Implementation of the EPIC Earthquake Early Warning System in the Bursa Province (Türkiye) and Its Surroundings

Abstract

Earthquake early warning systems aim to reduce the potential danger by providing a warning in the seconds before strong ground shaking occurs. In this study, we implemented EPIC, an early warning algorithm for Bursa province and its surroundings, which is a seismically active region. We replayed 104 earthquakes of M ≥ 3.5, which occurred in and around the study area between 2012 and 2021. We derived period and amplitude-based magnitude-scaling relationships using peak displacement amplitude ($Pd$) and predominant period ($T_p^{max}$) parameters of the first 4 s of P-wave arrivals. We investigated the performance of magnitude-scaling relationships through testing with real-time data. We observed an improvement when comparing the magnitude estimates made with the newly developed equations with the default equations used for California. We have also found that magnitude estimation with $Pd$ gives better results than $T_p^{max}$ for estimating the accurate final magnitude. We aim to adapt the EPIC early warning system, implemented for Bursa province and its surroundings, specifically for each region of Türkiye where the earthquake risk is high.

1. Introduction

While earthquake prediction studies continue worldwide, a growing focus is on reducing the damage caused by earthquakes. Loss of life and damage caused by destructive earthquakes can be reduced by using early warning systems. The United Nations [1] urged countries vulnerable to earthquakes to expand their efforts to establish, develop, and operate such systems. In consequence of recent advances in technology and a better understanding of the physical processes involved in earthquakes, Earthquake Early Warning Systems (EEWS) are rapidly improving [2]. They are now in operation in many countries around the world, including Japan [3], the USA [4], China [5,6], Mexico [7], Taiwan [8], South Korea [9], Italy [10], Israel [11], and Chile [12].

EEWS are the most effective way for reducing hazards of earthquakes. These systems cannot predict earthquakes but try to detect them to generate warnings. The EEWS infrastructures and algorithms use the propagation velocity difference between the P and S-waves. When an earthquake is detected, the system generates a real-time warning signal that is quickly transmitted to affected areas. This allows for timely actions, such as opening exit doors in buildings, ensuring escalators run towards exits, bringing elevators to the nearest floor, cutting off or controlling electricity, and slowing or stopping activities in facilities, such as factories, nuclear power plants, refineries, high-speed trains, subways, trams, and hospitals performing micro-surgery operations. Regional EEWS rely on seismic stations established in locations closest to the earthquake source to generate warnings, and the automatic transmission of alerts to areas in need.

Türkiye is located in the seismically highly active Alpine-Himalayan tectonic belt. One of the most seismically active fault zones in Türkiye is the North Anatolian Fault Zone (NAFZ). It often produces destructive and damaging earthquakes. Bursa province, along with its surrounding areas, is located in this active zone and has been exposed to numerous destructive earthquakes [13,14,15,16,17,18]. The study area is at high risk of earthquakes. The earthquake occurred on 28 February 1855, (I₀ = IX and Ms = 7.1) caused heavy damage, loss of life, and property in Bursa and its surroundings during the pre-instrumental period (<1900) [13,19,20]. During the instrumental period (>1900), important earthquakes that occurred in Bursa and its surroundings include the 15 April 1905 earthquake (Ms = 5.6), 3 August 1939 earthquake (Ms = 5.5), 15 September 1939 earthquake (Ms = 5.8), 13 November 1948 earthquake (Ms = 5.6), and 6 October 1964 earthquake (Ms = 6.8) [17] (Figure 1). The İzmit earthquake occurred on 17 August 1999 (Mw = 7.6) and caused severe loss of life and property and was also strongly felt in Bursa [21]. After the İzmit earthquake, some geo-scientists suggested that the next major earthquake would be on active faults located at the southwest end of the 1999 earthquake rupture [22,23,24,25]. Bulut et al. [26] reported that based on slip-deficit and historical observations, three segments in the Marmara Sea could produce major earthquakes (M > 7).

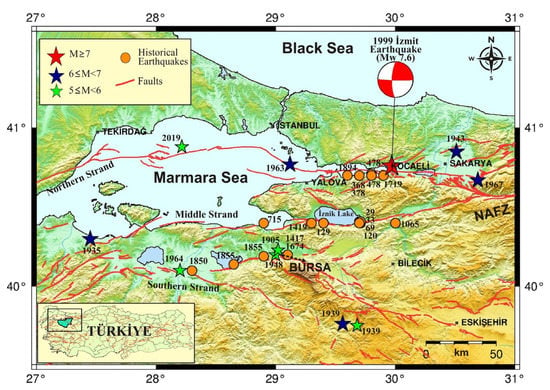
Figure 1. Tectonic elements of the Bursa province and its surroundings and location of significant historical and instrumental earthquakes. Faults shown are from Emre et al. [27]. Earthquake locations were compiled from [13,16,17,18,19]. NAFZ: North Anatolian Fault. Source mechanisms (red-white beach ball) of 17 August 1999, İzmit earthquake were obtained from Harvard CMT catalog. Inset shows the study region (box) in western Türkiye, and the green painted area in the box indicates Bursa province border.

Bursa, the fourth largest city in Türkiye located in the Marmara region, is a bustling hub of more than 3 million people and host to many heavy industries and historical structures. As an active player of the country’s economic growth and development, it is crucial to minimize the effects stemming from the seismic hazards. One of the most effective precautions in this regard is the establishment of an EEW system.

In this study, an EEWS has been set up by gathering the data where the stations located in and around study area into a single software of the seismometers and accelerometers belongs to Kocaeli University Earth and Space Sciences Research and Application Center (YUBAM), Disaster and Emergency Management Presidency (AFAD), and Bursa City Natural Gas Distribution Trade and Contracting Incorporated Company (Bursagaz). The widely used U.S. West Coast ShakeAlert’s Earthquake Point-source Integrated Code (EPIC) EEW algorithm [28,29] was utilized and customized for the region. We used two types of magnitude values, the first catalog was derived from Kandilli Observatory and Earthquake Research Institute (KOERI), the second was obtained from EPIC with the default parameters. We then replay the data using EPIC with new magnitude parameters to estimate the improvement in magnitude estimation and use real-time testing environments to demonstrate this improvement in a more complex environment.

2. EPIC Earthquake Early Warning System

EPIC is an algorithm that provides a warning for ground shaking, produced by earthquake waves. In this approach, a seismic station network is used to detect the first incident energy at the surface and convert the information in these low-amplitude waves into an estimate of the peak ground shaking that follows. The closest stations to the earthquake epicenter are the first to detect seismic energy [30]. The EPIC methodology identifies P-wave arrivals transmit from the sensors, determines the location of the earthquake using arrival times, and estimate its magnitude based on the epicentral distance and the peak displacement ($Pd$) [2]. Additionally, the maximum predominant period ($T_p^{max}$) in the 4 s following the P arrival is scaled with the magnitude of the earthquake. It then tries to estimate ground shaking using attenuation relations. All data is continuously collected, and as additional data is available from the first stations and additional stations, the hazard map can be updated every time. Since the most extensive ground-shaking observations are also made close to the epicenter, they can be integrated into the hazard assessment.

2.1. Estimation of Earthquake Location and Warning Time

EPIC uses at least four stations to generate robust and reliable alerts. The location of the earthquakes is determined by using the arrival times of the P waves. Following an earthquake, after the first four stations closest to the epicenter are triggered, a grid search method is used to find the location of the event. This method minimizes the error between observed and predicted values of arrival times [30].

The local warning time is the difference between the predicted S-wave arrival and the time the alert is issued. It can be estimated using the S wave arrival time curves along with the time of alert and location information. Using estimated values for S wave arrivals provides a conservative conclusion about the warning time [30].

2.2. Estimation of Rapid Earthquake Magnitude

Earthquake magnitude estimation is not only an important but also difficult part in EEW systems. Initial testing of the default system after implementation showed that the system worked well except for large discrepancies in magnitudes. A major focus of the manuscript is thus on describing the derivation of improved regression results for magnitude estimation. The magnitude, a measure of the energy released during an earthquake, is estimated using empirically derived linear relationships [31]:

$$M=5.39+1.23 lo{g}_{10}\left(Pd\right)+1.38 lo{g}_{10}\left(R\right)$$

(1)

where $Pd$ is the peak displacement (in cm) and R is epicentral distance (in km). The equation parameters, optimized for California, were derived using a global dataset (Northern and Southern California, Japan, and real-time data from California). The relationship had a mean magnitude error of 0.01, standard deviation of 0.31, and a correlation of 0.95 [31].

Wurman et al. (2007), using the data set from northern California, found the relationship between magnitude with $T_p^{max}$:

$$M=5.22+6.66 lo{g}_{10}\left(T_p^{max}\right)$$

(2)

3. Earthquake Early Warning System for Bursa Province (Türkiye) and Its Surroundings

3.1. Earthquake Early Warning System Algorithm (EPIC)

The EPIC algorithm is a regional point source algorithm [32]. The system will alert if P waves are detected by at least four stations and at least 40% of the stations are in the P phase wavefront area. Earthquake data is transmitted from Güralp sensors at stations to Scream software in .gcf format via LTE modem. It is then transmitted from Scream to Earthworm (the seismic data collection and automatic earthquake processing software) with the help of Scream2ew 7.6 software and is used by EPIC. When estimating the location of earthquakes, a grid search method is used in which the difference between the travel time calculated and observed is minimized. At this stage, the one-dimensional layered global velocity model AK135 [33] was preferred as the velocity model. The magnitude of the earthquake is obtained by the peak displacement ($Pd$) and the predominant period ($T_p^{max}$) calculated from the data at different stations [31]. As time progresses, new data continues to arrive, and all parameters (such as occurrence time, location, and size) are updated more accurately [29].

To ensure fast and reliable alerts, an EEWS needs to have a well-designed seismic network and algorithm that provides the longest possible warning time, accurate classification of shaking intensity, and a low rate of false or missed warnings. The optimal design of the network depends on various factors, including the seismotectonics of the region, available resources, and budget constraints [31,34]. In the case of Bursa province’s EEWS, 128 stations were utilized (99 being accelerometers and 29 being seismometers) (Figure 2). The station design was strategically placed and reinforced with existing stations to establish a reliable system. Accelerometers were installed in natural gas distribution points and public institutions’ gardens, while velocity sensors were placed in areas far from residential zones to allow for the closure of natural gas distribution valves and the cessation of heavy or sensitive machinery [35]. Tunç [35] also noted that a high station density could decrease the time required for a solution and warning.

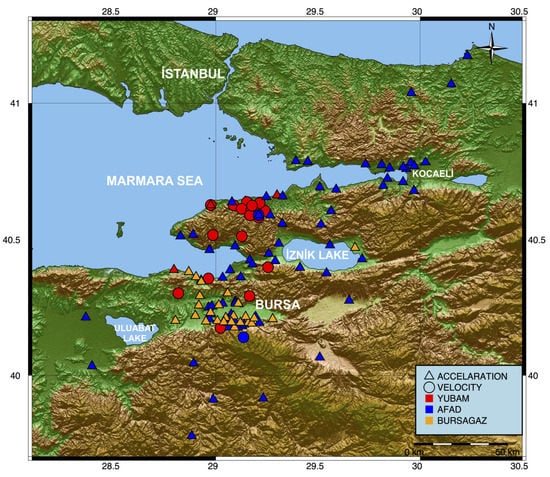
Figure 2. Station distribution in Bursa province and surrounding. The stations of YUBAM, AFAD, and Bursagaz are shown in red, blue, and orange colors, respectively. Triangle and circle refer to the type of sensor.

3.2. Determination of Magnitude Equation Coefficients for Bursa Province (Türkiye) and Its Surroundings

EPIC was developed and optimized for California. Sheen et al. [36] and Nof and Allen [11] found it beneficial to adjust the magnitude relation equations of EPIC in order to optimize EPIC for different regions, such as Korea and Israel, respectively. EEW applications frequently use relationships derived from the first few seconds of the P wave for earthquake magnitude estimation [31,37,38,39,40]. In this study, we evaluate $Pd$ and $T_p^{max}$ to estimate magnitude. For the magnitude- Pd scaling relationship, a linear regression model assumption was made between logarithmic $Pd$, observed magnitudes ($M$), and epicentral distance ($R$) [39]. The linear relationship between magnitude and $T_p^{max}$ is shown by the least squares fit between the $M$ and mean $T_p^{max}$ values from each station for each event [41,42].

Kandilli Observatory and Earthquake Research Institute-Regional Earthquake and Tsunami Monitoring Center [43] earthquake catalog consists of 275 earthquakes with a magnitude 3.5 < M < 7.0 between 1 January 2012, and 30 November 2021. A total of 275 earthquake data were examined and 104 earthquakes with data quality suitable for replaying in EPIC (Table 1) were studied. The seismic recordings used for regression analysis consist of strong motion and broadband waveforms. Following previous studies [39,42,44], we applied a 0.075 Hz high-pass Butterworth filter to the data. We used KOERI locations to calculate epicentral distances and P-wave onsets for each station and Matlab software (R2021b) to calculate $Pd$ and $T_p^{max}$ values from the first 4 s of the seismograms. Vertical component velocity seismograms were used in the analyses.

Table 1. List of earthquakes (M ≥ 3.5) recorded by KOERI that occurred in Bursa province and its surrounding area between 1 January 2012 and 30 November 2021.

No	Date	Origin Time (UTC)	Latitude	Longitude	Depth (km)	Magnitude
1	27 November 2013	04:13:37.5	40.846	27.919	10.8	4.7
2	11 March 2014	05:07:00.5	40.670	27.042	11.0	3.6
3	28 March 2014	03:59:51.2	40.422	26.134	13.2	4.5
4	1 June 2014	21:17:45.7	40.561	27.334	11.0	3.6
5	3 July 2014	05:04:46.1	40.209	27.933	11.8	4.5
6	3 August 2014	10:42:44.5	40.606	29.159	3.4	3.6
7	22 October 2014	17:11:05.6	40.407	30.115	7.5	4.5
8	6 December 2014	06:20:53.8	38.891	26.260	15.2	5.0
9	24 July 2015	06:54:10.1	40.251	26.305	10.7	4.6
10	24 July 2015	02:39:42.4	40.244	26.287	11.9	4.9
11	24 July 2015	01:26:00.7	40.243	26.303	11.2	4.5
12	10 September 2015	08:12:45.7	38.840	26.278	15.4	4.9
13	16 October 2015	04:35:07.0	40.446	29.166	5.4	3.5
14	26 October 2015	20:07:59.8	39.790	26.267	6.7	4.6
15	28 October 2015	16:20:02.0	40.822	27.764	14.3	4.5
16	5 December 2015	20:53:51.7	40.444	29.066	13.2	3.7
17	7 December 2015	20:57:51.1	40.707	27.431	10.3	3.7
18	28 March 2016	17:23:46.7	40.732	27.541	15.5	3.7
19	7 June 2016	04:09:45.6	40.265	29.152	15.8	4.6
20	7 June 2016	08:02:14.9	40.275	29.150	13.5	3.6
21	22 June 2016	23:35:59.7	40.705	29.223	7.6	3.7
22	25 June 2016	05:40:11.9	40.707	29.212	9.3	4.5
23	9 July 2016	14:20:51.3	40.707	29.195	9.5	3.8
24	17 July 2016	08:55:41.3	40.703	29.166	11.4	4.1
25	8 October 2016	23:02:46.6	40.614	28.945	5.5	3.7
26	6 February 2017	11:45:00.9	39.531	26.094	12.6	4.5
27	6 February 2017	10:58:01.2	39.525	26.100	13.9	5.3
28	6 February 2017	03:51:39.8	39.545	26.109	11.0	5.4
29	7 February 2017	02:24:02.9	39.524	26.124	12.7	5.3
30	8 February 2017	01:38:03.2	39.531	26.143	10.4	4.6
31	18 February 2017	23:19:24.9	40.270	27.177	12.9	3.6
32	28 February 2017	23:27:33.4	39.485	26.064	11.2	4.5
33	21 April 2017	14:12:21.0	38.651	27.601	13.1	5.1
34	27 March 2017	15:53:23.2	38.739	27.830	11.8	5.3
35	28 March 2017	04:38:19.5	38.738	27.794	10.6	4.5
36	12 June 2017	12:28:37.5	38.847	26.325	14.4	6.3
37	17 June 2017	03:40:36.9	38.918	26.243	12.7	4.8
38	21 July 2017	02:12:34.3	36.883	27.342	9.5	4.6
39	22 July 2017	22:12:32.2	40.018	27.141	13.2	4.3
40	25 July 2017	15:21:10.2	40.441	28.982	7.2	3.6
41	5 October 2017	23:54:42.3	40.838	28.340	13.9	3.6
42	4 November 2017	21:54:08.2	36.706	28.154	84.9	4.5
43	25 December 2017	05:13:50.0	38.575	26.736	17.5	4.8
44	3 March 2018	02:04:33.4	39.980	26.924	12.7	4.5
45	13 August 2018	08:57:09.1	40.661	27.356	17.2	3.7
46	6 September 2018	06:00:24.5	40.843	28.412	11.7	3.6
47	10 September 2018	23:02:55.3	37.180	30.634	105.7	4.9
48	4 December 2018	12:38:03.2	40.667	26.975	11.3	3.6
49	20 December 2018	06:34:24.4	40.600	28.977	7.3	4.6
50	5 January 2019	04:20:14.3	40.445	28.371	10.4	4.1
51	11 January 2019	16:09:56.4	40.282	28.857	5.2	3.9
52	15 February 2019	16:14:27.3	40.782	27.938	20.2	4.1
53	19 February 2019	21:33:55.0	40.386	27.157	11.5	4.1
54	19 February 2019	19:48:42.7	40.383	27.154	11.6	4.0
55	20 February 2019	00:27:57.4	40.392	27.154	6.8	3.6
56	24 February 2019	01:22:24.6	40.380	27.176	11.1	3.9
57	23 March 2019	15:17:59.1	40.812	27.754	18.1	3.7
58	23 March 2019	02:51:11.6	40.792	27.756	17.7	3.5
59	29 April 2019	18:02:43.3	39.400	26.319	11.6	4.5
60	9 March 2019	16:05:28.8	40.846	28.143	13.1	3.6
61	12 March 2019	22:24:08.6	39.331	27.922	7.7	4.5
62	25 March 2019	12:13:35.0	40.567	27.124	16.0	4.2
63	12 June 2019	22:44:50.4	40.723	27.444	14.5	3.6
64	8 August 2019	11:25:29.2	37.901	29.595	8.9	5.7
65	24 September 2019	08:00:21.4	40.875	28.212	9.9	4.7
66	26 September 2019	10:59:24.6	40.880	28.216	13.3	5.7
67	26 September 2019	15:39:21.1	40.845	28.250	14.8	3.5
68	26 September 2019	12:26:10.9	40.870	28.274	11.0	3.9
69	26 September 2019	12:17:09.3	40.870	28.273	9.3	3.9
70	26 September 2019	11:26:36.2	40.876	28.294	15.1	4.4
71	26 September 2019	07:32:06.6	40.878	28.221	7.6	3.8
72	27 September 2019	11:13:46.7	40.852	28.274	10.5	3.5
73	28 September 2019	11:03:03.2	40.869	28.283	14.8	3.8
74	29 September 2019	06:10:57.5	40.694	29.262	14.7	3.7
75	4 October 2019	15:54:30.6	40.312	27.255	15.0	3.6
76	5 October 2019	14:51:37.3	36.051	27.982	87.5	4.5
77	10 October 2019	17:09:39.9	40.711	29.270	4.6	3.5
78	10 December 2019	20:24:04.9	39.450	27.918	9.9	4.5
79	10 December 2019	20:14:02.7	39.445	27.925	9.2	5.0
80	11 January 2020	13:37:36.7	40.861	28.227	14.4	4.9
81	22 January 2020	20:17:38.5	39.064	27.848	11.6	4.6
82	22 January 2020	19:22:15.7	39.058	27.839	12.2	5.6
83	2 February 2020	11:36:40.1	39.089	27.866	13.7	4.5
84	2 February 2020	00:23:47.3	38.999	27.856	15.4	4.8
85	2 February 2020	00:57:43.2	40.836	28.184	14.4	3.9
86	18 February 2020	16:09:22.3	39.106	27.826	13.0	5.2
87	24 February 2020	02:43:33.3	38.991	27.877	10.4	5.0
88	1 April 2020	19:03:23.3	40.779	27.454	16.7	3.5
89	30 April 2020	10:09:46.1	37.004	28.532	8.4	4.6
90	26 June 2020	07:21:12.2	38.789	27.794	10.9	5.5
91	29 June 2020	04:06:23.8	36.714	28.225	73.2	4.7
92	16 July 2020	18:09:26.0	38.404	26.685	18.4	4.5
93	8 September 2020	21:57:23.5	40.701	27.420	13.6	4.6
94	24 September 2020	18:06:40.7	40.820	28.175	14.4	3.7
95	24 September 2020	13:38:31.2	40.813	28.144	13.7	4.3
96	30 October 2020	11:51:24.4	37.888	26.706	11.2	6.9
97	1 November 2020	07:05:12.4	37.811	26.960	8.6	4.5
98	5 November 2020	05:46:45.3	40.835	28.300	7.3	3.8
99	11 November 2020	06:49:45.4	37.853	26.968	8.0	4.7
100	1 February 2021	20:46:15.2	38.977	26.044	13.5	4.7
101	1 February 2021	13:10:15.1	38.949	26.061	10.0	4.8
102	1 February 2021	08:35:16.6	38.961	26.020	13.7	5.2
103	21 March 2021	21:33:56.5	40.516	28.153	7.7	3.6
104	19 June 2021	12:07:52.7	40.950	29.213	14.6	4.0

As a result, the best-fitting attenuation relationship for the resulting log($Pd$) is given as:

$$lo{g}_{10}\left(Pd\right)=-4.78+0.9M-1.34 lo{g}_{10}\left(R\right)$$

(3)

with a coefficient of determination of 0.639. Figure 3 contains a comparison of the observed $Pd$ values with the values estimated by Equation (3) for the magnitudes 3.0, 4.0, 5.0, 6.0, and 7.0, respectively, separately.

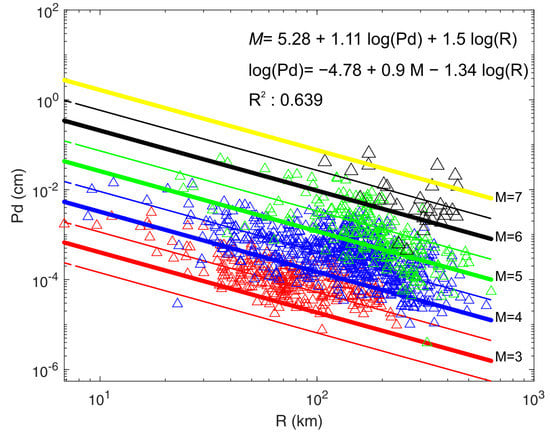
Figure 3. The relationships between $Pd$, epicentral distance (R), and catalog magnitude (M) calculated for each station. Each triangle is measured at a single site. Here, Pd is in cm, and R is in km. Thick lines are predictions based on Equation (4) for magnitudes 3 (red line), 4 (blue line), 5 (green line), 6 (black line), and 7 (yellow line), and thin lines are for magnitudes 2.5, 3.5, 4.5, 5.5, and 6.5, respectively.

When the regression result is reversed to estimate the magnitude using $Pd$ and R, the magnitude relationship is:

$$M=5.28+1.11 lo{g}_{10}\left(Pd\right)+1.5 lo{g}_{10}\left(R\right)$$

(4)

The linear relationship between $T_p^{max}$ and observed $M$ is:

$$M=4.88+1.97 lo{g}_{10}\left(T_p^{max}\right)$$

(5)

Figure 4 shows the relationship of $T_p^{max}$ calculated for each station and observed magnitude (M). The coefficient of determination of this relationship is 0.824. The relationship exhibits a good fit despite the scattering observed, especially for large earthquakes. The relation parameters obtained for the Bursa province and its surroundings are given in Equations (4) and (5). In the following, we implement Equations (4) and (5) in EPIC and replay the data in “simulated real-time” and “real-time”.

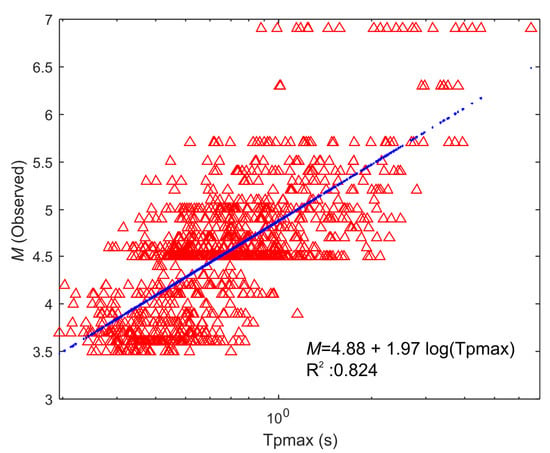
Figure 4. The relationship between $T_p^{max}$ (calculated for each station) and catalog magnitude (M).

4. Results and Discussion

After adjusting the magnitude relation equations based on past instrumental data and known catalog earthquake locations, we proceeded to evaluate the performance of the new equations using simulated real-time replays of recorded data and real-time processing. This evaluation is necessary since missing data, delays, and other operational difficulties may affect the results, and since the accuracy of the distance R calculation in real-time depends on the correct epicenter location, if the epicenter is mis-located, it can lead to an incorrect estimation of the magnitude. However, we were able to ensure a highly robust earthquake location due to the dense seismic network used in this study for the Bursa province and its surroundings. Hereafter, we will refer to the original magnitude relation equation as “default” (Equations (1) and (2)) [31,45] and the newly developed equation as “newly developed” (Equations (3) and (4)).

The epicenter distribution of earthquakes in the KOERI catalog and the epicentral distributions of the solutions obtained from the EPIC replayed dataset are shown in Figure 5. Square symbols represent KOERI solutions, and circles represent EPIC solutions. Errors are observed in the locations of some earthquakes. This is expected as performance declines for events outside the system. Nof and Allen [11] stated that large location errors are caused by events located further away from the network, and the system is suitable for in-network events and performs less well for out-of-network events. No parameter other than magnitude is estimated in the study. The observed difference is due to the different stations used while processing the replay solution. In real-time performance, there will be no difference in locations. Please note that in real-time playback, the algorithm uses multi-threading, which leads to different data orders each time.

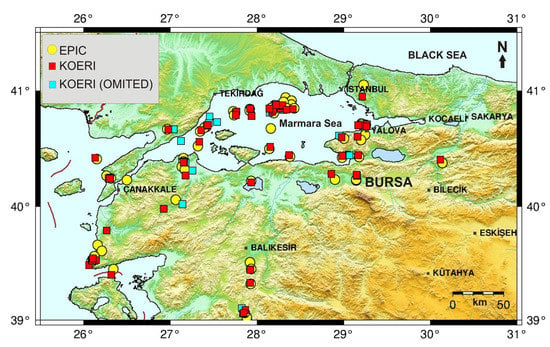
Figure 5. Epicenter distributions of the replayed earthquakes.

Figure 6 compares $Pd$ and $T_p^{max}$ calculated with the default and newly developed equations for each earthquake by observed magnitudes. When Figure 6a,b obtained with the default and newly developed equations are examined, it is observed that the scattering of the new equation is less. Although a small increase in standard deviation is observed, this is due to the scattering of some earthquakes smaller than M < 4. The distribution of $T_p^{max}$ against the catalog size of the default and newly developed equation is different (Figure 6c,d). Scattering is high in the graph by using the default equation. It is seen that the results of the analysis made with the newly developed equation show a better agreement between $T_p^{max}$ and the observed magnitudes compared to the default equation. Although an improvement in $T_p^{max}$ is observed, it is clear that $T_p^{max}$ is neither a good measure of magnitude estimation for default nor newly developed equations compared to $Pd$. The problem that $Pd$ reaching saturation for large earthquakes has been emphasized in previous studies [37,38,42]. In our study, the network’s magnitudes estimates agree with the newly developed equations. This can be explained by the near-field effects emphasized by Yamada and Mori [46]. Waveforms recorded by the strong motion sensor close to the source were used in the analysis. In this direction, values comparable to the catalog values were obtained despite the near-field effects.

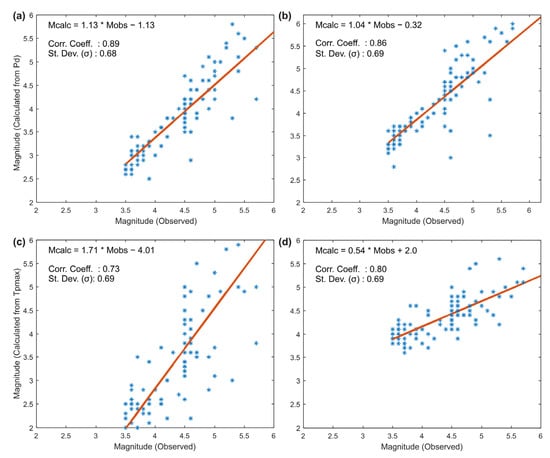
Figure 6. Magnitudes calculated from $Pd$ and $T_p^{max}$ versus the observed magnitude (a) magnitudes calculated using default equations for $Pd$, (b) magnitudes calculated using newly developed for $Pd$, (c) magnitudes calculated using default for $T_p^{max}$, (d) magnitudes calculated using newly developed for $T_p^{max}$.

In Figure 7, the errors of the magnitudes obtained by using $Pd$ and $T_p^{max}$ with the default and newly developed equations are given. When comparing $Pd$ was examined, the mean magnitude error is −0.57, the standard deviation 0.38, and the median −0.6 using the default settings. When the newly developed coefficients were used, mean magnitude error −0.13, standard deviation 0.41, and median −0.1 values were obtained. It is seen that the error of the solutions obtained from the newly developed equations for $Pd$ is lower than the error obtained with the default equation and even the median is very close to zero. Estimates based on $T_p^{max}$ with default relations resulted in a mean magnitude error of −0.88, a standard deviation of 1.15, and a median of −1.1. When newly developed relations are used, the mean magnitude error is 0.0, the standard deviation is 0.41, and the median is 0.0. An improvement was observed for $T_p^{max}$ when the magnitudes obtained using the default and newly developed equations were compared. However, when $Pd$ and $T_p^{max}$ are compared, we think $Pd$ provides more reliable results as a magnitude estimation measure, as mentioned before.

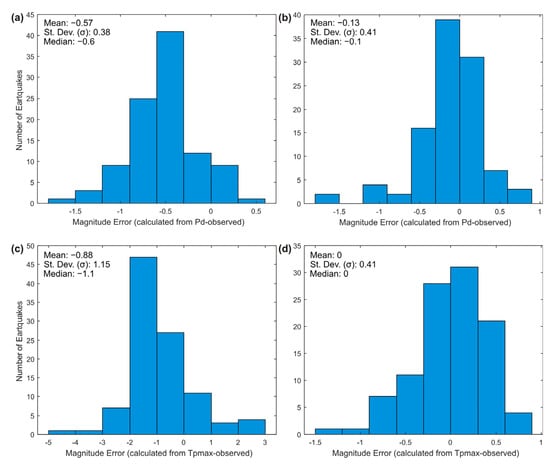
Figure 7. Histograms of errors for play-backed catalog dataset (a) magnitude errors using default equations for $Pd$, (b) magnitude errors using newly developed for $Pd$, (c) magnitude errors using default for $T_p^{max}$, (d) magnitudes errors using newly developed for $T_p^{max}$.

4.1. Latencies and Delays of the Seismic Network

Latency, delay, and packet size are critical factors in EEWS. While these terms are often used interchangeably, there are important physical differences between them that must be taken into account in early warning studies. Here, latency refers to the time between the P-wave onset at a station and the time data was packaged and transmitted along the signal path until it arrives at the data center. On the other hand, delay refers here only to the time it takes for the packaged signal to travel from the sensor to the data center along the transmission line. Packet size refers to the number of samples that are prepared for each transmission. These factors can have a significant impact on the speed and accuracy of early warning alerts. Understanding and minimizing latency and delay while optimizing packet size is essential for creating a fast and reliable EEW system [11,47,48].

The necessary data for the EEWS in Bursa and its surroundings are provided to YUBAM via AFAD and Bursagaz. However, since the data in the AFAD center passes several data servers and GSM technology is used for communication, latencies of the data are high. The delay time of some stations is more than 800 s due to the malfunction of the GPS. Therefore, when using an overall latency, the most accurate calculation would be to use the median time, measured as 4.6 s. Latencies of the data transmissions in the real-time analysis are given in Figure 8.

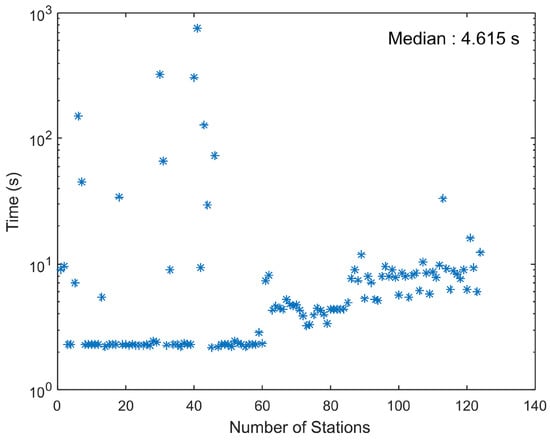
Figure 8. Latencies of stations transmitting data.

4.2. Real-Time Performance Observations

In this study, two servers were set up with EPIC to analyze earthquakes using the default and newly developed equations. Between 26 January 2022 and 25 June 2022, there are M ≥ 1.0 2662 earthquakes in KOERI catalogs. Since our station network is not as dense as KOERI, it did not detect small earthquakes occurring in areas outside of our network. Finally, our system has processed 363 earthquakes. Earthquake processing graphs generated by EPIC in real time are shown in Figure 9. While 536 earthquakes of M ≥ 2.5 were processed in KOERI catalogs, 139 earthquakes were processed with the default equation, and 236 earthquakes with the newly developed equation. The number of earthquakes processed M ≥ 3.5 is 60 for KOERI, 19 for the default equation, and 67 for the newly developed equation. The system overestimated the magnitude of 7 newly developed M = 3.4 earthquakes. When comparing the processed events by both systems, the default equation showed smaller magnitude estimates than the newly developed one. At the same time, the estimations made with the newly developed equation give results closer to the catalog magnitudes. This situation revealed a better result than the default relationship in estimating the magnitudes of the relationships derived from the EEW system established for Bursa province and its surroundings.

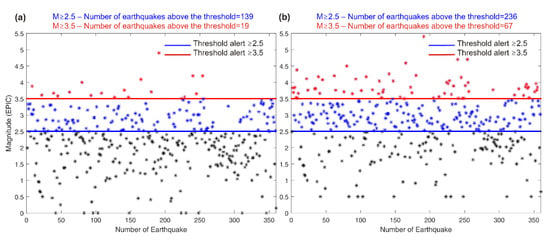
Figure 9. Between 26 January 2022 and 25 June 2022, using the real-time dataset, (a) default equations and (b) developed equations for earthquake magnitude estimation results. $Pd$-based magnitude scaling relationship was used in the calculations.

The 3 June 2022 Çaypınar (Balıkesir) Earthquake (M = 4.8)

An earthquake with M = 4.8 (KOERI) occurred on 3 June 2022, at 22:58:57.75 UTC in Çaypınar district of Balıkesir, southwest of Bursa. The epicenter of this earthquake is approximately 100 km away from Bursa city center (Figure 10). This earthquake was felt slightly in Bursa but did not cause any damage. The EPIC system, on the two different real-time servers, evaluated this earthquake in real-time, allowing the performance of the default and newly developed equations to be compared. The results of the first alert obtained are summarized in Table 2.

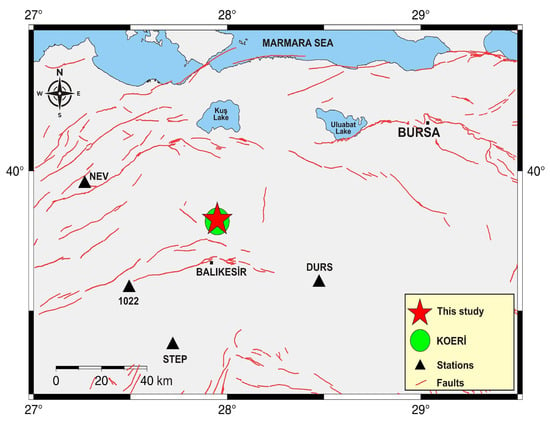
Figure 10. The 3 June 2022 Çaypınar (Balıkesir) earthquake (M = 4.8) epicenter map. The stations triggered after the earthquake are shown with a black triangle.

Table 2. EPIC performance using default and newly developed equations for the 3 June 2022 Çaypınar (Balıkesir) Earthquake (M = 4.8).

Event Date	Origin Time (UTC)	Latitude Longitude	Alert Time (UTC)	Magnitude Source	Magnitude
					M	${\mathit{T}}_{\mathit{p}}^{\mathit{m}\mathit{a}\mathit{x}}$	$\mathit{P}\mathit{d}$
3 June 2022	22:58:58.600	39.826 27.948	22:59:16.077	Default (Equations (1) and (2))	-	3.1	4.2
			22:59:14.868	Developed (Equations (4) and (5))	-	4.1	4.7
	22:58:57.750	39.820 27.948	-	KOERI catalog	4.8	-	-

While the estimated magnitude based on $Pd$ using the default equation was 4.2, it was observed that the result of the developed equation was 4.7. Considering the magnitude estimation based on $Pd$, the developed equation contains a lower error. When the results obtained with $T_p^{max}$ is compared, the difference is quite significant (magnitude 3.1 and 4.1, respectively, Table 2). Although the newly developed equation performs an excellent revision over the default equation, the result still contains apparent errors. As some researchers have indicated in previous studies, the reliability of the $Pd$-based magnitude scaling relationship is better than $T_p^{max}$ in our study [31,49].

Location error was 0.6 km and the alert issued 18.673 s and 17.118 s after catalog origin-time for the default equation and the newly developed one, respectively. As mentioned, latency is a key factor causing long delays in detecting and alerting the event. In this case, ~11.4 s of alert time is available for Bursa (assuming S-wave propagation velocity of 3.5 km/s) and a blind zone, where alert is delivered after the arrival of S-wave is about ~40 km. While this may seem like a weakness, it is usual since the earthquake occurred outside our seismic network. In a warning time of about 11 s, natural gas can be cut off; subways can be stopped safely, and elevators can be evacuated at the nearest floor. In short, this time is of great importance in preventing secondary disasters.

Thanks to the tests we have carried out, the average warning time for the Marmara Region is roughly 11 s. Of course, this varies depending on the distance from the event. Considering the calculation of the P wave, the process, and the network delay, there is a blind zone of approximately 60 km. To improve this, the number of stations should be increased, low latency hardware should be used, and the transmission cables in the stations should be designed as fiber optic.

Geoscientists emphasize that the next major earthquake will occur in Istanbul, where the western part of the NAF passes. According to the results obtained in this study, a warning time of approximately 8 s can be predicted for a possible Istanbul earthquake. In addition, when a possible Istanbul earthquake occurs, a blind zone of approximately 40–45 km occurs in Bursa.

5. Conclusions

The EPIC system is a useful tool that works in real-time in different regions [11,28,36,50] and aims to take precautions against seismic hazards. In short, the system aims to minimize disaster damage by generating warnings for an approaching ground shaking at certain times. EPIC estimates the magnitude using P waves peak displacement ($Pd$) and the dominant period ($T_p^{max}$). The epicenter of the event is located based on the grid search technique after the P wave triggering in at least four stations. The ground shaking can then be estimated using the attenuation relations of the location and magnitude of the event.

In this study, we aimed to adapt the EPIC EEW system for Bursa province and its surroundings. First, we optimized and, if necessary, modified seismic stations belonging to different seismological agencies in Bursa and its surroundings for robust data acquisition. We adjusted the magnitude relation equations by analyzing offline data from 104 earthquakes that occurred between 1 January 2012 and 30 November 2021. We tested the performance of the newly developed magnitude relationships both in replay mode and in real-time using EPIC. We observed an improvement in magnitude estimates made with the new equations compared with the default equations that are optimized for California. The improvement was demonstrated in real-time earthquake solutions for the 3 June 2023, Çaypınar (Balıkesir) earthquake (M = 4.8). We also concluded that a $Pd$-based scaling relationship is a good approach to deriving EEW magnitude estimates.

It is important to note that the number of earthquakes detected and analyzed by EPIC can vary depending on various factors, including the sensitivity of the system and the threshold values set for alarm levels. Additionally, the performance of the system can be affected by factors, such as network design, station placement, and real-time processing. However, the results presented in Figure 9 suggest that using the newly developed equation leads to the detection and analysis of a higher number of earthquakes with magnitudes greater than 2.5 compared to using the default equation. This highlights the importance of regularly updating and fine-tuning the algorithms used in EEW systems to improve their performance and effectiveness in providing early warnings.

The EEWS is currently running in test mode for Bursa and its surroundings. The system gives confidence with its robust and fast results. More precise magnitude estimation relationships can be determined by expanding the dataset with earthquakes that are likely to occur in the region. As a result, this study should be developed, and optimized magnitude relations should be obtained for Türkiye in general or for each region. In addition, optimizing the seismic network infrastructure to reduce delay times and blind zones is one of the most critical steps for an operational EEWS. Furthermore, connecting the EEWS to a robust dissemination system to allow alert delivery to the public and infrastructures should be of high priority for the decision makers and stakeholders.