Identification Method for Instantaneous Friction and Wear Energy Density Variation of High-Feed Milling Tool Flank
Abstract
:1. Introduction
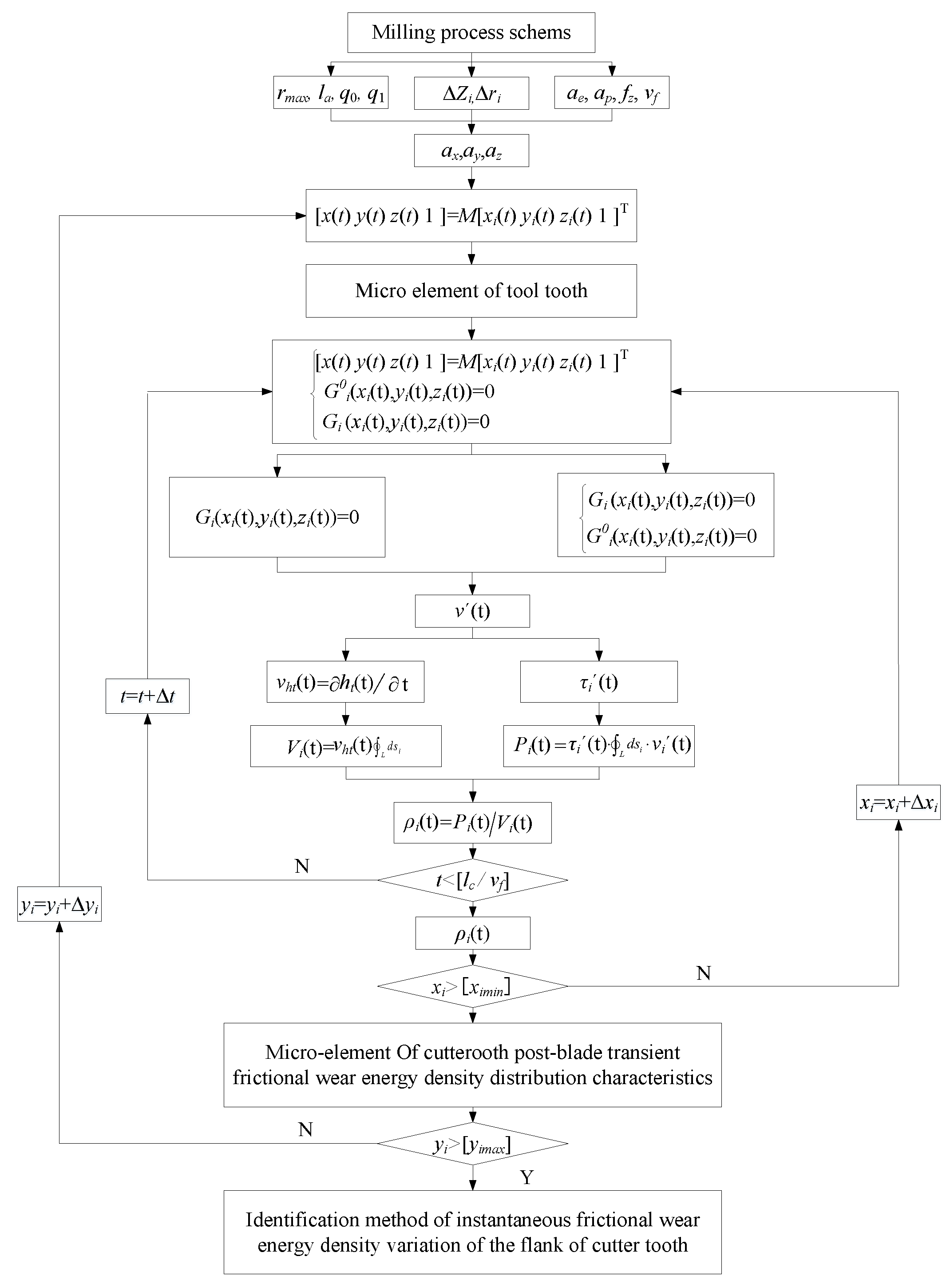
2. Instantaneous Wear Volume Model of the Tooth Flank
3. Method for Solving Instantaneous Friction Wear and Energy Density on the Tooth Flank
4. Variation of Friction and Wear Energy Density of the Tool Flank
5. Correlation Analysis between the Tool Flank Wear and Friction Wear Energy Density
6. Conclusions
- (1)
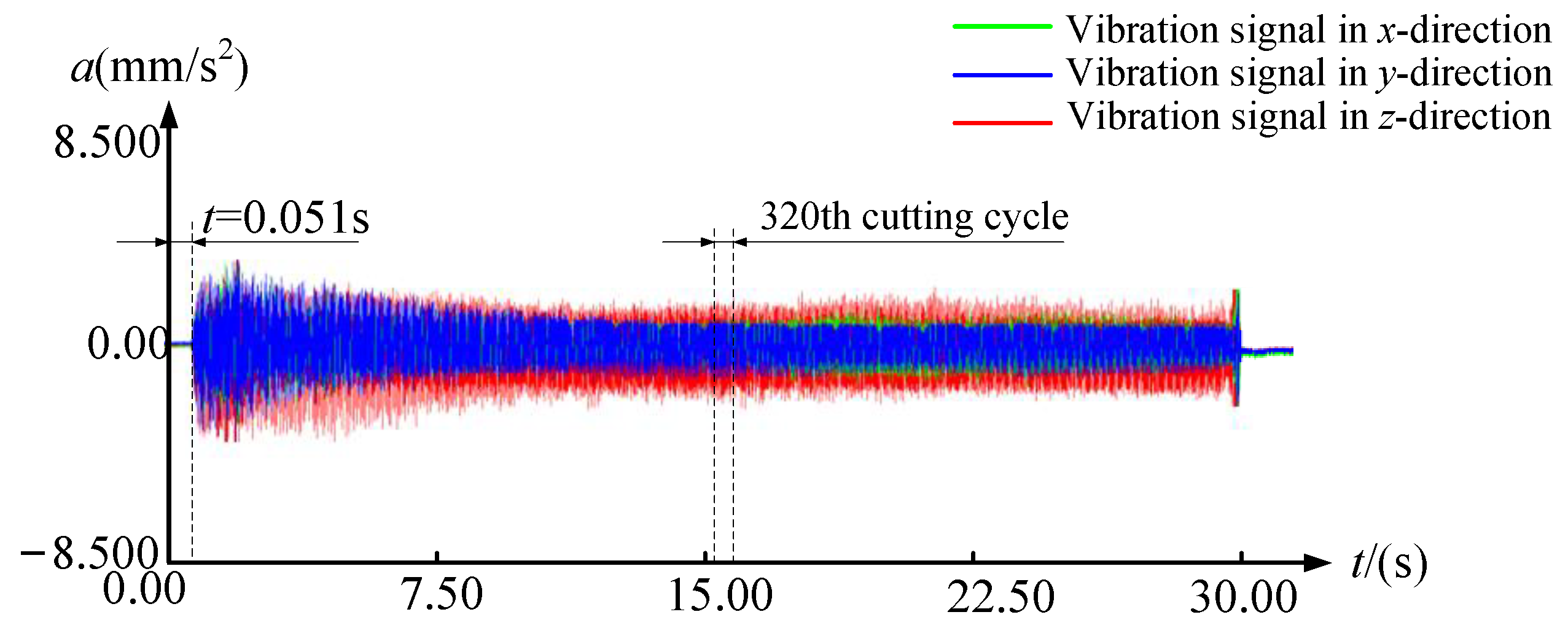
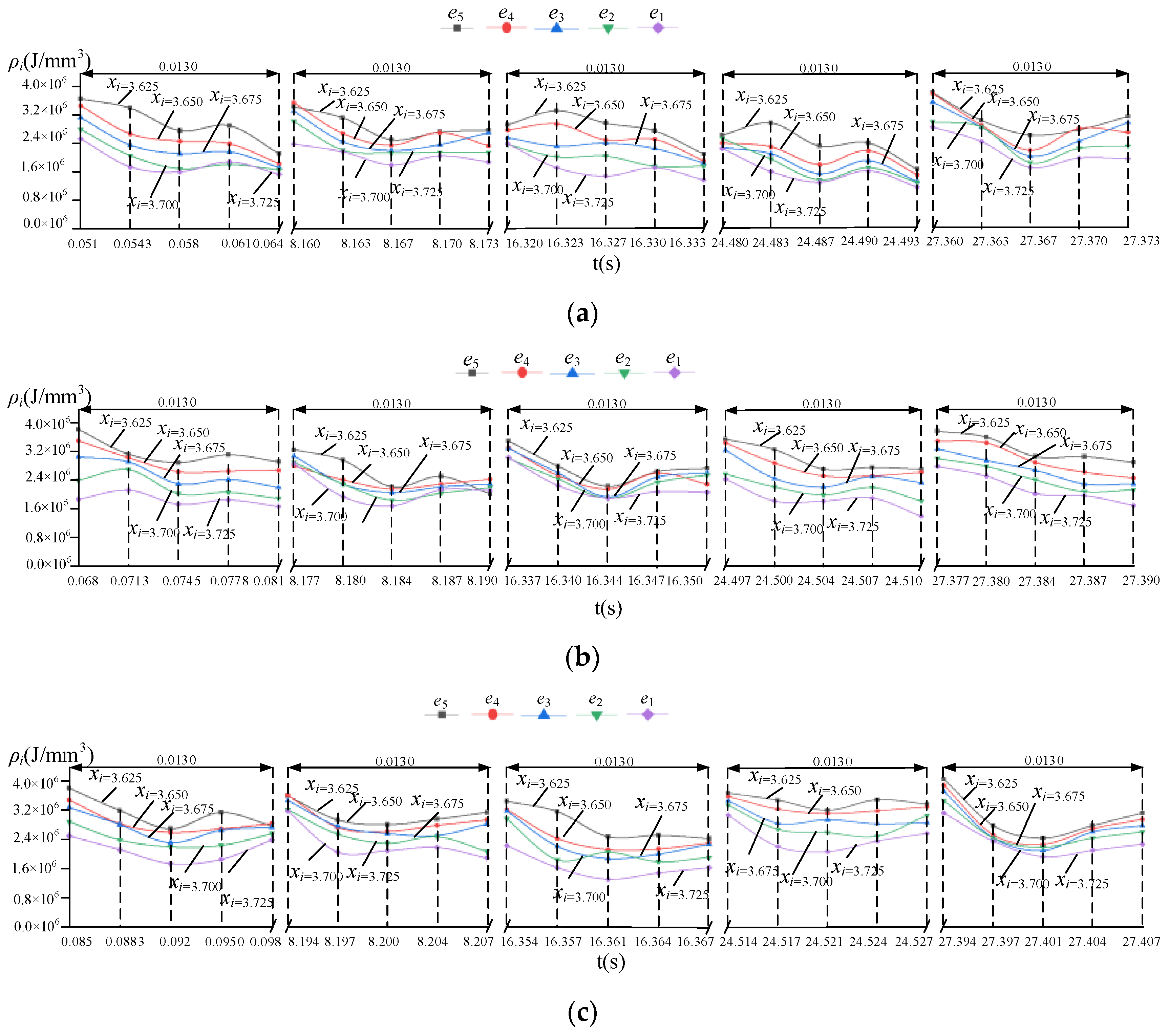
- A method for calculating the instantaneous pose on the flank face has been proposed. A calculation model of the instantaneous wear volume of the tool flank was established. The distribution and variation of the instantaneous wear volume of the cutter tooth’s flank face under milling vibration were revealed. The results show that the instantaneous wear depth and instantaneous wear volume on the flank face show unsteady variations with the contact angle and the cutting cycle, and there are obvious differences between different cutter teeth.
- (2)
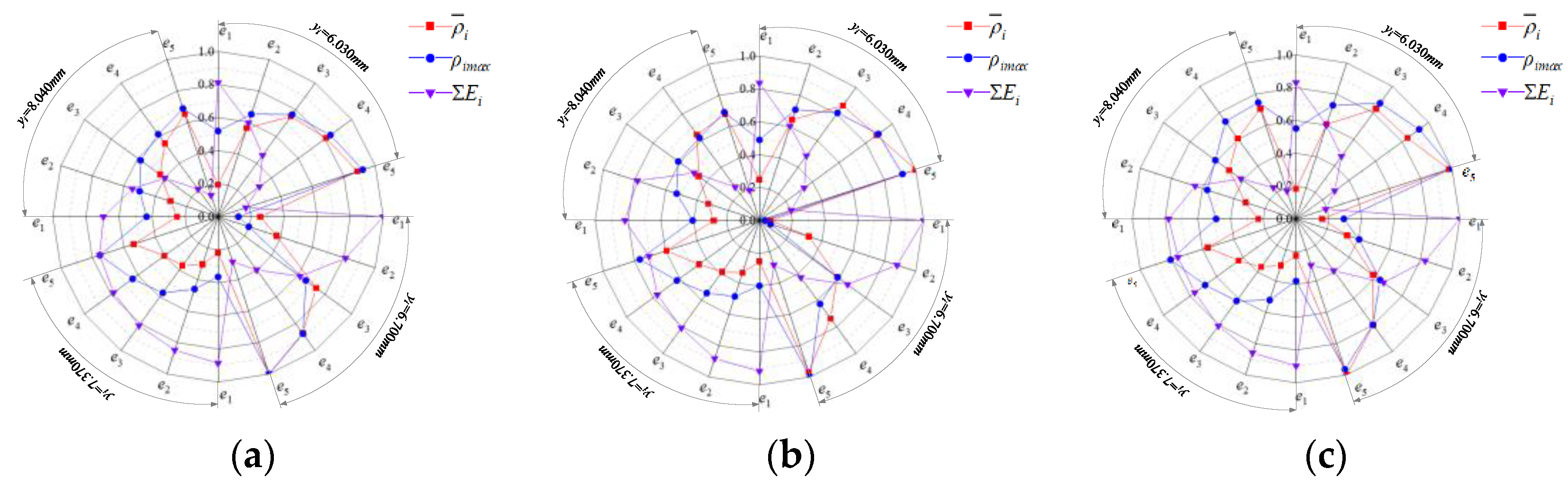
- The instantaneous pose and instantaneous friction velocity and the instantaneous friction stress and instantaneous friction energy consumption model of the micro-element on the cutter tooth were established, and the distribution of instantaneous friction energy consumption on the flank face was revealed. The correlation analysis results showed that the correlation between the cumulative friction energy consumption of the tool flank and the experimental results of the wear depth was greater than 0.860. This model can be used to identify and reveal the friction and wear characteristics. The response property of the friction and wear of the flank face to change the structure and position was revealed.
- (3)
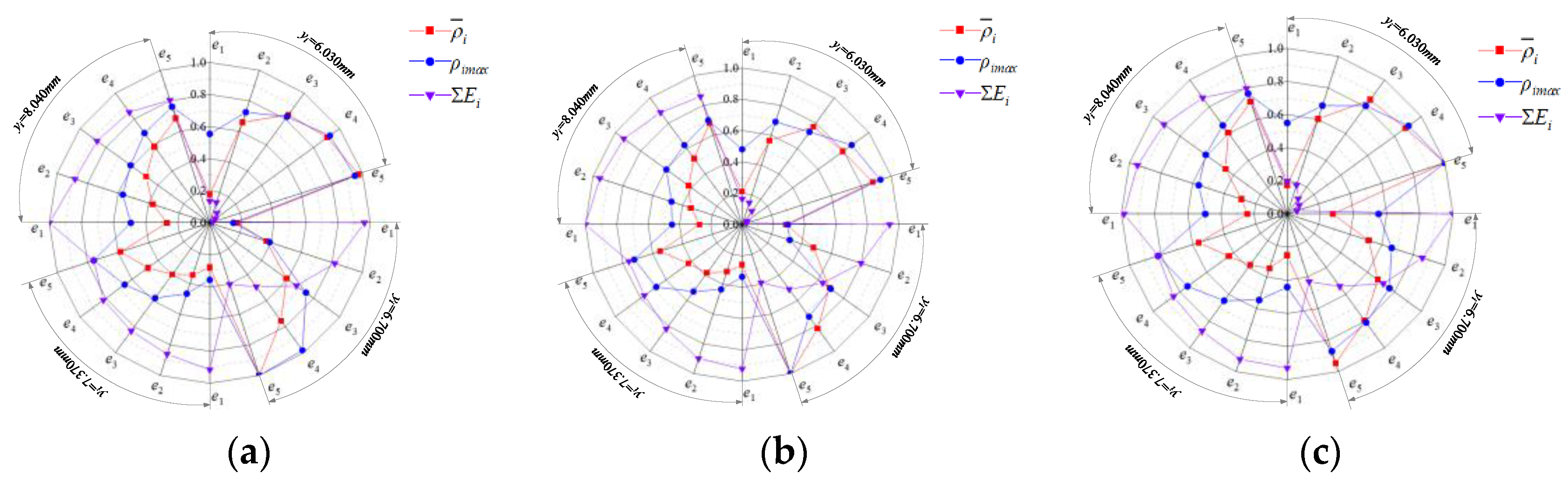
- An identification method for the instantaneous friction and wear energy density of the flank face has been proposed. The method revealed the difference in the dynamic relationship between the friction energy and wear on the flank of each cutter tooth of the milling cutter. The comparative analysis results of the process schemes showed that the method could be used to quantitatively characterize the diversity of the dynamic distribution of friction and wear on the flank face, and the milling process scheme can be evaluated accordingly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhao, P.; Zhang, L.; Jiang, B. Instantaneous friction energy consumption and its evolution of high energy efficiency milling cutter. J. Adv. Mech. Eng. 2022, 14, 16878132221095917. [Google Scholar] [CrossRef]
- Younas, M. Development and Analysis of Tool Wear and Energy Consumption Maps for Turning of Titanium Alloy (Ti6Al4V). J. Manuf. Process. 2021, 62, 613–622. [Google Scholar] [CrossRef]
- Giorjão, R.A.R.; Avila, J.A.; Escobar, J.D. The study of volumetric wearing of PCBN/W-Re composite tool during friction stir processing of pipeline steels (X70) plates. J. Adv. Manuf. Technol. 2021, 114, 1555–1564. [Google Scholar] [CrossRef]
- Lv, D.; Wang, Y.; Yu, X. Effects of Cutting Edge Radius on Cutting Force, Tool Wear, and Life in Milling of SUS-316L Steel. J. Adv. Manuf. Technol. 2020, 111, 2833–2844. [Google Scholar] [CrossRef]
- Kıvak, T. Optimization of surface roughness and flank wear using the Taguchi method in milling of Hadfield steel with PVD and CVD coated inserts. J. Meas. 2014, 50, 19–28. [Google Scholar] [CrossRef]
- Guo, X.L.; Deng, M.S.; Wang, J.X. Effects of geometric angle and cutting speed on cutting forces and tool wear of ceramic cutting tools during peripheral up-milling of high-density fiberboard. J. Mater. Wiss. Und Werkst. 2020, 51, 461–468. [Google Scholar] [CrossRef]
- Nooraie, R.Y.; Safari, M.; Pak, A. Tool wear estimation in machining based on the flank wear inclination angle changes using the FE method. J. Mach. Sci. Technol. 2019, 24, 425–445. [Google Scholar] [CrossRef]
- Li, F.; Liu, J. Optimization of milling process parameters and prediction of abrasive wear rate increment based on cutting force experiment. J. Adv. Mech. Eng. 2021, 13, 16878140211039972. [Google Scholar] [CrossRef]
- Su, Y.; Li, C.; Zhao, G.; Li, C.; Zhao, G. Prediction models for specific energy consumption of machine tools and surface roughness based on cutting parameters and tool wear. J. Proc. Inst. Mech. Eng. Part B 2021, 235, 1225–1234. [Google Scholar] [CrossRef]
- Zhang, X.; Han, C.; Luo, M.; Zhang, D. Tool Wear Monitoring for Complex Part Milling Based on Deep Learning. Appl. Sci. 2020, 10, 6916. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Z.; Zhao, J. Tool wear monitoring through online measured cutting force and cutting temperature during face milling Inconel 718. Int. J. Adv. Manuf. Technol. 2022, 122, 729–740. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, H.; Liu, D.; Wang, G.; Huang, C.; Yao, P. A Dual Compensation Strategy Based on Multi-Model Support Vector Regression for Tool Wear Monitoring. J. Meas. Sci. Technol. 2022, 33, 105601. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Li, H.; Wei, Q.; Deng, J.; Gao, Y. Experimental study on tool wear in milling CFRP/Ti laminated materials with diamond coated unit edge tool. J. Ferroelectr. 2022, 594, 166–174. [Google Scholar]
- Liang, J.; Gao, H.; Li, D. Study on milling tool wear morphology and mechanism during machining superalloy GH4169 with PVD-TiAlN coated carbide tool. J. Tribol. Int. 2023, 182, 108298. [Google Scholar] [CrossRef]
- Gowthaman, S.; Jagadeesha, T. Influence of radial rake angle and cutting conditions on friction during end milling of Nimonic 263. J. Int. J. Adv. Manuf. Technol. 2020, 109, 247–260. [Google Scholar] [CrossRef]
- Shi, K.N.; Zhang, D.H.; Liu, N.; Wang, S.B.; Ren, J.X.; Wang, S.L. A novel energy consumption model for milling process considering tool wear progression. J. Clean. Prod. 2018, 184, 152–159. [Google Scholar] [CrossRef]
- Choudhury, S.K.; Rath, S. In-process tool wear estimation in milling using cutting force model. J. Mater. Process. Technol. 2000, 99, 113–119. [Google Scholar] [CrossRef]
- Zheng, G.; Zhao, G.; Cheng, X.; Xu, R.; Zhao, J.; Zhang, H. Friction and wear performance of TiAlN/TiN coated tool against high-strength steel. J. Ceram. Int. 2018, 44, 6878–6885. [Google Scholar] [CrossRef]
- Baumann, R.; Bouraoui, Y.; Teicher, U. Tailored laser structuring of tungsten carbide cutting tools for improving their tribological performance in turning aluminum alloy Al6061 T6. J. Mater. 2023, 16, 1205. [Google Scholar] [CrossRef] [PubMed]
- Dou, J.; Jiao, S.; Xu, C. Unsupervised online prediction of tool wear values using force model coefficients in milling. J. Adv. Manuf. Technol. 2020, 109, 1153–1166. [Google Scholar] [CrossRef]
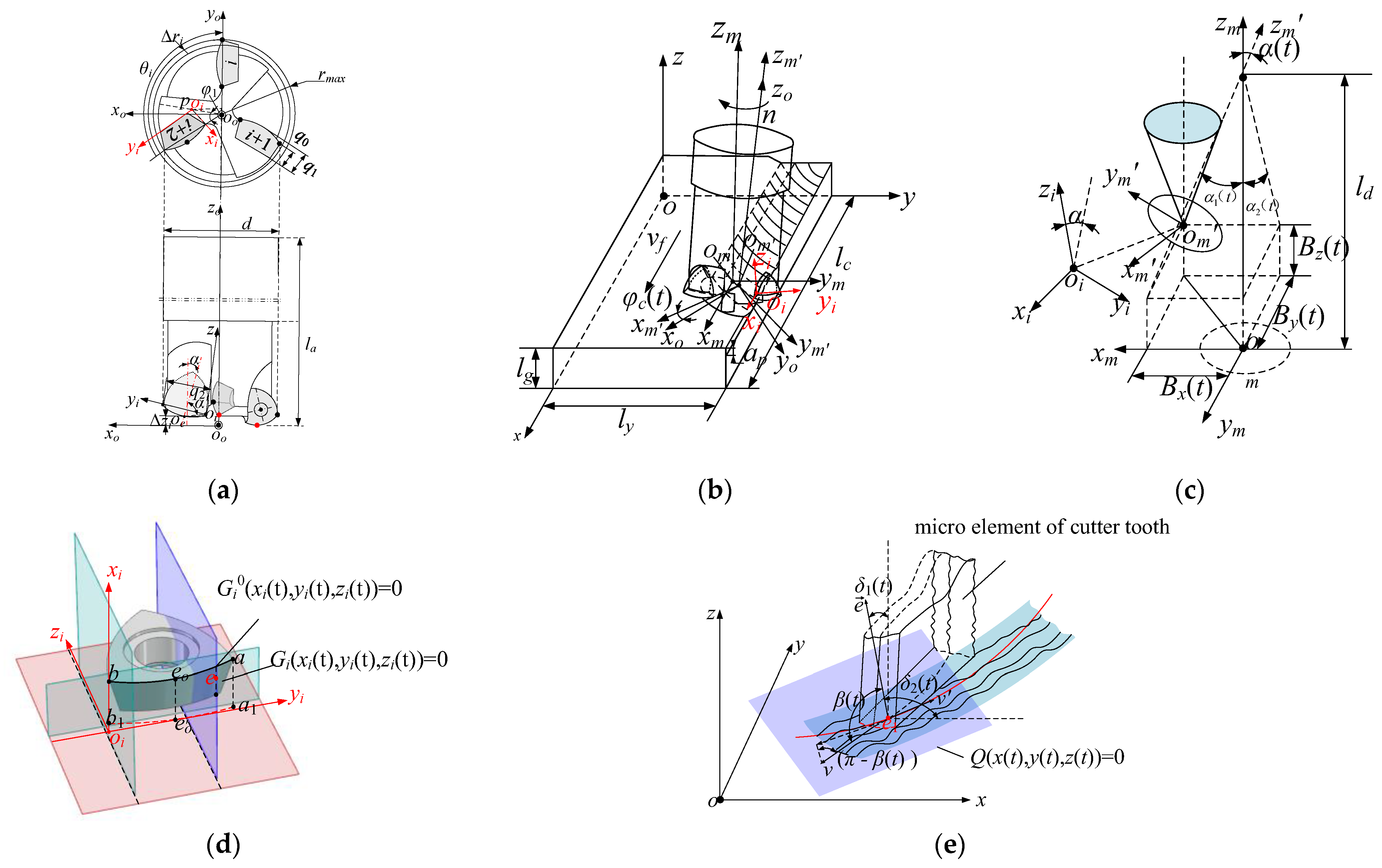
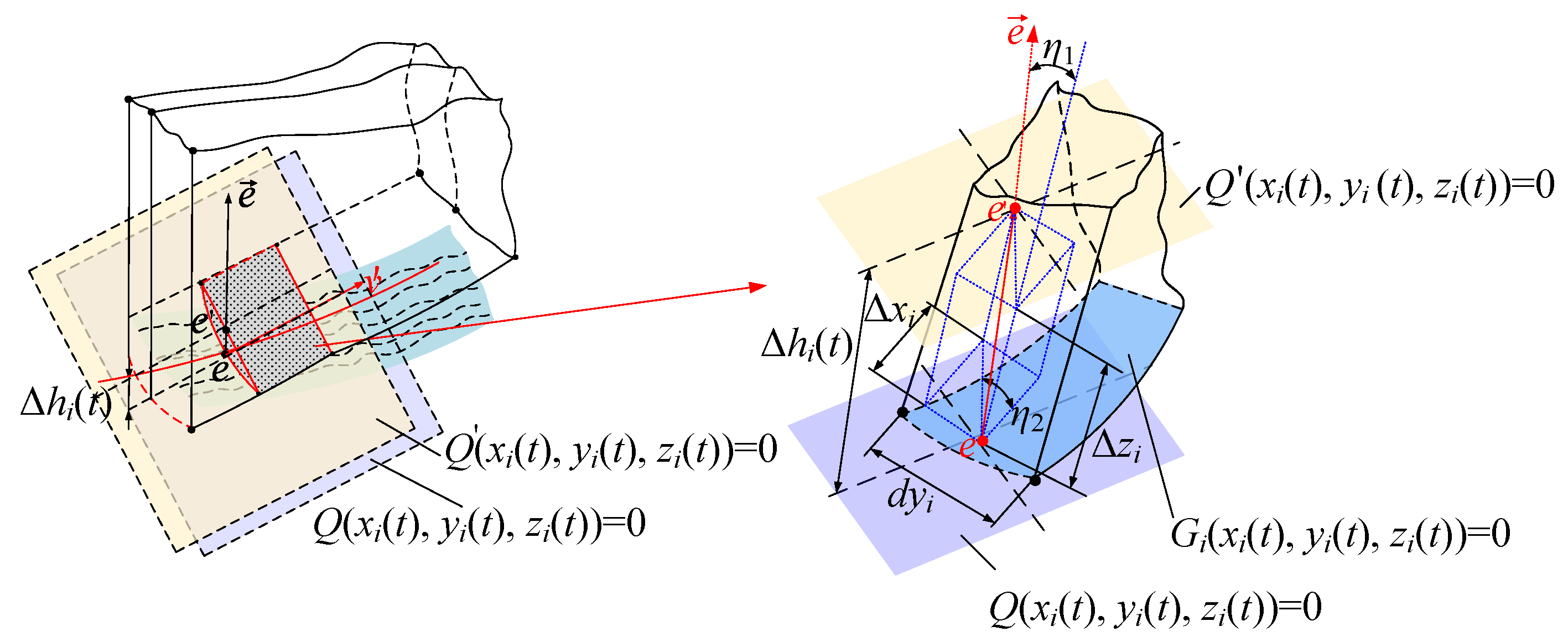
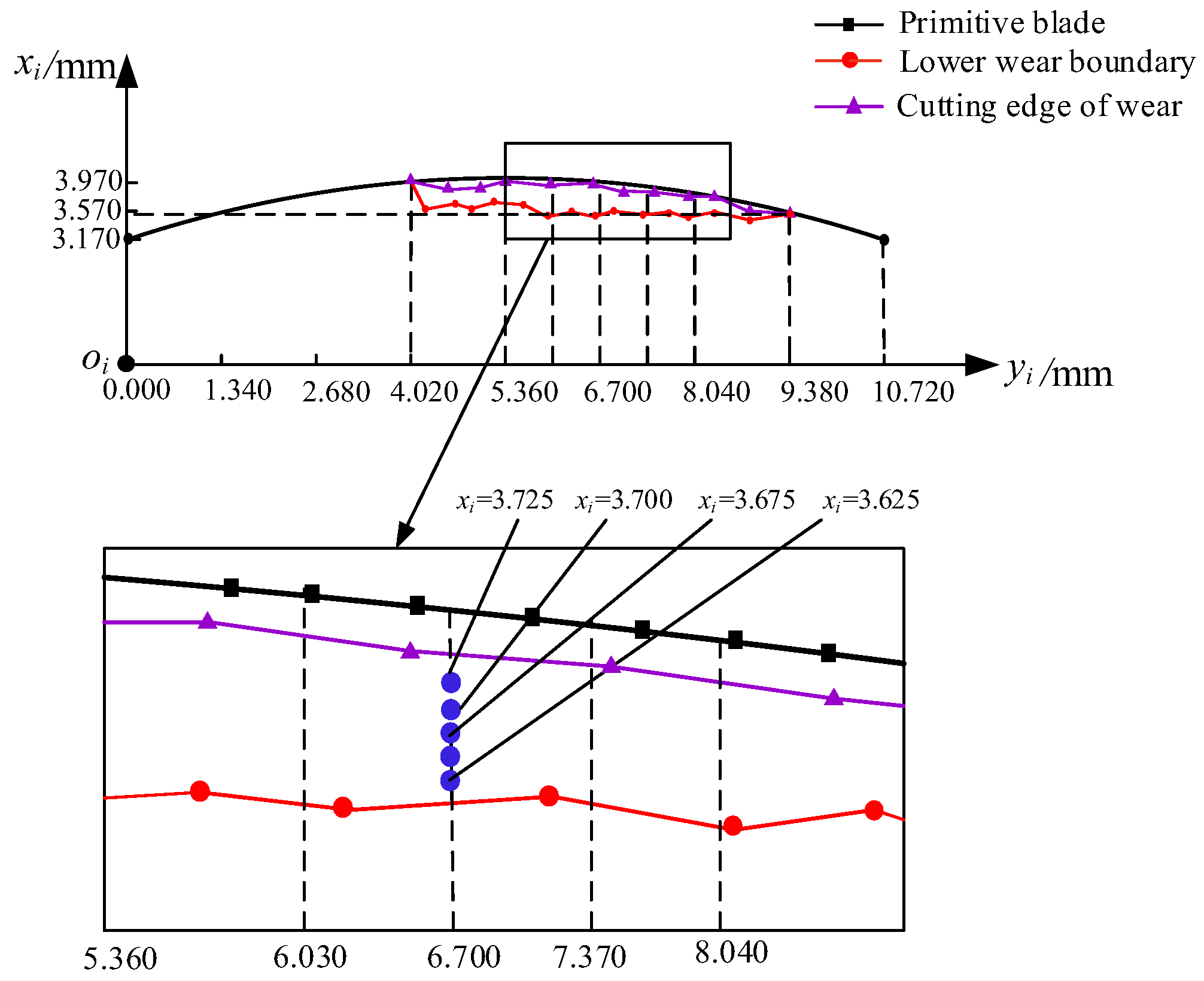
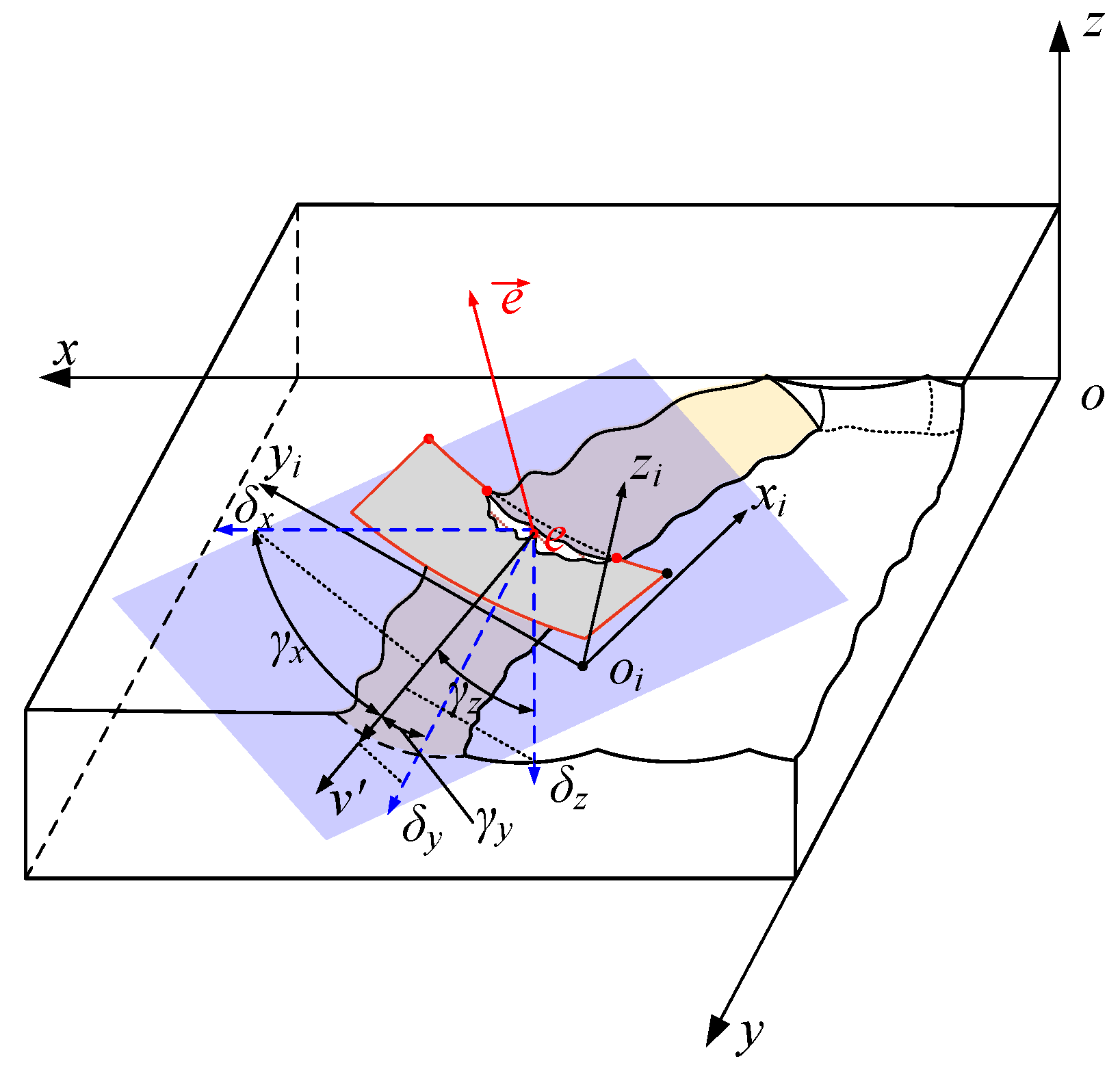
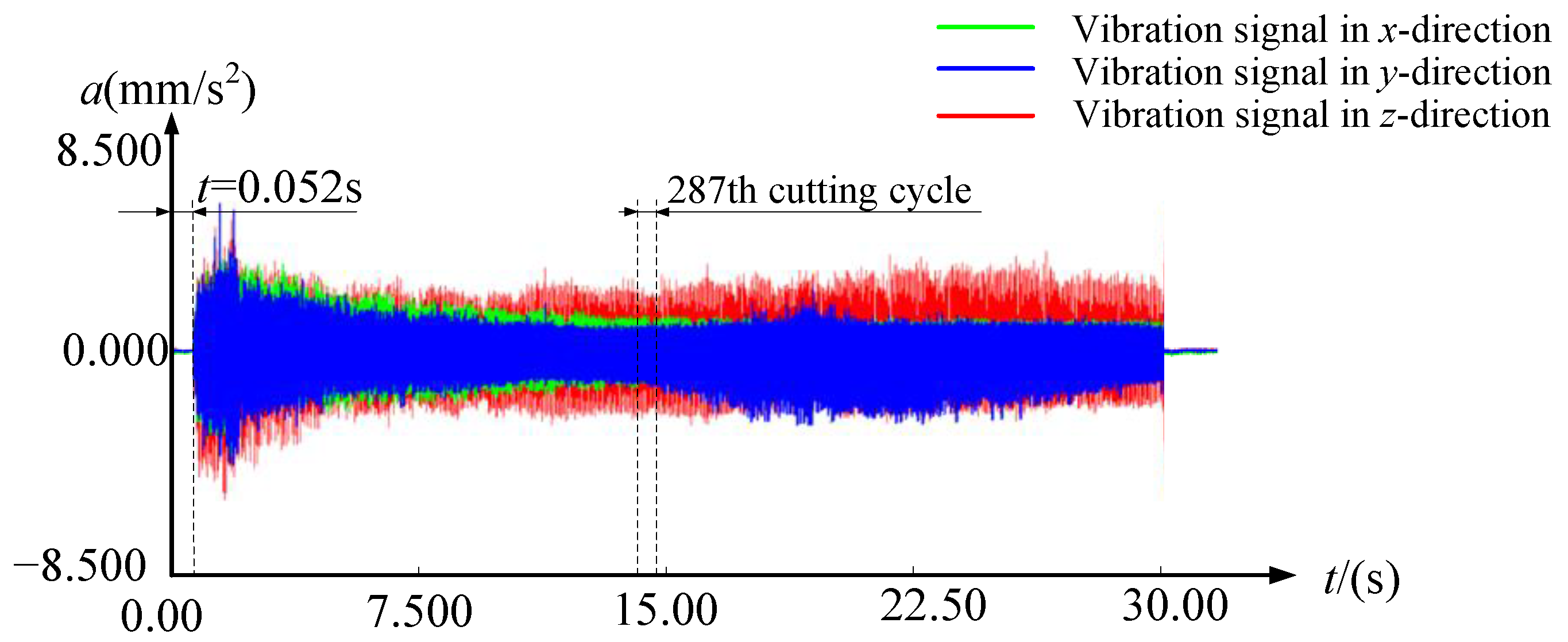
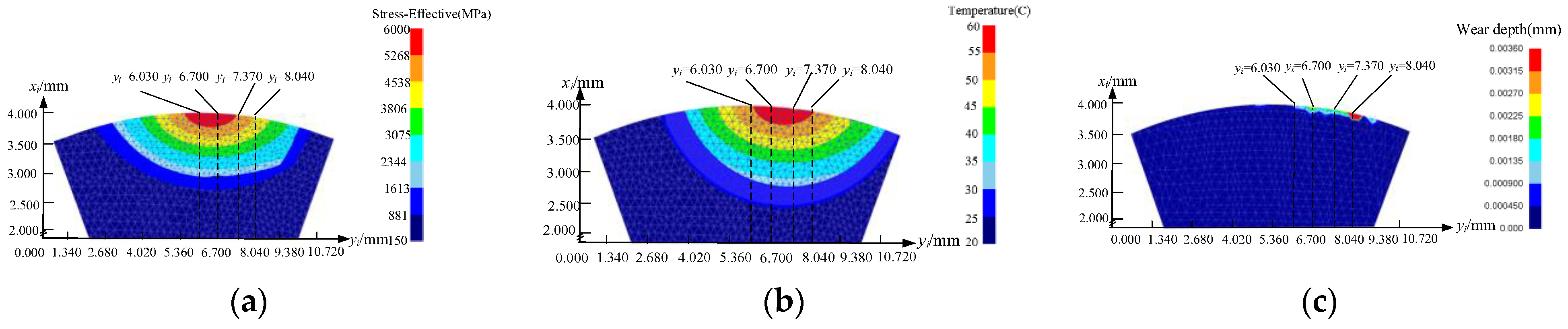
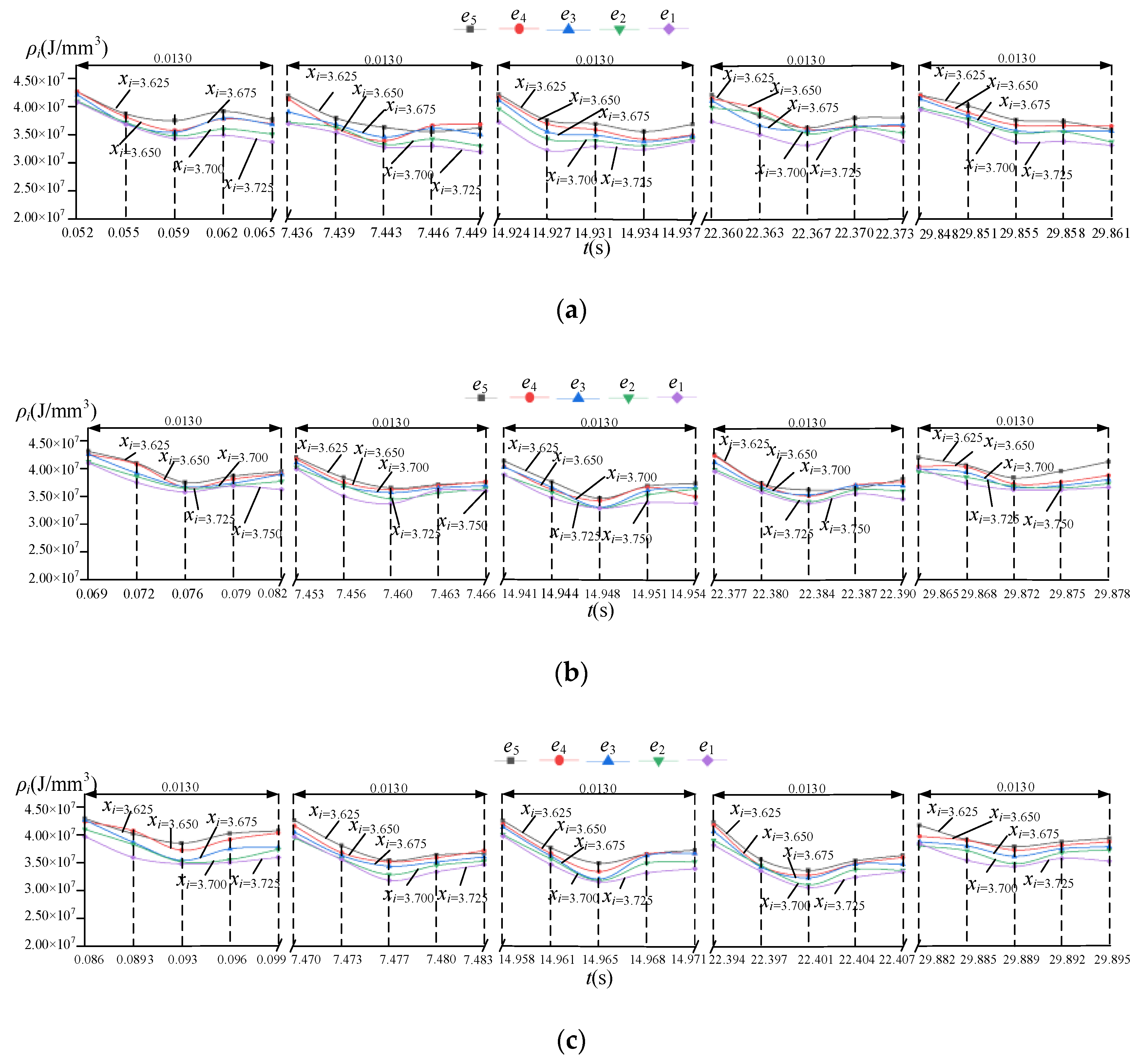
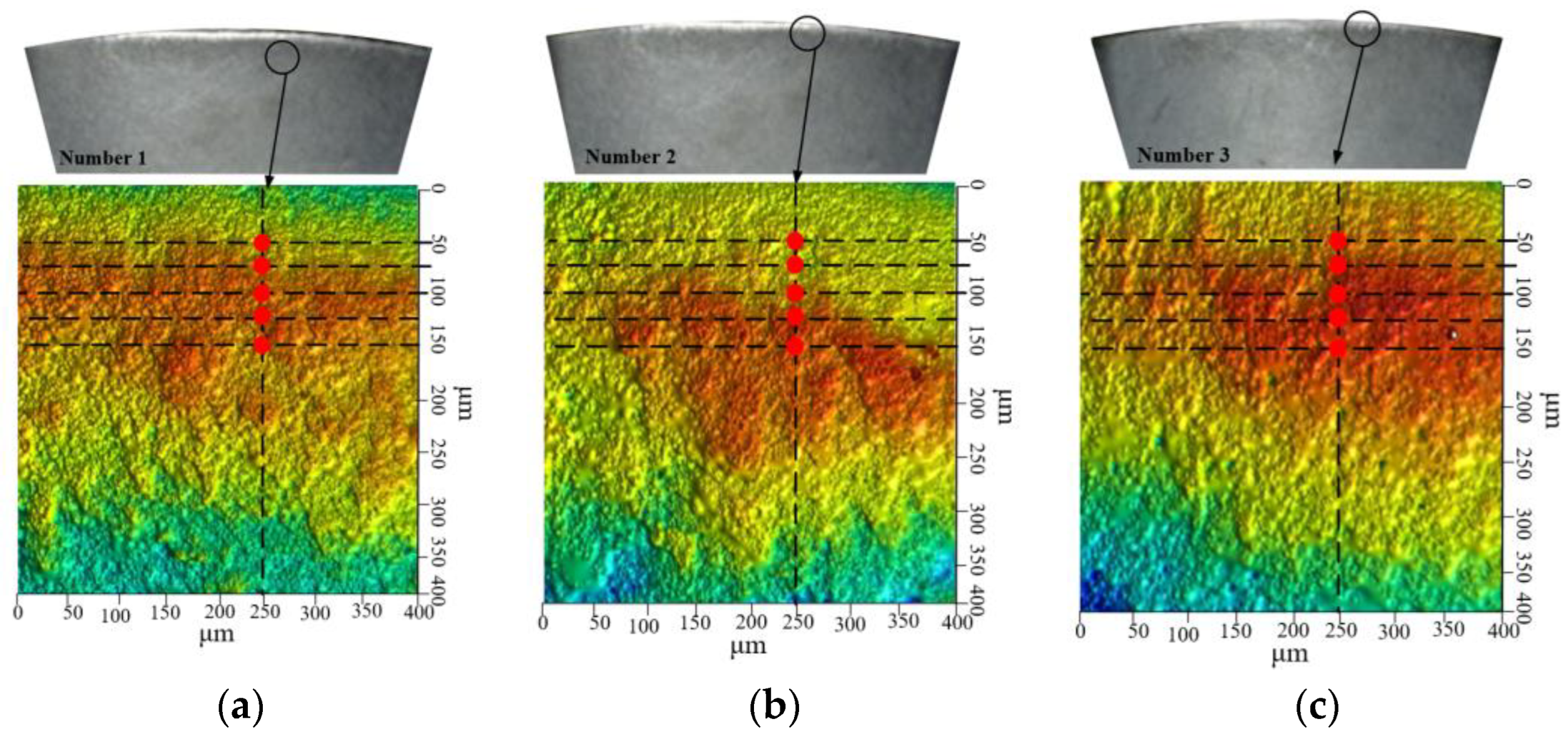
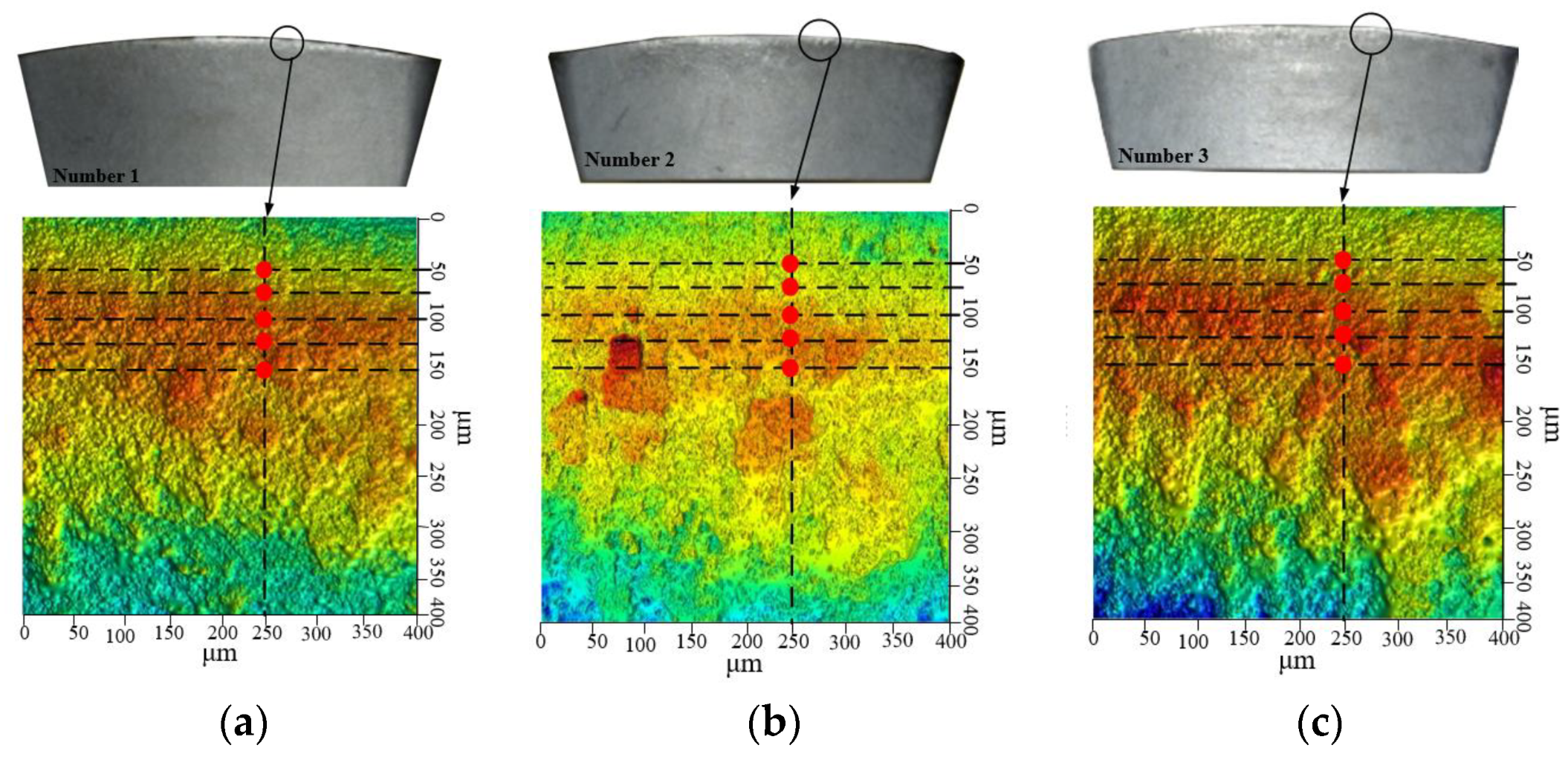
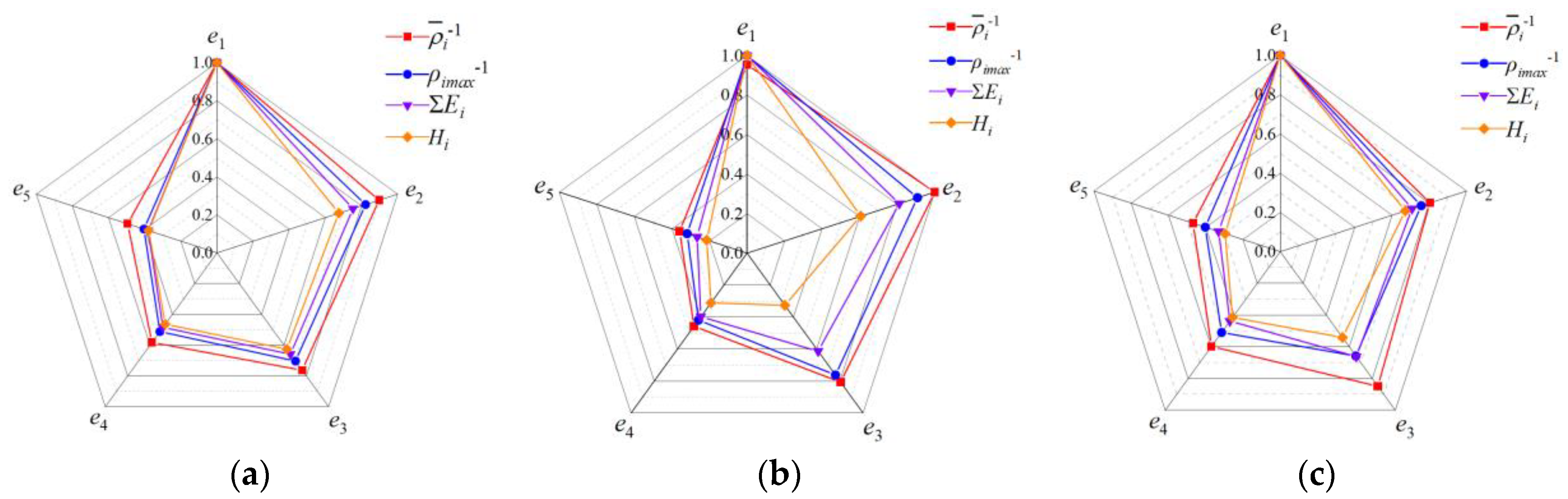

| Serial Number | Marameter | Meaning of Parameters |
|---|---|---|
| 1 | o-xyz | Workpiece coordinate system |
| 2 | oi-xiyizi | Cutter tooth coordinate system |
| 3 | o0-x0y0z0 | Cutting coordinate system without vibration |
| 4 | o0′-x0′y0′z0′ | Cutting coordinates system with vibration |
| 5 | om-xmymzm | Cutting coordinate system |
| 6 | lc | Length of the workpiece |
| 7 | lk | Width of the workpiece |
| 8 | lg | Height of the workpiece |
| 9 | vf | Cutter feed rate |
| 10 | n | Milling cutter speed |
| 11 | ap | Cutting depth |
| 12 | ae | Cutting width |
| 13 | φm(t) | Cutting time is the angle between the x0 axis and the xm′ axis when the cutting time is t |
| 14 | ψm(t) | Angle between the x0 axis and the xi axis when the cutting time is t |
| 15 | φ1 | Angle between oio0 and o0 and the line connecting the tip point |
| 16 | α(t) | Milling cutter attitude angle |
| 17 | α1(t) | Milling cutter attitude angle δ(t) projection angle in the xmomzv plane |
| 18 | α2(t) | Milling cutter attitude angle δ(t) projection angle in the ymomzm plane |
| 19 | Bx(t) | Vibration displacement in the xm direction |
| 20 | By(t) | Vibration displacement in the ym direction |
| 21 | Bz(t) | Vibration displacement in the zm direction |
| 22 | la | Amount of milling cutter overhang |
| 23 | q0, q1 | Distance from the lowest point of the tooth to the bottom surface of the tool tooth, distance from the tip to the bottom surface of the tooth |
| 24 | d | Diameter of the milling cutter |
| Tooth Error | Tooth Number | n (rpm) | vf (mm/min) | ap (mm) | ae (mm) | ||
|---|---|---|---|---|---|---|---|
| i = 1 | i = 2 | i = 3 | |||||
| Δzi (mm) | 0.000 | 0.001 | 0.003 | 1143 | 500 | 0.7 | 16 |
| Δri (mm) | 0.025 | 0.000 | 0.064 | ||||
| Cutter Tooth Error | Cutter Tooth Number | n (rpm) | vf (mm/min) | ap (mm) | ae (mm) | ||
|---|---|---|---|---|---|---|---|
| i = 1 | i = 2 | i = 3 | |||||
| Δzi (mm) | 0.007 | 0.003 | 0.000 | 1184 | 500 | 0.7 | 16 |
| Δri (mm) | 0.022 | 0.000 | 0.001 | ||||
| Cutter Tooth Number | Scheme 1 | Scheme 2 | ||||
|---|---|---|---|---|---|---|
| ∑Ei | ∑Ei | |||||
| Tooth 1 | 0.968 | 0.930 | 0.869 | 0.955 | 0.907 | 0.877 |
| Tooth 2 | 0.886 | 0.831 | 0.771 | 0.889 | 0.824 | 0.786 |
| Tooth 3 | 0.956 | 0.922 | 0.841 | 0.869 | 0.794 | 0.745 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Nie, Q.; Zhao, P.; Ma, Q.; Sun, S. Identification Method for Instantaneous Friction and Wear Energy Density Variation of High-Feed Milling Tool Flank. Appl. Sci. 2023, 13, 4807. https://doi.org/10.3390/app13084807
Jiang B, Nie Q, Zhao P, Ma Q, Sun S. Identification Method for Instantaneous Friction and Wear Energy Density Variation of High-Feed Milling Tool Flank. Applied Sciences. 2023; 13(8):4807. https://doi.org/10.3390/app13084807
Chicago/Turabian StyleJiang, Bin, Qiurui Nie, Peiyi Zhao, Qiang Ma, and Shuling Sun. 2023. "Identification Method for Instantaneous Friction and Wear Energy Density Variation of High-Feed Milling Tool Flank" Applied Sciences 13, no. 8: 4807. https://doi.org/10.3390/app13084807
APA StyleJiang, B., Nie, Q., Zhao, P., Ma, Q., & Sun, S. (2023). Identification Method for Instantaneous Friction and Wear Energy Density Variation of High-Feed Milling Tool Flank. Applied Sciences, 13(8), 4807. https://doi.org/10.3390/app13084807





