K-Means++ Clustering Algorithm in Categorization of Glass Cultural Relics
Abstract
1. Introduction
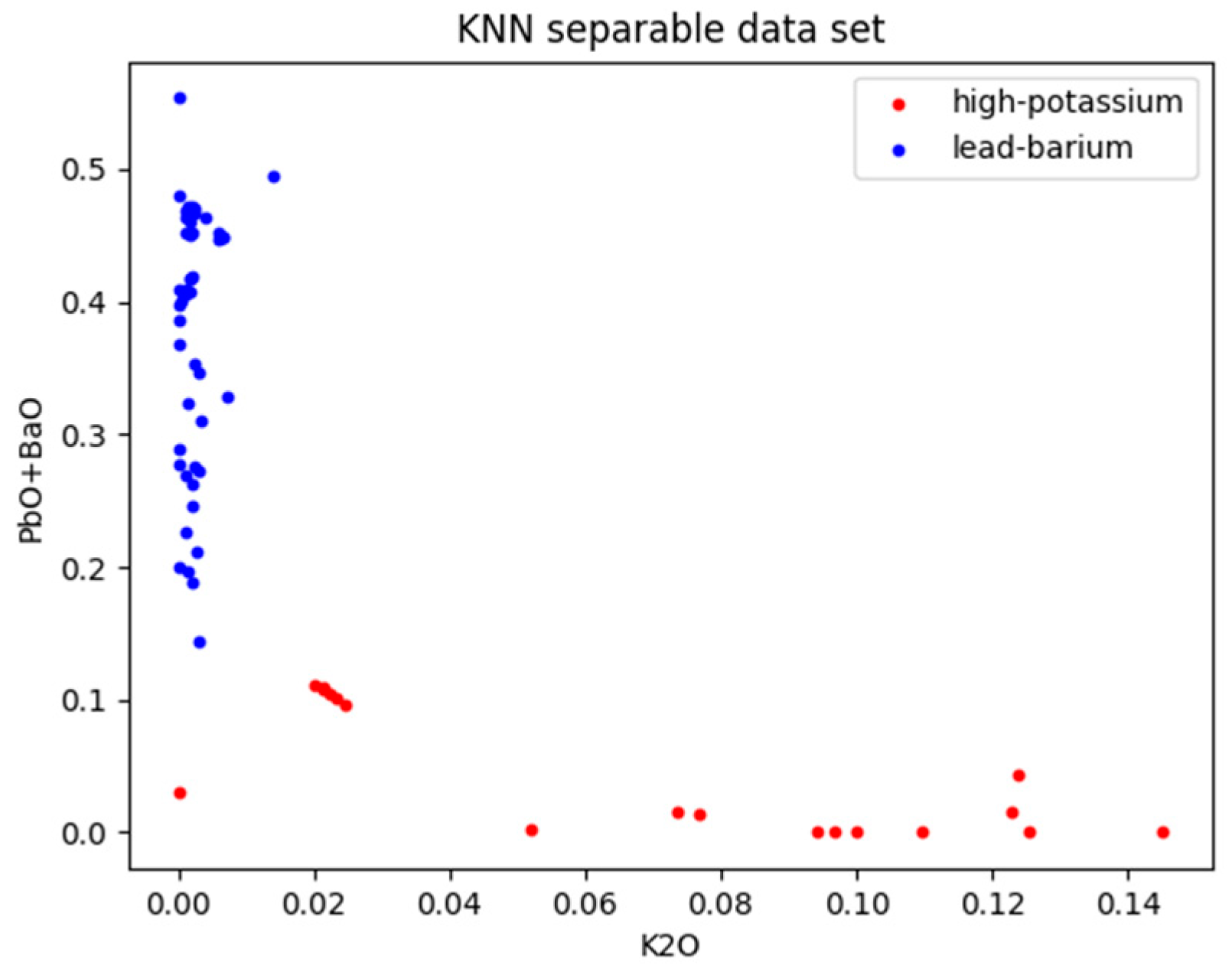
2. Classification Law of High-Potassium Glass and Lead–Barium Glass
2.1. Sample Data Acquisition and Exploratory Spatial Data Analysis
2.1.1. Data Overview
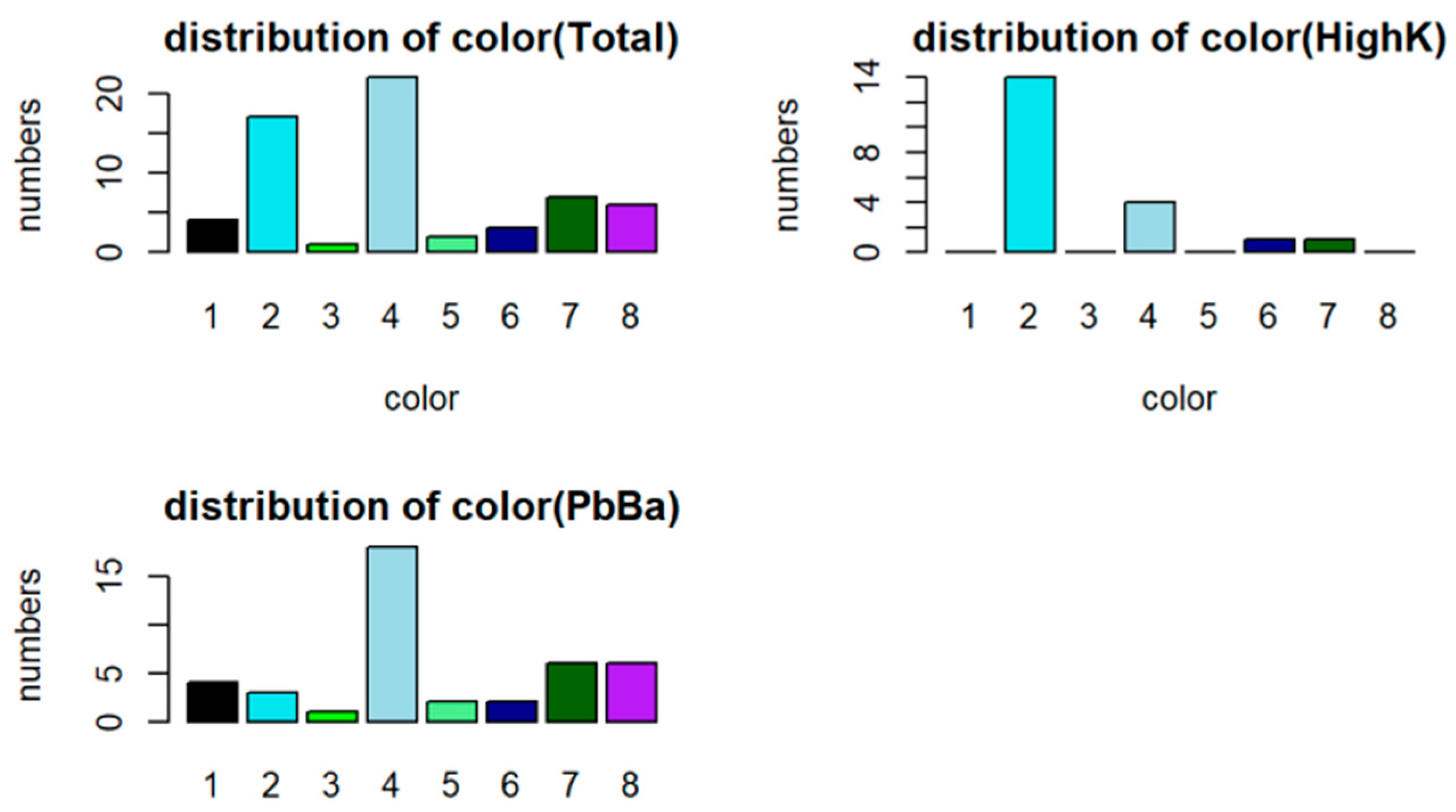
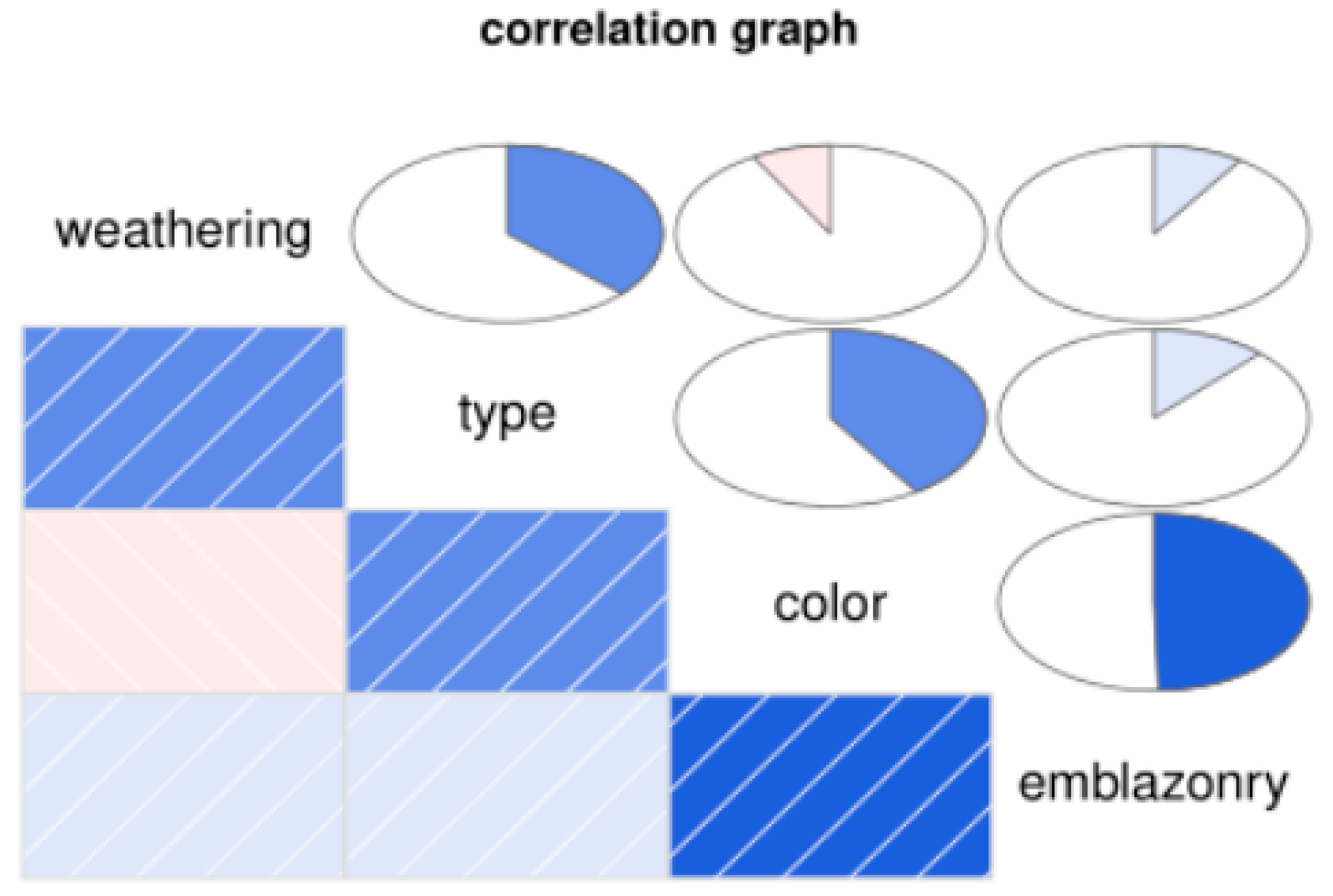
2.1.2. Exploratory Data Analysis
2.2. Analysis of Classification Laws Based on Sample Data
3. K-Means++ Subclass Classification
3.1. Prediction of the Chemical Composition Content before Weathering on Weathered Samples
- Use 35 unweathered samples, with 14 chemical compositions, as matrix X (35 × 14).
- Calculate the eigenvalue decomposition: .
- Choose the largest 3 eigenvalues and their eigenvectors, form matrix P (14 × 3).
- Calculate PCs for unweathered data: .
- Use 32 unweathered samples, with 14 chemical compositions, as matrix X1 (32 × 14).
- Calculate PCs for weathered data: .
3.2. K-Means++ Algorithm
4. Model Validity Analysis
4.1. Comparison Verification with Parent Classes
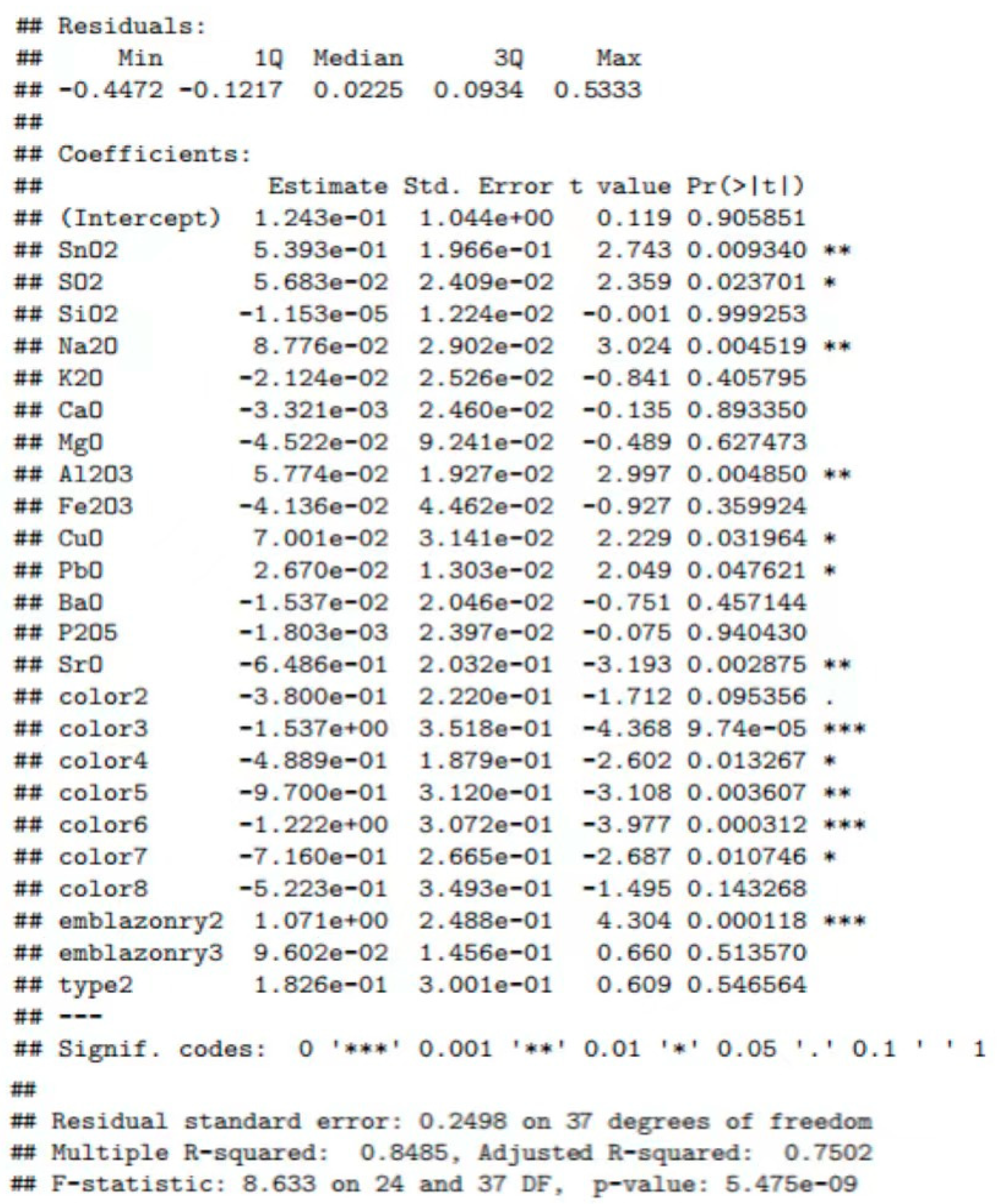
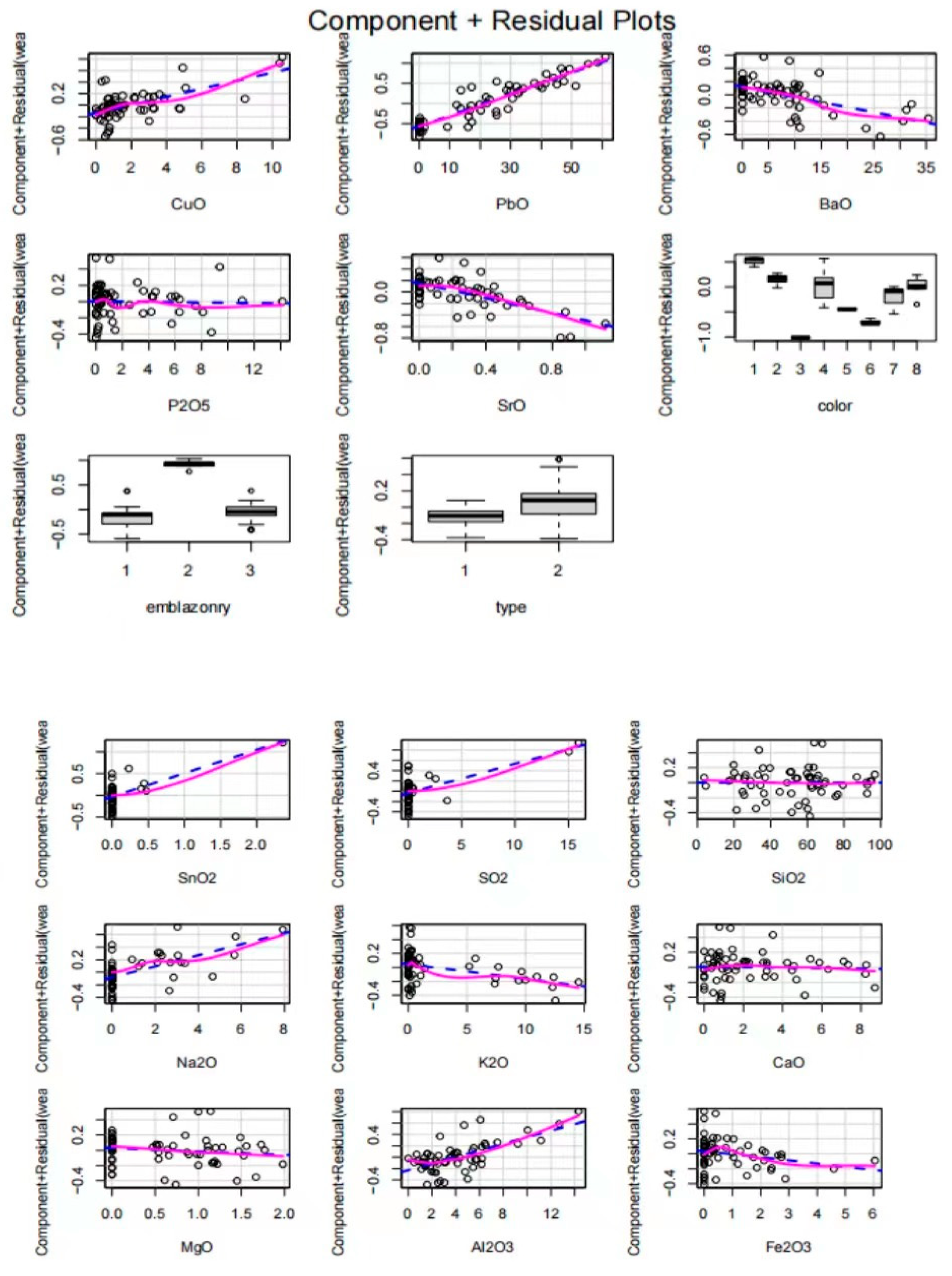
4.2. Significance Test of Linear Regression
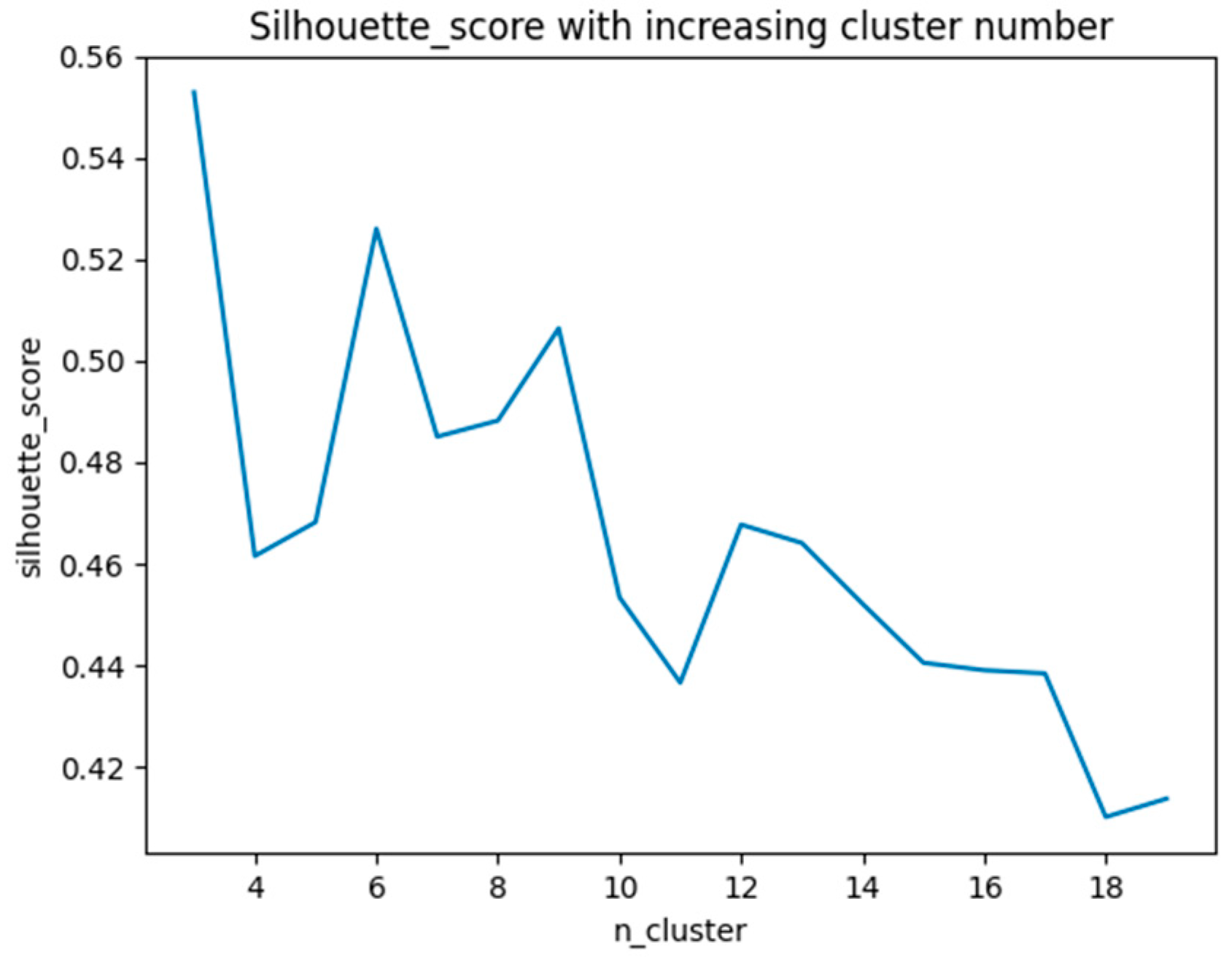
4.3. Silhouette Coefficient and Square Sum of Error
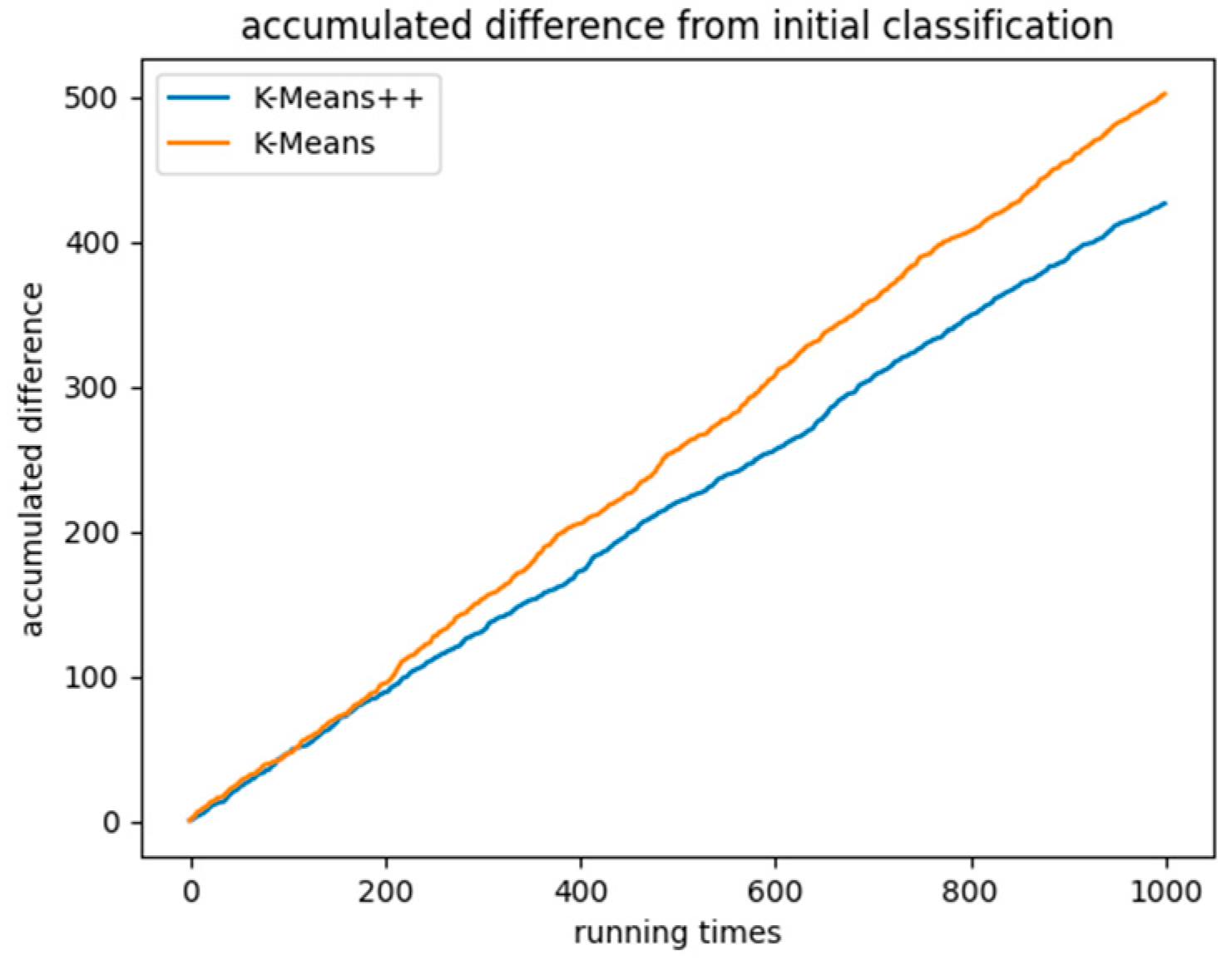
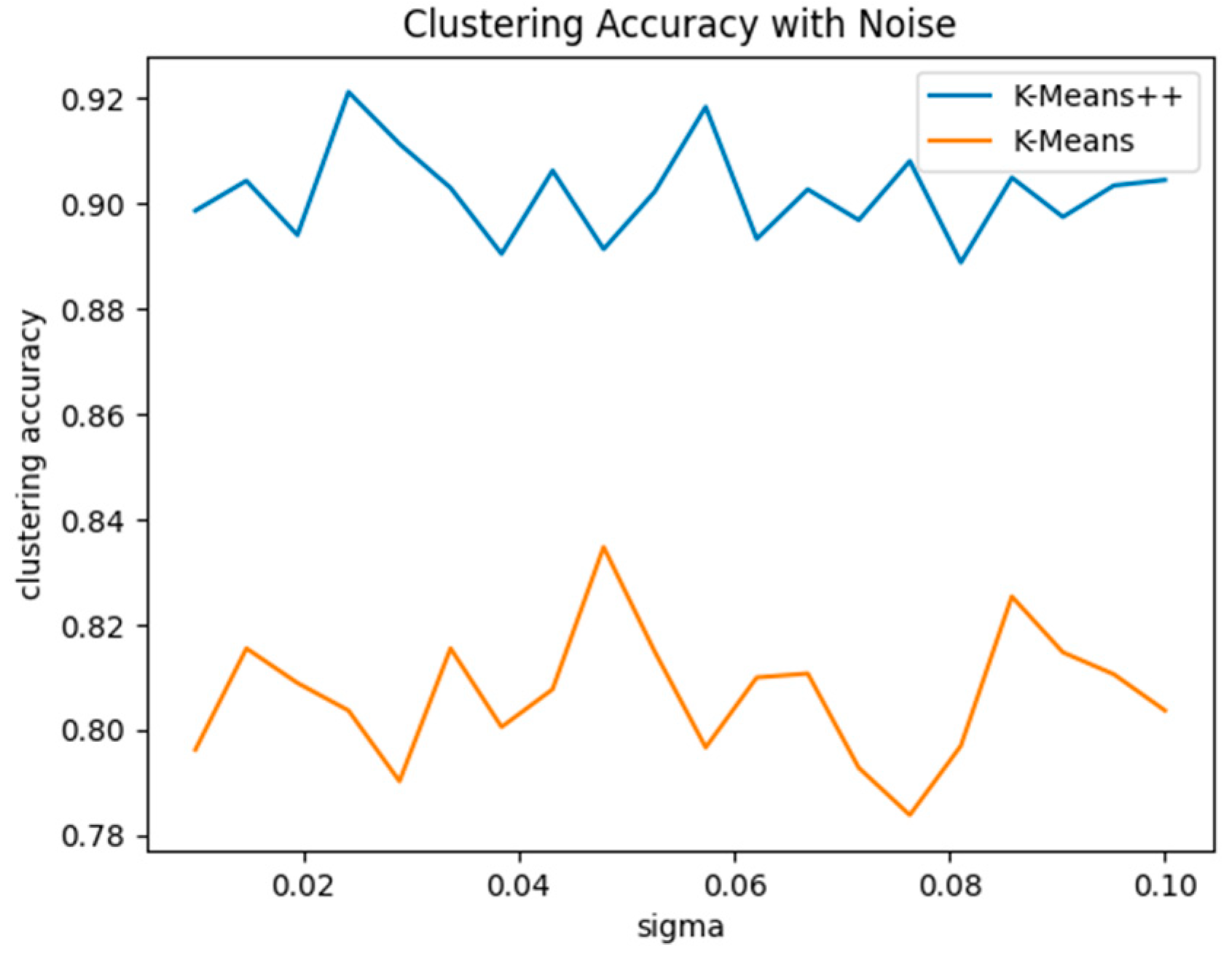
5. Model Sensitivity Analysis
6. Limitations and Future Work
6.1. Size of Glass Relics Data
6.2. Potential Improvement of K-Means++
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yin, Y. Component analysis of ancient glass products by association prediction. Contemp. Chem. Res. 2003, 1, 122–126. [Google Scholar]
- Cao, C.; Guo, H. Using fuzzy mathematics knowledge to classify the disease types of stone, ceramic and glass relics in the collection. J. Beijing Union Univ. 2009, 4, 58–60. [Google Scholar]
- Wang, C.; Tao, Y.; Chen, M.; Huang, M. Weathering of sodium-calcium-aluminum-magnesium silicate glass and alkali-lead silicate glass. Silic. Bull. 1989, 6, 1–9. [Google Scholar]
- Zhao, F.; Chen, B.; Chai, Y.; Dong, J.; Li, Q. The PXRF analysis and related issues of some glassware unearthed in Xi′an. Archaeol. Cult. Relics 2015, 4, 111–119. [Google Scholar]
- Feng, B. Construction and application of ancient glass beads database unearthed in China. Master’s Thesis, Northwest University, Xi’an, China, 2021. [Google Scholar]
- Zhang, L.; Li, H.; Chen, S.; Li, Z.; Ruan, M. Simulation method of glass composition and properties. J. Silic. 2022, 50, 2338–2350. [Google Scholar]
- Li, J. Glass defect detection based on deep learning. Master’s Thesis, Fujian University of Engineering, Fuzhou, China, 2021. [Google Scholar]
- Wang, Z.; Zhao, X.; Li, Z.; Guo, M.; Xiao, W.; Liu, Z. Original composition prediction and sub-classification method of weathered silicate glass based on machine learning. J. Silic. 2023, 51, 416–426. [Google Scholar]
- Yigit, H. A weighting approach for KNN classifier. In Proceedings of the 2013 International Conference on Electronics, Computer and Computation (ICECCO), Ankara, Turkey, 7–9 November 2013; pp. 228–231. [Google Scholar]
- Taneja, S.; Gupta, C.; Aggarwal, S.; Jindal, V. MFZ-KNN—A modified fuzzy based K nearest neighbor algorithm. In Proceedings of the 2015 International Conference on Cognitive Computing and Information Processing(CCIP), Noida, India, 3–4 March 2015; pp. 1–5. [Google Scholar]
- Kuang, Z. Optimization of KNN classification algorithm in high-dimensional data. Master’s Thesis, Guangdong University of Technology, Guangzhou, China, 2019. [Google Scholar]
- Angün, E.; Altınoy, A. A New Mixed-Integer Linear Programming Formulation for Multiple Responses Regression Clustering. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 1634–1639. [Google Scholar]
- Rani, A.J.M.; Parthipan, L. Clustering analysis by Improved Particle Swarm Optimization and K-means algorithm. In Proceedings of the IET Chennai 3rd International on Sustainable Energy and Intelligent Systems (SEISCON 2012), Tiruchengode, India, 27–29 December 2012; 2012; pp. 1–6. [Google Scholar]
- Dehariya, V.K.; Shrivastava, S.K.; Jain, R.C. Clustering of Image Data Set Using K-Means and Fuzzy K-Means Algorithms. In Proceedings of the 2010 International Conference on Computational Intelligence and Communication Networks, Bhopal, India, 26–28 November 2010; pp. 386–391. [Google Scholar]
- Li, B.; Guan, Y.; Gong, W.; Wei, X.; Xue, D. Density-based K-means initial clustering center selection algorithm. J. Suihua Univ. 2022, 42, 148–151. [Google Scholar]
- Zhang, S.; Chen, X. Dimensionality reduction of principal component analysis data based on mutual information credibility. J. Hubei Univ. Natl. (Nat. Sci. Ed.) 2019, 4, 425–430. [Google Scholar]
- Zhao, B. Discussion on the application of machine learning classification based on data dimensionality reduction. Mod. Inf. Technol. 2018, 2, 144–145. [Google Scholar]
- Dong, H. Comparative study of principal component analysis and linear discriminant analysis. Mod. Comput. (Prof. Ed.) 2016, 29, 36–40. [Google Scholar]
- Liu, Z.; Zhou, B.; Yu, L.; Niu, C.; Xu, X. K-means algorithm combining Pearson similarity and minimum spanning tree. J. Nanchang Inst. Technol. 2022, 41, 91–96. [Google Scholar]
- Zheng, R.; Zheng, X.; Huang, W. Fast sorting method for retired power batteries using improved K-means algorithm. J. Xiamen Univ. Technol. 2022, 30, 74–81. [Google Scholar]
- Murtagh, F.; Contreras, P. Algorithms for hierarchical clustering: An overview. Wiley Interdiscip. Rev.: Data Min. Knowl. Discov. 2012, 2.1, 86–97. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Yin, S.; Wang, T.; Xie, F.; Liu, L.; Qu, Z.; Zhang, B. Evaluation method of clustering results based on mutual information and contour coefficient. J. Ordnance Equip. Eng. 2020, 8, 207–213. [Google Scholar]
- Li, C.; Liu, Z.; Liu, S. Improved KNN data classification model based on linear regression method. J. Lanzhou Petrochem. Vocat. Tech. Coll. 2021, 3, 20–23. [Google Scholar]
- Sun, L.; Liu, M.; Xu, J. K-means clustering algorithm based on optimizing initial clustering center and contour coefficient. Fuzzy Syst. Math. 2022, 1, 47–65. [Google Scholar]





| Relic No. | Ornamentation | Type | Color | Weathering | Detection Point | SiO2 | CaO | MgO | Fe2O3 | PbO | … | Sum |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 01 | C | high-potassium | blue–green | unweathered | 01 | 69.33 | 6.32 | 0.87 | 1.74 | 97.61 | ||
| 02 | A | lead-barium | light green | weathered | 02 | 36.28 | 2.34 | 1.18 | 1.86 | 47.43 | 99.89 | |
| 03 | A | high-potassium | blue–green | unweathered | 03position1 | 87.05 | 2.01 | 0.25 | 100 | |||
| 03position2 | 61.71 | 5.87 | 1.11 | 2.16 | 1.41 | 98.88 |
| Clustering Name | Sample |
|---|---|
| 0 | 08 *, 08 Severe weathering point, 11, 20, 24, 26, 26 Severe weathering point. |
| 1 | 01, 03 Part 2, 04, 05, 06 Part 1, 06 Part 2, 13, 14, 16 |
| 2 | 02, 19, 30 Part 1, 30 Part 2, 34, 36, 38, 41, 43 Part 2, 49, 50, 51 Part 1, 52, 56, 57, 58 |
| 3 | 03 Part 1, 07, 09, 10, 12, 18, 21, 22, 27 |
| 4 | 23 unweathered point, 25 unweathered point, 28 unweathered point, 29 unweathered point, 31, 32, 33, 35, 37, 42 unweathered point 1, 42 unweathered point 2, 44 unweathered point, 45, 46, 47, 48, 49 unweathered point, 50 unweathered point, 53 unweathered point, 55 |
| 5 | 39, 40, 43 Part 1, 51 Part 2, 54, 54 Severe weathering point |
| Clustering Name | High-Potassium | Lead–Barium |
|---|---|---|
| 0 | 0 | 7 |
| 1 | 9 | 0 |
| 2 | 0 | 16 |
| 3 | 9 | 0 |
| 4 | 0 | 20 |
| 5 | 0 | 6 |
| Subclass Name | Subclass Number |
|---|---|
| Lead–barium high-copper | 0 |
| High-potassium and calcium | 1 |
| Lead–barium low-copper | 2 |
| High-potassium and low-calcium | 3 |
| Lead–barium mid-copper low-calcium | 4 |
| Lead–barium mid-copper high-calcium | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, J.; Yu, Z.; Cai, Y.; Wang, X. K-Means++ Clustering Algorithm in Categorization of Glass Cultural Relics. Appl. Sci. 2023, 13, 4736. https://doi.org/10.3390/app13084736
Meng J, Yu Z, Cai Y, Wang X. K-Means++ Clustering Algorithm in Categorization of Glass Cultural Relics. Applied Sciences. 2023; 13(8):4736. https://doi.org/10.3390/app13084736
Chicago/Turabian StyleMeng, Jie, Ziyang Yu, Yuxin Cai, and Xiuling Wang. 2023. "K-Means++ Clustering Algorithm in Categorization of Glass Cultural Relics" Applied Sciences 13, no. 8: 4736. https://doi.org/10.3390/app13084736
APA StyleMeng, J., Yu, Z., Cai, Y., & Wang, X. (2023). K-Means++ Clustering Algorithm in Categorization of Glass Cultural Relics. Applied Sciences, 13(8), 4736. https://doi.org/10.3390/app13084736






