The Seismic Resistance Analysis of Frame Structures and Wall Structures Using Ferrocement and Expanded Metal
Abstract
1. Introduction
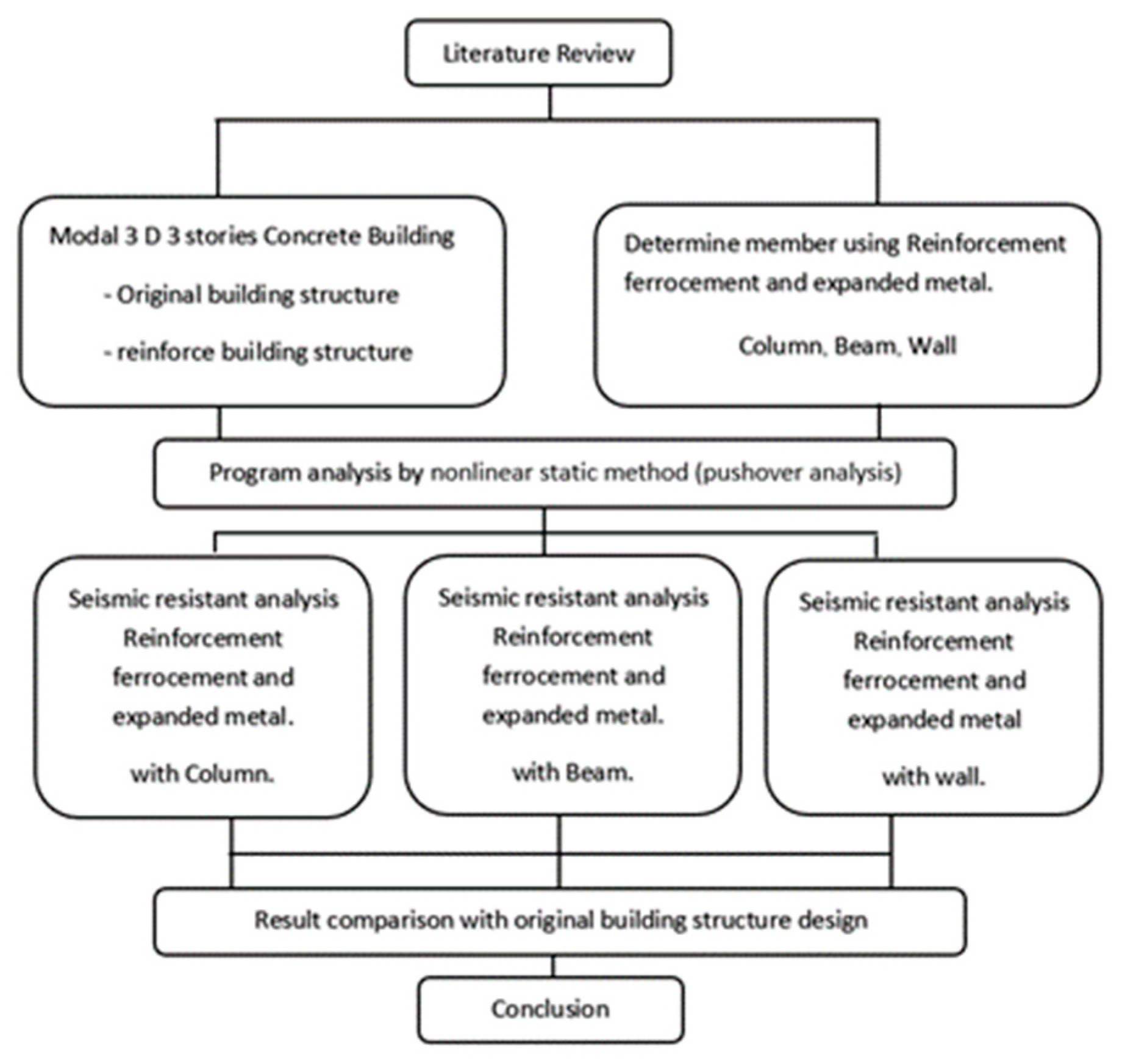
2. Materials and Methods
3. Reinforcement of the Frames of the Concrete Building Structure
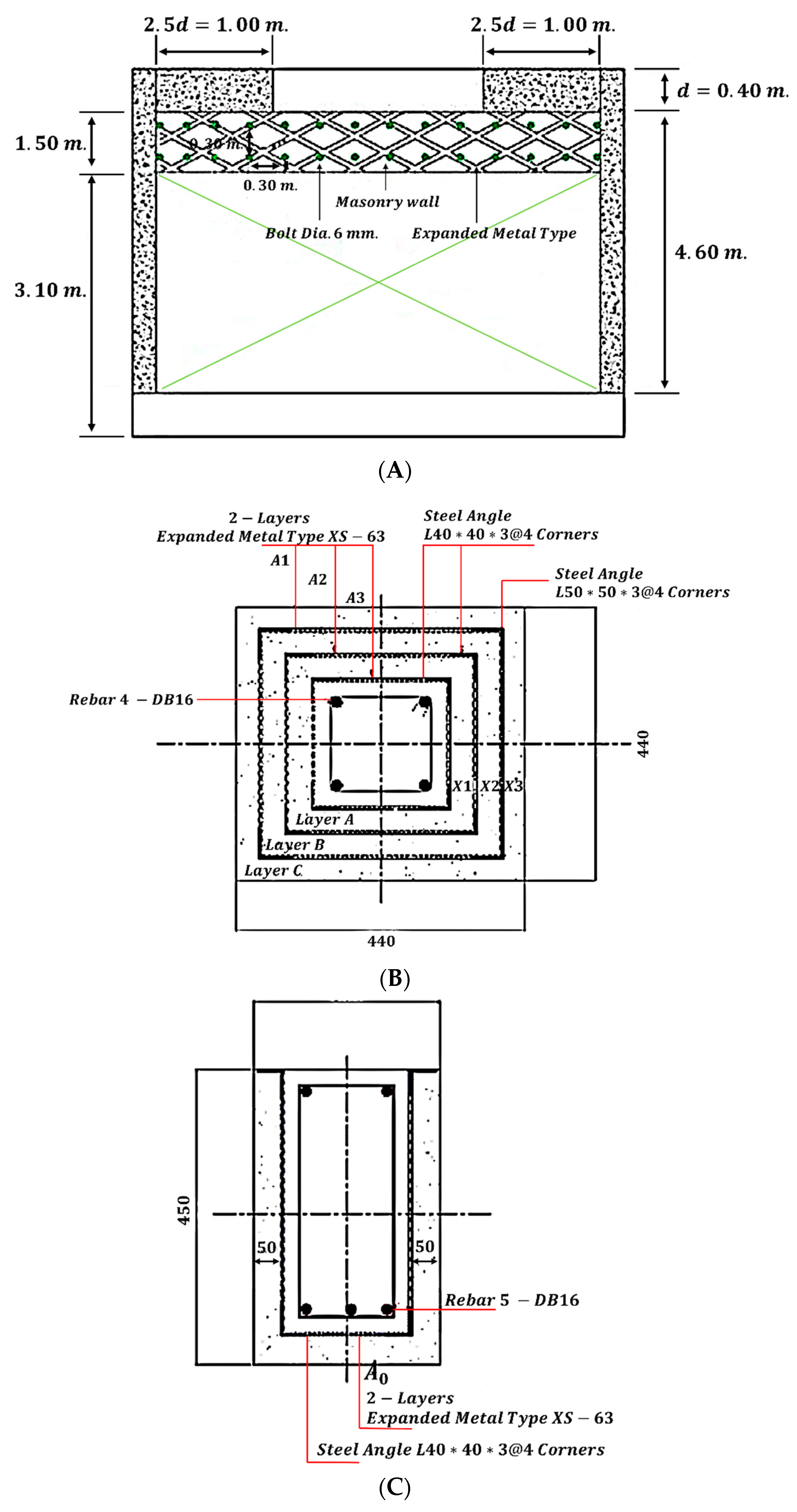
3.1. Reinforced Frames of the Concrete Model
- fys and fye = yield strength of the steel angle bar and expanded metal;
- Ss and Se = cross-sectional modulus of the steel angle bar and expanded metal;
- VBF = lateral load resistance of the reinforced rigid frame.
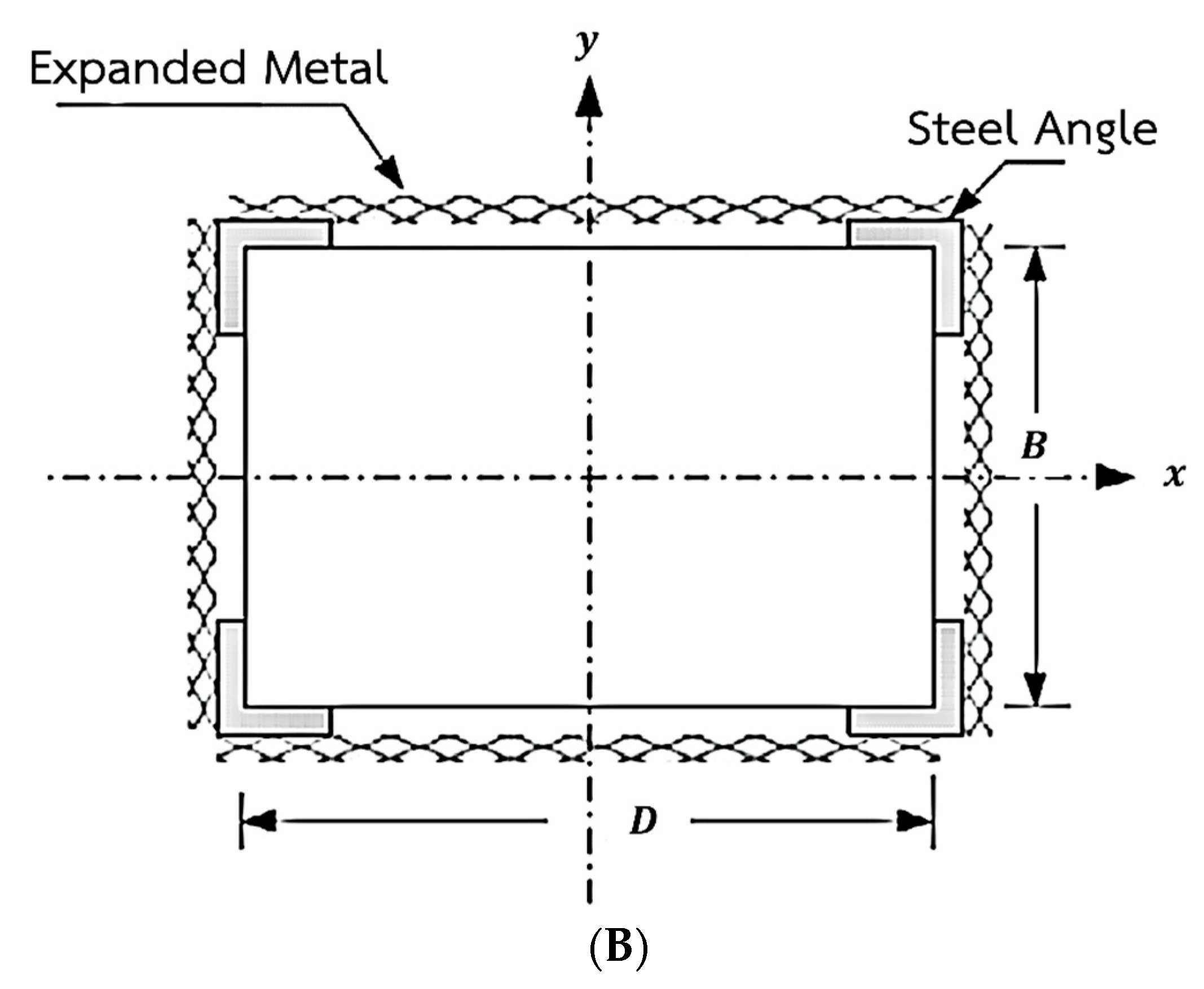
3.2. Reinforced Wall Frame Model
- is the allowable compressive stress of the brick wall prism, ,
- is the maximum compression of the brick wall prism
- Ø = 0.65, t = the thickness of the brick wall
- is the tilt angle of the diagonal compressive strength on the top of the brick wall.
- is the friction coefficient between the building frame and brick wall;
- is the ratio between the height and width of the building frame ;
- is the reduction factor of the pole .
4. Reinforcement of the Model Building
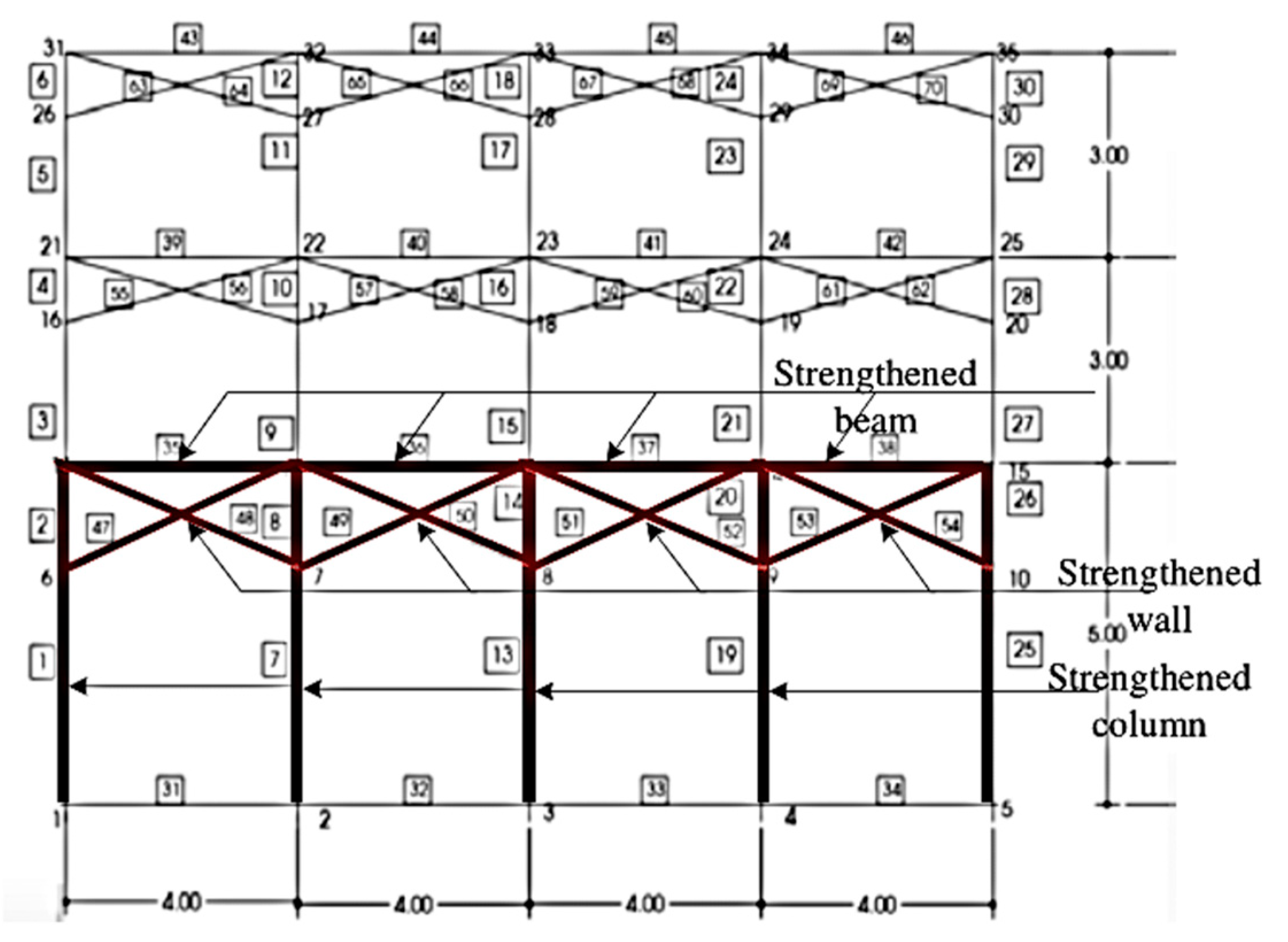
4.1. Sample Reinforcement of the Building
4.2. Sample Building Reinforcement Method
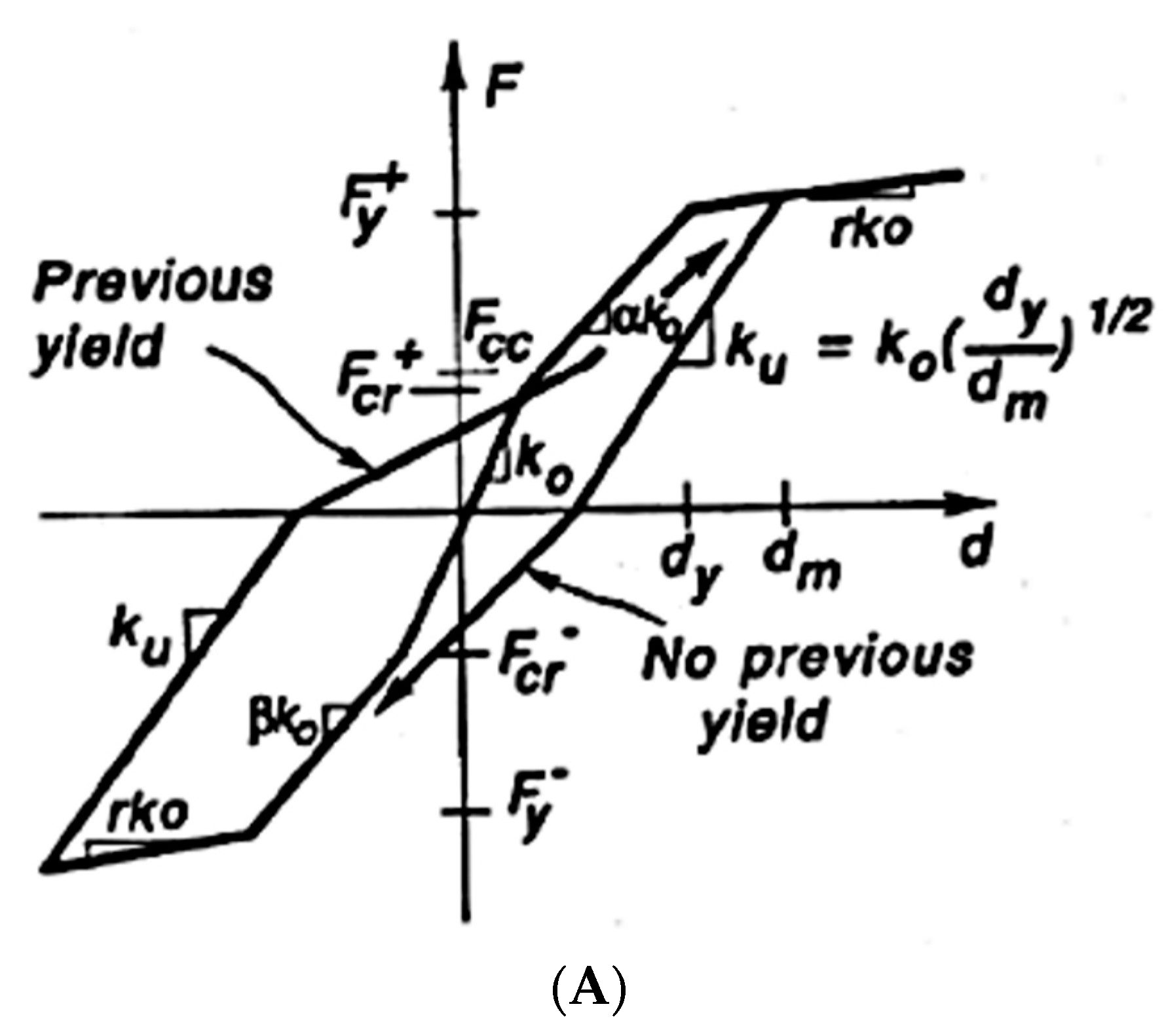
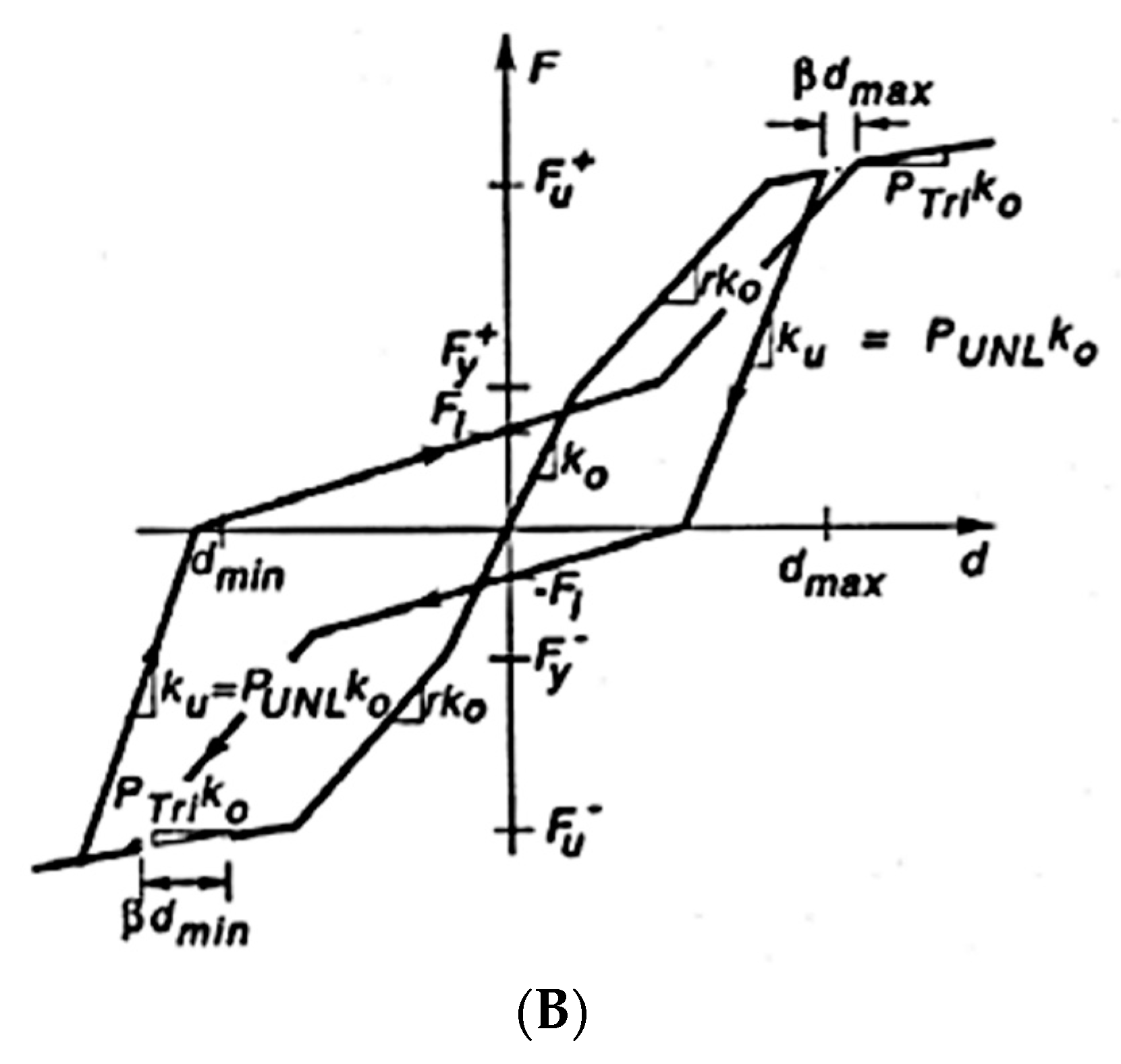
5. Reinforced Building Concrete Frame Analysis
- is the maximum deflection value of the system due to seismic force;
- is the maximum deflection value under monotonic loading;
- is the yield point of the structural system;
- is the hysteretic energy value of the structural system;
- is a constant which indicates the scale of damage by the response modal shape.
6. Conclusions
- (A)
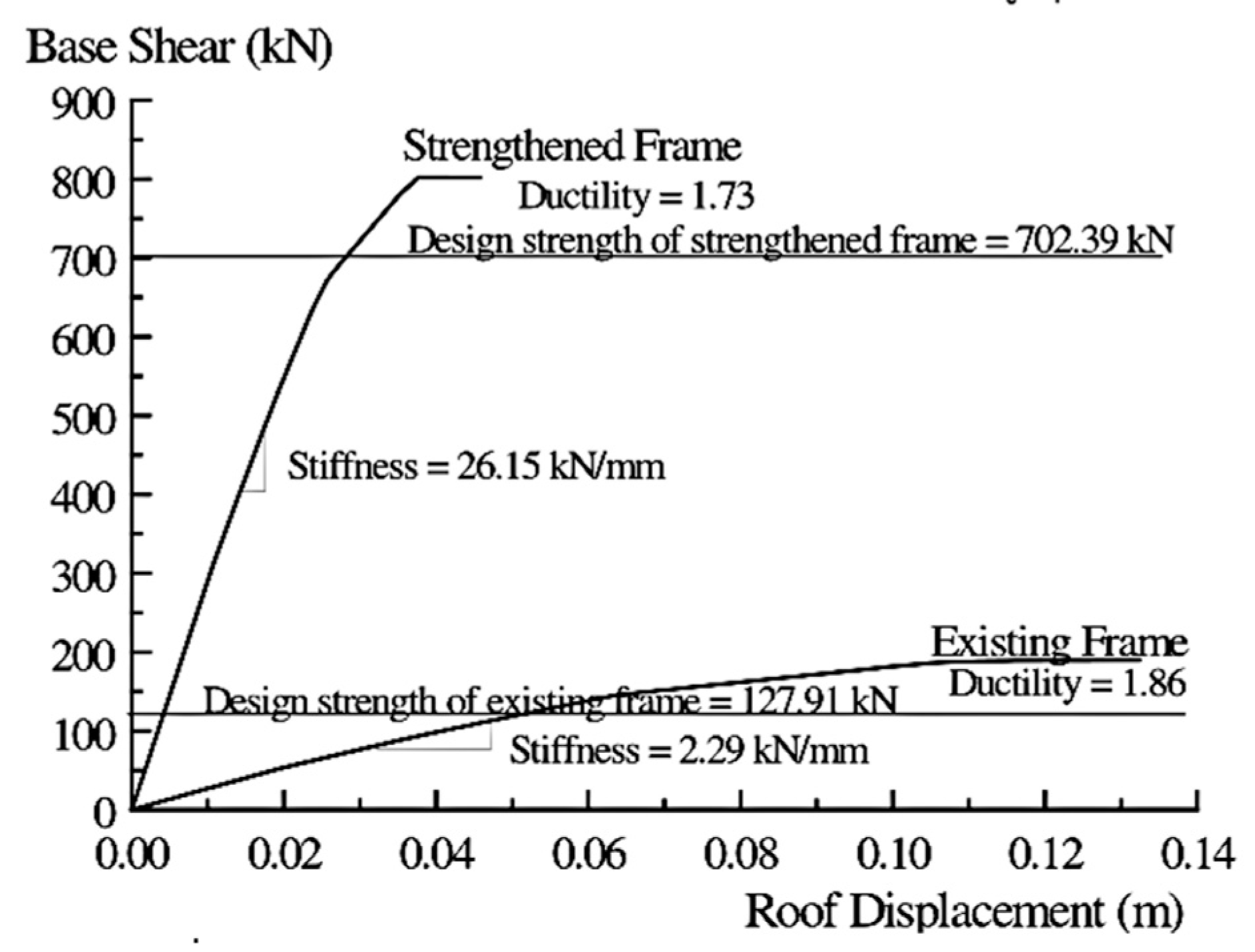
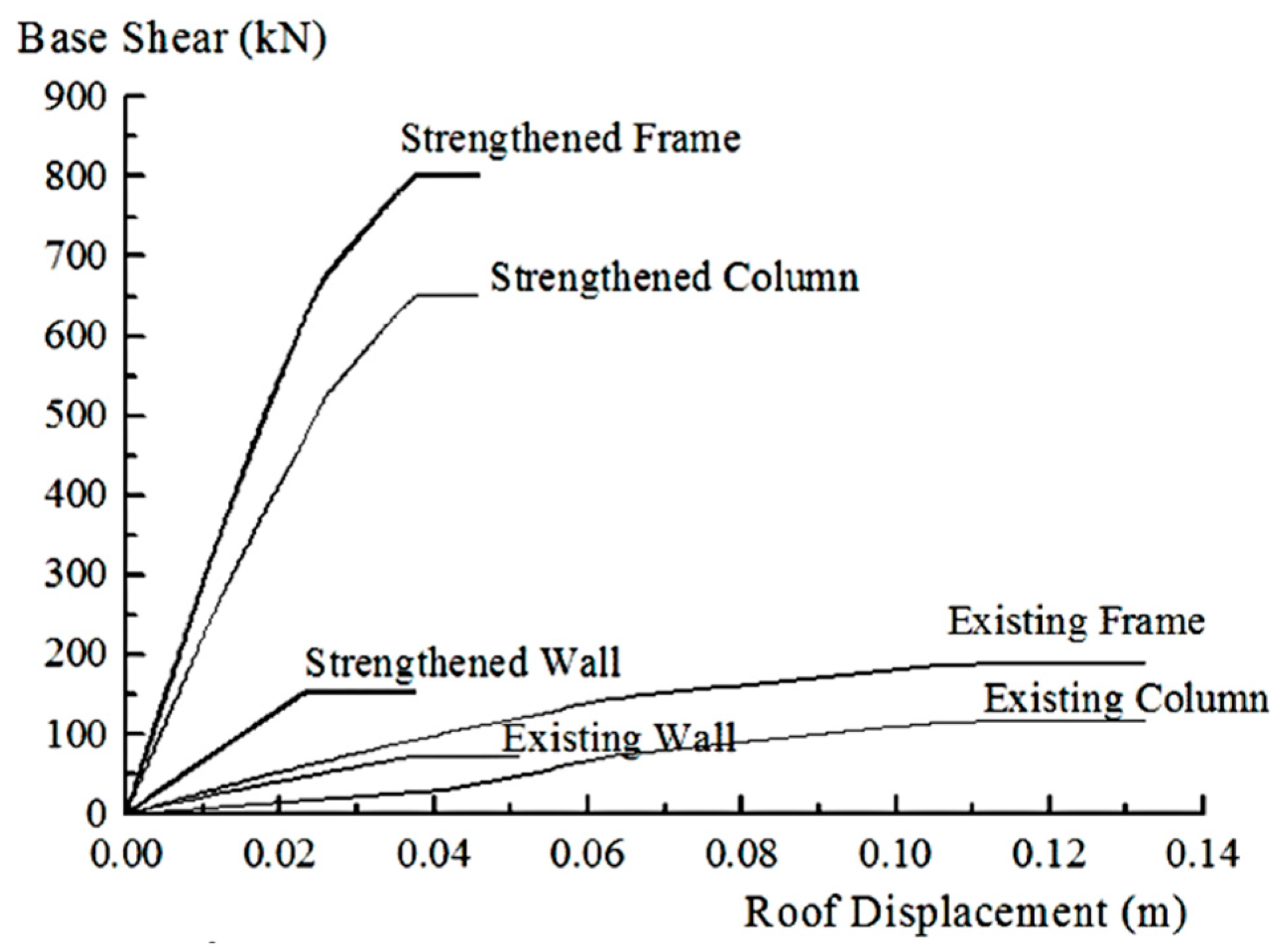
- The seismic resistance of the reinforced frame is 702.39 kN, higher than that of the original frame, which is 127.91 kN, with a difference in seismic resistance of approximately 14%. The seismic resistance value of the reinforced frame is 4.23 times higher than that of the original frame. The results of the reinforced columns, beams, and walls were obtained by splitting the column into parts. The column has a seismic resistance value that is increased by 5.54 times, and the walls have a seismic resistance value increased by 2.1 times. The seismic resistances of the reinforced columns and reinforced walls are 81% and 19% of the whole three-story concrete building structure, respectively.
- (B)
- The reinforced building structure’s frames have a higher stiffness value, increased by 11.42 times in comparison with the original building structure. The results of the reinforced columns show a stiffness value increase of 19.69 times. Additionally, the walls’ stiffness value is increased by 3.38 times. Therefore, the results show that the reinforcement of the frames, columns, and walls increased the stiffness values with respect to the concrete building structure.
- (C)
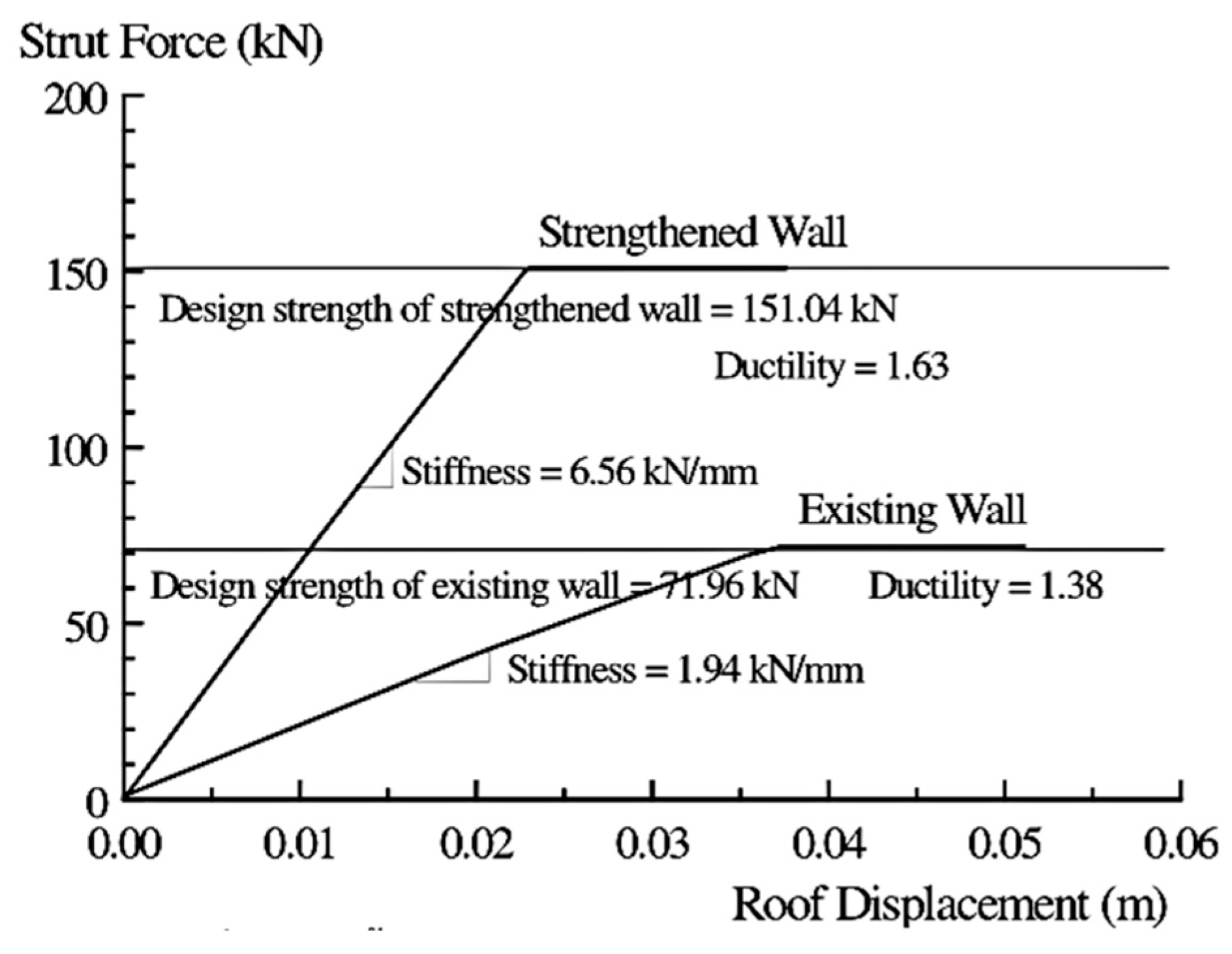
- The reinforced building structure’s frames have a ductility value of 1.73, which shows a decrease from the value of the original building structure, whose ductility value is 1.86. Furthermore, the reinforced columns’ ductility value is 1.64, a decrease from the value of the original building structure’s columns, whose ductility value is 1.89. On the contrary, the reinforced walls show an increase in their ductility value of 1.63, while the original walls’ ductility value is 1.38 times lower.
- (D)
- Reinforcement with the technique described in this paper can improve the performance of the original building structure by reducing the damage index to a safe level.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lukkunaprasit, P.; Ruangrassamee, A.; Boonyatee, T.; Chintanapakdee, C.; Jankaew, K.; Thanasisathit, N.; Chandrangsu, T. Performance of structures in the MW 6.1 mae lao earthquake in Thailand on May 5, 2014, and implications for future construction. J. Earthq. Eng. 2015, 20, 219–242. [Google Scholar] [CrossRef]
- Kazemi, M.T.; Morshed, R. Seismic shear strengthening of R/C columns with ferrocement jacket. Cem. Concr. Compos. 2005, 27, 834–842. [Google Scholar] [CrossRef]
- Leeanansaksiri, A.; Panyakapo, P.; Ruangrassme, A. Seismic capacity of masonry infilled RC frame strengthening with expanded metal ferrocement. Eng. Struct. 2018, 159, 110–127. [Google Scholar] [CrossRef]
- Longthong, S.; Panyakapo, P.; Ruangrassamee, A. Seismic Strengthening of RC Frame and Brick Infill Panel using Ferrocement and Expanded Metal. Eng. J. 2020, 24, 45–59. [Google Scholar] [CrossRef]
- Li, B.; Lam, E.S.S. Influence of interfacial characteristics on the shear bond behavior between concrete and ferrocement. Constr. Build. Mater. 2018, 176, 462–469. [Google Scholar] [CrossRef]
- Panyamul, S.; Panyakapo, P.; Ruangrassame, A. Seismic shear strengthening of reinforced concrete short columns using ferrocement with expanded metal. Eng. J. 2019, 23, 175–189. [Google Scholar] [CrossRef]
- Salinas, S.; Guzman, A.; Carrillo, J. Performance evaluation of structures with reinforced concrete columns retrofitted with steel jacketing. J. Build. Eng. 2021, 33, 101510. [Google Scholar] [CrossRef]
- Panyakapo, P. Seismic analysis of RC frame with brick infill panel strengthened by steel cage and expanded metal. Eng. J. 2021, 25, 29–44. [Google Scholar] [CrossRef]
- Amornpunyapat, R.; Panyakapo, P.; Panyakapo, M. Development of Lightweight Concrete Interlocking Block Panel with Water Treatment Sludge and Expanded Metal Ferrocement. Eng. J. 2021, 25, 81–97. [Google Scholar]
- Saneinejad, A.; Hobbs, B. Inelastic design of infilled frames. J. Struct. Eng. ASCE 1995, 6682, 560–634. [Google Scholar] [CrossRef]
- DPT. 1301/1302-61; Building Design Standards for Seismic Resistance. Department of Public Works and Town & Country Planning: Bangkok, Thailand, 2018.
- Carr, A.J. RUAUMOKO Computer Program; University of Canterbury: Christchurch, New Zealand, 2006. [Google Scholar]
- Saiidi, M.; Sozen, M.A. Simple and Complex Models for Nonlinear Seismic Response of Reinforced Concrete Structures; Report UILU–ENG-79-2031; Department of Civil Engineering, University of Illinois: Urbana, IL, USA, 1979. [Google Scholar]
- Stewart, W.G. The Seismic Design of Plywood Sheathed Shear Walls. Ph.D. Thesis, Department of Civil Engineering, University of Canterbury, Christchurch, New Zealand, 1987. [Google Scholar]
- Park, Y.J.; Ang, A.H. Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. ASCE 1985, 111, 722–739. [Google Scholar] [CrossRef]


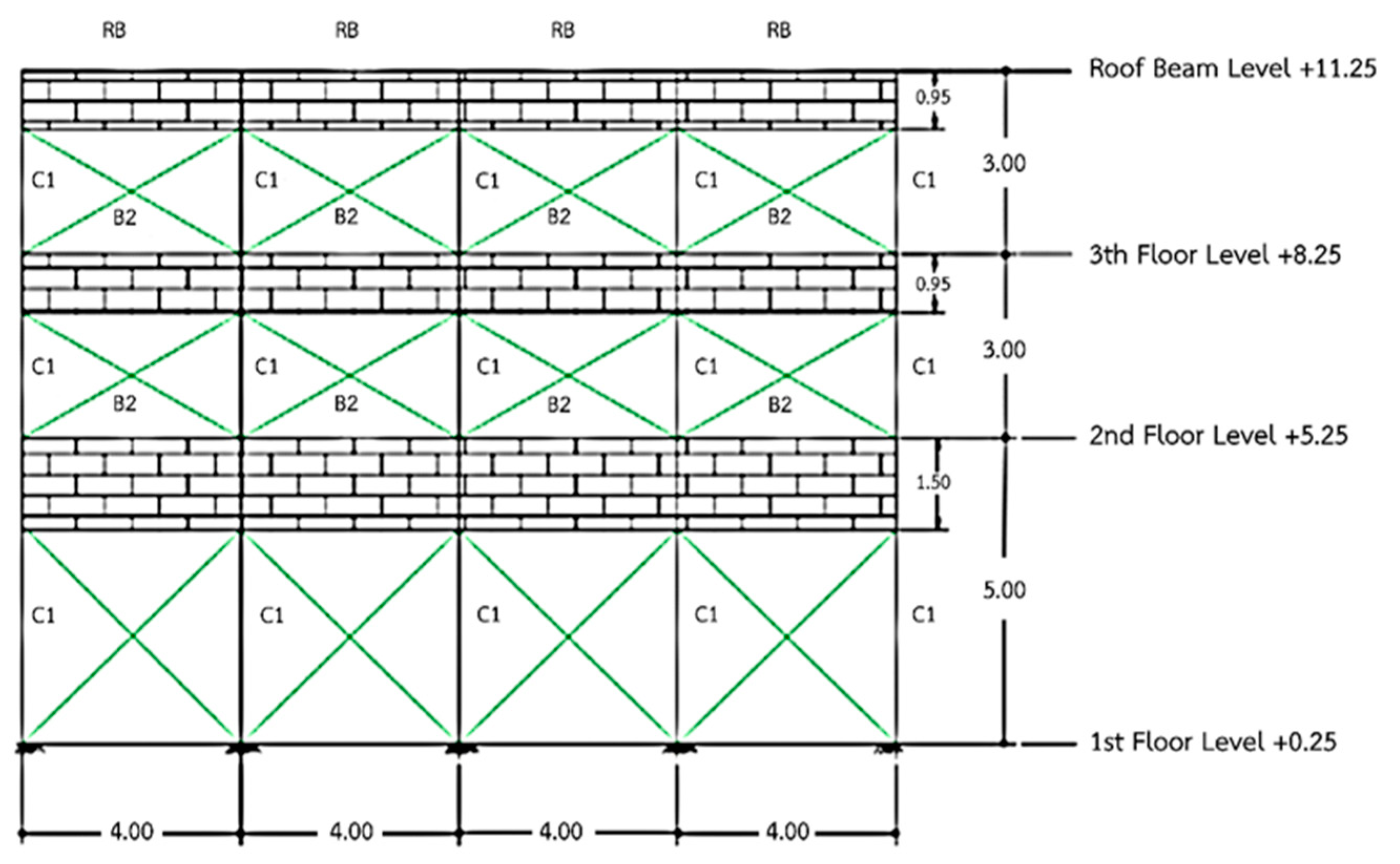



| Building | Size (mm.) | Main Reinforcement (mm.) | Stirrup Reinforcement (mm.) |
|---|---|---|---|
| C1 | 200 × 200 | 4DB16 | RB6@150 |
| B2 | 200 × 400 | 5DB16 | RB6@150 |
| RB | 200 × 400 | 4RB16 | RB6@150 |
| Parameter | Original Column | Reinforced Column |
|---|---|---|
| 30.05 | 30.05 | |
| - | 475.61 | |
| - | 505.66 | |
| 23.65 | 23.65 | |
| 11.19 | 110.27 |
| Parameter | Original Wall | Reinforced Wall |
|---|---|---|
| 0.085 | 0.1176 | |
| 89.81 | 124.26 | |
| 17.99 | 37.76 | |
| 22.38 | 220.54 | |
| 40.37 | 258.30 | |
| 127.91 | 702.39 |
| Structure | (s) | (g.) | (mm) | (mm) | |||
|---|---|---|---|---|---|---|---|
| Original | 1.3 | 1.03 | 1.01 | 1.04 | 0.32 | 114 | 137 |
| Reinforce | 1.3 | 1.25 | 1.03 | 0.36 | 0.94 | 39.9 | 48 |
| Structures | Stiffness (kN/mm) | Seismic Resistance (kN) | Ductility |
|---|---|---|---|
| The original frame | 2.29 | 127.91 | 1.86 |
| The reinforced frame | 26.15 | 702.35 | 1.73 |
| The original column | 1.07 | 55.95 | 1.89 |
| The reinforced column | 21.07 | 551.35 | 1.64 |
| The original wall | 1.94 | 71.96 | 1.38 |
| The reinforced wall | 6.56 | 151.04 | 1.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chonratana, Y.; Chatpattananan, V. The Seismic Resistance Analysis of Frame Structures and Wall Structures Using Ferrocement and Expanded Metal. Appl. Sci. 2023, 13, 4704. https://doi.org/10.3390/app13084704
Chonratana Y, Chatpattananan V. The Seismic Resistance Analysis of Frame Structures and Wall Structures Using Ferrocement and Expanded Metal. Applied Sciences. 2023; 13(8):4704. https://doi.org/10.3390/app13084704
Chicago/Turabian StyleChonratana, Yossakorn, and Vuttichai Chatpattananan. 2023. "The Seismic Resistance Analysis of Frame Structures and Wall Structures Using Ferrocement and Expanded Metal" Applied Sciences 13, no. 8: 4704. https://doi.org/10.3390/app13084704
APA StyleChonratana, Y., & Chatpattananan, V. (2023). The Seismic Resistance Analysis of Frame Structures and Wall Structures Using Ferrocement and Expanded Metal. Applied Sciences, 13(8), 4704. https://doi.org/10.3390/app13084704