Artificial Neural Networks for Navigation Systems: A Review of Recent Research

Abstract

Several machine learning (ML) methodologies are gaining popularity as artificial intelligence (AI) becomes increasingly prevalent. An artificial neural network (ANN) may be used as a “black-box” modeling strategy without the need for a detailed system physical model. It is more reasonable to solely use the input and output data to explain the system’s actions. ANNs have been extensively researched, as artificial intelligence has progressed to enhance navigation performance. In some circumstances, the Global Navigation Satellite System (GNSS) can offer consistent and dependable navigational options. A key advancement in contemporary navigation is the fusion of the GNSS and inertial navigation system (INS). Numerous strategies have been put out recently to increase the accuracy for jamming, GNSS-prohibited environments, the integration of GNSS/INS or other technologies by means of a Kalman filter as well as to solve the signal blockage issue in metropolitan areas. A neural-network-based fusion approach is suggested to address GNSS outages. The overview, inquiry, observation, and performance evaluation of the present integrated navigation systems are the primary objectives of the review. The important findings in ANN research for use in navigation systems are reviewed. Reviews of numerous studies that have been conducted to investigate, simulate, and integrate navigation systems in order to produce accurate and dependable navigation solutions are offered.

1. Introduction

Dead reckoning and position fixing are the two basic strategies of positioning classifications used in navigation. The inertial navigation system (INS) and the Global Positioning System (GPS), which is comprised of the Global Navigation Satellite System (GNSS), are the two most prevalent examples, respectively [1,2]. Over the past few decades, GPS and INS have been effectively integrated for real-world applications. Each does, however, have unique traits and limitations. A thorough examination of the existing literature on navigation systems is necessary because a significant amount of research has been conducted in the field of positioning systems. For instance, the GNSS navigation system offers accurate and semi-permanent position and speed data. Reduced accessibility and instability come from the threat to signal shadowing and multipath effects. A self-contained system that measures a vehicle’s linear and angular acceleration could serve as the guidance system. The drawback of INS is its drift error, which will continue to grow over time. As a result, the shortcomings of each technique are solved by the combination of the two systems.

GNSS is the most widely used approach in the disciplines of aviation, automatic craft technique and landing, land vehicle navigation and tracking, marine applications, and evaluation, among others. It is a navigational system that uses satellites to provide three-dimensional position and speed information. Despite being widely used, GNSS still must be able to provide consistent and accurate navigational solutions in some situations. The GNSS outage may occur whenever the vehicle travels through urban areas, tunnels, or enclosed spaces because the satellite signal is blocked. INS’s navigational accuracy decreases with time unless it is intermittently tagged by various sensors. Because of the inherent complementary operational characteristics of GNSS and INS systems, the combination of each method has provided the best possible resolution throughout the past decades. Furthermore, the combination of INS and an external navigation system, such as GNSS, could be a state-of-art technique for several application eventualities. In the integrated GNSS/INS navigation system, the GNSS resolution incorporates a consistent and semi-permanent stable accuracy that is employed to update the INS resolution. Furthermore, the INS settlement is subjected to bridging GNSS blackouts once a satellite signal is blocked. The GNSS/INS navigation system is becoming more and more fashionable because it offers consistent, accurate, and reliable navigation resolution. As long as the GNSS signals are usable, this navigation system calculates, estimates, and models the INS inaccuracy. As a result, it simultaneously provides accurate and fast navigation parameters.

For autonomous underwater vehicle (AUV) navigation, a navigation-grade INS in conjunction with a Doppler velocity log (DVL) is frequently employed. The precision of integrated navigation depends critically on whether or not the DVL can generate constant rate readings. Given the actual underwater working environment of AUVs, the DVL’s calculated value is subjected to outliers and even disruption. The well-trained network can forecast the velocity after the DVL fails, which can then be used for navigation in the future. Its benefit is that it enables time-varying noise adaptation and lessens outlier interference with the integrated navigation system. Figure 1 shows the different architectures for integrated navigation systems. The different methods of filtering approaches are the Kalman filter (KF), the extended Kalman filter (EKF), the unscented Kalman filter (UKF), the cubature Kalman filter (CKF), and the sequential Monte Carlo (SMC) approaches, among which the particle filter (PF) is the most well-known. The most fundamental and extensively used data fusion procedures in integrated navigation systems are KFs and their derivatives. The KF is an ideal estimate algorithm for Gaussian and linear approximations with the requirements of precise the system model and previous updated noise. Regrettably, the precision and robustness of conventional KFs are decreased by mistakes when modeling systems and the uncertainty of operating situations.

Figure 1. Example of integrated navigation systems: (a) GNSS/INS for air and land applications; (b) INS/DVL for underwater applications.

An adaptive Kalman filter (AKF) [3,4,5,6,7,8,9,10,11,12] can be used as the noise-adaptive filter for adjusting the noisy covariance matrices to satisfy the filter optimality criteria. The correlation- and covariance-matching techniques have made use of technological animations to predict the noise covariance. Making the inherent value of the covariance of the retained complies with its theoretical result is the fundamental tenet of the covariance-matching technique. To correct noisy estimates, the innovation-based estimation (IAE) [3,4,5,6,7,8] method has become quite effective. It combines fuzzy logic methodologies with membership functions created using the heuristic method. In contrast to sampling, the variational Bayesian (VB) [9,10,11,12] has been developed for a variety of models to achieve approximate posterior inference at a minimal computational cost.

Artificial neural networks (ANN) or neural networks (NN) [13] are built of straightforward components that work together. The quality and productivity of the NN enable it to estimate undetermined nonlinear input–output mapping. Due to the absence of estimators in the system model—i.e., it lacks the need for a mathematical model—NNs have been used to solve a wide range of issues. The NN has two unique characteristics: it can be generalized due to its nonlinearity, and it can be implemented in multi-input and multi-output arbitrary nonlinear mapping by altering the link weights. As a result, this makes the system’s real-time approximation more challenging. The deterministic methodology is a recognized and efficient technique for latency mitigation. Additionally, the NN’s widespread approximation property allows it to be used for the characterization of nonlinear systems. Like in nature, interconnections amongst constituents play a major role in networks’ function. The biological nervous system inspires these elements. By contrasting the outcome of an NN with the perceived target, an NN learns to fit the relationship. By changing the values of the connections (weights) between elements, an NN can be trained to carry out a certain task so that a different input leads to a particular target. Until the output of the network matches the target, the NN is changed based on a comparison between the output and the target. After that, it modifies the weight value until the error reaches the required accuracy.

The INS system can deliver precise navigational data quickly, and its accuracy will rapidly deteriorate over time. Therefore, it has been suggested that GNSS and INS be integrated to address their limitations. However, during GNSS process failures, the system will switch to a completely INS system navigation mode, and the effectiveness will be massively degraded. The features of the GNSS/INS integrated navigation system components in the situation of GNSS failures have been improved by using a variety of methods that have been presented to identify the GNSS signal outages. The addition of additional sensors to supply fresh reference data from other sources for the integrated navigation system, for which the odometer and maps are one remedy during GNSS failure. However, the price and size of the navigation system will rise correspondingly. Cornering, GNSS denial situations, the integration of employing KF, and several methods are also utilized to increase the perfection of GPS locations and to get over signal blockage in metropolitan areas. Neural networks are a popular choice for representing dynamic and complex processes since they have the potential to learn. To remove their influence from the estimation process, errors and noise are typically estimated using neural networks. In the event of a GPS signal failure, these strategies significantly improve GPS/INS integration. However, the localization systems are significantly impacted by severe multipath settings or prolonged non-line-of-sight (NLOS), and no improvement from its prior methodologies is realized. Although a few interesting implementations in complex visual detection and reduced AI computation have resulted from this research, a relatively intelligent mechanism has yet to be produced [14,15,16,17].

The rest of this manuscript is structured as follows: A overview of the application of neural networks in GPS is given in Section 2. The navigation incorporation utilizing state estimation approaches is introduced in Section 3. In Section 4, the development of the study on the neural network-enhanced navigation integration is covered. Section 5 outlines potential difficulties in the future. Conclusions are given in the final part.

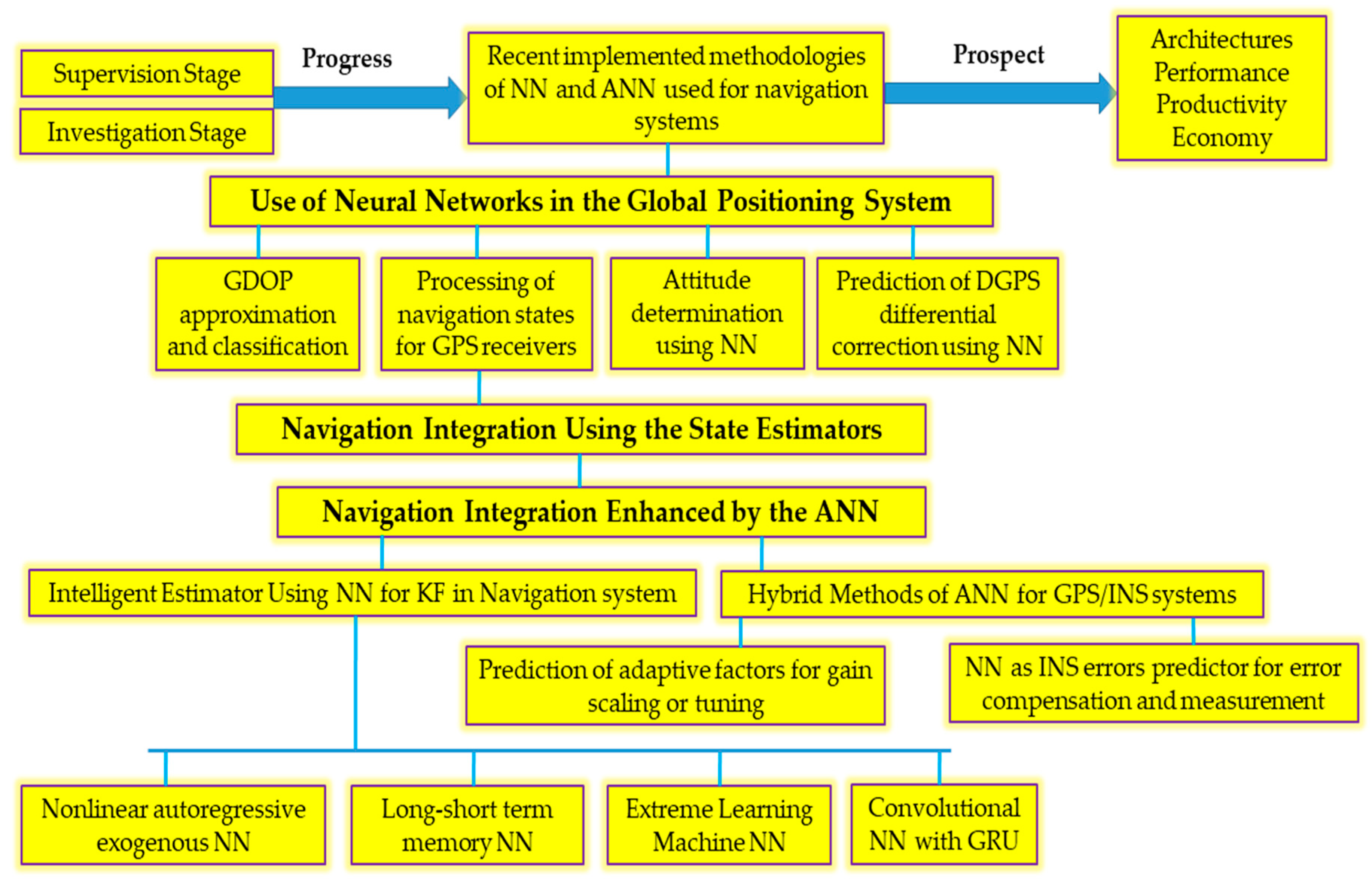
2. The Use of Neural Networks in the Global Positioning System

Machine learning (ML) enables artificial intelligence (AI) systems to learn from data. It is effective for nonlinear systems and is not reliant on the system’s mathematical model. The application overview of the ANN and NN in the navigation system has been subbmerized in Figure 2. The geometric dilution of precision (GDOP) approximation [13,14,15,16,17,18,19,20,21,22,23,24,25,26], GPS navigation processing [27,28,29], attitude determination using NNs [30], and prediction of differential DGPS correction message using NNs [31] are reviewed. It is a feature whose approaches—based on AI—may not ask for numerical methods of the system dynamics and observations, which is a key distinction between them and other forms of estimating methods. Figure 3 provides the overview of the NN training principle to approximate an unknown system model.

Figure 2. The outflow of ANN and NN in navigation system.

Figure 3. Overview of NN training principle.

2.1. GDOP Approximation and Classification

The most popular technique for training a multilayer feed-forward ANN; Figure 4 illustrates the back-propagation neural network (BPNN). In terms of the input, hidden, and output layers combined, it is simple to realize and performs exceptionally well. The BPNN has been the most widely used among all neural applications, although it is also acknowledged to have several limitations, such as slow learning. An NN may contain multiple layers. A bias vector, an output vector, and a weight matrix are present in each layer. A multi-layer network has multiple layers, each with a distinct function. To minimize the mean square error (MSE), the training algorithm influences the system parameters. As system results, the desired outcomes are useful.

Figure 4. The structure of a typical feed-forward neural network.

One can change the learning rates to decrease the training time, which will improve the BPNN. The paper’s major goal is to assess the mapping performance among four different network designs for approximating the GDOP function rather than to provide superior BPNN techniques. As a result, only the basic backpropagation algorithm is used. Additionally, the outcomes of the study can be used for other tasks, such as figuring out the eigenvalues of a matrix. Approximation and categorization of the GDOP using NN have been carried out effectively. The performances have been investigated and spoken about in [20]. Four types of NN classifiers—BPNN, OI Net, PNN, and general regression neural network (GRNN)—as well as two types of NN approximators—BPNN and GRNN, as shown in Figure 5—were studied. The BPNN has undoubtedly been the most widely used neural network across all applications, but it is also well known to have several flaws, particularly in slow learning. As a result, choosing the NNs requires balancing the needs of the user.

Figure 5. General GRNN architecture.

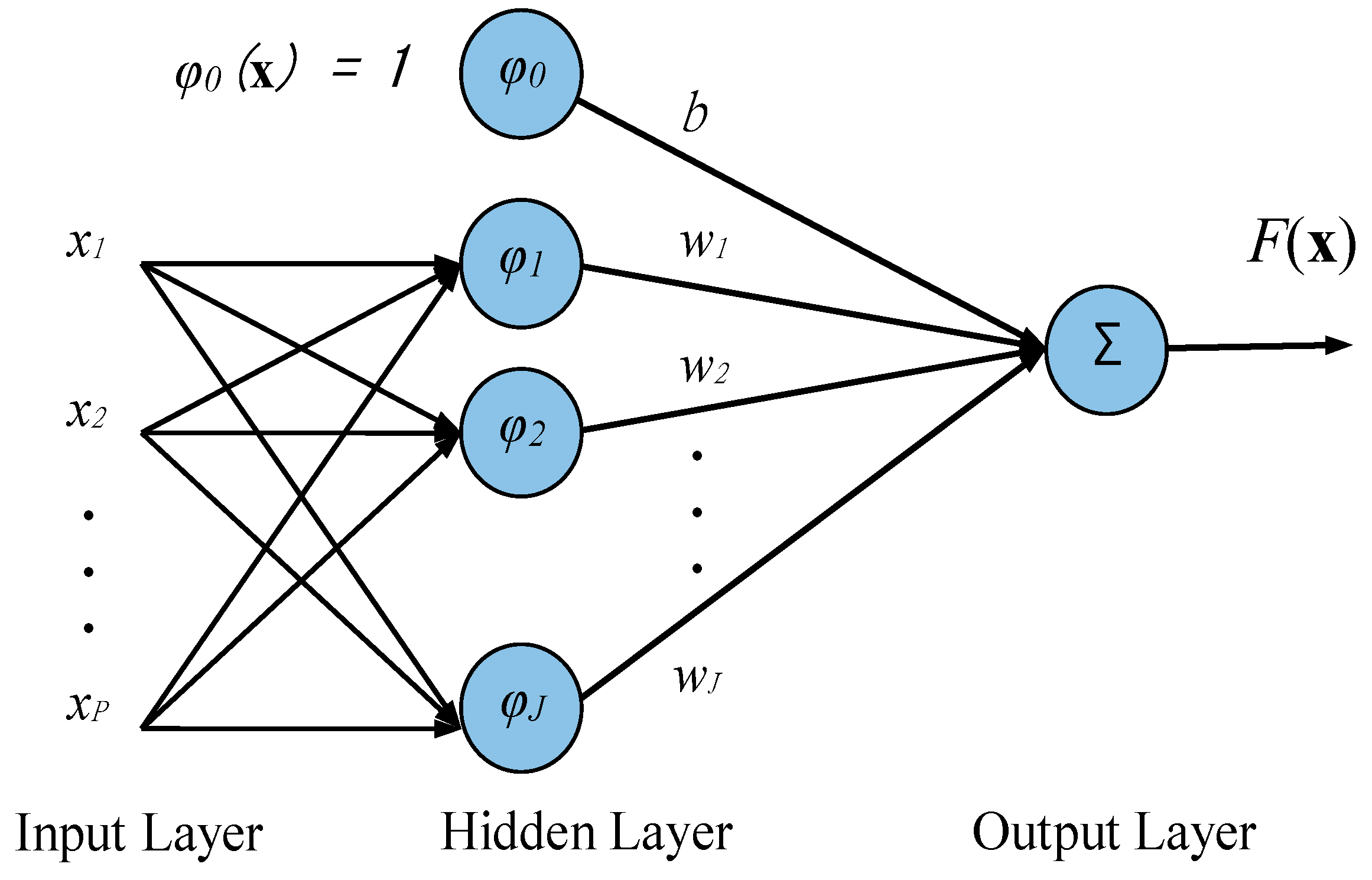
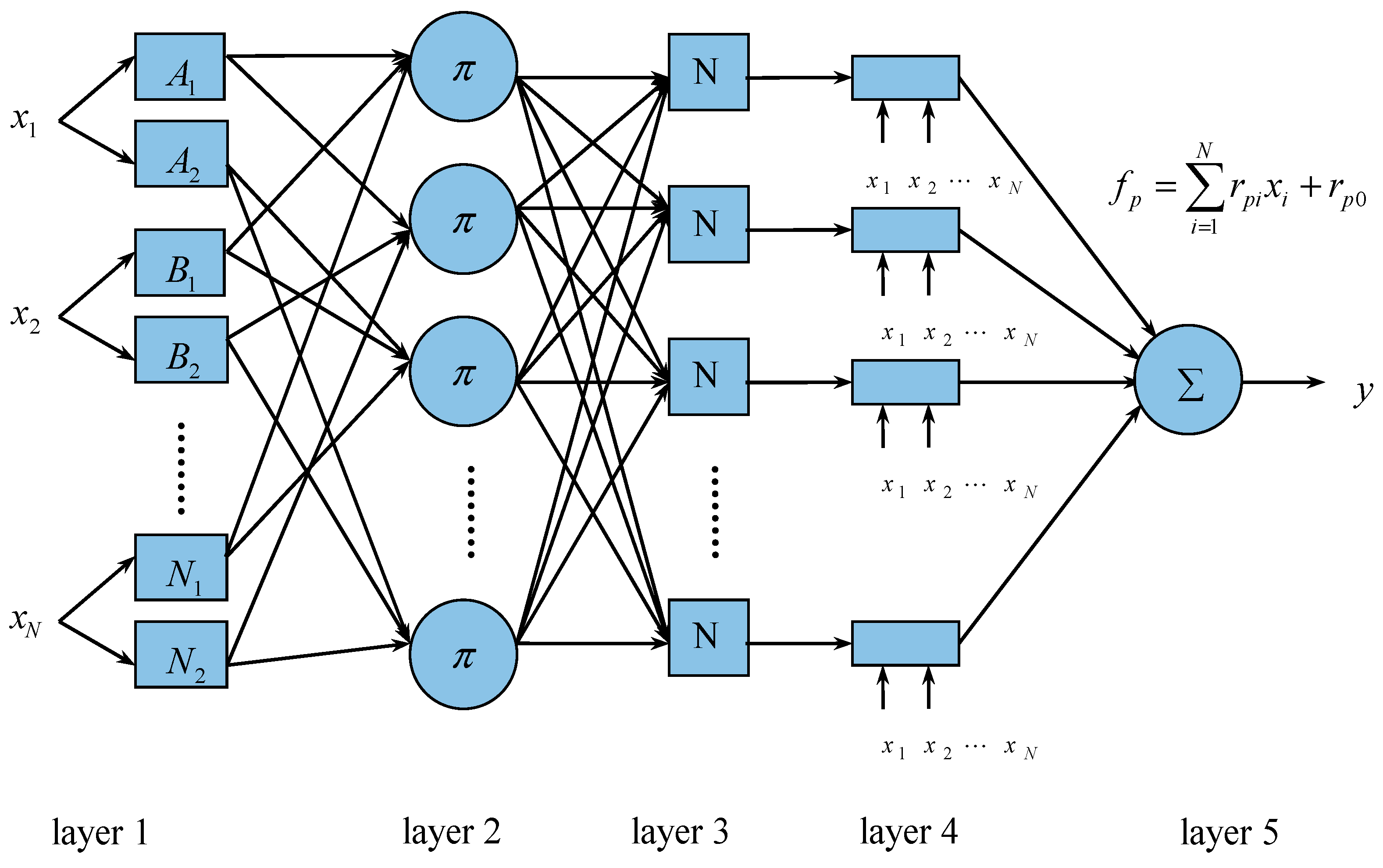
2.2. Processing for Navigation States for GPS Receivers

Blind signal separation, picture registration, and blind deconvolution are just a few examples of situations for which neural networks have been proposed as nonlinear filters. The receiver’s position and clock bias solutions are obtained from four or more GPS pseudorange measurements. One of the widely used methods aims at linearizing the equations and solving them with the least squares (LS) method based on an iteration technique. However, a digital computer frequently needs to adhere to the necessary computation time for real-time applications, where the solution can be acquired within a hundred nanoseconds. The continuous inversion of the matrix, which is typically necessary for finding LS solutions and GDOP computations in classic GPS receivers, is mostly carried out by the circuits of basic analog processors resembling neurons. Finally, the suggested system’s features and performance will be evaluated and contrasted with those offered by the traditional approach, which involves a digital computer in the matrix inversion process.

Nonlinear quadratic equations are used to solve for the location and bias of the receiver’s clock using multiple GPS pseudorange readings. Three-layer neural networks were used by Chansarkar [23] to offer a novel method for resolving the GPS pseudorange equations. In contrast to the linear least squares or EKF techniques used in conventional GPS receivers, the three-layer radial basis function (RBF) neural network in Figure 6 was created to solve the nonlinear GPS pseudorange equations directly. Chansarkar’s simulations exhibit consistent behavior even in poor geometry situations, in contrast to the conventional recursive least squares and EKF techniques, which are very sensitive to measurement mistakes. Input, hidden, and output layers make up the three-layer structure of an RBFNN. In addition, the neural network solution exhibits somewhat better noise performance under favorable geometry conditions than the anticipated iteration of the conventional least-squares solution. To assess the effectiveness of the trained neural network, computations with interrelated noisy models and additive white Gaussian noise have been analyzed.

Figure 6. Architecture of an RBFNN.

One common method aims to linearize the variables and use a recursive gradient-based LS technique to solve those. A digital computer frequently falls short of the required computation time for real-world implications—finding the answer is required in less than 100 nanoseconds, or its utilization is quite more costly. The conceptualization of two standard differential equation approaches and related circuits of analog processors that resemble neurons was used in [31,32] for the processing of GPS navigation. The study covers various ordinary differential equation formulation approaches and accompanying circuits of neuron-like analog processors. On the basis of the mean square error minimization criterion, a structure with a linear system of equations is solved and is frequently employed to determine positioning solutions. In GPS receivers, the circuits of basic neuron-like analog processors are primarily used. Second, computer simulation studies on single epoch and dynamic positioning were performed to confirm the effectiveness of the suggested strategy. Because it reduces the mean squared error of the observation, the LS estimation scheme may not be the ideal strategy when outliers are a concern. The L₁ and L_∞ criteria’s effectiveness in terms of outlier tolerance and GPS location are discussed in this research. For the purpose of GPS navigation processing, three ordinary differential equation derivation approaches and accompanying circuits of neuron-like analog L₁ (least-absolute), L_∞ (minimax), and L₂ (least-squares) architectures will be used. Finally, using computer simulation to base tests on a single epoch and execute kinematic positioning, researchers looked at how well the least absolute and minimax approaches fared in terms of outlier resistance when compared to the least squares method.

2.3. Attitude Determination Using NN

Jwo [30] has implemented the GPS as an interferometer for free posture estimation and carrier phase correlations. In computational methods, basic vectors are calculated by using the least square or Kalman filtering technique. However, if the baseline vector keys are produced using the least squares method, the actual posture results are intrinsically noisy. The KF makes an effort to reduce the estimation errors’ error variance. Although it necessitates a comprehensive previous recognition from the measurement noise and process noise covariance matrices, it will yield the best results. The KF will be replaced by a neural network state estimator that will be used in the attitude determination mechanism to estimate the attitude angles from noisy raw attitude solutions. When there is statistical knowledge uncertainty, using the neural network estimator instead of the Kalman filtering approach increases robustness.

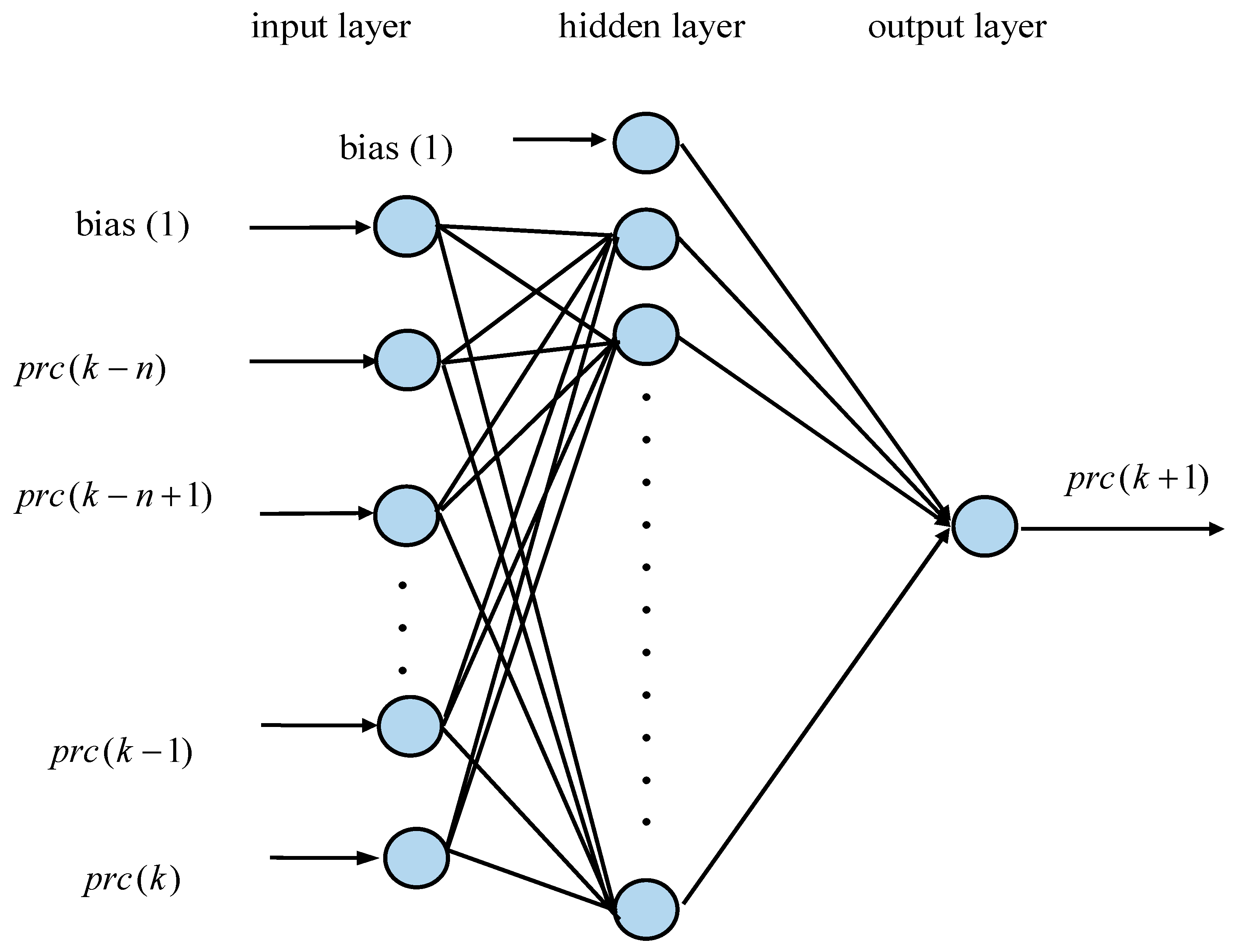
2.4. Prediction of DGPS Differential Correction Using NN

The autoregressive moving average (ARMA) neural network as shown in Figure 7 was proposed by Jwo [33] to predict data from DGPS pseudorange correction (PRC) message. The current work fits the profile of errors that are primarily controlled by ionospheric and tropospheric delays even without SA degradation. The ARMA NNs projected that PRC would give correction data with a large accuracy improvement when the PRC signal was temporarily lost. To construct the desired output of the PRC if the signals are lost, the stock market prediction methodology has been used in the NN input–output mapping architecture. The BPNN and GRNN types of ARMA NNs have both been used. The key advantage of employing GRNN during the training phase is the speed of computation. Results from the GRNN and BPNN are extremely similar in terms of accuracy. When the DGPS signals are temporarily absent, the accuracy of the system has greatly increased thanks to the inclusion of the ARMA NN mechanism.

Figure 7. Architecture of the ARMA neural network using the BPNN.

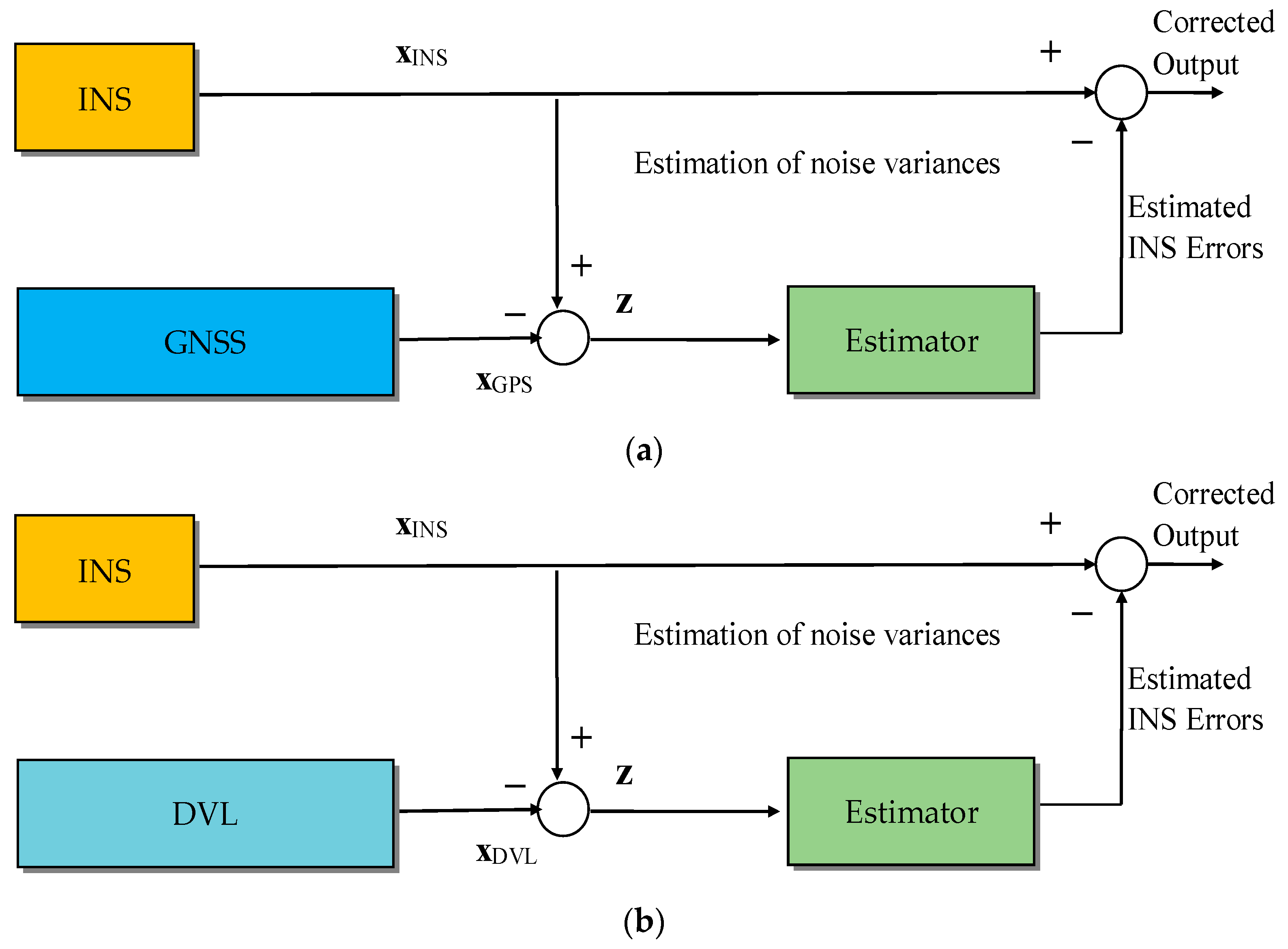
3. Navigation Integration Using the State Estimators

Navigation integration is typically carried out through the KF to estimate the system state variables and suppress the measurement noise. Different Bayesian filtering techniques, including the KF, EKF, UKF [34,35,36], CKF [37], and particle filter (PF) [36,38] techniques, are typically used in the data fusion algorithms of the INS/GPS-integrated navigation system to calibrate the navigation estimation error. In linear systems with white Gaussian noise, it is generally accepted that the KF makes use of the minimum mean square error (MMSE) as the best criterion. On the other hand, if the system’s dynamic and measurement models are accurately described, the KF leverages measurement updates to correct system state mistakes and restrict navigation solution errors. The noise statistics of the process provide the best estimates of a system’s states. Without measurement updates, the KF’s forecast diverges, and when GPS signals are not available, a combined GPS/INS navigation system’s performance may suffer quickly.

For nonlinear models, EKF employs an approximation technique to linearize the nonlinear system model. The state and observation equations are linearized using EKF using first-order Taylor reduction to enhance the conventional KF [38]. By constructing the linear differential equation, the nonlinear system is roughly approximated. It is straightforward to calculate the assessment in the Bayesian recursive formula since KF and EKF both turn the problem into a linear Gaussian model. The UKF is based on a method for mean and covariance propagation through a nonlinear mapping built using the unscented transform (UT) approach. The state vector is discretized as a minimum collection of sample points (sigma points), which approximates the second-order precision posterior mean and covariance of the random variable with a Gaussian distribution. To approximate the probability density distribution of a nonlinear function, UKF uses a set of predetermined samples. The EKF’s linearization method can only produce first-order accuracy. When the computing complexity is the same, the UKF performs better than the EKF. The aforementioned filtering algorithms for the high-dimensional process model are susceptible to a non-positive definite covariance matrix. Non-Gaussian noises, on the other hand, are commonly present in many real-world contexts and seriously degrade their functionality.

The KF, EKF, and UKF techniques have many significant flaws that prevent their application. They are unable to deal with the following two issues in particular: modeling non-Gaussian processes and observation noises and well as unidentified noise covariance matrices are the first two sources of noise. When the methods are coupled with colored noise, as is the case in several scenarios for practical implementation, the EKF cannot perform satisfactorily since the estimation outcomes are vulnerable to strong outliers and non-Gaussian noise. The CKF approximates the state mean and covariance of a nonlinear system with extra Gaussian noise using a collection of volume points based on the third-order spherical radial volume criteria. Theoretically, CKF is the approximation technique that comes closest to Bayesian filtering, and it is an effective tool for dealing with nonlinear system state estimates. For each integral point, CKF has the same weight, which is positive. Compared to UKF, CKF’s numerical stability is developing more rapidly. The resilience is decreased, and even the filter fails despite being impacted by the process model’s instability and the measured noise statics’ variability. In recent years, numerous academics have suggested enhanced CKF algorithms to address the aforementioned issues. The PF is computationally expensive for an online implementation even if it can handle the non-Gaussian, nonlinear system effectively.

The implementation of the Kalman family of filters needs a precise and logically valid statistical understanding of the process noise and measurement noise. Inadequate understanding of the noise statistics may cause filter divergence and substantially impair KF performance. Relativistic issues will arise if a filter’s theoretical operation and its real behavior do not correlate. The assumptions on the statistical database of disruption are violated in various of scenarios in which there are instabilities in the process model and noise characterization, because in many real-world scenarios, the availability of a well-defined model is unattainable because some observations are ignored in the modeling step and one approach for taking them into consideration is to consider an equivalent model influenced by uncertainty. Moreover, there are model assumptions in actual navigational applications that the continuous state-space model is unable to capture. Since the actual vehicle motions are the result of non-linear processes, the linear model contains modeling mistakes. It is necessary to predetermine the system model, the system’s beginning conditions, and the noise properties. It frequently happens that little prior knowledge of the operation is accessible.

The availability of a well-defined model is inappropriate in particular scenarios in which there are many uncertainties in the proposed system and noise interpretation. Predictions based on disruption statistics are violated due to a number of realistic applications, and some conditions are ignored in the modeling step. It is reasonable to suppose that an adaptive process will dynamically identify the system model uncertainties and modeling errors. Innovation-based adaptive estimating (IAE) and multiple-model-based adaptive estimation (MMAE), such as the interacting multiple models (IMM) [5,6,7,8] algorithm, are the two main approaches to AKFs that have been developed. The IMM algorithm has a configuration in which many model-matched state estimation filters operate in parallel and interact (exchange information) at each sampling period. By modifying the probabilities of each approach, which are utilized as weightings in the aggregate global state estimation, the algorithm performs soft switching between the various modes. The mode-conditioned forecast’s covariances as well as the variations between these estimates are taken into account in the covariance matrix linked to this combined estimate.

The noise data from the measurement sequence during the filtering process can be removed, and an IAE technique has been devised to estimate the process noise covariance Q_k and/or measurement noise covariance R_k. A bank of KFs with various parameters operates concurrently in an MMAE approach, and the weights of every sub-filter are aggressively changed in response to fresh assessments. The sub-filter with well-known parameters wins after a thorough study. The MMAE method, however, requires more resources and may not completely account for the true system model. Another drawback is that the parameter estimation method for both IAE and MMAE systems requires a sliding window over the measurement sequence, which causes inaccuracy and delay. Consequently, adaptive filters introduce more sophisticated components in integrated navigation systems. The selection in integrated navigation systems’ adaptive filters frequently uses fuzzy logic techniques. Such a selection selects the best sensors or dynamically modifies the noise covariance matrix. Target tracking may be manipulated well using interactive multiple models. Then the more accurate noise covariance matrix was estimated using the IMM technique. When used in an underwater environment, the IMM-adaptive robust cubature Kalman filter technique may successfully address the issues of measurement noise and typical statistical inaccuracy.

The technique makes use of VB learning to give a robust tracking capacity for time-varying noise covariance as well as an approximation of the noise strength. The VB approach is an inferential technique that approximates the real posterior distribution of hidden variables using a straightforward distribution, typically presuming that the disguised variables are unrelated to one another. In contrast to sampling methods, the VB has been created for a several models to perform preliminary posterior inference with a minimal computing cost. The typical filters for navigational state estimation and their improved algorithms are summarized in Table 1.

Table 1. The navigation filters and their improved algorithms.

Navigation Fusion Algorithm	Features
Linear Kalman filter algorithm	- Simple calculation and easy implementation
Nonlinear filter algorithms, including the EKF, UKF, and CKF	- Good processing capacity for nonlinear systems
Sequential Monte Carlo (SMC) approaches	- Particle filter (PF) is the well-known realization of the SMC approach
Adaptive filter algorithms	- Adapt to time-varying - Innovation-based adaptive estimating (IAE) and multiple-model-based adaptive estimation (MMAE) including the interacting multiple model (IMM) algorithm are the two main approaches. - The variational Bayesian (VB) learning algorithm analyzes the real posterior distribution of concealed parameters approximation using a straightforward distribution.
Neural-network-assisted filtering algorithm	- Simple, easy to learn, no need for systematic mathematical models - Good network predictability with real-time performance.
Deep learning improvement algorithm	- Improved accuracy - Good generalization capability.

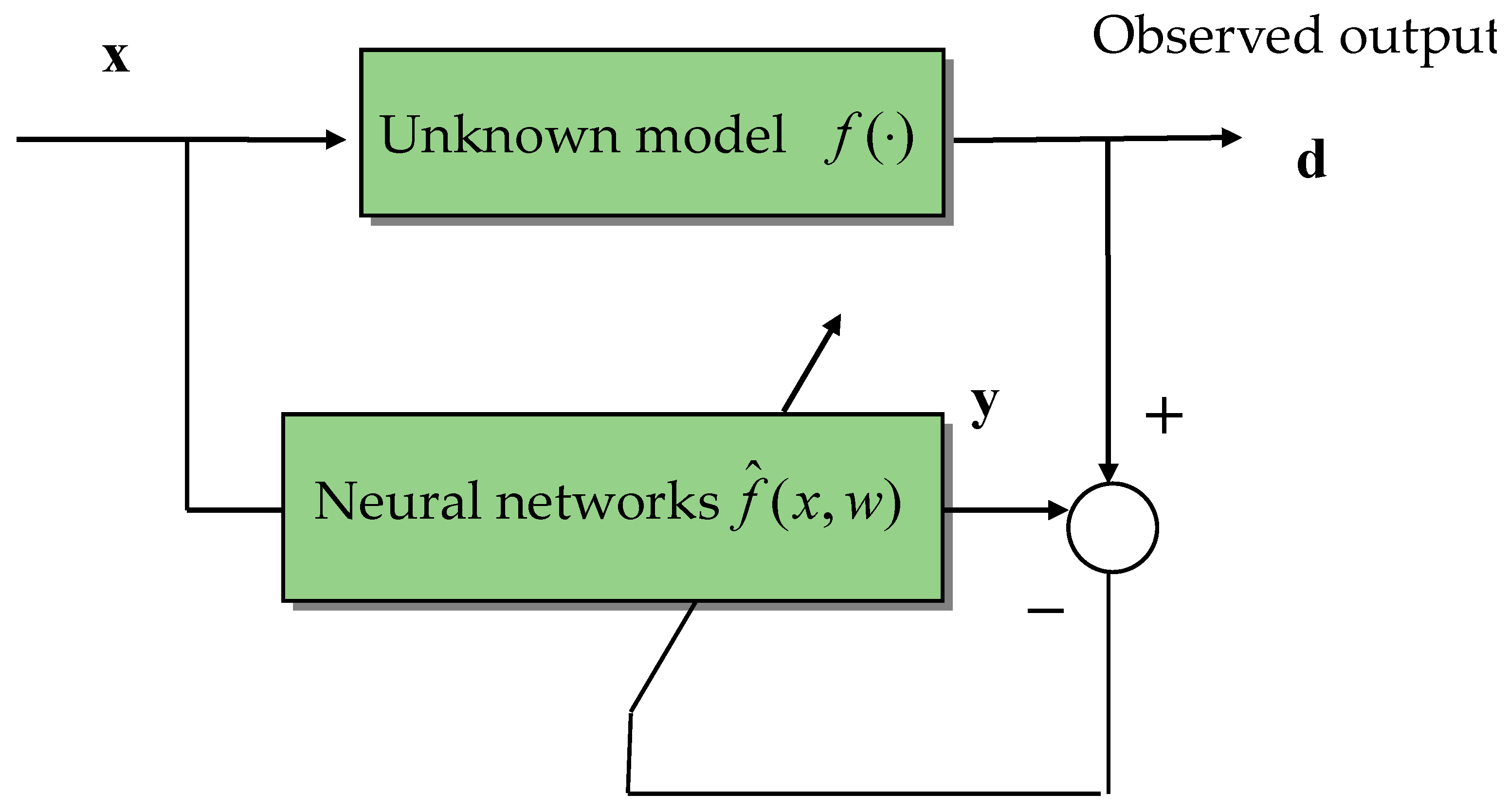
4. Navigation Integration Enhanced by the ANN

In complicated and hidden situations, inertial navigation is an essential component of vehicle navigation systems. There has been widespread use of the GNSS/INS combined system for land and air applications and DVL/INS for underwater applications. In general, the integration task makes considerable use of the EKF to obtain an accurate and consistent estimated position. In contrast, the lack of readings from the GNSS/INS EKF in the event of a GNSS signals failure, signal blockage, or jamming causes the navigation system’s accuracy to rapidly decline. To increase the integrated navigation system’s accuracy while GNSS failures, several fusion techniques have been investigated [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64]. Adding additional sensors to compensate for the lost GPS information and improve navigation accuracy is possible but comes at the cost of increased system complexity. Machine learning algorithms have become famous for mimicking the INS’s error propagation property and establishing a connection between updated vehicle dynamics and INS errors by using available GNSS signals to train the machine learning (ML) model. For the corrected INS mistakes caused by a lack of accurate measurements, such as GNSS failures, researchers have developed an error forecasting and compensating system based on artificial intelligence for GNSS/INS integration. The neural network has received considerable attention because of its useful nonlinear function estimation property and learning capacity. It has been frequently applied to integrated navigation error correction during GNSS failures. When GPS is unavailable, the neural network is used as an alternate integration mechanism to deliver superior navigational options.

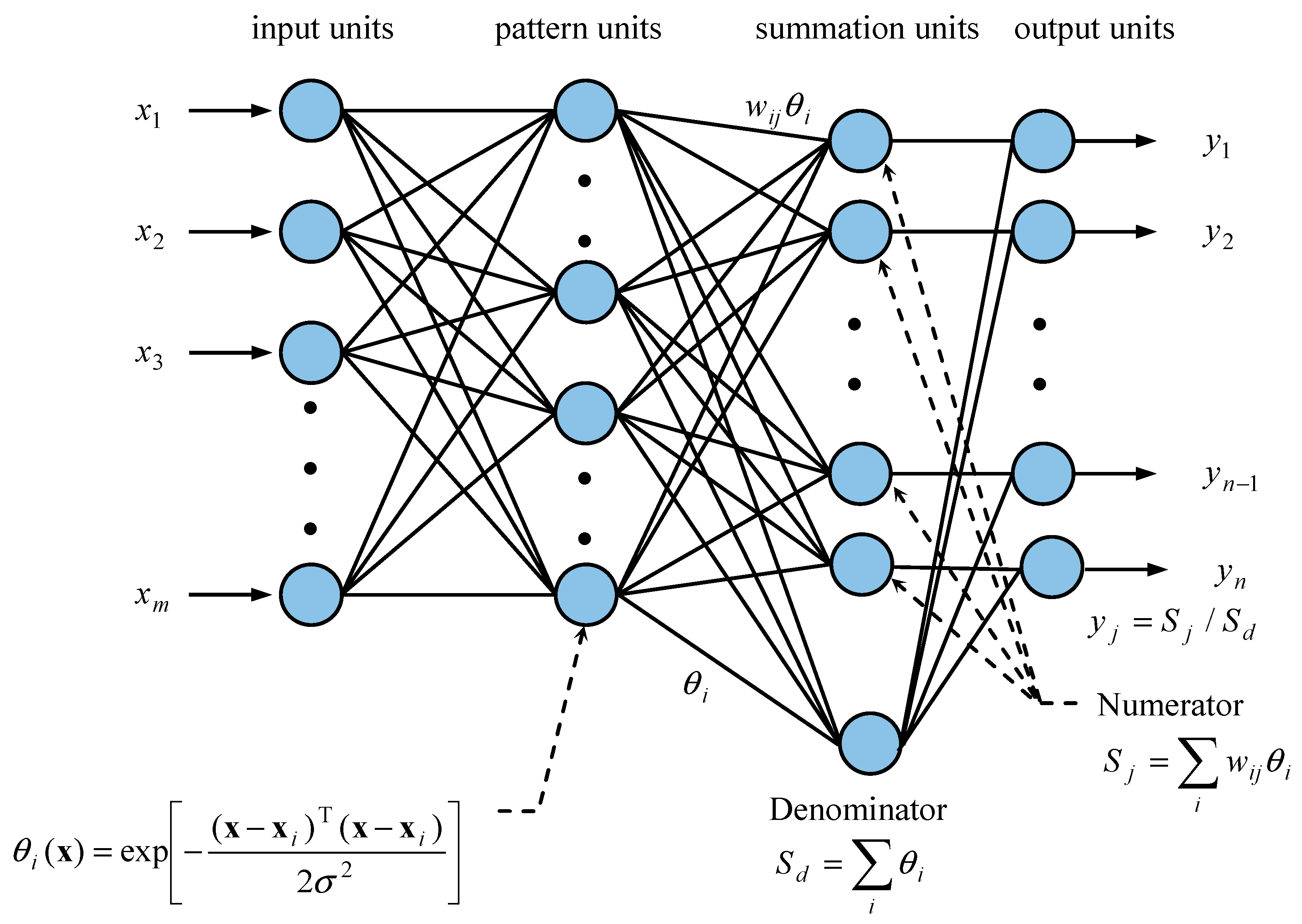
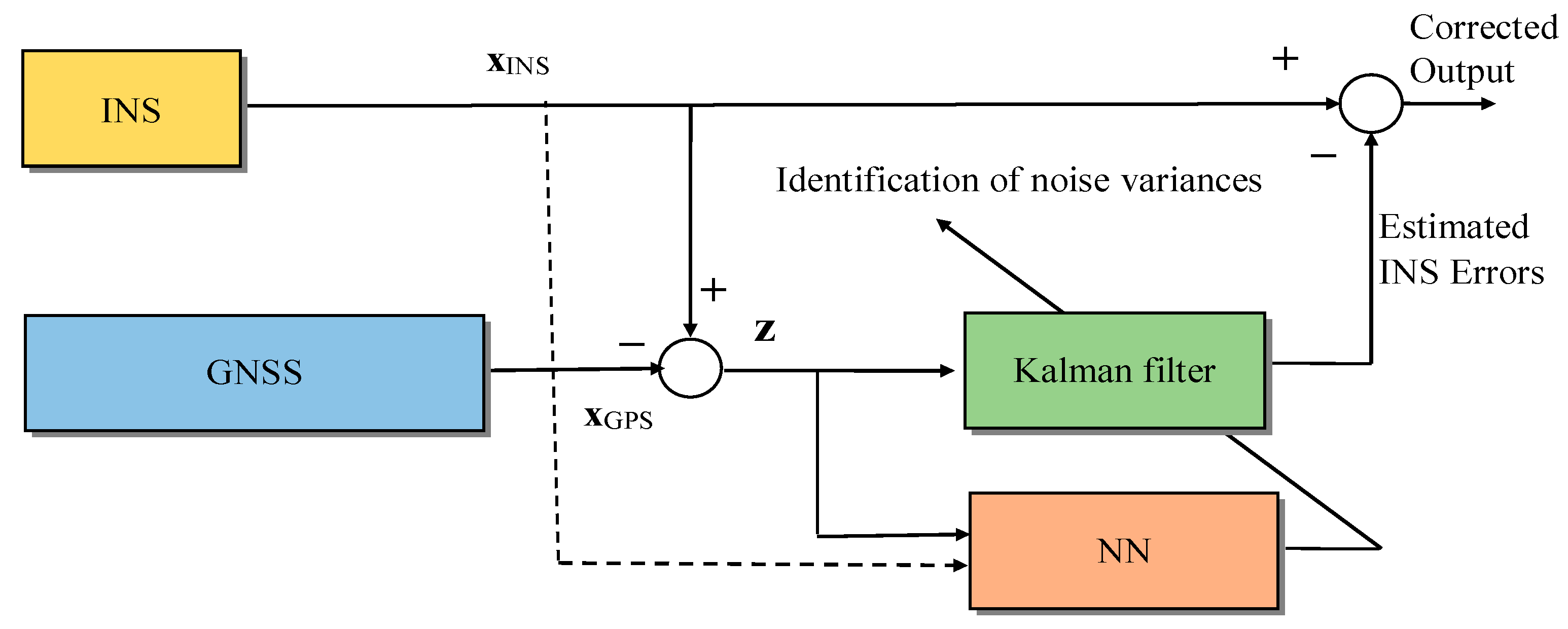
4.1. Intelligent Estimator Using an NN as a Replacement of KF for Data Fusion

The fact that it is not necessary to employ numerical methods in the simulation model and measurements with AI-based techniques is a key distinction between them and other forms of estimating methods, such as the Kalman filter. Several ANN-based approaches have been analyzed to take the place of KF as a state estimator. Instead of integrating the KF and the NN, this technique just substitutes one for the other. The main benefit of an NN over a KF is that it does not require any pre-existing statistical or mathematical models to choose a function that best maps inputs to outputs, such as the absolute location shown in Figure 8. Some methods, such as those based on multi-layer perceptron neural networks (MLPNNs) [65,66,67,68,69,70,71,72], RBFNNs [73,74,75,76,77,78,79,80,81,82,83,84], and adaptive neural fuzzy inference system (ANFIS) [85], were described for GPS/INS systems due to its capability to tackle the issue of nonlinearity. Due to their exceptional ability to model the nonlinear relationship, the aforementioned models were determined to have good performance. However, BP has drawbacks, including poor learning convergence velocity, artificial experience dependence, and a lack of accuracy.

Figure 8. Intelligent estimator using an NN as a replacement of KF for data fusion: (a) training mode; (b) predicting mode.

The fuzzy inference variables can be written as the NN weight vectors, and the FNN can be implemented as an NN framework. The “professional previous knowledge” is simple to transfer into the hazy if–then rules. With learning from the inferred data of individuals, the method can concurrently adopt the inference engine criteria and fine-tune the membership functions. The Takagi and Sugeno’s fuzzy inference-based ANFIS is a multilayer feed-forward network in which each node carries out a specific node operation on input variables. The ANFIS made of five layers has the architecture as shown in Figure 9.

Figure 9. The ANFIS architecture.

An important subset of deep learning that is frequently used for prediction is the recurrent neural network (RNN) [86,87], which can analyze the time-dependent data processing. Its output is structurally reliant on both the input at hand and the previous output. The hidden layer outputs of the RNN’s particular structure are kept in memory, which is treated as another input. The ability to link the current job with past information for the frame is the RNN’s most important benefit. In time series prediction, the state-based historical cues are well-predicted using sequence learning and RNNs. RNNs, differently from MLPs, use models in which the output is encoded into a hidden state and is a function of the inputs and outputs from the past. Unlike MLPs, RNNs can encode the information in the sequence itself and have a memory of the past outputs. This type of model can therefore be useful for learning from sequential data. However, back-propagation over time, a variation of back-propagation that takes temporality into account when computing the gradients, is typically used to train RNNs. When used for lengthy temporal sequences, this approach can cause many problems. The RNN units are made up of hidden state cells that predict events in the future by exploiting temporal signals, with better results than conventional methods. Short-term dependencies are possible with RNNs, and they can store large amounts of data about prior signals. The “vanishing gradient” is a training problem that is brought on by long-term dependencies, which the RNNs must be able to model. Figure 10 shows the block diagram for the proposed GNSS/INS integrated navigation with RNN training and prediction modes.

Figure 10. (a) Training and (b) prediction modes of GNSS/INS integrated navigation using RNN as the estimator.

In neural networks, the nodes in the buried layer are typically not connected. The hidden layer nodes in RNN, however, are connected and have both the input from the input layer and the input from the previously concealed layer as their inputs. Therefore, RNN networks are likewise realized via the time-back propagation algorithm. The “gradient disappearing phenomena” is caused by the activation function’s derivative multiplying with the input data sequence as it gets longer. This phenomenon is explained by the structure of an RNN and occurs when the input data sequence gets longer [87]. The weights are no longer updated as a result of this disappearance, which makes it challenging for the model to learn distant information. However, RNN suffers from the well-known gradient explosion and dispersion issues that lead to local extrema.

4.2. Hybrid Methods

Figure 11 demonstrates how combining KF and NN can improve GPS/INS integrated systems’ overall performances by overcoming their respective flaws. KF observations will not be updated if the GNSS signal is disrupted. When NNs support INS, navigation performance can be enhanced. To fill in the gaps left by GPS data disruptions, an NN-based fusion approach is suggested. A properly trained NN is capable of anticipating and correcting the interrupted position signal inaccuracy. Several designs were used to investigate an NN-aided adaptive EKF, including the prediction of adaptive factors for gain scaling or tuning, prediction of INS errors for error correction, and measurement reconfiguration. The hybrid methods essentially include the following three categories: (1) prediction of adaptive factors for gain scaling or tuning [57,58,59,60,61,88]; (2) an NN as the INS errors predictor for error compensation [57,59,69,78,79,80,81,82,89]; and (3) measurement reconfiguration based on an NN [76,90,91,92,93].

Figure 11. The block diagram of hybrid system for prediction of adaptive factors for gain scaling.

4.2.1. Prediction of Adaptive Factors for Gain Scaling or Tuning

It has also been extensively investigated and used to combine new artificial intelligence techniques with integrated navigation systems. The assumption is that the regression models and the adaptive data modeling are both distorted by minimal Gaussian white noise, which is essential for producing accurate estimation results. The EKF offers the best results when used as a navigation state estimator when the noise statistics for the measurement and system are completely understood. In reality, the noise changes with time, this degrades the estimation performance. A common adaptive method for estimating noise covariance matrices is the covariance matching method. The method aims at bringing the actual filter residuals into line with their covariance. However, if the window size is tiny, this innovation-based adaptive estimation produces very erratic results. A hierarchical neural network has been trained to identify the measurement noise covariance matrix in order to solve the problem. The link weights are then iteratively adjusted using the conjugate gradient method via the back-propagation algorithm.

These input–output linkages are mapped using an NN coupled with the updated KF measurement. The parameters utilized to correct KF gain are the outputs of the NN, while the inputs represent dynamic vehicle circumstances and fluctuations. These techniques typically use straightforward neural networks that must be trained in real time to fill in the necessary missing data. The innovative procedure that comes from the divergence between GPS and system state estimation provides details on measurement noise covariance R_k and process noise covariance Q_k. The limited information quality of Q_k and the link between Q_k and R_k are the two major barriers to the AKF of integrated navigation systems. Because Q_k instability can be effectively reflected in the observation sequence of the inertial measurement unit (IMU) in the SINS/GPS incorporated navigation system, Q_k can be located by identifying these patterns and looking through the basic information. The research employs artificial intelligence in a novel way to calculate inertial sensor noise.

During GNSS outages, the effectiveness of the GNSS/INS integrated navigation system would be decreased. The cost and complexity of the navigation system will rise, but this solution can produce good navigation performance. The multi-layer perceptron neural networks [66,67,68,69,70,71,72,73], radial basis function neural networks [74,75,76,77,78,79,80,81,82,83,84,85,86], and adaptive neuro-fuzzy inference systems [87] are a few examples of ANN-based techniques. Establishing an internal link between IMU/INS outputs and GPS data is the fundamental goal of ANN-based techniques. Furthermore, speed and/or attitude are utilised as inputs to improve prediction. Additionally, several previous data kinds (such as past 1-step and past 10-step data) are introduced to the inputs. Moreover, the model will become more sophisticated as a result of these additional inputs. As long as a GPS signal is present during the training phase, the system is operational. Given that there are fewer measurements in an INS than there are state parameters and that neural networks excel at approximation and at being nonlinear, adaptive, and fault-tolerant, the adaptive factor can be built using neural networks. The aforementioned techniques do not pre-filter IMU data to remove the noise from the first measurement, which will have an impact on the prediction.

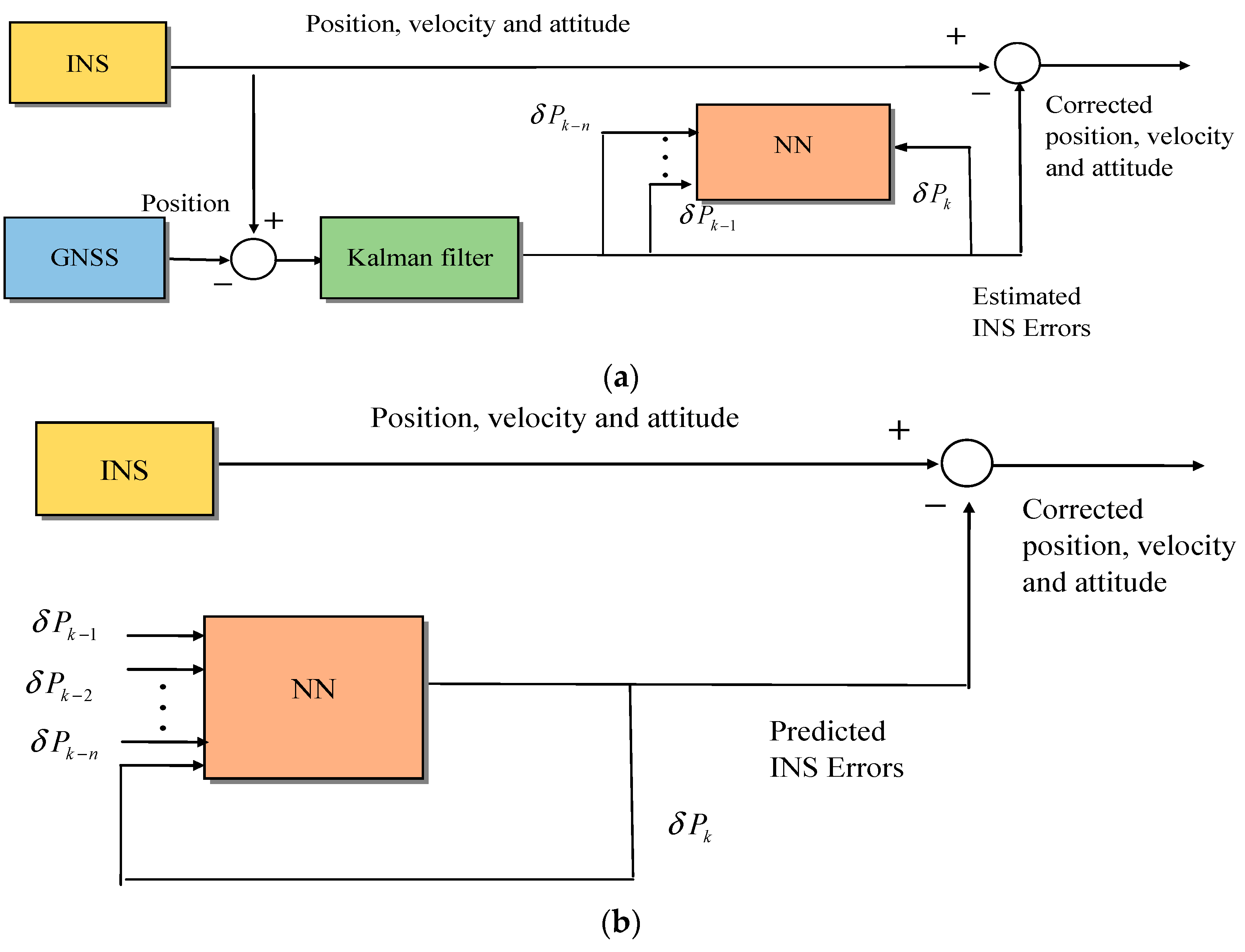
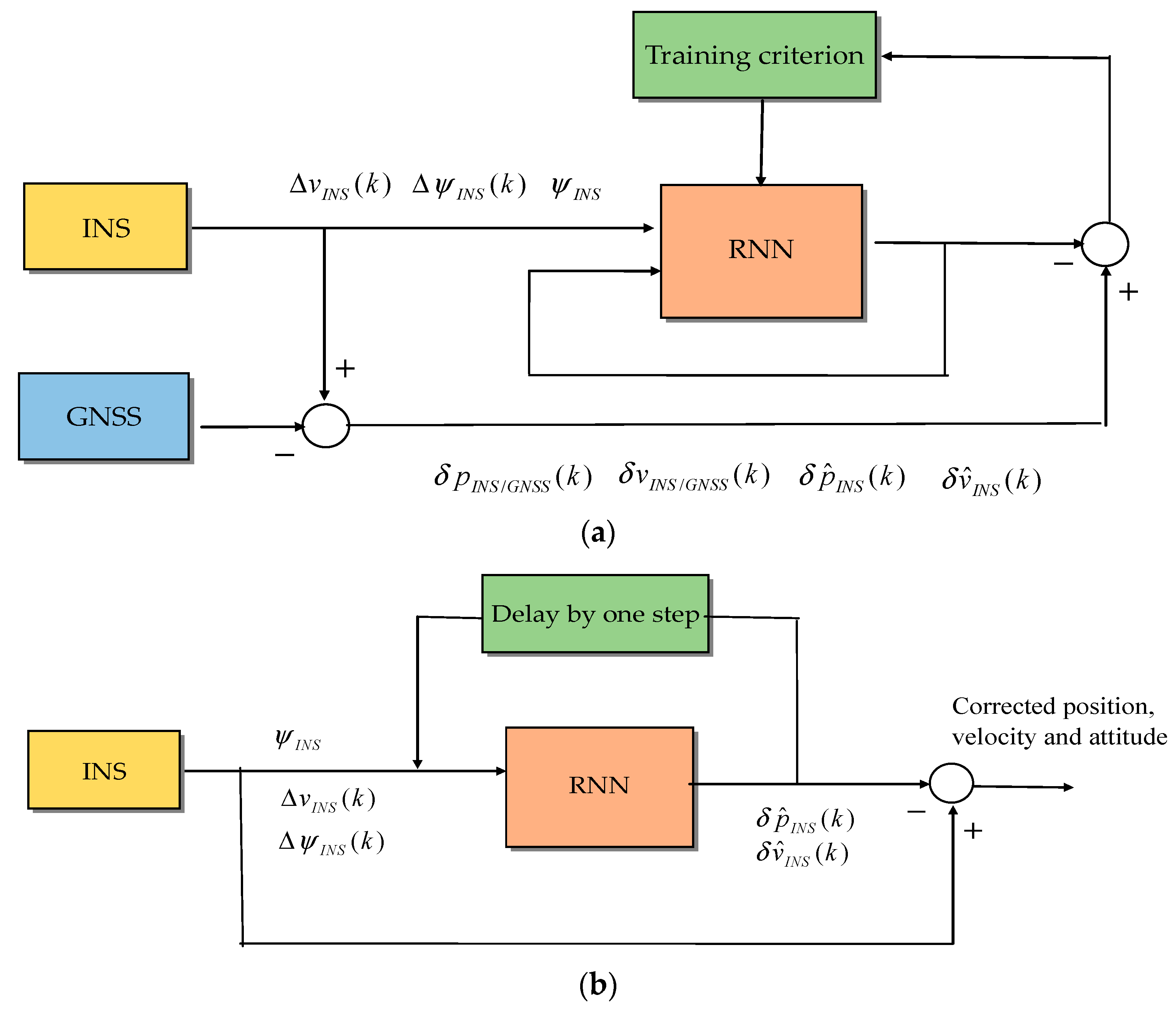
4.2.2. NN as the INS Errors Predictor for Error Compensation

There are numerous methods of enhancing the INS/GPS integrated navigation system when GPS is unavailable. The concept of mistake forecasting and compensating techniques is illustrated in Figure 12. In order to boost accuracy in the event of a GNSS signal blockage or INS failure, the NN accepts the INS position and time as inputs and outputs the position error. The biggest problem with INS is its “drift error,” which becomes worse as more travel is done. Because the IMU is a sensing free against external interference, it is feasible to develop a knowledge base regarding the relationship between motion sequences and sensor efficiency through metrics.

Figure 12. The training and prediction phases for error prediction and compensation.

If the NN is properly trained, the output keeps the EKF operating as if the GNSS were available for INS error correction. Most of the time, GNSS is accessible and can provide precise input for the ML algorithms during training and optimization. After training, the NN can be utilized to enhance the performance of the INS in urban settings and situations without GNSS. A conventional EKF is utilized in hybrid fusion techniques in addition to NNs that simulate INS or GNSS faults. To achieve high efficiency or to lessen the complexity of designs, these strategies mix estimate and intelligent procedures. The NN utilized in this method accepts the INS position and time as inputs and outputs the position error. The neural network, which was well trained while the GPS signal was present, is used to improve the INS measurements when the GPS signal is lost. In order to reduce the dependency on the INS errors, an input delay neural network (IDNN) has been developed to simulate INS position errors based on current and historical samples of INS positioning, and it performed better during GPS failures. The fundamental concept behind these neural network-based techniques for low-cost GPS and INS is to gather when GPS is accessible; INS data and KF results are used as a training dataset to train the neural network model. The outputs of the KF are then projected by a neural network to compensate for the INS inaccuracies during GPS outages.

A predictive approach is based on a linear basis function NN and an updated UKF improves the accuracy of position and velocity of the GPS/SINS-integrated navigation system, especially in the case of GPS signal outages. Additionally, to boost the dependability of the navigation system, a radial basis function NN and a nonstationary time series analysis are applied to forecast and compensate for the positional inaccuracy of the GPS/SINS incorporation in the presence of GPS signal outages. To address the low precision of vehicle inertial navigation in covert environments, ANFIS-based inertial navigation error estimation was developed. The findings imply that the ANFIS can significantly increase inertial navigation’s positioning accuracy. The error prediction by ANFIS was frequently greater at this point than the INS solution error of the multi-sequence experiment due to the modest INS solution error, and the effect was worse on the road segment with more bends. Future research should enlarge the training set of winding roads and modify the initial input values of the ANFIS model to accommodate this. When a signal is available, GPS displays its recommended outputs. The neural network then acquires accomplished navigational information by changing the synaptic weights. The learning algorithms lower the INS estimation error to achieve the best values for the system parameters as long as GPS signals are available.

In contrast to a conventional approach, a model predictive filter (MPF) is created by optimizing the network weights based on the neural network’s error correction utilizing system state variables. On the model predictive filter neural network (MPFNN) for INS error compensation, an NN learning technique is suggested to increase the positional precision of the GPS/INS combined navigation system in the absence of GPS. During GPS outages, MPFNN is used to anticipate INS inaccuracies. The MPF technique is used to correct the model error of neural networks during training to account for variations between the actual and desired output. A land vehicle navigation test was used to empirically confirm the performance of the suggested technique. According to comparison data, the suggested approach can successfully deliver extremely precise adjustments to the solo INS during GPS outages.

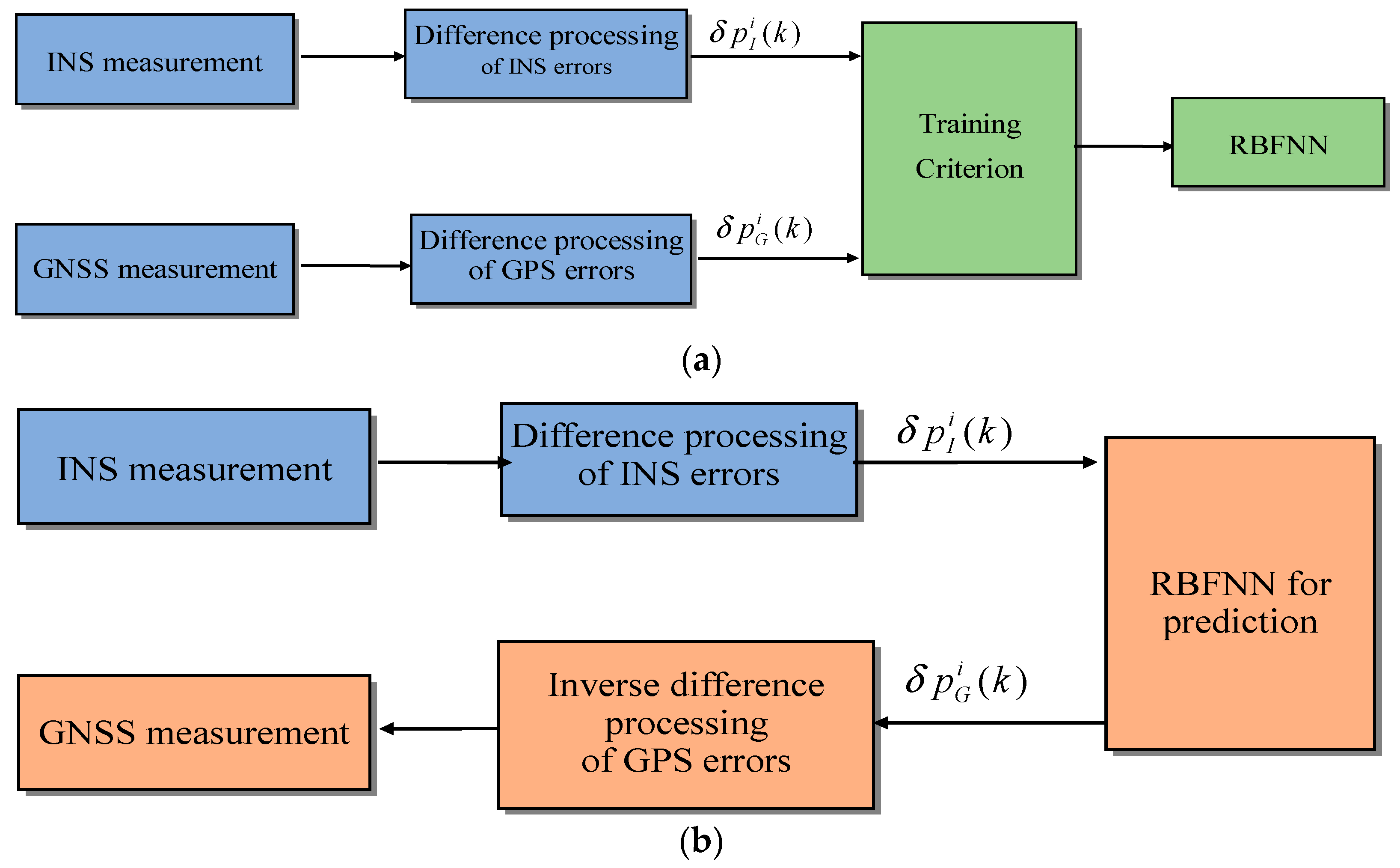
4.2.3. Measurement Reconfiguration Based on NN

A hybrid fusion technique is accepted to analyze the statistical correlation between sensor data and the GNSS positions advance during GNSS outages. During the GNSS accessibility time, KF merges the INS and GNSS data in order to gain more precise location and velocity information. When it is accessible, the GNSS is used as a reference. A framed knowledge base of the INS’s actions in specific vehicle motion outlines is created using the data from GNSS and INS. Multilayer feed-forward NNs with a back-propagation learning method were utilized in the literature to combine INS and DGPS data. Due to the presence of a GNSS and an INS, the combined navigation system offers a constant high-accuracy location. On the other hand, INS error divergence causes the navigation accuracy to unavoidably decrease during a GNSS outage. To predict the measurement of EKF during GNSS failures, the NN is directed when a GNSS signal is present.

Throughout training and optimization, GNSS is frequently accessible and can be used as a precise input for ML algorithms. After training, ML can be utilized to enhance the performance of the INS in urban settings and situations without GNSS in addition to the particular force and angular velocity produced by the inertial unit in the input. The model is simple structurally and does not fully utilize the historical data. As a result, the system’s response time will be sped up by using an extreme learning machine (ELM) NN to detect rapid GNSS signal failures and cut the detection time. To examine the effectiveness of forecasting the position increment of the GNSS system at the same time, different forms of historical data are input into the upgraded BPNN during GNSS failures. These methods’ major goal is to create a map between INS measurements and GNSS measurements, such as angles, forces, speeds, positions, and so forth. The NN is then trained using the SINS and GNSS measurements while the GNSS signals are present. A well-trained NN can provide virtual GNSS measurements after GNSS disruptions occur. INS/GPS integration algorithms based on MLPs and NNs have been proposed and applied to various types and grades of INS, intending to enhance the efficiency of the GPS and INS integrated system during GPS outages. To integrate data from an INS and DGPS using a multilayer perceptron NN, an NN-based satellite has been added to the multisensor system integration technique.

Although these methods can increase positioning accuracy, its real-time capabilities are constrained by the complexity of multilayer perceptron networks’ design and its online training procedures. To prepare the INS and GPS data for use with the NN, wavelet multi-resolution analysis (WMRA) is used. While the signals are present, EKF estimates the INS measurement errors, as well as the location, velocity, and attitude errors, and offers precise navigational solutions. In addition, the input of the EKF is a multi-layer NN that has been developed to map the driving behavior of the car using INS prediction errors for every GPS era. The NN can be used to anticipate INS mistakes for EKF measurement updates during signal blockages and hence enhance navigational solutions. The INS velocity, IMU outputs, and the length of signal outages are linked to a new model that predicts the GPS position increment. A land vehicle navigation test has been used to empirically assess the performance of the suggested approach. The test results show:

I.

During a GPS failure, the suggested model can effectively estimate the location increment and make up for the accumulation of INS errors.

II.

When the GPS measurements are absent, the advantage of a current design on localization becomes increasingly pronounced with time.

III.

The BPNN framework can adequately optimize both precision and computational burden by employing inputs for the past and present two-step data.

The measurement update of the KF during GPS outages was predicted using a mixed prediction method that includes the RBFNN and time series analysis. Without knowing how many neurons are contained in their buried layers, RBF networks can be used. Instead, throughout the training process, hidden neurons are formed dynamically to achieve the desired performance. When the two systems are cooperating, the measured raw data are typically used to train the RBF neural network in an RBFNN-assisted integrated navigation filtering process. When the GPS malfunctions, the inertial navigation system’s observed and calculated values are sent into the expected error value is calculated using a trained network model, and the inertial navigation system subsequently makes adjustments to generate the final navigational data. Superior estimation accuracy is provided by the integrated navigation system backed by the RBF neural network when short-term GPS data are absent.

These methods can significantly increase positioning precision despite using different prediction models than the pure INS mode. The loosely coupled GNSS/INS integration model is the main focus of the aforementioned research. A fusion technique based on RBFNN for bridging GPS failures was suggested for the closely coupled model. This algorithm used historical measurements to predict readings for the current window and then continued to predict measurements for the following window. In times of GPS failure, this technique can increase filtering accuracy. The RBFNN is much easier to create than other networks and has a higher learning speed and accuracy. To acquire the pseudo-GNSS measurement when the flawed measurement is identified, this paper employs the RBFNN. Better fault isolation and system reconfiguration are the goals of this.

The outcomes of the GPS/SINS KF and GPS KF are combined using the adaptive track fusion algorithm in the tightly coupled GPS/SINS-integrated navigation system based on adaptive multi-sensor track fusion. The lack of readings from the two KFs will cause the system’s accuracy to rapidly decline in the event of a GPS failure. To increase the accuracy of the navigation system during GPS failures, a radial-basis-function-neural-network-based solution for bridging GPS outages is given. This approach makes use of a radial basis function neural network to forecast the GPS/INS KF measurement during GPS outages, ensuring the filter’s consistent operation and dependable system performance. This RBF-based module’s main flaw was that it continued to train using all INS and GPS data that were accessible before the GPS outage, which we found to be unworkable and nearly impossible to apply in real time due to the lengthy training period. With the help of the adaptive track fusion algorithm, this research attempts to improve the precision of a tightly connected GPS/SINS integrated navigation system in the event of a GPS failure. The RBF neural network predicts observations of the differential pseudorange, differential pseudorange rate, and GPS/SINS KF so that the GPS/SINS KF can continue to function normally during GPS failures.

The reliability and accuracy of the tightly coupled GNSS/INS are ensured by appropriate fault isolation and a system reconfiguration methodology. However, a thorough comparison and analysis of their performances in the literature must be performed. This study compares their theoretical performances under various scenarios before analyzing their underlying concepts. The pseudo-GNSS measurement for the measurement reconfiguration is predicted using the RBFNN in Figure 13. Additionally, to make the switch from system testing to measuring reconstruction feasible, an adjustable modification criterion is offered while taking into account the variety of observation conditions. In the event of a GPS signal interruption, the error compensation model integrating the UKF and BPNN methods might offer continuous, accurate, and dependable vehicle navigation. The BPNN was updated while the GPS signal was active. The well-defined BPNN produced navigation estimation errors when the GPS signal was not available.

Figure 13. The (a) training and (b) prediction phases of RBFNN for measurement reconfiguration based on NN.

In addition, the GPS/INS inertial navigation system’s positioning accuracy is increased simultaneously when the GPS signal is obstructed and when it is enabled via the EKF and genetic algorithm (GA) neural network approach. In the absence of a genetic algorithm, the neural network optimizes the estimated EKF results. When the GPS signal is blocked, this successfully increases the positioning accuracy of the GPS/INS integrated navigation system. The integrated navigation system’s velocity accuracy still can be improved by using this technology. After the GPS signal was retrieved, the vehicle’s exact location was predicted using the interacting support vector machine for regression approach, which was trained using the GPS and INS data. Using the updated online support vector machine for a regression model to correct the positioning inaccuracy of the INS, the longitude and latitude coordinates of a vehicle were ascertained in the absence of a GPS signal.

Furthermore, inertial sensor and GPS data were fused in real time using neuro-fuzzy modules. Through the use of cross-validation by using a temporal frame throughout the update process, this research enhanced the performance of these modules. Uncompensated INS readings and DGPS measurements are combined using the INS/GPS integration approach based on ANNs. The commonly used sliding window technique is not taken into account by the ANFIS-based system. Therefore, the size of the temporal window used has a significant impact on the system’s accuracy. The findings demonstrated that the suggested system is a dependable, modeless, platform-independent module that does not require any a priori knowledge of the navigational tools being used as a cutting-edge SINS/GPS integration approach that makes use of the Hopfield NN and produces the best state estimation by reducing the Hopfield neural network’s energy function. Artificial neural networks could be used to create the “intelligent navigator,” a different INS/GPS integration strategy, for the upcoming generation of land vehicle navigation and positioning applications. Results from actual land vehicle tests showed that it is possible to use stored navigation knowledge to give accurate, real-time positioning data for standalone INS-based navigation. For comparatively brief periods of time without GPS, the KF outperformed intelligent navigation. The findings of this study significantly support the idea that for INS/GPS-integrated land vehicle navigation processes, the dynamic navigator might be the main mechanism.

The ANFIS-based module’s goal was to combine INS and GPS position data in real time. However, some restrictions on how the ANFIS parameters could be optimized while the system was in operation created a significant computational burden for real-time implementation. Fuzzy control is crucial because it improves the performance of a coupled GPS/INS for air and land navigation application during GPS signal loss. The use of a linguistic rule to represent complex, nonlinear, time-changing phenomena is a very beneficial and effective strategy. In their approach, a GPS/INS linked navigation system lacking GPS signals is intelligently assisted. The Z-12 GPS receiver and a navigation-grade INS were utilized to provide precise data for ANN, which is employed for multi-sensor systems and only works on location. The GPS/INS integration is based on artificial intelligence, and the AI-based INS/GPS integration methods have used an ANFIS by adopting a temporal-window-based cross-validation methodology during the training process. The suggested fuzzy system is trained using the same data to produce the corrected navigation data. The system will be able to complete its mission without GPS data using only the INS data and fuzzy correction algorithm. This work demonstrates the precision of trained ANFIS in the inability to retrieve data from a benchmark navigation system. The ANFIS is used to characterize the relationship between INS- and GPS-derived navigation data in order to precisely simulate vehicle dynamics and predict its location during GPS failures. It combines the advantages of fuzzy reasoning with neuro-computations. The intended ANFIS technology operates in predicting mode to determine location during periods of GPS signal interruption by shifting periodically depending on the INS velocity and azimuth.

The AKF can benefit from a navigation technique that uses a wavelet neural network (WNN) with random forest regression (RFR) to design the RFR-WNN to forecast INS errors during GPS failures. To increase forecast accuracy, a novel MLP network prediction model that establishes the relationship between INS information and GPS position increments was presented. The KF is enhanced by the addition of an adjusted factor to reduce the impact of the complexity environment and random mistakes on the filtering precision. AKF is used to repair INS inaccuracies. When GPS is functioning properly, a high-precision prediction model is built using RFR-WNN, and when GPS is malfunctioning, RFR-WNN provides the necessary observations for an AKF update. RFR is used to optimize the single WNN, which can increase generalizability and prediction accuracy to address the issue that the absence of comprehensive training data makes the single neural network model susceptible to classifier, unpredictability, and low prediction accuracy.

4.3. More Recent Development of NNs for Navigation System Designs

For the past few years, one of the most well-liked trends in scientific study has been deep learning. A subset of machine learning algorithms called deep learning [94,95,96,97,98,99] represents several levels of hierarchy and enables the construction of complex concepts from smaller ones. This section provides a review of the recent development of NNs for navigation system designs, including the following five categories: (1) nonlinear autoregressive exogenous neural network [90,100,101,102,103]; (2) long short-term memory (LSTM) NNs [89,91,92,104,105,106,107]; (3) extreme learning machine (ELM) NNs [93,103,108,109,110]; (4) gated recurrent unit (GRU) NNs [88,111,112,113,114]; and (5) convolutional neural networks (CNNs) [115,116,117] with GRU.

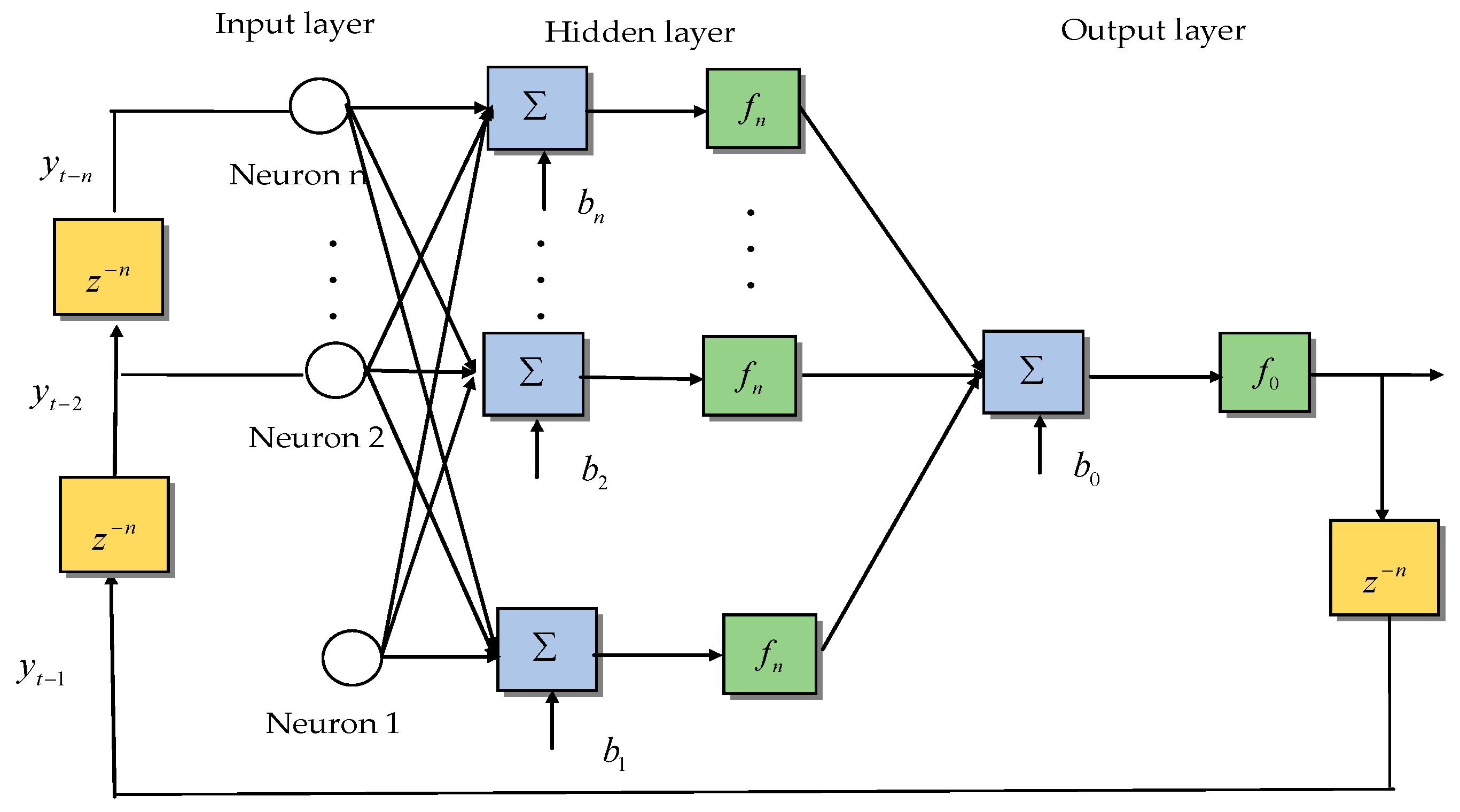
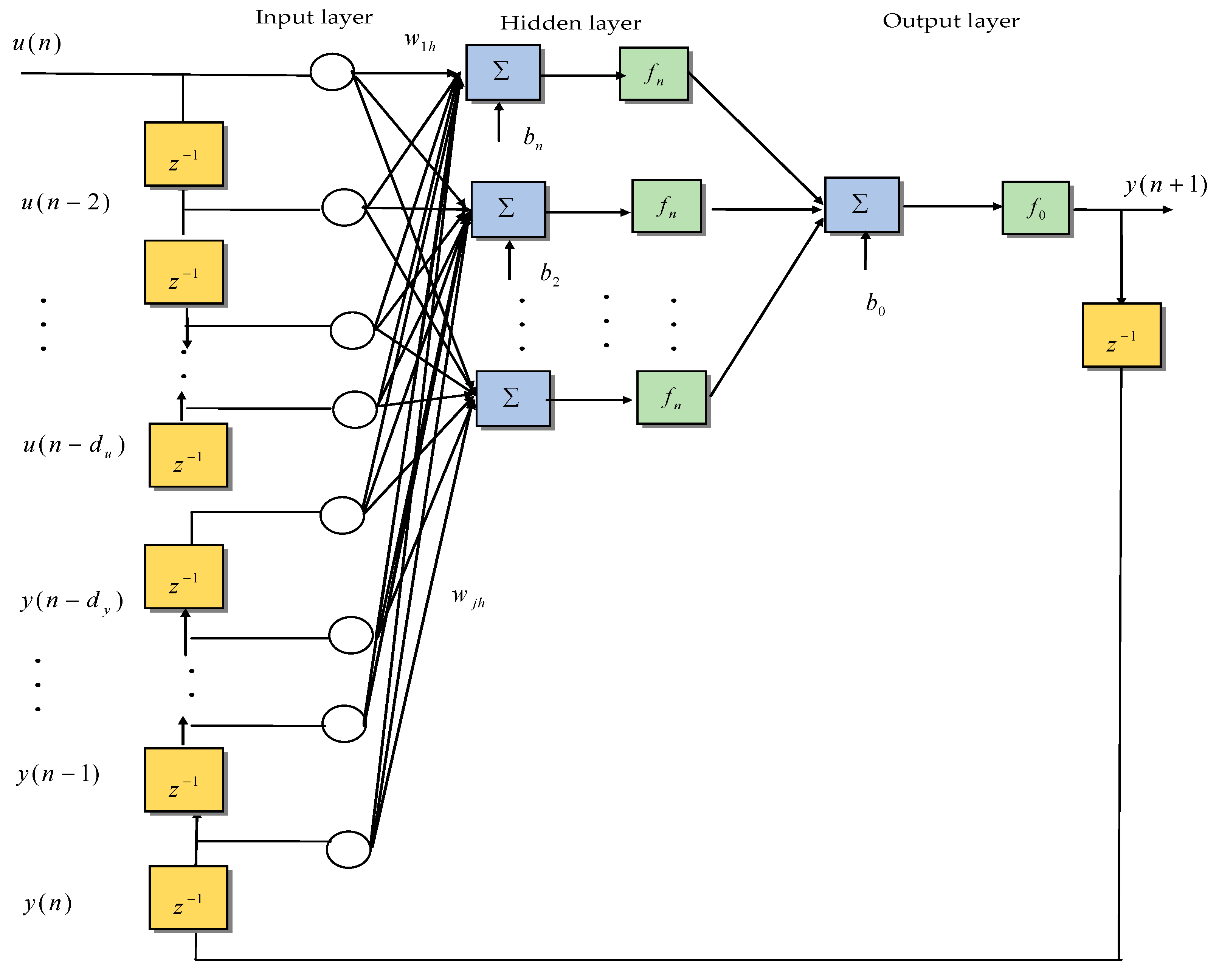
4.3.1. Nonlinear Autoregressive Exogenous Neural Network

Figure 14 shows a typical nonlinear autoregressive (NAR) NN, which is a feed-forward NN with three layers, namely the input, hidden, and output layers. A GPS/INS-fusion-based integrated system based on an autoregressive NN was proposed in which the time series forecasting field has made extensive use of a nonlinear autoregressive exogenous (NARX) neural network [104]. The system made use of the ANARX (additive nonlinear autoregressive exogenous) model, which is nonlinear autoregressive intelligent fusion technology. The findings demonstrated that in situations in which GPS measurement results in a time delay, the suggested system could still achieve the best positioning effect by utilizing the information from sensors already in place. Therefore, a method known as “NARX-aided UKF” has been studied to estimate the location during GPS outages, where the readings for UKF during GNSS signal losses are predicted using the NARX-based system. Additionally, an algorithm for INS error compensation that incorporates UKF and BPNN was created. Therefore, when GPS is available, UKF implements KF with excellent performance and guarantees high accuracy.

Figure 14. A typical NAR neural network.

In Figure 15, an NARX-NN model is presented, which can predict the velocity during DVL malfunction is built. A new SINS/DVL-integrated navigation process based on NNs is studied in light of the possibility that the DVL may malfunction during the missions. For underwater applications, velocity prediction can also be seen as a time varying forecasting issue. The NARX neural network is used because it can provide accurate predictions. The NN is updated by using the derived SINS and DVL parameters, body frame velocity, and its advancement while the DVL is available. When DVL is not accessible, the well-trained neural network’s velocity forecast is used to support SINS and keep the accuracy of integrated navigation high [102]. When specific circumstances arise, such as passing over marine life or the DVL going outside its maximum measuring range, the DVL will not keep the bottom lock and will not send velocity updates. Using partial basic data from the DVL and extra data, an extended loosely coupled (ELC) technique can provide virtual vehicle velocity to get around this issue. A hybrid strategy to predict the DVL data while it is malfunctioning. The predictor’s inputs are the past and present velocities acquired by SINS. In the absence of DVL, the research suggests an NN-based method to forecast body frame velocity. The literature on SINS/GNSS-integrated navigation has related approaches for related circumstances [90,101].

Figure 15. The architecture of NARX-NN model.

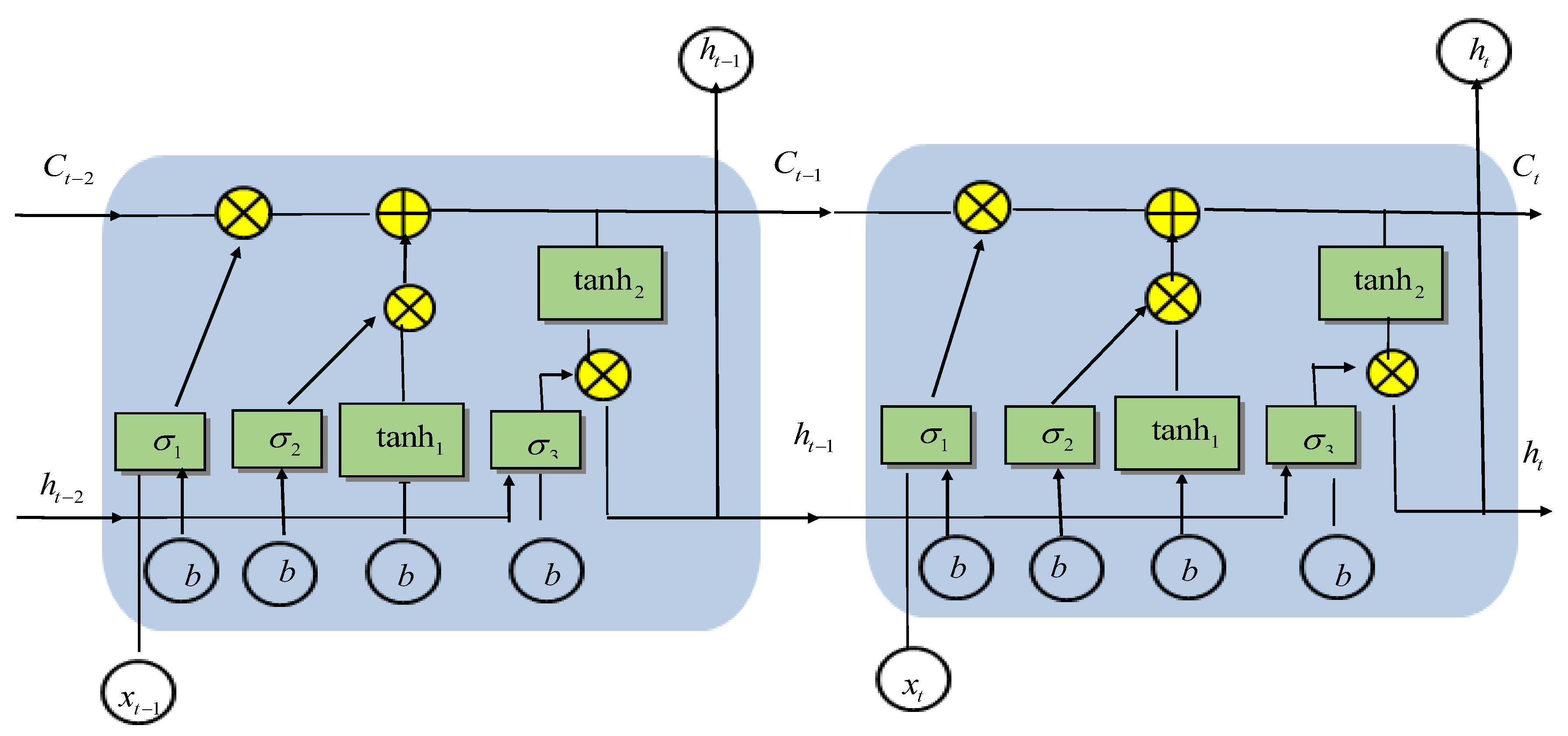
4.3.2. Long Short-Term Memory (LSTM) NN

The most popular deep neural networks for supervised learning include convolutional neural networks (CNNs), RNNs, reinforcement learning, and an RNN variant known as long short-term memory (LSTM) models. To create the approximation function, numerous hidden layers are typically stacked together and triggered in a series of steps. The term “depth” of a model refers to how many hidden layers are present, which explains how the term “deep learning” came to mean learning using models with many layers. When it comes to handling time sequence data and nonlinear system modeling, deep learning algorithms like RNNs offer several advantages over ML approaches because of their unique cycle unit. The inability of RNNs to compute long-term sequences led to the creation of LSTM by researchers. An enhanced RNN that is effective at handling these issues is the LSTM NN. To determine whether the supplied information is useful, LSTM also has the benefit of handling time series sequences with larger intervals and time delays in a cell. The LSTM approach significantly reduced the positioning inaccuracy, although it may have outperformed ANFIS.

The IMU core readings have complicated noise properties, as most approaches presume that NNs are constructed under optimal conditions without taking the precision of the labeled data into consideration. Before data fusion, a preprocessing method reduces uncertain noise in the raw values from inertial sensors. This research suggests a preprocessing data method that combines empirical mode decomposition (EMD) and wavelet threshold filtering (WTF) to treat the actual IMU raw measurement to acquire trustworthy and precise location data during GPS failures [106]. A self-learning navigation method that integrates data denoising and LSTM NN in conventional GNSS/INS integrated navigation is analyzed. The INS velocity and yaw as well as the output from the preprocessed IMU are used as the input of the LSTM model when the GNSS signal is available. The outcome is the GNSS position update. In order to correct INS navigation results when the GNSS signal is lost, the pre-processed IMU and INS information are put into the LSTM model to construct a pseudo-GNSS position and transmit it to the EKF. The EMD divides the noisy IMU signal, according to amplitude and frequency, into some intrinsic mode functions (IMFs). Then, the high-frequency IMFs are subjected to wavelet threshold filtering, which differentiates the useful data in the high-speed IMFs. Finally, to create a denoised signal, these IMFs are combined with low frequency IMFs and residual signals. The outcomes of the experiments demonstrate that the suggested navigation algorithm can greatly increase GNSS/INS integrated navigation accuracy and reliability during GNSS failures.

A learning model utilizing an RBFNN to map the INS position and location discrepancy between the INS and GPS was developed first. Then, an INS/GPS integration technique comprised of ANN was developed to fuse uncompensated INS and DGPS measurements for a variety of ANNs, i.e., complete counter propagation neural network (Full CPNN), RBFNN, BPNN, forward-only counter propagation neural network (FCPNN), CNN, adaptive resonance theory–counter propagation neural network (ART-CPNN), higher-order neural networks (HONN), and IDNN. Recently, several novel robust algorithms using NNs or support vector machines (SVM) in combination with EKF and ML techniques have demonstrated improved navigation performance. The majority of the systems discussed above rely on static neural networks, which only employ one-step INS data from the past and present without taking into account more historical vehicle dynamic data. It is understood that obtaining precise localization would be made more difficult by the requirement for historical vehicle dynamics via time series data. The aforementioned techniques are unable to maintain precise navigation results when GPS has a prolonged outage.

Deep learning recently demonstrated satisfactory performance in time sequence prediction, which includes speech and natural language processing. When working with lengthy sequences, RNNs may experience gradient disappearance and explosion. The MEMS-INS accuracy has been substantially improved by the development of LSTM, which was based on RNNs, to determine the INS inaccuracies according to the latest and previous records of the INS outcomes and denoise the MEMS-IMU signals. To calculate the pseudo-GPS, an LSTM focused on convolution NN can be used for readings to assist INS during GPS failures. In addition to the outer recurrence of RNNs, typical LSTM-gated cells in RNNs also feature an inside recurrenceThe internal state that cells store can be read from and written to. Gates regulate the entry, exit, and deletion of data from this cell state. They use their weights, much like a conventional neural network, to block or transmit information based on its significance and strength. Furthermore, RNN and LSTM neural networks were developed. The LSTM networks were created in an effort to address the RNNs’ long-term dependency. Creating a gating switch successfully addresses the RNN network’s long-term issues [87]. Recent studies have shown that LSTM can be useful in a variety of disciplines, including sustainable navigation. Robotics, ship trajectory prediction, and other industries have made extensive use of LSTM. The MLP network offers superior results and exhibits greater capability than conventional approaches. However, it is unable to manage long-term sequence management and historical dependencies in time-series data. These problems have caused the research community to focus more on CNN and RNN techniques. These techniques, however, were ineffective because of vanishing gradient issues and long-term effects.

A fusion technique based on LSTM-NN is proposed to obtain strong prediction performance, maintain the model’s simplicity, and adaptively incorporate historical data without increasing the additional inputs, thereby overcoming the limitations of existing ANN methods. The fundamental idea behind LSTM is presented in the following figure in Figure 16. LSTM is an RNN version that addresses RNNs’ drawbacks by modeling long-term dependencies using memory cells in place of the hidden layers of RNNs. An activation function and several gates, including input, output, and forget gates, are used by LSTM to represent and learn the behavior of time-based relations. To overcome GPS outages, an intelligent AKF built on deep neural networks, fuzzy logic for integrated navigation systems, and a fusion mechanism to deliver phony GPS location data are proposed. Empirical mode decomposition threshold filtering (EMDTF) and an LSTM NN make up the approach. Inertial sensors’ noise is removed by the EMDTF, which also gives more precise data for ensuing calculations. The LSTM predicts the pseudo-GPS position during GPS failures using the current specific forces and angular rates. To remove noise from IMU data, a preprocessing data technique based on EMDTF is described. Finally, the suggested methodology is used to navigate using the INS/GPS combined system [110].

Figure 16. Architecture of LSTM model.

For the unmanned aerial vehicle (UAV), a GPS/INS-integrated navigation system is suggested based on an LSTM NN. However, it can be difficult to manually specify the covariance noise value in KFs, which should dynamically adjust to the motion of the UAV. An LSTM-NN was chosen to create a cutting-edge end-to-end navigation technique because it contains specific contextual memory units that can automatically retain prior useful information. Experimental findings show that the suggested data-driven navigation strategy may accurately estimate the online UAV position without manually creating and modifying a mathematical model. For handling outliers, a reliable adaptive filter based on VB theory is suggested. Its benefit is that it enables time-varying noise adaptation and lessens outlier interference with the integrated navigation system. An RVBAKF/LSTM hybrid technique [90,92] was proposed to address the issue that when performing the work of an underwater vehicle, the underwater integrated navigation system is easily interrupted and the output is inaccessible. It is crucial to increase the fault tolerance of the integrated navigation system because given the value obtained, the DVL is subject to outliers or even discontinuation in the autonomous underwater vehicle’s (AUV) actual underwater learning environment. First, when the DVL output is standard, it chooses the SINS output linked to AUV velocities, such as velocity, attitude, angular velocity, and specific force, as the training input. The integrated navigation system receives pseudo-measurement results from the LSTM model if DVL output is disrupted. The technique can significantly increase the efficiency of the INS when the DVL output is stopped [92,102].

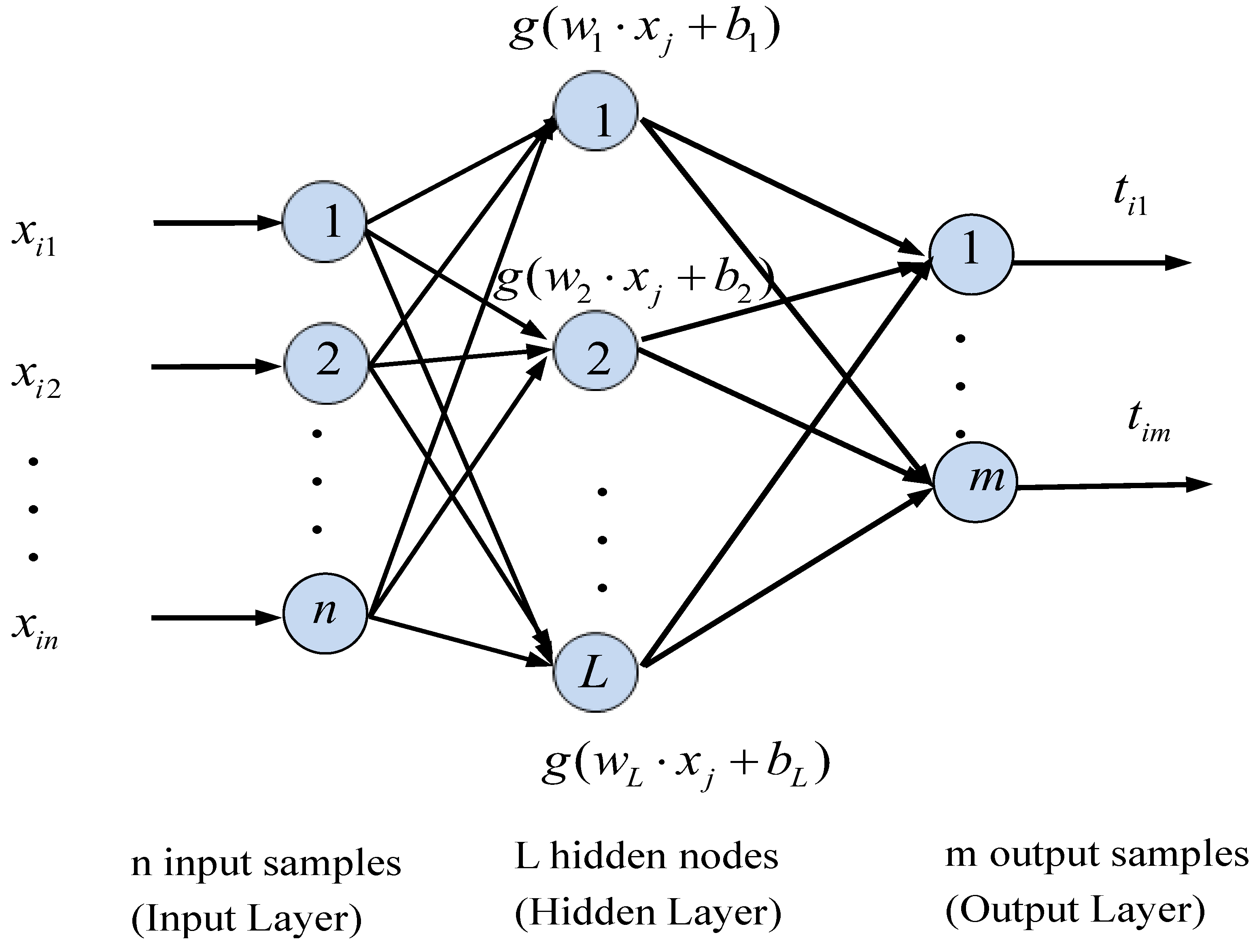
4.3.3. Extreme Learning Machine (ELM) NN

In order to lessen the ambiguous noise of the IMU raw measurements and offer reliable data for upcoming GPS/INS data fusion and training samples, a method for preprocessing the data based on EMD for wavelet denoising is created. The IMM-EKF approach is then suggested to increase the precision of the model training target result and the robustness of the KF output. Figure 17 presents a fresh, intelligent GPS/INS framework based on the ELM.

Figure 17. Basic schematic of ELM structure.

When the GPS is available, the denoised INS data and the outputs of the IMM-EKF are used to train the ELM while the GPS and denoised INS data are fused using the IMM-EKF. The ELM forecasts and corrects the INS position error during GPS failures. Three tests were run in the real field test to gauge the success of the suggested approach. The comparison of findings demonstrates that the suggested fusion method can greatly increase the precision and dependability of locating during GPS failures [88,109,110,111]. The wavelet-based denoising algorithm built on EMD is known as EMD-WD. An ANN-based fusion approach is suggested to address GNSS outages. The ELM network is first used to swiftly identify brief GNSS signal failures. The BPNN is then used to anticipate the overall output of GNSS following the output of the INS system, and the accuracy is increased by adopting the INS’s historical data in various steps. Extensive testing demonstrates that the integrated navigation fusion algorithm built on ELM and BPNN may significantly lower navigation errors when GNSS signals are interrupted. To balance the computational load and navigational precision, various algorithm alternatives are offered concurrently.

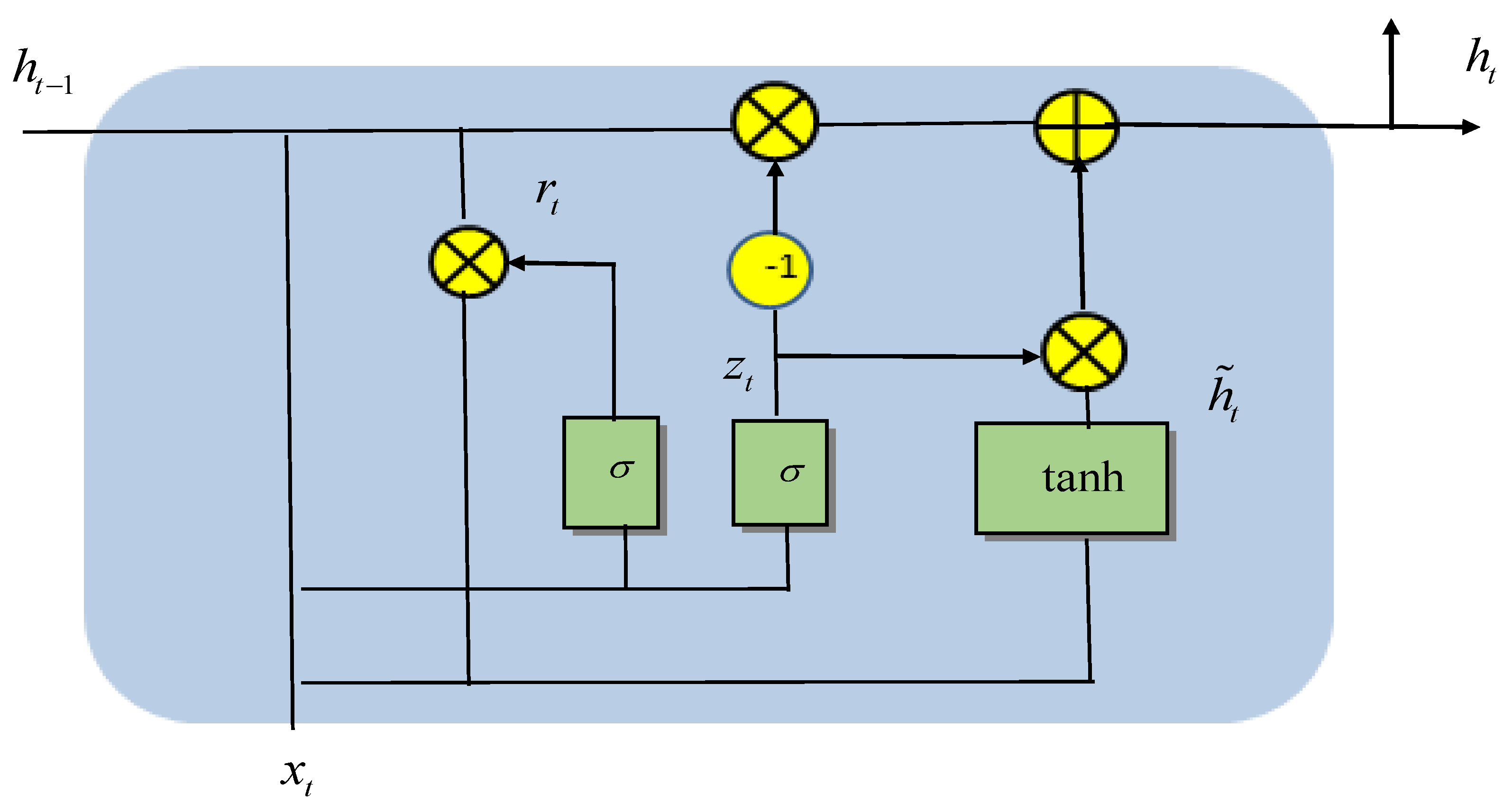
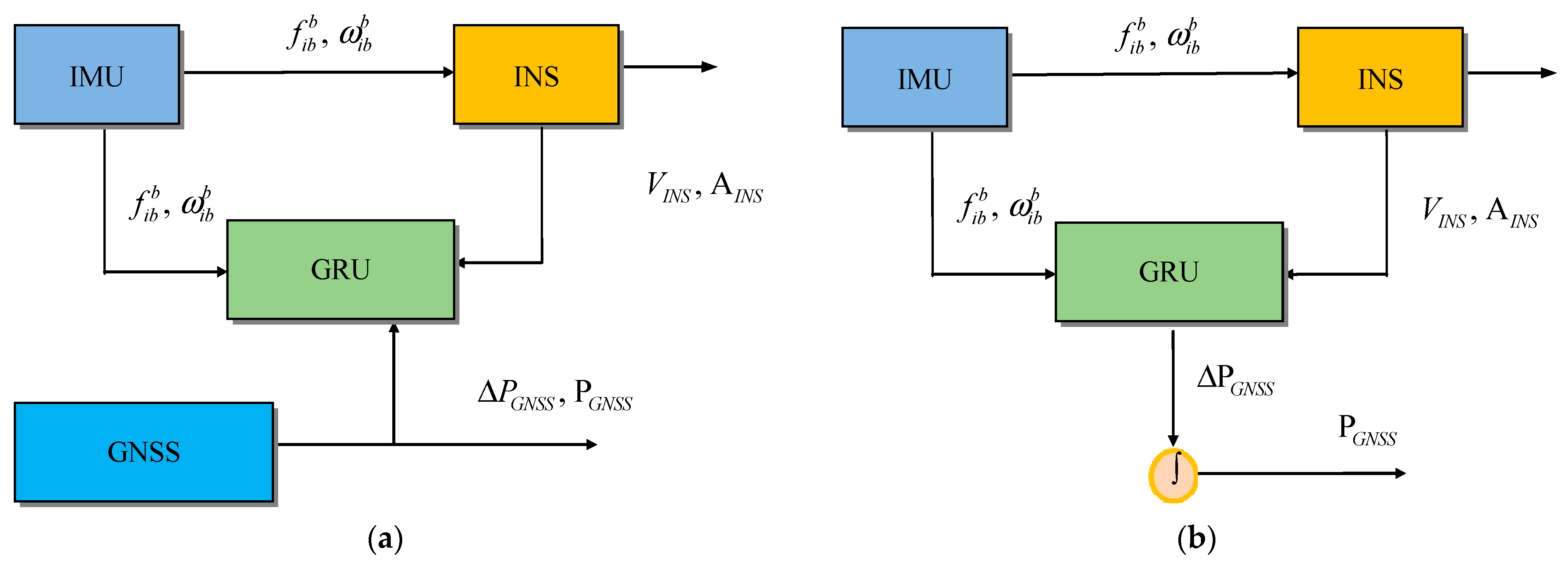
4.3.4. Gated Recurrent Unit (GRU) NN

The majority of neural networks, including RBF and MLP, are static networks. These networks’ primary drawback is that they can only store a limited amount of information from the past and can only use data from the most recent phase. The gated recurrent unit (GRU) was employed for the INS/GPS since the GRU is used for events connected to time series [88,111,112,113,114]. Figure 18 displays a hybrid method based on a GRU and an IMM-ARCKF. To address the uncertainty of the system model and measurement noise statics in the road applications of INS and GPS, the IMM-ARCKF technique is first presented. Then, a GRU neural network with two training and prediction modes is added to the INS/GPS. First, the GRU neural network operates in training mode when a GPS signal can be received. When there are GPS outages, the GRU neural network forecasts the GPS position increment. The experiment and analysis also assess the algorithm’s performance. The suggested algorithm can increase location accuracy during GPS outages, according to the experiment’s results.

Figure 18. The structure of GRU.

A hybrid algorithm based on GRU and AKF can be created to lessen the degradation, as shown in Figure 19. The GRU network is designed to forecast location changes during GNSS outages and has the advantages of high accuracy and efficiency. The GRU-predicted error accumulation is also taken into account in this research, and AKF is included as an additional method of enhancing navigation performance [101]. The basic KF, MLP-aided KF, LSTM-aided KF, and GRU-aided KF methods are all compared to the proposed hybrid algorithm, which is trained and tested on real-world road datasets. A useful solution for overcoming GNSS disruptions is the neural network. The performance analysis of different forms of neural networks indicates that both RNNs overcome the MLP in forecast positional variance, while the GRU surpasses the LSTM in model performance and training effectiveness.

Figure 19. Structure of GRU-aiding INS/GNSS integrated navigation: (a) training mode; (b) predicting mode.

4.3.5. Convolutional Neural Network (CNN) with GRU

The ELM has garnered considerable interest and attention in recent years from the scientific community because of its lightning-fast learning rate and exceptional generalization capabilities. As a result, the ELM is used and the RBFNN is contrasted with it. The simulation results demonstrate that by implementing the suggested strategy, the integrated navigation system’s accuracy is greatly increased, and in terms of both real-time capability and refinement power, the ELM gives the best performance.

Four one-dimensional CNNs [115,116,117,118,119,120] are used in the studied INS/GPS neural network (GI-NN) architecture to project IMU inputs into a high-logarithmic space for improved IMU feature extraction from sensor noise. To help the INS during GPS outages, a crucial hybrid fusion approach on the basis of GRU for load calculation reduction is devised. The GNSS/INS simultaneously incorporates the CNN and GRU. By using GI-NN to extract the IMU’s feature space from the sensor, it is possible to simplify calculations and boost measurement accuracy. Between navigational data and INS output, deep learning is primarily utilized to learn the velocity, attitude-specific force, and angular velocity. Additionally, to accurately calculate the INS error data and vehicle dynamic status, the GI-NN advanced fusion technique takes into account both the historical INS data and the current INS error. At the same time, the onboard computer saves the GPS and INS information to update the GI-NN model. When GPS signals are not available, the updated GI-NN model can forecast the GPS increment to maintain a reasonable level of navigational accuracy. In contrast with other NNs, GI-NN can boost measurement accuracy with a low computational load by extracting IMU spatial properties from sensor noise.

5. Advantage and Disadvantages of ANN in Navigation System

Current developments in ML have produced ANNs that are significantly more complicated and simpler to train than their predecessors. The LSTM architecture is one of the most significant developments [104]. To identify patterns in sequences, the LSTM technique learns from knowledge segments and stores in the form of series in memory. A filter in navigation can be thought of as a function of a series of machine assessments and feeds to produce a series of state estimates. As a result, LSTM ANNs can act like filters, but they are developed through updating on empirical data rather than by customizing filters based on past experience. By enhancing an existing filter, ANNs facilitate and filter data. The advantages of the augmentations include keeping the functionality of a verified filter with obtaining a major improvement via ANN augmentation. The augmentations involve offering corrections, adding measurements, and adjusting filter settings. This connection can be used by the learning algorithm to enhance the filter. ANNs are one type of system that can be used to extract information from knowledge. This now improves filter efficiency by raising the a priori knowledge of the issue.

The state modifications of ANN might be updated simply by presenting the error at each step of the time as the objective for guided outcome and generating estimation from the filter at every time interval. The ANN would then pick up on the mistakes the filter made at each time step. The ANN will overstate the error made by the filter at runtime. Since the filter employs updated state projections at the beginning of every time period, the state estimates produced by the filter have less error. This feedback must be included in the ANN output target at each time step in order to prevent the ANN from overestimating the filter’s mistakes. The ANN estimator will finally appear at a minimal area or saddle point after repeating this process, producing the same corrections in each iteration. As a result, the output expectation for the next upgrade will not be considerably altered. The additional step of recalculating the ANN’s goal output can make this process more complex.

6. Future Challenges

This article discusses the use of an ANN in the Global Navigation Satellite System, which includes the Global Positioning System and the Inertial Navigation System. The study also shows that depending on the application scenario, combining the INS with an external navigation system like GNSS may be a state-of-the-art method. Because it provides consistent, accurate, and dependable navigation resolution, the GNSS/INS navigation system is presented. The Kalman filter (KF), extended Kalman filter (EKF), unscented Kalman filter (UKF), cubature Kalman filter (CKF), sequential Monte Carlo (SMC) techniques, and particle filter (PF) are also explored as several filtering approaches. The geometric dilution of precision (GDOP) approximation, GPS navigation processing, attitude determination using NN, and prediction of differential DGPS correction using NN are reviewed. In addition to this, the most popular technique for training a multilayer feed-forward artificial neural network, the back-propagation neural network (BPNN), is analyzed. Two forms of NN approximators—BPNN and GRNN—as well as four types of NN classifiers—BPNN, OI Net, PNN, and general regression neural network (GRNN)—are well defended. The two main strategies for AKFs that have been established are innovation-based adaptive estimating (IAE) and multiple-model-based adaptive estimation (MMAE), which is similar to the interacting multiple models (IMM) algorithm. The technique uses variational Bayesian (VB) learning to give a robust tracking capacity for time-varying noise covariance and to approximate noise strength. Due to their ability to address the problem of non-linearity, various techniques, including those based on multi-layer perceptron neural networks (MLPNNs), RBFNNs, random forest regression (RFR), and adaptive neural fuzzy inference systems (ANFIS) were also described for GPS/INS systems.

A model will be trained using further datasets in future studies, and more data will be gathered under more challenging conditions. Some are listed below:

➢

The flexibility of neural networks to consistently modify their structure to the application can be linked to its significance for GPS/INS incorporation.

➢

However, for selecting an appropriate window size for real-time, practical applications requires considerable effort. Additionally, the efficiency of the approach is highly dependent on the vehicle’s state of movement and can be regained by using an ANN.

➢

The CNNs particular models are designed to take two-dimensional input data, including images or time series data. The linear regression procedure known as “convolution” is always included in at least one layer of the network and can be the source of the term for these topologies.

➢

The NNs that can be used to build waveforms for segments with curves differ from those that can be used for sequences with major roadways; this information may be obtained by subtracting the road curvature from the steering angle.

➢

A variety of neural networks and other machine learning techniques can be chosen to enhance the proposed model’s hidden layer and transfer function counts as well as the number of invisible neurons and parameters.

➢

By adding approaches that can offer a priori knowledge about the level of chaos of the time series, the recommended framework will perform better when choosing between adaptive, optimum, and robust estimators. When these strategies are paired with parallel computing activities, they might be able to train the methodology more effectively for longer prediction horizons.

➢

Displacements can grow to be impossibly large or incredibly small when they are accumulated over a long period. Expanding gradients can be shortened or compressed, making them simpler to solve. On the other hand, collapsing gradients may become too small for computers to express and for networks to learn from them with more efficiency.

➢

The vehicle’s movement depends on the capabilities of the vehicle and the layout of the route; an NN trained with measured data with a straight or curved road segment can provide a good location.

➢

Future research should enhance the series of twisting roads for practice and modify the initial input values of the ANN model to address the issues.

➢

Deep learning is a breakthrough in inertial navigation technology and can acquire more stability by using the trending ML technology.

7. Conclusions

Recently, machine learning techniques have gained popularity as artificial intelligence develops. To improve navigation performance, artificial neural networks have been the subject of substantial research. The entire results of artificial neural network research are explored for both the integration of the INS with GNSS and the usage of ANNs in the GNSS in navigation systems.

Furthermore, it is possible to employ an artificial neural network as a “mixed race” modeling technique without the necessity for a rigorous system physical model. It makes more sense to utilize the input and output data to describe the system behavior. The GNSS can sometimes provide dependable and consistent navigating solutions. The integration of GNSS with INS has been a significant development in modern navigation. Recently, several techniques have been suggested to enhance the GNSS/INS performance during GNSS failures. To improve navigational accuracy and overcome the signal blockage problem in urban metropolitans, various technologies such as jamming, GNSS-restricted environments, the integration of GPS/INS or other GNSS/INS using Kalman filter, and more based on artificial intelligence are also used. The output of the underwater integrated navigation system is subject to degradation in aquatic environments. In order to increase the error checking of the integrated navigation system, both the value obtained of the DVL and the real underwater working environments of autonomous underwater vehicles (AUV) are prone to anomalies or even dropouts. A highly credible adaptive filter built on the VB theory is recommended for managing against the outliers. The review’s main goals are an overview, a probe into, observation of, and an assessment of how well the current integrated navigation systems perform. To deal with GNSS disruptions, a neural network-based fusion strategy is recommended in this study.

Moreover, for an accurate and sustainable navigation solution, the reviews of different studies have been studied to explore, conclude, and combine navigation systems with neural network technology. The application of neural networks to GPS is detailed in this review. It introduces state estimation algorithms for GNSS/INS integration. A review of the development of neural network enhanced GNSS/INS integration study is explored. Future difficulties are also mentioned for the demonstration of deep learning technique in navigation system designs.