Heat Transfer Mechanism Investigation of Bubble Growth on the Superhydrophilic Nano-Structured Surface Using Moving Particle Semi-Implicit Method
Abstract
1. Introduction
2. Numerical Method and Calculation Procedure
2.1. Governing Equations
2.2. Particle Interaction Models
2.3. Higher Order Accurate Pressure Poisson Equation
2.4. The Surface Tension Model
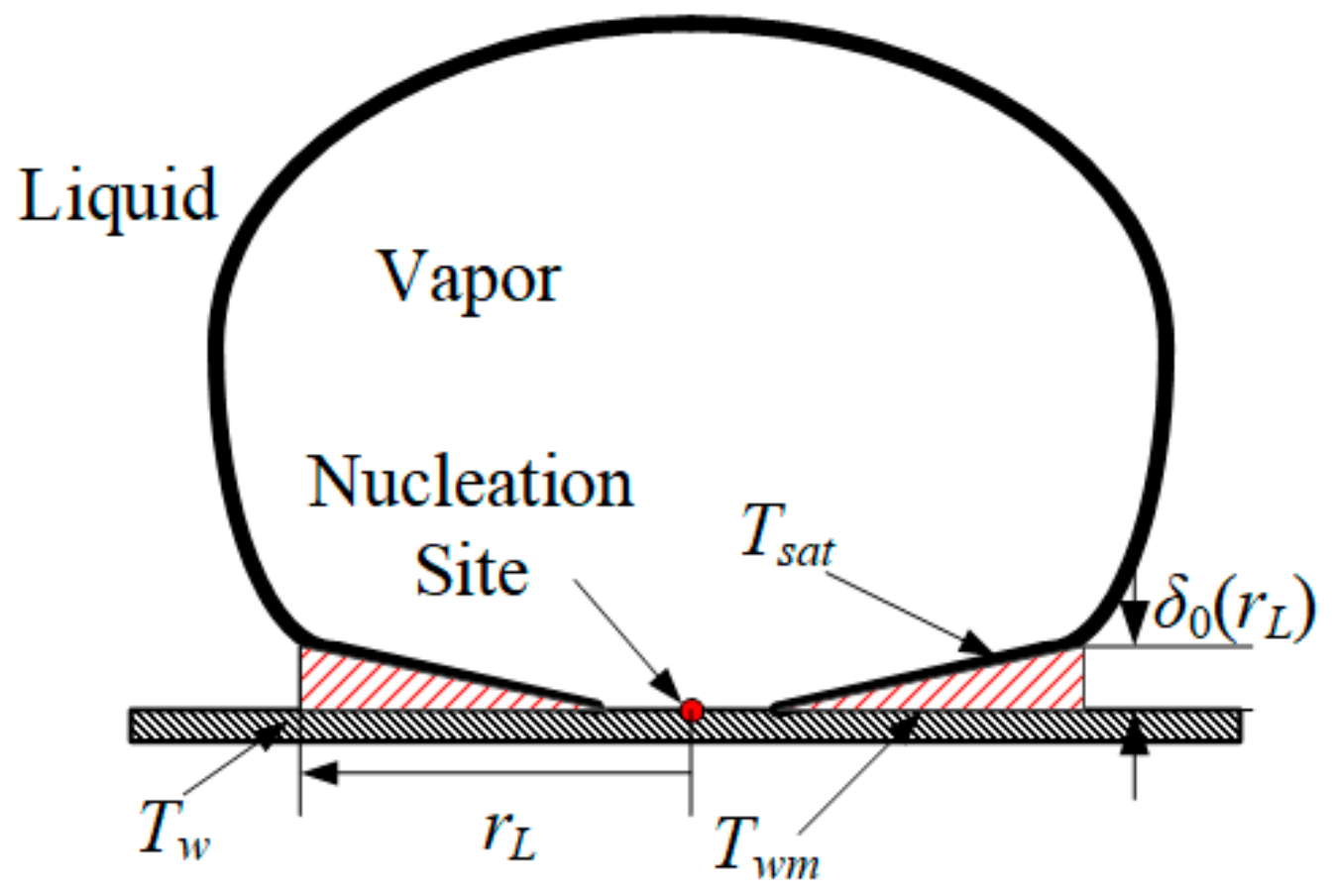
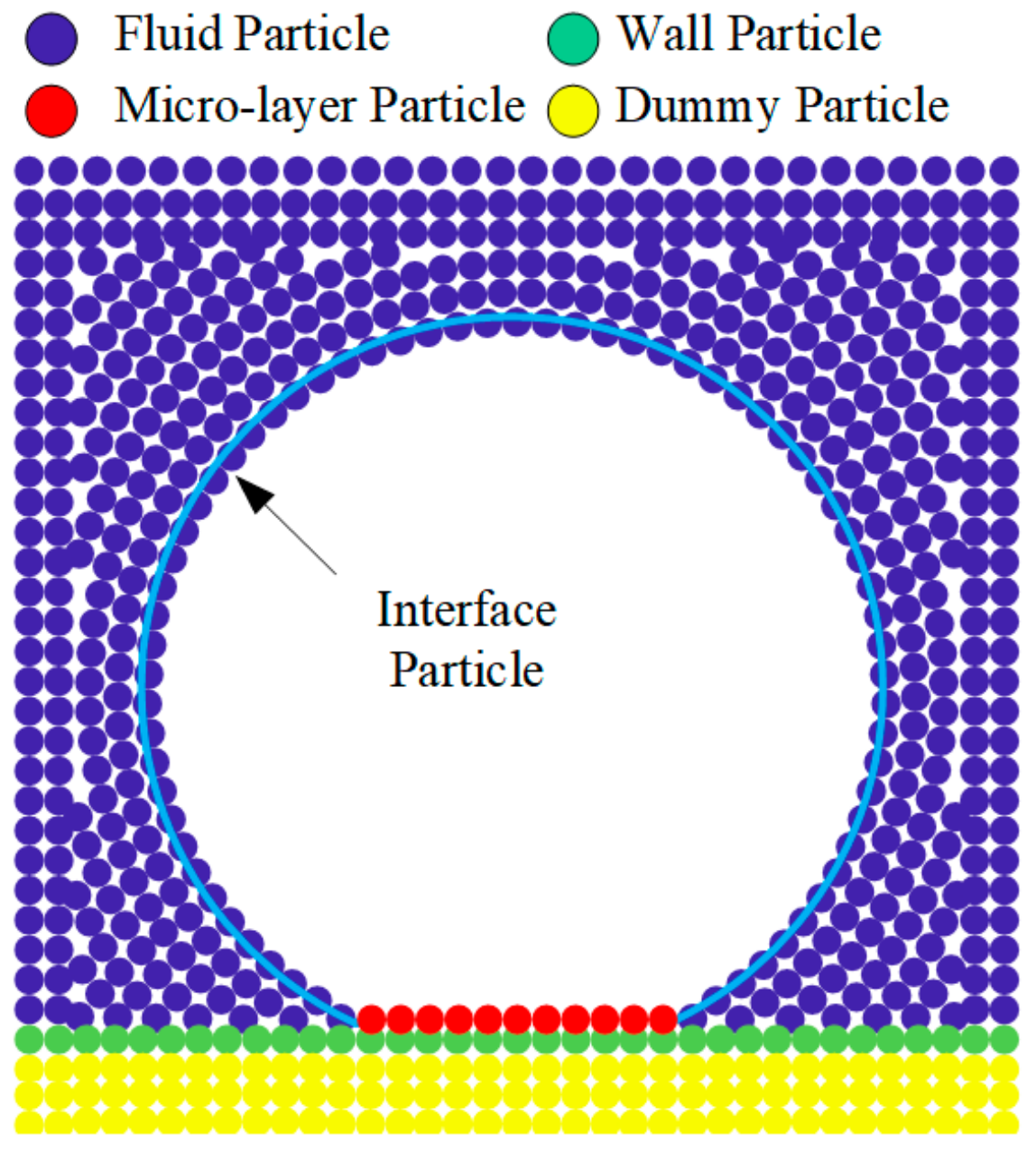
2.5. The Micro-Layer Model
- (1)
- We carried out a first calculation with C0 = 4.46 × 10−3.
- (2)
- We compared the calculated results with the experiment. If they were in good agreement, an appropriate C0 was achieved. Otherwise, we went to the next step.
- (3)
- We recalculated with the modified C0 and returned to the previous step.
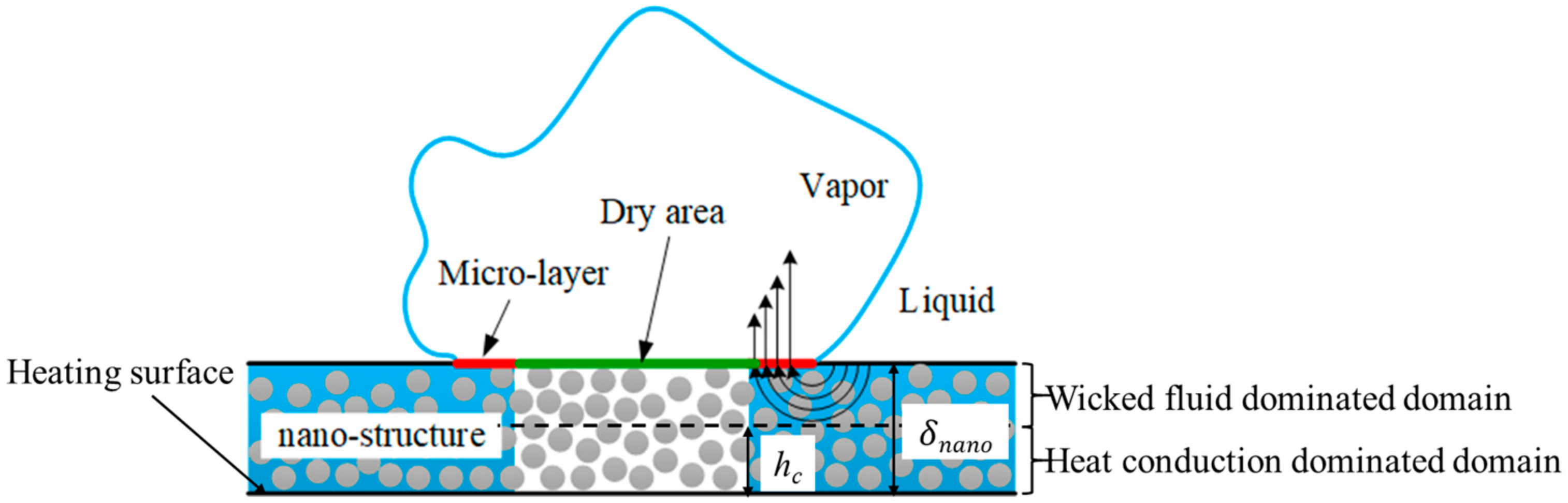
2.6. The Nano-Structure Model
2.7. The Bubble Volume Change Model
2.8. Calculation of the Domain and Boundary Conditions
2.9. The Time Step Control
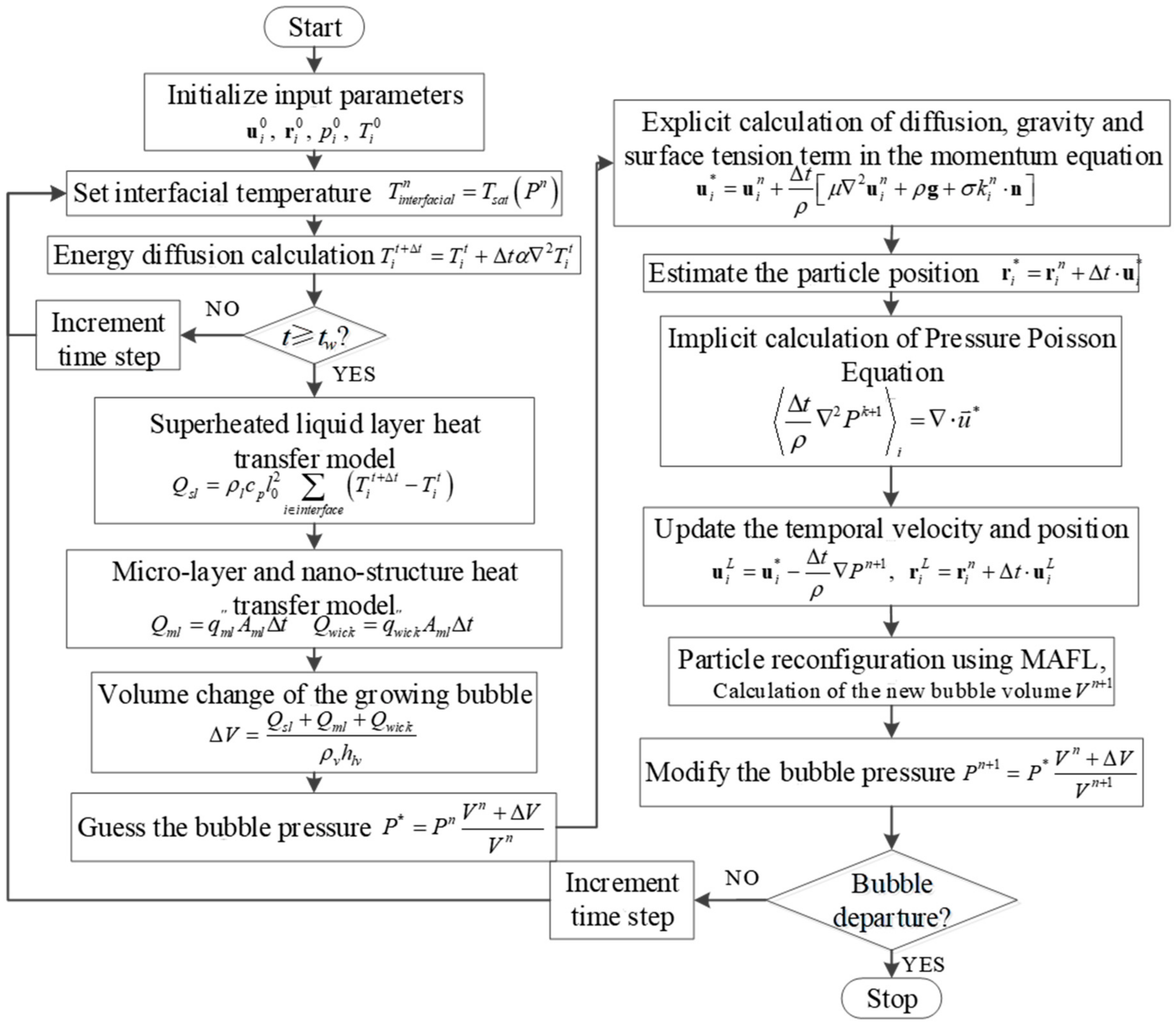
2.10. The Calculation Procedure
3. Validation
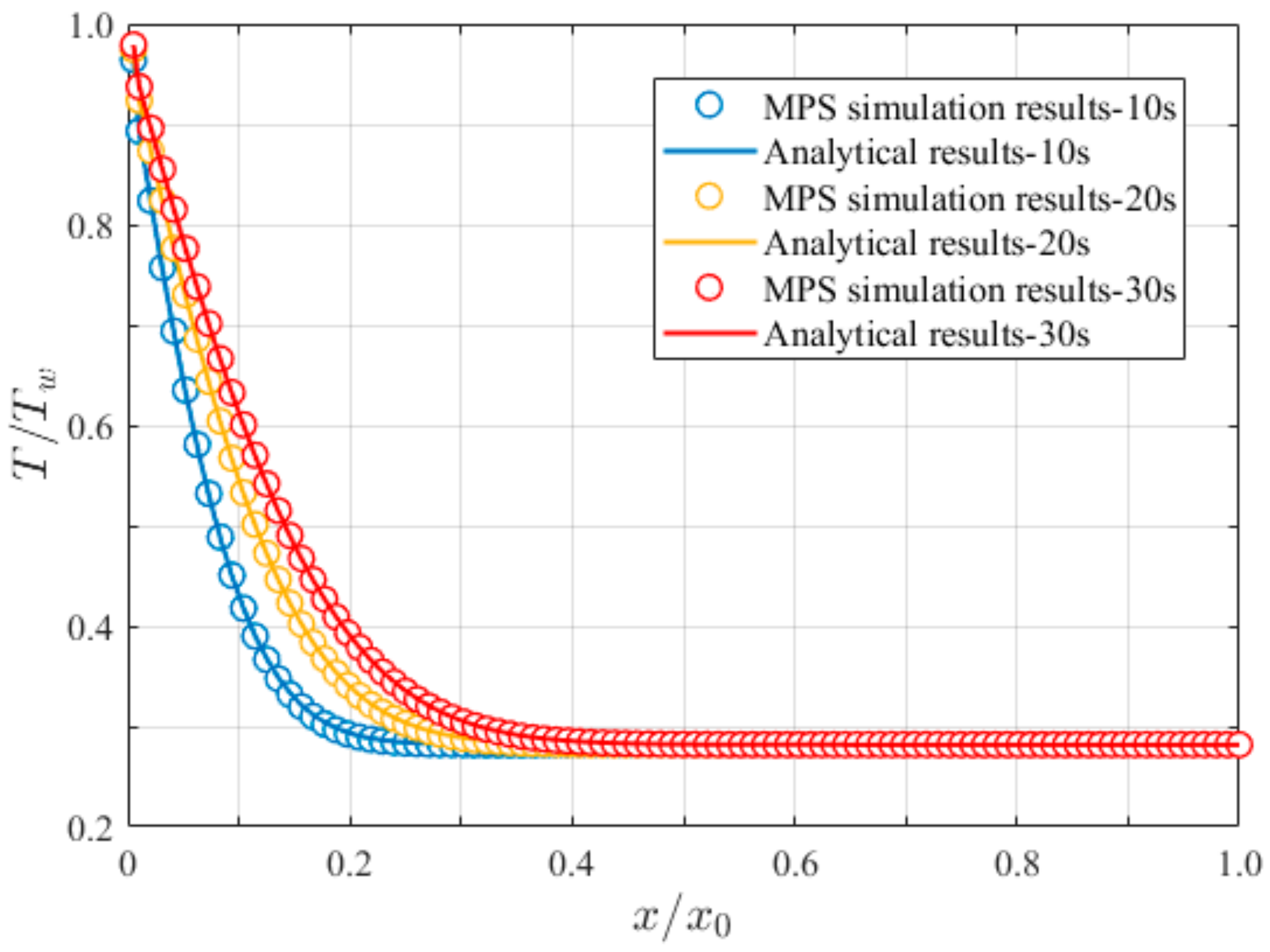
3.1. One-Dimensional Plate Heat Conduction
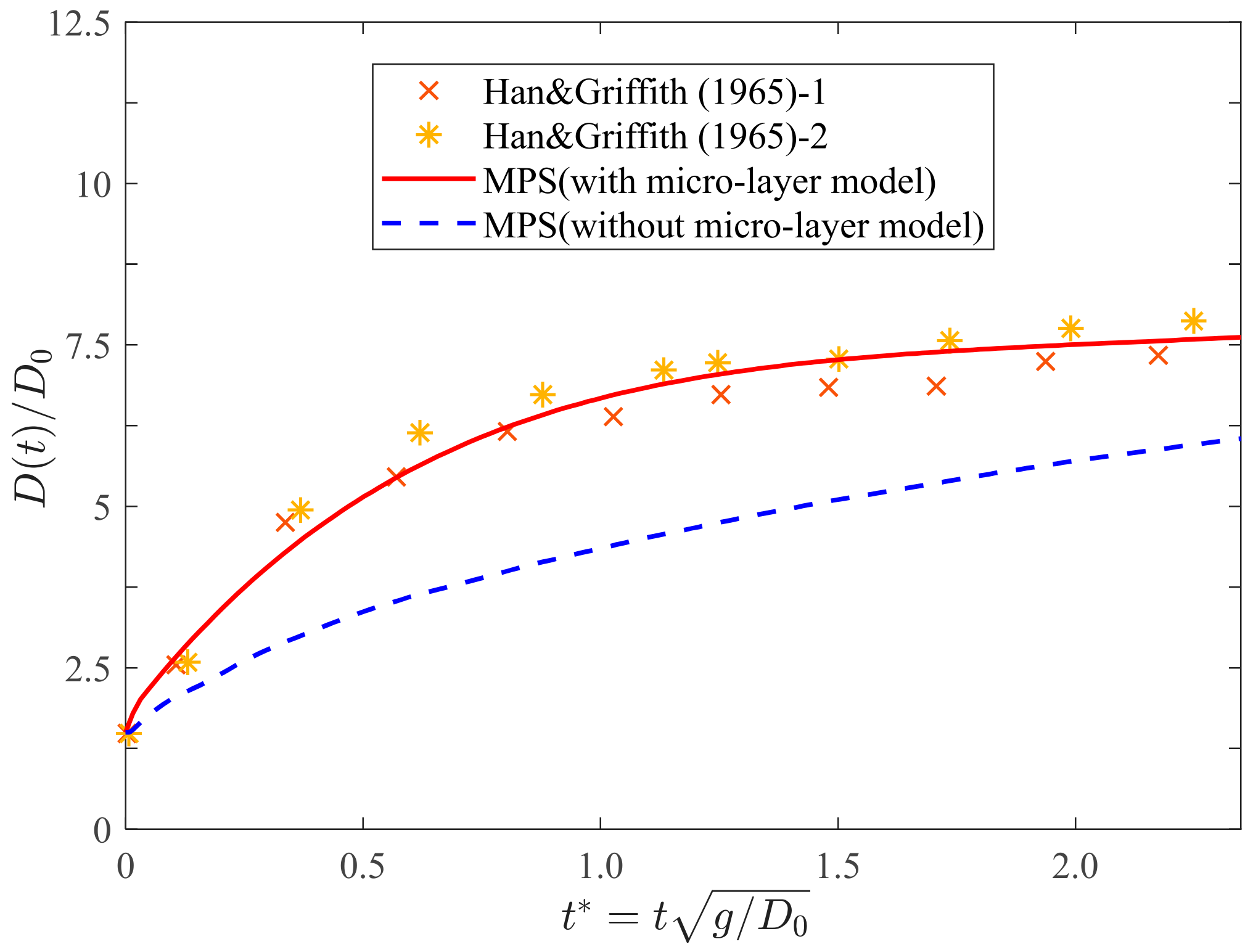
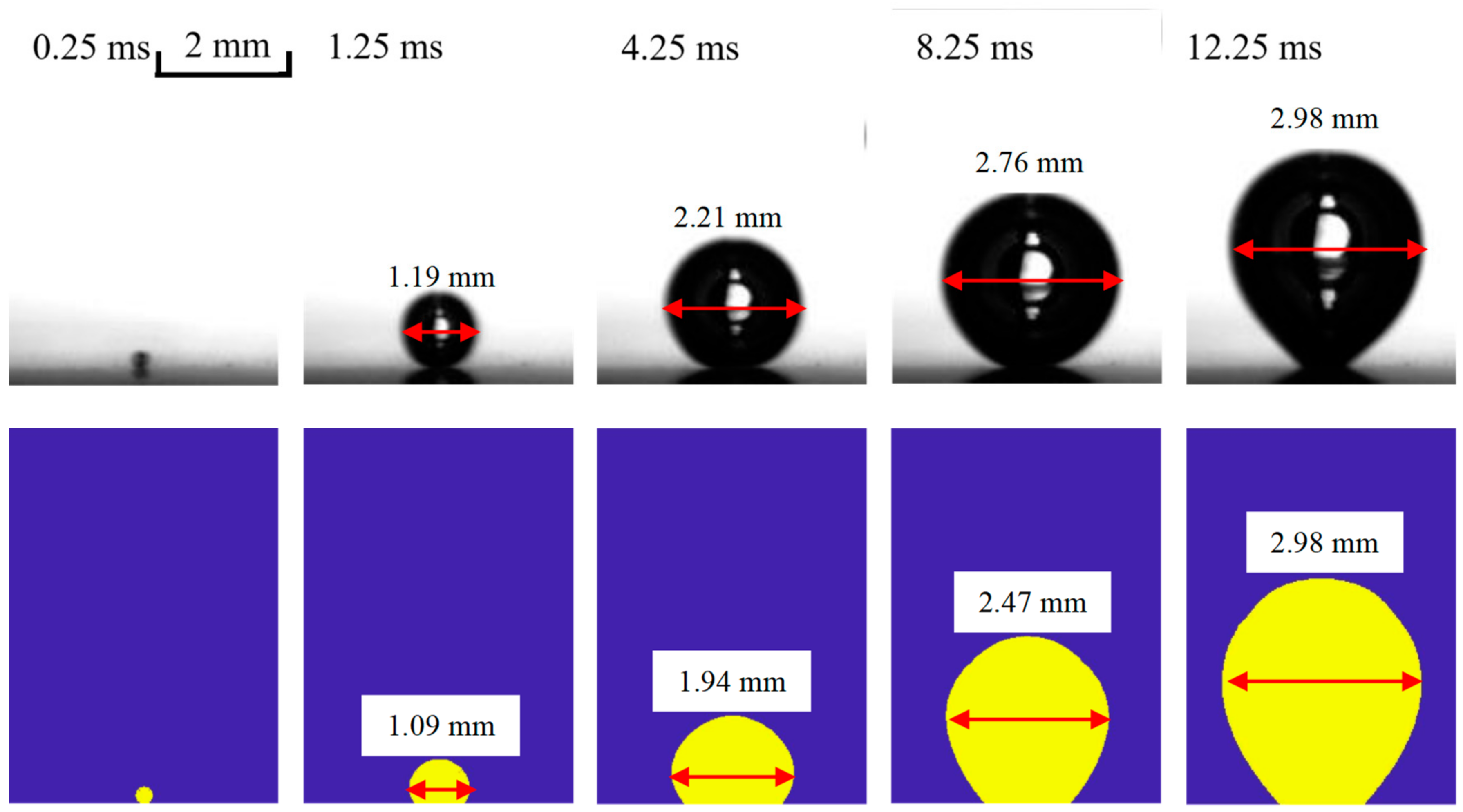
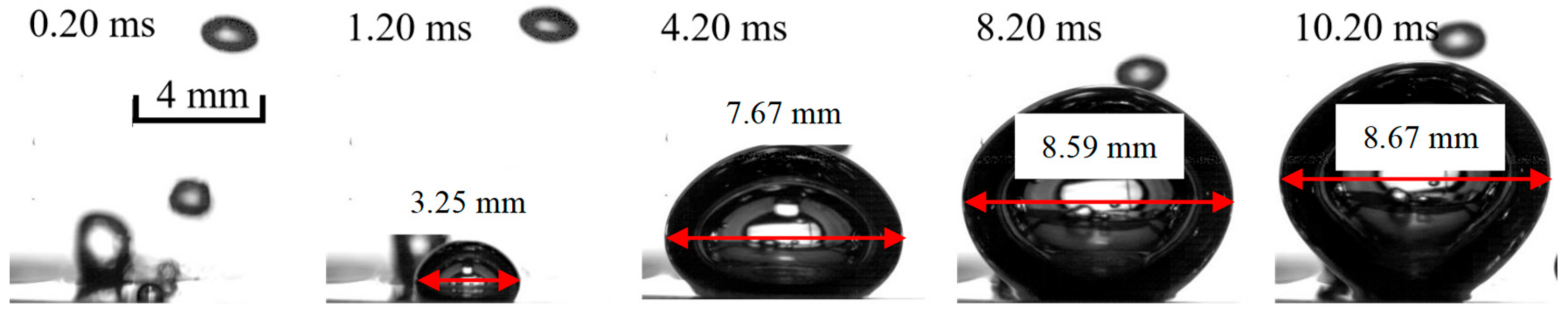
3.2. Pool Boiling on Bared Surfaces
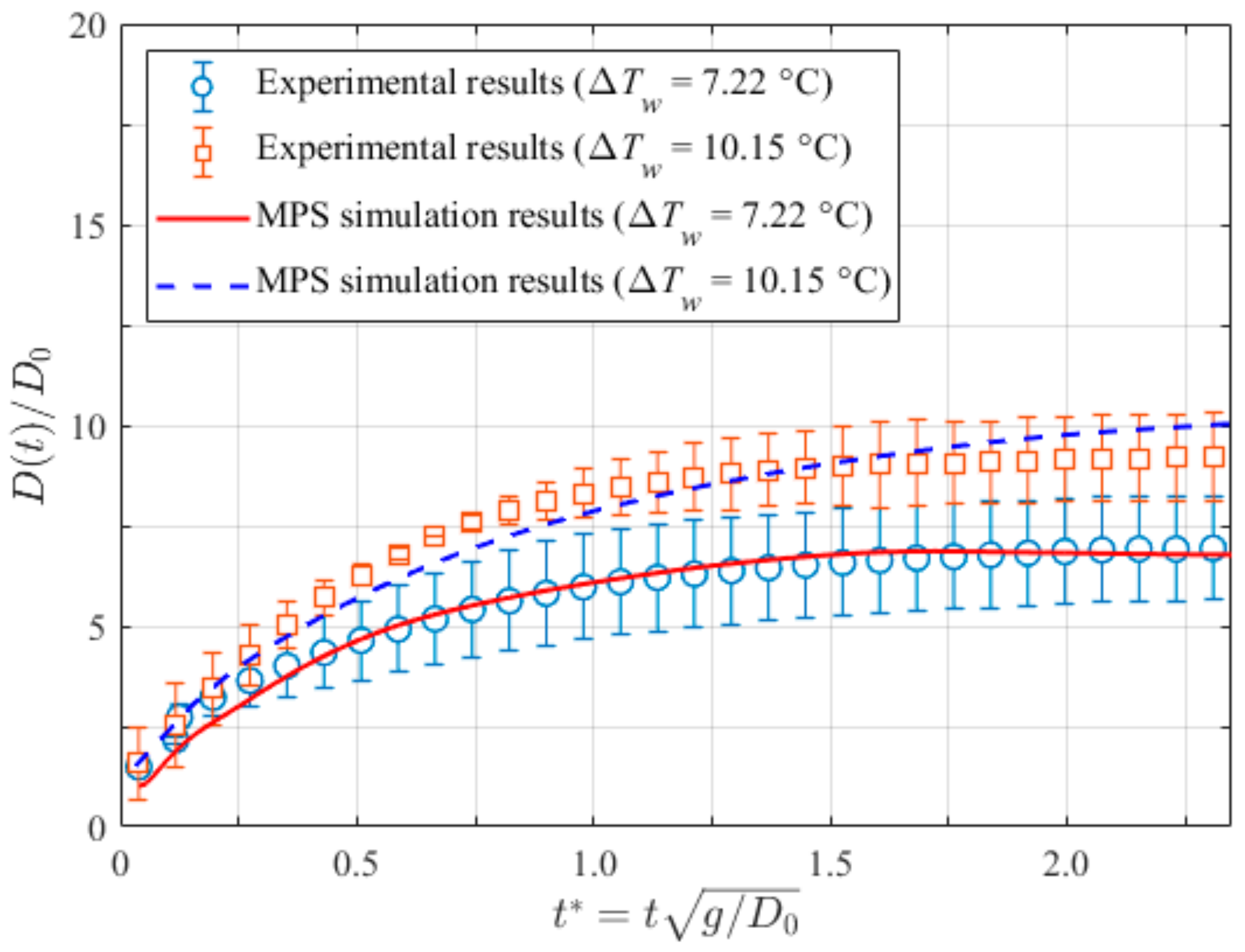
3.3. Pool Boiling on the Layer-by-Layer (LbL) Nano-Structured Surfaces
4. Results and Discussion
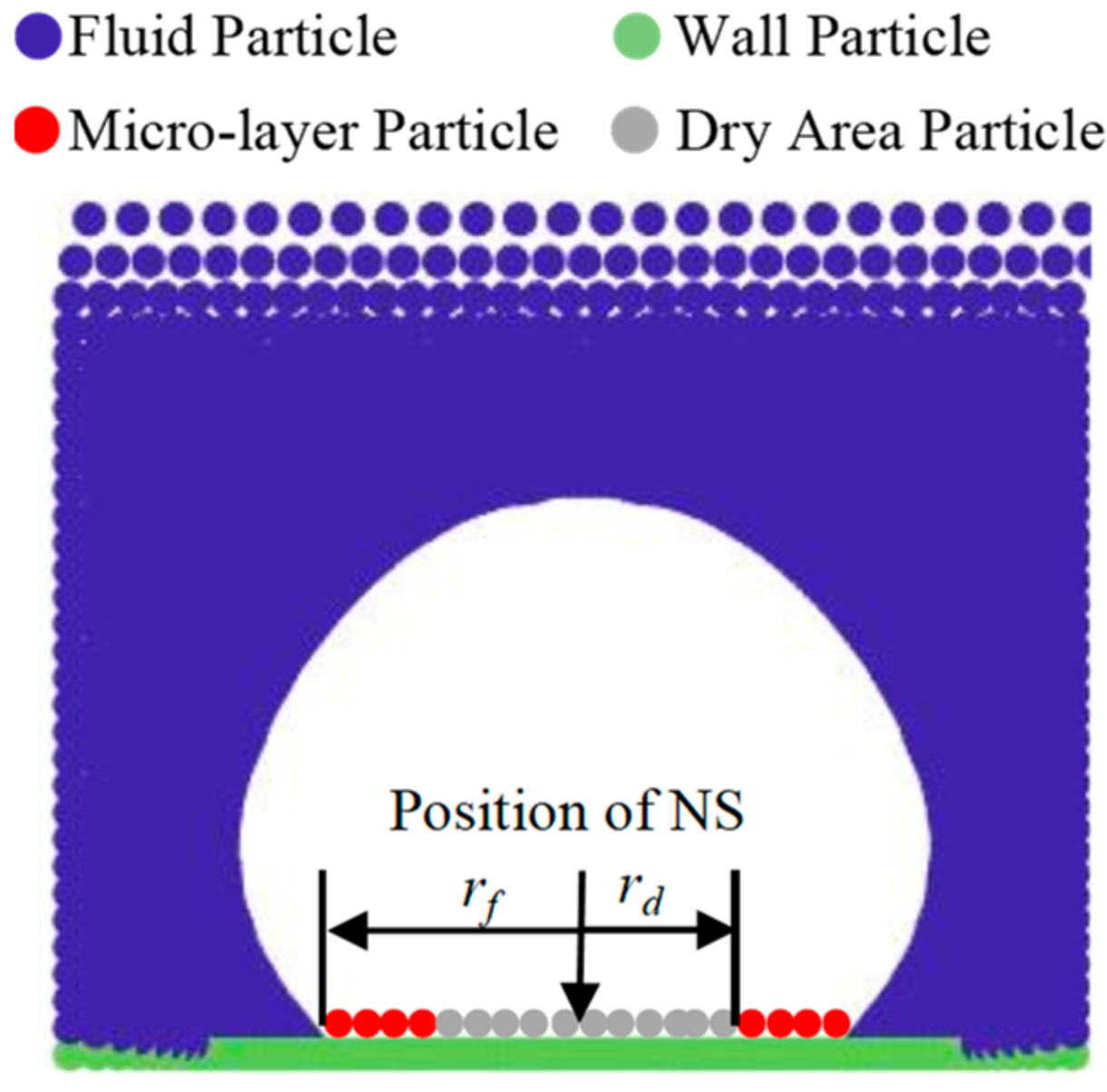
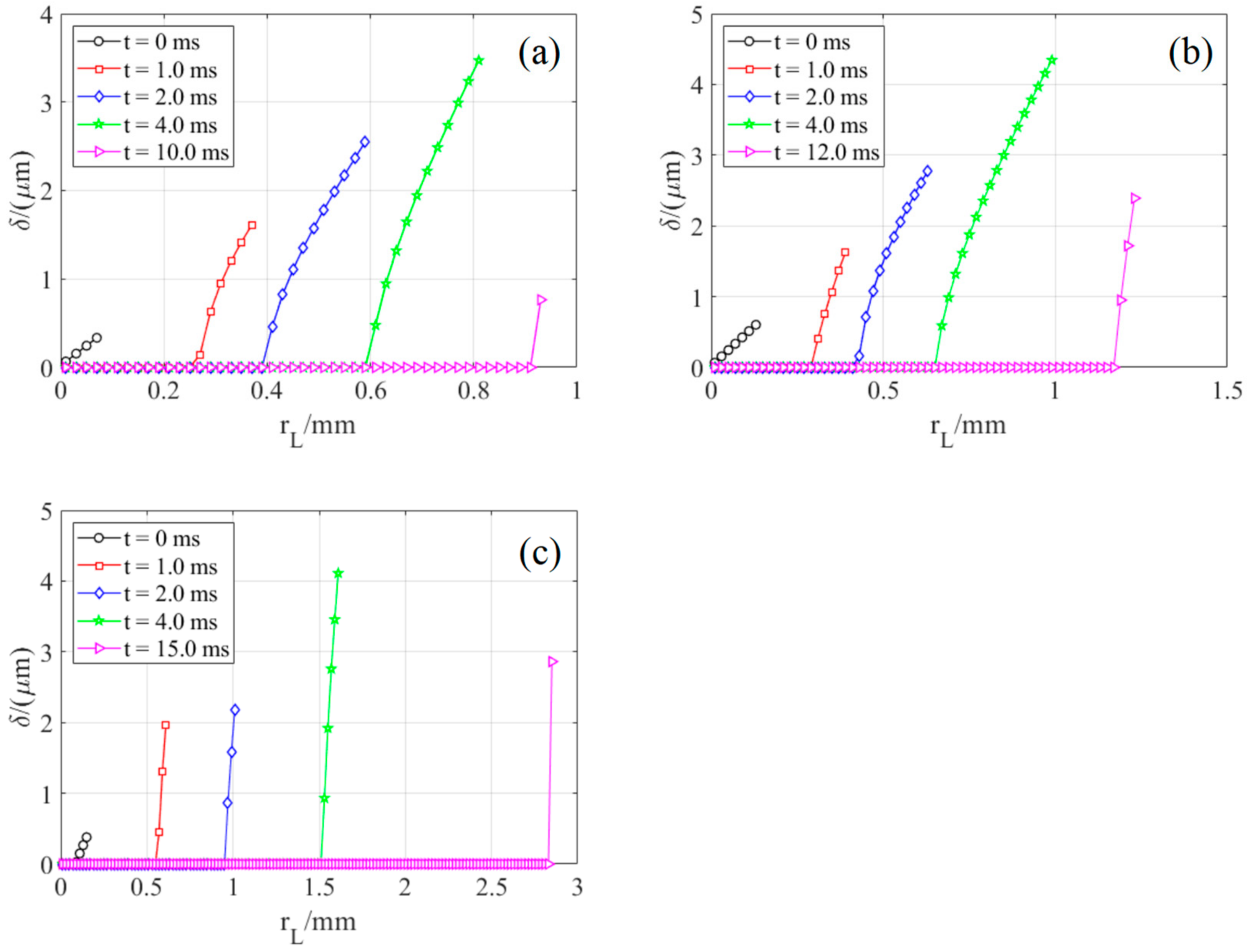
4.1. Variation of Micro-Layer Radius and Thickness
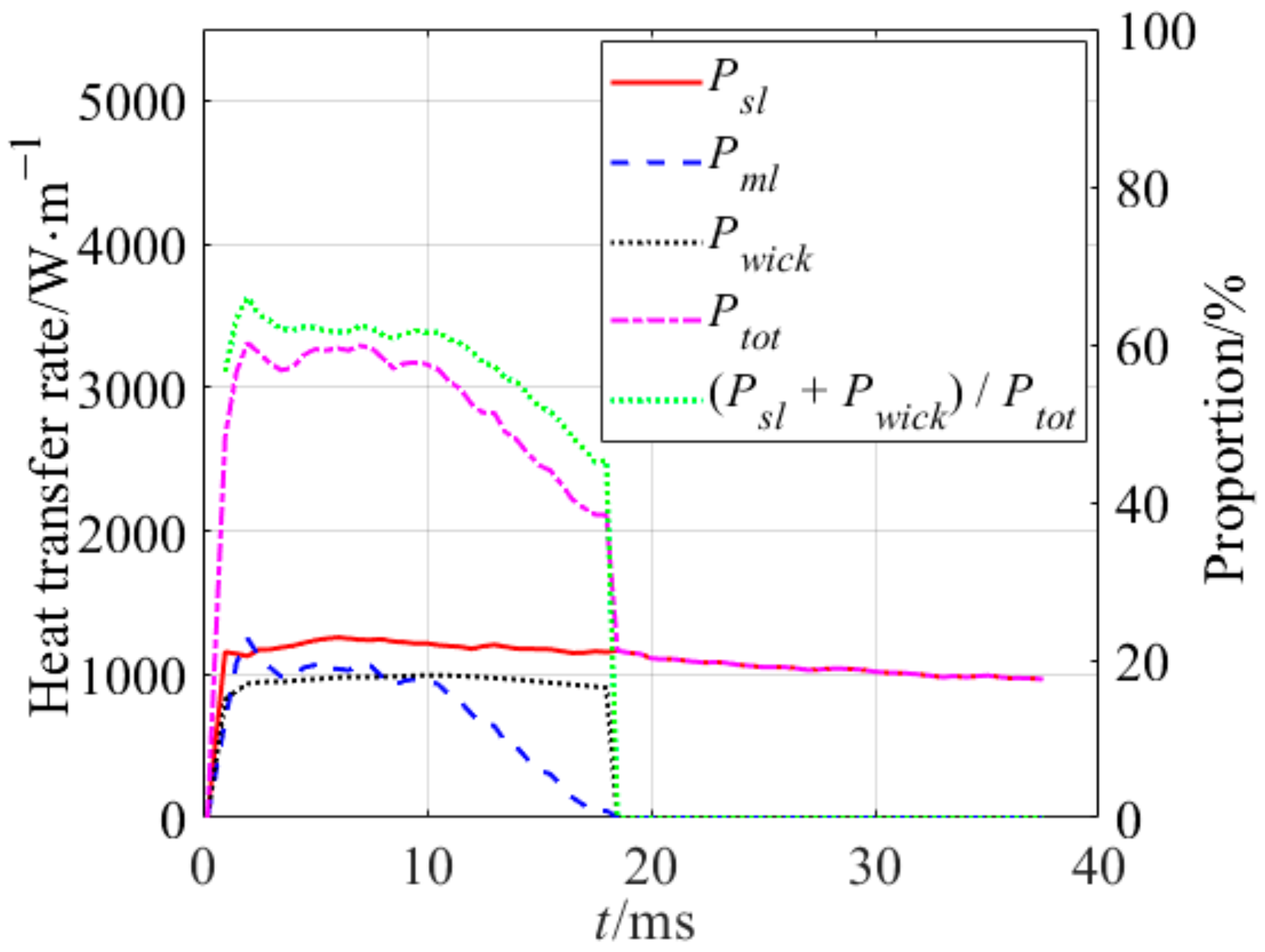
4.2. Analysis of Heat Transfer Process
5. Conclusions
- (1)
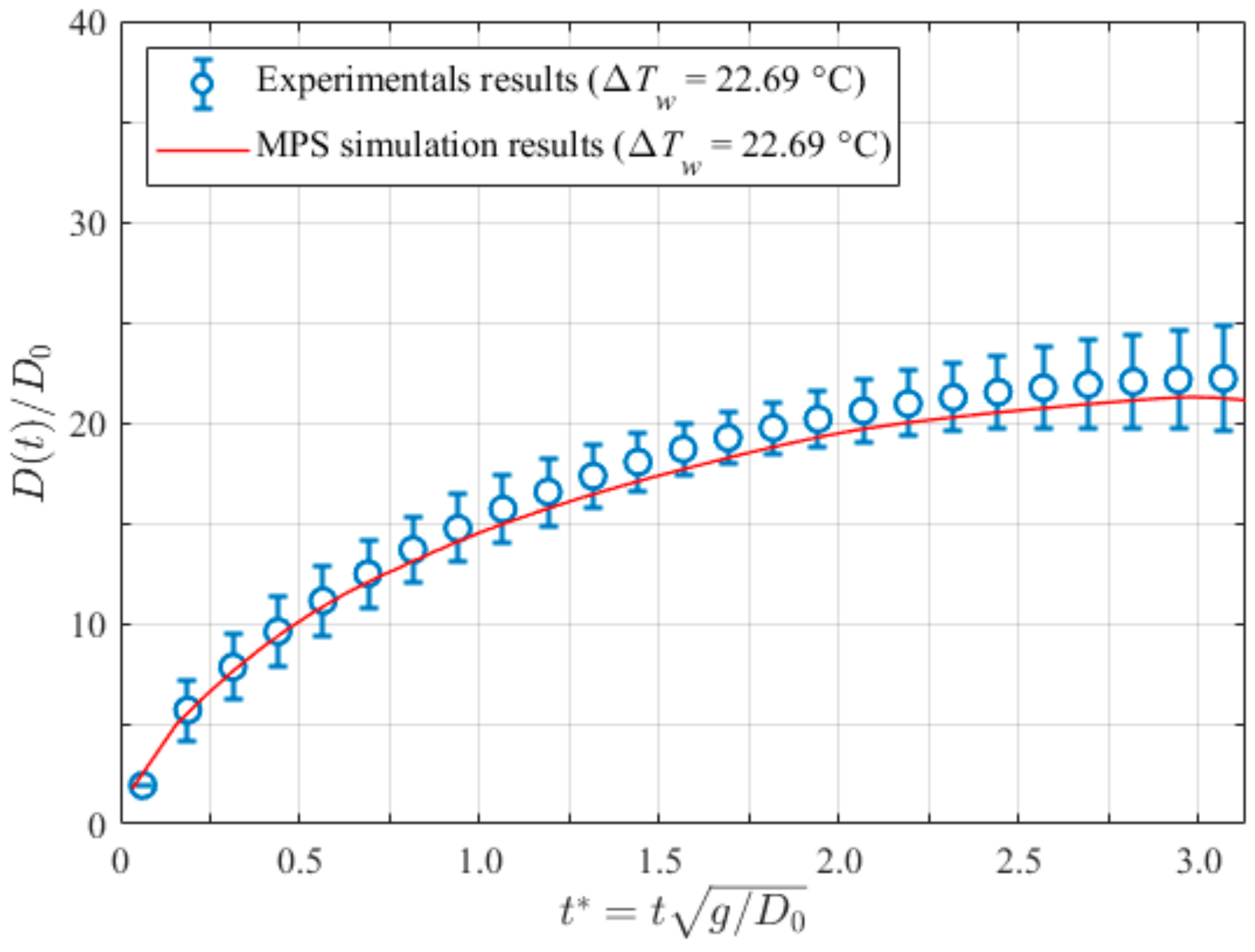
- Corresponding experiments were adopted as validations for the present method. The comparisons between the computed and experimental bubble growth rates showed great agreement. The maximum relative error was less than 5%, which reveals the robustness of the current method in simulating the growing bubble on both bared and nano-structured surfaces.
- (2)
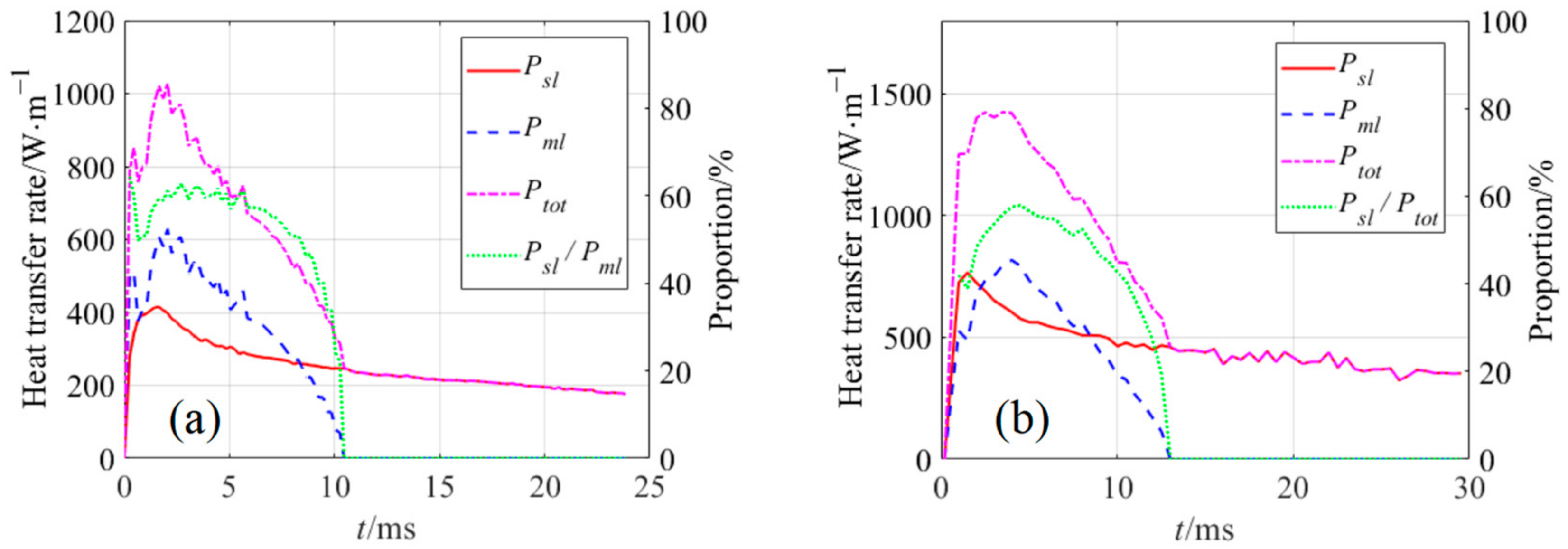
- Micro-layers beneath bubbles were investigated. Variations of their thickness and occupied area were successfully captured. The micro-layers’ max thickness was found to increase first and then decrease in all cases. The proportion of Pml in the bubble growth process on the bared surface was 40.55% at ΔTw = 7.22 °C and 32.23% at ΔTw = 10.15 °C, which is strong evidence that the micro-layer evaporation cannot be neglected during the pooling boiling simulation.
- (3)
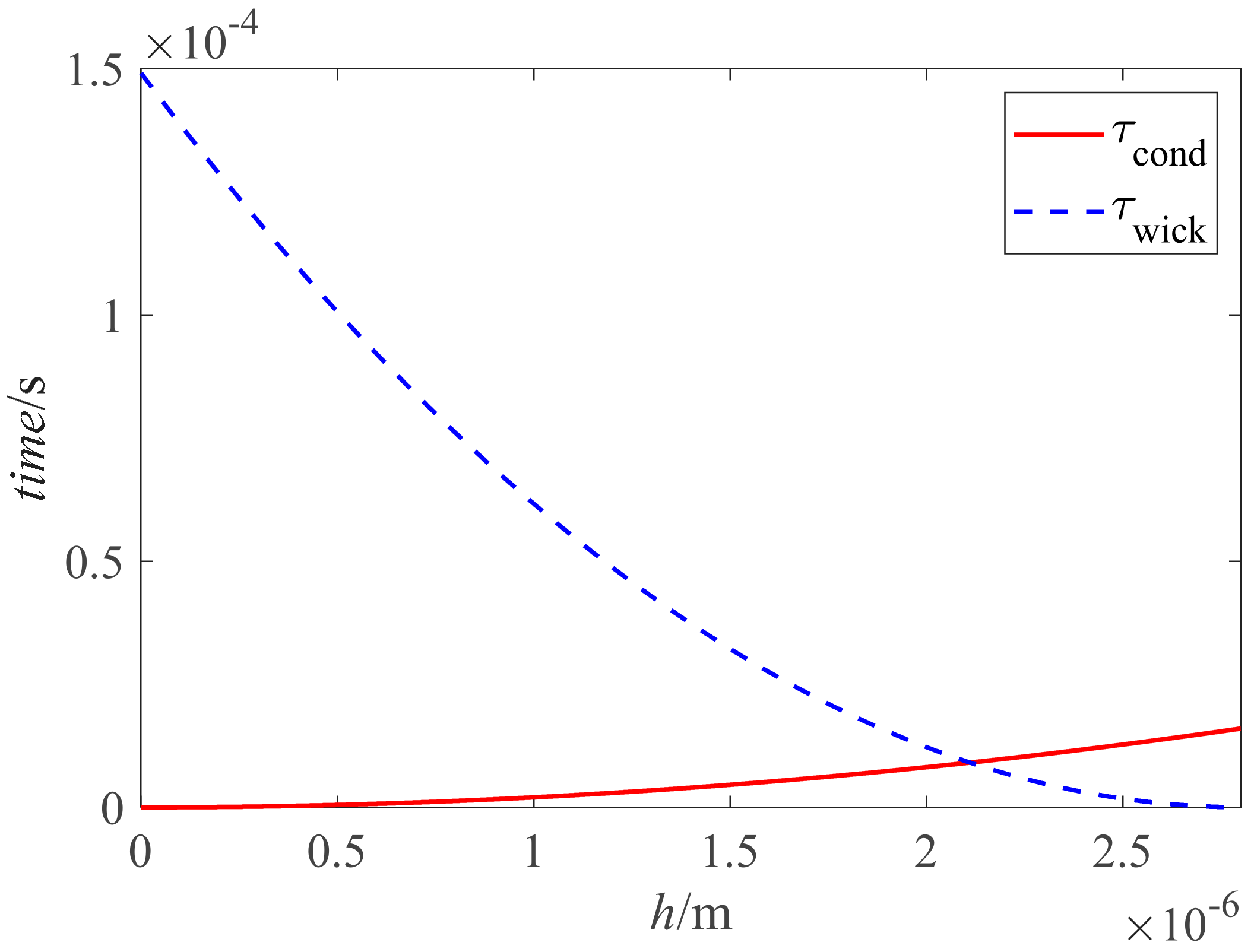
- The heat transfer process was investigated during bubble growth. The heat transfer contributions of the micro-layer and the wicked fluid were about 42.13% in the bubble growth on the nano-structured heater. The ratio of Pwick and Pml was 14:11.
- (4)
- The current research was the first attempt at directly simulating the bubble growth on the nano-structure. Simulations in this study give us a quantitative awareness of the heat transfer process during the bubble growth on the nano-structured surface.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kutateladze, S.S. Heat Transfer in Condensation and Boiling; AEC-tr-3770; US Atomic Energy Commission, Technical Information Service: Washington, DC, USA, 1952.
- Zuber, N. On the instability of boiling heat transfer. Trans. ASME 1958, 80, 711–720. [Google Scholar]
- Zuber, N. Hydrodynamic Aspects of Boiling Heat Transfer; AEC Report; United States Atomic Energy Commission, Technical Information Service: Washington, DC, USA, 1959.
- Chi-Yeh, H.; Griffith, P. The mechanism of heat transfer in nucleate pool boiling—Part I: Bubble initiaton, growth and departure. Int. J. Heat Mass Transf. 1965, 8, 887–904. [Google Scholar] [CrossRef]
- Lienhard, J.H.; Dhir, V.K. Hydrodynamic Prediction of Peak Pool-boiling Heat Fluxes from Finite Bodies. J. Heat Transf. 1972, 95, 152–158. [Google Scholar] [CrossRef]
- Dhir, V.K.; Liaw, S.P. Framework for a Unified Model for Nucleate and Transition Pool Boiling. J. Heat Transf. 1989, 111, 739–746. [Google Scholar] [CrossRef]
- Kandlikar, S.G. A Theoretical Model to Predict Pool Boiling CHF Incorporating Effects of Contact Angle and Orientation. J. Heat Transf. 2000, 123, 1071–1079. [Google Scholar] [CrossRef]
- Ahn, H.S.; Lee, C.; Kim, H.; Jo, H.; Kang, S.; Kim, J.; Shin, J.; Kim, M.H. Pool boiling CHF enhancement by micro/nanoscale modification of zircaloy-4 surface. Nucl. Eng. Des. 2010, 240, 3350–3360. [Google Scholar] [CrossRef]
- Chu, K.-H.; Enright, R.; Wang, E.N. Structured surfaces for enhanced pool boiling heat transfer. Appl. Phys. Lett. 2012, 100, 241603. [Google Scholar] [CrossRef]
- Kim, S.; Bang, I.; Buongiorno, J.; Hu, L. Surface wettability change during pool boiling of nanofluids and its effect on critical heat flux. Int. J. Heat Mass Transf. 2007, 50, 4105–4116. [Google Scholar] [CrossRef]
- Bang, I.C.; Chang, S.H. Boiling heat transfer performance and phenomena of Al2O3–water nano-fluids from a plain surface in a pool. Int. J. Heat Mass Transf. 2005, 48, 2407–2419. [Google Scholar] [CrossRef]
- Pham, Q.; Kim, T.; Lee, S.; Chang, S. Enhancement of critical heat flux using nano-fluids for Invessel Retention–External Vessel Cooling. Appl. Therm. Eng. 2012, 35, 157–165. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Liao, L. Sorption and agglutination phenomenon of nanofluids on a plain heating surface during pool boiling. Int. J. Heat Mass Transf. 2008, 51, 2593–2602. [Google Scholar] [CrossRef]
- Ahmed, O.; Hamed, M. Experimental investigation of the effect of particle deposition on pool boiling of nanofluids. Int. J. Heat Mass Transf. 2012, 55, 3423–3436. [Google Scholar] [CrossRef]
- Yu, L.; Sur, A.; Liu, D. Flow Boiling Heat Transfer and Two-Phase Flow Instability of Nanofluids in a Minichannel. J. Heat Transf.-Trans. Asme 2015, 137, 051502. [Google Scholar] [CrossRef]
- Paul, G.; Das, P.K.; Manna, I. Assessment of the process of boiling heat transfer during rewetting of a vertical tube bottom flooded by alumina nanofluid. Int. J. Heat Mass Transf. 2016, 94, 390–402. [Google Scholar] [CrossRef]
- Das, S.; Saha, B.; Bhaumik, S. Experimental study of nucleate pool boiling heat transfer of water by surface functionalization with SiO 2 nanostructure. Exp. Therm. Fluid Sci. 2016, 81, 454–465. [Google Scholar] [CrossRef]
- Stutz, B.; Morceli, C.H.S.; Da Silva, M.D.F.; Cioulachtjian, S.; Bonjour, J. Influence of nanoparticle surface coating on pool boiling. Exp. Therm. Fluid Sci. 2011, 35, 1239–1249. [Google Scholar] [CrossRef]
- Can, E.; Prosperetti, A. A level set method for vapor bubble dynamics. J. Comput. Phys. 2012, 231, 1533–1552. [Google Scholar] [CrossRef]
- Ryan, W.H.; Kuo, K.K. A ghost fluid method for compressible reacting flows with phase change. J. Comput. Phys. 2013, 235, 865–900. [Google Scholar]
- Ghosh, K.; Mukhopadhyay, A.; Sen, S.; Sanyal, D. A Sphericosymmetric VOF Approach for Investigating Immiscible Two-Phase Systems with One Liquid Phase. Numer. Heat Transf. Part A Appl. 2006, 50, 949–974. [Google Scholar] [CrossRef]
- Stephan, P.; Fuchs, T.; Wagner, E.; Schweizer, N. Transient local heat fluxes during the entire vapor bubble life time. In Proceedings of the ECI International Conference on Boiling Heat Transfer, Florianopolis, Brazil, 3–7 May 2009. [Google Scholar]
- Gerardi, C.; Buongiorno, J.; Hu, L.-W.; McKrell, T. Study of bubble growth in water pool boiling through synchronized, infrared thermometry and high-speed video. Int. J. Heat Mass Transf. 2010, 53, 4185–4192. [Google Scholar] [CrossRef]
- Cooper, M.G.; Lloyd, A.J.P. The microlayer in nucleate pool boiling. Int. J. Heat Mass Transf. 1969, 12, 895–913. [Google Scholar] [CrossRef]
- Lee, R.C.; Nydahl, J.E. Numerical Calculation of Bubble Growth in Nucleate Boiling from Inception Through Departure. J. Heat Transf. 1989, 111, 474–479. [Google Scholar] [CrossRef]
- Van Stralen, S.; Sohal, M.; Cole, R.; Sluyter, W. Bubble growth rates in pure and binary systems: Combined effect of relaxation and evaporation microlayers. Int. J. Heat Mass Transf. 1975, 18, 453–467. [Google Scholar] [CrossRef]
- Utaka, Y.; Kashiwabara, Y.; Ozaki, M. Microlayer structure in nucleate boiling of water and ethanol at atmospheric pressure. Int. J. Heat Mass Transf. 2013, 57, 222–230. [Google Scholar] [CrossRef]
- Utaka, Y.; Kashiwabara, Y.; Ozaki, M.; Chen, Z. Heat transfer characteristics based on microlayer structure in nucleate pool boiling for water and ethanol. Int. J. Heat Mass Transf. 2014, 68, 479–488. [Google Scholar] [CrossRef]
- Sato, Y.; Niceno, B. A depletable micro-layer model for nucleate pool boiling. J. Comput. Phys. 2015, 300, 20–52. [Google Scholar] [CrossRef]
- Chen, Z.; Utaka, Y. On heat transfer and evaporation characteristics in the growth process of a bubble with microlayer structure during nucleate boiling. Int. J. Heat Mass Transf. 2015, 81, 750–759. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, F.; Utaka, Y. Numerical simulation of thermal property effect of heat transfer plate on bubble growth with microlayer evaporation during nucleate pool boiling. Int. J. Heat Mass Transf. 2018, 118, 989–996. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, F.; Utaka, Y.; Chen, P.; Liang, C. An Improved Treatment on the Apparent Contact Angle of a Single-Bubble in Consideration of Microlayer for Simulations of Nucleate Pool Boiling. J. Therm. Sci. 2021, 30, 1951–1959. [Google Scholar] [CrossRef]
- Lee, W.; Son, G. Numerical simulation of boiling enhancement on a microstructured surface. Int. Commun. Heat Mass Transf. 2011, 38, 168–173. [Google Scholar] [CrossRef]
- Li, Q.; Yu, Y.; Zhou, P.; Yan, H. Enhancement of boiling heat transfer using hydrophilic-hydrophobic mixed surfaces: A lattice Boltzmann study. Appl. Therm. Eng. 2017, 132, 490–499. [Google Scholar] [CrossRef]
- Yu, Y.; Wen, Z.; Li, Q.; Zhou, P.; Yan, H. Boiling heat transfer on hydrophilic-hydrophobic mixed surfaces: A 3D lattice Boltzmann study. Appl. Therm. Eng. 2018, 142, 846–854. [Google Scholar] [CrossRef]
- Wang, W.; Huang, S.; Luo, X. MD simulation on nano-scale heat transfer mechanism of sub-cooled boiling on nano-structured surface. Int. J. Heat Mass Transf. 2016, 100, 276–286. [Google Scholar] [CrossRef]
- She, X.; Shedd, T.A.; Lindeman, B.; Yin, Y.; Zhang, X. Bubble formation on solid surface with a cavity based on molecular dynamics simulation. Int. J. Heat Mass Transf. 2016, 95, 278–287. [Google Scholar] [CrossRef]
- Liu, R.; Liu, Z. Study of boiling heat transfer on concave hemispherical nanostructure surface with MD simulation. Int. J. Heat Mass Transf. 2019, 143, 118534. [Google Scholar] [CrossRef]
- Rahman, M.M.; Ölçeroğlu, E.; McCarthy, M. Role of Wickability on the Critical Heat Flux of Structured Superhydrophilic Surfaces. Langmuir ACS J. Surf. Colloids 2014, 30, 11225. [Google Scholar] [CrossRef] [PubMed]
- Tetreault-Friend, M.; Azizian, R.; Bucci, M.; McKrell, T.; Buongiorno, J.; Rubner, M.; Cohen, R. Critical heat flux maxima resulting from the controlled morphology of nanoporous hydrophilic surface layers. Appl. Phys. Lett. 2016, 108, 243102. [Google Scholar] [CrossRef]
- Yoon, H.Y.; Koshizuka, S.; Oka, Y. Particle-Gridless Hybrid Method for Incompressible Flows. Int. J. Numer. Methods Fluids 1999, 30, 407–424. [Google Scholar] [CrossRef]
- Koshizuka, S.; Oka, Y. Moving-Particle Semi-Implicit Method for Fragmentation of Incompressible Fluid. Nucl. Sci. Eng. 1996, 123, 421–434. [Google Scholar] [CrossRef]
- Yoon, H.Y.; Koshizuka, S.; Oka, Y. Direct calculation of bubble growth, departure, and rise in nucleate pool boiling. Int. J. Multiph. Flow 2001, 27, 277–298. [Google Scholar] [CrossRef]
- Chen, R.; Tian, W.; Su, G.; Qiu, S.; Ishiwatari, Y.; Oka, Y. Numerical investigation on bubble dynamics during flow boiling using moving particle semi-implicit method. Nucl. Eng. Des. 2010, 240, 3830–3840. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, J.M. Numerical simulation on single bubble behavior during Al2O3/H2O nanofluids flow boiling using Moving Particle Simi-implicit method. Prog. Nucl. Energy 2015, 85, 130–139. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Son, G.; Ramanujapu, N.; Dhir, V.K. Numerical Simulation of Bubble Merger Process on a Single Nucleation Site During Pool Nucleate Boiling. J. Heat Transf. 2002, 124, 51–62. [Google Scholar] [CrossRef]
- Guo, K.; Chen, R.; Li, Y.; Tian, W.; Su, G.; Qiu, S. Numerical simulation of Rayleigh-Taylor Instability with periodic boundary condition using MPS method. Prog. Nucl. Energy 2018, 109, 130–144. [Google Scholar] [CrossRef]
- Guo, K.; Chen, R.; Qiu, S.; Tian, W.; Su, G. An improved Multiphase Moving Particle Semi-implicit method in bubble rising simulations with large density ratios. Nucl. Eng. Des. 2018, 340, 370–387. [Google Scholar] [CrossRef]
- Lancaster, P.; Salkauskas, K. Surfaces generated by moving least squares methods. Math. Comput. 1981, 37, 141–158. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. A higher order Laplacian model for enhancement and stabilization of pressure calculation by the MPS method. Appl. Ocean Res. 2010, 32, 124–131. [Google Scholar] [CrossRef]
- Chen, R.; Chen, L.; Guo, K.; Yamaji, A.; Furuya, M.; Tian, W.; Su, G.; Qiu, S. Numerical analysis of the melt behavior in a fuel support piece of the BWR by MPS. Ann. Nucl. Energy 2017, 102, 422–439. [Google Scholar] [CrossRef]
- Chen, R.H.; Tian, W.X.; Su, G.H.; Qiu, S.Z.; Ishiwatari, Y.; Oka, Y. Numerical investigation on coalescence of bubble pairs rising in a stagnant liquid. Chem. Eng. Sci. 2011, 66, 5055–5063. [Google Scholar] [CrossRef]
- Lee, W.; Son, G.; Yoon, H.Y. Numerical study of bubble growth and boiling heat transfer on a microfinned surface. Int. Commun. Heat Mass Transf. 2012, 39, 52–57. [Google Scholar] [CrossRef]
- Marek, R.; Straub, J. Analysis of the evaporation coefficient and the condensation coefficient of water. Int. J. Heat Mass Transf. 2001, 44, 39–53. [Google Scholar] [CrossRef]
- Kaviany, M. Principle of Heat Transfer in Porous Media; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Kim, H.D.; Kim, M.H. Effect of nanoparticle deposition on capillary wicking that influences the critical heat flux in nanofluids. Appl. Phys. Lett. 2007, 91, 014104. [Google Scholar] [CrossRef]
- Chen, H.; Sun, Y.; Xiao, H.; Liu, L. Numerical simulation of single bubble boiling on micro-pillar structure surface. Chem. Ind. Eng. Prog. 2019, 38, 4845–4855. (In Chinese) [Google Scholar]


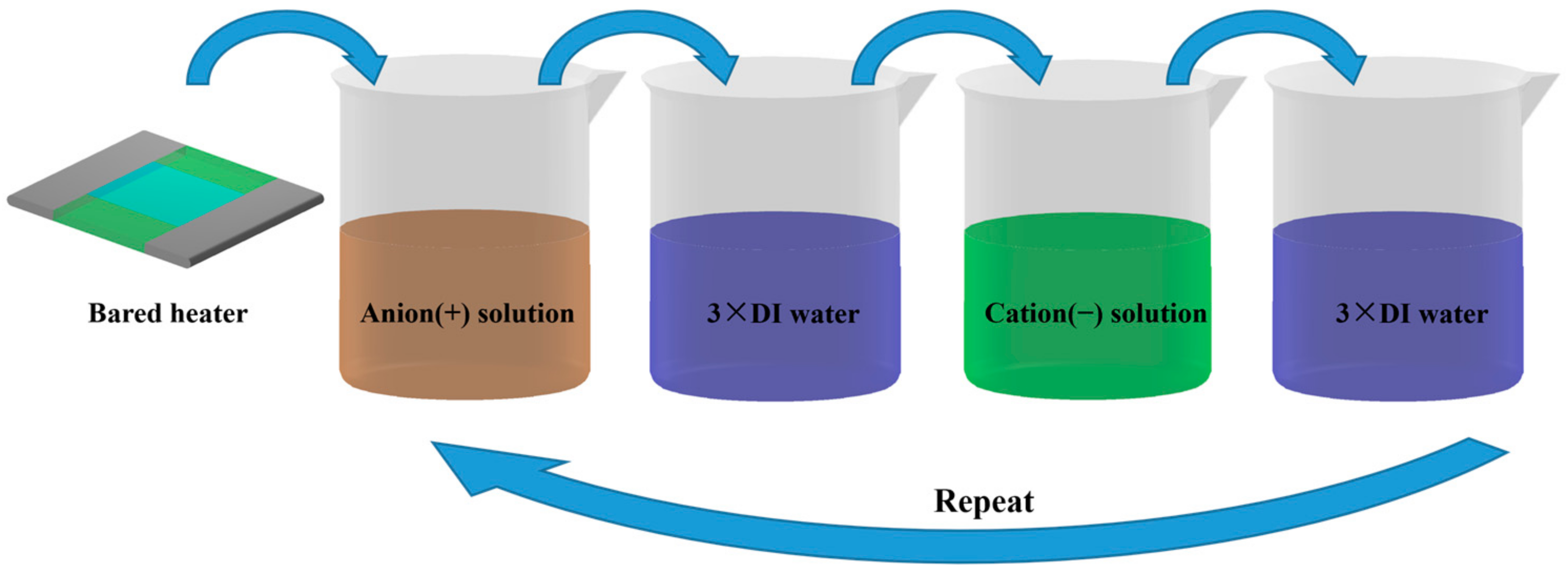
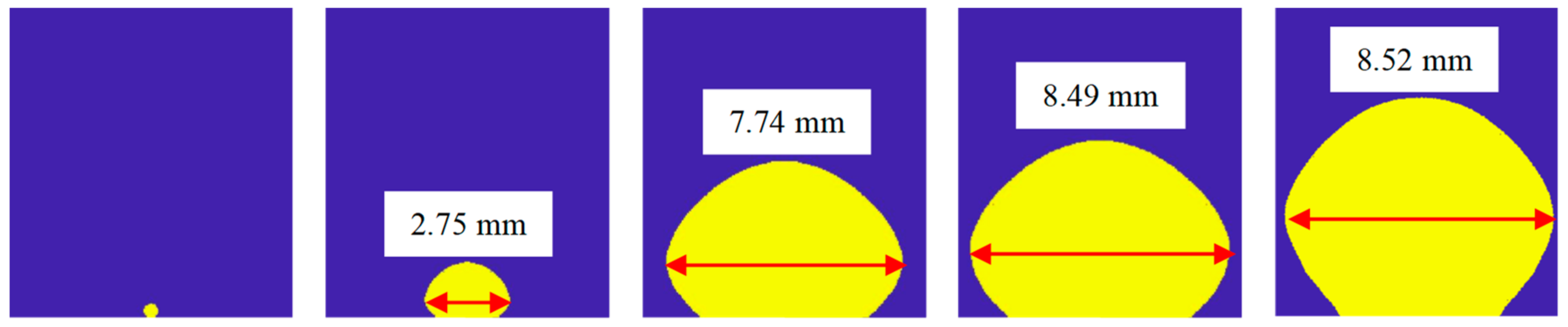
| No. of Bilayers | Size of Nano-Particle/nm | Thickness of the Nano-Sturcture/μm | Surface Roughness/nm | Porosity/% |
|---|---|---|---|---|
| 0 | N/A | 0 | <10 | N/A |
| 22 | 20 ± 2 | 0.50 ± 0.02 | 26 ± 3 | 63 ± 1 |
| 34 | 20 ± 2 | 0.93 ± 0.04 | 45 ± 6 | 63 ± 1 |
| 42 | 20 ± 2 | 1.18 ± 0.05 | 53 ± 8 | 63 ± 1 |
| 53 | 20 ± 2 | 1.42 ± 0.05 | 67 ± 20 | 63 ± 1 |
| 70 | 20 ± 2 | 1.90 ± 0.1 | 97 ± 19 | 63 ± 1 |
| 100 | 20 ± 2 | 2.76 ± 0.08 | 162 ± 25 | 63 ± 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, K.; Li, S.; Zhong, Y.; Chen, R.; Wang, M.; Qiu, S.; Tian, W.; Su, G. Heat Transfer Mechanism Investigation of Bubble Growth on the Superhydrophilic Nano-Structured Surface Using Moving Particle Semi-Implicit Method. Appl. Sci. 2023, 13, 4114. https://doi.org/10.3390/app13074114
Guo K, Li S, Zhong Y, Chen R, Wang M, Qiu S, Tian W, Su G. Heat Transfer Mechanism Investigation of Bubble Growth on the Superhydrophilic Nano-Structured Surface Using Moving Particle Semi-Implicit Method. Applied Sciences. 2023; 13(7):4114. https://doi.org/10.3390/app13074114
Chicago/Turabian StyleGuo, Kailun, Sijun Li, Yubao Zhong, Ronghua Chen, Mingjun Wang, Suizheng Qiu, Wenxi Tian, and Guanghui Su. 2023. "Heat Transfer Mechanism Investigation of Bubble Growth on the Superhydrophilic Nano-Structured Surface Using Moving Particle Semi-Implicit Method" Applied Sciences 13, no. 7: 4114. https://doi.org/10.3390/app13074114
APA StyleGuo, K., Li, S., Zhong, Y., Chen, R., Wang, M., Qiu, S., Tian, W., & Su, G. (2023). Heat Transfer Mechanism Investigation of Bubble Growth on the Superhydrophilic Nano-Structured Surface Using Moving Particle Semi-Implicit Method. Applied Sciences, 13(7), 4114. https://doi.org/10.3390/app13074114







