Abstract
A Sodium-cooled Fast Reactor (SFR) is one of the optimized candidates in Generation IV nuclear reactor systems, but safety is an essential issue for SFR development and application. Most knowledge was accumulated through SFR safety investigations, especially for Core Disruptive Accidents (CDAs). During the CDA of SFRs, the molten materials in the core region are likely to discharge into subcooled sodium and form a debris bed on the lower region of the reactor vessel. Noticing that elaboration on the characteristics and mechanisms of Debris Bed Formation (DBF) behavior should be essential for the subsequent analysis of debris bed coolability and accident progression through various experimental and modeling studies, much knowledge was obtained during the past decades. Motivated to promote future investigations on CDAs of SFRs, the previous experiments and modeling studies on DBF behavior are systematically reviewed and discussed in this paper. The experimental results showed that the flow-regime and accumulated-bed characteristics during DBF were influenced by varying parameters and realistic conditions. Through the modeling studies, several empirical models were proposed for predicting the flow regime and accumulated-bed characteristics in DBF. In addition, to promote further development of research, the future prospects concerning DBF behavior are also described.
1. Introduction
Over the 70-year period of nuclear power reactor development, the fission reactor concepts evolved from early prototype reactors (Generation I) to commercial power reactors (Generation II) and advanced Light Water Reactors (LWRs) with progressive designs (Generation III or III+). However, to develop advanced nuclear energy systems with increased safety, stronger economic competitiveness, less nuclear waste, and effective prevention of nuclear proliferation, Generation IV nuclear reactor systems have become a crucial research topic for global nuclear energy researchers in recent years [1]. A Sodium-cooled Fast Reactor (SFR) is considered a significant Generation IV nuclear reactor system due to its attractive breeding characteristic and extensive experience in construction and operations [2]. However, safety, a key issue for the development and application of nuclear energy, still requires enhancement and improvement for SFRs [1]. Though Core Disruptive Accidents (CDAs) should rarely occur thanks to the defense-in-depth strategy, the analysis of CDAs has attracted significant attention during SFR development because the designs of the SFR core are generally not in the most reactive configurations [3,4,5,6,7]. Therefore, it is crucial and necessary to assess the CDAs of SFRs from a safety standpoint. In a typical CDA of an SFR, the progression of the accidental event can be divided into four phases, including (1) the initiating phase [8,9,10], (2) the transition phase [11,12,13], (3) the post-accident material relocation (PAMR) phase [14,15,16,17], and (4) the post-accident heat removal (PAHR) phase [18,19,20,21,22]. During the PAMR phase, in a subcooled sodium pool, the molten fuel, structural components, and other materials may be discharged from the reactor core, rapidly quenched, and fragmented into solid debris due to interactions with the sodium coolant. After falling, the debris will accumulate in the lower plenum of the reactor vessel (or on the core-support structures) to form a debris bed. [23,24]. Figure 1 illustrates the debris bed formation. It is generally believed that the full fragmentation and solidification of the molten materials can be achieved in the case of a CDA of an SFR [25] forming debris beds consisting of solid particles or fragments of different sizes and porosity in the lower plenum [19,25,26,27].
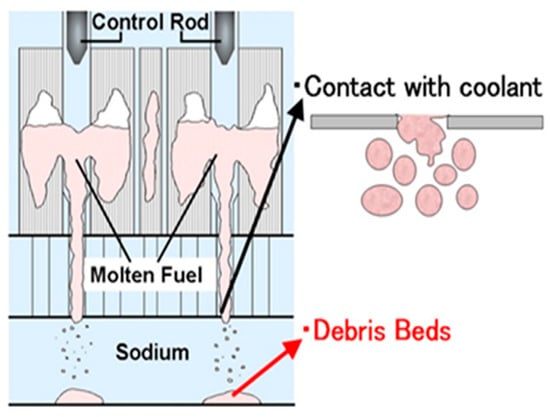
Figure 1.
Formation of the debris beds [24].
Considering that the debris bed configurations are of great essence to neutronic re-criticality and self-sustainable long-term coolability, adequate comprehensive evaluations for debris relocation in the CDA of an SFR are necessary to realize the In-Vessel Retention (IVR) for fuel debris [28,29,30]. On the other hand, focusing on the IVR of SFRs, relevant safety equipment (e.g., core catchers) is also recommended for employment below the reactor vessel to enlarge the safety margin [26,31]. It is expected that the stable removal of decay heat from the debris beds is achievable using core-catcher structures thanks to the natural convection of the sodium coolant. Noting that the characteristics of the debris beds can significantly impact their ability to remove decay heat, it is crucial to understand the characteristics and mechanisms of Debris Bed Formation (DBF), which are helpful in improving the design of SFR core catchers (such as their structures, retention capacities, and sizes) to further guarantees the safety IVR during the CDAs.
During the past decades, studies focusing on heat transfer within debris beds were performed [32,33,34,35,36,37,38,39,40,41]. In these investigations, in general, the initial debris bed shape was supposed to be homothetically piled [37], cylindrical [38], heap-like [40,41], and Gaussian-shaped [39] or conical [16,42,43,44]. Nevertheless, it was found that the geometries of debris beds (such as their heights) also significantly affect their heat removal capacity [45,46]. In the past few years, by assuming that the bed was initially conical (or convex), extensive investigations on the relocation phenomena of debris beds (termed as self-leveling) triggered by sodium boiling were performed [14,15,43,44,47,48,49,50]. Based on these investigations, the self-leveling mechanisms (e.g., bubble-particle interactions within particle beds) and characteristics (e.g., parametric influence on the leveling rate) were clarified. However, it should be noted that the complex multiphase flows, including solid debris, liquid coolant, and sodium vapor, involved in the DBF process can result in varying initial shapes of the debris bed, which in turn can influence the progression of severe accidents in SFRs. Hence, it Is of great importance to understand the characteristics and mechanisms of DBF behavior in severe accidents of SFRs.
Here, it should also be noted that in the context of the severe accidents of LWRs, the debris bed formation behavior was widely investigated with the aim of evaluating the debris bed coolability and subsequent Molten Core–Concrete Interaction (MCCI) [41,51,52,53,54,55,56], and many valuable findings were attained from these studies. However, due to the different thermal and hydraulic interactions made between the coolant and discharged molten core materials, it was found that the breakup and fragmentation of the discharged molten jet would be facilitated in SFRs because of the higher heat transfer between the two phases resulting from the direct liquid-liquid contact [27,57,58,59,60]. Therefore, in contrast to the LWR condition, wherein deep penetration of the discharged molten core jet likely occurred due to the vapor film formed between coolant and molten materials, the core materials are more easily fragmented into solid debris before reaching the reactor vessel or core catcher structures [27,57,58,59,60]. In addition, the debris size range in SFRs (e.g., 0.1 mm to several millimeters) is generally wider than that of LWRs (e.g., over several millimeters) [26,39,60,61], leading to varying debris bed formation characteristics.
Therefore, to elucidate the characteristics and mechanisms of DBF behavior in the case of an SFR, in the past decade, extensive experimental and modeling studies were performed separately at Kyushu University, the Japan Atomic Energy Agency (JAEA) [23,28,29,62,63,64], Indira Gandhi Centre for Atomic Research (IGCAR) [65], and Sun Yat-Sen University (SYSU) [24,66,67,68,69,70,71,72]. Figure 2 summarizes these investigations, which can be divided according to their different focal points: (1) investigations focusing on the overall accumulated-bed characteristics; and (2) investigations focusing on the flow regime characteristics. The research methodology used water and solid particles with different properties to simulate the liquid sodium and debris in CDAs. Solid particles were discharged into the water pool from the top by gravitation through a nozzle and accumulated at the bottom to form the particle bed. In the investigations focusing on the overall accumulated-bed characteristics [24,29,30,63,64,65,66], single-sized particles and mixed-sized solid particles in a range of 1.1~6.0 mm were employed, and some key parameters (e.g., particle type, nozzle height, and nozzle diameter) were quantitatively studied based on inter-particle interactions. It was found that concave or conical accumulated beds may be formed during DBF, dependent on the experimental conditions. Based on the experimental data, empirical models were developed to predict the key parameters that represented the accumulated characteristics (e.g., repose angle, mound, and bed height). However, it is noted that in these studies, the properties of the particles used cannot cover the entire range of typical debris formed in CDAs of SFRs (e.g., a size range from submillimeter to several millimeters), and the particle-fluid interactions are not clearly observable due to the limitations of the experimental setup. Therefore, a series of experimental and modeling studies were performed by focusing on the DBF flow-regime characteristics [24,66,67,68,69,70,71,72]. It was confirmed that due to the different inter-particle and particle-fluid interactions during different situations, four types of flow regime, including particle-suspension regime (Regime I), pool-convection dominant regime (Regime II), transitional regime (Regime III), and particle-inertia dominant regime (Regime IV), were found to form, leading to the formation of a flat bed, concave bed, trapezoid bed, and convex bed, respectively. Based on the different formation mechanisms of these flow regimes, an empirical model was developed to predict the DBF flow regime transitions, and its predictability was further extended owing to the knowledge accumulated from the experiments under more realistic conditions (e.g., mixed-sized particles and sodium boiling situations).
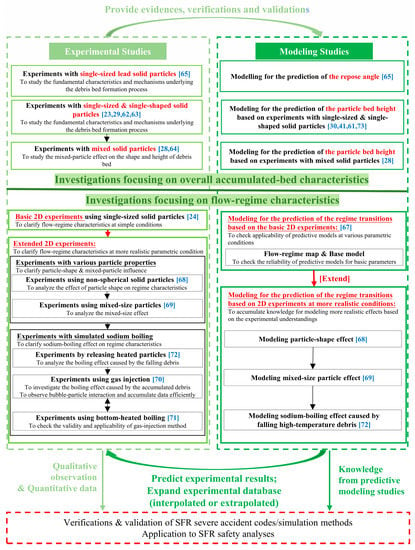
Figure 2.
Summary of experimental and modeling investigations on DBF behavior focusing on overall accumulated-bed characteristics [23,28,29,30,41,61,62,63,64,65,73] and flow-regime characteristics [24,67,68,69,70,71,72].
Considering the great importance of understanding DBF behavior to improve the safety evaluations of SFRs, a systematic review and critical discussion are performed in this paper based on experimental and modeling studies of DBF characteristics and mechanisms in the context of SFRs. The knowledge accumulated from valuable experimental evidence and reliable modeling predictions is significant to computer model improvement and verification and the optimization of the structural designs of the core catcher for SFRs, thereby promoting the development and application process of SFRs. The objective of this paper is to provide a comprehensive understanding of DBF characteristics and mechanisms in CDAs of SFRs through the systematic and critical review of previous experimental and modeling investigations. In Section 2, investigations focusing on overall accumulated-bed characteristics are introduced and summarized; while in Section 3, the investigation focuses on flow regime characteristics, which are described and discussed. Moreover, for the purpose of providing useful guidance and serving as a reference for further investigations regarding DBF behavior, a conclusion and a discussion of future prospects are described in Section 4 and Section 5, respectively.
2. Investigations Focusing on Overall Accumulated-Bed Characteristics
The characteristics of the accumulated bed formed after DBF behavior are crucial to the subsequent evaluation of debris bed heat removal. In IGCAR, experiments were conducted with high-density lead particles to develop an empirical model for predicting the repose angle of the formed debris bed [65]. At Kyushu University and JAEA, by employing single (i.e., single-sized and single-shaped) solid particles and mixed solid particles, some typical experimental parametric impacts on the overall accumulated-bed characteristics (e.g., bed height and shape) were clarified [23,28,29,62,63,64]. From their experiments, it was confirmed that under different experimental parameters, the debris bed’s geometrical shape would generally be convex or concave. Following the experimental investigations and to estimate and predict the bed height, the corresponding modeling investigations were carried out to develop an empirical predictive model [28,29], which is believed to be useful for expanding (interpolating or extrapolating) the experimental database and attaining more valuable knowledge. Based on the experimental data, an empirical model was first established for cases of single solid particles [29] and was then modified to be applicable to cases of mixed solid particles [28,29]. In this section, the investigations focusing on overall accumulated-bed characteristics are discussed.
2.1. Investigations with Single-Sized and Single-Shaped Solid Particles
2.1.1. Experimental Materials and Methods
Aimed at phenomenologically understanding the fundamental characteristics of DBF behavior, some pioneering simulated experiments by using water and single-sized and single-shaped solid particles to simulate sodium coolant and debris were conducted by Shamsuzzaman et al. [23,29,62,63] and Sudha et al. [65], concentrating on the overall accumulated-bed characteristics. Table 1 shows the comparison of material proprieties. Figure 3a shows the experimental system used by Sudha et al. [65], where a water tank measuring 27 × 36 × 38 cm and different release pipes were employed to obtain particle-releasing rates of 50~350 g/s. Nine experiments were performed by releasing a 1.7 kg single-sized spherical lead particle with a diameter of 1.8 mm into the water, transitioning from room temperature to 343K. Figure 3b displays the experimental apparatus, including a cylindrical container (375 mm inner diameter (Din), 1020 mm height) and an upper particle injection device followed by a cylindrical releasing nozzle. In total, 119 sets of experiments, including 43 sets using non-spherical particles, were conducted. To investigate the characteristics of accumulated particle beds, six key initial parameters, including particle density (ρp), particle diameter (dp), particle shape (spherical or non-spherical), particle volume (Vp, 3~10 L), nozzle diameter (dn, 20~40 mm), and nozzle height (Hn, 0.47~0.72 m), were considered. As shown in Figure 4, five important quantities related to bed characteristics, including the final bed height (Hb), final mound height (Hm), final mound dimple area (Adim), final dimple volume (Vdim), and final repose angle (θr) of the bed mound, were noted.

Table 1.
Comparison of material proprieties in experiments and reactor accidents (CDAs of SFRs) [24,29,68,74].
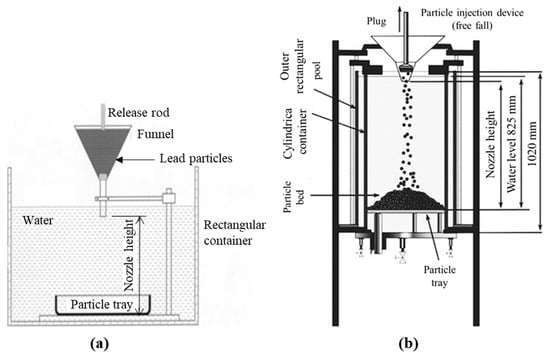
Figure 3.
Experimental system for the investigations focusing on overall accumulated-bed characteristics: (a) used by Sudha et al. [65], and (b) used by Shamsuzzaman et al. [29].
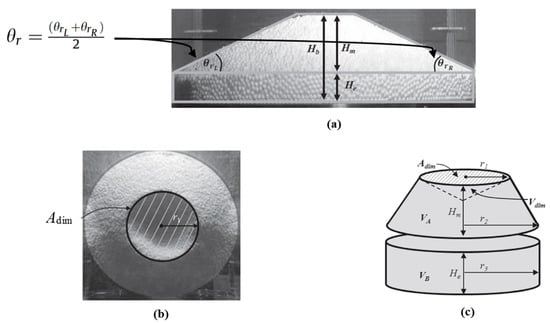
Figure 4.
Schematic illustrations of key quantities for representing the accumulated-bed characteristics. (a) Particle mound/bed height and repose angle; (b) dimple area; and (c) dimple volume [29].
2.1.2. Experimental Results and Discussion
Based on the experimental observations, it was initially confirmed that particle volume had no obvious impact on the final bed shape [23]. Then, through a series of experiments with Vp = 5 L, it was verified that, possibly due to the more significant impact of particle jets on the accumulated particle beds, more concave and flatter particle beds (i.e., particle beds with lower mound height, smaller repose angle, larger dimple area, and volume) could be attained when smaller-sized particles or a nozzle with larger diameter or higher placement were employed. In addition, it was confirmed that particle-shaped relevant characteristics (such as sphericity) could also effectively affect DBF behavior. Figure 5 shows the effect of particle shape. From this figure, it is observable that for non-spherical particles, potentially due to the smaller impacts of the falling particles on the accumulated particle beds and slower dissipation in lateral directions resulting from larger inter-particle friction [29], more particles accumulated on the bed center, leading to comparable higher particle mounds than those for the spherical cases. However, regarding the effect of particle density, the variations of Hm, Adim, and Vdim were found to be non-monotonous, although the repose angle seemed to decrease with the increase in particle density.
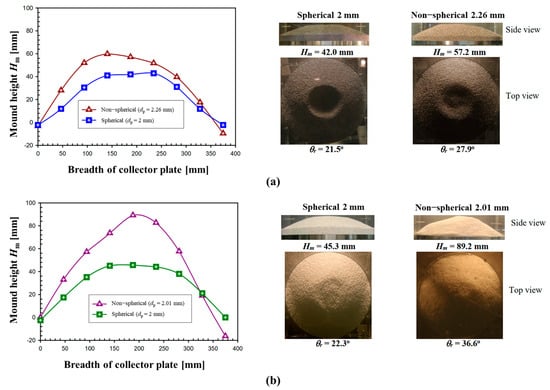
Figure 5.
Effect of particle shape on mound height (Hn = 720 mm, dn = 30 mm). (a) SS particle, and (b) Al2O3 particles [23,29].
In short, owing to these experiments employing single-sized and single-shaped particles, the fundamental characteristics of DBF were investigated, and the basic influences of particle size, nozzle height, and nozzle diameter on the overall accumulated-bed characteristics were revealed. Quantitative parametric analyses were performed, generally based on inter-particle interactions. Nevertheless, the effect of particle sphericity and density was not comprehensively identified. Moreover, more detailed characteristics and mechanisms during the DBF process (such as the particle-fluid interactions) were not comprehensively captured and explored.
2.1.3. Modeling Studies
For the purpose of modeling the important quantities characterizing DBF behavior, a predictive model focusing on Hb, which is one key factor indicating bed shape characteristics, was empirically established by Shamsuzzaman et al. [30,39,61,73]. By using Buckingham’s π theorem [75], the empirical model was established with the consideration of various parameters (see Equation (1)).
In Equation (1), the left side represents the similarity of geometry. For the right side, except the constant term k1, the first term uses the particle sphericity (ϕ), which was determined by Ergun’s equation (see Equation (2)) with the particle’s volume-equivalent diameter (dev) and measured pressure drop (ΔP), to evaluate the effect of particle shape (esp. for non-spherical particles); the characteristic dimensional similarities are represented by the second, third, and fourth terms; buoyancy influence is considered in the fifth term; while the sixth term points out volumetric similarities; the seventh term signifies the particle-jet Reynolds number with particle terminal velocity VT [76]; and the eighth term represents particle falling intensity. Furthermore, Table 2 lists the empirical indices in Equation (1) obtained by regression.
where Uf, ρf, and μf are the fluid superficial velocity, density, and viscosity; ε stands for the bed voidage (=).

Table 2.
Empirical constants in the predictive models for the particle bed (or mound) height.
By employing this model, relatively good agreement between the experimental and predicted particle bed heights was found (see Figure 6a). However, according to the quantitative analyses of the parametric impacts based on this model, it was recognized that, in general, the experimental results could not be predicted well for non-spherical particles [29]. This may indicate the inadequate estimation of the fictional particle-particle drag effect for non-spherical particles. Further, to attain more valuable knowledge on DBF behavior in reactor accidents, as shown in Figure 7, extrapolation of the predictive results was performed for spherical particle cases. It was found that within the fuel density range, an initial decrease but a gradual upward trend for Hb could be observed as the particle density increased. Possibly, this is because a larger frictional particle-particle drag resisted the lateral sedimentation of falling particles in cases of larger-density fuel particles [29].
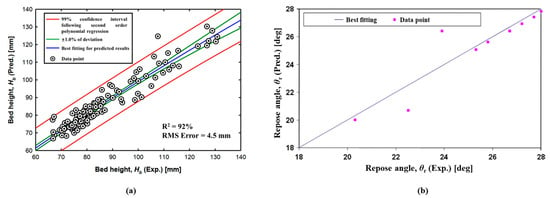
Figure 6.
Experimental and predicted results on (a) bed height and (b) repose angle (“Exp.” and “Pred.” mean experimental and predicted results, respectively) [63,65].
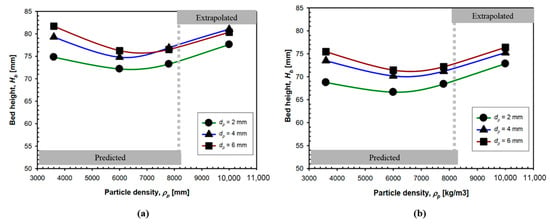
Figure 7.
Extrapolated data of the predicted bed heights with spherical fuel particles. (a) Hn = 720 mm, dn = 30 mm, and (b) Hn = 720 mm, dn = 40 mm [63].
On the other hand, Sudha et al. proposed a model to predict the repose angle under different experimental conditions by using Buckingham’s π theorem:
Figure 6b shows the experimental and predicted results. However, due to their limited experimental data, the model should be extended further with consideration of particle size, density, liquid properties, and experimental dimensions.
In a word, the empirical model proposed for predicting the particle bed heights and repose angles for DBF behavior in cases of single-sized and single-shaped particles can provide relatively reasonable predicted results in the case of spherical particles. However, it should be further improved to better and more rationally estimate the effects of non-spherical particles.
2.2. Investigations with Mixed Solid Particles
2.2.1. Experimental Materials and Methods
Noticing that after the melt-coolant interactions during actual severe SFR accidents, the debris particles are likely composed of heterogeneous mixtures [26], mixed-sized particles and mixed-density particles were utilized in the DBF experiments performed by Sheikh et al. [28,64]. The experimental system is shown in Figure 3b. For each experiment, the Vp and Hn were fixed at 5 L and 720 mm, respectively, and dp, dn, and the composition of particle mixtures were set as parameters. Al2O3, ZrO2, and SS particles of different sizes (2~6 mm) were utilized, respectively, to form the bicomponent or tricomponent mixed-sized particle mixture, and the volume of each component was the same. However, for composing mixed-density particle mixtures, Al2O3 and SS particles of the same size (2~6 mm) were employed with a volume mixing ratio of 1:3 to 3:1. To study the effect of mixed particles on DBF behavior, the apparent surface area of each particle component was measured at four typical horizontal cross sections of particle beds (see Figure 8).
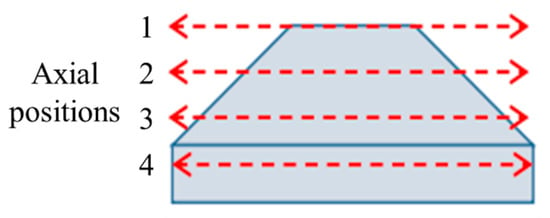
Figure 8.
Positions of measured apparent surface areas of beds (Position 1: particle bed top; Position 2: middle of particle mound; Position 3: bottom of particle mound; Position 4: bottom of particle bed) [64].
2.2.2. Experimental Results and Discussion
Figure 9 shows two typical measured results for mixed-sized and mixed-density cases. As shown in Figure 9, it was observed that, regardless of the mode adopted for mixing particles (namely mixed-sized or mixed-density), heavier particles tended to accumulate in the bed center while lighter particles (such as particles with smaller size or smaller density) would be pushed aside by collisions with heavier ones and, generally, disperse laterally during bed formation. Therefore, in such cases, particle beds with larger concavity and lower mound height were more likely to be formed. Furthermore, possibly due to the larger particle-particle friction, which may increase the difficulty for the accumulated bed to collapse under the impact of falling particles, the mixed-size particle mound heights were found to be higher than the single-size ones [28]. On the other hand, it was confirmed that at the mixed-sized bed summit, a larger number of smaller particles accumulated compared to the larger ones (see Figure 9a), especially in cases using a larger nozzle size or particles with larger size differences [64]. Meanwhile, for the bed summit in cases of mixed-density particles, a larger contribution was made by lighter particles (see Figure 9b), particularly when a larger nozzle size was employed [64]. This is possibly because, due to the larger particle-jet velocity, the heavier particles pushed the lighter particles aside as a result of the impact of the heavier particles on the lighter particles at the bed summit during the DBF process. Additionally, the effect of nozzle size (i.e., shorter and more concave/flat particle beds would form with larger nozzle size) was validated again in cases of mixed particles.
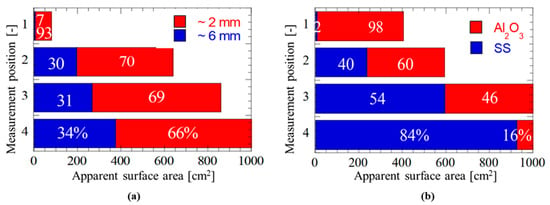
Figure 9.
Distribution of mixed particles for particle beds (dn = 40 mm). (a) Al2O3 mixed-sized particles (dp = 2 and 6 mm, mixing ratio = 1:1), and (b) Al2O3 and SS mixed-density particles (dp = 2 mm, mixing ratio = 1:1) [64].
2.2.3. Modeling Studies
To extend the model’s applicability for mixed particle situations, based on the 132 sets of experiments (119 for single-sized and single-shaped particles; 13 for mixed-sized particles), Equation (1) was modified as follows [28]:
In Equation (4), instead of particle sphericity ϕ, the particle surface area Ap was related to ϕ, and dp was used. Additionally, the values of the empirical constant indices are given in Table 2. Figure 10 illuminates the accuracy of the predicted Hb/dn results in accordance with Equation (4). Owing to this model, a good agreement between the experimental and predicted particle bed heights was achieved. In addition, for mixed-sized cases, higher mound heights can be reproduced, as observed in experiments through this model. Compared to the model proposed by Shamsuzzaman et al. (i.e., Equation (1)), this model can more reasonably predict the particle bed heights for non-spherical cases and mixed-sized cases [28].
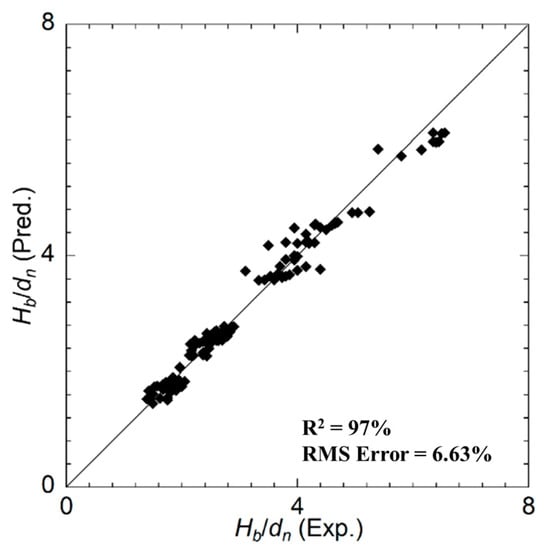
Figure 10.
Experimental and predicted Hb/dn values (“Exp.” and “Pred.” mean experimental and predicted results, respectively; Symbols in the figure show the data of experimental cases performed) [28].
In summary, by applying the model developed by Sheikh et al. [28], the particle bed height can be predicted well in both single-sized and mixed-sized cases. Nevertheless, it is worthwhile to emphasize again that it is not adequate to estimate the debris bed coolability solely via bed height because the decay heat removal capacity for the debris bed is also highly associated with the bed shape [45,46,77]. Therefore, to obtain a deeper and more comprehensive understanding of DBF behavior and an important factor representing bed characteristics, bed shapes are also required considerations in the modeling studies and predictions of various realistic conditions.
3. Investigations Focusing on Flow Regime Characteristics
Although the investigations focusing on the accumulated-bed characteristics discussed in the above section provide significant insights into understanding DBF behavior, it should be noted that: (1) due to the three-dimensional (3D) experimental system, the microscopic flow regime characteristics (e.g., fluid-solid interactions) during the DBF process were not carefully described and investigated, thereby lacking direct visualization evidence for understanding the mechanism of the different bed shapes formed; (2) some potential bed shapes may not have be found due to the rather finite range of experimental parameters (e.g., particle size), which did not encompass the whole property of ranges of the debris fragments and particles in the CDAs of SFRs [16,43]; (3) the effects of the possible liquid sodium boiling triggered from the debris decay heat during DBF progression were not taken into account; and (4) the shape of the debris bed, which is also an important factor affecting its heat removal capacity [45,46], was not be considered in the development of the empirical model.
Focusing on these points, a series of experimental and modeling studies, which is composed of 2 parts as shown in Figure 2, was promoted at SYSU to concentrate on the microscopic flow regime characteristics for DBF behavior [24,66,67,68,69,70,71]. In Part I, to clarify the basic mechanisms of flow regime transition and its characteristics, visualization experiments were performed in a two-dimensional (2D) system along with predictive modeling development. In Part II, the knowledge attained from the basic investigations conducted in Part I was validated by experiments of more realistic situations, and the predictability of the empirical model was extended for a variety of scenarios likely involved in actual severe SFR accidents. In this section, the investigations regarding DBF flow regime mechanisms and characteristics are described.
3.1. Investigations with Single-Sized Spherical Particles
3.1.1. Experimental Materials and Methods
Figure 11 shows the experimental visualization system for investigations focusing on flow regime characteristics. The main apparatus is a narrow quasi-2D viewing tank with a 1000 mm length (L) and 700 mm width (W). Recognizing that particle volume had no remarkable influence on DBF behavior [23], a 10 L particle volume was employed. As summarized in Table 1, when compared to the experiments focusing on the overall accumulated-bed characteristics, the experimental parameters cover the majority of ranges for the physical properties of debris (such as particle density and size) in actual severe accidents of SFRs. Furthermore, in addition to the particle density and size, the effects of additional various experimental parameters, including nozzle height (Hn = 110~130 cm), nozzle size (dn = 10~30 mm), and water depth (Hw = 0~60 cm), were studied. Additionally, the influence of the thickness (Wtank = 30~60 mm) of the tank was also investigated.
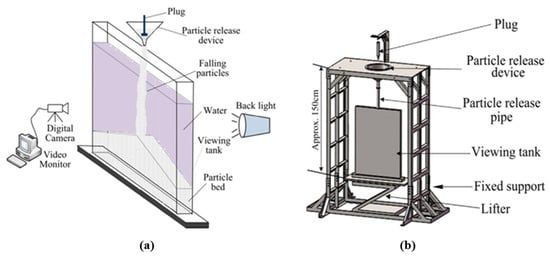
Figure 11.
Experimental Visualization system for investigations focusing on flow regime characteristics. (a) Schematic view of experimental system, and (b) detailed view of the main apparatus [24].
3.1.2. Experimental Results and Discussion
In light of experimental observations, pool convection and particle inertia were confirmed to be predominant in affecting flow regime characteristics during bed formation. As shown in Figure 12, due to their different predominance at varying parametric situations, four types of flow regimes were found to form, including the particle-suspension regime (Regime I), pool-convection dominant regime (Regime II), transitional regime (Regime III), and particle-inertia dominant regime (Regime IV). In Figure 13, the characteristics and mechanisms of each flow regime are described together with the effect of the different parameters. In general, the DBF process can be divided into two stages. Stage 1 is the particle-releasing stage, during which the falling particles are released from the nozzle to the upper area of the forming bed. In Stage 1, the nozzle outlet size and the properties of the released particles can significantly affect the releasing rate of particles, which subsequently influences the pool-convection intensity triggered by the falling particles and bed formation behavior. While Stage 2 is the particle accumulating stage (around the bottom area of the tank), during which the effects of particle inertia and particle-flow-induced pool convection play competing roles in determining the final bed shape. As shown in the final photos in Figure 12, after the particles are released and accumulated, four bed shapes, including flat, concave, trapezoid, and convex shapes, can be identified as a result of the different flow regime characteristics.

Figure 12.
Typical flow-regime characteristics (glass spherical particles, Hn = 110 cm, dn = 30 mm, Hw = 60 cm, and Wtank = 60 mm) (arrows represent the flow directions); (a) dp = 0.25 mm; (b) dp = 0.5 mm; (c) dp = 2 mm; and (d) dp = 8 mm [69].
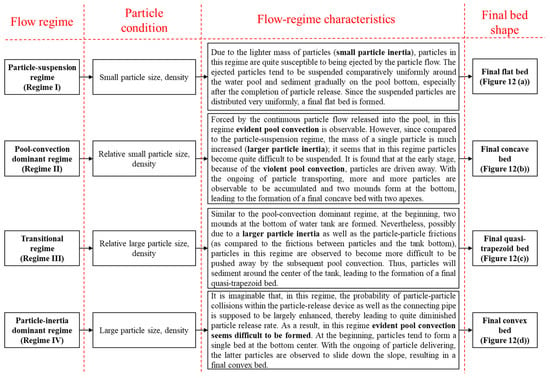
Figure 13.
Characteristics of flow regimes at different parametric situations.
As for the effect of experimental parameters, through qualitatively observing the particle bed formation process and quantitatively measuring the base angles and the vertex angles (see Figure 14), it was confirmed that, in general, a larger particle density and size could contribute to the particle inertia, thus resulting in the formation of greater-numbered flow regimes, consistent with the observations from above-mentioned 3D experiments focusing on accumulated-bed characteristics and resulting in more convex beds. Additionally, increasing the water depth would effectively facilitate the formation of pool convection (or enhance the intensity), resulting in the transition of greater-numbered regimes to lower-numbered ones, which indicates a tendency towards forming a more concave or flatter particle bed. Meanwhile, decreasing the nozzle size was expected to lead from a lower-numbered flow regime transit to a greater-numbered one because, in such a case, the resistance for discharging particles (such as frictions and collisions) was significantly strengthened, thus decreasing the particle discharging rate along with the predominance of pool convection. Moreover, similar to the observations of the experiments focusing on accumulated-bed characteristics, a slight tendency for particle bed to become flatter when the nozzle height increased was found because of more violent pool convections resulting from more remarkable differences in the velocity between the fluid flow and particle jet, although the flow regime transition did not emerge due to the rather limited range of parameters. Further, by varying the tank thickness, it was inferred that no remarkable variation in flow regime characteristics or bed geometry was observable, although the bed heights were changed due to the different cross-sectional areas.

Figure 14.
Illustrations for the base angle, vertex angle, and center angle. (a) Pool-convection dominant regime (Regime II), and (b) particle-inertia dominant regime (Regime IV) [24].
To summarize, according to the basic experiments focusing on flow regime characteristics with single-sized spherical particles, four typical flow regimes dependent on the particle inertia and pool convection were revealed during the DBF process under various parametric conditions, and it was confirmed that they would correspondingly lead to four different particle bed geometries due to their different characteristics and mechanisms. Through detailed parametric analyses based on inter-particle and flow-particle interactions, key factors (including dp, ρp, dn, Hn, and Hw) that affect the prominence of pool convection and particle inertia on flow regime transition were investigated. The consistent trends with the 3D experiments that focused on accumulated-bed characteristics and the confirmation of no noticeable impact of gap thickness on flow regime characteristics and bed geometry indicated the reliability and effectiveness of the experimental results under 2D conditions for SFR safety analysis.
3.1.3. Modeling Studies
Considering the mutual competition between the impacts of pool convection and particle inertia on changing the flow regime characteristics as discussed above, a judge index was proposed for predicting the flow regimes and bed shapes in the DBF process [67]:
where is the judge index; Iconvection and Iinertia are two dimensionless quantities that represent the prominences of pool convection and particle inertia, respectively; vpr stands for the average particle releasing rate estimated by , with the total particle volume Vp, as well as the releasing time t, measured in accordance with a duration of releasing the first particle to the last one from the nozzle; is the critical velocity for discharged particles to trigger the pool convection; a, b, c, d, and KB are empirical constants (see Table 3).

Table 3.
Values of the empirical constants in the predictive model for flow regimes and bed shapes.
Equation (5) is the so-called base model. Based on Equation (5), as shown in Figure 15a, the regime map, where different flow regimes are located in their individual regions, was proposed to predict flow regime transitions [67]. To clarify the regime boundaries between two neighboring regimes, three theoretical boundary values of I were suggested [67]. For example, Regime I is obtained when I ≥ 9.5; Regime II is attained when 1.5 ≤ I < 9.5; when 0.5 ≤ I <1.5, Regime III appears; and when I < 0.5, Regime IV emerges. Moreover, in addition to the regime map, the rationality and reliability of this model have been further confirmed and ensured through the parametric analyses on the values of I and experimental flow regime transitions [67]. On the whole, compared to the empirical models of Equations (1), (3) and (4) and focusing on the accumulated bed heights, the model of Equation (5) not only predicts the final bed shape but is also applicable in revealing flow regime transitions during DBF processes.
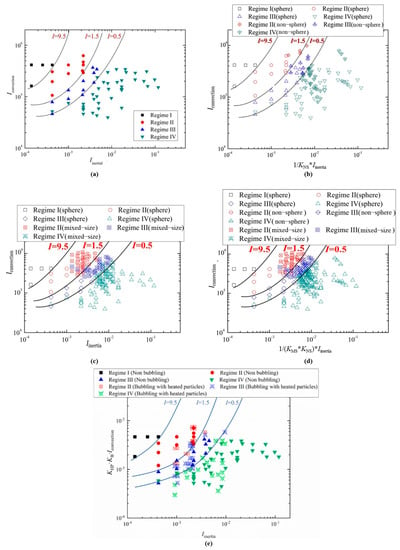
Figure 15.
Development of regime maps in accordance with the empirical model focusing on flow regime characteristics. (a) Single-sized spherical particles [67]; (b) single-sized and non-spherical particles with the extension scheme coupled [68]; (c) single-sized and mixed-sized spherical particles with the base model using da [69]; (d) single-sized and mixed-sized spherical particles with the extended model [69]; and (e) boiling condition with releasing heated particles [72].
3.2. Investigations with Single-Sized Non-Spherical Particles
3.2.1. Experimental Materials and Methods
The experimental system for studies with non-spherical particles is shown in Figure 11. To ensure a better balance between the operation of experiments and the reliability of experimental observations, the tank thickness, Wtank, was fixed at 60 mm, while Hw and dn varied from 60 to 80 cm and from 30 to 40 cm, respectively. In total, 46 experimental sets were conducted by employing non-spherical particles with different types (Al, Al2O3, ZrO2, SS, and Cu), sizes (dev from 0.50 to 5.62 mm), and shapes (dish, triangular prism, cylinder, and irregular shape) [67,68]. To evaluate the particle-shaped characteristics, the particle sphericities (ϕ) of non-spherical particles were also approximated in accordance with Ergun’s equation (see Equation (2)).
3.2.2. Experimental Results and Discussion
According to the experimental observations, it was found that by using particles with smaller sphericities (e.g., particles changed from a spherical shape to a non-spherical one), a greater-numbered flow regime is more probable to occur; in other words, a more convex particle bed would form. This may be understood by reasoning that the additional inter-particle collision and friction that resulted from shape-relevant parameters (e.g., eccentricity and roughness) were expected to reduce the particle releasing rate (i.e., cause less dominance of pool convection) through inhibiting particle movement within the particle releasing nozzle during the particle releasing stage and to restrict particle motion during the particle accumulating stage [68]. Compared to the experiments focusing on overall accumulated-bed characteristics, the consistent observations under non-spherical conditions confirm the effectiveness of the experimental results for SFR safety analysis again.
3.2.3. Modeling Studies
To better estimate the influence of particle shape, based on Geldart’s method [78,79], the VT for non-spherical particles was suggested to be modified as follows [80]:
where KT is a correction function associated with ϕ and the Reynolds number of particles determined by their dev and VT [78,79]; VTS is the terminal velocity of spherical particles sharing the same dev with non-spherical ones [68].
Further, in light of the aforementioned experimental analysis, it was found that during the particle-releasing stage, additional inter-particle interactions resulting from the shape-relevant characteristics would lead to less significant pool convection through the reduction of the particle releasing rate, which was already considered in the term vpr in the base model. Moreover, considering the falling process of particles into the pool, it can be understood that such inter-particle interactions would restrict the intensity of pool convection or, in other words, result in a more significant effect for particle inertia. In order to take this influence into account for the base model of Equation (5), an extension scheme, KNS, was proposed [68]:
where
Here, s1, s2, and s3 are empirical constants (see Table 3); Re is the Reynolds number of falling particles determined by . Concerning the reasonability of the proposed KNS, it can be understood that if particles are non-spherical (i.e., ϕ is smaller than 1.0), KNS becomes smaller than 1.0, leading to a smaller value of index I, indicating the possible emergence of a larger-numbered regime; while if particles are spherical (i.e., ϕ is 1.0), KNS becomes 1.0, and thus, the extended model will return to the base model developed in accordance with spherical particles (i.e., Equation (5)). As illustrated in Figure 15b, by using the extended model (i.e., Equation (7)), an extended regime map is attained for both spherical and non-spherical cases. According to the regime map depicted in Figure 15b, the reliability of the predicted results from the extended model is observed to be validated. On this basis, the potential for extending the applicability of the base model on DBF behavior under more realistic accidental situations was displayed to some degree.
3.3. Investigations with Mixed-Sized Spherical Particles
3.3.1. Experimental Materials and Methods
Regarding mixed-sized spherical particles, similarly, the experimental system shown in Figure 11 was employed with Wtank = 60 mm and varying nozzle diameters (30 and 45 cm), as well as water depths (60 and 80 cm). In the experiments, glass, Al2O3, ZrO2, and SS particle mixtures possessing differences in mixed diameter ratios (from 6:2 to 2:0.4) and volumetric mixed ratios (from 1:3 to 3:1) were utilized. In total, 76 sets of experiments were carried out [69].
3.3.2. Experimental Results and Discussion
Generally, the basic parametric effects (e.g., effects of Hw and dn) can also be validated in mixed-sized experiments. While focusing on the mixed-sized effect, it was found that by using particle mixtures with a larger number of smaller particles (i.e., smaller volumetric mixed ratio), due to their smaller particle inertia, the flow regimes during the DBF process tended to shift from bigger-numbered to lower-numbered regimes.
However, because of the differences in particle inertia exiting the particle components of different sizes, the existence of “intermediary cases” between two adjacent regimes (such as Regimes II and III) was observed in the experiments using mixed-sized spherical particles. In detail, although the impact of particle inertia and pool convection on DBF behavior were overall comparable for some specific cases, pool convection was probably only adequate in having an effective influence on pushing the smaller particles away while lacking the ability to significantly affect the motions of larger ones due to their larger inertia. These phenomena imply that under some specific accident situations (such as prominent sodium boiling), the stratifications and separations for different particle components in their mixtures, which are possibly able to influence the debris bed coolability, are likely to emerge because of the difference in component inertia [69], although more experiments should be performed to more deeply elaborate on the characteristics of particle separations and stratifications.
3.3.3. Modeling Studies
In order to predict the flow regimes for DBF behavior with mixed-sized spherical particles, there were two modeling approaches attempted by Cheng et al. [69]. The first one attempted to estimate the general hydraulic performance of mixed-sized particle mixtures by directly employing Equation (5) (i.e., the base model) with certain equivalent particle diameters, including four mean diameters (the mean number diameter, mean length diameter, area mean diameter (da, and volume mean diameter (dv)),
as well as a volume-equivalent diameter (devp) [81]:
In Equation (9), stands for the mean diameter of particles, r is the distribution type (r = 0, 1, 2, and 3 represent, respectively, number, length, area, and mean volume); np, j and dp, j are, respectively, the number and diameter of the j-th sized particles for the particle mixtures. While in Equation (9), εj and Vb, j represent the porosity and volume of particle beds constituted by the j-th sized particles, respectively.
In light of detailed analysis, as shown in Figure 15c, it was validated that through utilizing the base model with da, overall, results can be better predicted and attained in contrast to other mean diameters.
On the other hand, the second approach referred to the aforementioned extended model for non-spherical particles, attempting to develop an extension correlation, KMS, with consideration of the flow regime characteristics in cases of mixed-sized particles. Therefore, the extended model was developed as [69]:
where
In Equation (12), p1, p2, and p3 are empirical constants (see Table 3); is the extent of convergence of particle size distribution determined by using Ergun’s equation with dv to characterize the effective sphericity of the particle mixture. Considering the rationale of the establishment of KMS, it can be easily deduced that in single-sized spherical cases, equals 1.0, so KMS becomes 1.0; while for mixed-size spherical particles, is smaller than 1.0, so KMS becomes larger than 1.0, namely diminishing the effective impact of particle inertia, which corresponds well with the experimental observations.
With the rational and appropriate KMS, an extended regime map can be attained (see Figure 15d). In addition, to further validate the rationale of these two modeling approaches, the prediction results were also analyzed in accordance with the fundamental parametric effects (such as the effects of particle density and size and the effect of volumetric mixed ratio) on the flow regime transitions [69] observed in the experiments. Further, the extension potential of the model for application under more realistic accidental situations was again further confirmed.
3.4. Investigations on the Effect of Coolant Boiling Caused by Accumulated Debris
3.4.1. Experimental Studies Using the Gas-Injection Method
Recognizing that the decay heat of accumulated debris may lead to sodium coolant boiling, which possibly significantly affects DBF behavior, the gas-injection approach was utilized by Cheng et al. [71] to simulate the boiling conditions to elucidate their effect. Figure 16a shows the experimental system, which includes additional gas-injection apparatuses in comparison with that shown in Figure 11. For each experiment, nitrogen gas with a controlled flow rate (Qg = 0~50 L/min) was injected from the bottom of a liquid pool through an airstone, which was installed to guarantee a relatively uniform distribution of gas. In order to concentrate on the influence of the injected gas (i.e., the sodium boiling), Wtank, Vp, dn, and Hw were set at 60 mm, 10 L, 30 mm, and 60 cm, respectively. In total, 78 experimental sets were carried out by using various types of particles with different shapes, densities, and sizes.
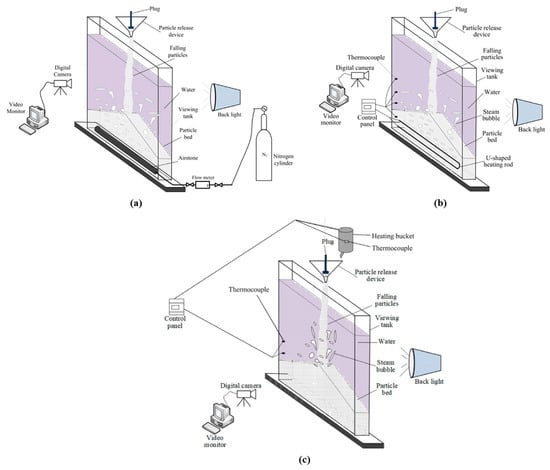
Figure 16.
Experimental systems for studies on sodium-boiling effects. (a) With gas injection; (b) with bottom heating; and (c) with the release of heated particles [70,71,72].
Considering different flow regime mechanisms and characteristics for different regimes, the key parametric effect (i.e., the effect of the gas flow rate Qg) on DBF was analyzed for each main regime (including Regime I, Regime II, and Regime IV) separately. Figure 17 shows the typical transit DBF behavior in gas-injection cases, while Figure 18 shows the influence of Qg on DBF behavior for different flow regimes. In experiments for Regime I, as Qg increased, despite no noticeable variations in flow regime or bed shapes (see Figure 17a), an evident increase in the maximum height of particles suspended (see the illustration of the height of particles suspended in the fourth photo of Figure 17a), as shown in Figure 18a, was found due to the larger impetus that drives the upward particle movements (esp. for smaller and lighter particles). Moreover, from Figure 18a, it is also observable that with a similar Qg, due to the difficulty for the upward gas-liquid flow to suspend the larger-sized (i.e., greater-inertia) particles, the peak value for the height of the particles suspended seemed to decrease when the particle size became larger. In addition, the difference in the height of particles suspended between the cases with 0.18 mm and 0.25 mm particle diameters was observed to be greatly reduced in comparison to that with 0.125 mm and 0.18 mm ones, indicating the non-negligible role of particle inertia in those cases (esp. under conditions without gas injection) and a probable flow regime transition with a further increase in particle size.

Figure 17.
Transit gas-injection DBF behavior for different flow regimes (glass spheres) (Arrows representing the visually-observed flow directions). (a) Regime I (dp = 0.125 mm, Qg = 20 L/min); (b) Regime II (dp = 0.5 mm, Qg = 10 L/min); and (c) Regime IV (dp = 6 mm, Qg = 50 L/min) [70].
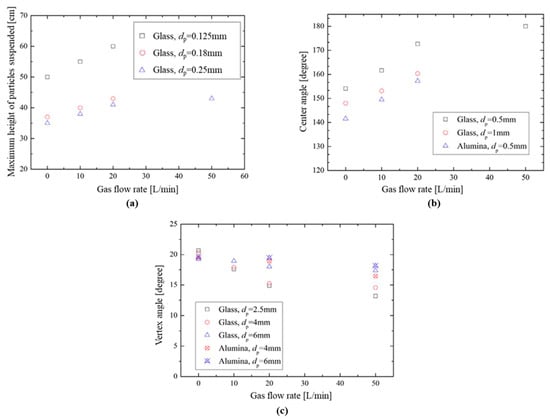
Figure 18.
Influence of gas flow rate on DBF behavior in cases of different flow regimes. (a) Regime I; (b) Regime II; and (c) Regime IV [70].
In regards to Regime II, it was found that with a larger Qg, a lower-numbered flow regime may emerge as a result of the greatly enhanced pool convection and the effect of larger-rate flows on diminishing the dominance of particle inertia (see Figure 12b and Figure 17b). More quantitatively, as shown in Figure 18b, by measuring the center angle (illustrated in Figure 14a), a gradual increment of the center angle could be found as Qg increased, revealing the trends for Regime II transit to Regime I.
However, in the case of Regime IV, as displayed in Figure 17c, although the intensity of pool convection was obviously enhanced in the early DBF stage, as the particles gradually accumulated, the accumulated particle bed possessing enough height was able to mitigate the gas-flow confluences, and thus, it was found that flow-regime transitions did not occur under the range of parameters considered. Nevertheless, owing to the quantitative measurement of the vertex angle (see Figure 14b), as shown in Figure 18c, the vertex angle apparently gradually decreased since a larger Qg was employed due to the promoted intensity of pool convection. Furthermore, an additional point that can be found from Figure 18c is that as Qg increased because of the positive role of pool convection in pushing away the particles, the differences in the vertex angles for the cases sharing the same Qg would enlarge, revealing a flattening tendency for the particle bed (i.e., the potential flow regime transitioned to a smaller-numbered one) with a greatly enhanced pool-convection intensity caused by a large gas flow rate.
In summary, regardless of the flow regimes, larger gas flow rates would significantly enhance the overall pool-convection intensity inside the whole pool and effectively impair the prominence of particle inertia, resulting in larger maximum heights of particles suspended or potential possibilities of transitioning larger-numbered regimes to smaller-numbered ones.
3.4.2. Experimental Studies Using the Bottom-Heated Method
Aimed at checking the applicability of the gas-injection approach in simulating coolant boiling due to the decay heat of debris, the experimental investigations using a bottom-heated approach to induce liquid boiling were carried out [71]. The experimental system is shown in Figure 16b. Compared to the experimental system shown in Figure 11, a heating tube with a U shape, which can supply heating power (P), was installed at the tank bottom. For the purpose of monitoring the transient temperatures in the pool, four thermocouples were installed at the axial positions of 15, 30, 45, and 60 cm. For each experiment, Wtank and Vp were fixed at 60 mm and 10 L, respectively; while dn, Hw, and P varied within the ranges of 30~40 mm, 45~80 cm, and 0~2580 W, respectively. In the experiments, pre-heated particles at 383K comprising different materials (glass, Al2O3, and ZrO2), diameters (0.125~6.0 mm), and shapes (sphere, irregular shape, and cylinder) were employed. In total, there were 72 sets of experiments conducted.
In light of the qualitative and quantitative experimental observations and similar to the gas-injection conditions, it was found that the steam bubbles produced from the tank bottom could generally play a role in enhancing the pool convection and weakening the particle inertia under boiling conditions. In addition, the aforementioned effects of different particle-related parameters (e.g., particle shape, density, and size) on the regime transitions were verified again under the bottom-heated boiling conditions. However, the influence of Hw on the characteristic angles for the particle beds was found to be inconsistent under boiling conditions in comparison to that under non-boiling conditions, which likely indicates two points concerning the mechanisms of DBF behavior in bubbling (including gas-injection and bottom-heated boiling) cases:
- (1)
- For the non-bubbling cases, pool convection is triggered by the falling particle jet and, thus, is limited within the center area. Therefore, the particles are driven away inside a relatively small region (such as around the two apexes of the bed). While for bubbling cases, due to the rather uniform distributions of bubbles in the pool, the influence area of pool convection is deemed to be wider.
- (2)
- Although increasing the water depth was found to generally enhance pool convection under non-bubbling conditions, for boiling conditions at a constant heating power, due to the larger water mass and the potentially enhanced heat dissipation resulting from larger heat-transfer areas within the environment, a higher water depth might also lead to reduced bubbling rate, thereby reducing the overall intensity of pool convection to some extent [71].
To quantitatively verify the applicability of the gas-injection approach to simulate coolant boiling, the influence of the bubbling approach was studied in different flow regimes by estimating the effective bubbling rates in accordance with measured characteristic quantities (namely, the maximum height of particles suspended and measured angles). Figure 19 shows the effect of the bubbling method in Regime IV. It was confirmed that, regardless of the particle type, the values of the characteristic quantities under the bottom-heated boiling condition at P = 2580 W were comparable to those under the gas-injection one within a relatively restricted range of Qg (10~20 L/min), revealing the probable existence of an equivalent quantity that can compare the two bubbling methods. Based on the temperature variations measured, owing to the thermocouples (see Figure 16b), and under the assumption that heat loss rate did not vary significantly within a fairly limited water temperature, the effective rate for bubbling, Qg,eff, was determined at nearly 18.49 L/min [71], which is within the range expected (i.e., 10~20 L/min) for P = 2580 W with Hw = 60 cm. Therefore, though further investigations with more elaborate considerations may still be required, to a certain degree, the reliability of the gas-injection approach for simulating coolant boiling was validated by the bottom-heated experiments, and additional gas-injection experiments with a wider range of Qg are expectable to elucidate the impact of boiling intensity on flow regime transition.
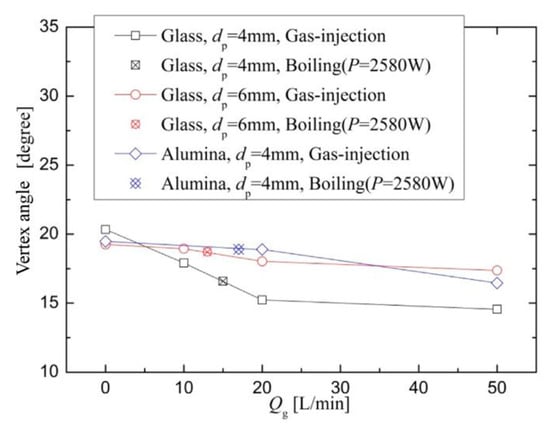
Figure 19.
Effect of bubbling method on vertex angle (Hw = 60 cm, dn = 30 mm, Regime IV).
In a word, the bubbles generated from sodium boiling are confirmed to have a promoting impact on pool convection and a dampening effect on particle inertia. Therefore, the flow regime characteristics may generally behave as lower-numbered ones in this case, as a result forming a more flattened bed.
3.5. Investigations on the Effect of Coolant Boiling Caused by Falling Debris
3.5.1. Experimental Materials and Methods
In addition to the boiling caused by the accumulated debris, it is also rationally expected that in actual severe SFR accidents, the high-temperature falling debris with decay heat may cause the coolant boiling to surround them during their falling process. Noticing this point, Xu et al. [72] performed a series of experiments by releasing heated particles to elucidate the effect of boiling caused by falling debris on DBF flow regime characteristics. Figure 16c displays the experimental system in which a heating bucket was employed to pre-heat the particles to the target temperature (Tp = 473~673 K). The water temperatures (358 K and 368 K) were selected to study the effect of liquid temperature. Other important parameters, including particle type (Alumina, Al2O3, ZrO2, and Steel), diameter (0.4~4 mm), and nozzle diameter (30~40 mm), were also considered.
3.5.2. Experimental Results and Discussion
Figure 20 shows the DBF flow regime characteristics with boiling liquid surrounding the falling particles. It was found that the mechanisms and effects of bubbling flow resulting from the falling particles worked differently than those generated by accumulated debris [72]. As shown in Figure 20, it was anticipated that the bubbling flows surrounding the falling debris would contribute to the centralization of the particle accumulation by means of two vortices and generate a counterforce against the central falling particle flow. This would mitigate the impact of pool convection resulting from discharged particles, which pushes the particles away to the peripherical areas resulting in lower-numbered regimes. However, in the case of boiling caused by falling particles, the dispersal of particles was averted from the central region of the water pool, leading to greater-numbered regimes. Further, parametric analyses confirmed that the flow regimes tended to transit to larger-numbered ones when higher particle and water temperatures were employed due to the enhanced bubbling flows surrounding the falling debris and restricting their dispersion [72]. In addition, particles with higher thermal conductivity were likely helpful in the effective heat transfer between particles and liquid, resulting in more intense boiling and the formation of greater-numbered regimes. Further, enlarging the nozzle diameter may cause non-monotonous flow-regime transitions. This is because the larger nozzle diameter would serve to accelerate the particle-releasing rate, which is expected to not only improve the intensities of particle-triggered pool convection but also facilitate bubble generation surrounding the falling particles.

Figure 20.
DBF flow-regime characteristics with boiling liquid surrounding the falling particles (Al2O3 spheres, dp = 0.5 mm, dn = 30 mm, and Tw = 368 K) (Arrows representing the visually-observed flow directions). (a) Regime II (Tp = 473 K); (b) Regime III (Tp = 523 K); and (c) Regime IV (Tp = 673 K) [72].
3.5.3. Modeling Studies
Considering the boiling resulting from the falling particles, an effective power, Peff, was taken into account to heat the liquid and generate the boiling [72]:
where Pg is the effective power to generate bubbles (or gas) by heated particles from the overheated water, and Pw stands for the effective power needed to heat the water to the boiling point from a subcooled status during particle discharging:
where TB represents the liquid boiling point, Tw is the initial water temperature, and Cw is the water’s specific heat. Then, the effective bubble generation rate, Qg,eff, can be derived:
where signifies the latent heat for boiling water.
To characterize the boiling effect on restraining the particle-induced pool convection, a dimensionless quantity, ψ, was defined [72]:
Similar to the above model extension, an extension scheme, KHP, accounting for the boiling effect caused by the falling debris, was proposed for incorporation into the previous model:
where
where Reg is the gas Reynolds number accounting for the boiling effect on centralizing the particle accumulations, and r1, r2, and r3 are the empirical constants given in Table 3. When ψ or Reg trends to zero (such as Qg,eff = 0 or vpr trends to ∞), indicating a negligible bubbling effect (e.g., minimal or non-intensive bubble generation or dominant particle-flow-induced convection), the value of KHP approaches 1, which restores the model to the base model that is suitable for non-bubbling cases. On the other hand, for cases where there is significant boiling during heated particle discharging, KHP is a positive value lower than 1 to consider the effects of boiling surrounding the falling particles on a regime transition to larger-numbered ones. Therefore, the proposed KHP was qualitatively reasonable.
Figure 15e shows the regime map with the consideration of KHP. It is seen that the model prediction and experimental observation show good agreement within the parameter ranges considered. While further analysis and validation may be required to examine the extrapolation and interpolation capabilities of the proposed KHP function under a wider range of experimental conditions, the introduction of the extension function suggests that the base model can be extended to predict the characteristics of DBF under more realistic situations for an accident to some extent.
4. Conclusions
Investigations on DBF behavior are important for the assessment of the PAMR phase in CDAs of SFRs and the evaluation of debris bed coolability, which is of great importance to the mitigation of accident consequences. Knowledge from experimental and modeling work can be applied to the evaluation and verification of SFR safety analysis codes. Recently, a large number of experiments and modeling studies on DBF behavior have been carried out considering the overall accumulated-bed characteristics and flow regime characteristics.
In the studies on DBF behavior focusing on the overall accumulated-bed characteristics, the key factors indicating the accumulated-bed characteristics (such as bed and mound heights, dimple area, and volume) were investigated in light of experiments in a cylindrical water pool to gain insight into the basic parametric effects on DBF behavior. It was confirmed that due to a more significant impact of particle jets on the accumulated particle beds, more concave and flatter particle beds (i.e., particle beds with a lower mound height, smaller repose angle, larger dimple area, and volume) could be attained when smaller-sized particles or a nozzle with larger diameter or higher placement were employed. However, in these experiments, only convex and concave beds were observed as a result of the relatively small parametric ranges. Considering the importance of bed height in evaluating the bed characteristics, two predictive models were empirically proposed for mound height and repose angle, and one was subsequently modified, becoming more applicable in predicting the bed height under more realistic accidental situations (i.e., the situations where debris are composed of mixed particles).
On the other hand, aimed at enabling experimental visualization and obtaining more comprehensive knowledge on the flow regime characteristics of DBF, additional parameters with wider ranges and more potential and realistic accidental situations (e.g., complex particle compositions in debris and coolant boiling resulting from the decay heat of debris) were considered in the experiments by using a narrow 2D viewing tank. From the experiments, it was confirmed that the opposed effects of pool convection and particle inertia result in different inter-particle and particle-fluid interactions and play a prominent role in flow regime transitions during the DBF process. Generally, four typical flow regimes, including particle-suspension, pool-convection dominant, transitional, and particle-inertia dominant regimes, were identifiable. Due to their different characteristics, after particle accumulation, four formed bed shapes, including flat, concave, trapezoid, and convex shapes, could be found, respectively. Larger particle inertia (e.g., resulting from particles with bigger sizes and densities) and lower intensity of pool convection (e.g., resulting from a lower liquid height or lower particle discharging rate) can promote the flow regime transition to a larger-numbered one, leading to the formation of a sharper bed summit geometry. Moreover, recognizing that information concerning the bed height was not adequate in analyzing the coolability of the debris bed because different debris bed shapes may possess the same bed height, another predictive model for flow regime transitions and final bed shape was developed in accordance with the parametric effects on flow regime characteristics.
Later, thanks to the extensive data and understanding accumulated from the experiments using non-spherical and mixed-sized particles, the applicable range of this model was further enlarged to include more realistic situations by introducing two corresponding extension schemes that characterize the relevant shape and mixed-sized influences on flow regime transition. Further, considering that in CDAs of SFRs, it is possible to heat and boil the sodium coolant due to the decay heat of the accumulated debris bed, the gas-injection approach, whose reliability was validated by the bottom-heated boiling experiments, was utilized to study the boiling effect on DBF behavior. It was found that the bubbles generated from sodium boiling can promote the intensity of pool convection and dampen the effect of particle inertia, leading to the flow regime transition to lower-numbered ones. However, on the contrary, from the experiments releasing heated particles into pre-heated water, it was confirmed that the boiling liquid caused by high-temperature falling debris promotes centralized particle accumulations and mitigates the impact of particle-induced pool convection. Based on the experimental understanding, an extension scheme was also successfully developed for cases releasing heated particles.
5. Discussion of Future Prospects
Though much valuable knowledge and understanding of DBF behavior have been accumulated through these previous experiments and modeling studies, it is expected that actual severe SFR accident conditions would be more complex than the conditions that have been taken into account. Therefore, in order to gain a more elaborate insight into the flow regime mechanisms and the characteristics of DBF behavior and to obtain more knowledge for SFR safety analysis, future investigations concerning DBF behavior phenomenology are required. Possible future experimental and modeling studies may involve but are not restricted to the following points:
- (1)
- Further analyses and validations of DBF characteristics in cases of multicomponent (i.e., more than three components) mixed-sized particles. As noted in Section 2 and Section 3, previous investigations under mixed-sized spherical particle conditions were carried out by only using bicomponent or a few tricomponent mixed-sized particle mixtures. To attain more reliable insights into DBF behavior under more realistic particulate situations, more experimental studies, as well as corresponding modeling verifications, with three (or even more) component mixed-size solid particles can be conducted.
- (2)
- Further experimental investigations on the characteristics of particle separation and stratification under mixed-size particle conditions. As mentioned in Section 3, from experiments focusing on flow regime characteristics, it was implied that the stratifications and separations of different particle components in the mixtures, which may affect the coolability of the debris beds, can possibly appear under some specific accident situations (e.g., significant sodium boiling) as a result of the differences in component inertia. Therefore, to study the characteristics of particle separations and stratifications, experiments using mixed-size particles can be carried out under the gas-injection method, which can effectively simulate the violent sodium boiling conditions.
- (3)
- Further experimental and modeling studies under mixed-density conditions. For the experimental studies, although fundamental mixed-density influences were preliminarily investigated through several experiments focusing on accumulated-bed characteristics, it is necessary to point out that due to the rather limited experimental parametric conditions and non-visual experimental processes, some potential valuable experimental evidence may have been missed. Therefore, mixed-density experiments should be continuously performed under more realistic parametric situations (e.g., smaller particle size and particle mixtures composed of components with densities comparable to the densities of debris in actual reactor accidents (such as MOX fuel and SS)) and in a visual quasi-2D water tank to study in detail the flow regime mechanism under mixed-density particle conditions. Again, since the particle inertia for mixed-density particle components is different, it is reasonable to imagine that particle separation and stratification phenomena may also be found and investigated in bubbling cases with mixed-density particles. Further, for the modeling studies, referring to the modeling developments regarding the molten-pool sloshing and debris bed self-leveling behaviors [81,82], some effective (or equivalent) density to estimate the overall density of the particle mixture can be tested by employing the base model. Further, the establishment of an extension scheme that can appropriately take the mixed-density effect into account can also be attempted.
- (4)
- Further modeling studies for bubbling conditions. To continuously extend the model’s predictability, an extension scheme can be developed for bubbling conditions. Preliminarily, considering the gas-injection cases, the modeling frameworks can be developed as follows:where KGI is a new extension scheme. Theoretically, KGI is required to ensure two points: (1) KGI should monotonously increase as Qg becomes larger to represent the effects of the gas flow rate on promoting pool convection and diminishing particle inertial impact; and (2) KGI should become 1.0 if no gas is injected (i.e., Qg = 0 L/min) to guarantee the applicability of the base model for non-bubbling cases.Here, it is also noted that the gas flow rate considered in our previous investigations may not cover the possible range of vapor flow rates from the drastic boiling induced by the accumulated debris beds in an actual CDA of an SFR [59,83]. Therefore, further experiments with wider ranges of gas flow rates may also be necessary to ensure the predictability of the extended model under accidental conditions.
- (5)
- Further investigations under large-scale 3D conditions. Although essentially consistent parametric effects on characteristics of DBF were confirmed in both 2D flow regime and 3D accumulated-bed experiments, it should be highlighted again that an insufficiently large range of parameters for the 3D accumulated-bed experiments in the comparison to that of actual accident conditions may cause the loss of valuable evidence (such as additional variation in particle bed shape). Through elaborately performing the large-scale 3D experiments, insights obtained from 2D flow-regime experiments are expectable to be further verified under the large-scale 3D conditions. It can be expected that a more applicable and dependable empirical model associating the flow regime and accumulated-bed characteristics can be developed for application in reactor safety assessments. In fact, referring to the previous modeling studies on debris bed self-leveling behavior [14,84], it can be expected that the flow regime boundary lines (or empirical constants) determined for the predictive model under 2D conditions can possibly vary to some degree for large-scale 3D predictions. Such a predictive model is supposed to be useful in the improved designs of in-vessel core catchers along with the developments and validations of SFR safety analysis codes.
Author Contributions
Formal analysis, R.X.; Investigation, R.X.; Data Curation, R.X. and S.C.; Writing—Original Draft Preparation, R.X.; Writing—Review and Editing, S.C. and R.X.; Supervision, S.C.; Project Administration, S.C.; Funding Acquisition, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
The current work is financially supported by Guangdong Basic and the Applied Basic Research Foundation, grant number 2022A1515011582, and the Science and Technology Program of Guangdong Province, grant number 2021A0505030026, in China.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | area | ρ | density |
| Ar | Archimedes number | σ | surface tension |
| C | specific heat | ϕ | particle sphericity |
| D | diameter of experimental device | ψ | quantities for characterizing |
| d | diameter | bubbling impact on restricting the | |
| mean diameter | particle-flow induced pool convection | ||
| Fr | Froude number | Ω | degree of convergence in particle |
| g | gravitational acceleration | size distribution | |
| H | height | ||
| hlg | latent heat of liquid | Subscripts | |
| L | length of experimental device | a | stands for an area mean term |
| m | mass | B | boiling |
| P | heating power | b | particle bed |
| ΔP | pressure-drop | c | critical value |
| Q | flow rate | dim | dimple |
| Re | Reynolds number | ev | stands for a volume-equivalent term |
| T | temperature | f | fluid |
| t | the time span between the first and last particles | g | gas |
| that flows out of the particle-releasing nozzle | in | inner container | |
| U | superficial velocity | ip | represents an initial value of particle |
| V | volume | j | j-th size particles |
| v | velocity | L | left |
| VT | particle terminal velocity | l | liquid |
| VTS | terminal velocity of a spherical particle with the | m | particle mound |
| volume-equivalent diameter of non-spherical particle | n | nozzle | |
| W | width of experimental device | p | particle |
| pr | particle releasing | ||
| Greek symbols | R | right | |
| ε | bed voidage | r | repose |
| θ | angle | tank | water tank |
| λ | thermal conductivity | v | stands for a mean volume term |
| μ | viscosity | w | water |
| Abbreviation | |||
| CDA | Core Disruptive Accident | PAHR | Post-Accident Heat Removal |
| DBF | Debris Bed Formation | PAMR | Post-Accident Material Relocation |
| IGCAR | Indira Gandhi Centre for Atomic Research | SFR | Sodium-cooled Fast Reactor |
| IVR | In-Vessel Retention | SS | Stainless Steel |
| JAEA | Japan Atomic Energy Agency | SYSU | Sun Yat-Sen University |
References
- OECD Nuclear Energy Agency. Technology Roadmap Update for Generation IV Nuclear Energy Systems; Generation IV International Forum (GIF); OECD Nuclear Energy Agency: Paris, France, 2014. [Google Scholar]
- Raj, B.; Chellapandi, P.; Rao, P.V. Sodium Fast Reactors with Closed Fuel Cycle; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Xu, R.; Cheng, S. Review of the molten-pool sloshing motion in case of Core Disruptive Accident: Experimental and modeling studies. Prog. Nucl. Energy 2021, 133, 103647. [Google Scholar] [CrossRef]
- Marchaterre, J.F. Overview of core disruptive accidents. Nucl. Eng. Des. 1977, 42, 11–17. [Google Scholar] [CrossRef]
- Maschek, W.; Li, R.; Matzerath Boccaccini, C.; Gabrielli, F.; Morita, K. Investigation on upper bounds of recriticality energetics of hypothetical core disruptive accidents in sodium cooled fast reactors. Nucl. Eng. Des. 2018, 326, 392–402. [Google Scholar] [CrossRef]
- Yamano, H. Thermal-Hydraulic Phenomena Contributing to Reactivity Mitigation in Core Disruptive Accidents of Fast Reactors. Ph.D. Thesis, Kyushu University, Fukuoka, Japan, 2009. [Google Scholar]
- Ohshima, H.; Kubo, S. Handbook of Generation IV Nuclear Reactors; Woodhead Publishing: Manchester, UK, 2016. [Google Scholar]
- Yamano, H.; Sato, I.; Tobita, Y. Development of technical basis in the initiating and transition phases of unprotected events for Level-2 PSA methodology in sodium-cooled fast reactors. Nucl. Eng. Des. 2012, 249, 212–227. [Google Scholar] [CrossRef]
- Sato, I.; Yamano, H.; Tobita, Y. Development of Severe Accident Evaluation Technology (Level 2 PSA) for Sodium-Cooled Fast Reactors—Identification of Dominant Factors in Initiating Phase of Unprotected Events. In Proceedings of the 2009 International Congress on Advances in Nuclear Power Plants (ICAPP’09), Tokyo, Japan, 10–14 May 2009. [Google Scholar]
- Yamano, H.; Tobita, Y.; Fujita, S. A three-dimensional neutronics-thermohydraulics simulation of core disruptive accident in sodium-cooled fast reactor. Nucl. Eng. Des. 2009, 239, 1673–1681. [Google Scholar] [CrossRef]
- Morita, K.; Matsumoto, T.; Emura, Y.; Abe, T.; Tatewaki, I.; Endo, H. Investigation on Sloshing Response of Liquid in a 2D Pool against Hydraulic Disturbance. In Proceedings of the Ninth Korea-Japan Symposium on Nuclear Thermal Hydraulics and Safety (NTHAS-9), Buyeo, Republic of Korea, 16–19 November 2014. [Google Scholar]
- Xu, R.; Cheng, S. Experimental and numerical investigations into molten-pool sloshing motion for severe accident analysis of sodium-cooled fast reactors: A review. Front. Energy Res. 2022, 10, 893048. [Google Scholar] [CrossRef]
- Tatewaki, I.; Morita, K.; Endo, H. A Study on Characteristics of Molten Pool Sloshing in Core Disruptive Accidents of Fast Reactors. In Proceedings of the 23rd International Conference on Nuclear Engineering: Nuclear Power-Reliable Global Energy (ICONE-23), Chiba, Japan, 17–21 May 2015. [Google Scholar]
- Xu, R.; Cheng, S. Debris Bed Self-Leveling Mechanism and Characteristics for Core Disruptive Accident of Sodium-Cooled Fast Reactor: Review of Experimental and Modeling Investigations. Sci. Technol. Nucl. Install. 2022, 2022, 2755471. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, R.; Cheng, H.; Liu, X.; Cheng, S. Numerical simulation of jet breakup phenomenon during severe accident of sodium-cooled fast reactor using MPS method. Ann. Nucl. Energy 2022, 172, 109087. [Google Scholar] [CrossRef]
- Cheng, S.; Yamano, H.; Suzuki, T.; Tobita, Y.; Nakamura, Y.; Zhang, B.; Matsumoto, T.; Morita, K. Characteristics of self-leveling behavior of debris beds in a series of experiments. Nucl. Eng. Technol. 2013, 45, 323–334. [Google Scholar] [CrossRef]
- Fauske, H.K.; Koyama, K. Assessment of fuel coolant interactions (FCIs) in the FBR core disruptive accident (CDA). J. Nucl. Sci. Technol. 2002, 39, 608–614. [Google Scholar] [CrossRef]
- Koyama, K.; Yamada, Y.; Hayakawa, S.; Watanabe, M.; Watanabe, O. Development of severe accident evaluation technology (level 2 PSA) for sodium-cooled fast reactors; dentification of Dominant Factors in Core Material Relocation and Heat Removal Phases. In Proceedings of the International Congress on Advances in Nuclear Power Plants (ICAPP’09), Tokyo, Japan, 10–14 May 2009. [Google Scholar]
- Suzuki, T.; Tobita, Y.; Nakai, R. Evaluation of recriticality behavior in the material-relocation phase for Japan sodium-cooled fast reactor. J. Nucl. Sci. Technol. 2015, 52, 1448–1459. [Google Scholar] [CrossRef]
- Bala Sundaram, G.; Velusamy, K. Effect of debris material composition on post accidental heat removal in a sodium cooled fast reactor. Nucl. Eng. Des. 2021, 375, 111065. [Google Scholar] [CrossRef]
- Lipinski, R.J. A Coolability Model for Postaccident Nuclear Reactor Debris. Nucl. Technol. 1984, 65, 53–66. [Google Scholar] [CrossRef]
- Lipinski, R.J.; Gronager, J.E.; Schwarz, M. Particle Bed Heat Removal with Subcooled Sodium: D-4 Results and Analysis. Nucl. Technol. 1982, 58, 369–378. [Google Scholar] [CrossRef]
- Shamsuzzaman, M.; Horie, T.; Fuke, F.; Kai, T.; Zhang, B.; Matsumoto, T.; Morita, K.; Tagami, H.; Suzuki, T.; Tobita, Y. Experimental Evaluation of Debris Bed Characteristics in Particulate Debris Sedimentation Behaviour. In Proceedings of the 21st International Conference on Nuclear Engineering, Chengdu, China, 29 July–2 August 2013. [Google Scholar]
- Lin, S.; Cheng, S.; Jiang, G.; Pan, Z.; Lin, H.; Wang, S.; Wang, L.; Zhang, X.; Wang, B. A two-dimensional experimental investigation on debris bed formation behavior. Prog. Nucl. Energy 2017, 96, 118–132. [Google Scholar] [CrossRef]
- Matsuba, K.; Isozaki, M.; Kamiyama, K.; Tobita, Y. Distance for fragmentation of a simulated molten-core material discharged into a sodium pool. J. Nucl. Sci. Technol. 2016, 53, 707–712. [Google Scholar] [CrossRef]
- Tentner, A.; Parma, E.; Wei, T.; Wigeland, R. Severe Accident Approach-Final Report; Evaluation of Design Measures for Severe Accident Prevention and Consequence Mitigation; Argonne National Laboratory: Argonne, IL, USA, 2010. [Google Scholar]
- Suzuki, T.; Kamiyama, K.; Yamano, H.; Kubo, S.; Tobita, Y.; Nakai, R.; Koyama, K. A scenario of core disruptive accident for Japan sodium-cooled fast reactor to achieve in-vessel retention. J. Nucl. Sci. Technol. 2014, 51, 493–513. [Google Scholar] [CrossRef]
- Sheikh, M.; Son, E.; Kamiyama, M.; Morioka, T.; Matsumoto, T.; Morita, K.; Matsuba, K.; Kamiyama, K.; Suzuki, T. Sedimentation behavior of mixed solid particles. J. Nucl. Sci. Technol. 2018, 55, 623–633. [Google Scholar] [CrossRef]
- Shamsuzzaman, M.; Horie, T.; Fuke, F.; Kamiyama, M.; Morioka, T.; Matsumoto, T.; Morita, K.; Tagami, H.; Suzuki, T.; Tobita, Y. Experimental study on debris bed characteristics for the sedimentation behavior of solid particles used as simulant debris. Ann. Nucl. Energy 2018, 111, 474–486. [Google Scholar] [CrossRef]
- Park, S.; Park, H.S.; Jeun, G.; Cho, B.J. Three-Dimensional Modeling of Debris Mixing and Sedimentation in Severe Accidents Using the Moving Particle Semi-Implicit Method Coupled with Rigid Body Dynamics. Nucl. Technol. 2013, 181, 227–239. [Google Scholar] [CrossRef]
- Vasilyev, B.A.; Shepelev, S.F.; Ashirmetov, M.R.; Poplavsky, V.M. BN-1200 Reactor Power Unit Design Development. In Proceedings of the International Conference on Fast Reactors and Related Fuel Cycles: Safe Technologies and Sustainable Scenarios (FR13), Paris, France, 4–7 March 2013. [Google Scholar]
- Harvey, J.; Narayanan, K.S.; Das, S.K.; Rao, E.V.H.M.; Lydia, G.; Malarvizhi, B.; Murthy, S.S.; Kumaresan, M.; Kasinathan, N.; Rajan, M. Assessment of Debris Bed Formation Characteristics Following Core Melt Down Scenario with Simulant System. In Proceedings of the 16th International Conference on Nuclear Engineering, Orlando, FL, USA, 11–15 May 2008. [Google Scholar]
- Ma, W.; Dinh, T.-N.; Buck, M.; Buerger, M. Analysis of the Effect of Bed Inhomogeneity on Debris Coolability. In Proceedings of the 15th International Conference on Nuclear Engineering (ICONE15), Nagoya, Japan, 22–26 April 2007. [Google Scholar]
- Yakush, S.; Kudinov, P.; Dinh, T.N. Modeling of Two-Phase Natural Convection Flows in a Water Pool with a Decay-Heated Debris Bed. In Proceedings of the 2008 International Congress on Advances in Nuclear Power Plants (ICAPP’08), Anaheim, CA, USA, 8–12 June 2008. [Google Scholar]
- Xiong, Z.; Cheng, S.; Xu, R.; Tan, Y.; Zhang, H.; Xu, Y. Experimental study on eutectic reaction between fuel debris and reactor structure using simulant materials. Ann. Nucl. Energy 2020, 139, 107284. [Google Scholar] [CrossRef]
- Hotta, A.; Akiba, M.; Morita, A.; Konovalenko, A.; Villanueva, W.; Bechta, S.; Komlev, A.; Thakre, S.; Hoseyni, S.M.; Sköld, P.; et al. Experimental and Analytical Investigation of Formation and Cooling Phenomena in High Temperature Debris Bed. J. Nucl. Sci. Technol. 2020, 57, 353–369. [Google Scholar] [CrossRef]
- Alvarez, D.; Amblard, M. Fuel Levelling. In Proceedings of the 5th Information Exchange Meeting on Post Accident Debris Cooling, Karlsruhe, Germany, 28–30 July 1982. [Google Scholar]
- Bürger, M.; Buck, M.; Schmidt, W.; Widmann, W. Validation and application of the WABE code: Investigations of constitutive laws and 2D effects on debris coolability. Nucl. Eng. Des. 2006, 236, 2164–2188. [Google Scholar] [CrossRef]
- Yakush, S.; Kudinov, P. Simulation of Ex-Vessel Debris Bed Formation and Coolability in a LWR Severe Accident. In Proceedings of the ISAMM-2009, Böttstein, Switzerland, 25–28 October 2009. [Google Scholar]
- Ma, W.; Dinh, T.-N. The effects of debris bed’s prototypical characteristics on corium coolability in a LWR severe accident. Nucl. Eng. Des. 2010, 240, 598–608. [Google Scholar] [CrossRef]
- Karbojian, A.; Ma, W.M.; Kudinov, P.; Dinh, T. A scoping study of debris bed formation in the DEFOR test facility. Nucl. Eng. Des. 2009, 239, 1653–1659. [Google Scholar] [CrossRef]
- Zhang, B.; Harada, T.; Hirahara, D.; Matsumoto, T.; Morita, K.; Fukuda, K.; Yamano, H.; Suzuki, T.; Tobita, Y. Experimental investigation on self-leveling behavior in debris beds. Nucl. Eng. Des. 2011, 241, 366–377. [Google Scholar] [CrossRef]
- Cheng, S.; Tagami, H.; Yamano, H.; Suzuki, T.; Tobita, Y.; Zhang, B.; Matsumoto, T.; Morita, K. Evaluation of debris bed self-leveling behavior: A simple empirical approach and its validations. Ann. Nucl. Energy 2014, 63, 188–198. [Google Scholar] [CrossRef]
- Cheng, S.; Tagami, H.; Yamano, H.; Suzuki, T.; Tobita, Y.; Taketa, S.; Nishi, S.; Nishikido, T.; Zhang, B.; Matsumoto, T.; et al. An investigation on debris bed self-leveling behavior with non-spherical particles. J. Nucl. Sci. Technol. 2014, 51, 1096–1106. [Google Scholar] [CrossRef]
- Takasuo, E. An experimental study of the coolability of debris beds with geometry variations. Ann. Nucl. Energy 2016, 92, 251–261. [Google Scholar] [CrossRef]
- Basso, S.; Konovalenko, A.; Yakush, S.E.; Kudinov, P. The effect of self-leveling on debris bed coolability under severe accident condi-tions. Nucl. Eng. Des. 2016, 305, 246–259. [Google Scholar] [CrossRef]
- Cheng, S.; Hirahara, D.; Tanaka, Y.; Gondai, Y.; Zhang, B.; Matsumoto, T.; Morita, K.; Fukuda, K.; Yamano, H.; Suzuki, T.; et al. Experimental investigation of bubbling in particle beds with high solid holdup. Exp. Therm. Fluid Sci. 2011, 35, 405–415. [Google Scholar] [CrossRef]
- Guo, L.; Morita, K.; Tobita, Y. Numerical simulations on self-leveling behaviors with cylindrical debris bed. Nucl. Eng. Des. 2017, 315, 61–68. [Google Scholar] [CrossRef]
- Tagami, H.; Cheng, S.; Tobita, Y.; Morita, K. Model for particle behavior in debris bed. Nucl. Eng. Des. 2018, 328, 95–106. [Google Scholar] [CrossRef]
- Li, C.-Y.; Wang, K.; Pellegrini, M.; Erkan, N.; Okamoto, K. Numerical Simulation and Validation of Debris Bed Self-Leveling Behavior with Mixed-Density Particles Using CFD-DEM Coupling Algorithm. Nucl. Technol. 2022, 208, 843–859. [Google Scholar] [CrossRef]
- Pohlner, G.; Vujic, Z.; Bürger, M.; Lohnert, G. Simulation of melt jet breakup and debris bed formation in water pools with IKE-JET/IKEMIX. Nucl. Eng. Des. 2006, 236, 2026–2048. [Google Scholar] [CrossRef]
- Sun, R.; Wu, L.; Ding, W.; Chen, R.; Tian, W.; Qiu, S.; Su, G. From melt jet break-up to debris bed formation: A review of melt evolution model during fuel-coolant interaction. Ann. Nucl. Energy 2022, 165, 108642. [Google Scholar] [CrossRef]
- Xiang, Y.; Thakre, S.; Ma, W.; Bechta, S. A scoping study on debris bed formation from metallic melt coolant interactions. Nucl. Eng. Des. 2021, 385, 111533. [Google Scholar] [CrossRef]
- Xiang, Y.; Deng, Y.; Fang, D.; Zhao, N.; Ma, W. Experimental investigation on ex-vessel debris bed formation using low melting-point melt of binary metals. Prog. Nucl. Energy 2023, 157. [Google Scholar] [CrossRef]
- Iwasawa, Y.; Sugiyama, T.; Abe, Y. Experiments of melt jet-breakup for agglomerated debris formation using a metallic melt. Nucl. Eng. Des. 2022, 386, 111575. [Google Scholar] [CrossRef]
- Modak, M.; Nirgude, V.V.; Park, H.S.; Choi, Y.J.; Seo, M.R. DAVINCI-SP tests for debris bed formation and spreading in a pool with center conical structure under two-phase condition. Nucl. Eng. Des. 2023, 405. [Google Scholar] [CrossRef]
- Kondo, S.; Konishi, K.; Isozaki, M.; Imahori, S.; Furutani, A.; Brear, D. Experimental study on simulated molten jet-coolant interactions. Nucl. Eng. Des. 1995, 155, 73–84. [Google Scholar] [CrossRef]
- Magallon, D.; Hohmann, H.; Schins, H. Pouring of 100-kg-Scale Molten UO2 into Sodium. Nucl. Technol. 1992, 98, 79–90. [Google Scholar] [CrossRef]
- Tobita, Y.; Kamiyama, K.; Tagami, H.; Matsuba, K.-I.; Suzuki, T.; Isozaki, M.; Yamano, H.; Morita, K.; Guo, L.; Zhang, B. Development of the evaluation methodology for the material relocation behavior in the core disruptive accident of sodium-cooled fast reactors. J. Nucl. Sci. Technol. 2016, 53, 698–706. [Google Scholar] [CrossRef]
- Mathai, A.M.; Sharma, A.K.; Anandan, J.; Malarvizhi, B.; Das, S.K.; Nashine, B.; Chellapandi, P. Investigation of fragmentation phenomena and debris bed formation during core meltdown accident in SFR using simulated experiments. Nucl. Eng. Des. 2015, 292, 87–97. [Google Scholar] [CrossRef]
- Yakush, S.; Kudinov, P.; Dinh, T.N. Multiscale Simulations of Self-Organization Phenomena in the Formation and Coolability of Corium Debris Bed. In Proceedings of the 13th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH-13), Kanazawa, Japan, 27 September–2 October 2009. [Google Scholar]
- Shamsuzzaman, M.; Horie, T.; Fuke, F.; Kai, T.; Zhang, B.; Matsumoto, T.; Morita, K.; Tagami, H.; Suzuki, T.; Tobita, Y. Experimental Investigation of Debris Sedimentation Behaviour on Bed Formation Characteristics. In Proceedings of the Eighth Japan-Korea Symposium on Nuclear Thermal Hydraulics and Safety (NTHAS8), Beppu, Japan, 9–12 December 2012. [Google Scholar]
- Shamsuzzaman, M.; Matsumoto, T.; Kamiyama, M.; Morioka, T.; Morita, K.; Tagami, H.; Suzuki, T.; Tobita, Y. Experimental study on sedimentation behavior of core debris. In Proceedings of the Ninth Korea-Japan Symposium on Nuclear Thermal Hydraulics and Safety (NTHAS9), Buyeo, Republic of Korea, 16–19 November 2014. [Google Scholar]
- Sheikh, M.; Son, E.; Kamiyama, M.; Morioka, K.; Matsumoto, T.; Morita, K.; Matsuba, K.; Kamiyama, K.; Suzuki, T. Experimental Investigation on Characteristics of Mixed Particle Debris in Sedimentation and Bed Formation Behavior. In Proceedings of the 11th International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Operation and Safety (NUTHOS-11), Gyeongju, Republic of Korea, 9–13 October 2016. [Google Scholar]
- Sudha, A.J.; Murthy, S.; Kumaresan, M.; Lydia, G.; Nashine, B.; Chellapandi, P. Experimental analysis of heaping and self-levelling phenomena in core debris using lead spheres. Exp. Therm. Fluid Sci. 2015, 68, 239–246. [Google Scholar] [CrossRef]
- Cheng, S.; Zhang, T.; Cui, J.; Gong, P.; Qian, Y. Insight from Recent Experimental and Empirical-Model Studies on Flow-Regime Charac-teristics in Debris Bed Formation Behavior. J. Nucl. Eng. Radiat. Sci. 2018, 4, 031003. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, S.; Jiang, G.; Yu, J.; Qian, Y.; Gong, P.; Cui, J. Development and analysis of a regime map for predicting debris bed formation behavior. Ann. Nucl. Energy 2017, 109, 658–666. [Google Scholar] [CrossRef]
- Cheng, S.; Gong, P.; Wang, S.; Cui, J.; Qian, Y.; Zhang, T.; Jiang, G. Investigation of flow regime in debris bed formation behavior with nonspherical particles. Nucl. Eng. Technol. 2018, 50, 43–53. [Google Scholar] [CrossRef]
- Cheng, S.; He, L.; Zhu, F.; Wang, J.; Xu, R.; Zhang, H.; Tan, Y.; Xu, Y. Experimental study on flow regimes in debris bed formation behavior with mixed-size particles. Ann. Nucl. Energy 2019, 133, 283–296. [Google Scholar] [CrossRef]
- Cheng, S.; Cui, J.; Qian, Y.; Gong, P.; Zhang, T.; Wang, S.; Jiang, G. An experimental investigation on flow-regime characteristics in debris bed formation behavior using gas-injection. Ann. Nucl. Energy 2018, 112, 856–868. [Google Scholar] [CrossRef]
- Cheng, S.; He, L.; Wang, J.; Zhu, F.; Cui, J. An experimental study on debris bed formation behavior at bottom-heated boiling condition. Ann. Nucl. Energy 2019, 124, 150–163. [Google Scholar] [CrossRef]
- Xu, R.; Cheng, S.; Xu, Y.; Tan, Y.; Zhang, H. Investigations on flow-regime characteristics during debris bed formation behavior in sodium-cooled fast reactor by releasing high-temperature particles. Nucl. Eng. Des. 2022, 395, 111866. [Google Scholar] [CrossRef]
- Dinh, N.; Ma, W.; Karbojian, A.; Kudinov, P.; Tran, C.T.; Hansson, C.R. Ex-Vessel Corium Coolability and Steam Explosion Energetics in Nordic Light Water Reactors; NKS-160; KTH-NPS-SARAM-071001; Royal Institute of Technology (KTH): Stockholm, Sweden, 2008. [Google Scholar]
- Shamsuzzaman, M.; Zhang, B.; Horie, T.; Fuke, F.; Matsumoto, T.; Morita, K.; Tagami, H.; Suzuki, T.; Tobita, Y. Numerical study on sedimentation behavior of solid particles used as simulant fuel debris. J. Nucl. Sci. Technol. 2014, 51, 681–699. [Google Scholar] [CrossRef]
- Buckingham, E. On Physically Similar Systems; Illustrations of the Use of Dimensional Equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Fan, L.-S.; Zhu, C. Principles of Gas-Solid Flows; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Chen, Y.; Ma, W. Development and application of a surrogate model for quick estimation of ex-vessel debris bed coolability. Nucl. Eng. Des. 2020, 370, 110898. [Google Scholar] [CrossRef]
- Geldart, D. Gas Fluidization Technology; John Wiley & Sons: Chichester, UK, 1986. [Google Scholar]
- Geldart, D. Estimation of basic particle properties for use in fluid—Particle process calculations. Powder Technol. 1990, 60, 1–13. [Google Scholar] [CrossRef]
- Cheng, S.; Li, X.; Liang, F.; Li, S.; Li, K. Study on sloshing motion in a liquid pool with non-spherical particles. Prog. Nucl. Energy 2019, 117, 103086. [Google Scholar] [CrossRef]
- Phan, L.H.S.; Ngo, P.M.; Miura, R.; Tasaki, Y.; Matsumoto, T.; Liu, W.; Morita, K. Self-leveling behavior of mixed solid particles in cylindrical bed using gas-injection method. J. Nucl. Sci. Technol. 2019, 56, 111–122. [Google Scholar] [CrossRef]
- Xu, R.; Cheng, S.; Li, S.; Cheng, H. Knowledge from recent investigations on sloshing motion in a liquid pool with solid particles for severe accident analyses of sodium-cooled fast reactor. Nucl. Eng. Technol. 2022, 54, 589–600. [Google Scholar] [CrossRef]
- Tagami, H.; Tobita, Y. Numerical Simulation for Debris Bed Behavior in Sodium Cooled Fast Reactor. In Proceedings of the 10th International Topical Meeting on Nuclear Thermal-Hydraulics, Operation and Safety (NUTHOS-10), Okinawa, Japan, 14–18 December 2014. [Google Scholar]
- Cheng, S.; Yamano, H.; Suzuki, T.; Tobita, Y.; Nakamura, Y.; Zhang, B.; Matsumoto, T.; Morita, K. Empirical correlations for predicting the self-leveling behavior of debris bed. Nucl. Sci. Tech. 2013, 24, 010602. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).