The Role of Fluid Overpressure on the Fracture Slip Mechanism Based on Laboratory Tests That Stimulating Reservoir-Induced Seismicity
Abstract
1. Introduction
2. Materials and Methods
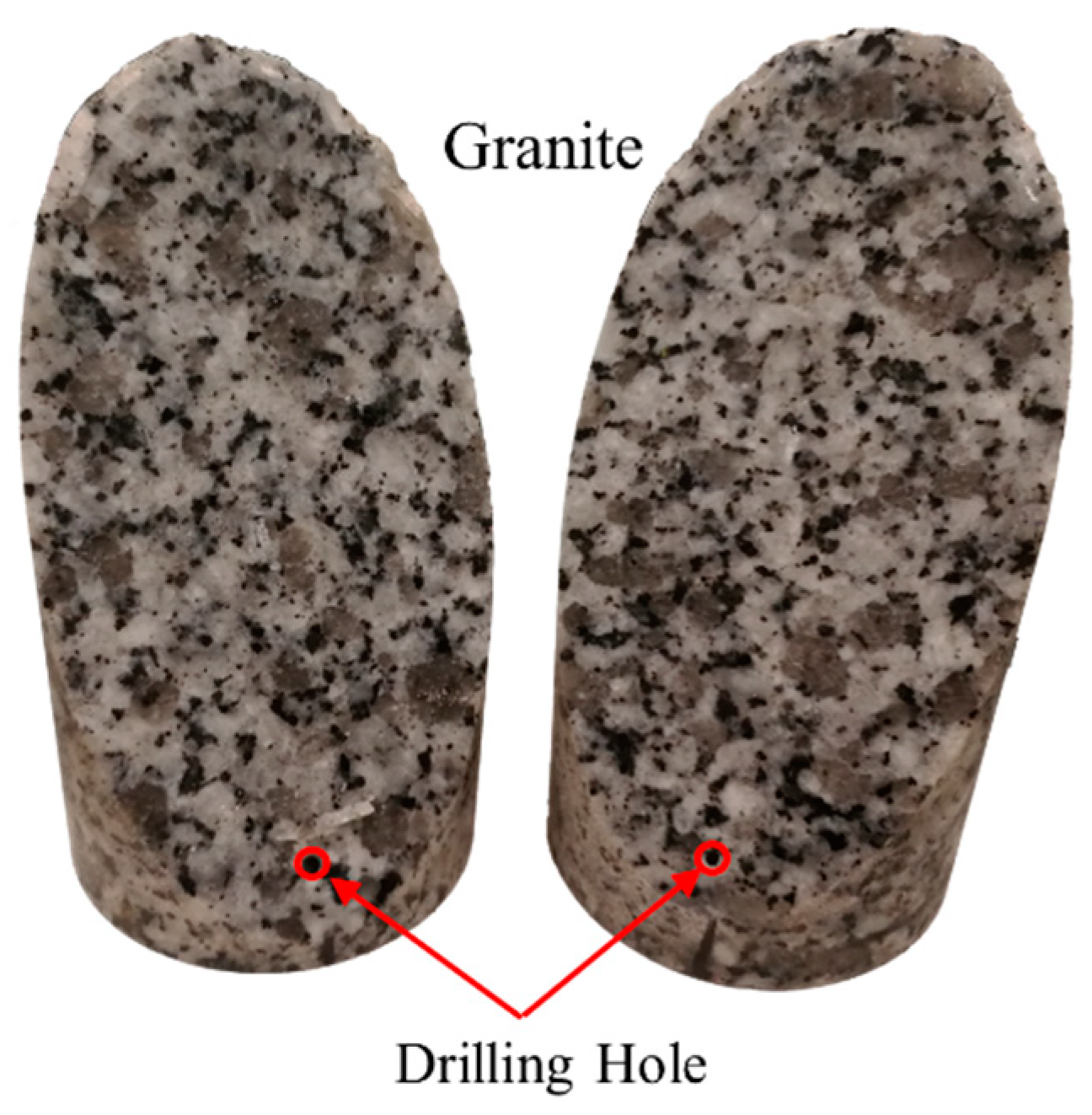
2.1. Setup and Sample Preparation
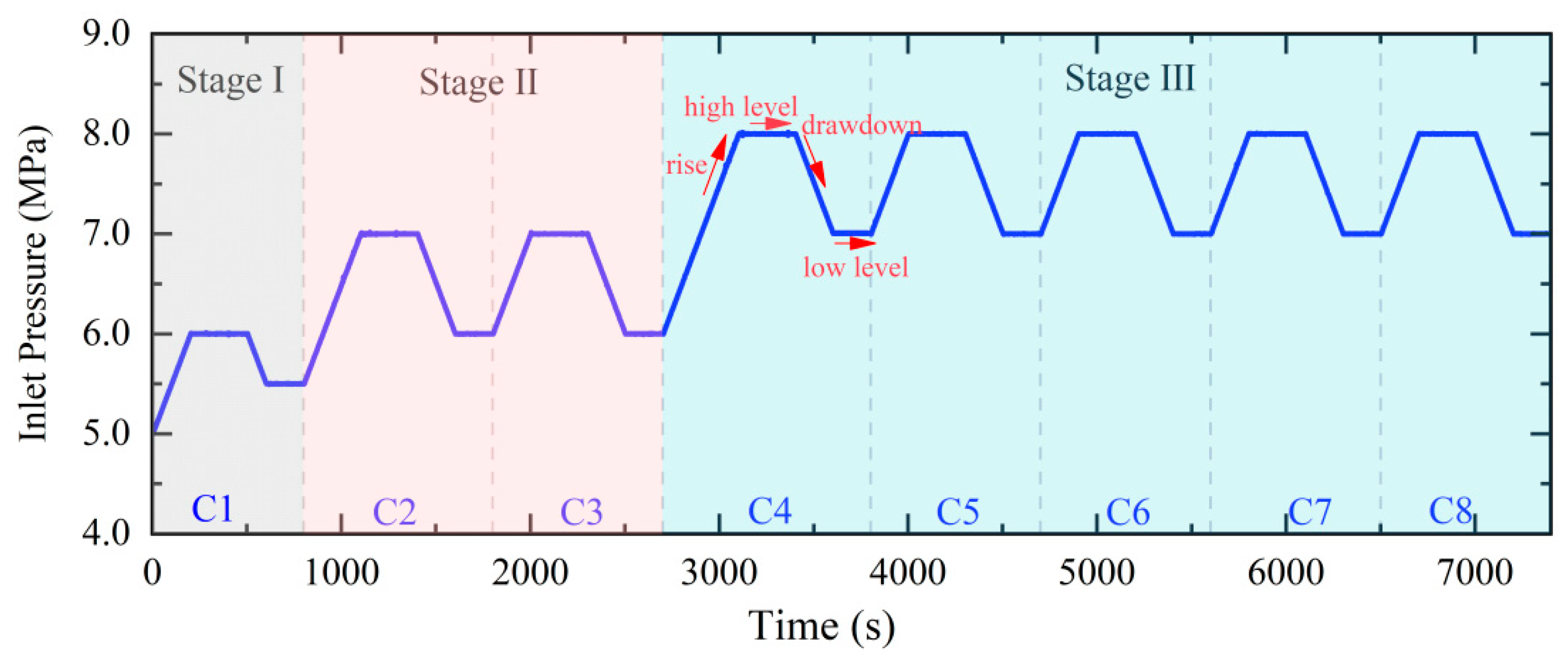
2.2. Experimental Procedure
3. Results
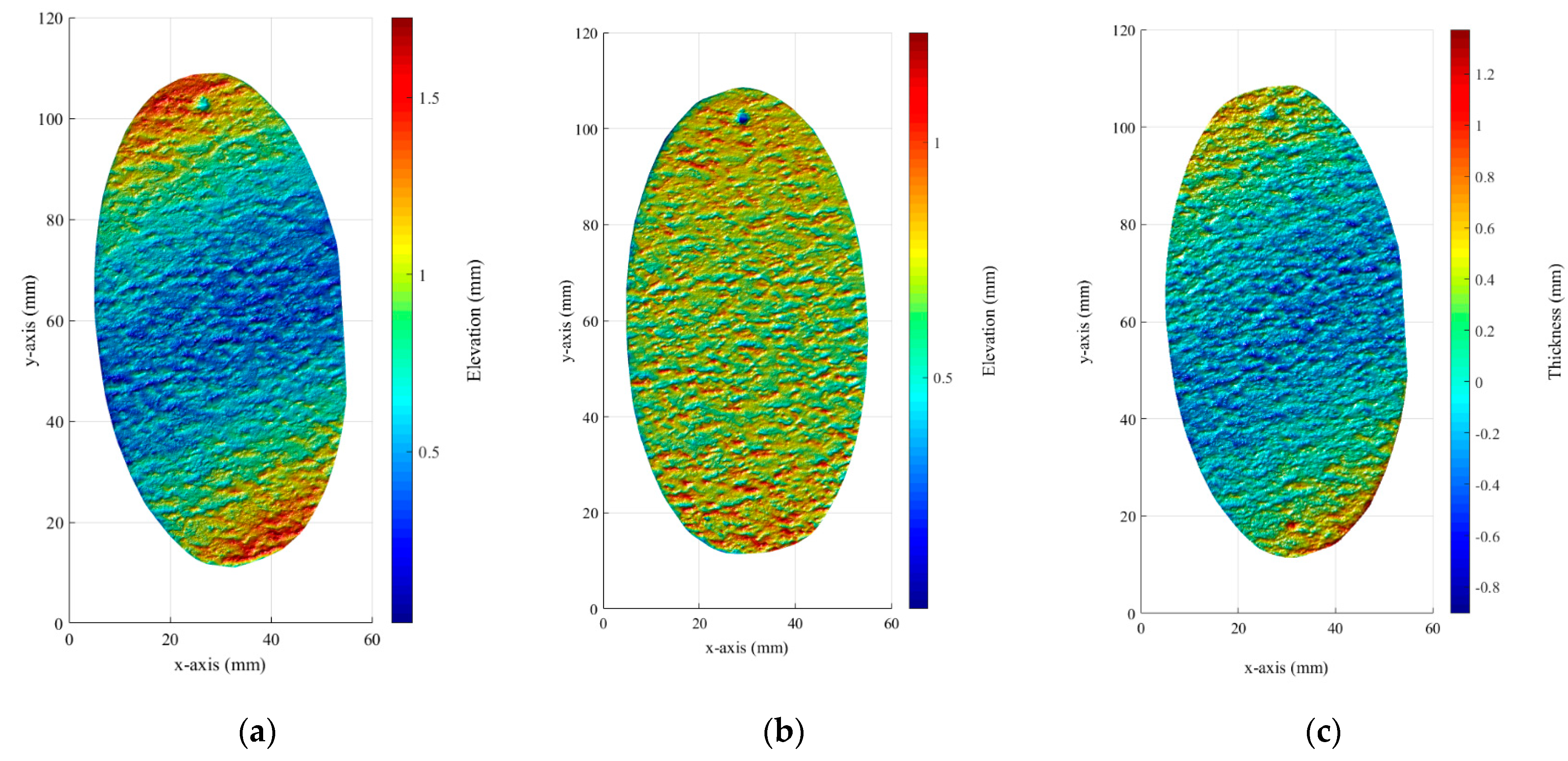
3.1. Roughness Alteration
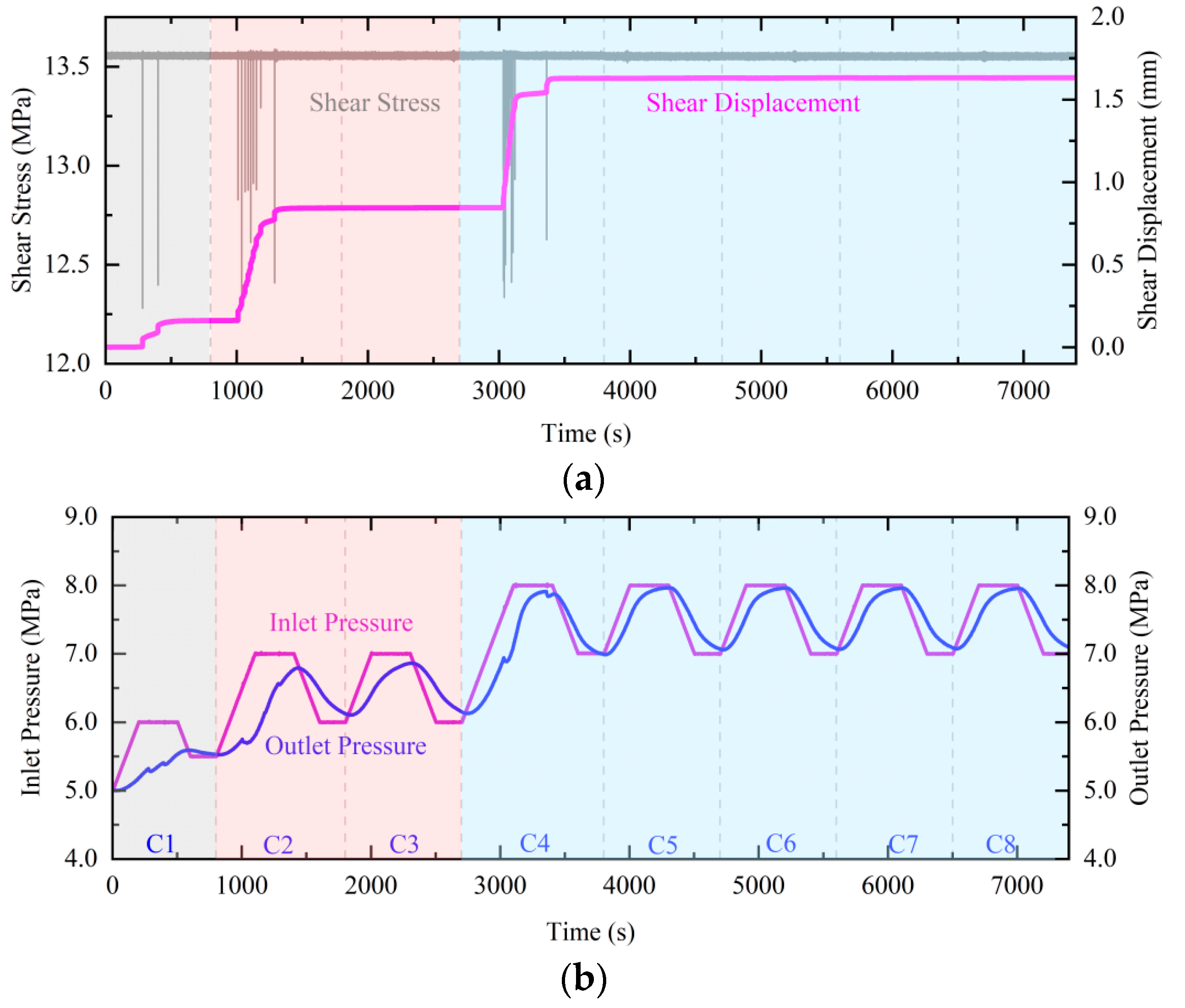
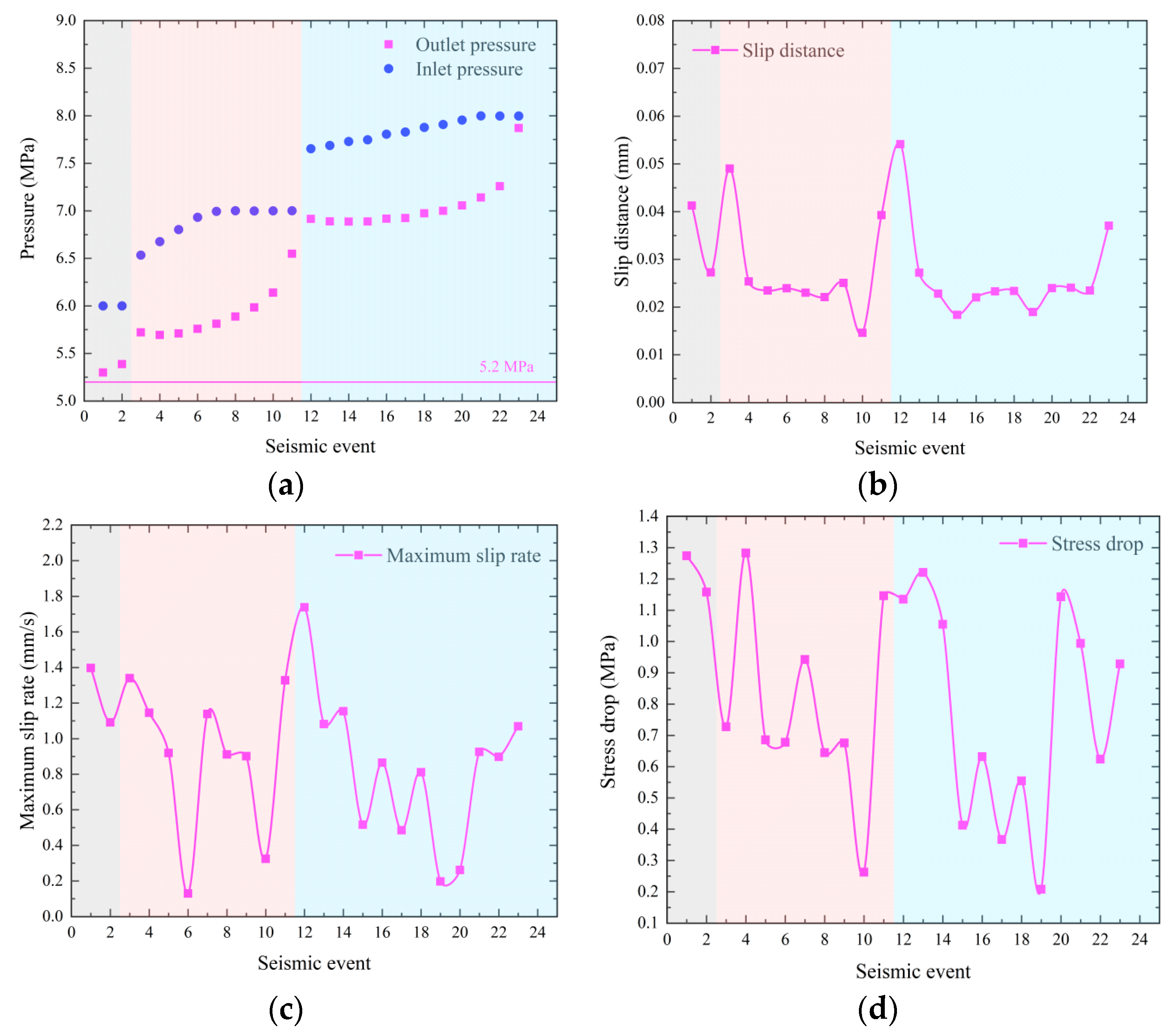
3.2. Mechanic Behavior of Fracture While Water Pressurization
4. Discussion
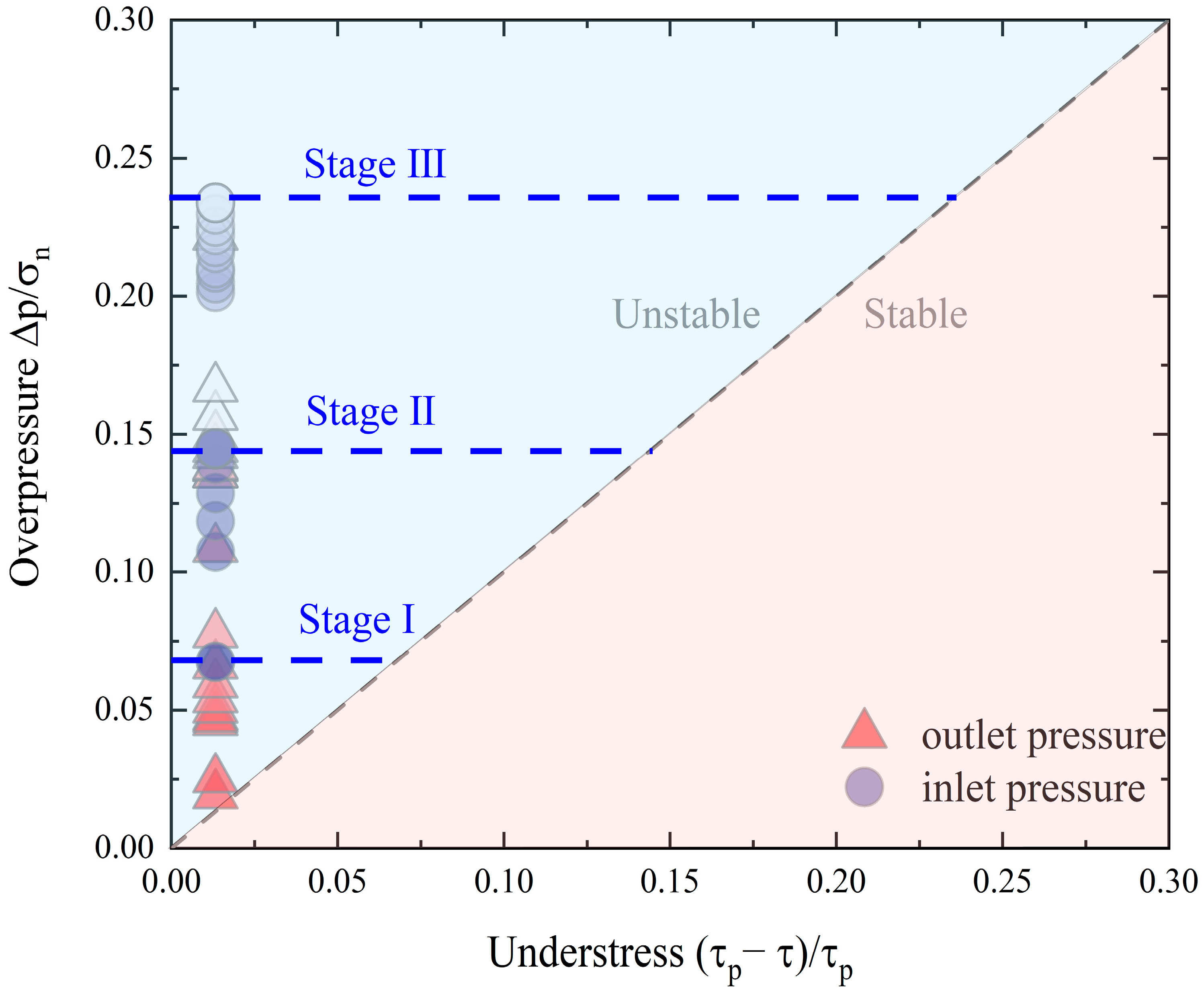
4.1. Overpressure in Fracture Reactivation
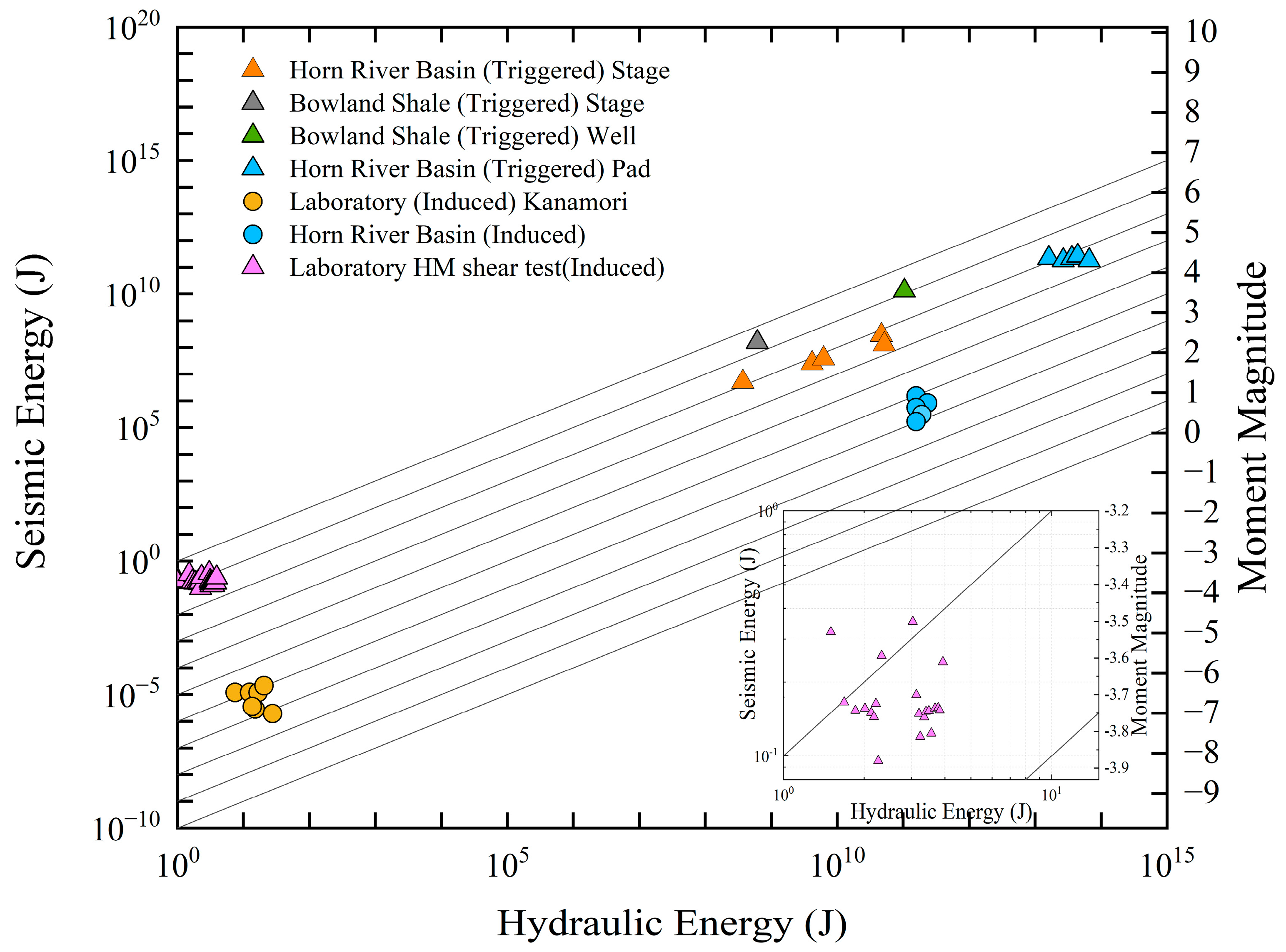
4.2. Hydraulic Energy and Seismic Energy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Elsworth, D.; Spiers, C.J.; Niemeijer, A.R. Understanding induced seismicity. Science 2016, 354, 1380–1381. [Google Scholar] [CrossRef]
- Baker, J.; Ellsworth, W.; Beroza, G.; Schultz, R. Risk-Informed Recommendations for Managing Hydraulic Fracturing–Induced Seismicity via Traffic Light Protocols. Bull. Seismol. Soc. Am. 2020, 110, 2411–2422. [Google Scholar] [CrossRef]
- Fang, Y.; den Hartog, S.A.M.; Elsworth, D.; Marone, C.; Cladouhos, T. Anomalous distribution of microearthquakes in the Newberry Geothermal Reservoir: Mechanisms and implications. Geothermics 2016, 63, 62–73. [Google Scholar] [CrossRef]
- Sibson, R.H. Earthquake Rupturing in Fluid-Overpressured Crust: How Common? Pure Appl. Geophys. 2014, 171, 2867–2885. [Google Scholar] [CrossRef]
- Sibson, R.H. Brittle-failure controls on maximum sustainable overpressure in different tectonic regimes. AAPG Bull. 2003, 87, 901–908. [Google Scholar] [CrossRef]
- Sibson, R.H. Controls on maximum fluid overpressure defining conditions for mesozonal mineralisation. J. Struct. Geol. 2004, 26, 1127–1136. [Google Scholar] [CrossRef]
- Nn, A.; Hs, B.; Ku, A. Fluid overpressure in subduction plate boundary caused by mantle-derived fluids-ScienceDirect. Earth Planet. Sci. Lett. 2020, 538, 116199. [Google Scholar]
- Cappa, F.; Scuderi, M.M.; Collettini, C.; Guglielmi, Y.; Avouac, J.-P. Stabilization of fault slip by fluid injection in the laboratory and in situ. Sci. Adv. 2019, 5, eaau4065. [Google Scholar] [CrossRef]
- Moernaut, J.; Wiemer, G.; Reusch, A.; Stark, N.; Batist, M.D.; Urrutia, R.; Bruno, L.; Kopf, A.; Strasser, M. The influence of overpressure and focused fluid flow on subaquatic slope stability in a formerly glaciated basin: Lake Villarrica (South-Central Chile). Mar. Geol. 2017, 383, 35–54. [Google Scholar] [CrossRef]
- Tingay, M.R.P.; Hillis, R.R.; Swarbrick, R.E. Origin of overpressure and pore-pressure prediction in the Baram province, Brunei. AAPG Bull. 2009, 93, 51–74. [Google Scholar] [CrossRef]
- Liu, Y.; He, Z.; He, S.; Zhang, D.; Li, T.; Wang, X. A new quantitative model and application for overpressure prediction in carbonate formation. J. Pet. Sci. Eng. 2021, 198, 108145. [Google Scholar] [CrossRef]
- Yujie, Z.; Xiaoli, L.; Enzhi, W. Influence of impoundment gravity and pore pressure on reactivation of faults. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 64. [Google Scholar] [CrossRef]
- Ye, Z.; Ghassemi, A. Injection-Induced Shear Slip and Permeability Enhancement in Granite Fractures. J. Geophys. Res. Solid Earth 2018, 123, 9009–9032. [Google Scholar] [CrossRef]
- Dugan, B.; Flemings, P.B. Overpressure and fluid flow in the new jersey continental slope: Implications for slope failure and cold seeps. Science 2000, 289, 288–291. [Google Scholar] [CrossRef]
- Gudmundsson, A. Fluid overpressure and stress drop in fault zones. Geophys. Res. Lett. 1999, 26, 115–118. [Google Scholar] [CrossRef]
- Osborne, M.J.; Swarbrick, R.E. Mechanisms for Generating Overpressure in Sedimentary Basins: A Reevaluation. AAPG Bull. 1997, 81, 1023–1041. [Google Scholar]
- Noël, C.; Passelègue, F.X.; Giorgetti, C.; Violay, M. Fault Reactivation During Fluid Pressure Oscillations: Transition From Stable to Unstable Slip. J. Geophys. Res. Solid Earth 2019, 124, 10940–10953. [Google Scholar] [CrossRef]
- Bell, M.L.; Nur, A. Strength changes due to reservoir-induced pore pressure and stresses and application to Lake Oroville. J. Geophys. Res. 1978, 83, 4469–4483. [Google Scholar] [CrossRef]
- Brown, M.R.M.; Ge, S. Distinguishing Fluid Flow Path from Pore Pressure Diffusion for Induced Seismicity. Bull. Seismol. Soc. Am. 2018, 108, 3684–3686. [Google Scholar] [CrossRef]
- Derode, B.; Guglielmi, Y.; De Barros, L.; Cappa, F. Seismic responses to fluid pressure perturbations in a slipping fault. Geophys. Res. Lett. 2015, 42, 3197–3203. [Google Scholar] [CrossRef]
- Ji, Y.; Wanniarachchi, W.A.M.; Wu, W. Effect of fluid pressure heterogeneity on injection-induced fracture activation. Comput. Geotech. 2020, 123, 103589. [Google Scholar] [CrossRef]
- Noël, C.; Pimienta, L.; Violay, M. Time-Dependent Deformations of Sandstone During Pore Fluid Pressure Oscillations: Implications for Natural and Induced Seismicity. J. Geophys. Res. Solid Earth 2019, 124, 801–821. [Google Scholar] [CrossRef]
- Scuderi, M.M.; Collettini, C.; Marone, C. Frictional stability and earthquake triggering during fluid pressure stimulation of an experimental fault. Earth Planet. Sci. Lett. 2017, 477, 84–96. [Google Scholar] [CrossRef]
- Violay, M.; Nielsen, S.; Spagnuolo, E.; Cinti, D.; Di Toro, G.; Di Stefano, G. Pore fluid in experimental calcite-bearing faults: Abrupt weakening and geochemical signature of co-seismic processes. Earth Planet. Sci. Lett. 2013, 361, 74–84. [Google Scholar] [CrossRef]
- Garagash, D.I.; Germanovich, L.N. Nucleation and arrest of dynamic slip on a pressurized fault. J. Geophys. Res. Solid Earth 2012, 117, B10. [Google Scholar] [CrossRef]
- Gischig, V.S. Rupture propagation behavior and the largest possible earthquake induced by fluid injection into deep reservoirs. Geophys. Res. Lett. 2015, 42, 7420–7428. [Google Scholar] [CrossRef]
- Dieterich, J.H. Time-dependent friction as a possible mechanism for aftershocks. J. Geophys. Res. 1972, 77, 3771–3781. [Google Scholar] [CrossRef]
- Ruina, A. Slip instability and state variable friction laws. J. Geophys. Res. Solid Earth 1983, 88, 10359–10370. [Google Scholar] [CrossRef]
- Goodfellow, S.D.; Nasseri, M.H.B.; Maxwell, S.C.; Young, R.P. Hydraulic fracture energy budget: Insights from the laboratory. Geophys. Res. Lett. 2015, 42, 3179–3187. [Google Scholar] [CrossRef]
- Kanamori, H.; Brodsky, E.E. The physics of earthquakes. Rep. Prog. Phys. 2004, 67, 1429–1496. [Google Scholar] [CrossRef]
- Ide, S.; Beroza, G.C. Does apparent stress vary with earthquake size? Geophys. Res. Lett. 2001, 28, 3349–3352. [Google Scholar] [CrossRef]
- Neda, B.; Eaton, D.W. Comparing energy calculations: Hydraulic fracturing and microseismic monitoring. In Proceedings of the 74th EAGE Conference and Exhibition Incorporating EUROPEC 2012, Copenhagen, Denmark, 4–7 June 2012. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Xu, C.; Song, D.; Liu, X.; Wang, E. The Role of Fluid Overpressure on the Fracture Slip Mechanism Based on Laboratory Tests That Stimulating Reservoir-Induced Seismicity. Appl. Sci. 2023, 13, 3382. https://doi.org/10.3390/app13063382
Zhu Y, Xu C, Song D, Liu X, Wang E. The Role of Fluid Overpressure on the Fracture Slip Mechanism Based on Laboratory Tests That Stimulating Reservoir-Induced Seismicity. Applied Sciences. 2023; 13(6):3382. https://doi.org/10.3390/app13063382
Chicago/Turabian StyleZhu, Yujie, Chen Xu, Danqing Song, Xiaoli Liu, and Enzhi Wang. 2023. "The Role of Fluid Overpressure on the Fracture Slip Mechanism Based on Laboratory Tests That Stimulating Reservoir-Induced Seismicity" Applied Sciences 13, no. 6: 3382. https://doi.org/10.3390/app13063382
APA StyleZhu, Y., Xu, C., Song, D., Liu, X., & Wang, E. (2023). The Role of Fluid Overpressure on the Fracture Slip Mechanism Based on Laboratory Tests That Stimulating Reservoir-Induced Seismicity. Applied Sciences, 13(6), 3382. https://doi.org/10.3390/app13063382









