Spherical Planting Inversion of GRAIL Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Spherical Planting Inversion
2.2. Model Studies
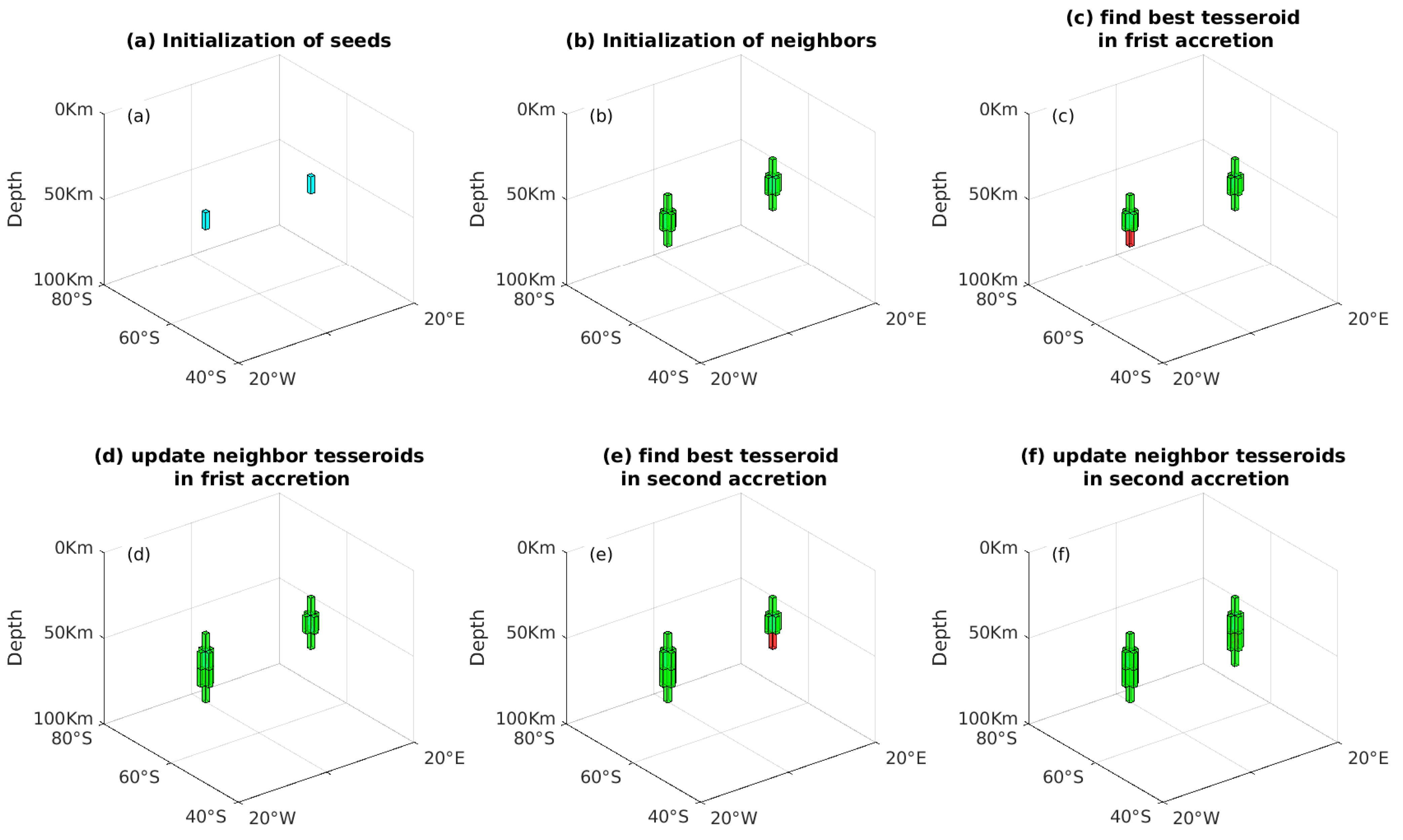
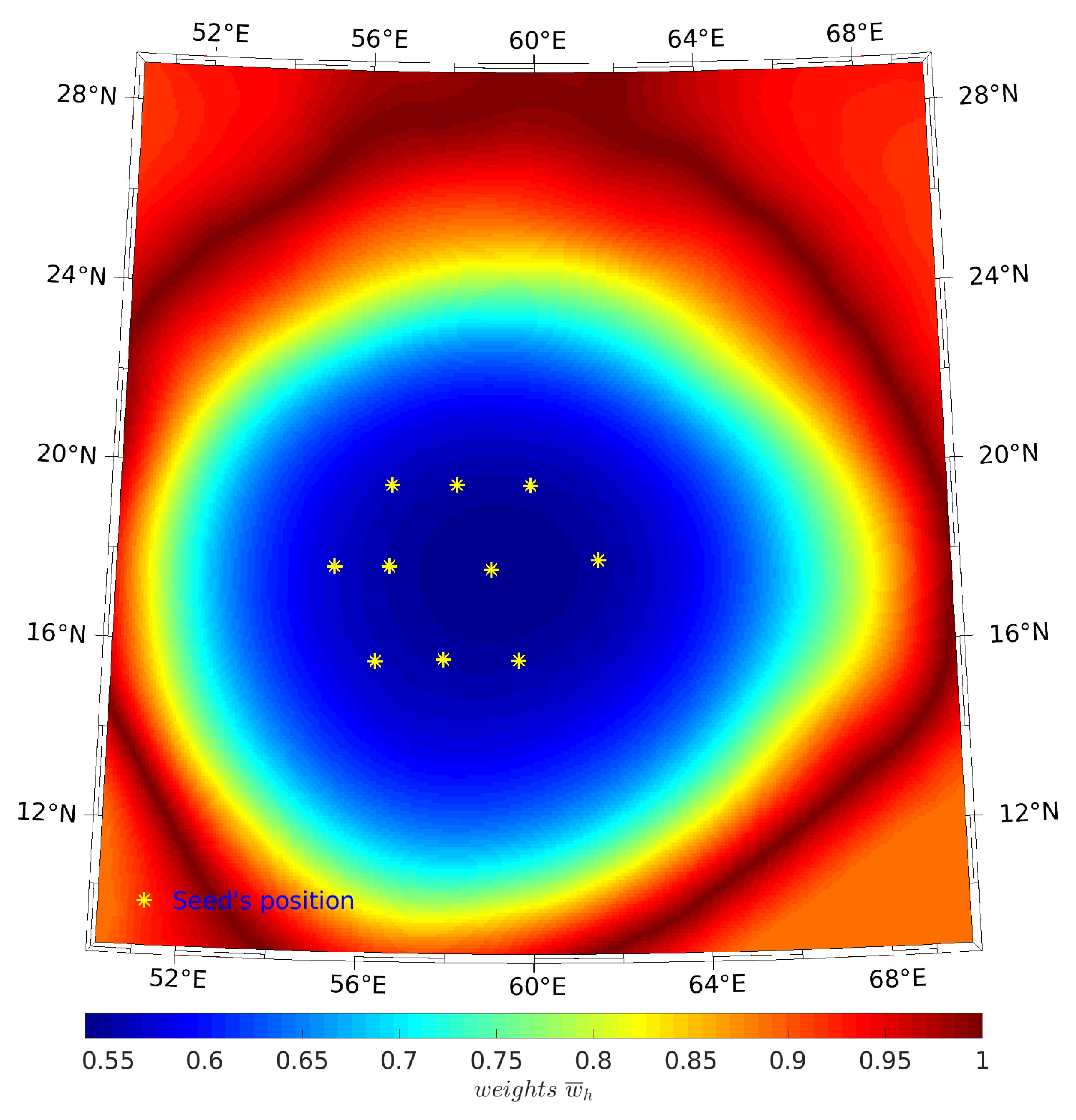
2.2.1. Verification of the Validity of the Novel Seed Weighting Function
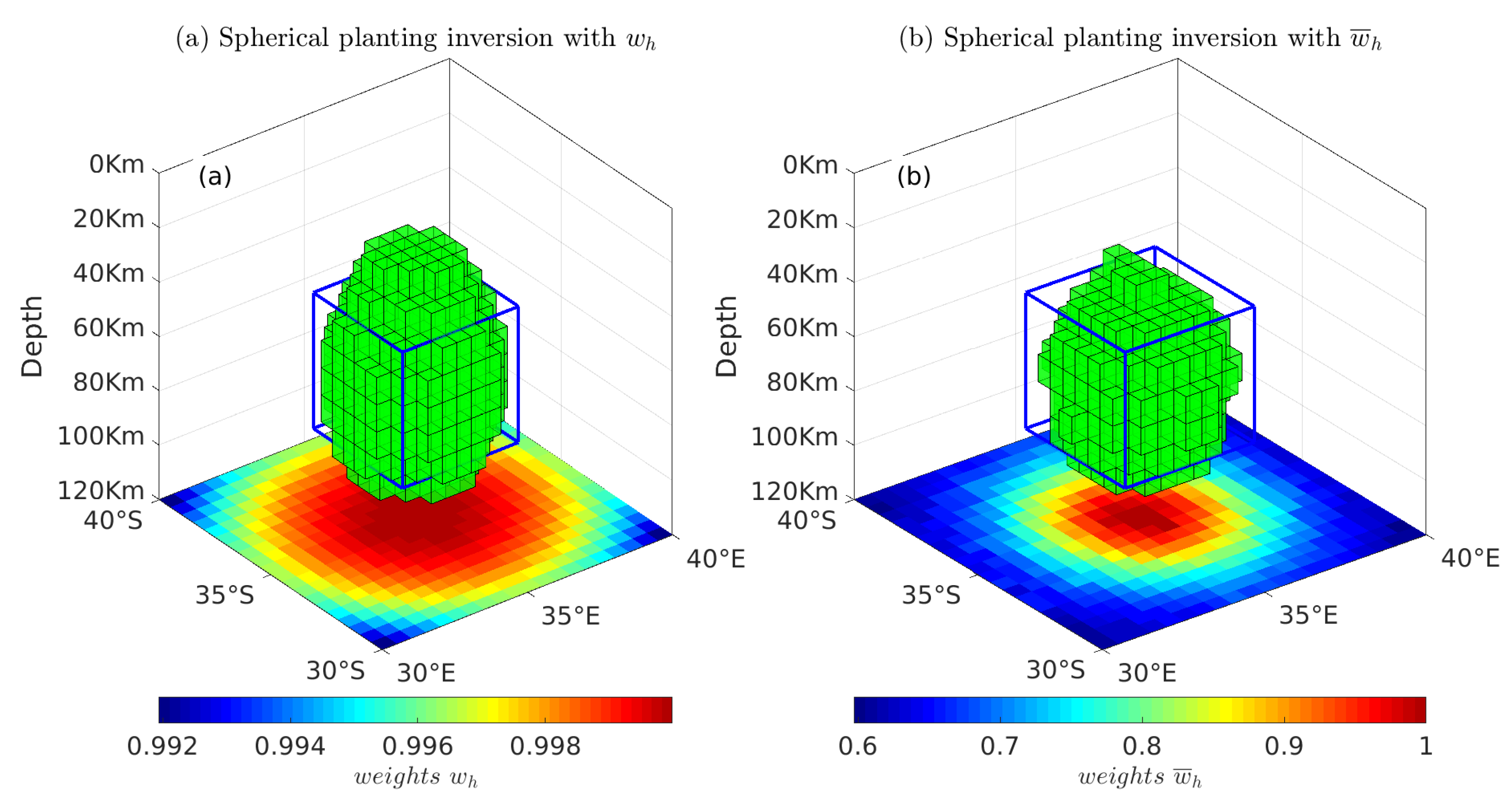
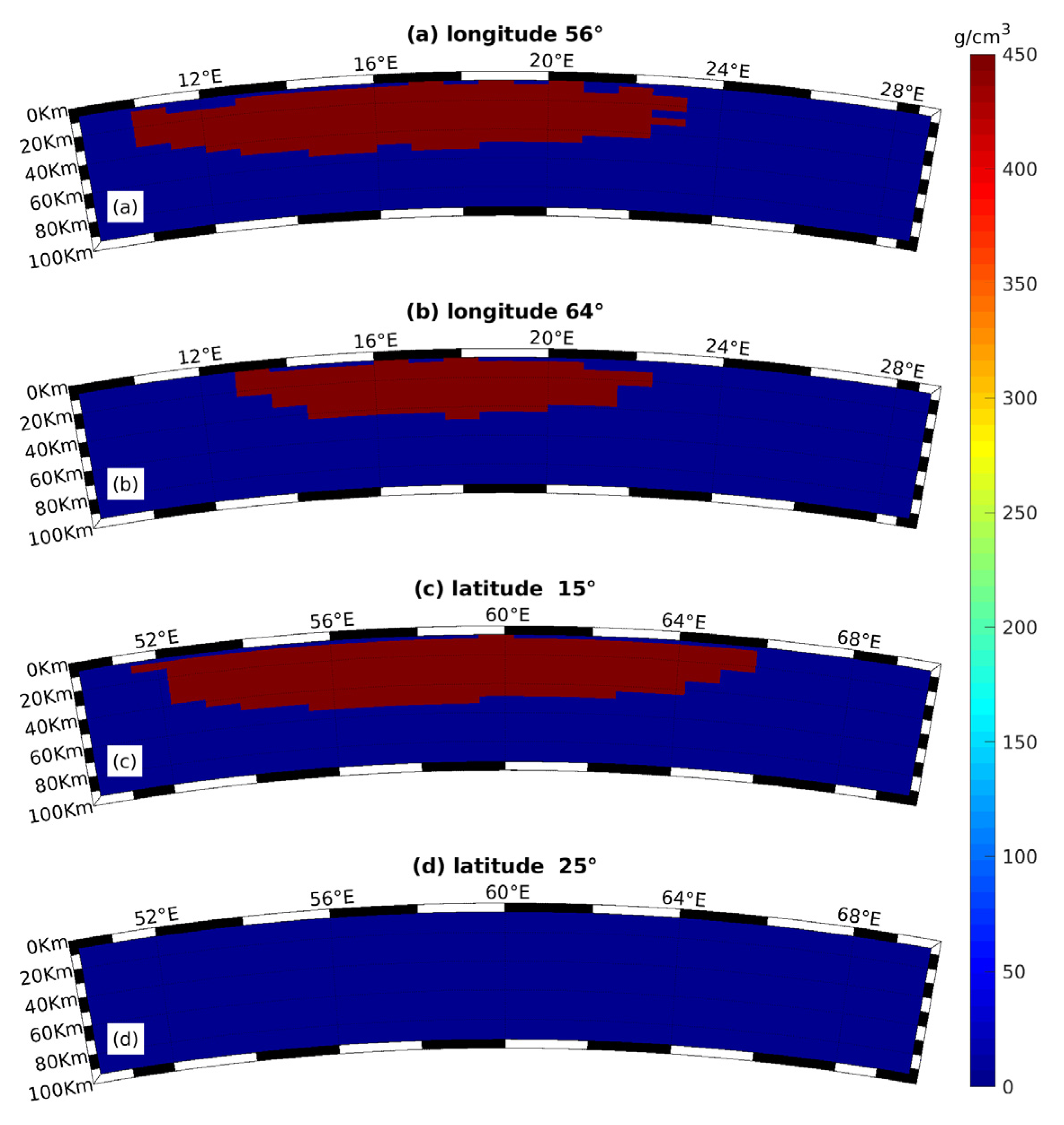
2.2.2. Verification of the Validity of Spherical Planting Inversion
3. Results
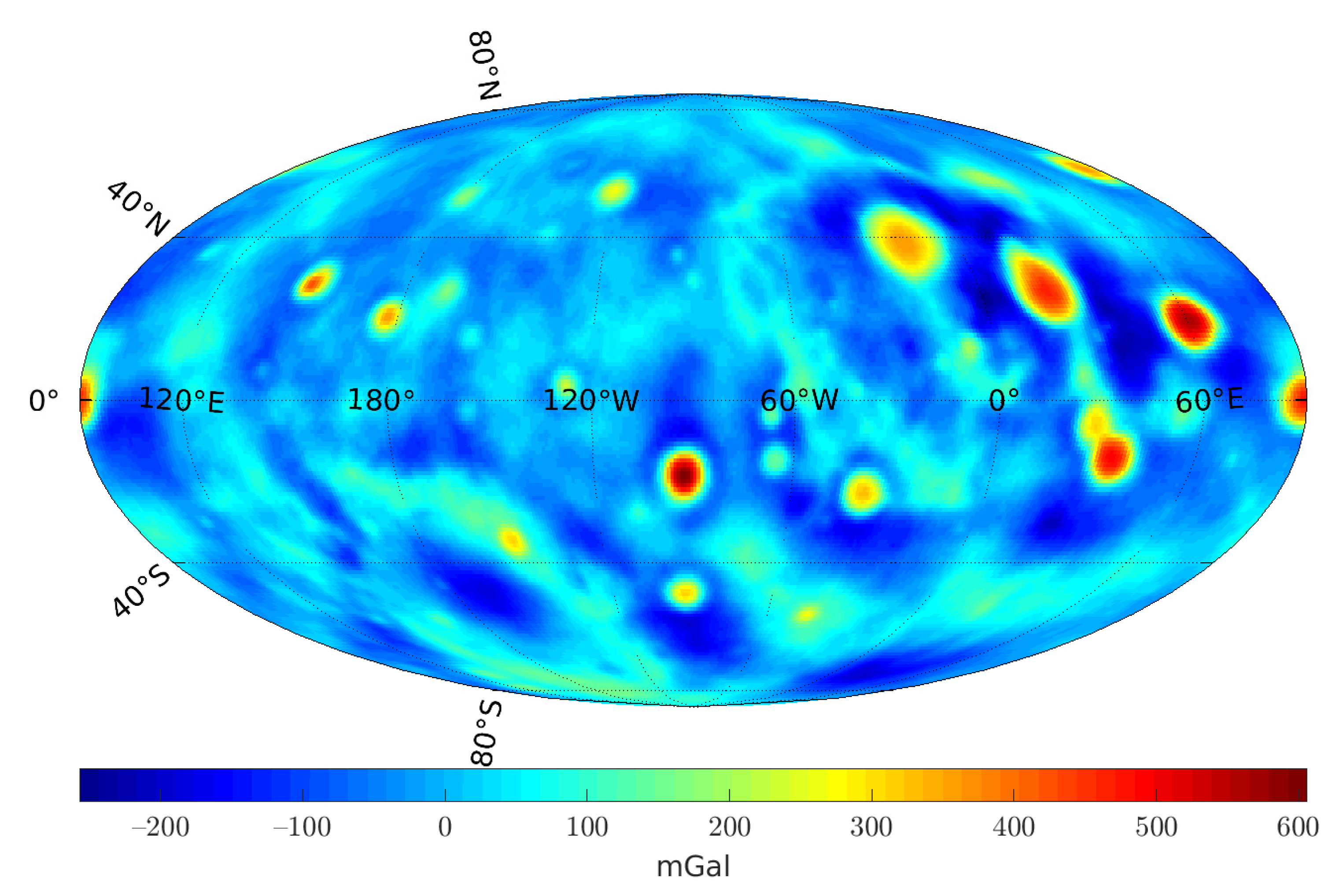
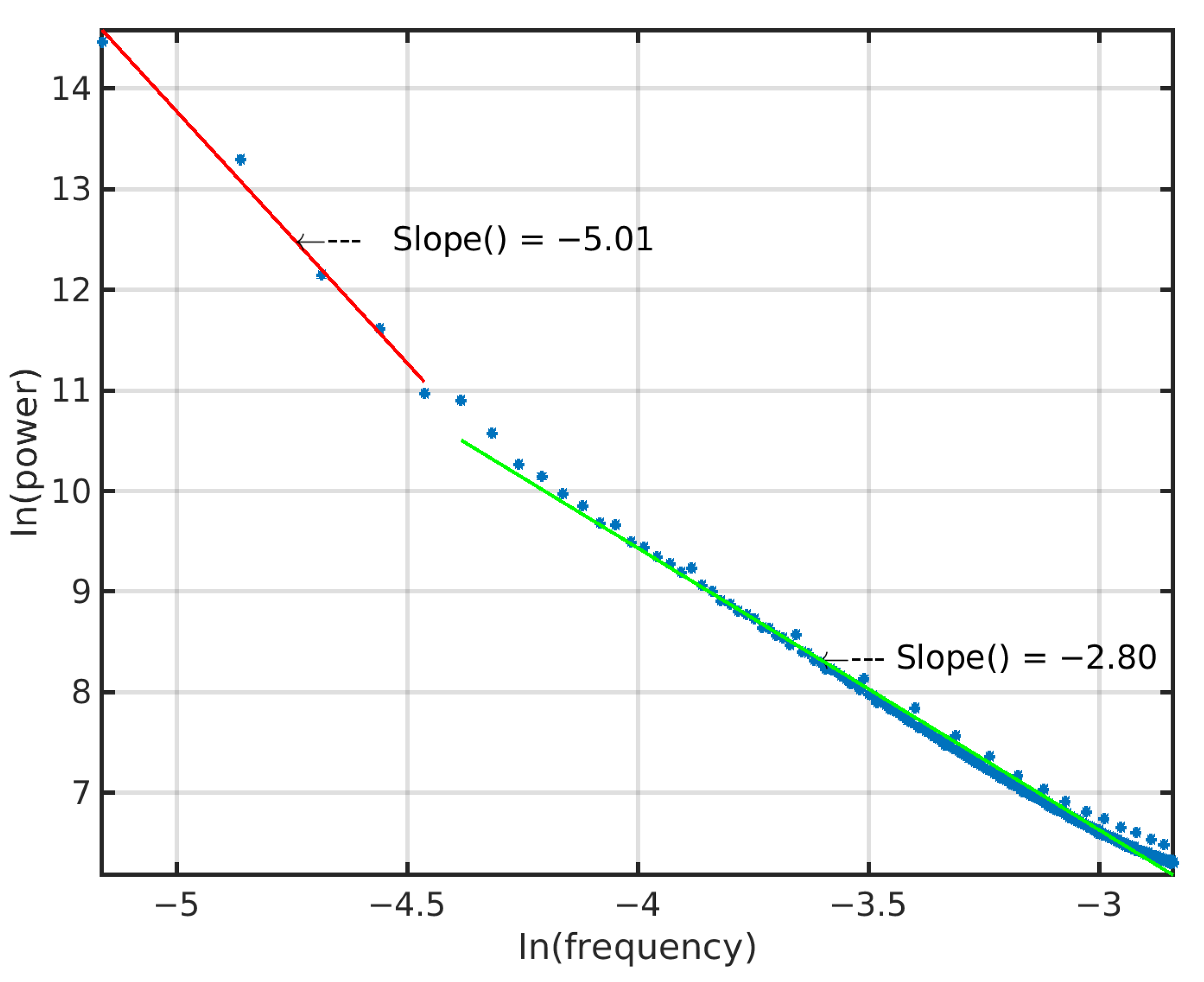
3.1. Data
3.2. Methodology
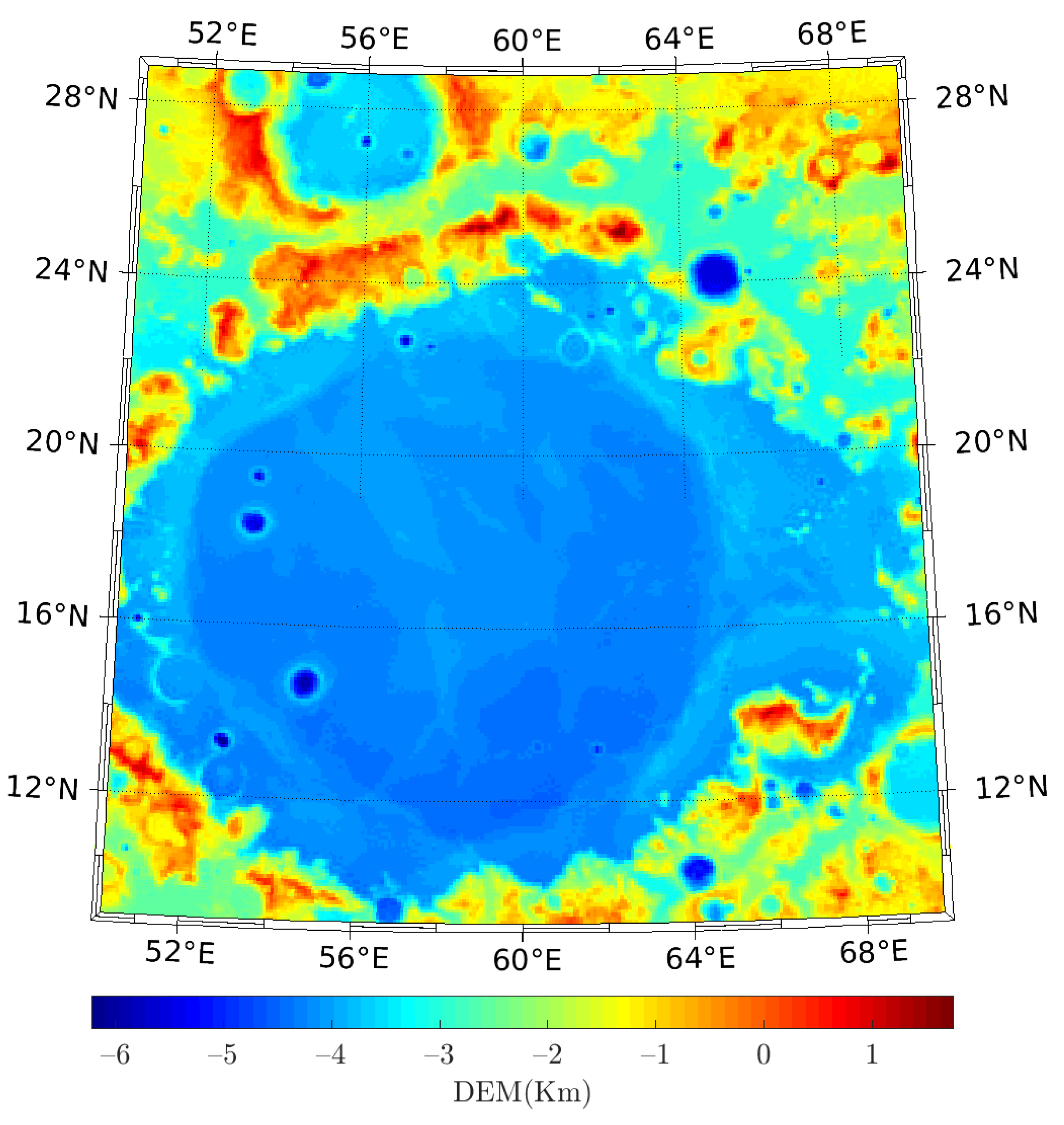
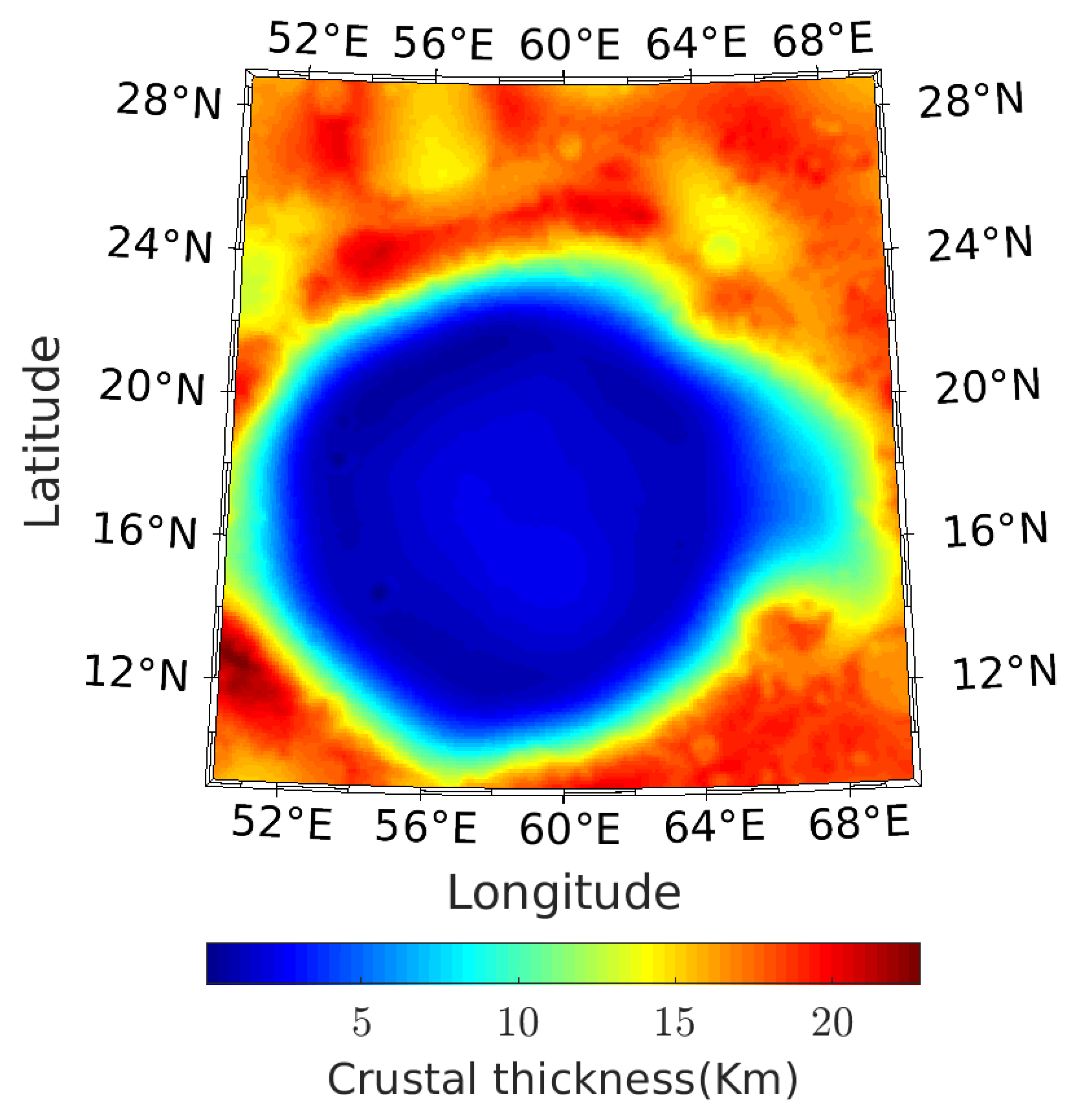
3.3. Spherical Planting Inversion of Mare Crisium
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farquharson, C.G.; Mosher, C.R.W. Three-dimensional modelling of gravity data using finite differences. J. Appl. Geophys. 2009, 68, 417–422. [Google Scholar] [CrossRef]
- Jahandari, H.; Bihlo, A.; Donzelli, F. Forward modelling of gravity data on unstructured grids using an adaptive mimetic finite-difference method. J. Appl. Geophys. 2021, 190, 104340. [Google Scholar] [CrossRef]
- Martyshko, P.; Ladovskii, I.; Byzov, D.; Tsidaev, A. Gravity Data Inversion with Method of Local Corrections for Finite Elements Models. Geosciences 2018, 8, 373. [Google Scholar] [CrossRef]
- Lelièvre, P.G.; Farquharson, C.G.; Hurich, C.A. Joint inversion of seismic traveltimes and gravity data on unstructured grids with application to mineral exploration. Geophysics 2012, 77, K1–K15. [Google Scholar] [CrossRef]
- Jahandari, H.; Farquharson, C.G. Forward modeling of gravity data using finite-volume and finite-element methods on unstructured grids. Geophysics 2013, 78, G69–G80. [Google Scholar] [CrossRef]
- Ren, Z.; Chen, C.; Pan, K.; Kalscheuer, T.; Maurer, H.; Tang, J. Gravity Anomalies of Arbitrary 3D Polyhedral Bodies with Horizontal and Vertical Mass Contrasts. Surv. Geophys. 2017, 38, 479–502. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C. Forward calculation of gravity and its gradient using polyhedral representation of density interfaces: An application of spherical or ellipsoidal topographic gravity effect. J. Geod. 2018, 92, 205–218. [Google Scholar] [CrossRef]
- Ren, Z.; Chen, C.; Zhong, Y.; Chen, H.; Kalscheuer, T.; Maurer, H.; Tang, J.; Hu, X. Recursive Analytical Formulae of Gravitational Fields and Gradient Tensors for Polyhedral Bodies with Polynomial Density Contrasts of Arbitrary Non-negative Integer Orders. Surv. Geophys. 2020, 41, 695–722. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, L. Analytical expressions for the gravitational vector field of a 3-D rectangular prism with density varying as an arbitrary-order polynomial function. Geophys. J. Int. 2017, 210, 1176–1190. [Google Scholar] [CrossRef]
- Ren, Z.; Tang, J.; Kalscheuer, T.; Maurer, H. Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method. J. Geophys. Res. Solid Earth 2017, 122, 79–109. [Google Scholar] [CrossRef]
- Zheng, W.; Xu, H. Progress in satellite gravity recovery from implemented CHAMP, GRACE and GOCE and future GRACE Follow-On missions. Geod. Geodyn. 2015, 6, 241–247. [Google Scholar] [CrossRef]
- Liang, Q.; Chen, C.; Li, Y. 3-D inversion of gravity data in spherical coordinates with application to the GRAIL data. J. Geophys. Res. Planets 2014, 119, 1359–1373. [Google Scholar] [CrossRef]
- Uieda, L.; Barbosa, V.C.F. Fast nonlinear gravity inversion in spherical coordinates with application to the South American Moho. Geophys. J. Int. 2016, 208, 162–176. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Y.; Yan, J.; Wang, H.; Rodriguez, J.A.P.; Qiu, Y. 3D inversion of full gravity gradient tensor data in spherical coordinate system using local north-oriented frame. Earth Planets Space 2018, 70, 1–23. [Google Scholar] [CrossRef]
- Zhao, G.; Chen, B.; Uieda, L.; Liu, J.; Kaban, M.K.; Chen, L.; Guo, R. Efficient 3-D Large-Scale Forward Modeling and Inversion of Gravitational Fields in Spherical Coordinates With Application to Lunar Mascons. J. Geophys. Res. Solid Earth 2019, 124, 4157–4173. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 1 arc-minute global relief model: Procedures, data sources and analysis. NOAA technical memorandum NESDIS NGDC-24. Natl. Geophys. Data Cent. NOAA 2009, 10, V5C8276M. [Google Scholar]
- Čuma, M.; Wilson, G.A.; Zhdanov, M.S. Large-scale 3D inversion of potential field data. Geophys. Prospect. 2012, 60, 1186–1199. [Google Scholar] [CrossRef]
- Čuma, M.; Zhdanov, M.S. Massively parallel regularized 3D inversion of potential fields on CPUs and GPUs. Comput. Geosci. 2014, 62, 80–87. [Google Scholar] [CrossRef]
- Moorkamp, M.; Jegen, M.; Roberts, A.; Hobbs, R. Massively parallel forward modeling of scalar and tensor gravimetry data. Comput. Geosci. 2010, 36, 680–686. [Google Scholar] [CrossRef]
- Zhao-Xi, C.; Xiao-Hong, M.; Liang-Hui, G.; Guo-Feng, L. Three-dimensional fast forward modeling and the inversion strategyfor large scale gravity and gravimetry data based on GPU. Chin. J. Geophys. 2012, 55, 4069–4077. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Pilkington, M. 3-D magnetic imaging using conjugate gradients. Geophysics 1997, 62, 1132–1142. [Google Scholar] [CrossRef]
- Commer, M.; Newman, G.A. New advances in three-dimensional controlled-source electromagnetic inversion. Geophys. J. Int. 2008, 172, 513–535. [Google Scholar] [CrossRef]
- Abubakar, A.; Habashy, T.M.; Li, M.; Liu, J. Inversion algorithms for large-scale geophysical electromagnetic measurements. Inverse Probl. 2009, 25, 1541–1548. [Google Scholar] [CrossRef]
- Sampietro, D.; Capponi, M. Seismic Constrained Gravity Inversion: A Reliable Tool to Improve Geophysical Models Away from Seismic Information. Geosciences 2021, 11, 467. [Google Scholar] [CrossRef]
- Zhang, R.; Li, T.; Zhou, S.; Deng, X. Joint MT and Gravity Inversion Using Structural Constraints: A Case Study from the Linjiang Copper Mining Area, Jilin, China. Minerals 2019, 9, 407. [Google Scholar] [CrossRef]
- Evrard, M.; Dumont, G.; Hermans, T.; Chouteau, M.; Francis, O.; Pirard, E.; Nguyen, F. Geophysical Investigation of the Pb–Zn Deposit of Lontzen–Poppelsberg, Belgium. Minerals 2018, 8, 233. [Google Scholar] [CrossRef]
- Pilkington, M.; Shamsipour, P. Noise reduction procedures for gravity-gradiometer data. Geophysics 2014, 79, G69–G78. [Google Scholar] [CrossRef]
- Liao, J.; Liu, H.; Li, W.; Guo, Z.; Wang, L.; Wang, H.; Peng, S.; Hursthouse, A. 3-D Butterworth Filtering for 3-D High-density Onshore Seismic Field Data. J. Environ. Eng. Geophys. 2018, 23, 223–233. [Google Scholar] [CrossRef]
- Davis, K.; Li, Y. Efficient 3D inversion of magnetic data via octree-mesh discretization, space-filling curves, and wavelets. Geophysics 2013, 78, J61–J73. [Google Scholar] [CrossRef]
- Cox, L.H.; Wilson, G.A.; Zhdanov, M.S. 3D inversion of airborne electromagnetic data using a moving footprint. Explor. Geophys. 2018, 41, 250–259. [Google Scholar] [CrossRef]
- Shin, Y.H.; Choi, K.S.; Xu, H. Three-dimensional forward and inverse models for gravity fields based on the Fast Fourier Transform. Comput. Geosci. 2006, 32, 727–738. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D. Fast inversion of large scale magnetic data using wavelets. SEG Tech. Program Expand. Abstr. 1997, 490–493. [Google Scholar] [CrossRef]
- Rene, R.M. Gravity inversion using open, reject, and “shape-of-anomaly” fill criteria. Geophysics 1986, 51, 988–994. [Google Scholar] [CrossRef]
- Camacho, A.G.; Montesinos, F.G.; Vieira, R. Gravity inversion by means of growing bodies. Geophysics 2000, 65, 95–101. [Google Scholar] [CrossRef]
- Uieda, L.; Barbosa, V. Robust 3D gravity gradient inversion by planting anomalous densities. Geophysics 2012, 77, G55–G66. [Google Scholar] [CrossRef]
- Uieda, L.; Barbosa, V.C.F. Use of the “shape-of-anomaly” data misfit in 3D inversion by planting anomalous densities. In Proceedings of the SEG Technical Program Expanded Abstracts 2012, Las Vegas, NV, USA, 4–9 November 2012. [Google Scholar] [CrossRef]
- Goossens, S.; Lemoine, F.G.; Sabaka, T.J.; Nicholas, J.B.; Mazarico, E.; Rowlands, D.D.; Loomis, B.D.; Chinn, D.S.; Neumann, G.A.; Smith, D.E. A Global Degree and Order 1200 Model of the Lunar Gravity Field Using GRAIL Mission Data; In Proceedings of the 47th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 21-25, March, 2016; p. 1484. [Google Scholar]
- Gómez-Ortiz, D.; Agarwal, B.N.P. 3DINVER.M: A MATLAB program to invert the gravity anomaly over a 3D horizontal density interface by Parker–Oldenburg’s algorithm. Comput. Geosci. 2005, 31, 513–520. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Neumann, G.A.; Nimmo, F.; Kiefer, W.S.; Taylor, G.J.; Melosh, H.J.; Phillips, R.J.; Solomon, S.C.; Andrews-Hanna, J.C.; Asmar, S.W.; et al. The Crust of the Moon as Seen by GRAIL. Science 2013, 339, 671–675. [Google Scholar] [CrossRef]
- Last, B.; Kubik, K. Compact gravity inversion. Geophysics 1983, 48, 713–721. [Google Scholar] [CrossRef]
- Barbosa, V.; Silva, J. Generalized compact gravity inversion. Geophysics 1994, 59, 57–68. [Google Scholar] [CrossRef]
- Ghalehnoee, M.H.; Ansari, A.; Ghorbani, A. Improving compact gravity inversion based on new weighting functions. Geophys. J. Int. 2016, 208, 546–560. [Google Scholar] [CrossRef]
- Stocco, S.; Godio, A.; Sambuelli, L. Modelling and compact inversion of magnetic data: A Matlab code. Comput. Geosci. 2009, 35, 2111–2118. [Google Scholar] [CrossRef]
- LaBrecque, D.J.; Owen, E.; Dailey, W.; Ramirez, A.L. Noise and occam’s inversion of resistivity tomography data. In SEG Technical Program Expanded Abstracts 1992; Society of Exploration Geophysicists: New Orleans, LA, USA, 1992; pp. 397–400. [Google Scholar] [CrossRef]
- Siripunvaraporn, W.; Sarakorn, W. An efficient data space conjugate gradient Occam’s method for three-dimensional magnetotelluric inversion. Geophys. J. Int. 2011, 186, 567–579. [Google Scholar] [CrossRef]
- Muller, P.M.; Sjogren, W.L. Mascons: Lunar mass concentrations. Science 1968, 161, 680–684. [Google Scholar] [CrossRef]
- Klokočník, J.; Kostelecký, J.; Cílek, V.; Kletetschka, G.; Bezděk, A. Gravity aspects from recent gravity field model GRGM1200A of the Moon and analysis of magnetic data. Icarus 2022, 384, 115086. [Google Scholar] [CrossRef]
- Yuan, F.; Xiao-hong, M.; Jun, W.; Zhao-xi, C. Study of the characteristics of lunar gravity field based on the model GRGM660PRIM. Prog. Geophys. 2018, 33, 2211–2218. [Google Scholar] [CrossRef]
- Spudis, P.D.; Sliz, M.U. Impact melt of the lunar Crisium multiring basin. Geophys. Res. Lett. 2017, 44, 1260–1265. [Google Scholar] [CrossRef]
- Rodionova, Z.F.; Zharkova, A.Y.; Grishakina, E.A.; Shevchenko, V.V. Topographic Features of the Lunar Maria and Basins. Sol. Syst. Res. 2021, 55, 183–199. [Google Scholar] [CrossRef]
- Wilhelms, D.E.; McCauley, J.F.; Trask, N.J. The Geologic History of the Moon; Professional Paper 1348; United States Government Printing Office: Washington, DC, USA, 1987. [Google Scholar]
- Lu, X.; Cao, H.; Ling, Z.; Fu, X.; Qiao, L.; Chen, J. Geomorphology, Mineralogy, and Geochronology of Mare Basalts and Non-Mare Materials around the Lunar Crisium Basin. Remote Sens. 2021, 13, 4828. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head, J.W.; Duxbury, T.H.; et al. Initial observations from the Lunar Orbiter Laser Altimeter (LOLA). Geophys. Res. Lett. 2010, 37, 1–6. [Google Scholar] [CrossRef]
- Lemoine, F.G.; Goossens, S.; Sabaka, T.J.; Nicholas, J.B.; Mazarico, E.; Rowlands, D.D.; Loomis, B.D.; Chinn, D.S.; Neumann, G.A.; Smith, D.E.; et al. GRGM900C: A degree 900 lunar gravity model from GRAIL primary and extended mission data. Geophys. Res. Lett. 2014, 41, 3382–3389. [Google Scholar] [CrossRef]
- Deng, Q.; Li, F.; Yan, J.; Ye, M.; Barriot, J.P. Degree-Depth Relation for Planetary Gravity Field Model Based on Wavelength. Earth Space Sci. 2022, 9, e2021EA002143. [Google Scholar] [CrossRef]
- Featherstone, W.E.; Hirt, C.; Kuhn, M. Band-limited Bouguer gravity identifies new basins on the Moon. J. Geophys. Res. Planets 2013, 118, 1397–1413. [Google Scholar] [CrossRef]
- Goossens, S.; Sabaka, T.J.; Wieczorek, M.A.; Neumann, G.A.; Mazarico, E.; Lemoine, F.G.; Nicholas, J.B.; Smith, D.E.; Zuber, M.T. High-Resolution Gravity Field Models from GRAIL Data and Implications for Models of the Density Structure of the Moon’s Crust. J. Geophys. Res. Planets 2020, 125, e2019JE006086. [Google Scholar] [CrossRef]
- Jansen, J.C.; Andrews-Hanna, J.C.; Li, Y.; Lucey, P.G.; Taylor, G.J.; Goossens, S.; Lemoine, F.G.; Mazarico, E.; Head, J.W.; Milbury, C.; et al. Small-scale density variations in the lunar crust revealed by GRAIL. Icarus 2017, 291, 107–123. [Google Scholar] [CrossRef]
- Jozwiak, L.M.; Head Iii, J.W.; Neumann, G.A.; Wilson, L. Observational constraints on the identification of shallow lunar magmatism: Insights from floor-fractured craters. Icarus 2017, 283, 224–231. [Google Scholar] [CrossRef]
- Andrews-Hanna, J.C.; Head, J.W.; Johnson, B.C.; Keane, J.T.; Kiefer, W.S.; McGovern, P.J.; Neumann, G.A.; Wieczorek, M.A.; Zuber, M.T. Ring faults and ring dikes around the Orientale basin on the Moon. Icarus 2018, 310, 1–20. [Google Scholar] [CrossRef]
- Hiesinger, H. New Views of Lunar Geoscience: An Introduction and Overview. Rev. Mineral. Geochem. 2006, 60, 1–81. [Google Scholar] [CrossRef]
- Stoffler, D. Cratering History and Lunar Chronology. Rev. Mineral. Geochem. 2006, 60, 519–596. [Google Scholar] [CrossRef]
- Golombek, M.P.; Anderson, F.S.; Zuber, M.T. Martian wrinkle ridge topography: Evidence for subsurface faults from MOLA. J. Geophys. Res. Planets 2001, 106, 23811–23821. [Google Scholar] [CrossRef]
- Taylor, S.R.; McLennan, S. Planetary Crusts: Their Composition, Origin and Evolution; Cambridge University Press: NY, UK, 2009; Volume 10. [Google Scholar]
- Spector, A.; Grant, F.S. Statistical models for interpreting aeromagnetic data. Geophysics 1970, 35, 293–302. [Google Scholar] [CrossRef]
- Mousa, A.; Mickus, K.; Al-Rahim, A. The thickness of cover sequences in the Western Desert of Iraq from a power spectrum analysis of gravity and magnetic data. J. Asian Earth Sci. 2017, 138, 230–245. [Google Scholar] [CrossRef]
- Ganguli, S.S.; Pal, S.K.; Singh, S.L.; Rao, J.; Balakrishna, B. Insights into crustal architecture and tectonics across Palghat Cauvery Shear Zone, India from combined analysis of gravity and magnetic data. Geol. J. 2020, 56, 2041–2059. [Google Scholar] [CrossRef]
- Ganguli, S.S.; Pal, S.K.; Sundaralingam, K.; Kumar, P. Insights into the crustal architecture from the analysis of gravity and magnetic data across Salem-Attur Shear Zone (SASZ), South-ern Granulite Terrane (SGT), India: An evidence of accretional tectonics. Episodes 2021, 44, 419–442. [Google Scholar] [CrossRef]
- de Souza, J.; Pires Rostirolla, S. A fast MATLAB program to estimate the multifractal spectrum of multidimensional data: Application to fractures. Comput. Geosci. 2011, 37, 241–249. [Google Scholar] [CrossRef]
- Essa, K.S.; Munschy, M.; Youssef, M.A.S.; Khalaf, E.E.D.A. Aeromagnetic and Radiometric Data Interpretation to Delineate the Structural Elements and Probable Precambrian Mineralization Zones: A Case Study, Egypt. Min. Metall. Explor. 2022, 39, 2461–2475. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Jolliff, B.L.; Khan, A.; Pritchard, M.E.; Weiss, B.P.; Williams, J.D.; Hood, L.L.; Righter, K.; Neal, C.R.; Shearer, C.K. New views of the moon. Rev. Min. Geochem 2006, 60, 221–364. [Google Scholar] [CrossRef]
- Wieczorek, M.A. Gravity and topography of the terrestrial planets. Treatise Geophys. 2015, 10, 153–193. [Google Scholar] [CrossRef]
- Besserer, J.; Nimmo, F.; Wieczorek, M.A.; Weber, R.C.; Kiefer, W.S.; McGovern, P.J.; Andrews-Hanna, J.C.; Smith, D.E.; Zuber, M.T. GRAIL gravity constraints on the vertical and lateral density structure of the lunar crust. Geophys. Res. Lett. 2014, 41, 5771–5777. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Beuthe, M.; Rivoldini, A.; Van Hoolst, T. Hydrostatic Interfaces in Bodies With Nonhydrostatic Lithospheres. J. Geophys. Res. Planets 2019, 124, 1410–1432. [Google Scholar] [CrossRef]
- Kiefer, W.S.; Macke, R.J.; Britt, D.T.; Irving, A.J.; Consolmagno, G.J. The density and porosity of lunar rocks. Geophys. Res. Lett. 2012, 39, L07201. [Google Scholar] [CrossRef]
- Corley, L.M.; McGovern, P.J.; Kramer, G.Y.; Lemelin, M.; Trang, D.; Gillis-Davis, J.J.; Taylor, G.J.; Powell, K.E.; Kiefer, W.S.; Wieczorek, M. Olivine-bearing lithologies on the Moon: Constraints on origins and transport mechanisms from M3 spectroscopy, radiative transfer modeling, and GRAIL crustal thickness. Icarus 2018, 300, 287–304. [Google Scholar] [CrossRef]
- May, D.A.; Knepley, M.G. Optimal, scalable forward models for computing gravity anomalies. Geophys. J. Int. 2011, 187, 161–177. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Y. Inversion of the density structure of the lithosphere in the North China Craton from GOCE satellite gravity gradient data. Earth Planets Space 2018, 70, 1–22. [Google Scholar] [CrossRef]
- Bühlmann, P.; Yu, B. Boosting with the L 2 loss: Regression and classification. J. Am. Stat. Assoc. 2003, 98, 324–339. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, G.; Zhang, D.; Cao, S.; Deng, Y.; Xu, G.; Liu, Y.; Zhu, Z.; Chen, P. Spherical Planting Inversion of GRAIL Data. Appl. Sci. 2023, 13, 3332. https://doi.org/10.3390/app13053332
Lu G, Zhang D, Cao S, Deng Y, Xu G, Liu Y, Zhu Z, Chen P. Spherical Planting Inversion of GRAIL Data. Applied Sciences. 2023; 13(5):3332. https://doi.org/10.3390/app13053332
Chicago/Turabian StyleLu, Guangyin, Dongxing Zhang, Shujin Cao, Yihuai Deng, Gang Xu, Yihu Liu, Ziqiang Zhu, and Peng Chen. 2023. "Spherical Planting Inversion of GRAIL Data" Applied Sciences 13, no. 5: 3332. https://doi.org/10.3390/app13053332
APA StyleLu, G., Zhang, D., Cao, S., Deng, Y., Xu, G., Liu, Y., Zhu, Z., & Chen, P. (2023). Spherical Planting Inversion of GRAIL Data. Applied Sciences, 13(5), 3332. https://doi.org/10.3390/app13053332





