New Approach of the Variable Fractional-Order Model of a Robot Arm
Abstract
1. Introduction
2. Mathematical Preliminaries
- —terminals of fractional differentiation,
- —fractional order.
- The notation represents an integral of fractional order.
2.1. Grünwald–Letnikov Definition
2.2. The Fractional Order Integrator
2.3. Fractional Derivative
Fractional Derivative Selected Properties
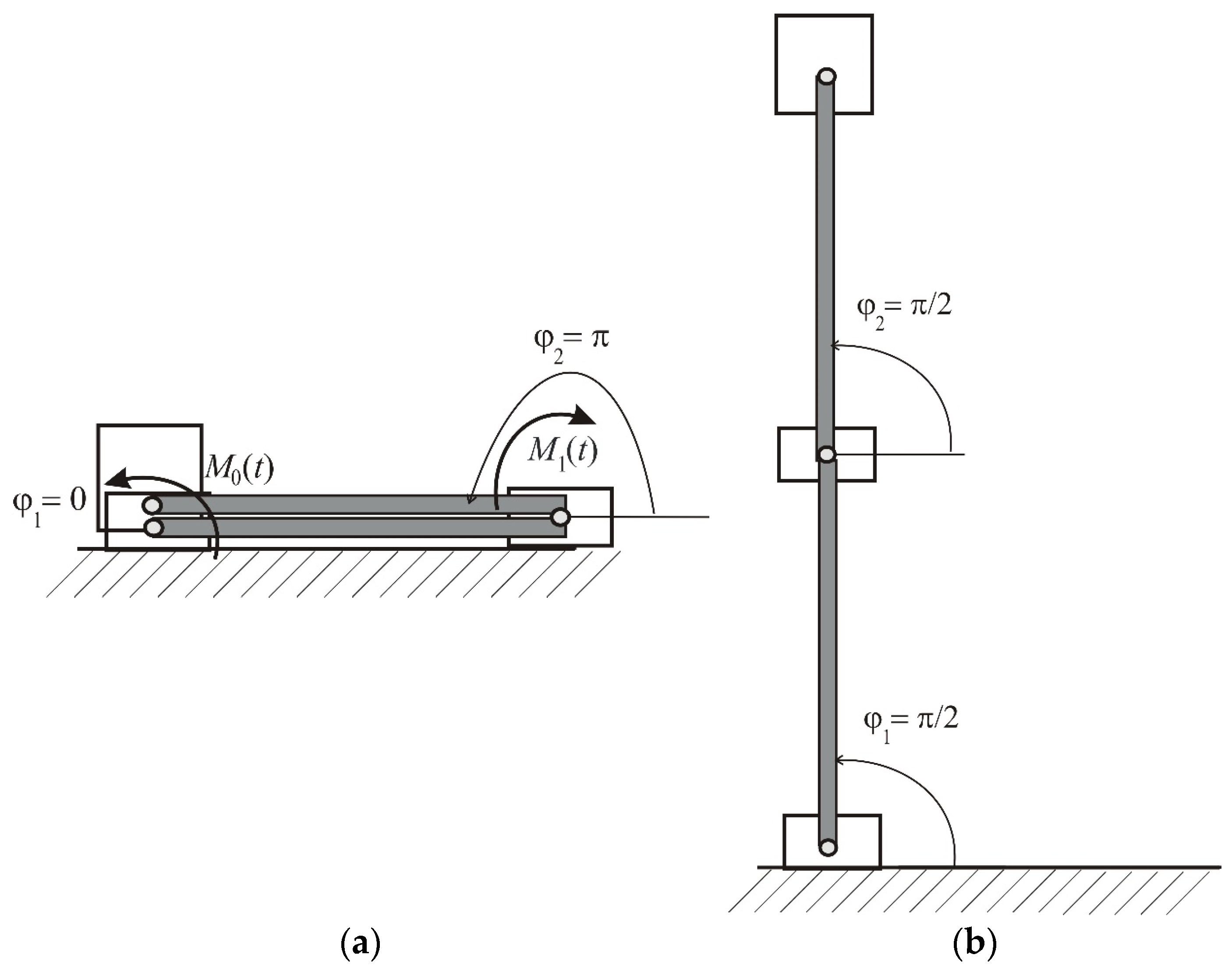
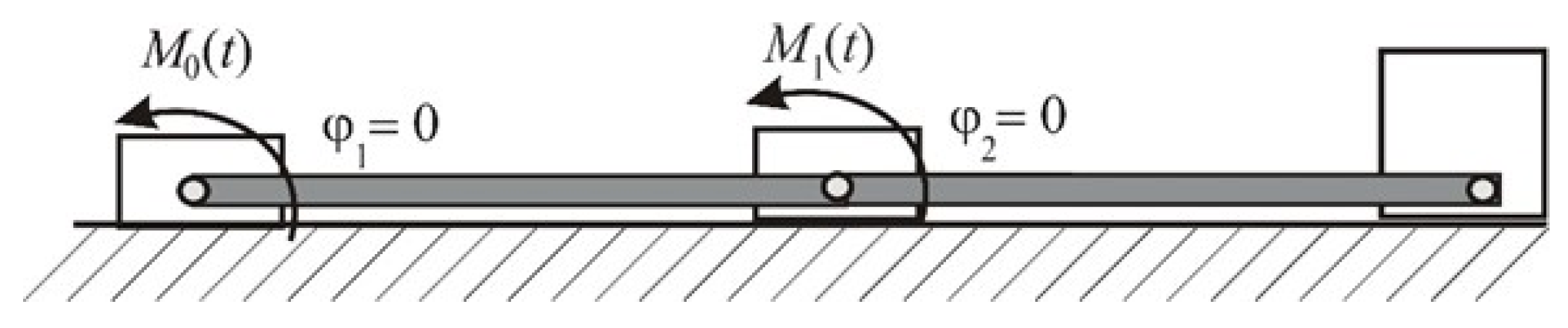
3. The Robot Arm Description
- m1 = 1.0 [kg]—the weight of the drive systems;
- m2 = 7.0 [kg]—total weight of the manipulator;
- m = 0.5 [kg]—weights of the manipulator links;
- l = 0.5 [m]—the length of the manipulator links;
- M0(t), M1(t)—driving torque.
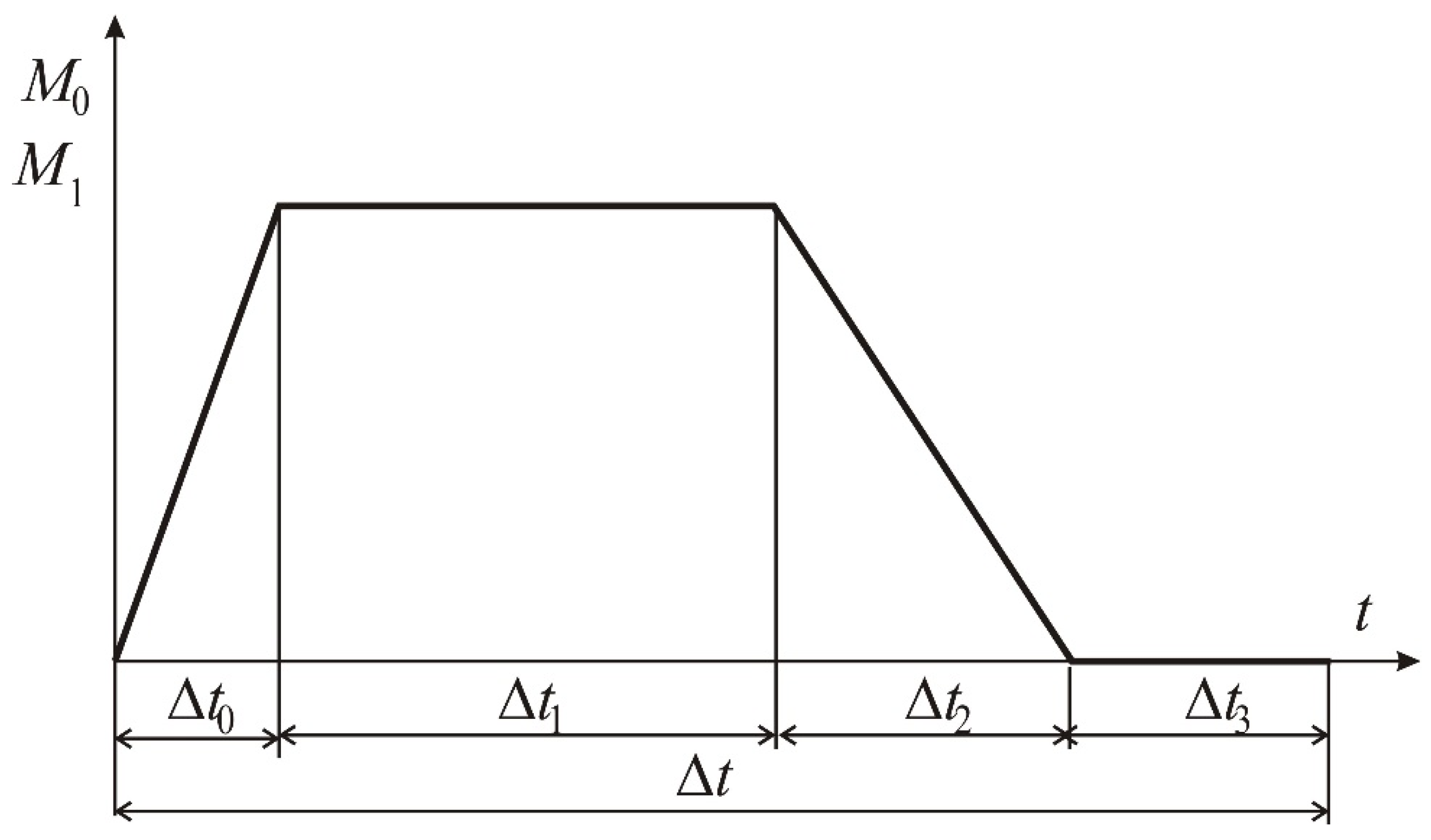
- M0, M1—fixed values of driving torque;
- Δt0—start-up phase, an increase of drive torques to the assumed fixed values;
- Δt1—phase of steady drive torques;
- Δt2—phase of reduction of drive torques to zero;
- Δt3—stop phase drive torques equal zero;
- l = 0.5 [m]—the length of the manipulator links.
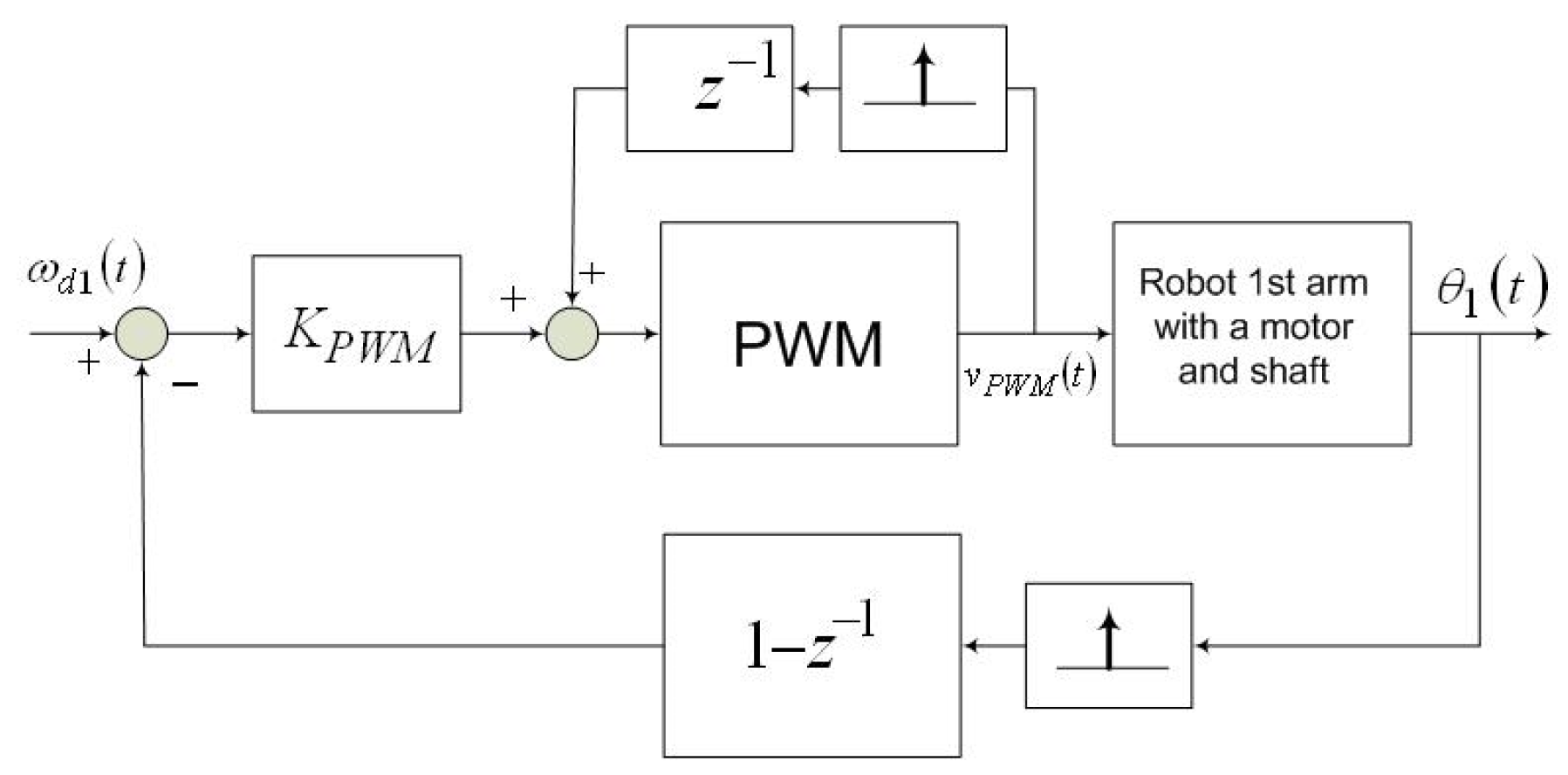
4. The Robot Arm’s Mathematical Models
4.1. Classical Mathematical Model (CM) of the Robot Arm
- —acceleration of the Earth,
- —lengths of the robot arm,
- —distance from the precedent joint to the arm centroid.
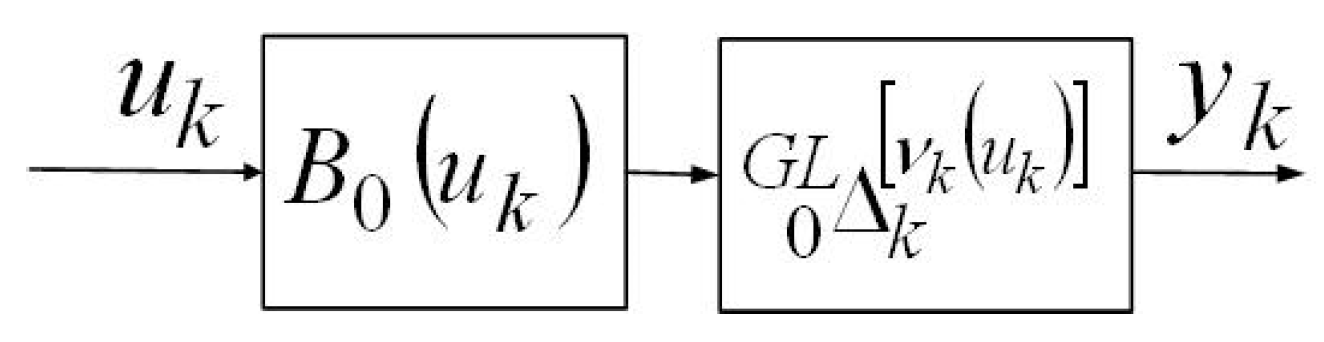
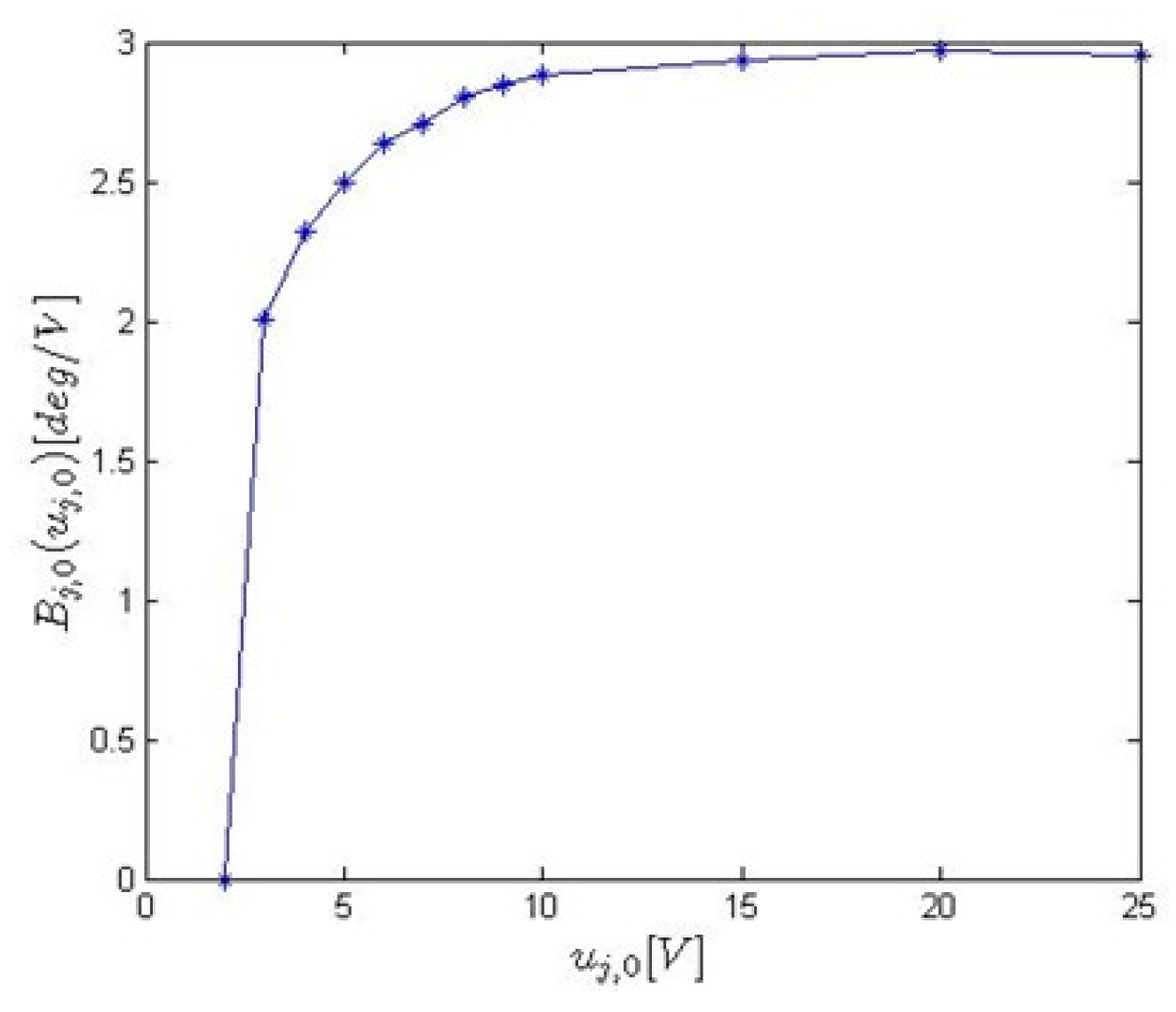
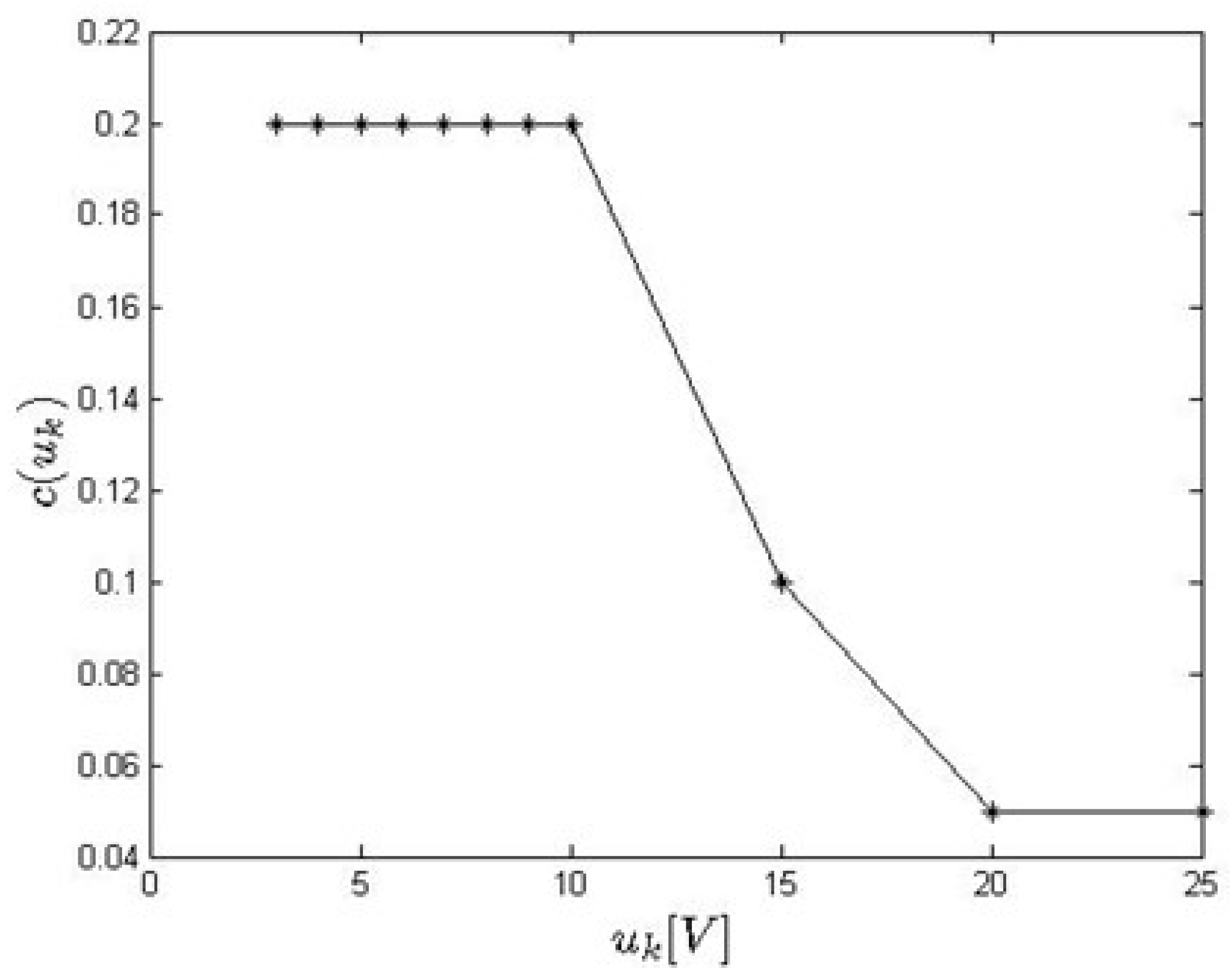
4.2. Variable Fractional-Order Mathematical Model (VFOM) of the Robot Arm
- —constant coefficients with ,
- —order functions,
- —order functions,
- —the robot arm input and output functions.
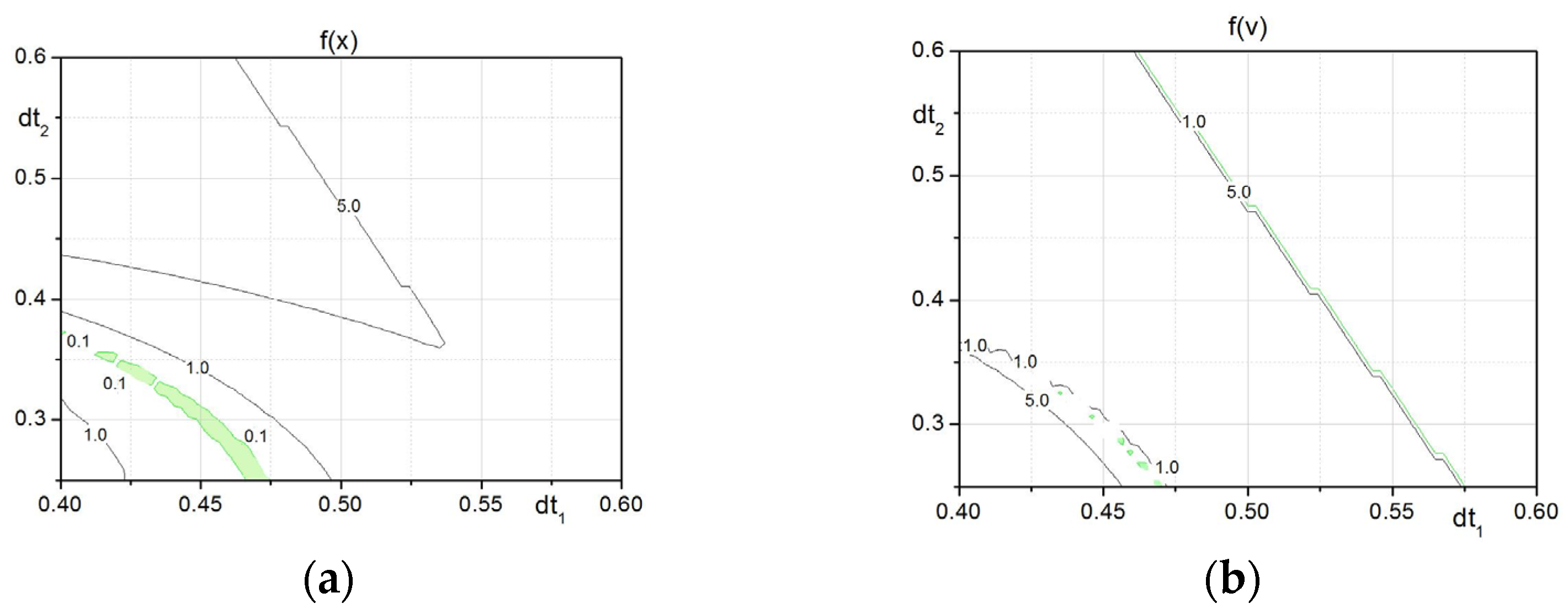
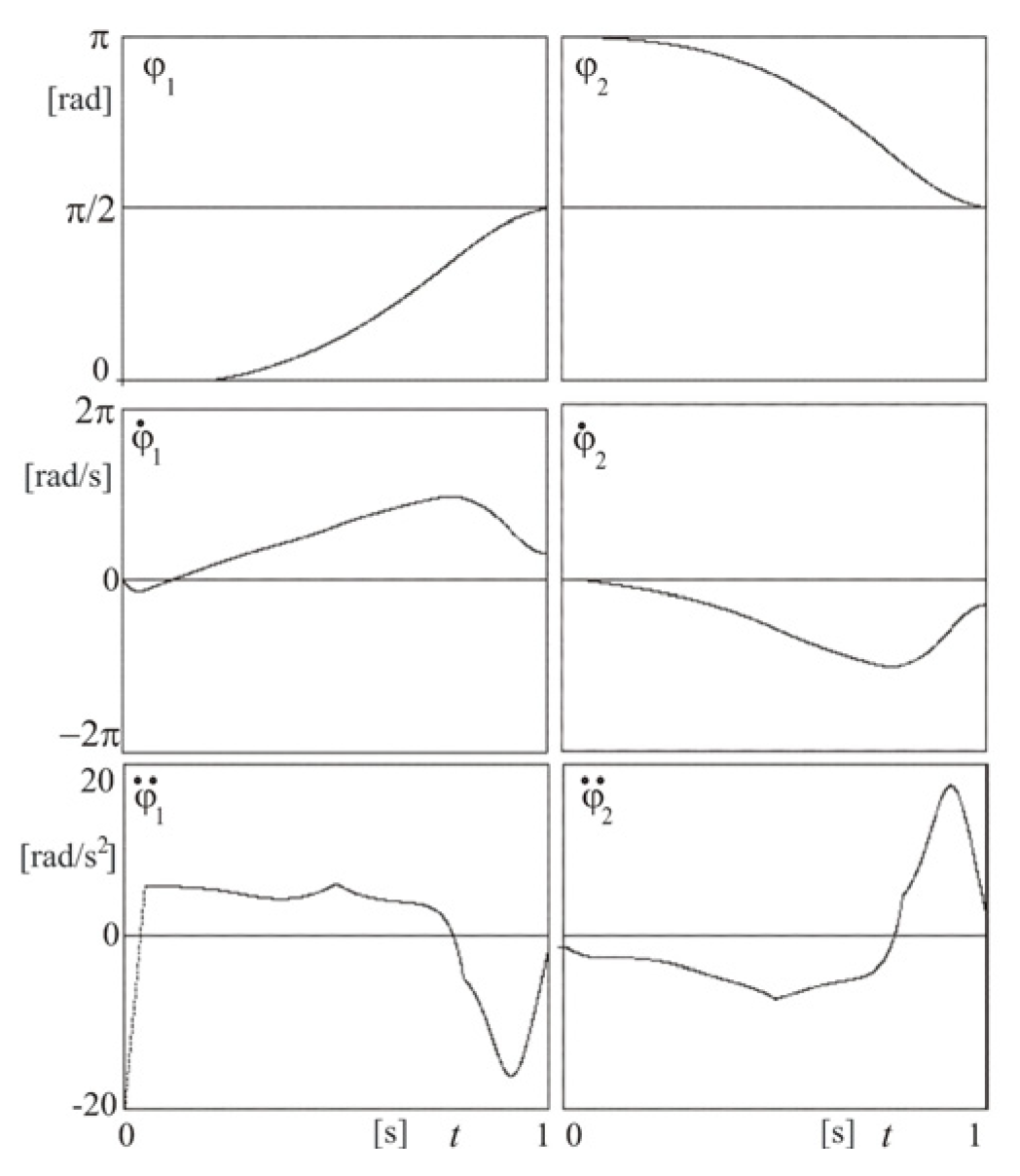
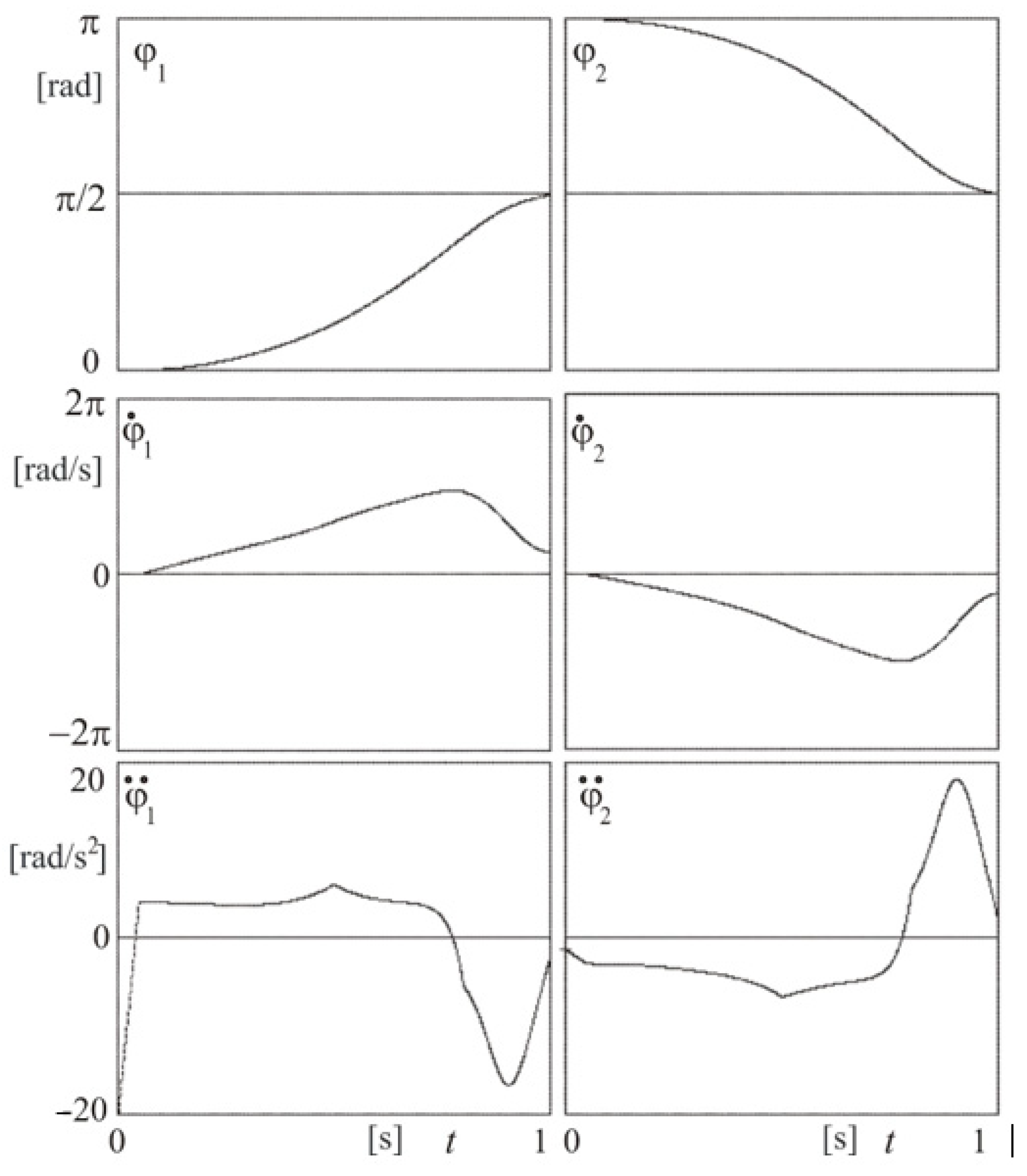
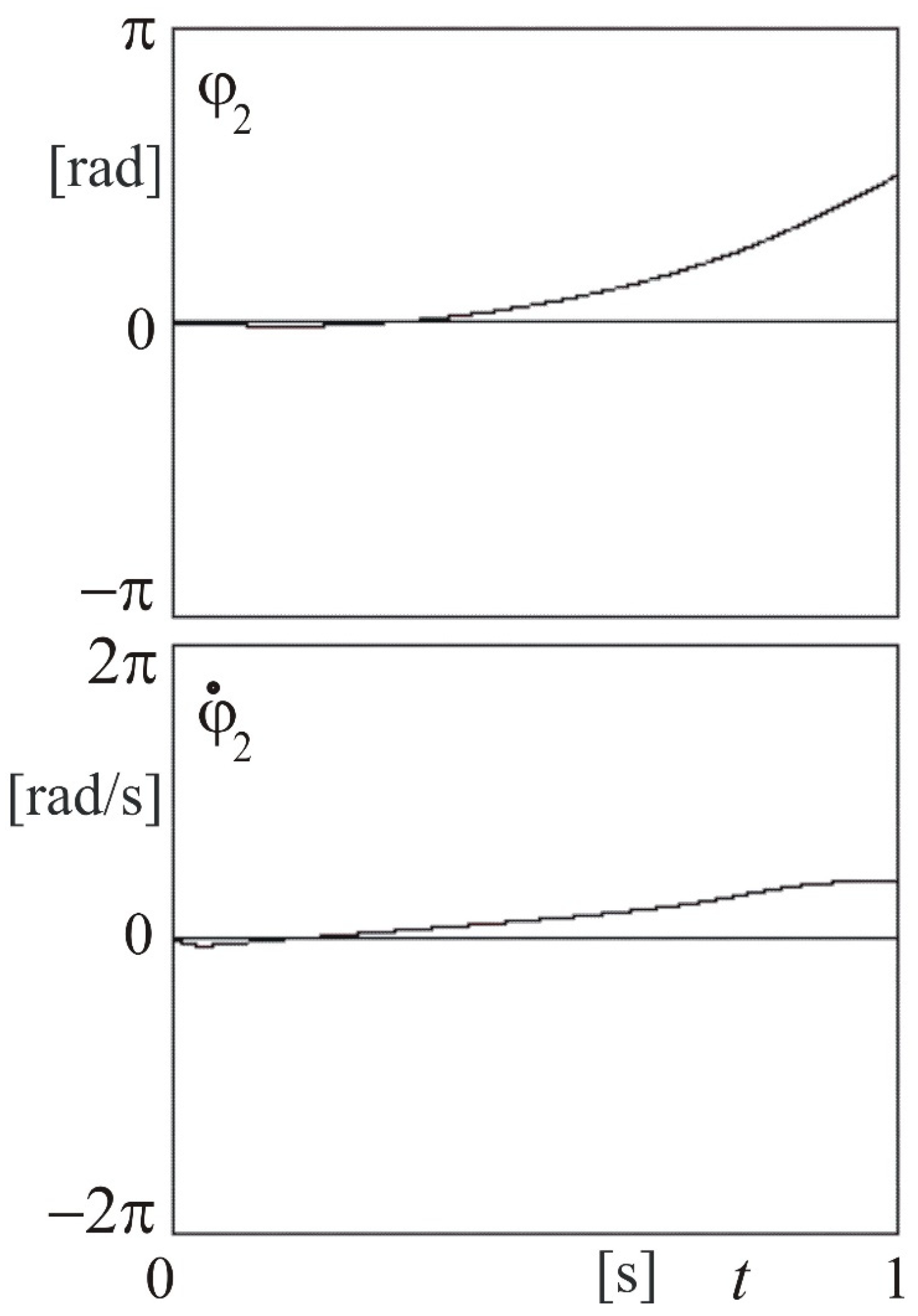
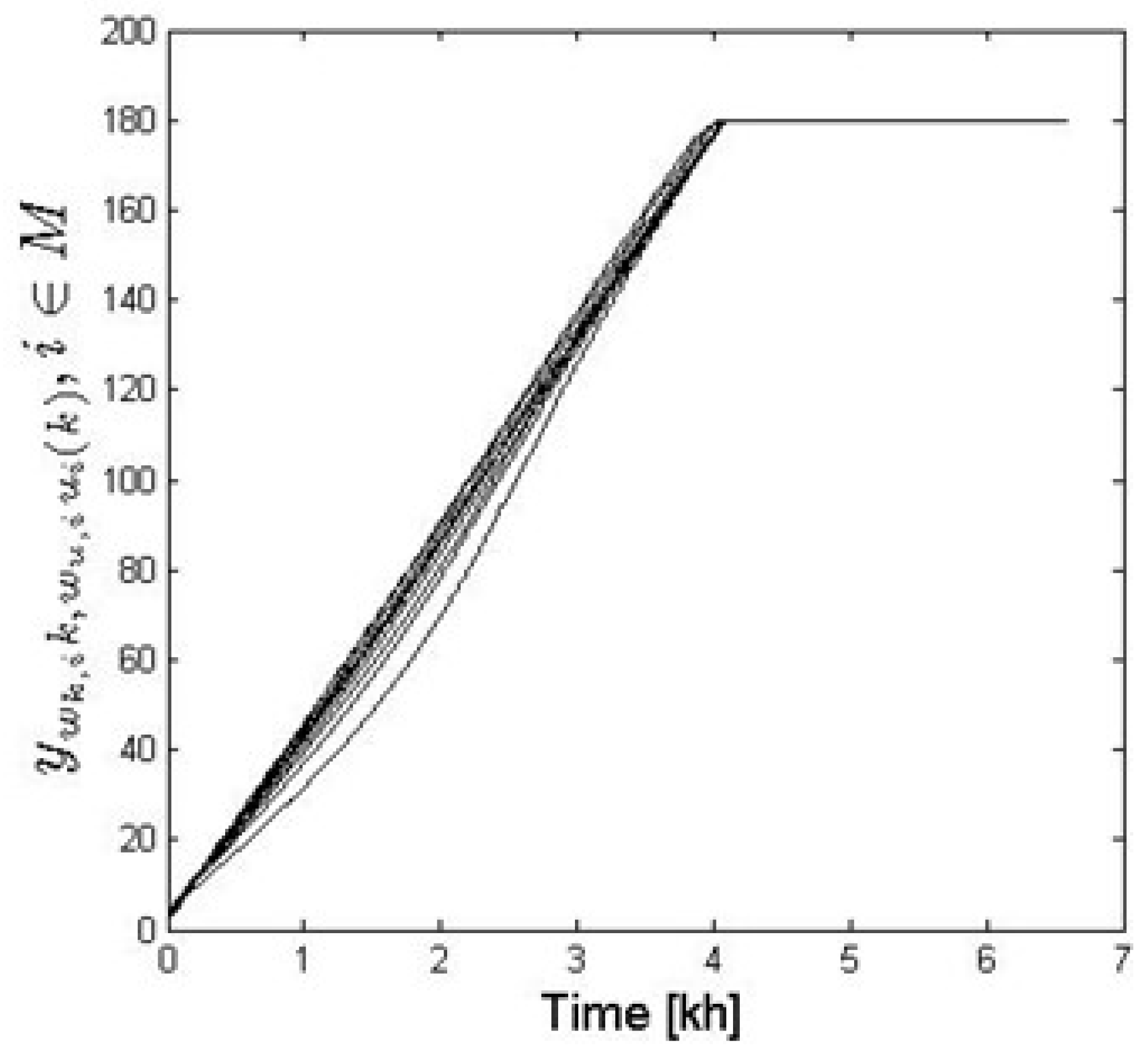
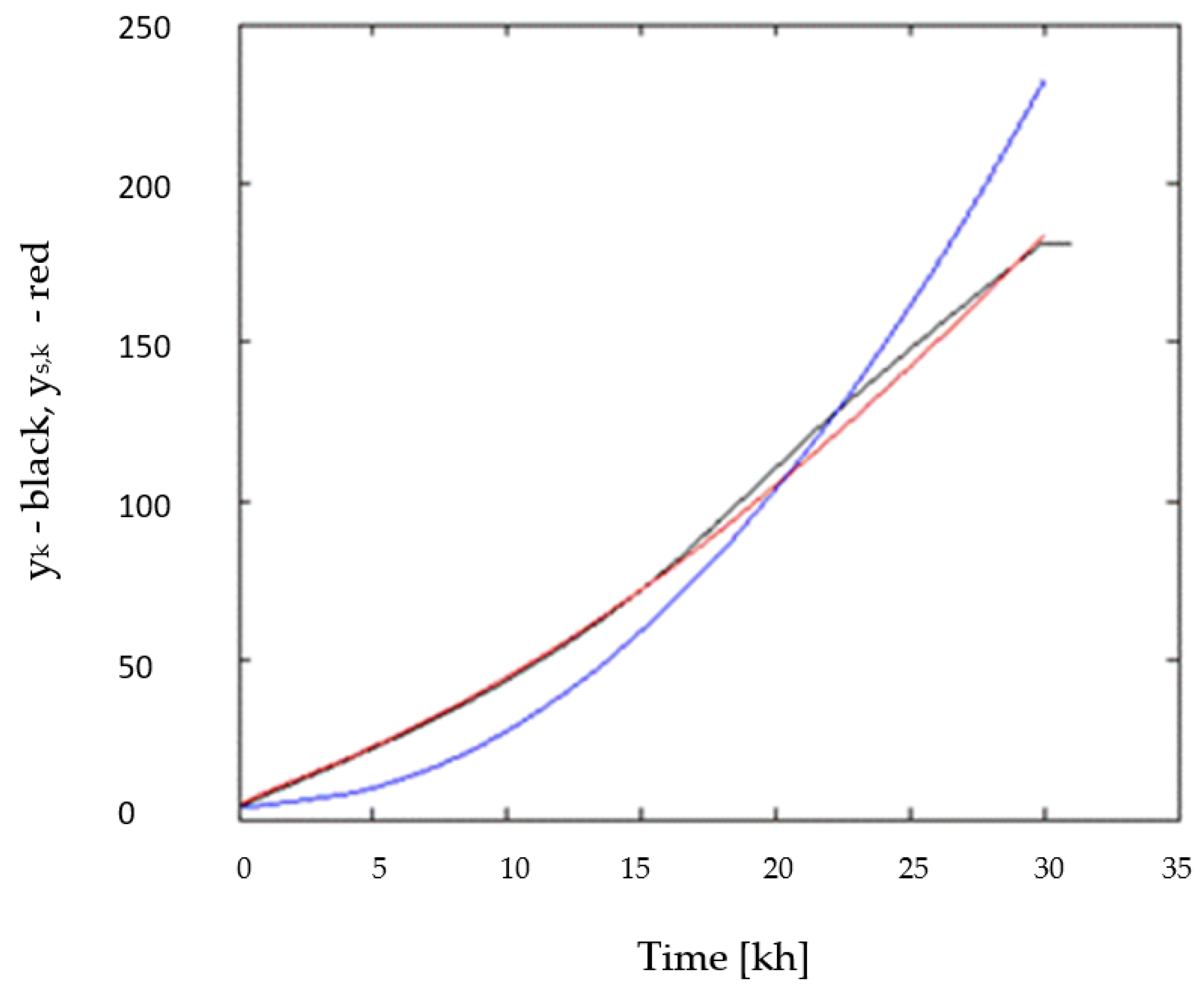
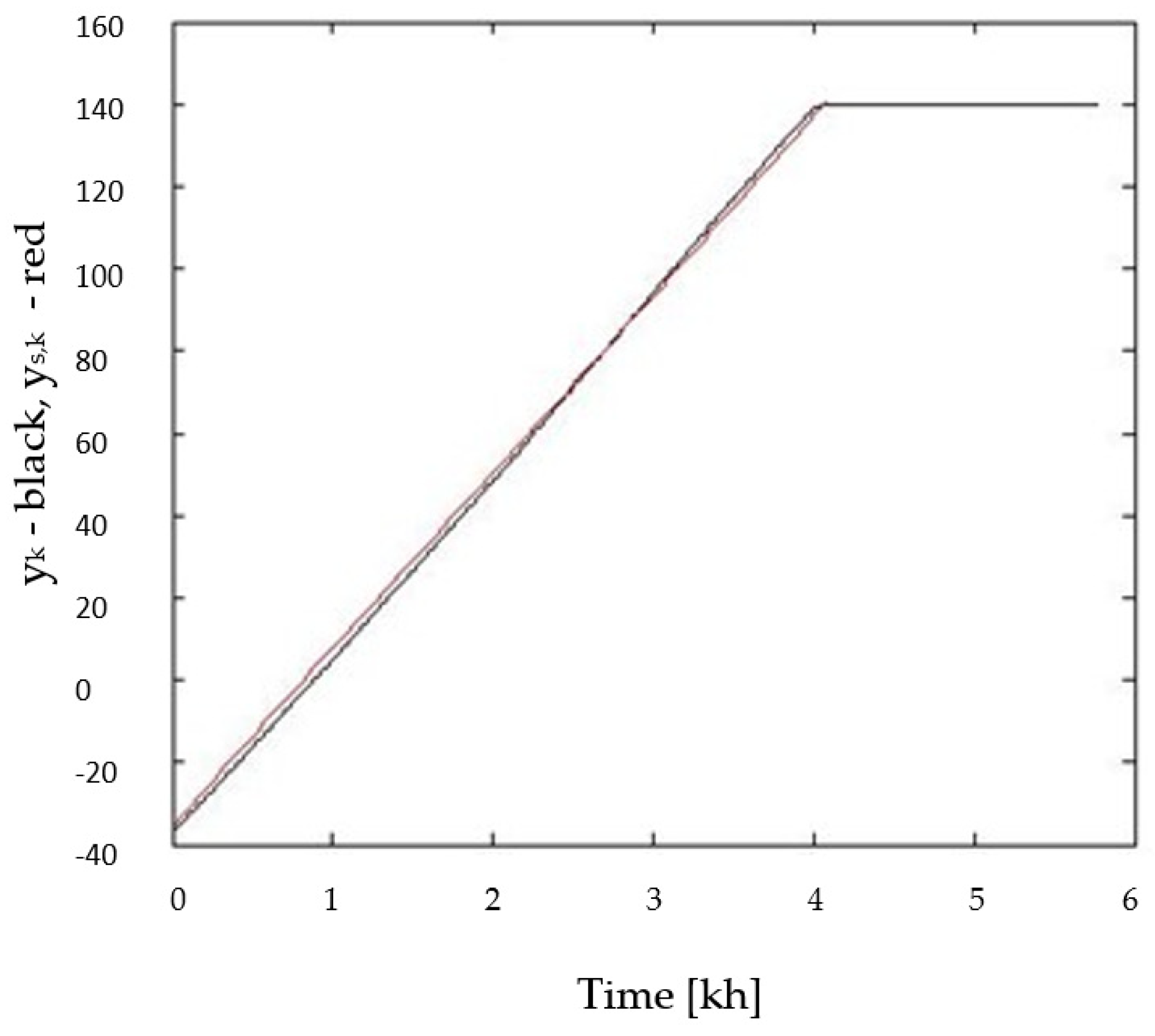
5. The Robot Arm Tests
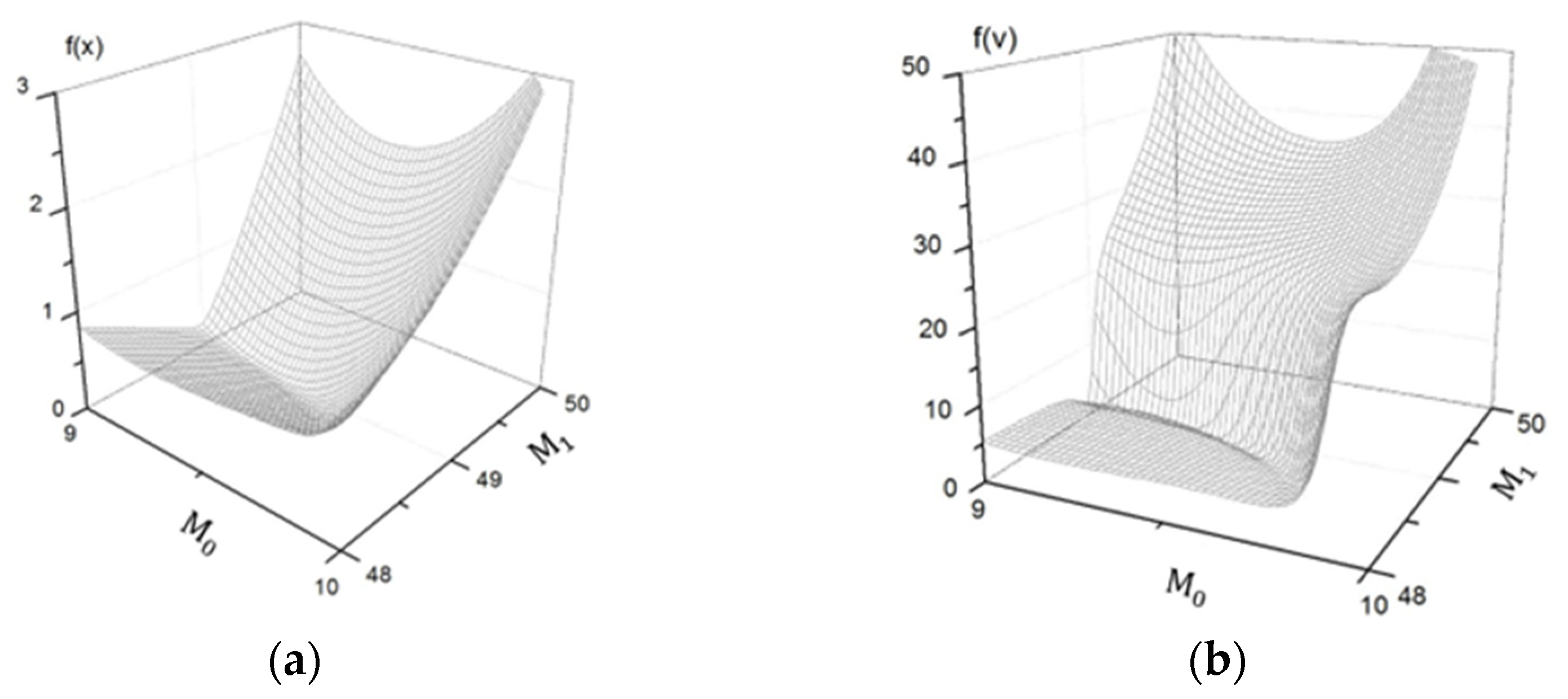
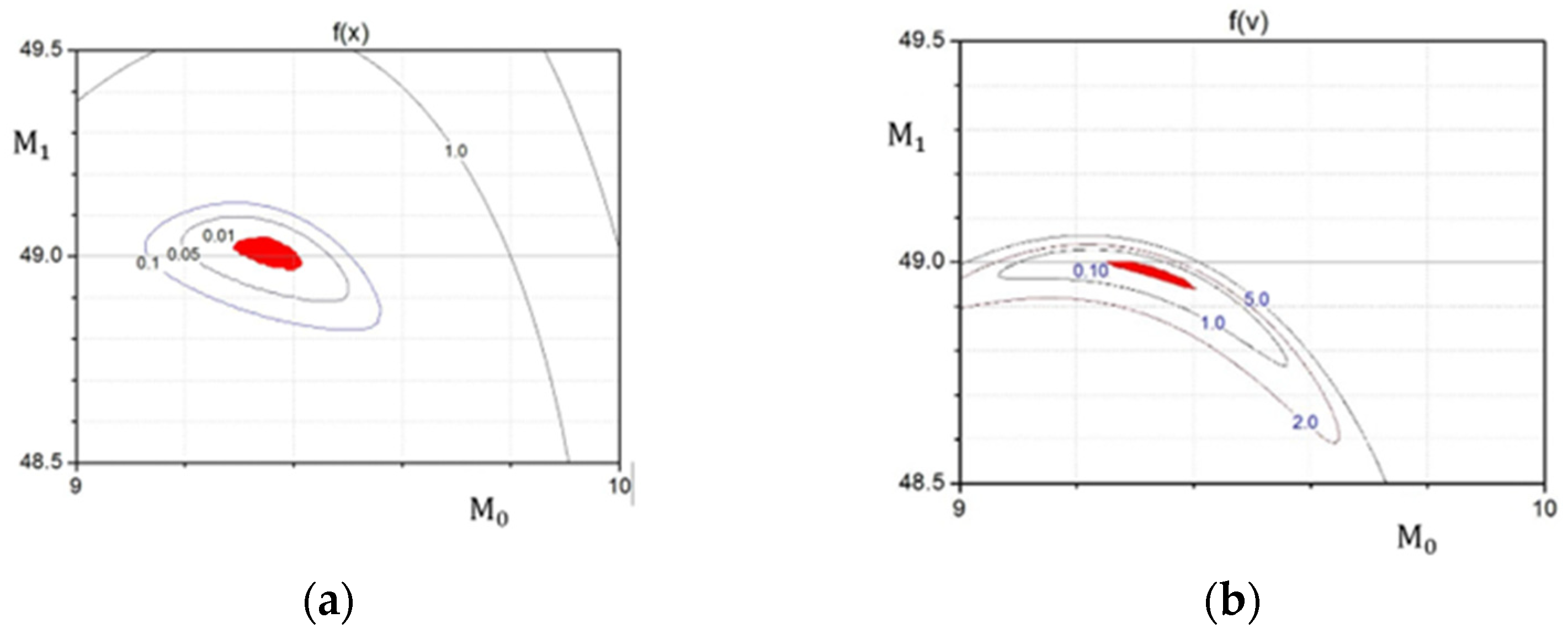
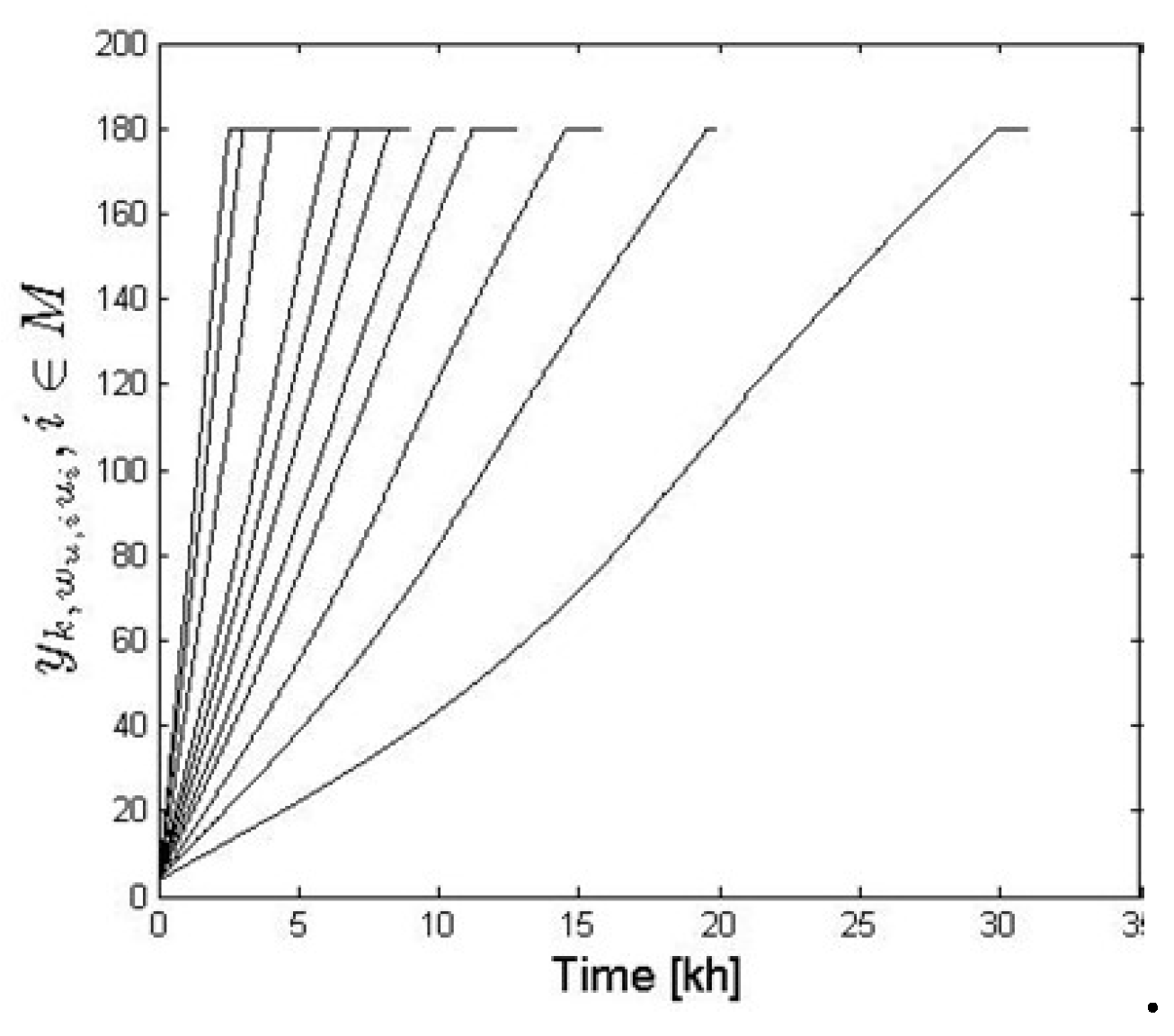
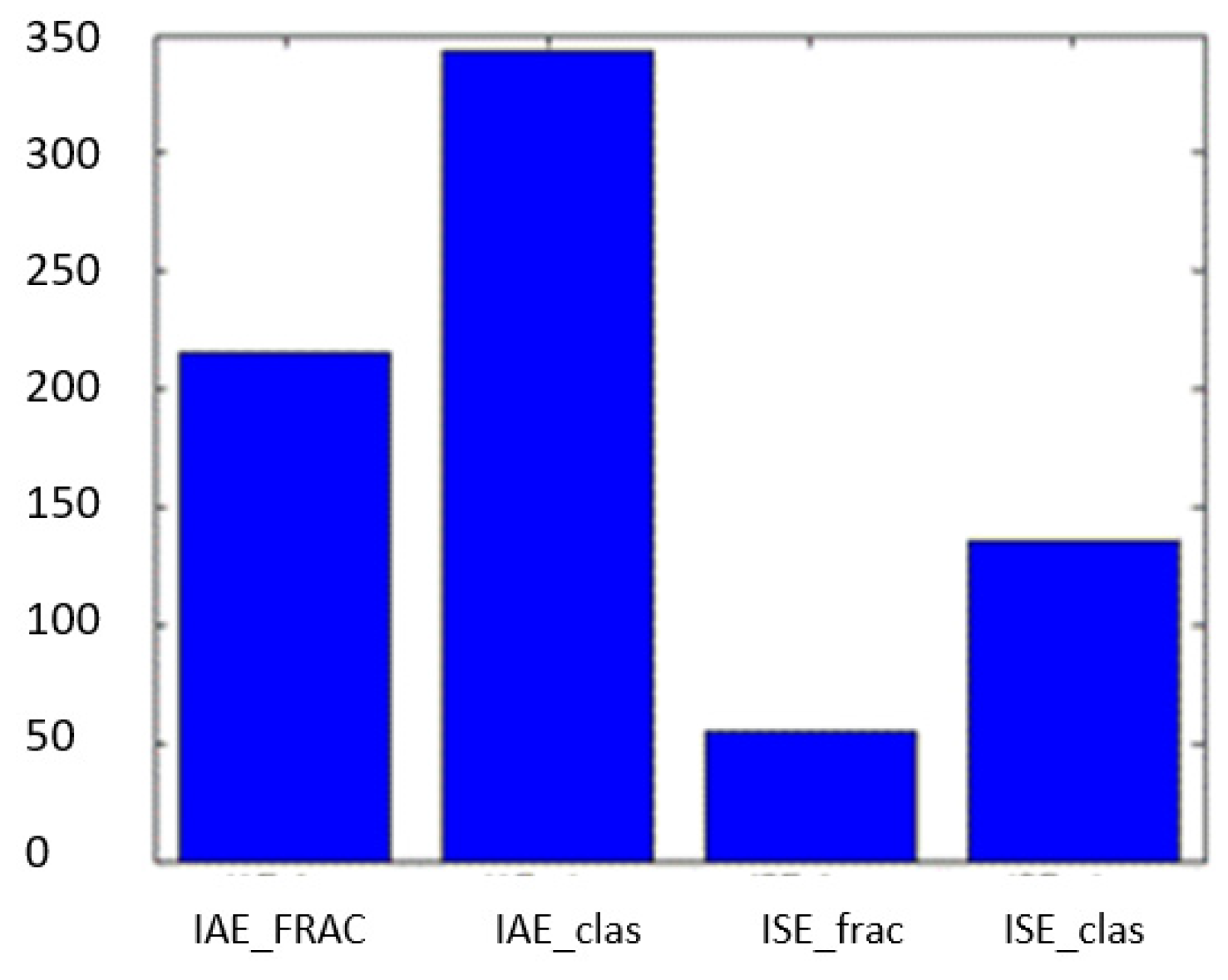
6. The VFOM and CM Parameters Selection
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Govindarajan, V.; Bhattacharya, S.; Kumar, V. Human-robot collaborative topological exploration for search and rescue applications. In Distributed Autonomous Robotic Systems; Springer: Tokyo, Japan, 2016; pp. 17–32. [Google Scholar]
- Brito, T.; Queiroz, J.; Piardi, L.; Fernandes, L.A.; Lima, J.; Leitão, P. A machine learning approach for collaborative robot smart manufacturing inspection for quality control systems. Procedia Manuf. 2020, 51, 11–18. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science Inc: New York, NY, USA, 2006; Volume 204. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. In An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Sabatier, J. Fractional order systems. Applications in modelling, identification, and control. J. Eur. Des. Systèmes Automatisés. RS Série JESA 2008, 42, 625. [Google Scholar]
- Spong, M.W.; Vidyasagar, M. Robot Dynamics, and Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1989. [Google Scholar]
- Alagoz, B.B.; Tepljakov, A.; Ates, A.; Petlenkov, E.; Yeroglu, C. Time-domain identification of One Noninteger Order Plus Time Delay models from step response measurements. Int. J. Model. Simul. Sci. Comput. 2019, 10, 1941011. [Google Scholar] [CrossRef]
- Garrappa, R.; Kaslik, E.; Popolizio, M. Evaluation of Fractional Integrals and Derivatives of Elementary Functions: Overview Tutorial. Mathematics 2019, 2, 7050407. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Podlubny, I.; Hernandez, A.; Feliu, V. Some approximations of fractional order operators used in control theory and applications. Fract. Calc. Appl. Anal. 2000, 3, 231–248. [Google Scholar]
- Rosario, J.M.; Didier, D.; Tenreiro Machado, J.A. Analysis of fractional-order robot axis dynamics. IFAC Proc. 2006, 39, 367–372. [Google Scholar] [CrossRef]
- Rhouma, A.; Sami, H. A Microcontroller Implementation of Fractional Order Controller. Int. J. Contr. Syst. Robot. 2017, 2, 122–127. [Google Scholar]
- Sierociuk, D.; Malesza, W. Fractional variable order anti-windup control strategy. Bull. Pol. Acad. Sci. Tech. Sci. 2018, 66, 427–432. [Google Scholar]
- Samko, S.; Ross, B. Integration and differentiation to a variable fractional order. Integr. Transf. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Sheng, H.; Sun, H.G.; Coopmans, C.; Chen, Y.Q.; Bohannan, G.W. A physical experimental study of variable-order fractional integrator and differentiator. Eur. Phys. J. Spec. Top. 2011, 193, 93–104. [Google Scholar] [CrossRef]
- Meng, R.; Yin, D.; Drapaca, C.S. A variable order fractional constitutive model of the viscoelastic behavior of polymers. Int. J. Non-Linear Mech. 2019, 113, 171–177. [Google Scholar] [CrossRef]
- Sierociuk, D.; Macias, M. Comparison of variable fractional order PID controller for different types of variable order derivatives. In Proceedings of the 14th International Carpathian Control Conference (ICCC), Rytro, Poland, 26–29 May 2013; pp. 334–339. [Google Scholar] [CrossRef]
- Ostalczyk, P. Variable-, fractional-order discrete PID controllers. In Proceedings of the 2012 17th International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2012; pp. 534–539. [Google Scholar] [CrossRef]
- Dabiri, A.; Moghaddam, B.P.; Machado, J.T. Optimal variable-order fractional PID controllers for dynamical systems. J. Comput. Appl. Math. 2018, 339, 40–48. [Google Scholar] [CrossRef]
- Ostalczyk, P.; Duch, P. Closed—Loop system synthesis with the variable-, fractional—Order PID controller. In Proceedings of the 2012 17th International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdroje, Poland, 27–30 August 2012. [Google Scholar] [CrossRef]
- Oziablo, P.; Mozyrska, D.; Wyrwas, M. Discrete-Time Fractional, Variable-Order PID Controller for a Plant with Delay. Entropy 2020, 22, 771. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Pan, F.; Xue, D. Variable-order fuzzy fractional PID controller. ISA Trans. 2015, 55, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Amini, M.; Waezi, Z.; Manthouri, M. Seismic control of the structures with active tuned mass damper and variable fractional order fuzzy proportional–integral–derivative controller. J. Vib. Control. 2022, 10775463221115451. [Google Scholar] [CrossRef]
- Ostalczyk, P.; Brzezinski, D.; Duch, P.; Łaski, M.; Sankowski, D. The variable, fractional-order discrete-time PD controller in the IISv1. 3 robot arm control. Open Phys. 2013, 11, 750–759. [Google Scholar] [CrossRef]
- Ostalczyk, P.W.; Duch, P.; Brzeziński, D.W.; Sankowski, D. Order functions selection in the variable-, fractional-order PID controller. In Advances in Modelling and Control of Non-Integer-Order Systems; Springer: Cham, Switzerland; pp. 159–170.
- Ostalczyk, P. Zarys rachunku różniczkowo—Całkowego ułamkowych rzędów. In Teoria i zastosowanie w automatyce, Komitet Automatyki i Robotyki Polskiej Akademii Nauk, Wydawnictwo Politechniki Łódzkiej. Monografie Tom 12; Łódź, Polska, 2008; Available online: http://repozytorium.p.lodz.pl/handle/11652/1843 (accessed on 28 January 2023).
- Ostalczyk, P. Discrete Fractional Calculus. In Applications in Control and Image Processing, Series in Computer Vision; World Scientific: Hackensack, NJ, USA, 2015; Volume 4, ISSN 2010-2143. [Google Scholar]
- Sierociuk, D.; Macias, M.; Malesza, W.; Sarwas, G. Dual Estimation of Fractional Variable Order Based on the Unscented Fractional Order Kalman Filter for Direct and Networked Measurements. Circuits Syst. Signal Process. 2016, 35, 2055–2082. [Google Scholar] [CrossRef]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-order Systems and Controls Fundamendals and Applications. In Advances in Industrial Control; Springer: London, UK, 2010. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bąkała, M.; Duch, P.; Ostalczyk, P. New Approach of the Variable Fractional-Order Model of a Robot Arm. Appl. Sci. 2023, 13, 3304. https://doi.org/10.3390/app13053304
Bąkała M, Duch P, Ostalczyk P. New Approach of the Variable Fractional-Order Model of a Robot Arm. Applied Sciences. 2023; 13(5):3304. https://doi.org/10.3390/app13053304
Chicago/Turabian StyleBąkała, Marcin, Piotr Duch, and Piotr Ostalczyk. 2023. "New Approach of the Variable Fractional-Order Model of a Robot Arm" Applied Sciences 13, no. 5: 3304. https://doi.org/10.3390/app13053304
APA StyleBąkała, M., Duch, P., & Ostalczyk, P. (2023). New Approach of the Variable Fractional-Order Model of a Robot Arm. Applied Sciences, 13(5), 3304. https://doi.org/10.3390/app13053304






