Modeling the Combined Effect of Travelers’ Contrarian Behavior, Learning and Inertia on the Day-to-Day Dynamics of Route Choice
Abstract
1. Introduction
- Introducing inertia into the dynamic process model representing the day-to-day evolution of the network state under mixed direct and contrarian route choices;
- Providing a more general statement of the fixed point stability conditions through the analysis of the Jacobian matrix of the resulting two-dimensional nonlinear dynamical system;
- Analyzing model behavior in the case of nonlinear link cost functions.
2. Method
2.1. Model Formulation
- (i = 1, 2) is the mean perceived cost of route i at the start of day t;
- (i = 1, 2) is the average flow-dependent cost actually experienced by users on route i;
- is the probability that a user who reconsiders their previous day’s choice will choose link 1 on day t, expressed as a function of the difference between day t’s perceived costs;
- () is a parameter quantifying the extent to which the most recent travel experience (“yesterday’s trip”) contributes to the formation of the cost perceived by users at the start of day t;
- () is a parameter representing the fraction of travelers who actually reconsider their previous day’s choice.
2.2. Fixed Point Stability Analysis
2.2.1. Fixed Point Stability in the Case of Linear Link Cost Functions
2.2.2. Fixed Point Stability in the Case of Fourth-Power Link Cost Functions
2.2.3. Discussion of Fixed Point Stability Results
- An adequately balanced mix of direct and contrarian subjects within the traveling population is conducive to fixed point stability, whereas strongly homogeneous route choice behaviors tend to trigger the occurrence of instabilities;
- The range of values ensuring fixed point stability depends on the inertia (α) and memory depth (β) parameters, as well as on the degree of sensitivity of costs to flows (γ) and of route choices to costs (μ);
- The stability regions defined by conditions (54) and (64) are not affected by a swap of the values of α and β or by a swap of the values of γ and μ;
- The width of the stability regions decreases as γ and/or μ increase. Unlike the latter parameters, which appear on both sides of expressions (54) and (64), α and β affect only the lower bound of the stability region. More specifically, it is easy to check that the derivatives of the left-hand sides of (54) and (64) with respect to α and β have a positive sign. In light of expressions (1)–(3), this suggests that appropriately reduced day-to-day cost and flow updating rates have the potential to offset the destabilizing effects of steeply increasing cost–flow functions and highly cost-sensitive route choice behaviors;
- Conditions (55), (56) and (65), (66) indicate that the composition of the traveling population in terms of direct/contrarian choice behaviors may become irrelevant when stability of the fixed point is already ensured by sufficiently small values of the other model parameters;
- Comparison of expressions (54) and (64) suggests that the stability region for fourth-power cost functions is twice as large as for linear cost functions. This circumstance can be explained by observing that, at the fixed point, the derivative of the fourth-power function is equal to , which is exactly half of the derivative of the linear cost function appearing in (54).
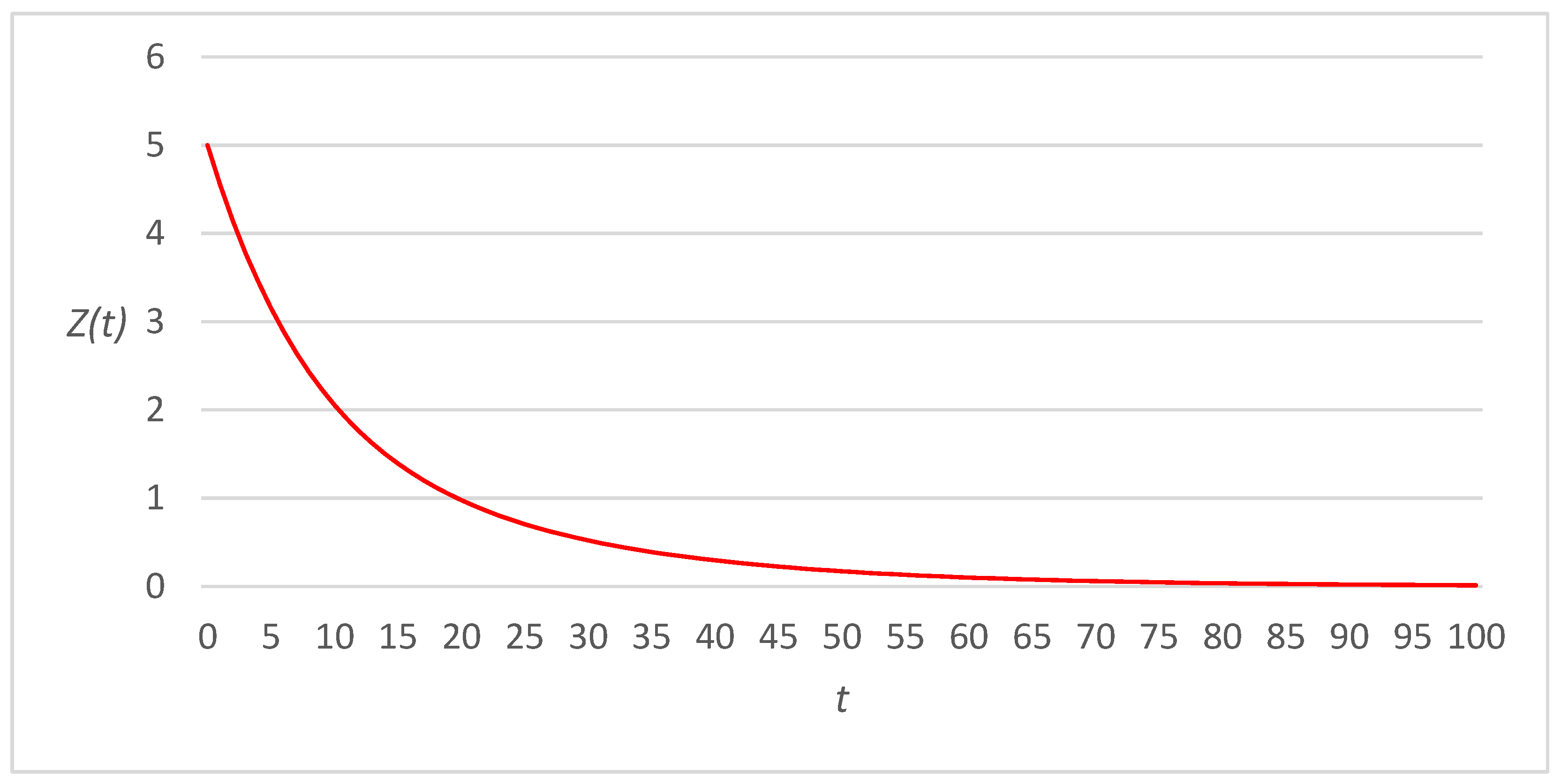
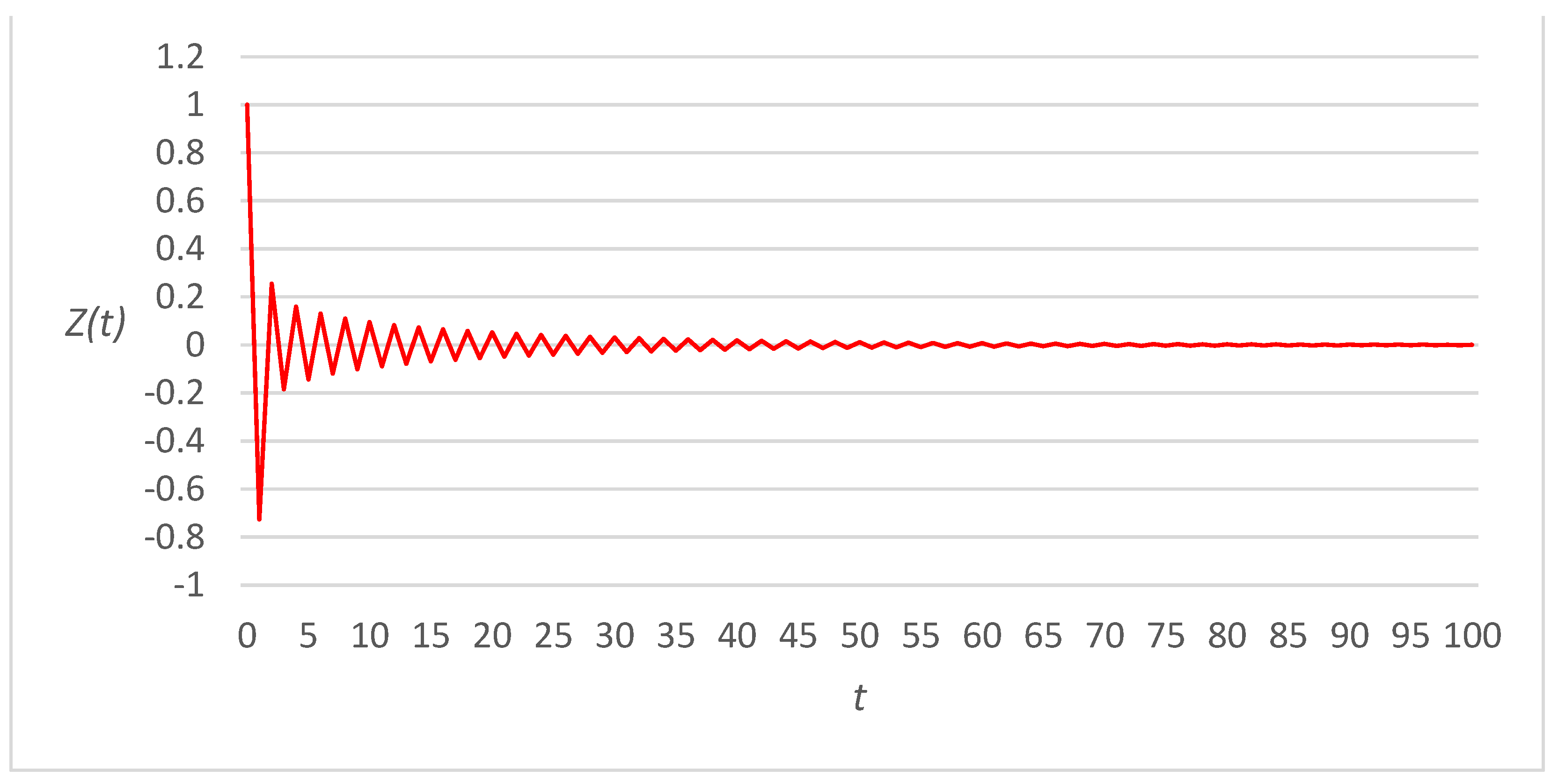
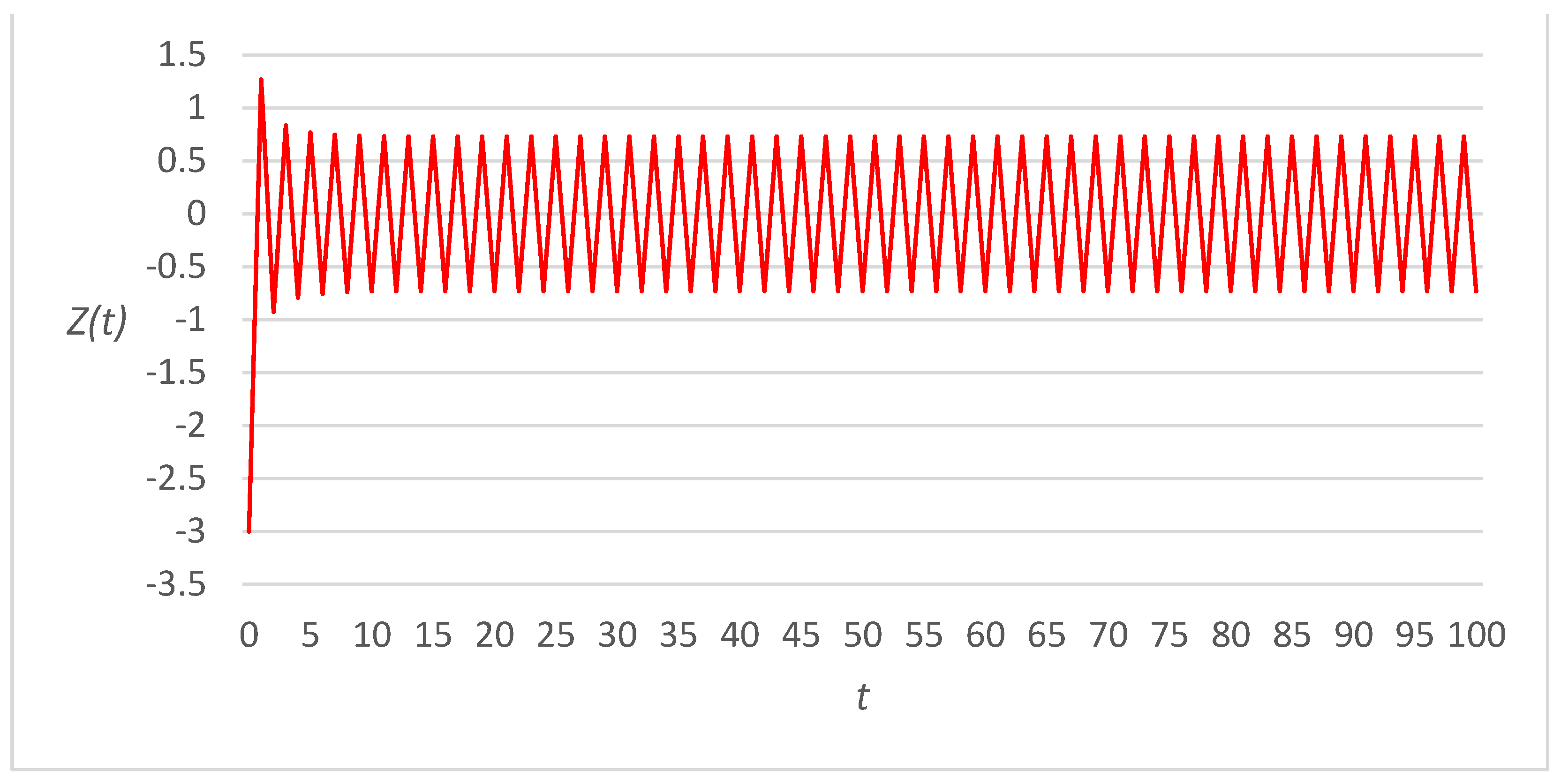
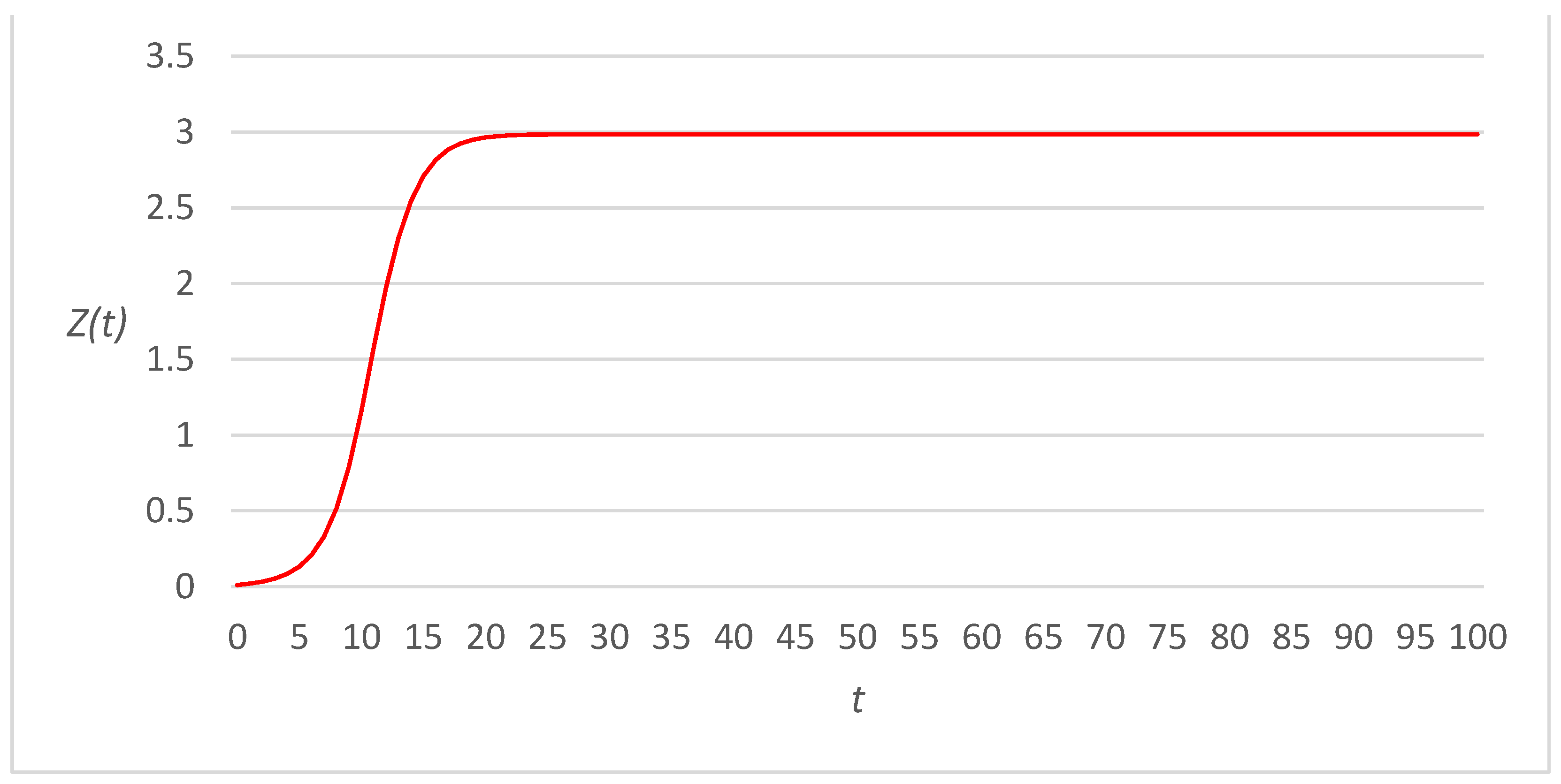
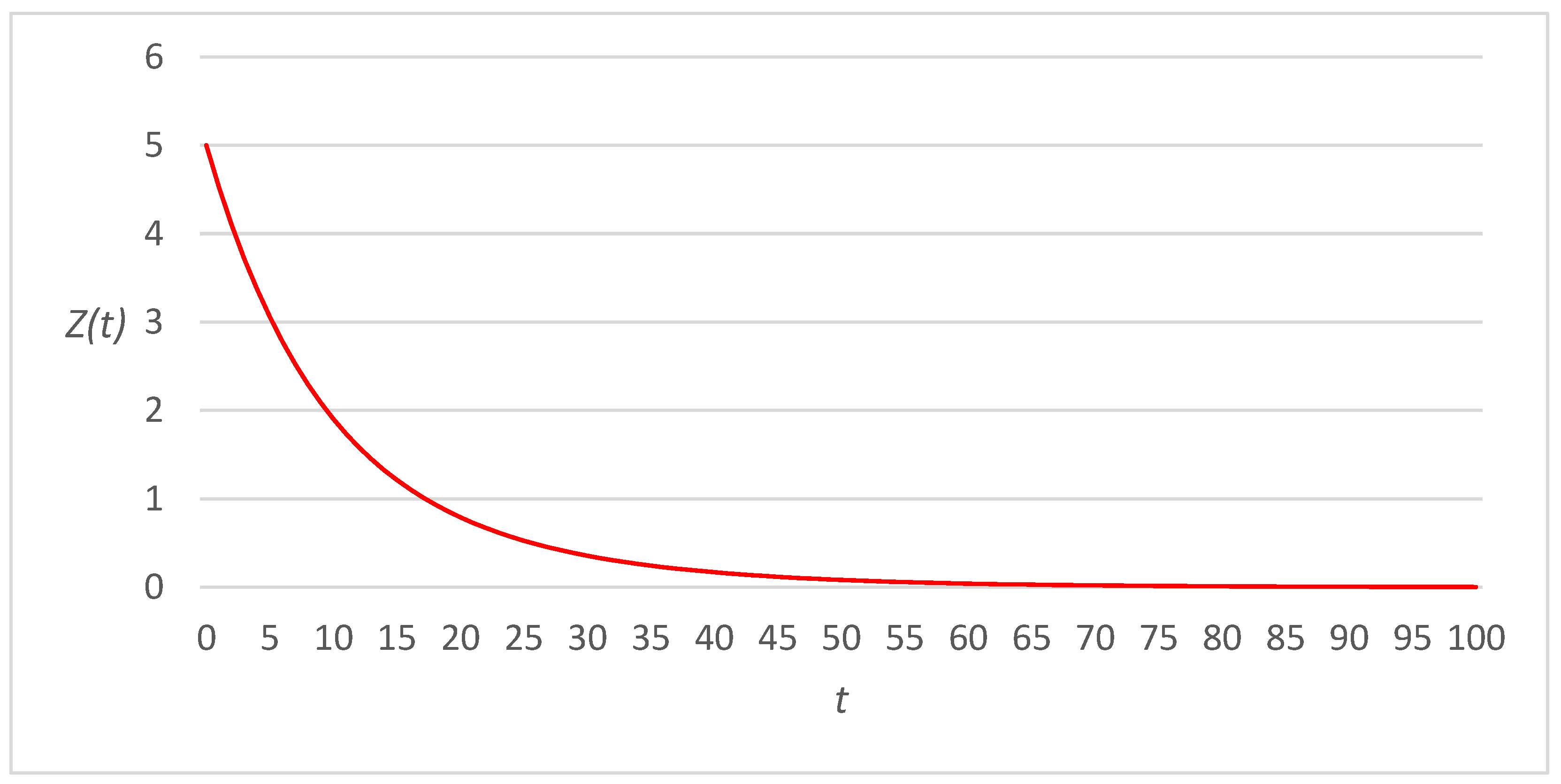
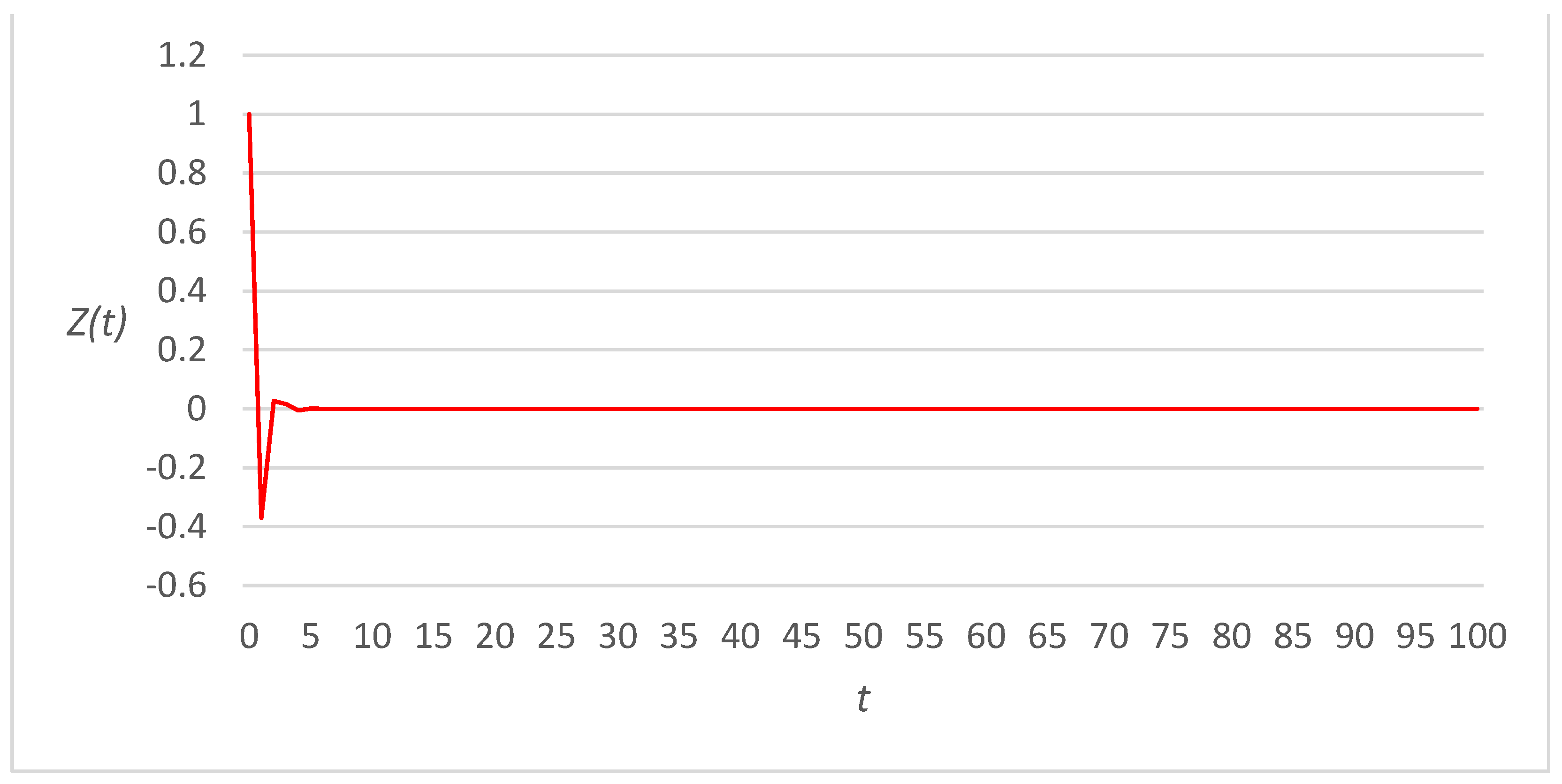
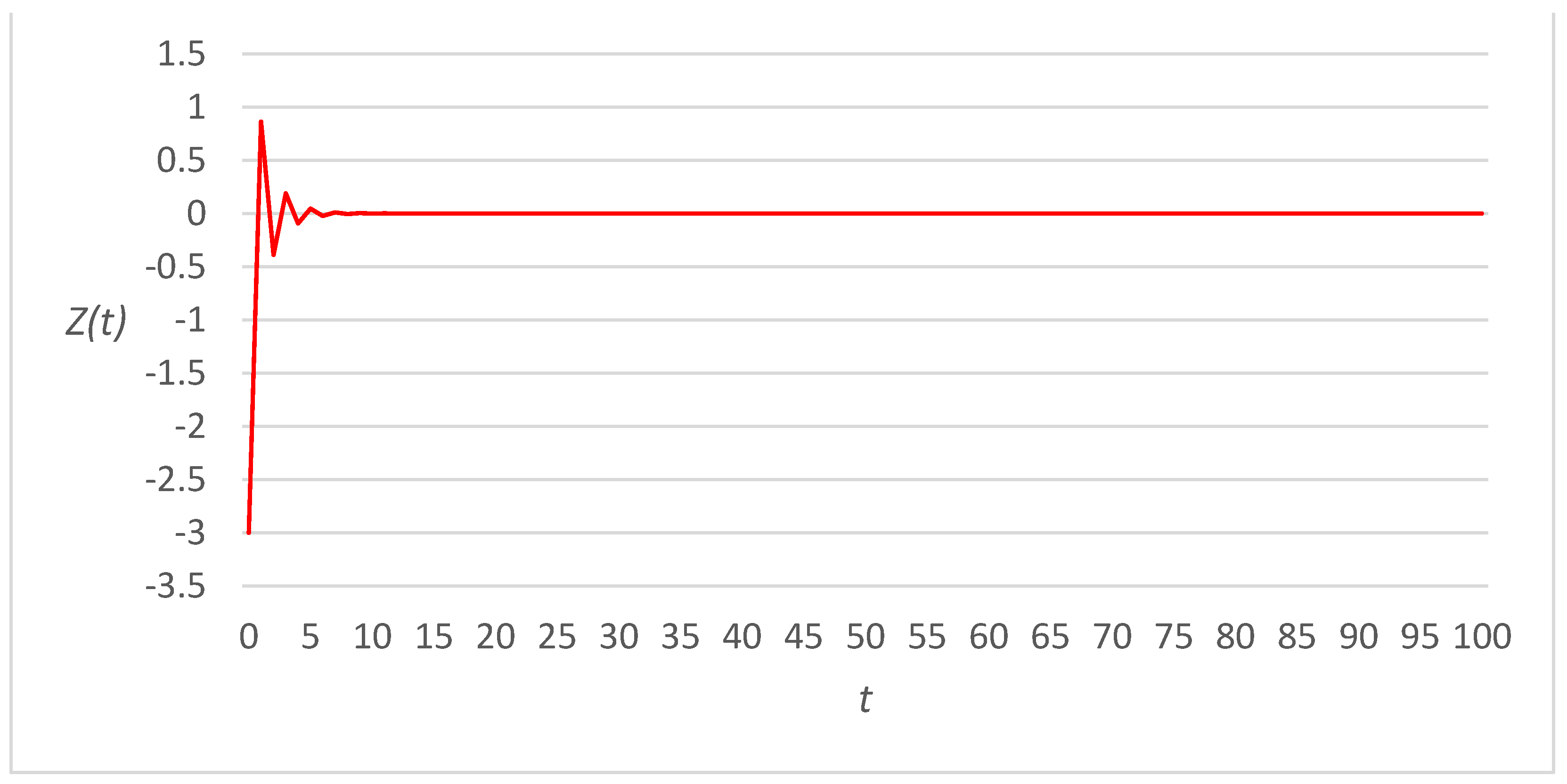
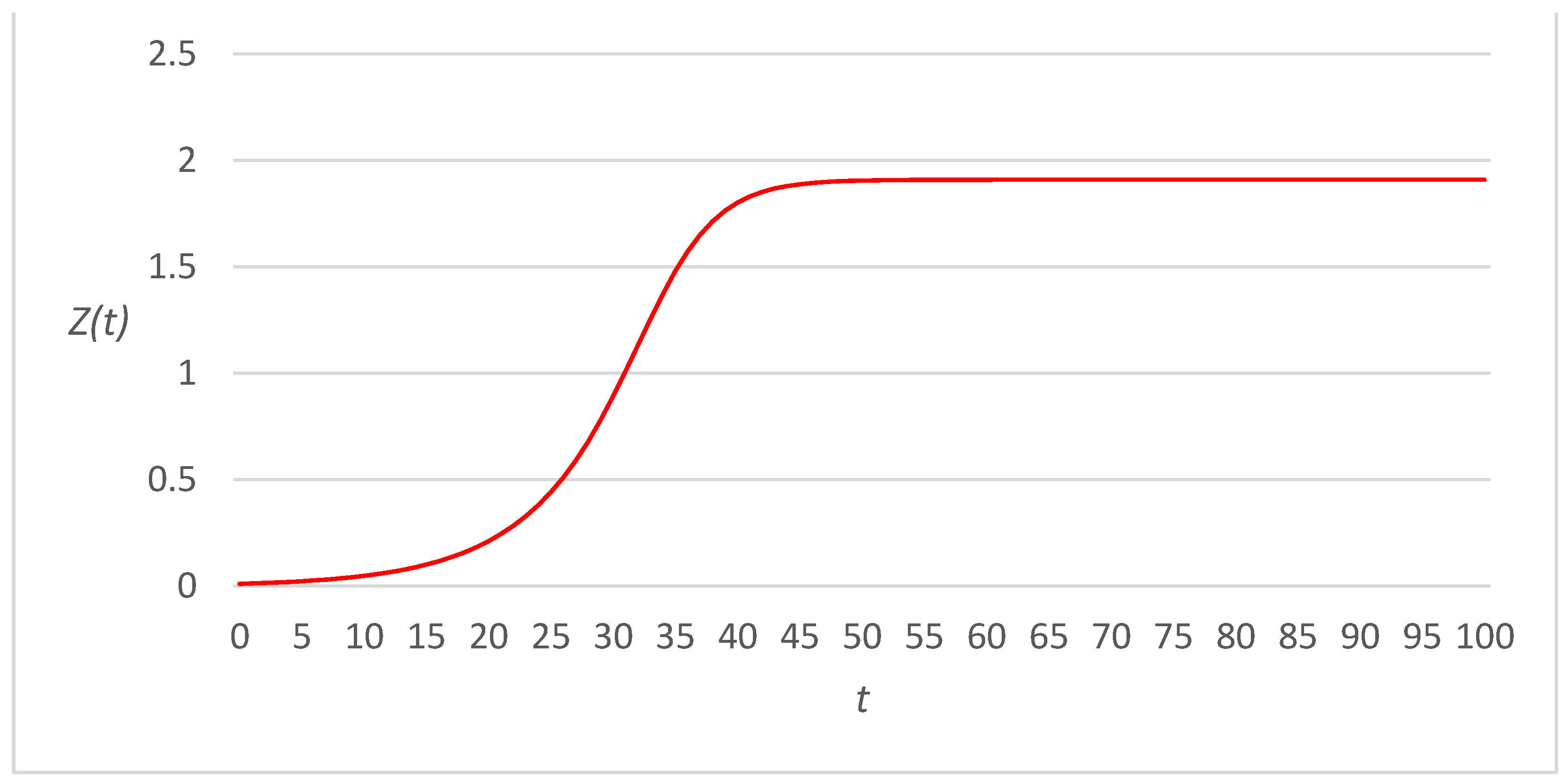
3. Numerical Examples
3.1. Linear Link Cost Functions
3.2. Fourth-Power Link Cost Functions
4. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Horowitz, J.L. The stability of stochastic equilibrium in a two-link transportation network. Transp. Res. B 1984, 18, 13–28. [Google Scholar] [CrossRef]
- Cantarella, G.E.; Cascetta, E. Dynamic processes and equilibrium in transportation networks: Towards a unifying theory. Transp. Sci. 1995, 29, 305–329. [Google Scholar] [CrossRef]
- Bie, J.; Lo, H.K. Stability and attraction domains of traffic equilibria in a day-to-day dynamical system formulation. Transp. Res. B 2010, 44, 90–107. [Google Scholar] [CrossRef]
- Meneguzzer, C. Dynamic process models of combined traffic assignment and control with different signal updating strategies. J. Adv. Transp. 2012, 46, 351–365. [Google Scholar] [CrossRef]
- Xiao, L.; Lo, H.K. Combined route choice and adaptive traffic control in a day-to-day dynamical system. Netw. Spat. Econ. 2015, 15, 697–717. [Google Scholar] [CrossRef]
- Xu, X.; Qu, K.; Chen, A.; Yang, C. A new day-to-day dynamic network vulnerability analysis approach with Weibit-based route adjustment process. Transp. Res. E 2021, 153, 102421. [Google Scholar] [CrossRef]
- Li, P.; Tian, L.; Xiao, F.; Zhu, H. Can day-to-day dynamic model be solved analytically? New insights on portraying equilibrium and accommodating autonomous vehicles. Transp. Res. B 2022, 166, 374–395. [Google Scholar] [CrossRef]
- Iida, Y.; Akiyama, T.; Uchida, T. Experimental analysis of dynamic route choice behavior. Transp. Res. B 1992, 26, 17–32. [Google Scholar] [CrossRef]
- Selten, R.; Chmura, T.; Pitz, T.; Kube, S.; Schreckenberg, M. Commuters route choice behavior. Games Econom. Behav. 2007, 58, 394–406. [Google Scholar] [CrossRef]
- Ben-Elia, E.; Shiftan, Y. Which road do I take? A learning-based model of route-choice behavior with real-time information. Transp. Res. A 2010, 44, 249–264. [Google Scholar] [CrossRef]
- Lu, X.; Gao, S.; Ben-Elia, E. Information impacts on route choice and learning behavior in a congested network: Experimental approach. Transp. Res. Rec. J. Transp. Res. Board 2011, 2243, 89–98. [Google Scholar] [CrossRef]
- Meneguzzer, C.; Olivieri, A. Day-to-day traffic dynamics: Laboratory-like experiment on route choice and route switching in a simple network with limited feedback information. Procedia Soc. Behav. Sci. 2013, 87, 44–59. [Google Scholar] [CrossRef]
- Rapoport, A.; Gisches, E.J.; Daniel, T.; Lindsey, R. Pre-trip information and route-choice decisions with stochastic travel conditions: Experiment. Transp. Res. B 2014, 68, 154–172. [Google Scholar] [CrossRef]
- Knorr, F.; Chmura, T.; Schreckenberg, M. Route choice in the presence of a toll road: The role of pre-trip information and learning. Transp. Res. F 2014, 27, 44–55. [Google Scholar] [CrossRef]
- Liu, S.; Guo, L.; Easa, S.M.; Yan, H.; Wei, H.; Tang, Y. Experimental study of day-to-day route-choice behavior: Evaluating the effect of ATIS market penetration. J. Adv. Transp. 2020, 2020, 8393724. [Google Scholar] [CrossRef]
- van Essen, M.; Thomas, T.; Chorus, C.; van Berkum, E. The effect of travel time information on day-to-day route choice behaviour: Evidence from a real-world experiment. Transp. B Transp. Dyn. 2019, 7, 1719–1742. [Google Scholar] [CrossRef]
- Wang, J.; Rakha, H. Empirical study of effect of dynamic travel time information on driver route choice behavior. Sensors 2020, 20, 3257. [Google Scholar] [CrossRef] [PubMed]
- Vacca, A.; Prato, C.G.; Meloni, I. Should I stay or should I go? Investigating route switching behavior form revealed preferences data. Transportation 2019, 46, 75–93. [Google Scholar] [CrossRef]
- Fusco, G.; Bracci, A.; Caligiuri, T.; Colombaroni, C.; Isaenko, N. Experimental analyses and clustering of travel choice behaviours by floating car big data in a large urban area. IET Intel. Transp. Syst. 2018, 12, 270–278. [Google Scholar] [CrossRef]
- Ye, H.; Xiao, F.; Yang, H. Exploration of day-to-day route choice models by a virtual experiment. Transp. Res. C 2018, 94, 220–235. [Google Scholar] [CrossRef]
- Li, W.; Ma, S.; Jia, N.; He, Z. An analyzable agent-based framework for modeling day-to-day route choice. Transp. A Transp. Sci. 2022, 18, 1517–1543. [Google Scholar] [CrossRef]
- Qi, H.; Jia, N.; Qu, X.; He, Z. Investigating day-to-day route choices based on multi-scenario laboratory experiments, Part I: Route-dependent attraction and its modeling. Transp. Res. A 2023, 167, 103553. [Google Scholar] [CrossRef]
- Camerer, C.F.; Ho, T.-H.; Chong, J.-K. A cognitive hierarchy model of games. Q. J. Econ. 2004, 119, 861–898. [Google Scholar] [CrossRef]
- Drehmann, M.; Oechssler, J.; Roider, A. Herding and contrarian behavior in financial markets: An internet experiment. Am. Econ. Rev. 2005, 95, 1403–1426. [Google Scholar] [CrossRef]
- Park, A.; Sgroi, D. Herding, contrarianism and delay in financial market trading. Euro. Econ. Rev. 2012, 56, 1020–1037. [Google Scholar] [CrossRef]
- Galariotis, E.C. Contrarian and momentum trading: A review of the literature. Rev. Behav. Financ. 2014, 6, 63–82. [Google Scholar] [CrossRef]
- Bagnoli, F.; Rechtman, R. Bifurcations in models of a society of reasonable contrarians and conformists. Phys. Rev. E 2015, 92, 042913. [Google Scholar] [CrossRef]
- Gambaro, J.P.; Crokidakis, N. The influence of contrarians in the dynamics of opinion formation. Physica A 2017, 486, 465–472. [Google Scholar] [CrossRef]
- Muslim, R.; Kholili, M.J.; Nugraha, A.R.T. Opinion dynamics involving contrarian and independence behaviors based on the Sznajd model with two-two and three-one agent interactions. Phys. D 2022, 439, 133379. [Google Scholar] [CrossRef]
- De Martino, A.; Giardina, I.; Marsili, M.; Tedeschi, A. Generalized minority games with adaptive trend-followers and contrarians. Phys. Rev. E 2004, 70, 025104. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.-X.; Zheng, D.-F.; Zheng, B.; Hui, P.M. Effects of contrarians in the minority game. Phys. Rev. E 2005, 72, 026134. [Google Scholar] [CrossRef] [PubMed]
- Bonsall, P. The influence of route guidance advice on route choice in urban networks. Transportation 1992, 19, 1–23. [Google Scholar] [CrossRef]
- Helbing, D.; Schönhof, M.; Stark, H.U.; Hołyst, J.A. How individuals learn to take turns: Emergence of alternating cooperation in a congestion game and the prisoner’s dilemma. Adv. Complex Syst. 2005, 8, 87–116. [Google Scholar] [CrossRef]
- Han, Q.; Timmermans, H.J.P.; Dellaert, B.G.C.; van Raaij, F. Route choice under uncertainty: Effects of recommendations. Transp. Res. Rec. J. Transp. Res. Board 2008, 2082, 72–80. [Google Scholar] [CrossRef]
- Qi, H.; Ma, S.; Jia, N.; Wang, G. Individual response modes to pre-trip information in congestible networks: Laboratory experiment. Transp. A Transp. Sci. 2019, 15, 376–395. [Google Scholar] [CrossRef]
- Meneguzzer, C. Contrarians do better: Testing participants’ response to information in a simulated day-to-day route choice experiment. Travel Behav. Soc. 2019, 15, 146–156. [Google Scholar] [CrossRef]
- Klein, I.; Ben-Elia, E. Emergence of cooperative route-choice: A model and experiment of compliance with system-optimal ATIS. Transp. Res. F 2018, 59, 348–364. [Google Scholar] [CrossRef]
- Bazzan, A.L.C.; Bordini, R.H.; Andrioti, G.K.; Vicari, R.M.; Wahle, J. Wayward agents in a commuting scenario (personalities in the minority game). In Proceedings of the Fourth International Conference on Multi Agent Systems, Boston, MA, USA, 10–12 July 2000. [Google Scholar]
- Alibabai, H.; Mahmassani, H.S. Foxes and sheep: Effect of predictive logic in day-to-day dynamics of route choice behavior. EURO J. Transp. Logist. 2016, 5, 53–67. [Google Scholar] [CrossRef]
- Meneguzzer, C. Day-to-day dynamics in a simple traffic network with mixed direct and contrarian route choice behaviors. Phys. A 2022, 603, 127841. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Guo, R.-Y.; Huang, H.-J. Day-to-day route choice in networks with different sets for choice: Experimental results. Transp. B Transp. Dyn. 2021, 9, 712–745. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; de Palma, A.; Kaysi, I. Dynamic network models and driver information systems. Transp. Res. A 1991, 25, 251–266. [Google Scholar] [CrossRef]
- Wahle, J.; Bazzan, A.L.C.; Klugl, F.; Schreckenberg, M. The impact of real-time information in a two-route scenario using agent-based simulation. Transp. Res. C 2002, 10, 399–417. [Google Scholar] [CrossRef]
- Ben-Elia, E.; Avineri, E. Response to travel information: A behavioural review. Transp. Rev. 2015, 35, 352–377. [Google Scholar] [CrossRef]
- Klein, I.; Levy, N.; Ben-Elia, E. An agent-based model of the emergence of cooperation and a fair and stable system optimum using ATIS on a simple road network. Transp. Res. C 2018, 86, 183–201. [Google Scholar] [CrossRef]
- Mansourianfar, M.H.; Gu, Z.; Waller, S.T.; Saberi, M. Joint routing and pricing control in congested mixed autonomy networks. Transp. Res. C 2021, 131, 103338. [Google Scholar] [CrossRef]
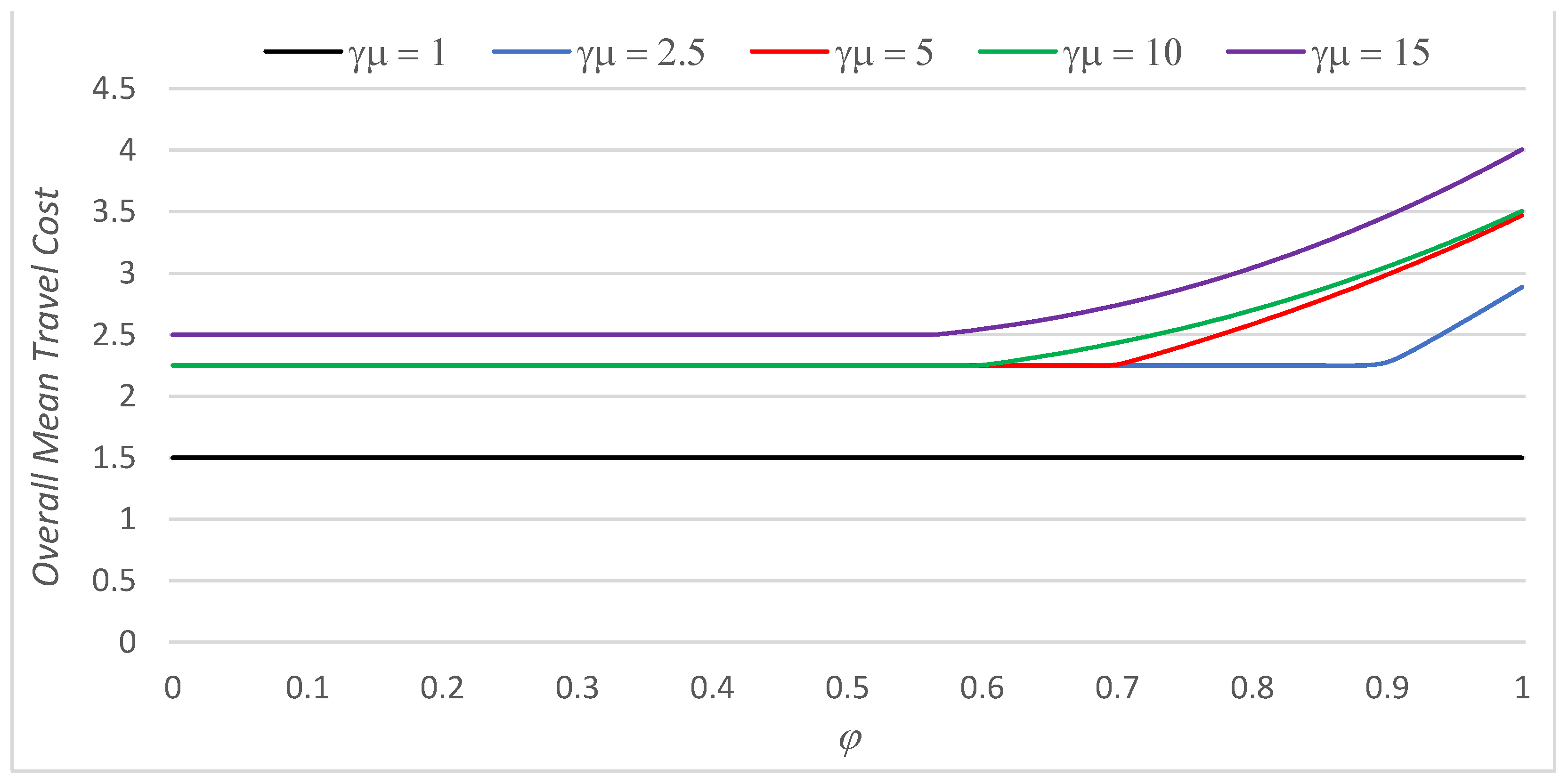
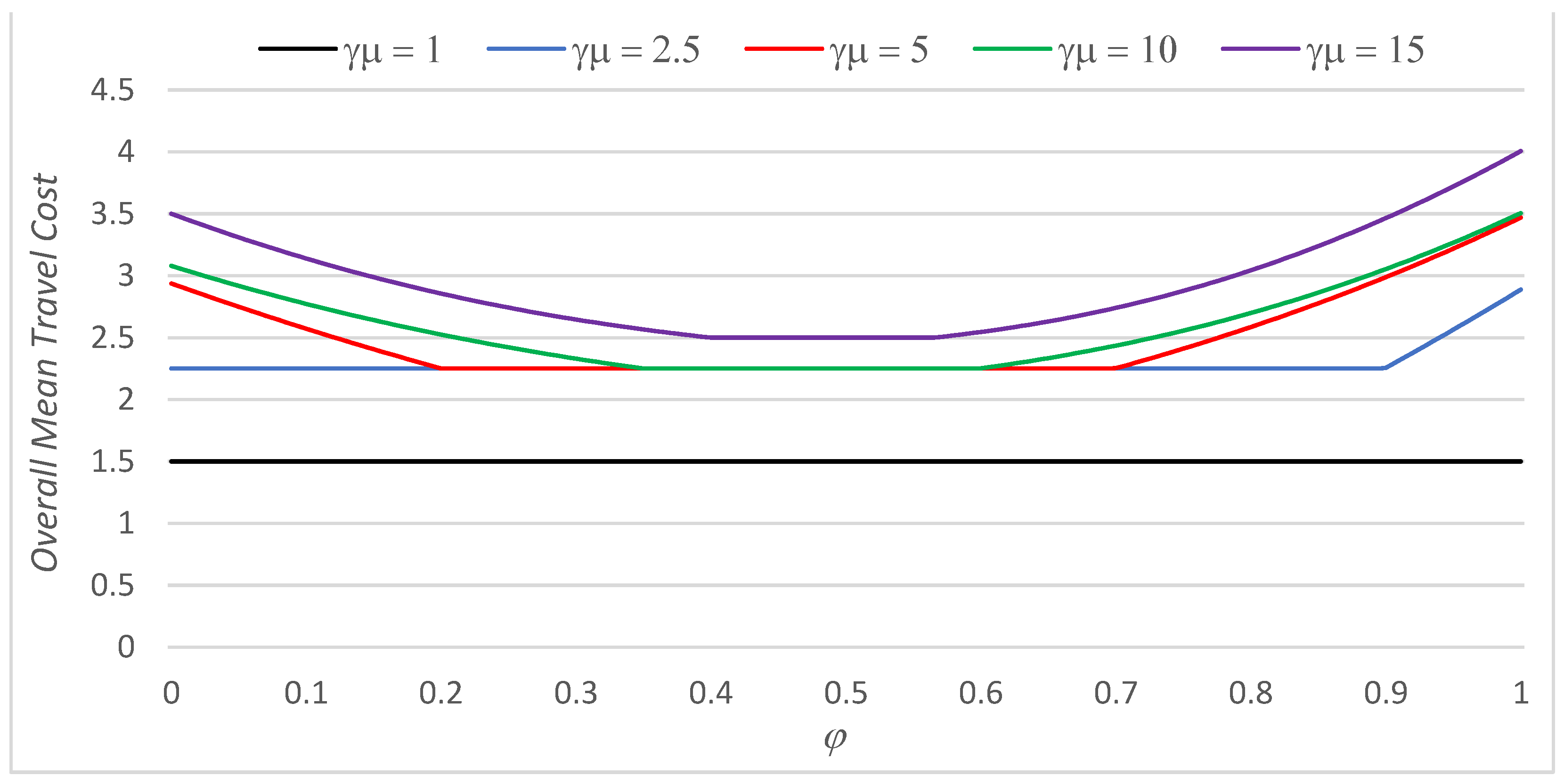
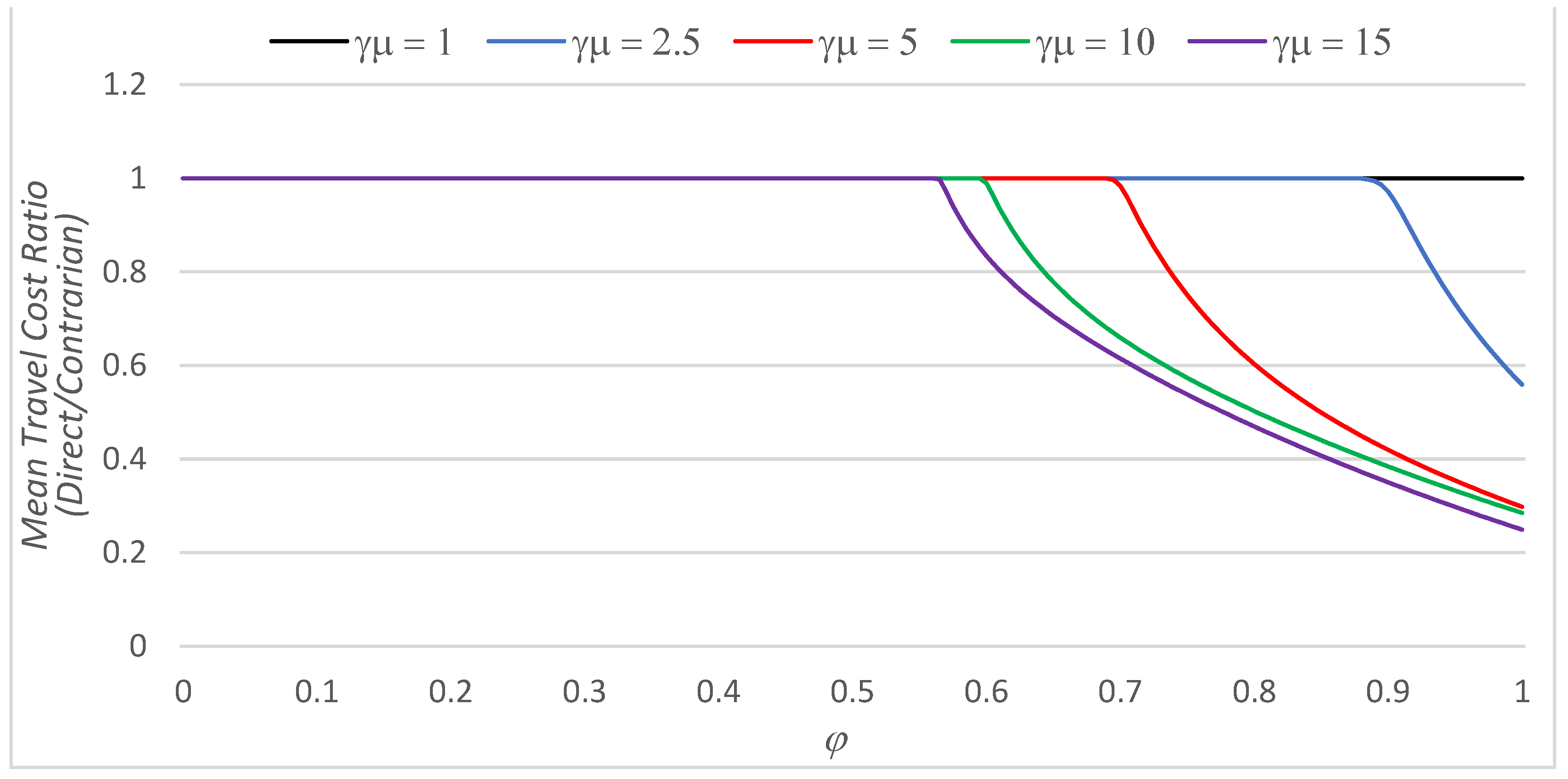
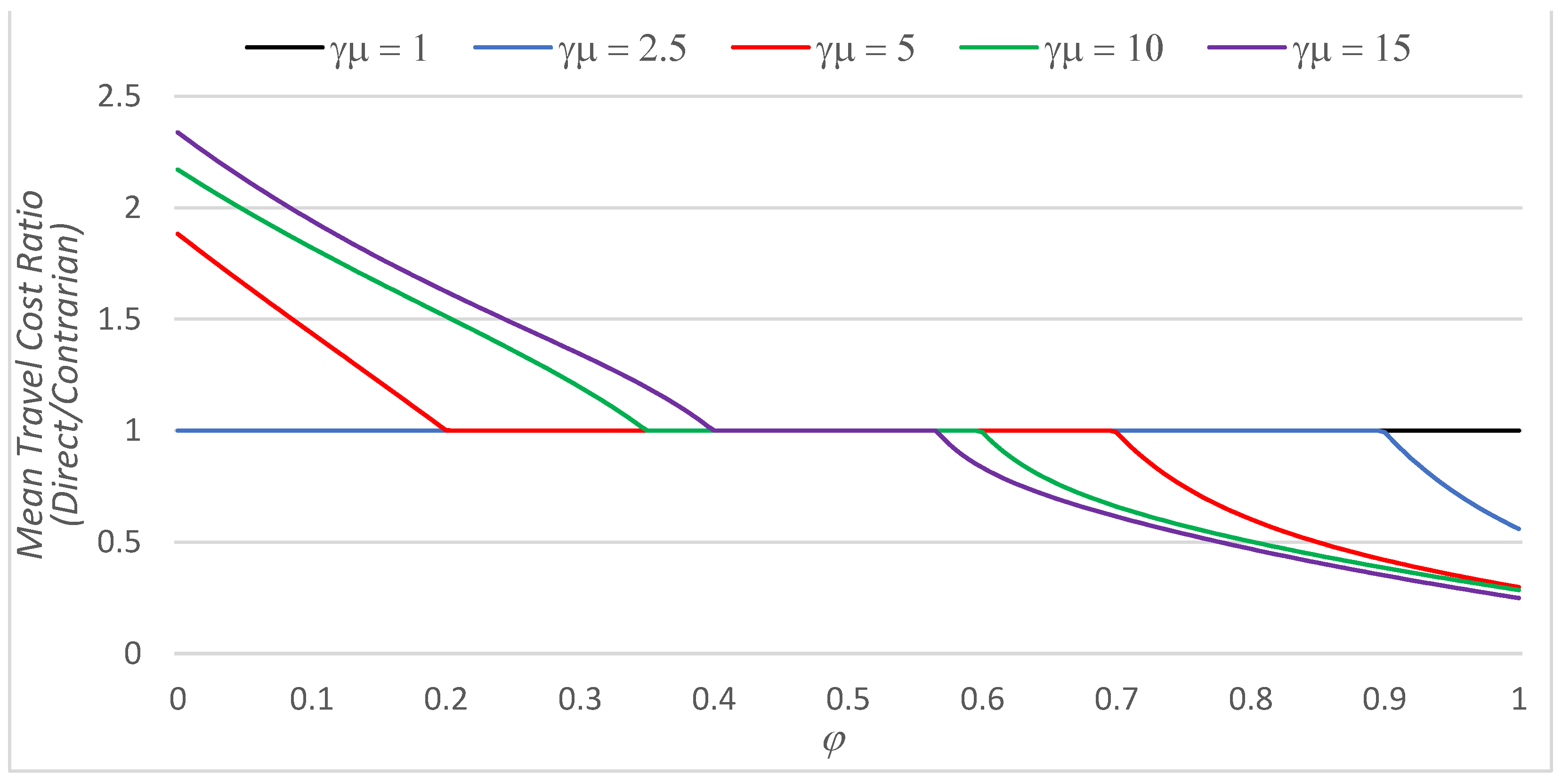
| α | β | φ Min | φ Max | |
|---|---|---|---|---|
| γμ = 1 | 0.1 | 0.1 | 0 | 1 |
| 0.5 | 0.5 | 0 | 1 | |
| 0.75 | 0.75 | 0 | 1 | |
| 0.9 | 0.9 | 0 | 1 | |
| 1 * | 1 * | 0 | 1 | |
| γμ = 2.5 | 0.1 | 0.1 | 0 | 0.9 |
| 0.5 | 0.5 | 0 | 0.9 | |
| 0.75 | 0.75 | 0 | 0.9 | |
| 0.9 | 0.9 | 0 | 0.9 | |
| 1 * | 1 * | 0.1 | 0.9 | |
| γμ = 5 | 0.1 | 0.1 | 0 | 0.7 |
| 0.5 | 0.5 | 0 | 0.7 | |
| 0.75 | 0.75 | 0 | 0.7 | |
| 0.9 | 0.9 | 0.2012 | 0.7 | |
| 1 * | 1 * | 0.3 | 0.7 | |
| γμ = 10 | 0.1 | 0.1 | 0 | 0.6 |
| 0.5 | 0.5 | 0 | 0.6 | |
| 0.75 | 0.75 | 0.2222 | 0.6 | |
| 0.9 | 0.9 | 0.3506 | 0.6 | |
| 1 * | 1 * | 0.4 | 0.6 | |
| γμ = 15 | 0.1 | 0.1 | 0 | 0.5667 |
| 0.5 | 0.5 | 0 | 0.5667 | |
| 0.75 | 0.75 | 0.3148 | 0.5667 | |
| 0.9 | 0.9 | 0.4004 | 0.5667 | |
| 1 * | 1 * | 0.4333 | 0.5667 |
| α | β | φ Min | φ Max | |
|---|---|---|---|---|
| γμ = 1 | 0.1 | 0.1 | 0 | 1 |
| 0.5 | 0.5 | 0 | 1 | |
| 0.75 | 0.75 | 0 | 1 | |
| 0.9 | 0.9 | 0 | 1 | |
| 1 * | 1 * | 0 | 1 | |
| γμ = 2.5 | 0.1 | 0.1 | 0 | 1 ** |
| 0.5 | 0.5 | 0 | 1 ** | |
| 0.75 | 0.75 | 0 | 1 ** | |
| 0.9 | 0.9 | 0 | 1 ** | |
| 1 * | 1 * | 0 ** | 1 ** | |
| γμ = 5 | 0.1 | 0.1 | 0 | 0.9 ** |
| 0.5 | 0.5 | 0 | 0.9 ** | |
| 0.75 | 0.75 | 0 | 0.9 ** | |
| 0.9 | 0.9 | 0 ** | 0.9 ** | |
| 1 * | 1 * | 0.1 ** | 0.9 ** | |
| γμ = 10 | 0.1 | 0.1 | 0 | 0.7 ** |
| 0.5 | 0.5 | 0 | 0.7 ** | |
| 0.75 | 0.75 | 0 ** | 0.7 ** | |
| 0.9 | 0.9 | 0.2012 ** | 0.7 ** | |
| 1 * | 1 * | 0.3 ** | 0.7 ** | |
| γμ = 15 | 0.1 | 0.1 | 0 | 0.6333 ** |
| 0.5 | 0.5 | 0 | 0.6333 ** | |
| 0.75 | 0.75 | 0.1296 ** | 0.6333 ** | |
| 0.9 | 0.9 | 0.3008 ** | 0.6333 ** | |
| 1 * | 1 * | 0.3667 ** | 0.6333 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meneguzzer, C. Modeling the Combined Effect of Travelers’ Contrarian Behavior, Learning and Inertia on the Day-to-Day Dynamics of Route Choice. Appl. Sci. 2023, 13, 3294. https://doi.org/10.3390/app13053294
Meneguzzer C. Modeling the Combined Effect of Travelers’ Contrarian Behavior, Learning and Inertia on the Day-to-Day Dynamics of Route Choice. Applied Sciences. 2023; 13(5):3294. https://doi.org/10.3390/app13053294
Chicago/Turabian StyleMeneguzzer, Claudio. 2023. "Modeling the Combined Effect of Travelers’ Contrarian Behavior, Learning and Inertia on the Day-to-Day Dynamics of Route Choice" Applied Sciences 13, no. 5: 3294. https://doi.org/10.3390/app13053294
APA StyleMeneguzzer, C. (2023). Modeling the Combined Effect of Travelers’ Contrarian Behavior, Learning and Inertia on the Day-to-Day Dynamics of Route Choice. Applied Sciences, 13(5), 3294. https://doi.org/10.3390/app13053294






