Prediction of Seismic Bearing Capacity Considering Nonlinearity and Dilatancy by Sequential Quadratic Programming
Abstract
1. Introduction
2. Methodology
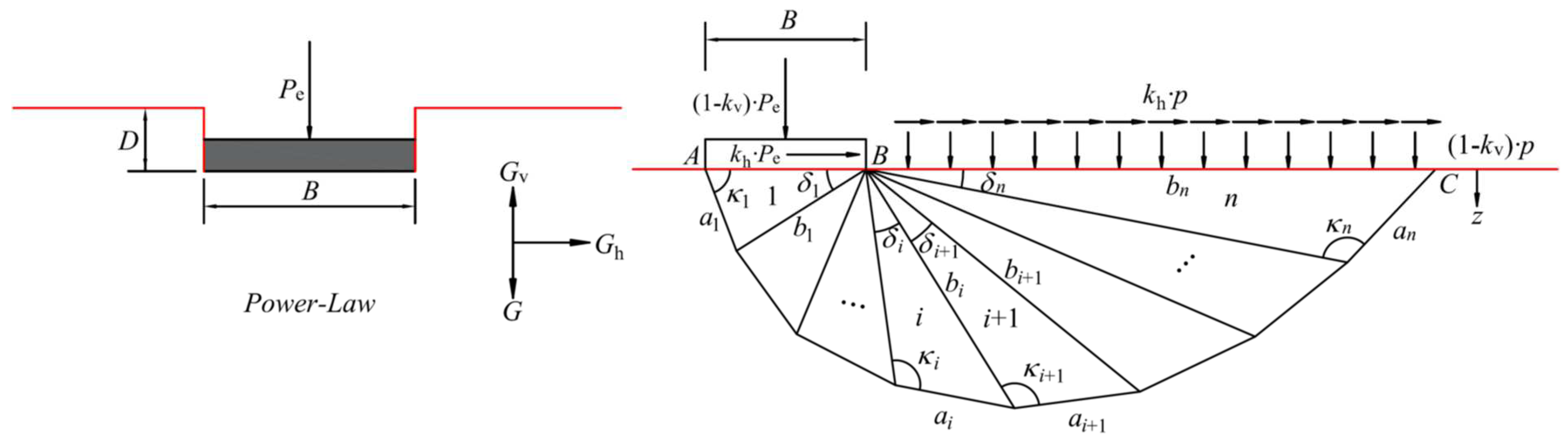
2.1. Kinematic Theorem of Limit Analysis
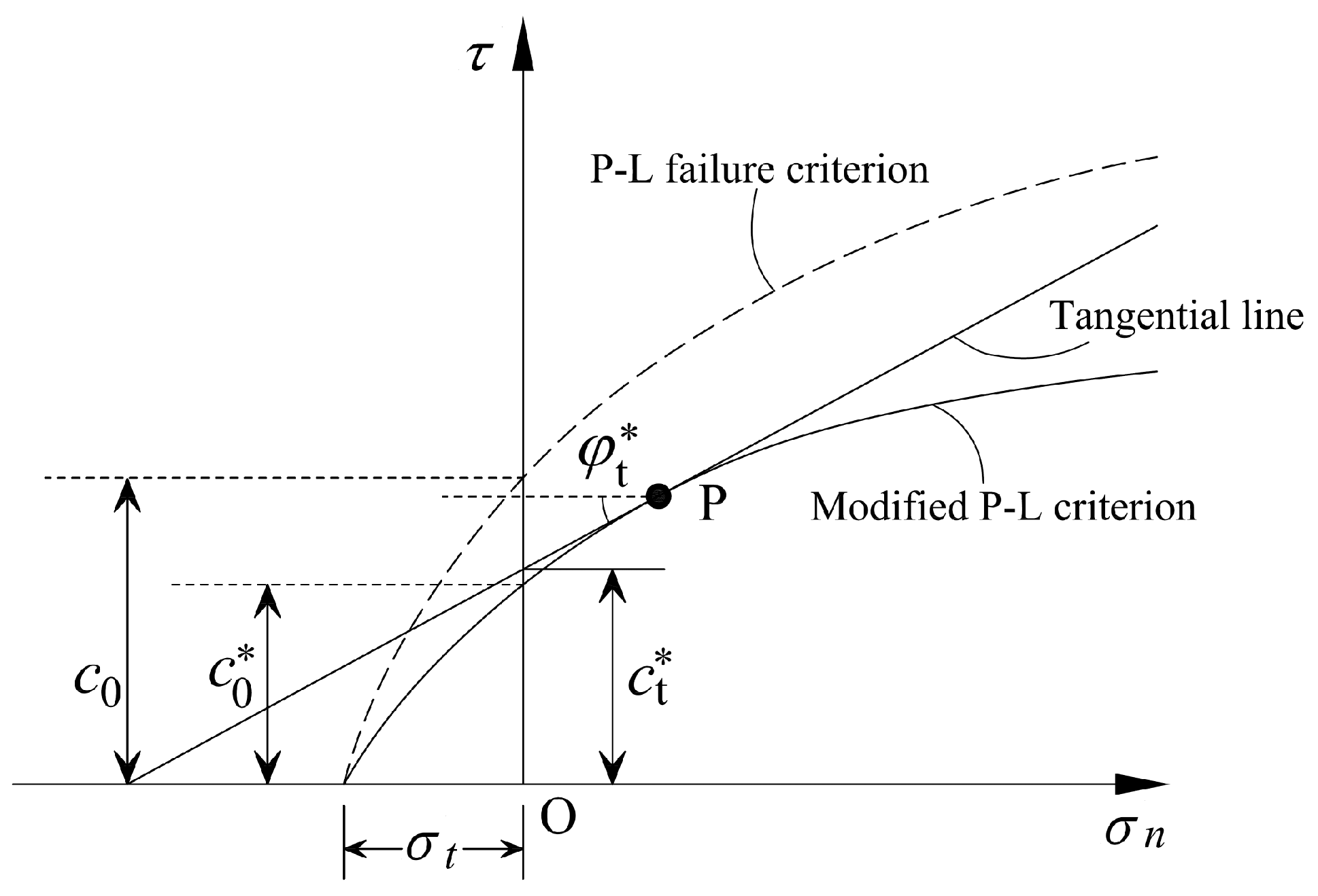
2.2. Nonlinear Failure Criterion of Dilatancy Soils
2.3. Non-Associative Flow Rule
3. Pseudo-Static Analysis of Ultimate Bearing Capacity
3.1. Rate of External Work and Internal Energy Dissipation
3.2. Seismic Ultimate Bearing Capacity
4. Numerical Results and Discussions
4.1. Comparisons
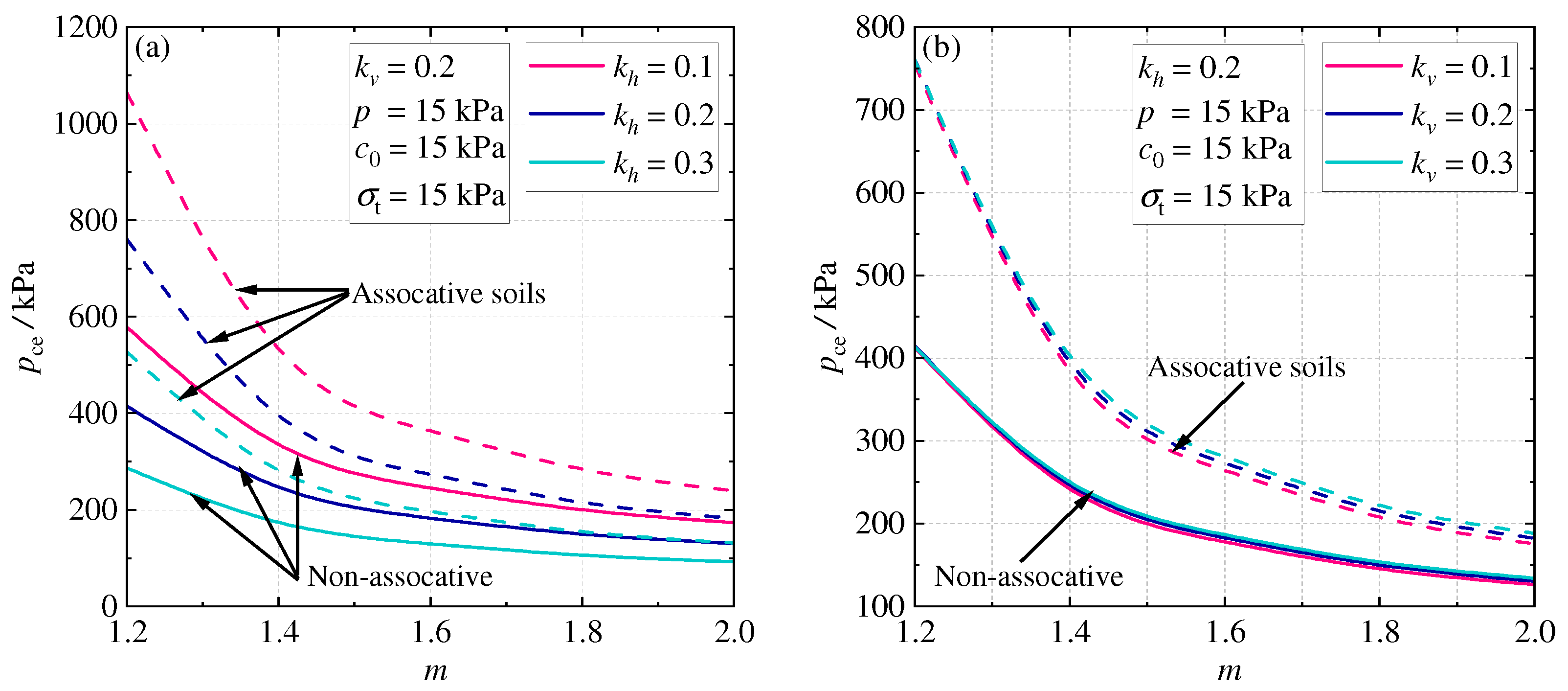
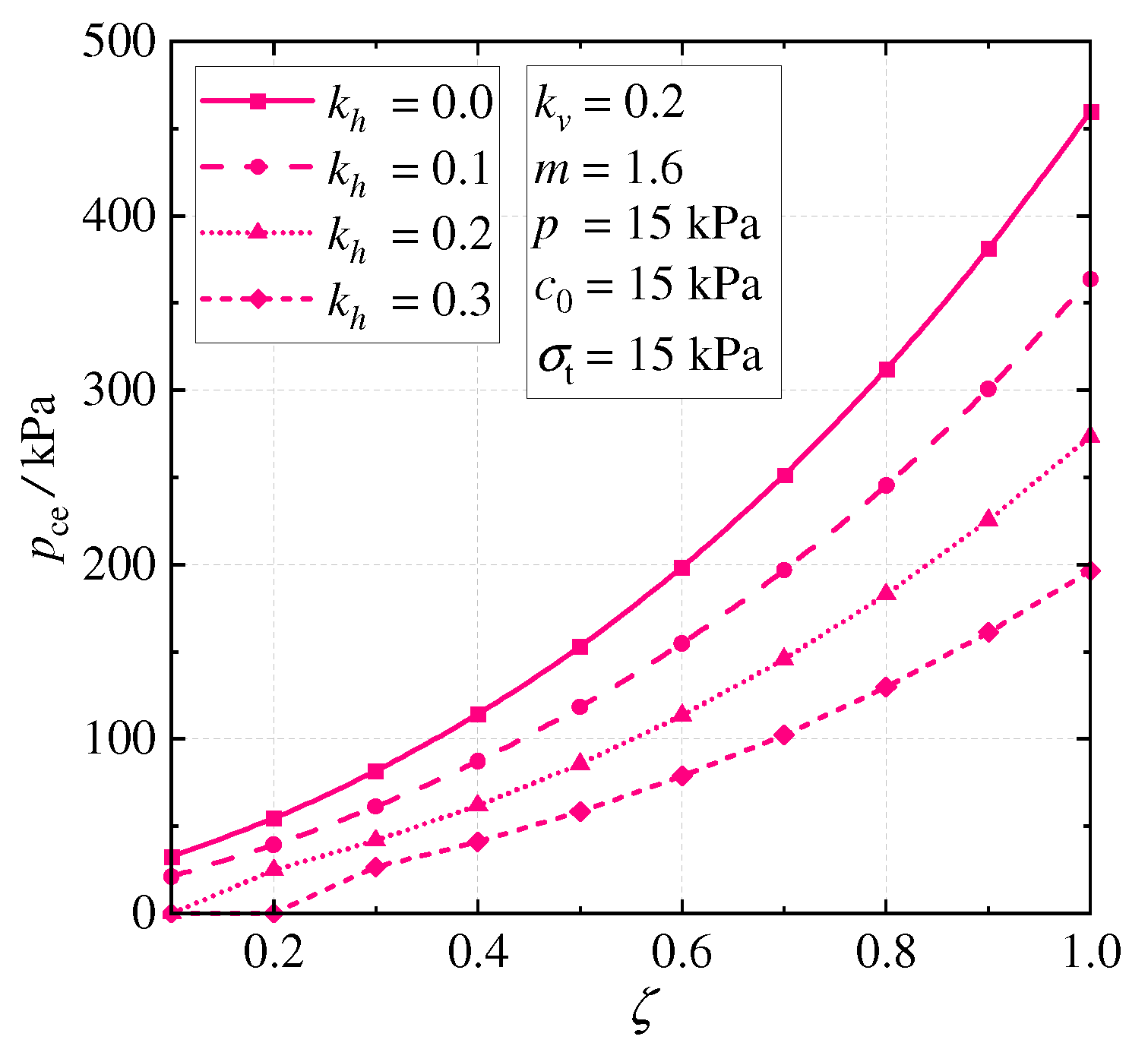
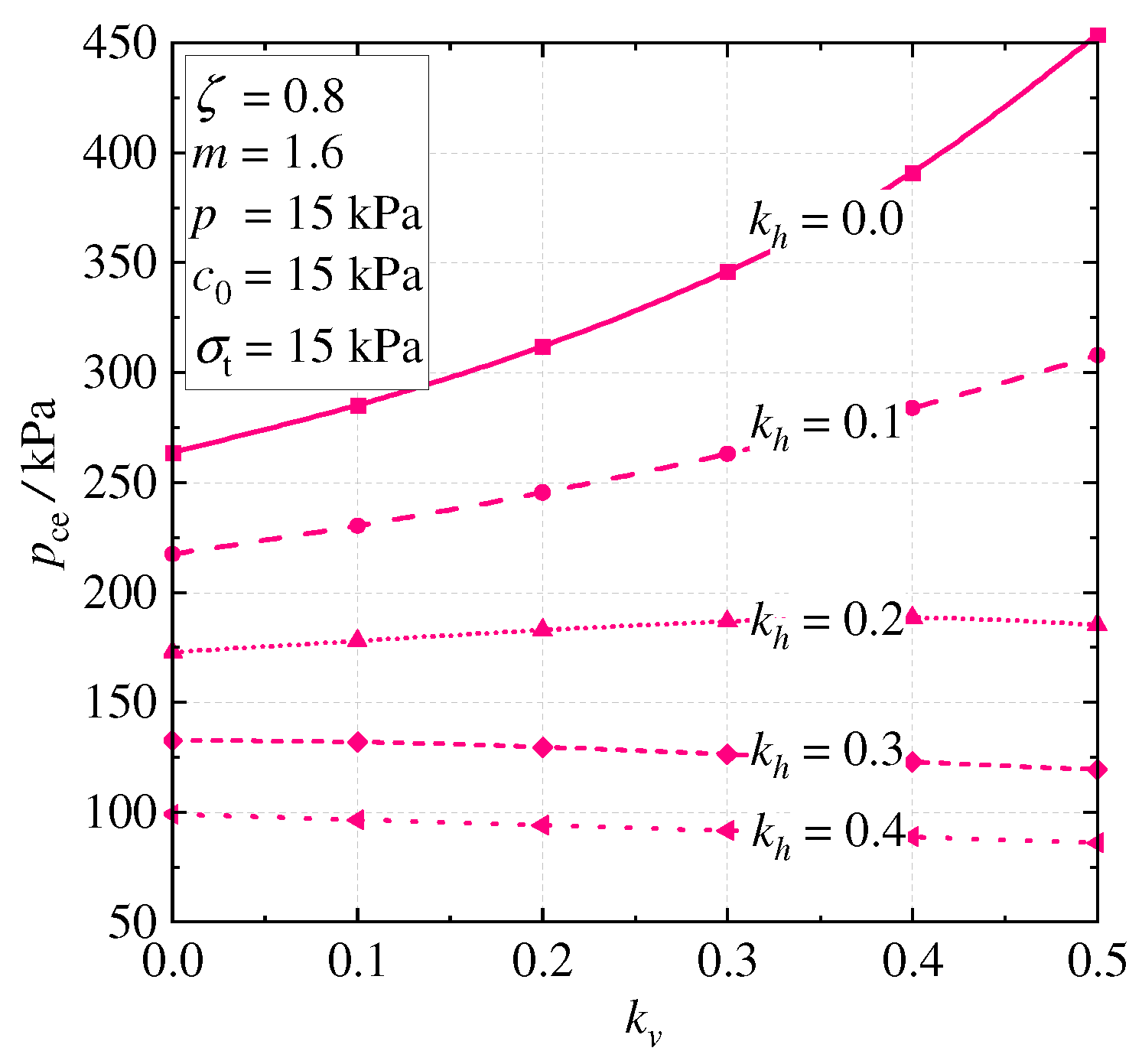
4.2. Parametric Study
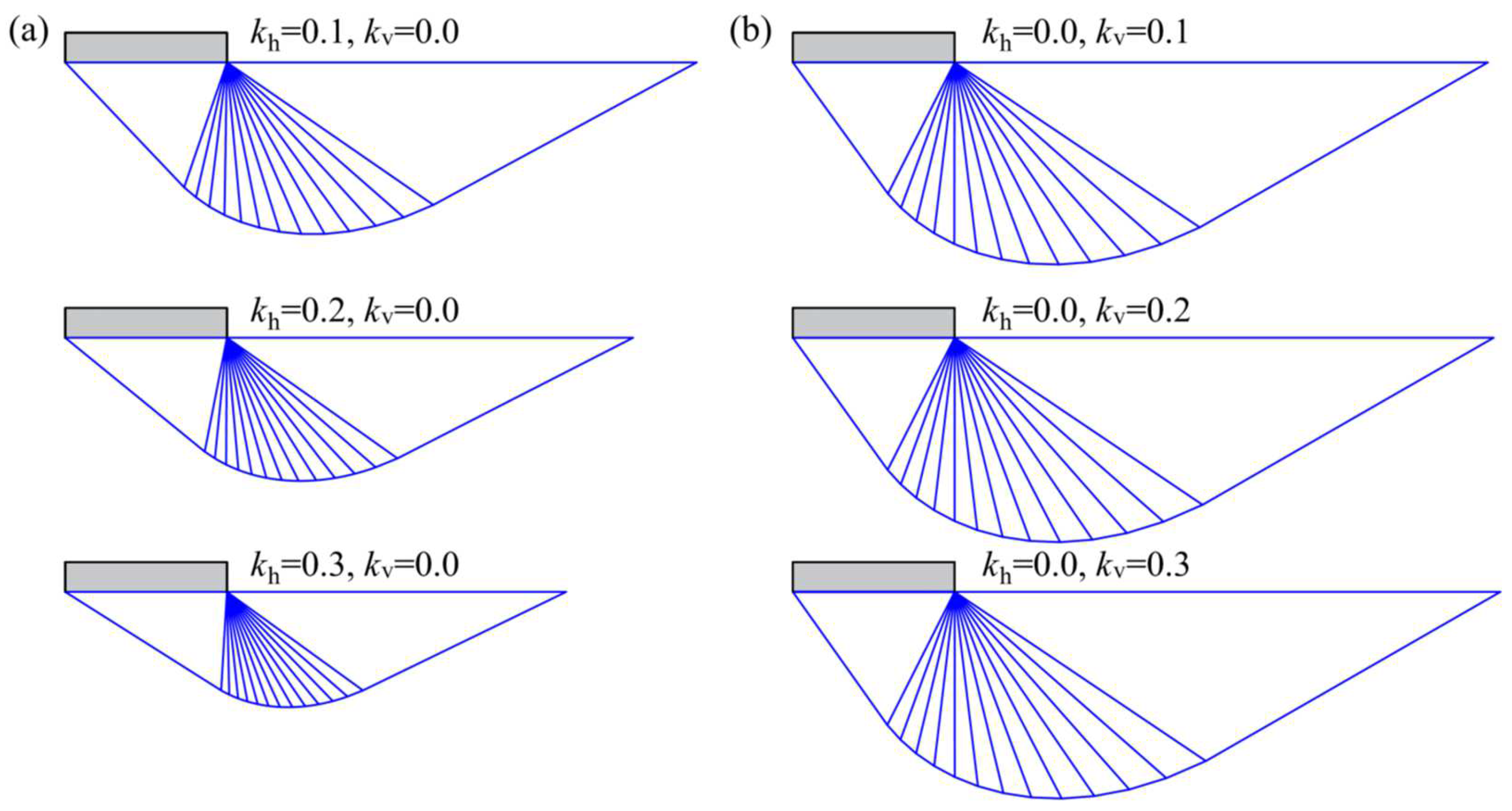
4.3. Critical Failure Surface
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| = velocity discontinuity of the ith block | = volume of failure body |
| = footing width | = velocity of the ith block |
| = velocity discontinuity of the ith block | = relative velocity between the ith block and the i + 1st block |
| = initial cohesion | = work rate achieved by earthquake loads |
| , = equivalent shear strength | = total external work rate |
| , = shear strength for non-associative materials | = work rate produced by |
| , = equivalent shear strength for non-associative materials | = work rate achieved by lateral soils |
| = buried depth of footing | = work rate achieved by soil weight |
| = work rate of internal energy | = angular variables of mechanism |
| = external body loads | = plastic strain rate |
| = gravity acceleration | = unit weight of soils |
| = dimensionless expressions | = angular variables of mechanism |
| , = seismic coefficients | = non-negative coefficient |
| = nonlinear coefficient | = angle between and vertical direction |
| = number of blocks | = effective stress |
| , , = bearing capacity factors | = normal stress at the failure surface |
| = load from the superstructure | = uniaxial tensile strength |
| = equivalent pressure of lateral soils | = shear stress at failure surface |
| = normalized bearing capacity | = equivalent shear stress |
| = area of failure surface | Ψ = dilatancy angle |
| = external surface loads | = dilatancy coefficient |
Appendix A
References
- Richards, R., Jr.; Elms, D.G.; Budhu, M. Seismic bearing capacity and settlements of foundations. J. Geotech. Eng. 1993, 119, 662–674. [Google Scholar] [CrossRef]
- Dormieux, L.; Pecker, A. Seismic bearing capacity of foundation on cohesionless soil. J. Geotech. Eng. 1995, 121, 300–303. [Google Scholar] [CrossRef]
- Silvestri, V.A. Limit equilibrium solution for bearing capacity of strip foundations on sand. Can. Geotech. J. 2003, 40, 351–361. [Google Scholar] [CrossRef]
- Yang, X.L.; Yin, J.H. Upper bound solution for ultimate bearing capacity with a modified Hoek-Brown failure criterion. Int. J. Rock Mech. Min. Sci. 2005, 42, 550–560. [Google Scholar] [CrossRef]
- Kumar, J.; Ghosh, P. Seismic bearing capacity for embedded footings on sloping ground. Géotechnique 2006, 56, 133–140. [Google Scholar] [CrossRef]
- Nguyen, H.C.; Vo-Minh, T. Calculation of seismic bearing capacity of shallow strip foundations using the cell-based smoothed finite element method. Acta. Geotech. 2022, 17, 3567–3590. [Google Scholar] [CrossRef]
- Zhong, J.H.; Li, Y.X.; Yang, X.L. Estimation of the seismic bearing capacity of shallow strip footings based on a pseudodynamic approach. Int. J. Geomech. 2022, 22, 04022143. [Google Scholar] [CrossRef]
- Zhong, J.H.; Hou, C.T.; Yang, X.L. Bearing capacity of foundations resting on rock masses subjected to Rayleigh waves. Soil Dyn. Earthq. Eng. 2023, 167, 107791. [Google Scholar] [CrossRef]
- Wang, N.; Xing, G.; Zhu, T.; Zhou, H.; Shi, Y. Propagating seismic waves in VTI attenuating media using fractional viscoelastic wave equation. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023280. [Google Scholar] [CrossRef]
- Huang, S.; Lyu, Y.; Sha, H.; Xiu, L. Seismic performance assessment of unsaturated soil slope in different groundwater levels. Landslides 2021, 18, 2813–2833. [Google Scholar] [CrossRef]
- Wu, M.; Ba, Z.; Liang, J. A procedure for 3D simulation of seismic wave propagation considering source-path-site effects: Theory, verification and application. Earthq. Eng. Struct. D 2022, 51, 2925–2955. [Google Scholar] [CrossRef]
- Zhai, S.Y.; Lyu, Y.F.; Cao, K.; Li, G.Q.; Wang, W.Y.; Chen, C. Seismic behavior of an innovative bolted connection with dual-slot hole for modular steel buildings. Eng. Struct. 2023, 279, 115619. [Google Scholar] [CrossRef]
- Huang, S.; Huang, M.; Lyu, Y. Seismic performance analysis of a wind turbine with a monopile foundation affected by sea ice based on a simple numerical method. Eng. Appl. Comp. Fluid. 2021, 15, 1113–1133. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yang, X.L. Pseudodynamic analysis of three-dimensional fissured slopes reinforced with piles. Int. J. Geomech. 2022, 23, 04022315. [Google Scholar] [CrossRef]
- Li, J.; Cheng, F.; Lin, G.; Wu, C. Improved hybrid method for the generation of ground motions compatible with the multi-damping design spectra. J. Earthq. Eng. 2022, 2022, 2095059. [Google Scholar] [CrossRef]
- Li, J.; Chen, M.; Li, Z. Improved soil–structure interaction model considering time-lag effect. Comput. Geotech. 2022, 148, 104835. [Google Scholar] [CrossRef]
- Li, J.; Zhou, L.; Li, S.; Lin, G.; Ding, Z. Soil–structure interaction analysis of nuclear power plant considering three-dimensional surface topographic irregularities based on automatic octree mesh. Eng. Struct. 2023, 275, 115161. [Google Scholar] [CrossRef]
- Keshavarz, A.; Nemati, M. Seismic bearing capacity analysis of reinforced soils by the method of stress characteristics. IJST-T. Civ. Eng. 2011, 35, 185–197. [Google Scholar] [CrossRef]
- Keshavarz, A.; Fazeli, A.; Sadeghi, S. Seismic bearing capacity of strip footings on rock masses using the Hoek–Brown failure criterion. J. Rock Mech. Geotech. 2016, 8, 170–177. [Google Scholar] [CrossRef]
- Casablanca, O.; Biondi, G.; Cascone, E.; Filippo, G.D. Static and seismic bearing capacity of shallow strip foundations on slopes. Géotechnique 2022, 72, 769–783. [Google Scholar] [CrossRef]
- Ghosh, S.; Debnath, L. Seismic bearing capacity of shallow strip footing with coulomb failure mechanism using limit equilibrium method. Geotech. Geol. Eng. 2017, 35, 2647–2661. [Google Scholar] [CrossRef]
- Izadi, A.; Mahsa, N.S.S.; Jamshidi Chenari, R.; Ghorbani, A. Pseudo-static bearing capacity of shallow foundations on heterogeneous marine deposits using limit equilibrium method. Mar. Georesour. Geotec. 2019, 37, 1163–1174. [Google Scholar] [CrossRef]
- Nouzari, M.A.; Jamshidi Chenari, R.; Payan, M.; Pishgar, F. Pseudo-static seismic bearing capacity of shallow foundations in unsaturated soils employing limit equilibrium method. Geotech. Geol. Eng. 2021, 39, 943–956. [Google Scholar] [CrossRef]
- Qin, C.B.; Chian, S.C. Kinematic analysis of seismic slope stability with a discretization technique and pseudo-dynamic approach: A new perspective. Géotechnique 2017, 68, 492–503. [Google Scholar] [CrossRef]
- Yilmazoglu, M.U.; Ozocak, A. Bearing Capacity of Shallow Foundations on Unsaturated Silty Soils. Appl. Sci. 2023, 13, 1308. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L.; Li, T.Z. Static and seismic stability assessment of 3D slopes with cracks. Eng. Geol. 2020, 265, 105450. [Google Scholar] [CrossRef]
- Sia, V.; Satyanaga, A.; Kim, Y. Effects of Heavy Rainfall on Shallow Foundations in Bukit Timah Granite in Singapore. Appl. Sci. 2022, 12, 9516. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Zhu, J.Q.; Yang, X.L. Three-dimensional active earth pressures for unsaturated backfills with cracks considering steady seepage. Int. J. Geomech. 2023, 23, 04022270. [Google Scholar] [CrossRef]
- Chen, W.; Liu, Q.; Wang, E. The Effect of the Water Table on the Bearing Capacity of a Shallow Foundation. Appl. Sci. 2022, 12, 6571. [Google Scholar] [CrossRef]
- Bralović, N.; Despotović, I.; Kukaras, D. Experimental Analysis of the Behaviour of Piled Raft Foundations in Loose Sand. Appl. Sci. 2023, 13, 546. [Google Scholar] [CrossRef]
- Yang, X.L.; Li, L.; Yin, J.H. Seismic and static stability analysis for rock slopes by a kinematical approach. Géotechnique 2004, 54, 543–549. [Google Scholar] [CrossRef]
- Zhong, J.; Hou, C.; Yang, X. Three-dimensional face stability analysis of rock tunnels excavated in Hoek-Brown media with a novel multi-cone mechanism. Comp. Geotech. 2023, 154, 105158. [Google Scholar] [CrossRef]
- Zhang, X.J.; Chen, W.F. Stability analysis of slopes with general nonlinear failure criterion. Int. J. Numer. Anal. Meth. Geomech. 1987, 11, 33–50. [Google Scholar] [CrossRef]
- Drescher, A.; Detournay, E. Limit load in translational failure mechanisms for associative and non-associative materials. Géotechnique 1993, 43, 443–456. [Google Scholar] [CrossRef]
- Yang, X.L.; Wang, J.M. Ground movement prediction for tunnels using simplified procedure. Tunn. Undergr. Space Technol. 2011, 26, 462–471. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L. Active earth pressure for soils with tension cracks under steady unsaturated flow conditions. Can. Geotech. J. 2018, 55, 1850–1859. [Google Scholar] [CrossRef]
- Huang, H.; Li, M.; Yuan, Y.; Bai, H. Theoretical analysis on the lateral drift of precast concrete frame with replaceable artificial controllable plastic hinges. J. Build. Eng. 2022, 62, 105386. [Google Scholar] [CrossRef]
- Zhang, C.; Kordestani, H.; Shadabfar, M. A combined review of vibration control strategies for high-speed trains and railway infrastructures: Challenges and solutions. J. Low Freq. Noise Vib. Act. Control 2023, 42, 272–291. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, J.; Zhang, W.; Liu, X. Experimental and numerical study of hooked-end steel fiber-reinforced concrete based on the meso-and macro-models. Compos. Struct. 2023, 309, 116750. [Google Scholar] [CrossRef]
- Sun, R.; Fu, L.; Cheng, Q.; Chiang, K.W.; Chen, W. Resilient Pseudorange Error Prediction and Correction for GNSS Positioning in Urban Areas. IEEE Internet Things J. 2023, in press. [Google Scholar] [CrossRef]
- Hou, C.; Zhong, J.; Yang, X. Three-dimensional stability assessments of a non-circular tunnel face reinforced by bolts under seepage flow conditions. Tunn. Undergr. Space Technol. 2023, 131, 104831. [Google Scholar] [CrossRef]
- Soubra, A.H. Upper-Bound Solutions for Bearing Capacity of Foundations. J. Geotech. Geoenviron. Eng. 1999, 125, 59–68. [Google Scholar] [CrossRef]
- Chen, W.F. Limit Analysis and Soil Plasticity; Elsevier Science: Amsterdam, The Netherlands, 1975. [Google Scholar] [CrossRef]
- Yang, X.L.; Yin, J.H. Slope stability analysis with nonlinear failure criterion. J. Eng. Mech. 2004, 130, 267–273. [Google Scholar] [CrossRef]
- Mabrouki, A.; Benmeddour, D.; Frank, R.; Mellas, M. Numerical study of the bearing capacity for two interfering strip footings on sands. Comput. Geotech. 2010, 37, 431–439. [Google Scholar] [CrossRef]

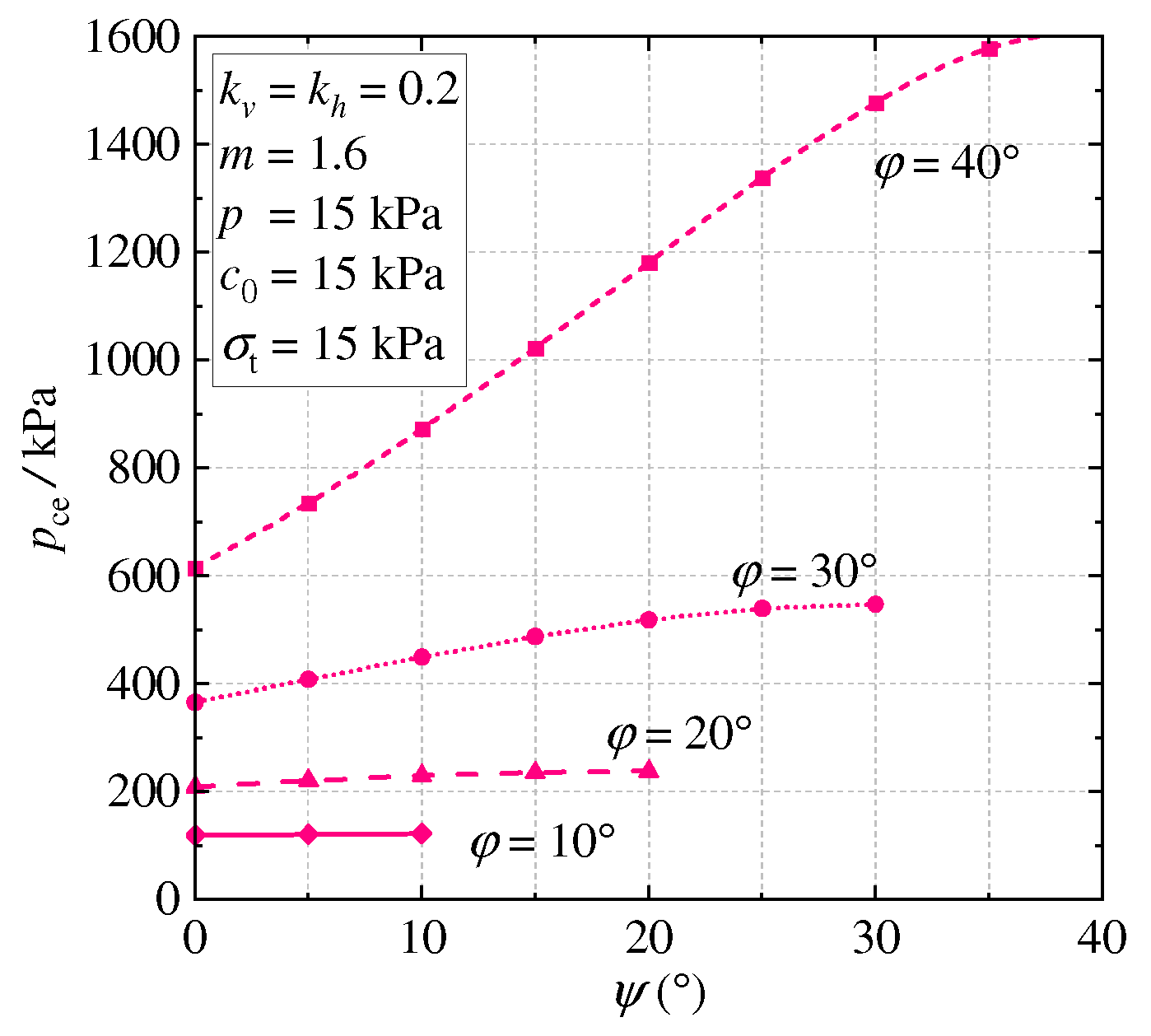



| Relative Error/% | |||||
|---|---|---|---|---|---|
| 2 | 37.85 | 28.65 | 47.89 | 1106.02 | - |
| 3 | 28.03 | 21.36 | 35.26 | 818.42 | 26.37 |
| 4 | 26.17 | 20.07 | 33.02 | 766.44 | 6.62 |
| 5 | 25.50 | 19.61 | 32.24 | 748.05 | 2.56 |
| 6 | 25.19 | 19.40 | 31.88 | 739.49 | 1.24 |
| 7 | 25.01 | 19.29 | 31.68 | 734.81 | 0.69 |
| 8 | 24.91 | 19.22 | 31.56 | 731.99 | 0.42 |
| 9 | 24.84 | 19.18 | 31.48 | 730.15 | 0.28 |
| 10 | 24.79 | 19.15 | 31.43 | 728.89 | 0.19 |
| 11 | 24.76 | 19.12 | 31.39 | 727.99 | 0.14 |
| 12 | 24.73 | 19.11 | 31.36 | 727.32 | 0.10 |
| 13 | 24.72 | 19.10 | 31.34 | 726.81 | 0.08 |
| 14 | 24.70 | 19.09 | 31.33 | 726.41 | 0.06 |
| 15 | 20 | 25 | 30 | |||||
|---|---|---|---|---|---|---|---|---|
| This Paper | Soubra [43] | This Paper | Soubra [43] | This Paper | Soubra [43] | This Paper | Soubra [43] | |
| 0 | 176.34 | 168.4 | 268.60 | 254.83 | 429.00 | 405.24 | 726.41 | 684.02 |
| 0.1 | 140.90 | 134.79 | 210.81 | 200.59 | 330.20 | 312.86 | 546.95 | 516.61 |
| 0.2 | 108.75 | 102.64 | 160.22 | 151.77 | 246.73 | 233.66 | 400.75 | 378.93 |
| 0.3 | 81.43 | 64.80 | 118.43 | 110.14 | 179.79 | 169.02 | 287.17 | 270.8 |
| 0.4 | 59.83 | 51.40 | 86.27 | 67.50 | 129.98 | 117.92 | 206.30 | 189.09 |
| 0.5 | 45.80 | 39.80 | 65.63 | 52.30 | 98.57 | 70.20 | 156.32 | 128.45 |
| 15 | 20 | 25 | 30 | |||||
|---|---|---|---|---|---|---|---|---|
| This Paper | Soubra [43] | This Paper | Soubra [43] | This Paper | Soubra [43] | This Paper | Soubra [43] | |
| 0 | 2.80 | 2.10 | 5.77 | 4.67 | 11.80 | 10.06 | 24.70 | 21.88 |
| 0.1 | 1.54 | 1.01 | 3.46 | 2.61 | 7.37 | 6.04 | 15.75 | 13.59 |
| 0.2 | 0.66 | 0.26 | 1.78 | 1.13 | 4.14 | 3.14 | 9.28 | 7.67 |
| 0.3 | 0.14 | - | 0.71 | 0.26 | 2.02 | 1.28 | 4.97 | 3.80 |
| 0.4 | - | - | 0.21 | - | 0.97 | 0.28 | 2.87 | 1.51 |
| 0.5 | - | - | - | - | 0.47 | - | 1.78 | 0.35 |
| 15 | 20 | 25 | 30 | |||||
|---|---|---|---|---|---|---|---|---|
| This Paper | Soubra [43] | This Paper | Soubra [43] | This Paper | Soubra [43] | This Paper | Soubra [43] | |
| 0 | 3.98 | 3.95 | 6.51 | 6.41 | 10.95 | 10.69 | 19.09 | 18.46 |
| 0.1 | 3.10 | 3.07 | 5.07 | 5.02 | 8.49 | 8.35 | 14.70 | 14.34 |
| 0.2 | 2.22 | 2.07 | 3.71 | 3.62 | 6.27 | 6.17 | 10.87 | 10.67 |
| 0.3 | 1.42 | - | 2.50 | 2.25 | 4.37 | 4.22 | 7.70 | 7.54 |
| 0.4 | 0.82 | - | 1.59 | - | 2.91 | 2.47 | 5.27 | 4.97 |
| 0.5 | 0.50 | - | 1.03 | - | 1.99 | - | 3.71 | 2.85 |
| 15 | 20 | 25 | 30 | |||||
|---|---|---|---|---|---|---|---|---|
| This Paper | Soubra [43] | This Paper | Soubra [43] | This Paper | Soubra [43] | This Paper | Soubra [43] | |
| 0 | 11.13 | 11.00 | 15.15 | 14.87 | 21.33 | 20.78 | 31.33 | 30.25 |
| 0.1 | 9.61 | 9.50 | 12.90 | 12.69 | 17.89 | 17.50 | 25.83 | 25.09 |
| 0.2 | 8.07 | 7.96 | 10.72 | 10.54 | 14.67 | 14.37 | 20.85 | 20.32 |
| 0.3 | 6.60 | 6.48 | 8.71 | 8.53 | 11.80 | 11.53 | 16.54 | 16.12 |
| 0.4 | 5.22 | 5.14 | 6.85 | 6.75 | 9.21 | 9.07 | 12.78 | 12.58 |
| 0.5 | 4.22 | 3.98 | 5.54 | 5.23 | 7.45 | 7.02 | 10.32 | 9.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, H.; Zhou, D. Prediction of Seismic Bearing Capacity Considering Nonlinearity and Dilatancy by Sequential Quadratic Programming. Appl. Sci. 2023, 13, 3215. https://doi.org/10.3390/app13053215
Liao H, Zhou D. Prediction of Seismic Bearing Capacity Considering Nonlinearity and Dilatancy by Sequential Quadratic Programming. Applied Sciences. 2023; 13(5):3215. https://doi.org/10.3390/app13053215
Chicago/Turabian StyleLiao, Hong, and De Zhou. 2023. "Prediction of Seismic Bearing Capacity Considering Nonlinearity and Dilatancy by Sequential Quadratic Programming" Applied Sciences 13, no. 5: 3215. https://doi.org/10.3390/app13053215
APA StyleLiao, H., & Zhou, D. (2023). Prediction of Seismic Bearing Capacity Considering Nonlinearity and Dilatancy by Sequential Quadratic Programming. Applied Sciences, 13(5), 3215. https://doi.org/10.3390/app13053215





