Development and Validation of an HPLC-UV Method for the Determination Bis(2-ethylhexyl) Phthalate Ester in Alcoholic Beverages
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemical and Reagents
2.2. Instrumentation
2.3. Procedure
2.4. Method Validation
2.4.1. Specificity
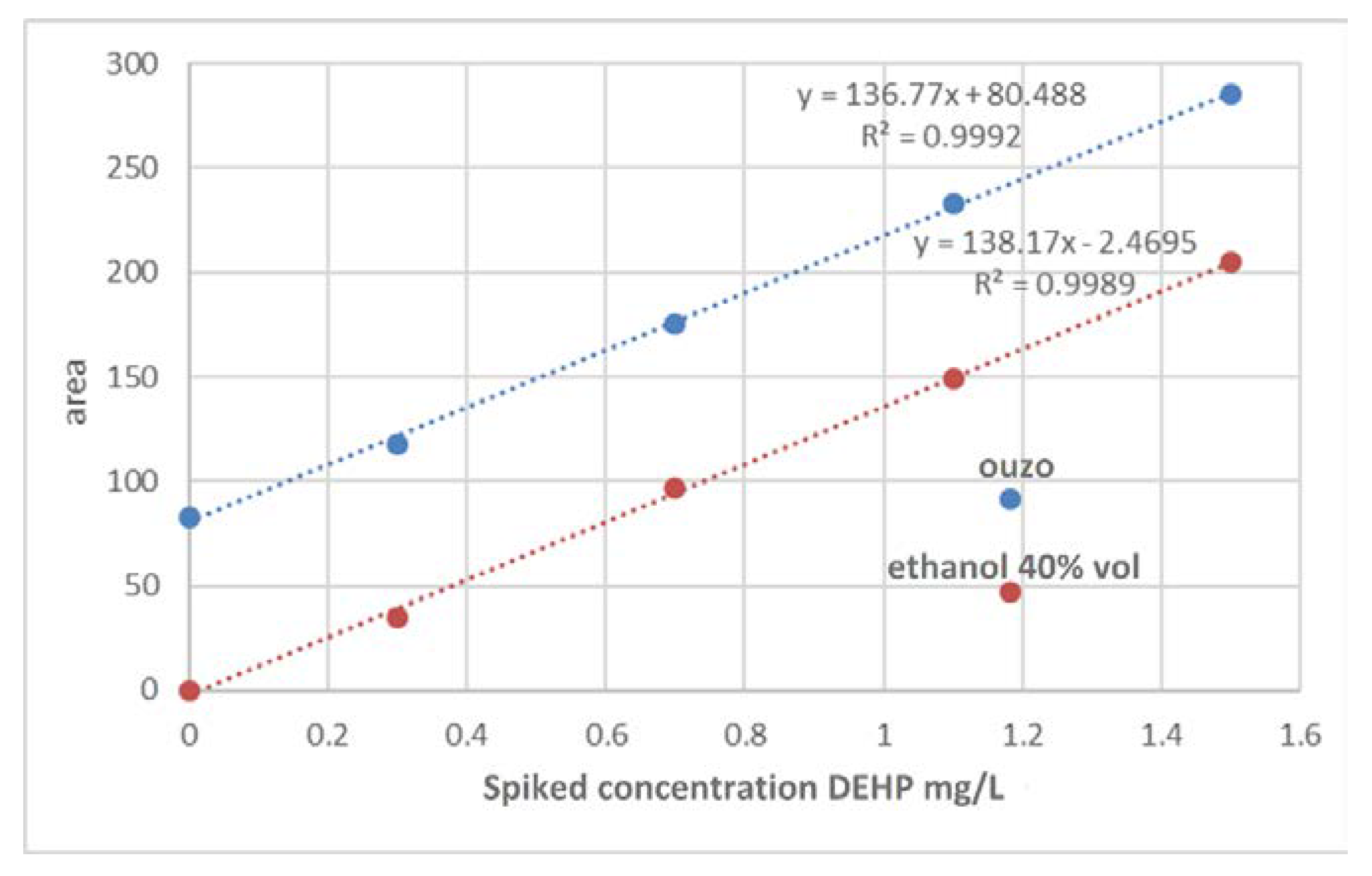
- In a real sample of Ouzo, 4 independent spikes of DEHP were made at concentrations of 0.3, 0.7, 1.1, and 1.5 mg/L and measured following the entire analytical procedure. Additionally, unspiked “ouzo” was measured. The spike was conducted by adding a small volume of a dense standard to avoid dilution of the sample.
- In pure solvent ethyl alcohol 40% v/v, 4 independent spikes of DEHP were made at concentrations of 0.3, 0.7, 1.1, and 1.5 mg/L and were measured following the entire analytical procedure. The pure solvent without spike was also measured.
2.4.2. Linearity
2.4.3. Limit of Detection (LOD) and Limit of Quantification (LOQ)
2.4.4. Accuracy
2.4.5. Precision
2.4.6. Range
2.4.7. Ruggedness
2.5. Assessment of Uncertainty
3. Results and Discussion
3.1. Specificity
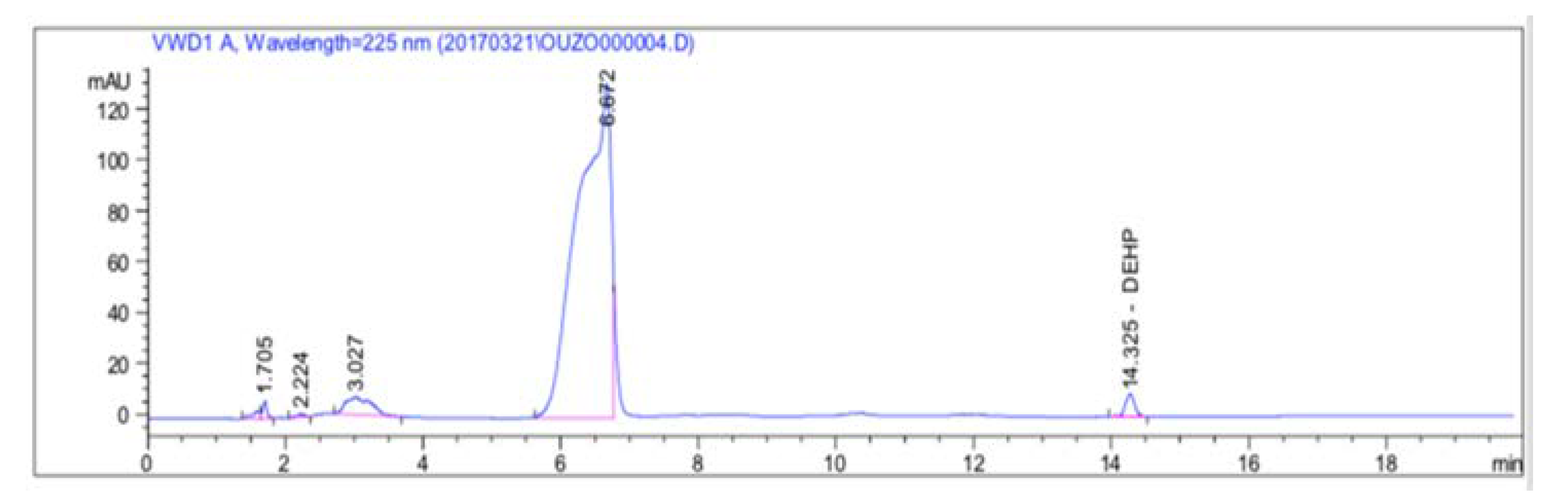
3.1.1. Elution Time and Separation Capacity of DEHP
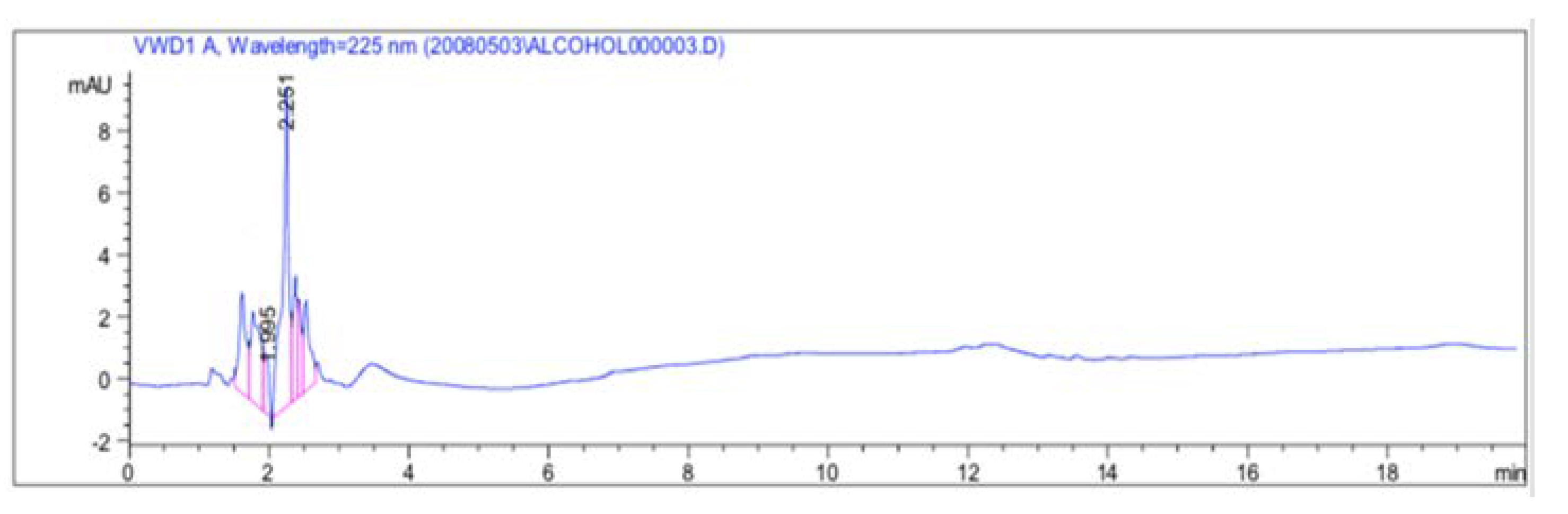
3.1.2. Ouzo Matrix Effect Check
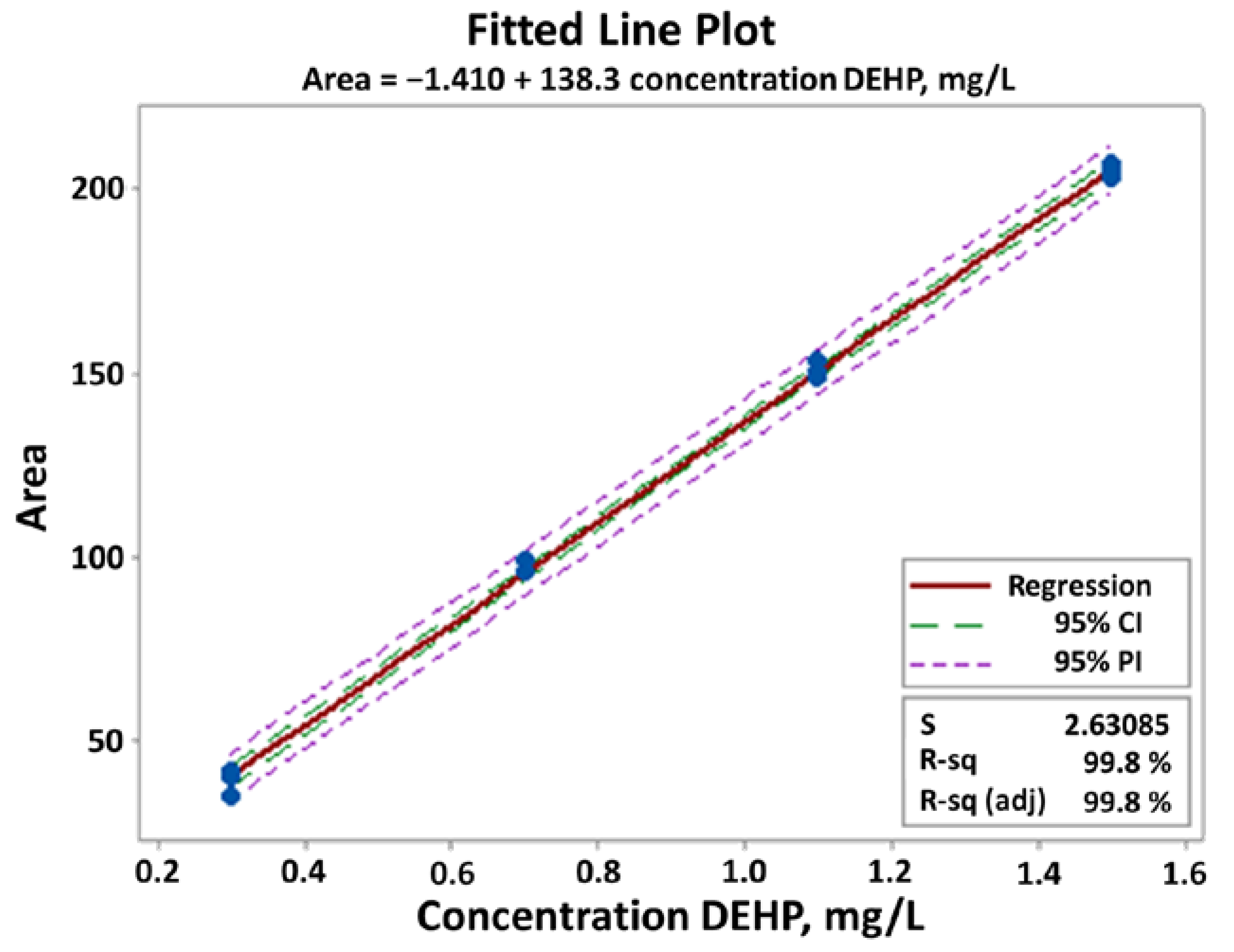
3.2. Linearity
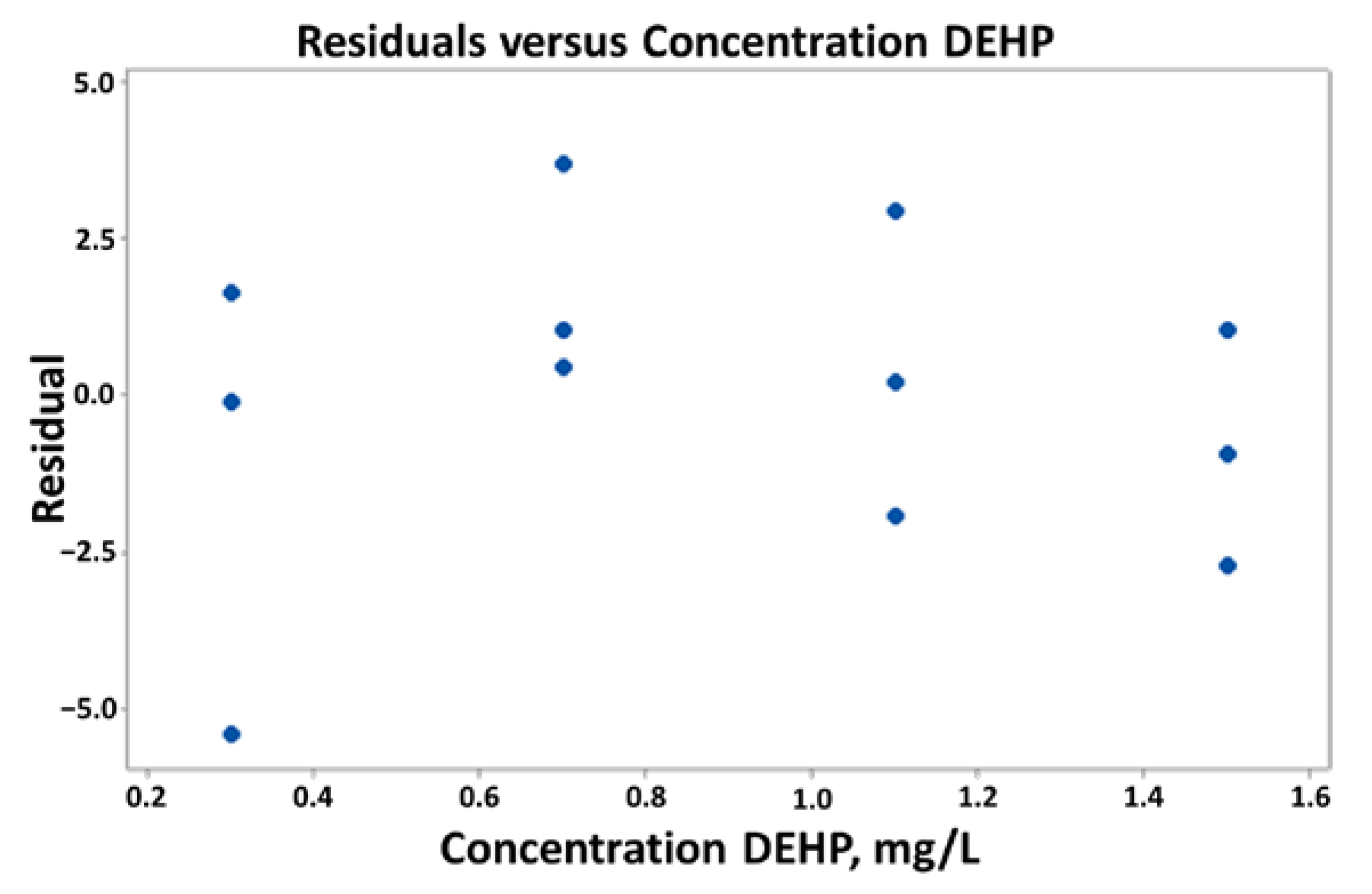
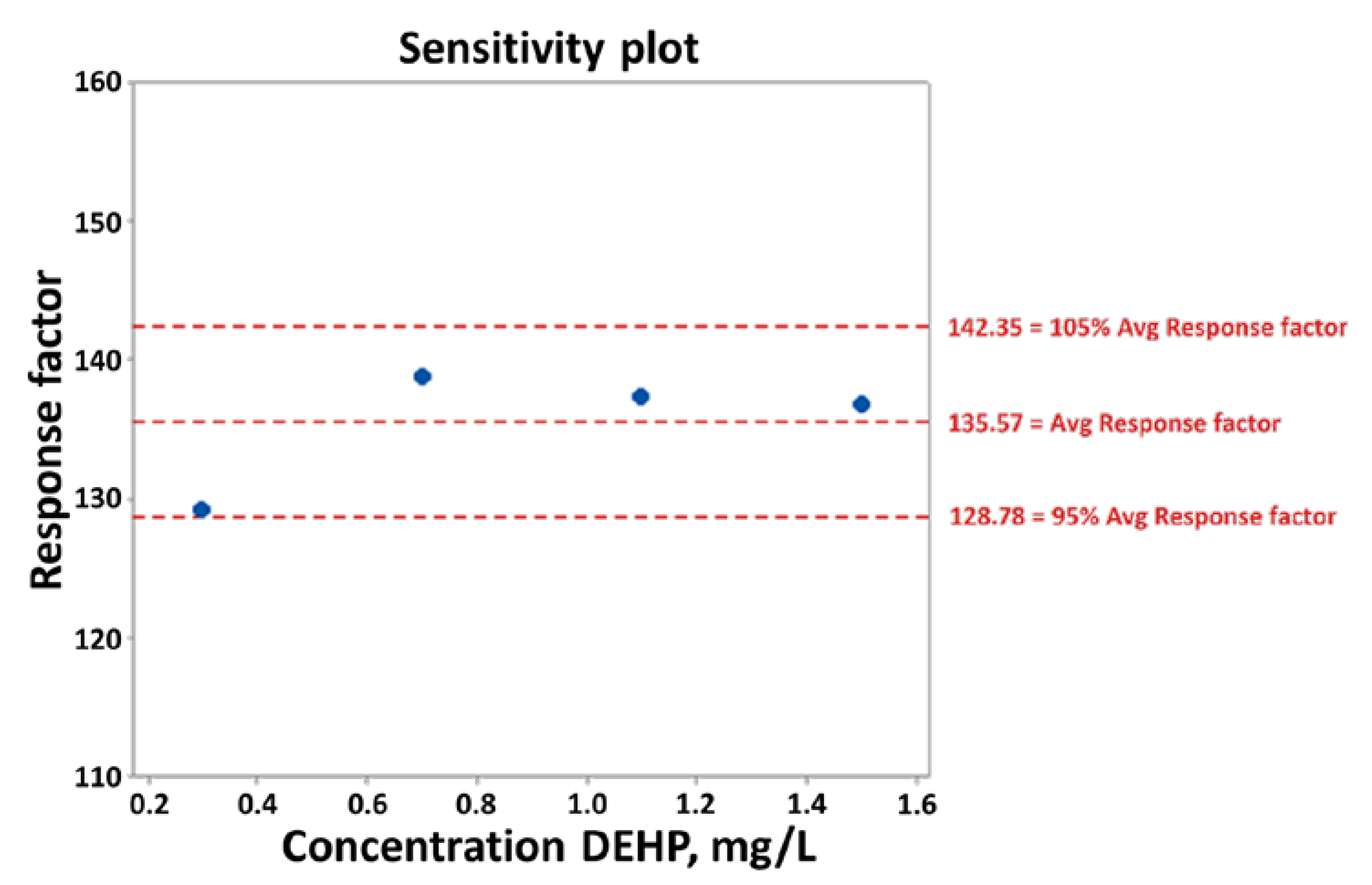
3.2.1. Statistical Data Checks
3.2.2. Simple Linear Regression
3.2.3. Linearity Checks (Linear Range)
3.3. Limit of Detection (LOD) and Limit of Quantification (LOQ)
3.4. Accuracy
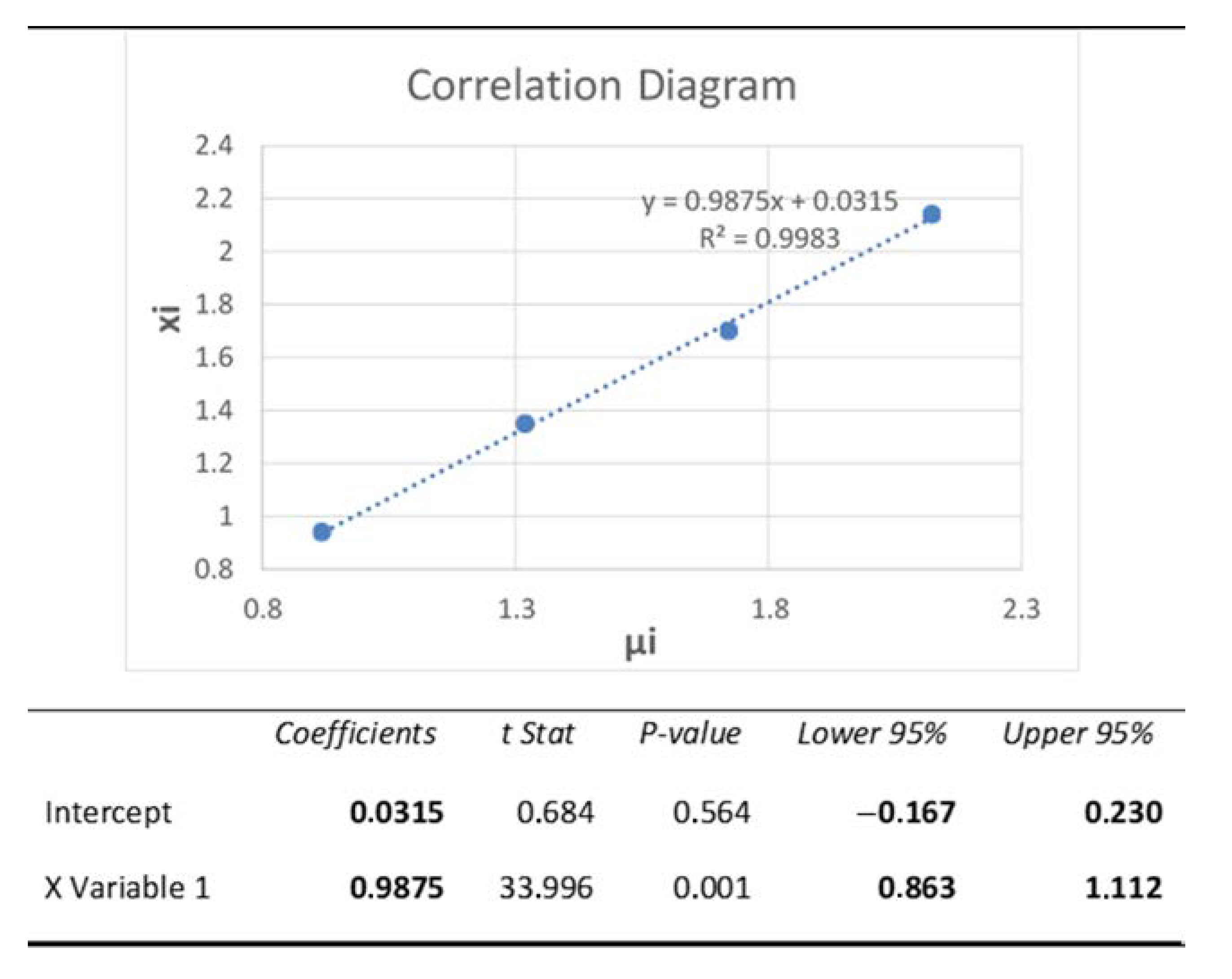
- For the slope b = 0.9875: H0: b = 1 vs. HA: b ≠ 1, to ascertain whether the value of b is statistically equal to monad, the 95% confidence interval of b should contain monad. From the regression analysis table, Figure 8 (below), CI 95% = (0.863; 1.112). Since CI includes monad we accept the null hypothesis, H0: b = 1. Therefore, we conclude that there is no “proportional” systematic error.
- For the intercept a = 0.0315: H0: a = 0 vs. HA: a ≠ 0, to ascertain whether the value of a is statistically equal to zero, the 95% confidence interval of a should contain zero. From the regression analysis table, Figure 8 (below), CI 95% = (−0.167; 0.230). Since CI includes zero, we accept the null hypothesis, H0: a = 0. Therefore, we conclude that there is no “standard” systematic error [9].
3.5. Precision
- Repeatability:
- −
- Standard deviation.
- −
- Relative standard deviation, from equation = 2.3%, as = 1.07 mg/L the average of the measurements in Table 7.
- −
- Limit of repeatability, from equation : rs = 0.069 mg/L, for two repeated measurements under repeatability conditions and 95% significance level.
- Intermediate precision:
| ANOVA: DEHP mg/L versus Day |
|---|
| Factor Type Levels Values |
| day random 8 1; 2; 3; 4; 5; 6; 7; 8 |
| Analysis of Variance for DEHP mg/L |
| Source DF SS MS F P |
| day 7 0.0122750 0.0017536 2.86 0.082 |
| Error 8 0.0049000 0.0006125 |
| Total 15 0.0171750 |
| S = 0.0247487 R-Sq = 71.47 R-Sq(adj) = 46.51% |
| Expected Mean |
| Square for Each |
| Term (using |
| Variance Error unrestricted |
| Source component term model) |
| 1 day 0.00057 2 (2) + 2 (1) |
| 2 Error 0.00061 (2) |
3.6. Range
3.7. Ruggedness
| Experiment | Factors | mg/L DEHP | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | |||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.07 | 1.03 |
| 2 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 1.00 | 1.02 |
| 3 | 1 | 2 | 2 | 1 | 1 | 2 | 2 | 1.03 | 1.03 |
| 4 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 1.00 | 1.05 |
| 5 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1.07 | 1.04 |
| 6 | 2 | 1 | 2 | 2 | 1 | 2 | 1 | 1.04 | 1.06 |
| 7 | 2 | 2 | 1 | 1 | 2 | 2 | 1 | 1.05 | 1.07 |
| 8 | 2 | 2 | 1 | 2 | 1 | 1 | 2 | 1.09 | 1.03 |
3.8. Assessment of Uncertainty
3.8.1. Calculation ubias,N
3.8.2. Calculation u(Rw)
3.8.3. Calculation of Combined Relative Uncertainty by NORDTEST
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Leebowitz, J.N.; Sarmiento, R.; Dugar, S.M.; Ethridge, M.W. Determination of six common phthalate plasticizers in grain neutral spirits and vodka. J. AOAC Int. 1995, 78, 730–735. [Google Scholar] [CrossRef]
- EU Commission Regulation No 10/2011. On plastic materials and articles intended to come into contact with food. Off. J. Eur. Union 2011.
- EU Commission Regulation No 2019/787. Definition, description, presentation and labelling of spirit drinks, the use of the names of spirit drinks in the presentation and labelling of other foodstuffs, the protection of geographical indications for spirit drinks, the use of ethyl alcohol and distillates of agricultural origin in alcoholic beverages, and repealing Regulation (EC) No 110/2008. Off. J. Eur. Union 2019.
- Del Carlo, M.; Pepe, A.; Sacchetti, G.; Compagnone, D.; Mastrocola, D.; Cichelli, A. Determination of phthalate esters in wine using solid-phase extraction and gas chromatography–mass spectrometry. Food Chem. 2008, 111, 771–777. [Google Scholar] [CrossRef]
- Russo, M.V.; Notardonato, I.; Avino, P.; Cinelli, G. Determination of phthalate esters at trace levels in light alcoholic drinks and soft drinks by XAD-2 adsorbent and gas chromatography coupled with ion trap-mass spectrometry detection. Anal. Methods 2014, 6, 7030–7037. [Google Scholar] [CrossRef]
- Shabir, G.A. Step-by-step analytical methods validation and protocol in the quality system compliance industry. J. Valid. Technol. 2005, 10, 314–325. [Google Scholar]
- Magnusson, B.; Örnemark, U. Eurachem Guide: The Fitness for Purpose of Analytical Methods—A Laboratory Guide to Method Validation and Related Topics, 2nd ed.; EURACHEM: Geel, Belgium, 2014; ISBN 978-91-87461-59-0. Available online: www.eurachem.org (accessed on 1 February 2020).
- Guideline, I.H.T. Validation of analytical procedures: Text and methodology. Q2 (R1) 2005, 1, 5. [Google Scholar]
- Koupparis, M. Open Courses University of Athen. 2017. Available online: http://opencourses.uoa.gr/modules/units/?course=CHEM100&id=2283 (accessed on 26 February 2023).
- Thompson, M.; Wood, R. Harmonized guidelines for internal quality control in analytical chemistry laboratories (Technical Report). Pure Appl. Chem. 1995, 67, 649–666. [Google Scholar] [CrossRef]
- Ermer, J.; Miller, J.H.M. Method Validation in Pharmaceutical Analysis: A Guide to Best Practice; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Taguchi, G.; Konishi, S. Taguchi Methods, Orthogonal Arrays and Linear Graphs, Tools for Quality Engineering; American Supplier Institute: Bingham Farms, MI, USA, 1987; pp. 35–38. [Google Scholar]
- Ellison, S.L.; Williams, A. Quantifying Uncertainty in Analytical Measurement; Eurachem/CITAC: Teddington, UK, 2012. [Google Scholar]
- Magnusson, B.; Naykki, T.; Hovind, H.; Krysell, M. NORDTEST Technical Report 537: Handbook for Calculation of Measurements Uncertainty in Environmental Laboratories; NORDTEST: Norbic, Oslo, 2012. [Google Scholar]
- Krause, S. Good analytical method validation practice, part I: Setting-up for compliance and efficiency. J. Valid. Technol. 2002, 9, 23–32. [Google Scholar]
- Association of Analytical Communities. Peer-Verified Methods Program, Manual on Policies and Procedures; Association of Analytical Communities: Rockville, MD, USA, 1998. [Google Scholar]
- Kaiser, H.J.; Ritts, B. Validation of Analytical Methods Used in Cleaning Validation. J. Valid. Technol. 2006, 10, 15–30. [Google Scholar]
- Danzer, K.; Currie, L. Guideline for calibration in analytical chemistry—Part 1. Fundamentals and single component calibration (IUPAC Recommendations 1998). Pure Appl. Chem. 1998, 70, 993–1014. [Google Scholar] [CrossRef]
- Barwick, V. Preparation of Calibration Curves-A Guide to Best Practice; LGC: Teddington, UK, 2003. [Google Scholar]
- Shrivastava, A.; Gupta, V.B. Methods for the determination of limit of detection and limit of quantitation of the analytical methods. Chron. Young Sci. 2011, 2, 21–25. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Espejo, F.; Armada, S. Determination of volumetric coefficients of thermal expansion in alcoholic beverages and aqueous ethanol–sucrose mixtures by differential volume measurements. Food Bioprocess Technol. 2012, 5, 2805–2818. [Google Scholar] [CrossRef]

| Factor | Levels | ||
|---|---|---|---|
| Regular Value | Deliberate Change | ||
| 1 | 2 | ||
| A | Concentration of methanol solution in acetonitrile | 1.00% | 0.99% |
| Β | Gradient of mobile phase solvents: A: Ultrapure water B: Acetonitrile with 1% methanol | −3 min A: 37.5%, B: 62.5% −10 min A: 0%, B: 100% −20 min A: 0%, B: 100% −22 min A: 37.5%, B: 62.5% | −3 min A: 36.5%, B: 63.5% −10 min A: 1%, B: 99% −20 min A: 1%, B: 99% −22 min A: 36.5%, B: 63.5% |
| C | Mobile phase flow rate | 1.00 mL/min | 0.98 mL/min |
| D | Column oven temperature | 25.0 °C | 25.5 °C |
| E | Wave length | 225 nm | 226 nm |
| Experiment | Parameter | ||||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 2 | 2 | 2 | 2 |
| 3 | 1 | 2 | 2 | 1 | 1 | 2 | 2 |
| 4 | 1 | 2 | 2 | 2 | 2 | 1 | 1 |
| 5 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| 6 | 2 | 1 | 2 | 2 | 1 | 2 | 1 |
| 7 | 2 | 2 | 1 | 1 | 2 | 2 | 1 |
| 8 | 2 | 2 | 1 | 2 | 1 | 1 | 2 |
| A’ part | Concentration Level | Duplicate Per Level | DEHP Concentration, mg/L | Area |
| 1 | 1 | 0.3 | 34.65 | |
| 1 | 2 | 0.3 | 41.72 | |
| 1 | 3 | 0.3 | 39.98 | |
| 2 | 1 | 0.7 | 96.47 | |
| 2 | 2 | 0.7 | 99.12 | |
| 2 | 3 | 0.7 | 95.86 | |
| 3 | 1 | 1.1 | 148.80 | |
| 3 | 2 | 1.1 | 153.69 | |
| 3 | 3 | 1.1 | 150.97 | |
| 4 | 1 | 1.5 | 205.14 | |
| 4 | 2 | 1.5 | 207.12 | |
| 4 | 3 | 1.5 | 203.34 | |
| B’ part | SUMMARY | |||
| DEHP Concentration, mg/L | Mean Value Area | Standard Deviation, s | RSD,% | |
| 0.3 | 38.78 | 3.684 | 9.498 | |
| 0.7 | 97.15 | 1.733 | 1.784 | |
| 1.1 | 151.15 | 2.450 | 1.621 | |
| 1.5 | 205.20 | 1.891 | 0.921 | |
| Xi,sp | Known Concentration, μi (μi = xi, sp + x0, x0 = 0.62) | Method under Validation, xi |
|---|---|---|
| 0.3 | 0.92 | 0.94 |
| 0.7 | 1.32 | 1.35 |
| 1.1 | 1.75 | 1.70 |
| 1.5 | 2.12 | 2.14 |
| Day: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DEHP mg/L: | 1.11 | 1.05 | 1.09 | 1.06 | 1.04 | 1.01 | 1.07 | 1.09 | 1.05 | 1.03 | 1.10 | 1.06 | 1.10 | 1.14 | 1.04 | 1.06 |
| Analysis of Variance |
|---|
| Source DF Adj SS Adj MS F-Value p-Value |
| A 1 0.003025 0.003025 5.48 0.041 |
| B 1 0.000025 0.000025 0.05 0.836 |
| C 1 0.000100 0.000100 0.18 0.680 |
| D 1 0.000625 0.000625 1.13 0.313 |
| E 1 0.000400 0.000400 0.72 0.415 |
| Error 10 0.005525 0.000553 |
| Lack-of-Fit 2 0.000625 0.000313 0.51 0.619 |
| Pure Error 8 0.004900 0.000613 |
| Total 15 0.009700 |
| Measurement | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| recovery Ri% | 93 | 94 | 93 | 91 | 95 | 91 | 92 | 97 | 95 | 92 | 91 | 91 |
| Measurement | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | |
| recovery Ri% | 93 | 94 | 91 | 90 | 94 | 91 | 92 | 92 | 93 | 94 | 91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gemenetzis, E.G.; Alygizakis, N.A. Development and Validation of an HPLC-UV Method for the Determination Bis(2-ethylhexyl) Phthalate Ester in Alcoholic Beverages. Appl. Sci. 2023, 13, 3194. https://doi.org/10.3390/app13053194
Gemenetzis EG, Alygizakis NA. Development and Validation of an HPLC-UV Method for the Determination Bis(2-ethylhexyl) Phthalate Ester in Alcoholic Beverages. Applied Sciences. 2023; 13(5):3194. https://doi.org/10.3390/app13053194
Chicago/Turabian StyleGemenetzis, Evangelos G., and Nikiforos A. Alygizakis. 2023. "Development and Validation of an HPLC-UV Method for the Determination Bis(2-ethylhexyl) Phthalate Ester in Alcoholic Beverages" Applied Sciences 13, no. 5: 3194. https://doi.org/10.3390/app13053194
APA StyleGemenetzis, E. G., & Alygizakis, N. A. (2023). Development and Validation of an HPLC-UV Method for the Determination Bis(2-ethylhexyl) Phthalate Ester in Alcoholic Beverages. Applied Sciences, 13(5), 3194. https://doi.org/10.3390/app13053194







