Study of the Interaction between Regular Waves and a Wind-Fish Combined Structure

Abstract

The combination of a wind turbine and fish cage (wind-fish) is able to solve the complex issue of power supply for deep-sea aquaculture. Nevertheless, the hydrodynamic coupling between the fish cage and the wind turbine foundation is increasingly complex, and there is little research on the related hydrodynamics. In this paper, the hydrodynamic research on the wind turbine foundation and fish cage structure is carried out using numerical simulation, in which the porous medium model is adopted to simulate the effects of the fish cage on the flow field. By analyzing the hydrodynamic characteristics of the combined structure of an offshore wind turbine and aquaculture cage under the action of regular waves, the load on both the cage in the combined structure and the wind turbine foundation, and the overall load on the combined structure of offshore wind turbine and cage are obtained. The effects of wave parameters, structural dimensions, cage submergence depth, and biological attachment on cage load, wind turbine foundation load, and overall load of the combined structure are analyzed. The results demonstrate that the wind turbine foundation is persistently the central part of the combined structure. The wave height, water depth, and degree of attachment of marine organisms all have different effects on the amplitude of the structural load. In contrast, the wave period, cage geometry, and cage submergence depth have no significant effects on the amplitude of the structural load. In addition to the water depth, other factors will affect the proportion of the load on the wind turbine foundation and the total load as well.

1. Introduction

On one hand, deep-sea aquaculture reduces the negative impact of fisheries on the environment. On the other hand, it provides a more natural aquaculture environment; therefore, it can obtain fishery products with better quality, which is more advantageous than offshore aquaculture [1]. However, as deep-sea aquaculture is far from the coast, how to supply power for deep-sea aquaculture facilities has become a vital issue restricting the development of deep-sea aquaculture. The combination of wind turbines and fish cages can solve the complex power supply problem of deep-sea cage culture. Nonetheless, since the marine ranching and offshore wind power are located in the same sea area, it remains unknown whether the hydrodynamic forces between them will have adverse effects on each other. Therefore, it is urgent to carry out a hydrodynamic analysis of the combined deep-sea aquaculture cage and wind turbine structure, to explore the hydrodynamic characteristics of the deep-sea aquaculture structure and wind turbine foundation, and to provide necessary technical support for the subsequent research and implementation of far-reaching offshore wind farms and marine ranching.

Great progress has been made in the research of offshore wind turbines and fish cages. At present, a series of numerical simulation methods have been established to study the hydrodynamic characteristics of a wind turbine foundation, employing ANSYS software to calculate the stress and strain changes, and to analyze the influence of tower top mass, wind turbine structure gravity, and seawater on the natural frequency of the wind turbine foundation structure [2,3]. The finite element software ABAQUS is also used to analyze the dynamic response of offshore wind turbines [4]. Several numerical simulation models of wind turbines coupled with hydrodynamic forces have been proposed to identify the damping of the wind turbine foundation mode [5]. The hydrodynamic characteristics of offshore wind turbines under wave, wind, tidal current and extreme sea conditions have also been numerically simulated and analyzed [6,7,8,9,10]. In addition, the dynamic characteristics of the offshore wind turbine supporting structures under different wave steepness parameters [11,12], water depth parameters [13,14,15], and wave loads [16,17,18] are widely studied.

For the study of hydrodynamic characteristics of cages in marine pastures, the numerical simulation methods extensively used to simulate mesh structure mainly include the modal analysis method [19,20] and the porous medium method [21], whose effectiveness is verified by comparison with the experimental results. A series of studies have been carried out on the hydrodynamic characteristics of the cage under different sea conditions. Kristiansen et al. explored the load variation of aquaculture cages and mooring devices under the combined action of waves and currents, as well as the sensitivity of numerical results to multiple parameters and models, and came to the conclusion that the cage devices did not need to use extremely fine numerical grids [22,23,24]. Xu et al. [25,26,27] established the finite element model of the cage structure under the action of waves, analyzed the deformation and stress of the cage in regular waves, and predicted the stress of the net panels under extreme wave action. Lader et al. discussed the dynamic characteristics of the cage under the action of regular waves, irregular waves and water flow by numerical simulation [28,29,30]. Moreover, the submergence characteristics of a single-point mooring (SPM) cage system under the action of regular waves [31] and random waves [32] were investigated. It was found that the cage system has an obvious response to the increase in wave height; the degree of submergence of irregular waves is less than that of regular waves, and the cage is in a dynamic stable state after submergence. Ma et al. developed a semi-analytical solution to investigate the wave interference and corresponding dynamic responses of the submerged flexible fish cage array [33]. Liu et al. analyzed the yield and fatigue phenomena of the cage floating structure under excessive and long-term wave loads [34]. Mjåtveit et al. simulated two types of typical gravity cages, with circular and square shapes, for the purpose of comparing their cage deformations, cultivation volumes, and towing forces under different current conditions [35]. Cheng et al. conducted time-domain simulations to study the effects of the main design parameters on cage culture quantity and resistance [36]. Wang et al. investigated the tensions within the net twines, the loads on the connectors and the cross-sectional forces/moments on the main steel structures of vessel-shaped fish cages [37].

Previous studies are almost a separate exploration of the hydrodynamic characteristics of wind turbines or cages. The research on the combination of wind turbines and cages is in the preliminary stage of development. The combined structure of fixed offshore wind turbines and deep-water and offshore aquaculture cages has significant advantages of efficient space utilization and sufficient combination between structures. However, the interaction mechanism between structures and the influence mechanism of the marine environment on structures are extremely complex. It is difficult to carry out field measurement and physical model test, and the research cost is also quite high. Currently, there are many basic technical problems which need to be explored and solved in depth and in detail. Therefore, it is necessary to use the numerical simulation method in this paper to study the hydrodynamic characteristics of the combined structure of a deep-sea aquaculture cage with fixed offshore fan under the action of waves, and to study the effect of wave factors and cage size on the combined structure. Therefore, it is necessary to study not only the hydrodynamic characteristics of the combined structure of offshore wind turbines and cages under wave action using the numerical simulation method in this paper, but also the effect of wave factors and cage size on the stress of the combined structure.

2. Numerical Simulation

To simulate the hydrodynamic characteristics of the combined structure of offshore wind turbines and marine ranches under the action of waves, a three-dimensional numerical wave flume capable of generating regular waves is established based on the Navier–Stokes equation in this paper. On the basis of the multiphase flow solver in OpenFOAM, the control equations of the offshore wind turbine and cage combined structures are solved. For the purpose of improving the calculation efficiency, the porous medium model is used to simulate the cage part of the combined structure.

2.1. Control Equation

In this paper, the load and flow field of the combined structure of wind turbine and cage under wave action are studied in a numerical wave tank. The fluctuation is described by the Reynolds-Averaged Navier–Stokes equations (RANS) as follows [38],

Continuity equation:

$$\frac{\partial u_i}{\partial x_i}=0$$

(1)

Momentum equation:

$$\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left[(v+v_t)(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i})\right]+g_i$$

(2)

where u is the velocity; x is the coordinate; p is the pressure; g is the gravitational acceleration; t is the time; and ρ is the fluid density.

The porous medium model is used to simulate the cage structure in the ocean The control equation of the cage is mainly based on the corresponding control equation of the wave field, adding porosity and introducing Darcy’s law. See Formulas (3) and (4) for the specific control equation [39].

Continuity equation:

$$\rho \frac{\partial u_i}{\partial x_i}=0$$

(3)

Momentum equation:

$$\frac{\partial }{\partial t}(\rho u_i)+u_j\frac{\partial }{\partial x_j}(\rho u_i)=-\frac{\partial p}{\partial x_i}+\rho g_i+\mu (\frac{{\partial }^2{u}_i}{\partial x_j^2}+\frac{{\partial }^2{u}_j}{\partial x_i^2})+S_i$$

(4)

where ρ is the fluid density; μ is the momentum viscosity of the fluid; u_i and u_j are average velocity components; t is the time; p is the pressure; ν is the velocity vector; g_i is the acceleration of gravity; i and j are 1, 2, 3, etc.; and S_i is the source term of the momentum equation in porous medium.

2.2. Porous Media Model

The fish cage is an integral part of the combined structure, and the wire in the mesh structure can be regarded as a small cylinder. Several small cylinders are connected into a mesh through nodes. Due to the large number of small cylinders, it will be a great burden for numerical simulation if it is directly simulated and calculated. Therefore, this paper adopts the porous medium model (see Figure 1 for the schematic diagram) to simulate the flow-blocking effect of the mesh and selects a reasonable flow-blocking coefficient to make the porous medium have the same flow-blocking effect as mesh.

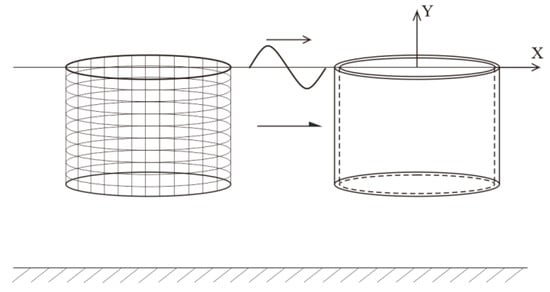
Figure 1. Schematic diagram of porous medium model.

Outside the porous medium region, the source term S_i in the momentum equation is equal to 0. In the porous medium region, Forchheimer put forward the expression of pressure gradient when water flows through the porous medium region at a certain velocity based on Darcy’s law in 1901. The calculation of S_i is shown in Formulas (5)–(7),

$$S_i=a{u}_i+b\left|u_i\right|u_i=-(\lambda D+\frac{1}{2}\rho \overrightarrow{\left|u\right|}{F}_{ij})\overrightarrow{u}$$

(5)

$$S_i=-C_{ij}\frac{1}{2}\rho \left|\overrightarrow{u}\right|\overrightarrow{u}$$

(6)

$$C_{ij}=\left(\begin{array}{ccc}{C}_n& 0& 0\\ 0& C_t& 0\\ 0& 0& C_t\end{array}\right)$$

(7)

where a and b are constant coefficients; λ is the thickness of the porous medium; D is the cylinder diameter; C_ij is the porosity coefficient matrix of the porous medium; C_n is the normal resistance coefficient; C_t is the tangential resistance coefficient, and porosity coefficient is expressed in m⁻¹.

The directions of resistance F_d and lift F_l of the porous medium are parallel and perpendicular to the flow direction, respectively. See Formulas (8) and (9) for specific expressions [39],

$$\overrightarrow{F_d}=C_n\frac{1}{2}\rho \lambda A\left|\overrightarrow{u}\right|\overrightarrow{u}$$

(8)

$$\overrightarrow{F_l}=C_t\frac{1}{2}\rho \lambda A\left|\overrightarrow{u}\right|\overrightarrow{u}$$

(9)

where λ and A is the thickness and the area of porous medium, respectively. In addition, the drag and lift can also be calculated by empirical formulas, as shown in Formulas (10) and (11),

$$F_d=\frac{1}{2}\rho C_{d}A{u}_0^2$$

(10)

$$F_l=\frac{1}{2}\rho C_{t}A{u}_0^2$$

(11)

where u₀ is the free flow rate.

The drag coefficient C_d and lift coefficient C_t can be calculated as follows,

$$C_d=(1+10{\mathrm{Re}}^{-2/3})\left(8.03S_n{}^2-0.74S_n+0.12\right)$$

(12)

$$C_l=\left(0.57S_n-3.54S_n{}^2+10.1S_n{}^3\right)\sin \left(2\alpha \right)$$

(13)

where α is the angle of attack of the mesh, that is, the angle between the mesh and the direction of water flow on the horizontal plane; and S_n is the net solidity. When the mesh is perpendicular to the direction of water flow, and its resistance values at different flow velocities are known, C_n can be obtained by fitting the curve between the cage resistance and the flow velocity with the least square method.

2.3. Calculation Method of Structural Load

The ratio D/L of the cross-sectional dimension D to the wavelength L of offshore wind turbine foundation is less than 0.2. For small-scale cylindrical structures, the empirical formula proposed by Morison in 1950 is commonly used to calculate the wave loads. See Formula (14) for the calculation of the total wave force f,

$$f=f_D+f_I=\frac{1}{2}{C}_D{\rho }_{w}D{u}_x\left|u_x\right|+C_M\rho \frac{\pi D^2}{4}\frac{\partial u_x}{\partial t}$$

(14)

where f_D is the horizontal drag force; f_I is the horizontal inertial force; u_x is the velocity component; D is the diameter of the column; ρ_w is the density of seawater; C_D and C_M are the drag force coefficient and inertia force coefficient, respectively. According to the suggestion of Code for Classification and Construction of Fixed Offshore Platforms, C_D equal to 1.2 and C_M equal to 2.0 are selected in this paper.

2.4. Free Surface Tracking

The VOF method has the advantages of small storage, favorable form, and less calculation error, so this paper selects the VOF method as the free surface tracking method. The VOF uses a scalar function between 0 and 1 to simulate the position of a free surface, where 0 indicates that the grid is filled with gas, and 1 means that the grid is filled with liquid. Except for these two aforementioned cases, it is considered that there is an interface between the two fluids in the grid, namely, the free surface. The density and viscosity of the fluid in a single grid are shown in Formula (15),

$$\begin{array}{l}\rho =\alpha {\rho }_w+(1-\alpha ){\rho }_a\\ \mu =\alpha {\mu }_w+(1-\alpha ){\mu }_a\end{array}$$

(15)

where ρ_w and ρ_α is the density of water and air, respectively; μ_w and μ_α is the dynamic viscosity of water and air, respectively; α is the ratio of unit water volume to grid volume; α_w is the volume fraction of water; and α_a is the volume fraction of air. The volume fractions α_w and α_a can be obtained by calculation, as shown in Formula (16),

$$\begin{array}{c}\frac{\partial {\alpha }_w}{\partial t}+\frac{\partial u_f{\alpha }_w}{\partial x_i}+\frac{\partial u_{c,i}{\alpha }_w(1-{\alpha }_w)}{\partial x_i}=0\\ {\alpha }_a=1-{\alpha }_{ve}\end{array}$$

(16)

$$u_{c,i}=\min \left[c_{\alpha }\left|u_i\right|\max (\left|u_i\right|)\right]$$

(17)

where $\frac{\partial u_{c,i}\alpha (1-\alpha )}{\partial x_i}$ is the manual compression item; u_c,i is the artificial compression speed to keep the interface sharp; and c_a is the coefficient, which is usually 1 by default.

2.5. Numerical Wave Making and Wave Attenuation

Waves2Foam, a third-party wave-making and wave-absorbing tool based on the C++ environment, has been extensively used on the OpenFOAM platform, so this paper applies Waves2Foam to simulate the wave generation and wave absorption.

(1)

Regular wave generation

The horizontal velocity distribution of the numerical wave tank is as follows:

$$u(x,z,t)=H\omega [\frac{\cosh k(z+h)}{\sinh kh}\cos (kx-\omega t)+\frac{3}{4}Hk\frac{\cosh 2k(z+h)}{{\sinh }^{4}kh}\cos (2kx-2\omega t)]$$

(18)

The velocity distribution in the vertical direction, that is, the velocity distribution in the water depth direction is described as:

$$w(x,z,t)=H\omega [\frac{\sinh k(z+h)}{\sinh kh}\sin (kx-\omega t)+\frac{3}{4}Hk\frac{\sinh 2k(z+h)}{{\sinh }^{4}kh}\sin (2kx-2\omega t)]$$

(19)

The wave surface of the wave is expressed as:

$$\eta =H\left[-\frac{Hk}{2\sinh 2kh}+\cos (kx-\omega t)+\frac{Hk}{4}\frac{\cosh kh(2{\cosh }^{2}kh+1)}{{\sinh }^{3}kh}\cos (2kx-2\omega t)\right]$$

(20)

where $\omega$ is the frequency of the wave; k is the number of waves; H is the wave amplitude; and h is the water depth of the numerical flume.

(2)

Wave elimination

The Waves2Foam solver uses a relaxation zone for wave attenuation, and defines the relaxation function in the solver, as shown in Formula (21).

$$\begin{array}{l}{\chi }_R(\xi )=1-\frac{\exp ({\xi }^{3.5})-1}{\exp (1)-1}\\ \xi \in \left[0,1\right]\end{array}$$

(21)

This function makes the values of the starting point of the relaxation zone 1, the ending point 0, and the middle of the relaxation zone between 0 and 1. In the relaxation zone, the velocity of fluid and the volume fraction of the wave surface are constantly updated in time steps. See Formula (22) for the specific expression,

$$\psi ={\chi }_R{\psi }_{computed}+(1-{\chi }_R){\psi }_{t\arg et}$$

(22)

where $\psi$ is the volume fraction or velocity of the fluid; ${\psi }_{computed}$ is the updated volume fraction or velocity calculated in real time in the relaxation zone; and ${\psi }_{t\arg et}$ is the theoretical value corresponding to the entrance, with the exit value of 0. Figure 2 is the schematic diagram of fluid volume fraction. The value of the volume fraction is mainly based on the relative position from the static water surface, which is 0 above the static water surface and 1 below it.

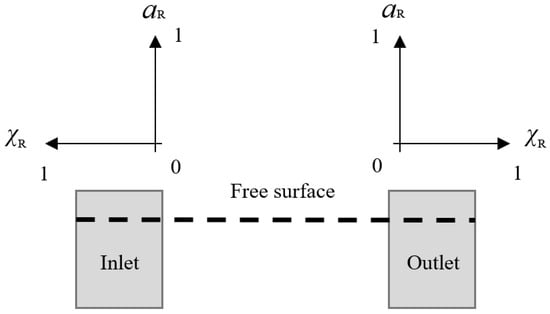
Figure 2. Schematic diagram of fluid volume fraction.

2.6. Model Settings and Boundary Conditions

A scale model of 1:30 is used for numerical simulation. Figure 3 implies an established numerical wave flume with a length of 15 m, a width of 4 m, and a height of 2 m. The diameter D of the cage is 2 m, while that of the wind turbine foundation is 0.17 m, placed in the center of the bottom of the sink. The cage height H is 0.5 m, the length of the wave-making area is 4 m, and the length of the wave-absorbing area is 5 m. Three wave height meters are arranged in front, inside, and behind the combined structure along the x-direction of the center line.

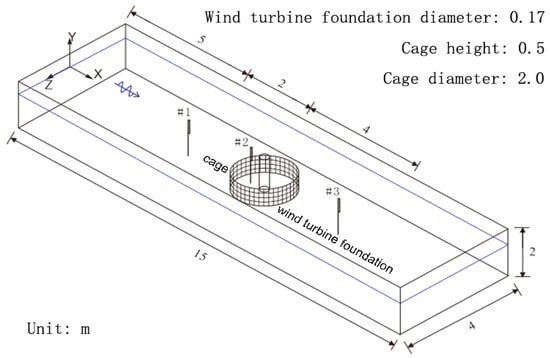
Figure 3. Boundary conditions of numerical flume.

The inlet boundary of the numerical flume is defined as the wave inlet boundary, while the outlet at the right end is the wave outlet boundary, and the boundary between the top of the numerical flume and the air is the free outflow boundary. The pressure condition is the total boundary condition obtained according to the velocity and atmospheric pressure. For the side wall and bottom surface of the numerical flume, they are identifiable fixed nonslip boundaries. The foundation structure of the wind turbine adopts an impenetrable nonslip boundary. The mesh arrangement of the numerical flume is given in Figure 4. Both the horizontal mesh size and the vertical mesh size are 0.02 m, and the mesh around the water surface and the structure is refined.

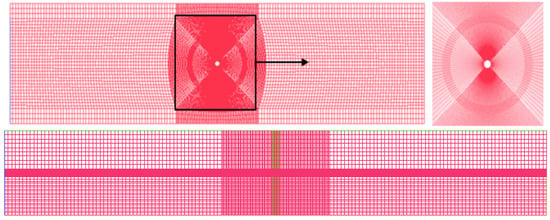
Figure 4. The mesh arrangement of the numerical flume with wind-fish combined structure.

3. Results

The hydrodynamic characteristics of the combined structure of offshore wind turbines and deep-sea aquaculture cages under the action of regular waves are explored. The effects of different wave parameters (wave height, period, and water depth), structure size, structure location (i.e., the diving depth of the cage), as well as biological attachment on the structural load are analyzed.

3.1. Wave Environmental Factors

The hydrodynamic load of the wind-fish combined structure is an important component of the structural design, and the wave environmental factors have a significant influence on the hydrodynamic load. Therefore, it is beneficial to understand the influence of wave environmental factors on the design of the wind-fish combined structure. A total of seven wave conditions with three different wave heights, three different periods and three different water depths are set up to compare the effects of wave heights, wave periods and water depths on structural loads. Specific design parameters are shown in Table 1. The cage height H_net is 0.5 m, the diameter D_net is 2 m and the net solidity Sn is 0.27.

Table 1. Regular wave environment parameters.

No.	Wave Height (m)	Period (s)	Water Depth (m)	Wave Steepness	Submergence Depth (m)
1	0.10	1.4	1.0	0.034	0
2	0.12	1.4	1.0	0.040	0
3	0.14	1.4	1.0	0.047	0
4	0.12	1.2	1.0	0.054	0
5	0.12	1.6	1.0	0.032	0
6	0.12	1.4	1.4	0.039	0
7	0.12	1.4	1.8	0.039	0

Note: (1) Wave conditions 1–3 are mainly used to explore the influence of different wave heights on the load of combined structures and individual structures. (2) Wave conditions 2, 4, and 5 are mainly used to explore the influence of different periods on the load of combined structures and individual structures. (3) Wave conditions 2, 6, and 7 are mainly used to explore the influence of different water depths on the load of combined structures and individual structures.

Figure 5, Figure 6 and Figure 7 depict the time domain curve and frequency domain diagram of the combined structure under different wave heights, periods, and water depths. It can be seen from the comparison that the horizontal wave load on the combined structure increases with the increase in wave height. The change of wave period has little effect on the horizontal wave load on the combined structure, whereas with the variation of water depth, the horizontal wave load on the combined structure increases slowly, and the wave crest occurs slightly earlier. In the frequency domain diagram, one times the frequency is inertial force, and two times the frequency is drag force. The analysis illustrates that the inertial force dominates among the three, while the drag force is weak.

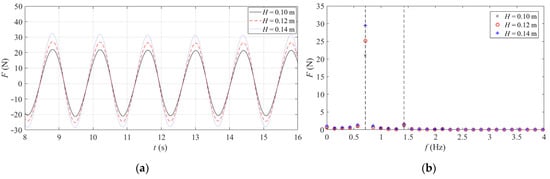
Figure 5. Load duration curve and spectrum of combined structure under different wave heights. (a) Time domain curve. (b) Frequency domain diagram.

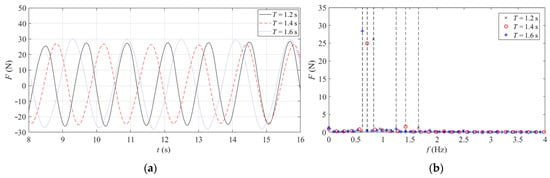
Figure 6. Load duration curve and spectrum diagram of combined structure under different periods. (a) Time domain curve. (b) Frequency domain diagram.

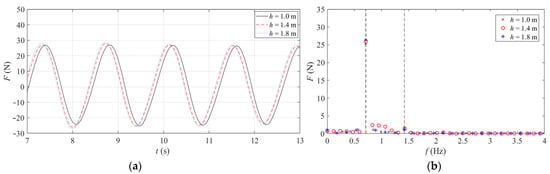
Figure 7. Load duration curve and spectrum of combined structure under different water depths. (a) Time domain curve. (b) Frequency domain diagram.

In the composite structure, the sensitivity of the horizontal load on cages and wind turbines to the change of wave factor is different. In order to explore the influence of different wave factors on the safety of the combined structures, Figure 8 is the distribution diagram of the hydrodynamic load of the combined structure under different wave heights, wave periods, and water depths. Table 2 shows the proportion of the maximum horizontal load on the wind turbine foundation.

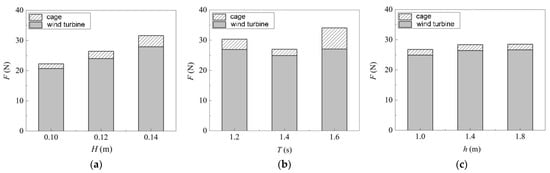
Figure 8. Hydrodynamic load distribution on the combined structure under different wave heights (a), wave periods (b), and water depths (c).

Table 2. Maximum horizontal load distribution and proportion of combined structure under different wave factors.

	Case No.	Wind Turbine Foundation Load (N)	Cage Load (N)	Proportion of Wind Turbine Load
Different wave heights	1	20.70	1.56	94%
	2	24.00	2.43	91.53%
	3	27.90	3.72	88.6%
Different periods	4	26.91	3.42	88.72%
	2	24.91	2.08	92.29%
	5	27.07	6.99	79.48%
Different water depths	2	24.91	1.86	93.05%
	6	26.42	1.95	93.13%
	7	26.65	1.86	93.48%

The results illustrate that with the increase in wave height, the proportion of the maximum horizontal load of offshore wind turbines gradually decreases from 94% to 88.6%, indicating that the cage has more obvious wave resistance. With the increase in the wave period, the maximum horizontal load proportion of the wind turbine foundation increases first and then decreases. Synchronously, the existence of the wind turbine foundation has a significant impact on the load on the cage in different periods. However, an increase in water depth does not significantly change the proportion of maximum horizontal load on the offshore wind turbines. In general, the load on the wind turbine foundation is obviously greater than that on the fish cage when the degree of adhesion of marine organisms to the fish cage is small.

3.2. The Influence of the Geometrical Dimensions of the Cage

The fish yield in the fish cage is affected by the dimensions of the cage. However, the dimensions of the cage are also determined by the power supply of the wind turbine. In addition, the hydrodynamic load on the fish cage can be also transferred to the foundation of the wind turbine. Thus, it is beneficial to understand the influence of the geometrical dimensions of the fish cage on the safety design of the combined structure. The diameter and height of the cage are important factors to be considered when designing cage dimensions. Three different cage heights and six different diameters of the cages are set in this paper, and the specific design parameters are shown in Table 3. The wave height is 0.12 m, the period is 1.4 s, the water depth is 1 m, and the cage is commonly at the liquid level.

Table 3. Size parameters of cage.

Case No.	Height of Cage (m)	Diameter of Cage (m)	Density of Cage	Submergence Depth (m)
8	0.3	2.0	0.27	0
9	0.5	2.0	0.27	0
10	0.7	2.0	0.27	0
11	0.5	1.2	0.27	0
12	0.5	1.4	0.27	0
13	0.5	1.6	0.27	0
14	0.5	1.8	0.27	0
15	0.5	2.2	0.27	0

Note: (1) Cases No. 8–10 are mainly used to explore the influence of different cage heights on the load of combined structures and individual structures; (2) Cases No. 9 and 11–15 are mainly to explore the influence of the diameter of the cage on the load of the combined structure and the individual structure.

The forces on the combined structure with different cage sizes are shown in Figure 9 and Figure 10. It can be seen that the increase in cage height does not significantly affect the horizontal wave load on the combined structure. An increase in the diameter of the cage results in no obvious change in the trend of the horizontal wave load on the composite structure. The inertial force dominates the load on a combined structure, while the drag force is weak.

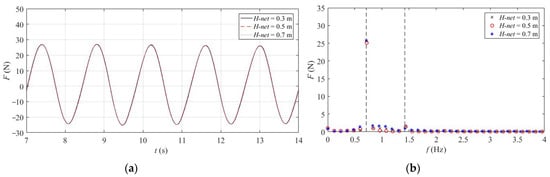
Figure 9. Load duration curve and spectrum of combined structure under different cage heights. (a) Time domain curve. (b) Frequency domain diagram.

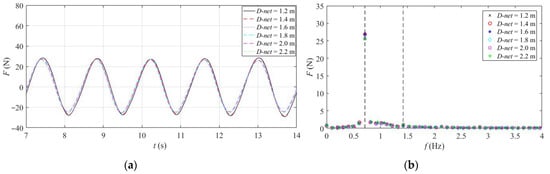
Figure 10. Load duration curve and spectrum of combined structure under different diameters of the cages. (a) Time domain curve. (b) Frequency domain diagram.

Table 4 and Figure 11 present the maximum horizontal load proportion. The results show that with the increase in cage height, the proportion of the maximum horizontal load of the wind turbine foundation gradually decreases from 93.28% to 91.06%, showing that the wave-making resistance of cage gradually increases, mainly because the increase in cage height increases the effective area of the cage. With the increase in the diameter of the cage, the proportion of the maximum horizontal load of the offshore wind turbine gradually increases from 80.21% to 93.67%, indicating that the influence of the cage’s wave resistance on the load on the wind turbine’s foundation structure is gradually reduced. The wind turbine foundation bears the primary load on the combined structure.

Table 4. Maximum horizontal load distribution and proportion of the combined structure under different cage heights and diameters.

	Case No.	Wind Turbine Foundation Load (N)	Cage Load (N)	Proportion of Wind Turbine Load
Different cage heights	8	24.97	1.80	93.28%
	9	24.91	2.08	92.67%
	10	24.94	2.45	91.06%
Different cage diameters	11	26.51	6.54	80.21%
	12	26.22	6.40	80.38%
	13	26.29	5.25	83.35%
	14	24.63	3.15	88.67%
	9	24.91	2.08	91.18%
	15	25.16	1.70	93.67%

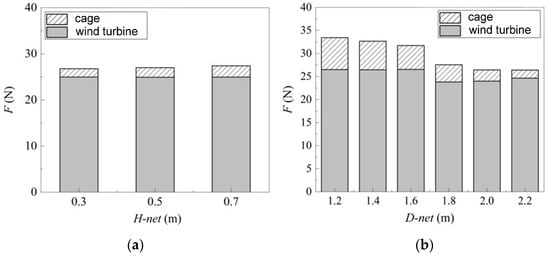
Figure 11. Hydrodynamic load distribution of the combined structure under different cage heights (a) and diameters (b).

3.3. Other Influencing Factors

As a permeable structure, long-term exposure to the marine environment and the attachment of marine organisms will also threaten the safety of the composite structure. Therefore, this paper studies the influence of different cage submergence depths and different degrees of attachment of marine organisms on the load on the combined structure. The degree of attachment of marine organisms mainly corresponds to different cage densities. In this paper, seven different cage submergence depths and two cage densities are set, and the specific design parameters are shown in Table 5. The wave height is 0.12 m, the period is 1.4 s, and the water depth is 1 m.

Table 5. Parameters of other influencing factors.

Case No.	Height of Cage (m)	Diameter of Cage (m)	Solidity of Cage	Submergence Depth (m)
16	0.5	2.0	0.27	0.00
17	0.5	2.0	0.27	0.04
18	0.5	2.0	0.27	0.06
19	0.5	2.0	0.27	0.08
20	0.5	2.0	0.27	0.30
21	0.5	2.0	0.27	0.60
22	0.5	2.0	0.27	0.90
23	0.5	2.0	0.13	0.00

Note: (1) Cases No. 16–22 mainly explore the influence of cage submergence depth on the load on the combined structure and individual structure. (2) Cases No. 16 and 23 mainly explore the influence of cage compactness on the load on combined structures and individual structures.

As can be seen from Figure 12 and Figure 13, with the increase in the diving depth of the cage, the horizontal wave load on the combined structure shows little change. The increase in the density of the cage will lead to an increase in the effective area; afterwards, the horizontal wave load on the combined structure will also increase. The load on the combined composite structure is still dominated by the inertial force, with a weak drag force.

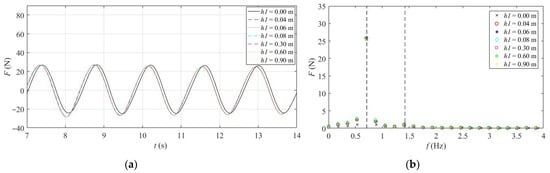
Figure 12. Load duration curve and spectrum of the combined structure under different cage submergence depths. (a) Time domain curve. (b) Frequency domain diagram.

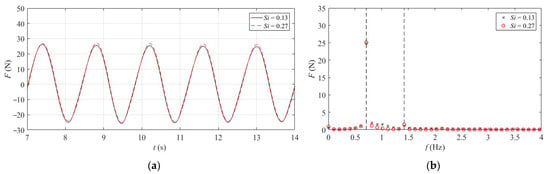
Figure 13. Load duration curve and spectrum diagram of combined structure under different levels of marine organism attachment. (a) Time domain curve. (b) Frequency domain diagram.

Table 6 and Figure 14 indicate the proportion of the maximum horizontal load on the wind turbine foundation under different submergence depths and cage plugging rates. The results portray that the proportion of the maximum horizontal load on offshore wind turbines gradually increases from 93.05% to 99.78% with the increase in the diving depth of the cage, indicating that the wave-blocking effect of the cage on the wind turbine foundation becomes weaker and weaker. However, with the increase in the degree of adhesion of marine organisms, the proportion of the maximum horizontal load on the offshore wind turbine decreases from 97.35% to 93.05%, demonstrating that increased adhesion of marine organisms increases the wave resistance of the cage.

Table 6. Distribution and proportion of the maximum horizontal load on the combined structure caused by different cage submergence depths and cage plugging rates.

	Case No.	Wind Turbine Foundation Load (N)	Cage Load (N)	Proportion of Wind Turbine Load
Different submergence depths	16	24.91	1.86	93.05%
	17	26.66	1.67	94.11%
	18	26.62	1.59	94.36%
	19	26.71	1.45	94.85%
	20	26.74	0.81	97.05%
	21	26.72	0.17	99.36%
	22	26.68	0.06	99.78%
Different plugging rates	1	24.99	0.68	97.35%
	3	24.91	1.86	93.05%

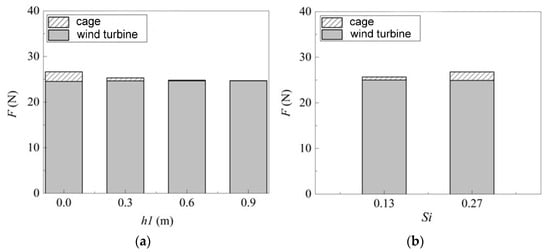
Figure 14. Hydrodynamic load distribution on the combined structure under different cage submergence depths (a) and cage plugging rates (b).

4. Conclusions

It is found that, among the wave parameters, the wave height affects the amplitude of the load on the combined structure. The higher the wave height, the greater the load on the combined structure, the more pronounced the wave resistance of the cage, and the smaller the load proportion on the wind turbine foundation. The period influences the phase of the maximum load of the combined structure, whereas it has little influence on the magnitude of the load. In contrast, the wind turbine foundation load first decreases and then increases with the increase in the wave period. The increase in water depth induces the horizontal wave load on the combined structure to increase slowly and the time of wave crest to occur slightly earlier, but it has little effect on the load proportion on the wind turbine foundation. The geometric size of the cage has no significant effect on the load. With the increase in cage height, the proportion of the wind turbine foundation load decreases, while with the increase of the diameter of the cage, the proportion of fan foundation load increases. Different diving depths of the cage have little effect on the load on the combined structure, but the more significant the diving depth, the greater the proportion of wind turbine load. The degree of adhesion of different marine organisms directly affects the wave resistance of the cage structure, leading to the increase in the load on the combined structure. In contrast, the wind turbine foundation load proportion will be significantly smaller. Notably, the wind turbine foundation is commonly the central part of the load-bearing combined structure.