An Efficient Computational Approach for Inverse Kinematics Analysis of the UR10 Robot with SQP and BP-SQP Algorithms
Abstract
1. Introduction
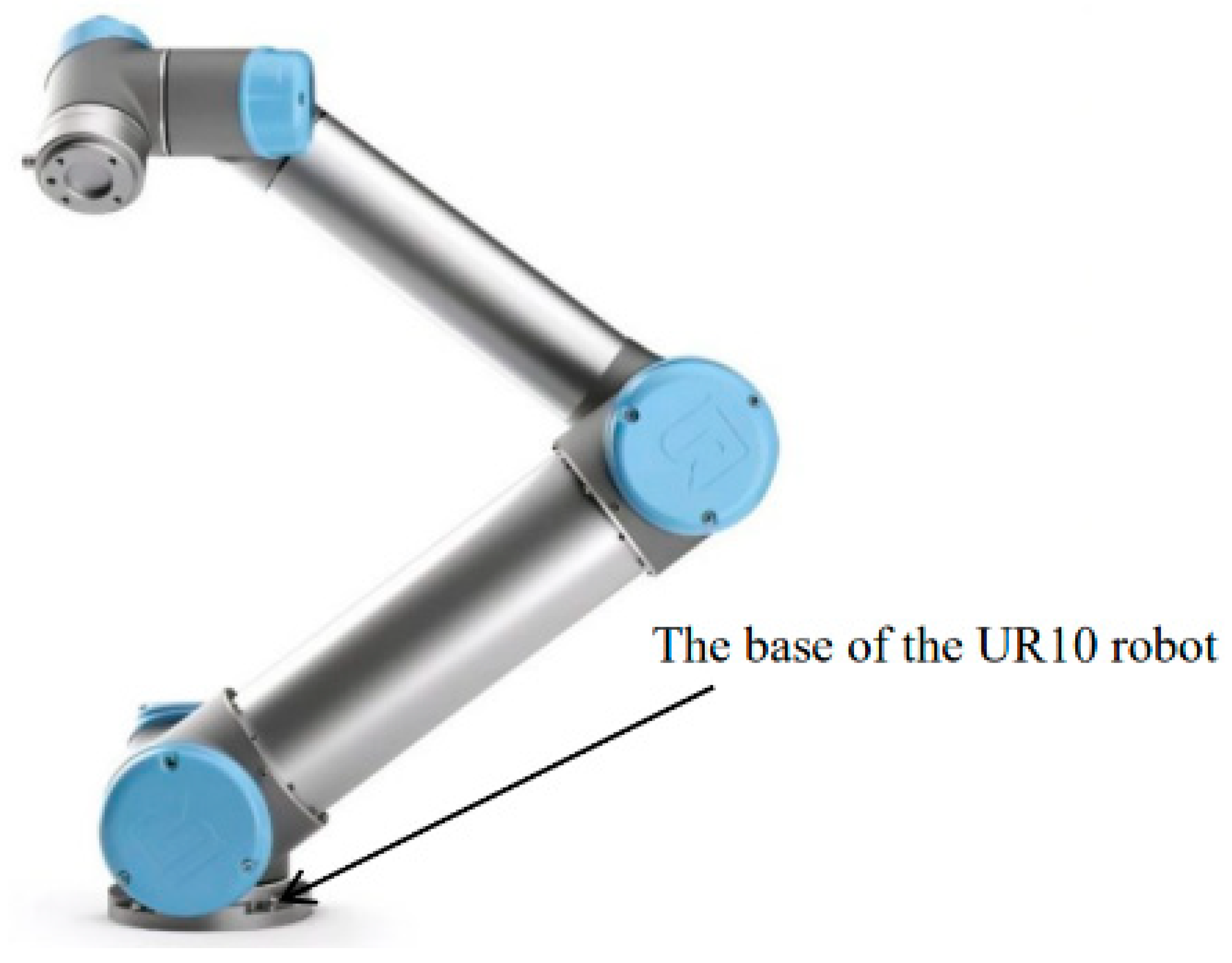
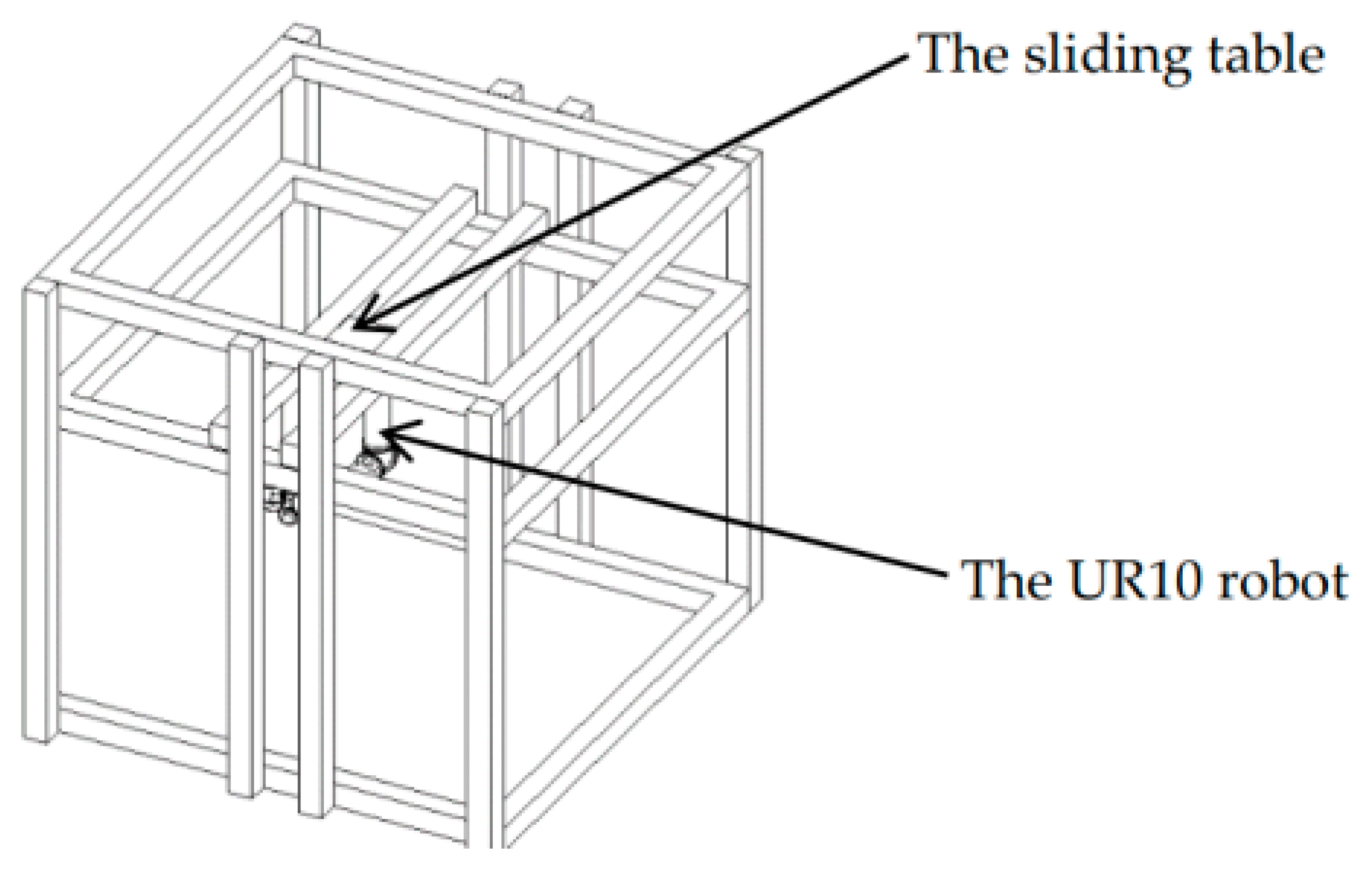
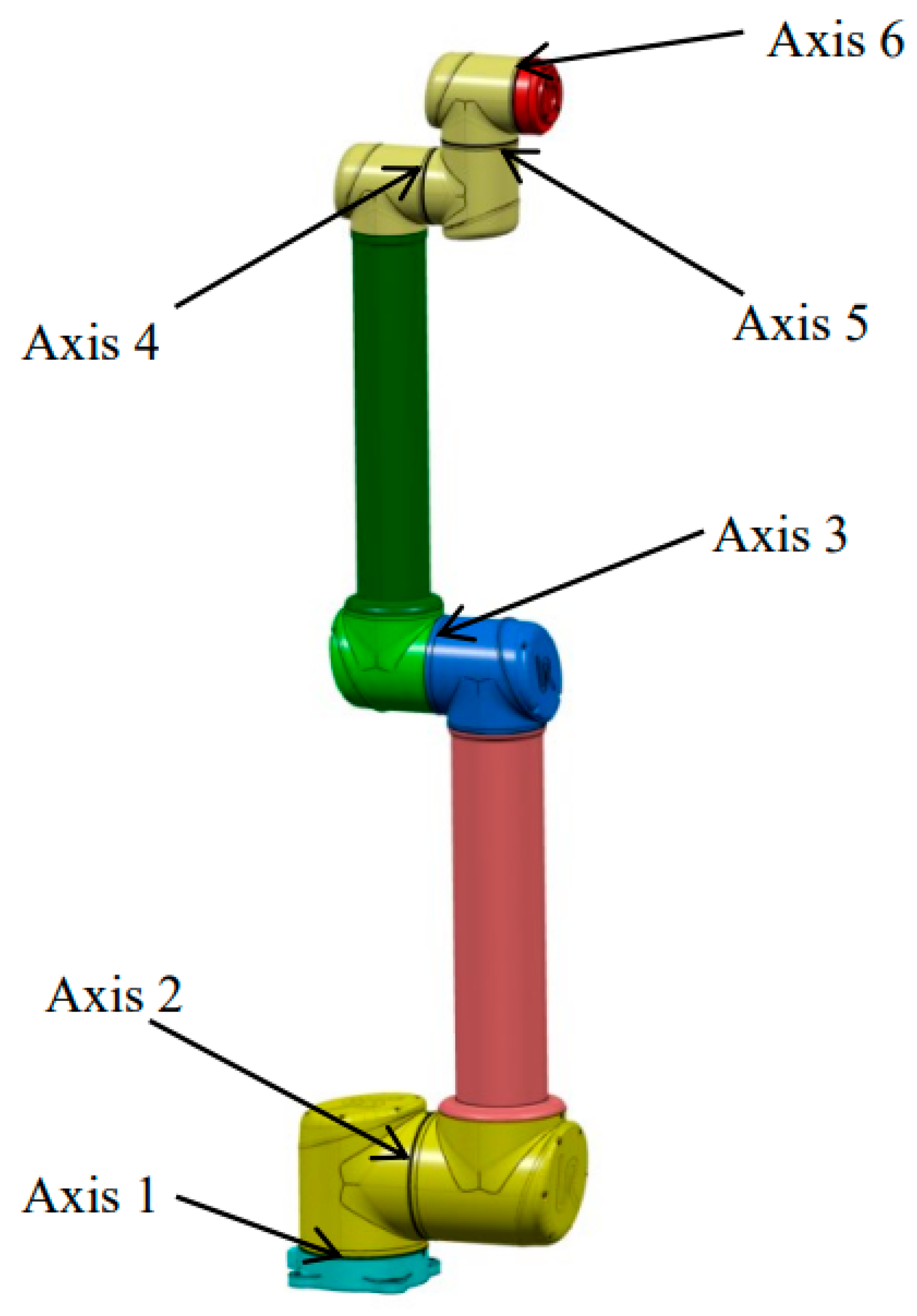
2. The Physical Model of the UR10 Robot
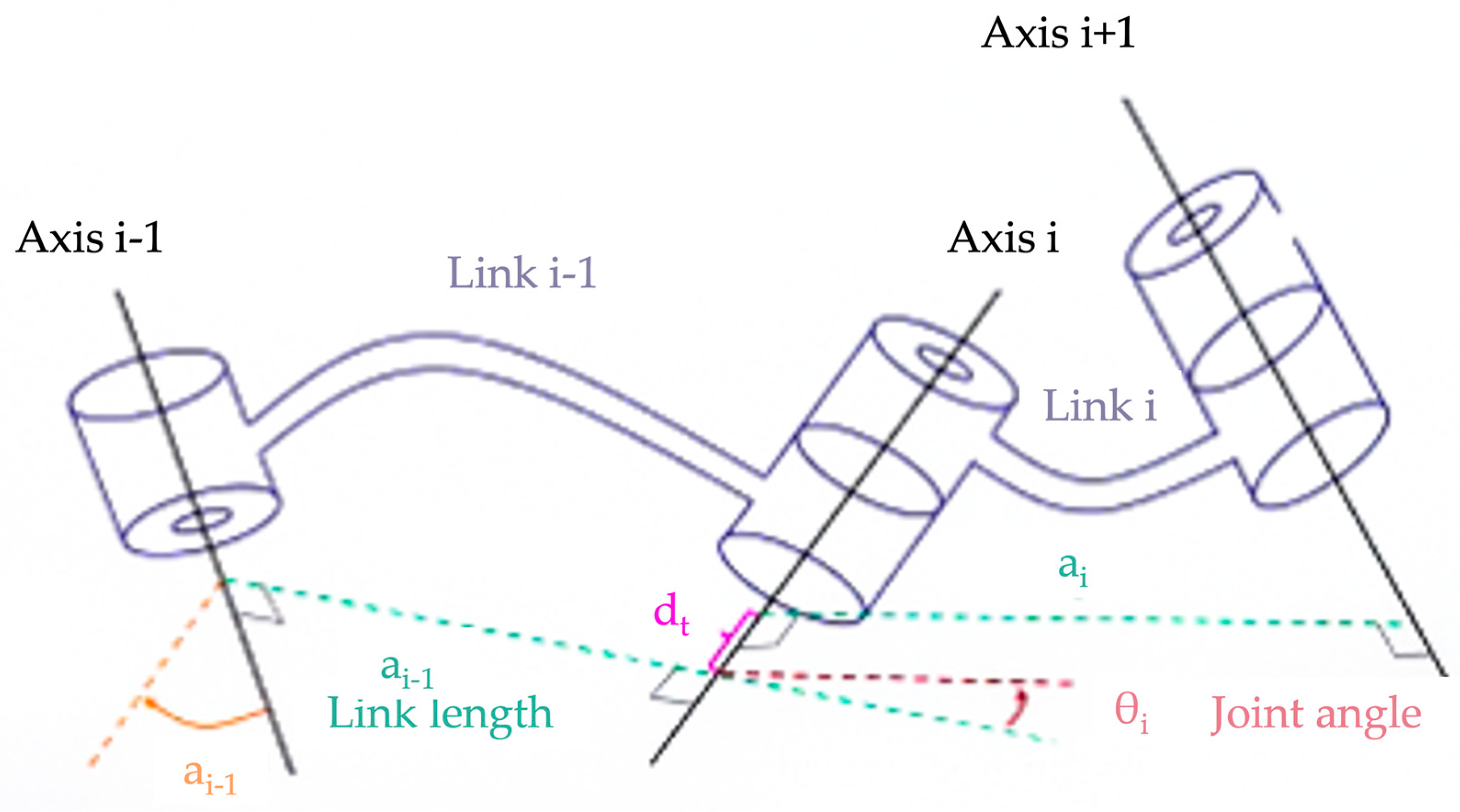
3. The Kinematics Model of the UR10 Robot
4. The Forward Kinematics Analysis
5. Inverse Kinematics Analysis
5.1. The Closed-Form Solution of Inverse Kinematics
5.2. The SQP Algorithm for Inverse Kinematics
5.3. The Solution of the Inverse Kinematics Model with the BP-SQP Algorithm
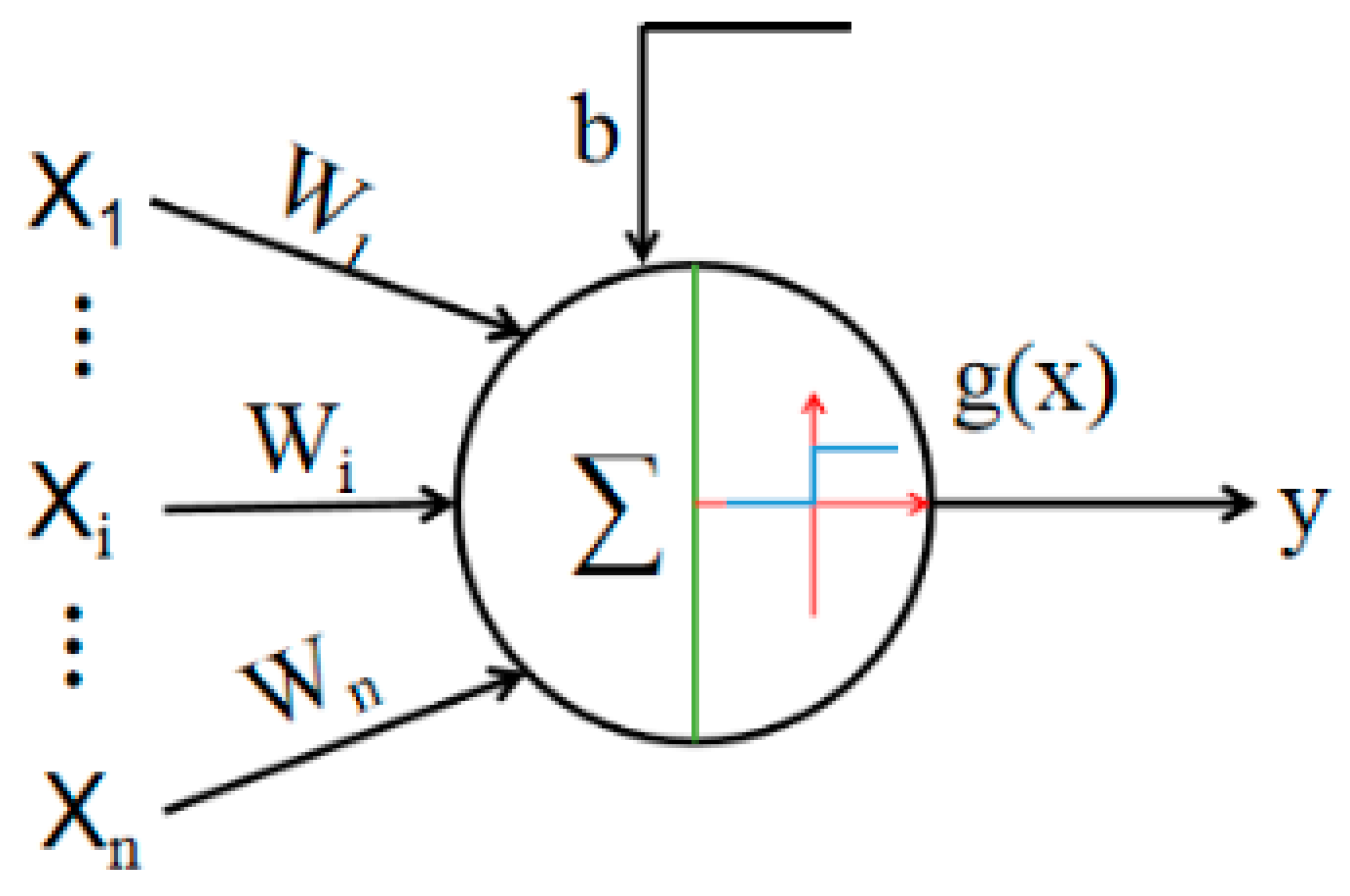
5.3.1. Forward Propagation of Neural Networks
5.3.2. Back Propagation of Neural Networks
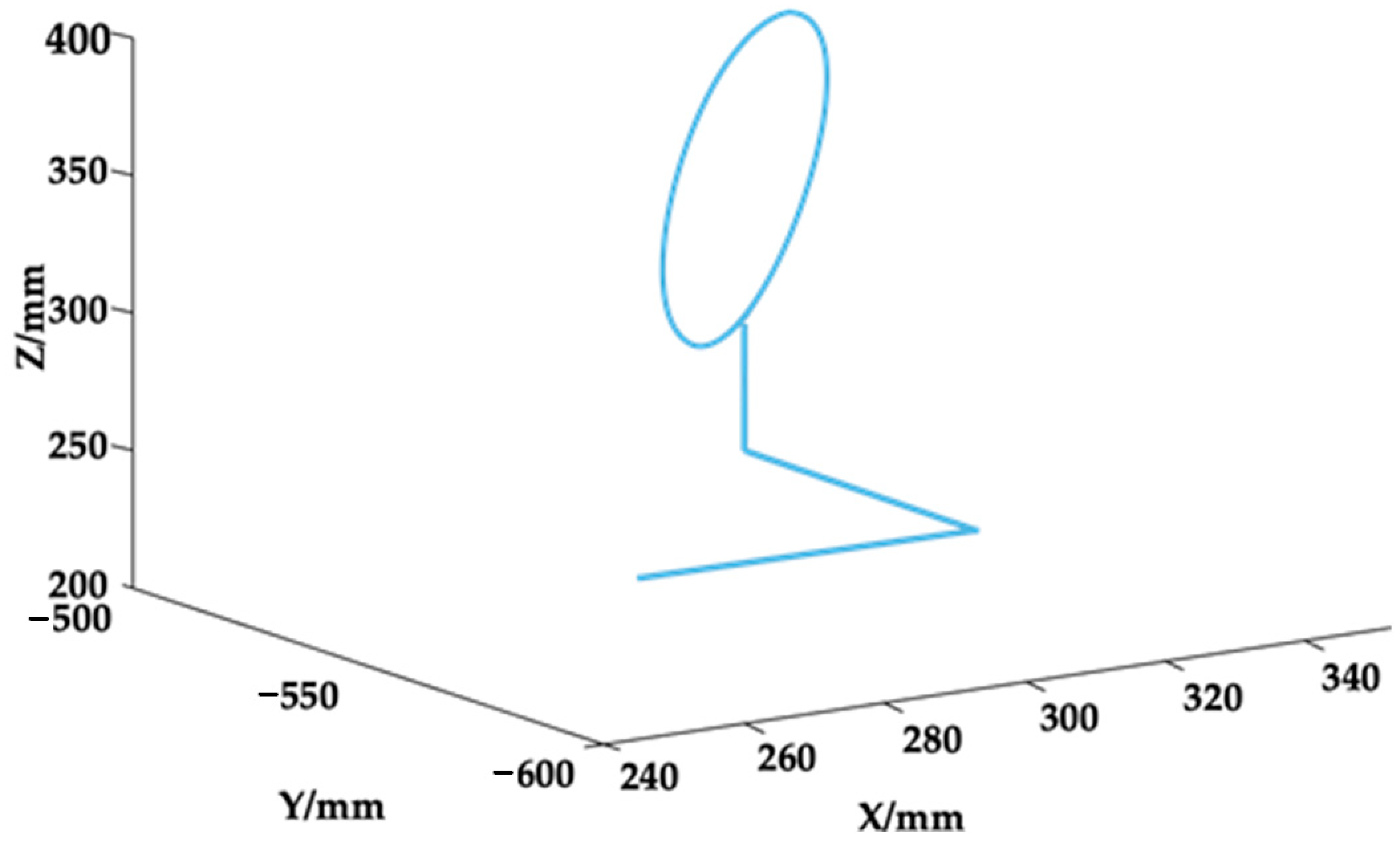
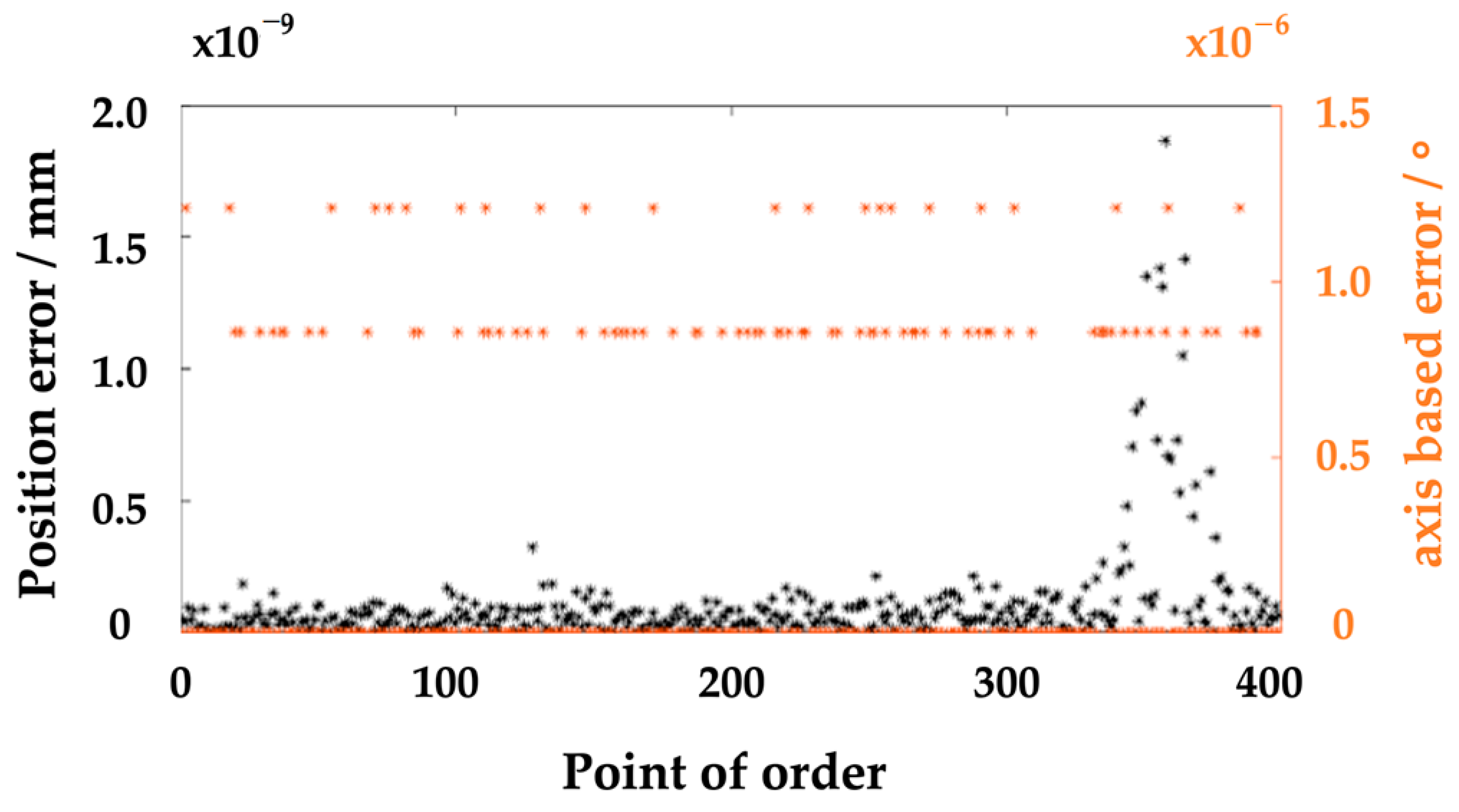
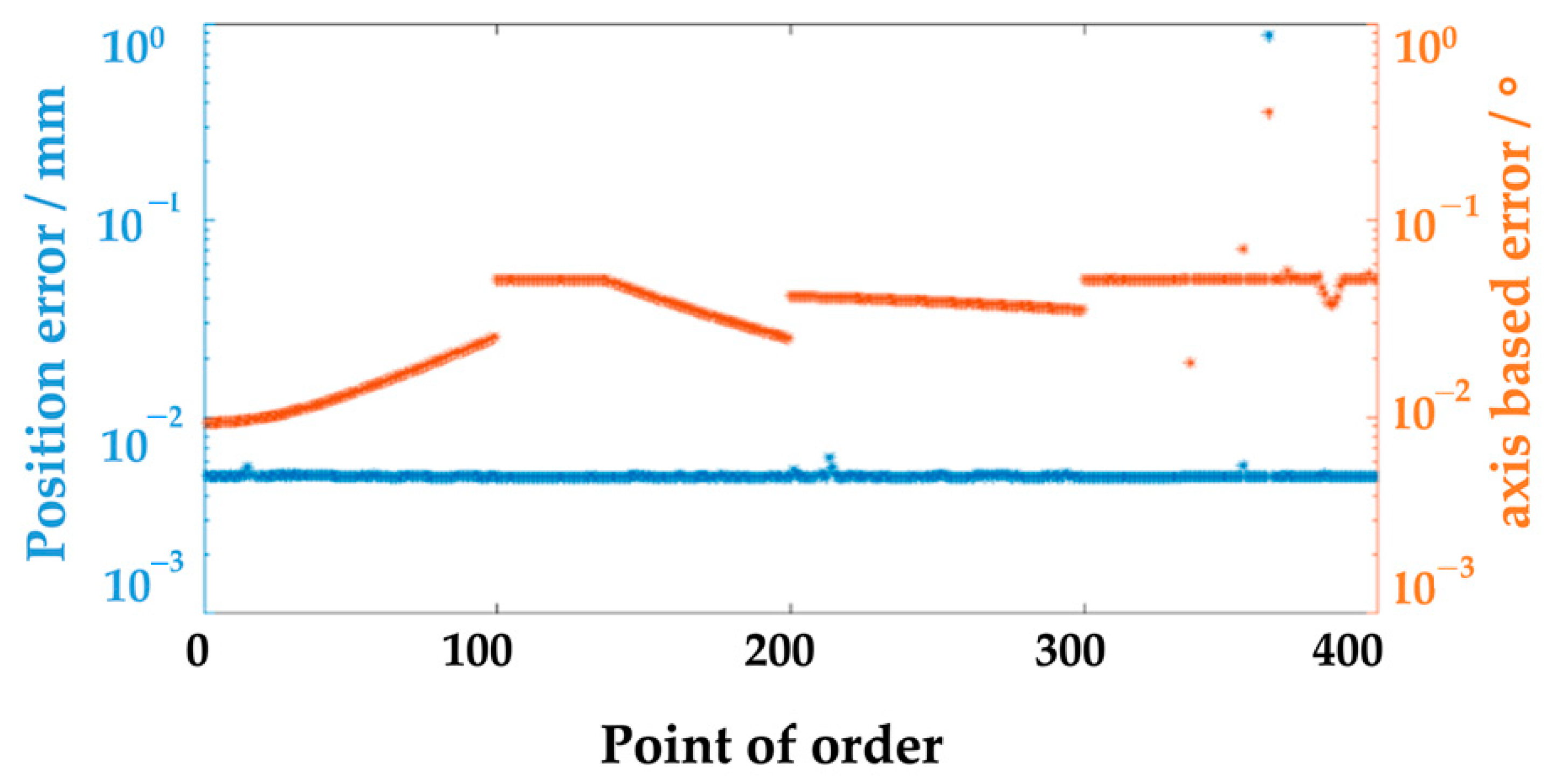
6. Simulation Based on Inverse Kinematics
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moreira, A.P.; Neto, P.; Vidal, F. Special Issue on Advances in Industrial Robotics and Intelligent Systems. Appl. Sci. 2023, 13, 1352. [Google Scholar] [CrossRef]
- Xiao, Y.; Jiang, J.; Yang, D.; Li, J.; Wu, J.; Chen, Y. Research on Mechanism and Measurement Model for the Effects of Path Dependence on Human Error in Space Station Manipulator Tasks. Symmetry 2022, 14, 753. [Google Scholar] [CrossRef]
- Kampmann, P.; Kirchner, F. Integration of Fiber-Optic Sensor Arrays into a Multi-Modal Tactile Sensor Processing System for Robotic End-Effectors. Sensors 2014, 14, 6854–6876. [Google Scholar] [CrossRef]
- Guerra, E.; Munguia, R.; Grau, A. Monocular SLAM for Autonomous Robots with Enhanced Features Initialization. Sensors 2014, 14, 6317–6337. [Google Scholar] [CrossRef]
- Chang, C.; Han, Z.; Li, X.; Sun, S.; Qin, J.; Fu, H. A Non-Geodesic Trajectory Design Method and Its Post-Processing for Robotic Filament Winding of Composite Tee Pipes. Materials 2021, 14, 847. [Google Scholar] [CrossRef]
- Wang, J.; Liang, F.; Zhou, H.; Yang, M.; Wang, Q. Analysis of Position, Pose and Force Decoupling Characteristics of a 4-UPS/1-RPS Parallel Grinding Robot. Symmetry 2022, 14, 825. [Google Scholar] [CrossRef]
- Huang, H.; Xu, H.; Chen, F.; Zhang, C.; Mohammadzadeh, A. An Applied Type-3 Fuzzy Logic System: Practical Matlab Simulink and M-Files for Robotic, Control, and Modeling Applications. Symmetry 2023, 15, 475. [Google Scholar] [CrossRef]
- Tatum, R.; Lucas, D.; Weaver, J.; Perkins, J. Geometrically motivatied inverse kinematics for an arm with 7 degrees of freedom. In Proceedings of the OCEANS 2015-MTS/IEEE WASHINGTON, Washington, DC, USA, 19–22 October 2015; pp. 1–6. [Google Scholar]
- Liu, H.S.; Zhou, W.N.; Lai, X.B.; Zhu, S. An Efficent Inverse Kinematic Algorithm for a PUMA560-Structured Robot Manipulator. Int. J. Adv. Robot. Syst. 2013, 10, 236. [Google Scholar] [CrossRef]
- Bai, Y.; Luo, M.; Pang, F. An Algorithm for Solving Robot Inverse Kinematics Based on FOA Optimized BP Neural Network. Appl. Sci. 2021, 11, 7129. [Google Scholar] [CrossRef]
- Kramar, V.; Kramar, O.; Kabanov, A. An Artificial Neural Network Approach for Solving Inverse Kinematics Problem for an Anthropomorphic Manipulator of Robot SAR-401. Machines 2022, 10, 241. [Google Scholar] [CrossRef]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 84–85. [Google Scholar]
- Zhao, G.; Jiang, D.; Liu, X.; Tong, X.; Sun, Y.; Tao, B.; Kong, J.; Yun, J.; Liu, Y.; Fang, Z. A Tandem Robotic Arm Inverse Kinematic Solution Based on an Improved Particle Swarm Algorithm. Front. Bioeng. Biotechnol. 2022, 10, 832829. [Google Scholar] [CrossRef] [PubMed]
- Duka, A.-V. Neural Network based Inverse Kinematics Solution for Trajectory Tracking of a Robotic Arm. Procedia Technol. 2014, 12, 20–27. [Google Scholar] [CrossRef]
- Gan, J.Q.; Oyama, E.; Rosales, E.M.; Hu, H. Quick look a complete analytical solution to the inverse kinematics of the pioneer 2 robotic arm. Robotica 2005, 23, 123–129. [Google Scholar] [CrossRef]
- Sudharsan, J.; Karunamoorthy, L. Derivation of Forward and Inverse Kinematics of 8—Degrees of Freedom Based Bio-Inspired Humanoid Robotic Arm. Adv. Mater. Res. 2014, 984–985, 1245–1252. [Google Scholar] [CrossRef]
- Deng, H.; Xie, C. An improved particle swarm optimization algorithm for inverse kinematics solution of multi-DOF serial robotic manipulators. Soft Comput. 2021, 25, 13695–13708. [Google Scholar] [CrossRef]
- Liu, S.; Zhu, S.; Wang, X. Real-time high-precision inverse kinematics algorithm for general 6R robots based on matrix decomposition. J. Mech. Eng. 2008, 44, 304–309. [Google Scholar] [CrossRef]
- Lü, S.; Zhang, D.; Liu, H. The inverse kinematics spinor equation of 6R robot based on Wu method. J. Mech. Eng. 2010, 46, 35–41. [Google Scholar]
- Liao, B.; Shang, J.; Ernest, A.; Wang, X. Five degree of freedom inverse kinematics of anthropomorphic arm based on ergodic iteration method. Mech. Des. Res. 2011, 27, 25–28. [Google Scholar]
- Si, Y.; Jia, Q.; Chen, G.; Sun, H. A complete solution to the inverse kinematics problem for 4-DOF manipulator robot. In Proceedings of the 2013 IEEE 8th Conference on Industrial Electronics and Applications (ICIEA), Melbourne, VIC, Australia, 19–21 June 2013; pp. 1880–1884. [Google Scholar] [CrossRef]
- Lin, Y.; Min, H. Inverse kinematics of modular manipulator robot with shoulder offset based on geometric method mixed with analytical method algorithm. In Proceedings of the 2015 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Shenyang, China, 8–12 June 2015; pp. 1198–1203. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, W.; Meng, D. Inverse kinematics solution method of redundant space manipulator based on arm angle parameterization. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 6022–6027. [Google Scholar]
- Yu, L.; Wang, W.; Wang, Z.; Gu, Q.; Wang, L. An analytical solution acquisition method for inverse kinematics of robots not satisfying pieper criterion. Robot 2016, 38, 486–494. [Google Scholar]
- Li, Q.; Zhao, L.; Li, R.; Liu, R.; Feng, Y.; Zhang, P. Inverse kinematics and workspace analysis of SPR+UPS+UPR parallel mechanism. Packag. Eng. 2020, 41, 213–218. [Google Scholar]
- Cui, M.; Wu, J.; Li, R.; Wang, X.; Zhang, J. Inverse kinematics and reachable workspace analysis of 3-URPR parallel mechanism. Packag. Eng. 2020, 41, 196–201. [Google Scholar]
- Yang, S. Improved drosophila optimization algorithm for inverse kinematic solutions of redundant robots. Mech. Strength 2020, 42, 7. [Google Scholar]
- Xie, X.; Fan, S.; Zhou, X.; Li, Z. Inverse solution of robotic arm kinematics based on improved differential evolutionary algorithm. Robotics 2019, 41, 8. [Google Scholar]
- Wang, J.; Yang, M.; Liang, F.; Feng, K.; Zhang, K.; Wang, Q. An Algorithm for Painting Large Objects Based on a Nine-Axis UR5 Robotic Manipulator. Appl. Sci. 2022, 12, 7219. [Google Scholar] [CrossRef]
- Kucuk, S.; Bingul, Z. Inverse kinematics solutions for industrial robot manipulators with offset wrists. Appl. Math. Model. 2014, 38, 1983–1999. [Google Scholar] [CrossRef]
- Bingül, Z.; Karahan, O. Dynamic identification of Staubli RX-60 robot using PSO and LS methods. Expert Syst. Appl. 2011, 38, 4136–4149. [Google Scholar] [CrossRef]

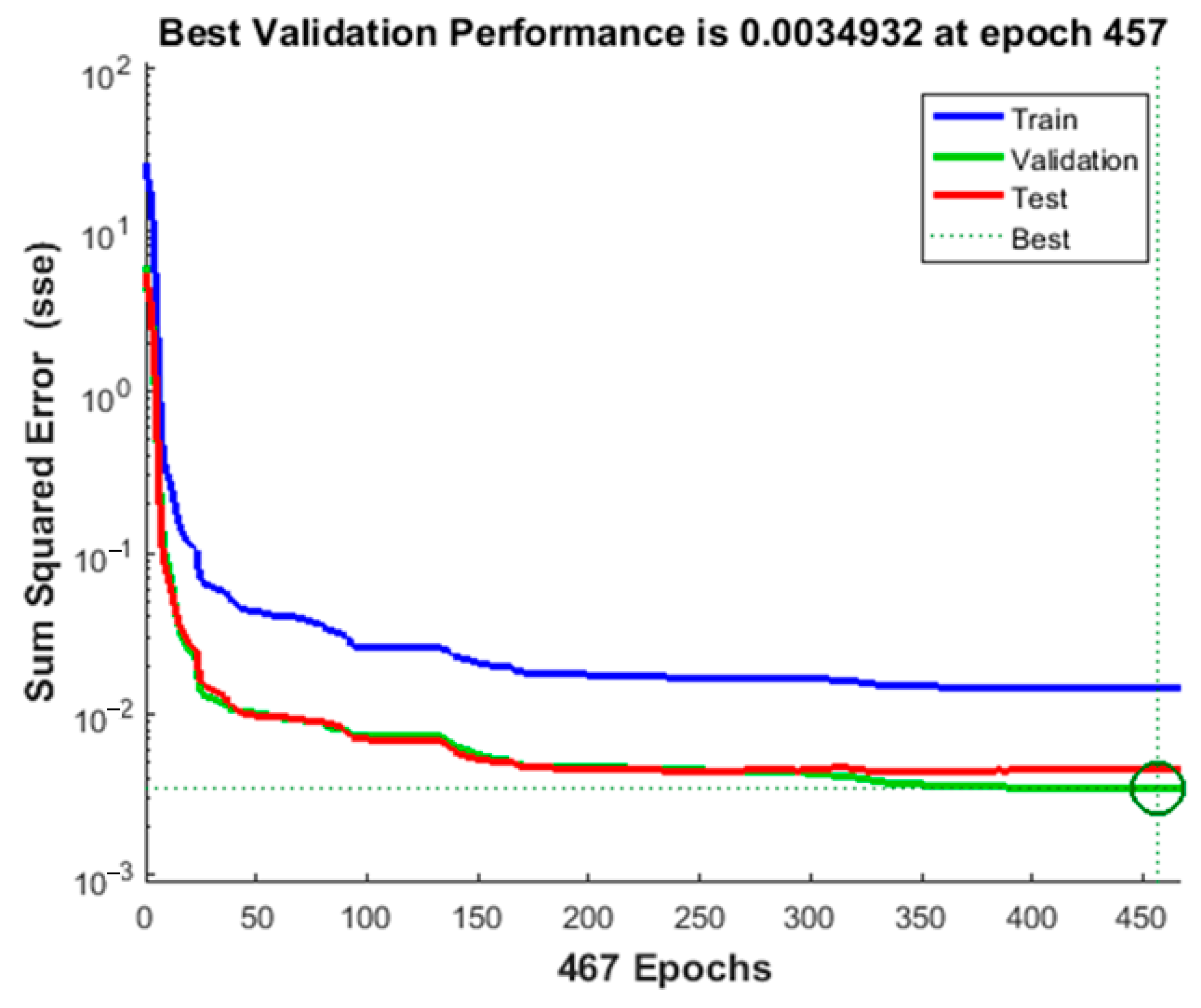
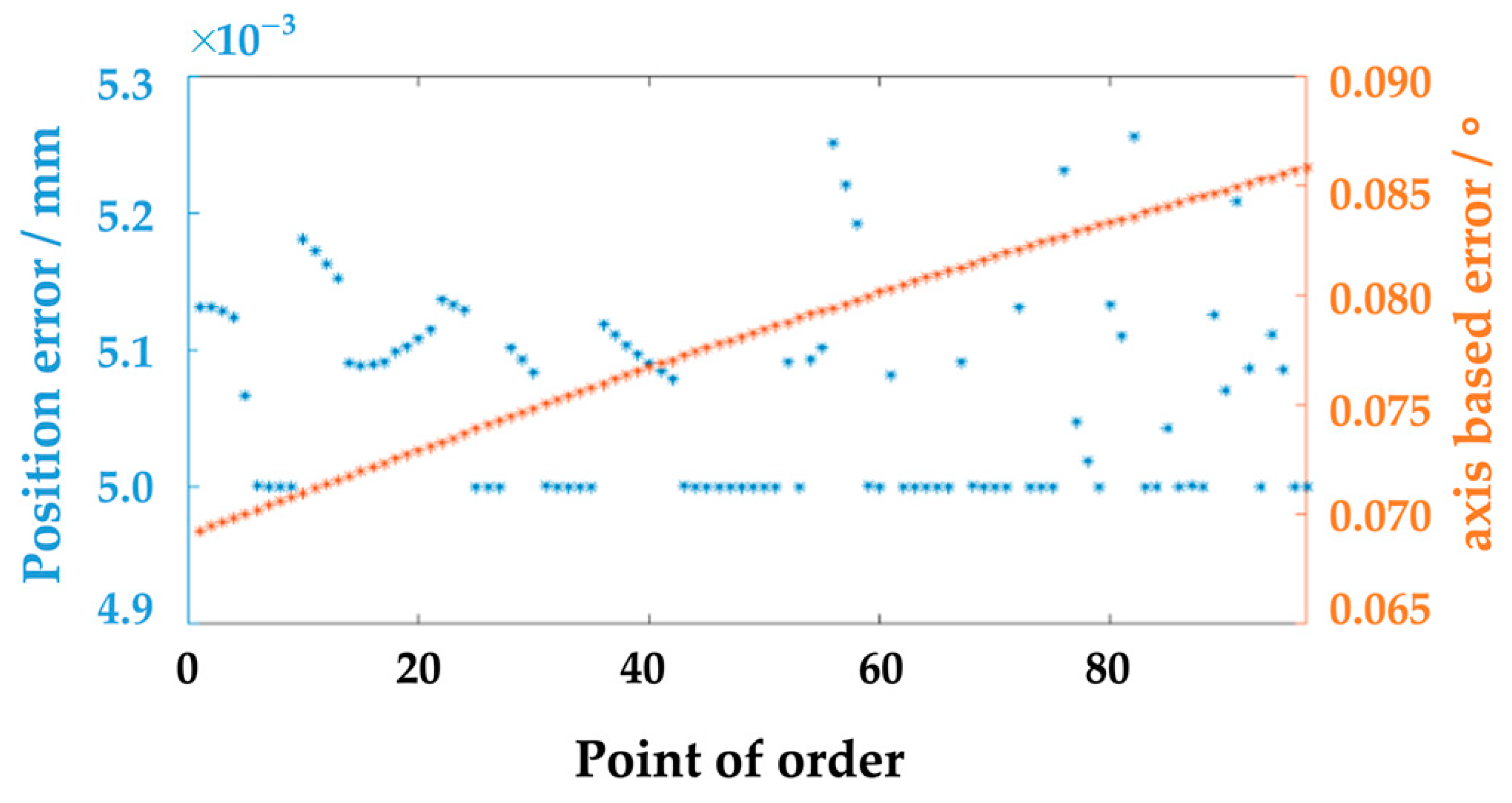
| Type | Success Rate | Time/s | Algorithmic Premise | Optimal Solution |
|---|---|---|---|---|
| The closed-form solution | 100% | 78.8 | Target pose determination | no |
| The SQP algorithm | 99.5% | 37 | Target position and axis determination | yes |
| The BP-SQP algorithm | 100% | 4.2 | Target location and axis determination, a certain number of samples | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Liu, J.; Zhang, X.; Wang, J.; Li, X.; Tu, X.; Chen, S.; Wang, C.; Huang, Q. An Efficient Computational Approach for Inverse Kinematics Analysis of the UR10 Robot with SQP and BP-SQP Algorithms. Appl. Sci. 2023, 13, 3009. https://doi.org/10.3390/app13053009
Huang Y, Liu J, Zhang X, Wang J, Li X, Tu X, Chen S, Wang C, Huang Q. An Efficient Computational Approach for Inverse Kinematics Analysis of the UR10 Robot with SQP and BP-SQP Algorithms. Applied Sciences. 2023; 13(5):3009. https://doi.org/10.3390/app13053009
Chicago/Turabian StyleHuang, Yizhe, Jiaen Liu, Xuwei Zhang, Jun Wang, Xiao Li, Xikai Tu, Shuisheng Chen, Chenlin Wang, and Qibai Huang. 2023. "An Efficient Computational Approach for Inverse Kinematics Analysis of the UR10 Robot with SQP and BP-SQP Algorithms" Applied Sciences 13, no. 5: 3009. https://doi.org/10.3390/app13053009
APA StyleHuang, Y., Liu, J., Zhang, X., Wang, J., Li, X., Tu, X., Chen, S., Wang, C., & Huang, Q. (2023). An Efficient Computational Approach for Inverse Kinematics Analysis of the UR10 Robot with SQP and BP-SQP Algorithms. Applied Sciences, 13(5), 3009. https://doi.org/10.3390/app13053009






