1. Introduction
Hydraulic turbines are complex structures presenting a runner submerged in water and a shaft in air that are designed to operate at their best efficiency point (BEP). However, the introduction of intermittent renewable energy sources in the electrical grid, such as solar and wind power, is forcing them to operate for longer periods of time in off-design and transient conditions [
1,
2,
3]. Under these circumstances, hydraulic turbines are subjected to more deleterious phenomena and transient events [
1,
2,
3], which can cause fatigue cracks and high-amplitude rotor vibrations if a resonance occurs [
4,
5]. In order to avoid resonances, it is of paramount importance to measure and precisely calculate the natural frequencies of hydraulic turbines in air and water under non-rotating and rotating conditions.
Previous studies showed that there are many similarities between the mode shapes of some specific runners, such as Francis runners, and those of a disk [
6,
7,
8,
9]. More specifically, some modes of both a Francis runner and a disk are characterized by the number of nodal diameters (ND) and circles (NC). The present investigation was thus performed on a structure composed of a disk clamped to a shaft supported by two bearings, resembling a hydraulic turbine rotor system.
The modal responses of disk-like structures with or without blades in air have been investigated extensively. For instance, the presence of mistuned blades or shaft misalignments has been found to alter their natural frequencies [
10,
11]. It has also been observed that high rotating speeds increase the natural frequencies [
12,
13,
14,
15,
16]. However, other authors have concluded that this effect might be neglected at low rotating speeds [
17].
Similarly, the modal response of disk-like structures in water has also attracted the attention of researchers. It has been proven experimentally and numerically that their natural frequencies decrease compared to those in air. The added mass effect has been considered to be primarily responsible for this frequency drop [
17,
18,
19]. It has also been observed that the added mass is altered when a solid body is close to a rigid surface, resulting in an additional decrease in its natural frequencies [
18,
19]. Additionally, the rotation has been found to influence the natural frequencies and mode shapes of submerged disks, even at low rotating speeds. For instance, the ND vibration modes evolve from standing mode shapes under non-rotating conditions to traveling mode shapes under rotating conditions. Under non-rotating conditions, the displacements of each point of the disk are either in phase or out of phase, while under rotating conditions the displacements are phase-shifted, resulting in a wave traveling over the disk [
17,
20,
21,
22].
Understanding how the modal response and, more specifically, the natural frequencies are transmitted from a rotating frame to a stationary frame is indispensable in order to design and optimize structural health monitoring systems in hydraulic turbines, as they have a runner submerged in water which is not easily accessible. Hamid et al. [
23] established an analytical correlation between the natural frequencies of a rotating disk in air measured from the rotating and from the stationary frames and then proved it experimentally. It was concluded that the relation between the measurements from the two different reference frames depended on the rotating speed and the mode shape. Later, Presas et al. [
24,
25] investigated the correlation between the natural frequencies of a submerged disk, measured from the rotating frame using accelerometers and from the stationary frame using a laser displacement sensor. In air, the laser displacement sensor measured two shifted natural frequencies for each single natural frequency measured from an on-board position. Nonetheless, in water, the laser displacement sensor only measured one shifted natural frequency for each single natural frequency measured on board.
Most of the previous studies employed the experimental modal analysis technique to extract the modal responses of disks, including their natural frequencies and mode shapes. An experimental modal analysis requires an actuator in order to excite the structure and sensors to measure its response. Subsequently, the frequency response function between the excitation and the measured response can be calculated, as can the mode shapes, the damping ratios and the natural frequencies. The selection of the actuator is a key part of the experiment. The traditional exciters, such as an instrumented hammer or a shaker, are useless in submerged structures because of limitations to accessibility or due to the fact that they might influence the modal parameters. In these specific conditions, exciters such as piezoelectric PZT patches have proven to be useful [
26,
27,
28,
29,
30,
31,
32]. These studies demonstrated that the natural frequencies, mode shapes and damping ratios can be extracted from the response of a structure that is excited using PZT patches, even when they are not calibrated. This fact simplifies the experiment since the relation between the voltage and the dynamic force of a PZT patch is unknown and is not linear in the entire frequency range.
Although there is an extensive bibliography on modal responses of disk-like structures, experimental investigations which assess novel modal testing techniques using PZT patches or rotating speed ramp-ups as exciters while measuring the responses from on-board and off-board positions in rotating and submerged systems have not been carried out. To deepen the insight in the modal responses of rotating structures also requires further investigations using numerical methods to simulate their modal responses.
This article presents a study using different experimental and numerical methods to perform the modal analysis of rotating structures submerged in water. The paper is organized in five sections. First, it starts with the introduction. In the second section, the test rig, the instrumentation and the experimental methodology are presented. In the third section, the numerical models are introduced, and in the fourth section, the results are described and discussed. Finally, the main conclusions are summarized in the fifth section.
2. Experimental Investigation
2.1. Test Rig Description
The test rig used for this study consisted of a stainless-steel disk that could be submerged into a plexiglass tank full of water and coupled to a shaft (see
Figure 1a). The test rig was placed in the laboratory of the Barcelona Fluids & Energy Lab (IFLUIDS) research group at the UPC. The disk–shaft structure was supported by two bearings placed on an aluminum frame. The aluminum frame was a modular structure that permitted changing the distance between the bearings. Nonetheless, in the current study, all the tests were performed with the same bearing configuration. The two bearings were a roller type with high radial stiffness, preventing radial displacements of the shaft. A variable-speed DC motor (Motor, SQ75, Crouzet) was bolted on the aluminum frame and connected to the shaft through a cog belt and a driven pulley. Using the cog belt and the driven pulley, the structure could be rotated at different rotating speeds with the DC motor. The DC motor was controlled with a software that permitted adjusting the rotating speed during stationary operation and adjusting the frequency range and the acceleration during transient ramps. The plexiglass tank of water was cylindrical and permitted the flow to be visualized through its walls.
As
Figure 1b shows, the shaft was equipped with two slip rings: one mounted at the top of the shaft and the other one in the middle of the shaft. The slip ring at the top of the shaft, indicated in
Figure 2a as the “end of shaft slip ring”, had 20 circuit connections (Slip Ring, SR20M, Michsci), and it was used to transmit the signals of several strain gauges located on board to the data acquisition system placed off board. The slip ring in the middle of the shaft, indicated in
Figure 2b as the “lateral slip ring”, had six circuit connections (Slip Ring, B6-2, Michsci), and it was used to transmit the signal of an accelerometer located on board to the data acquisition system and to feed a piezoelectric PZT patch located on board with a signal from the data acquisition system.
2.2. Instrumentation
In order to measure the modal response of the structure, the test rig was equipped with several sensors placed in specific locations to precisely detect different mode shapes (see
Figure 3a). Concretely, the disk was equipped with three on-board waterproof triaxial strain gauges, SG1, SG2 and SG3 (Strain Gauge, WFRA-3-120-17-3LDBB-F, Tokyo Measuring Instruments Laboratory), glued to the bottom of the disk and one on-board ICP accelerometer, A0 (Accelerometer, 352C34, PCB Piezotronics), glued to the top of the disk. This accelerometer is not waterproof, and it was used only in the case of having the disk in air. Additionally, five off-board laser displacement sensors, D0, D1, D2, D3 and D4 (Displacement Laser, ILD1320-10, Micro-Epsilon), were placed along the shaft line and the disk (see
Figure 3b). Due to their measuring range (20–30 mm), the laser sensor pointing at the disk was also used only in the case of having the disk in air. Additionally, two off-board triaxial accelerometers, AUB and ALB (Accelerometer, 356A16, PCB Piezotronics), were placed in the outside housing of the bearings to measure the vibrations transmitted from the shaft (see
Figure 3c).
The excitation of the structure was performed using an impact hammer (Hammer, 086C03, PCB Piezotronics) and a piezoelectric PZT patch (PZT patch, P-876.A12, PI Ceramic) glued to the bottom of the disk (see
Figure 3a). The rotating speed ramp-up test excited the structure with the force induced by the mechanical rotor imbalance.
The digitalization and recording of the signals were performed using the National Instruments compact DAQ NI-cDAQ-9185 chassis equipped with three input modules: (i) the current module NI-9253 for the laser displacement sensors, (ii) the IEPE acceleration module NI-9231 for the accelerometers and (iii) the voltage module NI-9235 for the strain gauge measurements. In order to generate a frequency-varying voltage to feed the PZT patch, the output voltage module NI-9262 was employed. A LabVIEW code was used to synchronize the acquisition and to record all the signals, which were sampled at 4267 Hz.
2.3. Methodology
The experimental modal tests of the disk–shaft assembly were performed by exciting the structure using an instrumented hammer, a PZT patch and a transient ramp-up (see
Figure 4).
Due to the difficulty of performing hammer impacts when the disk was in water or rotating, the hammer was only used when the disk was not rotating in air. The rowing hammer technique was employed to identify the natural frequencies and mode shapes of the disk up to 300 Hz. A total of 10 impacts were performed in different positions of the disk, as presented in
Figure 5a. Subsequently, the frequency response functions (FRF) between the accelerometer and the hammer signals were computed, obtaining their real and imaginary parts, as shown in
Figure 5b. The FRF was calculated using a force-exponential window to minimize signal leakage. Additionally, the FRF was averaged with a RMS method and using five impacts given in each position. The natural frequencies of the structure were identified directly from the frequency peaks of the FRFs, and the mode shapes were obtained from the amplitudes and signs of the frequency peaks of the imaginary part of the FRFs.
The modal test was also performed using a PZT patch. In the current study, this alternative method to perform a modal test was first validated by comparing the results obtained with the hammer and the PZT patch when the disk was in air without rotation. Subsequently, the PZT patch was used to perform the modal analysis with the disk rotating in air and water. The disk was tested in air at 0, 50, 100, 150, 200, 250 and 300 rpm and in water at 0 and 50 rpm. Tests in water were carried out only up to 50 rpm because at higher rotating speeds the water leaked through some sensors’ sealing, reaching the electrical connections and producing unreliable measurements. The PZT patch was fed a frequency-varying voltage that swept over different frequency ranges and excited the natural frequencies of the disk, which were then identified from the increase in the amplitude of the structural response at each resonance. The peaks of the signal were identified from a spectrum built using the maximum values of a waterfall spectrum for each frequency bit over the entire temporal duration of the signal (see
Figure 6b). The waterfall spectra were calculated using a short-time Fourier transform (STFT) (see
Figure 6a). A resolution of 0.142 Hz was obtained in the equivalent spectrum of
Figure 6b using a Hanning window with an FFT block size of 30,000 points and a sliding time segment with a 10% time increment between two consecutive FFT blocks. The chirps were performed in different frequency ranges of 0–100 Hz, 100–200 Hz and 200–300 Hz for 100 s and in the range of 0–300 Hz for 300 s.
Finally, a transient ramp-up test from 0 to 300 rpm with a duration of 120 s was performed to excite the natural frequencies with the mechanical imbalance. The increase in the amplitude of the structural response at certain frequencies was identified using the same methodology applied to the PZT patch tests. From these frequency peaks, the natural frequencies were directly identified.
3. Numerical Analysis
A series of numerical structural and acoustic–structural models, to perform modal analysis and harmonic analysis, were built with the commercial software ANSYS® 2022R2.
First, a numerical model only consisting of the structural parts of the test rig, the disk and the shaft, was built in order to calculate the natural frequencies of the non-rotating disk in air. The material of the shaft and the disk was considered standard stainless-steel, whose properties were already defined in the “General Materials” engineering data source of ANSYS®. The discretization of the bodies was performed using a combination of tetrahedral and hexahedral elements. Subsequently, a mesh refinement process was performed to determine the optimal element mesh size that provided an accurate solution with a low computational cost. The optimal mesh used for the discretization of the structural part had a total of 43,826 elements and 88,796 nodes. The bearings were modeled using body–ground bushing connections and by adjusting the stiffness coefficients in the radial and axial directions.
Second, the previous numerical model was enlarged with an acoustic region corresponding to the fluid domain, reproducing the surrounding water inside the tank in order to obtain the natural frequencies of the non-rotating disk in water. The density and the speed of sound of the water were considered to be 1000 kg/m3 and 1430 m/s, respectively. The acoustic region was modeled through tetrahedral elements, which assumed that the fluid was inviscid, irrotational, compressible and without mean flow. The structural boundary conditions were the same as in the case of having the disk in air. The nodes of the solid elements in contact with the fluid were defined as a fluid–solid interface. In this case, the optimal mesh used for the discretization of both the structural and acoustic domains had a total of 495,222 elements and 829,056 nodes.
For both air and water simulations, piezoelectric properties were added into the numerical models to simulate the excitation induced by a frequency-varying chirp applied to the PZT patch glued to the disk. The simulated piezoelectric patch (P-876.A12) was composed of a piezoceramic PIC255 layer, called the active layer, sandwiched between two thin encapsulating polymers, called the soft layer, which electrically insulated and applied prestress to the active layer (see
Figure 7). The coupling of the acoustic, structural and piezoelectric physical models of the system was performed using the ANSYS
® extension called “Piezo and Mems”. The piezoelectric material’s electrical behavior was defined by introducing the piezoelectric constants provided by the manufacturer in the stress–charge form [
33]. Additionally, the polarized direction was set perpendicular to the disk surface. By doing so, a voltage between the two faces of the active layer of the patch could be defined, and the strain induced by the applied voltage to the patch could be simulated [
34]. The boundary conditions were the same as in the case of having the disk in air or water. All in all, structural–piezoelectric and acoustic–structural–piezoelectric harmonic analyses were performed to simulate chirp excitations between 0 and 300 Hz.
4. Results
4.1. Results in Air
4.1.1. Natural Frequencies of the Non-Rotating Disk in Air
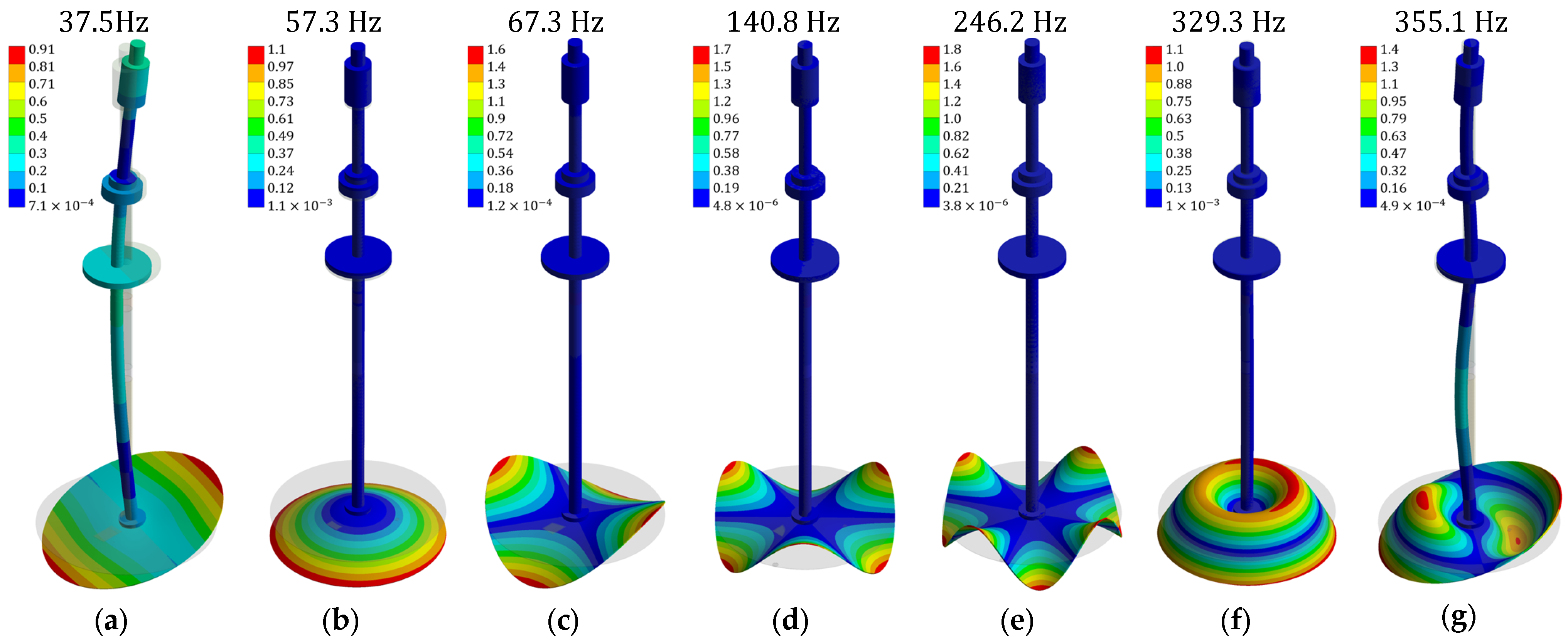
Figure 8 presents the natural frequencies and corresponding mode shapes of the non-rotating disk in air, calculated through a numerical modal analysis. The 1ND presents the lowest natural frequency, with a value of 37.5 Hz. Subsequently, there are the 0NC, 2ND, 3ND, 4ND and 1NC, with values of 57.3 Hz, 67.3 Hz, 140.8 Hz, 246.2 Hz and 329.3 Hz, respectively. The combined mode 1NC+1ND presents the highest natural frequency in the investigated range of frequencies, with a value of 355.1 Hz. The same mode shapes and natural frequencies were also obtained numerically with a harmonic analysis in which the system was excited with a chirp signal.
Figure 9 shows a frequency response and some mode shapes calculated using the harmonic analysis.
In this section, the presented experimental natural frequencies of the non-rotating disk in air were obtained using both the rowing hammer technique and a chirp applied with the PZT patch. In the current study, both experimental methodologies resulted in the same natural frequencies as in previous investigations [
26,
27]. Subsequently, these results were compared with the numerical predictions.
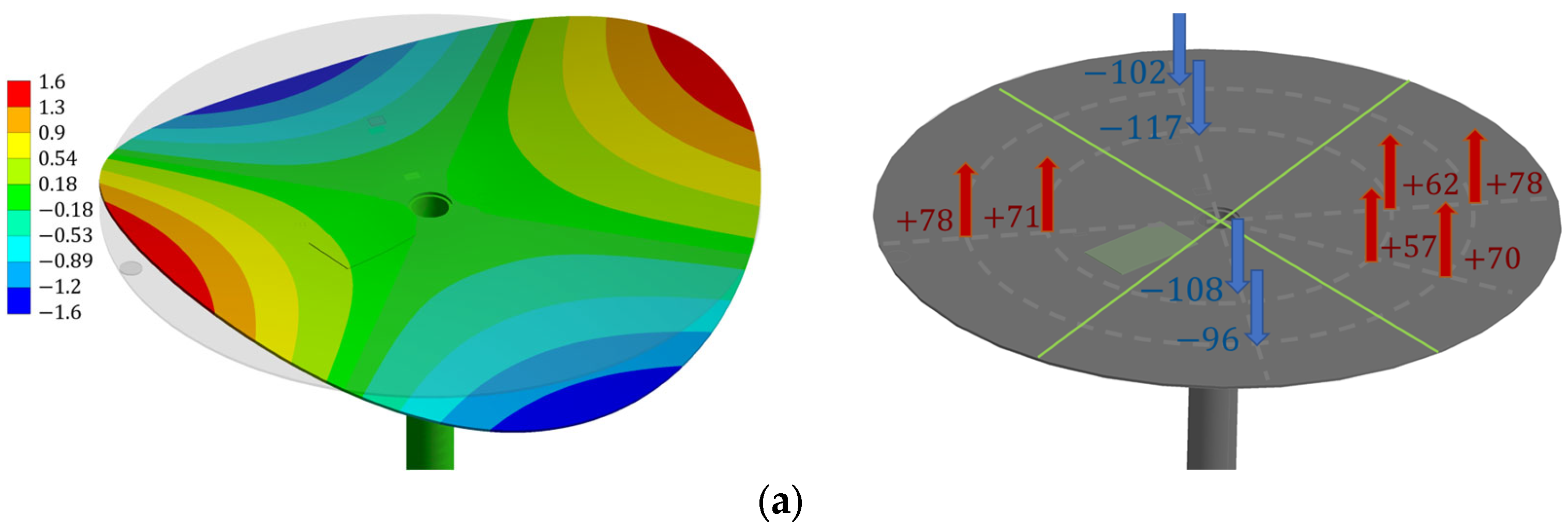
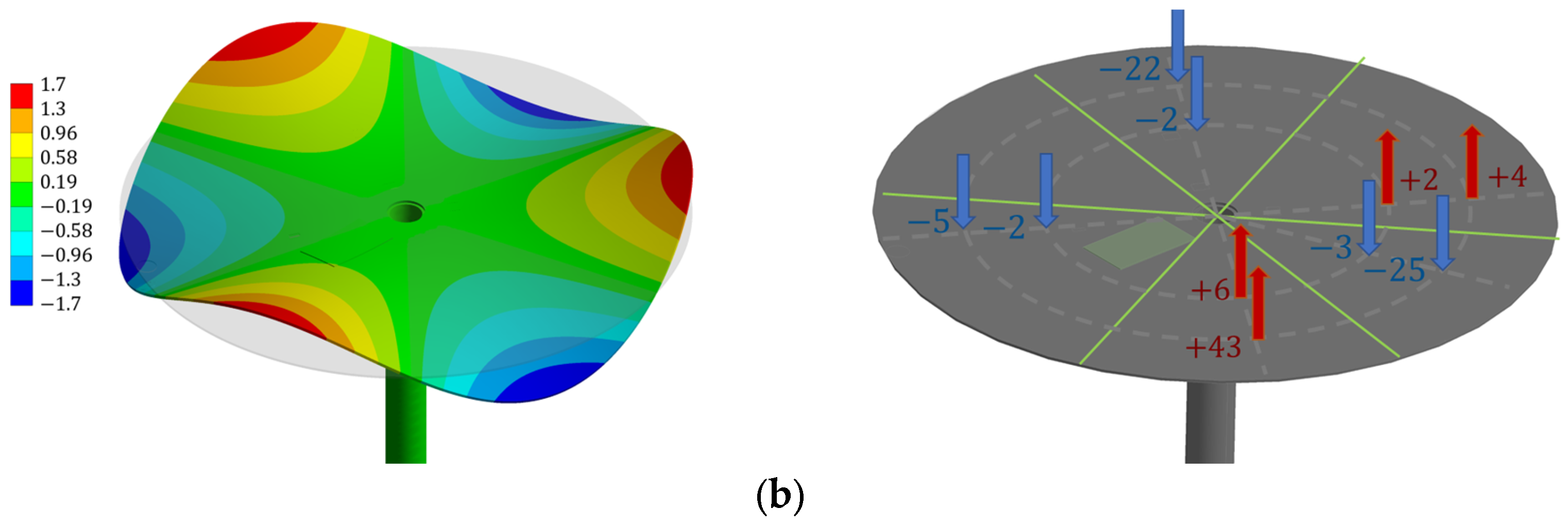
Figure 10 shows the numerical mode shapes of the 2ND and 3ND modes (plotted in the left column) and the corresponding experimental results (plotted in the right column). This figure shows that the number of nodal diameters and their positions (see the green lines) were captured numerically. Moreover, the highest relative displacements were usually found on the external perimeter of the disk in both the numerical and experimental results. In general, the numerical mode shapes were in close agreement with the experimental mode shapes.
Table 1 shows a comparison of the numerical and experimental natural frequencies. The absolute percentage of the deviation between the results was lower than 7% for the diametral modes, 1ND, 2ND, 3ND and 4ND, whereas the discrepancy was higher for the circular modes, 0NC and 1NC, and the combined mode, 1NC+1ND, where the deviation increased up to 28%. This higher discrepancy may have been associated with the uncertainties in the bearings’ properties, which influence the NC modes more than the ND modes.
4.1.2. Experimental Detection of the Natural Frequencies of the Non-Rotating Disk in Air
Figure 11 shows the spectra of the structural response measured by different sensors mounted at different locations when the disk was not rotating in air. As the sensors measured different physical magnitudes, i.e., acceleration, strain or displacement, all the spectra were normalized using their maximum values in the range of 0 to 100 Hz. The accelerometers placed on the lower and upper bearings in the radial direction (ALB
y and AUB
y) primarily detected the 1ND at 39.8 Hz, while the accelerometers in the axial direction (ALB
x and AUB
x) primarily detected the 0NC at 41.2 Hz. The 1ND resulted in radial displacements on the bearings and was consequently detected by ALB
y and AUB
y, whereas the 0NC resulted in axial displacements, and thus it was detected by ALB
x and AUB
x. Both on-board sensors, the strain gauge SG3_9 and the accelerometer A0 detected the 2ND at 69.1 Hz with similar relative amplitudes. However, SG3_9 detected the 1ND at 39.8 Hz with a higher relative amplitude than A0 because the latter was mounted close to the nodal line of the 1ND mode shape, producing a low acceleration at that point. Finally, D0, D1 and D2 primarily detected the natural frequency associated with the 1ND at 39.8 Hz because their measuring directions coincided with the main displacement direction of this mode on the disk and shaft. Therefore, the locations of the sensors had a strong influence on which natural frequencies could be detected. A sensor may not have detected a natural frequency because it was located on a nodal position or because its measuring direction did not coincide with the main displacement direction of the corresponding mode shape.
4.1.3. Influence of Rotation on the Natural Frequencies of the Disk in Air
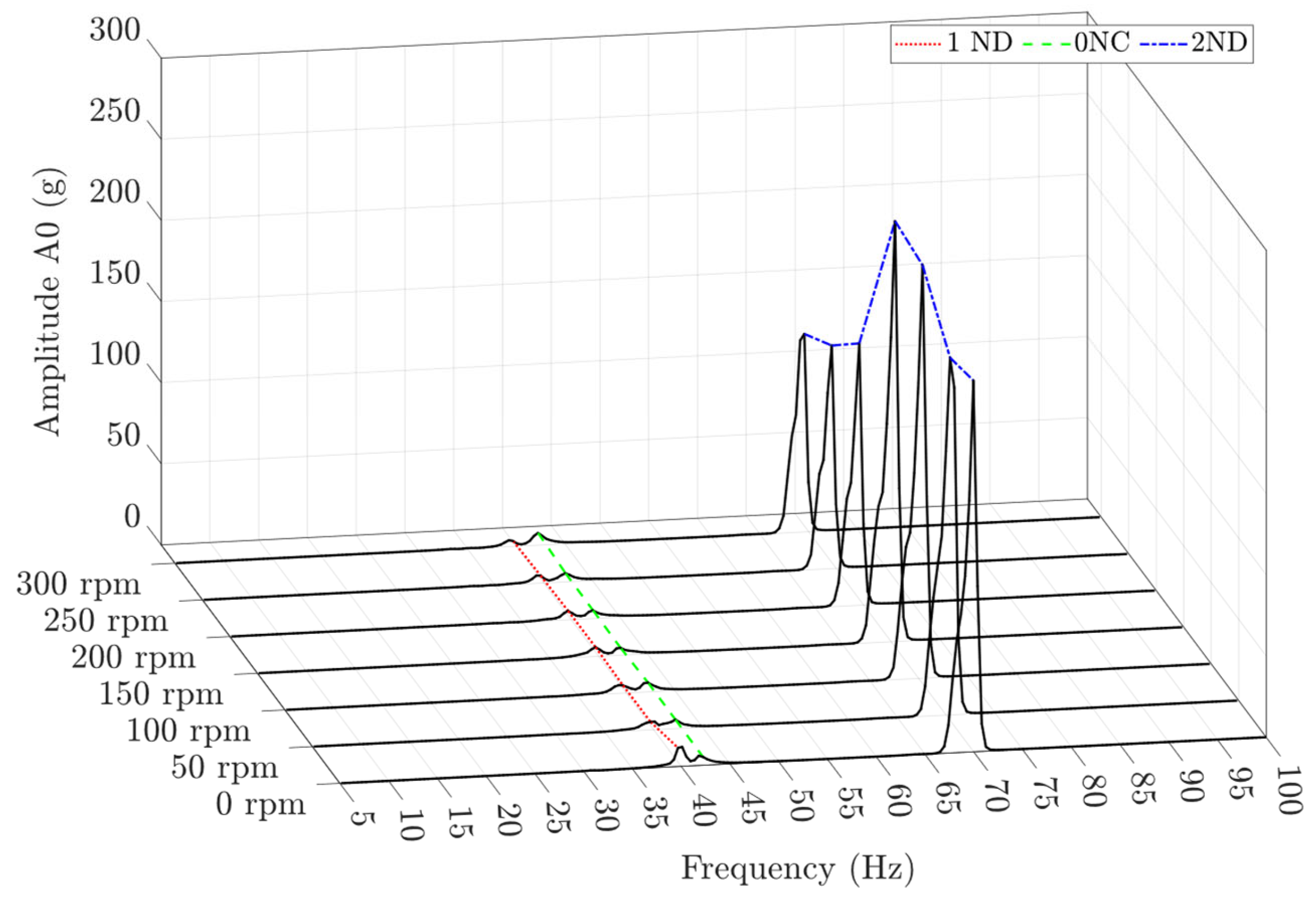
Figure 12 shows the spectra in the range of 5 to 100 Hz of the structural response measured by the on-board accelerometer at different rotating frequencies. The spectrum at 0 rpm presented three frequency peaks corresponding to the 1ND at 39.8 Hz, the 0NC at 41.2 Hz and the 2ND at 69.1 Hz. All these modes were also detected at higher rotating frequencies, from 50 rpm to 300 rpm, at the same frequencies. Similar to the conclusions of [
17], the current results suggest that the natural frequency detected from an on-board position,
, is independent of the rotating speed. This also agrees with the observations of [
12,
13,
14], who concluded that the rotating speed influences the natural frequencies, but this influence begins at higher rotating speeds than those tested in the present study.
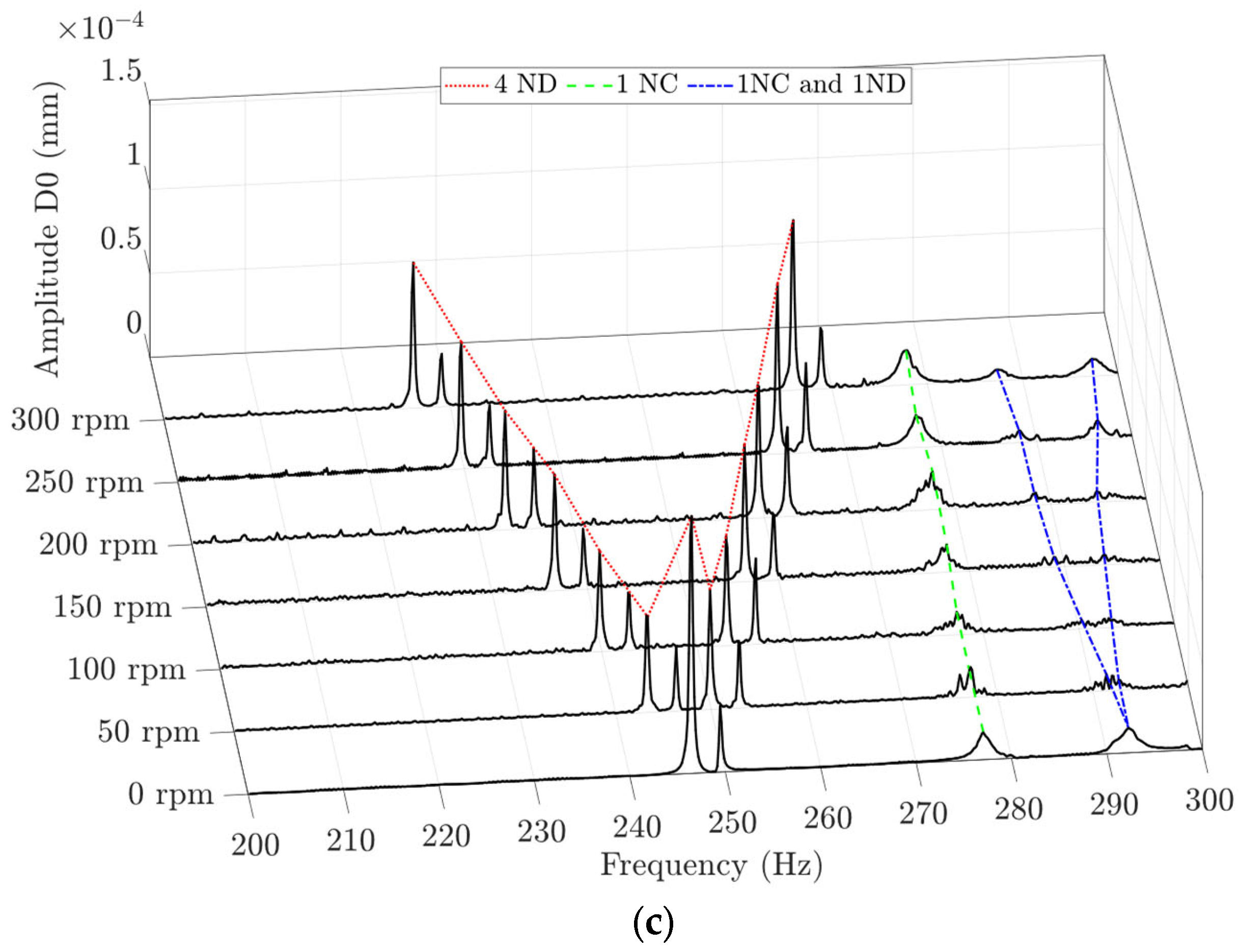
Figure 13 shows the spectra in the ranges of 16 to 100 Hz (a), 100 to 200 Hz (b) and 200 to 300 Hz (c) measured by the D0 mounted off board and pointing directly at the disk. The spectra at 0 rpm presented seven frequency peaks corresponding to the 1ND at 39.8 Hz, the 0NC at 41.2 Hz, the 2ND at 69.1 Hz, the 3ND at 147.1 Hz, the 4ND at 246.5 Hz, the 1NC at 277.1 Hz and the 1NC+1ND at 292.3 Hz. When the rotating speed was increased, the single frequency peaks corresponding to the 1ND, 2ND, 3ND, 4ND and 1NC+1ND were split into two frequency peaks: one with a higher value and the other with a lower value. The higher and lower frequency values increased and decreased, respectively, when the rotating speed of the disk increased. Moreover, this increase or decrease in frequency depended on the number of NDs of the mode shape. On the other hand, the single frequency peaks corresponding to 0NC and 1NC were not split, and they always presented the same frequency value. As also observed by [
23,
24,
25], the natural frequency detected by the D0,
, of an ND mode has been found to be dependent on the rotating speed of the disk,
, and the number of nodal diameters,
, based on the following expression:
Figure 14 shows the spectra in the range of 200 to 320 Hz measured by the off-board accelerometer mounted on the upper bearing in the radial direction, AUB
y, at different rotating speeds. The spectrum at 0 rpm presented three frequency peaks corresponding to the 4ND at 246.5 Hz, the 1NC at 277.1 Hz and the 1NC+1ND at 292.3 Hz. When the rotating speed was increased, the single frequency peak corresponding to the 4ND was split into two frequency peaks: one with a higher value and the other with a lower value. The higher and lower frequencies increased and decreased, respectively, when the rotating speed of the disk increased. On the other hand, the single frequency peak corresponding to 1NC was not split, and it always presented the same frequency value. Finally, the 1NC+1ND mode shape divided into three frequency peaks when the disk rotated: one with a higher value, another with a lower value and the last one with the same frequency value. The higher and lower frequencies increased and decreased, respectively, when the rotating speed of the disk increased. The third frequency presented the same value at different rotating speeds. The 1NC+1ND was therefore transmitted to the bearing housing partially like an ND mode and partially like an NC mode. Roig et al. [
35] also observed that the axial vibration of a rotating rotor is transmitted from the rotor to the supporting structure at the same frequency. Unlike to the transmission equation of D0 see Equation (1), in this case, the natural frequency detected by the accelerometer,
, of an ND mode only depended on the
based on the following expression:
These results indicate that the positions of the sensors had a great impact on the natural frequency detected when the disk was rotating. The detected natural frequency strongly depended on the reference frame of the sensor and if the sensor was able to measure displacements of the disk directly or remote vibrations on a bearing housing.
4.2. Results in Water
4.2.1. Natural Frequencies of the Non-Rotating Disk in Water
In this section, the presented experimental natural frequencies of the non-rotating disk in water were obtained using the frequency-varying PZT patch excitation method. Additionally, an acoustic–structural modal analysis was used to simulate the natural frequencies and mode shapes.
Table 2 shows the numerical and experimental natural frequencies corresponding to the 0NC, 1ND, 2ND, 3ND, 4ND, 1NC and 1NC+1ND. The discrepancy between the numerical and experimental results was lower than 10% for most of the modes. Exceptionally, the 1NC presented a discrepancy slightly higher than 10%.
The mode shapes and natural frequencies of the disk in water, simulated using an acoustic–structural modal analysis, were also computed using a harmonic analysis in which the structure was excited with a PZT patch. The mode shapes and natural frequencies calculated using both the modal analysis and the harmonic analysis were similar.
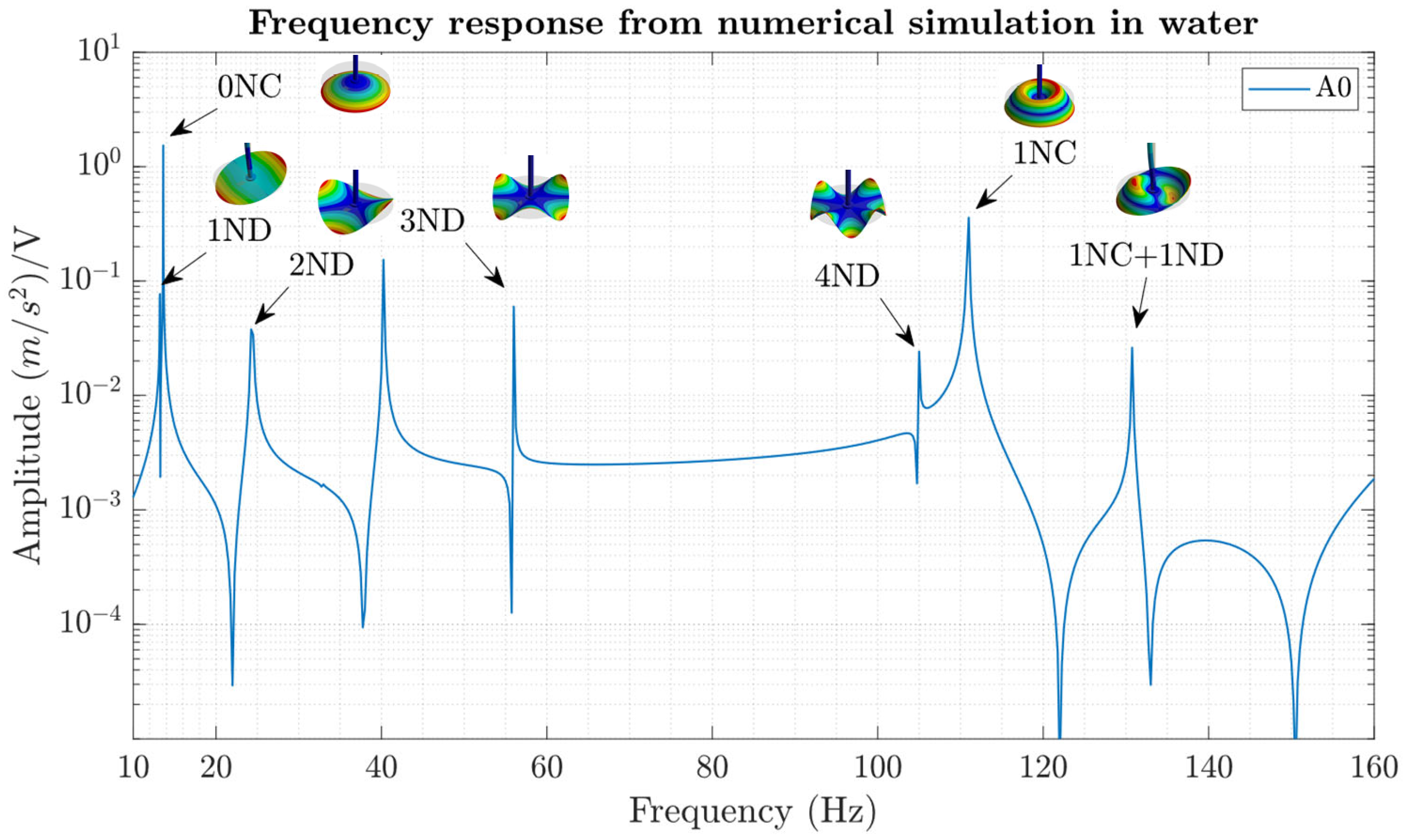
Figure 15 shows the numerical frequency response and some mode shapes calculated using the harmonic analysis. It can be seen that in addition to the frequency peaks corresponding to the natural frequencies of the disk itself, there were other frequency peaks that were associated with natural frequencies dominated by the shaft, which demonstrates that the PZT patch, which was located on the disk, was also able to excite natural frequencies of other components.
4.2.2. Influence of Rotation on the Natural Frequencies of the Disk in Water
Figure 16 shows the spectra of the structural response measured by different sensors mounted at different locations when the disk was not rotating and rotating in water. As the sensors measured different physical magnitudes, i.e., acceleration or strain, all the spectra were normalized using their maximum values in the range of 0 to 100 Hz. The spectrum at 0 rpm of the strain gauge SG3_9 shows two frequency peaks corresponding to the 1ND at 13.1 Hz, with a higher amplitude, and to the 2ND at 22 Hz, with a lower amplitude. At 50 rpm, the single frequency peaks associated with the 1ND and the 2ND were split into two frequency peaks. This split of a natural frequency detected from an on-board position was not observed in air, so it indicates that the hydrodynamic forces induced by the disk vibration in water were responsible for this effect. The splitting of natural frequencies measured from an on-board position when a disk was submerged in water and rotated was also observed by other authors [
17].
4.3. Comparison of the Natural Frequencies and Mode Shapes of the Non-Rotating Disk in Air and Water
Figure 17 shows the spectra of the structural responses measured by different sensors mounted at different locations when the disk was not rotating in air and water. All the spectra were normalized using their maximum values in the range of 0 to 100 Hz. All sensors detected the frequency peak associated with the 1ND at 39.8 Hz in air and the corresponding frequency peak at 13.1 Hz in water. Among all sensors, the 2ND frequencies at 69.1 Hz in air and at 22 Hz in water were only detected by SG2_6. Both natural frequencies decreased in value when the disk was submerged in water, which was due to the added mass effect. The peak corresponding to the 1ND at 39.8 Hz was lower in amplitude than the peak corresponding to the 2ND at 69.1 Hz measured by SG2_6 in air. Nonetheless, the peak corresponding to the 1ND at 13.1 Hz was higher in amplitude than the peak corresponding to the 2ND at 22 Hz measured by SG2_6 in water. This may indicate that the mode shape in water had rotated relative to that in air. Consequently, SG2_6 was close to a nodal diameter of the 1ND in air, whereas it was close to a nodal diameter of 2ND in water. Escaler et al. [
36] also observed that the mode shapes in water may change with respect to those in air.
Table 3 shows the numerical and experimental natural frequencies of the 1ND, 0NC, 2ND, 3ND, 4ND, 1NC and 1NC+1ND in air and water and the corresponding frequency reduction ratios (FRRs), calculated as:
where
and
are the natural frequencies in air and water, respectively. The circular mode shapes always presented higher FRRs than the diametral mode shapes. Additionally, those with a lower number of NCs or NDs also presented higher FRRs. For this reason, the 1ND presented a lower frequency than the 0NC in air but a higher frequency in water. Therefore, the NC modes, especially those with few nodal circles, accelerated more water resulting in higher added masses. Finally, we can also see that the numerical and experimental FRRs were in close agreement.
4.4. Detection of Natural Frequencies through a Transient Ramp-Up
A transient rotating speed ramp-up from 0 to 300 rpm was employed to excite the structure.
Figure 18 shows the spectra measured in air by the accelerometer mounted on the disk during the ramp-up, in orange, and during the chirp excitation using the PZT patch, in blue. The spectra show that all the natural frequencies of the disk, corresponding to the 1ND at 39.8 Hz, the 0NC at 41.2 Hz, the 2ND at 69.1 Hz, the 3ND at 147.1 Hz, the 4ND at 246.5 Hz, the 1NC at 277.1 Hz and the 1NC+1ND at 292.3 Hz were excited by the mechanical imbalance or its harmonics and were accurately measured by the on-board accelerometer. The natural frequencies in the low-frequency band presented higher amplitudes than those in the high-frequency band because they were excited by the first harmonics of the mechanical imbalance, which have a higher level of energy. Other natural frequencies in the low-frequency band, associated with the supporting structure, were also excited during the ramp-up. These natural frequencies were not excited when using a localized excitation on the disk, such as with the PZT patch.
Figure 19 shows the spectra measured in water by the accelerometer mounted on the lower bearing in a radial direction, ALBy, during a ramp-up, in orange, and during a chirp excitation using the PZT patch, in blue. These spectra show that most of the natural frequencies of the disk corresponding to the 1ND and 0NC at around 13 Hz, the 2ND at 22 Hz, the 3ND at 51.8 Hz and the 1NC+1ND at 128.9 Hz were accurately measured by the off-board accelerometer. It is probable that the other natural frequencies of the disk, corresponding to the 4ND and 1NC, were also excited by the mechanical imbalance and its harmonics, but they were not measured with precision from the bearing housing. Additional natural frequencies associated with the supporting structure were also excited and measured from the bearing housing.
5. Conclusions
This paper presents an experimental and numerical investigation of the modal response of a disk–shaft structure not rotating and rotating in air and water. The numerical and experimental modes of vibration were in close agreement. The maximum deviations between the natural frequencies of the ND family modes were 6.2% in air and 9.2% in water, and those of the NC family modes were 28% in air and 10.8% in water.
The natural frequencies of the disk could be detected using on-board and off-board sensors, as long as they were not mounted on a nodal position and they were oriented along the main displacement direction of the mode shape.
From on-board positions, the detected natural frequencies of ND modes in water depended on the rotating speed. Meanwhile, the detected natural frequencies of NC modes in air or water and of ND modes in air did not depend on the rotating speed. From off-board positions, the detected natural frequencies of ND modes in water depended on the rotating speed and the number of NDs, if measured from the disk displacements, and only on the rotating speed, if measured from vibrations.
The FRRs tended to decrease with the mode order, presenting the highest value for the 0NC mode.
Finally, the piezoelectric PZT patches and the rotating speed ramp-ups were proved to be reliable methods to excite the natural frequencies of rotating structures submerged in water. These methods have the potential to be applied in hydraulic turbines for the identification of natural frequencies of the rotor in actual operating conditions.
Future work should focus on achieving a more precise determination of the natural frequencies using off-board sensors located on the bearings, particularly when the structure is in water and rotating at higher speeds. For this purpose, it is recommended to use on-board sensors under non-rotating conditions in order to identify the transmissibility functions and the most optimal off-board measuring positions.
Author Contributions
Conceptualization, R.R. and X.E.; methodology, R.R., X.S.-B. and X.E.; software, X.S.-B.; validation, R.R. and X.E.; investigation, R.R., X.S.-B. and X.E.; writing—original draft preparation, R.R. and X.S.-B.; writing—review and editing, R.R., X.S.-B. and X.E.; supervision, X.E.; funding acquisition, X.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union’s Horizon H2020 research and innovation program under grant agreement No. 814958.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Trivedi, C.; Cervantes, M.J.; Gandhi, B.K.; Dahlhaug, O.G. Pressure measurements on a high-head Francis turbine during load acceptance and rejection. J. Hydraul. Res. 2014, 52, 283–297. [Google Scholar] [CrossRef]
- Trivedi, C.; Gandhi, B.K.; Cervantes, M.J. Effect of transients on Francis turbine runner life: A review. J. Hydraul. Res. 2013, 51, 121–132. [Google Scholar] [CrossRef]
- Goyal, R.; Gandhi, B.K.; Cervantes, M.J. PIV measurements in Francis turbine—A review and application to transient operations. Renew. Sustain. Energy Rev. 2018, 81, 2976–2991. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Y.; Wang, Z. A Review of Fatigue Damage Mechanism in Hydro Turbines. Renew. Sustain. Energy Rev. 2016, 54, 1–14. [Google Scholar] [CrossRef]
- Presas, A.; Luo, Y.; Wang, Z.; Guo, B. Fatigue life estimation of Francis turbines based on experimental strain measurements: Review of actual data and future trends. Renew. Sustain. Energy Rev. 2019, 102, 96–110. [Google Scholar] [CrossRef]
- Rodriguez, C.; Egusquiza, E.; Escaler, X.; Liang, Q.; Avellan, F. Experimental investigation of added mass effects on a Francis turbine runner in still water. J. Fluids Struct. 2006, 22, 699–712. [Google Scholar] [CrossRef]
- Liang, Q.; Rodríguez, C.; Egusquiza, E.; Escaler, X.; Farhat, M.; Avellan, F. Numerical simulation of fluid added mass effect on a Francis turbine runner. Comput. Fluids 2007, 36, 1106–1118. [Google Scholar] [CrossRef]
- Huang, X.; Egusquiza, E.; Valero, C.; Presas, A. Dynamic behaviour of pump-turbine runner: From disk to prototype runner. IOP Conf. Ser. Mater. Sci. Eng. 2013, 52, 022036. [Google Scholar] [CrossRef]
- Presas, A.; Valero, C.; Huang, X.; Egusquiza, E.; Farhat, M.; Avellan, F. Analysis of the dynamic response of pump-turbine runners—Part I: Experiment. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 052015. [Google Scholar] [CrossRef]
- Pust, L.; Pesek, L. Vibration of circular bladed disk with imperfections. J. Bifurc. Chaos 2011, 10, 2893–2904. [Google Scholar] [CrossRef]
- Heo, J.W.; Chung, J. Vibration analysis of a flexible rotating disk with angular misalignment. J. Sound Vib. 2004, 274, 821–841. [Google Scholar] [CrossRef]
- Lamb, H.; Southwell, R.V. The vibrations of spinning discs. Proc. R. Soc. London 1921, 99, 272–280. [Google Scholar]
- Campbell, W. The protection of steam turbine disk wheels from axial vibration. Trans. ASME 1924, 46, 272–280. [Google Scholar]
- Southwell, R.V. On the free transverse vibrations of a uniform circular disc clamped at its centre and on the effects of rotation. Proc. R. Soc. London 1922, 101, 133–153. [Google Scholar]
- Tang, Q.; Li, C.; She, H.; Wen, B. Analysis of frequency and mode shape of rotating-flexible disk-drum coupled structure with non-continuous conections. Int. J. Mech. Sci. 2021, 190, 106004. [Google Scholar] [CrossRef]
- She, H.; Li, C. Effects of centrifugal stiffening and spins softening on nonlinear modal characteristics of cyclic blades with impact-friction coupling. Nonlinear Dyn. 2022, 110, 3229–3254. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. Influence of the rotation on the natural frequencies of a submerged-confined disk in water. J. Sound Vib. 2015, 337, 161–180. [Google Scholar] [CrossRef]
- Askari, E.; Jeong, K.-H.; Amabili, M. Hydroelastic vibration of circular plates immersed in a liquid-filled container with free surface. J. Sound Vib. 2013, 332, 3064–3085. [Google Scholar] [CrossRef]
- Valentín, D.; Presas, A.; Egusquiza, E.; Valero, C. Experimental study on the added mass and damping of a disk submerged in a partially fluid-filled tank with small radial confinement. J. Fluids Struct. 2014, 50, 1–17. [Google Scholar] [CrossRef]
- Louyot, M.; Nennemann, B.; Monette, C.; Gosselin, F. Modal analysis of a spinning disk in a dense fluid as a model for high head hydraulic turbines. J. Fluid Struct. 2020, 94, 102965. [Google Scholar] [CrossRef]
- Nennemann, B.; Monette, C.; Braun, O.; Biner, D.; Münch-Alligné, C. Eigenfrequencies of rotating discs in dense fluid: Imposed modal motion approach. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012072. [Google Scholar] [CrossRef]
- Horisberger, W.M.; Monette, B.; Sick, C.; Dual, M. Experimental modal analysis of disk-like rotor-stator system coupled by viscous liquid. J. Fluids Struct. 2019, 88, 198–215. [Google Scholar]
- Mehdigholi, H. Forced Vibration of Rotating Discs and Interaction with Non-Rotating Structures; Imperiall College of Science, Technology and Medicine: London, UK, 1991. [Google Scholar]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. On the detection of the natural frequencies and mode shapes of submerged rotating disk-like structures from the casing. Mech. Syst. Signal Process. 2015. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U.; Weber, W. Natural frequencies of rotating disk-like structures submerged viewed from the stationary frame. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 082023. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Egusquiza, M.; Bossio, M. On the use of PZT-Patches as Exciters in Modal Analysis: Application to Submerged Structures. Proceedings 2017, 1, 32. [Google Scholar] [CrossRef]
- Presas, A.; Valentin, D.; Egusquiza, E.; Valero, C.; Seidel, U. Feasibility of Using PZT Actuators to Study the Dynamic Behaviour of a Rotating Disk due to Rotor-Stator Interaction. Sensors 2014, 14, 11919–11942. [Google Scholar] [CrossRef]
- De La Torre, O.; Escaler, X.; Egusquiza, E.; Farhat, M. Experimental investigation of added mass effects on a hydrofoil under cavitation conditions. J. Fluids Struct. 2013, 39, 173–187. [Google Scholar] [CrossRef]
- Solemslie, B.W.; Ostby, P.T.; Iliev, I. Decomposition of the structural response of the Francis-99 runner during resonance. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012093. [Google Scholar] [CrossRef]
- Kumar, Y.; Kumar, K.M. Modal Analysis for Optimezed Placement of Piezoelectric Patches on a Composite Beam Structure. Mater. Today Proc. 2018, 5, 21135–21139. [Google Scholar] [CrossRef]
- Presas, A.; Luo, Y.; Wang, Z.; Valentin, D.; Egusquiza, M. A Review of PZT Patches Applications in Submerged Systems. Sensors 2018, 18, 2251. [Google Scholar] [CrossRef] [PubMed]
- Valentin, D.; Presas, A.; Valero, C.; Egusquiza, M.; Jou, E.; Egusquiza, E. Influence of the hydrodynamic damping on the Dynamic response of Francis turbine runners. J. Fluids Struct. 2019, 90, 71–89. [Google Scholar] [CrossRef]
- COMSOL INC. Piezoelectric Materials: Understanding the Standards. Available online: https://www.comsol.com/blogs/piezoelectric-materials-understanding-standards/ (accessed on 13 October 2022).
- Sánchez-Botello, X.; de la Torre, O.; Roig, R.; Costa-Castelló, R.; Escaler, X. PZT actuators as on-board instruments to reduce vibrations and strains in submerged structures. IOP Conf. Ser. Earth Environ. Sci. 2022, 1079, 012097. [Google Scholar] [CrossRef]
- Roig, R.; Sanchez-Botello, X.; Escaler, X.; Mulu, B.; Högström, C.-M. On the Rotating Vortex Rope and Its Induced Structural Response in a Kaplan Turbine Model. Energies 2022, 15, 6311. [Google Scholar] [CrossRef]
- Escaler, X.; De La Torre, O. Axisymmetric vibrations of a circular Chladni plate in air and fully submerged in water. J. Fluids Struct. 2018, 82, 432–445. [Google Scholar] [CrossRef]
Figure 1.
(a) The test rig mounted in the laboratory. (b) Geometry and dimensions of the test rig.
Figure 1.
(a) The test rig mounted in the laboratory. (b) Geometry and dimensions of the test rig.
Figure 2.
(a) End-of-shaft SR-series slip ring assembly. (b) Lateral B-series slip ring assembly.
Figure 2.
(a) End-of-shaft SR-series slip ring assembly. (b) Lateral B-series slip ring assembly.
Figure 3.
(a) Scheme of the position of the instrumentation used during the tests (bottom and lateral views). (b) Laser displacement sensors mounted on the shaft. (c) Triaxial accelerometers mounted on the lower and upper housings of the bearings.
Figure 3.
(a) Scheme of the position of the instrumentation used during the tests (bottom and lateral views). (b) Laser displacement sensors mounted on the shaft. (c) Triaxial accelerometers mounted on the lower and upper housings of the bearings.
Figure 4.
Scheme of the methodologies used to perform the experimental modal tests.
Figure 4.
Scheme of the methodologies used to perform the experimental modal tests.
Figure 5.
(a) Scheme of the impact positions on the disk excited using the instrumented hammer and (b) the real and imaginary parts of the averaged FRF between the on-board accelerometer and the hammer signals.
Figure 5.
(a) Scheme of the impact positions on the disk excited using the instrumented hammer and (b) the real and imaginary parts of the averaged FRF between the on-board accelerometer and the hammer signals.
Figure 6.
(a) Waterfall result obtained from the STFT analysis of SG3_8 when the disk was submerged in water and rotating at 50 rpm while excited with a chirp signal ranging from 0 to 100 Hz. (b) Maximum spectrum of the STFT, showing the different natural frequencies in water.
Figure 6.
(a) Waterfall result obtained from the STFT analysis of SG3_8 when the disk was submerged in water and rotating at 50 rpm while excited with a chirp signal ranging from 0 to 100 Hz. (b) Maximum spectrum of the STFT, showing the different natural frequencies in water.
Figure 7.
(a) Numerical model of the test rig when the disk was submerged inside the tank of water. (b) Close-up around the piezoelectric patch model, with its active and soft layers indicated and the disk flipped to see the PZT in detail.
Figure 7.
(a) Numerical model of the test rig when the disk was submerged inside the tank of water. (b) Close-up around the piezoelectric patch model, with its active and soft layers indicated and the disk flipped to see the PZT in detail.
Figure 8.
Numerical modes of vibration of the non-rotating disk in air: (a) 1ND; (b) 0NC; (c) 2ND; (d) 3ND; (e) 4ND; (f) 1NC; (g) 1NC+1ND.
Figure 8.
Numerical modes of vibration of the non-rotating disk in air: (a) 1ND; (b) 0NC; (c) 2ND; (d) 3ND; (e) 4ND; (f) 1NC; (g) 1NC+1ND.
Figure 9.
Numerical frequency response obtained from a harmonic analysis when the disk was not rotating in air.
Figure 9.
Numerical frequency response obtained from a harmonic analysis when the disk was not rotating in air.
Figure 10.
Numerical (left) and experimental (right) mode shapes of the non-rotating disk in air: (a) 2ND and (b) 3ND.
Figure 10.
Numerical (left) and experimental (right) mode shapes of the non-rotating disk in air: (a) 2ND and (b) 3ND.
Figure 11.
Maximum normalized spectra of the STFT measured from several sensors when the disk was excited with a chirp in the range of 0–100 Hz.
Figure 11.
Maximum normalized spectra of the STFT measured from several sensors when the disk was excited with a chirp in the range of 0–100 Hz.
Figure 12.
Maximum spectra of the STFT of the on-board accelerometer when the disk was excited in air with a chirp in the range of 0 to 100 Hz at different rotating speeds.
Figure 12.
Maximum spectra of the STFT of the on-board accelerometer when the disk was excited in air with a chirp in the range of 0 to 100 Hz at different rotating speeds.
Figure 13.
(a) Maximum spectra of the STFT of the D0 when the disk was excited with chirps in air in the ranges of 0 to 100 Hz (a), 100 to 200 Hz (b) and 200 to 300 Hz (c) at different rotating speeds.
Figure 13.
(a) Maximum spectra of the STFT of the D0 when the disk was excited with chirps in air in the ranges of 0 to 100 Hz (a), 100 to 200 Hz (b) and 200 to 300 Hz (c) at different rotating speeds.
Figure 14.
Maximum spectra of the STFT of the radial accelerometer, AUBy, when the disk was excited in air with a chirp in the range of 200 to 300 Hz at different rotating speeds.
Figure 14.
Maximum spectra of the STFT of the radial accelerometer, AUBy, when the disk was excited in air with a chirp in the range of 200 to 300 Hz at different rotating speeds.
Figure 15.
Numerical frequency response obtained from a harmonic analysis of the non-rotating disk in water.
Figure 15.
Numerical frequency response obtained from a harmonic analysis of the non-rotating disk in water.
Figure 16.
Maximum normalized spectra of the STFT measured from several sensors when the disk (non-rotating and rotating) was excited with a chirp in the range of 0–100 Hz in water.
Figure 16.
Maximum normalized spectra of the STFT measured from several sensors when the disk (non-rotating and rotating) was excited with a chirp in the range of 0–100 Hz in water.
Figure 17.
Maximum normalized spectra of the STFT measured from several sensors when the disk was excited with a chirp in the range of 0–100 Hz in air and water.
Figure 17.
Maximum normalized spectra of the STFT measured from several sensors when the disk was excited with a chirp in the range of 0–100 Hz in air and water.
Figure 18.
Maximum spectra of the STFT of A0 when exciting the disk with a chirp applied using the PZT patch, in blue, or using a ramp-up, in orange, in air.
Figure 18.
Maximum spectra of the STFT of A0 when exciting the disk with a chirp applied using the PZT patch, in blue, or using a ramp-up, in orange, in air.
Figure 19.
Maximum spectra of the STFT of ALBy when exciting the disk with a chirp applied using the PZT patch, in blue, or using a ramp-up, in orange, in water.
Figure 19.
Maximum spectra of the STFT of ALBy when exciting the disk with a chirp applied using the PZT patch, in blue, or using a ramp-up, in orange, in water.
Table 1.
Natural frequencies obtained from numerical and experimental modal analyses of the non-rotating disk in air.
Table 1.
Natural frequencies obtained from numerical and experimental modal analyses of the non-rotating disk in air.
| Mode Shape | Numerical Simulation | Experimental Modal Test | Discrepancy |
|---|
| 1ND | 37.5 Hz | 39.8 Hz | 6.2% |
| 0NC | 57.3 Hz | 41.2 Hz | 28.0% |
| 2ND | 67.3 Hz | 69.1 Hz | 2.7% |
| 3ND | 140.8 Hz | 147.1 Hz | 4.5% |
| 4ND | 246.2 Hz | 246.5 Hz | 0.1% |
| 1NC | 329.3 Hz | 277.1 Hz | 15.9% |
| 1NC+1ND 1 | 355.1 Hz | 292.3 Hz | 17.7% |
Table 2.
Natural frequencies obtained from numerical and experimental modal analyses of the non-rotating disk in water.
Table 2.
Natural frequencies obtained from numerical and experimental modal analyses of the non-rotating disk in water.
| Mode Shape | Numerical Simulation | Experimental Modal Test | Discrepancy |
|---|
| 0NC | 13.0 Hz | 12.1 Hz | 7.1% |
| 1ND | 12.9 Hz | 13.1 Hz | 1.4% |
| 2ND | 24.3 Hz | 22.0 Hz | 9.2% |
| 3ND | 55.8 Hz | 51.8 Hz | 7.3% |
| 4ND | 104.9 Hz | 101.0 Hz | 3.8% |
| 1NC | 110.6 Hz | 122.6 Hz | 10.8% |
| 1NC+1ND 1 | 128.2 Hz | 128.9 Hz | 0.5% |
Table 3.
Frequency reduction ratios (FRRs) obtained from numerical and experimental modal analyses of the non-rotating disk in air and water.
Table 3.
Frequency reduction ratios (FRRs) obtained from numerical and experimental modal analyses of the non-rotating disk in air and water.
| Mode Shape | Numerical | Experimental | FRR
Numerical | FRR
Experimental |
|---|
| Air | Water | Air | Water |
|---|
| 1ND | 37.5 Hz | 12.9 Hz | 39.8 Hz | 13.1 Hz | 65.55% | 67.10% |
| 0NC | 57.3 Hz | 13.0 Hz | 41.2 Hz | 12.1 Hz | 77.27% | 70.66% |
| 2ND | 67.3 Hz | 24.3 Hz | 69.1 Hz | 22.0 Hz | 63.91% | 68.11% |
| 3ND | 140.8 Hz | 55.8 Hz | 147.1 Hz | 51.8 Hz | 60.34% | 64.80% |
| 4ND | 246.2 Hz | 104.9 Hz | 246.5 Hz | 101.0 Hz | 57.38% | 59.02% |
| 1NC | 329.3 Hz | 110.6 Hz | 277.1 Hz | 122.6 Hz | 66.41% | 55.75% |
| 1NC+1ND 1 | 355.1 Hz | 128.2 Hz | 292.3 Hz | 128.9 Hz | 63.90% | 55.91% |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).