Hazard Model: Epidemic-Type Aftershock Sequence (ETAS) Model for Hungary
Abstract
1. Introduction
1.1. Motivation
1.2. Aim of the Study
1.3. Background
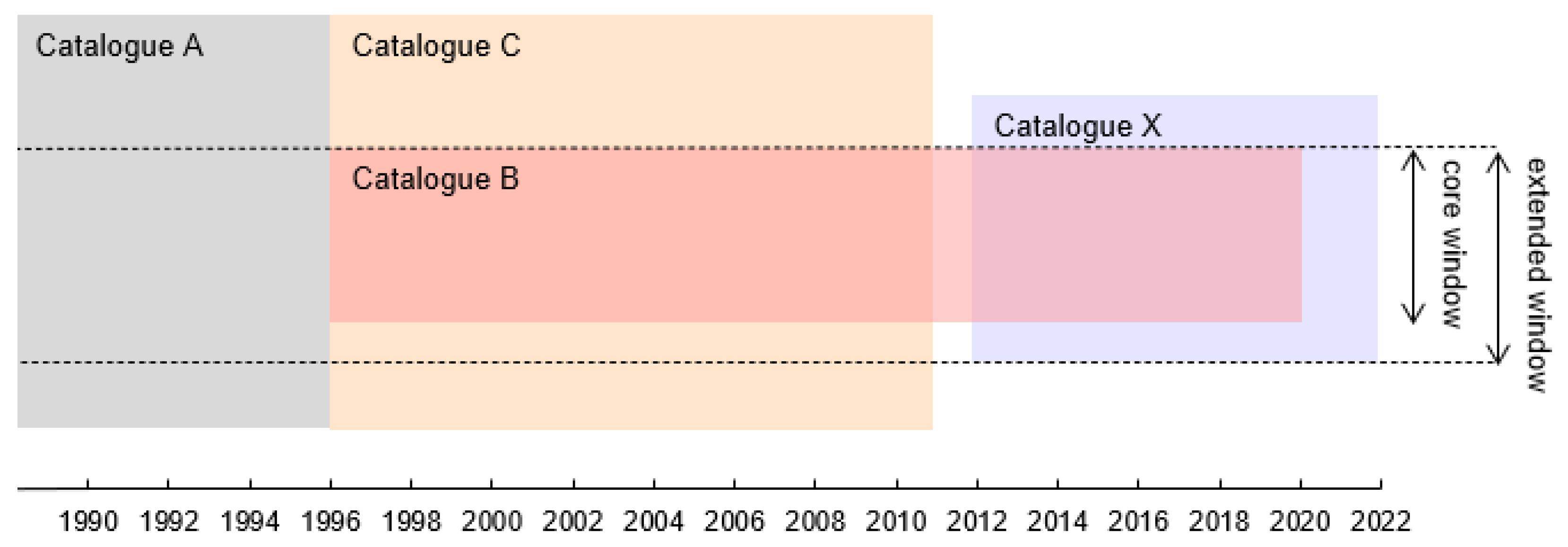
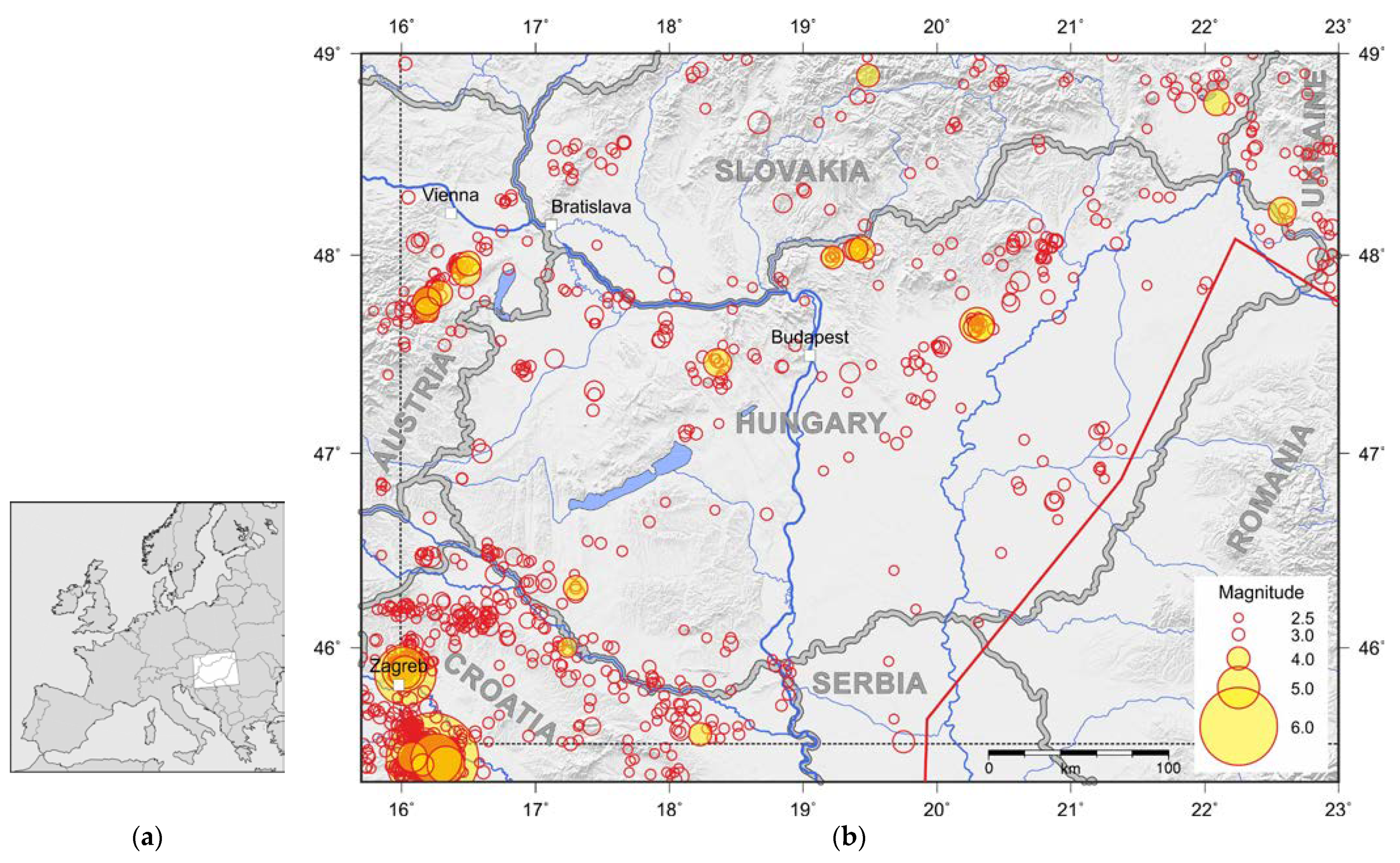
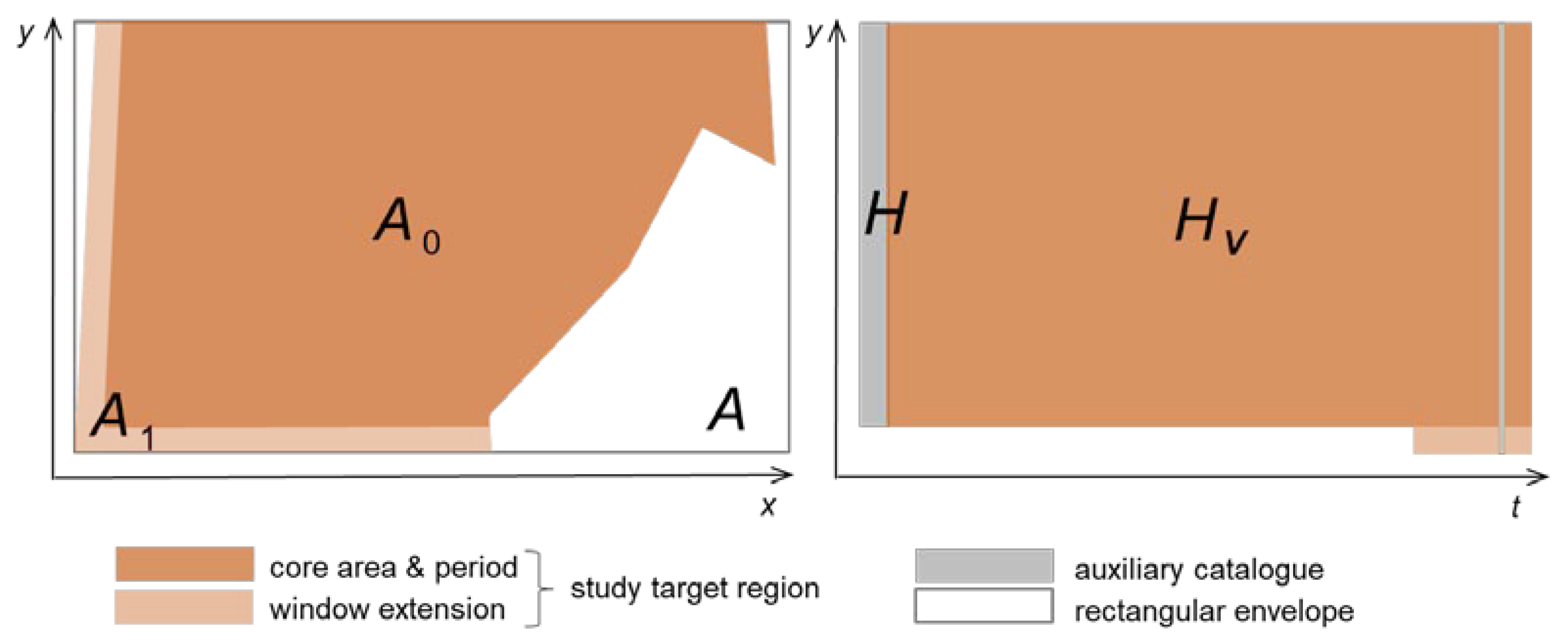
2. Data
- Catalogue A: Historical catalogue for the period 456 A.D. to 1995 [21], collected from several primary sources, partly instrumental and partly macroseismic. The number of events included in the extended window that reach the magnitude threshold is 2402. Due to obvious data quality limitations, these events are not used directly for ETAS parameter fitting but only as data for subsequent model downscaling.
- Catalogue B: Instrumental catalogue covering the core window and the period 1996 to 2019, based on the recordings of the Hungarian seismograph network [19]. The number of events reaching the magnitude threshold is 654.
- Catalogue C: Instrumental catalogue data for the period 1996 to 2010, collected and merged from international sources [22,23,24]. While some of the underlying sources are continuously updated, the merged dataset is only available to the end of 2010. The number of events included in the extended window that reach the magnitude threshold is 1107, partly overlapping with catalogue B data in the core window.
- Catalogue X: Initial event list (IEL) data covering the period 2012 to 2021 [25], based on the recordings of the Hungarian seismograph network. IEL data are an interim phase of the yearly updates of the Hungarian instrumental earthquake catalogue (catalogue B). Geographical coverage is wider than the core window by a margin of 0.2 degrees latitude and 0.3 degrees longitude in all directions. Automated preliminary epicenter determinations are post-processed for the monthly publications of the list, which may result in some coordinate shifts across the window boundary. Thus, the western and southern edge of the extended window corresponds approximately to the geographical scope of the IEL. The number of events from IEL included in the extended window that reach the magnitude threshold is 2313, fully overlapping with catalogue B data in the core window in the period 2012 to 2019.
3. Epidemic-Type Aftershock Sequence (ETAS) Modelling Methods
3.1. Model Formulation
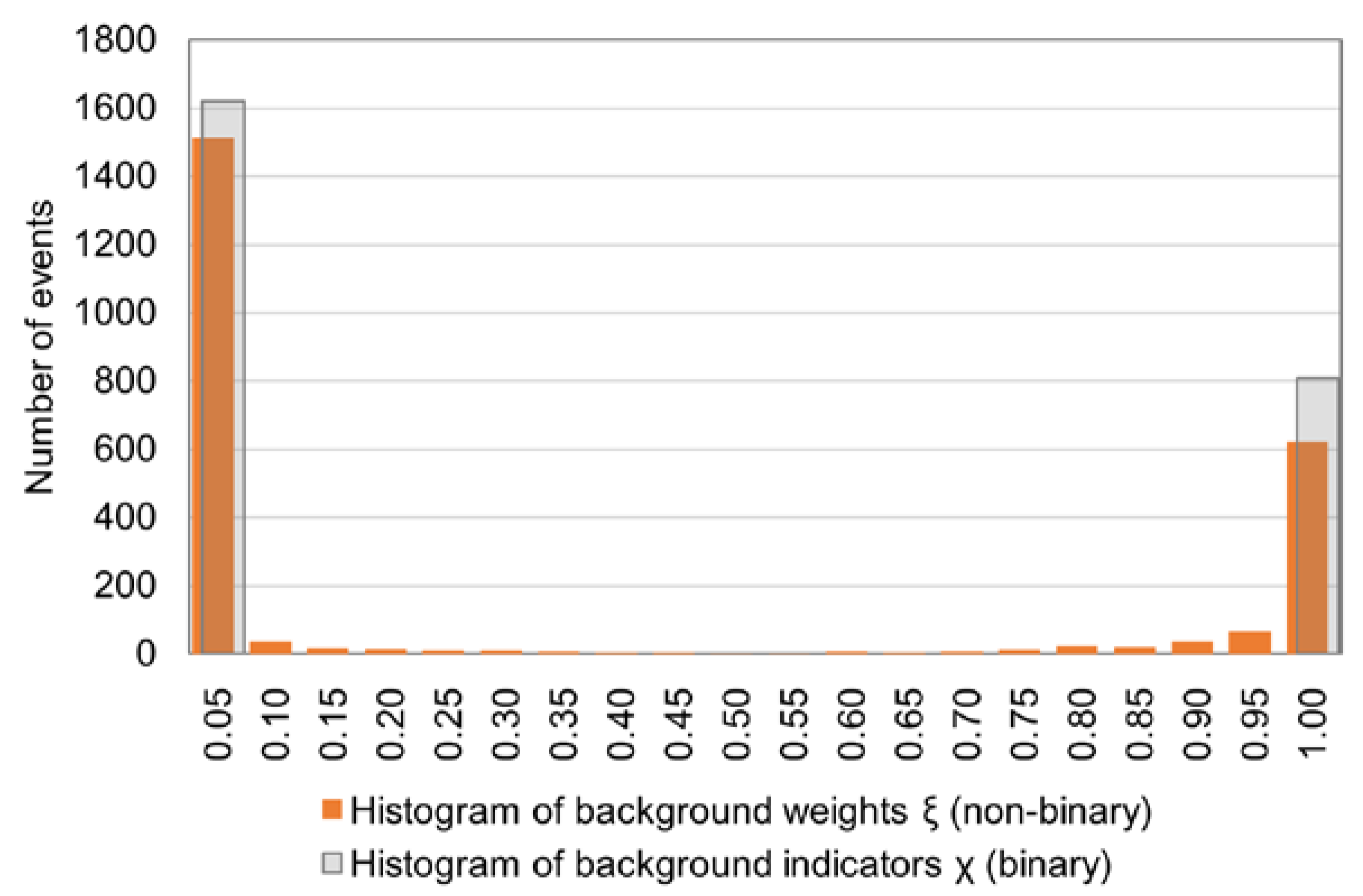
3.2. Parameter Fitting
- kernel smoothing for ;
- log-likelihood optimization for ;
- follow-on declustering steps based on the ETAS model.
4. Modelling Results
4.1. ETAS Parameters
4.2. Parameter Ranges
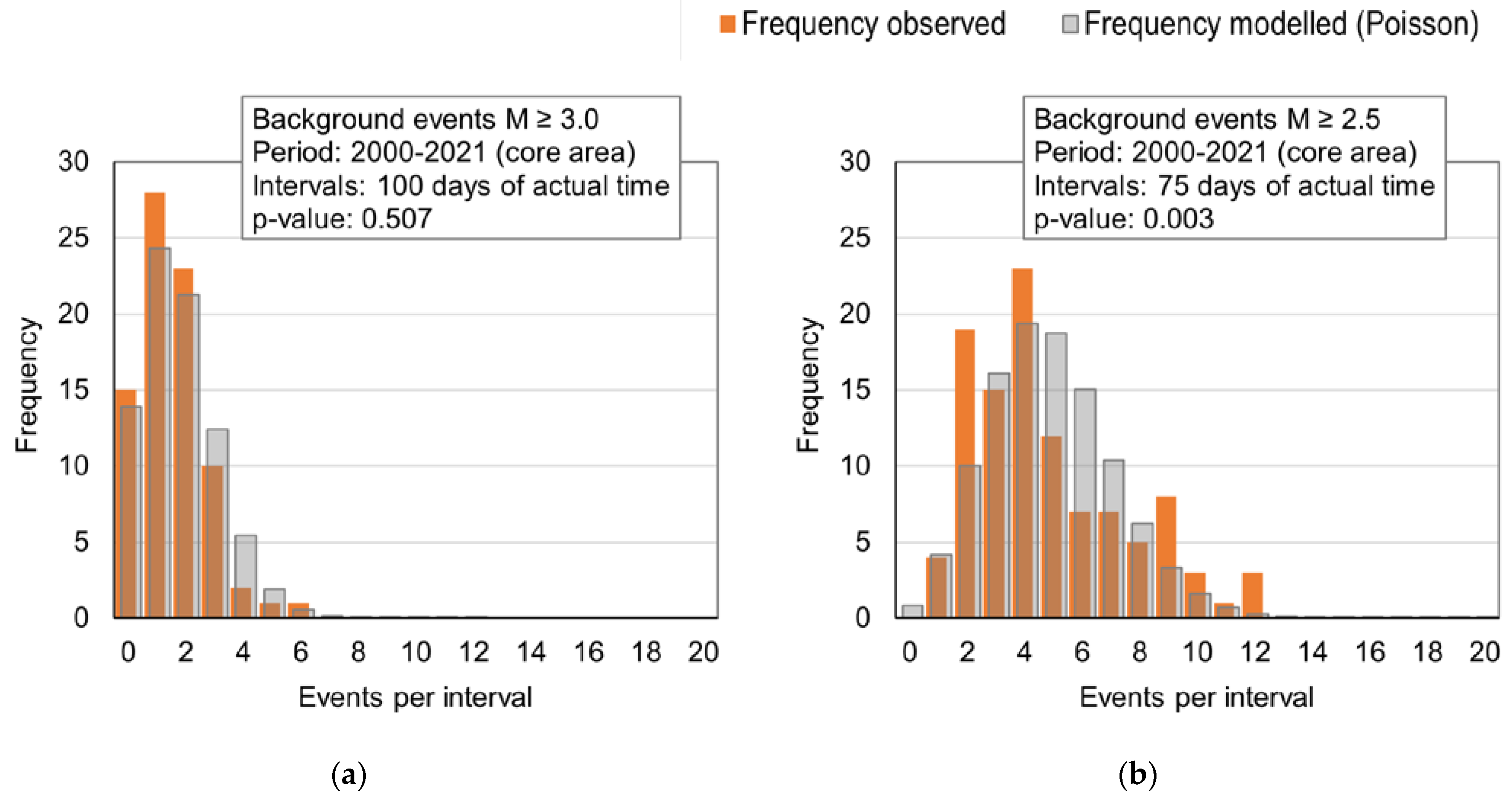
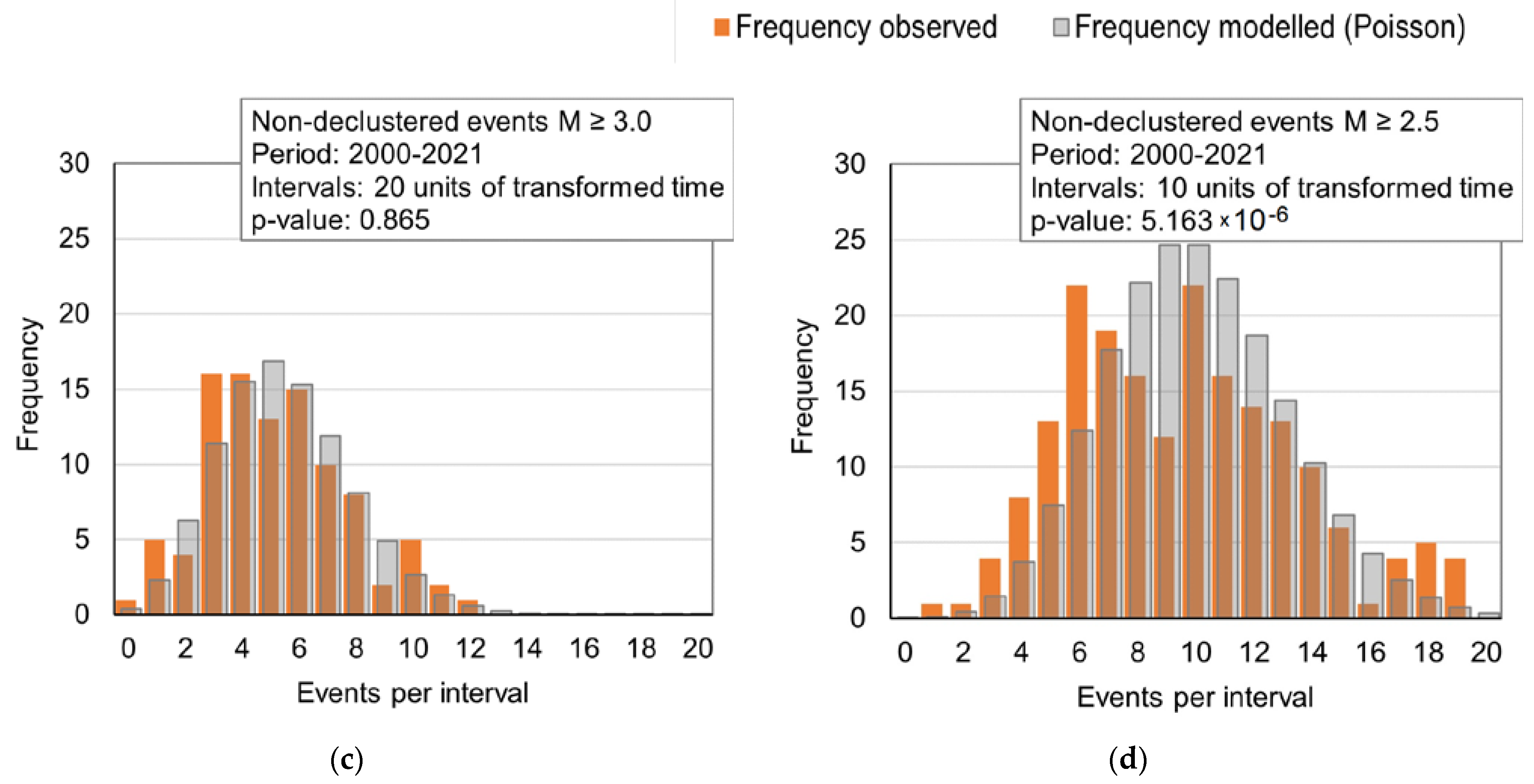
4.3. Event Accumulation Test
4.4. Poisson Goodness-of-Fit Test
4.5. Distance Test
4.6. Time Lag Test
4.7. Triggering Ability Test
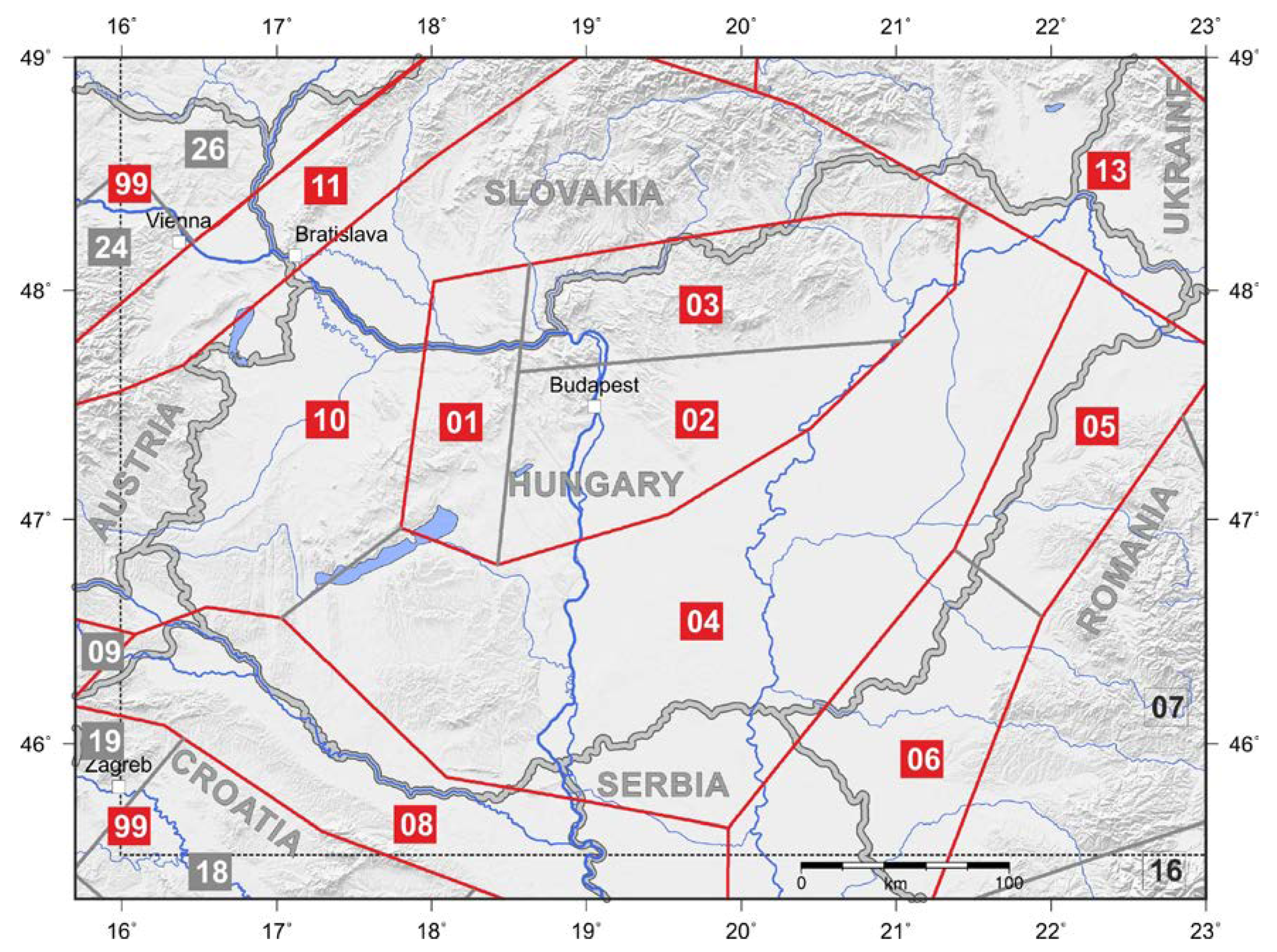
5. Parameter Downscaling Methods
5.1. Motivation for Downscaling
5.2. Maximum Likelihood Estimation with Variable Observation Periods
5.3. Transformed Time Estimates
- Parameter is obtained by solving Equation (18) for the non-declustered event set in the transformed time, and is set equal to .
- The scaling factor is set such that for the non-declustered event set in the transformed time, where is calculated according to Equation (19).
6. Parameter Downscaling Results
6.1. Downscaled Parameters
6.2. Sensitivity of the Downscaled Parameters
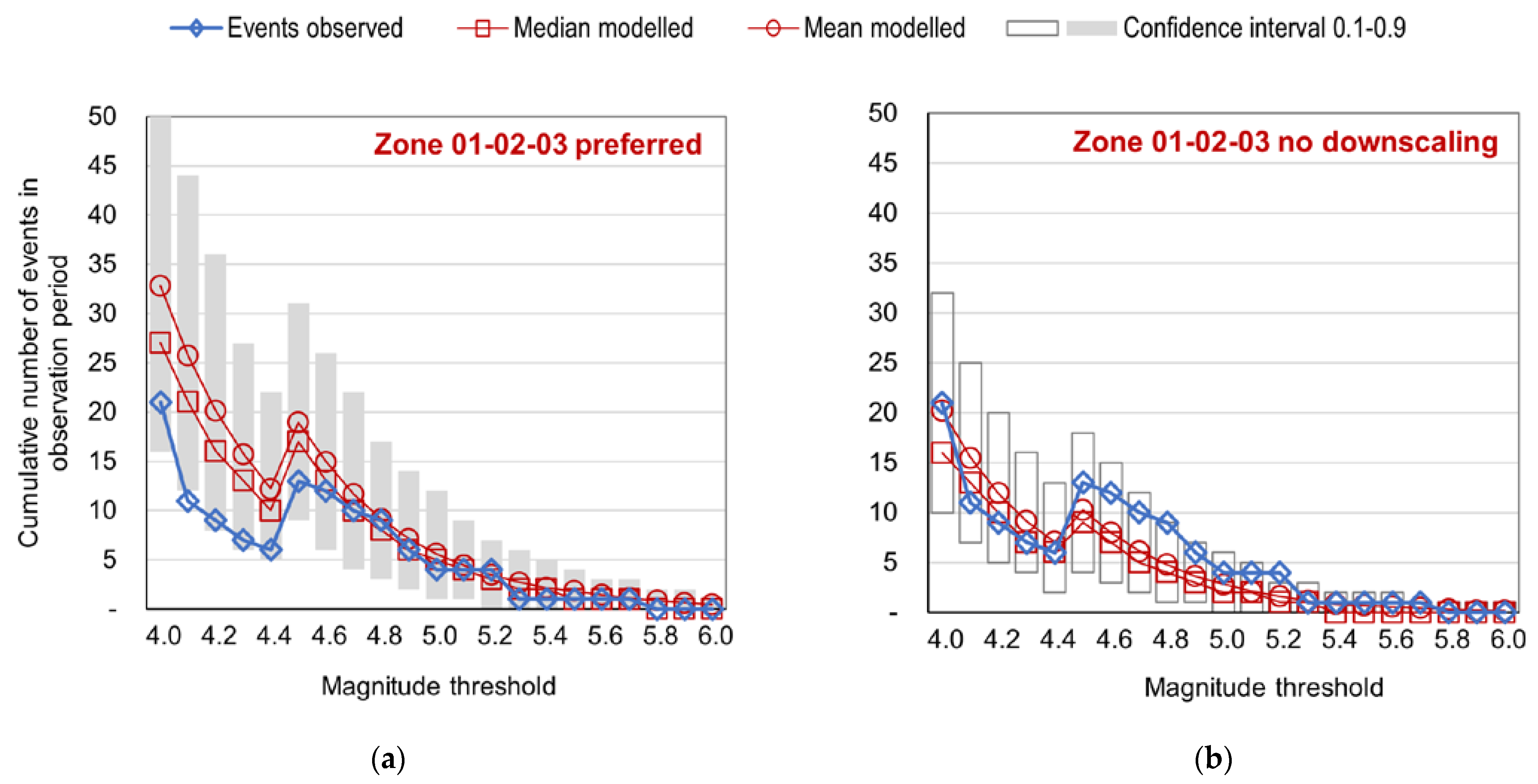
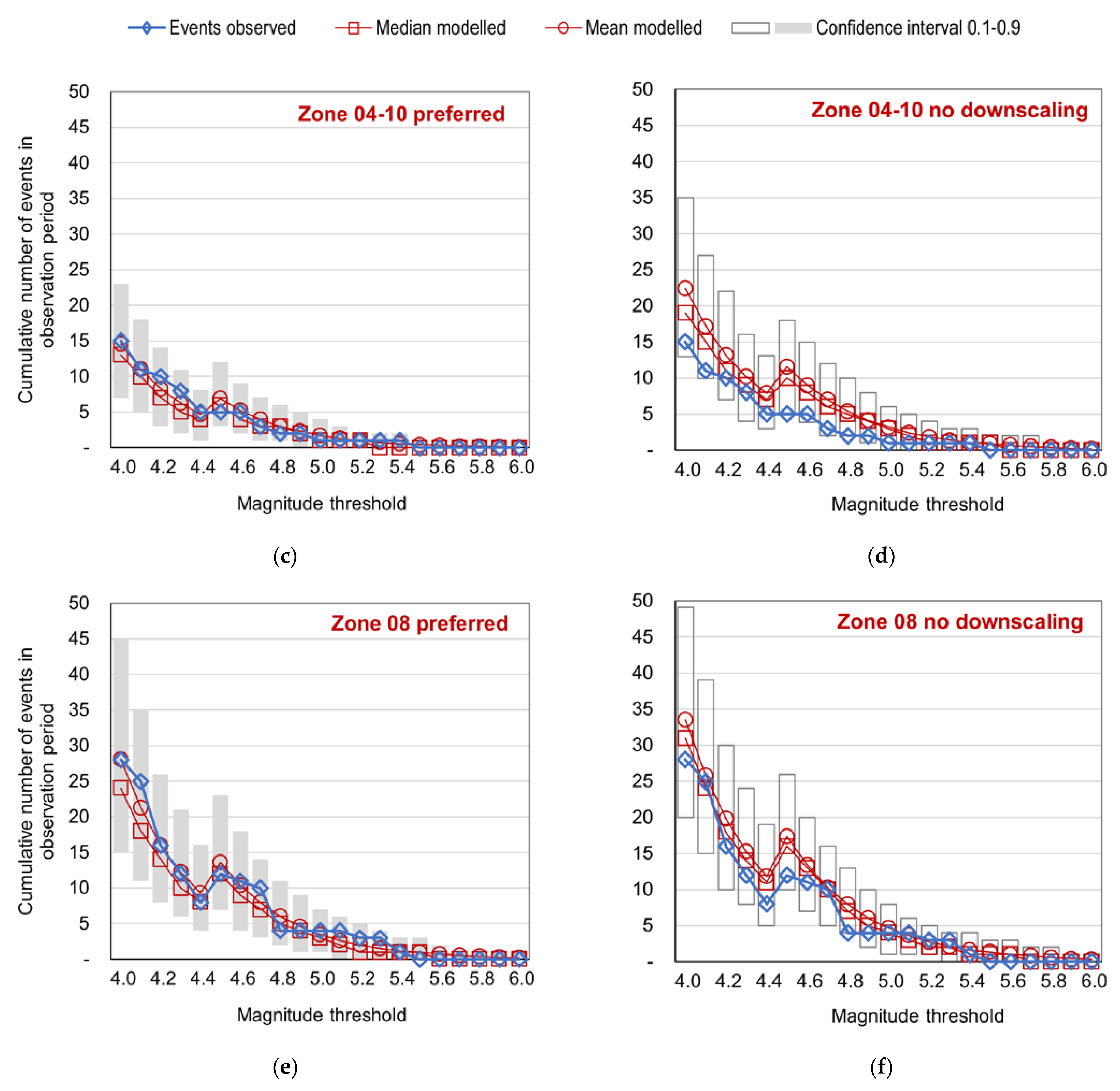
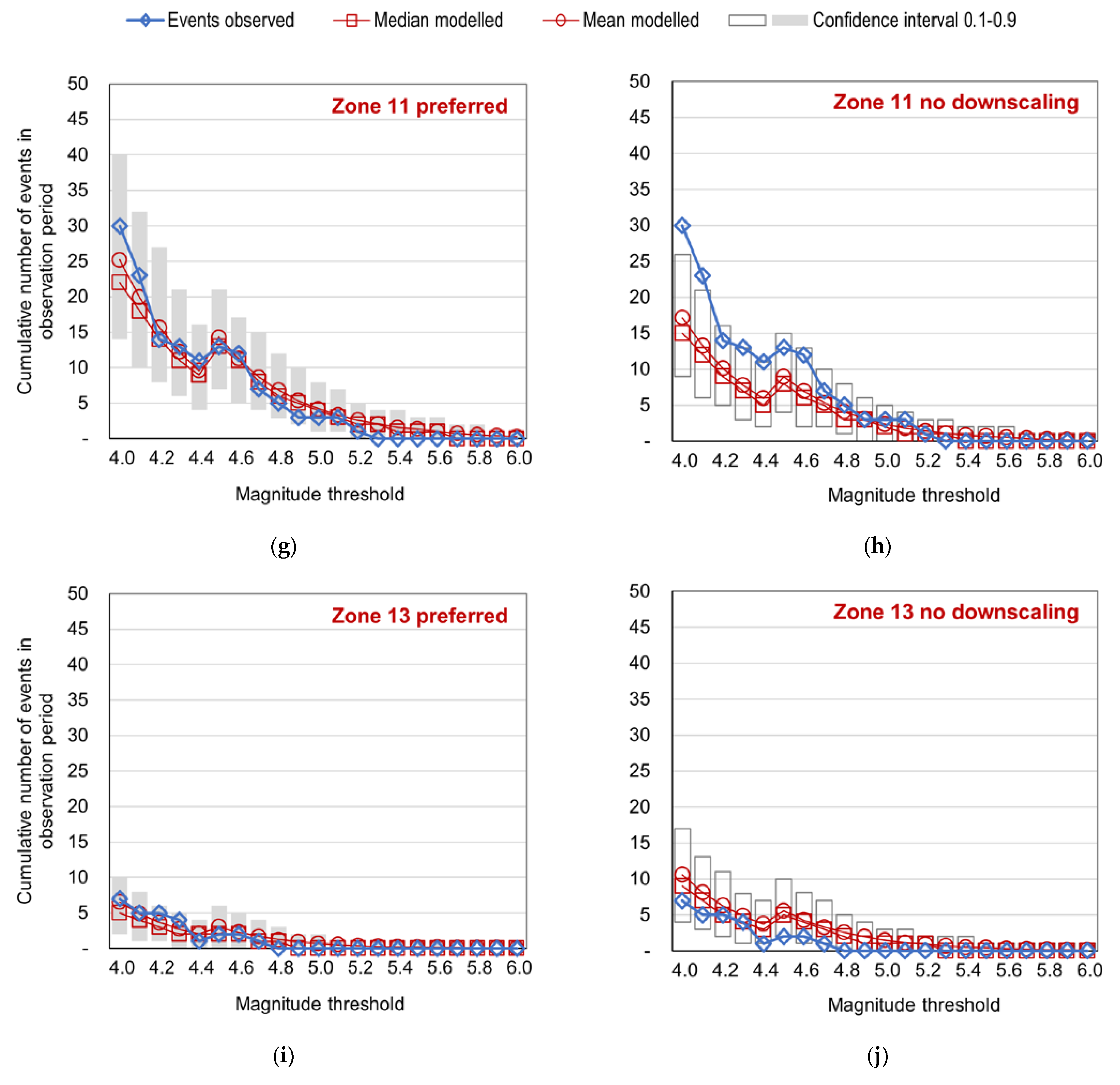
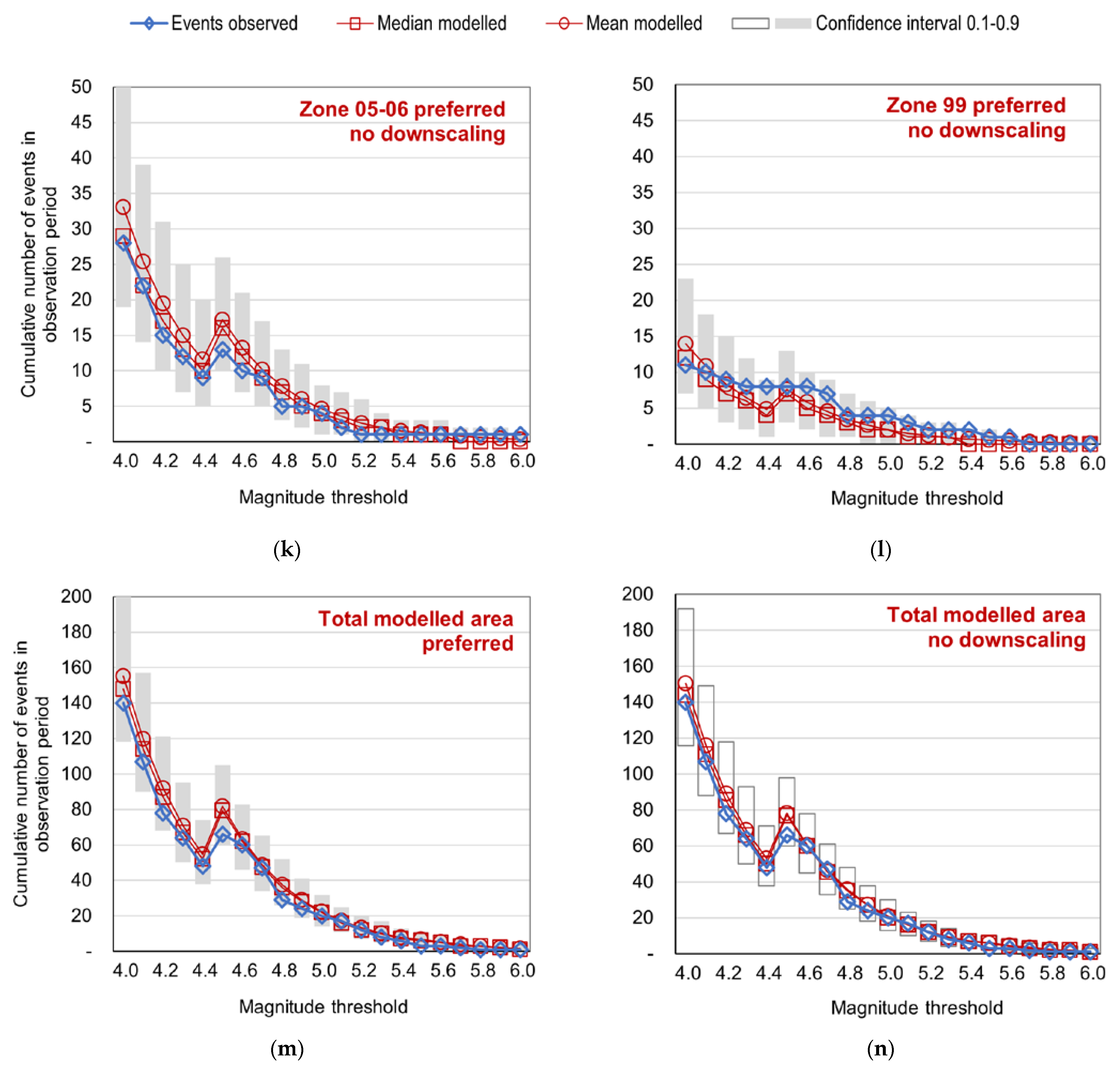
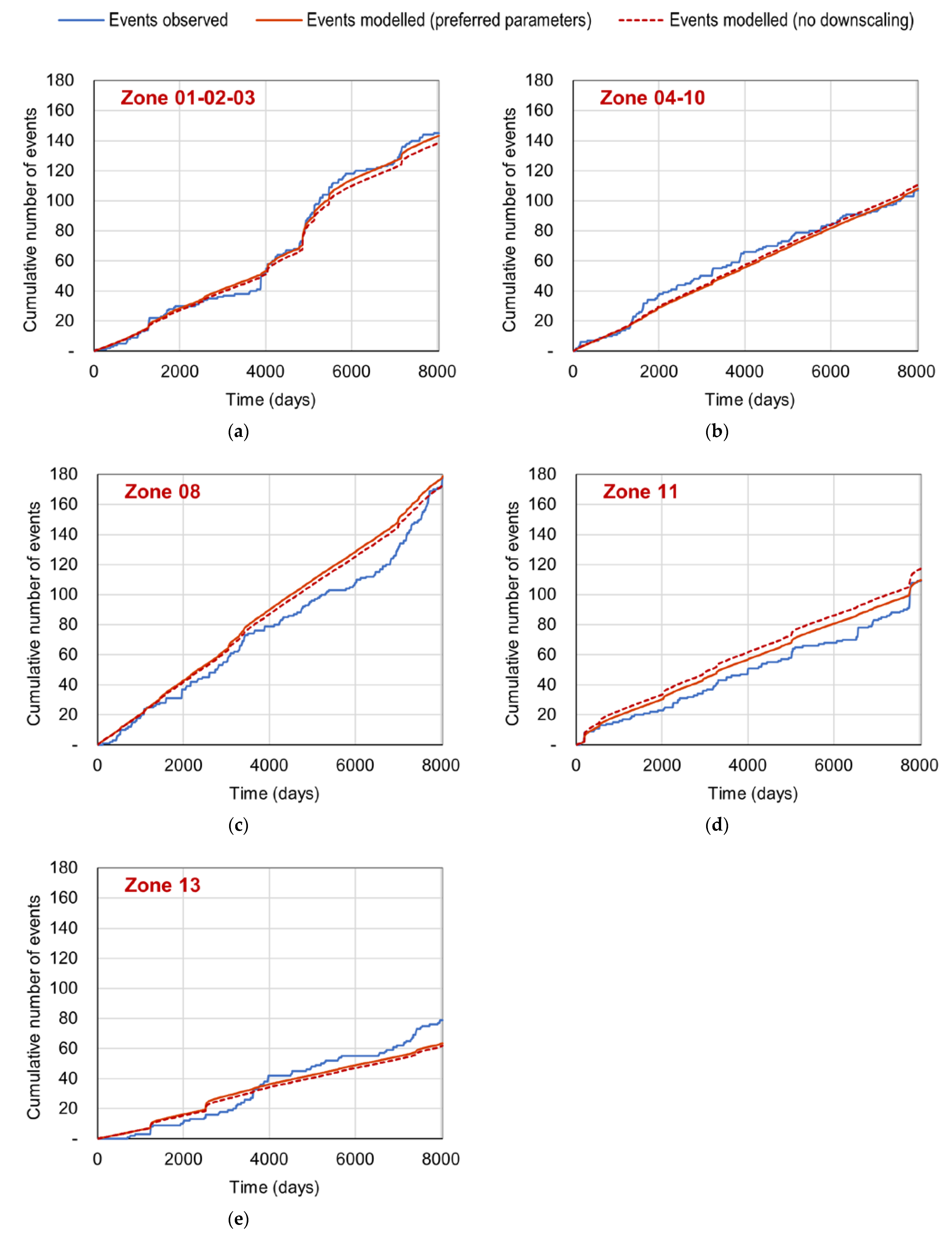
6.3. Test of Long-Term Event Numbers by Zone
6.4. Test of Event Accumulation by Zone, 2000–2021
7. Discussion and Conclusions
- Poisson goodness-of-fit tests of the modelled versus the observed process show a satisfactory fit for events , which is appropriate for application in insurance. On the other hand, the same tests show significant deviations from the model at the magnitude threshold . These deviations at low magnitudes likely result from the inhomogeneities of the observed process between earthquake clusters, from data deficiencies, and possibly also from boundary effects at the edge of the modelled area or at the magnitude threshold.
- A stretched exponential time response function is used in the model. Based on the results of the event accumulation and time lag tests, we conclude that this time response form is appropriately fitted to the observed data. Deviations from the theoretical curve in the time lag test occur at very short time periods due to early aftershock incompleteness and at long time periods due to the time bounds of the observed catalogue. The modelled branching ratio implies a stable process. A systematic comparison of the stretched exponential function against the more commonly used modified Omori law as an alternative, however, was not part of this study.
- The model uses a Gaussian space response function with an allowance for epicenter error. The results of the standardized distance test show a good fit between the model and the observed data. The km value of the error parameter is consistent with the horizontal error estimates of the underlying catalogue. On the other hand, the fitted parameter possibly also absorbs a correction for a deviation of the data from the Gaussian space response model or from the constraint. An indication for this is that the 42-m value of the parameter is unlikely to reflect the aftershock radius of events by itself.
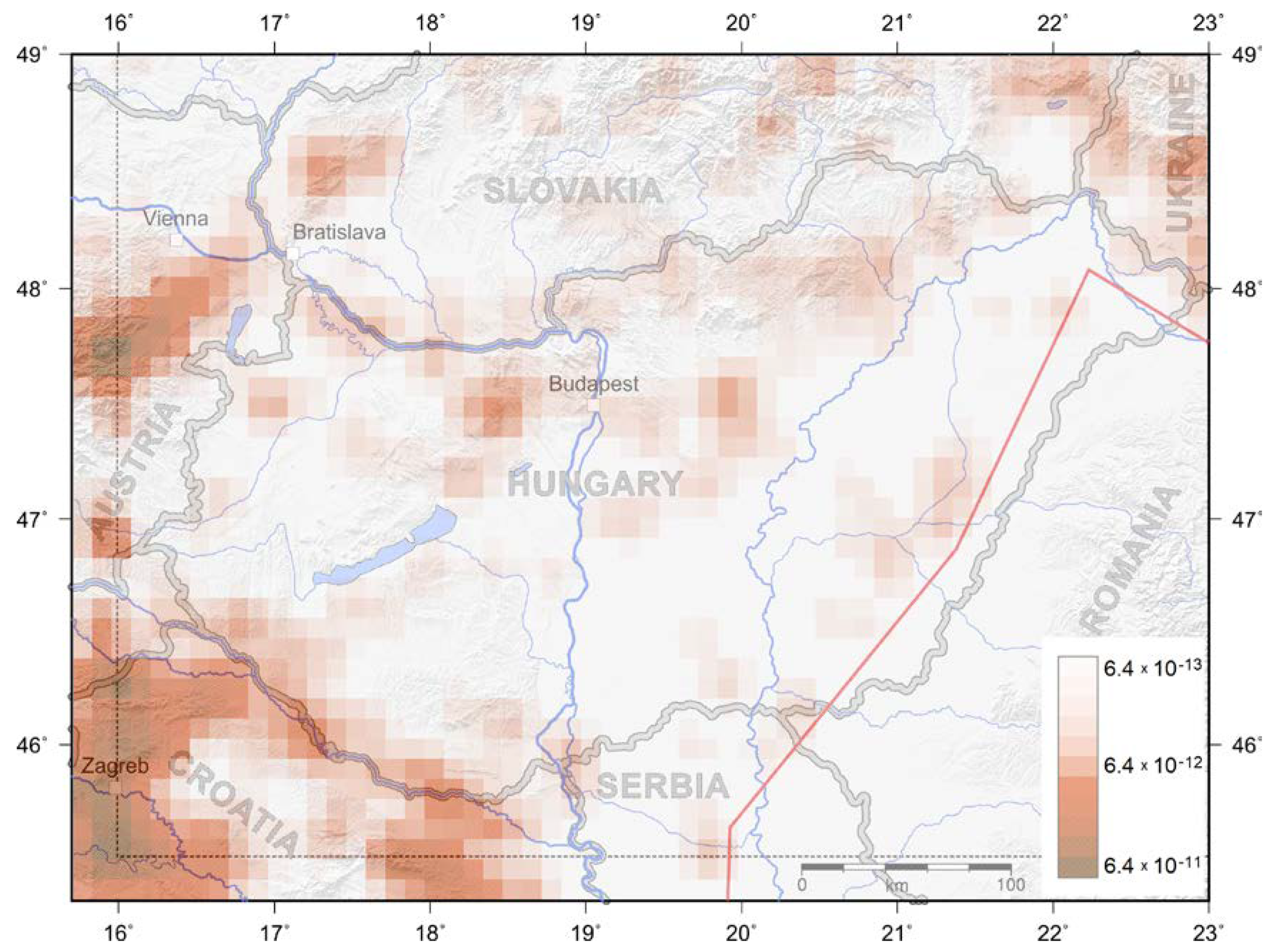
- After the overall ETAS parameter estimation, parameter adjustments for regional zones (downscaling) were also calculated. In this step, historical catalogue data going back to 1700 were incorporated. Despite the known limitations of the historical catalogue, we find it important that, in an insurance model for a moderately active region like Hungary, the most destructive historical events are taken into account for parameterization and for model testing. Even after the inclusion of historical events, the dataset used for downscaling is still dominated by recent instrumental data which have a lower magnitude threshold of completeness. The modelled event numbers were tested against long-term historical observations in the magnitude range relevant for insurance losses. For the total modelled area, the test outcomes show a good fit both with and without downscaling, with the modelled median numbers falling slightly closer to the observations with the non-downscaled parameters. However, downscaling provides clear improvements to the results by zone. While the parameters of the overall model are subject to significant uncertainties, the tests indicate that the downscaled parameters are only moderately sensitive to the variations of the overall parameters.
- For a Hungarian model, the central Zone 01–02–03 is especially important. In this zone, the downscaled model overestimates long-term event numbers in the 4.0–4.5 magnitude range. On the other hand, it gives better-fitting and more conservative results than the original parameterization for magnitudes , which is desirable in the case of a model for insurance applications. Zone 01–02–03 has experienced some notable event clusters in the 2000–2021 period, corresponding to the Oroszlány 2011, Tenk 2013, and Érsekvadkert-Iliny 2013–2015 events. The observed overall event accumulation in the zone is well-fitted to the downscaled model, as shown in Figure 13a; however, this graph masks the inhomogeneities between the two 2013 event sequences, which were geographically distant but overlapped in time.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Directive 2009/138/EC of the European Parliament and of the Council of 25 November 2009 on the Taking-Up and Pursuit of the Business of Insurance and Reinsurance (Solvency II). Available online: https://eur-lex.europa.eu/eli/dir/2009/138/oj (accessed on 5 February 2023).
- Commission Delegated Regulation (EU) 2015/35 of 10 October 2014 Supplementing Directive 2009/138/EC of the European Parliament and of the Council on the Taking-Up and Pursuit of the Business of Insurance and Reinsurance (Solvency II). Available online: https://eur-lex.europa.eu/eli/reg_del/2015/35/oj (accessed on 5 February 2023).
- Petrinjski Potresi: Prosinac 2020.—Prosinac 2021.—Geofizički Odsjek. Godina Dana od Razornog Potresa Kod Petrinje. Available online: https://www.pmf.unizg.hr/geof/seizmoloska_sluzba/potresi_kod_petrinje/2020–2021 (accessed on 16 December 2022).
- Oros, E.; Placinta, A.O.; Popa, M.; Diaconescu, M. The 1991 Seismic Crisis in the West of Romania and Its Impact on Seismic Risk and Hazard Assessment. Environ. Eng. Manag. J. 2019, 19, 609–623. [Google Scholar] [CrossRef]
- Ogata, Y. Statistical models for earthquake occurrences and residual analysis for point processes. J. Am. Stat. Assoc. 1988, 83, 9–27. [Google Scholar] [CrossRef]
- Ogata, Y. Space-Time Point-Process Models for Earthquake Occurrences. Ann. Inst. Stat. Math. 1998, 50, 379–402. [Google Scholar] [CrossRef]
- Zhuang, J.; Ogata, Y.; Vere-Jones, D. Stochastic Declustering of Space-Time Earthquake Occurrences. J. Am. Stat. Assoc. 2002, 97, 369–380. [Google Scholar] [CrossRef]
- Zhuang, J.; Ogata, Y.; Vere-Jones, D. Analyzing earthquake clustering features by using stochastic reconstruction. J. Geophys. Res. 2004, 109, B05301. [Google Scholar] [CrossRef]
- Hardebeck, J. Appendix S–Constraining Epidemic Type Aftershock Sequence (ETAS) Parameters from the Uniform California Earthquake Rupture Forecast, Version 3 Catalog and Validating the ETAS Model for Magnitude 6.5 or Greater Earthquakes. In Uniform California Earthquake Rupture Forecast, Version 3 (UCERF3)—The Time-Independent Model, Field, E.H., Biasi, G.P., Bird, P., Dawson, T.E., Felzer, K.R., Jackson, D.D., Johnson, K.M., Jordan, T.H., Madden, C., Michael, A.J., et al., U.S. Geological Survey Open-File Report 2013–1165, 97 p., California Geological Survey Special Report 228, and Southern California Earthquake Center Publication 1792. Available online: https://pubs.usgs.gov/of/2013/1165/ (accessed on 5 February 2023).
- Veen, A.; Schoenberg, F.P. Estimation of Space–Time Branching Process Models in Seismology Using an EM–Type Algorithm. J. Am. Stat. Assoc. 2008, 103, 614–624. [Google Scholar] [CrossRef]
- Ogata, Y.; Zhuang, J. Space–time ETAS models and an improved extension. Tectonophysics 2006, 413, 13–23. [Google Scholar] [CrossRef]
- Mignan, A. Modeling aftershocks as a stretched exponential relaxation. Geophys. Res. Lett. 2015, 42, 9726–9732. [Google Scholar] [CrossRef]
- Stallone, A.; Marzocchi, W. Empirical evaluation of the magnitude-independence assumption. Geophys. J. Int. 2019, 216, 820–839. [Google Scholar] [CrossRef]
- Turcotte, D.L.; Holliday, J.R.; Rundle, J.B. BASS, an alternative to ETAS. Geophys. Res. Lett. 2007, 34, L12303. [Google Scholar] [CrossRef]
- Zhuang, J.; Werner, M.J.; Harte, D.S. Stability of earthquake clustering models: Criticality and branching ratios. Phys. Rev. E 2013, 88, 062109. [Google Scholar] [CrossRef]
- Guo, Y.; Zhuang, J.; Zhou, S. A hypocentral version of the space–time ETAS model. Geophys. J. Int. 2015, 203, 366–372. [Google Scholar] [CrossRef]
- Guo, Y.; Zhuang, J.; Zhou, S. An improved space-time ETAS model for inverting the rupture geometry from seismicity triggering. J. Geophys. Res. Solid Earth 2015, 120, 3309–3323. [Google Scholar] [CrossRef]
- Seif, S.; Mignan, A.; Zechar, J.D.; Werner, M.J.; Wiemer, S. Estimating ETAS: The effects of truncation, missing data, and model assumptions. J. Geophys. Res. Solid Earth 2016, 122, 449–469. [Google Scholar] [CrossRef]
- Magyarországi Földrengések Évkönyve. Hungarian Earthquake Bulletin 1995–2019; GeoRisk: Budapest, Hungary, 1996–2020; HU ISSN 1219-963X; Available online: http://www.georisk.hu/Bulletin/bulletinh.html (accessed on 5 February 2023).
- MABISZ: A Decemberi Földrengések Magyar Kárbejelentéseinek a Száma Meghaladja a Horvátországit. Available online: https://mabisz.hu/a-decemberi-foldrengesek-magyar-karbejelenteseinek-a-szama-meghaladja-a-horvatorszagit/ (accessed on 16 December 2022).
- Zsíros, T. A Kárpát-Medence Szeizmicitása és Földrengés Veszélyessége: Magyar Földrengés Katalógus (456–1995), MTA GGKI: Budapest, Hungary, 2000. Available online: https://mek.oszk.hu/04800/04801/ (accessed on 5 February 2023).
- International Seismological Centre. On-Line Bulletin. 2022. Available online: https://doi.org/10.31905/D808B830 (accessed on 29 April 2021).
- U.S. Geological Survey. Available online: https://earthquake.usgs.gov/earthquakes/search/ (accessed on 29 April 2021).
- Grünthal, G.; Wahlström, R.; Stromeyer, D. The unified catalogue of earthquakes in central, northern, and northwestern Europe (CENEC)—Updated and expanded to the last millennium. J. Seism. 2009, 13, 517–541. [Google Scholar] [CrossRef]
- GeoRisk—Földrengés Mérnöki Iroda—Earthquake Engineering. Havi Földrengés Tájékoztató (Monthly EQ list). Available online: http://www.georisk.hu/Tajekoztato/tajekoztato.html (accessed on 5 February 2023).
- Woessner, J.; Laurentiu, D.; Giardini, D.; Crowley, H.; Cotton, F.; Grünthal, G.; Valensise, G.; Arvidsson, R.; Basili, R.; Demircioglu, M.B.; et al. The 2013 European Seismic Hazard Model: Key components and results. Bull. Earthq. Eng. 2015, 13, 3553–3596. [Google Scholar] [CrossRef]
- Utsu, T. Aftershock and earthquake statistics (I): Some parameters which characterize an aftershock sequence and their interrelations. J. Fac. Sci. Hokkaido Univ. 1969, 3, 129–195. [Google Scholar]
- Hainzl, S.; Christophersen, A.; Enescu, B. Impact of Earthquake Rupture Extensions on Parameter Estimations of Point-Process Models. Bull. Seism. Soc. Am. 2008, 98, 2066–2072. [Google Scholar] [CrossRef]
- Felzer, K.R.; Becker, T.W.; Abercrombie, R.E.; Ekström, G.; Rice, J.R. Triggering of the 1999MW7.1 Hector Mine earthquake by aftershocks of the 1992MW7.3 Landers earthquake. J. Geophys. Res. Atmos. 2002, 107, ESE 6-1–ESE 6-13. [Google Scholar] [CrossRef]
- Fletcher, R.; Powell, M.J.D. A Rapidly Convergent Descent Method for Minimization. Comput. J. 1963, 6, 163–168. [Google Scholar] [CrossRef]
- Burkhard, M.; Grünthal, G. Seismic source zone characterization for the seismic hazard assessment project PEGASOS by the Expert Group 2 (EG1b). Swiss J. Geosci. 2009, 102, 149–188. [Google Scholar] [CrossRef]
- Wang, Q.; Schoenberg, F.P.; Jackson, D.D. Standard Errors of Parameter Estimates in the ETAS Model. Bull. Seism. Soc. Am. 2010, 100, 1989–2001. [Google Scholar] [CrossRef]
- Weichert, D.H. Estimation of the earthquake recurrence parameters for unequal observation periods for different magnitudes. Bull. Seism. Soc. Am. 1980, 70, 1337–1346. [Google Scholar] [CrossRef]
- Tóth, L.; Győri, E.; Mónus, P.; Zsíros, T. Seismic Hazard in the Pannonian Region. In The Adria Microplate: GPS Geodesy, Tectonics and Hazards; Pinter, N., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 369–384. [Google Scholar] [CrossRef]




| Iteration | (1/Day) | (1/Day) | (km) | (km) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0970 | 0.0675 | 0.0049 | 0.4178 | 0.2533 | 2.6021 | 0.0426 | 2.3464 | −16,613.68 |
| 2 | 0.1136 | 0.0646 | 0.0049 | 0.4186 | 0.2519 | 2.6021 | 0.0418 | 2.3325 | −16,569.50 |
| 3 | 0.1144 | 0.0644 | 0.0049 | 0.4184 | 0.2517 | 2.6021 | 0.0417 | 2.3395 | −16,569.11 |
(1/Day) | (km) | (km) | |||||
|---|---|---|---|---|---|---|---|
| Parameter ranges from 20 simulations | |||||||
| min | 0.1031 | 0.0044 | 0.3694 | 0.2200 | 0.0389 | 2.2394 | 0.44 |
| max | 0.1284 | 0.0056 | 0.5148 | 0.2805 | 0.0455 | 2.4919 | 0.49 |
| Parameters calculated with alternative magnitude of the Petrinja mainshock | |||||||
| 0.1142 | 0.0052 | 0.4011 | 0.2700 | 0.0481 | 2.3035 | 0.49 | |
| 0.1148 | 0.0045 | 0.4401 | 0.2308 | 0.0357 | 2.3842 | 0.44 | |
| Magnitude | Begin | End | (Days) |
|---|---|---|---|
| 2000 | 2021 | 8036 | |
| 1995 | 2021 | 9862 | |
| 1970 | 2021 | 18,993 | |
| 1880 | 2021 | 51,865 | |
| 1750 | 2021 | 99,346 | |
| 1750 | 2021 | 99,346 | |
| 1700 | 2021 | 117,609 | |
| 1700 | 2021 | 117,609 |
| Zone | (1/Day) | (km) | (km) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 01–02–03 | 0.0101 | 0.0066 | 0.4184 | 0.2517 | 2.4406 | 0.0486 | 2.3395 | 191 | 0.60 |
| 04–10 | 0.0113 | 0.0037 | 0.4184 | 0.2517 | 2.8073 | 0.0366 | 2.3395 | 139 | 0.39 |
| 08 | 0.0174 | 0.0048 | 0.4184 | 0.2517 | 2.7404 | 0.0416 | 2.3395 | 233 | 0.49 |
| 11 | 0.0092 | 0.0054 | 0.4184 | 0.2517 | 2.3869 | 0.0438 | 2.3395 | 151 | 0.47 |
| 13 | 0.0059 | 0.0031 | 0.4184 | 0.2517 | 2.8651 | 0.0335 | 2.3395 | 60 | 0.33 |
| 05–06 * | 0.0170 | 0.0049 | 0.4184 | 0.2517 | 2.6021 | 0.0417 | 2.3395 | 68.5 ** | 0.47 |
| 99 * | 0.0078 | 0.0049 | 0.4184 | 0.2517 | 2.6021 | 0.0417 | 2.3395 | 63 | 0.47 |
| Zone | Alternative | (1/Day) | (km) | (km) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 01–02–03 | 0.0101 | 0.0067 | 0.4011 | 0.2700 | 2.4414 | 0.0545 | 2.3035 | 0.60 | |
| 0.0101 | 0.0065 | 0.4401 | 0.2308 | 2.4423 | 0.0429 | 2.3842 | 0.60 | ||
| 04–10 | 0.0113 | 0.0038 | 0.4011 | 0.2700 | 2.8070 | 0.0410 | 2.3035 | 0.39 | |
| 0.0113 | 0.0037 | 0.4401 | 0.2308 | 2.8073 | 0.0323 | 2.3842 | 0.39 | ||
| 08 | 0.0174 | 0.0049 | 0.4011 | 0.2700 | 2.7400 | 0.0466 | 2.3035 | 0.49 | |
| 0.0174 | 0.0047 | 0.4401 | 0.2308 | 2.7414 | 0.0368 | 2.3842 | 0.49 | ||
| 11 | 0.0092 | 0.0054 | 0.4011 | 0.2700 | 2.3870 | 0.0490 | 2.3035 | 0.47 | |
| 0.0092 | 0.0052 | 0.4401 | 0.2308 | 2.3872 | 0.0387 | 2.3842 | 0.47 | ||
| 13 | 0.0059 | 0.0032 | 0.4011 | 0.2700 | 2.8651 | 0.0376 | 2.3035 | 0.33 | |
| 0.0059 | 0.0031 | 0.4401 | 0.2308 | 2.8680 | 0.0296 | 2.3842 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szabó, P.; Tóth, L.; Cerdà-Belmonte, J. Hazard Model: Epidemic-Type Aftershock Sequence (ETAS) Model for Hungary. Appl. Sci. 2023, 13, 2814. https://doi.org/10.3390/app13052814
Szabó P, Tóth L, Cerdà-Belmonte J. Hazard Model: Epidemic-Type Aftershock Sequence (ETAS) Model for Hungary. Applied Sciences. 2023; 13(5):2814. https://doi.org/10.3390/app13052814
Chicago/Turabian StyleSzabó, Péter, László Tóth, and Judith Cerdà-Belmonte. 2023. "Hazard Model: Epidemic-Type Aftershock Sequence (ETAS) Model for Hungary" Applied Sciences 13, no. 5: 2814. https://doi.org/10.3390/app13052814
APA StyleSzabó, P., Tóth, L., & Cerdà-Belmonte, J. (2023). Hazard Model: Epidemic-Type Aftershock Sequence (ETAS) Model for Hungary. Applied Sciences, 13(5), 2814. https://doi.org/10.3390/app13052814







