Analysis of the Ventilation Performance of a Solar Chimney Coupled to an Outdoor Wind and Indoor Heat Source
Abstract
:1. Introduction
2. Materials and Methods
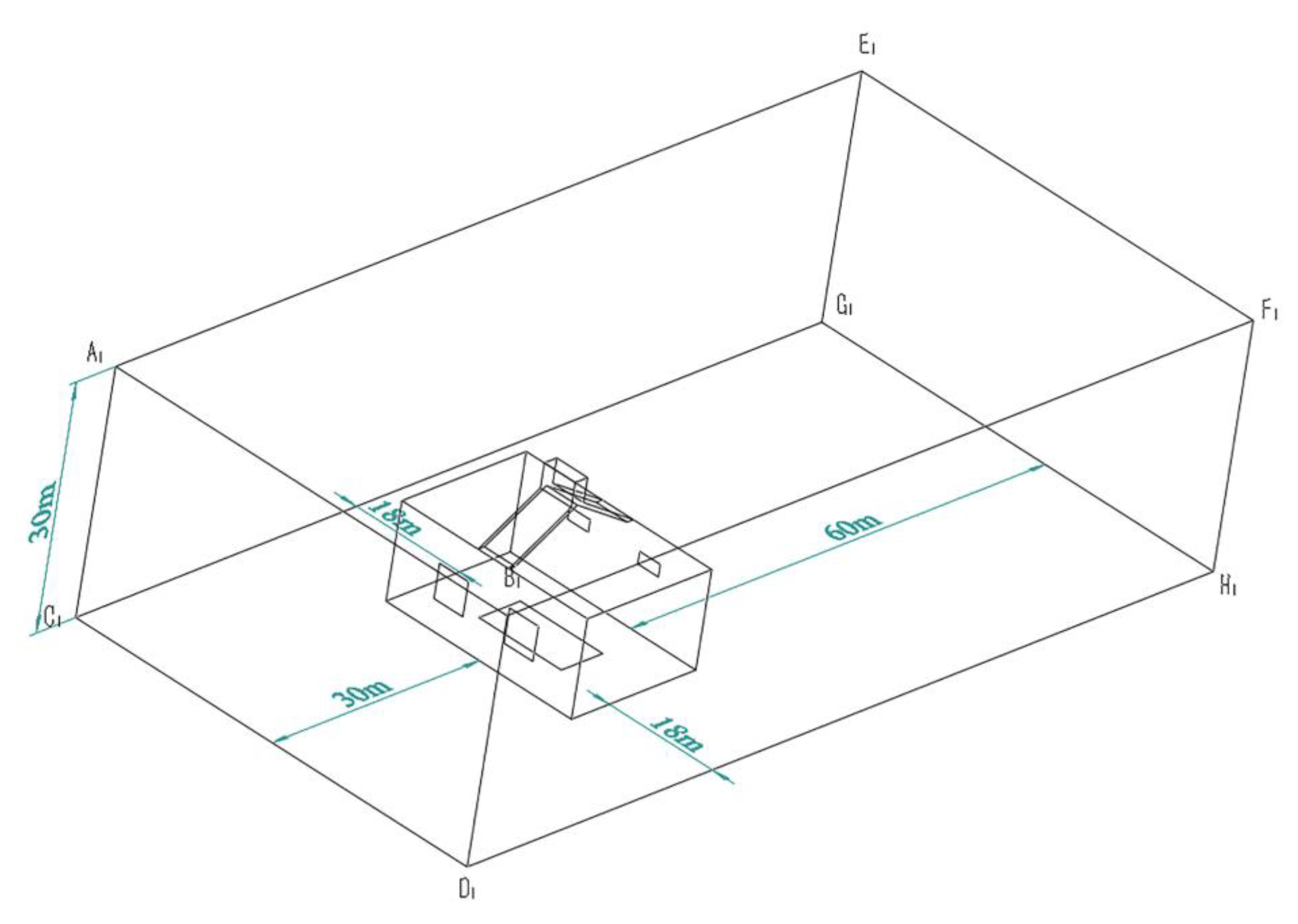
2.1. Physical Model
2.2. Calculation Area
2.3. Mathematical Models
2.4. Boundary Conditions
3. Validation
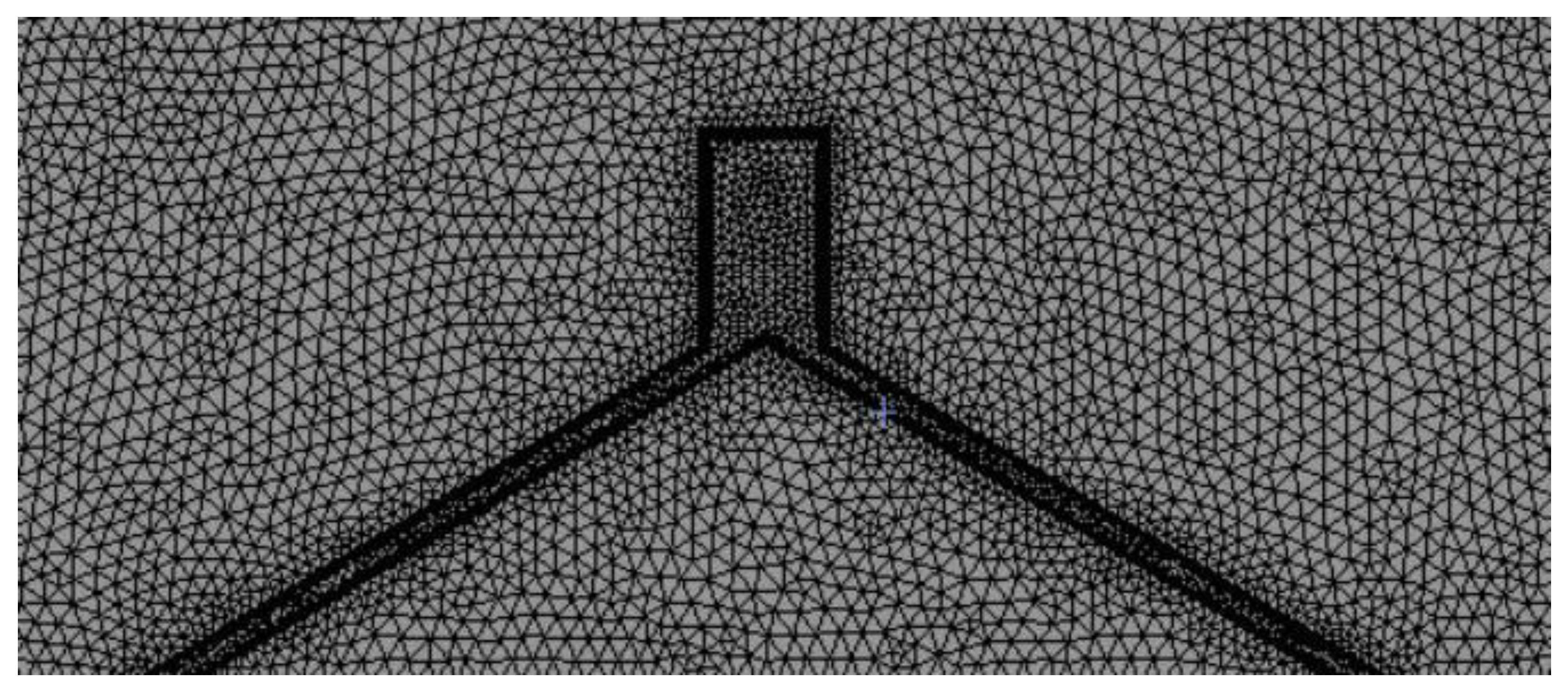
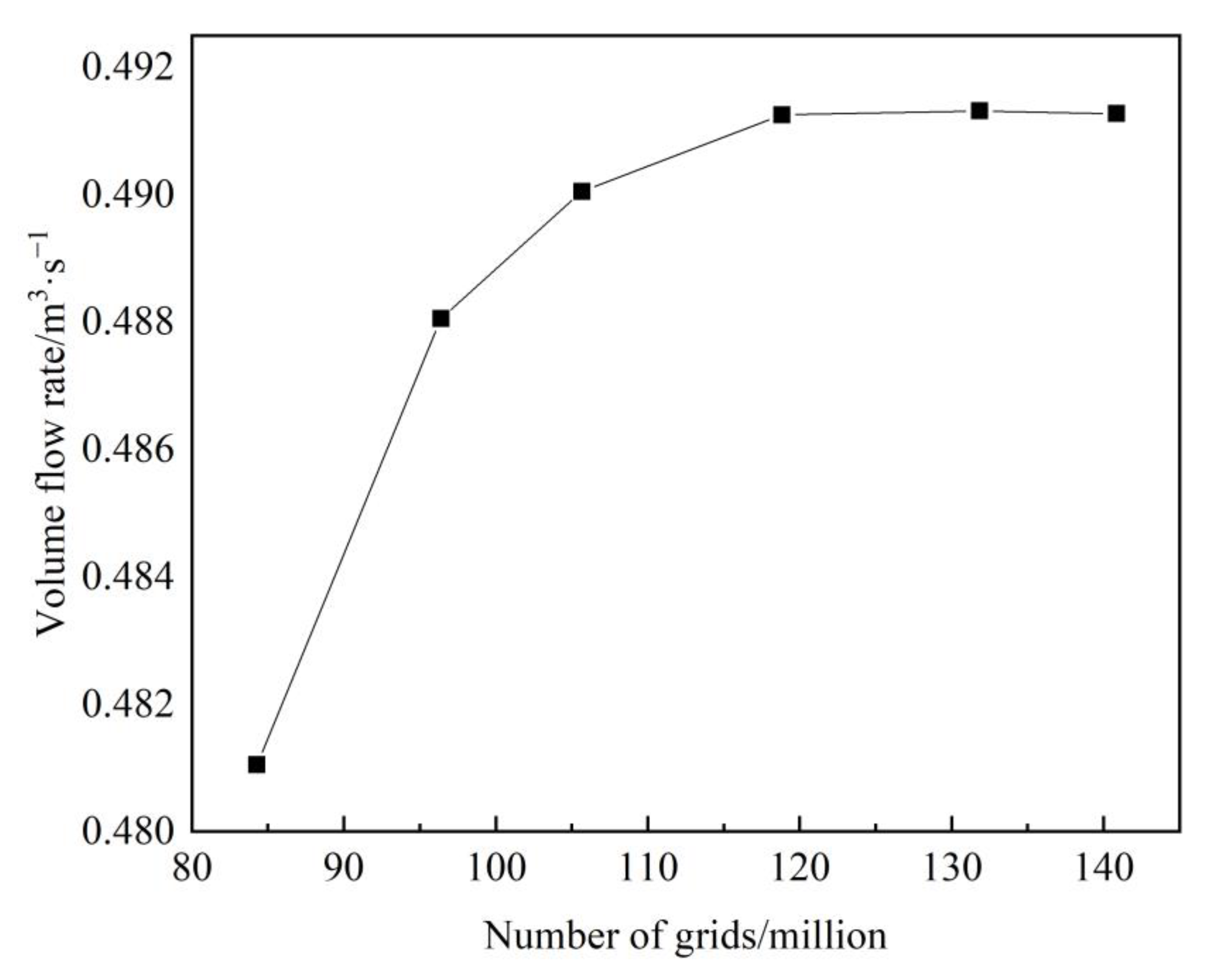
3.1. Mesh Independence Verification
3.2. Model Validation
4. Results and Discussion
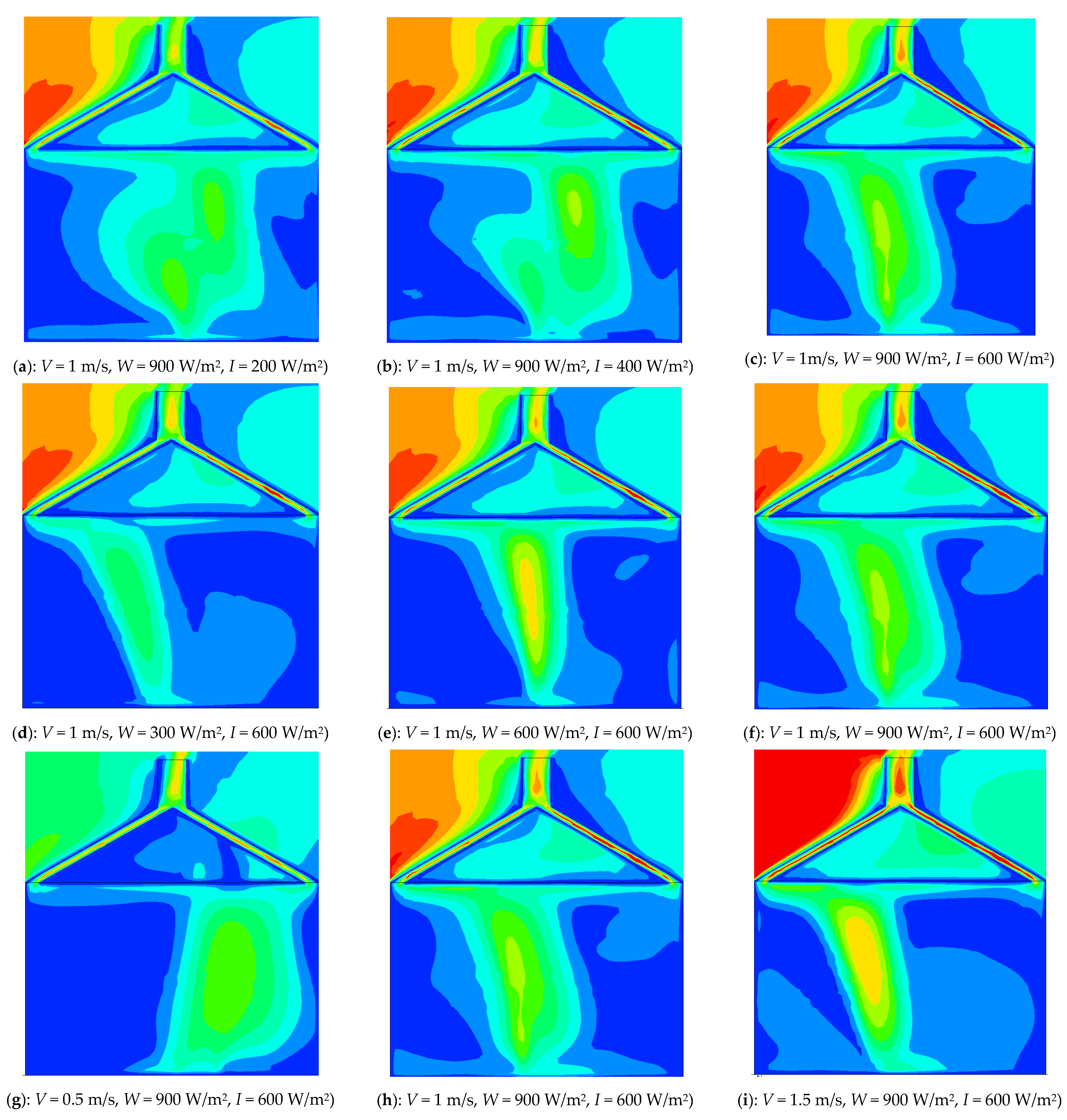
4.1. Indoor Air Velocity Distribution at X = 4.5 m
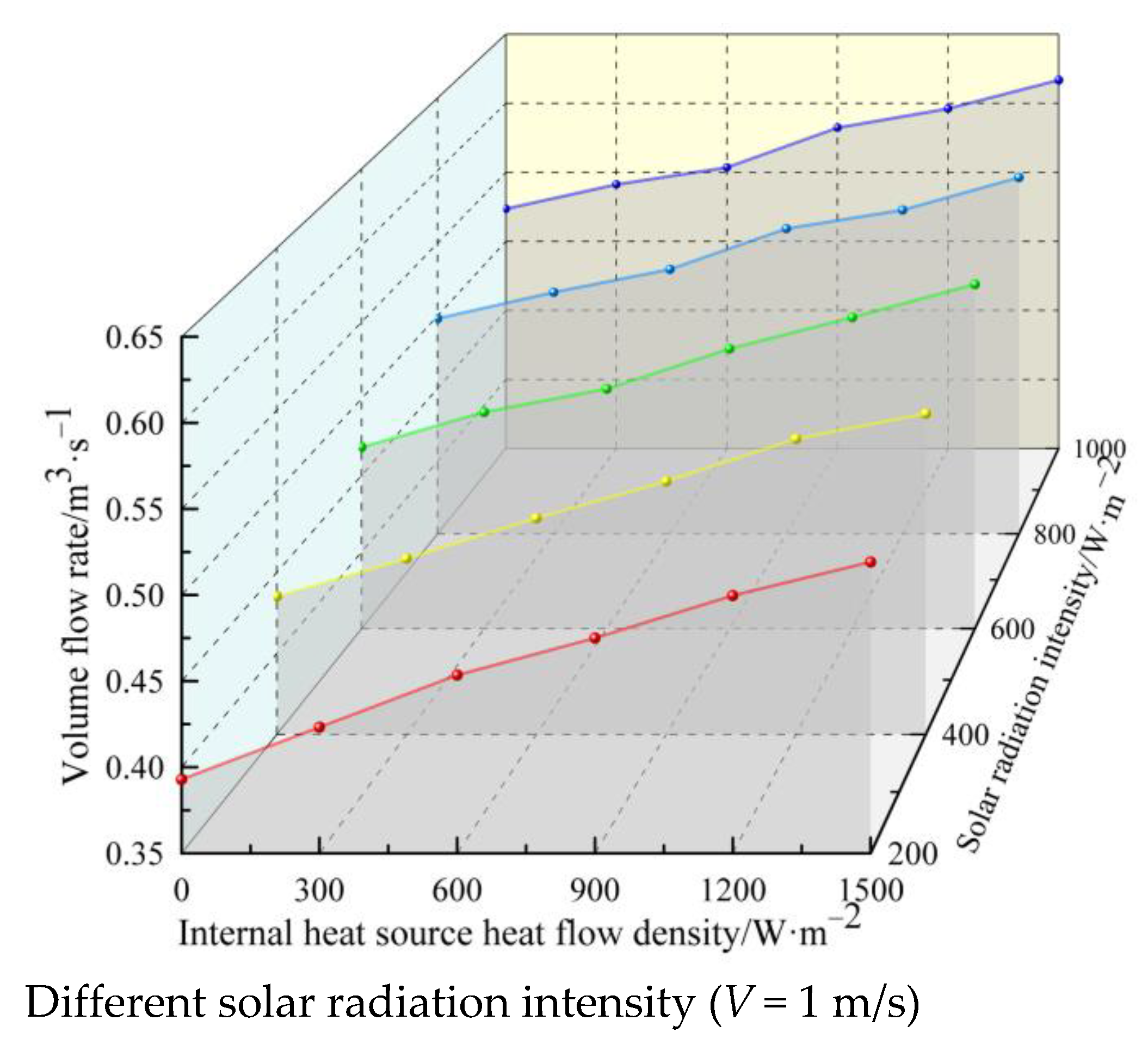
4.2. Variation of Ventilation Volume with Solar Radiation Intensity
4.3. Change of Ventilation Rate with Heat Flux of Indoor Heat Source
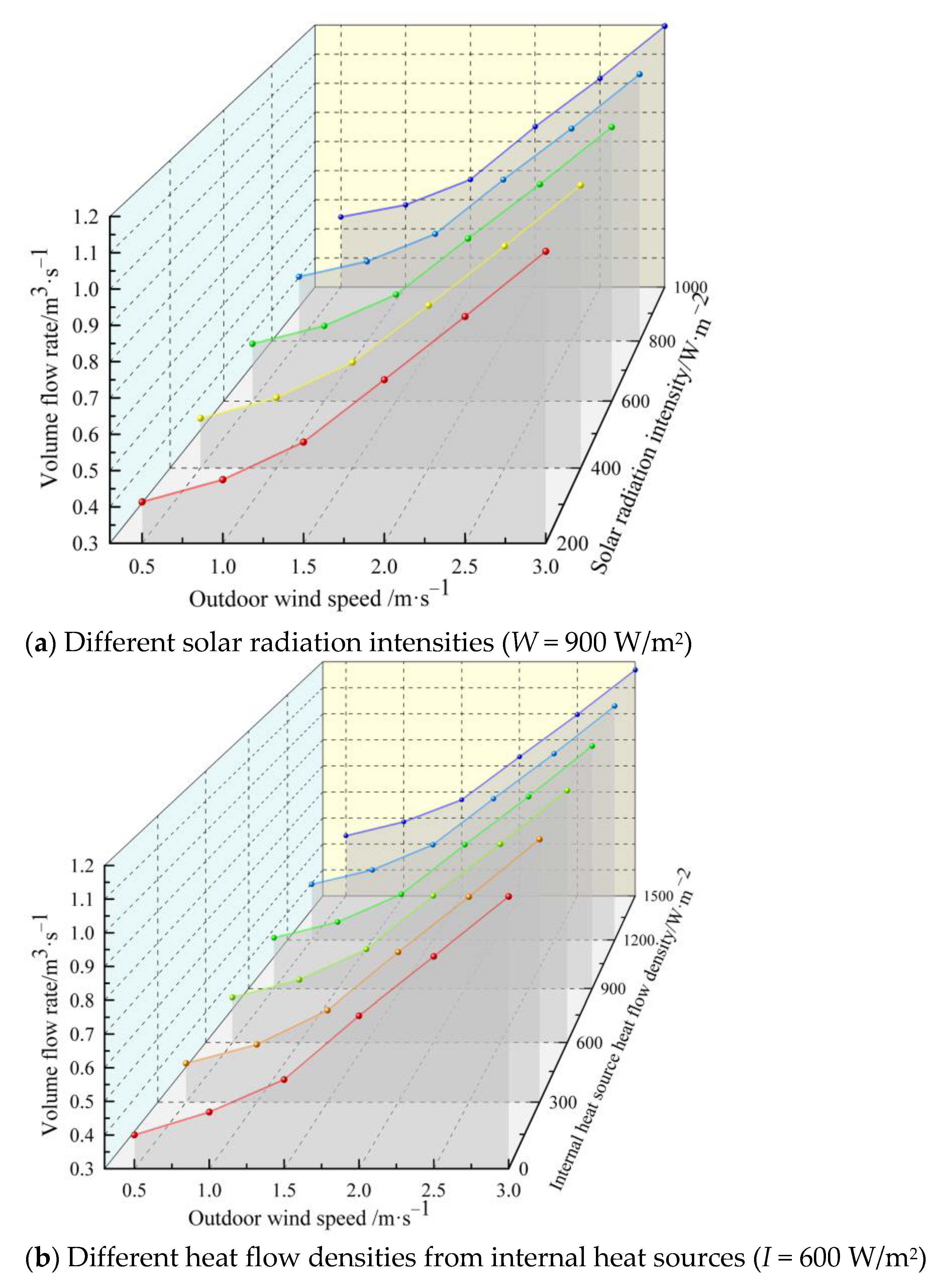
4.4. Change of Ventilation Volume with Outdoor Wind Speed
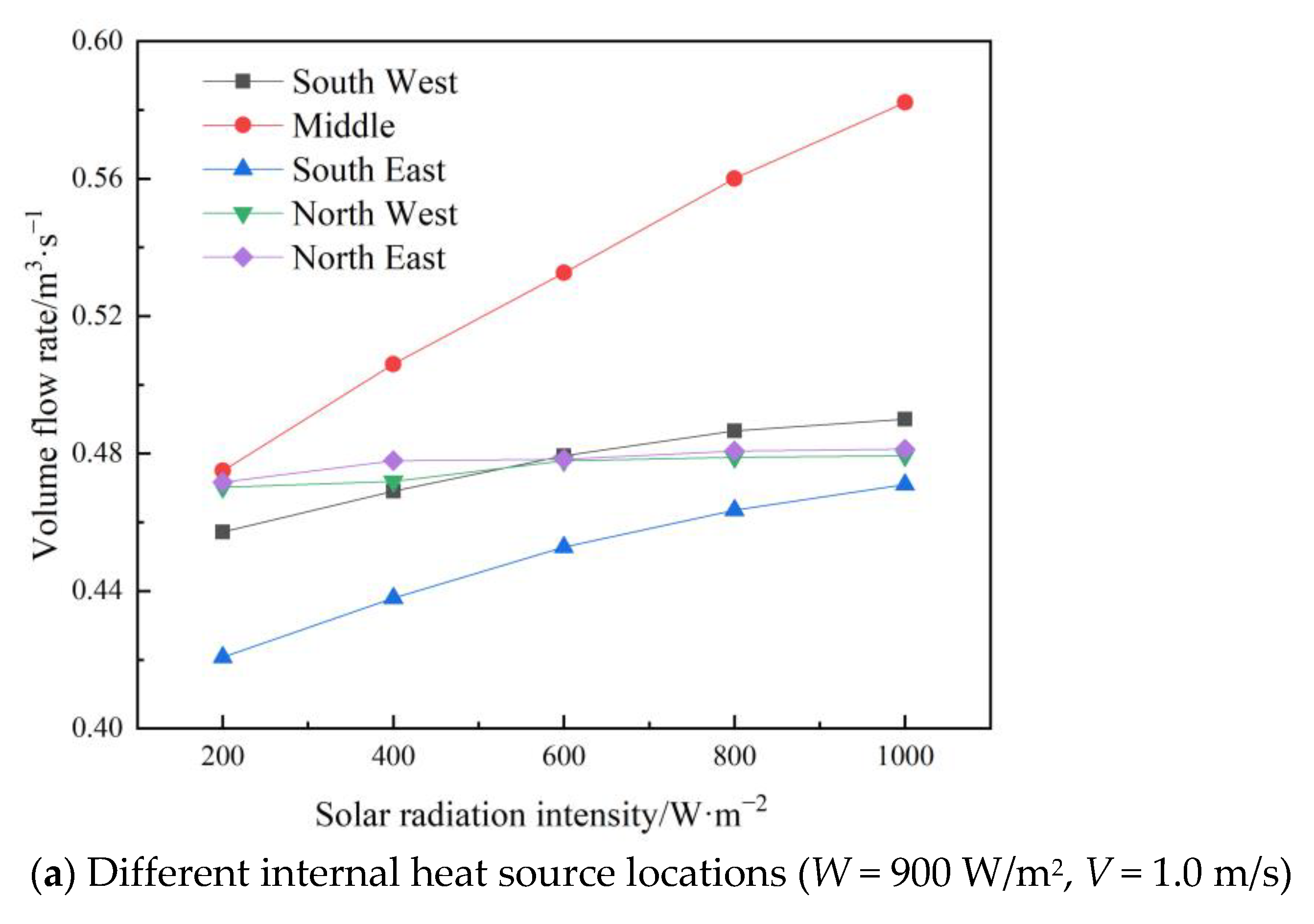
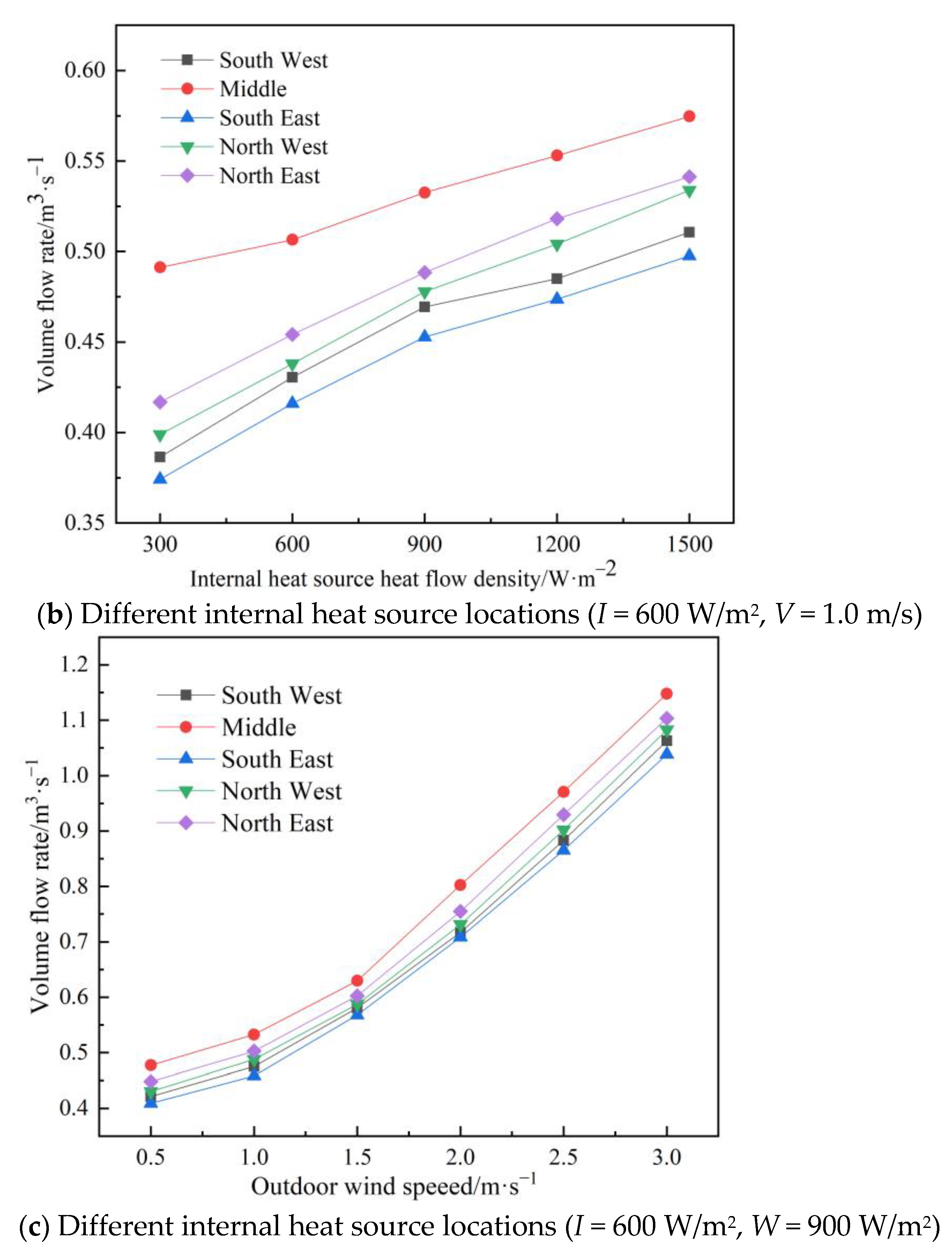
4.5. Variation of Ventilation with the Position of the Internal Heat Source
4.6. Variation of Ventilation Volume with Solar Chimney Inlet Width
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tan, X.; Lai, H.; Gu, B.; Zeng, Y.; Li, H. Carbon emission and abatement potential outlook in china’s building sector through 2050. Energy Policy 2018, 118, 429–439. [Google Scholar] [CrossRef]
- Gao, X.Y.; Fan, B.Y.; Zhang, H.G. Research on the application of solar heating systems in the construction of new rural areas. J. Sol. Energy 2009, 30, 1653–1657. [Google Scholar]
- Wang, L.; Chen, S.K.; Li, R. Study on the influencing factors and optimal design of the composite ventilation system of tunnel and solar chimney. Renew. Energy 2017, 35, 218–223. [Google Scholar]
- Bassiouny, R.; Korah, N.S.A. Effect of solar chimney inclination angle on space flow pattern and ventilation rate. Energy Build. 2009, 41, 190–196. [Google Scholar] [CrossRef]
- Hong, S.; He, G.; Ge, W. Annual energy performance simulation of solar chimney in a cold winter and hot summer climate. Build. Simul. 2019, 12, 847–856. [Google Scholar] [CrossRef]
- Luo, X.L.; Wang, Y.P.; Liang, J.; Qi, J.; Su, W.; Yang, Z.; Chen, J.; Wang, C.; Chen, Y. Improved correlations for working fluid properties prediction and their application in performance evaluation of sub-critical Organic Rankine Cycle. Energy 2019, 17, 122–137. [Google Scholar] [CrossRef]
- AboulNaga, M.M.; Abdrabboh, S.N. Improving night ventilation into low-rise buildings in hot-arid climates exploring a combined wall-roof solar chimney. Renew. Energy 2000, 19, 47–54. [Google Scholar] [CrossRef]
- Zavala-Guillén, I.; Xamán, J.; Hernández-Pérez, I.; Hernández-Lopéz, I.; Gijón-Rivera, M.; Chávez, Y. Numerical study of the optimum width of 2a diurnal double air-channel solar chimney. Energy 2018, 147, 403–417. [Google Scholar] [CrossRef]
- Lal, S. Experimental, CFD simulation and parametric studies on modified solar chimney for building ventilation. Appl. Sol. Energy 2014, 50, 37–43. [Google Scholar] [CrossRef]
- Khedari, J.; Rachapradit, N.; Hirunlabh, J. Field study of performance of solar chimney with air-conditioned building. Energy 2003, 28, 1099–1114. [Google Scholar] [CrossRef]
- Hou, Y.C.; Li, H.; Li, A.G. Experimental and theoretical study of solar chimneys in buildings with uniform wall heat flux. Sol. Energy 2019, 193, 244–252. [Google Scholar] [CrossRef]
- Rabani, M. Cooling performance of a passive hybrid system consisted of domed roof and solar chimney: A numerical approach. Int. J. Green Energy 2022, 19, 435–454. [Google Scholar] [CrossRef]
- Dhahri, M.; Nekoonam, S.; Hana, A.; Mamdouh, E.H.A.; Müslüm, A.; Mohsen, S.; Habib, S. Thermal performance modeling of modified absorber wall of solar chimney-shaped channels system for building ventilation. J. Therm. Anal. Calorim. 2021, 145, 1137–1149. [Google Scholar] [CrossRef]
- He, G.Q.; Lv, D. Enhancing solar chimney ventilation efficiency by insertion of transparent panel. J. Zhejiang Univ. Eng. Sci. 2021, 55, 2260–2266. [Google Scholar]
- Liu, H.; Li, P.; Yu, B.; Zhang, M.; Tan, Q.; Wang, Y.; Zhang, Y. Contrastive Analysis on the Ventilation Performance of a Combined Solar Chimney. Appl. Sci. 2022, 12, 156. [Google Scholar] [CrossRef]
- Leticia, O.N.; Fernando, M.S. Simulation and measurements of wind interference on a solar chimney performance. J. Wind. Eng. Ind. Aerodyn. 2018, 179, 135–145. [Google Scholar]
- Wang, Q.Y.; Zhang, G.M.; Li, W.Y.; Shi, L. External wind on the optimum designing parameters of a wall solar chimney in building. Sustain. Energy Technol. Assess. 2020, 42, 98–108. [Google Scholar] [CrossRef]
- Gao, N.; Yan, Y.; Sun, R.; Lei, Y. Natural Ventilation Enhancement of a Roof Solar Chimney with Wind-Induced Channel. Energies 2022, 15, 6492. [Google Scholar] [CrossRef]
- Shi, L. Impacts of wind on solar chimney performance in a building. Energy 2019, 185, 55–67. [Google Scholar] [CrossRef]
- Lin, Y.; Xu, Z.Y. Buoyancy-driven flows by a heat source at different levels. Int. J. Heat Mass Transfer. 2013, 58, 312–321. [Google Scholar] [CrossRef]
- Gao, X.P.; Li, A.G.; Yang, C.Q. Study on thermal stratification of an enclosure containing two interacting turbulent buoyant plumes of equal strength. Build. Environ. 2018, 141, 236–246. [Google Scholar] [CrossRef]
- Barrios, G.; Huelsz, G.; Rechtman, R. Heat transfer and flow transitions of a thermal plume generated by a heating element on the enclosure bottom wall. Eur. J. Mech. B/Fluids 2019, 77, 17–24. [Google Scholar] [CrossRef]
- Dhahri, M.; Aouinet, H.; Sammouda, H. Numerical approximation of air flow temperature distribution and thermal comfort in buildings. Sci. Afr. 2020, 8, 11–18. [Google Scholar]
- Dhahri, M.; Aouinet, H.; Mhamdi, N. CFD analysis of the effect of uniformly sheared air flow on natural ventilation in building. Int. J. Ambient Energy 2019, 43, 915–921. [Google Scholar] [CrossRef]
- Miyazaki, T.; Akisawa, A.; Kashiwagi, T. The effects of solar chimneys on thermal load mitigation of office buildings under the Japanese climate. Renew. Energy. 2006, 31, 987–1010. [Google Scholar] [CrossRef]
- Arce, J.; Jimenez, M.J.; Guaman, J.D.; Heras, M.; Alvarez, G.; Xamán, J. Epxerimental study for natural ventilation on a solar chimney. Renew. Energy. 2009, 34, 2928–2934. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, G.M.; Yang, W.; Huang, D.; Cheng, X.; Setunge, S. Determining the influencing factors on the performance of solar chimney in buildings. Renew. Sustain. Energy Rev. 2018, 88, 223–238. [Google Scholar] [CrossRef]
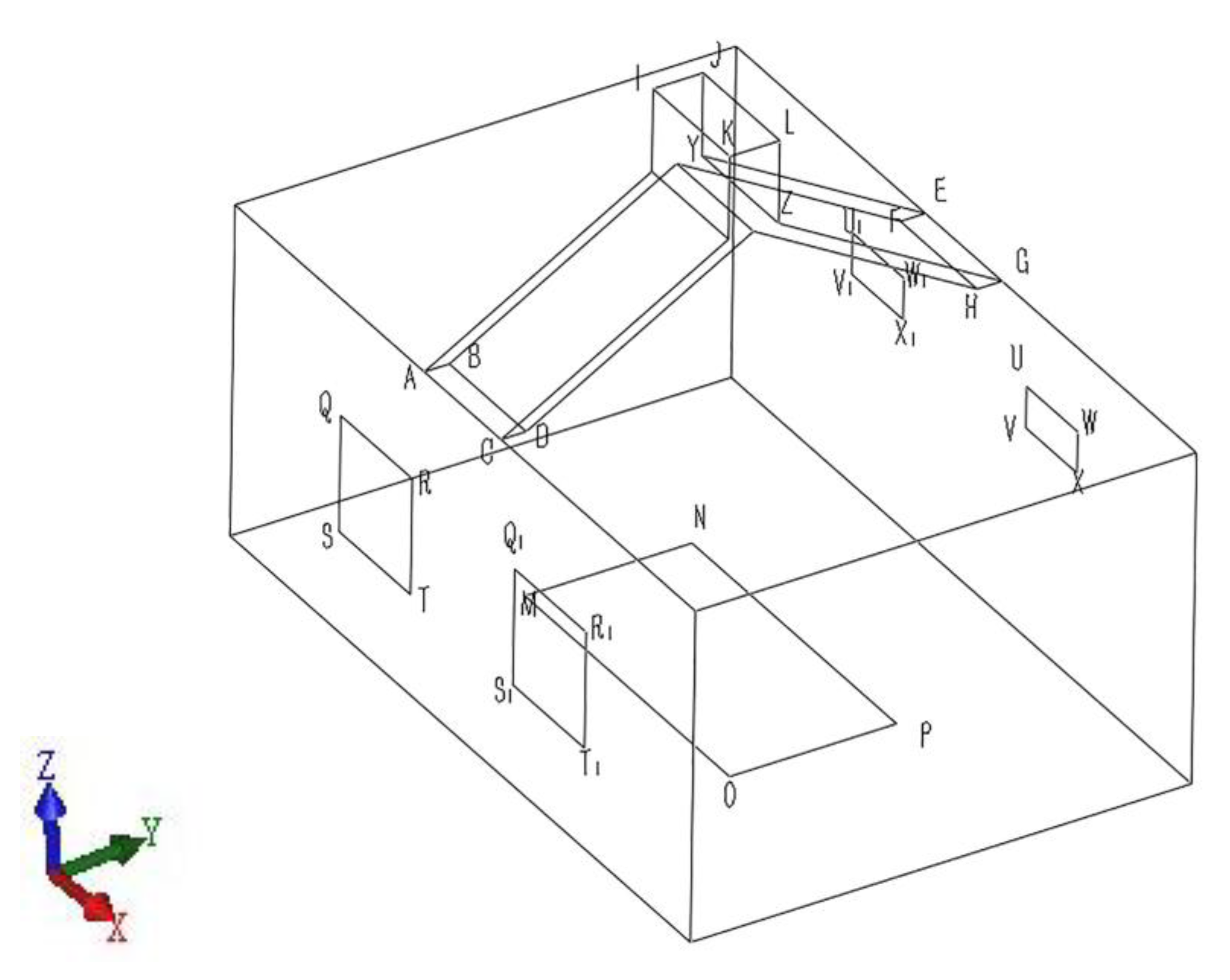


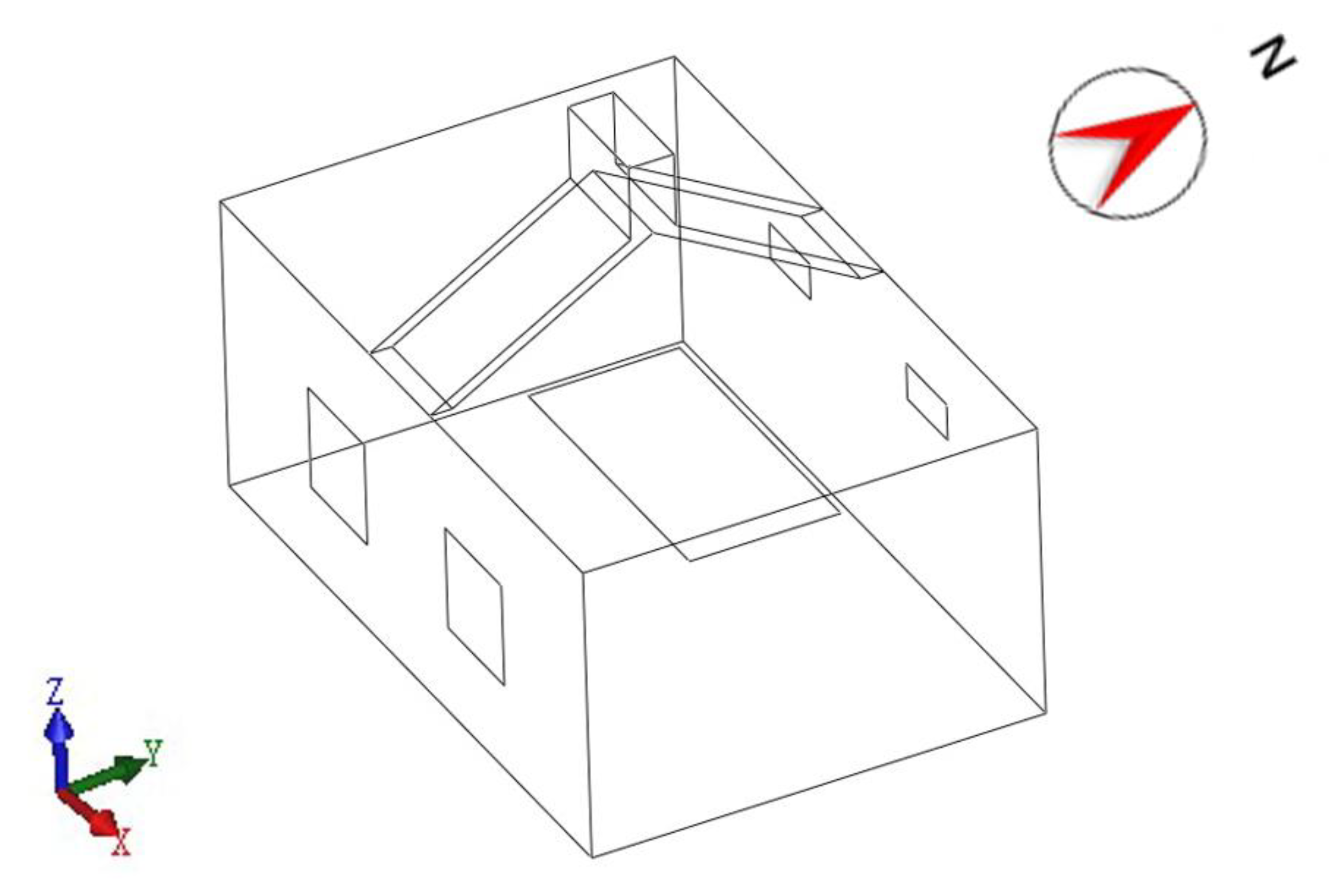

| Enclosed Area | Meaning |
|---|---|
| QRST, Q1R1S1T1 | South window |
| UVWX, U1V1W1X1 | North window |
| MNOP | Indoor heat source |
| ABCD, EFGH | Air inlet |
| IJKL | Air outlet |
| BDFH, JLYZ | Heat collecting walls |
| ACKI, EGYZ | Glass cover plate |
| Material | Thickness | Density | Heat Conductivity Coefficient | Specific Heat Capacity | Solar Radiation | ||
|---|---|---|---|---|---|---|---|
| mm | kg/m3 | W/(m·k) | J/(kg·k) | Transmittance | Reflectance | Absorption Rate | |
| Glass cover plate | 3 | 2500 | 0.75 | 837.4 | 0.84 | 0.1 | 0.06 |
| Polyvinyl chloride | 50 | 100 | 0.047 | 1380 | 0 | 0.05 | 0.95 |
| Air | — | 1.205 | 0.0259 | 1005.43 | 1 | 0 | 0 |
| Insulated walls | 200 | 1800 | 0.814 | 879 | 0 | 1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, S.; Ge, Z.; Xu, J.; Xie, J.; Xie, Z.; Zhang, S.; Li, J. Analysis of the Ventilation Performance of a Solar Chimney Coupled to an Outdoor Wind and Indoor Heat Source. Appl. Sci. 2023, 13, 2585. https://doi.org/10.3390/app13042585
Yue S, Ge Z, Xu J, Xie J, Xie Z, Zhang S, Li J. Analysis of the Ventilation Performance of a Solar Chimney Coupled to an Outdoor Wind and Indoor Heat Source. Applied Sciences. 2023; 13(4):2585. https://doi.org/10.3390/app13042585
Chicago/Turabian StyleYue, Shuaikun, Zhong Ge, Jian Xu, Jianbin Xie, Zhiyong Xie, Songyuan Zhang, and Jian Li. 2023. "Analysis of the Ventilation Performance of a Solar Chimney Coupled to an Outdoor Wind and Indoor Heat Source" Applied Sciences 13, no. 4: 2585. https://doi.org/10.3390/app13042585
APA StyleYue, S., Ge, Z., Xu, J., Xie, J., Xie, Z., Zhang, S., & Li, J. (2023). Analysis of the Ventilation Performance of a Solar Chimney Coupled to an Outdoor Wind and Indoor Heat Source. Applied Sciences, 13(4), 2585. https://doi.org/10.3390/app13042585







