Course Recommendation Based on Enhancement of Meta-Path Embedding in Heterogeneous Graph

Abstract

The main reason students drop out of online courses is often that they lose interest during learning. Moreover, it is not easy for students to choose an appropriate course before actually learning it. Course recommendation is necessary to address this problem. Most existing course recommendation methods depend on the interaction result (e.g., completion rate, grades, etc.). However, the long period required to complete a course, especially large-scale online courses in higher education, can lead to serious sparsity of interaction results. In view of this, we propose a novel course recommendation method named HGE-CRec, which utilizes context formation for heterogeneous graphs to model students and courses. HGE-CRec develops meta-path embedding simulation and meta-path weight fusion to enhance the meta-path embedding set, which can expand the learning space of the prediction model and improve the representation ability of meta-path embedding, thereby avoiding tedious manual setting of the meta-path and improving the effectiveness of the resulting recommendations. Extensive experiments show that the proposed approach has advantages over a number of existing baseline methods.

1. Introduction

In recent ten years the growth rate of distance education has been impressive, enabling students from all over the world to study courses at low cost. Many distance learning platforms, such as Coursera and edX, provide a large number of online courses and attract millions of registered users. The goal of users (students) is to master knowledge through course learning. The ongoing surge in the number of courses requires effective recommendation methods to help learners find suitable courses [1]. The recommendation accuracy is very important in regard to improving the service quality of online course platforms [2,3].

The purpose of course learning is to master new knowledge or improve the level of mastery of previously learned knowledge. Course learning is different from reading or browsing news, newsletters, and documents. The learning process is continuous (usually a semester), and the interactive objects (e.g., teacher, course video, subject) are diverse. For example, a higher education course on the XuetangX platform (xuetangx.com), e.g., Introduction to Machine Learning, lasts for 12 weeks and has 6–7 sections per week, while Introduction to Psychology is a 12-week course with 5–7 sections per week. Another example can be found in higher education courses on the edX (edx.org) platform, such as Big Data and Education, each of which are 8 weeks long and require 6–12 h per week. The Architectural Imagination course takes 10 weeks and 3–5 h per week. However, massive online course resources place students in danger of becoming lost in the large amount of information present at any time during the learning process [1]. In addition, the diversity of interactive objects enables relationships between students and students, students and courses, and courses and courses, even if these relationships are indirect or potential. The network in the real world is complex, with maany different elements affecting each other.

The traditional methods of modeling the real world with homogeneous networks neglect the impact of multi-source heterogeneous elements, while heterogeneous graphs (abbr. HG) have proved to be an effective method for modeling graph structures composed of multiple entities and relationships [4,5]. The advantage of HG is that it fully and intuitively uses the heterogeneous network structure in the dataset [6]. However, the main disadvantage is that it needs to manually design the meta-path, which is difficult to achieve optimally in real practice. Unfortunately, most existing methods do not solve these problems.

Faced with the aforementioned problems and issues, in this paper we propose a course recommendation method based on an enhancement of HG meta-path embedding (abbr. HGE-CRec). First, we use the skip-gram algorithm to generate the original meta-path embedding. Then, Graph Convolutional Networks (abbr. GCN) are utilized to generate simulated meta-path embedding based on the construction of the original meta-paths, enriching the dataset used for HG meta-path embedding. Third, we adopt a Graph Attention Network (abbr.GAT) to aggregate the neighboring node information of each node on the meta-path in order to enrich the semantics of node embedding. Fourth, a nonlinear method is adopted to fuse all information in order to enhance the node embedding of the meta-paths. Finally, the enhanced embedding is combined with a Matrix Factorization-based model to predict ratings for students and courses. We compare and analyze HGE-CRec with other existing Matrix Factorization-based recommendation models using two real-world online course datasets and two general open datasets dealing with HIN embedding-based recommendation research.

In brief, the contributions of this paper can be summarized based on the following three perspectives:

• We propose a novel course recommendation method based on heterogeneous graph embedding, and our experiments prove that the performance of this method is better than existing methods.
• We propose a novel solution for enhancing the embedding of the meta-path in HG.
• Extensive experiments on four real-world datasets demonstrate the effectiveness of the proposed approach. In addition, we show that the proposed approach can maintain good performance even in the absence of meta-path data.

The rest of this paper is organized as follows. We briefly review related works in Section 2. In Section 3, we introduce preliminaries and important notation. In Section 4, we describe the framework and implementation of HGE-CRec. The extensive experimental studies we conducted are described in Section 5. Finally, we provide our conclusions in Section 6.

2. Related Work

In this section, we first review related research about course recommendation. Then, we define and explain the meaning of exercise difficulty and revisit existing methods for predicting exercise difficulty.

2.1. Course Recommendation System

In the educational domain, personalized learning recommender system have been a research hotspot. Traditional recommendation methods have applications in personalized course recommendation, such as content-based filtering [7,8], collaborative filtering [9,10], and Hybrid-based course recommendation systems [11]. Due to the hierarchical structure of knowledge concepts in curricula, research into ontology-based course recommendations [1,12,13] have received extensive attention. Generally, an administrator is required to operate an operational course recommender system. The administrator can adjust the algorithm parameters to generate more accurate learning log-based recommendations, monitor user feedback on the courses recommended by the system, and adjust the algorithm parameters according to actual situation to ensure the normal operation of the system. Traditional recommendation methods mostly come from the field of e-commerce. They regard courses as commodities, students as customers, and course learning behaviors as commodity purchase behaviors. However, course selection behavior is essentially different from commodity purchase behavior. When comparing learning content to movies or books, the cognitive state of the student and the learning content may change over time and context [14,15,16]. Learning a course generally takes a relatively long period of time, and constantly consumes students’ attention and energy. In addition, students intend to achieve good grades through a course, which strongly affects students’ level of satisfaction towards the course. Furthermore, due to changes in their level of knowledge mastery, students’ preference for courses is not persistent; that is, after completing a course and mastering relevant knowledge, their preference for courses with similar knowledge concepts decreases. Student satisfaction with a course should not be equated with preference, as course recommendation methods based on student preference have certain limitations. In [17], the authors pointed out that student satisfaction with course learning is significantly affected by teachers, course content, curriculum, and grades. Recently, the satisfaction of students has become an important factor in research on course recommendation. In [18], course recommendation based on learning performance prediction was proposed. A number of course recommendation methods focus on the characteristics and behavior data of students in the learning system. For example, [19] proposed a recommendation method for learning objects based on the integration of social signals, interests, and learner user preferences in an e-learning system. The authors of [20] proposed a course recommender system that uses extracted rules to find suitable courses according to student behaviors and preferences. In [21], a path that satisfies students’ limited time while maximizing their grades is used to make lesson-by-lesson recommendations. Similar to other recommendation systems, course recommendation systems must face the cold start problem, meaning that it is difficult to recommend courses for new students. The literature [22] points out that when there are insufficient data in one domain and relatively rich data in another, transfer learning can be used to overcome the cold-start problem when the two domains are explicitly or implicitly related. In addition, with sufficient data from the source domain, transfer learning and collaborative filtering can be used in combination to extract knowledge in order to improve the accuracy of recommendations in the target domain [23].

2.2. Heterogeneous Information Network Embedding-Based Recommendation

In natural and social systems, interacting components form interconnected networks, which can be referred to as complex information networks. These networks are homogeneous, containing the same type of objects and links; however, most real systems contain multiple types of interacting components, and as such can be modeled as heterogeneous information networks (abbr. HIN). HIN consist of multiple types of nodes and links, and have been proposed as a powerful information modeling method [24] able to naturally model complex objects and their rich relations. Figure 1 shows the HIN of two course datasets. HIN embedding, which aims to embed multiple types of nodes into a low-dimensional space, has received growing attention as well. Heterogeneous information networks can naturally model complex objects and their rich relations in recommender systems, as in such systems objects are of different types and links among objects represent different relations. In [25], the authors propose an approach to evaluate the similarity of items or users in HIN. In [26], the authors proposed an MF-based recommendation method that uses the entity similarity calculated on a heterogeneous information network based on a meta-path algorithm. In [27], a collaborative filtering method on a weighted heterogeneous information network was proposed. This method is constructed by connecting users and items with the same rating. It can flexibly integrate heterogeneous information to make recommendations through weighted meta-paths and weighted integration methods. In order to take full advantage of the relationship heterogeneity in information networks, the authors of [28] introduced metapath-based latent features to represent the connectivity between users and items along different types of paths. The network embedding approach is more resistant to sparse and noisy data. Considerable research has been done on representation learning for HIN. Broadly speaking, the existing works on HIN embedding can be categorized into four types: random walk-based methods, decomposition-based methods, deep neural network-based methods, and task-specific methods. In [6], an HIN embedding-based approach for recommendation was proposed. In [29], the authors exploited the attention-guided walk model in a heterogeneous information network to selectively sample discriminative attributes and representative explanation meta-paths to explain the recommendations.

3. Preliminary

The term Heterogeneous Graph is used uniformly in the descriptions in this paper. Because the graph structure means that it contains more comprehensive information and rich semantics, it has been widely used in many data mining tasks. In this section, we first introduce several definitions used in this article, including the HG and the meta-path of the HG. Then, we illustrate the working process of performance prediction using meta-path embedding. Several important notations are listed in

Table 1. Important notations used in this paper.

Notation	Description
$G=(V,E)$	The heterogeneous graph
A	The set of the types of node
P	A meta-path
$\mathsf{\Gamma }$	The set of the meta-path
$A_t$	The type of node t
$|N^{A_t}(v)|$	The number of nodes of type $A_t$ in the neighbor of node v.
$M^a$	An adjacency matrix of HG.
$e^{(l)}$	A node embedding on the l meta-path.
$e_u^{(U)},e_i^{(I)}$	The finally embedding of user u and item i.
${\widehat{r}}_{u,i}$	The rating predicted by user u on item i.
$u_u,v_i$	The potential factors for user u and item i

, and we present a more detailed explanation of their role in this context.

Definition 1

(Heterogeneous Graph). (1) Given a graph $G=\{V,E\}$, where V and E are the node set and relation set, respectively, if there is a mapping function $\varphi (·)$ of node type and a mapping function $\theta (·)$ of edge type which map the nodes $v\in V$ and edges $e\in E$ to the specific types A and C, respectively, then this type graph is a heterogeneous graph. (2) If $\left|A\right|+\left|C\right|>1$, then G is a heterogeneous graph and $G=\{A,C\}$ is called heterogeneous graph (abbr. HG) schema. The schematic of a heterogeneous graph of a course is shown in Figure 1.

Definition 2

(Meta-path of HG). A meta-path is defined as a sub-path that links two different nodes in a heterogeneous graph. In this study, a meta-path is denoted as a path in the form of $B_1\stackrel{C_1}{⟶}{B}_2\stackrel{C_2}{⟶}\dots \stackrel{C_l}{⟶}{B}_l$ which describes a composite relation $C=C_1\circ C_2\circ \cdots \circ C_l$ between entity $B_1$ and $B_{i+1}$, where ∘ denotes the composition operator on relations.

Definition 3

(Reciprocal Relationship of HG Embedding). Given the HG embedding of a course, denoted by $\overrightarrow{c}$, and a student, denoted by $\overrightarrow{s}$, the reciprocal relationship between them is an interactive module Θ, e.g., $\mathcal{R}=\mathsf{\Theta }(\overrightarrow{c},\overrightarrow{s})$, where $\mathcal{R}$ is the representation of the interactive result.

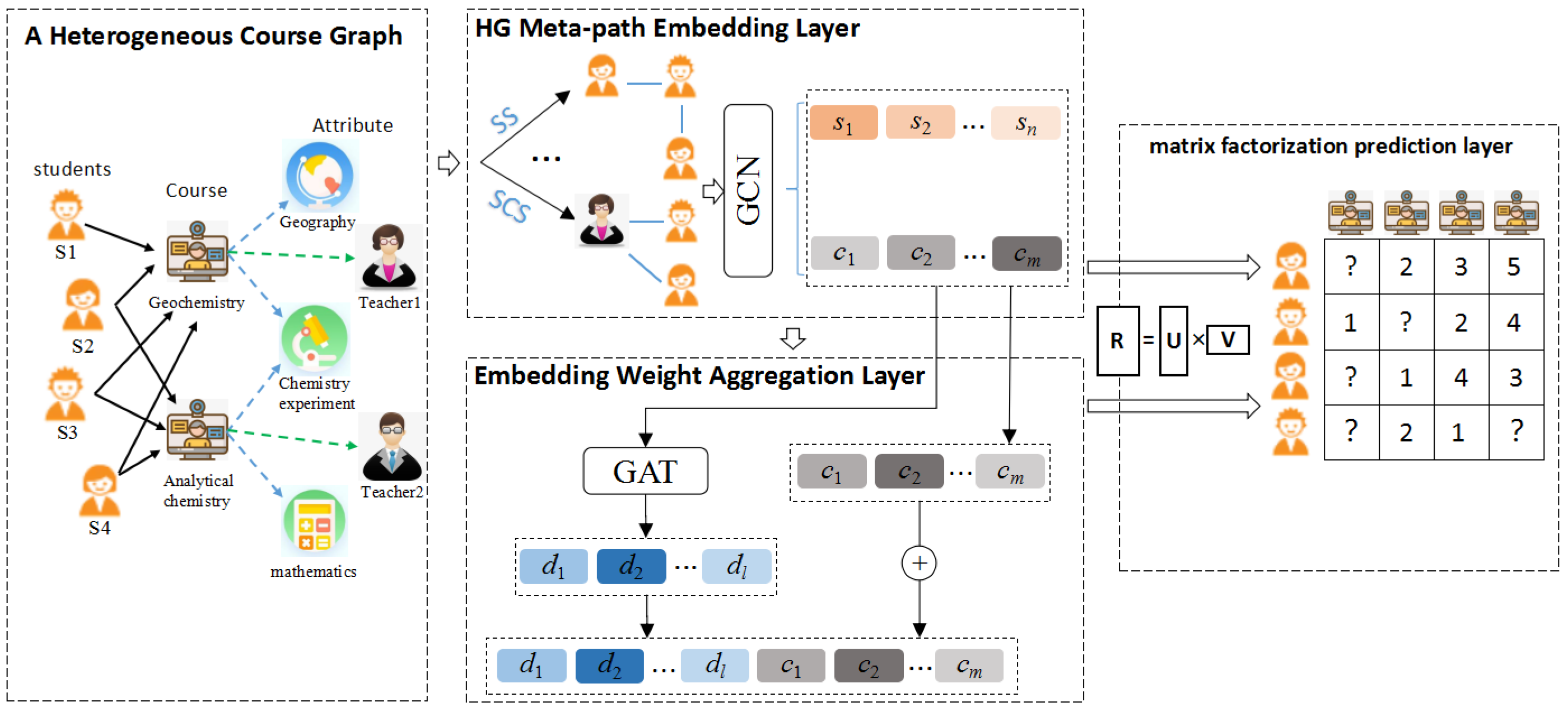
4. Proposed Approach for Course Recommendation

In this section, we propose a novel method for course recommendation based on HG meta-path embedding. For simplicity, in the following presentation we use the short name “HGE-CRec” for our proposed method. The framework of HGE-CRec is shown in Figure 2. As shown in the figure, HGE-CRec is a triple-layer architecture model that takes students’ ratings of each course as the output. The first layer is named the Meta-path Embedding Layer (MEL), the second layer is named the Embedding Weight Aggregation Layer (EWAL), and the third layer is named the Matrix Factorization based Prediction Layer (MFPL). The MEL generates meta-path embeddings for heterogeneous graphs and employs a GCN to simulate more meta-path embeddings. The EWAL employs GAT to aggregate neighbor node embeddings and concatenate them with the original embeddings. The MFPL uses a matrix factorization framework to predict students’ ratings on courses. The details of MEL, EWAL, and MFPL are illustrated in Section 4.1, Section 4.2 and Section 4.3.

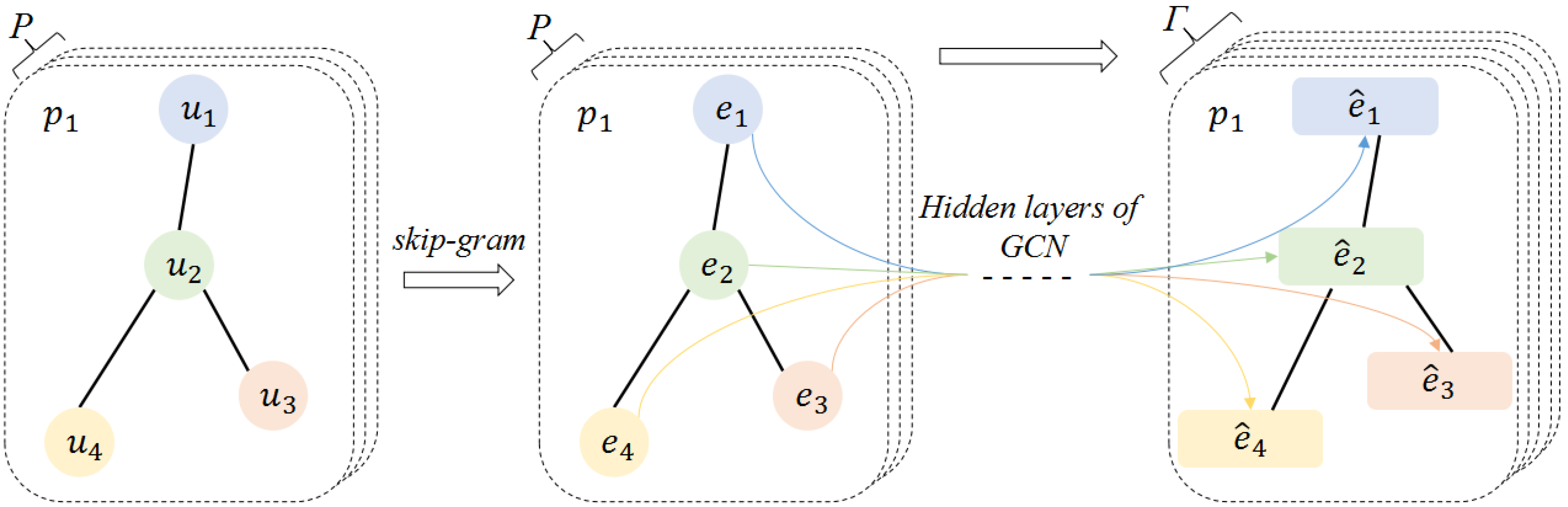
4.1. Meta-Path Embedding Layer

4.1.1. Original Meta-Path Embedding

This module is used to generate the embedding of nodes on meta-paths of the heterogeneous graph. For this task, the meta-paths of the heterogeneous graph are generally sampled first, then the nodes on the sampled meta-paths are embedded. This module uses a meta-path based Deep Walk (abbr. MDK) to generate node embedding on each meta-path. MDK combines the random walk and word2vec algorithms. First, the heterogeneous graph is sampled and filtered for node sequences of various meta-paths, then the skip-gram algorithm in word2vec is used to map the node sequences into low-dimensional space:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill R(n_{t+1}=y|n_t=x,P)=\left\{\begin{array}{cc}\frac{1}{|N_{A_{t+1}}(x)|},\hfill & \hfill (x,y)\in E,\mathsf{\Phi }(y)=A_{t+1}\\ 0,\hfill & \hfill (x,y)\in E,\mathsf{\Phi }(y)\ne A_{t+1}\\ 0,\hfill & \hfill (x,y)\notin E\end{array}\right.\end{array}\end{array}$$

where $n_t$ represents the t-th node of the walk, x is a set of the node type which includes $A_t$, $|N_{A_{t+1}}(x)|$ represents the number of nodes with node type $A_{t+1}$ among the neighbors of node x, and $R(n_{t+1}=y|n_t=x,P)$ represents the probability for a given node x of selecting a node y which represents the constraints of meta-path P. This regular sampling can ensure uniform sampling of various heterogeneous types of nodes under the constraint of the meta-path P to obtain the node sequence $X=[x_1,x_2,x_3,\dots ,x_n]$ of various meta-paths. Next, in order to improve the training efficiency of meta-path nodes, we filter X, that is, we keep nodes of the same type as the starting node, map nodes of the same type to the same space, form a new homogeneous node sequence $\widehat{X}$, and then pass embedding methods to generate embedded representations of the filtered nodes.

Next, the skip-gram algorithm is used to generate node embeddings of $\widehat{x}$. The skip-gram algorithm adopts the principle of similarity of adjacent nodes, uses the central node to predict the context node, and obtains the embedding of the target node after continuous iterative optimization. Skip-gram is a three-layer network structure consisting of an input layer, hidden layer, and output layer. It first generates a node sequence according to the size of the window, then takes the central node of the sequence as input and continuously maximizes the occurrence probability of its neighbor nodes, and finally obtains the embeddings of all nodes. The optimization objective of this algorithm is as follows:

$$L=\underset{f}{max}\sum _{u\in V}logPr(N_u|f(u)),$$

(1)

where f is a function that maps each node u to a d-dimensional space vector, e.g., $f=V\to R^d$, u is the current node, $N_u$ is the neighbor node of the u node obtained through the meta-path, and Stochastic Gradient Descent is used to optimize L.

4.1.2. Simulated Meta-Path Embedding

Using the method in the previous section, the embeddings generated under each meta-path in the heterogeneous graph can be obtained. In order to gather more neighbor information to improve the learning effect of node feature representation, this module uses GCN to aggregate the information of neighbor nodes to generate more meta-path node embeddings. As Figure 2 shows, a GCN model inside $MEL$ is used to achieve this task; that is, more meta-path node embeddings are simulated by using GCN to aggregate neighbor embeddings for the node embeddings of the initial meta-path, thereby generating new node embeddings. The schematic of this process is shown in Figure 3.

For a heterogeneous graph $G=(V,E)$, $M^a$ denotes an adjacency matrix of G generated from the set of filtered meta-path sampling sequences $\widehat{X}$; $M^a$ is added as an identity matrix I for extension, e.g., $M^a=M^a+I$. Then, we have a matrix D

$$D_{ii}=\sum _j{M}_{ij}^a,$$

(2)

where D denotes a diagonal matrix of the node degree. Then, the GCN is used to generate the embeddings of the simulated meta-path following the process in Equation (3):

$$\begin{array}{c}\hfill {\widehat{e}}^P=softmax(D^{-\frac{1}{2}}{M}^a{D}^{-\frac{1}{2}}LeakyReLU(D^{-\frac{1}{2}}{M}^a{D}^{-\frac{1}{2}}{e}^P{W}_0^P)W_1^P),\end{array}$$

(3)

where ${\widehat{e}}^P$ denotes the simulated meta-path embeddings, $e^P$ denotes the original ones, and $W_0^P$ and $W_1^P$ represent the trainable weight matrix.

4.2. Embedding Weight Aggregation Layer

4.2.1. Aggregation of Meta-Path Embedding Based on Attention Mechanism

In order to aggregate the neighbor information of each node, EWAL adopts a GAT mechanism to update the embedding representation of each node to form a new node embedding vector. For each meta-path embedding, including the original meta-path embedding and the simulated meta-path embedding, Equation (4) can be used to generate a new node embedding for each node under each meta-path:

$$t_{v,j}^{(l)}=LeakyReLU({\eta }^{(l)T}·[W^{(l)}{e}_v^{(l)}\left|\right|W^{(l)}{e}_j^{(l)}]),$$

(4)

where $e_v^{(l)}$ represents the embedding of node v under the l-th meta-path, $t_{v,j}^{(l)}$ represents the contribution of features of neighbor j to node v under the l-th meta-path, ${\eta }^{(l)T}$ represents the attention parameter vector under the lth meta-path, $W^{(l)}$ represents the trainable weight matrix, and $\left|\right|$ represents the splicing operation between vectors. Then, we can use Equation (5) for normalization:

$$a_{i,j}^{(l)}=\frac{exp(t_{vj}^{(l)})}{{\sum }_{k=1}^{k\in N_v}exp(t_{vk}^{(l)})}$$

(5)

After the weighted average of the neighborhood features of node v is obtained according to contribution $a_{i,j}^{(l)}$, a nonlinear conversion function $\sigma$ is added to obtain the new features of node v, i.e., ${\tilde{e}}_v^{(l)}$. Equation (6) shows this process:

$${\tilde{e}}_v^{(l)}=\sigma (\sum _{j\in N_v}{a}_{vj}^{(l)}{W}^{(l)}{e}_j^{(l)})$$

(6)

In order to better learn the correlation between nodes and neighbors, the module uses the multi-header attention mechanism to perform K times attention operations, then splices the K times of the results, as shown in Equation (7):

$${\tilde{e}}_v^{(l)}(K)=\underset{k=1}{\overset{K}{\left|\right|}}\sigma (\sum _{j\in N_v}{[a_{vj}^{(l)}]}^k{[W^{(l)}]}^k{e}_j^{(l)}),$$

(7)

where ${[a_{vj}^{(l)}]}^k$ represents the normalized neighbor contribution weight to node v on the k attention header under the l meta-path, and ${[W^{(l)}]}^k$ represents the trainable weight matrix on the k attention header under the l meta-path.

In order to retain the embedded information before and after updating the node, the embedded information before and after the update is spliced, meaning that the final embedded dimension after splicing is twice the previously embedded dimension. Both the user node and the project node need to undergo graph attention network aggregation embedding.

The framework of GAT Embedding is shown in Figure 4.

4.2.2. Fusion of Meta-Path Embedding

Next, we use nonlinear depth fusion method to fuse all of the different kinds of embedded information of the meta-path into the embedded information targeted at a single node. This embedding fusion transformation can transform the embedding into a more appropriate form, improving the recommendation performance.

With a node $v\in V$, we can find the embedded representation set of v nodes ${\{e_v^{(l)}\}}_{l=1}^{\left|\mathsf{\Gamma }\right|}$, where $\mathsf{\Gamma }$ is a set of meta-paths that include the original meta-paths and the simulated meta-paths, and $e_v^{(l)}$ represents the embedded information of node v under meta-path l. Taking the user node as an example, the nonlinear depth fusion function $\mathcal{M}(·)$ provided below can be used to fuse the embedded information of each user node u, as shown in Equation (8):

$$\mathcal{M}(\{e_u^{(l)}\})=\sigma (\sum _{l=1}^{\left|\mathsf{\Gamma }\right|}{W}_u^{(l)}\sigma (M^{(l)}{e}_u^{(l)}+b^{(l)})),$$

(8)

where $M^{(l)}\in R^{D\times d}$ is the conversion matrix under path l, $b^{(l)}\in R^D$ is the offset vector under path l, and $W_u^{(l)}$ is the preference weight of user v under meta-path l. The function $\sigma (·)$ is a nonlinear function. Here, the sigmoid function is used. For the fusion of embedded information of project nodes, a fusion method consistent with the embedded information of the user nodes is adopted. The algorithm for enhancing meta-path embedding is shown in Algorithm 1.

Algorithm 1: Algorithm for enhancing meta-path embedding

Input: the heterogeneous graph G; the adjacency matrix $M^a$; the meta-path sets $P^{(U)}$ for users and $P^{(I)}$ for items.     Output: the enhanced meta-path embedding set of users and items: ${\{e_u^{(l)}\}}_l^{|{\mathsf{\Gamma }}^{(U)}|}$,${\{e_i^{(l)}\}}_l^{|{\mathsf{\Gamma }}^{(I)}|}$. 1: Get original meta-path embedding sets ${\{e_i^{(l)}\}}_l^{|P^{(I)}|}$ and ${\{e_u^{(l)}\}}_l^{|P^{(U)}|}$ of G by using skip-gram 2: for$e_i^{(l)}$ in ${\{e_i^{(l)}\}}_l^{|P^{(I)}|}$ do 3:    ${\tilde{e}}_i^{(l)}\leftarrow GCN(e_i^{(l)},M^a)$. {Equation (3)} 4:    ${\mathsf{\Gamma }}^{(I)}\leftarrow \{e_i^{(l)},{\tilde{e}}_i^{(l)}\}$. {Get a set including two types meta-path embedding.} 5: end for 6: for${\overline{e}}_i^{(l)}$ in ${\mathsf{\Gamma }}^{(I)}$ do 7:    $t_{i,j}^{(l)}\leftarrow GAT({\overline{e}}_i^{(l)},{\overline{e}}_j^{(l)})$. {${\overline{e}}_j^{(l)}$ is the embedding of the neighbor node j. Equation (4)} 8:    $a_{i,j}^{(l)}\leftarrow normalize(t_{i,j}^{(l)})$. {Equation (5)} 9:    ${\widehat{e}}_i^{(l)}\leftarrow F(a_{i,j}^{(l)},e_j^{(l)})$. {Equation (6), Equation (7)} 10:    $e_i^{(l)}\leftarrow Con(e_i^{(l)},{\widehat{e}}_i^{(l)})$. Update $e_i^{(l)}$ by connecting ${\widehat{e}}_i^{(l)}$. 11: end for 12: for$e_u^{(l)}$ in ${\{e_u^{(l)}\}}_l^{|P^{(U)}|}$ do 13:    ${\tilde{e}}_u^{(l)}\leftarrow GCN(e_u^{(l)},M^a)$. {Equation (3)} 14:    ${\mathsf{\Gamma }}^{(I)}\leftarrow \{e_u^{(l)},{\tilde{e}}_u^{(l)}\}$. {Get a set including two types meta-path embedding.} 15: end for 16: for${\overline{e}}_u^{(l)}$ in ${\mathsf{\Gamma }}^{(U)}$ do 17:    $t_{u,j}^{(l)}\leftarrow GAT({\overline{e}}_u^{(l)},{\overline{e}}_j^{(l)})$. {${\overline{e}}_j^{(l)}$ is the embedding of the neighbor node j. Equation (4)} 18:    $a_{u,j}^{(l)}\leftarrow normalize(t_{u,j}^{(l)})$. {Equation (5)} 19:    ${\widehat{e}}_u^{(l)}\leftarrow F(a_{u,j}^{(l)},e_j^{(l)})$. {Equation (6), Equation (7)} 20:    $e_u^{(l)}\leftarrow Con(e_u^{(l)},{\widehat{e}}_u^{(l)})$. Update $e_u^{(l)}$ by connecting ${\widehat{e}}_u^{(l)}$. 21: end for 22: return${\{e_u^{(l)}\}}_l^{|{\mathsf{\Gamma }}^{(U)}|}$,${\{e_i^{(l)}\}}_l^{|{\mathsf{\Gamma }}^{(I)}|}$.

4.3. Matrix Factorization-Based Prediction Layer

The MFPL module uses Matrix Factorization to predict the grade of students on courses. The HGE-CRec model proposed in this paper combines HG meta-path embedding with Matrix Factorization, and further combines the embedded vectors of users u and items i obtained from MEL and EWAL into the Matrix Factorization model. The prediction process of the rating is shown in Eqution (9):

$${\widehat{r}}_{u,i}=u_u^T·v_i+\alpha ·e_u^T·{\gamma }_i+\beta ·{\gamma }_u^T·e_i,$$

(9)

where ${\widehat{r}}_{u,i}$, u, and i belong to the rating matrix $\mathcal{R}$, $e_u$ is the embedding of the user after merging the embedding vectors of different meta-paths, and $e_i$ is the embedding of the item after merging the embedding vectors of different meta-paths, that is, the result of merging function $\mathcal{M}(·)$ in Equation (8). In order to keep the form consistent, the hidden factors ${\gamma }_i$ and ${\gamma }_u$ are introduced to multiply the embedding vectors $e_u$ and $e_i$, respectively, while $\alpha$ and $\beta$ are adjustable parameters.

In order to provide the model with better generalization ability and prevent overfitting, regular constraints can be added to the loss function. For modeling scenarios of heterogeneous information networks, heterogeneous regular terms need to be added. The final optimization goal is shown in Eqution (10):

$$\begin{array}{cc}\hfill & \ell =\sum _{<u,i,r_{u,i}>\in \mathcal{R}}{(r_{u,i}-{\widehat{r}}_{u,i})}^2+\hfill \\ \hfill & \lambda \sum _u({\Vert U_u\Vert }_2+{\Vert V_i\Vert }_2+{\Vert {\gamma }_u\Vert }_2+{\Vert {\gamma }_i\Vert }_2+{\Vert {\mathbb{E}}_u\Vert }_2+{\Vert {\mathbb{E}}_i\Vert }_2),\hfill \end{array}$$

(10)

where ${\widehat{r}}_{u,i}$ is the prediction score calculated using Equation (9), $\lambda$ is the regularization parameter, ${\mathbb{E}}_u$ is the parameter set of the function $\mathcal{M}(·)$ for users, and ${\mathbb{E}}_i$ is the parameter set of the function $\mathcal{M}(·)$ for items. The model training uses Gradient Descent to obtain the partial derivative, then updates the variables according to the direction of the negative gradient. After multiple iterations, the low-dimensional matrix is updated continuously until the algorithm finally converges; the parameters of Equation (10) are updated according to the following formula:

$$\begin{array}{c}\hfill U_u\leftarrow U_u-\eta ((r_{u,i}-{\widehat{r}}_{u,i})V_i+{\lambda }_U{U}_u)\end{array}$$

(11)

$$\begin{array}{c}\hfill {\mathbb{E}}_{u,l}\leftarrow {\mathbb{E}}_{u,l}-\eta (-\alpha (r_{u,i}-{\widehat{r}}_{u,i}){\gamma }_u{\nabla }^{(U)}+{\lambda }_{\mathbb{E}}{\mathbb{E}}_{u,l}),\end{array}$$

(12)

$$\begin{array}{c}\hfill V_i\leftarrow V_i-\eta ((r_{u,i}-{\widehat{r}}_{u,i})U_u+{\lambda }_V{V}_i)\end{array}$$

(13)

$$\begin{array}{c}\hfill {\mathbb{E}}_{i,l}\leftarrow {\mathbb{E}}_{i,l}-\eta (-\alpha (r_{u,i}-{\widehat{r}}_{u,i}){\gamma }_i{\nabla }^{(I)}+{\lambda }_{\mathbb{E}}{\mathbb{E}}_{i,l}),\end{array}$$

(14)

$$\frac{\partial e_i^{(l)}}{\partial {\mathbb{E}}_{i,l}}=\left\{\begin{array}{cc}{W}_i^{(l)}\sigma (X_a)\sigma (X_f)(1-\sigma (X_a))(1-\sigma (X_f))e_i^{(l)},\hfill & \mathbb{E}=M;\hfill \\ \\ W_i^{(l)}\sigma (X_a)\sigma (X_f)(1-\sigma (X_a))(1-\sigma (X_f)),\hfill & \mathbb{E}=b;\hfill \\ \\ \sigma (X_a)\sigma (X_f)(1-\sigma (X_a)),\hfill & \mathbb{E}=W,\hfill \end{array}\right.$$

(15)

The algorithm for training HGE-CRec is shown in Algorithm 2.

Algorithm 2: HGE-CRec training algorithm

Input: the heterogeneous graph G; the adjacency matrix $M^a$; the rating matrix $\mathcal{R}$; the adjustable parameters $\alpha$, $\beta$; the regularization parameter $\lambda$; the learning rate coefficients for integrating embedding features; the enhanced meta-path embedding sets ${\{e_u^{(l)}\}}_l^{|{\mathsf{\Gamma }}^{(U)}|}$ for users and ${\{e_i^{(l)}\}}_l^{|{\mathsf{\Gamma }}^{(I)}|}$ for items.     Output: ${\widehat{r}}_{u,i}$, the users and items feature matrices U and V; the weights of users and items HG embedding; the weights of feature interaction matrix and; the parameters in the fusion function of embedding 1: Get enhanced meta-path embedding sets ${\{e_u^{(l)}\}}_l^{|{\mathsf{\Gamma }}^{(U)}|}$ and ${\{e_i^{(l)}\}}_l^{|{\mathsf{\Gamma }}^{(I)}|}$ by using Algorithm 1 2: Initialize $U,V,{\gamma }^{(U)},{\gamma }^{(I)},{\mathbb{E}}_u,{\mathbb{E}}_i$ by standard normal distribution; 3: while termination criterion is not satisfied do 4:    $r_{u,i}\leftarrow$ Randomly select a tuple $<u,i>\in R$ 5:    Update $U_u$ and $V_i$ by a typical MF model; 6:    for $e_u^{(l)}$ in ${\mathsf{\Gamma }}^{(U)}$ do 7:      ${\nabla }^{(U)}\leftarrow \frac{\partial e_u^{(l)}}{\partial {\mathbb{E}}_{u,l}}$ {Equation (15)}; 8:      Update ${\mathbb{E}}_{u,l}$ by Equation (12); 9:    end for 10:    Update ${\gamma }_u^{(U)}$ by Equation (11); 11:    for $e_i^{(l)}$ in ${\mathsf{\Gamma }}^{(I)}$ do 12:      ${\nabla }^{(I)}\leftarrow \frac{\partial e_i^{(l)}}{\partial {\mathbb{E}}_{i,l}}$ {Equation (15)}; 13:      Update ${\mathbb{E}}_{i,l}$ by Equation (14); 14:    end for 15:    Update ${\gamma }_i^{(I)}$ by Equation (13); 16: end while 17: return$U,V,{\gamma }^{(U)},{\gamma }^{(I)},{\mathbb{E}}_u,{\mathbb{E}}_i$

5. Experiments

In this section, we conduct extensive experimental studies to verify the effectiveness and advantages of our approach. To this end, we compare the recommendation performance produced by HGE-CRec with several baselines on four datasets.

5.1. Datasets

In order to verify the effective of our proposed approach, the experiments are carried on four real datasets: two large-scale online courses datasets, Scholat and CNPC, and two other datasets, Yelp and Movielens, which are commonly used in research on HIN embedding-based recommendation. CNPC, Yelp, and Movielens are public datasets.

Table 2. Statistics for nodes and relationships in the datasets.

Datasets	Relations (A-B)	Number (A)	Number (B)	Number (A-B)
	Student-Course	25,293	1670	53,988
	Student-Unit_of_study	150,563	5753	150,563
Scholat	Student-Research_field	150,563	6458	150,563
	Course-School	3168	344	3168
	Course-Type	3168	13	3168
	Course-Teacher	3168	1060	7846
	User-Course	224,914	238	325,199
	User-Learner_type	32,719	7	32,719
CNPC	User-Age	224,914	4	224,914
	Course-Discipline	238	10	238
	Course-Course_length	238	79	238
	User-Business	16,239	14,284	198,397
	User-User	10,580	10,580	158,590
Yelp	User-Compliment	14,411	11	76,875
	Business-City	14,267	47	14,267
	Business-Category	14,180	511	40,009
	User-Movie	943	1682	100,000
	User-User	943	943	47,150
Movielens	User-Occupation	943	21	943
	User-Age	943	8	943
	Movie-Movie	1682	1682	82,798
	Movie-Genre	1682	18	2891

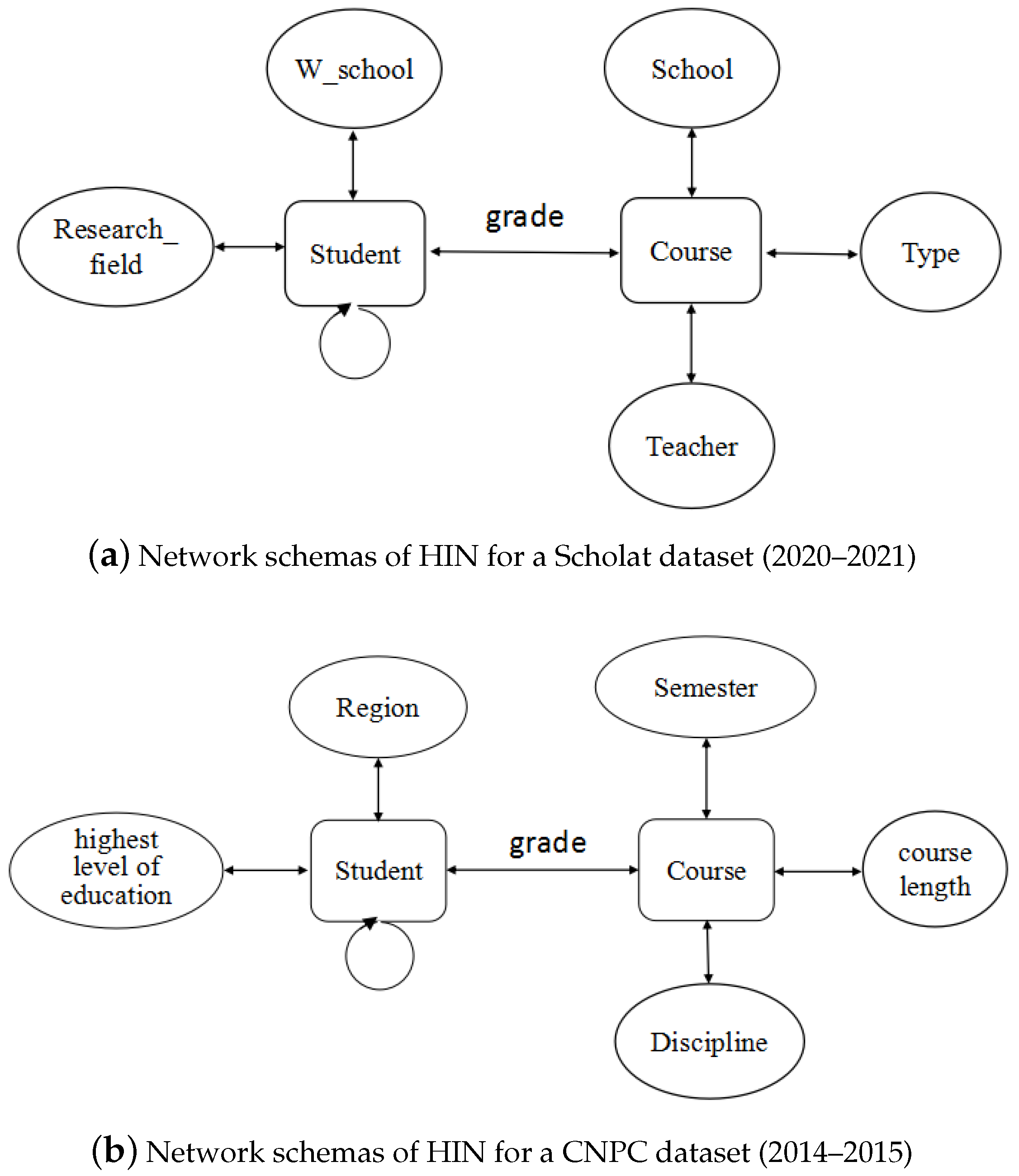
presents statistical information about the nodes and relationships in these datasets.

• Scholat
  This dataset is from a real academic social course platform (scholat.com) which provides courses offered by Chinese universities, including undergraduate and graduate courses. The courses involve computer science, economics, pedagogy, and other disciplines. The student profiles include the school, grade, major, courses learned, etc. The dataset used in our experiment contains 3168 courses, 150,563 users, and 1,237,485 course visit records for the 2020–2021 academic year. The frequency of students’ attendance of courses represents information about student interest in the course. In this experiment, we scaled the attendance frequency to an interval.
• CNPC (https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/26147, accessed on 28 September 2022)
  This dataset consists of the Canvas Network Open Course (canvas.net), which hosts open online courses, including Massive Open Online Courses (MOOCs) that are freely available to participants around the world. The dataset used in our experiments is from January 2014 to September 2015, including 224,914 users and 238 courses as well as various attribute information on users’ social relations, forums, users, and courses. The courses include ten disciplines, e.g., mathematics, statistics, and education.
• Yelp (https://www.yelp.com/dataset/documentation/main, accessed on 30 September 2022)
  This dataset comes from the largest merchant rating website in the United States, yelp.com. The dataset records user ratings of merchants, the users’ social relationship, and attribute information on users and merchants, including 16,239 users, 14,282 merchants, and 198,397 ratings.
• Movielens (http://files.grouplens.org/datasets/movielens/ml-100k-README.txt, accessed on 30 September 2022)
  The Movielens dataset is a classic movie recommendation dataset from movielens.org. Movielens-100k was selected for this experiment. This dataset has 943 users, 1682 movies, and 100,000 scores, and contains social relationship and attribute information between users and movies.

For the proposed model, the interactive data between students and courses is the most important. In addition, we are concerned about the characteristics that are conducive to the formation of the rich meta-paths from datasets, such as course type and teacher or student school and type. Based on the statistical analysis in Table 2, we defined the meta-paths in all four datasets, as shown in

Table 3. Meta-paths of the four datasets.

Scholat	CNPC	Yelp	Movielens
S-C-S, C-S-C, S-C-Te-C-S, C-Te-C, C-Ty-C, S-C-Ty-C-S, S-C-Sc-C-S, C-Sc-C	U-C-U, C-U-C, U-C-D-C-U, C-D-C, U-C-Co-C-U, C-Co-C	U-B-U, B-U-B, U-B-Ci-B-U, B-Ci-B, U-B-Ca-B-U, B-Ca-B	U-M-U, M-U-M, U-M-G-M-U, M-G-M, M-M, U-M-M-U

.

5.2. Experimental Setup

In this subsection, we first clarify the implementation details of the experimental setup used for HGE-CRec. Then, we introduce the comparison baselines and evaluation metrics used in the experiments.

5.2.1. Baselines

This experiment selects three baseline methods to carry out comparative experiments with the proposed approach: PMF, SoMF, and HERec.

• PMF [30]: This is a recommended algorithm for classical probability matrix factorization models which decomposes the scoring matrix into two low-dimensional matrices.
• SoMF [31]: In this algorithm, social relations have the characteristics of social regularization items, helping to integrate social relations into basic recommendations in the matrix factorization model.
• HERec [6]: This classical recommendation algorithm based on heterogeneous information network embedding adopts the random walk strategy based on the meta-path to generate the embedding, then integrates the embedded fusion into the matrix factorization model for recommendation.

5.2.2. Evaluation Metrics

This experiment selects two indicators commonly used in research on recommendation systems, namely, the Mean Absolute Error (MAE) and Root Mean Square Error (RMSE), as the evaluation indicators of the model. MAE and RMSE calculate the prediction accuracy by calculating the deviation between the predicted user score and the actual user score. The smaller the MAE and RMSE, the higher the recommendation quality.

The MAE can be expressed by Equation (16):

$$MAE=\frac{1}{|D_{test}|}\sum _{(i,j)\in D_{test}}|r_{i,j}-{\widehat{r}}_{i,j}|.$$

(16)

The RMSE can be expressed by Equation (17):

$$RMSE=\sqrt{\frac{1}{|D_{test}|}{\sum }_{(i,j)\in D_{test}}{(r_{i,j}-{\widehat{r}}_{i,j})}^2}.$$

(17)

where $r_{i,j}$ is the real rating of item j by user i, ${\widehat{r}}_{i,j}$ is the predicted score of user i on item j, and $D_{test}$ is the test set of the scoring records.

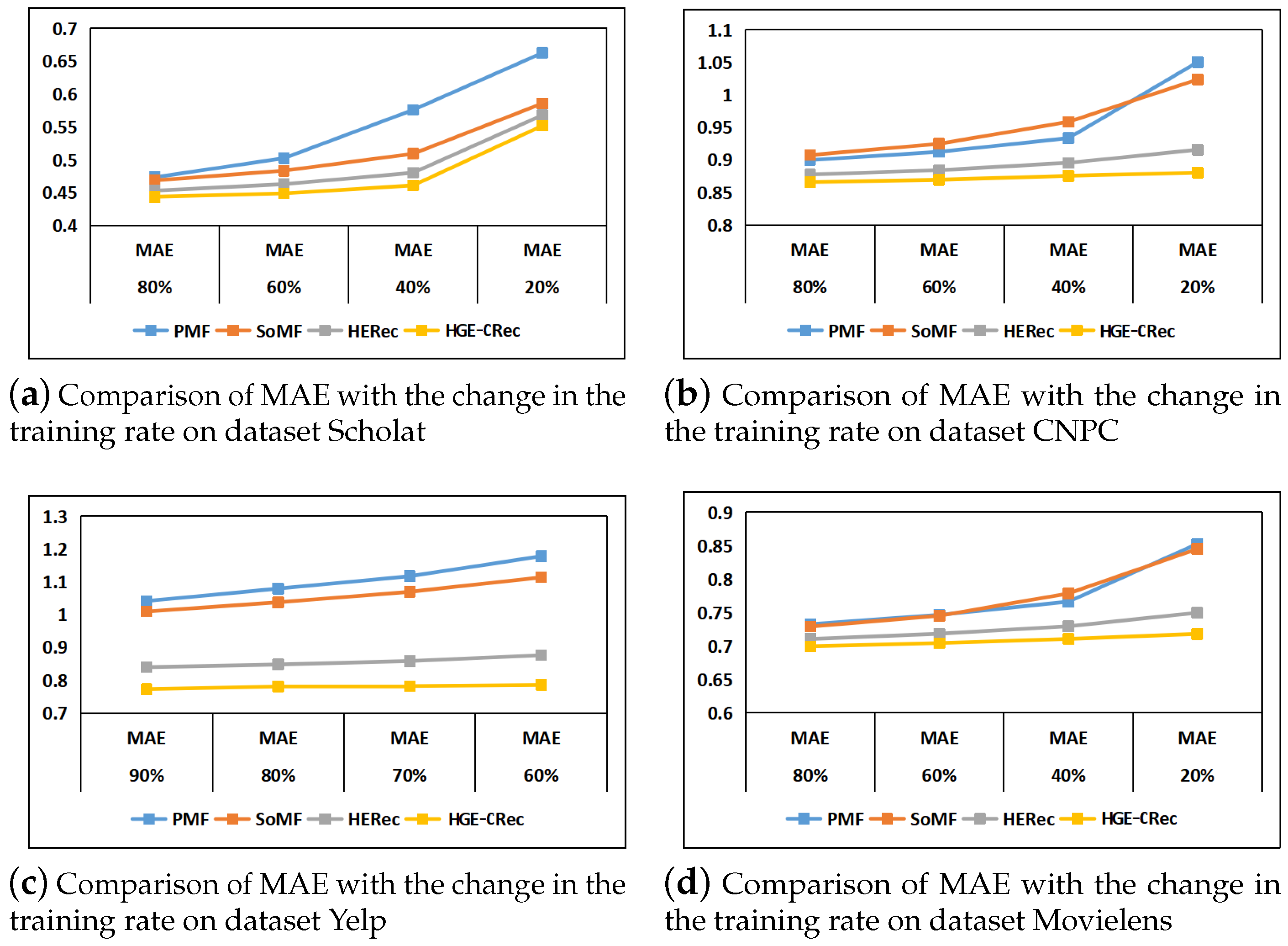
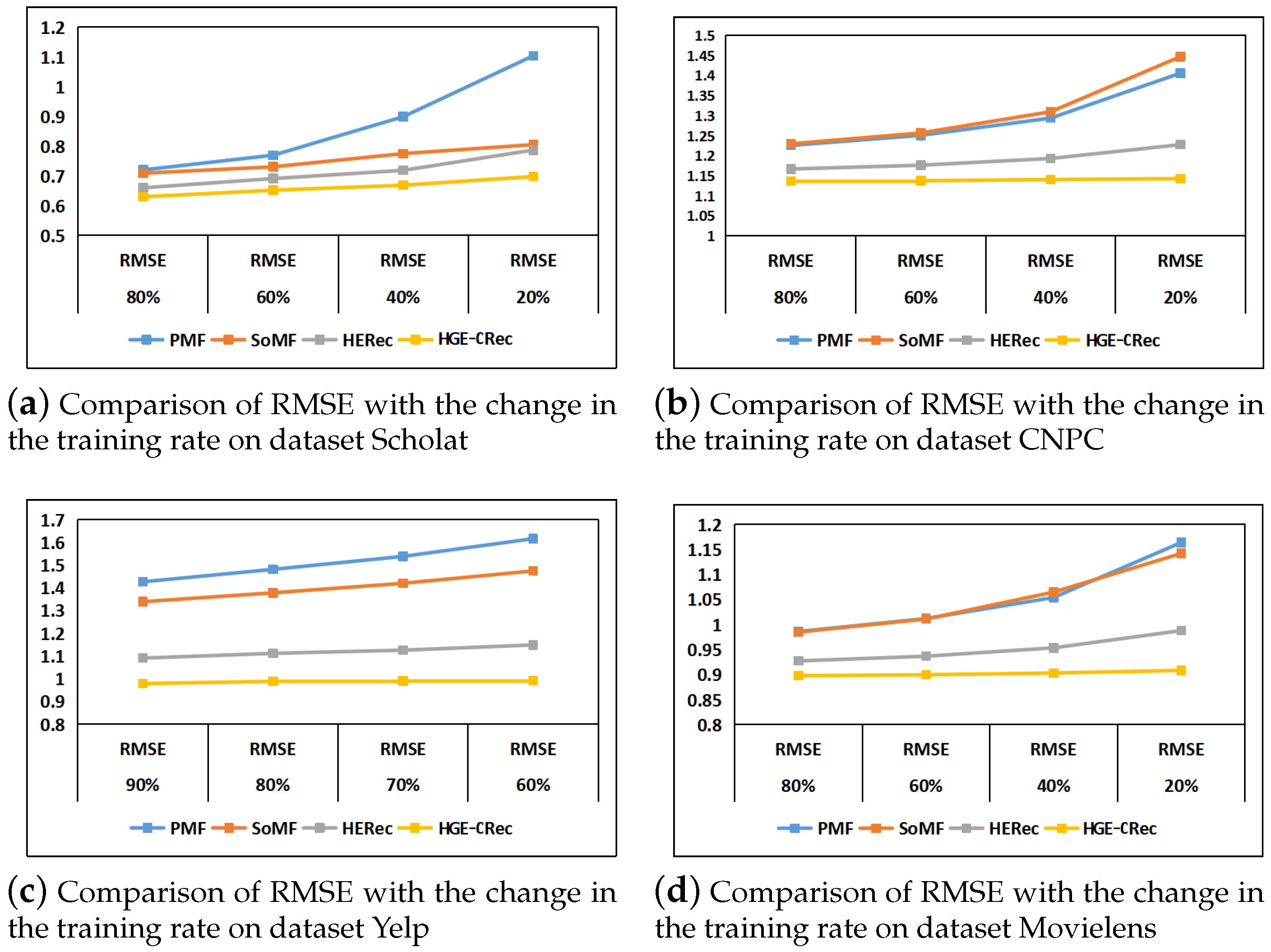
5.3. Results of the Comparative Experiment

This subsection illustrates the comparative experimental results using the proposed approach and baseline methods on four datasets.

For each dataset, the preference (or score) record data are divided into a training set and a test set. For the Scholat, CNPC, and Movielens datasets, four training segmentation ratios are set, namely, 80%, 60%, 40%, and 20%; For the Yelp dataset, because it is more sparse than the other three datasets, four larger training ratios are set, namely, 90%, 80%, 70%, and 60%. For each ratio, teen evaluation sets are randomly generated, then the results are averaged to the final results, which as shown in

Table 4. Results on Scholat.

Training Rate	Metrics	PMF	SoMF	HERec	HGE-CRec
80%	MAE	0.4732	0.4685	0.4529	$0.4435$
	RMSE	0.7199	0.7087	0.6596	$0.6294$
60%	MAE	0.5023	0.4832	0.4627	$0.4486$
	RMSE	0.7693	0.7303	0.6908	$0.6516$
40%	MAE	0.5758	0.5090	0.4801	$0.4608$
	RMSE	0.8988	0.7748	0.7185	$0.6683$
20%	MAE	0.8302	0.5856	0.5677	$0.5516$
	RMSE	1.4199	0.8048	0.7866	$0.6976$

,

Table 5. Results on CNPC.

Training Rate	Metrics	PMF	SoMF	HERec	HGE-CRec
80%	MAE	0.8998	0.9074	0.8775	$0.8658$
	RMSE	1.2254	1.2293	1.1666	$1.1361$
60%	MAE	0.9124	0.9248	0.8843	$0.8695$
	RMSE	1.2504	1.2563	1.1761	$1.1374$
40%	MAE	0.9335	0.9585	0.8955	$0.8754$
	RMSE	1.2934	1.3092	1.1928	$1.1403$
20%	MAE	1.0504	1.0236	0.9156	$0.8805$
	RMSE	1.4053	1.4465	1.2273	$1.1428$

,

Table 6. Results on Yelp.

Training Rate	Metrics	PMF	SoMF	HERec	HGE-CRec
90%	MAE	1.0412	1.0095	0.8395	$0.7723$
	RMSE	1.4268	1.3392	1.0907	$0.9787$
80%	MAE	1.0791	1.0373	0.8475	$0.7804$
	RMSE	1.4816	1.3782	1.1117	$0.9884$
70%	MAE	1.1170	1.0694	0.8580	$0.7817$
	RMSE	1.5387	1.4201	1.1256	$0.9899$
60%	MAE	1.1778	1.1135	0.8759	$0.7853$
	RMSE	1.6167	1.4748	1.1488	$0.9928$

and

Table 7. Results on Movielens.

Training Rate	Metrics	PMF	SoMF	HERec	HGE-CRec
80%	MAE	0.7324	0.7289	0.7103	$0.6992$
	RMSE	0.9862	0.9851	0.9274	$0.8980$
60%	MAE	0.7463	0.7450	0.7181	$0.7041$
	RMSE	1.0121	1.0112	0.9369	$0.8998$
40%	MAE	0.7661	0.7784	0.7293	$0.7104$
	RMSE	1.0542	1.0650	0.9536	$0.9033$
20%	MAE	0.8527	0.8451	0.7495	$0.7179$
	RMSE	1.1641	1.1423	0.9881	$0.9086$

.

Table 4, Table 5, Table 6 and Table 7 show a comparison of the two indicators, MAE and RMSE, with respect to the recommended results using the proposed approach and baseline methods on the four datasets.

Figure 5 shows the results on the four datasets in terms of MAE. Compared with the baselines, the line when using HGE-CRec is gentler in terms of MAE as the training ratio changes from 80% to 20%. In other words, the MAE growth of HGE-CRec is lower than the other three baselines. The same can be observed for all of the datasets.

Figure 6 shows the results on the four datasets in terms of RMSE. Compared with the baselines, the line when using HGE-CRec is gentler in terms of RMSE as the training ratio changes from 80% to 20%. In other words, as for MAE, the growth in RMS for EHGE-CRec is lower than for the other three baselines. Again, this can be observed for all of the datasets.

Moreover, from Figure 5 and Figure 6 it can be seen that the experimental results curves of the proposed approach is flat compared to the baselines, indicating that the effectiveness of the proposed approach is more stable than the baselines.

5.4. Ablation Study

In this section, we conduct an ablation study of the proposed approach through two experiments.

5.4.1. Component Adjustment

The first experiment observes the changes in the performance of the various approaches by adjusting the model’s components. The HGE-CRec proposed in this paper uses GCN and GAT to improve the meta-path embedding after generating the original meta-path embedding. The first source of improvement is realized by using GCN to generate the simulated meta-path embedding, which enhances the meta-path embedding and expands the range of sample feature distribution. The second improvement is to use GAT to aggregate the various kinds of meta-path embedding based on neighbor weights. In order to explore the effect of these two improvements on the model, an ablation study of the component was set up using the following models for comparison:

• HGE-CRec${}_{GCN}$
  Only the first part of the HGE-CRec model’s meta-path embedding is improved, that is, while GCN is used to generate analog meta-path embedding, GAT is not used to aggregate various kinds of meta-path embedding based on neighbor weight.
• HGE-CRec${}_{GAT}$
  Only the second part of the HGE-CRec model’s meta-path embedding is improved, that is, while GAT is used to aggregate the original meta-path embedding based on the neighbor weights, GCN is not used to generate simulated meta-path embeddings.

The training ratio was uniformly 80%. The experimental results of the above models on the four datasets are shown in

Table 8. Results of ablation study on component adjustment.

Dataset	Metrics	HGE-CRec${}_{\mathit{GCN}}$	HGE-CRec${}_{\mathit{GAT}}$	HGE-CRec
Scholat	MAE	0.4528	0.4435	0.4435
	RMSE	0.6598	0.6295	0.6294
CNPC	MAE	0.8775	0.8658	0.8658
	RMSE	1.1667	1.1362	1.1361
Yelp	MAE	0.8479	0.7807	0.7804
	RMSE	1.1111	0.9880	0.9884
Movielens	MAE	0.7103	0.6992	0.6992
	RMSE	0.9272	0.8981	0.8980

.

It can be seen from the experimental results that HGE-CRec${}_{GCN}$ has the weakest effect, which means that only the first part of the improvement has no significant impact on the model; slight jitter is observed during the training process, with a slight increase or decrease. This further indicates that, based on the premise of there being sufficient of original meta-path embeddings, more analog meta-path embeddings are generated by aggregating neighborhood information, and there is little improvement on the model. That is, when meta-path embedding reaches a sufficient amount, saturation occurs and it is of little significance to add meta-path embedding. The effect of HGE-CRec${}_{GAT}$ is significantly improved, showing that the improvement in the second part has a good impact on the model. Furthermore, this shows that using GAT to aggregate the neighbor embedding information of each node based on weight can effectively improve the performance of the model. That is, by learning the influence weight of different neighbors on nodes in the meta-path, the node representation can be enriched and the accuracy of prediction can be improved.

5.4.2. Meta-Path Embedding Adjustment

From the above component adjustment experiment, it can be observed that the effect of the first source of model improvement does not result in a significant effect. Our analysis indicates that the reason for this is that the embedding of the selected meta-path from the dataset becomes saturated. In order to verify this hypothesis, the simulation experiment described in this section was designed to simulate whether the GCN can simulate the embedding of meta-paths in the case of insufficient meta-paths in the dataset (i.e., the embedding of meta-paths is not saturated), expand the range of feature distribution for the meta-paths embedded in the sample, and improve the recommendation effect. The design of the analog element path ablation experiment is described below.

Assuming that each dataset only provides one meta-path, a comparative experiment was conducted to investigate whether GCN can be used to simulate the embedding of meta-paths without considering the weight aggregation of GAT embedding. This experiment adopted a unified meta-path; the type of meta-path was User-Item-User and the training rate was 80%. The model that does not use GCN to simulate the embedding of meta-paths is named HGE-CRec${}_{None-OneMP}$, the model embedded by GCN analog meta-path is named HGE-CRec${}_{GCN-OneMP}$, and the results of the analog element path ablation experiment for the four datasets are shown in

Table 9. Results of meta-path embedding enhancement.

Datasets	Metrics	HGE-CRec${}_{\mathit{None}-\mathit{OneMP}}$	HGE-CRec${}_{\mathit{GCN}-\mathit{OneMP}}$
Scholat	MAE	0.4559	0.4533
	RMSE	0.6719	0.6604
CNPC	MAE	0.8808	0.8795
	RMSE	1.1784	1.1682
Yelp	MAE	0.8804	0.8529
	RMSE	1.1607	1.1283
Movielens	MAE	0.7136	0.7112
	RMSE	0.9360	0.9298

.

The results of this experiment verify that in the case of insufficient meta-paths the use of a graph convolution network to aggregate neighbor information to generate more analog meta-path embedding can improve the experimental results. The method of adding small sample data to GCN can generate more embedded data for recommendation, improving the accuracy of small-sample training data in the final recommendation process. This further shows that the HGE-CRec proposed in this paper can be applied to datasets with insufficient meta-paths. In addition, the traditional predefined meta-path depends on the manual definition provided by researchers. In order to find a better predefined meta-path, a large number of experiments need to be carried out. HGE-CRec effectively expands the range of the feature distribution of the meta-path embedding sample by using GCN to generate more simulated meta-path embedding. For cases with only a small number of meta-paths, the best effect that can be achieved by manually predefined meta-paths can be obtained. From this point of view, the proposed model is conducive to relieving the complexity and uncertainty of manually predefined meta-paths.

6. Conclusions

This paper proposes a course recommendation model, HGE-CRec, based on heterogeneous graph and Graph Neural Network and adopts a heterogeneous graph approach to model multi-source heterogeneous information in the scenario of course recommendation for distance education. The proposed HGE-CRec model uses GCN and GAT to improve the meta-path embedding process in HG. Specifically, after using the skip-gram algorithm to generate the original meta-path embeddings, GCN is used to generate new embeddings to simulate more meta-path embeddings, effectively expanding the range of feature distribution of the meta-path embedded samples. Next, GAT is used to learn the neighborhood contribution degree, aggregate the neighbor embedding information of nodes, and obtain the node embedding vector with importance semantics. The node embedding vectors of different meta-paths are weighted nonlinearly and aggregated to form the low dimensional embedding vectors of each node, and the recommendation is implemented under the framework of matrix decomposition.

Data sparsity is a difficult problem in large-scale online course recommendation. The model proposed in this paper uses a heterogeneous graph structure to represent online course learning and expands the relationship domain of entities (e.g., students, courses) through the meta-paths, thereby alleviating the problem of data sparsity. This work can expand recommendation methods for large-scale online courses from a local perspective to a global perspective, providing a reference for further optimization of online course platforms. On the whole, our proposed model fully considers the different contributions of different neighbors and distinguishes the weight of different neighbor embeddings in order to better model the heterogeneous graph and improve the recommendation effect. Moreover, traditional meta-path generation methods rely on researchers manually predefining the meta-path. In order to find a better meta-path, repeated experiments need to be carried out. Using graph convolution network to generate new embeddings for simulation of more meta-paths might be a good way to solve this problem, as defining only a few meta-paths can already achieve a better effect than that achieved by manually predefining the meta-path. In this way, the problem of tedious and uncertain manual adjustment of predefined meta-paths can be solved. In our future work, we intend to make our model more flexible and extensible. For example, by considering the prevalence of streaming education as a global trend [32], this model can be adjusted to recommend interdisciplinary and cross-domain courses by adding attribute variables to generate meta-paths in the model. In addition, the extension of our framework into an advanced version with further consideration of the multi-modal information of courses and the social network behavior of learners [33] could potentially enrich the knowledge concept representation.