Seismic Performance of Ductile Column with Rectangular Hollow Cross-Section in RC Building
Abstract
1. Introduction
2. Experimental Program
2.1. Specimen Details
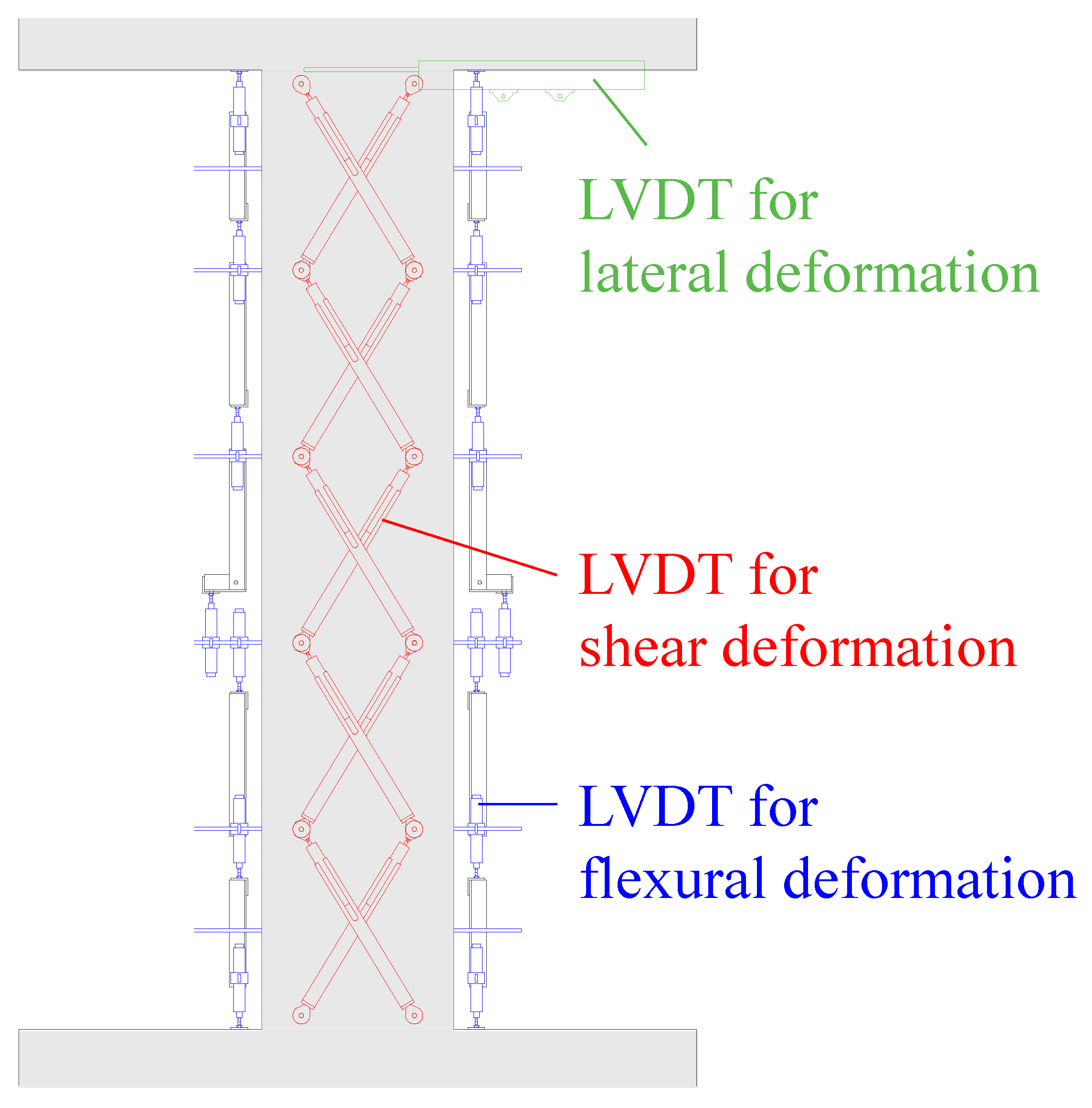
2.2. Loading Program and Instrumentation
3. Experiment Results
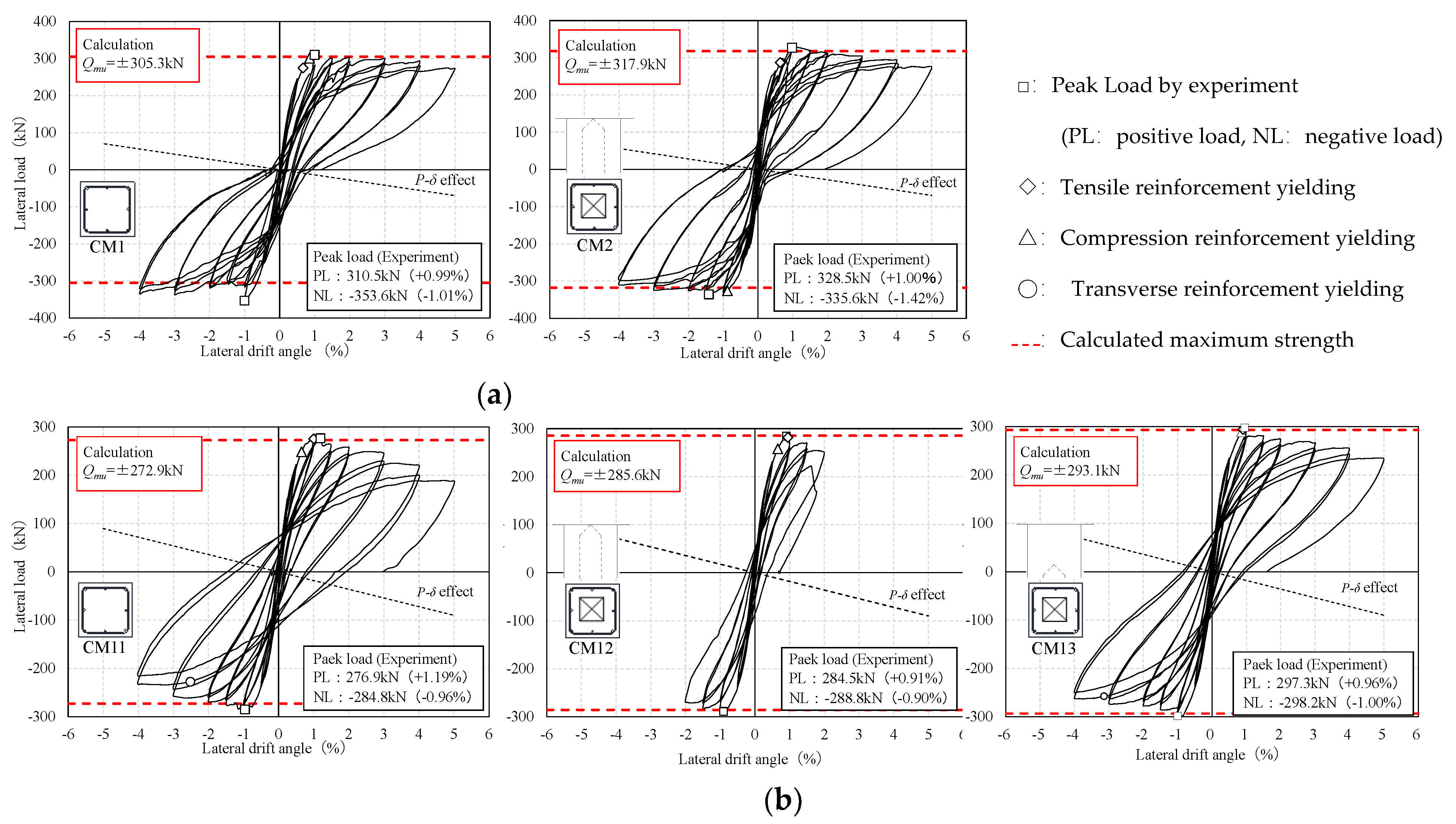
3.1. Failure Process and Hysteresis Curve of N-Series (η = 0.16)
3.2. Failure Process and Hysteresis Curve of S-Series (η = 0.3)
4. Discussion
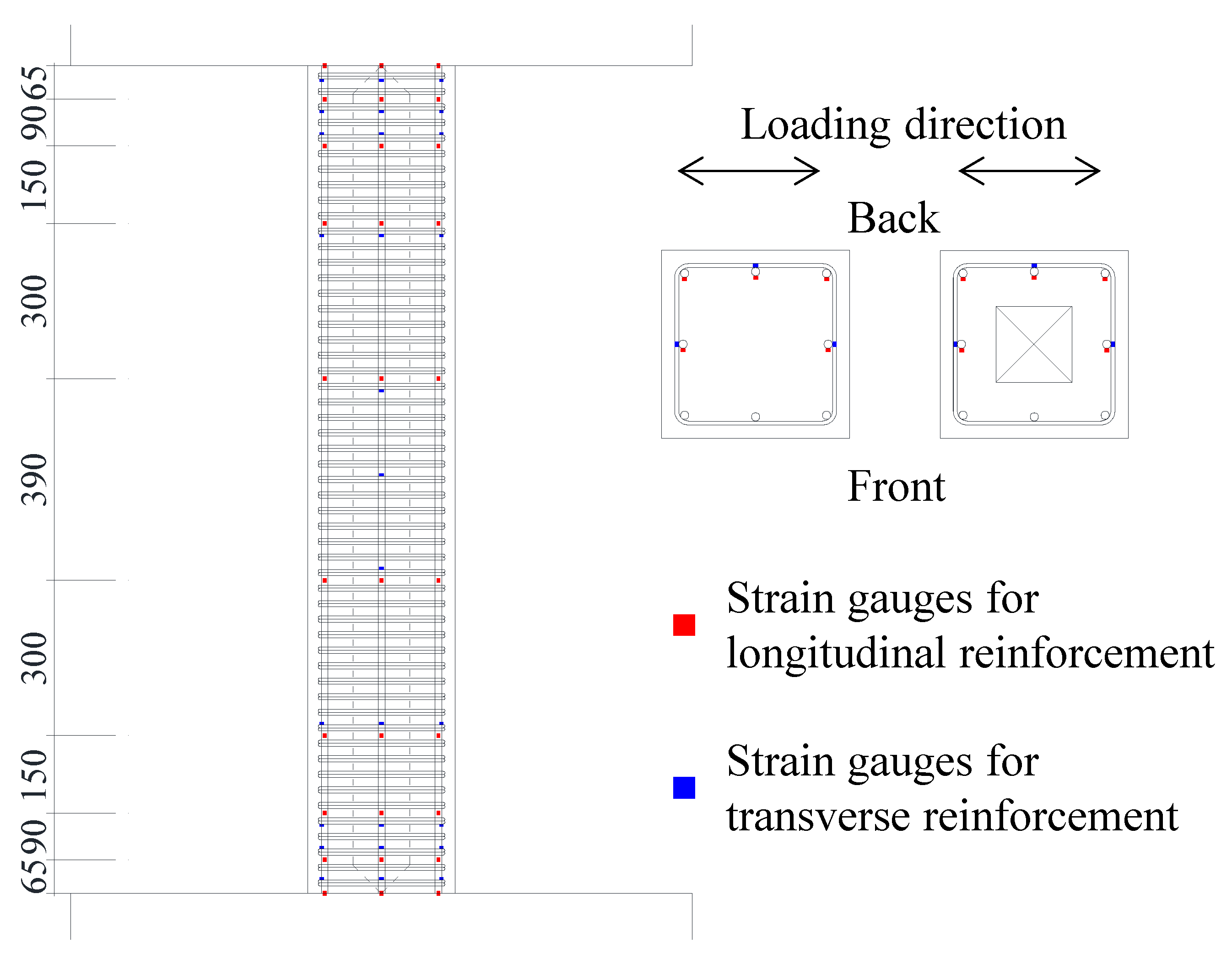
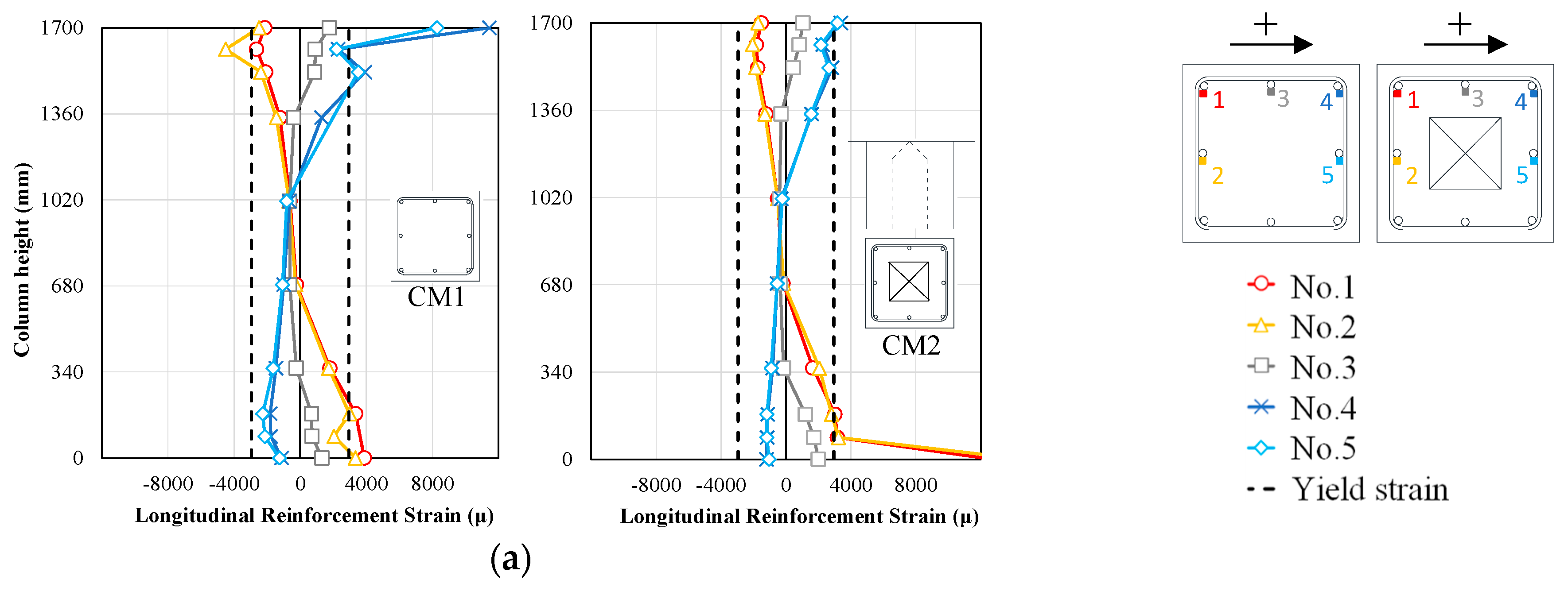
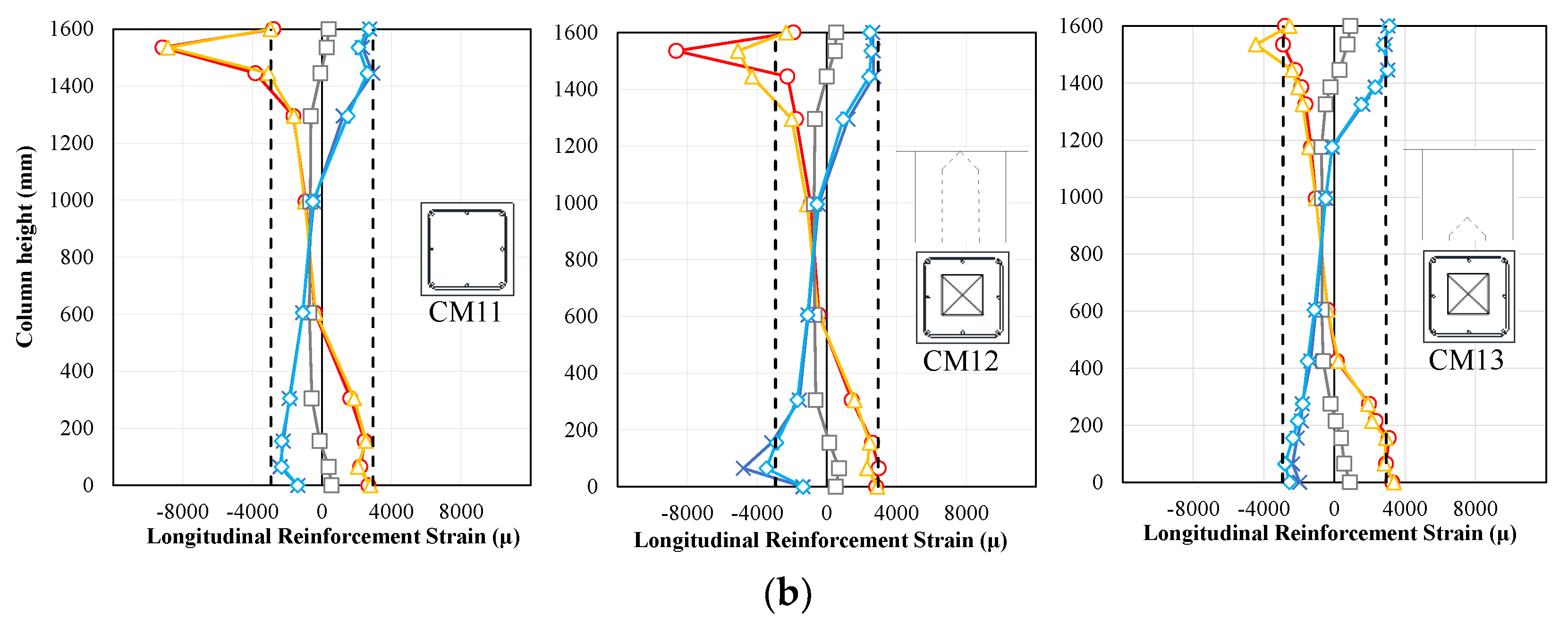
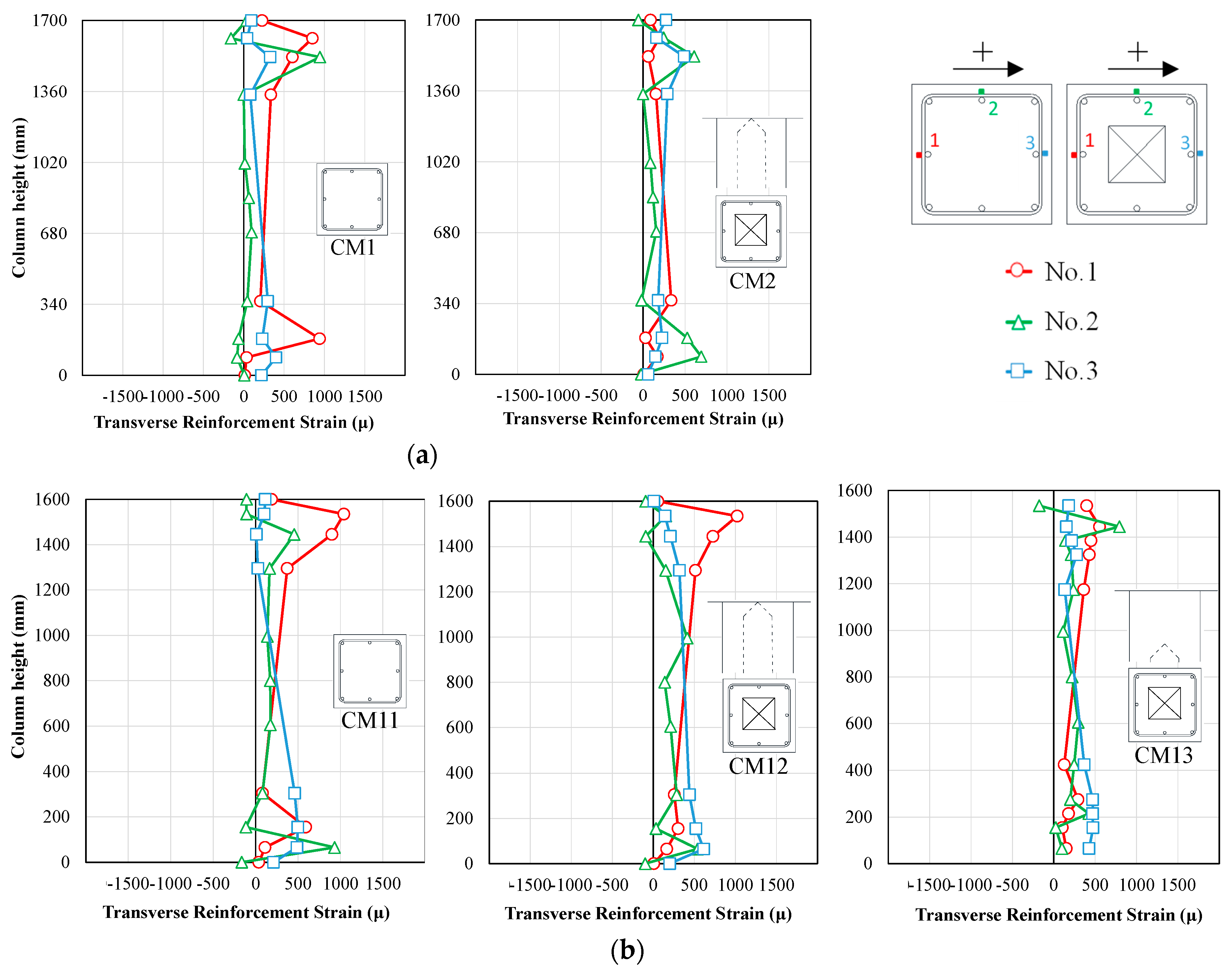
4.1. Strain Distribution of Reinforcement
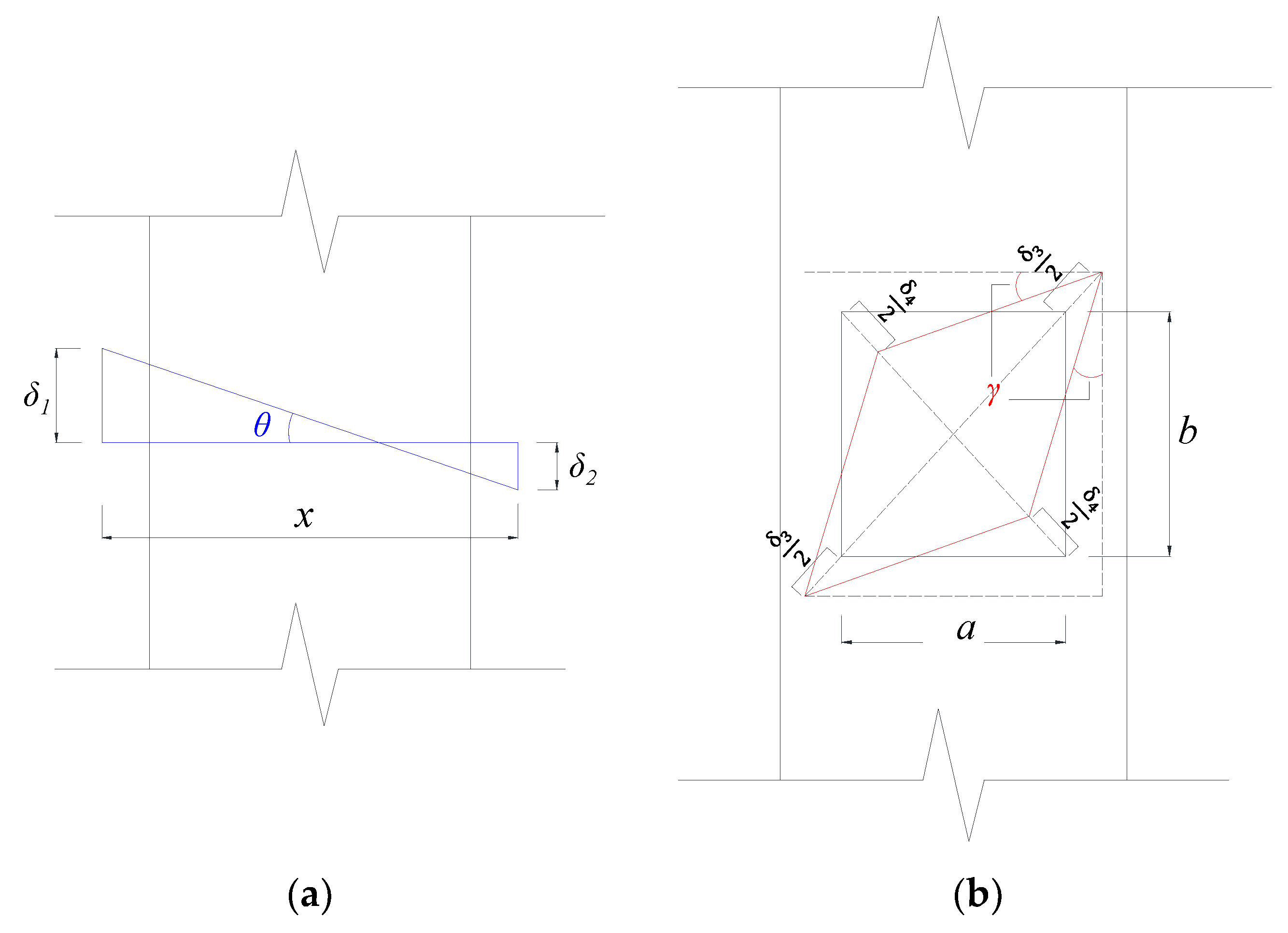
4.2. Flexural and Shear Deformation Distribution
4.3. Equivalent Viscous Damping Ratio
4.4. Neutral Axis Location
4.5. Finite Element Analysis
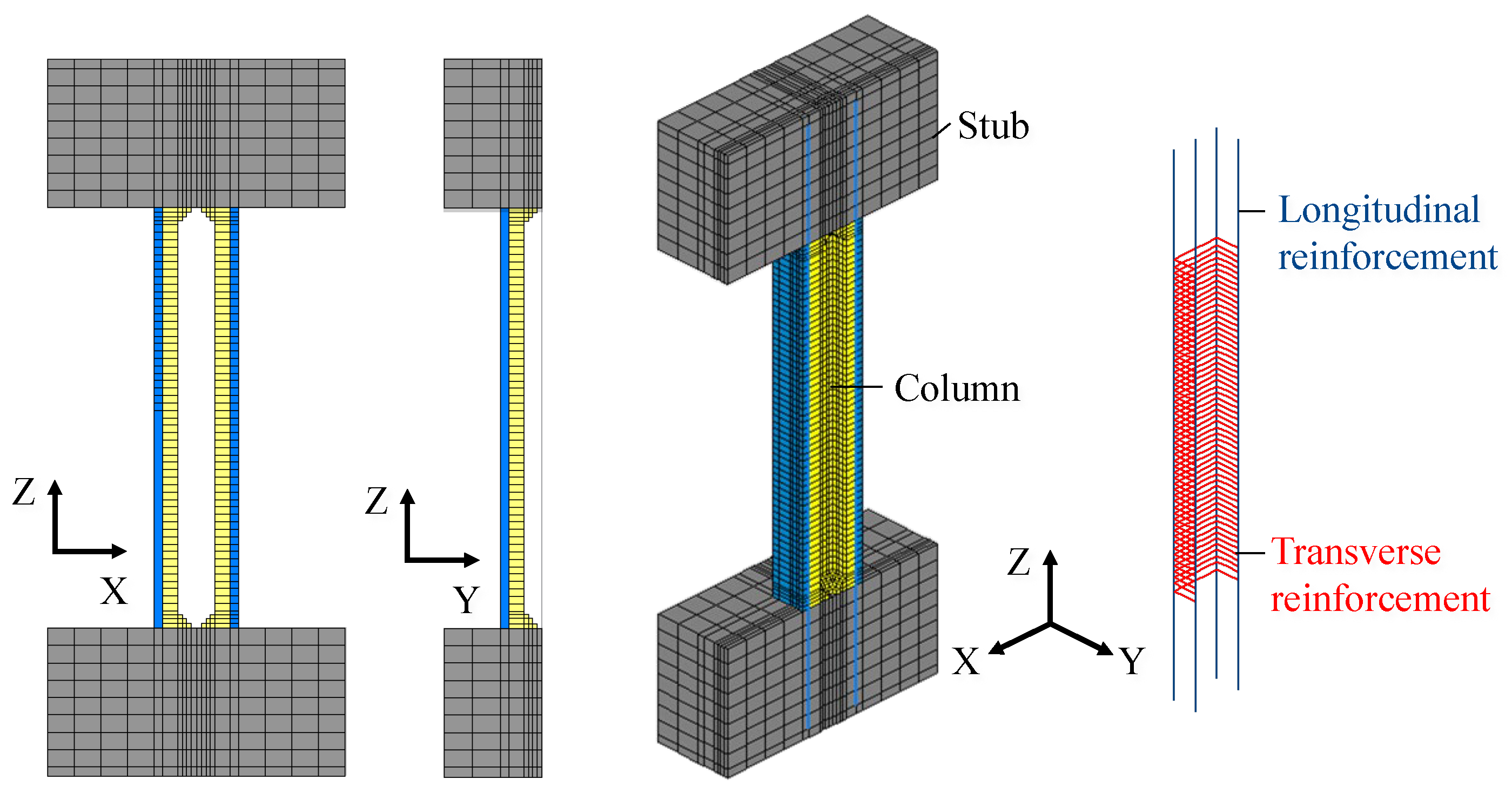
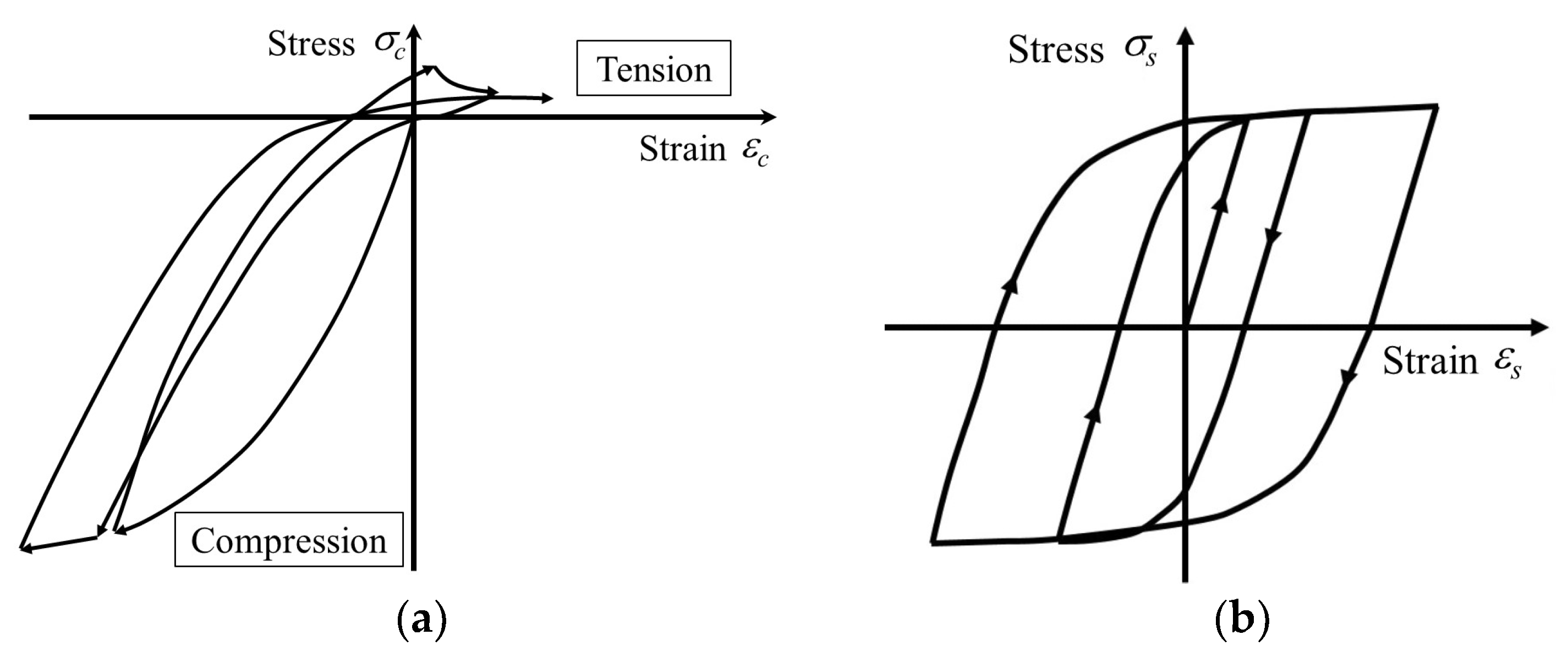
4.5.1. Analysis Outline
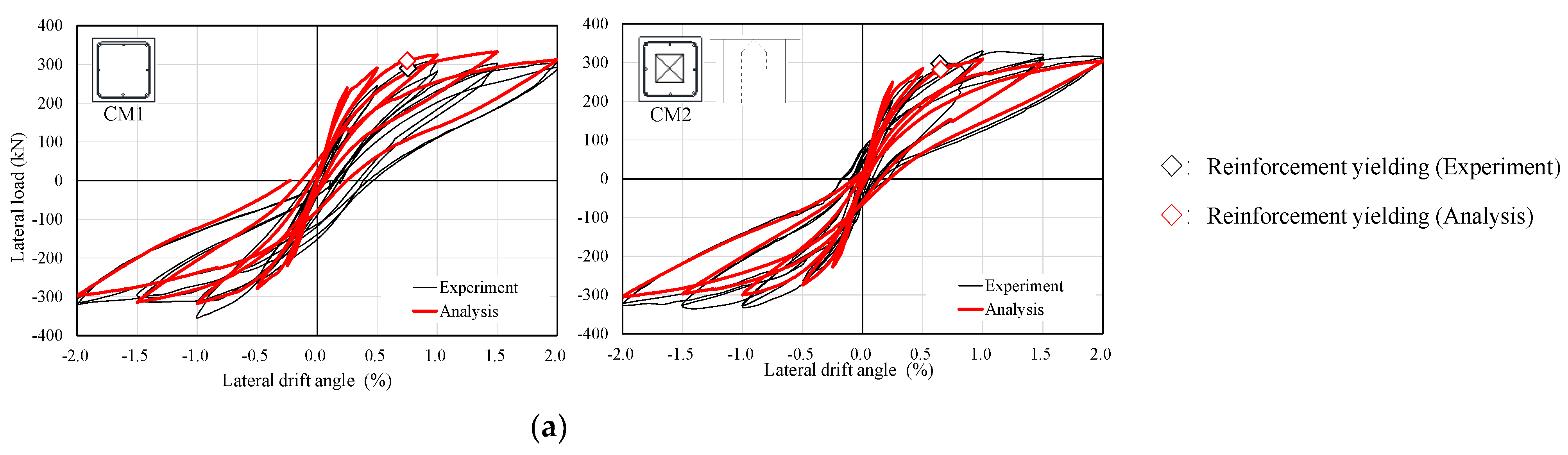
4.5.2. Analysis Result
5. Conclusions
- 1.
- Although the moment of inertia and cross-sectional area decreased in the hollow-sectioned column, by using higher strength concrete with a higher Young’s modulus, the initial lateral stiffness of the hollow-sectioned column could be reproduced as that of the solid-sectioned column.
- 2.
- In the hollow-sectioned columns, the experimental maximum strength was 1.00~1.06 times the ultimate flexural strength estimated by the cross-sectional analysis using plane section assumption, and the calculations showed good agreement with the experiments. Accordingly, the maximum strength evaluation by the plane section assumption is also effective for the RC columns with rectangular hollow cross-sections.
- 3.
- Under an axial force ratio of 0.16, the structural performances between hollow- and solid-sectioned columns were found to be almost equivalent, because their hysteresis curves, failure patterns, strain distributions of reinforcement, flexural and shear deformations, and energy absorption capacity were almost the same.
- 4.
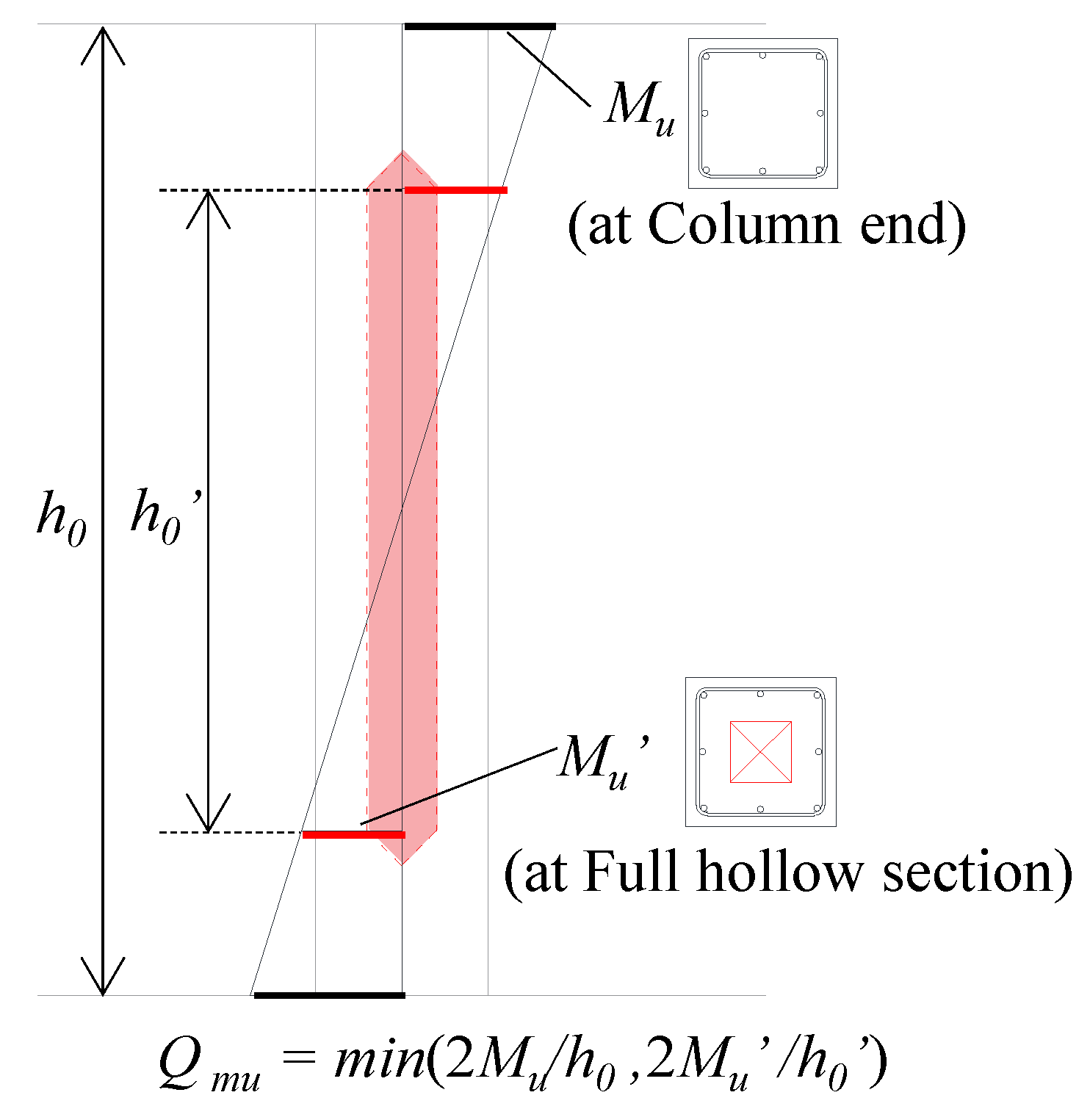
- In the hollow-sectioned specimen CM12 with an axial force ratio of 0.3, the structural performance was almost the same until the 2.0% drift angle; however, sudden deterioration of the load-bearing capacity occurred at the second loading cycle, with concrete compressive failure occurring at the plastic hinge region near the column end. Such brittle failure was induced by the location of the neutral axis at the ultimate flexural state, which was estimated to exist beyond the flange of the hollow cross-section.
- 5.
- In the hollow-sectioned specimen CM13 with an axial force ratio of 0.3, the position of hollow sections was, therefore, planned at 0.75D from the column end, beyond the plastic hinge regions. Then, the structural performance between the hollow- and solid-sectioned columns was found to be almost the same.
- 6.
- The relationship between the magnitude of the compressive axial force and the neutral axis location at the ultimate flexural state was found to be one of the crucial factors for the deformation capacity and the application scope of RC columns with rectangular hollow cross-sections. If the neutral axis is located within the flange of the cross-section, the concrete compressive stress does not work on the hollow section; therefore, the compressive stress distribution of concrete, at the plastic hinge region, would be similar to that of a solid cross-section. On the other hand, if the neutral axis exists on the web of plastic hinge regions, the concrete compressive stress on the hollow cross-section is likely to increase abruptly, due to the concrete crushing, at around the ultimate flexural state.
- 7.
- The nonlinear FEM analysis was carried out to further grasp the structural behaviors of the rectangular hollow sectioned columns. The drift angles of reinforcement yielding, the maximum strength, and the hysteresis curves by the analysis reasonably corresponded with the experiments. The compressive stress concentration of concrete at the hollow-cross section near the column end was also observed from the minimum principal stress distribution by the analysis, which is considered to result in abrupt brittle failure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| b | column width |
| b′ | column width excluding hollow cross-section |
| D | cross-section height of column |
| d | effective cross-section height of column |
| Es | Young’s modulus |
| εcu | ultimate concrete strain at the compression fiber |
| Fc | compressive strength of concrete |
| h0 | clear height |
| h0′ | height between both full hollow sections |
| η | axial force ratio |
| j | moment arm length from compressive to tensile resultant force |
| M/Q | shear span ratio |
| Mu | ultimate flexural moment capacity at solid section |
| Mu′ | ultimate flexural moment capacity at fully hollowed section |
| N | axial force |
| pt | longitudinal tensile reinforcement ratio |
| pw | transverse reinforcement ratio |
| Qmu | ultimate flexural strength |
| Qsu,mean | ultimate shear strength |
| R | drift angle |
| r | hollow section ratio |
| σ0 | axial stress |
| σwy | yield strength of transverse reinforcement |
| heq | equivalent viscous damping ratio |
References
- Chung, Y.S.; Han, G.H.; Lee, K.K.; Lee, D.H. Quasistatic test for seismic performance of circular hollow RC bridge pier. J. Earthq. Eng. Soc. Korea 1999, 3, 41–54. (In Korean) [Google Scholar]
- Lee, J.H.; Choi, J.H.; Hwang, D.K.; Kwahk, I.J. Seismic Performance of Circular Hollow RC Bridge Columns. J. Civ. Eng. 2015, 19, 1456–1467. [Google Scholar] [CrossRef]
- Osada, K.; Yamaguchi, T.; Ikeda, S. Seismic performance and the strengthening of hollow circular RC piers having reinforced cut-off planes and variable wall thickness. Concr. Res. Technol. 1999, 10, 13–24. (In Japanese) [Google Scholar] [CrossRef]
- Ranzo, G.; Priestley, M.J.N. Seismic performance of large RC circular hollow columns. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Sun, C.H.; Kim, I.H. Improvement of seismic detailing of bridge columns with hollow sections. J. Earthq. Eng. Soc. Korea 2011, 15, 75–78. (In Korean) [Google Scholar]
- Whittaker, D.; Park, R.; Carr, A.J. Experimental tests on hollow circular concrete columns for use in offshore concrete platforms. In Proceedings of the Pacific Conference on Earthquake Engineering, Wairakei, New Zealand, 5–8 August 1987. [Google Scholar]
- Yeh, Y.-K.; Mo, Y.L.; Yang, C.Y. Seismic performance of hollow circular bridge piers. ACI Struct. J. 2001, 98, 62–871. [Google Scholar]
- Won, D.; Kim, S.; Seo, J.; Kang, Y.J. Experimental study of composite hollow RC column under uniaxial compressive load. Appl. Sci. 2019, 9, 373. [Google Scholar] [CrossRef]
- Liang, X.; Sritharan, S. Effects of confinement in circular hollow concrete columns. J. Struct. Eng. 2018, 144, 1–13. [Google Scholar] [CrossRef]
- Calvi, G.M.; Pavese, A.; Rasulo, A.; Bolognini, D. Experimental and numerical studies on the seismic response of RC hollow bridge piers. Bull. Earthq. Eng. 2005, 3, 267–297. [Google Scholar] [CrossRef]
- Han, Q.; Du, X.; Zhou, Y.; Lee, G.C. Experimental study of hollow rectangular bridge column performance under vertical and cyclically bilateral loads. Earthq. Eng. Eng. Vib. 2013, 12, 433–445. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Behavior of ductile hollow reinforced concrete columns. Bull. N. Z. Soc. Earthq. Eng. 1983, 16, 273–290. [Google Scholar]
- Pinto, A.; Molina, J.; Tsionis, G. Cyclic tests on large-scale models of existing bridge piers with rectangular hollow cross-section. Earthq. Eng. Struct. Dyn. 2003, 32, 1995–2012. [Google Scholar] [CrossRef]
- Shen, Y.; Gu, S. Shake table test for reinforced concrete hollow rectangular pier. J. Archit. Civ. Eng. 2018, 35, 28–133. [Google Scholar]
- Shen, Y.; Wei, B. Shaking Table Test Study on Seismic Performance of Hollow Rectangular Piers. Adv. Civ. Eng. 2019, 2019, 7508759. [Google Scholar] [CrossRef]
- Mo, Y.L.; Nien, I.C. Seismic performance of hollow high-strength concrete bridge columns. J. Bridge Eng. 2002, 7, 338–349. [Google Scholar] [CrossRef]
- Yeh, Y.-K.; Mo, Y.L.; Yang, C.Y. Full-scale tests on rectangular hollow bridge piers. Mater. Struct. 2002, 35, 117–125. [Google Scholar] [CrossRef]
- Yeh, Y.-K.; Mo, Y.L.; Yang, C.Y. Seismic performance of rectangular hollow bridge columns. J. Struct. Eng. 2002, 128, 60–68. [Google Scholar] [CrossRef]
- Kim, S.; Hong, H.; Han, T. Behavior of an internally confined hollow reinforced concrete column with a polygonal cross-section. Appl. Sci. 2021, 11, 4302. [Google Scholar] [CrossRef]
- Martínez-Martín, F.; Yepes, V.; González-Vidosa, F.; Hospitaler, A.; Alcalá, J. Optimization design of RC elevated water tanks under seismic loads. Appl. Sci. 2022, 12, 5635. [Google Scholar] [CrossRef]
- Kondo, I.; Suzuki, T.; Sugino, H. Damage control design of flexible RC tall building using high-strength materials. AIJ J. Technol. Des. 2001, 14, 73–78. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Morooka, S.; Kunieda, H.; Ogiwara, Y. Estimation of bending rigidity and stress concentration of circular hole void slab. AIJ J. Technol. Des. 2002, 67, 133–137. (In Japanese) [Google Scholar]
- Matsushita, F.; Shibata, S.; Nakamura, F.; Asano, T. Durability improvement for autoclaved aerated concrete (AAC): Development of high carbonation-resistant AAC. AIJ J. Technol. Des. 1999, 5, 33–36. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Architectural Institute of Japan (AIJ). AIJ Standard for Structural Calculation of Reinforced Concrete Structures; Architectural Institute of Japan: Tokyo, Japan, 2018. [Google Scholar]
- Popovics, S. A Numerical Approach to the Complete Stress-Strain Curve of Concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- ITOCHU Techno-Solutions Corporation. Concrete Structures Non-Linear Finite Element Analysis Program FINAL ver.11; ITOCHU Techno-Solutions Corporation: Tokyo, Japan, 2019. (In Japanese) [Google Scholar]
- Naganuma, K.; Ohkubo, M. An analytical model for reinforced concrete panels under cyclic stresses. J. Struct. Constr. Eng. 2000, 536, 135–142. (In Japanese) [Google Scholar] [CrossRef]
- Ahmad, S.H.; Shah, S.P. Complete Triaxial Stress-Strain Curve for Concrete. J. Struct. Div. 1982, 108, 728–742. [Google Scholar] [CrossRef]
- Naganuma, K. Stress-strain relationship for concrete under triaxial compression. J. Struct. Constr. Eng. 1995, 474, 163–170. (In Japanese) [Google Scholar] [CrossRef]
- Nakamura, H.; Higai, T. Compressive Fracture Energy and Fracture Zone Length of Concrete. Semin. Post Peak Behav. RC Struct. Subj. Seism. Load 1999, 2, 259–272. [Google Scholar]
- Ottosen, N.S. A failure criterion for concrete. J. Eng. Mech. 1977, 103, 527–535. [Google Scholar] [CrossRef]
- Izumo, J.; Shima, H.; Okamura, H. Analytical model for reinforced concrete panel elements subjected to in-plane forces. In Proceedings of the Japan Concrete Institute, Tokyo, Japan, 1–3 July 1987. (In Japanese). [Google Scholar]
- Ciampi, V.; Eligehausen, R.; Bertero, V.V.; Popov, E.P. Analytical Model for Concrete Anchorages of Reinforcing Bars under Generalized Excitations; Report NO. UCB/EERC-82/23; University of Berkeley: Berkeley, CA, USA, 1982. [Google Scholar]
- Naganuma, K.; Yonezawa, K.; Kurimoto, O.; Eto, H. Simulation of nonlinear dynamic response of reinforced concrete scaled model using three-dimensional finite element method. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Architectural Institute of Japan (AIJ). Design Guidelines for Earthquake Resistant Reinforced Concrete Buildings Based on Inelastic Displacement Concept; Architectural Institute of Japan: Tokyo, Japan, 1999. [Google Scholar]
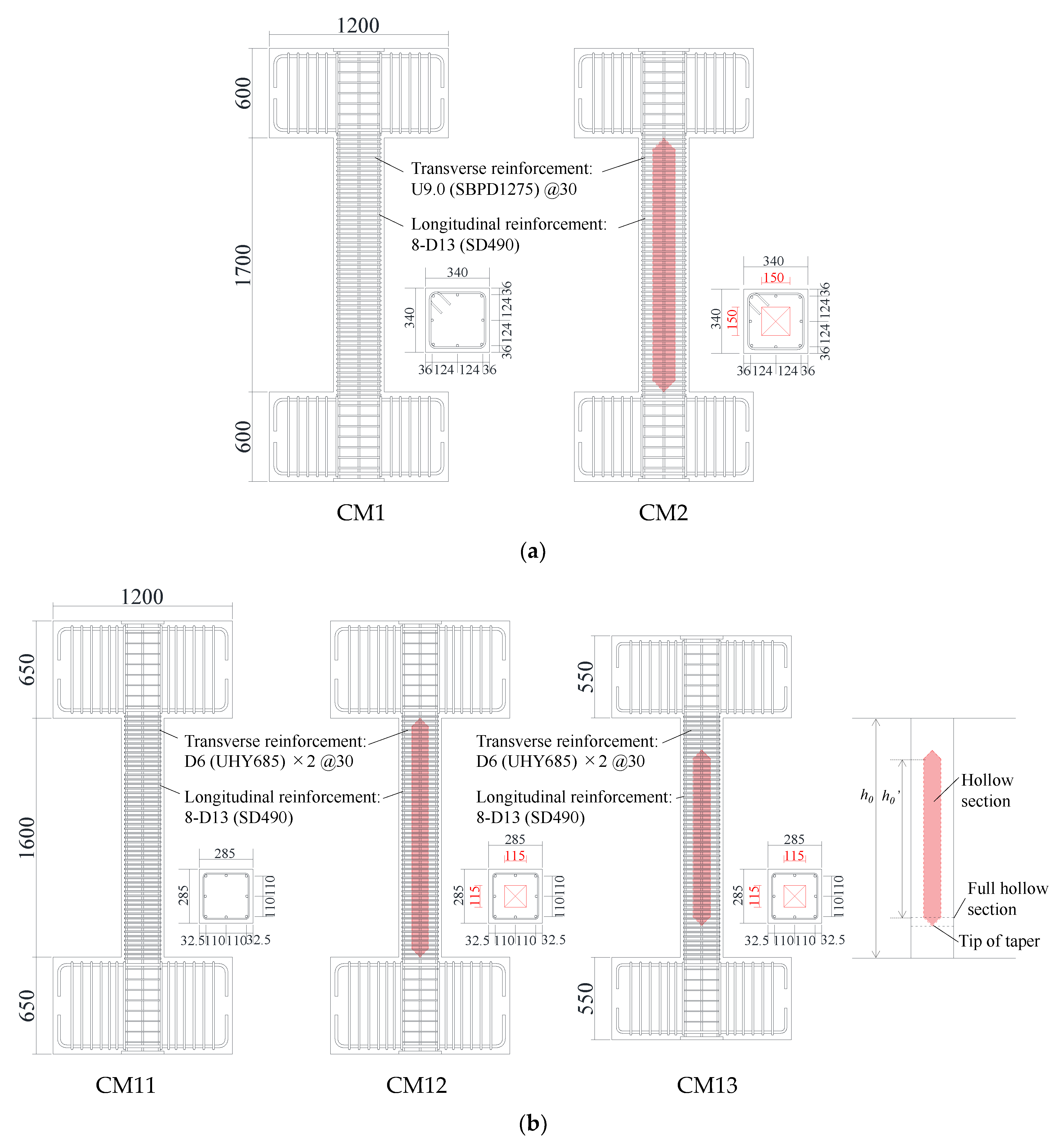








| Series | Specimen | Cross-Section | Tip Position of Taper *b | Longitudinal Reinforcement | Transverse Reinforcement | Axial Force (kN) (η: Axial Force Ratio) | |
|---|---|---|---|---|---|---|---|
| Solid/ Hollow | r *a | ||||||
| N | CM1 | solid | 1.00 | 8-D13 (SD490) | U9.0@30 (SBPD1275) | 1400 (0.16) | |
| CM2 | hollow | 0.81 | 0D | ||||
| S | CM11 | solid | 1.00 | 8-D13 (SD490) | D6 × 2@30 (UHY685) | 1800 (0.28) | |
| CM12 | hollow | 0.84 | 0D | 1800 (0.30) | |||
| CM13 | 0.75D | 1800 (0.28) | |||||
| Yield Strength (MPa) *a | Yield Strain (μ) *a | |
|---|---|---|
| D13 (SD490) | 537 | 2944 |
| D6 (UHY685) | 700 | 5426 |
| U9.0 (SBPD1275) | 1373 | 8884 |
| Series | Specimen | Compressive Strength (MPa) | Tensile Strength (MPa) |
|---|---|---|---|
| N | CM1 | 74 | 4.47 |
| CM2 | 93 | 4.85 | |
| S | CM11 | 78 | 4.11 |
| CM12 | 88 | 4.60 | |
| CM13 | 95 | 4.38 |
| Series | Specimen | Cement | Water | Sand | Gravel | Admixture | |
|---|---|---|---|---|---|---|---|
| S1 *a | S2 *b | ||||||
| N | CM1 | 523 | 188 | 538 | 370 | 700 | 6.54 |
| CM2 | 672 | 188 | 387 | 264 | 850 | 8.74 | |
| S | CM11 | 523 | 188 | 538 | 370 | 700 | 6.54 |
| CM12 | 672 | 188 | 387 | 264 | 850 | 8.74 | |
| CM13 | 672 | 188 | 387 | 264 | 850 | 8.74 | |
| Series | Specimen | Qmu (kN) | Qsu,mean (kN) | Qsu,mean/Qmu |
|---|---|---|---|---|
| N | CM1 | 305.3 | 598.7 | 1.96 |
| CM2 | 317.9 | 435.3 | 1.37 | |
| S | CM11 | 272.9 | 442.0 | 1.62 |
| CM12 | 285.6 | 321.6 | 1.13 | |
| CM13 | 293.1 | 327.9 | 1.12 |
| Series | Specimen | Experiment (kN) | Calculation (Cross-Sectional Analysis) (kN) | Experiment/Calculation | ||
|---|---|---|---|---|---|---|
| Positive Loading | Negative Loading | Positive Loading | Negative Loading | |||
| N | CM1 | 310.5 | −353.6 | 305.3 | 1.02 | 1.16 |
| CM2 | 328.5 | −335.6 | 317.9 | 1.03 | 1.06 | |
| S | CM11 | 276.9 | −284.8 | 272.9 | 1.01 | 1.04 |
| CM12 | 284.5 | −288.8 | 285.6 | 1.00 | 1.01 | |
| CM13 | 297.3 | −298.2 | 293.1 | 1.01 | 1.02 | |
| Series | Specimen | Calculation (FEM) (kN) | Experiment (kN) | Calculation (FEM)/Experiment | |||
|---|---|---|---|---|---|---|---|
| Positive L. | Negative L. | Positive L. | Negative L. | Positive L. | Negative L. | ||
| N | CM1 | 332.7 | −317.2 | 310.5 | −353.6 | 1.07 | 0.90 |
| CM2 | 308.9 | −305.7 | 328.5 | −335.6 | 0.94 | 0.91 | |
| S | CM11 | 253.6 | −235.8 | 276.9 | −284.8 | 0.92 | 0.83 |
| CM12 | 275.7 | −255.4 | 284.5 | −288.8 | 0.97 | 0.88 | |
| CM13 | 279.3 | −246.3 | 297.3 | −298.2 | 0.94 | 0.83 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, K.; Yamazaki, K.; Takahashi, R. Seismic Performance of Ductile Column with Rectangular Hollow Cross-Section in RC Building. Appl. Sci. 2023, 13, 2234. https://doi.org/10.3390/app13042234
Jin K, Yamazaki K, Takahashi R. Seismic Performance of Ductile Column with Rectangular Hollow Cross-Section in RC Building. Applied Sciences. 2023; 13(4):2234. https://doi.org/10.3390/app13042234
Chicago/Turabian StyleJin, Kiwoong, Kaede Yamazaki, and Ryo Takahashi. 2023. "Seismic Performance of Ductile Column with Rectangular Hollow Cross-Section in RC Building" Applied Sciences 13, no. 4: 2234. https://doi.org/10.3390/app13042234
APA StyleJin, K., Yamazaki, K., & Takahashi, R. (2023). Seismic Performance of Ductile Column with Rectangular Hollow Cross-Section in RC Building. Applied Sciences, 13(4), 2234. https://doi.org/10.3390/app13042234






