Improved Surrounding Rock Classification Method for the Middle Rock Pillar of a Small Clear-Distance Tunnel
Abstract
:1. Introduction
2. Middle Rock Pillar Classification Index Analysis
2.1. Factors Influencing the Stability of the Middle Rock Pillar
2.1.1. Characteristics of Middle Rock Pillar
2.1.2. External Human Factors
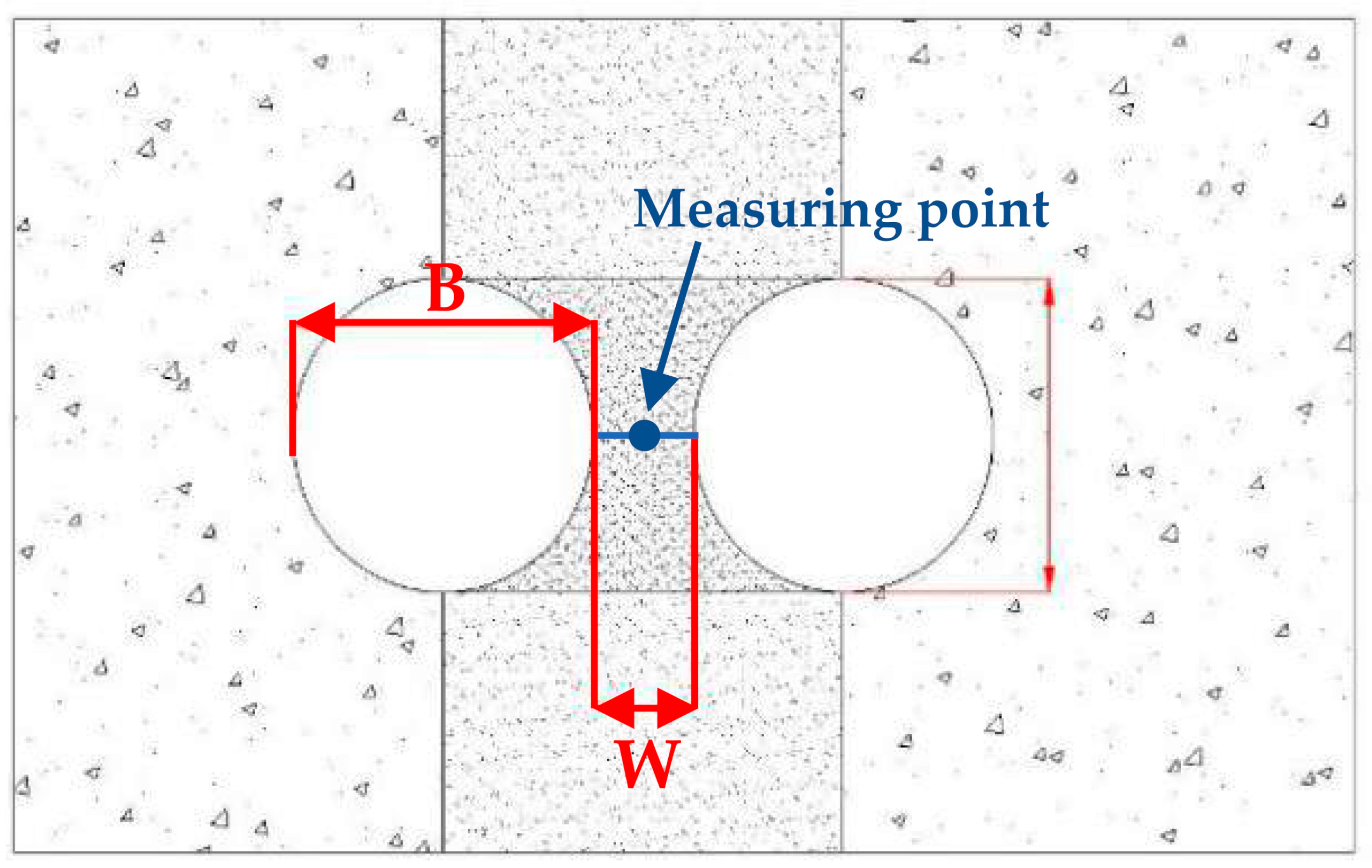
2.2. Geometrical Index
2.3. Physical Index
2.3.1. Integrity
2.3.2. Permeability
2.3.3. Combination of Main Structural Plane and Tunnel Axis
2.4. Mechanics Index
2.4.1. Hardness
2.4.2. Initial Stress State
3. Middle Rock Pillar Classification Method
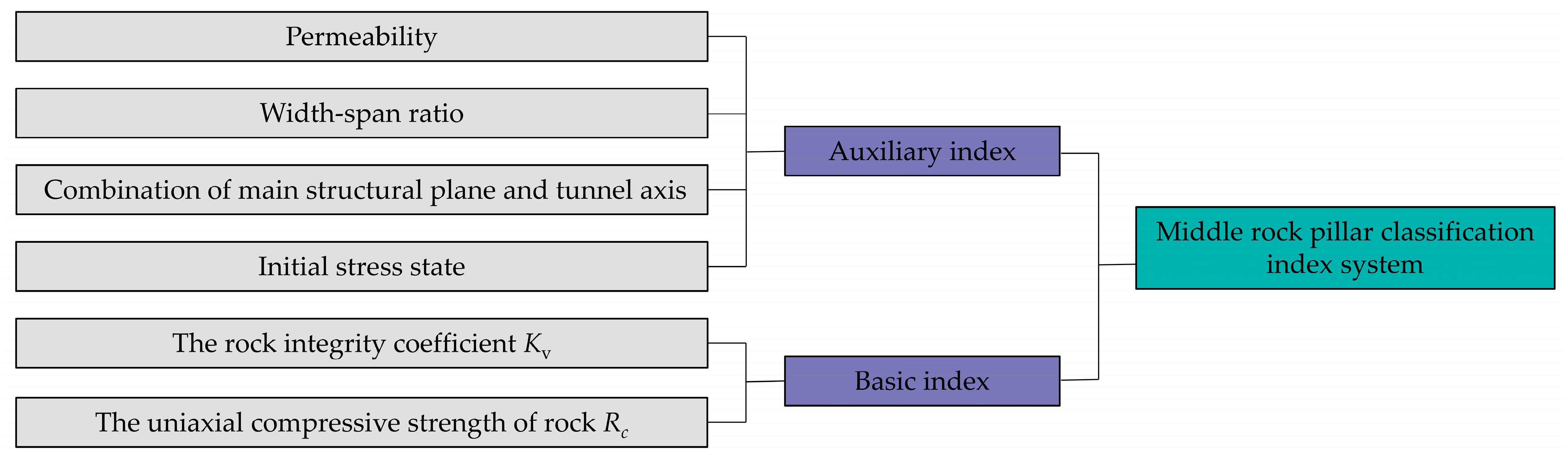
3.1. Middle Rock Pillar Classification Index System
- (1)
- We determined the primary and secondary relationships of each index and classified them into levels. The main index is the strength and stability of various middle rock pillars, which is a common factor in various rock masses and belongs to the basic index. Secondary indices varied according to different engineering design types, occurrence conditions, and site conditions, which belong to the auxiliary index. The basic quality and foundation frame were first determined by the basic index, and then the basic quality was modified according to the auxiliary index.
- (2)
- Each classification index should be independent of the others, and the influence of a single index should correspond to the properties of a single aspect of the rock mass. For example, the degree of weathering of a rock mass cannot be used as a basic index because it affects both the strength and integrity of the rock mass.
- (3)
- Through a combination of qualitative and quantitative descriptions, an index system was established to improve the accuracy of classification through a comprehensive evaluation.
3.2. Basic Index Score
3.2.1. Rock Integrity Coefficient Kv
3.2.2. Uniaxial Compressive Strength of Rock Rc
3.3. Auxiliary Index Score
3.3.1. Permeability
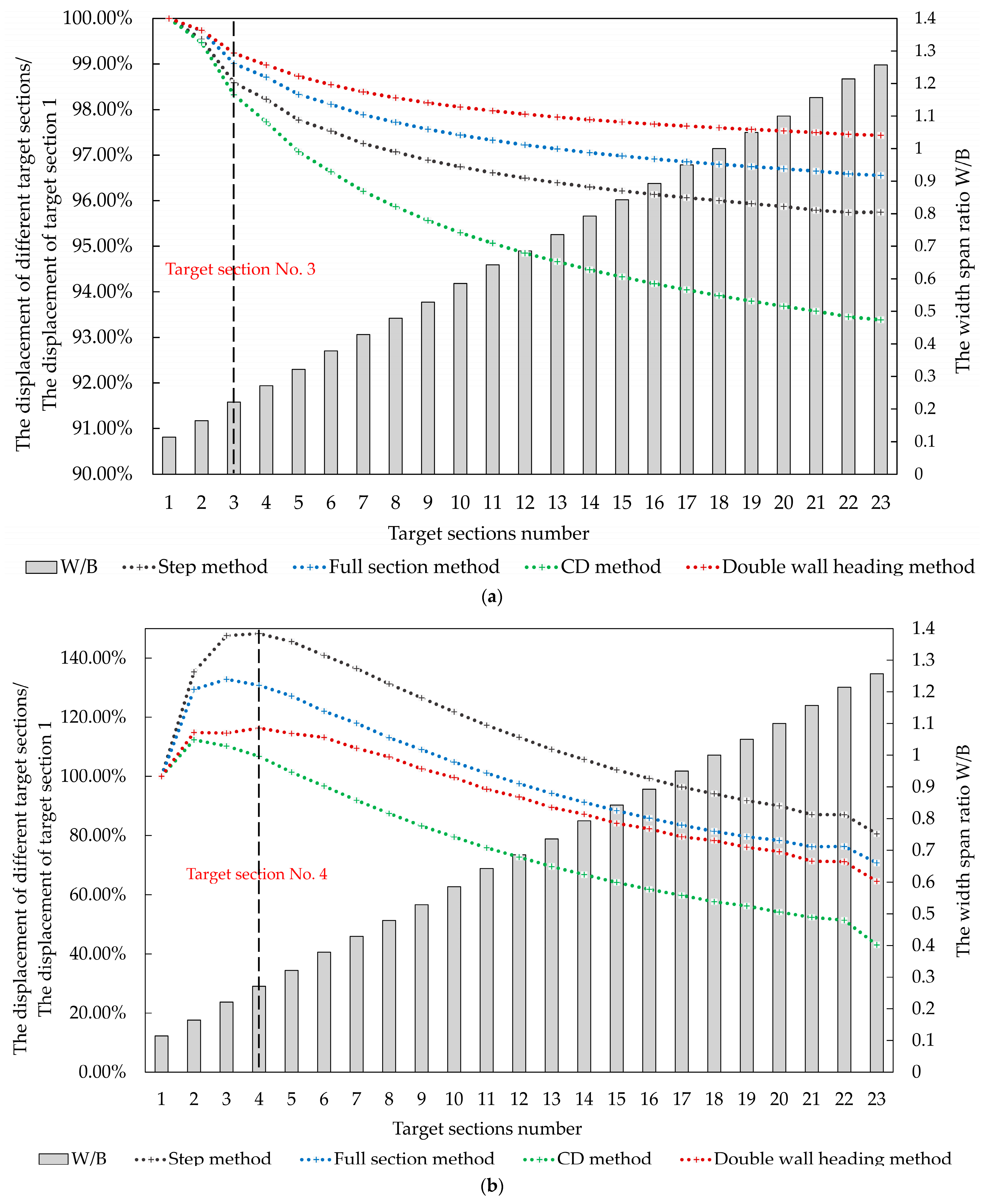
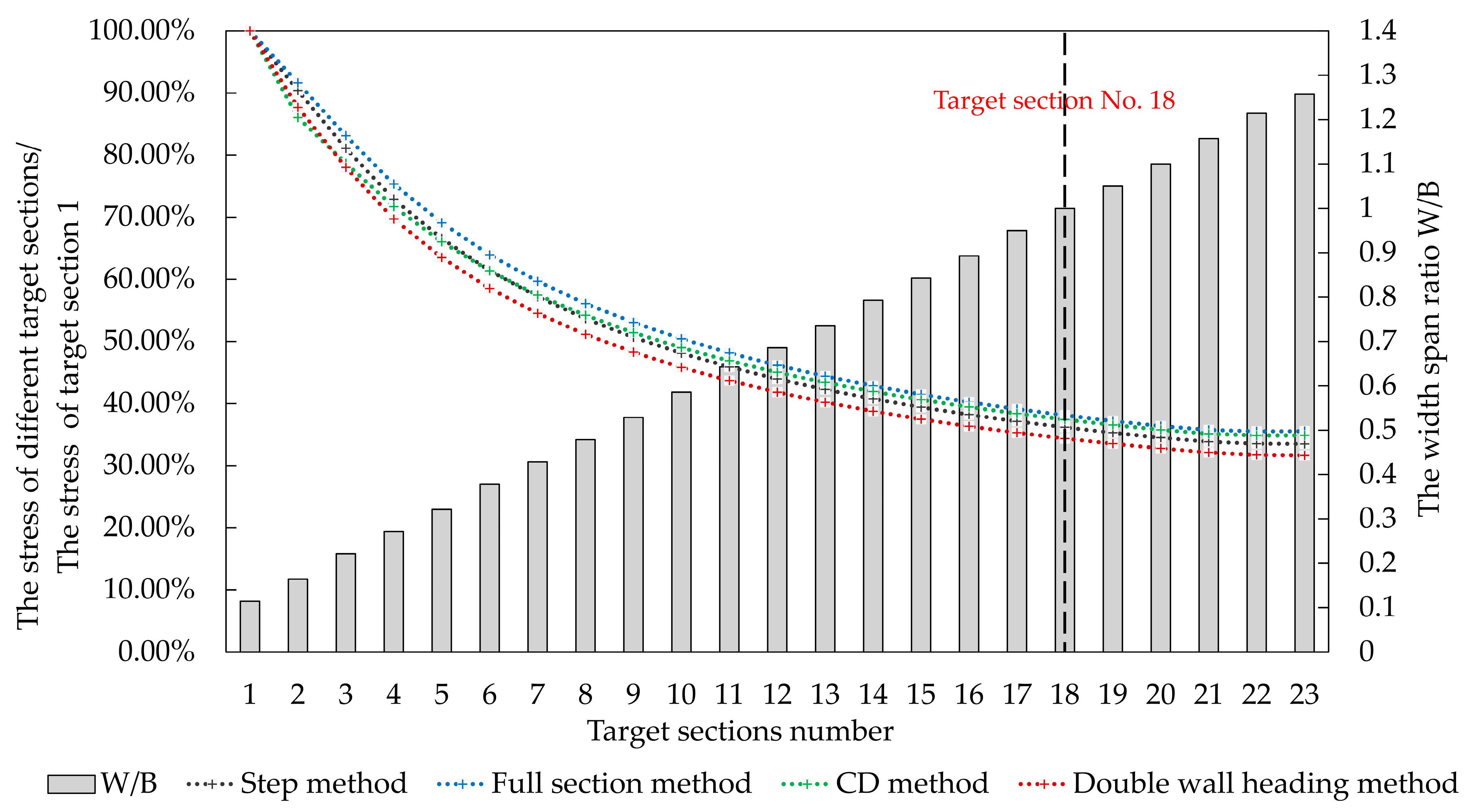
3.3.2. Width–Span Ratio
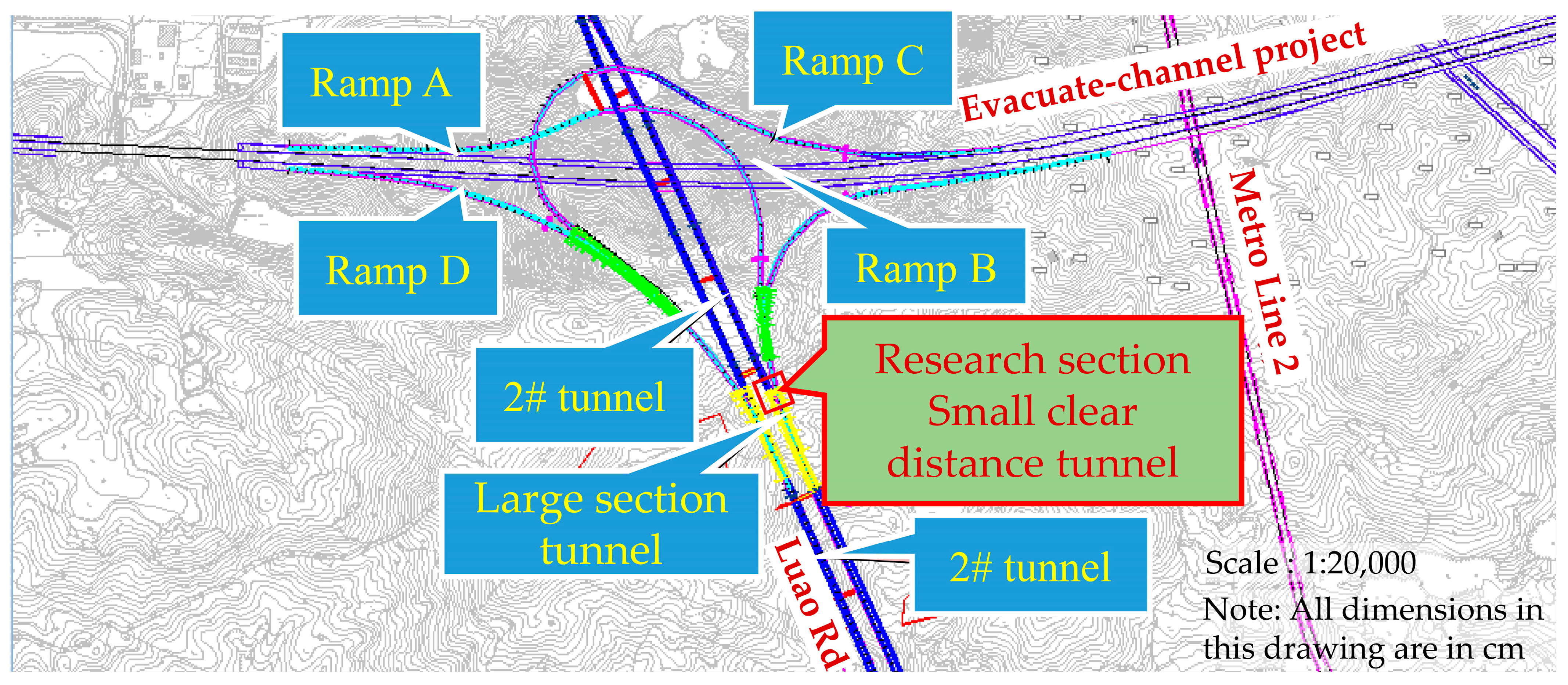
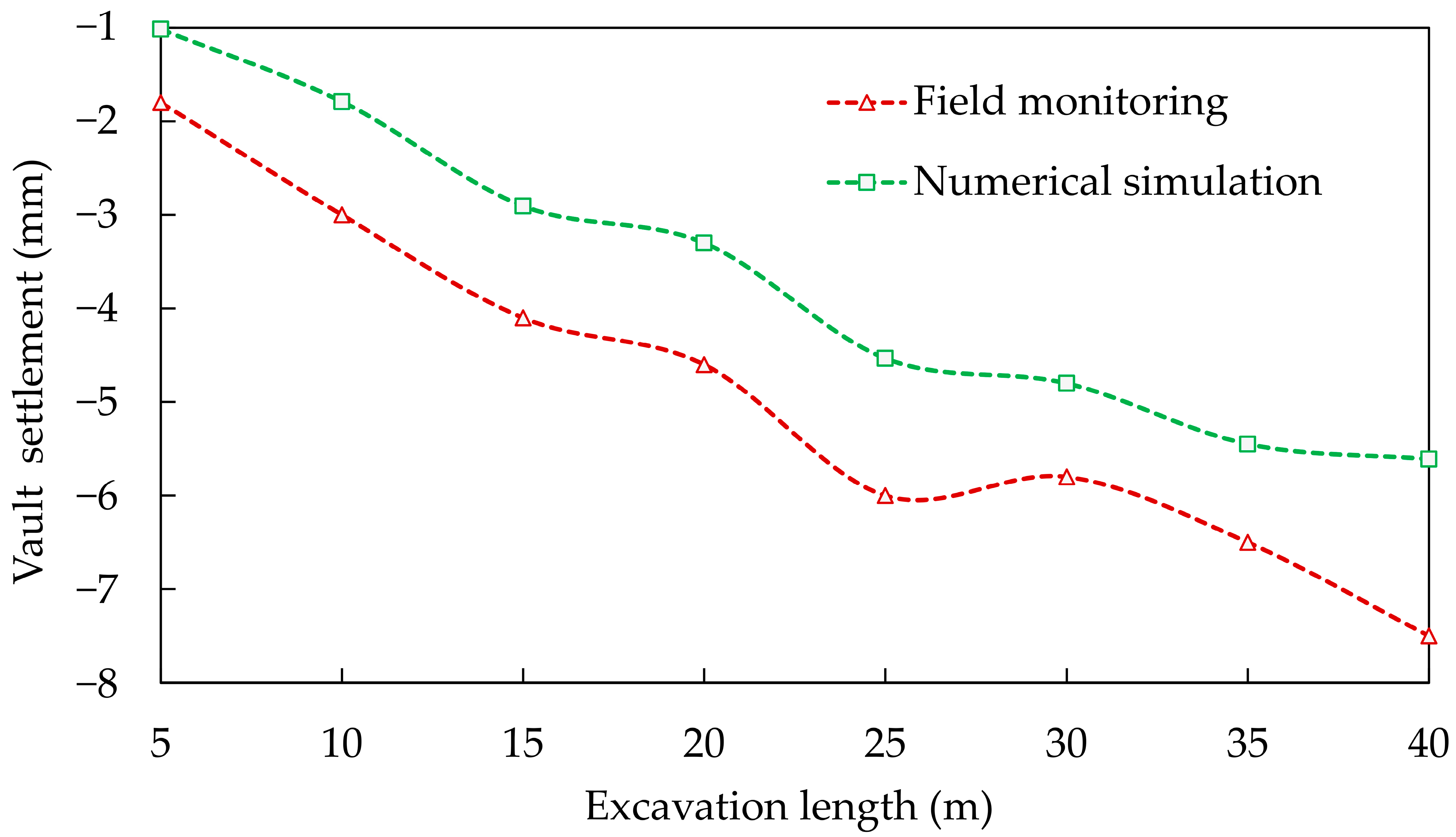
Engineering Background
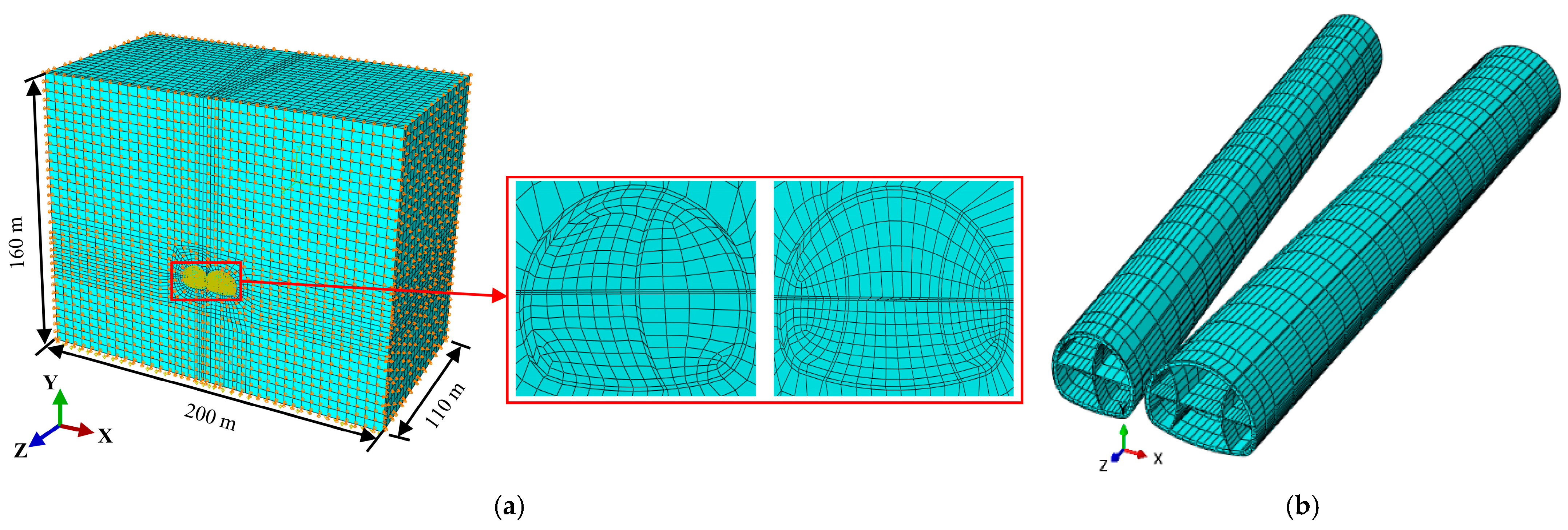
Numerical Model Establishment
Numerical Model Validation
Numerical Simulation Analysis
3.3.3. Combination of Main Structural Plane and Tunnel Axis
3.3.4. Initial Stress State
3.4. Middle Rock Pillar Grade Determination
- (1)
- Among the basic indices and auxiliary indices of the middle rock pillar, each index was graded by different numerical ranges, and the corresponding scores also had a range. To determine the specific evaluation scores, a linear corresponding method was adopted, that is, if the uniaxial compressive strength Rc was 50 MPa (Table 7). It can be observed that the rock was between 30 and 70 MPa and belonged to general hard rock, and the corresponding score was between 26 and 34. The corresponding linear score value should be 30, that is, T2 is 30.
- (2)
- The total score of the middle rock pillar, T, is the sum of T1 to T6.
- (3)
- The total score T reflects the comprehensive value of the various indices of the middle rock pillar. The maximum value of T is 96, which is less than 0 in the most unfavorable case. If T < 0, then it is treated as T = 0.
4. Application of Middle Rock Pillar Classification Method
4.1. Engineering Background
4.2. Application of Middle Rock Pillar Classification Standard
5. Conclusions
- (1)
- Six indices affecting the quality of the middle rock pillar were selected in terms of three aspects: geometric, physical, and mechanical factors, including the integrity, hardness, combination of the main structural planes of the middle rock pillar and tunnel axis, permeability, initial stress state, and geometric state.
- (2)
- The classification index system of the middle rock pillar was established from the two dimensions of the basic and auxiliary indices. Basic indices include integrity coefficient and uniaxial compressive strength. Auxiliary indices include permeability, width–span ratio, combination of main structural plane and tunnel axis, and initial stress state.
- (3)
- The scoring method of subtracting the score of the auxiliary index on the basis of the score determined by the basic index can more accurately reflect the quality of the middle rock pillar quality.
- (4)
- According to the score calculated from the evaluation of the middle rock pillar classification standard, the middle rock pillar was divided into five grades: I, II, III, IV, and V.
- (5)
- The improved classification standard solved the uncertainty problem caused by discrete rock mass parameters and subjective human factors, and the research results provided support for tunnel construction design and support parameter optimization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, H.B.; Li, P.F.; Ma, G.W. Stability analysis of the middle soil pillar for asymmetric parallel tunnels by using model testing and numerical simulations. Tunn. Undergr. Sp. Tech. 2021, 108, 103686. [Google Scholar] [CrossRef]
- Li, S.H.; Li, P.F.; Zhang, M.J. Analysis of additional stress for a curved shield tunnel. Tunn. Undergr. Sp. Tech. 2021, 107, 103675. [Google Scholar] [CrossRef]
- Dai, S.S. Study on surrounding rock classification and parameter acquisition method of mountain highway tunnel. J. Catastropho. 2019, 34, 77–81. [Google Scholar] [CrossRef]
- Chandar, K.R.; Deo, S.N.; Baliga, A.J. Prediction of Bond’s work index from field measurable rock properties. Int. J. Miner. Process. 2016, 157, 134–144. [Google Scholar] [CrossRef]
- Lin, Y.M. Theory and Practice of Rock Classification; Metallurgical Industry Press: Beijing, China, 1996. [Google Scholar]
- Chen, C.Y.; Wang, G.R. Discussion on the interrelation of various rock mass quality classification systems at home and abroad. Chin. J. Rock Mech. Eng. 2002, 21, 1894–1900. [Google Scholar] [CrossRef]
- Barton, N.R.; Lien, R.; Lunde, J. Engineering Classification of Rock Masses for the Design of Tunnel Support. Rock Mech. Rock Eng. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Barton, N.R. Some new Q-value correlations to assist in site characterisation and tunnel design. Int. J. Rock Mech. Min. 2002, 39, 185–216. [Google Scholar] [CrossRef]
- Laubscher, D.H. Class distinction in rock masses. 2T Coal Gold, Base Miner. S. Afr. 1975, 13, 37–50. [Google Scholar] [CrossRef]
- Laubscher, D.H. A geomechanics classification system for the rating of rock mass in mine design. J. S. Atr. Inst. Min. Metal. 1990, 90, 257–273. [Google Scholar]
- Laubscher, D.H.; Jakubec, J. The MRMR rock mass rating classification system in mining practice. MassMin 2000, 7, 413–421. [Google Scholar]
- Wang, S.C.; He, F.L.; Li, C.S. Rock Mass Classification of Tunnel Engineering; Southwest Jiaotong University Press: Chengdu, China, 2006. [Google Scholar]
- Cai, M.F. Rock Mechanics and Engineering; Science Press: Beijing, China, 2000. [Google Scholar]
- GB/T 50218-94; National Standard of the People’s Republic of China. Standard for Engineering Classification of Rock Masses. China Building Industry Press: Beijing, China, 1995.
- TB 10003-99; Industrial Standard of the People’s Republic of China. Code for Design on Tunnel of Railway. China Railway Press: Beijing, China, 1999.
- JTG D70-2004; Industrial Standard of the People’s Republic of China. Code for Design of Road Tunnel. China Communications Press: Beijing, China, 2004.
- JTG F60-2009; Industrial Standard of the People’s Republic of China. Technical Specifications for Construction of Highway Tunnel. China Communications Press: Beijing, China, 2009.
- GB/T 50218-2014; National Standard of the People’s Republic of China. Standard for Engineering Classification of Rock Mass. China Planning Press: Beijing, China, 2014.
- Peng, N.; Gan, L.K. Fuzzy comprehensive evaluation method in rock classification of in-situ expansion tunnel. Adv. Mater. Resear. 2011, 261–263, 1567–1572. [Google Scholar] [CrossRef]
- Duan, L.D.; Song, C.B. Application of BP Neural Network in the Rapid Classification of Surrounding Rock. China Saf. Sci. J. 2010, 20, 41–45+177. [Google Scholar] [CrossRef]
- Liang, H.R.; Wang, Y.D.; Peng, H.; Liu, J.F.; Yan, X. Classification of Soft Surrounding Rock of Tunnel Based on Normal Cloud Theory. J. Chongqing Jiaotong Univ. 2021, 40, 82–87. [Google Scholar] [CrossRef]
- Yang, G.; Li, T.B.; Ma, C.C.; Meng, L.B.; Zhang, H.G.; Ma, J.J. Intelligent rating method of tunnel surrounding rock based on one-dimensional convolutional neural network. J. Intell. Fuzzy Syst. 2022, 42, 2451–2469. [Google Scholar] [CrossRef]
- Ma, J.J.; Li, T.B.; Li, X.; Zhou, S.L.; Ma, C.C.; Wei, D.Q.; Dai, K.K. A probability prediction method for the classification of surrounding rock quality of tunnels with incomplete data using Bayesian networks. Sci. Rep. 2022, 12, 19846. [Google Scholar] [CrossRef]
- Xue, Y.G.; Li, Z.Q.; Qiu, D.H.; Zhang, L.W.; Zhao, Y.; Zhang, X.L.; Zhou, B.H. Classification model for surrounding rock based on the pca-ideal point method: An engineering application. Bull. Eng. Geol. Environ. 2019, 78, 3627–3635. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, L.; Wang, J.; Ma, H.S.; Cai, S.L.; Pu, S.K.; Duan, J.L.; Gao, L.; Li, E.B. Research on deformation prediction of tunnel surrounding rock using the model combining firefly algorithm and nonlinear auto-regressive dynamic neural network. Eng. Comput. 2021, 37, 1443–1453. [Google Scholar] [CrossRef]
- Jiang, F.; He, P.; Wang, G.; Zheng, C.C.; Xiao, Z.Y.; Wu, Y.; Lv, Z.H. Q-method optimization of tunnel surrounding rock classification by fuzzy reasoning model and support vector machine. Soft Comput.—A Fusion Found. Methodol. Appl. 2022, 1–14. [Google Scholar] [CrossRef]
- Niu, W.; Li, T.; Xiong, G.; Zhang, G. Support vector machines based intelligent rock mass classification method. J. Eng. Geol. 2011, 19, 88–92. [Google Scholar] [CrossRef]
- Liu, H.X.; Li, W.S.; Zha, Z.Y.; Jiang., W.J.; Xu, T. Method for surrounding rock mass classification of highway tunnels based on deep learning technology. Chin. J. Geotech. Eng. 2018, 40, 1809–1817. [Google Scholar] [CrossRef]
- Jiang, Q.; Song, S.G.; Li, T.; Wang, K.; Gu, R.H. Study on Surrounding Rock Stability of Small Clear-Distance Twin Highway Tunnel with Eight Lanes. Geotech. Geol. Eng. 2019, 37, 593–598. [Google Scholar] [CrossRef]
- Gong, J.W.; Xia, C.C.; Lei, X.W. Analysis of filed measurement and theoretical calculation on rock pressure in shallow buried twin tunnels with small spacing. Chin. J. Rock Mech. Eng. 2010, 29 (Suppl. S2), 4139–4145. [Google Scholar]
- Zhang, W.G.; Anthony, T.C. Numerical study of pillar stresses and interaction effects for twin rock caverns. Int. J. Numer. Anal. Met. 2014, 39, 193–206. [Google Scholar] [CrossRef]
- GB50287–2016; National standard of the People’s Republic of China. Code for Hydropower Engineering Geological Investigation. China Planning Press: Beijing, China, 2016.
- TB 10003-2016; Industrial Standard of the People’s Republic of China. Code for Design on Tunnel of Railway. China Railway Press: Beijing, China, 2016.
- JTG 3370. 1-2018; Industrial Standard of the People’s Republic of China. Specifications for Design of Highway Tunnels Section 1 Civil Engineering. China Communications Press: Beijing, China, 2018.
- Li, S.B.; Zhang, Y.G.; Cao, M.Y.; Wang, Z.N. Study on Excavation Sequence of Pilot Tunnels for a Rectangular Tunnel Using Numerical Simulation and Field Monitoring Method. Rock Mech. Rock Eng. 2022, 55, 3507–3523. [Google Scholar] [CrossRef]
- Yong, Z.; He, H.W.; Li, P.F. Key Techniques for the Construction of High-Speed Railway Large-Section Loess Tunnels. Engineering 2018, 4, 254–259. [Google Scholar] [CrossRef]
- Wang, H.N.; Utili, S.; Jiang, M.J. An analytical approach for the sequential excavation of axisymmetric lined tunnels in viscoelastic rock. Int. J. Rock Mech. Min. Sci. 2014, 68, 85–106. [Google Scholar] [CrossRef]
- Daraei, A.; Zare, S.; Ghorbani, M. A new multi-graph approach for selecting the sequential excavation method of civil tunnels. Tunn. Undergr. Sp. Tech. 2019, 91, 102999. [Google Scholar] [CrossRef]
- He, C. Highway Small Clear Distance Tunnel; China Communications Press: Beijing, China, 2015. [Google Scholar]

| Classification Basis | Integrity Degree (Kv) | ||||
|---|---|---|---|---|---|
| Integrity | Relative Integrity | Relatively Broken | Broken | ||
| Extremely Integrity | More Integrity | ||||
| Classification of Tunnel Rock Mass (Ministry of Railways) | >0.85 | 0.85–0.65 | 0.65–0.45 | 0.45–0.25 | <0.25 |
| Classification of Surrounding Rock of Underground Engineering of Hydropower Station (Ministry of Water Resources and Electric Power) | >0.75 | 0.75~0.45 | 0.45~0.2 | <0.2 | |
| State | Dry | Slightly Damp | Occasional Water Seepage | Frequent Water Seepage | Massive Water Seepage |
|---|---|---|---|---|---|
| Water yield (L/min × 10 m) | 0 | <10 | 10–25 | 25–125 | >125 |
| Hydraulic pressure (MPa) | 0 | 0 | <0.1 | 0.1~0.25 | >0.25 |
| Left Side Tunnel Assessment | Right Side Tunnel Assessment | Comprehensive Assessment | ||||
|---|---|---|---|---|---|---|
| Included Angle between Structural Plane Strike and Tunnel Axis | Inclination of Structural Plane | Grade Score | Included Angle between Structural Plane Strike and Tunnel Axis | Inclination of Structural Plane | Grade Score | |
| 60°–90° | 60°–90° | 1 | 60°–90° | 60°–90° | 1 | 1.00 |
| 30°–60° | 0.9 | 30°–60° | 0.9 | 0.81 | ||
| 0°–30° | 0.8 | 0°–30° | 0.8 | 0.64 | ||
| 60°–90° | 60°–90° | 1 | 30°–60° | 60°–90° | 0.7 | 0.70 |
| 30°–60° | 0.9 | 30°–60° | 0.6 | 0.54 | ||
| 0°–30° | 0.8 | 0°–30° | 0.7 | 0.56 | ||
| 60°–90° | 60°–90° | 1 | 0°–30° | 60°–90° | 0.6 | 0.60 |
| 30°–60° | 0.9 | 30°–60° | 0.5 | 0.45 | ||
| 0°–30° | 0.8 | 0°–30° | 0.6 | 0.48 | ||
| 30°–60° | 60°–90° | 0.7 | 60°–90° | 60°–90° | 1 | 0.70 |
| 30°–60° | 0.6 | 30°–60° | 0.9 | 0.54 | ||
| 0°–30° | 0.7 | 0°–30° | 0.8 | 0.56 | ||
| 30°–60° | 60°–90° | 0.7 | 30°–60° | 60°–90° | 0.7 | 0.49 |
| 30°–60° | 0.6 | 30°–60° | 0.6 | 0.36 | ||
| 0°–30° | 0.7 | 0°–30° | 0.7 | 0.49 | ||
| 30°–60° | 60°–90° | 0.7 | 0°–30° | 60°–90° | 0.6 | 0.42 |
| 30°–60° | 0.6 | 30°–60° | 0.5 | 0.30 | ||
| 0°–30° | 0.7 | 0°–30° | 0.6 | 0.42 | ||
| 0°–30° | 60°–90° | 0.6 | 60°–90° | 60°–90° | 1 | 0.60 |
| 30°–60° | 0.5 | 30°–60° | 0.9 | 0.45 | ||
| 0°–30° | 0.6 | 0°–30° | 0.8 | 0.48 | ||
| 0°–30° | 60°–90° | 0.6 | 30°–60° | 60°–90° | 0.7 | 0.42 |
| 30°–60° | 0.5 | 30°–60° | 0.6 | 0.30 | ||
| 0°–30° | 0.6 | 0°–30° | 0.7 | 0.42 | ||
| 0°–30° | 60°–90° | 0.6 | 0°–30° | 60°–90° | 0.6 | 0.36 |
| 30°–60° | 0.5 | 30°–60° | 0.5 | 0.25 | ||
| 0°–30° | 0.6 | 0°–30° | 0.6 | 0.36 | ||
| Hardness | Hard Rock | Soft Rock | ||||
|---|---|---|---|---|---|---|
| Extremely Hard | Relatively Hard | General Hard | General Soft | Relatively Soft | Extremely Soft | |
| Rc (MPa) | >120 | 70–120 | 30–70 | 15–30 | 5–15 | <5 |
| Representative rock | Unweathered granite, gneiss, diorite, quartzite, siliceous limestone, etc. | Slightly weathered and weakly weathered marble, tuff, dolomite, magmatic rock, etc. | Strongly weathered extremely hard rock, weakly weathered hard rock, sandy mudstone, siltstone, mudstone, etc. | Mudstone, coal, argillaceous cemented sandstone, conglomerate, etc. | Completely weathered rocks | |
| Initial Stress State of the Middle Rock Pillar | Main Phenomenon | The Strength Stress Ratio S | |
|---|---|---|---|
| Hard Rock | Soft Rock | ||
| Extremely high stress | Excavation may cause rock bursts. Many new fractures. | The caking phenomenon of rock core. Sustained large displacement. | <4 |
| Medium~High stress | Rock mass peeling and falling off of tunnel wall. Poor cavern formation. | Significant displacement of tunnel wall rock mass. Persistent displacement. | 4–8 |
| Low stress | Weak initial stress state. The strength of rock mass is conducive to stability. | >8 | |
| Classification Basis | Integrity Degree | |||||
|---|---|---|---|---|---|---|
| Extremely Integrity | More Integrity | Relative Integrity | Relatively Broken | More Broken | Extremely Broken | |
| The rock integrity coefficient Kv | >0.9 | 0.8~0.9 | 0.6~0.8 | 0.4~0.6 | 0.2~0.4 | 0.2 |
| Score T1 | 42~50 | 34~42 | 26~34 | 18~26 | 10~18 | 10 |
| Hardness Degree | Hard Rock | Soft Rock | ||||
|---|---|---|---|---|---|---|
| Extremely Hard | Relatively Hard | General Hard | General Soft | Relatively Soft | Extremely Soft | |
| Rc | >120 | 70~120 | 30~70 | 15~30 | 5~15 | 5 |
| Score T2 | 42~50 | 34~42 | 26~34 | 18~26 | 10~18 | 10 |
| State | Dry | Slightly Damp | Occasional Water Seepage | Frequent Water Seepage | Massive Water Seepage |
|---|---|---|---|---|---|
| Water yield (L/min × 10 m) | 0 | 10 | 10~25 | 25~125 | >125 |
| Hydraulic pressure (MPa) | 0 | 0 | 0.1 | 0.1~0.25 | >0.25 |
| Score T3 | 0 | −2 | −4~−2 | −8~−4 | −16 |
| Materials | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Cohesion (MPa) | Friction Angle (°) |
|---|---|---|---|---|---|
| Surrounding rock | 2200–2300 | 6–10 | 0.25–0.3 | 2.0 | 39–50 |
| Primary lining support | 2500 | 30 | 0.20 | / | / |
| Secondary lining support | 2500 | 32.5 | 0.15 | / | / |
| Temporary support | 7900 | 200 | 0.30 | / | / |
| Width Span Ratio W/B | 0.3 | 0.3~1.0 | 1.0~1.5 | 1.5~2 | 2~2.5 | >2.5 |
|---|---|---|---|---|---|---|
| Impact degree | Extremely large | Relatively large | Slightly large | Large | Less | Small |
| Score T4 | −16 | −16~−12 | −12~−8 | −8~−4 | −4~−2 | 0 |
| Comprehensive Assessment | 0.36~0.45 | 0.48~0.54 | 0.56~0.64 | 0.7~1 |
|---|---|---|---|---|
| Influence of middle rock pillar stability | Most unfavorable | Unfavorable~Slightly unfavorable | Slightly favorable~Favorable | Most favorable |
| Score T5 | −16 | −12~−6 | −5~−3 | −2 |
| The Strength Stress Ratio S | 4 | 4~6 | 6~8 | >8 |
|---|---|---|---|---|
| Initial stress state | Extremely high stress | High stress | Medium stress | Low stress |
| Score T6 | −16 | −12~−6 | −6~−4 | −2 |
| Grade | I | II | III | IV | V | |
|---|---|---|---|---|---|---|
| Total Score T | 73 < T ≤ 96 | 57 < T ≤ 73 | 38 < T ≤ 57 | 20 < T ≤ 38 | T ≤ 20 | |
| Basic property | Integrity | More integrity~Extremely integrity | Relative integrity~More integrity | Relatively broken~Relative integrity | More broken~Relatively broken | Extremely broken~More broken |
| Hardness | Relatively hard~Extremely hard | General hard~Relatively hard | General soft~General hard | Relatively soft~General soft | Extremely soft~Relatively soft | |
| Auxiliary property | Permeability | Dry | Slightly damp | Slightly damp~Occasional water seepage | Frequent water seepage~Frequent water seepage | Massive water seepage |
| Width span ratio | Extremely large | Relatively large | Slightly large~Large | Less~Small | Small | |
| Combination of main structural plane and tunnel axis | Most unfavorable | Most unfavorable | Unfavorable~Slightly unfavorable | Slightly favorable~Favorable | Most favorable | |
| Initial stress state | Low stress~Medium stress | Low stress~Medium stress | Low stress~High stress | High stress~Extremely high stress | High stress~Extremely high stress | |
| Influencing Factors of Construction | Adjustment | Influencing Factors of Construction | Adjustment |
|---|---|---|---|
| Excavation scheme | Adopt the reinforcement scheme with temporary support | Footage | Reduce footage |
| Stagger distance of tunnel face | Reduce the stagger distance of the tunnel face | Stagger distance between two tunnels | Reduce the stagger distance between two tunnels |
| Excavation sequence | When the conditions are met, the ramp shall be excavated first | Advanced reinforcement measures | Opposed anchors and grouting |
| Index | T1 | T2 | T3 | T4 | T5 | T6 | T |
|---|---|---|---|---|---|---|---|
| Score | 31.6 | 37.78 | −4 | −16 | −5 | −2 | 42.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Cao, A.; Wu, Z.; Liu, X.; Li, Z.; Lin, L.; Liu, X.; Li, H.; Sun, Y. Improved Surrounding Rock Classification Method for the Middle Rock Pillar of a Small Clear-Distance Tunnel. Appl. Sci. 2023, 13, 2130. https://doi.org/10.3390/app13042130
Wang J, Cao A, Wu Z, Liu X, Li Z, Lin L, Liu X, Li H, Sun Y. Improved Surrounding Rock Classification Method for the Middle Rock Pillar of a Small Clear-Distance Tunnel. Applied Sciences. 2023; 13(4):2130. https://doi.org/10.3390/app13042130
Chicago/Turabian StyleWang, Jianxiu, Ansheng Cao, Zhao Wu, Xuezeng Liu, Zonghai Li, Lihua Lin, Xiaotian Liu, Huboqiang Li, and Yuanwei Sun. 2023. "Improved Surrounding Rock Classification Method for the Middle Rock Pillar of a Small Clear-Distance Tunnel" Applied Sciences 13, no. 4: 2130. https://doi.org/10.3390/app13042130
APA StyleWang, J., Cao, A., Wu, Z., Liu, X., Li, Z., Lin, L., Liu, X., Li, H., & Sun, Y. (2023). Improved Surrounding Rock Classification Method for the Middle Rock Pillar of a Small Clear-Distance Tunnel. Applied Sciences, 13(4), 2130. https://doi.org/10.3390/app13042130






