Abstract
Dendrite, a typical geological pattern, is developed along the bedding plane in limestone and dolomite strata in Jinzigou area, Zhoukoudian, Beijing, China, with a self-similar dendritic morphology. In order to reveal the dynamic mechanism of its formation, the diffusion-limited aggregation method, a model of fractal growth, was selected to simulate the microscopic dynamic mechanism of its formation. Take an L × L square lattice, with L = 200 lattices, 20,000 particles, and L = 250 lattices, 30,000 particles, for simulation. Obtain the simulation results of the dendritic pattern and the intermediate results with 8057 and 10,827 random particles released in the simulation process with 20,000 particles. The results show that the pattern is a typical fractal pattern formed in the process of fractal growth, with a fractal dimension of about 1.6. Its morphology is characterized by fractal geometry, and the dynamic mechanism of its formation is the fractal growth phenomenon generated by self-organizing criticality. The growth process is a nonlinear and non-equilibrium evolutionary process, which is dynamic and far from equilibrium. It is consistent with the fractal dimension of Zhoukoudian dendrite (1.52–1.78). Diffusion-limited aggregation (DLA) is a typical growth process in fractal growth. It leads to the growth of randomly branching structures that closely resemble various important systems in the earth sciences, providing a theoretical basis for revealing the nature of complex geological processes.
1. Introduction
Dendrite, a typical multi-branching formation, with a bushy, or feather-like pattern, is a kind of dendritic film, much like the impression of bryophytes or algae, which is mainly produced in the bedding plane, joint, fissure or mineral surface, cleavage plane, etc., of limestone, dolomite, marble, sandstone, etc. [1]. Because of its plant-like appearance, it is often mistaken for plant fossils (Figure 1). The name comes from the Greek word dendron (δένδρον), which means “tree,” since the crystal’s structure resembles that of a tree [2]. It has long been recorded in the literature of the Song and Yuan Dynasties of China [3].

Figure 1.
Dendrites in Zhoukoudian, Beijing, China. JZG01, JZG02, and JZG04 are limestone; JZG03 is marble.
Dendrite samples were collected in Jinzigou area, Zhoukoudian, Beijing (Figure 1), and developed in the limestone of the Majiagou Formation and marble of the Jingeryu Formation; they are iron dendrites. Morphological observation of dendrite shows that its local pattern and overall pattern have a high degree of morphological similarity, or self-similarity, which means that the dendritic pattern of dendrite has fractal geometric morphological characteristics. Here, the similar morphology is determined by the micro dynamic mechanism. To a certain extent, it can be approximately considered as a geochemical gene [4,5,6,7,8,9], just as genes determine biological characteristics.
Since the fractal term was creatively proposed by mathematician Mandelbrot in 1967 [10,11,12], with the gradual growth, maturity, and development of fractal itself, it has been cited by many disciplines and departments, and, at the same time, shows the vitality of fractal application in various disciplines. This is because it can reveal the essential structure of nature and describe the actual life of human beings [13,14,15]. It is an intuitive geometric language to describe the motion of chaos. In fact, it is a mathematical system in closer agreement with the real world, integrating many nonlinear science contents.
Earth sciences are concerned with extremely diverse sets of strongly interacting and synergetic phenomena [16,17,18]. In order to better understand these phenomena, it is often necessary to accurately describe complex structures and their evolution far from equilibrium. The development of fractal geometry has provided a valuable new approach towards the quantitative description of the statistical properties of various structures ranging in size from large molecules to continental coastlines [11,12]. In recent years, many simple non-equilibrium growth models have been developed [18], one of which is the diffusion-limited aggregation model (DLA), introduced by Witten and Sander [19].
As for the formation of dendrite, it is generally believed that it is the result of the infiltration and diffusion precipitation of iron and manganese solutions along the bedding surface or fracture surface after the formation of rock [1]. It is tree-like pattern of some crystal aggregates of oxide of iron and manganese, exhibits fractal morphological structural characteristics, and should be the growth pattern formed by fractal growth [14,15]. In order to investigate the dynamic mechanism of the dendrite formation, the diffusion-limited aggregation model, a typical growth process in fractal growth, was selected to simulate the micro dynamic mechanism of its formation, providing a reference for revealing the formation essence of dendrite.
As mentioned above, dendrite has only been mentioned in a few studies, and it is only a very simple introduction, without systematic discussion, especially regarding the dynamic mechanism of its formation. In fact, dendrite is a typical geological pattern, representing a large class of important systems and structures in geoscience, such as fault systems, sand dune ripples, rock cracks, mud cracks, river networks, mineral growth, ore vein morphology, and the deposit formation process. Although the characteristics of these systems or structures are very obvious, we do not know the micro-dynamic mechanism of their formation process. The study of the dynamic mechanism of the formation of dendrite provides a good example for the in-depth understanding and discussion of the micro-dynamic mechanism of the formation of many similar typical geological phenomena (or patterns).
As we know, the natural system is very complex. Specifically, it is a complex system, a dynamic system far from equilibrium, a nonlinear and non-equilibrium evolutionary system. We hope to promote an understanding of the nature of natural phenomena and deepen the understanding of non-equilibrium phenomena by elaborating the microscopic dynamic mechanism of dendrite, one of the typical phenomena in nature. After all, most processes in nature are non-equilibrium, rather than equilibrium, processes. Non-equilibrium and nonlinear processes are the essence of nature.
2. Model
Diffusion-limited aggregation (DLA) is a typical growth process in fractal growth. This model is a very convincing model of fractal growth, proposed by Witten and Sander of the University of Michigan in 1981, aiming at describing the diffusion and condensation process of coal ash, soot, or metal powder suspended in the atmosphere. It is a fractal growth process, far from the equilibrium state [19,20,21,22].
The DLA model also shows the fractional power-law behavior of correlation function [19]. This model is a variant of the Eden model, and its initial state is a seed particle at the origin of the lattice. A second particle is added at some random site, far away from the origin. The particle walks randomly until it reaches a position adjacent to the seed. Then the walking particles become part of the cluster. Subsequently, another particle is introduced at a random distance, and it randomly walks until it joins the cluster, and so on. If a particle touches the boundary of the lattices during its random walk, it will be removed and introduced into another particle [18,23].
DLA is an important and valuable model for simulating random growth process. The mathematical model describing the growth of diffusion limited aggregation is the Laplace equation. The growth probability of the surface of the growth structure is given by the scalar field (or gradient perpendicular to the surface) Φ(r), obeying Laplace equation
with boundary conditions Φ(r) = 0 at all positions r occupied by the cluster and Φ(r) = 1 (or some other constant value) for . Singularities are avoided by choosing a finite size to use the Laplace equation. In the DLA model, the probability P(r) of random walk particles visiting the lattice site at position r is proportional to Φ(r). This can be easily seen by comparing the discretized Laplace equation
with the equation
that describes the probability of a random walk particle visiting a lattice site (i, j), that is, the probability of visiting its nearest neighboring lattice site [18]. Here, Φ(i, j) is the value of the scalar potential associated with the position lattice site (i, j) on the square lattice, and P(i, j) is the probability that a random walk particle will be found at the position of the lattice site.
In summary, the DLA process of thousands of particles, overall, forms a distribution of particle concentration (or the probability distribution of finding particles). This concentration is large away from the growth center and zero at the edge of the clustered cluster. Therefore, a concentration gradient is formed from the distance to the edge of the cluster, which can be described by the first and second equations of Fick diffusion [20].
The first Fick diffusion equation describes the diffusion particle flow j as being equal to the product of the concentration gradient ∇ϕ and the diffusion coefficient D:
The Fick diffusion second equation shows that the change in concentration over time is equal to the concentration of the diffusion particle flow.
Here, j is the diffusion particle flow, and D is the diffusion coefficient. Because j is pointing in the direction in which the concentration gradient ∇ϕ is decreasing, it has a minus sign in front of it. If the particles are diffused on a large enough square lattice, and the clustered clusters are small enough, the change in the concentration of the diffused particles over time can be considered as zero for most of lattices, and thus Equation (1) can be obtained.
3. Method
As mentioned above, this model has the following properties and characteristics: this kind of fractal structure follows the Laplacian equation of a movable boundary in the formation process; in the process of condensed growth, the condensed particles exhibit irregular diffusion motion in the Laplacian concentration field; the interface of the growth clusters shows complex and unstable properties [24].
The rules of the DLA model can be summarized as follows: take a square in two-dimensional Euclidean space and divide it into many small squares to form a square lattice. A stationary particle is placed on a lattice site near the center of the lattice as a seed, and a particle is randomly generated at a distance from the seed particle. It makes a random walk on each lattice site due to Brownian motion. The result is a collision with a seed particle, in which case, the particle attaches to the seed particle and combines with it to form a cluster. The second step is to walk to the edge of the lattice, so that the particle is absorbed and disappears. Then, a second particle is randomly produced, and the process is repeated until it becomes attached to the cluster or absorbed by the boundary. After this process is repeated many times, the connected set of a square will grow outward from the original square, as shown in Figure 2. Particles exhibit Brownian motion, so when the particle is released, it is specified to move to the adjacent left, right, top, and bottom squares with a probability of one-quarter, and this process continues until the particle leaves the boundary, or reaches the cluster.
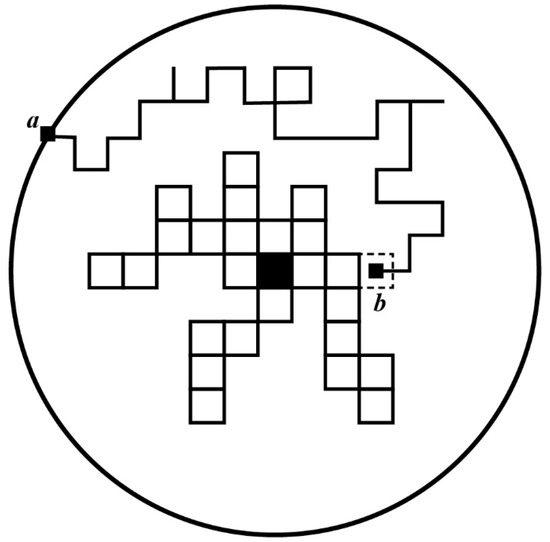
Figure 2.
Growth rules of diffusion-limited aggregation (DLA) models.
Based on the classical DLA model and MATLAB, the dendritic morphology and growth process of the dendrite are simulated.
Take an L × L square lattice and set a fixed particle in the center of the plane as a seed. The random function rand is used to randomly generate a particle in the plane, and the particle moves irregularly on the plane by Brownian motion. If the generated particle collides with the seed, it will be attached to the seed and form particle clusters. This process is repeated until a dendritic aggregate is formed in the lattice.
In computer simulation, first, set the size of the square grid as L = 200 or 250 and use the axis function to set the size of the square grid to L × L. Sparse function is used to generate an L × L all-zero sparse matrix, and then the seed position and seed number are set. The random function rand is used to generate random particles. Then, use the draw function to dynamically demonstrate the motion pattern of random particles. Determine the position of the random particles, count the number of “seed cluster” particles adjacent to random particles, and finally, graph these positions.
4. Result and Discussion
Figure 3 shows the computer simulation results of the DLA model, with L = 200 lattice and 20,000 particles. Figure 3a,b shows the simulated growth results when 8057 and 10,827 random particles are released, respectively, and Figure 3c shows the dendritic graph obtained after running the program (20,000 particles). From Figure 3, it can be clearly seen that the tree branches simulated by the DLA model continue to grow upward. It seems that the larger DLA cluster has more arms and fills the space more evenly than does the smaller cluster; its fractal dimension is 1.59 (Figure 4).
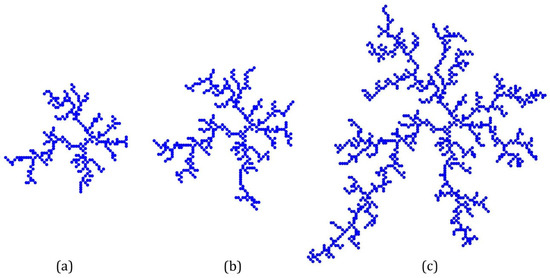
Figure 3.
The dendritic pattern simulated by DLA (200 × 200 lattice, 20,000 particles). (a,b) the intermediate results of DLA simulation with 8057 particles (a) with 10,827 particles (b); (c) the result of DLA simulation with 20,000 particles.
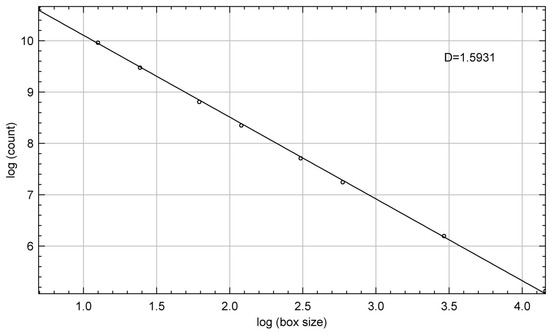
Figure 4.
Fractal dimension of dendritic pattern simulated by 20,000 particles (as shown in Figure 3).
Figure 5 shows the computer simulation results of the DLA model, with lattice L = 250 and 30,000 random particles. This dendritic fractal pattern is relatively complex. Particles grow outward from the central seed. The dendritic pattern formed is gradually complicated. The fractal dimensions of the dendritic pattern shown in Figure 3 and Figure 5 were calculated, using the box dimension method, to be 1.59 and 1.64, respectively (Figure 4 and Figure 6).

Figure 5.
Dendritic pattern simulated by DLA (250 × 250 lattice, 30,000 particles).
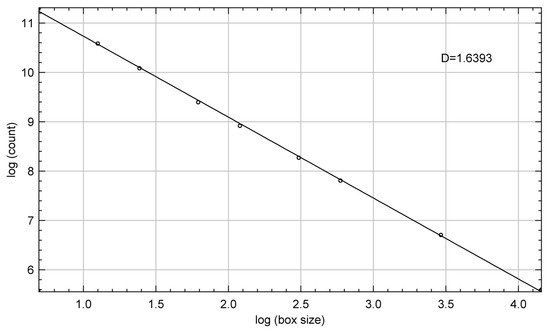
Figure 6.
Fractal dimension of dendritic pattern simulated by 30,000 particles (as shown in Figure 5).
In order to explore the simulation effect of the DLA model, the author selected four samples of dendrite—JZG01, JZG02, JZG03, and JZG04—in Zhoukoudian area for comparative analysis (Figure 1). The fractal dimension calculation method is the same as that of the simulated dendritic pattern, namely, the box dimension method. Through four steps: extraction analysis location → image processing → image binary matrix data extraction → data statistical analysis, the box dimension method was used to calculate the morphological fractal dimension of the four samples in Zhoukoudian area. The results show that the fractal dimension of the four samples is 1.61, 1.67, 1.78, and 1.52, respectively, ranging from 1.52 to 1.78, with an average value of 1.65. The local fractal dimension of JZG03 is 1.77, while the overall fractal dimension is 1.78, indicating that the local pattern of the dendrite shows self-similarity to the overall pattern; that is, the dendritic pattern of dendrite has fractal characteristics. The fractal dimensions of the dendritic pattern simulated by the DLA model are 1.59 and 1.64, which are consistent with the fractal dimensions of Zhoukoudian dendrite. The simulation effect is good, which essentially reveals the microscopic dynamic mechanism of dendrite formation.
From the above, the agglomeration group (cluster) formed by the DLA model exhibits fractal characteristics. Moreover, previous studies have shown that the fractal dimension of DLA is independent of the lattice type [20]. The fractal dimension of the obtained DLA figure remains unchanged when the square lattice is changed into a triangular lattice [20], its fractal dimension does not increase with the increase in the spatial dimension, and it has a stable value [25].
DLA also has a screening effect [20]. The reason for the generation of branches with different sizes is that, due to the tortuous random motion trajectory of the particles, the branches that extend from the outside of the cluster have a greater probability of acquiring particles, which prevents the particles from intruding into the inside. This screening effect makes the clusters grow in the structure by continuously branching outward [26].
Figure 3 and Figure 5 also show that, in the process of the random walking and outward growth of the particles, due to the high probability of obtaining particles from the branches extending outside the cluster, particles cannot invade into the interior. This screening effect makes the cluster grow continuously according to the outward branching structure, forming a complex dendritic pattern.
According to the above analysis, it is believed that the formation of dendrite is a fractal pattern formed in the process of fractal growth, that is, the microscopic dynamic mechanism of its formation.
In recent years, studies regarding fractal growth have developed rapidly [27,28,29,30,31]. According to the latest research results, fractal growth phenomena caused by self-organized criticality can be generally summarized into three main models: Laplace, percolation, and oscillation. For dendritic growth, these can be divided into two cases, the first being dendritic solidification, forming a solid dendritic pattern, and the second being viscous fingering, forming a fluid dendritic pattern. Under appropriate conditions, both can be studied using the DLA model.
Moreover, this dynamic mechanism reveals that the growth process is a dynamic process far from equilibrium, and it is also a nonlinear and non-equilibrium evolutionary process. It can be used to explain a large class of fractal formation processes in nature, such as fluid movement, dielectric breakdown, electrodeposition process, crystal growth in liquid film, viscous fingering, non-dendritic growth, loose rock dissolution and seismic cracking, etc. [32,33,34,35,36,37]. Therefore, it has attracted widespread attention, deepening the understanding of non-equilibrium phenomena. It has been widely used in some irreversible growth processes far from equilibrium. For example, Yu applied it to the study of mineral deposits [15,38,39,40,41,42], suggesting that the formation of mineral deposits is a fractal growth process, and that the dynamic mechanism of the formation of super-large deposits and ore-concentration areas constitutes the dynamics of fractal growth. In other words, super-large deposits and ore-concentration areas are realized and completed through the onset of ore formation followed by the snowball effect.
The diffusion-limited aggregation model, as well as various related models, have led to the growth of random branching structures that closely resemble various important systems in earth sciences. Although most processes in nature involve multiple mechanisms, the DLA model alone seems unlikely to provide an adequate understanding of these processes. However, the DLA model is one of the most striking examples of complex pattern generation using simple models and algorithms. It has become the dominant paradigm for pattern formation far from equilibrium, and it provides valuable examples for a wide range of natural phenomena. It gives us the first insight into the microscopic processes involved in the growth of branching structures, as well as the importance of random events or distributions to these growth phenomena. Above all, it does provide a good theoretical model for the formation mechanism of many typical geological phenomena (or patterns), such as fault systems, river networks, mineral growth, ore vein morphology and deposit formation process, etc.
5. Conclusions
The morphology of dendrite has fractal geometry characteristics, and in fact, the dynamic mechanism of its formation is the fractal growth phenomenon generated by self-organizing criticality. The growth process is a dynamic process far from equilibrium, which is a nonlinear and non-equilibrium evolutionary process. The diffusion-limited aggregation (DLA) model in the fractal growth theory can satisfactorily simulate the growth process and the formed pattern, which essentially reveals the microscopic dynamic mechanism of dendrite formation. The fractal dimensions of the simulated pattern are 1.59 and 1.64, which are consistent with the fractal dimensions of Zhoukoudian dendrite. DLA has led to the growth of random branching structures that closely resemble various important systems in the earth sciences, providing possibilities for revealing the nature of complex geological processes, and also for deepening the understanding of non-equilibrium phenomena.
Author Contributions
N.L.: conceptualization, methodology, formal analysis, data curation, and writing—original draft; Y.H.: conceptualization, data curation, and visualization; S.X.: investigation, formal analysis, and data curation; L.X.: formal analysis and data curation; Y.W.: conceptualization and investigation; J.L.: investigation and data curation; P.L.: investigation and data curation; Q.G.: conceptualization and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Fundamental Research Funds for the Central Universities, China (Grant No. 2652018285).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We greatly appreciate the comments from the anonymous reviewers and editors for their valuable suggestions to improve the quality of this manuscript.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Manutchehr-Danai, M. Dictionary of Gems and Gemology; Springer: Berlin, Germany, 2009; pp. 241–242. [Google Scholar]
- Nanjwade, B.K.; Bechra, H.M.; Derkar, G.K.; Manvi, F.V.; Nanjwade, V.K. Dendrimers: Emerging polymers for drug-delivery systems. Eur. J. Pharm. Sci. 2009, 38, 185–196. [Google Scholar] [CrossRef] [PubMed]
- Lin, J. The colorful world of dendrite. Jewel. Gold 2022, 2, 68–69. (In Chinese) [Google Scholar]
- Gong, Q.J.; Yan, T.T.; Wu, X.; Li, R.K.; Wang, X.Q.; Liu, N.Q.; Li, X.L.; Wu, Y.; Li, J. Geochemical gene: A promising concept in discrimination and traceability of geological materials. Appl. Geochem. 2022, 136, 105133. [Google Scholar] [CrossRef]
- Wu, Y.; Gong, Q.J.; Liu, N.Q.; Wu, X.; Yan, T.T.; Xu, S.C.; Li, W.J. Classification of geological materials on geochemical lithogenes: Illustration on a case study in Gejiu area of Yunnan Province, China. Appl. Geochem. 2022, 146, 105460. [Google Scholar] [CrossRef]
- Gong, Q.J.; Liu, N.Q.; Wu, X.; Yan, T.T.; Fan, T.Q.; Li, X.L.; Liu, M.X.; Li, R.K.; Albanese, S. Using regional geochemical survey data to trace anomalous samples through geochemical genes: The Tieshanlong tungsten deposit area (Southeastern China) case study. J. Geochem. Explor. 2020, 219, 106637. [Google Scholar] [CrossRef]
- Li, R.K.; Liu, N.Q.; Gong, Q.J.; Wu, X.; Yan, T.T.; Li, X.L.; Liu, M.X. Construction, test and application of a geochemical gold metallogene: Case studies in China. J. Geochem. Explor. 2019, 204, 1–11. [Google Scholar] [CrossRef]
- Li, J.; Gong, Q.J.; Zhang, B.M.; Liu, N.Q.; Wu, X.; Yan, T.T.; Li, X.L.; Wu, Y. Construction, test and application of a Tungsten metallogene named MGW11: Case studies in China. Appl. Sci. 2023, 13, 606. [Google Scholar] [CrossRef]
- Hou, Z.G.; Gong, Q.J.; Liu, N.Q.; Jiang, B.; Li, J.; Wu, Y.; Huang, J.X.; Gu, W.X. Elemental abundances of moon samples based on statistical distributions of analytical data. Appl. Sci. 2023, 13, 360. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractal: Form, Chance and Dimension; Freeman: San Francisco, CA, USA, 1977; pp. 1–365. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982; pp. 1–460. [Google Scholar]
- Zhang, J.Z. Fractal; Tsinghua University Press: Beijing, China, 2011; pp. 1–310. (In Chinese) [Google Scholar]
- Yu, C.W. The Complexity of Geosystems (Book 1); Geological Publishing House: Beijing, China, 2003; pp. 282–344. (In Chinese) [Google Scholar]
- Yu, C.W. Fractal Growth of Mineral Deposits at the Edge of Chaos (Book 2); Anhui Education Press: Hefei, China, 2006; pp. 105–174. (In Chinese) [Google Scholar]
- Liu, N.Q.; Peng, N.; Gong, Q.J.; Liu, Y.S.; Yu, C.W.; Albanese, S. Spatio-temporal synchronization in complex ore-forming systems: Mesoscale case study in south China. J. Geochem. Explor. 2021, 231, 106873. [Google Scholar] [CrossRef]
- Yu, C.W.; Peng, N. Regional Ore Zonality of the Nanling Region; Geological Publishing House: Beijing, China, 2009; pp. 1–256. (In Chinese) [Google Scholar]
- Barton, C.C.; La Pointe, P.R. Fractals in Petroleum Geology and Earth Processes; Springer: New York, NY, USA, 1995; pp. 227–259. [Google Scholar]
- Witten, T.A.; Sander, L.M. Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon. Phys. Rev. Lett. 1981, 47, 1400–1403. [Google Scholar] [CrossRef]
- Witten, T.A.; Sander, L.M. Diffusion-Limited Aggregation. Phys. Rev. B 1983, 27, 5686–5697. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-Organized Criticality: An Explanation of 1/f Noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef]
- Sander, M.L. Diffusion-limited aggregation: A kinetic critical phenomenon. Contemp. Phys. 2000, 41, 203–218. [Google Scholar] [CrossRef]
- Meakin, P. Fractals, Scaling and Growth Far From Equilibrium; Cambridge University Press: Cambridge, UK, 1998; pp. 1–674. [Google Scholar]
- Gao, R.; Xie, S.Y.; Tao, J.D. Simulation for the fractal aggregation growth on the platform of MATLAB. J. Southwest China Norm. Univ. Nat. Sci. Ed. 2005, 30, 83–86, (In Chinese with English Abstract). [Google Scholar]
- Satpathy, S. Dielectric breakdown in three dimensions: Result of numerical simulation. Phys. Rev. B 1986, 33, 5093–5095. [Google Scholar] [CrossRef]
- Rosenstock, H.B.; Marquardt, C.L. Cluster formation in two-dimensional random walks: Application to photolysis of silver halides. Phys. Rev. B 1980, 22, 5797–5809. [Google Scholar] [CrossRef]
- Stanley, H.E.; Ostrowsky, N. Random Fluctuations and Pattern Growth: Experiments and Models; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; pp. 1–355. [Google Scholar]
- Vicsek, T. Fractal Growth Phenomena; World Scientific: Singapore, 1992; pp. 312–319. [Google Scholar]
- Bunnde, A.; Havlin, S. Fractals and Disorder Systems; Springer: Berlin, Germany, 1996; pp. 1–407. [Google Scholar]
- Jamtveit, B.; Meakin, P. Growth, Dissolution and Pattern Formation in Geosystems; Kluwer Academic Publishers: Dordrecht, Germany, 1999; pp. 1–409. [Google Scholar]
- Ben-Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2000; pp. 1–315. [Google Scholar]
- Nittman, J.; Daccord, G.; Stanley, H.E. Fractal growth of viscous fingers: Quantitative characterization of a fluid instability phenomenon. Nature 1985, 314, 141–144. [Google Scholar] [CrossRef]
- Meek, J.M.; Craggs, J.D. Electrical Breakdown of Gases; Wiley: New York, NY, USA, 1978; Volume 15, pp. 182–185. [Google Scholar]
- Grier, D.; Ben-Jacob, E.; Clarke, R.; Sander, L.M. Morphology and microstructure in electrochemical deposition of zinc. Phys. Rev. Lett. 1986, 56, 1264–1267. [Google Scholar] [CrossRef]
- Brady, R.M.; Ball, R.C. Fractal growth of copper electrodeposits. Nature 1984, 309, 225–228. [Google Scholar] [CrossRef]
- Ben-Jacob, E.; Shochet, O.; Tenenbaum, A.; Cohen, I.; Czirok, A.; Vicesek, T. Generic modeling of cooperative growth pattern in bacterial colonies. Nature 1994, 368, 46–49. [Google Scholar] [CrossRef]
- Sidoravicius, V.; Stauffer, A. Multi-particle diffusion limited aggregation. Invent. Math. 2019, 218, 491–571. [Google Scholar] [CrossRef]
- Yu, C.W. Larger ore deposit and metallogenic districts at the edge of chaos. Earth Sci. Front. 1999, 6, 195–229. [Google Scholar]
- Yu, C.W. Fractal Growth of Mineral Deposits at the Edge of Chaos (Book 1); (In Chinese). Anhui Education Press: Hefei, China, 2006; pp. 1–9, 161–200. [Google Scholar]
- Yu, C.W. Fractal growth of ore-forming dynamical systems at the edge of chaos, a new metallogeny and methodology (First half). Earth Sci. Front. 2001, 8, 9–28. [Google Scholar]
- Yu, C.W. Fractal growth of ore-forming dynamical systems at the edge of chaos, a new metallogeny and methodology (Second half). Earth Sci. Front. 2001, 8, 471–489. [Google Scholar]
- Yu, C.W. Fractal growth of ore-forming dynamic systems at the edge of chaos: A new metallogeny and methodology. Bull. Mineral. Petrol. Geochem. 2002, 21, 103–113. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).