Experience Replay Optimisation via ATSC and TSC for Performance Stability in Deep RL

Abstract

Catastrophic forgetting is a significant challenge in deep reinforcement learning (RL). To address this problem, researchers introduce the experience replay (ER) concept to complement the training of a deep RL agent. However, the buffer size, experience selection, and experience retention strategies adopted for the ER can negatively affect the agent’s performance stability, especially for complex continuous state action problems. This paper investigates how to address the stability problem using an enhanced ER method that combines a replay policy network, a dual memory, and an alternating transition selection control (ATSC) mechanism. Two frameworks were designed: an experience replay optimisation via alternating transition selection control (ERO-ATSC) without a transition storage control (TSC) and an ERO-ATSC with a TSC. The first is a hybrid of experience replay optimisation (ERO) and dual-memory experience replay (DER) and the second, which has two versions of its kind, integrates a transition storage control (TSC) into the first framework. After comprehensive experimental evaluations of the frameworks on the pendulum-v0 environment and across multiple buffer sizes, retention strategies, and sampling ratios, the reward version of ERO-ATSC with a TSC exhibits superior performance over the first framework and other novel methods, such as the deep deterministic policy gradient (DDPG) and ERO.

1. Introduction

In recent years, deep RL has made some strides in game AI [1], energy [2], stock trading [3], health [4], autonomous driving [5], and many more. The experience replay (ER) concept is a vital component of the success of these RL applications. According to Lin et al. [6], ER allows an RL agent to change its current policy by reusing previously experienced data. It also aids the agent in making better decisions when it encounters similar states and speeds up its learning. However, not all experiences (transitions) benefit the agent’s training [7]. There is a need to harness important experiences to stabilise and improve the agent’s performance, but this becomes a challenge when dealing with a stochastic world where the agent seldom obtains quality and relevant experiences. As a result, it is imperative to store and efficiently use essential experiences.

For ER to be successful, there is the need to carefully understand the strategies required to determine the experiences to store, the ones to select for training the agent, and those to retain when the replay buffer is full. With a standard experience replay process, the agent, through an exploration and exploitation mechanism, selects an action in a state, takes that action, and receives a reward and a new state from its environment. The transition tuple (state, action, reward, and the new state), also known as experience, is stored in a fixed-length replay buffer. After storage, a selection strategy randomly samples a mini-batch of the stored experiences to train the agent. This process repeats until the attainment of a performance threshold. A retention mechanism is applied to ensure that relevant experiences are maintained when the replay buffer is full. The selection and retention strategies are employed to facilitate the effective use of data and reduce the cost of interactions with the agent’s environment.

Over the years, researchers have developed novel approaches for experience selection and retention. Algorithms such as deep Q-network (DQN) [8], prioritised experience replay (PER) [9], combined experience replay (CER) [10], deep deterministic policy gradient (DDPG) [11], episodic memory deep Q-Network (EMDQN) [12], selective experience replay (SER) [13], prioritised sequence experience replay (PSER) [14], experience replay optimisation (ERO) [15], and attentive experience replay (AER) [16] use a single replay buffer, while others, such as the double experience replay (DER) [17] algorithm, rely on a double buffer (also called dual memory). Again, some algorithms uniformly replace or remove experiences at random, while others use prioritisation strategies to delete experiences from the buffer. It is worth noting that experience selection is not only influenced by how to retain experiences when the replay buffer is full, but also by what to store in the buffer. Thus, it is essential to study the relationship between the storage, selection, and retention mechanisms applied in ER. The following are the main contributions of this paper:

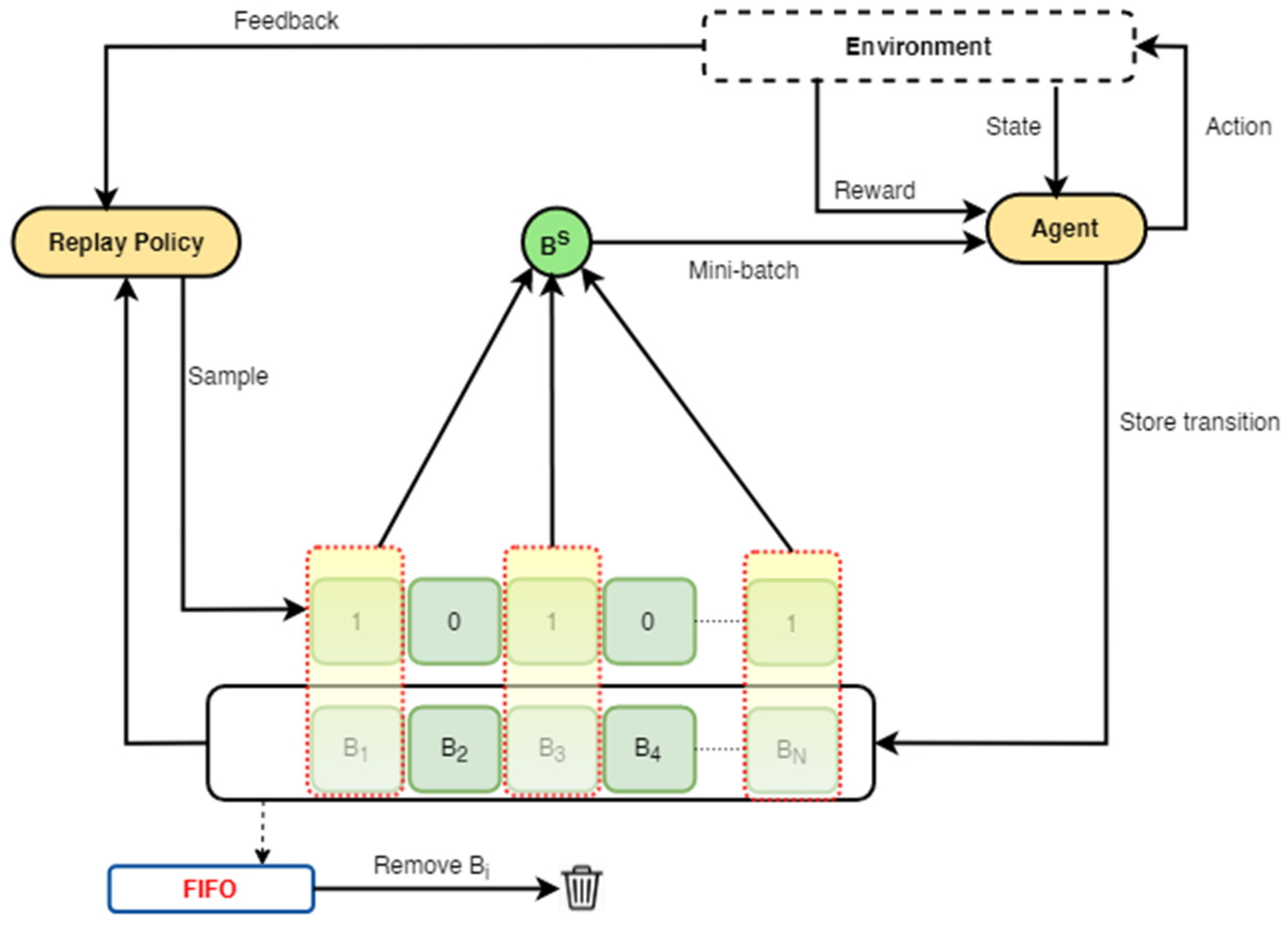
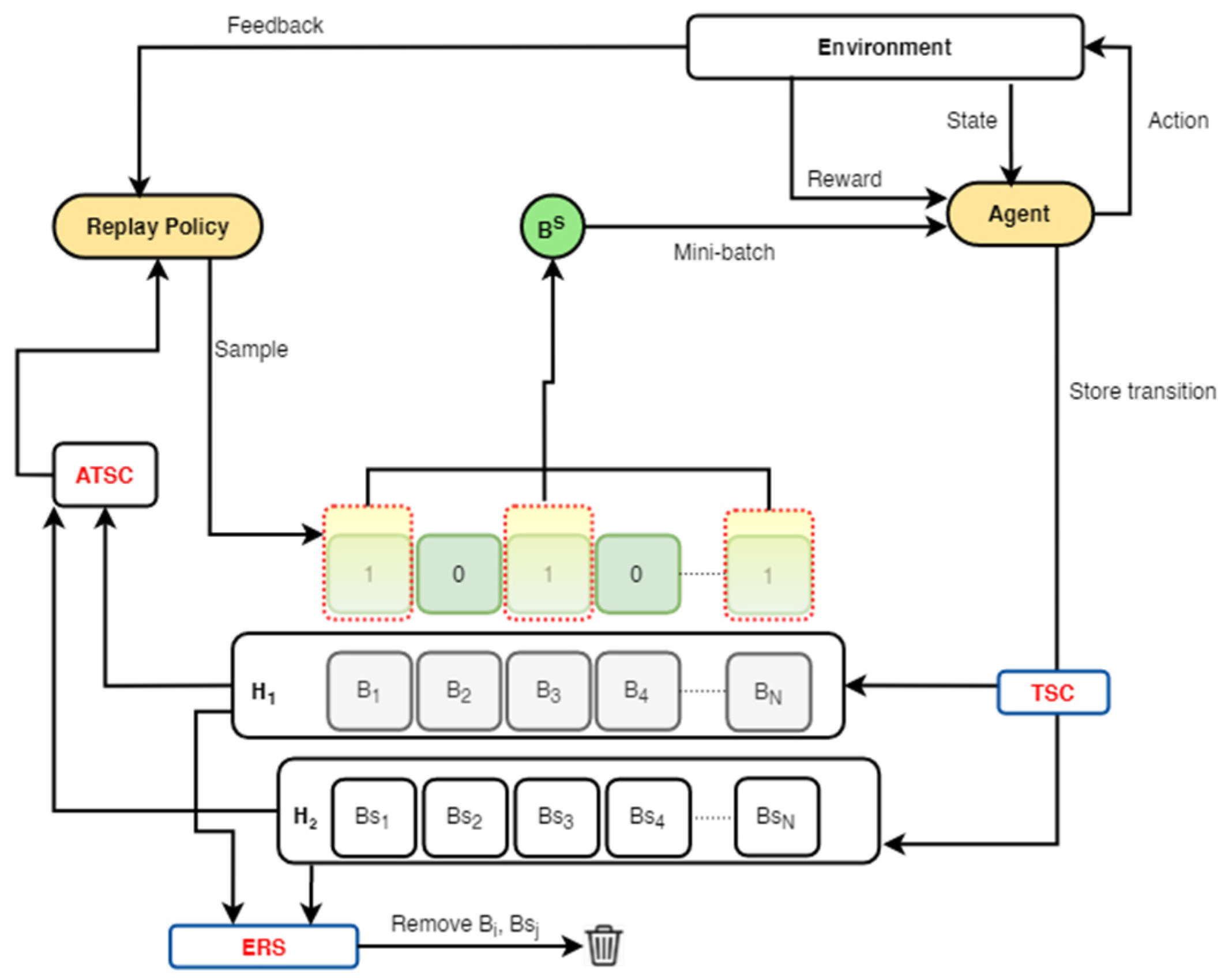
• To effectively improve the performance stability of ERO, an alternating transition selection control (ATSC) and a dual memory are introduced into the standard ERO to design a first framework. The ATSC uses a selection ratio to sample transitions from the dual memory into the replay policy network to promote complementary and stable learning.
• A transition storage control (TSC), which uses either a reward or a temporal difference error (TDE) threshold, is further integrated into the first framework to ensure that more rewarding and diverse transitions are frequently stored in the dual memory.

To better comprehend the operations of the frameworks and to validate their efficacy, they are primarily evaluated on the Pendulum-v0 of the OpenAI Gym [18] platform. Subsequently, the frameworks are tested on the MountainCarContinuous-V0, LunarLanderContinuous-v2, and BipedalWalker-v3 environments. The experiments demonstrate that the reward version of ERO-ATSC with a TSC exhibits superior performance over the first framework and other novel algorithms, such as the deep deterministic policy gradient (DDPG) and experience replay optimisation (ERO).

The rest of the paper is organised as follows: Section 2 presents a brief review of related works on ER techniques. Section 3 highlights the single and dual replay buffer frameworks, and Section 4 focuses on the experimental setup. Section 5 discusses the results and Section 6 presents the conclusion and recommendation.

2. Related Works

With advancements in deep learning and deep reinforcement learning, researchers seek to retain the knowledge acquired by a deep neural network as it trains to find solutions to diverse problems. In recent times, the focus has been on continual learning, where a trained neural network continues to learn. However, continual learning faces the challenge of catastrophic forgetting [19,20,21,22]. A neural network will adjust its weights to a specific problem, task A, but will forget these weights when the same network begins to train on a different task. This behaviour can be harmful to generalisation and continual learning. To ensure that the network is scalable and can train on multiple and complex tasks without forgetting, researchers suggest developing and adopting different strategies and algorithms. While some suggest training a neural network with regularisation approaches, such as learning without forgetting (LWF) [23] and elastic weight consideration (EWC) [21], others such as Han et al. [24] opt for dynamic network architecture, and some also suggest complementary learning systems (memory with replay strategies) [8,9,13,15,17,25].

ER is one of the oldest but relevant mechanisms employed to complement neural network training. Lin [6] introduced the ER concept in his reinforcement learning research but the DQN algorithm [8] brought it to the limelight. In ER, previous data are stored in a buffer and repeatedly reused with new data to train the neural network. However, the successful operation of ER hinges on some selection and retention mechanisms that require careful design and implementation. This section briefly reviews experience retention and selection strategies but throws much on the latter.

2.1. Experience Retention Strategies and Algorithms

The ER mechanism has three major stages: storing experiences in the buffer, retaining or removing experiences when the replay buffer is full, and selecting experiences to be replayed. When a deep RL agent observes a state, that state is fed into the deep neural network, and the network predicts the q-values of all possible actions in the state. Afterwards, an exploration–exploitation technique (for example, epsilon-greedy) selects an action in the observed state. A new state is observed and a feedback reward is given to determine the value of the action taken. The agent transits from one state to another until it reaches a terminal state. The transition tuple (state, action, reward, and new state) can be stored directly in the buffer or may be stored based on some threshold mechanisms. Since some actions are more rewarding than others and the agent aims to maximise its accumulated reward, it is vital to adopt efficient mechanisms to retain relevant experiences and remove less relevant ones when the buffer is full.

An experience retention strategy may be implemented sequentially, uniformly, or prioritised. The standard ER uses the First-In-First-Out (FIFO) approach, where it sequentially overwrites old experiences with new ones when the buffer is full. The experiences are removed without considering their relevance to the agent’s performance [26]. Another approach is to replace experiences in the first half of the buffer with new ones when the buffer is full. Moreover, a replay buffer that is big enough to store all experiences can be used [7]. However, this approach can be detrimental to training stability, as experiences that may hamper learning progress continue to stay in the buffer. In the reservoir approach, experiences are uniformly at random, overwritten with new ones. Furthermore, experiences can be overwritten stochastically based on their relevance to learning [26]. Table 1 presents a list of algorithms and their ER strategies.

2.2. Experience Selection Strategies and Algorithms

The effectiveness of experience selection or sampling is rated not only by the sample outcome, but also by the strategies implemented to produce the needed outcome. Irrespective of the experience selection strategy adopted, the sampling mechanism may be uniform or prioritised but not sequential; sequential sampling will generate highly correlated experiences and eventually prevent the agent from learning. However, a uniform or prioritised sampling will reduce the cost of training, break the correlation between transitions, and improve sampling efficiency and learning stability.

Many selection strategies have been developed and combined with some RL algorithms to solve simple and complex problems. The DQN algorithm of Mnih et al. [8] combines a deep convolutional neural network with the standard ER and the Q-learning [27] method to solve the challenging Atari 2600 games; in this approach, the experiences are selected uniformly at random. Each experience in the replay buffer has an equal probability or chance of being selected for replay. For a set of experiences, E(e₁, e₂, …, e_n), the probability of any experience is given as Pi = 1/n. Contrary to uniform sampling, some selection strategies draw inspiration from the prioritised sweeping [28] technique and, therefore, assign higher selection probability to experiences that are deemed important and can generate good returns. Prioritised strategies assign importance to experiences based on temporal difference error (TDE) [9], reward [13,15], frequency of selection [17], distribution of transitions [13], and even the similarities between states [16]. While some selection strategies are fully prioritised (only the highest priority transitions are selected), others have a parameter to regulate the level of prioritisation. The parameterised prioritisation makes it flexible to scale from uniform to fully prioritised sampling.

Schaul et al. [9] present a prioritised experience replay (PER), where experiences with higher TDE are selected frequently. This situation can result in a loss of diversity but can be addressed with stochastic prioritisation. However, prioritisation can create a bias, which can also be corrected with importance sampling. While Horgan et al. [29] extend prioritised experience replay to a distributed setting, Zha et al. [15] use a replay policy (neural network) combined with both uniform and prioritised selection techniques to select transitions for replay. Luo and Li handle state-action space diversity by over-sampling under-represented experiences in a non-diverse state-action space. Sun et al. [15,16] also sample experiences based on the similarities between the states of those experiences and the state of the agent. They equally focus on experiences that are frequently visited.

Just as multiple neural networks are used in some RL algorithms to enhance training stability [8,11,15,26,30,31], recent works in ER are exploring the use of a dual-memory architecture. The dualism may come in the form of long and short memory [32] or main and cache [33]. It may also be differentiated based on the sources of the replay data or the ratio of selection from the dual memory. Olin-Ammentorp et al. [32] rely on the complementary learning system of the human brain (interaction between the cortical and hippocampal networks) to design a dual memory (short-term and long-term) replay architecture. However, their design was implemented in a discrete state-action space. Ko and Chang [33] use the main memory to store diverse experiences and cache memory to manage the frequently used experiences to train the neural network. On the other hand, a ratio can be employed to alternate the sampling of relevant experiences from one memory and recent experiences from another memory [17]. Table 1 shows a tabulated summary of some RL algorithms and their adopted ER strategies.

Table 1. Some RL algorithms and their ER strategies √.

Ref.	Algorithm	Sampling Strategy		Retention Strategy
		Uniform	Priority	Sequential	Uniform	Priority
[8]	Deep Q-Network (DQN)	√		√
[9]	Prioritised Experience Replay (PER)	√		√
[11]	Deep Deterministic Policy Gradient (DDPG)	√		√
[12]	Episodic Memory Deep Q-Network (EMDQN)	√		√
[13]	Selective Experience Replay (SER)	√			√	√
[14]	Prioritised Sequence Experience Replay (PSER)		√	√
[15]	Experience Replay Optimisation (ERO)	√	√	√
[16]	Attentive Experience Replay (AER)	√	√	√
[17]	Double Experience Replay (DER)	√	√	√
[26]	Prioritised Stochastic Memory Management (PSMM)	√				√
[30]	Twin Delayed Deep Deterministic Policy Gradient (TD3)	√		√
[31]	Proximal Policy Optimisation (PPO)	√		√
[33]	Dual Memory Structure (DMS)	√	√	√		√

Table 1. Some RL algorithms and their ER strategies √.

Ref.	Algorithm	Sampling Strategy		Retention Strategy
		Uniform	Priority	Sequential	Uniform	Priority
[8]	Deep Q-Network (DQN)	√		√
[9]	Prioritised Experience Replay (PER)	√		√
[11]	Deep Deterministic Policy Gradient (DDPG)	√		√
[12]	Episodic Memory Deep Q-Network (EMDQN)	√		√
[13]	Selective Experience Replay (SER)	√			√	√
[14]	Prioritised Sequence Experience Replay (PSER)		√	√
[15]	Experience Replay Optimisation (ERO)	√	√	√
[16]	Attentive Experience Replay (AER)	√	√	√
[17]	Double Experience Replay (DER)	√	√	√
[26]	Prioritised Stochastic Memory Management (PSMM)	√				√
[30]	Twin Delayed Deep Deterministic Policy Gradient (TD3)	√		√
[31]	Proximal Policy Optimisation (PPO)	√		√
[33]	Dual Memory Structure (DMS)	√	√	√		√

The uniform sampling or retention strategy is simple to implement but samples or retains transition irrespective of their relevance to learning. The prioritised sampling or retention strategy increases the frequency of selecting relevant transitions but has exponential computational complexity as well as probability tuning difficulties. The sequential retention strategy is popular and simple to implement but sequentially replaces old transitions irrespective of their relevance to learning.

3. General Framework for ERO-ATSC

This section presents a brief transition from the standard ER technique to the ERO framework. Again, the section provides a detailed formulation of two comprehensive frameworks of the ERO algorithm. While the first framework combines ERO with a dual memory and an ATSC, the second framework puts together ERO, a double memory, an ATSC and a TSC mechanism. The section further shows an investigation of the effect of different retention strategies and buffer sizes on the stability and performance of the two frameworks, considering the varying sampling ratios.

3.1. ERO and Alternating ERO

The ERO algorithm is extended with a dual-memory selection strategy to demonstrate the idea of stabilising and improving the agent’s performance through complementary learning. This section presents the operation mechanism of the ERO framework and the proposed alternating transition selection framework.

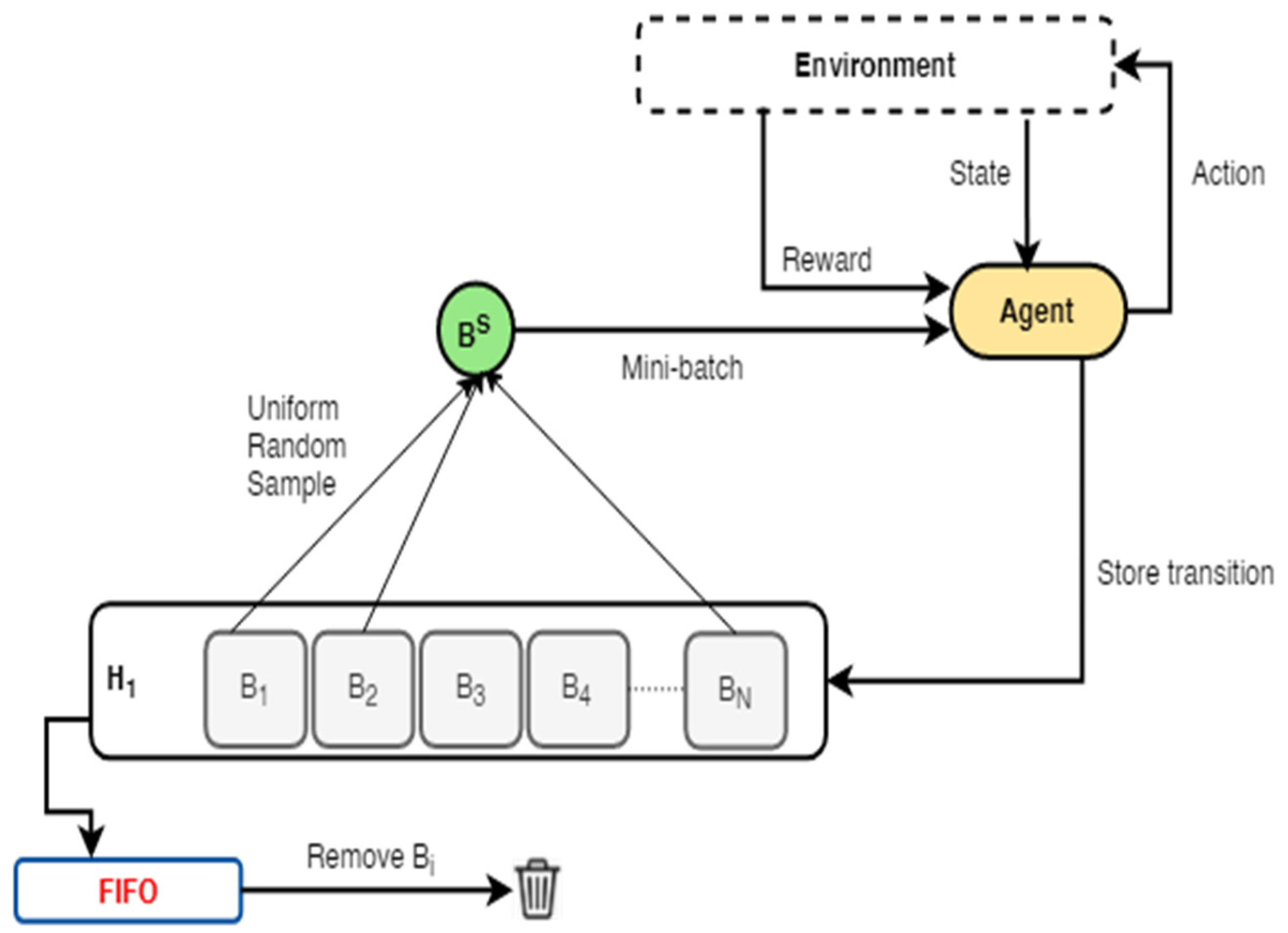
3.1.1. ERO Framework

ERO is a novel framework that uses a neural network to predict replay transitions. It is used to enhance the experience selection mechanism in the DDPG algorithm [9]. As illustrated in Figure 1 and Figure 2, a replay policy is combined with the standard ER framework to form the ERO framework. The transitions generated by the agent’s choices of actions are stored in the replay buffer and subsequently sampled into the replay policy after a specified number of transitions are buffered. The replay policy prioritises the transitions through a Boolean (0, 1) vectorisation process based on the TDEs. Transitions with Boolean number 1 are uniformly sampled to train the agent. When the replay buffer is full, the naive FIFO retention strategy is used to retain experiences in the standard ER and ERO frameworks. However, in this study, an enhanced sequential retention strategy is used for the experience retention mechanism of the ERO framework.

Figure 1. An illustration of the standard experience replay (ER) framework. A specified batch size of transitions is uniformly sampled at random from the replay buffer to train the agent. When the buffer is full, the First-In-First-Out (FIFO) retention strategy is applied to ensure that older transitions are replaced with newer ones.

Figure 2. An illustration of experience replay optimisation (ERO). A specified batch size of transitions is sampled from the replay buffer, using a replay policy (deep neural network), to train the agent. When the buffer is full, the First-In-First-Out (FIFO) retention strategy is applied to ensure that older transitions are replaced with newer ones.

The replay policy of ERO relies on Equations (1)–(4), and the notations used are clearly explained in Table 2.

$$\lambda =\left\{\varphi \left(f_{B_i}|{\theta }^{\varphi }\right)| B_i\in B\right\} \in {ℝ}^N$$

(1)

$$B^s=\left\{B_i|B_i\in B \mathsf{\Lambda } I_i=1\right\}$$

(2)

$$r^r=r_{\pi }^c-r_{{\pi }^{,}}^c$$

(3)

$$P\left(I|\varphi \right)={\displaystyle \sum }_{j:B_j\in B^{batch}}{r}^r\nabla {\theta }^{\varphi }\left[I_i\log \varphi +\left(1-I_i\right)\log \left(1-\varphi \right)\right]$$

(4)

where $\varphi$ denotes the function approximator and $B_i$ is a transition in the replay buffer $B$. ${\theta }^{\varphi }$ denotes the parameters of $\varphi$, $f_{B_i}$ is a feature vector, and N is the number of transitions in a mini-batch. The priority score function is expressed as $\varphi \left(f_{B_i}|{\theta }^{\varphi }\right)\in \left(0,1\right)$, with the priority score represented by Lambda $\left(\lambda \right)$. $I_i \in \left\{0,1\right\}$ is a Bernoulli distribution of sample $B^s$. The replay reward, cumulative reward of current policy, and cumulative reward of previous policy are denoted as $r^r,$ $r_{\pi }^c$, and $r_{{\pi }^{\prime }}^c$ respectively.

Table 2. Symbols and notations used in this section.

Notation	Explanation
$\varphi$	Function approximator
$B$	Replay buffer
$B_i$	A transition in the replay buffer B
${\theta }^{\varphi }$	Parameters of the function approximator
$f_{B_i}$	Feature vector
$\lambda$	Priority score
$r^r$	Cumulative reward
$r_{\pi }^c$	Cumulative reward of current policy
$r_{{\pi }^{\prime }}^c$	Cumulative reward of previous policy
$B^s$	A specified batch size of sampled transitions

3.1.2. Alternating Transition Selection Framework

Since Lin [6] introduced experience replay in his reinforcement learning research, many strategies have evolved for experience selection and retention. Most of these strategies use a single buffer. However, in recent times, researchers have been exploring the use of dual memory for experience replay. Consequently, we design and investigate an alternating selection strategy that harnesses the strength of ERO and dual memory. Figure 3 and Figure 4 show the design of two experience replay optimisation with alternating transition selection control (ERO-ATSC) frameworks; Figure 4 has a TSC but Figure 3 does not.

Figure 3. Framework 1: this framework combines experience replay optimisation (ERO) with a dual memory and an alternating transition selection control (ERO-ATSC) without a transition storage control (TSC) mechanism. Transitions from the environment are stored in only H1. When a specified mini-batch size is reached, the replayed transitions from H1 are stored in H2. The ATSC uses a defined ratio to sample a mini-batch of transitions from either H1 or H2 into the replay policy network. These transitions are vectorised and prioritised and uniformly sampled at random to train the agent. Feedback from the training environment is sent to the replay policy network for policy evaluation.

Figure 4. Framework 2: this framework combines experience replay optimisation (ERO) with a dual memory and an alternating transition selection control (ERO-ATSC) with a transition storage control (TSC) mechanism. Transitions from the environment are stored in only H1. When a specified mini-batch size is reached, the replayed transitions from H1 are stored in H2. The ATSC uses a defined ratio to sample a mini-batch of transitions from either H1 or H2 into the replay policy network. These transitions are vectorised and prioritised and uniformly sampled at random to train the agent. Feedback from the training environment is sent to the replay policy network for policy evaluation.

In the first framework, the double experience replay (DER) strategy, proposed by Han et al. [17], is combined with the ERO’s replay policy. We store transitions from the environment into only H1. When replay begins in H1, the replayed transitions from H1 are stored in H2. Subsequently, the ATSC uses a predetermined ratio to sample a mini-batch of transitions from either H1 or H2. The mini-batch is further vectorised, prioritised by the replay policy, and uniformly sampled to train the agent. Afterwards, the replay policy takes feedback from the training environment to assess its performance.

Conversely, in the second framework, as indicated in Figure 4 and elaborated with Algorithm 1, we alter the DER strategy with the addition of a TSC mechanism. We store only transitions that meet the TSC threshold into H2 instead of the replayed data from H1. We store transitions from the environment into the replay buffers H1 or H2 or both depending on how well they meet the storage threshold. When a transition meets a specified reward threshold of the TSC, it is stored in both buffers. However, if the transition does not meet the required threshold, it is only stored in H1. Again, at a specific sampling ratio, the ATSC samples a mini-batch of transitions from either H1 or H2. These transitions are vectorised and prioritised by the replay policy and uniformly sampled for training the agent. After training, the replay policy receives feedback for policy evaluation.

Algorithm 1: ERO-ATSC with TSC

Given:       An off-policy RL algorithm DDPG Sampling strategies (S1, S2) from replay where: S1 and S2 samples with ERO       Return strategies (F1, F2) where F1 and F2 are FIFO and Enhanced-FIFO Reward threshold (Rt), sampling ratio ($\lambda$), mini-batch size (Mb)

1: Initialise DDPG and replay buffer H1, H2

2: observe state (S0) and choose action (a0) using DDPG

3:  for episode =1, M do

4:       observer (st; rt; st+1)

5:       store transition (st, at, rt, st+1) in H1 to follow ERO

6:       if rt > Rt then

7:             store transition (st, at, rt, st+1) in H2 to follow ERO

8:       end if

9:       for t = 1; T do

10:             if size (H2) > Mb then

11:                     with S1, S2, and sampling ratio λ, sample transition from                       H1 and H2

12:             else

13:                      with S1, sample transition from H1

14:             end if

15:            update weight according to DDPG

16:     end for

17:     if H1 is full then

18:         use F2

19:     end if

20:     if H2 is full then

21:         use F1

22:     end if

23: end for

4. Method

In this section, we detail the experimental environment and the configuration settings used in our experiments.

4.1. Environmental Setup

To evaluate, compare, and confirm the efficiency of our frameworks, we perform our experiments on the Pendulum-v0, a classical control environment on the OpenAI Gym [18] platform. OpenAI Gym is a software that offers a standard interface comprising multiple but different environments to help RL researchers. We opt for Pendulum-v0 because of its complex continuous task, suitable for the DDPG [9] algorithm. The Pendulum-v0 is a version of the classical inverted pendulum swing-up problem based on the classic control theory. It has a pendulum that requires a force at its free end to set it in motion. The agent’s focus is to repeatedly swing up the pendulum from its initial random position until it stands upright with its centre of gravity right above the fixed point. It has a continuous action space of −2.0 and 2.0 for its minimum and maximum force, respectively. It also has three continuous observation spaces made up of x and y co-ordinates and an angular velocity of the pendulum. While the angular velocity is between −8.0 and 8.0, the x and y co-ordinates have values that range between −1.0 and 1.0.

4.2. Parameter Settings

ERO extends the selection strategy of the vanilla DDPG algorithm with a novel replay policy using a single replay memory. This study extends the ERO algorithm with an alternating transition selection control mechanism and a dual memory. Nonetheless, the configurations and hyperparameters conform to ERO and the OpenAI DDPG stable baseline [34]. To improve our findings, experiments are conducted. Two threshold values are adopted and applied to perform ablative and additive experiments: the sampling ratio for the ATSC of both frameworks and the storage threshold for only the TSC in the second framework.

After performing preliminary experiments, TSC threshold values between −5 and −1 are identified and adopted. These values are negative because of the initial downward random position of the pendulum. The ATSC ratios are set to 90:10, 50:50, and 10:90 percentages stipulated in the DER experiment. The frameworks’ learning stability is evaluated on multiple buffer sizes of 1 × 10⁶ (1,000,000), 1 × 10⁵ (100,000), 1 × 10⁴ (10,000), and 1 × 10³ (1000). The FIFO and the enhanced FIFO retention strategies are equally assessed. In all, the experiments are conducted on an Intel(R) Xeon(R) CPU E3-1220 v6 @ 3.00 GHz (4CPUs) with 32 GB RAM and Windows Server 2012R2 operating system. The hyperparameters used are outlined in Table 3.

Table 3. Some parameters used in the implementation of the two frameworks.

Hyperparameter	Value
Batch size	64
Actor learning rate	1 × 10−4
Critic learning rate	1 × 10−3
Gamma	0.99
Eval steps	100
Eval episodes	10
Environment complexity (seed)	1 × 106

5. Results and Discussion

In this section, we commence our discussion with careful observation of the results from both frameworks. We then compare the performance of the two frameworks with a critical interest in the retention strategy used, the sampling ratio selected, and the choice of buffer size. In Table 4, we give clarity to the notations that are used in the presentation of the results.

Table 4. List of major notations.

Notation	Explanation
H1	The first replay buffer
H2	The second replay buffer
F1	First-In-First-Out (FIFO)
F2	Enhanced FIFO
F1F1	Both H1 and H2 use F1
F1F2	H1 uses F1 and H2 uses F2
F2F2	Both H1 and H2 use F2
F2F1	H1 uses F2 and H2 uses F1
R1	Experiences are selected from H1 and H2 with a ratio of 1:1
R2	Experiences are selected from H1 and H2 with a ratio of 9:1
R3	Experiences are selected from H1 and H2 with a ratio of 1:9

The discussion in this section commences with careful observation of the results from both frameworks, followed by a performance comparison of the two frameworks with a critical interest in the retention strategy used, the sampling ratio selected, and the choice of buffer size. Firstly, we conduct multiple experiments on Framework 1 across the three sampling ratios, the four dual retention strategies, and the four replay buffer sizes. Since the aim of the agent is to accumulate rewards, the frameworks are evaluated based on the mean returns, which is a summation of all rewards during an episode (subsequences of agent–environment interactions) divided by the number of episodes. The bigger the return, the better the performance. Equations (5) and (6) show how the mean return is computed:

$$G_t=R_{t+1}+R_{t+2}+R_{t+3}+\dots +R_T$$

(5)

$$\mathrm{Mean} \mathrm{return}=\frac{G_t}{Number of episodes}$$

(6)

where $G_t$ is the return, $R_{t+1}$ is the reward at time step t, and T is the final time step.

From Figure 5a–d, we observe that, while the sampling ratio of 1:1 records the worst return, the sampling ratio of 9:1 has the best and most consistent performance across the buffers and retention strategies. The output in these figures shows that Framework 1 is not heavily influenced by the retention strategy but by the sampling ratio. Thus, a higher selection frequency from a buffer with more diverse and recent transitions is essential for the stable performance of the RL agent. Additionally, the sampling ratio of 1:9 produces a rise in performance across the four retention strategies as the buffer size increases. The performance of the 1:1 sampling ratio declines for the F1F2 and the F2F2 strategies as the buffer size moves from 1 × 10⁵ to 1 × 10⁶.

Figure 5. Performance of Framework 2 across multiple buffer sizes, retention strategies, and sampling ratios. (a) Framework 1 is evaluated using the FIFO for both replay buffers; (b) Framework 1 is evaluated using FIFO for the first replay buffer and enhanced FIFO for the second replay buffer; (c) Framework 1 is evaluated using enhanced FIFO and FIFO for the first and second replay buffers, respectively; (d) Framework 1 is evaluated using enhanced FIFO for both replay buffers.

The second set of experiments follows the same setting as the previous experiments but includes a TSC threshold. The implementation begins with a reward threshold and continues with a TDE threshold. After multiple implementations of Framework 2 with reward thresholds from −1 to −5, the reward of −1 is selected, since it generates the median return across the four retention mechanisms. Subsequently, an equal number of multiple experiments are conducted, and the results are shown in Figure 6a–d. Again, the sampling ratio of 9:1 displays the best and most consistent performance across the four buffer sizes. The ratio of 1:1 still demonstrates the minimum performance with an apparent declining return on the F1F2 retention strategy. This scenario occurs for buffer sizes from 1 × 10⁴ to 1 × 10⁶. Thus, it is instructive to note that an equal rate of experience selection from both replay buffers, especially in the first framework, is not healthy for the successful training of the RL agent.

Figure 6. Performance of Framework 2 across multiple buffer sizes, retention strategies, and sampling ratios. (a) Framework 2 is evaluated using the FIFO retention strategy for both replay buffers; (b) Framework 2 is evaluated using FIFO for the first replay buffer and enhanced FIFO for the second replay buffer; (c) Framework 2 is evaluated using enhanced FIFO and FIFO for the first and second replay buffers, respectively; (d) Framework 2 is evaluated using enhanced FIFO for both replay buffers.

After identifying the superiority of Framework 2 over Framework 1, an evaluation of the former is repeated but with a TDE threshold. The implementation occurs with the exact buffer sizes and retention strategies but with a 9:1 sampling ratio and a threshold of |TDE| < 1. This approach is more flexible and easily applicable for continual learning; it does not require the foreknowledge of a reward function to implement the TSC threshold. Focusing on our objectives and upon establishing that the sampling ratio of 9:1 has the best performance in both frameworks, the memory and retention strategy results are extracted and analysed. Table 5 and Table 6 present the compared results of Framework 1 and the two versions of Framework 2. We ascertain the framework with the most stable results across buffer sizes by computing the average returns across the four buffer sizes. As shown in Table 5, the F2F1 retention strategy proves superior and serves as a basis for comparing the performance of the frameworks across all four buffer sizes.

Table 5. The average performance of the frameworks across the buffer sizes with a sampling ratio of 9:1.

Frameworks	F1F1	F1F2	F2F1	F2F2
Framework 1	−188.42	−191.34	−177.50	−206.28
Framework 2 (Reward)	−180.103	−179.95	−170.71	−180.31
Framework2 (TDE)	−192.87	−192.56	−170.18	−172.47

Table 6. The performance of the 9:1 sampling ratio on the frameworks across multiple buffer sizes using the F2F1 retention strategy.

Frameworks	1 × 106	1 × 105	1 × 104	1 × 103
Framework 1	−188.28	−156.43	−182.50	−182.76
Framework 2 (Reward)	−155.43	−155.46	−-179.53	−192.42
Framework2 (TDE)	−157.58	−160.97	−173.80	−188.39

Despite their competitive performance, as indicated in Figure 7 and Table 7, the reward version of the proposed framework outperforms the others. This is because the TSC ensures that more relevant transitions are selected for storage and training. It equally ensures a better distribution of transitions to prevent overfitting and underfitting during the agent’s training. In effect, it boosts the generalisation of the framework. Additionally, the ATSC coupled with the dual memory promote complementary and stable learning. While the dual memory offers a more diverse storage of transitions, the ATS timeously alternate the selection of these transitions for learning. It is also insightful to note that a wrong choice of retention strategy or sampling ratio can hamper the performance of the framework.

Figure 7. Performance of algorithms on the Pendulum-v0 environment.

Table 7. The performance of Framework 2 using the F2F1 retention strategy, a sampling ratio of 9:1, and a replay buffer of 1e6 across other continuous environments.

Environments	Framework 2 (Reward)	Framework 2 (TDE)
Pendulum-v0	−155.43	−157.58
MountainCarContinuous-v0	−1.86	−1.87
LunarLanderContinuous-v2	−20.77	−32.02
BipedalWalker-v3	−6.60	−131.83

It can be observed in Table 6 that both versions of Framework 2 have a higher average return than Framework 1 and, accordingly, show a more consistent growth as the buffer size increases from 1 × 10³ to 1 × 10⁶. Nonetheless, it can be argued that identifying the suitable reward threshold for a continuous state-action problem can be very challenging and time-consuming, especially for problems with complex reward functions. Under such conditions, a TDE threshold will be a better option.

6. Conclusions

The significant finding of our study is that a dual memory with an alternating transition selection strategy can improve the stability of the deep deterministic policy gradient (DDPG) algorithm across multiple buffer sizes. The experience replay optimisation (ERO) and dual-memory experience replay (DER) methods are combined to formulate the experience replay optimisation via alternating transition selection control (ERO-ATSC) with transition storage control (TSC) and the ERO-ATSC without TSC frameworks. The frameworks are further evaluated on different buffer sizes, sampling ratios, and experience retention strategies. The findings reveal that a sampling ratio of 9:1 and a retention strategy of F2F1 (first replay buffer uses enhanced FIFO and the second buffer uses FIFO) produce the steadiest average performance across the four buffer sizes. Though both versions of ERO-ATSC with TSC have competitive results and demonstrate the highest performance among the evaluated algorithms, the reward version proves superior in reward accumulation. In future, we hope to extend the proposed framework (ERO-ATSC with TSC) to automatically predict the reward threshold.