Nonlinear Vibrations of Carbon Nanotubes with Thermal-Electro-Mechanical Coupling

Abstract

Carbon nanotubes (CNTs) have wide-ranging applications due to their excellent mechanical and electrical properties. However, there is little research on the nonlinear mechanical properties of thermal-electro-mechanical coupling. In this paper, we study the nonlinear vibrations of CNTs by a thermal-electro-mechanical coupling beam theory. The Galerkin method is used to discretize the partial differential equation and obtain two nonlinear ordinary differential equations that describe the first- and second-order mode vibrations. Then, we obtain the approximate analytical solutions of the two equations for the primary resonance and the subharmonic resonance using the multi-scale method. The results indicate the following three points. Firstly, the temperature and electric fields have a significant influence on the first-mode vibration, while they have little influence on the second-mode vibration. Under the primary resonance, when the load amplitude of the second mode is 20 times that of the first mode, the maximal vibrational amplitude of the second is only one-fifth of the first. Under the subharmonic resonance, it is more difficult to excite the subharmonic vibration at the second-order mode than that of the first mode for the same parameters. Secondly, because the coefficient of electrical expansion (CEE) is much bigger than the coefficient of thermal expansion (CTE), CNTs are more sensitive to changes in the electric field than the temperature field. Finally, under the primary resonance, there are two bifurcation points in the frequency response curves and the load-amplitude curves. As a result, they will induce the jump phenomenon of vibrational amplitude. When the subharmonic vibration is excited, the free vibration term does not disappear, and the steady-state vibration includes two compositions.

1. Introduction

In 1991, carbon nanotubes (CNTs) were discovered by Iijima [1], and their excellent mechanical, chemical, electrical properties have since, extensively attracted the attention of researchers [2,3,4,5,6]. CNTs are formed by the crimping of graphene sheets in a particular direction. Moreover, researchers observed the flexoelectric effect in CNTs [7]. The lattice of graphene is symmetrical, and the uniform deformation of graphene will not lead to polarization. When graphene is curling into CNTs, the symmetry of the lattice may break and may induce the piezoelectric effect. The second-order flexible electric effect in graphene can be caused by the strain gradient. In fact, the strain gradient changes the position of ions, leading to the asymmetric redistribution of electron density [8,9]. Ahmadi has described in detail the zigzag and armchair $\gamma$-graphene-acetylene nanotubes using the Density functional theory function and non-equilibrium Green’s function methods. He also reported the application prospect of these devices in nano transistors and switching memory circuits [10,11,12]. At the same time, CNTs also have technical potential in field emission, nano-electronic devices, micro-electro-mechanical system, biosensing, high-frequency nanoelectronics, and so on [13,14,15,16,17]. These applications are used in many physical fields, such as temperature and electrostatic fields. Tombler’s results show that, when CNTs are deformed under a transverse concentrated load, their conductivity decreases greatly [18]. This experiment is of great significance, showing that the coupling effect should be specially considered [19]. CNTs can be employed in a variety of technical applications when combined with a polymer composite material to create carbon nanotube-reinforced composites [20]. In these applications, the influence of the temperature field is usually accompanied. However, it is necessary to comprehensively research the thermal-electro-mechanical coupling of CNTs [21]. Because CNTs are curled by graphene and the thickness of graphene is uncertain, the stiffness of CNTs cannot be determined by the classical beam model. This means that the bending and stretching stiffness must be considered separately [22,23,24]. For example, Huang established a thermal-electro-mechanical coupling nanobeam model of CNTs with independent bending and stretching stiffness [23]. This nanobeam model describes the axial load and radial load of the beam. Generally, when the beam is subjected to axial load and radial load, curvature and axial strain will occur [25].

From the above discussion, one can find that CNTs have extensive applications. However, their mechanical properties under the multi-field coupling conditions have received little attention. For example, the deformations of CNTs when the ambient temperature and the applied voltage at both ends of the beam change have not been studied in depth thus far. However, this is common in nanoelectromechanical systems. In fact, Huang [23] proposed a beam model for the first time to describe the mechanical properties of a CNT under thermal and electric fields.

This paper will further analyze the model proposed by Huang [23]. Because it is difficult to solve partial differential equations, the Galerkin method [26] is used to discretize the partial differential equation into ordinary differential equations. The accuracy of the Galerkin truncation depends on the order of truncation. Therefore, the first-order and second-order mode vibration equations of the partial differential equation are used in this paper. We will solve the two vibration equations using the multi-scale method [27,28]. The steady-state solutions response to the primary resonance and the subharmonic resonance are obtained. The effect of temperature and electric fields on steady-state motion can be discovered by the analytical solutions. The accuracy of the solutions is checked by numerical calculations.

The main motivation of this paper is to study the nonlinear vibrations of carbon nanotubes with thermal-electro-mechanical coupling. In Section 2, the Galerkin method is used to obtain the reduced-order model of nanobeam. In Section 3, the multi-scale method is used to obtain approximate solutions of the main resonance and subharmonic resonance of nanobeam. In Section 4, the influence of the temperature and electric field on the system is discussed by the approximate solutions. We summarize the results in Section 5.

2. Materials and Methods

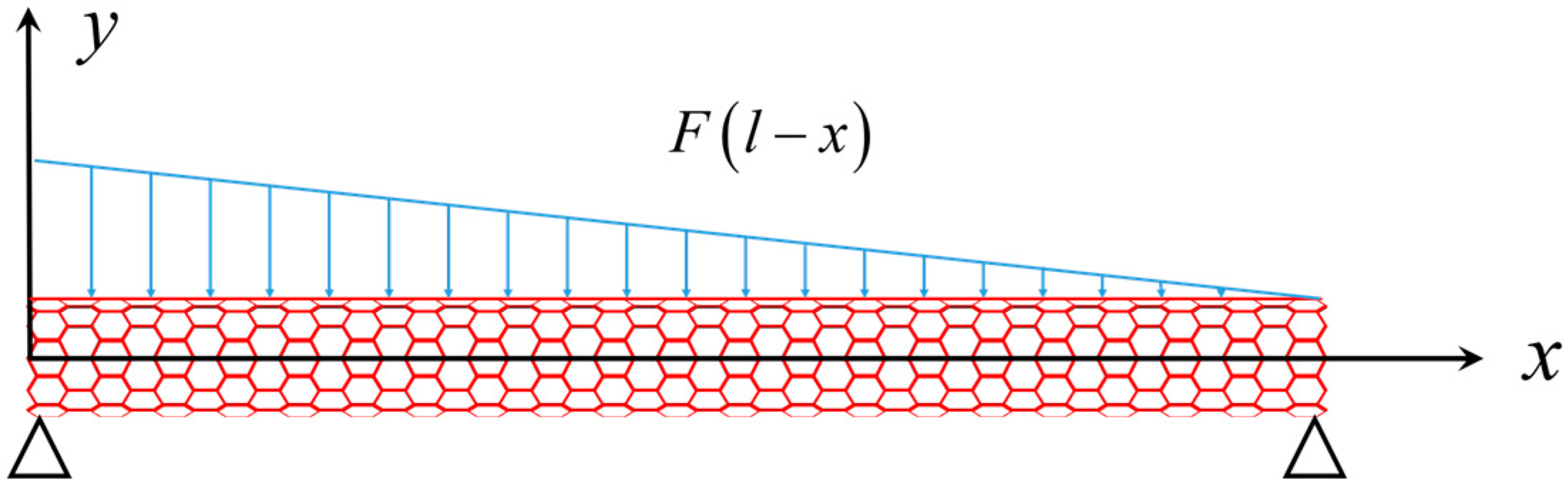
Thermal-Electro-Mechanical Coupling Beam Model of CNTs

In Reference [23], Huang expanded the deformation energy in extensional stiffness, bending stiffness, the CEE, and the CTE. Then, using the Hamiltonian principle, he obtained a partial differential equation that models the dynamical properties of CNTs with thermal-electro-mechanical coupling. The equation can be shown as:

$$\begin{array}{l}m\frac{{\partial }^{2}w}{\partial t^2}+k_S\left(k_{U}U+k_{T}T\right)\frac{{\partial }^{2}w}{\partial x^2}+k_B\frac{{\partial }^{4}w}{\partial x^4}-\frac{k_S\left(1+k_{U}U+k_{T}T\right)}{2l^2}\frac{{\partial }^{2}w}{\partial x^2}\underset{0}{\overset{l}{\int }}{\left(\frac{\partial w}{\partial x}\right)}^{2}dx\\ -k_B\{12\frac{\partial w}{\partial x}\frac{{\partial }^{2}w}{\partial x^2}\frac{{\partial }^{3}w}{\partial x^3}+3{\left(\frac{\partial w}{\partial x}\right)}^2\frac{{\partial }^{4}w}{\partial x^4}+3{\left(\frac{{\partial }^{2}w}{\partial x^2}\right)}^3\}=f\left(x,t\right).\end{array}$$

(1)

Here $m$ is the mass per unit length of CNTs; $l$ is the length of CNTs; $k_S$ is the extensional stiffness; $k_B$ is the bending stiffness; $k_U$ is the CEE; and $k_T$ is the CTE. Normally, there is no piezoelectric effect in isotropic materials [29]. However, if graphene is curled into CNTs, its hexagonal symmetry will be distorted and may cause the piezoelectric effect of tubes. This causes strain due to the external electric field, and the strain is proportional to the field strength [30].

Equation (1) is the plane motion equation of CNTs. If a CNT is treated as a beam with two hinged ends, its boundary conditions are:

$$w=\frac{{\partial }^{2}w}{\partial x^2}=0,\hspace{1em}at\hspace{1em}x=0,l.$$

(2)

We can add a linear damping term $\overline{C}{\partial }^{5}w/\partial t\partial x^4$ to Equation (1) to obtain the equation of motion with damping dissipation as:

$$\begin{array}{l}m\frac{{\partial }^{2}w}{\partial t^2}+\overline{C}\frac{{\partial }^{5}w}{\partial t\partial x^4}+k_S\left(k_{U}U+k_{T}T\right)\frac{{\partial }^{2}w}{\partial x^2}\\ +k_B\frac{{\partial }^{4}w}{\partial x^4}-\frac{k_S\left(1+k_{U}U+k_{T}T\right)}{2l^2}\frac{{\partial }^{2}w}{\partial x^2}{{\displaystyle \underset{0}{\overset{l}{\int }}\left(\frac{\partial w}{\partial x}\right)}}^{2}dx\\ -k_B\{12\frac{\partial w}{\partial x}\frac{{\partial }^{2}w}{\partial x^2}\frac{{\partial }^{3}w}{\partial x^3}+3{\left(\frac{\partial w}{\partial x}\right)}^2\frac{{\partial }^{4}w}{\partial x^4}+3{\left(\frac{{\partial }^{2}w}{\partial x^2}\right)}^3\}=f\left(x,t\right).\end{array}$$

(3)

Sakharova used molecular dynamics calculations to obtain the following parameters: extensional stiffness $k_s=\alpha \left(d-d_0\right)$ and bending stiffness $k_B=\beta {\left(d-d_0\right)}^3$, where $\alpha =1128.15\mathrm{nN}/\mathrm{nm}$, and $\beta =142.54\mathrm{nN}/\mathrm{nm}$ [2]. In this paper, we will take $\left(10,10\right)$ single walled carbon nanotubes (SWCNTs) as an example. Therefore, the tube’s diameter is $d=1.356\mathrm{nm}$, and the parameter $d_0=2.7\times {10}^{-7}\mathrm{nm}$. Because the $d_0$ is much smaller than tube’s diameter $d$, we use $d_0=0$. This makes $k_S=1.53\times {10}^3\mathrm{nN}$ and $k_B=0.355\times {10}^3\mathrm{nN}\cdot {\mathrm{nm}}^2$. The CTE is $k_T=6.0\times {10}^{-6}{\mathrm{K}}^{-1}$ from Reference [31], and the CEE is $k_U=0.025\mathrm{nm}/\mathrm{V}$, which is obtained through the linear fitting FDT calculations [30].

For convenience, we reduce Equation (3) to a dimensionless form. Letting $\tilde{w}=w/l,\tilde{x}=x/l,\tilde{t}={\omega }_{0}t$, we obtain:

$$\begin{array}{l}P\frac{{\partial }^2\tilde{w}}{\partial {\tilde{x}}^2}+Q\frac{{\partial }^4\tilde{w}}{\partial {\tilde{x}}^4}+C\frac{{\partial }^5\tilde{w}}{\partial \tilde{t}\partial {\tilde{x}}^4}+R\frac{{\partial }^2\tilde{w}}{\partial {\tilde{x}}^2}{{\displaystyle \underset{0}{\overset{l}{\int }}\left(\frac{\partial \tilde{w}}{\partial \tilde{x}}\right)}}^{2}dx\\ -S\{12\frac{\partial \tilde{w}}{\partial \tilde{x}}\frac{{\partial }^2\tilde{w}}{\partial {\tilde{x}}^2}\frac{{\partial }^3\tilde{w}}{\partial {\tilde{x}}^3}+3{\left(\frac{\partial \tilde{w}}{\partial \tilde{x}}\right)}^2\frac{{\partial }^4\tilde{w}}{\partial {\tilde{x}}^4}+3{\left(\frac{{\partial }^2\tilde{w}}{\partial {\tilde{x}}^2}\right)}^3\}=\overline{f}\left(x,t\right),\end{array}$$

(4)

Here,

$$\begin{array}{l}P=\frac{k_S\left(k_{U}U+k_{T}T\right)}{m{\omega }_0^2{l}^2},\hspace{1em}R=\frac{k_S\left(1+k_{U}U+k_{T}T\right)}{2m{\omega }_0^2{l}^2},\\ Q=\frac{k_B}{m{\omega }_0^2{l}^4},\hspace{1em}S=\frac{k_B}{m{\omega }_0^2{l}^6},\hspace{1em}C=\frac{\overline{C}}{m{\omega }_0{l}^4}.\end{array}$$

(5)

To reveal the load’s influence on the second-order mode, we consider a linear load $F\left(l-x\right)$, as shown in Figure 1:

In this paper, we will focus on the nonlinear mechanical properties of $\left(10,10\right)$ SWCNT with thermal-electro-mechanical coupling. Dimensionless Equation (4) is a partial differential equation. It is difficult to find an accurate analytical solution for the equation. Therefore, we use the Galerkin method [26] to obtain an approximate solution. We assume that the solution of the equation is:

$$\tilde{w}={\displaystyle \sum _{j=1}^n{\eta }_j\left(t\right)\sin \left(j\pi x\right)}.$$

(6)

For the analysis of the first and second order mode, we take $n=2$ in Equation (6) and substitute it into Equation (4). Then, we multiply $\sin \left(\pi x\right)$ on the two sides of the equation and the interval integral in $\left[0,1\right]$ (the Galerkin integral [26,32]) to obtain the vibrational equation of the first mode. That of the second mode can be obtained by multiplying $\sin \left(2\pi x\right)$ on the two sides, then, the integral in $\left[0,1\right]$. Therefore, we obtain the following equations:

$$\begin{array}{l}{\ddot{\eta }}_1+c_1{\dot{\eta }}_1+k_{11}{\eta }_1+k_{12}{\eta }_1{\eta }_2^2+k_{13}{\eta }_1^3=F_1,\\ {\ddot{\eta }}_2+c_2{\dot{\eta }}_2+k_{21}{\eta }_2+k_{22}{\eta }_1^2{\eta }_2+k_{23}{\eta }_2^3=F_2.\end{array}$$

(7)

In Equation (7), the dot on the letter indicates the derivative in time. The parameters of Equation (7) are:

$$\begin{array}{l}{k}_{11}=1-\frac{{\pi }^2{k}_S\left(k_{U}U+k_{T}T\right)}{m{\omega }_0^2{l}^2},\hspace{1em}{k}_{12}=\frac{{\pi }^4{k}_S\left(1+k_{U}U+k_{T}T\right)}{m{\omega }_0^2{l}^4}-\frac{30{\pi }^6{k}_B}{m{\omega }_0^2{l}^6},\\ k_{13}=\frac{{\pi }^4{k}_S\left(1+k_{U}U+k_{T}T\right)}{4m{\omega }_0^2{l}^4}-\frac{3{\pi }^6{k}_B}{2m{\omega }_0^2{l}^6},\hspace{1em}{F}_1=\frac{4}{ml{\omega }_0^2\pi }f,\\ k_{21}=16-\frac{4{\pi }^2{k}_S\left(k_{U}U+k_{T}T\right)}{m{\omega }_0^2{l}^2},\hspace{1em}{k}_{22}=\frac{{\pi }^4{k}_S\left(1+k_{U}U+k_{T}T\right)}{m{\omega }_0^2{l}^4}-\frac{30{\pi }^6{k}_B}{m{\omega }_0^2{l}^6},\\ k_{23}=\frac{4{\pi }^4{k}_S\left(1+k_{U}U+k_{T}T\right)}{m{\omega }_0^2{l}^4}-\frac{96{\pi }^6{k}_B}{m{\omega }_0^2{l}^6},\hspace{1em}{F}_2=\frac{2}{ml{\omega }_0^2\pi }f,\\ c_1=\frac{\overline{C}}{m{\omega }_0{l}^4},\hspace{1em}{c}_2=\frac{16\overline{C}}{m{\omega }_0{l}^4},\hspace{1em}{c}_2=16c_1.\end{array}$$

(8)

From the buckling theory of elastic columns, one can know that the CNTs will lose stability if $k_{11}=0$. This case means that the critical temperature is a function of the critical electric field and critical length, as shown in Figure 2.

We can find from Figure 2 that the electric field has a greater impact on the thermal-electro-mechanical coupling model of CNTs than the temperature field due to $k_U\gg k_T$. This means that the electric field has an outstanding influence on the stiffness of CNTs. From the data of quantum calculations, the CEE is always bigger than the CTE. For example, using Hartree-Fock and density functional quantum mechanics simulations [30], Guo obtained a CEE of about $k_U=0.025 \mathrm{nm}/\mathrm{V}$. However, Jiang obtained a CTE of about $6.0\times {10}^{-6} {\mathrm{K}}^{-1}$ [31] through the nonequilibrium Green’s function method. In fact, the source of thermal or electrical expansion may require further theoretical and experimental research.

3. Results

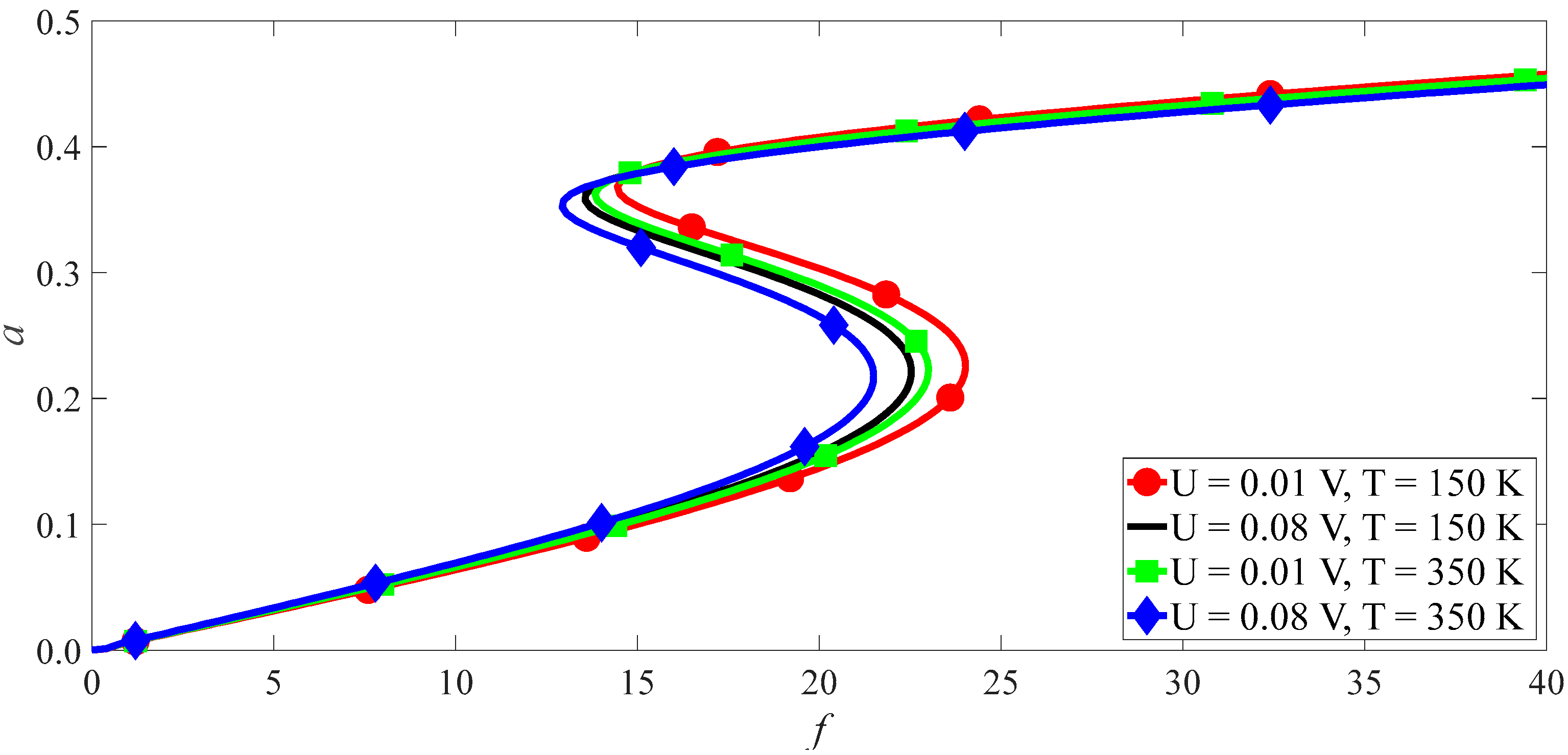
3.1. Primary Resonance of SWCNTs

When $\mathrm{\Omega }$ is close to ${\omega }_j$ and there is no internal resonance between the two modes, vibrations of the two model are uncoupled. Therefore, the coupling term of Equation (7) can be removed [28] and the equation is rewritten as:

$${\ddot{\eta }}_j+c_j{\dot{\eta }}_j+k_{j1}{\eta }_j+k_{j3}{\eta }_j^3=F_j\cos \mathrm{\Omega }t,\hspace{1em}j=1,2.$$

(9)

For the study of primary resonance, we introduce $\epsilon$ for perturbation, where $\epsilon$ is a small parameter. Here, $\epsilon =0.01$ is used, and Equation (9) is rewritten as

$${\ddot{\eta }}_j+{\omega }_j^2{\eta }_j+2\epsilon {\overline{c}}_j{\dot{\eta }}_j+\epsilon {\overline{k}}_{j3}{\eta }_1^3=\epsilon f_j\cos \omega \overline{t},\hspace{1em}j=1,2.$$

(10)

Here, ${\omega }_j^2=k_{j1}$, and Equation (10) will be solved by the multi-scale method [32]. We expand ${\eta }_i$ as follows:

$${\eta }_j={\eta }_{j0}\left(T_0,T_1\right)+\epsilon {\eta }_{j1}\left(T_0,T_1\right)+\cdots .$$

(11)

In Equation (11), $T_0={\epsilon }^{0}t$, $T_1=\epsilon t$, and here, it is

$$\frac{\mathrm{d}}{dt}=D_0+\epsilon D_1,\hspace{1em}\frac{d^2}{d{t}^2}=D_0^2+2\epsilon D_0{D}_1+{\epsilon }^2{D}_1^2.$$

(12)

Substituting Equations (11) and (12) into Equation (10), and making the coefficients of the same order $\epsilon$ equal, we obtain [32]

$${\epsilon }^0:\hspace{1em}{D}_0^2{\eta }_{j0}+{\omega }_j^2{\eta }_{j0}=0.$$

(13)

$$\epsilon :\hspace{1em}{D}_0^2{\eta }_{j1}+{\omega }_j^2{\eta }_{j1}=-2D_0{D}_2{\eta }_{j0}-2{\overline{c}}_j{D}_0{\eta }_{j0}-{\overline{k}}_{j3}{\eta }_{j0}^3+\frac{1}{2}{f}_j\cos \left(\mathrm{\Omega }{T}_0\right).$$

(14)

Let the solution of the equation of order ${\epsilon }^0$ be:

$${\eta }_{j0}=A\left(T_1\right)\exp \left(i{\omega }_j{T}_0\right)+cc.$$

(15)

where $cc$ is the complex conjugate terms of the previous terms and $A_1$ is a real function of $T_1$. Substituting Equation (15) into Equation (14), we obtain

$$\begin{array}{cc}{D}_0^2{\eta }_{j1}+{\omega }_j^2{\eta }_{j1}& =\left[-2i{\omega }_j\left(A^{\prime }+{\overline{c}}_{j}A\right)-3{\overline{k}}_{j3}{A}^2\overline{A}\right]\exp \left(i{\omega }_j{T}_0\right)\\ & -{\overline{k}}_{j3}{A}^3\exp \left(3i{\omega }_j{T}_0\right)+\frac{1}{2}{f}_j\exp \left[i\left(\mathrm{\Omega }{T}_0\right)\right]+cc.\end{array}$$

(16)

where the apostrophe represents the derivative with respect to $T_1$. The dimensionless detuning parameter $\sigma$ is introduced to make the excitation frequency $\Omega ={\omega }_j+\epsilon \sigma$. We eliminate the secular term and obtain:

$$2i{\omega }_j\left(A^{\prime }+{\overline{c}}_{j}A\right)+3{\overline{k}}_{j3}{A}^2\overline{A}=\frac{1}{2}{f}_j\exp \left(i\sigma T_j\right).$$

(17)

Introducing a polar form for $A$, we obtain:

$$A=\frac{1}{2}a\exp \left(i\beta \right).$$

(18)

where $a$ and $\beta$ are real functions of $T_1$. Substituting Equation (18) into Equation (17), and separating the real part and imaginary part, we obtain:

$$\{\begin{array}{l}{a}^{\prime }=-{\overline{c}}_{j}a+\frac{1}{2{\omega }_j}{f}_j\sin \gamma \\ a{\beta }^{\prime }=\frac{3}{8}\frac{{\overline{k}}_{j3}}{{\omega }_j}{a}^2-\frac{1}{2{\omega }_j}{f}_j\cos \gamma .\end{array}$$

(19)

where $\gamma =\sigma T_1-\beta$. When $a^{\prime }={\beta }^{\prime }=0$, the steady state motion appears; therefore:

$$\{\begin{array}{l}0=-{\overline{c}}_{j}a+\frac{1}{2{\omega }_1}{f}_j\sin \gamma \\ a\sigma =\frac{3}{8}\frac{{\overline{k}}_{j3}}{{\omega }_j}{a}^3-\frac{1}{2{\omega }_j}{f}_j\cos \gamma .\end{array}$$

(20)

From Equation (20), we obtain

$$\left[{\overline{c}}_j^2+{\left(\sigma -\frac{3}{8}\frac{{\overline{k}}_{j3}}{{\omega }_j}{a}^2\right)}^2\right]a_j^2=\frac{f_j^2}{4{\omega }_j^2}.$$

(21)

Equation (21) indicates that the response amplitude $a$ is a function of $\sigma$ and the excitation amplitude $f_j$. Substituting Equation (18) into Equation (15), and then substituting the result into Equation (11), one can obtain the first order approximate solution of Equation (10).

$$u=a\cos (\mathrm{\Omega }t-\gamma )+O\left(\epsilon \right)=a\cos \left({\omega }_{j}t+\epsilon \sigma t-\gamma \right)+O\left(\epsilon \right).$$

(22)

Here, $a$ and $\sigma$ are given by Equation (21), and ${\omega }_j^2=k_{j1}$$\left(j=1,2\right)$.Therefore, from Equation (21), we can draw Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.

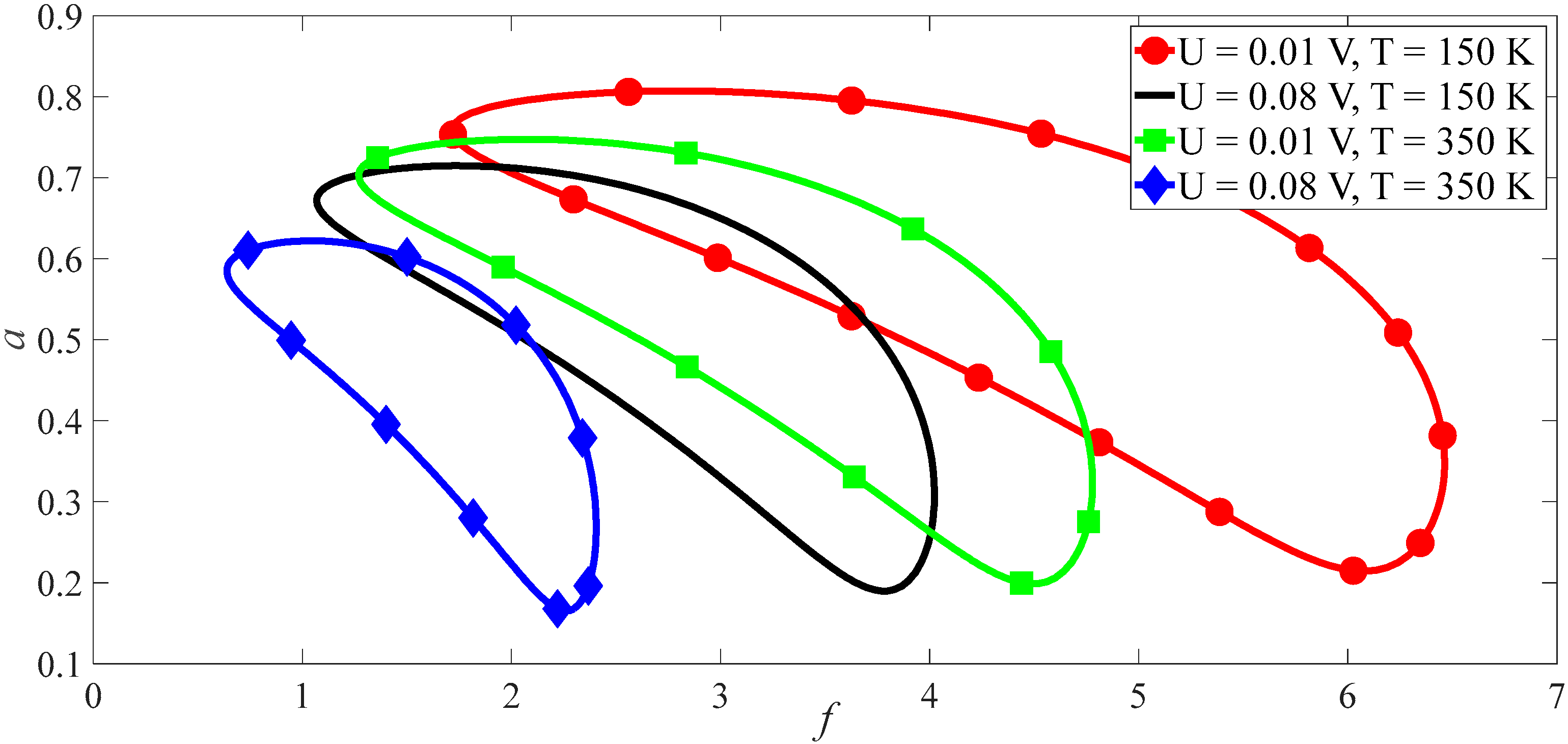
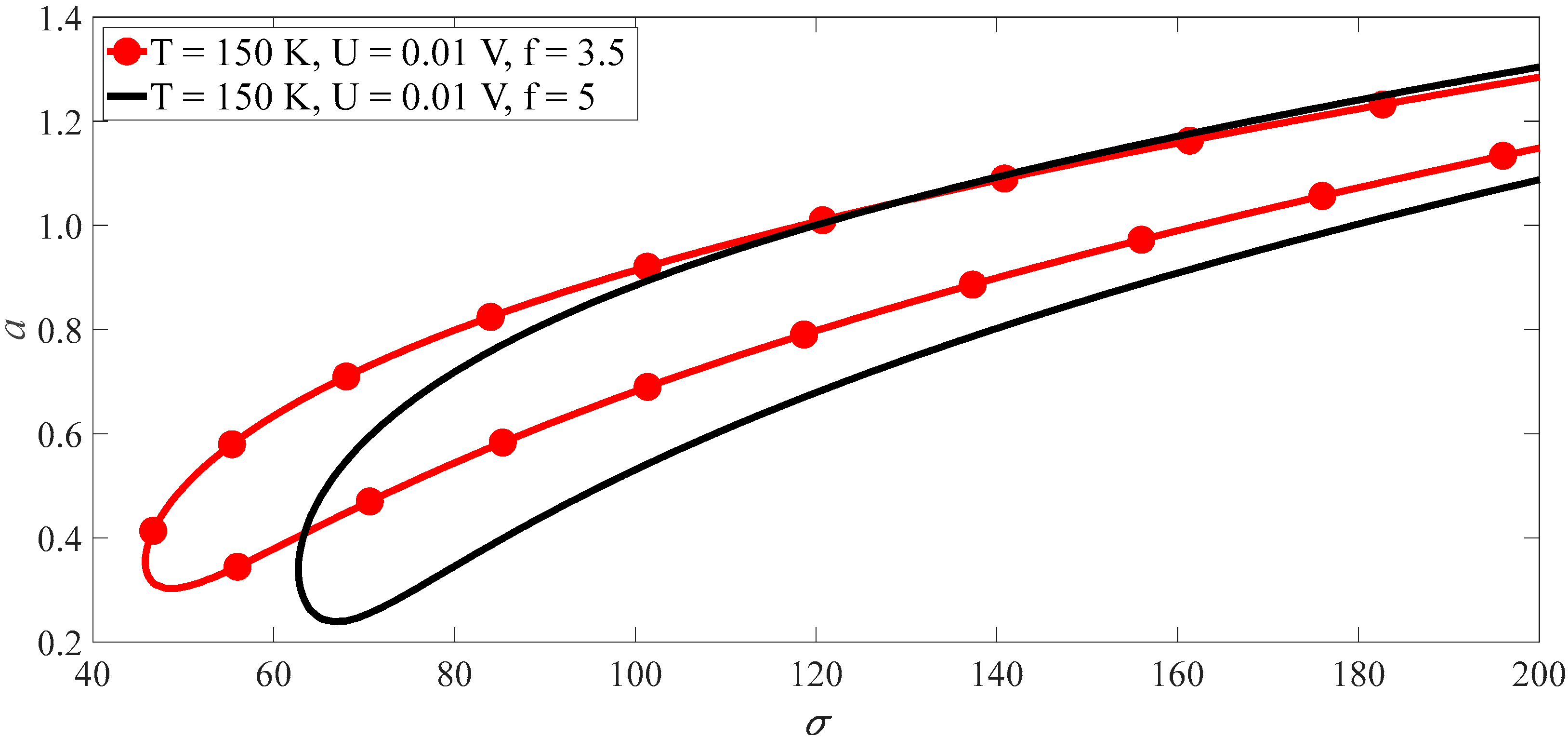
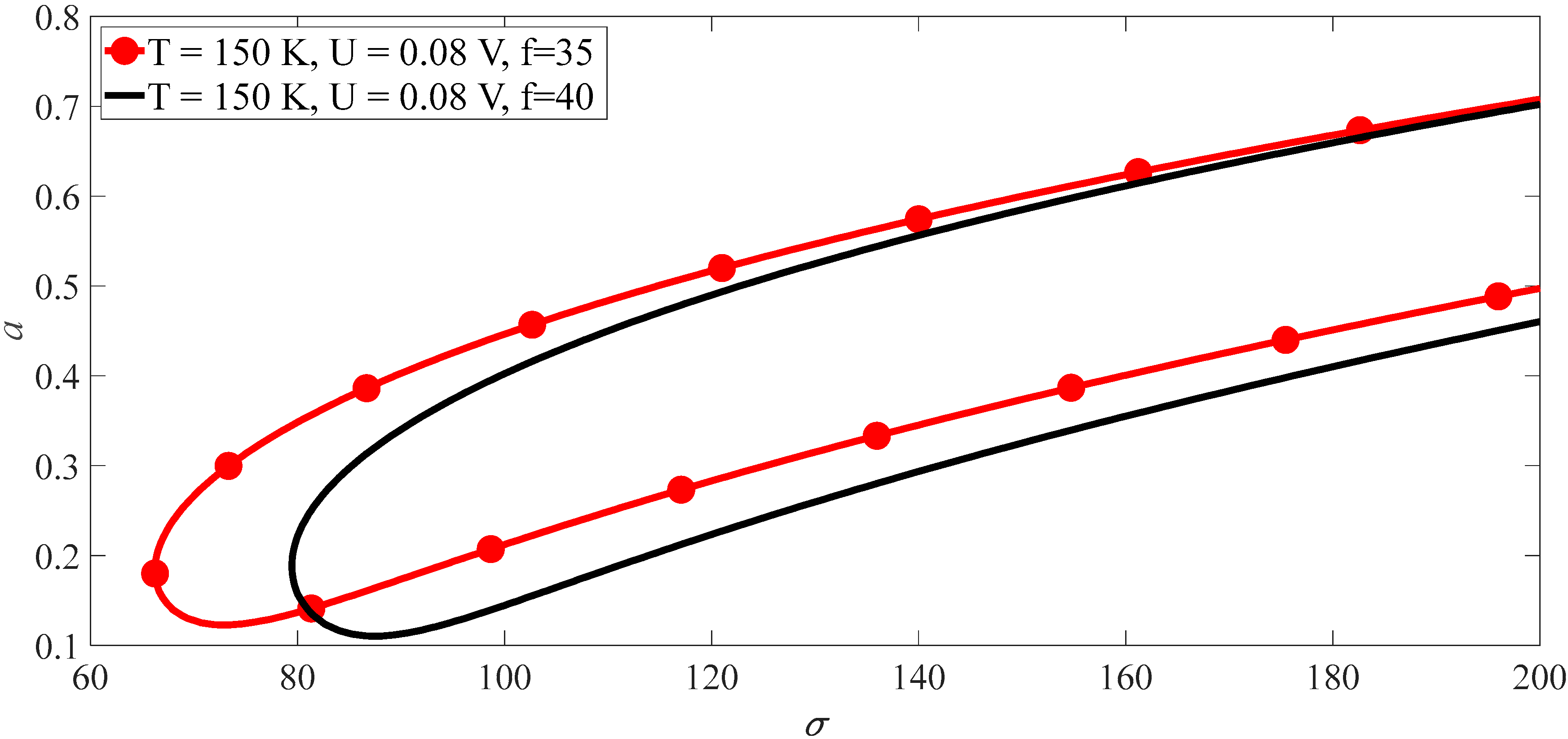
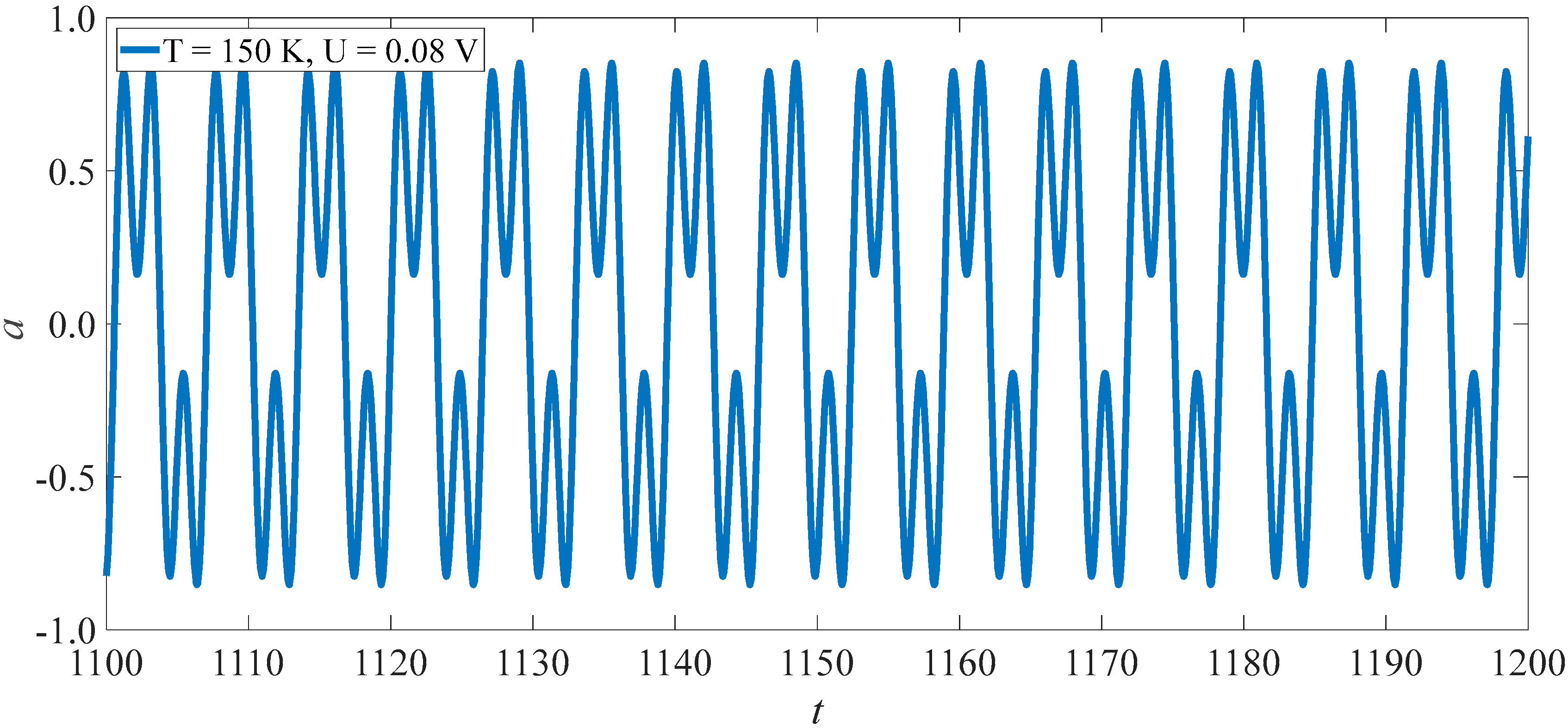
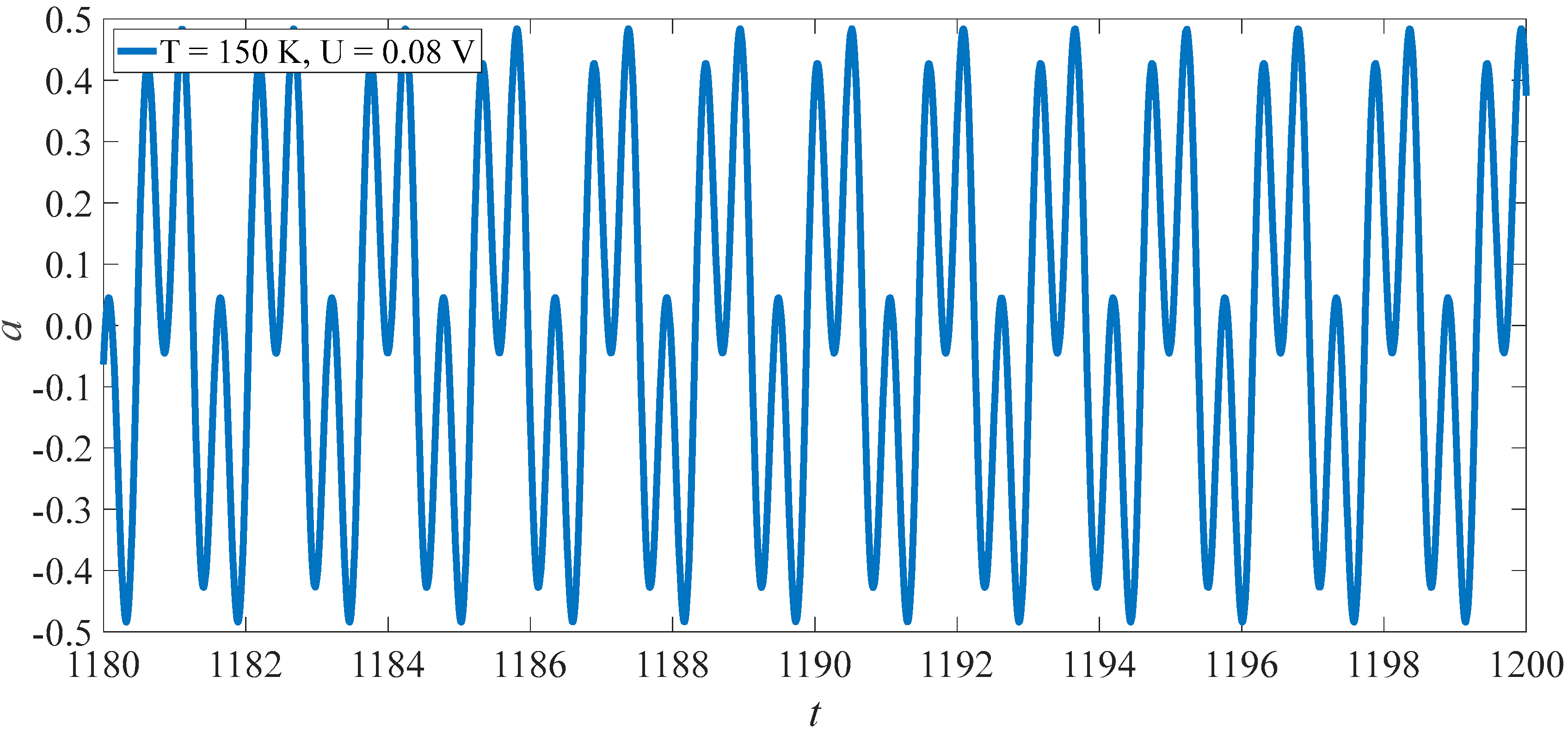
3.2. Subharmonics Resonance of SWCNTs

When $\mathrm{\Omega }$ is far away from ${\omega }_j$, a large vibrational amplitude requires a large exciting amplitude. In this paper, we will study the subharmonic resonant. Therefore, we rewrite Equation (9) as:

$${\ddot{\eta }}_j+{\omega }_j^2{\eta }_j+2\epsilon {\overline{c}}_j{\dot{\eta }}_j+\epsilon {\overline{k}}_{j3}{\eta }_1^3=f_j\cos \omega \overline{t},\hspace{1em}j=1,2.$$

(23)

The seeking form of the solution is:

$${\eta }_j={\eta }_{j1}\left(T_0,T_1\right)+\epsilon {\eta }_{j2}\left(T_0,T_1\right)$$

(24)

Substituting Equation (24) into Equation (23) and aking the coefficients of order $\epsilon$ equal, we obtain [32]:

$${\epsilon }^0:\hspace{1em}{D}_0^2{\eta }_{j1}+{\omega }_j^2{\eta }_{j1}=f_j\cos \left(\mathrm{\Omega }{T}_0+{\tau }_j\right)$$

(25)

$$\epsilon :\hspace{1em}{D}_0^2{\eta }_{j2}+{\omega }_j^2{\eta }_{j2}=-2D_0{D}_1{\eta }_{j1}-2{\overline{c}}_j{D}_0{\eta }_{j1}-{\overline{k}}_{j3}{\eta }_{j1}^3$$

(26)

The form of the solution of Equation (25) is:

$${\eta }_{j1}=A\left(T_1\right)\exp \left(i{\omega }_j{T}_0\right)+\mathrm{\Lambda }\left(T_1\right)\exp \left(i\mathrm{\Omega }{T}_0\right)+cc$$

(27)

where $cc$ stands for the complex conjugate of the preceding terms and $\mathrm{\Lambda }=\frac{1}{2}{f}_j{\left({\omega }_j^2-{\mathrm{\Omega }}^2\right)}^{-1}$. When Equation (27) is brought into Equation (26), we can obtain:

$$\begin{array}{l}{D}_1^2{\eta }_{j2}+{\omega }_j^2{\eta }_{j2}=-\left[2i{\omega }_j\left(A^{\prime }+{\overline{c}}_{j}A\right)+6{\overline{k}}_{j3}A{\mathrm{\Lambda }}^2+3{\overline{k}}_{j3}{A}^2\overline{A}\right]\exp \left(i{\omega }_j{T}_0\right)\\ -{\overline{k}}_{j3}\{A^3\exp \left(3i{\omega }_j{T}_0\right)+{\mathrm{\Lambda }}^3\exp \left(3i\mathrm{\Omega }{T}_0\right)+3A^2\mathrm{\Lambda }\exp \left(i\left(2{\omega }_j+\mathrm{\Omega }\right)T_0\right)\\ +3{\overline{A}}^2\mathrm{\Lambda }\exp \left(i\left(\mathrm{\Omega }-2{\omega }_j\right)T_0\right)+3A{\mathrm{\Lambda }}^2\exp \left(i\left({\omega }_j+2\mathrm{\Omega }\right)T_0\right)\\ +3A{\mathrm{\Lambda }}^2\exp \left(i\left({\omega }_j-2\mathrm{\Omega }\right)T_0\right)\}-\mathrm{\Lambda }\left[2i{\overline{c}}_j\mathrm{\Omega }+3{\overline{k}}_{j3}{\mathrm{\Lambda }}^2+6{\overline{k}}_{j3}A\overline{A}\right]\exp \left(i\mathrm{\Omega }{T}_0\right)+cc\end{array}$$

(28)

Introducing a dimensionless detuning parameter $\sigma$, the exciting frequency can be written as $\mathrm{\Omega }=3{\omega }_j+\epsilon \sigma$, and eliminating the duration terms of $\exp \left[i\left(\mathrm{\Omega }-2{\omega }_j\right)T_0\right]$, we obtain:

$$2i{\omega }_j\left(A^{\prime }+{\overline{c}}_{j}A\right)+6{\overline{k}}_{j3}A{\mathrm{\Lambda }}^2+3{\overline{k}}_{j3}{A}^2\overline{A}+3{\overline{k}}_{j3}\mathrm{\Lambda }{\overline{A}}^2\exp \left(i\sigma T_1\right)=0$$

(29)

Introducing the polar form of $A$, hawse obtain:

$$A=\frac{1}{2}a\exp \left(i\beta \right),$$

(30)

where $a$ and $\beta$ are real functions. Substituting Equation (30) into Equation (29) and separating the real part and imaginary parts, we obtain:

$$\{\begin{array}{l}{a}^{\prime }=-{\overline{c}}_{j}a-\frac{3{\overline{k}}_{j3}\mathrm{\Lambda }}{4{\omega }_j}{a}^2\sin \left(\sigma T_1-3\beta \right)\\ a{\beta }^{\prime }=\frac{3{\overline{k}}_{j3}}{{\omega }_1}\left({\mathrm{\Lambda }}^2+\frac{1}{8}{a}^2\right)a+\frac{3{\overline{k}}_{j3}\mathrm{\Lambda }}{4{\omega }_j}{a}^2\cos \left(\sigma T_1-3\beta \right).\end{array}$$

(31)

The equations can be transformed into an autonomous system, if we assume:

$$\gamma =\sigma T_1-3\beta .$$

(32)

The result is:

$$\{\begin{array}{l}{a}^{\prime }=-{\overline{c}}_{j}a-\frac{3{\overline{k}}_{j3}\mathrm{\Lambda }}{4{\omega }_j}{a}^2\sin \gamma \\ a{\gamma }^{\prime }=\left(\sigma -\frac{9{\overline{k}}_{j3}{\mathrm{\Lambda }}^2}{{\omega }_j}\right)a-\frac{9{\overline{k}}_{j3}}{8{\omega }_j}{a}^3-\frac{9{\overline{k}}_{j3}\mathrm{\Lambda }}{4{\omega }_j}{a}^2\cos \gamma .\end{array}$$

(33)

If $a^{\prime }={\gamma }^{\prime }=0$, the steady state motion will occur. This corresponds to the solution of the following equation:

$$\{\begin{array}{l}{\overline{c}}_{j}a=-\frac{3{\overline{k}}_{j3}\mathrm{\Lambda }}{4{\omega }_j}\sin \gamma \\ \left(\sigma -\frac{9{\overline{k}}_{j3}{\mathrm{\Lambda }}^2}{{\omega }_j}\right)a-\frac{9{\overline{k}}_{j3}}{8{\omega }_j}{a}^3=\frac{9{\overline{k}}_{j3}\mathrm{\Lambda }}{4{\omega }_j}{a}^2\cos \gamma .\end{array}$$

(34)

Taking the squares of the two equations, then adding them to delete $\gamma$, we obtain:

$$\left[9{\overline{c}}_j^2+{\left(\sigma -\frac{9{\overline{k}}_{j3}{\mathrm{\Lambda }}^2}{{\omega }_j}-\frac{9{\overline{k}}_{j3}}{8{\omega }_j}{a}^2\right)}^2\right]a^2=\frac{81{\overline{k}}_{j3}^2{\mathrm{\Lambda }}^6}{16{\omega }_j^2}{a}^4.$$

(35)

According to Equation (35), We know $a=0$ or:

$$9{\overline{c}}_j^2+{\left(\sigma -\frac{9{\overline{k}}_{j3}{\mathrm{\Lambda }}^2}{{\omega }_j}-\frac{9{\overline{k}}_{j3}}{8{\omega }_j}{a}^2\right)}^2=\frac{81{\overline{k}}_{j3}^2{\mathrm{\Lambda }}^6}{16{\omega }_j^2}{a}^2.$$

(36)

The equations are a quadratic function solution of $a^2$, and their solution is:

$$a^2=p\pm {\left(p^2-q^2\right)}^{1/2},$$

(37)

Here,

$$p=\frac{8{\omega }_j\sigma }{{\overline{k}}_{j3}}-6{\mathrm{\Lambda }}^2,\hspace{1em}q=\frac{64{\omega }_j^2}{81{\overline{k}}_{j3}^2}\left[9{\overline{c}}_j^2+{\left(\sigma -\frac{9{\overline{k}}_{j3}{\mathrm{\Lambda }}^2}{{\omega }_j}\right)}^2\right].$$

(38)

We notice that $q$ is always positive; therefore, there is a nontrivial free vibration amplitude if $p>0$ and $p^2\ge q$. This means ${\mathrm{\Lambda }}^2<\frac{4{\omega }_j\sigma }{27{\overline{k}}_{j3}}$ and $\frac{{\overline{k}}_{j3}{\mathrm{\Lambda }}^2}{{\omega }_j}\left(\sigma -\frac{63{\overline{k}}_{j3}{\mathrm{\Lambda }}^2}{8{\omega }_j}\right)-2{\overline{c}}_j^2\ge 0$. Because ${\overline{k}}_{j3}>0$, $\sigma$ is positive, we can write the first-order approximation solution as:

$$u=a\cos \left[\frac{1}{3}\left(\mathrm{\Omega }t-\gamma \right)\right]+f_j{\left({\omega }_j^2-{\mathrm{\Omega }}^2\right)}^{-1}\cos \mathrm{\Omega }t+O\left(\epsilon \right).$$

(39)

In Equation (39), $a$ and $\gamma$ are given by Equation (34). There, $j=1$ means the first mode and $j=2$ means the second mode.

4. Discussion

4.1. Primary Resonance

We can obtain the visible pattern of the relationship between the vibration amplitude and the parameters from Equation (21), as shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. These Figures reveal the influence of the temperature field and the electric field on vibrations for the primary resonance. For the first mode (Figure 3), the initial value of the numerical solutions for the low branch is $\left({\eta }_1,{\dot{\eta }}_1\right)=\left(0.6,0\right)$, and, at the high branch, it is $\left({\eta }_1,{\dot{\eta }}_1\right)=\left(0.6,0\right)$. For the second mode (Figure 4), the initial value of the numerical solutions at the low branch is $\left({\eta }_1,{\dot{\eta }}_1\right)=\left(0.012,0\right)$, and, at the high branch it is $\left({\eta }_1,{\dot{\eta }}_1\right)=\left(0.36,0\right)$. From Figure 3 and Figure 4, it can be found that the multi-scale method is accurate. Figure 5 shows that the second mode is hardly excited when the first mode is excited. For example, when the load amplitude of the second mode is 20 times that of the first mode, the maximal vibrational amplitude of the second is only one-fifth of the first, as shown in Figure 5. It is found from Figure 6 that the maximum amplitudes with detuning parameters will increase when the temperature field and electric field increase, and the region being in multi values will also become larger. This rule agrees also with the second mode; however, the temperature field and electric field have a smaller effect than the first, as shown in Figure 7.

From Equation (21), we also obtain the curves of vibration amplitudes and loads for the first and second modes, as shown in Figure 8 and Figure 9. The two figures show that the temperature and electric fields impact outstandingly the vibration amplitudes of the first mode, while the influence is weak on the second mode. Furthermore, there are two bifurcation points in the frequency-response curves and the load-amplitude curves. They will induce the jump phenomenon of vibrational amplitude. These details of the jump have been discussed in reference [28].

4.2. Subharmonics

Through Equation (36)we can draw the vibration amplitude with the model frequency as a function of other parameters (as shown in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18). These figures reveal the relationship between subharmonic amplitude, temperature field, and electric field. These figures support the following main conclusions.

First, it is more difficult to excite the subharmonic vibration at the second-order mode than that of the first mode for the same parameters, as shown in Figure 10.

Second, the first mode is more sensitive to temperature and electric fields than the second mode, as shown in Figure 11, Figure 12, Figure 13 and Figure 14.

Finally. The numerical simulations of Equation (9) are operated using the Runge–Kutta method for the first mode with the initial value $\left({\eta }_1,{\dot{\eta }}_1\right)=\left(0.012,0\right)$ and the second mode with the initial value $\left({\eta }_1,{\dot{\eta }}_1\right)=\left(0.2,0\right)$. These simulations show that the analytical solutions are accurate, as shown in Figure 15, Figure 16, Figure 17 and Figure 18.

5. Conclusions

In this paper, the nonlinear vibrations of a $\left(10,10\right)$ SWCNT are studied by a thermal-electro-mechanical coupling nanobeam theory for the primary resonance and subharmonic resonance. This model includes independent extensional stiffness and bending stiffness. We obtain nonlinear ordinary differential equations for the first and second modes by the Galerkin method. Then, their approximate analytical solutions are obtained by the multiple scale method for the primary resonance and subharmonic resonance. The solutions are used to discuss the influences of the electric and temperature fields on the vibrations of the structure. Moreover, we check the accuracy of the approximate analytical solutions using the Runge–Kutta method. The main conclusions are as follows.

(1)

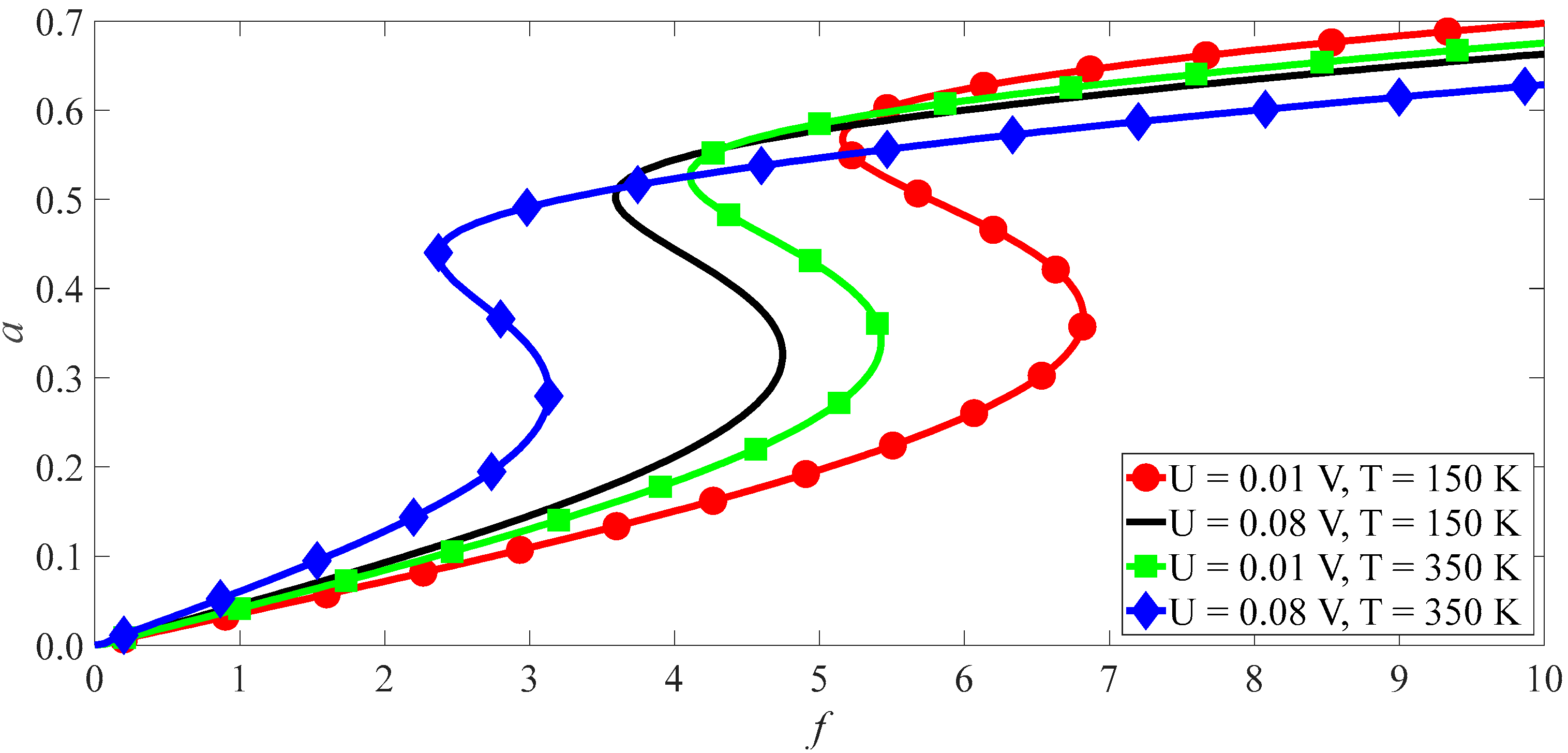
Under the primary resonance and subharmonics, the nonlinear vibrations of the first mode are more sensitive to the temperature and electric fields than the second mode. For the primary resonance, when the load amplitude of the second mode is 20 times of the first mode, the maximal vibrational amplitude of the second is only one-fifth of the first. For the subharmonics, it is more difficult to excite the subharmonic vibration at the second-order mode than at the first mode.

(2)

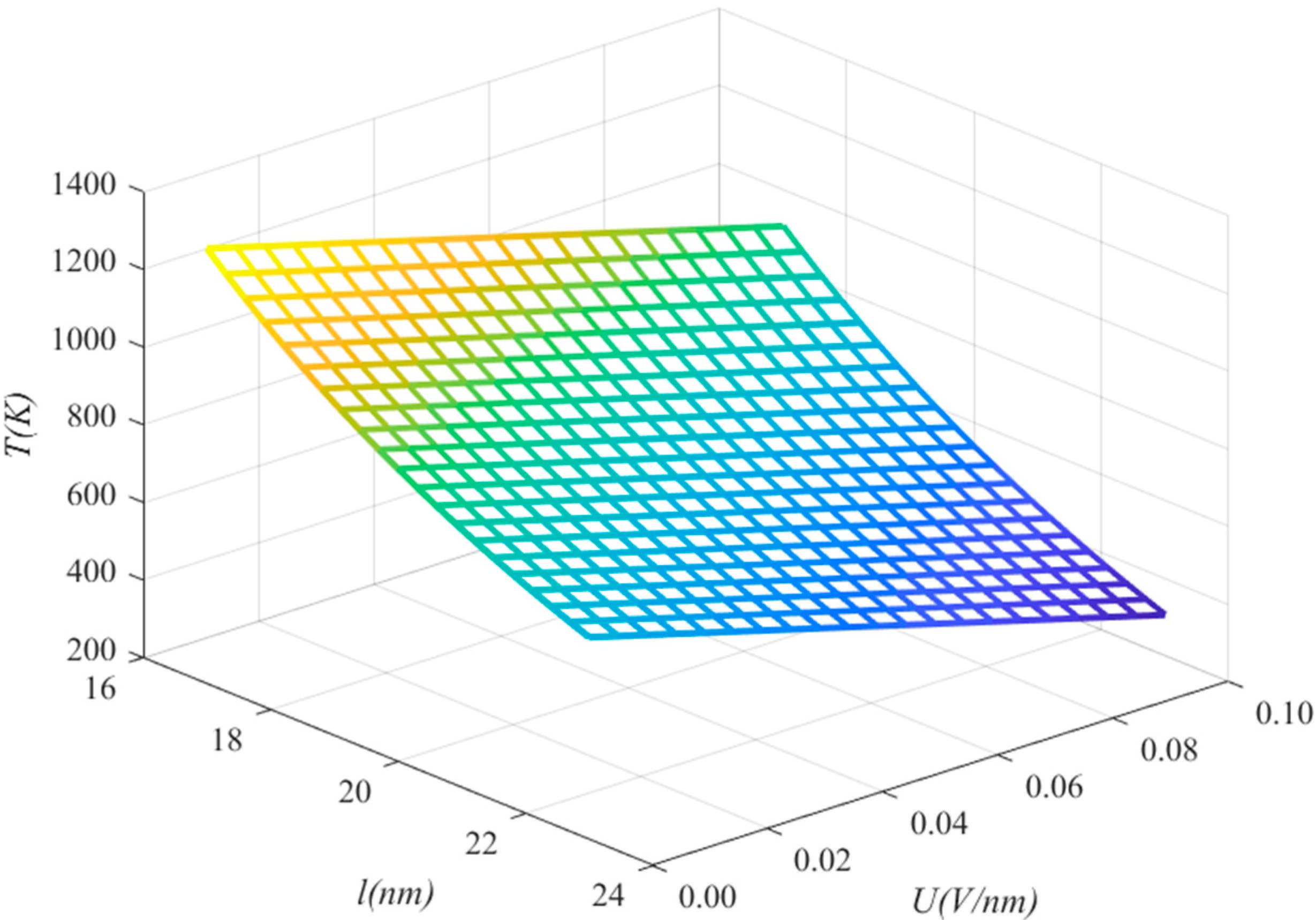
Since the CEE is far greater than the CTE, the electric field has more outstanding influence on an SWCNT’s vibration than the temperature.

(3)

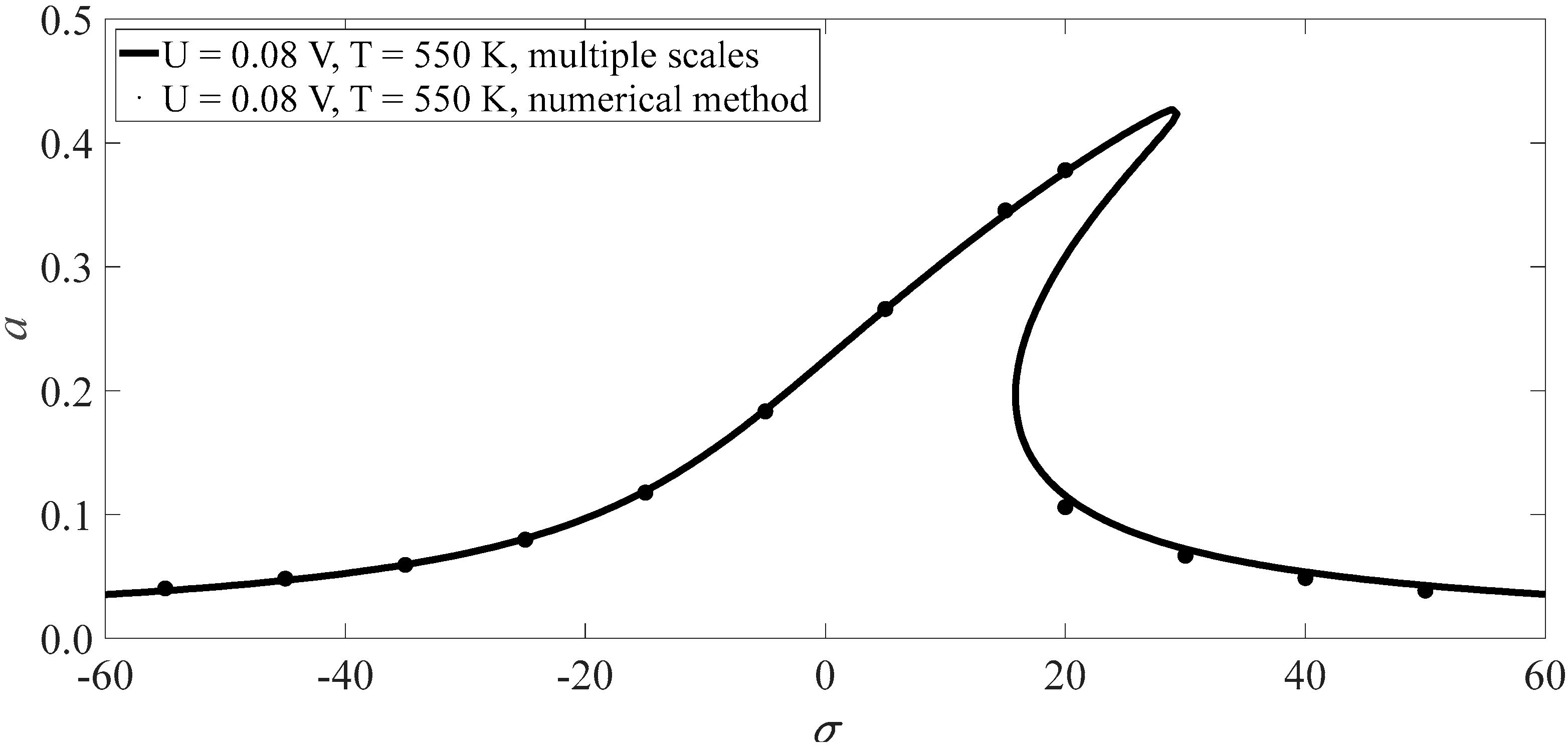
There is only one vibrational component with the model frequency in the primary resonance, in which the jump of vibrational amplitude may be induced by changes in the load’s frequency or amplitude. Further, there are two vibrational components in the subharmonic resonance, and the two components have approximate vibrational amplitude.