Abstract
The tackifying effect of resins used in the tire industry highly depends on the compatibility and interaction strength with the rubber matrix. Here, uncured and cured styrene/butadiene rubber compounds, either in the presence or absence of a hydrocarbon aromatic tackifying resin, were studied by means of high-resolution and time-domain solid-state NMR (SSNMR) techniques to investigate resin/polymer interactions and the effect of the resin on the dynamics of polymer chains. 13C direct excitation and cross-polarization spectra, combined with low-field measurements of 1H T1 and analysis of 1H on-resonance free-induction decay, provided information on the dynamic heterogeneity of the samples and the degree of mixing between the resin and the rubber matrix. Moreover, 1H T1 and T1ρ relaxation times at variable temperatures were used to investigate the effect of resin on both segmental dynamics activated at the glass transition and collective polymer dynamics. SSNMR findings were discussed in relation to crosslink density and Tg data. The obtained results show that the resin is intimately mixed with the polymer, while maintaining its rigid character. A slowdown of segmental dynamics, related to an increase in Tg, was found as a consequence of resin addition, while no effect was evidenced on fragility and collective polymer dynamics.
1. Introduction
Elastomer-based compounds are widely employed in the tire industry thanks to the possibility to tune their applicative properties by modifying their formulation. Usually, they are composed of one or more polymers, such as natural rubber or synthetic polymers (isoprene rubber, butadiene rubber, styrene/butadiene rubber), which are subjected to vulcanization in the presence of a vulcanizing agent and other ingredients, including fillers, stabilizers, processing oils and resins, with the purpose of providing defined mechanical proprieties to the final product [1]. In particular, resins are employed in the tire industry for the following three different functions: as tackifiers; as reinforcing agents; and as curing agents [2]. Specifically, tackifying resins are added to modify the rheological behavior of the rubber compound, with the final aim of favoring the processability of the uncured compound, promoting filler dispersion and improving mechanical properties of tires, such as rolling resistance and wet traction [1,2,3,4,5,6,7]. The achievement of precise requirements in the final product strongly depends on the polymer–resin miscibility, which in turn is related to physico-chemical characteristics of the resin itself, such as the softening point, glass transition temperature (Tg), viscosity, chemical structure and molecular weight [6,7,8,9,10,11,12,13,14]. Indeed, the presence of resin alters the dynamics of the polymer chains, resulting in a modification of the viscoelastic behavior and final mechanical properties of the vulcanizate [14,15,16]. In this frame, the comprehension of the relationship between macroscopic proprieties of technological interest and structural and dynamic features arising from polymer–resin interactions at the molecular level plays a key role in rationalizing the design of new materials with improved performances. A common way to evaluate polymer–resin miscibility and to predict the effect of resin on the mechanical behavior of the final product relies on monitoring the Tg of the vulcanizate upon resin addition. This is often conducted either by calorimetric measurements [12,17,18] or by dynamic mechanical analyses [6,7,8,9,10,11,19]; in the latter case, the tanδ curve as a function of temperature is measured, whose profile is directly influenced by the change in Tg and provides a way to predict the behavior of the vulcanized blend in terms of rolling resistance and wet traction. Other studies investigate the effect of resins on the dynamic [13,14,15], viscoelastic [16], and mechanical [17,18,20,21] properties of rubbers.
Solid-state NMR spectroscopy (SSNMR) represents a valuable technique to gain insight into the structure and dynamics of polymeric materials [22,23,24,25,26]. In particular, 1H time-domain (TD) SSNMR experiments can be exploited to measure 1H spin–lattice relaxation times in the laboratory frame (T1) and in the rotating frame (T1ρ), as well as 1H spin–spin relaxation times (T2), which depend on the modulation of 1H-1H dipolar couplings by molecular motions, thus providing information on the dynamics of polymer chains [27,28,29,30,31]. In addition, in the case of multicomponent systems with domain sizes lower than tens of nm (or nm), the T1′s (or T1ρ′s) of protons in different dynamic environments tend to be averaged to a single value due to the spin diffusion phenomenon, thus allowing an assessment of the structural homogeneity of a sample. Moreover, one can also benefit from magic angle spinning (MAS), high-power decoupling, and cross-polarization (CP) techniques to obtain high-resolution SSNMR 13C spectra, which yield both structural and dynamic information on each component of the composite [22,24]. Thanks to the wealth of information that can be obtained, SSNMR has been successfully employed to investigate the dynamic and structural properties of elastomer compounds and vulcanizates. However, to the best of our knowledge, it has not previously been employed to characterize the effect of resins on elastomer structure and dynamics.
In this work, TD and high-resolution SSNMR techniques were applied to investigate uncured and cured styrene/butadiene rubber compounds, either in the presence or absence of the tackifying resin Kristalex™ 5140, a low molecular weight (Mn = 1690 g/mol) α-methylstyrene/styrene copolymer characterized by excellent thermal stability, a high softening point (413 K) and a glass transition temperature of 363 K [32]. 13C high-resolution SSNMR spectra and analyses of on-resonance 1H free-induction decays (FIDs) were used to investigate the structural properties and dynamic and structural heterogeneity of the samples. Information on the heterogeneity of the samples was also obtained from 1H T1 and T1ρ. Moreover, 1H T1 and T1ρ measured at different temperatures and at different magnetic fields were exploited to characterize the dynamics of the polymeric chains on a wide range of motion timescales. In particular, we took advantage of field-cycling (FC) NMR relaxometry to measure 1H T1 on a wide range of Larmor frequencies (0.01–35 MHz). The NMR results were discussed in comparison with data on crosslink density and glass transition temperature, two macroscopic properties of interest for rubber applications that are usually affected by the addition of resins. This comparison allowed the effect of the resin on the structure and dynamics of the polymer chains in the rubber compound and the corresponding vulcanizate to be correlated with these applicative properties. Moreover, information could be obtained on the degree of mixing between polymer and resin.
2. Materials and Methods
2.1. Samples
All samples were provided by Pirelli Tyre SpA (Milano, Italy). The sample indicated as SBR consists of a blend of styrene/butadiene rubber (39.5% styrene, vinyl content on the dienic portion 38.5%, Mn = 530,000 g/mol, Mw = 750,000 g/mol), treated distillated aromatic extract (TDAE) as plasticizer oil, carbon black (N100 series, surface area: 158 m2/g) as a reinforcing filler and a vulcanization package containing sulfur, N-cyclohexyl-2-benzothiazole sulfenamide (CBS), zinc oxide and stearic acid. Sample SBR_k has the same formulation as SBR, but it also contains Kristalex™ 5140 resin (poly(α-methylstyrene-co-styrene), Synthomer, Mn = 1690 g/mol, Mw = 4750 g/mol). vSBR and vSBR_k indicate samples obtained by the vulcanization of SBR and SBR_k, respectively. All compounds were mixed in a 1.5 L internal mixer (Harburg Freudenberger, Hamburg, Germany) in a two-step mixing process. In the first step, all ingredients, except the vulcanization system, were mixed for 200 s, reaching a dumping temperature of approximately 413 K with a rotor speed of 75 rpm. In the second step, the vulcanization system was added, and the compound was finalized by mixing for 120 s at 313 K with a rotor speed of 50 rpm, and the maximum dumping temperature was set at 383 K. vSBR and vSBR_k were vulcanized at 443 K for 10 min.
The composition of the samples is reported in detail in Table 1.

Table 1.
Sample composition in phr (parts per hundred rubber).
2.2. Differential Scanning Calorimetry and Equilibrium Swelling Experiments
Differential scanning calorimetry (DSC) measurements were carried out with a DSC Mettler-Toledo 820 instrument. Thermal cycles between 183 and 473 K were performed. The cooling/heating rate was 10 K/min. For all samples, Tg was determined as the intersection point of the two tangents to the DSC curve at the endothermic step. The obtained values are reported in Table 2.

Table 2.
Tg values obtained by DSC experiments and crosslink density (1/Mc) values determined by equilibrium swelling experiments.
Equilibrium swelling experiments were performed in duplicate to determine the crosslink density (1/Mc, where Mc is the average molar mass between two adjacent crosslinks) of vSBR_k and vSBR. The samples were weighed and then soaked in toluene for 72 h in the dark. Thereafter, they were dried with absorbent paper and quickly weighed. After being dried overnight in an oven at 343 K under vacuum, the samples were weighed again in order to determine the amount of adsorbed solvent. 1/Mc values were then calculated using the Flory–Rehner equation [33]. The obtained 1/Mc values are reported in Table 2.
2.3. SSNMR Experiments
1H on-resonance FIDs were recorded at 303 K on a Niumag permanent magnet interfaced with a Stelar PC-NMR console, working at a 1H Larmor frequency of 20.8 MHz and equipped with a single-channel static 5 mm probe. Specifically, the mixed Magic Sandwich Echo (MSE) pulse sequence was applied [23] using a total echo duration τMSE = 6 (4τφ + 2τ90), with τφ = 1.5 μs and τ90 = 3.3 μs. For compounds and vulcanizates, a dwell time of 1 μs was used and 3k data points were acquired. For Kristalex™ 5140, the dwell time was 0.1 μs and 2k data points were acquired. A total of 200 scans were accumulated using a recycle delay of 0.5 s for the compounds and vulcanizates, and one of 1 s for Kristalex™ 5140. The experimental MSE 1H FIDs were analyzed by a discrete approach using a non-linear least-square fitting procedure implemented in the Mathematica® environment [34]. For all samples, 1H longitudinal relaxation time, T1, values were also measured at 303 K using the inversion recovery pulse sequence coupled with a solid echo pulse scheme (IRSE), with delay times ranging from 1 ms to 0.5 s in the case of the vulcanized samples and from 1 ms to 1 s for Kristalex™ 5140. All IRSE experiments were acquired using 4–16 scans and recycle delays of 0.5 and 1 s for vulcanized samples and Kristalex™ 5140, respectively.
13C high-resolution SSNMR experiments and 1H T1ρ measurements were performed on a Bruker Avance Neo spectrometer working at Larmor frequencies of 500.13 and 125.77 MHz for 1H and 13C nuclei, respectively, using a double-resonance 4 mm CP-MAS probe. 90° pulses with a duration of 4.3 μs and 4.1 μs were employed for 1H and 13C excitation, respectively. 13C direct excitation (DE) spectra under MAS were recorded on vSBR and vSBR_k using a recycle delay of 20 s, optimized to obtain quantitative measurements and accumulating 1600 scans. 1H–13C CP/MAS spectra were recorded on vulcanized samples and on Kristalex™ 5140 by applying a linear ramp on the 13C channel during the contact time, using a constant 1H spin-lock field of 69 kHz. To investigate CP dynamics, contact times ranging from 0.05 to 4 ms were employed for vSBR and vSBR_k, while for Kristalex™ 5140, contact times ranged from 0.05 to 10 ms; 1000 transients were accumulated, using a recycle delay of 4 s. All 13C experiments were recorded at 303 K, applying the SPINAL-64 scheme during acquisition for high-power proton decoupling. An MAS frequency of 5 kHz was used to avoid spinning instability due to the elastic character of the samples. 1H T1ρ measurements were performed at different temperatures between 303 and 343 K and under static conditions by applying a spin-lock field of 46 kHz for durations ranging from 0.4 to 20 ms.
1H longitudinal relaxation rates, R1 = 1/T1, were measured in a 0.01−35 MHz Larmor frequency range at different temperatures by means of a Stelar Spin Master FFC-2000 FC NMR relaxometer. The switching time was 3 ms, while the 90° pulse duration was 10.9 μs, and a single scan was acquired. Prepolarized and non-prepolarized pulse sequences were used below and above 12 MHz, respectively. The polarizing and detection frequencies were set at 25 and 16.3 MHz, respectively, while all other parameters were optimized for each experiment. All the 1H magnetization curves vs. time were reproduced using a monoexponential function, with errors on 1H R1 lower than 3%. Samples were cut into small pieces and loaded in a 10 mm NMR glass tube. Measurements were performed every 10 K from 303 K to 393 K. The sample temperature was controlled within ±0.1 K by a Stelar VTC90 variable temperature unit. Considering the adopted instrumental conditions, R1 values higher than 1000 s−1 were disregarded.
3. Results and Discussion
3.1. Structural Characterization and Degree of Mixing
The presence of domains with different molecular mobility in the samples was investigated through the analysis of on-resonance 1H FIDs acquired using the MSE pulse sequence [35]. Indeed, this analysis allowed protons in different dynamic environments to be distinguished on the basis of spin–spin relaxation times, 1H T2, whose values monotonically increase as the degree of mobility increases [35,36,37,38,39,40].
Figure 1 shows the 1H FIDs obtained for all samples at 303 K. The curves were fitted to a linear combination of three functions (Equation (1)), each characterized by a decay time T2,i and multiplied by a fractional weight Wi (i = g, e1, e2) [38,41,42].
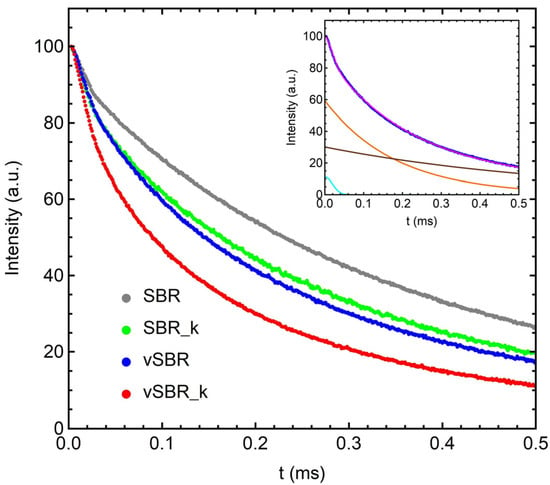
Figure 1.
Expansion of the first 0.5 ms of the experimental 1H FIDs of the investigated samples at 303 K. The inset shows the experimental curve (blue) and the total fitting function (magenta) obtained for vSBR, together with the single contributions of the Gaussian (cyan), intermediate-T2 (orange), and long-T2 (brown) exponential functions.
The first function is a Gaussian function (g), representative of the fraction of protons in rigid environments. The other two are exponential functions (e1, e2), ascribable to protons in regions of intermediate and fast mobility. An example of FID fitting is shown in the inset of Figure 1, while the best fit values of Wi and T2,i are reported in Table 3.

Table 3.
Weight percentages (Wi) and T2,i values obtained as best-fitting parameters from the analysis of the 1H FIDs of the investigated samples through Equation (1).
For all the analyzed samples, a small proton fraction associated to the Gaussian function was detected, with a very short T2 on the order of 20–30 μs, ascribable to molecular fragments with highly restricted mobility, including polymer segments involved in physical and chemical constraints, such as entanglements and crosslinks, and in interactions with filler particles. The two exponential components are instead characterized by longer T2 values ranging from ~100 to ~800 μs, and they account for most of the protons in the polymer chain segments and for protons in liquid-like components, including TDAE and dangling chains.
By passing from the uncured to the vulcanized samples, an increase in Wg and a concomitant decrease in the T2 values of both exponential functions were observed. This effect can be ascribed to the formation of chemical crosslinks between the polymer chains, causing a reduction in molecular mobility. As the resin was added, an increase in the rigid fraction on the order of 5–8% was observed, accompanied by a decrease in both T2,e1 and T2,e2 values. Because the 1H FID of pure resin can be nicely reproduced by a Gaussian function characterized by a T2 value of 20 μs (Figure S1), the higher Wg values obtained for SBR_k and vSBR_k can reasonably be ascribed to a contribution of the resin protons to the Gaussian component. Indeed, it was estimated that the resin protons account for 10% of the total proton content in both samples. Furthermore, the decrease in T2,e1 and T2,e2 values reflects a slowdown of the dynamics of all the other components of the samples, mainly the polymer, induced by the presence of resin.
In order to ascribe the regions at different mobilities to different sample components, 13C high-resolution SSNMR experiments were carried out on vSBR and vSBR_k. In particular, 13C DE/MAS spectra were recorded to obtain quantitative spectra, while 1H-13C CP/MAS spectra selectively highlighted the more rigid components of the samples. In fact, the CP process relies on the magnetization transfer from abundant (1H) to rare (13C) nuclei mediated by the heteronuclear dipolar interaction, enhancing the detection of 13C nuclei in close proximity to protons in rigid environments. Furthermore, the CP dynamics is strongly influenced by molecular motions, as they directly affect the extent of dipolar interaction, as well as 1H T1ρ, and can be studied by analyzing CP spectra recorded at different contact times.
The 13C DE/MAS spectra acquired for vSBR and vSBR_k are reported in Figure 2a,b. Both spectra presents broad signals, mainly due to the distribution of chemical shifts typical of amorphous materials. Specifically, a group of signals at low chemical shifts (0–50 ppm) is present, ascribable to the aliphatic carbon nuclei of the polymer and TDAE, and to naphthenic carbons in TDAE. In the spectrum of vSBR_k, an additional contribution from CH2 carbons of Kristalex™ 5140 can be observed between 30 and 50 ppm. At higher chemical shifts (100–160 ppm), signals from aromatic and alkene carbons were detected. In the spectrum of vSBR_k, it is also possible to observe low intensity signals at about 167 and 87 ppm due to the first-order spinning sidebands of the tertiary aromatic carbons of the resin. In the 13C CP/MAS spectra, recorded with a short contact time of 0.2 ms (Figure 2c,d), signals arising from rigid domains are enhanced, showing broader lines with respect to the DE spectra. In particular, the signals of resin carbons are favored compared to those of SBR, as can be seen from the higher intensity of the spinning sidebands. The isotropic signal and the corresponding sidebands of aromatic tertiary carbons of Kristalex™ 5140 were assigned on the basis of the 1H-13C CP spectrum recorded for the resin under the same experimental conditions (Figure 2e). Interestingly, the observation of spinning sidebands for Kristalex™ 5140 in the spectra of vSBR_k indicates that the resin maintains a rigid character even when blended with the polymer, in agreement with the results from 1H FID analysis.
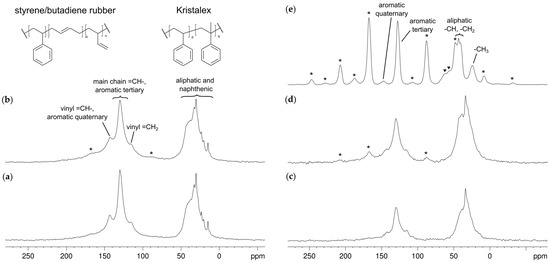
Figure 2.
13C DE/MAS spectra of (a) vSBR and (b) vSBR_k recorded using a recycle delay of 20 s. 1H-13C CP/MAS spectra of (c) vSBR, (d) vSBR_k and (e) Kristalex™ 5140 recorded using a contact time of 0.2 ms and a recycle delay of 4 s. Spinning sidebands are marked with an asterisk; impurities are marked with a filled triangle. All spectra were recorded using an MAS frequency of 5 kHz.
The CP dynamics was then studied for the tertiary aromatic carbons in pure Kristalex™ 5140 and in vSBR_k and compared with that of aromatic/alkene carbons in vSBR and vSBR_k (see Supplementary Materials). Interestingly, the 1H T1ρ of the aromatic protons of the resin in pure Kristalex™ 5140 (~9 ms) is significantly longer than that measured in both vSBR_k and vSBR (0.6–1 ms) (Table S1). This seems to be ascribable to the proton spin diffusion between resin and polymer domains occurring in vSBR_k and suggests that in this sample the resin is intimately mixed with the polymer. To this regard, further information could be obtained by the low-resolution measurement of 1H T1: mono-exponential trends for the relaxation curves were obtained for all the samples and 1H T1 values of 114, 66 and 74 ms were measured for pure Kristalex, vSBR and vSBR_k, respectively. Although these values are quite similar, these results seem to confirm an intimate mixing (on a tens of nm scale) between resin and polymer in vSBR_k.
3.2. Characterization of Dynamics
The dynamic properties of all samples were investigated by means of FC NMR experiments for the measurement of 1H spin–lattice relaxation rates (R1 = 1/T1) at variable Larmor frequencies, from 0.01 to 35 MHz. In fact, 1H spin–lattice relaxation is driven by the modulation of the 1H-1H dipolar couplings by molecular motions. The dependence of 1H R1 on frequency (ν or ω = 2πν), called nuclear magnetic relaxation dispersion (NMRD), can be described by a linear combination of spectral densities, J(ω), which are the Fourier transform of the autocorrelation functions of motion [43]. For polymers far above Tg, R1 dispersions are mainly governed by segmental dynamics, that is local motions within the Kuhn segment, activated at the glass transition. Segmental dynamics, also referred to as “glassy” dynamics, is responsible for the so-called α-relaxation. Additional contributions to R1 dispersions arise from collective motions involving longer and longer chain portions, indicated as polymer dynamics. The contribution to R1(ω) arising from segmental dynamics can be well represented using the Cole–Davidson spectral density, while contributions from polymer dynamics result in power law dependences of the type R1(ω) ∝ ω−γ, with different values of the γ exponent depending on the motional regime as defined by the mostly accepted tube–reptation theory [44,45,46]. Therefore, FC NMR has proven to be an effective technique to characterize the dynamics of polymers far above glass transition over a broad range of characteristic motion times [47,48]. In particular, it has been successfully applied to obtain information on segmental and polymer dynamics in polymer melts and vulcanized rubbers [49,50,51,52,53,54]. For this aim, R1(ω) data are usually transformed to the susceptibility representation, χ″(ω) = ω R1(ω), and χ″(ωτs) master curves are built from χ″(ω) curves acquired at different temperatures by exploiting the frequency–temperature superposition (FTS) principle [55,56] to determine the values of the correlation time for segmental dynamics, τs. At low temperatures, χ″(ω) curves show a maximum, and the high-frequency branch of the curves, which mainly arises from the contribution of segmental dynamics (), can be fitted to Equation (2):
using the Cole–Davidson spectral density function:
with 0 < βCD ≤ 1. Thus, τs values can be obtained from τCD using the relation τs = βCDτCD. At higher temperatures, the χ″(ω) curves do not show a maximum, and the frequency axis is scaled until they overlap the curves obtained at lower temperatures to build the master curve. In this case, τs can be determined as the frequency scaling factor.
Here, 1H NMRD curves were acquired for all the investigated samples at different temperatures in the 303–393 K range. In Figure 3a, the curves recorded at 303, 333 and 363 K are reported as examples. In Figure S3, the corresponding χ″(ω) curves are also shown.
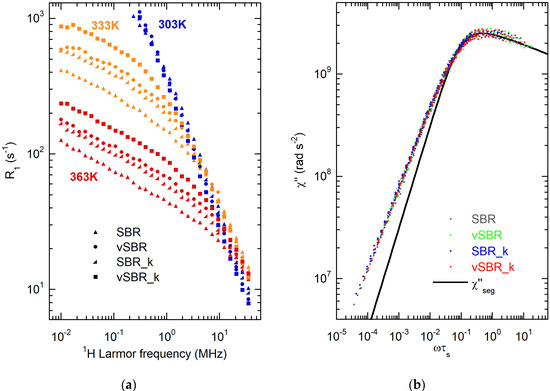
Figure 3.
(a) 1H NMRD curves for the investigated samples at the indicated temperatures. (b) Susceptibility master curves of the indicated samples; the black line represents the contribution of the segmental dynamics to the χ′′(ωτs) master curve of SBR_k.
For all samples, at low temperatures, R1 shows a power law dependence on Larmor frequency with γ ≅ 1, suggesting that R1 relaxation is dominated by segmental dynamics (Regime 0). Correspondingly, the χ″(ω) curves display a maximum associated with the condition ωτs ≅ 1, which shifts towards lower frequencies passing from uncured to vulcanized samples. Moreover, SBR_k and vSBR_k show χ″(ω) maxima at lower frequencies than the corresponding samples without Kristalex™ 5140. These results indicate a slowdown of segmental dynamics as a consequence of both crosslinking and resin addition, in agreement with the higher Tg values measured by DSC (Table 2). At T ≥ 323 K, the NMRD curves show two regions with different power law dependences. A region with γ values in the range 0.7–0.8, with γ decreasing by increasing the temperature, was detected at higher frequencies, ascribable to the overlap of Regime 0 with the Rouse regime (Regime I of the tube–reptation model). At lower frequencies, a region with γ of 0.25–0.28 was observed, which is attributable to the Rouse regime. For all samples, R1 increases with increasing temperature at high frequencies, while it decreases at lower frequencies, with a shift in the crossover point between Regime 0 and Regime I toward lower frequencies, due to the corresponding increase in τs.
For each sample, the NMR susceptibility χ″(ω) curves obtained at different temperatures were combined together to build χ″(ωτs) master curves, under the assumption that the FTS principle holds true, to obtain τs values. χ″(ω) curves at 303 K were fitted to Equation (2) in order to obtain τs. βCD was found to be 0.12, in agreement with the value determined for SBR samples in a previous work [52]. At the remaining temperatures, τs values were determined as the frequency scaling factors used to build the master curves. The χ″(ωτs) master curves obtained for all samples are shown in Figure 3b, while the values of τs as a function of 1000/T are reported in Figure 4a. The obtained χ″(ωτs) master curves cover a frequency range of six decades and display characteristic shapes that well reflect the different dynamic regimes described above: at a high frequency, the contribution of segmental dynamics is dominant, while polymer dynamics assumes a significant importance for ωτs < 0.1.
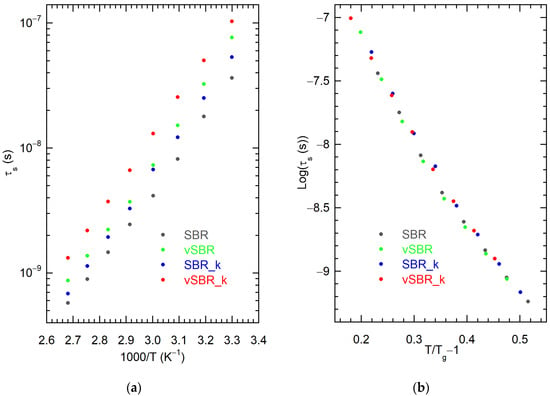
Figure 4.
(a) Correlation times for segmental dynamics, τs, vs. 1000/T and (b) Logτs vs. (T/Tg − 1) for the indicated samples. Tg values were determined by DSC measurements (Table 2). Errors on τs are lower than 5%.
As expected from the trend of the maxima of the χ″(ω) curves, τs values are longer in the vulcanized samples (vSBR, vSBR_k) with respect to the uncured ones (SBR, SBR_k), and in samples containing the resin (SBR_k, vSBR_k) with respect to those without it (SBR, vSBR). The increase in τs upon vulcanization is ascribable to the formation of crosslinks, which restrict segmental dynamics, also resulting in increased Tg (Table 2). The addition of the resin, although lowering the efficiency of vulcanization, as it was observed when comparing the crosslink density of vSBR and vSBR_k (Table 2), yielded a slowdown of segmental dynamics, paralleled by an increase in Tg. Similar trends in τs upon resin addition to rubber matrices were found in investigations of α-relaxation by broadband dielectric spectroscopy [13,14,15]
For all samples, τs values show, as expected, decreasing trends by increasing the temperature (Figure 4a). However, quantitative analyses of these trends in terms of the commonly used Vogel−Fulcher−Tammann (VFT) function to obtain information on polymer fragility is hampered by the limited temperature range investigated. On the other hand, hints on the variation of fragility upon vulcanization or resin addition can be achieved by plotting Logτs as a function of (T/Tg − 1) according to Equation (4):
Equation (4) is obtained by recasting the VFT equation [57]. In Equation (4), m is the fragility index, τ0 is the pre-exponential factor of the VFT equation and the value of τs at the glass transition (τs(Tg)) is, by definition, a constant (100 s) [58]. If τ0 and m do not change significantly, all samples are expected to exhibit the same behavior. Indeed, in our case, using Tg values determined by DSC in (T/Tg − 1), a good superposition was observed for the Logτs curves of all the samples (Figure 4b). These results indicate that both crosslinking by vulcanization and resin addition do not significantly affect the polymer fragility index, which yields a measurement of the rapidity with which segmental dynamics slow down upon approaching the glass transition by decreasing the temperature. Unchanged polymer fragility upon vulcanization was also reported for rubbers with low crosslinking degrees [52]. On the other hand, the addition of resin was previously found to increase the fragility index at high resin concentrations [13], suggesting that in our case the amount of resin was too low to show such an effect.
For the vulcanized samples, the dynamics at low frequency was further investigated by analyzing 1H spin–lattice relaxation in the rotating frame (T1ρ). Although an estimate of 1H T1ρ was already obtained by analyzing the CP dynamics, 1H T1ρ data were more accurately measured at a spinlock field (ω1/2π) of 46 kHz by means of a dedicated experiment with direct 1H detection. At all the investigated temperatures (from 303 to 343 K), the relaxation curves can be well reproduced by the combination of two exponential functions , with Wa ≅ 40–90%, T1ρ,a ≅ 0.6–2.3 ms, Wb ≅ 10–60% and T1ρ,b ≅ 5–11 ms, which is very similar for vSBR and vSBR_k, as shown in Table S2. The effect of spin diffusion, which tends to average out differences between intrinsic relaxation times, makes a physical interpretation of the individual T1ρ components very difficult. Nevertheless, dynamic information could be obtained by looking at the population weighted rate average , which is not affected by spin diffusion [29] (Table S3). As shown in Figure 5, 1H decreases by increasing the temperature for both vSBR and vSBR_k, indicating the presence of dynamic processes in the fast motion regime. In agreement with R1 measurements, higher values were measured for vSBR_k, which shows a higher Tg, indicating a slowdown of dynamics induced by the presence of the resin. In order to better understand the origin of relaxation, the contribution of segmental dynamics () at different temperatures was calculated from Equation (5):
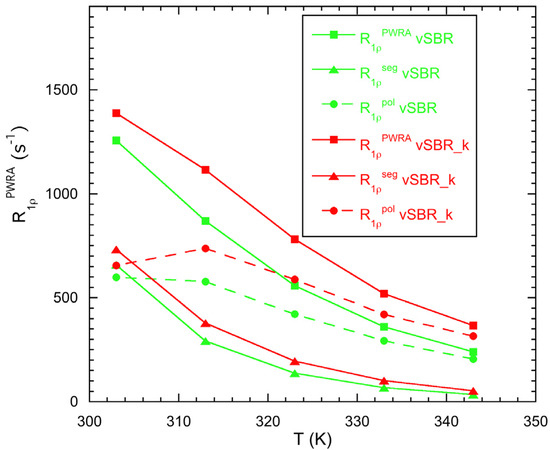
Figure 5.
1H R1ρPWRA (experimental), R1ρseg (calculated) and R1ρpol(calculated) vs. temperature for the indicated samples. The lines are plotted to guide the eye.
The values of τs obtained from the analysis of 1H NMRD curves and reported in Figure 4 were used for the calculation. As we can see, shows a decreasing trend with increasing temperature, but it accounts for only a fraction, ranging from about 52% at 303 K to 14% at 343 K, of the experimental 1H . This confirms the increasing contribution of collective polymer dynamics in the kHz frequency range as the temperature increases. The contribution of polymer dynamics was estimated as the difference (Figure 5, Table S3), under the assumption of statistical independence and time-scale separation between segmental and polymer dynamics. increases by decreasing the temperature, approaching a maximum at 303–313 K that corresponds to the condition ω1τpol ≅ 1. These results suggest the presence of Rouse motions with characteristic correlation times (τpol) on the order of tens of μs in the investigated temperature range.
4. Conclusions
In this work, the effects of the tackifying resin Kristalex™ 5140 on the structural and dynamic properties of SBR compounds of interest to the tire industry were investigated through a combination of high-resolution and TD SSNMR techniques. To this end, uncured and cured SBR compounds, either in the absence or presence of 15 phr of resin, as well as a pure Kristalex™ 5140 sample, were studied, and the obtained results were discussed in comparison with Tg and crosslink density data.
From the “macroscopic” point of view, an increase in Tg and a slight decrease in crosslink density were observed as a consequence of resin addition. From the “microscopic” point of view, the resin was found to be intimately mixed with the polymer in the rubber matrix, while maintaining its rigid character. Moreover, the resin induced a slowdown of segmental dynamics of the polymer in both uncured and cured samples, while it did not affect the polymer fragility and the spectrum of collective polymer motions in the Rouse regime.
In conclusion, the obtained results showed for the first time that SSNMR can provide very useful information on the degree of mixing and interaction between resin and polymer in rubber compounds. This information could help the comprehension of the molecular origin of the observed macroscopic and mechanical properties, which is fundamental to drive research towards formulations with improved and optimized performances.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app13031939/s1, Figure S1: 1H FID (black points) and Gaussian fitting function (green line) obtained for Kristalex; Figure S2: Integral intensities of the 13C CP/MAS signals (points) and fitting functions (black lines) obtained for vSBR (a), vSBR_k (b) and Kristalex (c) as a function of the contact time τCP; Figure S3: 1H NMR susceptibility curves of the investigated samples at the indicated temperatures. Table S1: TCH and T1ρ values obtained from the analysis of the CP curves for the investigated samples; Table S2: 1H T1ρ,i values and relative weight percentages (Wi) obtained for vSBR and vSBR_k at the investigated temperatures; Table S3: 1H R1ρPWRA (experimental), R1ρseg (calculated) and R1ρpol (calculated) obtained for vSBR and vSBR_k at the investigated temperatures.
Author Contributions
M.P. and F.N. (Francesca Nerli) contributed equally to this work. Conceptualization, M.G., F.M., F.N. (Francesca Nardelli) and L.C.; methodology, all authors; software, M.P., F.N. (Francesca Nerli), F.M. and F.N. (Francesca Nardelli); validation, M.P., F.N. (Francesca Nerli), F.M. and F.N. (Francesca Nardelli); formal analysis, M.P., F.N. (Francesca Nerli), F.M., F.N. (Francesca Nardelli), L.C. and M.C.; investigation, F.M., F.N. (Francesca Nardelli), M.P., F.N. (Francesca Nerli) and L.C.; resources, M.C., L.G., L.C., F.M. and M.G.; data curation, M.P., F.N. (Francesca Nerli), F.M., F.N. (Francesca Nardelli), L.C. and M.C.; writing—original draft preparation, F.M., F.N. (Francesca Nardelli), L.C., M.P., F.N. (Francesca Nerli), M.G. and M.C.; writing—review and editing, all authors; visualization, F.M., F.N. (Francesca Nardelli), M.P. and F.N. (Francesca Nerli); supervision, M.C., L.G. and M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Acknowledgments
CISUP (Center for Instrument Sharing-University of Pisa) is acknowledged for the use of the Bruker Avance Neo 500 solid-state NMR spectrometer. M.P. acknowledges MUR (Ministero dell’Università e della Ricerca) for the project PON 2014–2020 (D.M. 1061/2021), entitled “Tecnologie abilitanti per l’introduzione di materiali sostenibili nella formulazione di gomme: caratterizzazione di materiali elastomerici mediante spettroscopia e rilassometria NMR”. F.N. (Francesca Nerli) is grateful to GIDRM (Gruppo Italiano Discussione Risonanze Magnetiche) for the AnnaLaura Segre-Donatella Capitani fellowship.
Conflicts of Interest
M.C. and L.G. are Pirelli Tyre’s employees and contributed to the experimental work and to the manuscript writing. All other authors declare no conflict of interest.
References
- Rodgers, B.; Waddell, W. Chapter 9—The Science of Rubber Compounding. In The Science and Technology of Rubber, 4th ed.; Mark, J.E., Erman, B., Roland, C.M., Eds.; Academic Press: Boston, MA, USA, 2013; pp. 417–471. [Google Scholar]
- Stuck, B. Tackifying, Curing, and Reinforcing Resins. In Rubber Technology; Carl Hanser Verlag GmbH & Co. KG: München, Germany, 2020; pp. 641–651. [Google Scholar]
- Powers, P.O. Resins Used in Rubber. Rubber Chem. Technol. 1963, 36, 1542–1570. [Google Scholar] [CrossRef]
- Kim, S.W.; Lee, G.H.; Heo, G.S. Identification of Tackifying Resins and Reinforcing Resins in Cured Rubber. Rubber Chem. Technol. 1999, 72, 181–198. [Google Scholar] [CrossRef]
- Aubrey, D.W. The Nature and Action of Tackifier Resins. Rubber Chem. Technol. 1988, 61, 448–469. [Google Scholar] [CrossRef]
- Vleugels, N.; Pille-Wolf, W.; Dierkes, W.K.; Noordermeer, J.W.M. Understanding the Influence of Oligomeric Resins on Traction and Rolling Resistance of Silica-Reinforced Tire Treads. Rubber Chem. Technol. 2015, 88, 65–79. [Google Scholar] [CrossRef]
- Indriasari; Noordermeer, J.; Dierkes, W. Incorporation of Oligomeric Hydrocarbon Resins for Improving the Properties of Aircraft Tire Retreads. Appl. Sci. 2021, 11, 9834. [Google Scholar] [CrossRef]
- Class, J.B.; Chu, S.G. The Viscoelastic Properties of Rubber–Resin Blends. I. The Effect of Resin Structure. J. Appl. Polym. Sci. 1985, 30, 805–814. [Google Scholar] [CrossRef]
- Class, J.B.; Chu, S.G. The Viscoelastic Properties of Rubber–Resin Blends. II. The Effect of Resin Molecular Weight. J. Appl. Polym. Sci. 1985, 30, 815–824. [Google Scholar] [CrossRef]
- Class, J.B.; Chu, S.G. The Viscoelastic Properties of Rubber–Resin Blends. III. The Effect of Resin Concentration. J. Appl. Polym. Sci. 1985, 30, 825–842. [Google Scholar] [CrossRef]
- L’Heveder, S.; Sportelli, F.; Isitman, N.A. Investigation of Solubility in Plasticised Rubber Systems for Tire Applications. Plast. Rubber Compos. 2016, 45, 319–325. [Google Scholar] [CrossRef]
- Lindemann, N.; Finger, S.; Karimi-Varzaneh, H.A.; Lacayo-Pineda, J. Rigidity of Plasticizers and Their Miscibility in Silica-Filled Polybutadiene Rubber by Broadband Dielectric Spectroscopy. J. Appl. Polym. Sci. 2022, 139, 52215. [Google Scholar] [CrossRef]
- Lindemann, N.; Schawe, J.E.K.; Lacayo-Pineda, J. Kinetics of the Glass Transition of Silica-Filled Styrene–Butadiene Rubber: The Effect of Resins. Polymers 2022, 14, 2626. [Google Scholar] [CrossRef]
- Liang, J.; Chang, S.; Feng, N. Effect of C5 Petroleum Resin Content on Damping Behavior, Morphology, and Mechanical Properties of BIIR/BR Vulcanizates. J. Appl. Polym. Sci. 2013, 130, 510–515. [Google Scholar] [CrossRef]
- Yin, C.; Zhao, X.; Zhu, J.; Hu, H.; Song, M.; Wu, S. Experimental and Molecular Dynamics Simulation Study on the Damping Mechanism of C5 Petroleum Resin/Chlorinated Butyl Rubber Composites. J. Mater. Sci. 2019, 54, 3960–3974. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, J.; Lu, Y.; Dong, D.; Wang, W.; Zhang, L. A Combined Molecular Dynamics Simulation and Experimental Method to Study the Compatibility between Elastomers and Resins. RSC Adv. 2018, 8, 14401–14413. [Google Scholar] [CrossRef]
- Dae Han, C.; Kim, J.; Man Baek, D.; Gun Chu, S. Viscoelastic Behavior, Order-Disorder Transition, and Phase Equilibria in Mixtures of a Block Copolymer and an Endblock-Associating Resin. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 315–341. [Google Scholar] [CrossRef]
- Harper, M.; Tardiff, J.; Haakenson, D.; Joandrea, M.; Knych, M. Tire Tread Performance Modification Utilizing Polymeric Additives. SAE Int. J. Veh. Dyn. Stab. NVH 2017, 2, 179–189. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, R.; Wemyss, A.M.; Du, A.; Bao, X.; Geng, X.; Wan, C. Damping and Electromechanical Behavior of Ionic-Modified Brominated Poly(Isobutylene- Co -Isoprene) Rubber Containing Petroleum Resin C5. Ind. Eng. Chem. Res. 2022, 61, 3063–3074. [Google Scholar] [CrossRef]
- Ye, N.; Wu, Z.; Wu, X.; Lu, Y.; Zhang, L. Performance Enhancement of Polymerized, Functionalized Solution Styrene–Butadiene Rubber Composites Using Oligomeric Resin towards Extremely Safe and Energy-Saving Tires. Polymers 2022, 14, 2928. [Google Scholar] [CrossRef]
- Wu, C.; Wu, G.; Wu, C. Dynamic Mechanical Properties in Blends of Poly(Styrene-b-Isoprene-b-Styrene) with Aromatic Hydrocarbon Resin. J. Appl. Polym. Sci. 2006, 102, 4157–4164. [Google Scholar] [CrossRef]
- Schmidt-Rohr, K.; Spiess, H.W. Multidimensional Solid-State NMR and Polymers; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Saalwächter, K.; Spiess, H.W. Solid-State NMR of Polymers. In Polymer Science: A Comprehensive Reference; Matyjaszewski, K., Möller, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 185–219. [Google Scholar]
- Saalwächter, K.; Reichert, D. Polymer Applications of NMR. Encycl. Spectrosc. Spectrom. 2016, 695–708. [Google Scholar] [CrossRef]
- Zhang, R.; Miyoshi, T.; Sun, P. NMR Methods for Characterization of Synthetic and Natural Polymers; Royal Society of Chemistry: London, UK, 2019. [Google Scholar]
- Müller, K.; Geppi, M. Chapter 8—Application of SSNMR to Selected Classes of Systems. In Solid State NMR: Principles, Methods and Applications; Wiley-VCH: Weinheim, Germany, 2021; pp. 447–530. [Google Scholar]
- Saalwächter, K. Microstructure and Molecular Dynamics of Elastomers as Studied By Advanced Low-Resolution Nuclear Magnetic Resonance Methods. Rubber Chem. Technol. 2012, 85, 350–386. [Google Scholar] [CrossRef]
- Besghini, D.; Mauri, M.; Simonutti, R. Time Domain NMR in Polymer Science: From the Laboratory to the Industry. Appl. Sci. 2019, 9, 1801. [Google Scholar] [CrossRef]
- Geppi, M.; Harris, R.K.; Kenwright, A.M.; Say, B.J. A Method for Analysing Proton NMR Relaxation Data from Motionally Heterogeneous Polymer Systems. Solid State Nucl. Magn. Reson. 1998, 12, 15–20. [Google Scholar] [CrossRef] [PubMed]
- Forte, C.; Geppi, M.; Malvaldi, M.; Mattoli, V. Dynamics of an Amorphous Polymer by an Improved NMR Approach Based on the Simultaneous Analysis of 1H and 13C Relaxation Times. J. Phys. Chem. B 2004, 108, 10832–10837. [Google Scholar] [CrossRef]
- Martini, F.; Borsacchi, S.; Spera, S.; Carbonera, C.; Cominetti, A.; Geppi, M. P3HT/PCBM Photoactive Materials for Solar Cells: Morphology and Dynamics by Means of Solid-State NMR. J. Phys. Chem. C 2013, 117, 131–139. [Google Scholar] [CrossRef]
- TECHNICAL DATA SHEET Kristalex™ 5140 Hydrocarbon Resin. Available online: www.synthomer.com/Media/tds/Kristalex%205140%20Hydrocarbon%20Resin.pdf (accessed on 23 January 2023).
- Saville, B.; Watson, A.A. Structural Characterization of Sulfur-Vulcanized Rubber Networks. Rubber Chem. Technol. 1967, 40, 100–148. [Google Scholar] [CrossRef]
- Mathematica, Version 12; Wolfram Research, Inc.: Champaign, IL, USA, 2010.
- Maus, A.; Hertlein, C.; Saalwächter, K. A Robust Proton NMR Method to Investigate Hard/Soft Ratios, Crystallinity, and Component Mobility in Polymers. Macromol. Chem. Phys. 2006, 207, 1150–1158. [Google Scholar] [CrossRef]
- Papon, A.; Saalwächter, K.; Schäler, K.; Guy, L.; Lequeux, F.; Montes, H. Low-Field NMR Investigations of Nanocomposites: Polymer Dynamics and Network Effects. Macromolecules 2011, 44, 913–922. [Google Scholar] [CrossRef]
- Räntzsch, V.; Haas, M.; Özen, M.B.; Ratzsch, K.F.; Riazi, K.; Kauffmann-Weiss, S.; Palacios, J.K.; Müller, A.J.; Vittorias, I.; Guthausen, G.; et al. Polymer Crystallinity and Crystallization Kinetics via Benchtop 1H NMR Relaxometry: Revisited Method, Data Analysis, and Experiments on Common Polymers. Polymer 2018, 145, 162–173. [Google Scholar] [CrossRef]
- Borsacchi, S.; Sudhakaran, U.P.; Calucci, L.; Martini, F.; Carignani, E.; Messori, M.; Geppi, M. Rubber-Filler Interactions in Polyisoprene Filled with in Situ Generated Silica: A Solid State NMR Study. Polymers 2018, 10, 822. [Google Scholar] [CrossRef]
- Nardelli, F.; Martini, F.; Lee, J.; Lluvears-Tenorio, A.; La Nasa, J.; Duce, C.; Ormsby, B.; Geppi, M.; Bonaduce, I. The Stability of Paintings and the Molecular Structure of the Oil Paint Polymeric Network. Sci. Rep. 2021, 11, 1–13. [Google Scholar] [CrossRef]
- Perez, M.G.; Lima, A.P.; Moraes, T.B.; Chaves, E.G.; Ruiz, N.M.D.S.; dos Santos Teixeira, S.C.; Honorato, H.D.A.; de Menezes, S.M.C.; deAzevedo, E.R. 1H Time Domain NMR to Probe Microstructural and Mobility Changes in Polyamide 11 Exposed to H2S Scavengers. What Type of Information Can Be Assessed? Polym. Degrad. Stab. 2022, 202, 110001. [Google Scholar] [CrossRef]
- Schäler, K.; Roos, M.; Micke, P.; Golitsyn, Y.; Seidlitz, A.; Thurn-Albrecht, T.; Schneider, H.; Hempel, G.; Saalwächter, K. Basic Principles of Static Proton Low-Resolution Spin Diffusion NMR in Nanophase-Separated Materials with Mobility Contrast. Solid State Nucl. Magn. Reson. 2015, 72, 50–63. [Google Scholar] [CrossRef]
- Hansen, E.W.; Kristiansen, P.E.; Pedersen, B. Crystallinity of Polyethylene Derived from Solid-State Proton NMR Free Induction Decay. J. Phys. Chem. B 1998, 102, 5444–5450. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Clarendon Press: Oxford, UK; London, UK, 1961. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Science Publication: Oxford, UK; London, UK, 1986. [Google Scholar]
- de Gennes, P.G. Reptation of a Polymer Chain in the Presence of Fixed Obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Rouse, P.E. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Kimmich, R.; Fatkullin, N. Polymer Chain Dynamics and NMR. Adv. Polym. Sci. 2004, 170, 1–113. [Google Scholar] [CrossRef]
- Stapf, S.; Lozovoi, A. Chapter 13. Field-Cycling Relaxometry of Polymers. In Field-Cycling NMR Relaxometry; Kimmich, R., Ed.; The Royal Society of Chemistry: Cambridge, UK, 2018; pp. 322–357. [Google Scholar]
- Kariyo, S.; Stapf, S. Influence of Cross-Link Density and Deformation on the NMR Relaxation Dispersion of Natural Rubber. Macromolecules 2002, 35, 9253–9255. [Google Scholar] [CrossRef]
- Kariyo, S.; Stapf, S. NMR Relaxation Dispersion of Vulcanized Natural Rubber. Solid State Nucl. Magn. Reson. 2004, 25, 64–71. [Google Scholar] [CrossRef]
- Kariyo, S.; Stapf, S. Restricted Molecular Dynamics of Polymer Chains by Means of NMR Field Cycling Relaxometry. Macromol. Chem. Phys. 2005, 206, 1300–1310. [Google Scholar] [CrossRef]
- Martini, F.; Carignani, E.; Nardelli, F.; Rossi, E.; Borsacchi, S.; Cettolin, M.; Susanna, A.; Geppi, M.; Calucci, L. Glassy and Polymer Dynamics of Elastomers by 1H Field-Cycling NMR Relaxometry: Effects of Cross-Linking. Macromolecules 2020, 53, 10028–10039. [Google Scholar] [CrossRef] [PubMed]
- Nardelli, F.; Martini, F.; Carignani, E.; Rossi, E.; Borsacchi, S.; Cettolin, M.; Susanna, A.; Arimondi, M.; Giannini, L.; Geppi, M.; et al. Glassy and Polymer Dynamics of Elastomers by 1H-Field-Cycling NMR Relaxometry: Effects of Fillers. J. Phys. Chem. B 2021, 125, 4546–4554. [Google Scholar] [CrossRef] [PubMed]
- Nardelli, F.; Calucci, L.; Carignani, E.; Borsacchi, S.; Cettolin, M.; Arimondi, M.; Giannini, L.; Geppi, M.; Martini, F. Influence of Sulfur-Curing Conditions on the Dynamics and Crosslinking of Rubber Networks: A Time-Domain NMR Study. Polymers 2022, 14, 767. [Google Scholar] [CrossRef] [PubMed]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Ding, Y.; Sokolov, A.P. Breakdown of Time−Temperature Superposition Principle and Universality of Chain Dynamics in Polymers. Macromolecules 2006, 39, 3322–3326. [Google Scholar] [CrossRef]
- Blochowicz, T.; Gainaru, C.; Medick, P.; Tschirwitz, C.; Rössler, E.A. The Dynamic Susceptibility in Glass Forming Molecular Liquids: The Search for Universal Relaxation Patterns II. J. Chem. Phys. 2006, 124, 134503. [Google Scholar] [CrossRef]
- Kremer, F.; Schönhals, A. Broadband Dielectric Spectroscopy; Kremer, F., Schönhals, A., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).