Novel Method for Bridge Structural Full-Field Displacement Monitoring and Damage Identification
Abstract
1. Introduction
2. Full-Field Displacement Monitoring of a Structure Based on Natural Texture Feature Monitoring
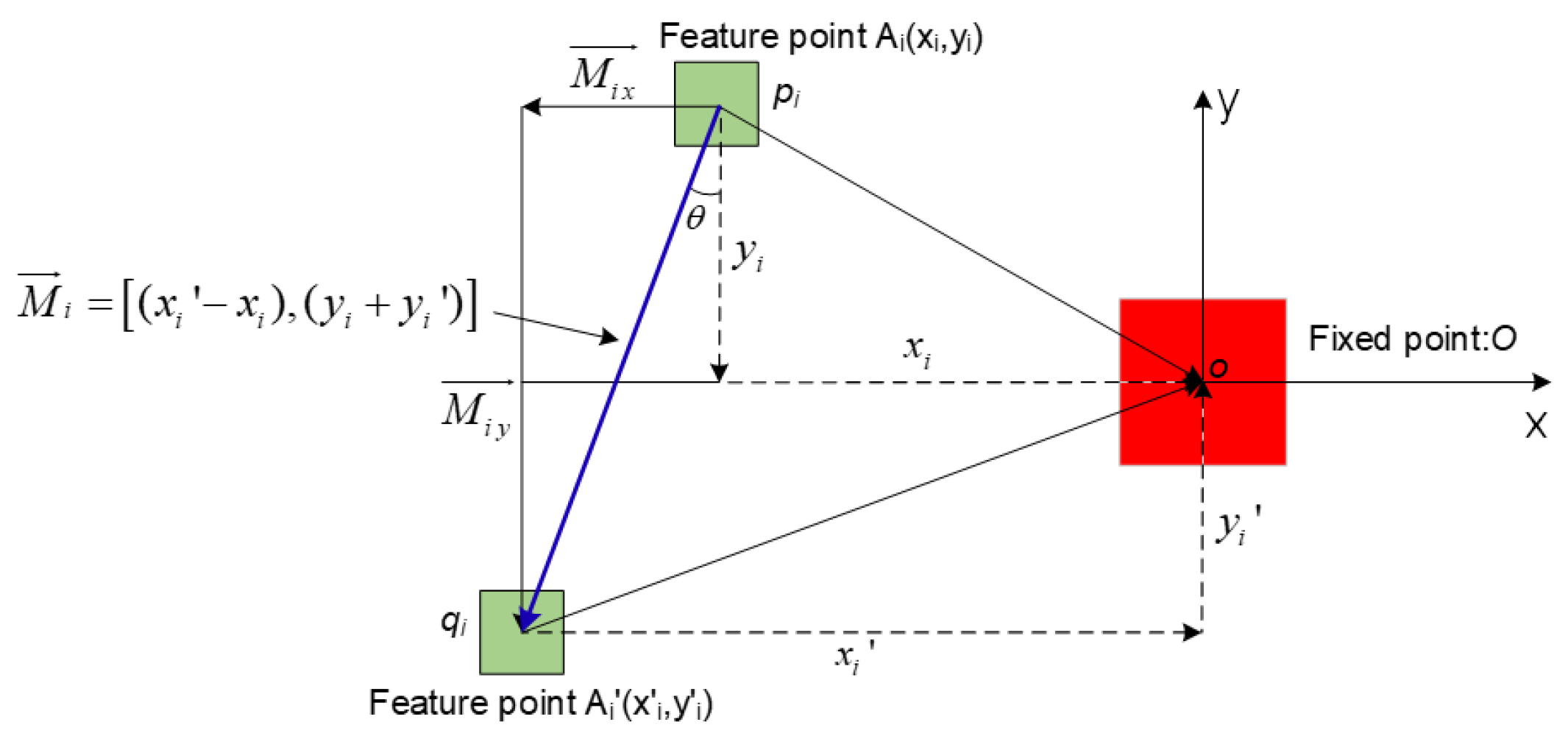
2.1. Full-Field Displacement Vector (FFDV) Point Source Generation Method
2.2. Calculation Method of the Structure’s FFDV
2.3. Full-Field Displacement Monitoring Test of the Structure
2.4. Calibration of Test Beam’s Image Monitoring Resolution
2.5. The Structure’s Full-Field Displacement Monitoring Results under Natural Texture Conditions
2.6. Validation of the Structure’s FFDV Accuracy
2.7. Monitoring Steps of Structural Full-Field Displacement
3. Damage Identification Method Based on FFDV Monitoring
3.1. Analysis of Damage Identification Index Applicable to FFDV Monitoring
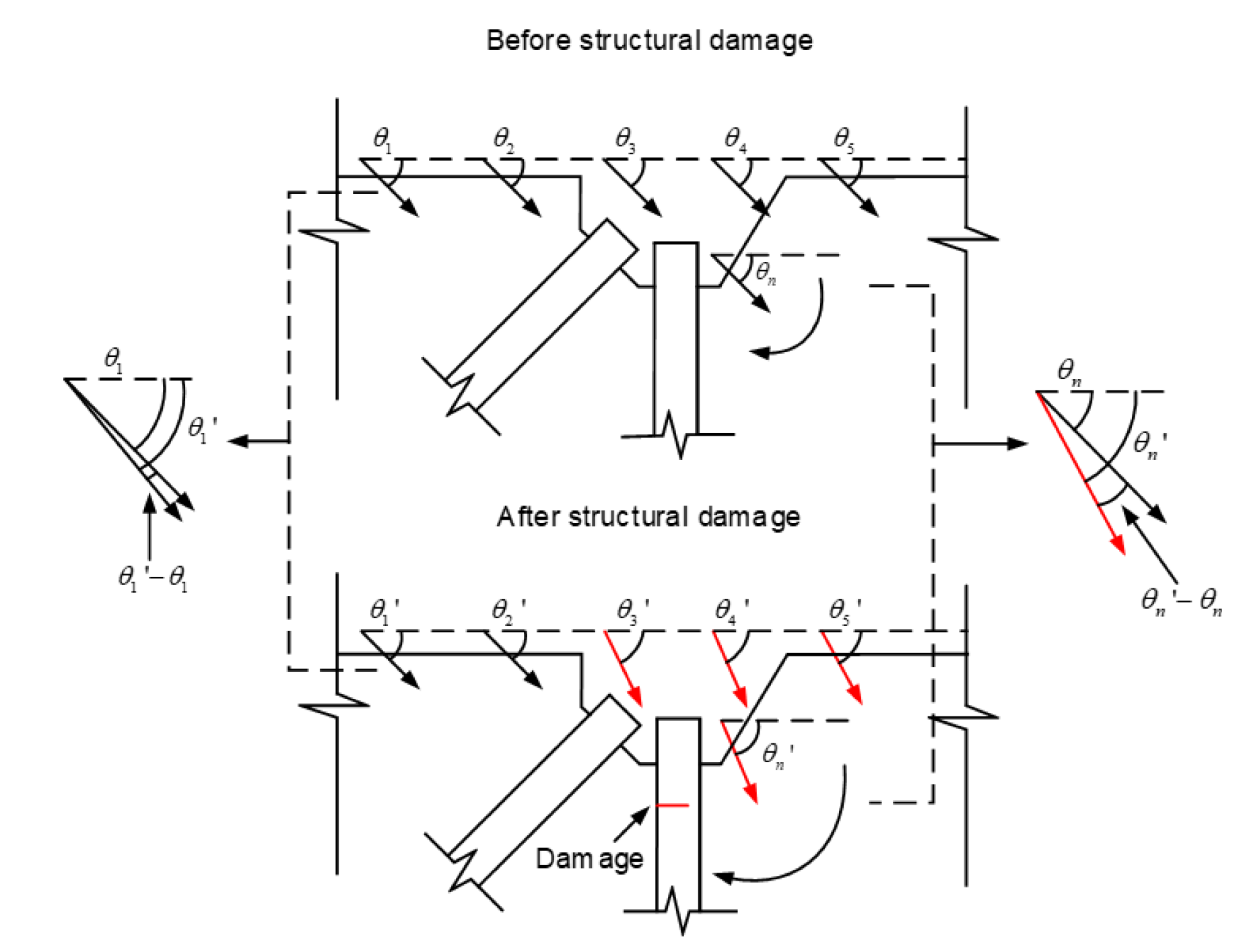
3.2. Damage Identification Index for the FFDV of the Structure
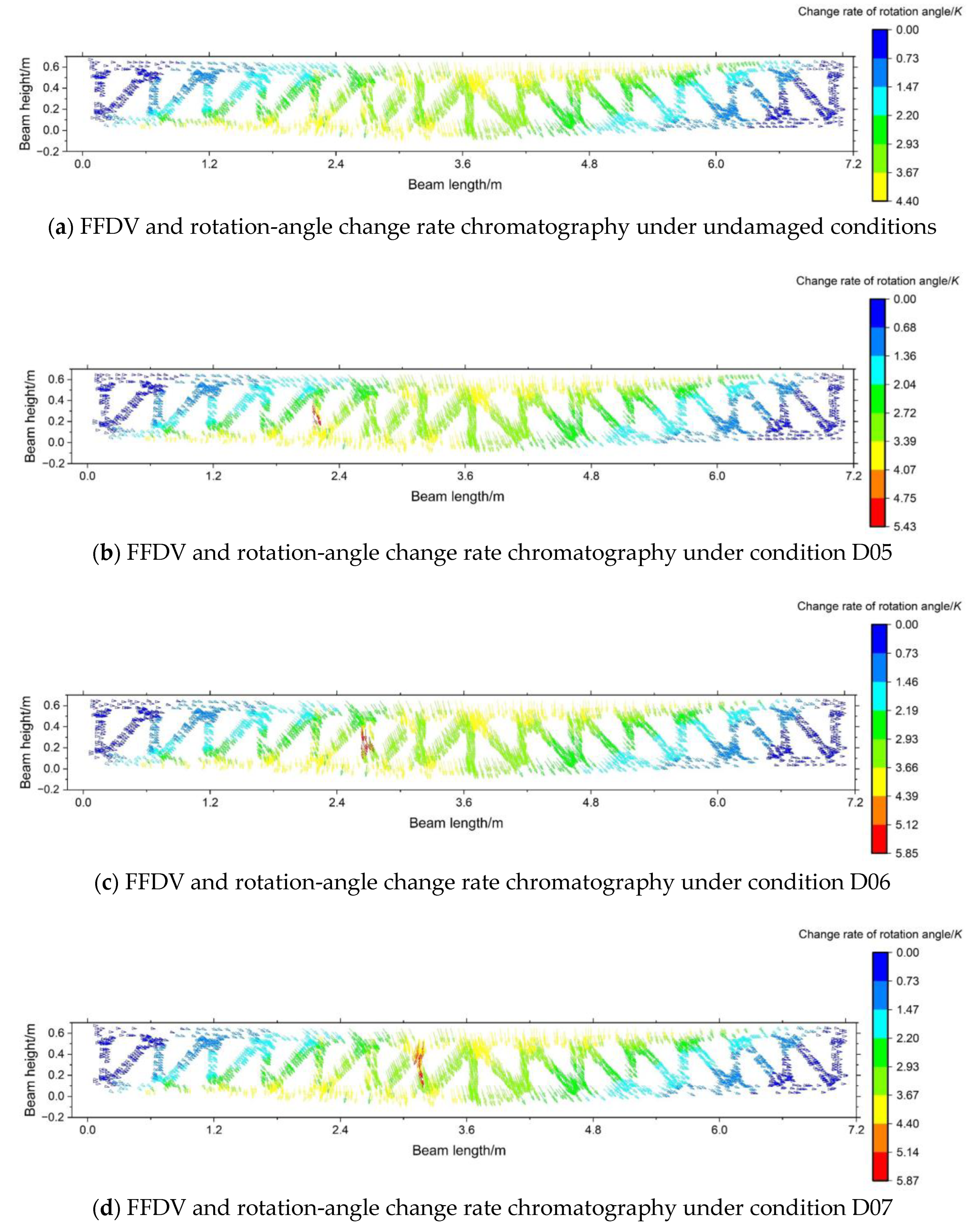
3.3. Validation of FFDV’s Rotation-Angle Change Rate Damage Identification Index
3.4. Damage Identification Program for the Structure Based on the Rotation-Angle Change Rate of the FFDV
4. Conclusions
- The image scale-invariant feature transform (SIFT) algorithm can be used to extract the natural texture features of a structure surface. Arranging a fixed point can constrain the positions of the feature points on the structure surface before and after deformation. The FFDV of the structure surface can be extracted by calculating the relative positional relationships between the feature points and the fixed point before and after deformation.
- A method to calibrate the monitoring resolution of structural images was proposed. The method calibrates the monitoring resolution by using the length of the feature line and the number of pixels represented by the feature line. The calibration results showed that the monitoring resolution of the test beam image in this study was 0.1771 mm.
- Results obtained with 3D laser scanning validated the accuracy of the FFDV of the structure. The validation results showed that the maximum absolute error of the full-field vector length was 0.48 mm and that the maximum absolute error of the rotation angle was 0.82°, indicating that the extracted displacement vector can accurately reflect the full-field displacement characteristics of a structure.
- The displacement vector of a structurally damaged section has been shown to indicate an abnormal rotation angle. Based on this finding, a damage identification index was proposed considering changes in rotation-angle rate. The index was proven to be applicable in the full-field displacement monitoring of the structure. Furthermore, the identification effect of this index was validated via various tests. The validation results showed that the identification index indicated an abnormal peak response at the damage location, validating the accuracy of the index in damage location identification.
- The structural FFDV extraction method expands conventional structural deformation monitoring data. Improving monitoring data dimensions renders the damage signal more intuitive, which is beneficial in solving the damage identification challenges caused by sparse monitoring data.
- The full-field displacement monitoring method proposed in this work demonstrated favorable results in the laboratory. However, actual bridge structural environments are more complicated than the laboratory environment. In particular, the noise in images is more significant. Therefore, the noise-interference problem associated with this method is recommended as a subject for future studies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, J.; Lee, K.-C.; Jeong, S.; Lee, Y.-J.; Sim, S.-H. Long-term displacement measurement of full-scale bridges using camera ego-motion compensation. Mech. Syst. Signal Process. 2020, 140, 106651. [Google Scholar] [CrossRef]
- Ngeljaratan, L.; Moustafa, M.A. Structural health monitoring and seismic response assessment of bridge structures using target-tracking digital image correlation. Eng. Struct. 2020, 213, 110551. [Google Scholar] [CrossRef]
- Meng, L.; Zou, J.; Liu, G. Research on the Design and Automatic Recognition Algorithm of Subsidence Marks for Close-Range Photogrammetry. Sensors 2020, 20, 544. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.Z.; Celik, O.; Catbas, F.N.; O’Brien, E.J.; Taylor, S. Structural displacement monitoring using deep learning-based full field optical flow methods. Struct. Infrastruct. Eng. 2020, 16, 51–71. [Google Scholar] [CrossRef]
- Chen, G.; Liang, Q.; Zhong, W.; Gao, X.; Cui, F. Homography-based measurement of bridge vibration using UAV and DIC method. Measurement 2020, 170, 108683. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, C.; Jiang, S.; Zhang, J.; Duan, W.H. Noncontact cable force estimation with unmanned aerial vehicle and computer vision. Comput. Civ. Infrastruct. Eng. 2020, 36, 73–88. [Google Scholar] [CrossRef]
- Yu, S.; Xu, Z.; Su, Z.; Zhang, J. Two flexible vision-based methods for remote deflection monitoring of a long-span bridge. Measurement 2021, 181, 109658. [Google Scholar] [CrossRef]
- Lee, Z.-K.; Bonopera, M.; Hsu, C.-C.; Lee, B.-H.; Yeh, F.-Y. Long-term deflection monitoring of a box girder bridge with an optical-fiber, liquid-level system. Structures 2022, 44, 904–919. [Google Scholar] [CrossRef]
- Lee, Z.K. Bridge Safety Monitoring Integrated System with Full Optical Fiber and the Method for Sensing Thereof. Japanese Patent No. 5, 542, 980, 21 March 2014. [Google Scholar]
- Lee, Z.K. Bridge Safety Monitoring Integrated System with Full Optical Fiber and the Method for Sensing Thereof. US Patent No. 9, 183, 739, 16 August 2015. [Google Scholar]
- Lee, Z.K. Optical Fiber Sensing Method. Unitary Patent No. EP3457105, 21 December 2020. [Google Scholar]
- Quqa, S.; Martakis, P.; Movsessian, A.; Pai, S.; Reuland, Y.; Chatzi, E. Two-step approach for fatigue crack detection in steel bridges using convolutional neural networks. J. Civ. Struct. Health Monit. 2021, 12, 127–140. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, H.; Huang, M. A deep learning-based fine crack segmentation network on full-scale steel bridge images with complicated backgrounds. IEEE Access 2021, 9, 114989–114997. [Google Scholar] [CrossRef]
- Peng, X.; Zhong, X.; Zhao, C.; Chen, A.; Zhang, T. A UAV-based machine vision method for bridge crack recognition and width quantification through hybrid feature learning. Constr. Build. Mater. 2021, 299, 123896. [Google Scholar] [CrossRef]
- Feroz, S.; Dabous, S.A. UAV-Based Remote Sensing Applications for Bridge Condition Assessment. Remote Sens. 2021, 13, 1809. [Google Scholar] [CrossRef]
- Dan, D.H.; Dan, Q. Automatic recognition of surface cracks in bridges based on 2D-APES and mobile machine vision. Measurement 2021, 168, 108429. [Google Scholar] [CrossRef]
- Khayatazad, M.; De Pue, L.; De Waele, W. Detection of corrosion on steel structures using automated image processing. Dev. Built Environ. 2020, 3, 100022. [Google Scholar] [CrossRef]
- Huang, I.; Chen, P.; Chen, S. Automated bridge coating defect recognition using U-net fully convolutional neural networks. J. Chin. Inst. Civ. Hydraul. Eng. 2021, 33, 605–617. [Google Scholar]
- Jin Lim, H.; Hwang, S.; Kim, H.; Sohn, H. Steel bridge corrosion inspection with combined vision and thermographic images. Struct. Health Monit. 2021, 20, 3424–3435. [Google Scholar] [CrossRef]
- Rahman, A.; Wu, Z.Y.; Kalfarisi, R. Semantic Deep Learning Integrated with RGB Feature-Based Rule Optimization for Facility Surface Corrosion Detection and Evaluation. J. Comput. Civ. Eng. 2021, 35, 04021018. [Google Scholar] [CrossRef]
- Prasanna, P.; Dana, K.J.; Gucunski, N. Automated Crack Detection on Concrete Bridges. IEEE Trans. Autom. Sci. Eng. 2016, 13, 591–599. [Google Scholar] [CrossRef]
- Sarvestani, A.A.; Eghtesad, M.; Fazlollahi, F.; Goshtasbi, A.; Mokhtari, K. Dynamic Modeling of an Out-Pipe Inspection Robot and Experimental Validation of the Proposed Model using Image Processing Technique. Iran. J. Sci. Technol. Trans. Mech. Eng. 2016, 40, 77–85. [Google Scholar] [CrossRef]
- Yeum, C.M.; Dyke, S.J. Vision-Based Automated Crack Detection for Bridge Inspection. Comput. Aided Civ. Infrastruct. Eng. 2015, 30, 759–770. [Google Scholar] [CrossRef]
- Morgenthal, G.; Hallermann, N.; Kersten, J. Framework for automated UAS-based structural condition assessment of bridges. Autom. Constr. 2019, 97, 77–95. [Google Scholar] [CrossRef]
- Zhong, X.; Peng, X.; Shen, M. Study on the feasibility of identifying concrete crack width with images acquired by unmanned aerial vehicles. China Civ. Eng. J. 2019, 52, 56–65. [Google Scholar]
- Liang, Y.; Cai, S.; Feng, Q.P.E. appearance inspection technology of Wuhan Tianxingzhou Yangtze River Bridge Cable Based on UAV aerial photography. J. Geod. Geodyn. 2019, 39, 1207–1210. [Google Scholar]
- Lin, W.; Sun, Y.; Yang, Q.; Lin, Y. Real-time comprehensive image processing system for detecting concrete bridges crack. Comput. Concr. 2019, 23, 445–457. [Google Scholar]
- La, H.M.; Dinh, T.H.; Pham, N.H. Automated robotic monitoring and inspection of steel structures and bridges. Robotica 2019, 37, 947–967. [Google Scholar] [CrossRef]
- Li, X.K.; Gao, C.; Guo, Y.C. Cable surface damage detection in cable-stayed bridges using optical techniques and image mosaicking. Opt. Laser Technol. 2019, 110, 36–43. [Google Scholar] [CrossRef]
- Cha, Y.J.; You, K.; Choi, W. Vision-based detection of loosened bolts using the Hough transform and support vector machines. Autom. Constr. 2016, 71, 181–188. [Google Scholar] [CrossRef]
- Huang, J.; Liu, J.; Gong, H.; Deng, X. A comprehensive review of loosening detection methods for threaded fasteners. Mech. Syst. Signal Process. 2021, 168, 108652. [Google Scholar] [CrossRef]
- Chen, L.; Xiong, H.; Yang, Z.; Long, Y.; Ding, Y.; Kong, Q. Preload measurement of steel-to-timber bolted joint using piezoceramic-based electromechanical impedance method. Measurement 2022, 190, 110725. [Google Scholar] [CrossRef]
- Tang, Z.F.; Sui, X.D.; Duan, Y.F.; Zhang, P.F.; Yun, C.B. Guided wave-based cable damage detection using wave energy transmission and reflection. Struct. Control. Health Monit. 2021, 28, e2688. [Google Scholar] [CrossRef]
- Cao, J.L.; Xu, L.; Guo, S.S.; Ding, D.X. A New Automatic Seamless Image Stitching Algorithm Based on the Gray Value of Edges. Appl. Mech. Mater. 2014, 496–500, 2241–2245. [Google Scholar] [CrossRef]
- Yan, W.; Liu, C. Three projective transformations for image stitching. Opt. Precis. Eng. 2015, 23, 2724–2731. [Google Scholar] [CrossRef]
- Song, F.; Lu, B. An Automatic Video Image Mosaic Algorithm Based on SIFT Feature Matching. Adv. Intell. Syst. Comput. 2013, 181, 879–886. [Google Scholar]
- Qiang, D.; Jinghong, L.; Chao, W. Image Mosaic Algorithm Based on Improved BRISK. J. Electron. Inf. Technol. 2017, 39, 444–450. [Google Scholar]
- Li, Y.; Li, G.; Gu, S.; Long, K. Image mosaic algorithm based on area blocking and SIFT. Opt. Precis. Eng. 2016, 24, 1197–1205. [Google Scholar]
- Ma, Y.; Ren, Z. Image Mosaic Method Based on Improved SIFT Feature Detection Algorithm. Lect. Notes Electr. Eng. 2014, 270, 771–779. [Google Scholar]










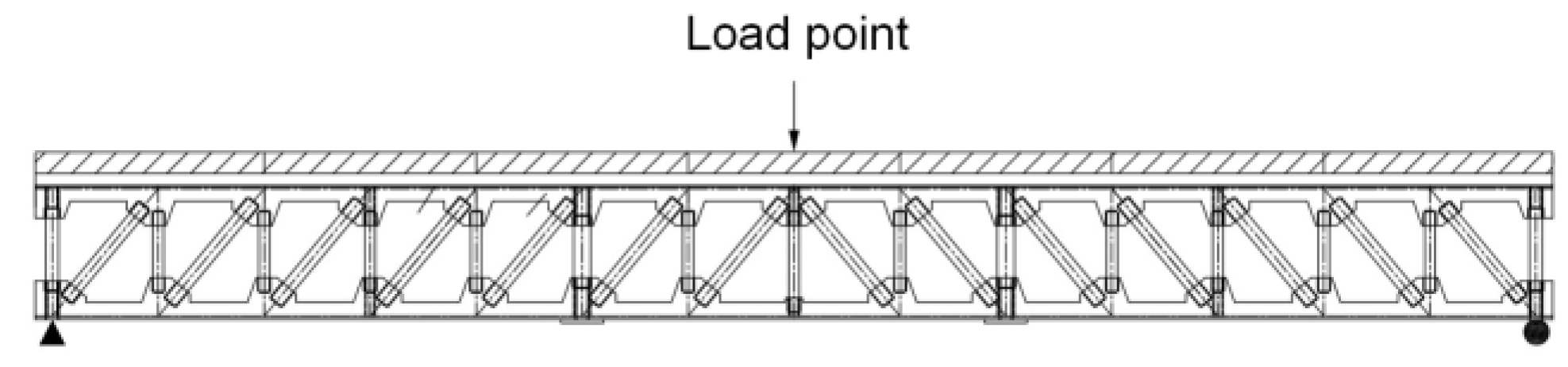
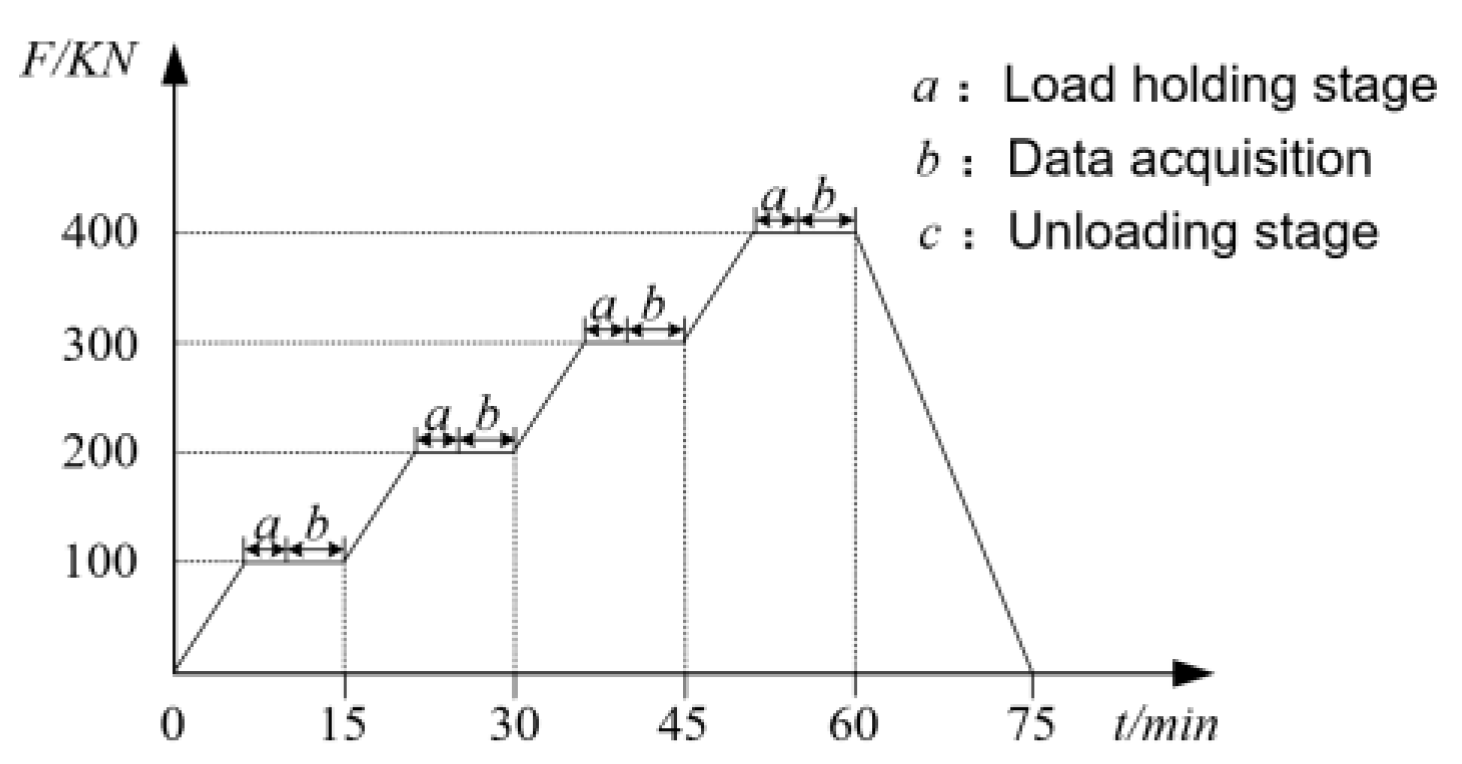

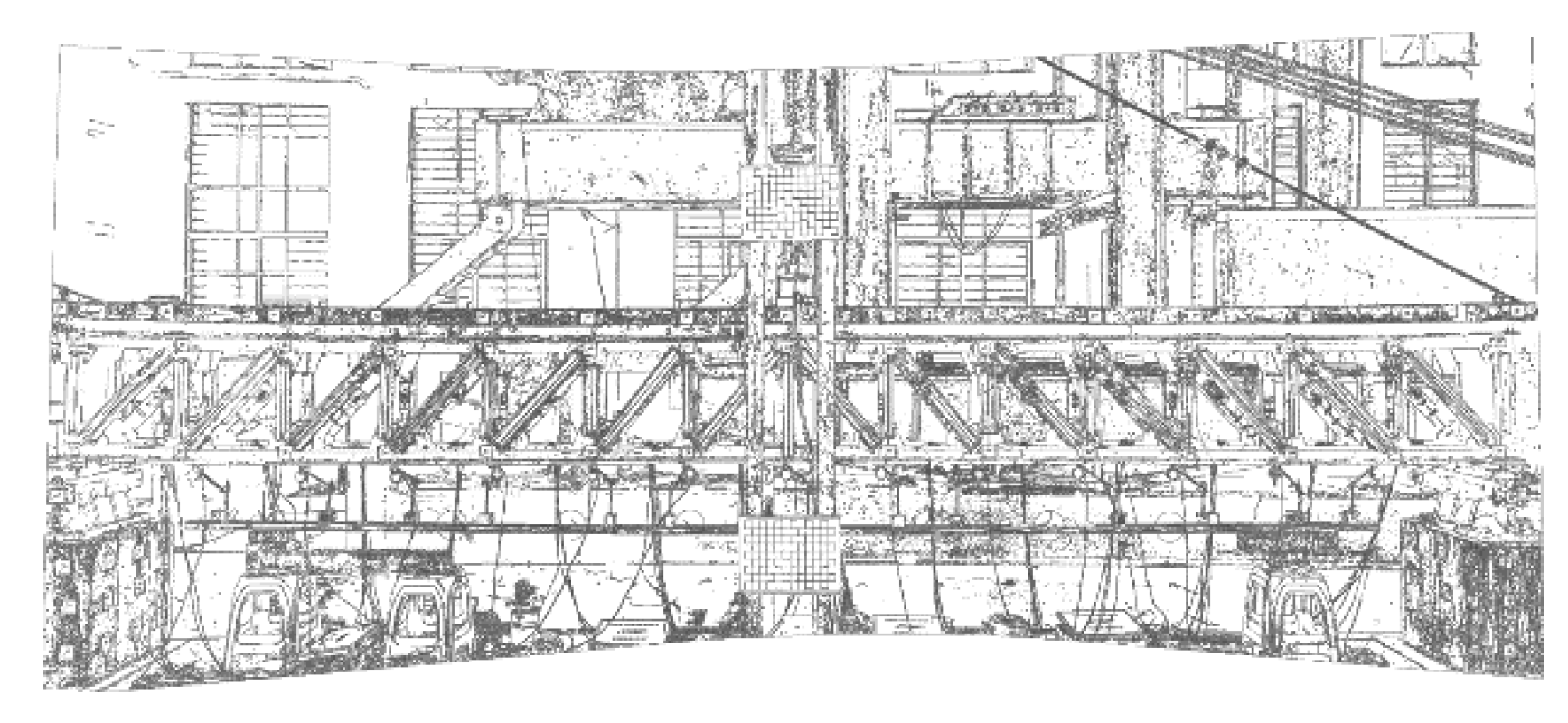



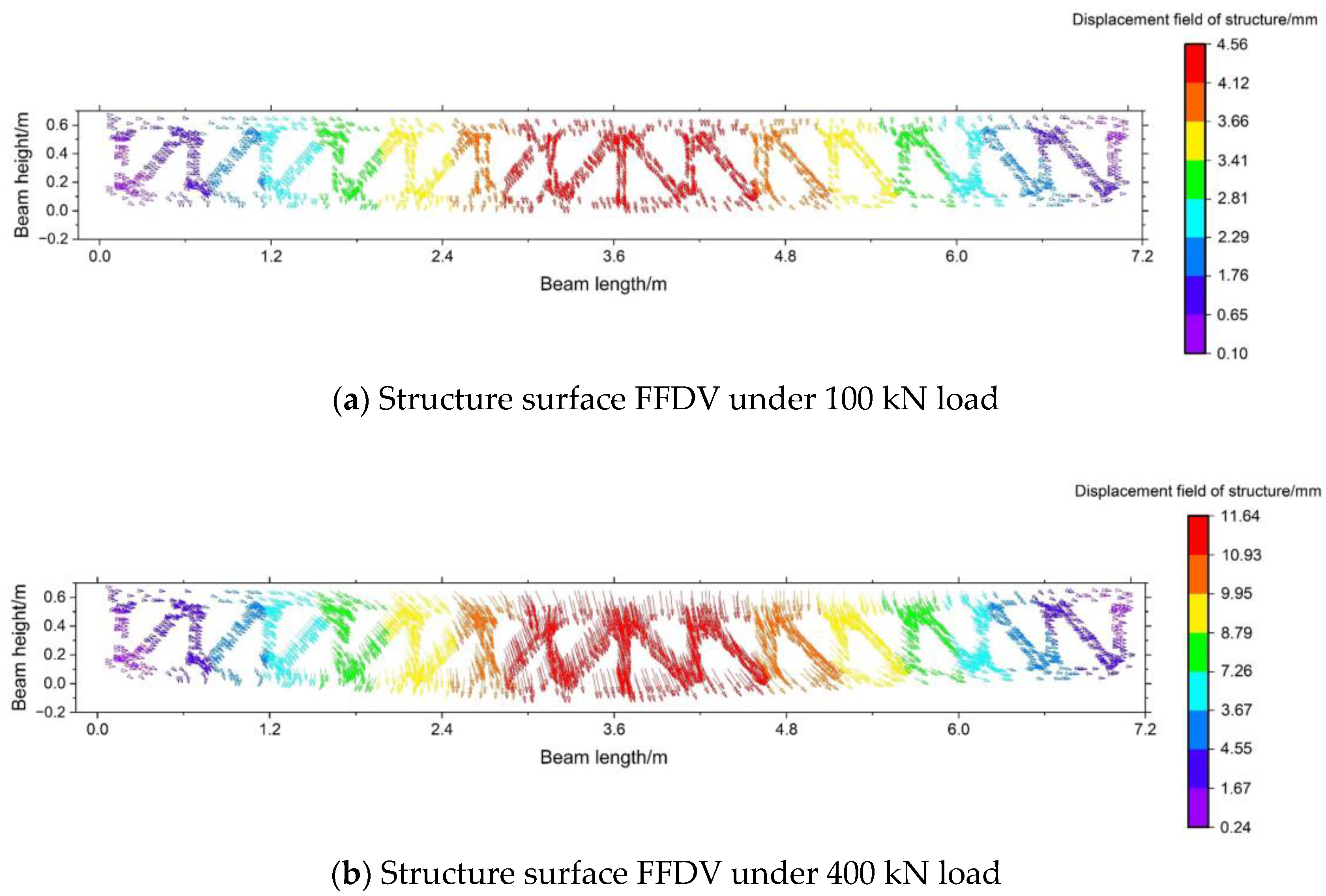
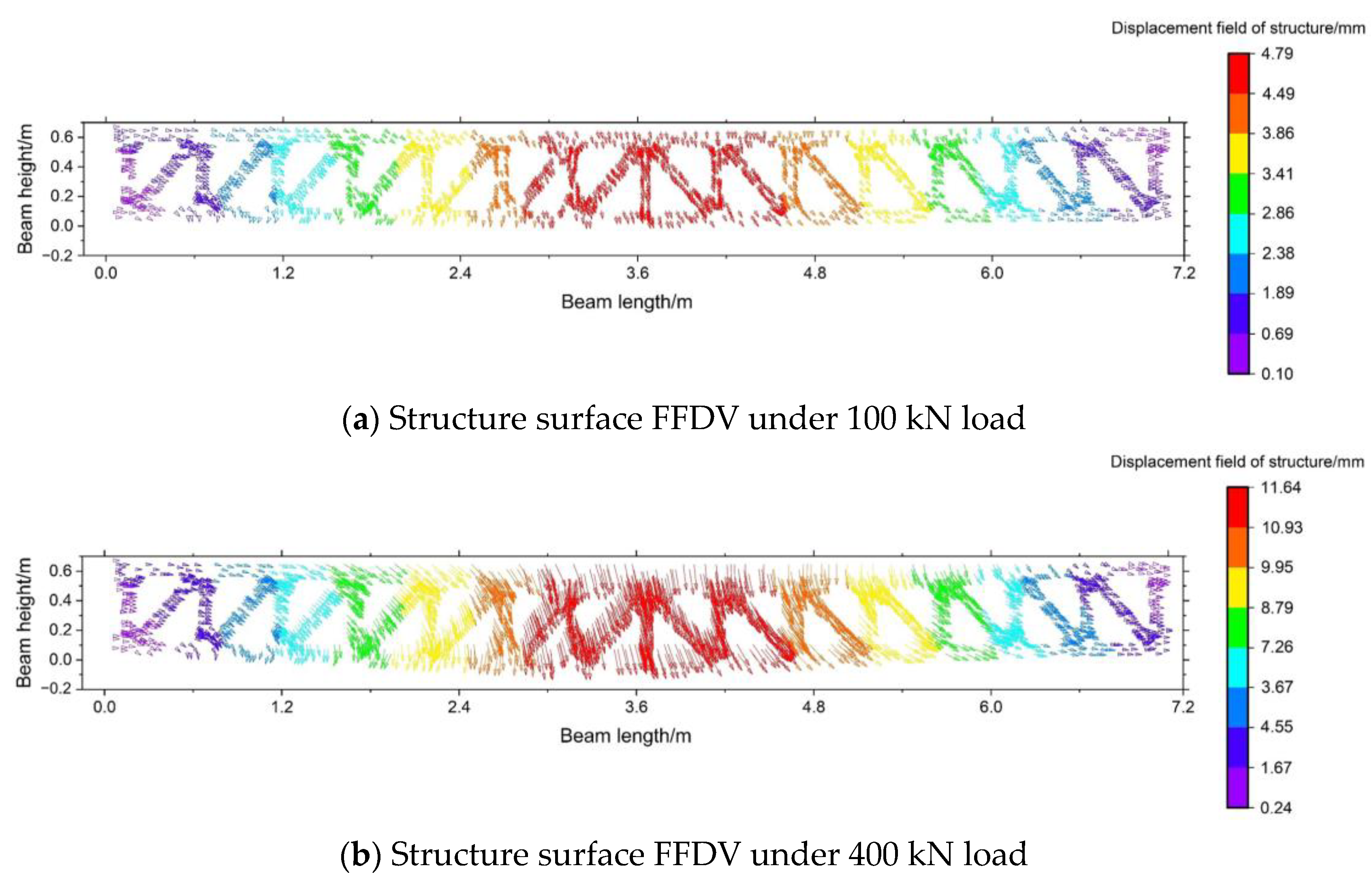
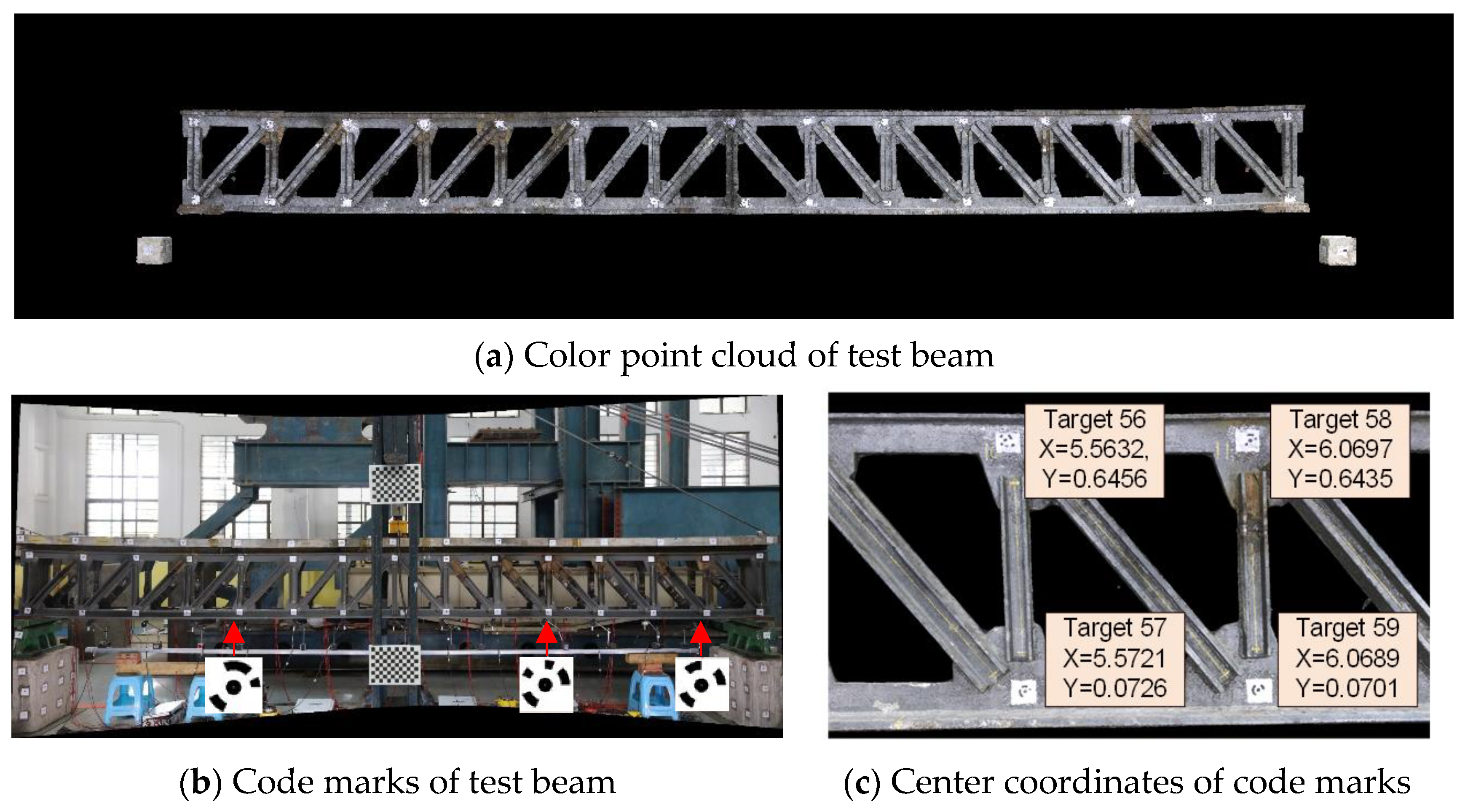



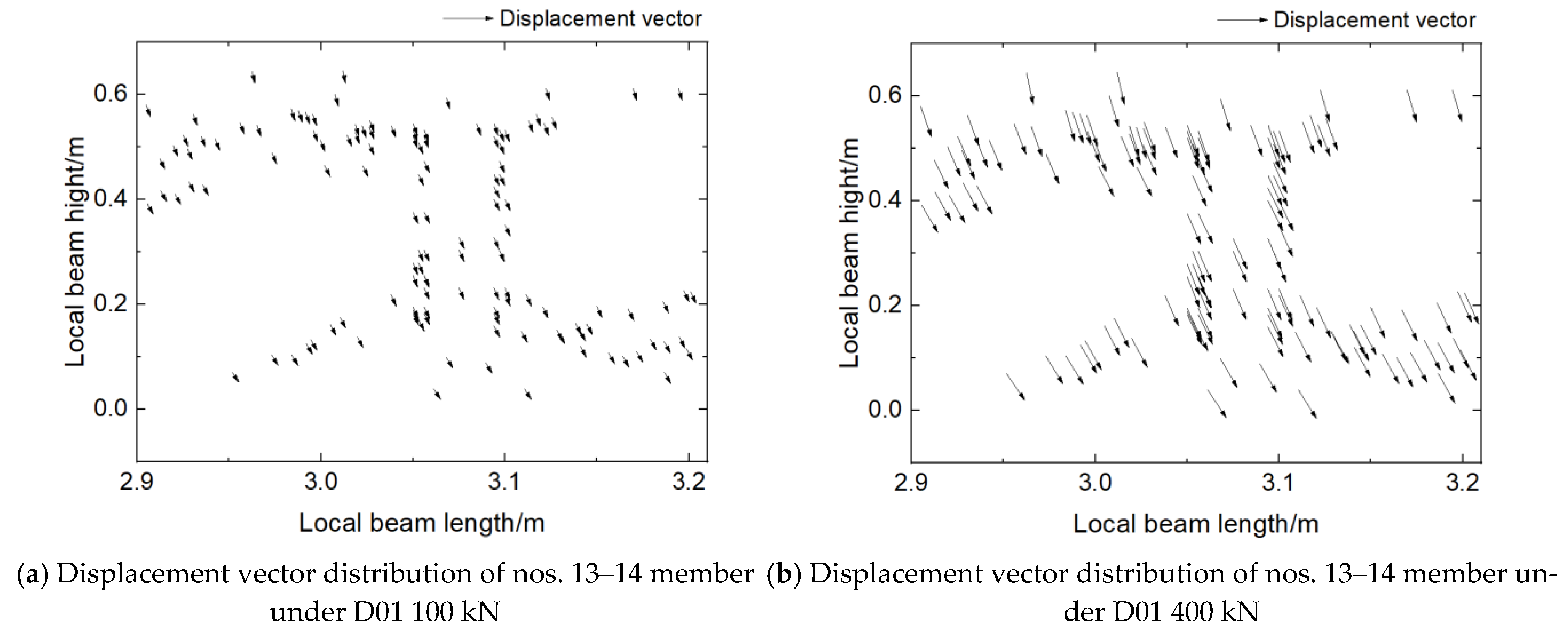

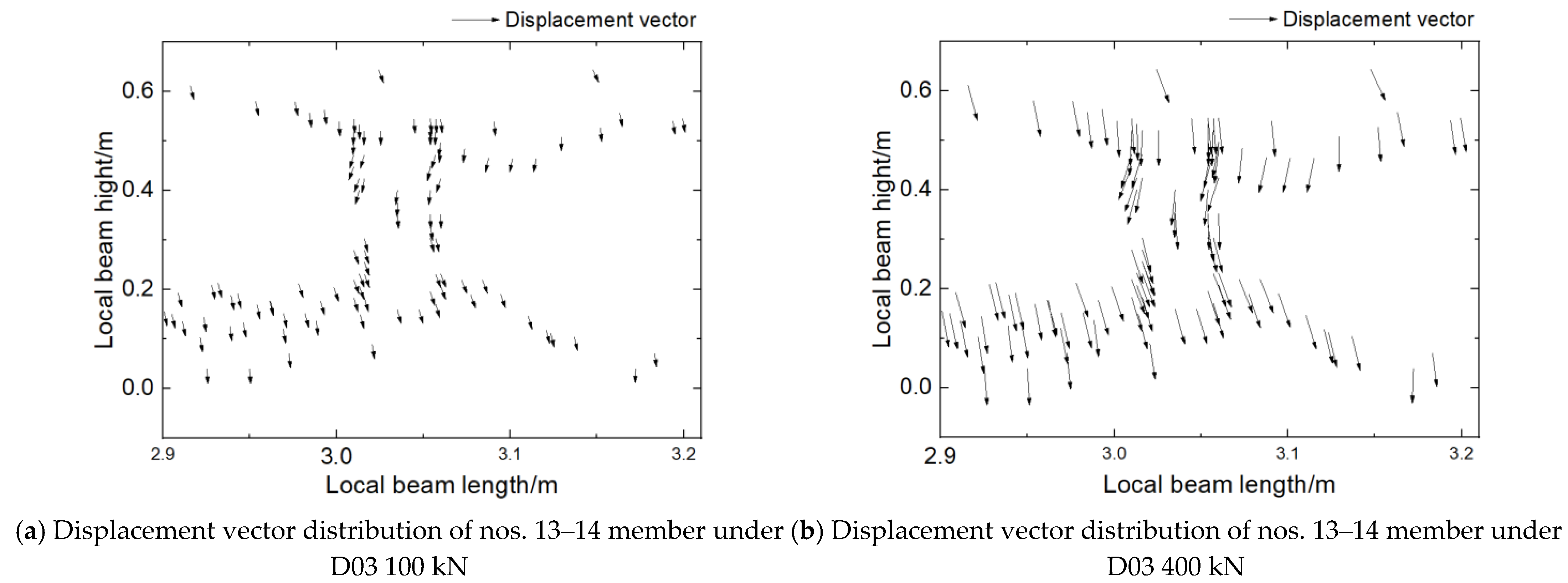


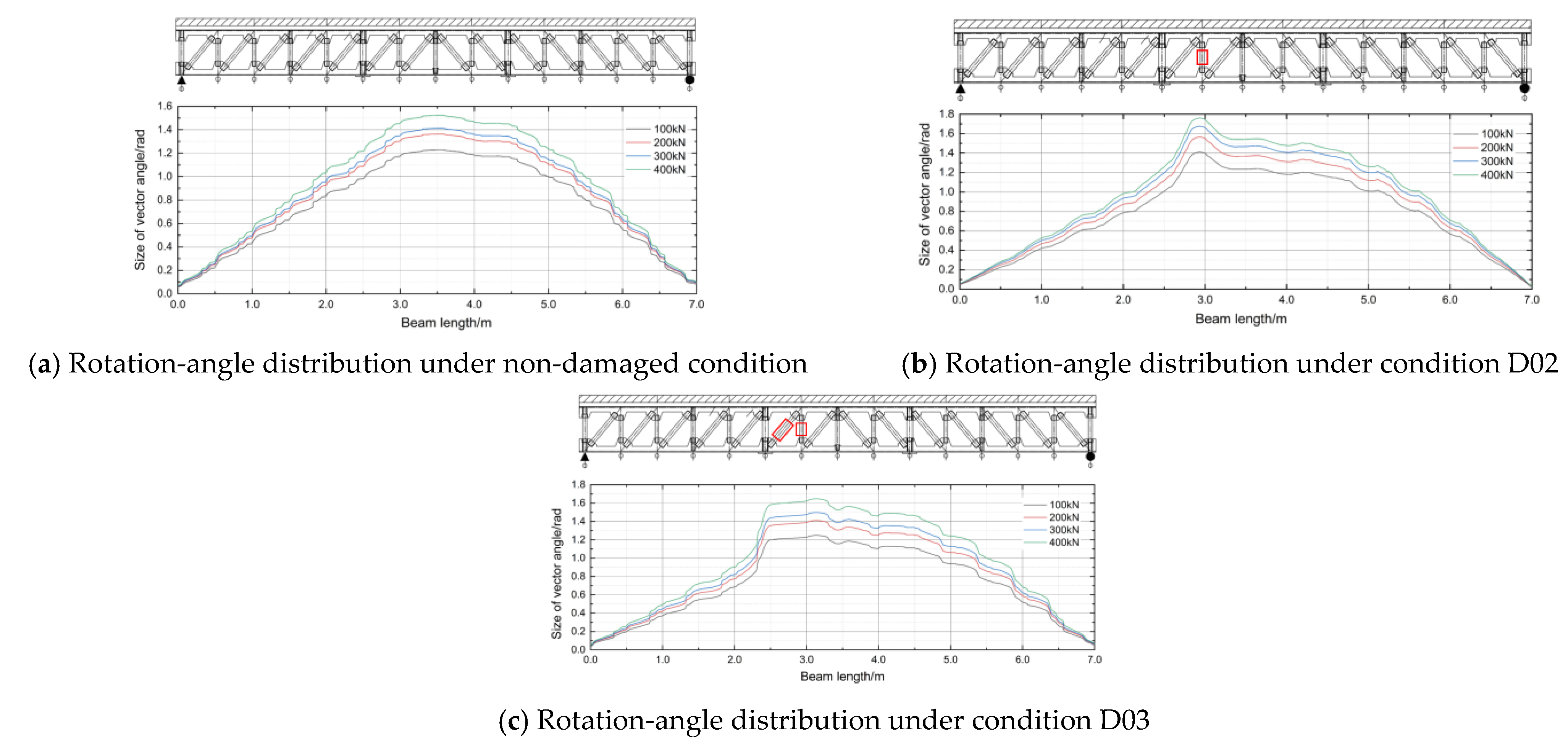




| Damage Condition | Member Type | Member No. | No. of Damaged Members | Damage Order |
|---|---|---|---|---|
| D01 | - | - | 0 | - |
| D02 | Vertical member | 13–14 | 1 | 1 |
| D03 | Vertical member Inclined member | 13–14 and 12–13 | 2 | 2 |
| Vertical Bar No. | No. of Pixels | Calibration Line Length/mm | Calibration Value mm/px | Average Value |
|---|---|---|---|---|
| 1–2 | 1986 | 367.17 | 0.1849 | 0.1771 mm/px |
| 3–4 | 1999 | 359.21 | 0.1797 | |
| 5–6 | 1993 | 360.10 | 0.1807 | |
| 7–8 | 1991 | 357.30 | 0.1795 | |
| 9–10 | 1998 | 356.32 | 0.1783 | |
| 11–12 | 1994 | 312.39 | 0.1567 | |
| 13–14 | 1989 | 355.91 | 0.1789 | |
| 15–16 | 2654 | 453.94 | 0.1710 | |
| 17–18 | 1982 | 356.83 | 0.1800 | |
| 19–20 | 1993 | 321.44 | 0.1613 | |
| 21–22 | 1988 | 357.77 | 0.1800 | |
| 23–24 | 1987 | 356.75 | 0.1795 | |
| 25–26 | 1994 | 361.37 | 0.1812 | |
| 27–28 | 1989 | 363.10 | 0.1826 | |
| 29–30 | 1983 | 359.47 | 0.1813 |
| Load Level | Deformation Extraction Position | Measured Value of Dial Indicator R1/mm | Extracted Deformation Value R2/mm | S = R2 − R1 /mm | Error Value |S|/R1/% |
|---|---|---|---|---|---|
| 100kN | 2080 | 2.92 | 2.95 | 0.03 | 1.03% |
| 3580 | 3.63 | 3.47 | −0.16 | 4.41% | |
| 5080 | 2.93 | 2.97 | 0.04 | 1.37% | |
| 200kN | 2080 | 4.76 | 4.71 | −0.05 | 1.05% |
| 3580 | 5.46 | 5.33 | −0.13 | 2.38% | |
| 5080 | 5.02 | 4.85 | −0.17 | 3.39% | |
| 300kN | 2080 | 6.45 | 6.33 | −0.12 | 1.86% |
| 3580 | 7.34 | 7.38 | 0.04 | 0.54% | |
| 5080 | 6.34 | 6.44 | 0.1 | 1.58% | |
| 400kN | 2080 | 8.18 | 8.04 | −0.14 | 1.71% |
| 3580 | 9.41 | 9.33 | −0.08 | 0.85% | |
| 5080 | 8.32 | 8.06 | −0.26 | 3.13% |
| Damage Condition | Member No. | No. of Damaged Members | Degree of Damage | Load Level | Damage Order |
|---|---|---|---|---|---|
| D04 | - | 0 | - | 300 kN | - |
| D05 | 9–10 | 1 | 50% | 1 | |
| D06 | 11–12 | 1 | 2 | ||
| D07 | 13–14 | 1 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, X.; Chu, X.; Zhu, W.; Zhou, Z.; Luo, R.; Meng, J. Novel Method for Bridge Structural Full-Field Displacement Monitoring and Damage Identification. Appl. Sci. 2023, 13, 1756. https://doi.org/10.3390/app13031756
Duan X, Chu X, Zhu W, Zhou Z, Luo R, Meng J. Novel Method for Bridge Structural Full-Field Displacement Monitoring and Damage Identification. Applied Sciences. 2023; 13(3):1756. https://doi.org/10.3390/app13031756
Chicago/Turabian StyleDuan, Xin, Xi Chu, Weizhu Zhu, Zhixiang Zhou, Rui Luo, and Junhao Meng. 2023. "Novel Method for Bridge Structural Full-Field Displacement Monitoring and Damage Identification" Applied Sciences 13, no. 3: 1756. https://doi.org/10.3390/app13031756
APA StyleDuan, X., Chu, X., Zhu, W., Zhou, Z., Luo, R., & Meng, J. (2023). Novel Method for Bridge Structural Full-Field Displacement Monitoring and Damage Identification. Applied Sciences, 13(3), 1756. https://doi.org/10.3390/app13031756






