Numerical Study of the Flow of Pollutants during Air Purification, Taking into Account the Use of Eco-Friendly Material for the Filter—Mycelium

Abstract

To improve air quality, it is customary to apply technological measures to isolate or retain pollutants by influencing the polluted stream in various ways to effectively remove the pollutants. One of the most commonly used measures is a filter, in which the air flow passes through a porous aggregate. A variety of filter materials allows very selective and precise cleaning of the air flow in non-standard or even aggressive microclimate conditions. In this paper, the environmental aspect of the used materials is discussed, and a theoretical model of an adapted mycelium is proposed as an alternative to the use of filter materials to predict air flow purification. In the created numerical model of an idealized filter, several cases are considered when the pore size of the mycelial fillers reaches 1.0, 0.5 and 0.1 mm, and the feed flow velocity reaches 1–5 m/s. Moreover, in the mycelium itself, the flow velocity can decrease and approach the wall to a value of 0.3 m/s, which is estimated for additional numerical studies of interaction with the surface. These preliminary studies are aimed at establishing indicative theoretical parameters for favorable air flow movement in the structure of the mycelium.

1. Introduction

The use and properties of mycelium can be analyzed from different angles, one of which is a problem is related to the environmental damage of the used fillers and the use of raw materials. The use of materials and resources in industry has increasingly been directed toward waste-free technology and/or reduced material/energy requirements during production and operation. In current activities, artificial synthetic materials, composites and metamaterials have been increasingly used, and so have the use of cheap but low-quality raw materials, such as for plastics (including fly ash), glass, metal, construction waste (marble dust waste) and wood (paper and pulp), as well as for other applications [1,2,3]. The use of such materials is beneficial due to their relatively low cost at the initial stage of production, but the damage they cause to the environment in the presence of a waste can be very high. In addition, their processing is particularly complex and wasteful.

The use of raw materials, especially non-renewable or slowly renewable ones, does not comply with the principles of sustainable development in the creation of technologies, structures and products and is clearly doomed to extinction due to an ever-increasing financial burden on account of its limited quantity and the principles of a circular economy. It is always necessary to consider how the resulting waste is treated during its service life, whether the feedstock is biodegradable, recyclable or recovered for new use, which is essentially the goal of the circular economy [4,5,6,7]. Based on studies, it has been established that more than 35% of the total energy/raw material requirements for the entire life cycle of a building is spent on the construction of the building [8].

Another problem is the use of filter surfaces, which are often changed due to rapid contamination. The materials of conventional designs are often substituted to meet needs, the adaptation of which allows the appropriate characteristics of such a design to be achieved. One example is the technological increase in the porosity of biochar to increase the sorption capacity of pollutants [9,10,11]. Another direction is the use of filter surfaces to trap various foreign phases in the air, water, soil and other media.

One of the most popular fiber filtration technologies is used to purify air flow. Such technologies include dry filters, such as bag filters, HEPA filters, etc., or their modifications together with cyclones or electrostatic filters. The inserts used to operate such filters are made of fibrous artificial or natural material, and to improve their properties, they are impregnated, reinforced with a metal frame or otherwise treated. Taking into account the fact that the production of these materials even before they are used in the filter creates a lot of pollution, their service life is short, because if any defect appears on the surface of the fiber, such a filler must be replaced with a new one. The resulting amounts of unusable fillers are recycled, which further increases the relative rate of pollution per unit of volume of air cleaned, and if such material cannot be processed, the waste goes into incinerators or landfills, which are currently the last and least desirable way to handle waste. In each case, filter materials are selected by taking into account process parameters, including the operating temperature and the physical and chemical properties of the filtered material (abrasiveness, stickiness, particle size and erosion resistance). The most widely used synthetic materials or various types of composites, including polypropylene, polyamide, acrylic, PPS (polyphenylene sulfide), glass fiber and PTFE (polytetrafluoroethylene), are non-degradable materials that emit organic compounds that are harmful to the human body [12].

Another problem is that there is little research on products that can be considered renewable using natural fillers. Research is underway on the use of sustainable aggregates, including biofoams, to replace commonly used petroleum-based materials. Mycelial filler, as a new material, can vary depending on the polysaccharides, lipids and chitin included in its composition, and it is attractive in that it is easily adapted and produced, has a wide range of mechanical and thermal insulation properties and is also easy to process [13,14]. Mycelium, as a filler, has an original structure, consisting of many branches in a three-dimensional space for a nutrient substrate, i.e., for sugar, absorption and transport for further growth [15]. Its biological nature somewhat limits its use at temperatures above 60 °C due to tissue death, but this neutralization/sterilization method can be used for regeneration until acceptable conditions are restored and the process can be repeated. In most studies, mycelium was studied using this material for packaging, but no studies were found where this material was considered not only as a volumetric object, but also using it in complex engineering issues, a special purpose object (for example, a tube through which air will pass). Moreover, using mycelium to filter the air.

From an ecological point of view, mycelium is a real “green raw material” because it consists of biological tissue. Mycelium-based objects do not cause significant pollution problems and avoid environmental risks due to increasing urbanization and populations [16]. At present, attempts have been made to apply eco-design to find a target area for such a new material, taking into account the mechanical properties of the material, for example, for packaging, shoes or interior details, but they are limited to research on mycelium [17]. Applied research on mycelium and composites containing mycelium has been carried out by replacing conventional building materials [13] and thus has also aimed to improve the properties of conventional materials and to reduce production and operating costs, energy consumption and general environmental pollution [18]. Studies have been conducted to reduce environmental pollution in outer space through the use of mycelial composite panels that absorb particulate matter at a low concentration of about 45 µg/m³ (in this case, PM10) [19]. A study was conducted comparing the physicochemical properties of foams based on grown mycelium and hot-pressed panels (lignocellulose substrate), and it was found that the sound absorption and heat absorption of the mycelium are significantly worse [20].

When solving problems related to the use of mycelium as a material, it is important to determine what the problem is and what the predicted result can be. In general, the purpose of this work was to study the possibilities of using mycelium as a filler and/or a raw material for air filtration. Numerical modeling was aimed at studying such filter media and using pore matrices of different porosities, corresponding to different types of mycelia and the movement of air flow, as well as its change through the media. This may allow the design of an experimental stand (in the stand using biological material) in future stages, the selection of a suitable mycelium structure, a reduction in pressure loss, and its use for air filtration by trapping particulate matter.

The main working hypotheses are as follows: when the filler has a pore size of 50 µm and its porosity is 0.2, then a pressure drop of up to 10 Pa occurs. By using a filler instead of a pore size of 20 µm and a porosity of 0.2, another filler with a pore size of 10 µm and a porosity of 0.2 can reduce pressure drops by up to 30%. Various types of mycelia can be used to potentially form a filler, whose properties are close to the desired physical properties.

There are also important general observations related to the use and analysis of mycelial material. Cellulose–mycelia foam was investigated by Hoda [21]. Here, it is proposed as a technology to develop the use of fungal mycelium, the vegetative part of a fungus, through a porous scaffold of cellulose-based foam.

Experimental and isothermal studies on the sorption of Congo red by a modified mycelial biomass of wood-rotting fungus was investigated by Binupriya et al. [22]. They showed that the autoclaved biomass of T. versicolor is an effective adsorbent for the removal of Congo red from aqueous solutions.

The identification of ectomycorrhizal mycelium in soil horizons was given by Renske et al. [23,24]. They mentioned that their study demonstrates that molecular identification methods provide a novel tool for future studies on EM fungal community dynamics. The preparation and characterization of mycelium as a bio-matrix in the fabrication of bio-composites was given by Shakir et al. [25]. In this work, morphological observations confirmed the presence of mycelium networks, which can be used as a potential bio-matrix in bio-composites. A review of the material function of mycelium-based bio-composites is given by Yang et al. [26]. They mentioned that, even though mycelium-based composites show advantages in their mechanics, light weight and many environmentally friendly features, they have limitations and challenges for large-scale applications. A study on the mechanical properties of the latex–mycelium composite was given by He et al. [27]. A study on mycelial pellets for the alleviation of membrane fouling in a membrane bioreactor was given by Xiao et al. [28]. This study provided a proof-of-concept demonstration of using mycelial pellets as bio-carriers to mitigate membrane fouling, making treatment by membrane bioreactors more efficient, more reliable and more sustainable. The metal-binding capacity of arbuscular mycorrhizal mycelium was investigated by Joner et al. [29,30]. They mentioned that fungal adaptations that enhance such filtering, e.g., extracellular adsorption or intracellular fungal sequestration, may be important mechanisms to reduce the exposure of herbivores and people to toxic metals, such as increased anthropogenic loads.

A study on the mycelial effects on phage retention during transport in a microfluidic platform was given by Ghanem et al. [31]. They mentioned that mycelia–phage interactions may further be exploited for the development of novel strategies to reduce or hinder the transport of undesirable (bio) colloidal entities in environmental filter systems. The mechanical behavior of mycelium-based particulate composites was investigated by Islam et al. [32]. They mentioned that fillers work both as nutrition for hyphae during growth and as reinforcement during mechanical functions. The mechanical possibilities of mycelium materials were investigated by Lelivelt [33]. They mentioned that composites exhibit the Mullins effect and hysteresis under cyclic compression—a behavior similar to that of unfilled mycelium. A designed study on the applications of mycelium biocomposites in architecture was given by Kırdök et al. [34]. In their work, the authors sought to consider the potential of using mycelium for the production of biocomposites in construction.

The goal of our work is to propose a possible concept for modeling mycelium as a biocomposite material with a complex structure. To achieve the goal, the following two essential tasks were set: In the case of different predicted parameters, the first task was to analyze the movement of air flow in the proposed filter model, whose material consists of mycelium. The second task was to determine the behavior of pollutants/particles during their interaction with the surface of the mycelium (inner surface of the filter).

2. Problem Formulation and Insights

The task was set from the point of view of applications, answering the question of whether it is possible to use such an ecological filter with an organic origin. Mycelium is a natural polymeric composite fibrous material. First, we tried to answer this question using numerical experiments. In the beginning, we studied how air flows in the filter and how pollutant particles interact with the inner surface of the filter. Previous studies have shown that filtration speed and efficiency are two different parameters of effective filtration. This is due to the fact that increasing the speed of air purification affects the quality of air purification. Therefore, in this paper, we tried to determine the optimal speed at which the filter can theoretically be considered effective. The composition of the considered filter includes mycelium, the mechanical properties of which correspond to a soft material. A filter made from this material is likely to trap particles quickly at the beginning of air purification but may be ineffective later. Through numerical experiments, we tried to understand this phenomenon by studying the interaction of pollutant particles with the surface of the mycelium, to see how deep the particle can penetrate, and to partially elucidate the possibility of filter clogging. Although the filter we used contained soft mycelium, we would also like to study a filter made of a composite material (with mycelium), the use of which is also described in the known literature. Thus, this paper considers not only closed-cycle production but also a new niche for the use of an organic, easily processed and therefore environmentally inert material, the properties and structure of which can be chosen no less effectively than traditional filter media. Further studies should also include a deeper analysis of the interaction of particles with the inner surface of the composite filter.

In the process of extracting contaminants, solid particles cause them to interact with the filter surface. From the point of view of mechanics, mycelium, as a material, is much softer than the solid particles of pollutants. This aspect is important both in evaluating the efficiency of a filter during filter growth/manufacturing and in predicting its durability. To study the behavior of the filter, a theoretical numerical simulation of the interaction of particles with the surface of the mycelium was carried out using the method of discrete elements. To assess filter contamination, the constructed theoretical model indicated the depth of the penetration of the solid particles. Based on the obtained results, we developed recommendations regarding filter life (in terms of the use of the filter).

3. Methods and Tools

3.1. Air Flow Study

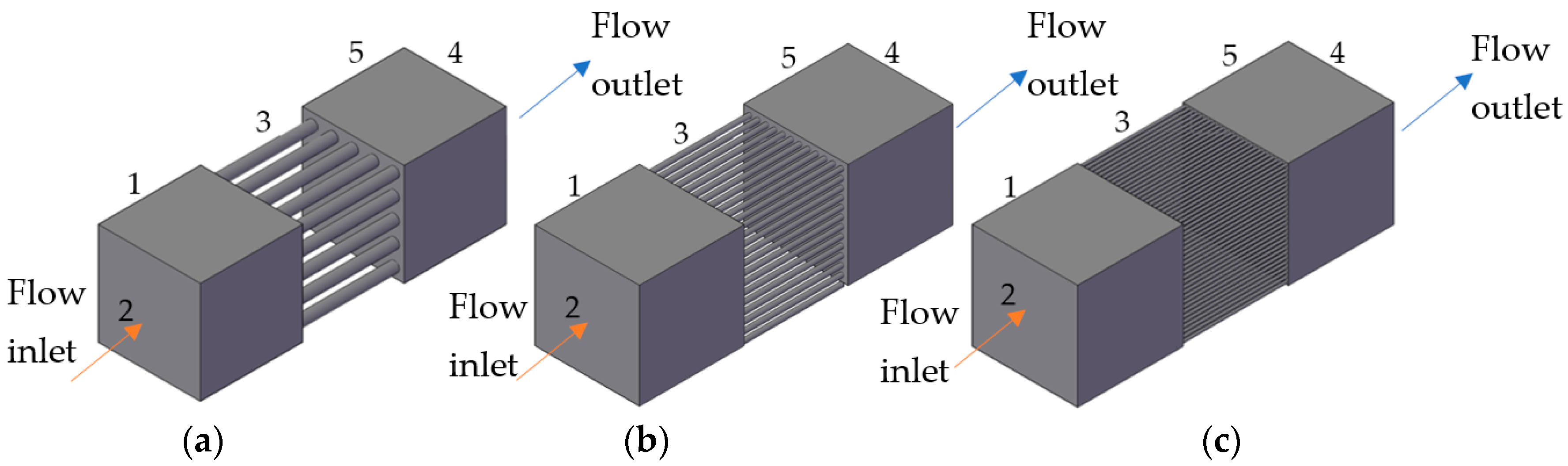
We created and applied a model of a porous filler and a gas flow object flowing through it. The object under consideration was created using the AutoCad graphical editor, consisting of three basic structures with an inflow channel (1), an inflow (inlet) plane (2), a zone of idealized longitudinal pores (3), an outflow plane (outlet) (4) and a channel outflow (5).

In this work, the emphasis is not on the accuracy of the geometry, but on the dynamics of the movement of the air flow itself, which is useful to understand before designing. In future stages, detailed studies will be carried out on a natural stand based on the results of this work.

For the model, the following analogous parameters of all three objects were taken: the sides of the inlet or outlet channel (mm) were 0.5 × 0.5 × 0.5; the length of the zone of idealized longitudinal pores was 0.5 mm; and the accepted pore sizes (diameter of longitudinal cylinders) for objects I, II and III were 50 µm, 20 µm and 10 µm, respectively. A wide range of model cases was researched for comparison with other studies [13,18,34,35,36,37]. These cases were adopted in order to analyze the main trends for the application of this mycelium media for filtration.

The shape of mycelium pores is not strictly defined. Depending on their type, the shape of mycelium of naturally growing fungi can be a straight cylinder, cone, fiber, cube, etc. [13,14,15,38,39]. Most often, mycelium pairs are formed artificially according to the need in cylinders, plates, dog-bone shapes, V-shapes and others. In this study, to simplify the initial investigation of such a structure, an idealized case of pores with a regular cylindrical shape and corresponding length compared to the inlet and outlet channels was applied. The size of the cylinders was chosen based on examples of easily grown mycelial cultures. One of the smallest pores with a diameter equal to 10 µm, an intermediate case of 20 µm and larger ones with a diameter of 50 µm were accepted. An essential condition that must be met is that the pore size must be relatively small for its application as a filter material to be effective. The pore shape can have a dual effect on the performance of such technology, the first of which is that the irregular geometry of mycelium pores as channels can cause additional obstacles for solid particles as pollutants to be retained, and this increases cleaning efficiency. On the other hand, the tortuosity of the filter medium can increase the aerodynamic drag of such a system, so it is necessary to control the amount of supplied air flow.

These cases are intended to detect the influence of the porosity of mycelium media, having a significant influence on the collection of solid particles depending on the granulometric composition of the separated particles. In other works, different densities of the mycelial filler have been used: about 0.050 g/cm³ [15], within the range of 0.015–0.075 g/cm³ [40], and within the range of 0.090–0.599 g/cm³ [18]. Pores of the microstructure of filler composites can reach 1–2 µm [41], but in most cases, their average size is about 20–50 µm. The total density of the filler (mycelium) was taken to be isotropic and equal to 300 kg/m³. For each porous filler, only the diameter and the number of longitudinal cylinders varied. Thus, the structure was composed of cylinders along and across 5 × 5 elements for object I (Figure 1a), 12 × 12 for object II (Figure 1b) and 25 × 25 for object III (Figure 1c). Schemes of these three structures are presented in Figure 1.

Air flow studies were carried out using the ANSYS Fluent program. In future stages, natural studies and model validation will be carried out to check the accuracy of the model. Three computational grids with different details were prepared for each of the three structures. The grid with the highest average quality index, but not lower than 0.85, was chosen as the optimal grid. Thus, the grids of object I consisted of 6678, 537,168 and 5,192,530 elements. The element size was chosen to be 5 × 10⁻⁴ m, 5 × 10⁻⁵ m and 5 × 10⁻⁶ m, respectively. For the min size, the mesh was defeatured, in particular defeaturing the size and capture curvature, specifically the min size curvature, and the min size was 5 × 10⁻⁵ m, 5 × 10⁻⁶ m and 5 × 10⁻⁷ m. In all cases, smoothing was set to medium. The first one, with an average quality index of 0.98, was chosen as the optimal one (an error of up to 2% is acceptable). Similarly, object II grids consisted of 66,370, 394,278 and 2,431,316 elements. The element size was chosen to be 2 × 10⁻⁴ m, 2 × 10⁻⁵ m, 1 × 10⁻⁵ m, respectively. For the min size, the mesh was defeatured, in particular defeaturing the size and capture curvature, specifically the min size curvature, and the min size was 2 × 10⁻⁵ m, 1 × 10⁻⁵ m and 5 × 10⁻⁶ m. In all cases, smoothing was set to medium. The first one, with an average quality index of 0.97, was chosen as the best one (permissible error up to 3%). Object III had 2,092,359, 2,113,120 and 2,114,437 elements, and the first one, with an average quality indicator of 0.95, was chosen as the optimal one (permissible error up to 5%). The element size was chosen to be 5 × 10⁻³ m, 5 × 10⁻⁴ m and 1 × 10⁻⁴ m, respectively. The mesh was defeatured, and in particular, the defeaturing size for all three mesh options was 5 × 10⁻⁸ m. For the min size, the capture curvature and, in particular, the min size curvature was 5 × 10⁻³ m, 5 × 10⁻⁴ m and 5 × 10⁻⁵ m. In all cases, smoothing was set to medium. Tetrahedra were chosen as the mesh extension parameters.

To create the model, the laminar viscosity model was applied, and the stationary type was chosen. The main model parameters and explicit pseudotransitional relaxation factors are provided in

Table 1. Main model parameters.

Parameter	Values/Method Type	References, Source
Density of the material (mycelium)	300 kg/m3	[13,14,15]
Initial gauge pressure	0 Pa	-
Gauge pressure in the discharge channel	0 Pa	-
Direction of the reverse flow	Normal to the boundary	-
Solution of the pressure–velocity dependence	Second-order discretization of pressure and momentum	-
Relaxation factors
Pressure	0.5	-
Momentum	0.5	-
Density	1.0	-
Volume forces	1.0	-
Initialization	Hybrid	-

.

To analyze the model solution and obtain results for each case, calculations were performed after at least 1000 iterations until the residuals of all variables (continuity, x-, y- and z-velocity) did not reach a level of no more than 10⁻⁵.

3.2. Particle Interaction Study

Newton’s second law is used to describe the interaction particles. The general expression for the forces acting on a particle can be given as follows:

$$m_i\frac{d^2{\mathit{x}}_i}{d{t}^2}={\mathit{F}}_i\left(t\right)$$

(1)

where $m_i$ and vector x_i (bold letter means vector) are the mass and position of the i-th particle. The vector ${\mathit{F}}_i\left(t\right)={\displaystyle \sum }_j{\mathit{F}}_{i,j}\left(t\right)$ corresponds to the resultant forces acting on particle i in the event of possible interaction.

If we define the normal orientation of contact by the unit vector $\mathit{N}$, the force vector ${\mathit{F}}^{\mathit{N}}=F^N\mathit{N}$ may be described by the time-dependent scalar variable $F^N\left(t\right)$ [31]. The interaction of a particle in the normal direction can be described by five forces of different nature:

$$F^N\left(t\right)=F_{deform}^N\left(t\right)+F_{attr}^N\left(t\right)+F_{attr-diss}^N\left(t\right)$$

(2)

where $F_{deform}^N\left(t\right)$ is the particle deformation force in the normal direction (Hertz model); $F_{attr}^N\left(t\right)$ is the force of attraction of a particle in the normal direction; and $F_{attr-diss}^N\left(t\right)$ is the dissipative force of a particle in the normal direction associated with adhesion [32]. A more detailed description of the model can be found in [31,32,33,34].

Estimating the action of the normal force $F^N\left(t\right)$, the adhesive–dissipative interaction of a particle with a surface can be divided into two parts (Figure 2).

The first part comprises approach (S-L) and detachment (A-D’). When approaching and detaching, the particle experiences the action of the adhesive force and, accordingly, moves a certain distance from the interacting surface, and its displacement is considered negative. The second part includes loading (L-U) and unloading (U-A). During loading and unloading, the particle comes into contact with the surface, it is deformed, and the displacement is considered positive. As seen in Figure 2, a negative normal force corresponds to attraction, and a positive normal force corresponds to repulsion, according to Chlebnikovas and Jasevičius [42,43]. If it does not have enough energy to detach at point D’, it returns, and sticking process occurs. In this work, the sticking process was not analyzed.

The initial data are presented in

Table 2. Initial data.

Objects	Initial Parameters	Values	References, Source
Glass particle (pollution)	Diameter, $d_i$	$1 \mathsf{\mu }\mathrm{m}$	-
	Radius, $R_i$	$0.5 \mathsf{\mu }\mathrm{m}$	-
	Initial interaction distance, $h_S$	$0.4 \mathrm{nm}$	[42]
	Initial velocity, ${\upsilon }_0$	−0.3 cm/s	-
	mass, $m_i$	$\approx 1.293\mathrm{pg}$ (picograms)	-
	Density, ${}_i$	$\approx 2376 \mathrm{kg}/{\mathrm{m}}^3$	[43]
	Young’s modulus, $E_i$	$80.1 \mathrm{Gpa}$	[43]
	Poisson’s ratio, ${}_i$	0.27	[43]
Mycelium	Density, ${\rho }_j$	680 $\mathrm{g}/{\mathrm{cm}}^3$	[44]
	Young’s modulus, $E_j$	$550 \mathrm{Mpa}$	[44]
	Poisson ratio, ${\nu }_j$	$0.3$	[44]
Simulation	Time step	$0.1 \mathrm{ps}$ (picoseconds)	-

.

4. Results

The results presented in this article are divided into two parts. In the beginning, results related to the air flow studies of the mycelial material/filter are presented. Next, the interaction of the microparticle with the surface of the mycelium is considered.

4.1. Results of the Study of Air Flow

We numerically evaluated the processes of the movement of gas flows in a porous filler. The use of a new material/filler in a technological process requires a deep analysis of the properties of this material, the study of ongoing processes and the determination of application conditions. In this paper, a fundamental scientific evaluation of a new material consisting of mycelium was chosen as a structural element for air flow filtration technology. Based on the results of the numerical simulation study, the task was to determine the significant advantages and disadvantages of this meta-material, taking into account the dynamics of a moving gas flow, various porous structures that comprise the filler, the effect on the process of air flow movement and the aerodynamics of such a system that would be applied to air for flow filtering, comprising indicators/indexes for the physical model.

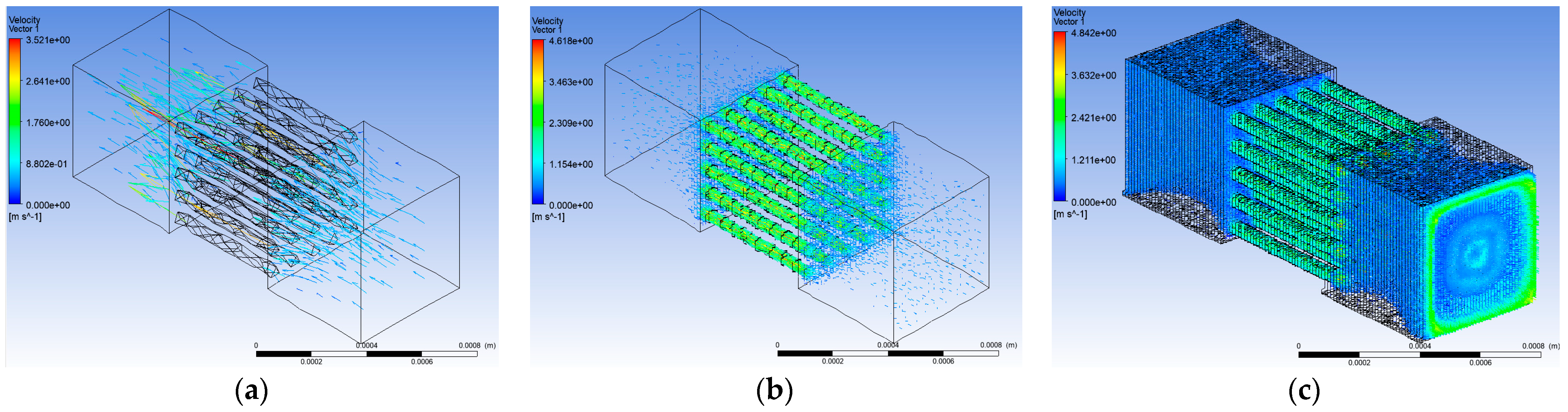
The air flow velocity vector, in an idealized porous filler, was formed in the models of the three structures with different pore sizes using computational grids of three parts: the model of case I with low, middle and high detalization (Figure 3).

Studies have shown that, at an inflow velocity through the inlet plane of 0.5 m/s, the maximum air flow velocity occurs in the middle of the cylindrical part of the pore and remains high at the exit to the outlet cubic channel. The average values between all three models of detailing, when reaching a pore size of 50 µm, ranged from 2.5 to 2.9 m/s.

The obtained digital data for each case show that the median speeds were 1.76 m/s, 2.31 m/s and 2.42 m/s, for cases 1, 2 and 3 of detail, respectively. However, maximum values occurred only in special cases when air was distributed over the pore cylinders of the mycelium, as well as along the axis of the pore cylinder for cases with medium detail. When considering the general situation of the entire object, the average velocity values decreased and were obtained in the intervals of 0.9–1.76 m/s, 1.15–2.31 m/s and 1.21–2.42 m/s, respectively, for the three details with a pore size of 50 µm. The maximum velocity in the model was determined in the cylindrical section of the pair ¾ of the length in the center of the cross section, which reached 4.8 m/s at the maximum grid detail, provided that the length of the cylindrical part of the steam pair was the same as the inlet cubical channel and the outlet cubical channel. It was noted that, when the air flow entered the outlet cubical channel, due to local pressure losses at the outlet, the velocity decreased by about 1.8 times, and with further attenuation, it reached an average of 1.5 m/s.

The distribution of absolute values changed slightly when the pore size reached 20 µm, which was the most common case in terms of mycelium pore size (Figure 4). In this case, while maintaining the same inflow velocity (0.5 m/s), the air flow velocity in the medium detail model reached 1.3–1.5 m/s, and in the low and high detail models, it reached 1.1–1.3 m/s and 1.7–1.8 m/s. It was assumed that, for a structure with such a pore size, a low-resolution mesh is insufficient due to large velocity fluctuations throughout the analyzed model. In the case of high detail, the velocity spread between the minimum and maximum was also significant, but the most noticeable deviations were associated with uneven flow in pores, where the velocity changed quite sharply from 1.3 to 2.2 m/s. According to the model of medium detail, it was assumed that the maximum speed of the air flow reached 2.5 m/s, as well as in the cylindrical part of the pore approaching the outlet cubical channel, and after entering this zone, the speed decreased to 0.7 m/s.

The results of modeling the structure with the smallest pores (10 µm) show that the models of all three parts generated a fairly similar situation. Namely, the average air flow velocity was about 0.65–0.8 m/s, and the maximum speed was about 1.2 m/s. It was also noted that, both during inflow into the cylindrical part of the pore and after outflow from it, the air flow velocity was quite the same and sharply decreased, reaching a value of approximately 0.3 m/s. In the pair itself, the speed increased quite strongly and reached 1.0–1.1 m/s. Compared to other cases, the resulting air flow was low due to pressure losses in such a system. When flowing into the cylindrical part of the pore with the smallest possible diameter, the flow lost much more energy in general, and its static pressure decreased. However, due to the extremely small size of the pore diameter, which, in this case, was 10 µm, the air flow rate in the pores remained sufficient to overcome other losses. Pressure increased toward the exit to the output cube channel.

The object under study was composed of an inflow channel and an outflow channel with a large volumetric space, which were connected through micro-sized cylinders imitating mycelial pores. The air flow supplied through the inflow plane was distributed evenly over the entire area of the inflow channel, and as it approached the distribution to the mycelial pore cylinders, flow retention occurred, which increased the flow pressure. At the entrance to the cylinder of the mycelial pore, the flow was reduced aerodynamically due to a local obstacle. Studies have shown that the air flow regains dynamic pressure as it moves through the microcylinder, and at about the middle of the mycelium cylinder, the flow velocity reaches its maximum values. Air flow movement continued to slow down slightly due to path losses, and at the exit to the outlet channel, a sudden rarefaction of the air and a drop in the air flow velocity occurred again. This also occurred due to a sudden change in the cross-section from a micro-cylinder to an outflow channel with a large volumetric space, analogous to the inflow case. These phenomena were inevitable and will be studied in detail in practical experimental studies in a laboratory. By applying this technology, the optimal amount of supplied air flow can be studied in real conditions, and the mycelium space of different volumes can be designed. One of the most important tasks is to determine the aerodynamic load of this technology and the optimal amount of cleaned air according to the size of the structure.

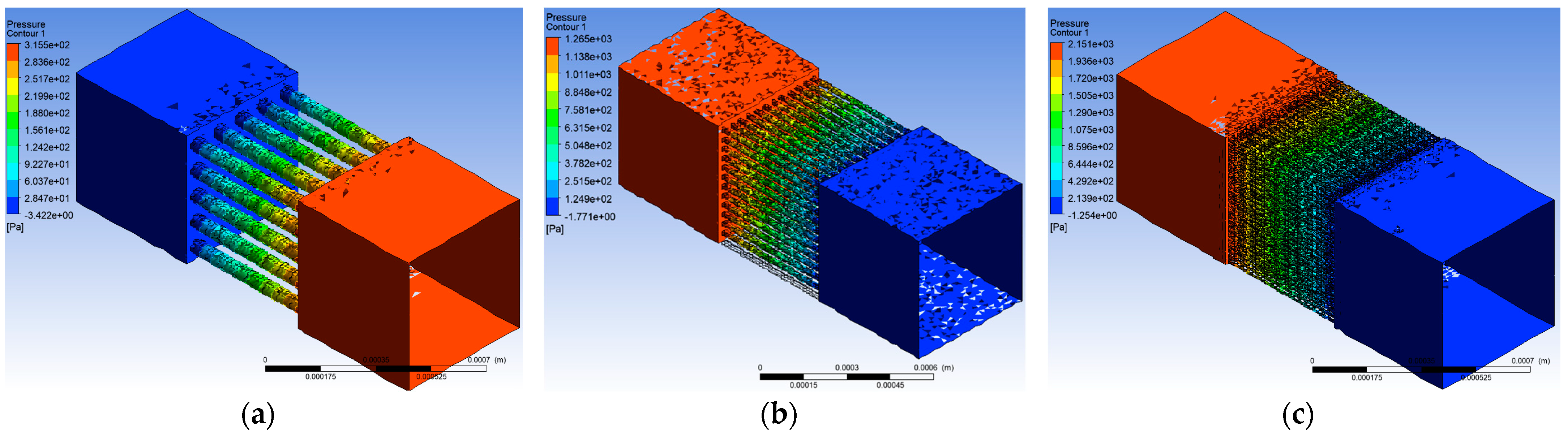
For a detailed analysis of the filtration process, it is important to study the structure of pressure losses on surfaces. To ensure a suitable air supply, the main surface pressure distributions were analyzed (Figure 5). In the initial zone, when the inflow velocity reached 0.5 m/s, a pressure of about 300 Pa was reached. The construction of the object was based on a proportional comparison of all elements, i.e., the length of the input channel cube corresponded to the length of the cylindrical part in a ratio of 1:1 and was simultaneously equal to the length of the output channel cube. As can be seen, the pressure at the pore inlet decreased by about 70 Pa and reached 220–235 Pa. Reaching the middle of the cylindrical part of the pore, it decreased and reached about 180 Pa, and at the end of the pore, it reached about 60 Pa. When evaluating the pressure drops of other pore sizes, it can be said that the values changed proportionally. For example, with a pore size of 20 µm, the inlet pressure reached 1200–1300 Pa, and at the outlet, it decreased to 650–790 Pa. and reached 120–150 Pa at the end of the pore. In the model analyzing the smallest pore size of 10 µm, a relatively high-pressure of 2150 Pa was created at the inlet, which decreased to 1350–1500 Pa in the pores and 250–300 Pa at the end of the pore. A similar trend continued in models of other parts.

The model extracted the distribution of air flow trajectories and, being important for the filtering device, the passage of the characteristic velocity of these lines through the entire structure of the porous object, which characterizes the mycelial filler (Figure 6).

The generated flow distributions showed that, at a size of 50 µm, the air flow uniformly passed through the entire structure and maintained a speed of about 1.2 m/s in the exit plane. With pore sizes of 20 µm and 10 µm, the velocities were less and equal to 0.6 m/s and 0.3 m/s. Considering these results, it can be assumed that, when designing a physical object and planning an experimental study, the use of a filler consisting of 10 μm mycelium pores may not be rational due to extremely low residual air flow. It is likely that 20 µm pores can be used in filtration processes, in which higher air flow rates are used to keep the air flow from losing its carrier capacity or to clean up low-density air flow contaminated with particulates. The energy flux is sufficient to displace particles from the inlet channel into the porous structure.

4.2. Results of the Study of Particle Interaction

For the next part of the study, an analysis of the interaction of a particle with a surface is presented, in which the particle was at a distance of h_S = 0.4 nm (Table 2) from the interacting surface at the considered time instance. Based on previous studies [44,45,46,47,48], it is important to take this distance into account, because, from such a certain distance, the acting force of adhesive attraction becomes sufficient to attract the particle to the interacting surface (in our case, this is the surface of the mycelium).

Therefore, when studying the interaction of a pollutant particle with a surface, the velocity value was used, taking into account the previous part of the study of this paper. The velocity value was approximately equal to υ₀ = 0.3 cm/s (Table 2) near the surface of the tube where the particle was located, so the particle velocity here was much lower compared to the center of the mycelium pore/cylindrical tube (taking into account the cross section).

As mentioned before, according to the results of the numerical experiments, the initial velocity of the particle’s impact on the plane of the mycelium filter material was 0.3 m/s. The surface was assumed to be flat. Particle velocities in both normal and tangential directions at different angles could be calculated using the following equation:

$${\upsilon }_0^N=sin{\phi }_0;\hspace{1em}\hspace{1em}{\upsilon }_0^T=cos{\phi }_0$$

(3)

The initial angles of impact into plane ${\phi }_0$ were chosen to be 10°, 20° and 30°, respectively. At these angles, the initial velocities were as follows:

• When ${\phi }_{0,1}=10$, then ${\upsilon }_{0,1}^T=0.29544\mathrm{m}/\mathrm{s}$; ${\upsilon }_{0,1}^N=0.052094\mathrm{m}/\mathrm{s}$;
• When ${\phi }_{0,2}=20$, then ${\upsilon }_{0,2}^T=0.2819078\mathrm{m}/\mathrm{s}$; ${\upsilon }_{0,2}^N=0.102606\mathrm{m}/\mathrm{s}$;
• When ${\phi }_{0,3}=30$, then ${\upsilon }_{0,3}^T=0.2598076\mathrm{m}/\mathrm{s}$; ${\upsilon }_{0,3}^N=0.150\mathrm{m}/\mathrm{s}$.

As a first step in studying the impact of a pollutant particle on the mycelium surface, this study was idealized, and it was assumed that air resistance at an initial distance of 0.4 nm (Figure 2, point S) of the particle from the surface is not estimated/not applicable. Further studies will be devoted to assessing the additional effect of air resistance.

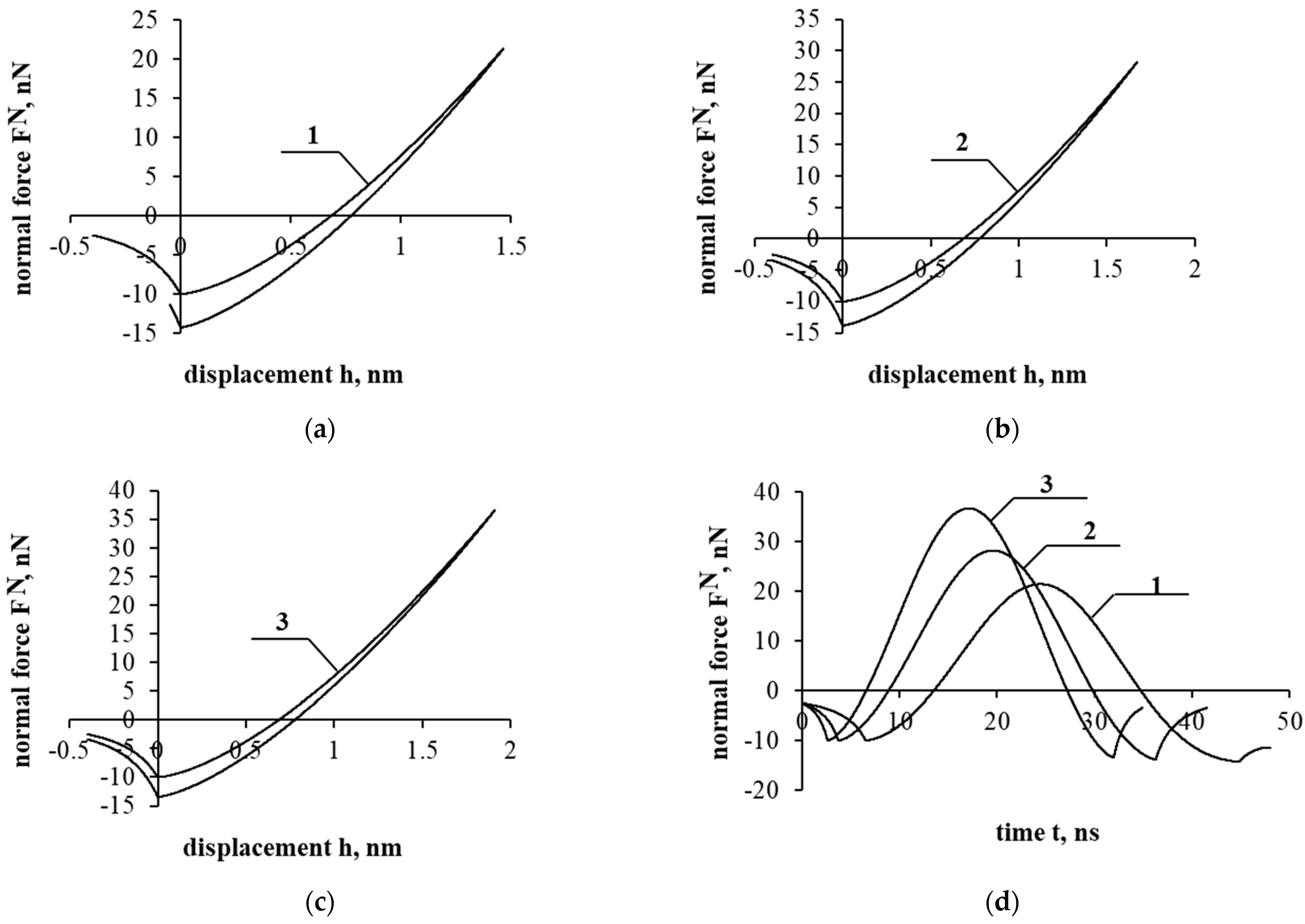
Now we would like to present the results. This paper presents the interaction of a glass particle with the surface of the mycelium. The interaction of the particle upon impact on the surface at different angles was studied. The results presented below (Figure 7 and Figure 8) show that, at a small angle, the particle was likely to stick to the mycelium surface. Figure 7a shows the dependence of the force on the displacement after the impact, and when the particle separated, it could not return to the initial distance from which the interaction began. Therefore, having reached point D’ (Figure 2), further movement would involve a sticking process, which was not considered in this work. The velocity value, after reaching this point, was zero (Figure 7f, case 1). At a larger interaction angle, the particle bounced off the interacting surface with the corresponding velocity (Figure 7f, cases 2 and 3). Research shows that, when particles pass through an air filter, their movement at a slight angle to the interacting surface results in sticking. On the one hand, its ability to catch microparticles is a good feature, but the problem of filter clogging time remains. Therefore, further research should focus on both filter clogging and the size of the “pore/hole” of the mycelium. The pores must determine both the efficiency and the rate of clogging.

The dynamics of the normal force are additionally shown in Figure 7d. It was observed that, as the angle increased, the maximum values of both the normal force and the achieved displacement increased, and the duration of the interaction decreased. The velocity values (Figure 7f) increased as it approached the surface, and when the maximum normal force and displacement were reached, the velocity had a zero value. Then, the particle changed direction to the opposite one, and the detachment process began. In this case, when the particle changed direction, the velocity had the opposite (positive) sign.

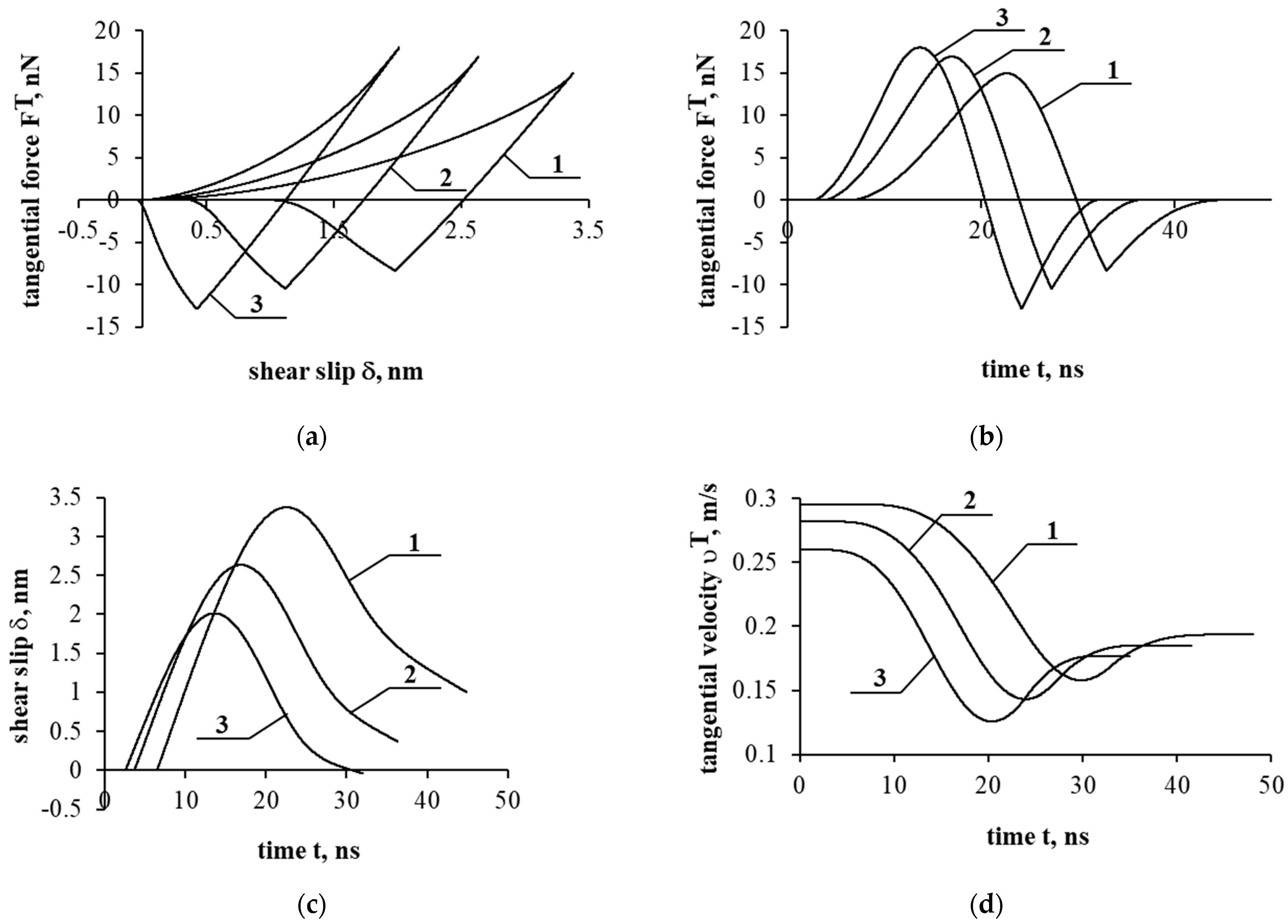
Now, the interaction/contact in the tangential direction is considered (Figure 8). It should be noted that contact occurred at a relatively short distance (up to 3.5 nm); therefore, in the simulation, it was assumed that the interaction would occur with a flat surface. As in the case of normal interaction, an increase in the angle of interaction led to an increase in the value of the normal force, and the duration of the interaction decreased. In contrast to the usual interaction, at a small angle, the achieved particle displacement in the tangential direction (shear slip) increased. Moreover, when moving in the tangential direction during contact, the particle moved both forward and backward (Figure 8c). Particle contact in the tangential direction included slip and elastic deformation (at the end of the contact). By observing the velocity graphs, it could be seen that the velocity values settled at the corresponding value at the end of the contact. After the particle bounced, because the interaction was at an angle, as expected, the particle continued to move in the tangential direction as well. In all cases, at the end of the contact, the value of the tangential force equal to zero was reached. It should also be noted that, when the particle was at a certain distance from the interacting surface, there was no interaction in the tangential direction, because the adhesive force acted only in the normal direction.

Taking into account the presented results (Figure 7 and Figure 8), as mentioned in the formulation of the problem, because the mycelium material itself is relatively soft, the particles tended to penetrate (Figure 7e) into the material as well as stick to the surface at small interaction angles. Therefore, in order to increase the efficiency of the filter, a filter containing smaller diameter pores can be selected. In this case, the circulation of the air flow slows down, and the particles tend to stick to the surface even more. However, the filter clogs faster, so a more efficient filter may become less durable. When developing these filters for specific materials, all requirements for them must be evaluated. The required pore size must be chosen so that the flow rate on the pore wall results not only in good adhesion but also in the durability of the filter.

It should be noted that, from the point of view of modeling, because the adhesion during interaction acts in the normal direction, the description of the tangential force becomes more complicated. As the results showed, when considering the interaction in the tangential direction (along the interacting surface), different particle behavior can occur. When a particle moves in a tangential direction at a small distance of nanometers, the particle can slide over the surface (Figure 8a) and even return to the initial interaction position (Figure 8c). In the future, if possible, research should continue in cooperation with the manufacturers of this material. Moreover, additional studies related to the search for an effective filter should be carried out.

It should also be noted that mycelium is a material of biological origin. The question of modifying a mycelial filter from a biological point of view remains open regarding its applications, including not only the extraction of particles but also the destruction of viruses in the filter.

5. Conclusions

• A numerical model of the idealized geometry flow through a mycelium porous zone was researched. The results show that the average air flow rate is equal to 2.7 m/s, 1.5 m/s and 0.7 m/s in the mycelium pores in the cases of 50 µm, 20 µm and 10 µm pore diameters, respectively, when the inflow rate through the air channel is equal to 0.5 m/s.
• Mycelium filling, which is promising for air flow filtration, depending on the size of the pores in the range of 10–50 µm in diameter, makes a pressure drop from 240 Pa to 1800 Pa throughout the air flow path. The largest local pressure losses in the system are located at the end of the mycelium pores and at the outflow into the outflow channel.
• Research shows that, when particles pass through an air filter, their interaction at a low angle to the interacting surface results in sticking. This is important when choosing a mycelium material for making a filter.
• The question of filter clogging time remains open, so further research should focus on both filter clogging and mycelium pore/hole size. The pores determine both the efficiency of the filter and its clogging rate.