A Comparison between Two Statistical Methods for Gear Tooth Root Bending Strength Estimation Starting from Pulsator Data
Abstract
1. Introduction
- From the fatigue point of view, the tooth root stress history is different. On the one hand, in pulsator tests, the stress trend is sinusoidal with R > 0. On the other hand, in the MG case, the tooth root stress presents a peculiar stress trend that is influenced by the load sharing between teeth pairs (and the related tooth deformability). This difference is typically solved by means of corrective coefficients that modify the SN curve (e.g., [22]).
- From the statistical point of view, it must be considered that pulsator tests are performed on selected teeth rather than on the complete gears. Furthermore, not all teeth of a gear can be tested. Commonly, statistical tools are adopted here.
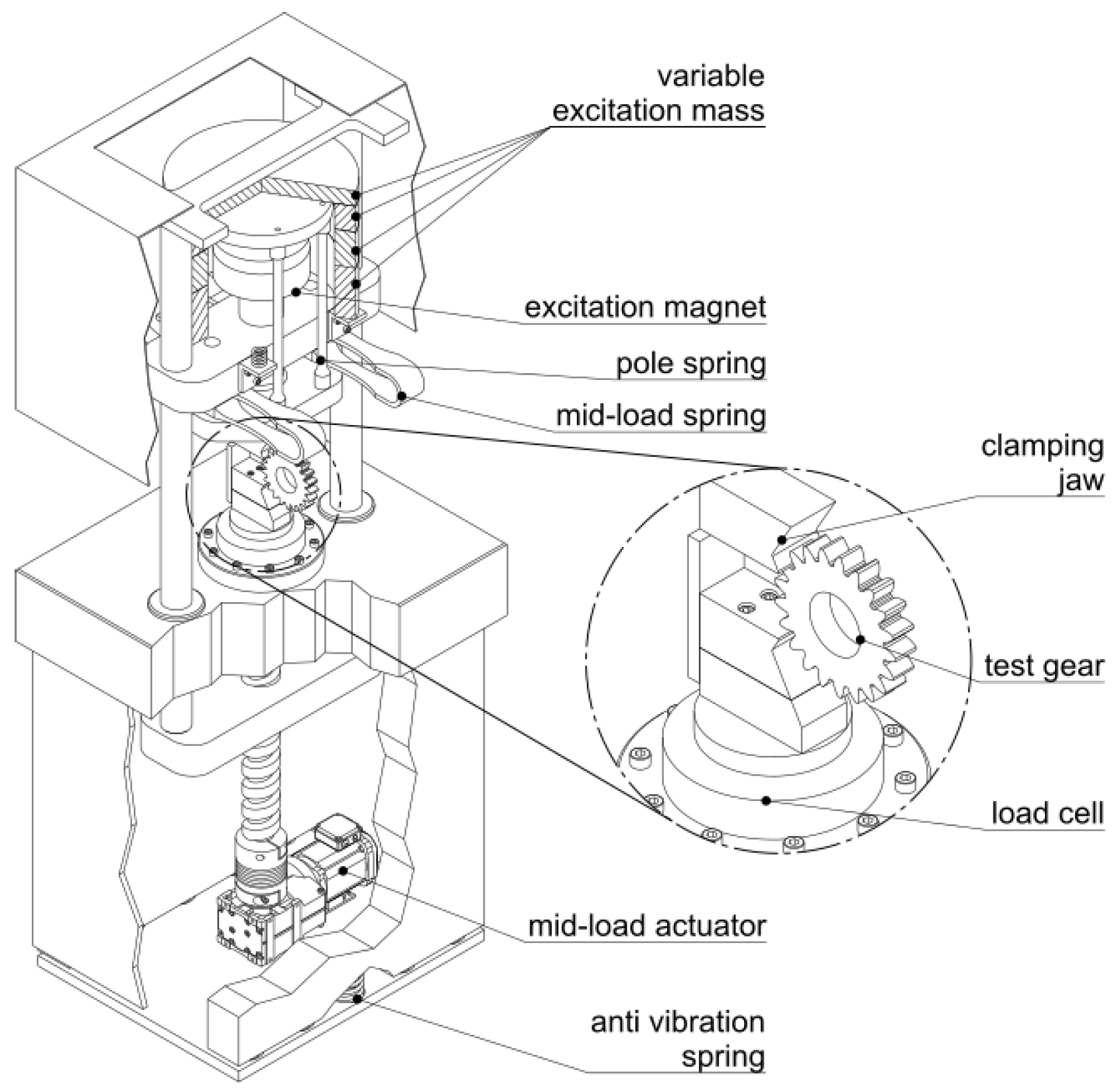
2. Experimental Procedure for Tooth Root Bending Fatigue Testing
3. The Pulsator to Running Gears Problem
- 1.
- Pulsator tests and MG have different loading conditions, as, in the first, a sinusoidal load is applied at a fixed position, while in the latter, the load changes both the magnitude (due to the load sharing between teeth pairs) and the point of application (as the contact point between teeth changes during gear meshing).
- 2.
- The stress ratio R is different as pulsator tests are required to work at , while in the MG gear case, the tooth root stress moves to a positive maximum (typically when the contact is at the outer point of a single tooth in contact) to a negative minimum (due to the extension of the compression field from the adjacent tooth, e.g., [4,5,38]), thus at a load ratio (e.g., [39]).
- 3.
- The crack initiation location seems to be different. Indeed, certain experimental findings of Winkler et al. [40] and Fuchs et al. [36,41,42,43,44] possibly imply that in the pulsator test case, crack initiation is much more likely to occur at the surface, while in the MG case, a slightly increased risk for subsurface crack initiation can be observed. However, their findings are based on investigations on shot-peened gears made from high-cleanliness steels. Furthermore, a different runout level was considered for pulsator and MG tests. Moreover, considering all the data available [36,40,41,42,43,44], and further results from experimental investigations at FZG that have not been published yet, it can be assumed that there is not a different crack location for common case-hardened gear steels for both compared testing methods (i.e., pulsator and MG). Therefore, the effect of the crack initiation location will not be discussed here.
- 4.
- The statistical behavior of pulsator and MG tests is different. In pulsator tests, the failed teeth are predetermined and are those that are loaded within the pulsator test rig (for each test run, two teeth are in the symmetric configuration); furthermore, not all the gear teeth can be tested. On the other hand, in the MG case, all the gear teeth are loaded during a test run, and the gear failure is the result of the failure of the weakest gear tooth (e.g., [22,29,37,45,46,47]).
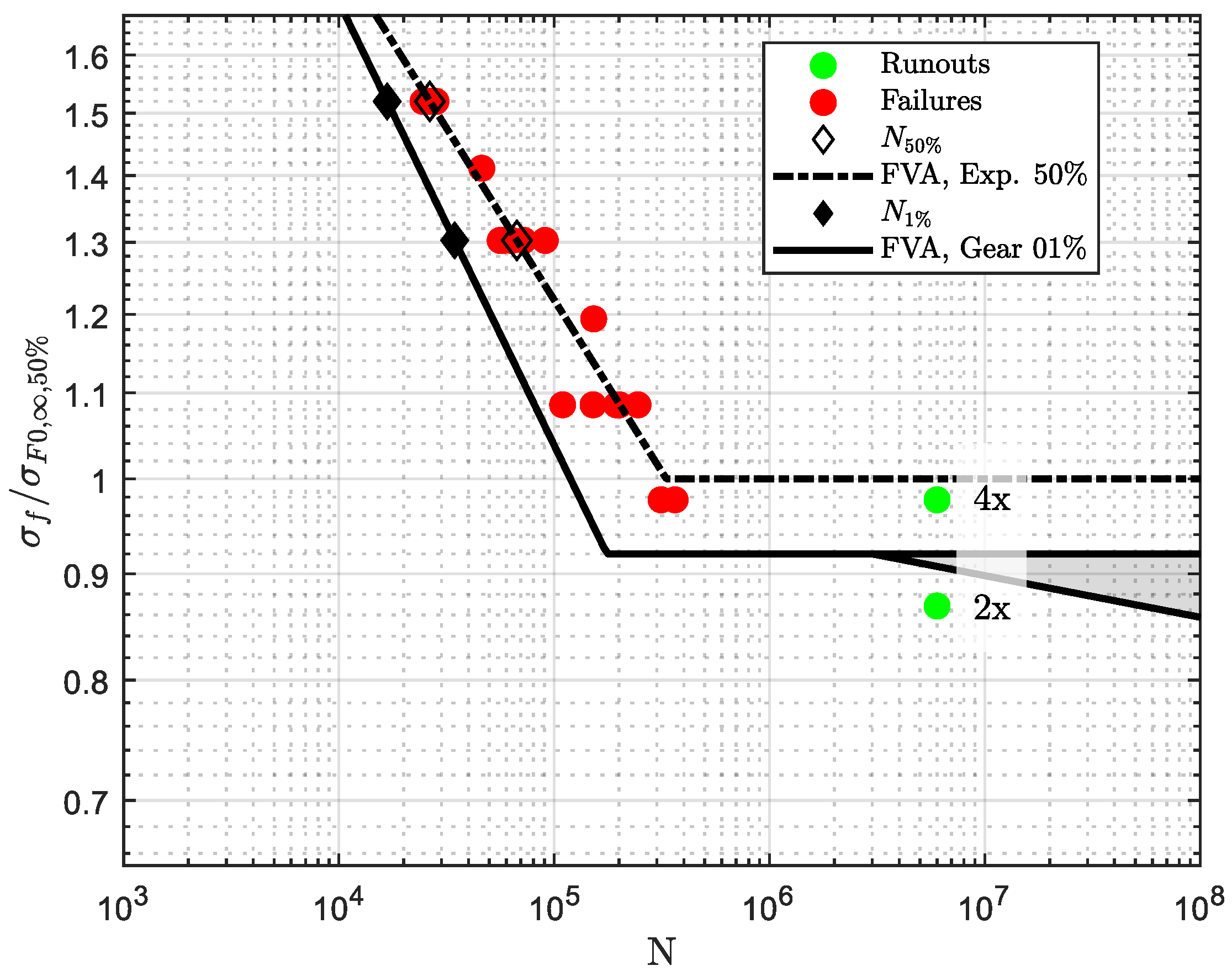
4. Method 1: FVA Approach Based on FZG Research
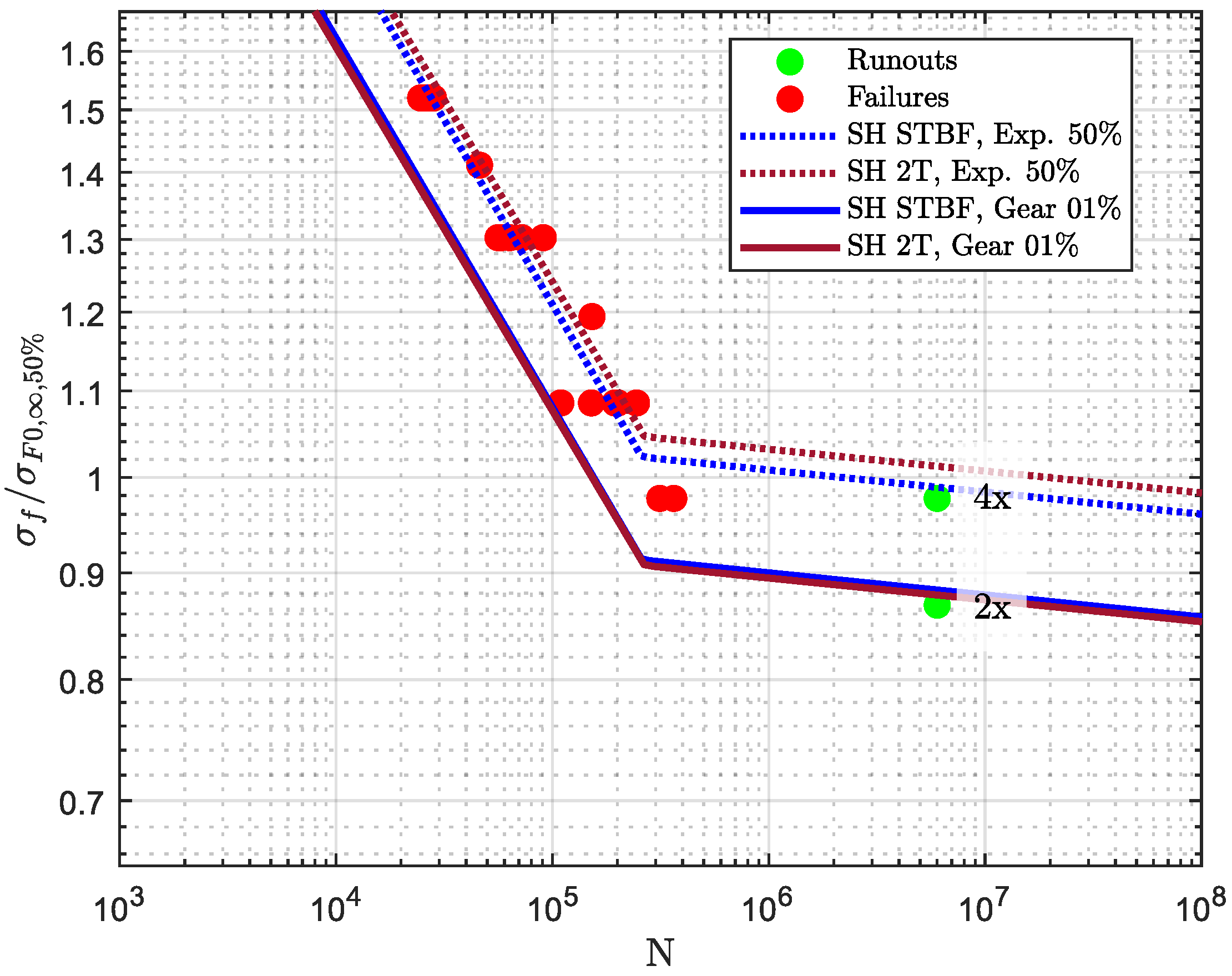
5. Method 2: Maximum Likelihood and Statistic of Extremes (ML&SoE)
- 1.
- If the experimental points are considered as they are, that is, if the fact that the symmetric test configuration works on two teeth is not considered, the only observed surviving specimen is the one that reaches the runout level. The elaboration performed with such considerations is called “STBF” as they are the experimental points obtained directly from the pulsator/STBF testing machine.
- 2.
- If the fact that the symmetric test configuration works on two teeth is considered, it must be considered that the experimental point is not composed only of failed and surviving specimens but by the compresence of both. This can be easily understood by looking at the experimental points. On the one hand, if one of the two teeth fails (i.e., a failure according to the STBF consideration), the other has survived. That is, a failure occurring within the test is both an observed value (i.e., the failed tooth) and randomly right-censored data (i.e., the survived tooth). On the other hand, if the runout level is reached (i.e., a runout according to the STBF consideration), both tested teeth have reached the runout level. Therefore, different statistical considerations must be taken into account in the 2T case. The elaboration performed with such considerations will be called “2T” as two teeth are taken into consideration.
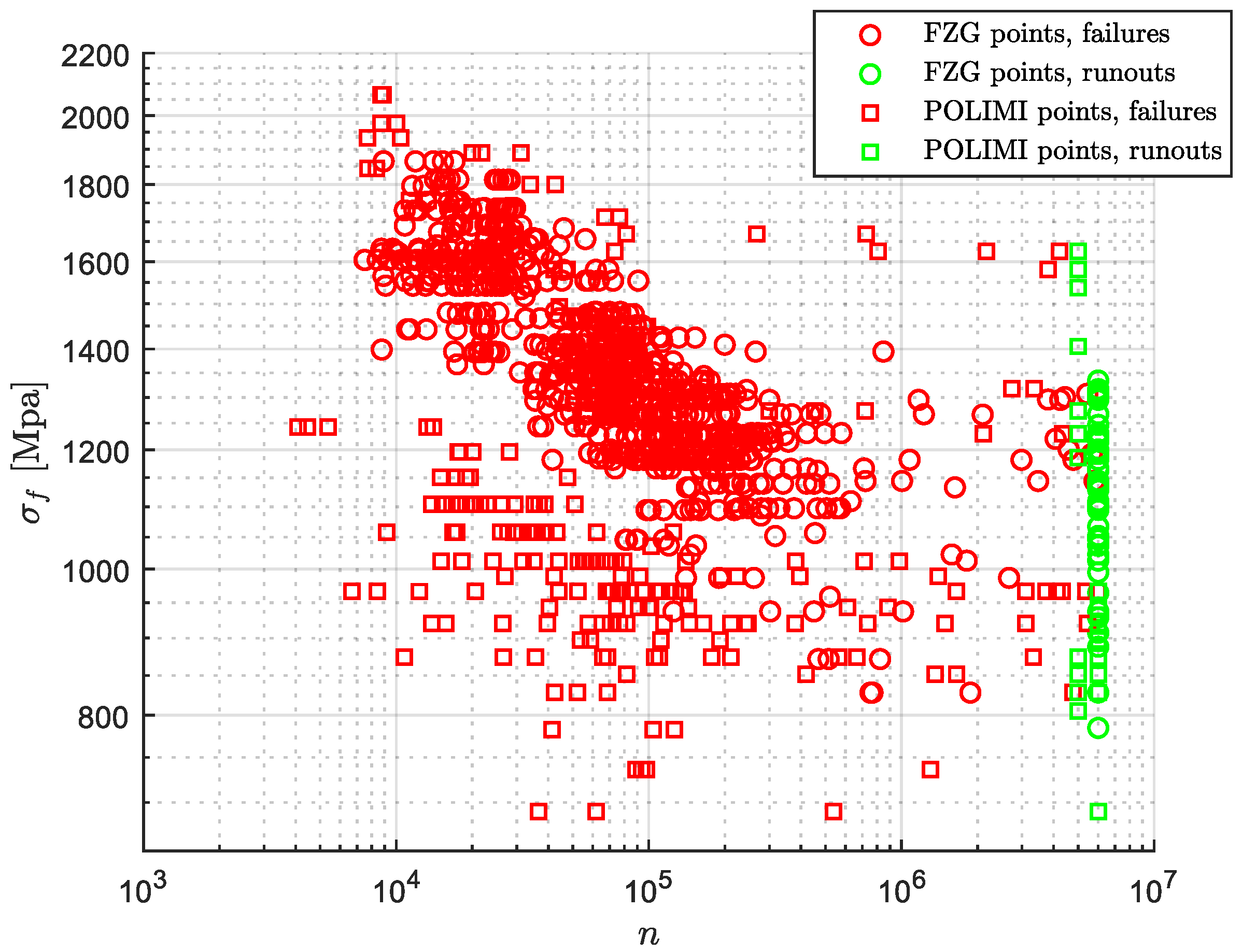
6. Adopted Database
7. Evaluation Study: Comparison between the Two Models
8. Extended Investigations on Method 2
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Acronym
| CDF | Cumulative Distribution Function |
| ML | Maximum Likelihood |
| MG | Meshing Gear |
| LR | Likelihood Ratio |
| PF | Profile Likelihood |
| Probability Density Function | |
| STBF | Single Tooth/Teeth Bending Fatigue |
| SoE | Statistics of Extremes |
Nomenclature
| Parameter of Hück method | |
| Stress/load step, mainly considered in Hück method | |
| Generic model parameter | |
| Estimated parameter | |
| Constrained parameter | |
| Confidence interval of the estimated parameter | |
| Parameter of Hück method | |
| Gear CDF | |
| STBF CDF | |
| 2T CDF | |
| Number of tests on the load level, Hück’s method | |
| Conversion factor acc. to Stahl for 50 % to 1 % failure probability | |
| Corrective coefficient acc. to Rettig | |
| Limited life slope | |
| Long life slope | |
| Likelihood | |
| Log-likelihood | |
| 50% experimental lifetime | |
| 1% gear failure probability lifetime | |
| Spindel-Haibach model coordinate (together with ) | |
| Standard deviation | |
| Logarithmic standard deviation | |
| Spindel-Haibach standard deviation in the direction | |
| Spindel-Haibach standard deviation in the direction, limited life region | |
| Spindel-Haibach standard deviation in the direction, long life region | |
| Stress | |
| Spindel-Haibach model coordinate (together with ) | |
| Experimental endurance limit for 50 % failure probability | |
| Gear endurance limit for 1 % failure probability | |
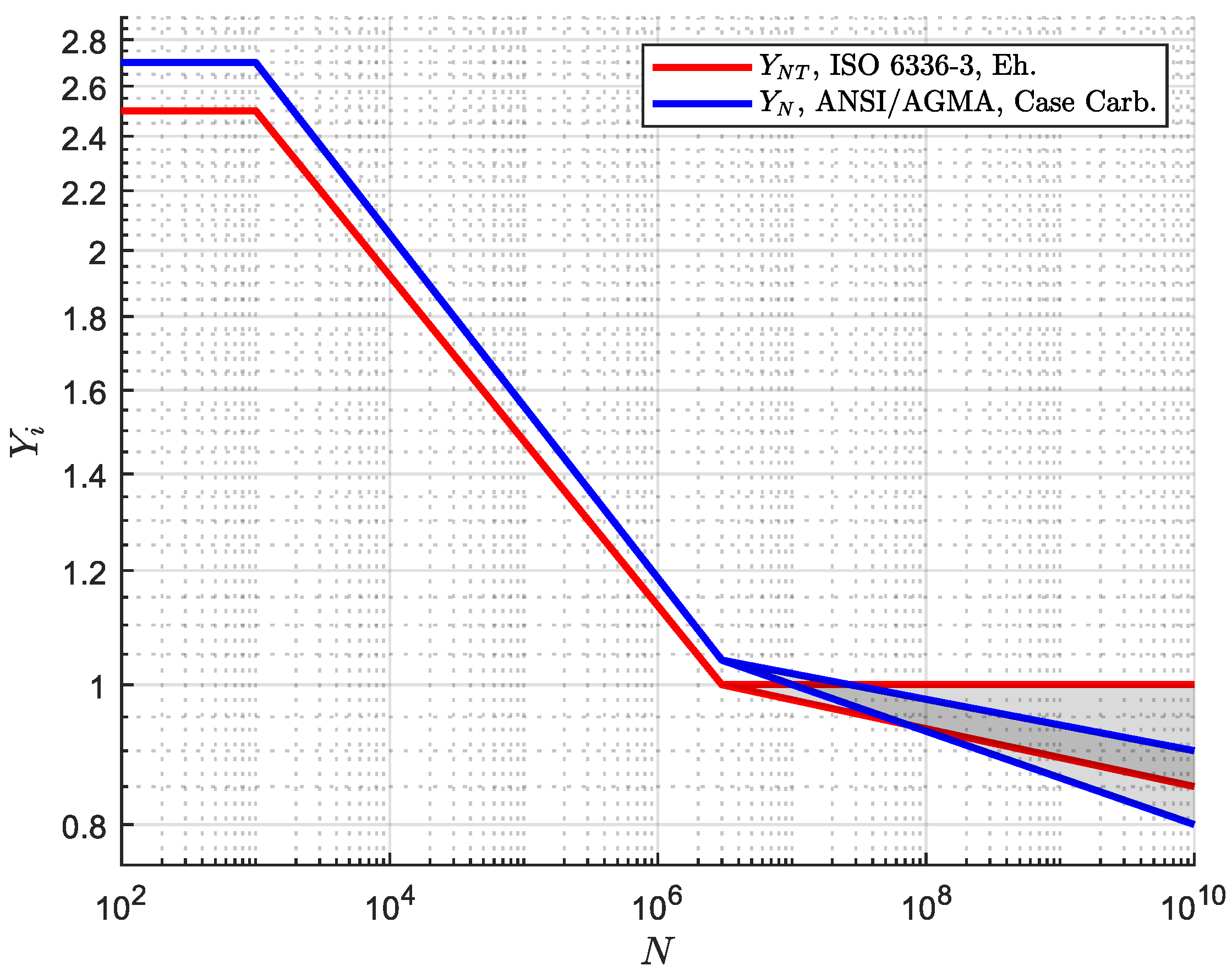
| Life factor acc. to ANSI/AGMA 2001 | |
| Life factor acc. to ISO 6336-3 |
Appendix A. Maximum Likelihood Estimation of the Experimental Tooth Root Fatigue Fracture SN Curve
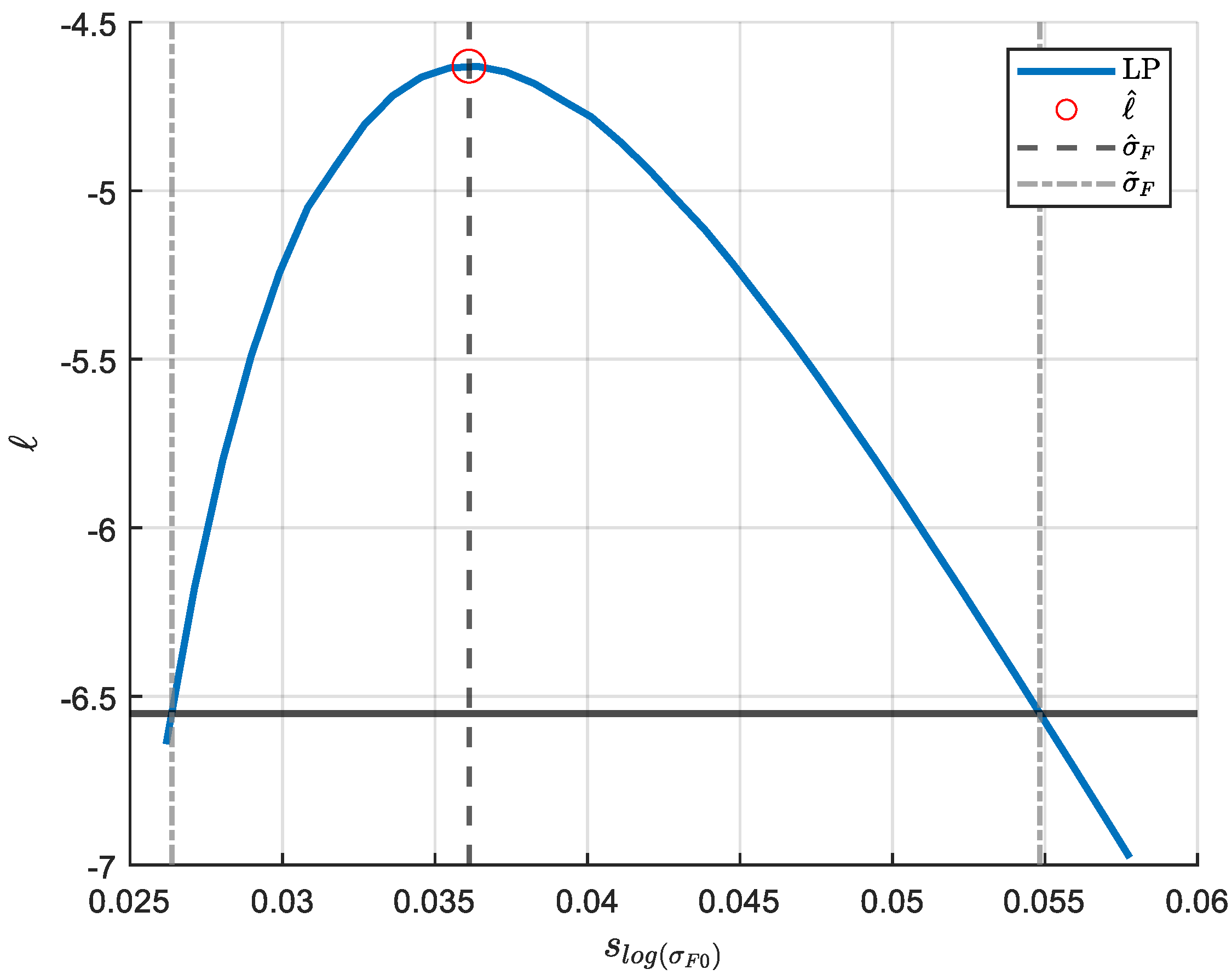
Appendix B. Profile Likelihood and Likelihood Ratio Profile
References
- Aktiengesellschaft, M. Maag Gear-Book: Calculation and Manufacture of Gears and Gear Drives for Designers and Works Engineers; Maag Gear-Wheel Co: Zurich, Switzerland, 1963. [Google Scholar]
- Dudley, D.; Townsend, D. Manuale Degli Ingranaggi - Edizione Italiana; Tecniche nuove: Milano, Italy, 1996. [Google Scholar]
- Henriot, G. Manuale Pratico Degli Ingranaggi; Tecniche nuove: Milano, Italy, 1993. [Google Scholar]
- Fernandes, P. Tooth bending fatigue failures in gears. Eng. Fail. Anal. 1996, 3, 219–225. [Google Scholar] [CrossRef]
- Davoli, P.; Conrado, E.; Michaelis, K. Recognizing gear failures. Mach. Desing. 2007. Available online: http://hdl.handle.net/11311/274596 (accessed on 14 January 2022).
- ISO 6336-3:2019; Calculation of Load Capacity of Spur and Helical Gears—Part 3: Calculation of Tooth Bending Strength. International Organization for Standardization: Geneva, Switzerland, 2019. Available online: https://www.iso.org/standard/63822.html (accessed on 7 January 2022).
- ANSI AGMA 2001-D04; Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth. American Gear Manufacturers Association: Alexandria, VA, USA, 2004. Available online: http://www.agma.org (accessed on 8 August 2022).
- ISO 6336-6:2019; Calculation of Load Capacity of Spur and Helical Gears—Part 6: Calculation of Service Life under Variable Load. International Organization for Standardization: Geneva, Switzerland, 2019. Available online: https://www.iso.org/standard/63823.html (accessed on 26 January 2022).
- Hong, I.J.; Kahraman, A.; Anderson, N. A rotating gear test methodology for evaluation of high-cycle tooth bending fatigue lives under fully reversed and fully released loading conditions. Int. J. Fatigue 2019, 133, 105432. [Google Scholar] [CrossRef]
- Bonaiti, L.; Concli, F.; Gorla, C.; Rosa, F. Bending fatigue behaviour of 17-4 PH gears produced via selective laser melting. Procedia Struct. Integr. 2019, 24, 764–774. [Google Scholar] [CrossRef]
- Concli, F.; Bonaiti, L.; Gerosa, R.; Cortese, L.; Nalli, F.; Rosa, F.; Gorla, C. Bending Fatigue Behavior of 17-4 PH Gears Produced by Additive Manufacturing. Appl. Sci. 2021, 11, 3019. [Google Scholar] [CrossRef]
- Olsson, E.; Olander, A.; Öberg, M. Fatigue of gears in the finite life regime—Experiments and probabilistic modelling. Eng. Fail. Anal. 2016, 62, 276–286. [Google Scholar] [CrossRef]
- Lambert, R.; Aylott, C.; Shaw, B. Evaluation of bending fatigue strength in automotive gear steel subjected to shot peening techniques. Procedia Struct. Integr. 2018, 13, 1855–1860. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Xu, Z.-Z.; Shin, G.-S.; Lyu, S. A study on the evaluation of bending fatigue strength for 20CrMoH gear. Int. J. Precis. Eng. Manuf. 2013, 14, 1339–1343. [Google Scholar] [CrossRef]
- Lisle, T.J.; Little, C.P.; Aylott, C.J.; Shaw, B.A. Bending fatigue strength of aerospace quality gear steels at ambient and elevated temperatures. Int. J. Fatigue 2022, 164, 107125. [Google Scholar] [CrossRef]
- Dengo, C.; Meneghetti, G.; Dabalà, M. Experimental analysis of bending fatigue strength of plain and notched case-hardened gear steels. Int. J. Fatigue 2015, 80, 145–161. [Google Scholar] [CrossRef]
- Meneghetti, G.; Dengo, C.; Conte, F.L. Bending fatigue design of case-hardened gears based on test specimens. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 1953–1969. [Google Scholar] [CrossRef]
- John, J.; Li, K.; Li, H. Fatigue Performance and Residual Stress of Carburized Gear Steels Part I: Residual Stress. SAE Int. J. Mater. Manuf. 2008, 1, 718–724. [Google Scholar] [CrossRef]
- Dowling, W.E.; Donlon, W.T.; Copple, W.B.; Chernenkoff, R.A.; Darragh, C. Bending Fatigue Behavior of Carburized Gear Steels: Four-Point Bend Test Development and Evaluation. J. Passeng. Cars 1996, 105, 1330–1339. Available online: https://www.jstor.org/stable/44720852 (accessed on 1 August 2022).
- Spice, J.J.; Matlock, D.K.; Fett, G. Optimized Carburized Steel Fatigue Performance as Assessed with Gear and Modified Brugger Fatigue Tests. J. Mater. Manuf. 2002, 111, 589–597. Available online: https://www.jstor.org/stable/44718684 (accessed on 1 August 2022).
- Kuhn, H.; Medlin, D.; Osman, T.M.; Rigney, J.D.; Weaver, M.; Stevenson, M.; Kalpakjian, S.; House, J.W.; Gillis, P.P.; Robinson, R.M.; et al. Mechanical Testing of Gears. In ASM Handbook; ASM International: Materials Park, OH, USA, 2000; Volume 8, pp. 861–872. [Google Scholar] [CrossRef]
- Rettig, H. Ermittlung von Zahnfußfestigkeitskennwerten auf Verspannungsprüfständen und Pulsatoren-Vergleich der Prüfverfahren und der gewonnenen Kennwerte. Antriebstechnik 1987, 26, 51–55. [Google Scholar]
- Stahl, K.; Michaelis, K.; Höhn, B.-R. FVA Research Project 304, Final Report No. 580—Life Time Statistics—Statistical Methods for Estimation of the Machine Element Life Time and Reliability, and Exemplary Application on Gears (German: Lebensdauerstatisktik—Statistische Methoden zur Beurteilung von Bauteillebensdauer und Zuverlässigkeit und ihre beispielhafte Anwendung auf Zahnräder); FVA-Forschungsheft: Frankfurt am Main, Germany, 1999. [Google Scholar]
- Hein, M.; Geitner, M.; Tobie, T.; Stahl, K.; Pinnekamp, B. Reliability of gears—Determination of statistically validated material strength numbers. In Proceedings of the American Gear Manufacturers Association Fall Technical Meeting 2018, Oak Brook, IL, USA, 24–26 September 2018. [Google Scholar]
- Tobie, T.; Matt, P. FVA Guideline 563 I—Recommendations for the Standardization of Load Capacity Tests on Hardened and Tempered Cylindrical Gears; FVA: Frankfurt am Main, Germany, 2012. [Google Scholar]
- Hein, M. Zur Ganzheitlichen Betriebsfesten Auslegung und Prüfung von Getriebezahnrädern. Ph.D. Dissertation, Tecnhical university of Munich, Munic, Germany, 2018. [Google Scholar]
- Bonaiti, L.; Gorla, C. Estimation of gear SN curve for tooth root bending fatigue by means of maximum likelihood method and statistic of extremes. Int. J. Fatigue 2021, 153, 106451. [Google Scholar] [CrossRef]
- Bonaiti, L.; Rosa, F.; Rao, P.M.; Concli, F.; Gorla, C. Gear root bending strength: Statistical treatment of Single Tooth Bending Fatigue tests results. Forsch. Ing. 2021, 86, 251–258. [Google Scholar] [CrossRef]
- Seabrook, J.B.; Dudley, D.W. Results of a Fifteen-Year Program of Flexural Fatigue Testing of Gear Teeth. J. Eng. Ind. 1964, 86, 221–237. [Google Scholar] [CrossRef]
- Akata, E.; Altınbalık, M.; Çan, Y. Three point load application in single tooth bending fatigue test for evaluation of gear blank manufacturing methods. Int. J. Fatigue 2004, 26, 785–789. [Google Scholar] [CrossRef]
- Buenneke, R.W.; Slane, M.B.; Dunham, C.R.; Semenek, M.P.; Shea, M.M.; Tripp, J.E. Gear Single Tooth Bending Fatigue Test. Transactions 1982, 91, 3266–3274. Available online: https://about.jstor.org/terms (accessed on 5 August 2022).
- J1619_201712; Single Tooth Gear Bending Fatigue Test. SAE International: Warrendale, PA, USA, 2017. Available online: https://www.sae.org/standards/content/j1619_201712/ (accessed on 5 August 2022).
- Gorla, C.; Rosa, F.; Conrado, E.; Albertini, H. Bending and contact fatigue strength of innovative steels for large gears. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 2469–2482. [Google Scholar] [CrossRef]
- Wildhaber, E. Measuring tooth thickness of involute gears. Amer. Mach. 1923, 59, 551. [Google Scholar]
- Test rigs. Available online: https://www.ifa.ruhr-uni-bochum.de/ifa/dienste/pruefstaende.html.en (accessed on 21 October 2022).
- Fuchs, D.; Schurer, S.; Tobie, T.; Stahl, K. On the determination of the bending fatigue strength in and above the very high cycle fatigue regime of shot-peened gears. Forsch. im Ingenieurwesen 2021, 86, 81–92. [Google Scholar] [CrossRef]
- Hong, I.; Teaford, Z.; Kahraman, A. A comparison of gear tooth bending fatigue lives from single tooth bending and rotating gear tests. Forsch. Ing. 2022, 86, 259–271. [Google Scholar] [CrossRef]
- Vučković, K.; Čular, I.; Mašović, R.; Galić, I.; Žeželj, D. Numerical model for bending fatigue life estimation of carburized spur gears with consideration of the adjacent tooth effect. Int. J. Fatigue 2021, 153, 106515. [Google Scholar] [CrossRef]
- Rao, S.B.; Schwanger, V.; McPherson, D.R.; Rudd, C. Measurement and Validation of Dynamic Bending Stresses in Spur Gear Teeth. In Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference—DETC2005, Long Beach, CA, USA, 24–28 September 2005; pp. 755–764. [Google Scholar] [CrossRef]
- Winkler, K.; Schurer, S.; Tobie, T.; Stahl, K. Investigations on the tooth root bending strength and the fatigue fracture characteristics of case-carburized and shot-peened gears of different sizes. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 7338–7349. [Google Scholar] [CrossRef]
- Fuchs, D.; Schurer, S.; Tobie, T.; Stahl, K. New Consideration of Non-Metallic Inclusions Calculating Local Tooth Root Load Carrying Capacity of High-Strength, High-Quality Steel Gears. Available online: www.geartechnology.com (accessed on 13 July 2022).
- Fuchs, D.; Schurer, S.; Tobie, T.; Stahl, K. A model approach for considering nonmetallic inclusions in the calculation of the local tooth root load-carrying capacity of high-strength gears made of high-quality steels. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 7309–7317. [Google Scholar] [CrossRef]
- Fuchs, D.; Schurer, S.; Tobie, T.; Stahl, K. Investigations into non-metallic inclusion crack area characteristics relevant for tooth root fracture damages of case carburised and shot-peened high strength gears of different sizes made of high-quality steels. Forsch. Ing. 2019, 83, 579–587. [Google Scholar] [CrossRef]
- Fuchs, D.; Rommel, S.; Tobie, T.; Stahl, K. Fracture analysis of fisheye failures in the tooth root fillet of high-strength gears made out of ultra-clean gear steels. Forsch. Ing. 2021, 85, 1109–1125. [Google Scholar] [CrossRef]
- Mcpherson, D.R.; Rao, S.B. Methodology for translating single-tooth bending fatigue data to be comparable to running gear data. Gear Technol. 2008, 6, 42–51. [Google Scholar]
- Rao, S.B.; Mcpherson, D.H. Experimental characterization of bending fatigue strength in gear teeth. Gear Technol. 2003, 20, 25–32. [Google Scholar]
- Li, M.; Xie, L.-Y.; Li, H.-Y.; Ren, J.-G. Life Distribution Transformation Model of Planetary Gear System. Chin. J. Mech. Eng. 2018, 31, 24. [Google Scholar] [CrossRef]
- Concli, F.; Maccioni, L.; Bonaiti, L. Reliable gear design: Translation of the results of single tooth bending fatigue tests through the combination of numerical simulations and fatigue criteria. WIT Trans. Eng. Sci. 2021, 130, 111–122. [Google Scholar] [CrossRef]
- Concli, F.; Fraccaroli, L.; Maccioni, L. Gear Root Bending Strength: A New Multiaxial Approach to Translate the Results of Single Tooth Bending Fatigue Tests to Meshing Gears. Metals 2021, 11, 863. [Google Scholar] [CrossRef]
- Concli, F.; Maccioni, L.; Fraccaroli, L.; Bonaiti, L. Early Crack Propagation in Single Tooth Bending Fatigue: Combination of Finite Element Analysis and Critical-Planes Fatigue Criteria. Metals 2021, 11, 1871. [Google Scholar] [CrossRef]
- Bonaiti, L.; Bayoumi, A.B.M.; Concli, F.; Rosa, F.; Gorla, C. Gear Root Bending Strength: A Comparison Between Single Tooth Bending Fatigue Tests and Meshing Gears. J. Mech. Des. 2021, 143, 1–17. [Google Scholar] [CrossRef]
- Petersen; Link, R.; Pascual, F.; Meeker, W. Analysis of Fatigue Data with Runouts Based on a Model with Nonconstant Standard Deviation and a Fatigue Limit Parameter. J. Test. Evaluation 1997, 25, 292. [Google Scholar] [CrossRef]
- Mao, T.; Liu, H.; Wei, P.; Chen, D.; Zhang, P.; Liu, G. An improved estimation method of gear fatigue strength based on sample expansion and standard deviation correction. Int. J. Fatigue 2022, 161. [Google Scholar] [CrossRef]
- Dixon, W.J.; Mood, A.M. A Method for Obtaining and Analyzing Sensitivity Data. J. Am. Stat. Assoc. 1948, 43, 109–126. [Google Scholar] [CrossRef]
- Alnahlaui, A.; Tenberge, P. Improved Method for the Determination of Tooth Root Endurance Strength. In Proceedings of the International Conference on Gears 2022, Munich, Germany, 12–14 September 2022. [Google Scholar]
- Geitner, M.; Tobie, T.; Stahl, K. FVA research project 610 IV, final report no. 1432—Materials 4.0—Comprehensive statistical data analysis to evaluate the influence of material and heat treatment properties on the load carrying capacity of gears (German: Werkstoffe 4.0-Erweiterte Datenanalyse zur Bewertung des Einflusses von Werkstoff- und Wärmebehandlungseigenschaften auf die Zahnradtragfähigkeit); FVA-Forschungsheft: Frankfurt am Main, Germany, 2021. [Google Scholar]
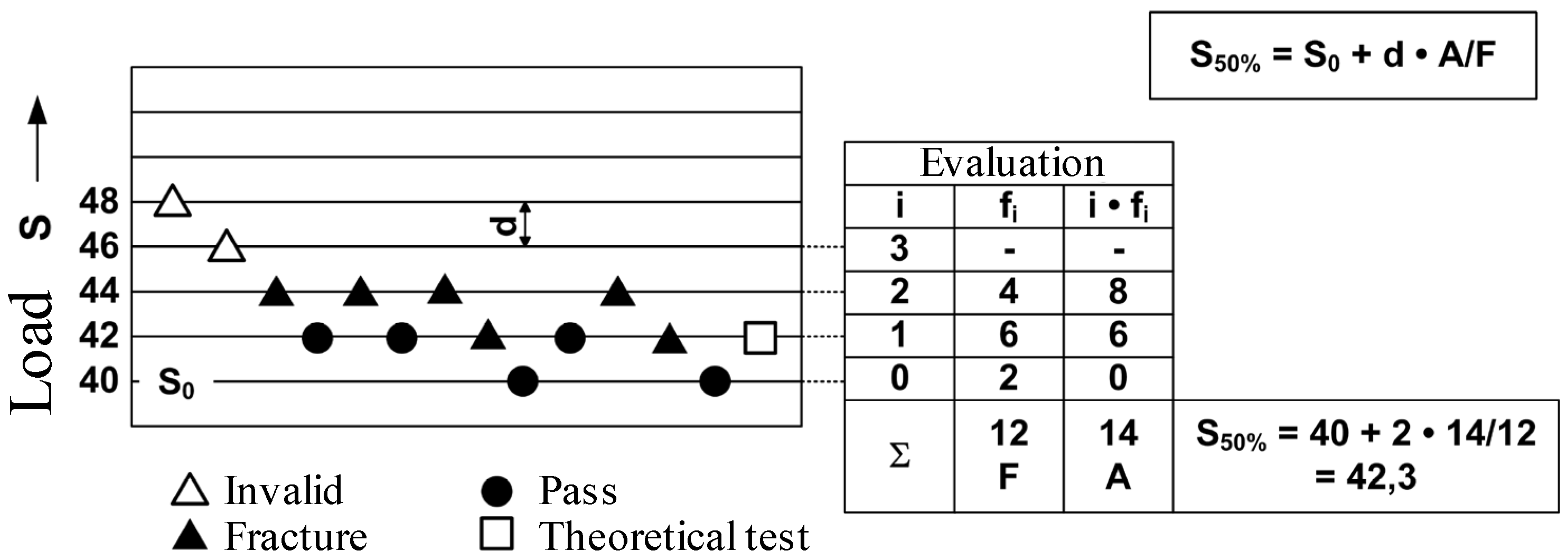
- Hück, M. Ein verbessertes Verfahren für die Auswertung von Treppenstufenversuchen. Mater. Werkst. 1983, 14, 406–417. [Google Scholar] [CrossRef]
- Hösel, T.; Joachim, F. Zahnflankenwälzfestigkeit unter Berücksichtigung der Ausfallwahrscheinlichkeit. Antriebstechnik 1978, 17. [Google Scholar]
- Rossow, E. Eine einfache Rechenschiebernäherung an die den normal scores entsprechenden Prozentpunkte. Qualitätskontrolle 1964, 9, 146–147. [Google Scholar]
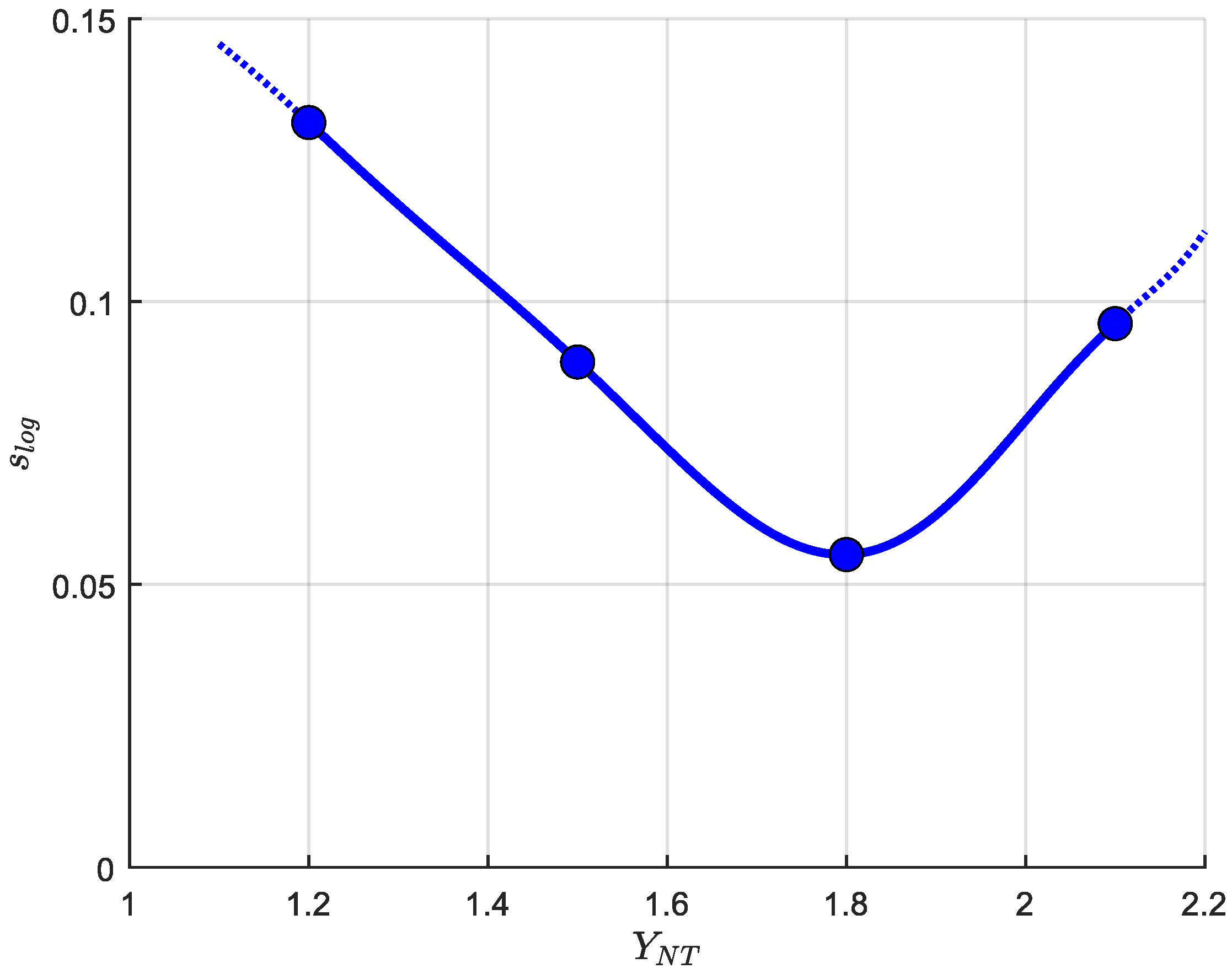
- Spindel, J.; Haibach, E. Some Considerations in the Statistical Determination of the Shape of S-N Curves; ASTM International: West Conshohocken, PA, USA, 1981; p. 89. [Google Scholar] [CrossRef]
- Beretta, S. Affidabilità Delle Costruzioni Meccaniche; Springer: Milan, Italy, 2009. [Google Scholar] [CrossRef]
- Urbano, M.F.; Cadelli, A.; Sczerzenie, F.; Luccarelli, P.; Beretta, S.; Coda, A. Inclusions Size-based Fatigue Life Prediction Model of NiTi Alloy for Biomedical Applications. Shape Mem. Superelasticity 2015, 1, 240–251. [Google Scholar] [CrossRef]
- Nelson, W. Applied Life Data Analysis; Wiley: Hoboken, NJ, USA, 1982. [Google Scholar] [CrossRef]
- Nelson, W. Accelerated Testing: Statistical Models, Test Plans and Data Analyses; John Wiley & Sons: Hoboken, NJ, USA, 2004; p. 601. [Google Scholar]
- Winkler, K.J.; Tobie, T.; Stahl, K. Influence of grinding zones on the tooth root bending strength of case carburized gears. Forsch. Ing. 2021, 86, 661–671. [Google Scholar] [CrossRef]
- Gasparini, G.; Mariani, U.; Gorla, C.; Filippini, M.; Rosa, F. Bending fatigue tests of helicopter case carburized gears: Influence of material, design and manufacturing parameters. Gear Technol. 2009, 68–76. Available online: www.geartechnology.com (accessed on 22 October 2022).
- Gorla, C.; Rosa, F.; Conrado, E. Bending Fatigue Strength of Case Carburized and Nitrided Gear Steels for Aeronautical Applications. Int. J. Appl. Eng. Res. 2017, 12, 11306–11322. Available online: http://www.ripublication.com (accessed on 2 August 2022).
- Castillo, E.; Mínguez, R.; Conejo, A.J.; Pérez, B.; Fontenla, O. Estimating the parameters of a fatigue model using Benders’ decomposition. Ann. Oper. Res. 2011, 210, 309–331. [Google Scholar] [CrossRef]
- Pascual, F.G.; Meeker, W.Q. Estimating Fatigue Curves With the Random Fatigue-Limit Model. Technometrics 1999, 41, 277–289. [Google Scholar] [CrossRef]
- Lorén, S. Estimating fatigue limit distributions under inhomogeneous stress conditions. Int. J. Fatigue 2004, 26, 1197–1205. [Google Scholar] [CrossRef]
- Castillo, E.; Fernández-Canteli, A. A compatible regression Weibull model for the description of the three-dimensional fatigue σM–N–R field as a basis for cumulative damage approach. Int. J. Fatigue 2021, 155, 106596. [Google Scholar] [CrossRef]
- Canteli, A.F.; Castillo, E.; Blasón, S.; Correia, J.; de Jesus, A. Generalization of the Weibull probabilistic compatible model to assess fatigue data into three domains: LCF, HCF and VHCF. Int. J. Fatigue 2022, 159, 106771. [Google Scholar] [CrossRef]
- Freudenthal, A.M.; Gumbel, E.J. Physical and Statistical Aspects of Fatigue. Adv. Appl. Mech. 1956, 4, 117–158. [Google Scholar] [CrossRef]
- Beretta, S.; Clerici, P.; Matteazzi, S. The effect of sample size on the confidence of endurance fatigue tests. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 129–139. [Google Scholar] [CrossRef]
- Loren, S. Fatigue limit estimated using finite lives. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 757–766. [Google Scholar] [CrossRef]
- Lorén, S.; Lundström, M. Modelling curved S–N curves. Fatigue Fract. Eng. Mater. Struct. 2005, 28, 437–443. [Google Scholar] [CrossRef]
- Pascual, F.G. Theory for Optimal Test Plans for the Random Fatigue-Limit Model. Technometrics 2003, 45, 130–141. [Google Scholar] [CrossRef]
- Miller, R.; Nelson, W. Optimum Simple Step-Stress Plans for Accelerated Life Testing. IEEE Trans. Reliab. 1983, R-32, 59–65. [Google Scholar] [CrossRef]
- Horstman, R.; Peters, K.; Gebremedhin, S.; Meltzer, R.; Vieth, M.B.; Nelson, W. Fitting of Fatigue Curves with Nonconstant Standard Deviation to Data with Runouts. J. Test. Eval. 1984, 12, 69–77. [Google Scholar] [CrossRef]
- Mitra, E.D.; Hlavacek, W.S. Parameter estimation and uncertainty quantification for systems biology models. Curr. Opin. Syst. Biol. 2019, 18, 9–18. [Google Scholar] [CrossRef]
- Meeker, W.Q.; Escobar, L.A. Teaching about Approximate Confidence Regions Based on Maximum Likelihood Estimation. Am. Stat. 1995, 49. [Google Scholar] [CrossRef]
- Wiel, S.V.; Meeker, W. Accuracy of approx confidence bounds using censored Weibull regression data from accelerated life tests. IEEE Trans. Reliab. 1990, 39, 346–351. [Google Scholar] [CrossRef]


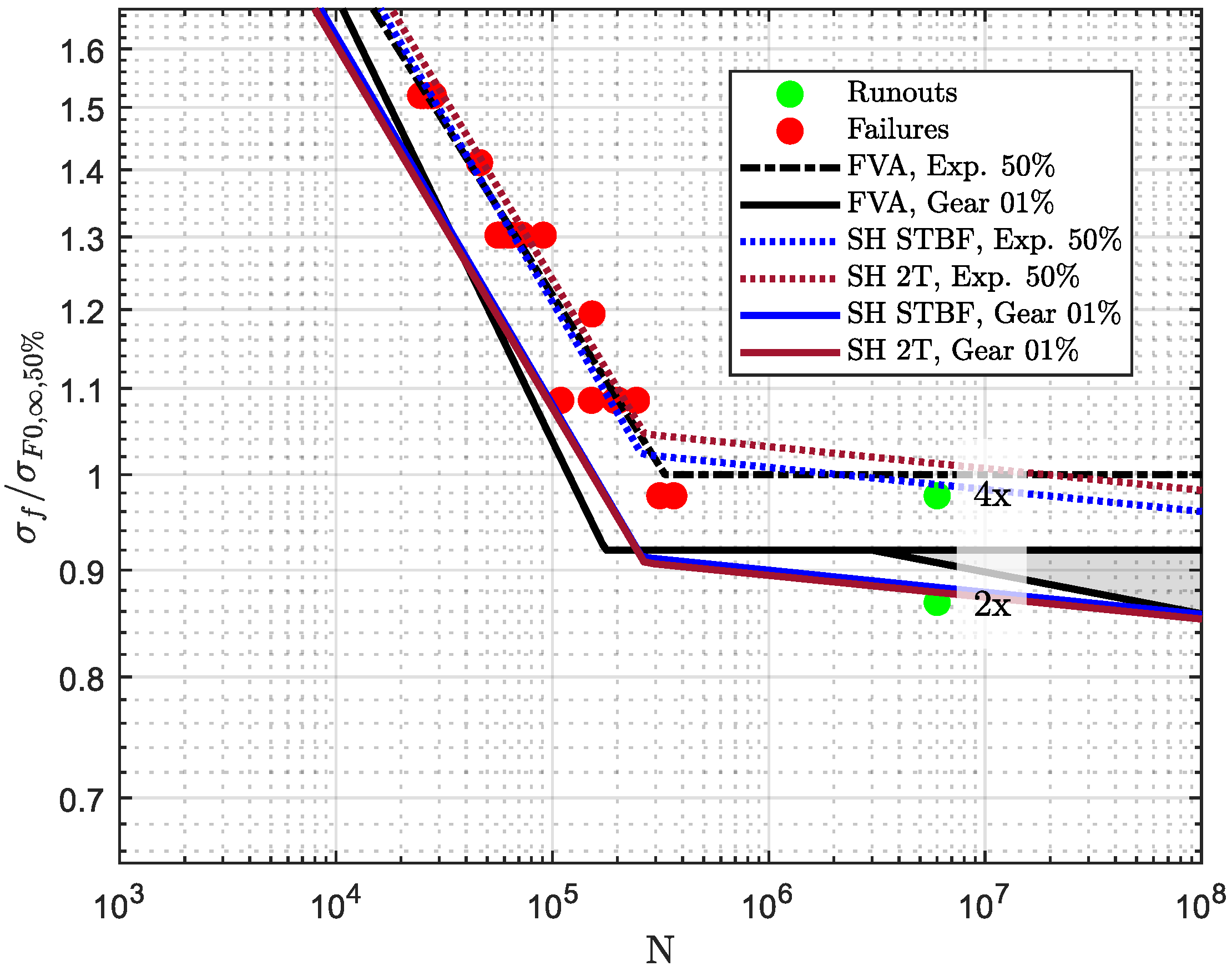


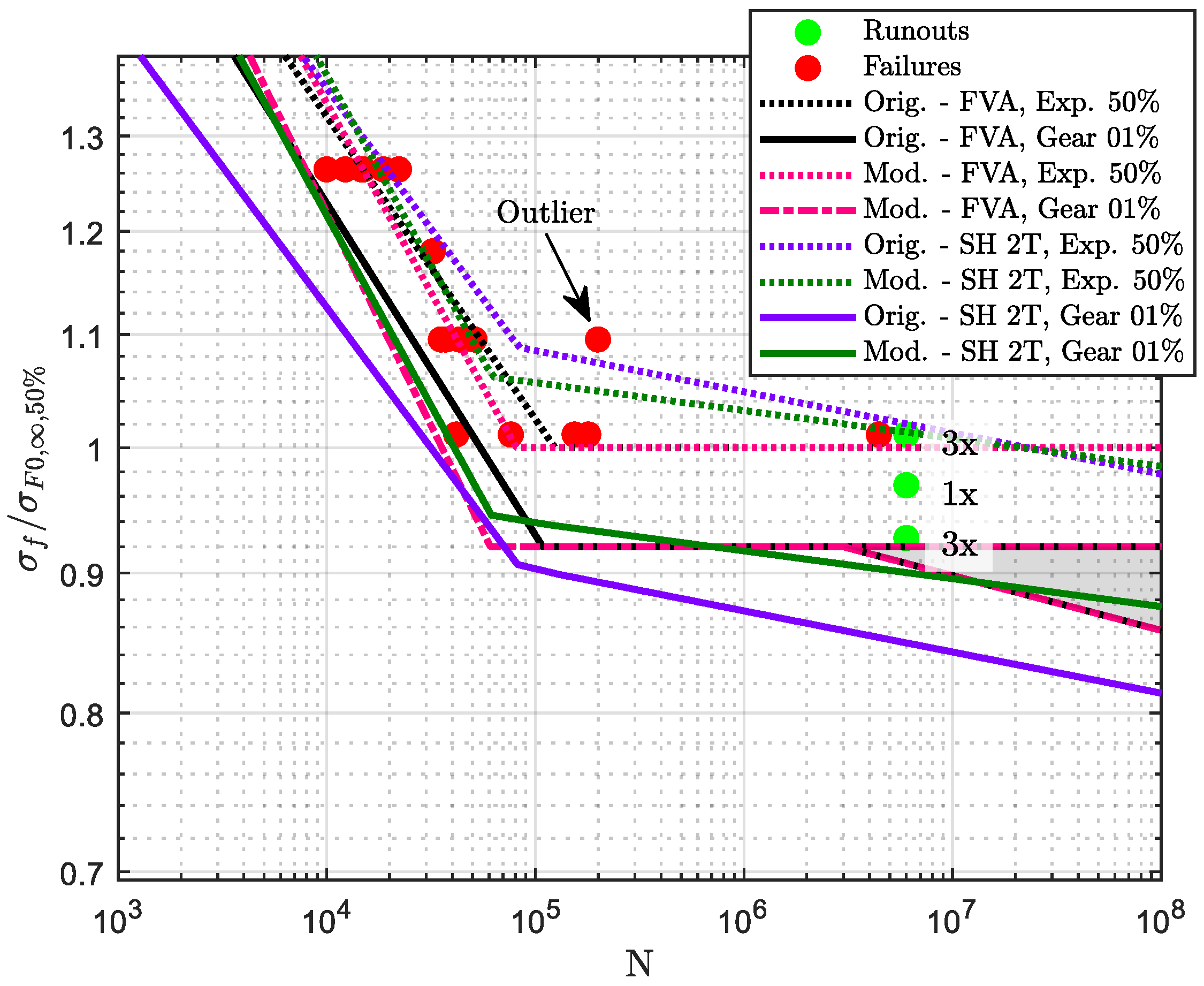
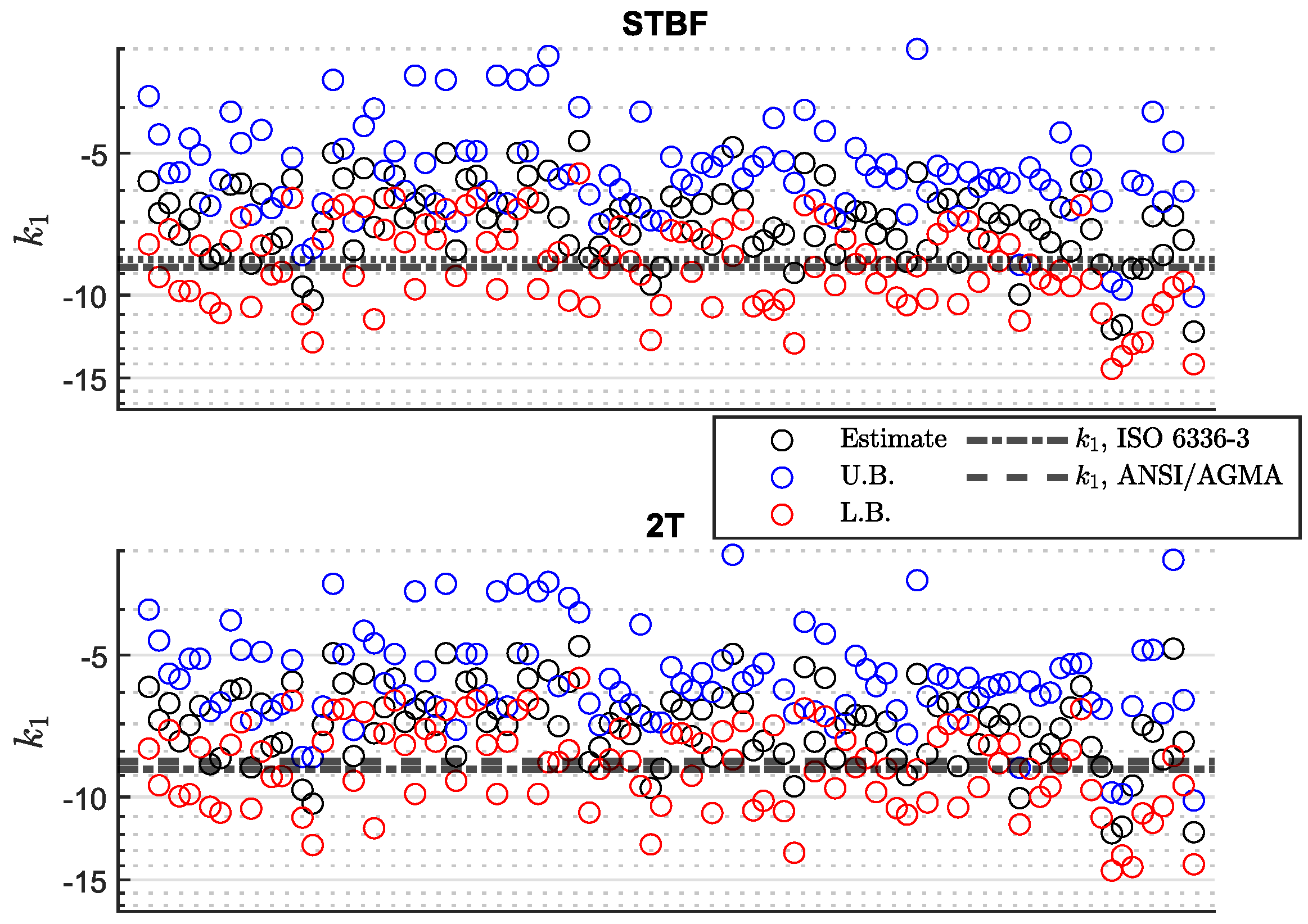
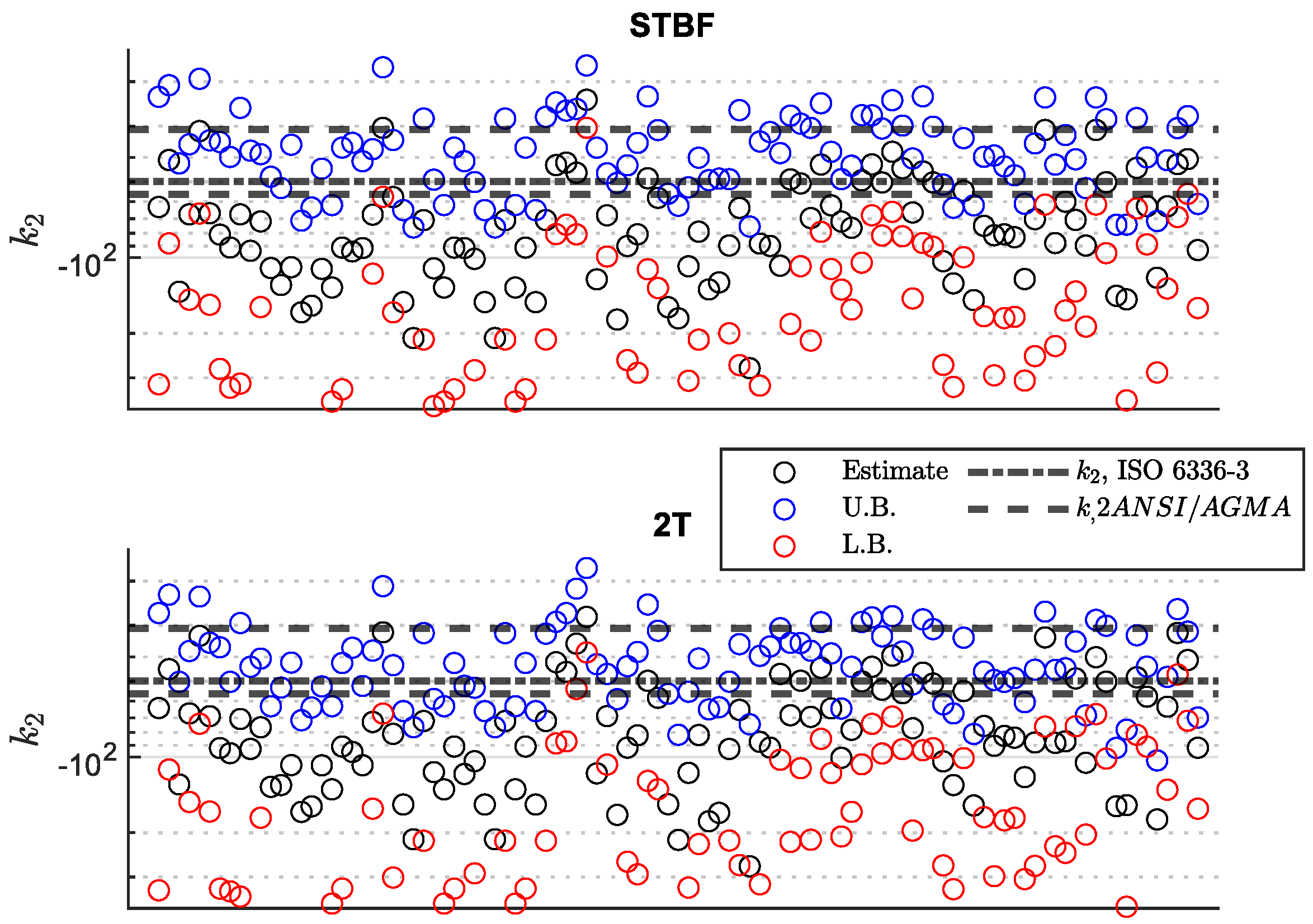

| Year | Reference | Short Summary |
|---|---|---|
| 2009 | [66] | Presentation and analysis of a part of POLIMI points |
| 2017 | [67] | Presentation and analysis of a part of POLIMI points |
| 2018 | [24] | Partial statistical analysis of FZG points |
| 2019 | [40] | Presentation and discussion of selected FZG campaigns |
| 2021 | [56] | Partial statistical analysis of FZG points with focus on effects of materials and heat treatments properties |
| 2022 | [65] | Presentation and discussion of selected FZG campaigns |
| 2021–2022 | [27,28] | Presentation and analysis of a part of POLIMI points |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonaiti, L.; Geitner, M.; Tobie, T.; Gorla, C.; Stahl, K. A Comparison between Two Statistical Methods for Gear Tooth Root Bending Strength Estimation Starting from Pulsator Data. Appl. Sci. 2023, 13, 1546. https://doi.org/10.3390/app13031546
Bonaiti L, Geitner M, Tobie T, Gorla C, Stahl K. A Comparison between Two Statistical Methods for Gear Tooth Root Bending Strength Estimation Starting from Pulsator Data. Applied Sciences. 2023; 13(3):1546. https://doi.org/10.3390/app13031546
Chicago/Turabian StyleBonaiti, Luca, Michael Geitner, Thomas Tobie, Carlo Gorla, and Karsten Stahl. 2023. "A Comparison between Two Statistical Methods for Gear Tooth Root Bending Strength Estimation Starting from Pulsator Data" Applied Sciences 13, no. 3: 1546. https://doi.org/10.3390/app13031546
APA StyleBonaiti, L., Geitner, M., Tobie, T., Gorla, C., & Stahl, K. (2023). A Comparison between Two Statistical Methods for Gear Tooth Root Bending Strength Estimation Starting from Pulsator Data. Applied Sciences, 13(3), 1546. https://doi.org/10.3390/app13031546