Numerical and Experimental Analysis of the Oil Flow in a Planetary Gearbox
Abstract
1. Introduction
Literature Review
2. Materials and Methods
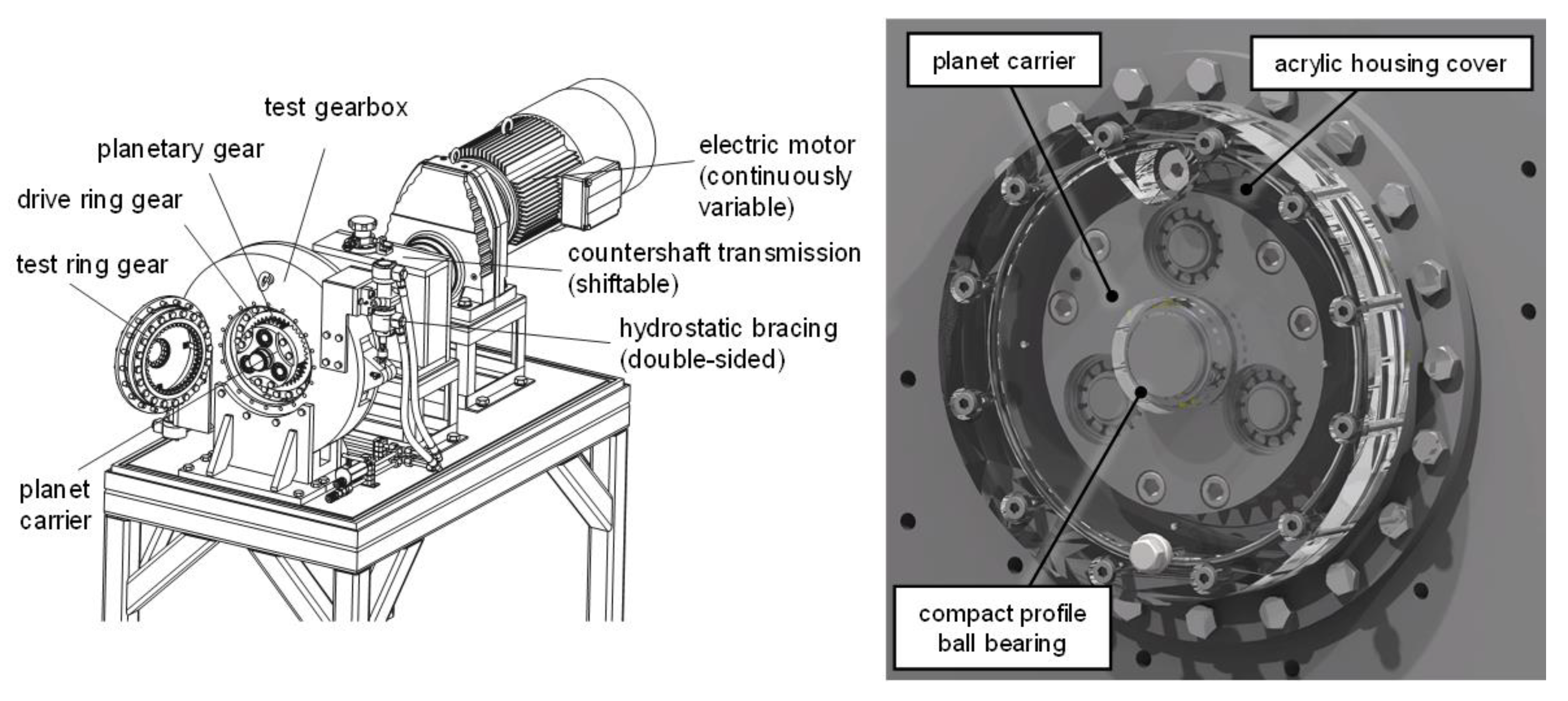
2.1. Object of Investigation
2.2. Operating Conditions
2.3. Mathematical Description and Governing Equations
2.4. CFD Modeling of the Oil Flow
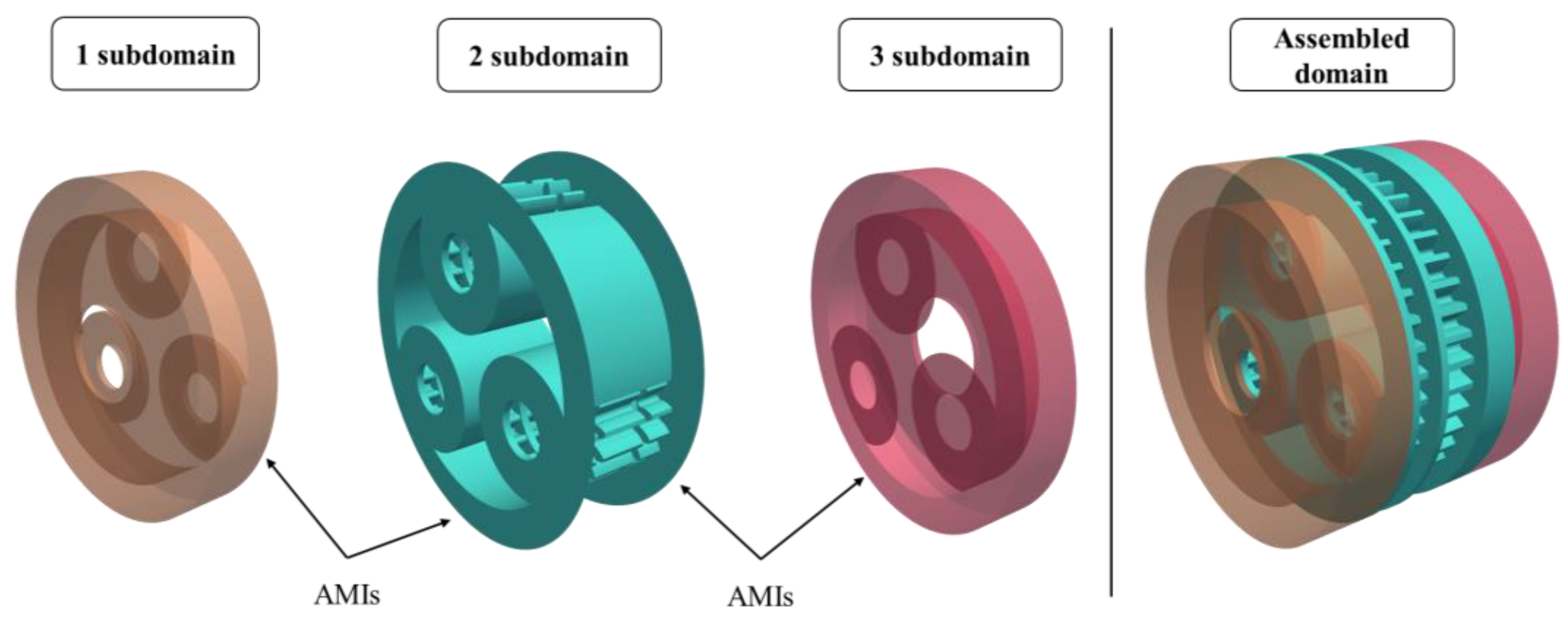
2.4.1. Geometrical Considerations
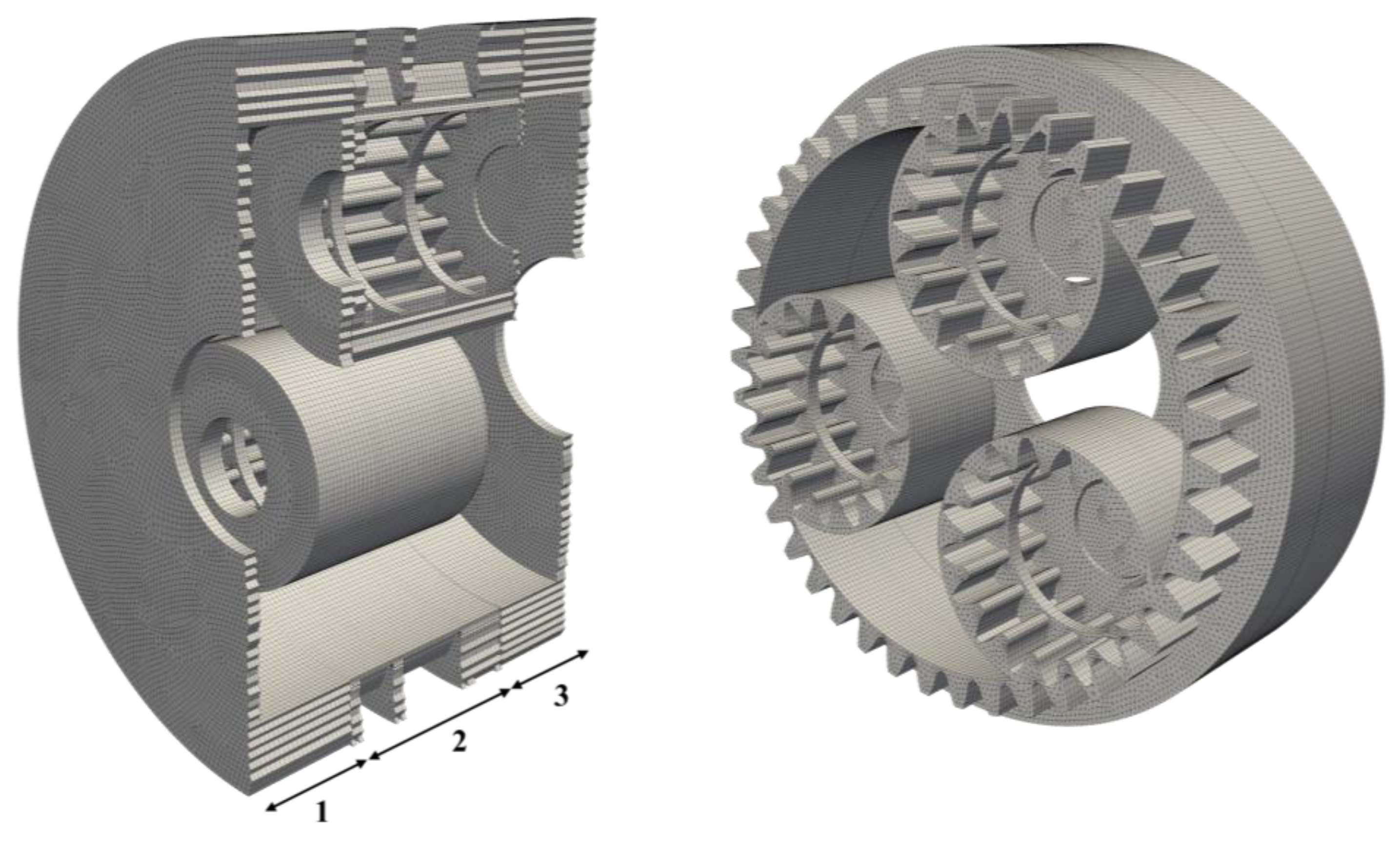
2.4.2. Meshing Approach
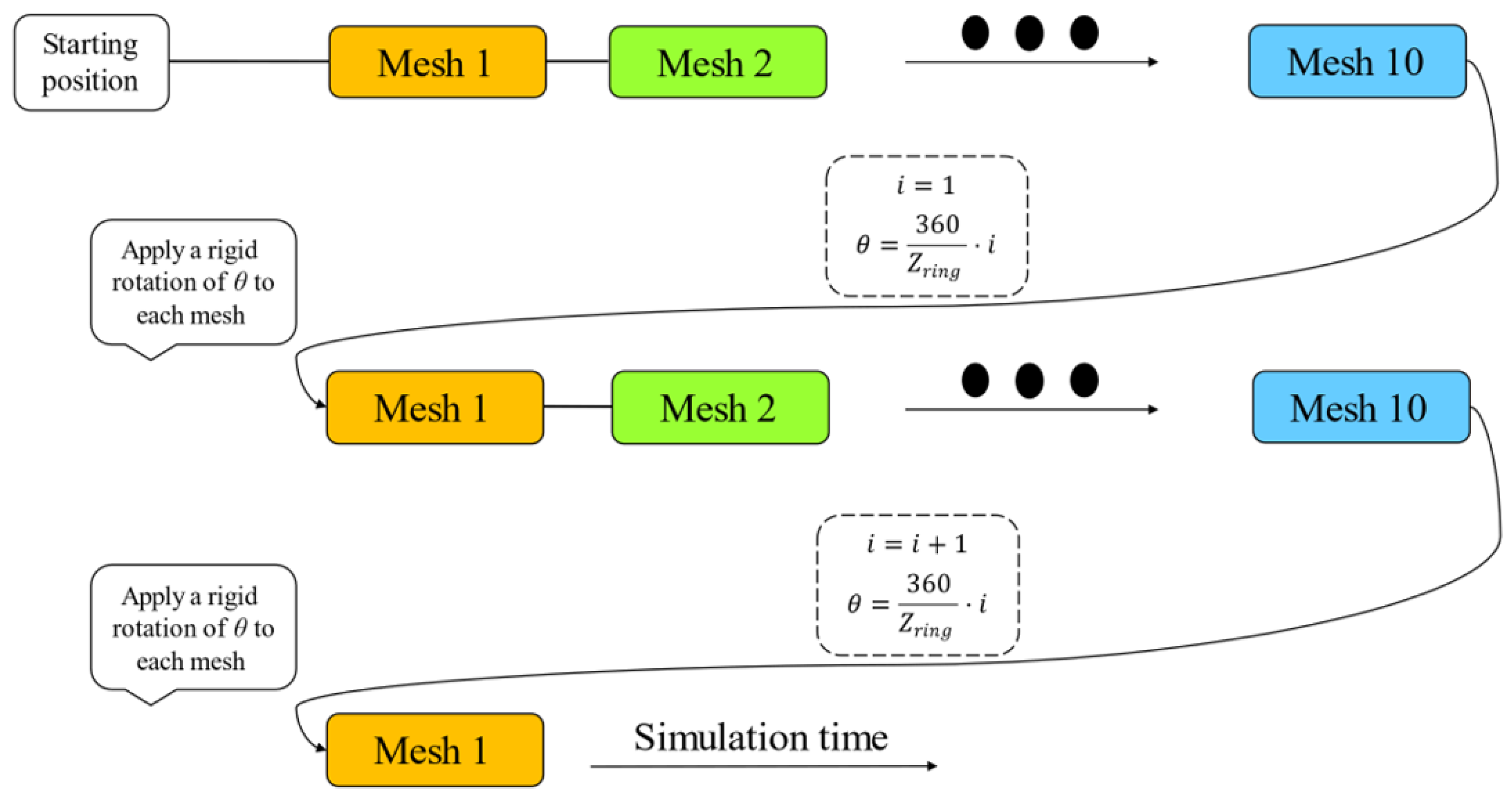
2.4.3. Mesh-Handling Approach
2.4.4. Boundary Conditions and Numerical Settings
2.4.5. Computational Performance
3. Results and Discussion
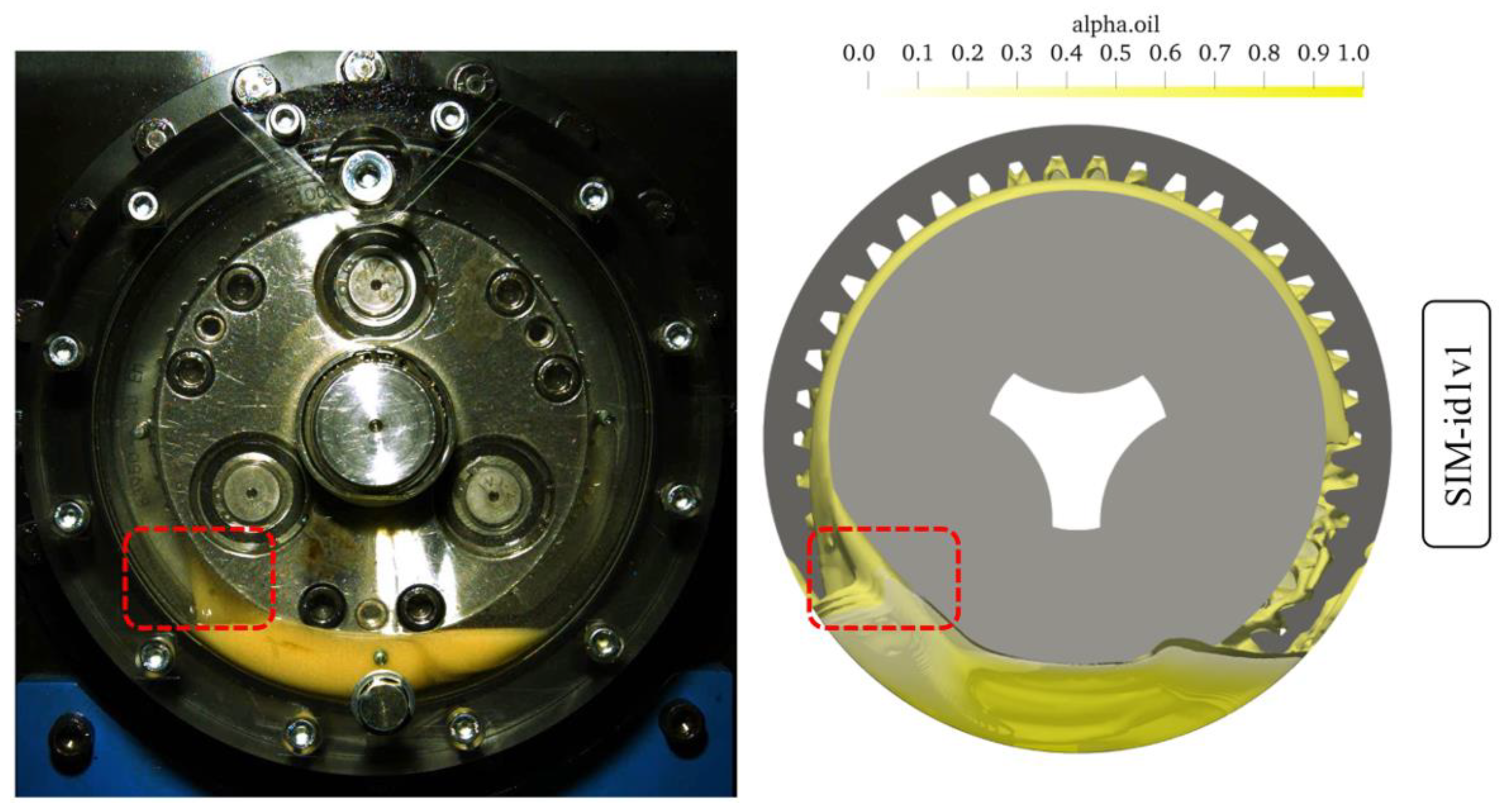
3.1. Comparison of Numerical and Experimental Results
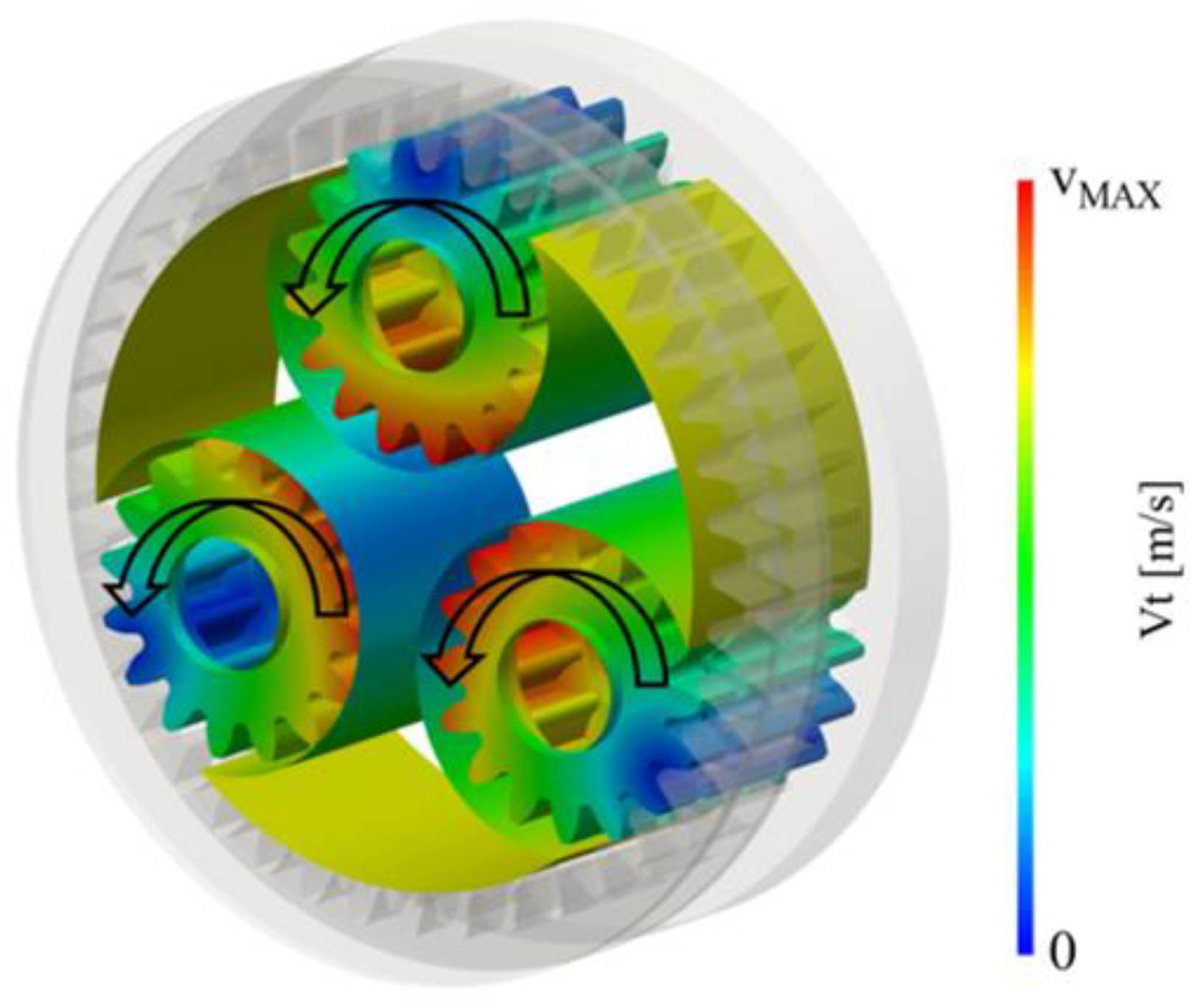
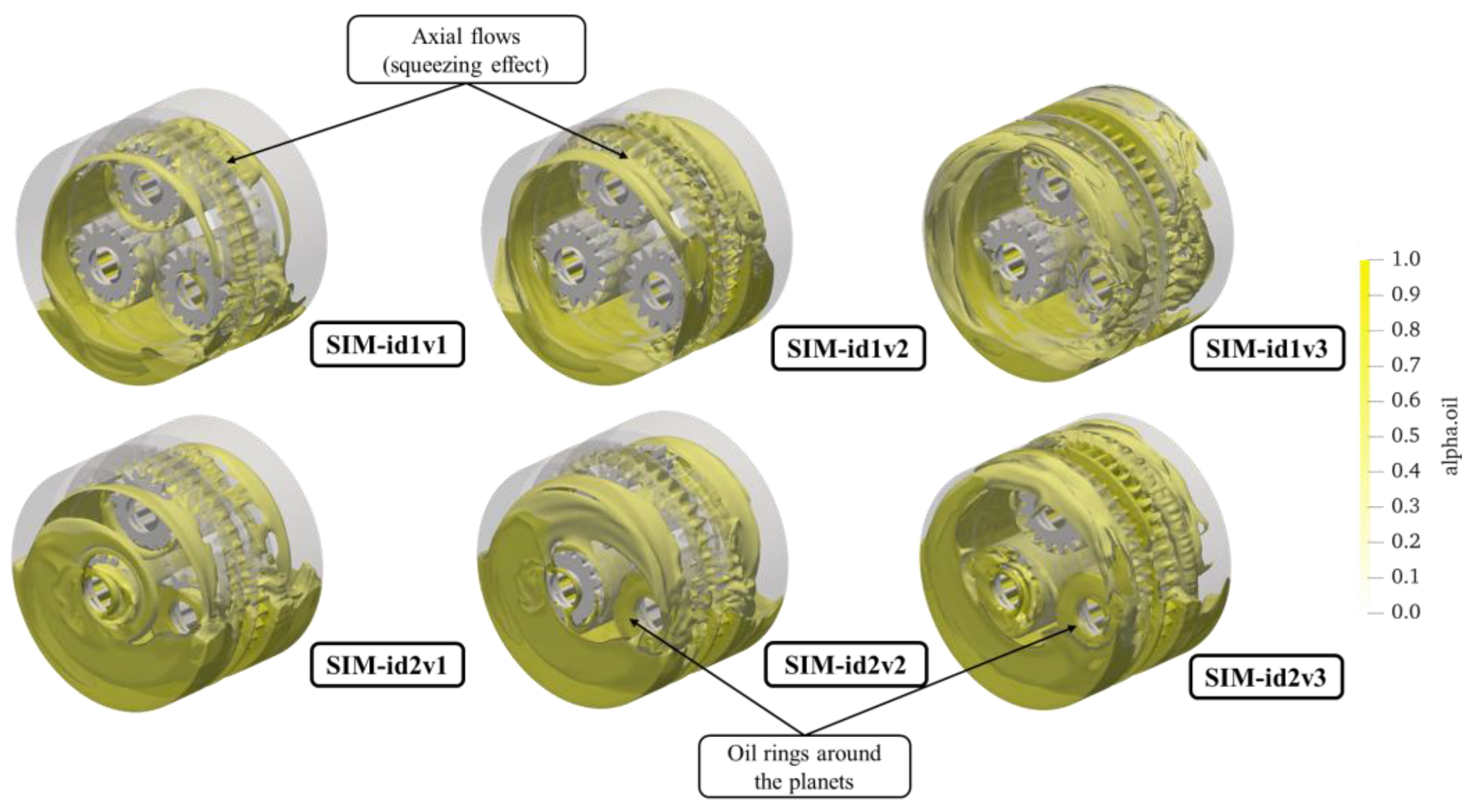
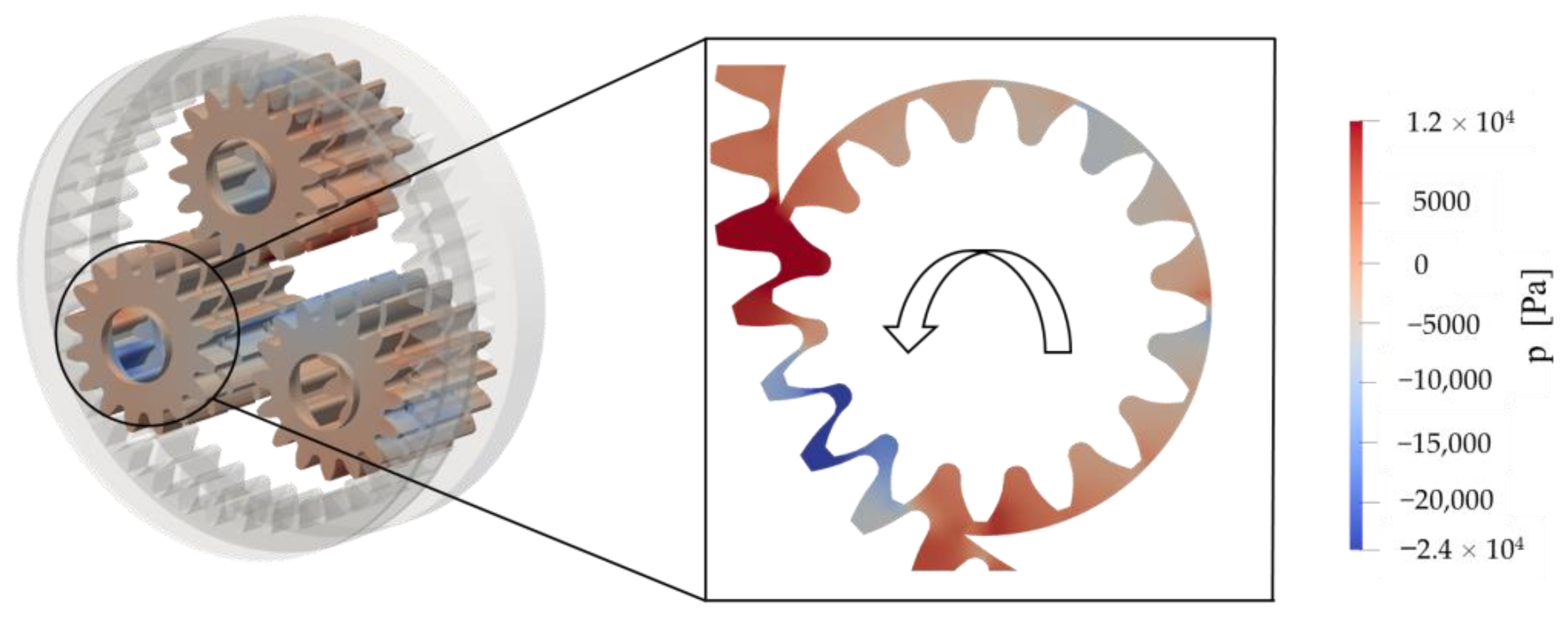
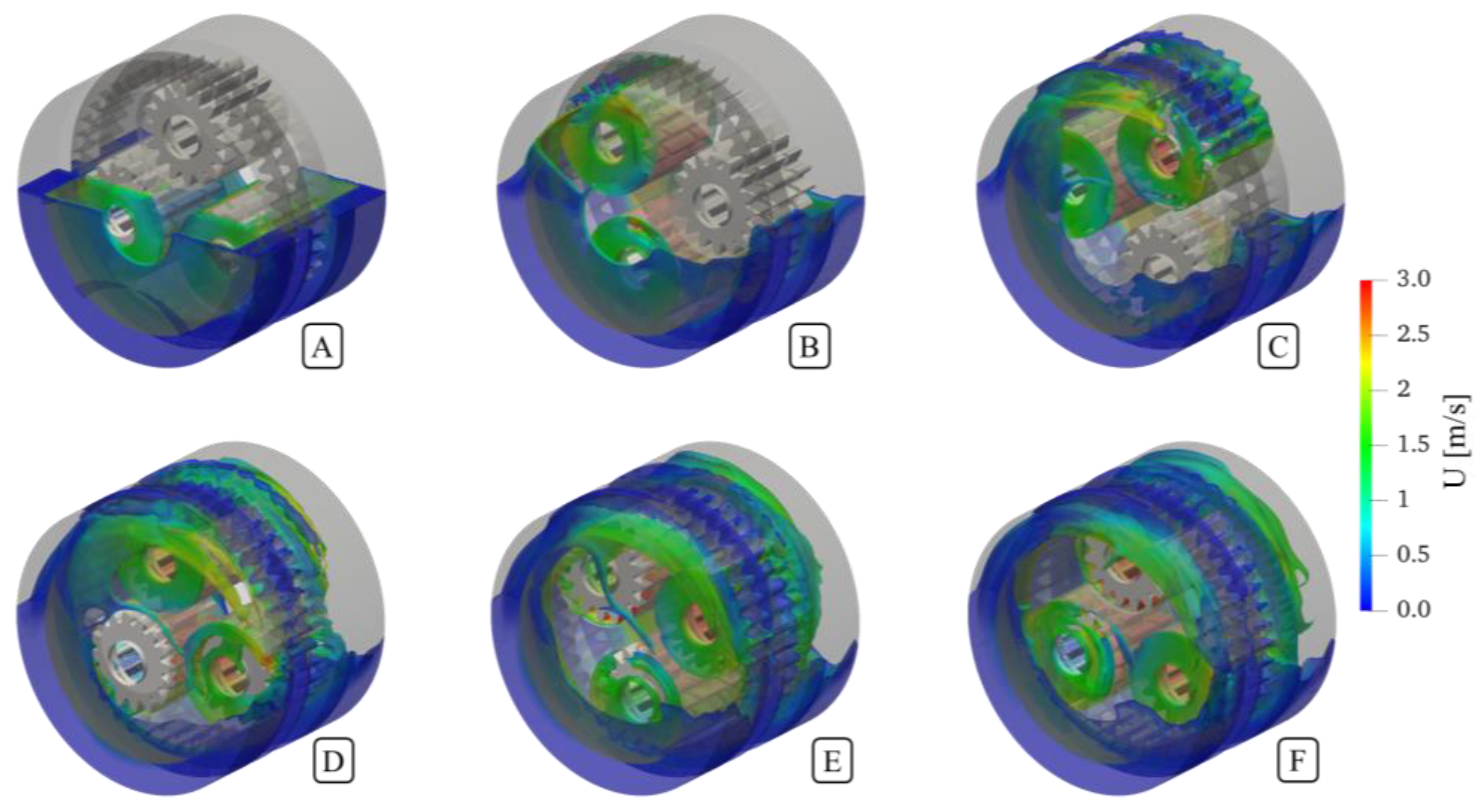
3.2. Details of the Oil Flow in the Planetary Gearbox
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schudy, J. Untersuchungen Zur Flankentragfähigkeit von Außen-Und Innenverzahnungen. Einflüsse Auf Das Grübchen-, Grauflecken- Und Verschleißverhalten, Insbesondere Bei Langsam Laufenden Getriebestufen. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2010. [Google Scholar]
- Liu, H.; Standl, P.; Sedlmair, M.; Lohner, T.; Stahl, K. Efficient CFD Simulation Model for a Planetary Gearbox. Forsch. Ing. 2018, 82, 319–330. [Google Scholar] [CrossRef]
- Gold, P.W.; Hermsmeier, J.; Goedecke, O.; Assman, C. Untersuchung Der Leerlaufverluste in Einem Planetengetriebe Für Windkraftanlagen Mit Mine-Ralölbasischen Und Biologisch Schnell Abbaubaren Schmierstoffen. VDI Berichte 1999, 1460, 217–230. [Google Scholar]
- Kettler, J. Ölsumpftemperatur von Planetengetrieben; FVA Heft 639; FVA: Frankfurt am Main, Germany, 2002. [Google Scholar]
- da Costa, D. Power Loss in Planetary Gear Transmissions Lubricated with Axle Oils. Master’s Thesis, University of Porto, Porto, Portugal, 2015. [Google Scholar]
- Höhn, B.R.; Stahl, K.; Schudy, J.; Tobie, T.; Zornek, B. FZG Rig-Based Testing of Flank Load-Carrying Capacity Internal Gears. Gear Technol. 2012, 60–69. [Google Scholar]
- de Gevigney, J.D.; Changenet, C.; Ville, F.; Velex, P.; Becquerelle, S. Experimental Investigation on No-Load Dependent Power Losses in a Planetary Gear Set. In Proceedings of the International Gear Conference, Valencia, Spain, 4–5 March 2013; pp. 1101–1112. [Google Scholar]
- Boni, J.-B.; Neurouth, A.; Changenet, C.; Ville, F. Experimental investigations on churning power losses generated in a planetary gear set. J. Adv. Mech. Des. Syst. Manuf. 2017, 11, JAMDSM0079. [Google Scholar] [CrossRef]
- Boni, J.-B.; Changenet, C.; Ville, F. Analysis of Flow Regimes and Associated Sources of Dissipation in Splash Lubricated Planetary Gear Sets. J. Tribol. 2021, 143, 111805. [Google Scholar] [CrossRef]
- Maccioni, L.; Concli, F. Computational Fluid Dynamics Applied to Lubricated Mechanical Components: Review of the Approaches to Simulate Gears, Bearings, and Pumps. Appl. Sci. 2020, 10, 8810. [Google Scholar] [CrossRef]
- Bianchini, C.; Da Soghe, R.; Errico, J.D.; Tarchi, L. Computational Analysis of Windage Losses in an Epicyclic Gear Train. In Proceedings of the Turbo Expo, Charlotte, NC, USA, 26–30 June 2017; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2017; Volume 5B. [Google Scholar]
- Bianchini, C.; Da Soghe, R.; Giannini, L.; Fondelli, T.; Massini, D.; Facchini, B.; D’Errico, J. Load Independent Losses of an Aeroengine Epicyclic Power Gear Train: Numerical Investigation. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Concli, F. Austempered Ductile Iron (ADI) for gears: Contact and bending fatigue behavior. Procedia Struct. Integr. 2018, 8, 14–23. [Google Scholar] [CrossRef]
- Concli, F.; Conrado, E.; Gorla, C. Analysis of power losses in an industrial planetary speed reducer: Measurements and computational fluid dynamics calculations. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 228, 11–21. [Google Scholar] [CrossRef]
- Concli, F. Thermal and efficiency characterization of a low-backlash planetary gearbox: An integrated numerical-analytical prediction model and its experimental validation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 230, 996–1005. [Google Scholar] [CrossRef]
- Concli, F. Low-Loss Gears Precision Planetary Gearboxes: Reduction of the Load Dependent Power Losses and Efficiency Estimation through a Hybrid Analytical-Numerical Optimization Tool [Hochleistungs- Und Präzisions-Planetengetriebe: Effizienzschätzung Und Reduzierun. Forsch. Ing. 2017, 81, 395–407. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C. Numerical modeling of the churning power losses in planetary gearboxes: An innovative partitioning-based meshing methodology for the application of a computational effort reduction strategy to complex gearbox configurations. Lubr. Sci. 2017, 29, 455–474. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C. CFD Simulation of Power Losses and Lubricant Flows in Gearboxes. In Proceedings of the American Gear Manufacturers Association Fall Technical Meeting 2017, Colombus, OH, USA, 22–24 October 2017; pp. 2–14. [Google Scholar]
- OpenFOAM. Available online: https://www.openfoam.com (accessed on 20 December 2022).
- Cho, J.; Hur, N.; Choi, J.; Yoon, J. Numerical Simulation of Oil and Air Two-Phase Flow in a Planetary Gear System Using the Overset Mesh Technique. In Proceedings of the Open Archives of the 16th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, ISROMAC 2016, Honolulu, HI, USA, 10–15 April 2016. [Google Scholar]
- Benek, J.; Steger, J.; Dougherty, F.C. A Flexible Grid Embedding Technique with Application to the Euler Equations. In Proceedings of the 6th Computational Fluid Dynamics Conference, Danvers, CO, USA, 13–15 July 1983; p. 1944. [Google Scholar]
- Benek, J.; Buning, J.; Steger, J. A 3-D Chimera Grid Embedding Technique. In Proceedings of the 7th Computational Physics Conference, Cincinnati, OH, USA, 15–17 July 1985; p. 1523. [Google Scholar]
- STAR-CCM+. Available online: www.plm.automation.siemens.com (accessed on 8 December 2022).
- ANSYS FLUENT. Available online: www.ansys.com (accessed on 8 December 2022).
- Höhn, B.R.; Stahl, K.; Schudy, J.; Tobie, T.; Zornek, B. Investigations on the Flank Load Carrying Capacity in the Newly Developed FZG Back-to-Back Test Rig for Internal Gears. In Proceedings of the Fall Technical Meeting; AGMA: Cincinnati, OH, USA, 2011. [Google Scholar]
- Laukotka, E.M. Referenzöle—Datensammlung; FVA Heft 660; FVA: Frankfurt am Main, Germany, 2003. [Google Scholar]
- Versteeg, H.K. An Introduction to Computational Fluid Dynamics—The Finite Volume Method; Pearson Education: London, UK, 1995. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions; Imperial College of Science, Technology and Medicine: London, UK, 2002. [Google Scholar]
- Farrell, P.E.; Maddison, J.R. Conservative interpolation between volume meshes by local Galerkin projection. Comput. Methods Appl. Mech. Eng. 2011, 200, 89–100. [Google Scholar] [CrossRef]
- Python. Available online: https://www.python.org/ (accessed on 8 December 2022).
- SALOME. Available online: http://www.salome-platform.org (accessed on 8 December 2022).
- Mastrone, M.N.; Concli, F. CFD simulations of gearboxes: Implementation of a mesh clustering algorithm for efficient simulations of complex system’s architectures. Int. J. Mech. Mater. Eng. 2021, 16, 1–19. [Google Scholar] [CrossRef]
- Bash. Available online: www.gnu.org/software/bash (accessed on 8 December 2022).
- Concli, F.; Schaefer, C.T.; Bohnert, C. Innovative Meshing Strategies for Bearing Lubrication Simulations. Lubricants 2020, 8, 46. [Google Scholar] [CrossRef]
- Taylor, G.I. VIII. Stability of a viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. London Ser. A 1923, 223, 289–343. [Google Scholar] [CrossRef]
- Concli, F.; Della Torre, A.; Gorla, C.; Montenegro, G. A New Integrated Approach for the Prediction of the Load Independent Power Losses of Gears: Development of a Mesh-Handling Algorithm to Reduce the CFD Simulation Time. Adv. Tribol. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C. A CFD analysis of the oil squeezing power losses of a gear pair. Int. J. Comput. Methods Exp. Meas. 2014, 2, 157–167. [Google Scholar] [CrossRef]
- Korsukova, E.; Morvan, H. Preliminary CFD Simulations of Lubrication and Heat Transfer in a Gearbox. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition GT2017, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Fondelli, T.; Massini, D.; Andreini, A.; Facchini, B. Three-Dimensional CFD Analysis of Meshing Losses in a Spur Gear Pair. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition GT2018, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Li, J.; Qian, X.; Liu, C. Comparative study of different moving mesh strategies for investigating oil flow inside a gearbox. Int. J. Numer. Methods Heat Fluid Flow 2022. [Google Scholar] [CrossRef]





| Unit | Ring gear | Planet Gear | |
|---|---|---|---|
| Center distance (a) | mm | 59 | |
| Normal module (mn) | mm | 4.5 | |
| Number of teeth (z) | - | 42 | 16 |
| Face width (b) | mm | 16 | 14 |
| Tip diameter (da) | mm | 185.0 | 82.5 |
| Pressure angle (αn) | ° | 20 | |
| Helix angle (β) | ° | 0 | |
| Profile shift coeff. (x) | - | 0.1817 | 0.2962 |
| Unit | Value | |
|---|---|---|
| Kinematic viscosity (40 °C) | mm2/s | 95 |
| Kinematic viscosity (100 °C) | mm2/s | 10.7 |
| Density (40 °C) | kg/m3 | 864 |
| Simulation Name | Lubricant Filling Level | Planet Carrier Speed nt in rpm | Planet Gears Speed np,abs in rpm | Tangential Speed at Pitch Circle vt in m/s |
|---|---|---|---|---|
| SIM-id1v1 | 3∙mn | 81 | 132 | 0.8 |
| SIM-id1v2 | 162 | 263 | 1.6 | |
| SIM-id1v3 | 324 | 526 | 3.2 | |
| SIM-id2v1 | centerline | 81 | 132 | 0.8 |
| SIM-id2v2 | 162 | 263 | 1.6 | |
| SIM-id2v3 | 324 | 526 | 3.2 |
| Max Non-Orthogonality [°] | Max. Skewness [-] | ||
|---|---|---|---|
| Initial mesh | Displaced mesh | Initial mesh | Displaced mesh |
| 50.7 | 66.1 | 1.6 | 2.8 |
| Convergence criterion | 1 × 10−5 |
| Maximum Courant number | 1 |
| Pressure solver | PCG (preconditioned conjugate gradient) |
| Velocity solver | PBiCG (stabilized preconditioned bi-conjugate gradient) |
| Time derivative discretization | First order implicit Euler scheme |
| Velocity discretization | Second order linear-upwind scheme |
| Convection of the volumetric fraction | Second order van Leer scheme |
| GRAMC | General Approach | Net Gain % | |
|---|---|---|---|
| Simulation time for the analyzed gearbox (1 planet carrier rotation) | 20 h | 400 h | 95% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mastrone, M.N.; Hildebrand, L.; Paschold, C.; Lohner, T.; Stahl, K.; Concli, F. Numerical and Experimental Analysis of the Oil Flow in a Planetary Gearbox. Appl. Sci. 2023, 13, 1014. https://doi.org/10.3390/app13021014
Mastrone MN, Hildebrand L, Paschold C, Lohner T, Stahl K, Concli F. Numerical and Experimental Analysis of the Oil Flow in a Planetary Gearbox. Applied Sciences. 2023; 13(2):1014. https://doi.org/10.3390/app13021014
Chicago/Turabian StyleMastrone, Marco Nicola, Lucas Hildebrand, Constantin Paschold, Thomas Lohner, Karsten Stahl, and Franco Concli. 2023. "Numerical and Experimental Analysis of the Oil Flow in a Planetary Gearbox" Applied Sciences 13, no. 2: 1014. https://doi.org/10.3390/app13021014
APA StyleMastrone, M. N., Hildebrand, L., Paschold, C., Lohner, T., Stahl, K., & Concli, F. (2023). Numerical and Experimental Analysis of the Oil Flow in a Planetary Gearbox. Applied Sciences, 13(2), 1014. https://doi.org/10.3390/app13021014









