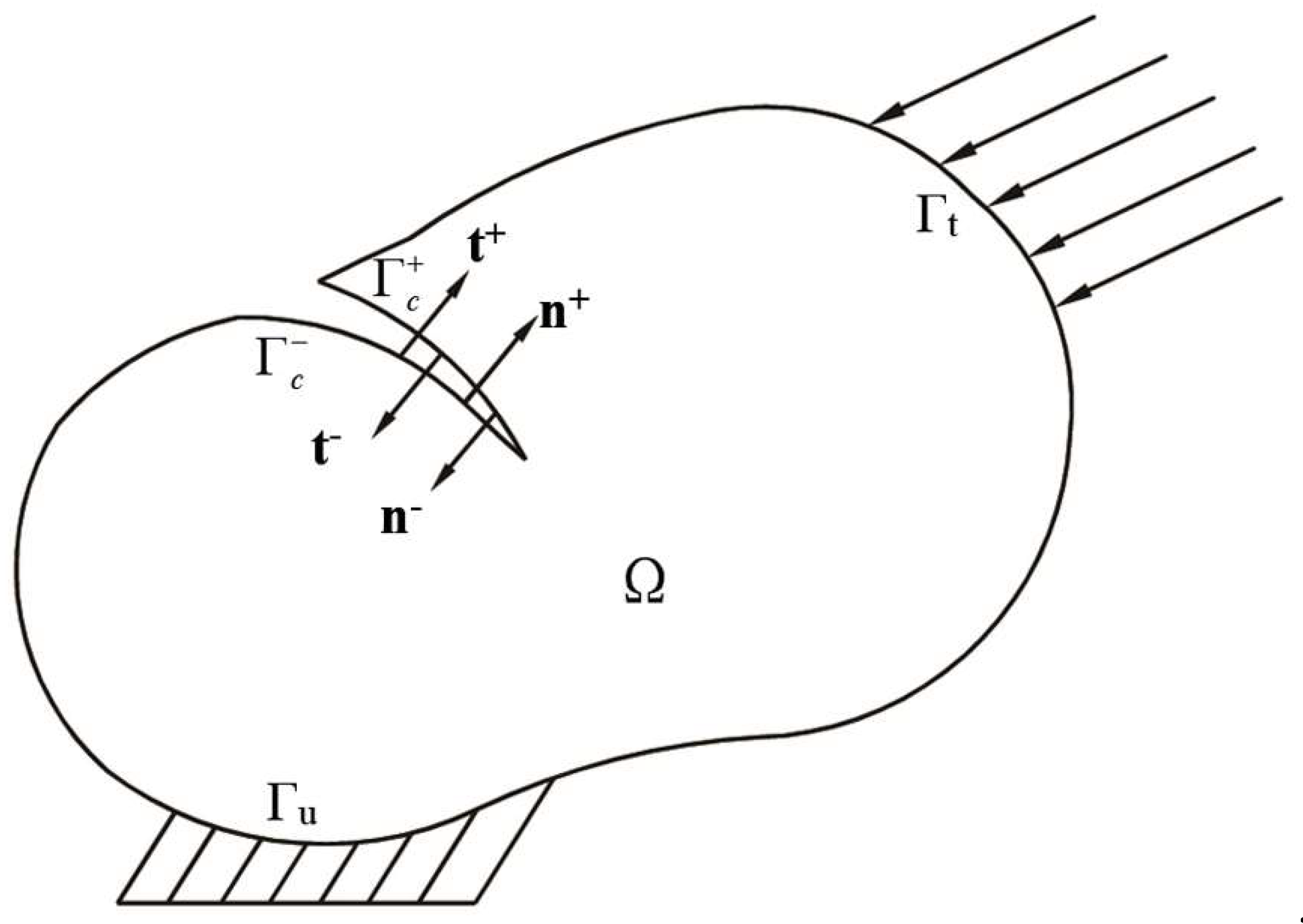
1. Introduction
Masonry-infilled RC frame structures are widely built in seismically active areas around the world [
1]. The observation of post-earthquake damage has shown that the interaction between the infill and the bounding frame has a significant impact on the seismic performance of these structures that may or may not be beneficial [
2,
3]. Therefore, it is always important to consider the behavior of the frame–infill wall interaction in seismic regions.
A large number of numerical methods have been proposed in the literature to consider the nonlinear behavior of masonry-infilled frames. Generally, two main modeling approaches are used for the cracking and damage behavior of the masonry material, these being the continuum approach and the discretization approach. In the continuum approach, the infill is usually modeled as a homogenized continuum and the weakness of mortar joints is smeared out in the entire wall. It has been widely adopted in the past due to its efficiency of calculation and convenience of implementation [
4,
5,
6,
7,
8,
9,
10,
11,
12], which allows it to be used for the seismic performance analysis of actual large-scale structures [
13,
14]. In this approach, the crack and damage propagation path is represented by a zone in which the load-bearing capacity is gradually lost. The best-known model of this approach is the smeared cracking model, which was pioneered with the fixed smeared cracking model [
15,
16], then extended to the rotating smeared cracking model [
17,
18,
19]. Furthermore, in order to consider the anisotropy and post-peak softening behavior caused by the presence of mortar in masonry walls, some heterogeneous continuum models with the features of orthotropic elastic-plastic behavior with softening have been proposed [
20,
21,
22].
In the discretization approach, continuum elements are combined with interface elements to separately represent masonry units, mortar joints and unit–mortar interfaces. In fact, mortar joints and unit-mortar interfaces are usually reduced to interfaces for computational efficiency. With this approach, different failure modes can be captured in an accurate manner. Therefore, it is also widely used in a lot of literature to explore the detailed structural behavior of masonry-infilled RC frames [
23,
24,
25,
26,
27,
28,
29,
30].
In addition, some novel simulation methods have been proposed for the comprehensive consideration of computational efficiency and simulation accuracy. Milani [
31] proposed a homogenization model of masonry walls at a structural level by uniformly discretizing the wall into rigid triangular elements and nonlinear interface elements. Pirsaheb et al. [
32,
33] proposed a novel multi-pier (MP) method to analyze the in-plane behavior of masonry walls, especially for walls with openings. With this MP method, Khaleghi et al. [
34,
35] predicted the load-bearing capacity and stiffness of masonry walls by the application of machine learning, which greatly improves calculation efficiency.
In the analysis of masonry-infilled RC frames, the choice of numerical method depends on the accuracy and detail required. The uncertainties of the frame–infill wall interaction may result in different failure modes, which leads to complexity in the numerical analysis. The discretization approach is usually preferred to describe the failure behavior of masonry-infilled RC frames in detail. In this approach, however, interface elements are required to be preset in the modeling process before the analysis to represent the potential cracking behavior. Shing [
36,
37] tried to add interface elements into the modeling of columns to model the diagonal shear failure in the columns according to the experimental observation of cracking behavior. However, in frame members and masonry blocks, the diagonal cracks and many distributed cracks may develop in an arbitrary manner; it is therefore difficult to preset interface elements in the modeling procedure. For this reason, Stavridis and Shing [
25] introduced a great many of horizontal, vertical and diagonal interface elements in columns to cover potential crack-propagation paths.
Considering the inherent mesh dependence in the interface element and the complication of a finite element discretization scheme, this approach is still not satisfactory for dealing with the arbitrary crack-propagation problem [
38]. Therefore, an extended finite element method (XFEM) is introduced and combined with interface elements to predict the response of masonry-infilled RC frame structures. XFEM is an effective numerical method for solving discontinuous problems. This paper focuses on the implementation aspects of a numerical simulation of masonry-infilled RC frame structures using XFEM, and presents a feasible and effective means to incorporate XFEM into the finite element analysis program FEAP [
39]. Some critical and difficult parts in the implementation of XFEM are also explained in detail.
Research Significance
The failure of masonry-infilled RC frame structures has been very common in past earthquakes. The existence of the infill wall affects the load-bearing capacity and failure mode of such structures. Due to the complexity of the interaction between the infill wall and the bounding frame, and the numerous factors affecting the structural behavior, it is not easy to determine the failure behavior of infilled RC frames. Therefore, it is desirable and challenging to explore this failure behavior in detail using accurate numerical methods. To this end, the discretization approach combining continuous elements and interface elements is a widely used approach. To overcome the difficulty of arbitrary crack propagation in this approach, XFEM is introduced into this study to simulate the cracking behavior of frame concrete and masonry units, and the key elements in the implementation of XFEM are elaborated. Finally, numerical examples show the effectiveness of the proposed model. The study will help academics better understand the performance of masonry-infilled RC frame structures, and help readers to extend its application to a broader class of problems.
3. Numerical Implementation of XFEM
FEAP is an open source structural analysis program for solving linear and nonlinear problems in solid mechanics and other subject areas. It allows users to add new elements, material modules or command language statements to meet some specific application requirements.
In this paper, the operation of incorporating the XFEM capabilities within FEAP is broken down into the following subcategories: 1. nodal degrees of freedom; 2. input material parameters; 3. information passing; 4. numerical integration strategy; 5. constitutive relations; 6. assembly procedure; 7. output for post-processing; 8. crack-propagation strategy. Of all these tasks, Task 8 is implemented by adding a macro command with the name “UMACR1”, and the incorporation of all the others is implemented in a user-developed element. Different tasks are carried out according to the values of the parameter ISW passed as the 11th parameter in the user element subprogram “ELMTnn”. The implementation frameworks of extended finite elements for concrete and masonry block are very similar, except for some differences in implementation details due to the different enrichment types. Detailed descriptions for the implementation of these eight tasks are elaborated in the following sections.
3.1. Nodal Degrees of Freedom
In a classical finite element modeling for a two-dimensional problem, two degrees of freedom at each node are usually needed in solid elements to perform the continuum mechanics analysis, which correspond to nodal displacements in two coordinate directions. In XFEM, as described in Equation (1), apart from the classical degrees of freedom, there are several additional enriched degrees of freedom that should be introduced for the displacement field description, and these enriched degrees of freedom are also associated with the corresponding element nodes [
40]. To be more specific, two enriched degrees of freedom at each node are needed for the modified Heaviside enrichment, and eight enriched degrees of freedom at each node are built for the crack tip enrichment.
In this study, two types of extended finite element modules are built in FEAP using a user subprogram called “ELMTnn”: one is programed to simulate the behavior of concrete for columns and beams, and the other is used for the masonry blocks in the infill panel. The difference in enrichment type for two modules leads to different numbers of required nodal degrees of freedom. For masonry elements, two enriched degrees of freedom per node associated with the modified Heaviside enrichment are added. For concrete elements, ten enriched degrees of freedom per node associated with both the modified Heaviside and crack tip enrichments are used. It should be pointed out that multiple cracks are allowed in the modeling. Specifically, if either the modified Heaviside or crack tip enrichment is activated, degrees of freedom numbered 3, 4 or 5–12 are correspondingly used to perform the subsequent work. If two modified Heaviside enrichments for two cracks are activated at the same node, the degrees of freedom 3–6 are used. If modified Heaviside and crack tip enrichments associated with two different cracks are activated, the degrees of freedom 3–12 are all adopted. Two crack tip enrichments at the same node and more than one crack intersecting in the same element are not considered in this paper. If needed, the number of degrees of freedom should be appropriately set according to the desired analysis type.
Furthermore, there are usually several element types used to perform the analysis, and these elements have different numbers of degrees of freedom. In the first part of an input file for FEAP, the value of NDF (maximum number of unknowns per node) is required to show the problem size information. For an element whose NSD (the number of specified degrees of freedom) is less than NDF, it may not be necessary to have the additional degrees of freedom activated. In FEAP, therefore, a convenient method is provided to automatically eliminate the degrees of freedom with values greater than NSD, by inserting the following codes into the user element subroutine for the ISW = 1 task.
DO i = NSD + 1, NDF
IX(i) = 0
END DO
For concrete and masonry-block elements, the NSD values are specified as 12 and 4, respectively. This avoids the need to specify appropriate fixed boundary conditions for the unused values.
Additionally, some element types in FEAP may have more than two degrees of freedom at each node. For instance, apart from two degrees of freedom, the frame element has an additional degree of freedom, numbered ‘3′, to represent the bending behavior. The use of the same location for additional degrees of freedom in the XFEM introduces a limitation in application. However, users might define alternative degree-of-freedom assignments to deal with this conflict.
3.2. Input Material Parameters
In FEAP, the program allows users to define their own parameters that are stored in the array ud(*). In this study, a subroutine “uimate(ud)” is built under the ISW = 1 task to define various user parameters, and a sample module is shown as follows:
subroutine uimate(ud)
c Purpose: Input material parameters for material models
implicit none
c Common blocks
character text(2)*15
logical pcomp, errck, tinput, inputs
real*8 ev(10),ud(*)
inputs = .true.
do while(inputs)
errck = .true.
do while(errck)
errck = TINPUT(text,1,ev,9)
end do ! while
c 1 Youngs.Modulus 2 Poissons.Ratio
if (PCOMP(text(1),’EEnu’,4)) then
ud(1) = ev(1)
ud(2) = ev(2)
c Initial state vector of interface s0 r0 u0
elseif (PCOMP (text(1),’q0q0′,4)) then
ud(3) = ev(1)
ud(4) = ev(2)
ud(5) = ev(3)
c Stiffnesses of interface Dnn Dtt
elseif (PCOMP(text(1),’DnDt’,4)) then
ud(6) = ev(1)
ud(7) = ev(2)
c Check end of data
elseif (PCOMP (text(1),’ ‘,4)) then
inputs = .false.
endif
end do ! while
end |
The subroutine “TINPUT” is a standard input subprogram in FEAP. The subroutine “PCOMP” is used to compare character strings for a match and upper/lower case differences are ignored. “EEnu”, “q0q0” and “DnDt” are command names set by users. A conflict between user-set command names and standard FEAP command names should be prevented.
To input the user parameters, the mesh “MATErial” command should include associated statements. A sample command sequence in an input file can adopt the following format:
MATErial ma
USER n
EEnu E nu
q0q0 s r miu
DnDt Dn Dt
where ma represents the material number, n represents the user element number (1 for a concrete element and 2 for a masonry-block element in this study).
3.3. Information Passing
In FEAP, conventional information such as material parameters, element nodal solution parameters and element nodal coordinates is provided to the user element subroutine through data passed as arguments. For user-defined information such as crack geometry and enrichment types, FEAP also provides options for each user element to create and manage user data arrays through the common block.
In XFEM, the crack propagation is completely independent of the finite element mesh. Naturally, we can represent cracks as contiguous piecewise linear segments, with new crack segments added as cracks propagate. That means a user array containing a series of vertex coordinates is needed to describe the crack geometry information. FEAP allows users to add allocation for their own arrays by calling a subprogram “UALLOC”. However, it is not easy to determine the length of the data array since the number of vertices for each crack and number of cracks are constantly changing as cracks propagate and new cracks are initiated. In addition, some extra attention must be paid to the management of user-defined arrays. Therefore, an alternative approach is proposed in this study to describe the crack geometry information by utilizing element-history variables.
In FEAP, element-history variables are provided for each element to manage additional variables that constantly change during the solving process. It is a user’s choice to decide what is retained in each history-variable type. Generally, element history variables are set to store internal variables for constitutive relations. In this study, the coordinates of intersections between the crack and element edges as well as the vertices of the crack lying inside the current element are also recorded in the corresponding element history variables. With these data, plotting piecewise linear crack segments of each element will automatically form the distribution of all crack curves. In this method, it is easy to specify the amount of history variables associated with the crack geometry information, although it may waste some storage space due to the duplicate records of some intersects in adjacent elements. Meanwhile, this method also eases the implementation of element partitioning, the determination of integration points and the calculation of enrichment functions for integration points, since the intersection coordinates of the crack and element edges have been stored.
In addition, nodal enrichment types for each element should be stored in element history variables, too. Because more than one enrichment may be included at the same node to deal with a multiple-cracks situation, five numbers (i.e., 0 for no enrichment, 1 for modified Heaviside enrichment, 2 for crack tip enrichment, 3 for two modified Heaviside enrichments, 6 for one modified Heaviside enrichment and one crack tip enrichment) have been defined to represent crack-enrichment information. It should be noted that the appropriate enrichment type indicates the associated enriched degrees of freedom, which further ensures the implementation of an appropriate assembly.
3.4. Numerical Integration Strategy
In this study, an efficient numerical integration strategy is adopted to accurately assemble the contribution to the weak form on both sides of the crack surface. This strategy is simple yet effective, and it is also capable of adapting to much more complex crack-propagation problems.
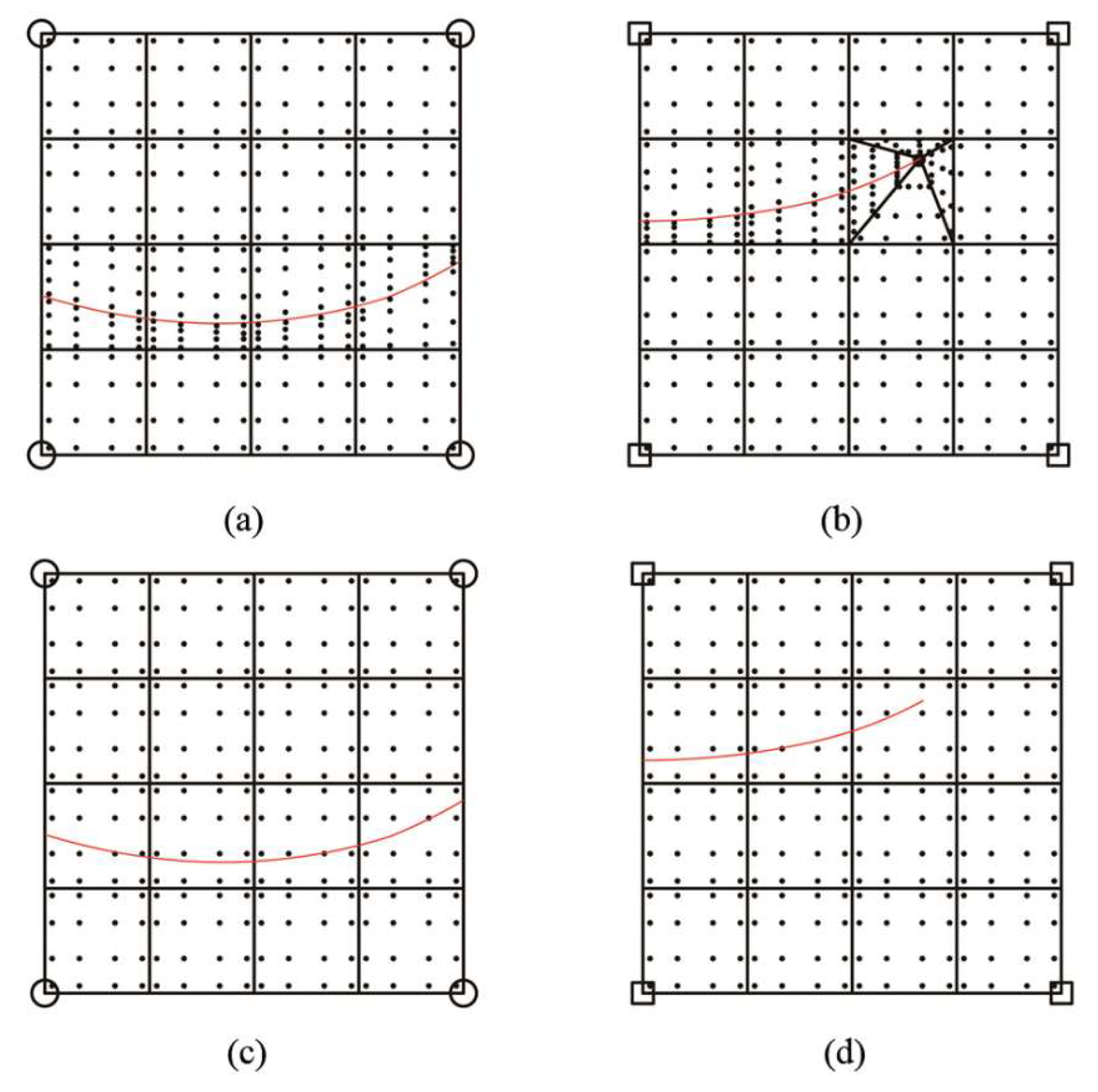
The elements cut by the crack are firstly subdivided into 16 sub-quadrilaterals, as shown in
Figure 2. Following this, two sets of subdivision strategies are adopted to remedy the integration error due to the incompatibility between the sub-quadrilateral edges and the crack surface [
51]. To be specific, one set with sub-elements compatible with the crack surface is used to compute the global stiffness matrix, as shown in
Figure 2a,b, and the other set with sub-elements independent of the crack surface is used for residual vector and plastic flow, as denoted in
Figure 2c,d. For each sub-element, four-order standard Gauss–Legendre quadrature is used to determine the location of integration points.
In the first set of the sub-element division strategy (as shown in
Figure 2a,b), sub-quadrilaterals that cracks pass through are further divided into several sub-blocks according to the intersection of the crack surface with the sub-quadrilateral. Considering that the crack propagation occurs in an arbitrary manner in a finite element solution domain during the analysis, there should be a series of intersection situations that may occur. In the following, the possible intersection situations are summarized in detail, and the division strategy of sub-quadrilaterals for each case is elaborated.
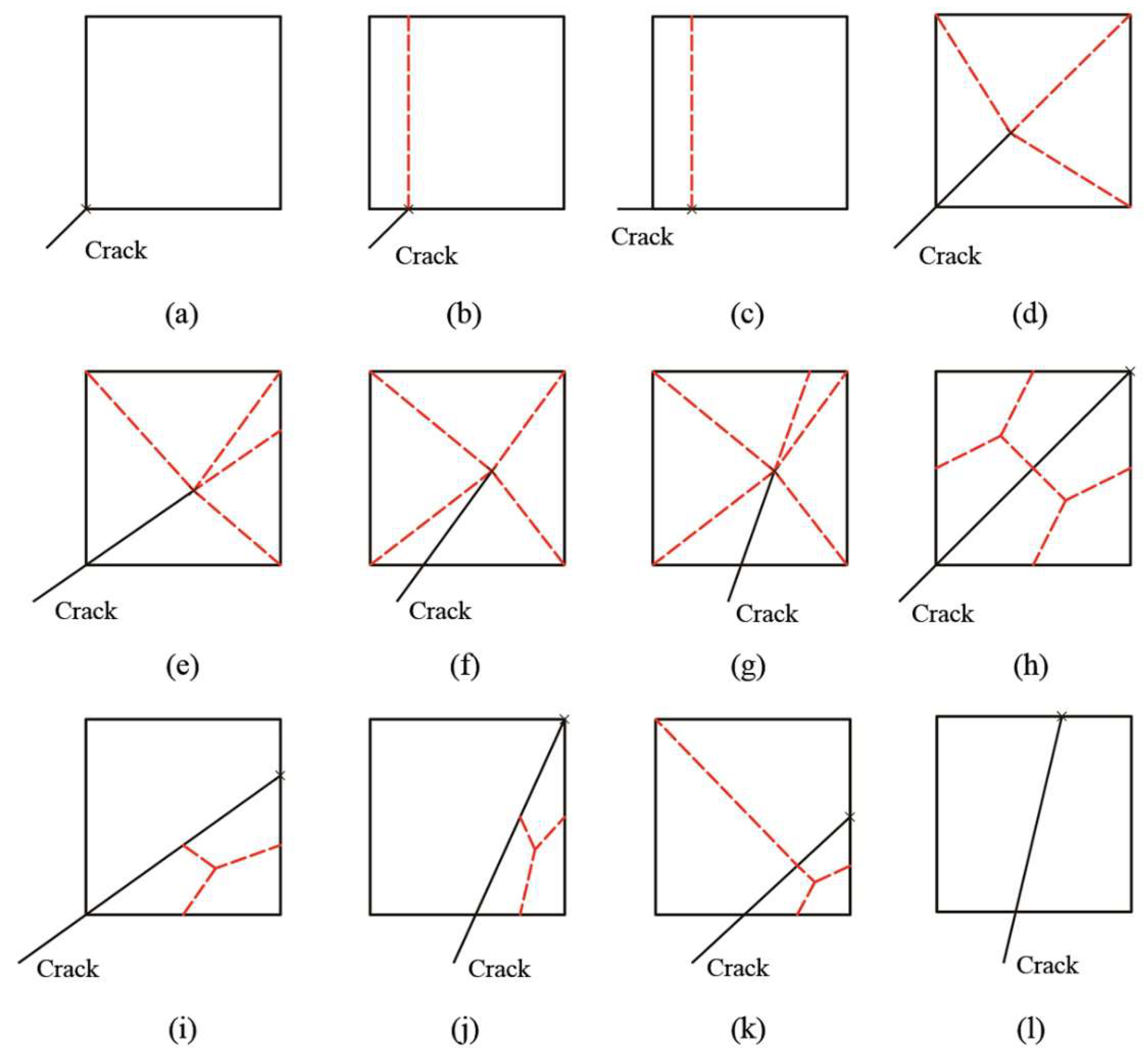
In
Figure 3, the subdivision strategy of the sub-quadrilaterals with a crack tip is presented. First of all, the subdivision for three simple intersection situations (the crack tip touches the boundary of a sub-quadrilateral but not penetrate it) is shown in
Figure 3a–c.
A sub-quadrilateral is subdivided into four to six triangles with the crack tip as a common vertex if the crack tip lies in the sub-quadrilateral but not on the boundary, as illustrated in
Figure 3d–g. In order to integrate the function on a triangle within a prescribed accuracy, a mapping scheme with a two-step coordinate transform is adopted in this study, as depicted in
Figure 4. Each triangle is firstly mapped on a reference isosceles right-angled triangle; then, this reference triangle is further mapped on a reference square with a side of length 2 by Duffy coordinate transform [
52].
A sub-quadrilateral is further divided into a set of quadrilaterals; if it is penetrated by a straight crack and the crack tip lies on the boundary, see
Figure 3h–l. That is, a triangle is further divided into three sub-quadrilaterals by connecting the midpoint of each side and the centroid of the triangle.
For a sub-quadrilateral that is penetrated by the crack but does not contain the crack tip, the subdivision strategy is illustrated in
Figure 5. Similar to crack tip cases, two simple division situations without an actual division needed are firstly presented in
Figure 5a,b. In
Figure 5c–e, the sub-quadrilaterals containing a crack tip before (
Figure 3d–g) have been cut through by the propagating crack. Similar to the division strategy shown in
Figure 3d–g, these sub-quadrilaterals are also divided into a set of triangles for consistency, and the same mapping scheme is also adopted for each triangle. Following this, a sub-quadrilateral penetrated by a straight crack is divided into several quadrilaterals (see
Figure 5f–i) in the same manner as the division strategy shown in
Figure 3h–l.
With the above strategy, sub-quadrilaterals cut by the cracks are divided into several simple geometric figures (triangles and quadrilaterals), and the location and number of integration points are then determined. It should be mentioned that the subdivision information is not stored in the procedure since the intersection situations for the subdivision may vary during the numerical analysis; it is calculated when required.
3.5. Constitutive Relations
In order to precisely model the nonlinear behavior of masonry-infilled RC frame structures, the rational bulk material constitutive relation (Equation (12)) and discrete interface constitutive relation (Equation (13)) are required to properly consider the distributed crushing and cracking behavior of the concrete and masonry blocks. For this purpose, two of constitutive relation subroutines called “umatmises” and “umatinterface” are built.
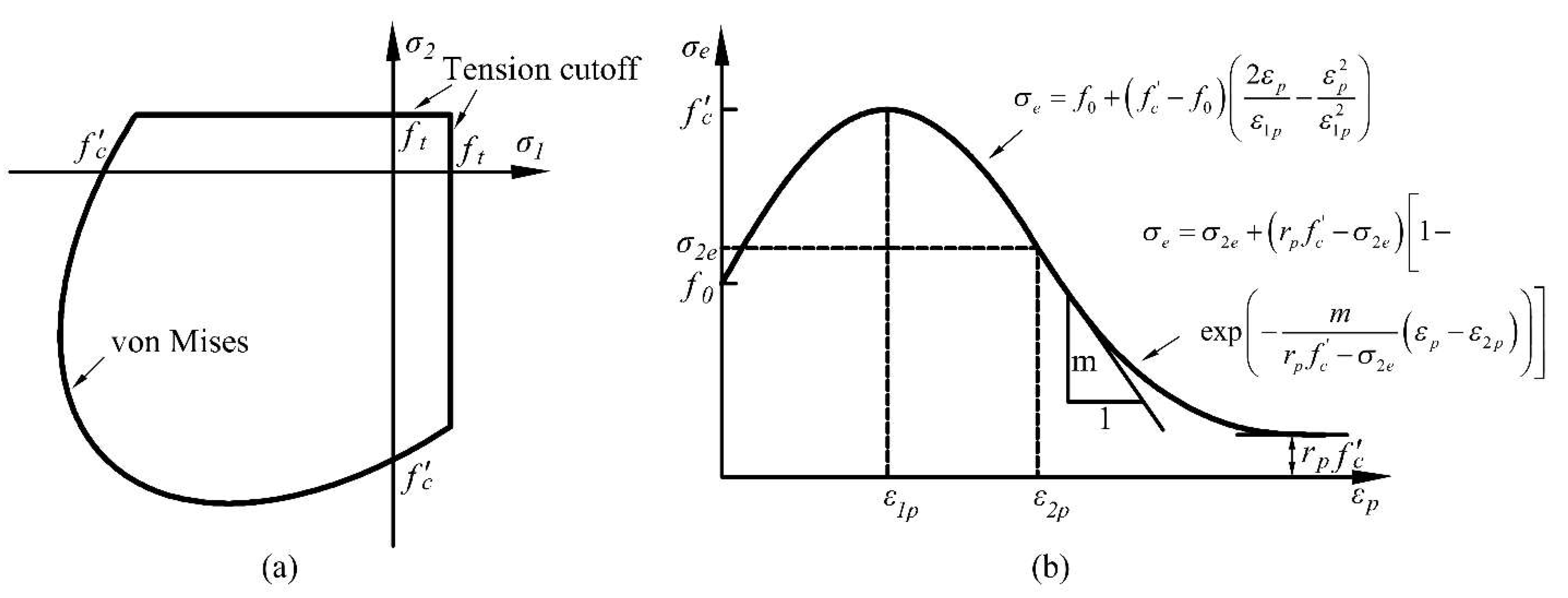
Firstly, an elastic-plastic constitutive model called J2-plasticity model [
53] is employed in this study to model the crushing process of concrete and masonry blocks, as depicted in
Figure 6. In this model, a yield criterion combining the von Mises yield criterion and tension cutoff criterion are adopted, as displayed in
Figure 6a. The von Mises yield criterion can be written in the following format:
where J
2 is second invariant of the deviatoric stress. For plane stress state,
. Therefore, the second invariant of the deviatoric stress tensor can be expressed as [
54]:
where
and
.
Moreover,
σe is effective stress and
εp is effective plastic strain. The effective stress is a function of the effective plastic strain, which governs the isotropic strain hardening/softening law. The function is described as a parabolic function followed by an exponential decay function, which is determined by the material parameters
f0,
fc,
ε1p and
ε2p, as shown in
Figure 6b.
In this analysis, the implementation of the constitutive relation is in the rate form, and it can be described as follows: upon discretization in time, the stress vector and effective plastic strain in the current step are given; then in the next step, a new stress vector and effective plastic strain are updated in a prescribed strain rate. To be specific, elastic predictor stress vector is firstly obtained through the current stress vector, stiffness matrix and strain rate. Together with the current effective plastic strain, the value of the yield function is then calculated. If the value is negative, the elastic predictor stress vector is the new admissible stress vector for the next step; or an iteration procedure is preformed to correct the predictor stress vector and effective plastic strain, until the yield function is equal to zero within a permissible tolerance. Finally, the stress vector and effective plastic strain at the next step are updated.
The discrete interface constitutive relation in Equation (13) usually plays an important role in modeling the failure behavior of masonry-infilled frames due to the weak performance of cracks. In this study, a precise discrete constitutive relation [
28,
36,
38,
55] is employed to model the cracking behavior of the concrete and masonry blocks, and it is able to simulate the degradation of tensile strength and tensile stiffness, normal compaction, shear dilatation and decreases in friction surface roughness under combined normal and shear tractions.
The interface displacement discontinuity w is decomposed into three displacement modes, i.e., the conventional elastic and plastic displacements, as well as a geometric part to account for the reversible dilatation caused by the wedging effect of asperity surfaces. A hyperbolic yield criterion [
28] is adopted to deal with the yielding of the crack surface in both tension-shear and compression-shear regions. It can be expressed in the following format:
where s is material tensile strength, r is the radius of curvature at the vertex, and μ is the slope of asymptotes of the hyperbola, which represents the frictional coefficient of the crack. These three parameters govern the state of yield surfaces, and can be combined into a state vector q. In addition, a non-associated flow rule, in which two different forms are adopted according to the normal tensile or compressive stress state, is used in this study to improve the numerical stability [
56].
Similarly, an elastic predictor-plastic corrector method is also adopted here to update the new stress vector and state vector q for a given stress vector, state vector q at the current step, and interface displacement increment dw for the next step. Some details of the discrete interface constitutive relation can be found in [
28,
56,
57].
3.6. Assembly Procedures
When implementing the user element program in the environment of XFEM, the element partitioning discussed in
Section 3.4 is executed once the ISW = 3 and 6 tasks are activated. After the location of integration points is obtained according to the appropriate subdivision, a loop over all the integration points of each element is specified to compute the element tangent matrix and residual vector of the continuous part. The standard shape functions and their derivatives at each integration point are firstly calculated. If the modified Heaviside enrichment is activated for at least one node, the value of
function at each integration point is computed. In addition, the values of
at element nodes are also computed since the shifted-based enrichment is used. Analogously, for the activated crack tip enrichment, the values of crack tip functions
and their derivatives at each integration point, along with the nodal values of
are calculated. With these values, the strain-displacement element matrix B is subsequently constructed. The stiffness matrix and residual vector for the continuous part are then calculated.
Moreover, the stiffness and residual contributions from the discontinuity surface are also needed, once a crack has occurred in the element. For each segment of crack surfaces, the shape function matrix Ncoh and transformation matrix M at each Gauss integration point are calculated according to Equations (14) and (21). Subsequently, the stiffness matrix and residual vector for the discontinuity surface are obtained.
3.7. Output for Post-Processing
During the analysis, it is necessary to output the element variables, nodal projections and the crack information into an output file for post-processing, and this can be realized under the ISW = 4 and 8 tasks in the user element subroutine of FEAP. In this study, the subdivision with 16 uniform sub-quadrilaterals is used for storing element variables, and command “Stress” is used to output the corresponding information. Meanwhile, commands “Displacement” and “Reaction” are also adopted to store the nodal displacements and nodal reactions into the output file. With these data, a post-processing program for load capacity and damage patterns is built to investigate the failure process of masonry-infilled RC frames.
Alternatively, some post-processing software can be used to obtain the same failure results. For this, however, the instructions for the specific adopted software must be strictly followed when writing the output file, which also requires an additional program to modify the format of the output file.
In addition, it should be mentioned that the output commands do not have to be executed in each solution step. In fact, these commands are executed every ten steps in this study to prevent an oversized output file.
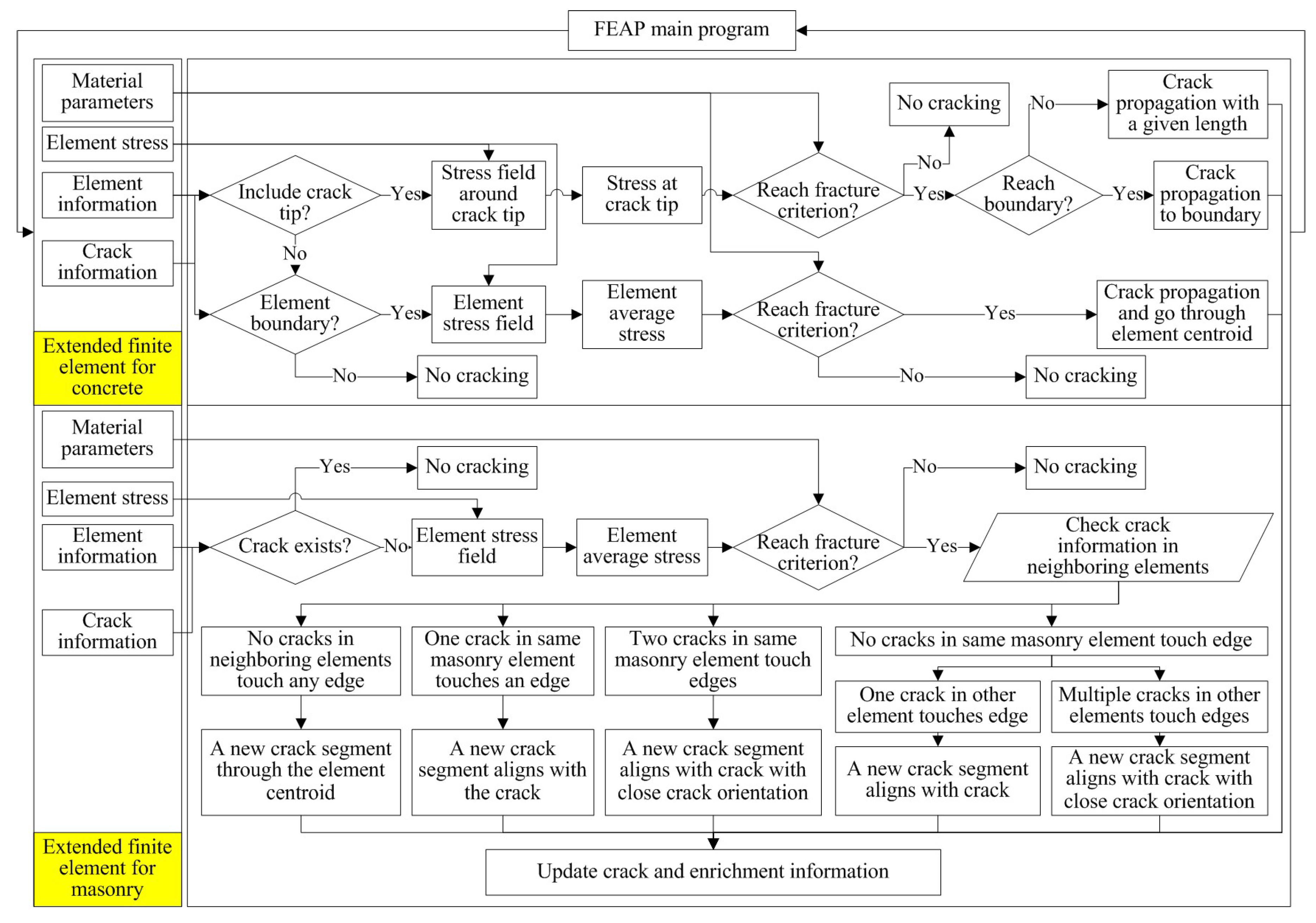
3.8. Crack-Propagation Strategy
FEAP allows users to add their own macro commands to realize some specific functions, which are performed by adding a subroutine called “UMACRn”. In this study, a macro command with name “CKPG” is built to check the element crack-propagation criterion and to update the crack and enrichment information, and its implementation process is shown in
Figure 7.
In previous literature, only one or a few cracks are allowed to occur, and the starting position of cracks is usually prescribed before carrying out the numerical analysis. Some good results have been achieved in these numerical analyses; however, it will become much more difficult to ensure cracks propagate properly in real structures, since a large number of cracks may occur and affect each other. Therefore, an appropriate crack-propagation strategy is proposed in this study, so that the crack can propagate in a rational way.
In this study, the maximum principal stress criterion is adopted as the fracture criteria, which means a new crack segment normal to the major principal stress direction is specified if the major principal stress reaches the tensile strength. For a real structure, however, if a new crack segment occurs once the fracture criterion is satisfied, there could be numerous distributed cracks occurring. This may lead to a locking problem if these cracks cannot be properly connected. In this study, a new crack segment is allowed to occur only if it starts at the free edge of a finite element mesh, or it is an extension of the existing cracks. It should be mentioned that the propagation strategies used for concrete and blocks are different due to the difference in the enrichment of the two materials.
For concrete members, two steps are included. Firstly, the elements containing the crack tip are checked. A new crack segment with a given length is added if the stress around the crack tip reaches the fracture criterion. Next, the elements located on the boundary of the mesh and without enriched degrees of freedom activated are checked. A new crack segment that passes through the element centroid is inserted if the average element stress is beyond the tensile strength of concrete.
For masonry blocks, one crack segment can pass through one element at one time. At each loading step, the fracture criterion is checked within every finite element to determine if a crack segment may initiate. If so, the direction of this potential crack segment is also calculated. Following this, the crack information of neighboring elements is checked. If there are no cracks that touch any edges of the current element, the crack segment is simply placed through the centroid of the current element. For elements in the same block with the current element, if only one crack in the neighboring elements touches an edge of the current element, the new crack segment is forced to align with the crack of the neighboring element; if there are two cracks in two neighboring elements that could potentially be aligned with the new crack segment, the new crack is then aligned with the one of the neighboring element whose angle of orientation is closest to that of the new crack. If no cracks in the neighboring elements could be aligned with the crack in the current element of the same block, a similar method is used to align the crack of the current element with the crack of those elements in the neighboring block; please see
Figure 7 for the implementation process.
As the crack propagates, the information for the cracks, enrichment and the crack tips is updated and stored in the corresponding locations of the element history variables, as described in
Section 3.3.
4. Numerical Verification
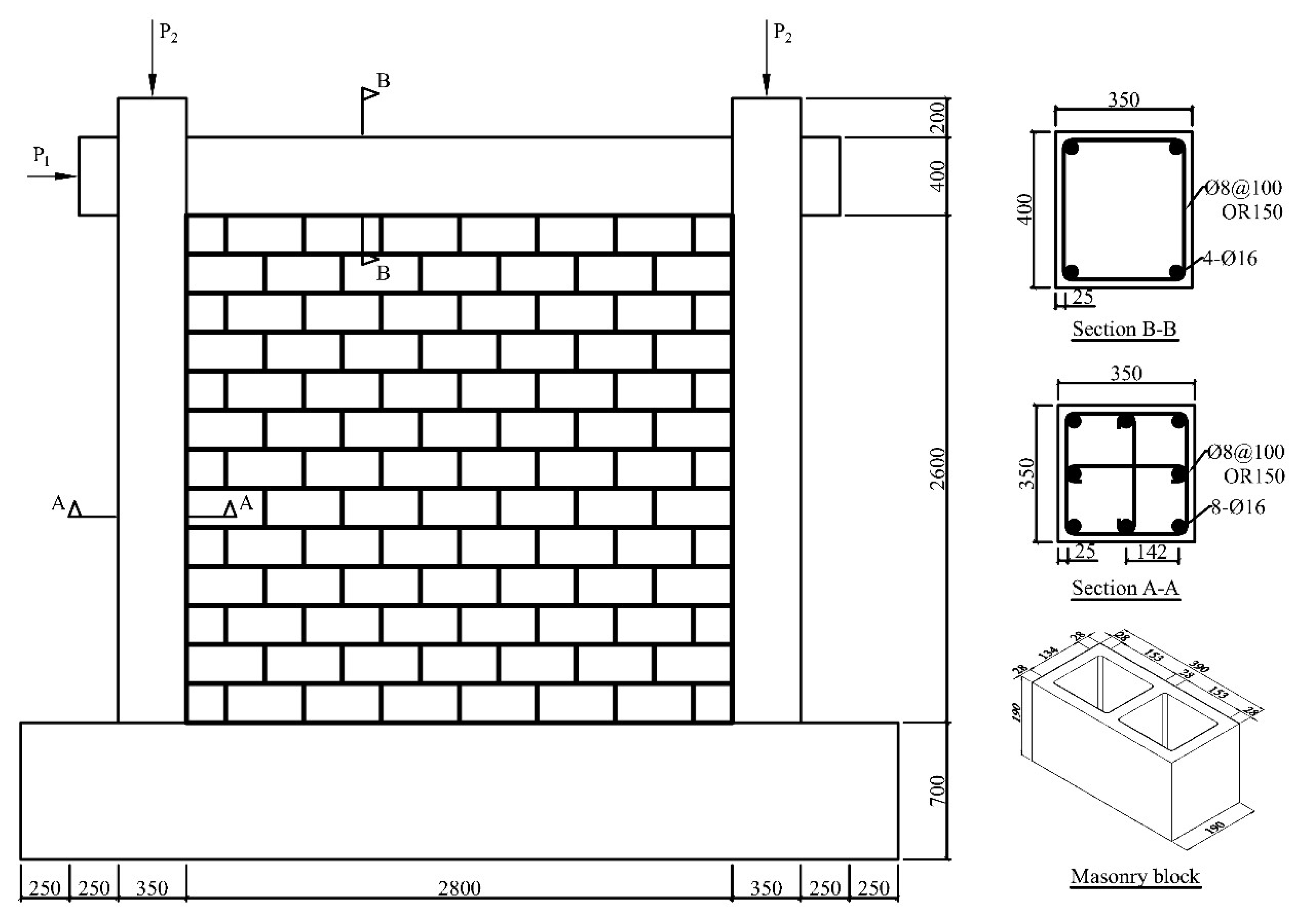
Two full-scale one-story one-bay RC frame specimens with and without infill walls are utilized to demonstrate the effectiveness of the proposed modeling [
58]. The geometry and design information for test specimens is displayed in
Figure 8. In the test, the concrete hollow block of 390 × 190 × 190 mm
3 is used to construct the infill wall. The thickness of the bed and head joints is 10 mm. A vertical compressive load of 700 kN is firstly applied on the top of two columns and is kept constant during the test. Following this, a series of lateral reversed cyclic loads are applied on the two ends of the beam.
Finite element modeling for two specimens are created in FEAP by inputting a series of parameters, such as dimensions, numbers of the reinforcement and material properties, into the programed modeling routine. The thickness of the infill panel is chosen to be two face shells of 56 mm thickness. The base of the model is fixed in all directions. The material parameters for the compressive behavior of the concrete members and masonry blocks are summarized in
Table 1. The input parameters of the discrete cracks’ constitutive relations used for concrete cracks, masonry cracks and mortar joints are listed in
Table 2.
To properly model the behavior of masonry-infilled RC frames, there is need of a systematic calibration process to define various parameters for the proposed finite element modeling. The compressive parameters of concrete material are determined with the data from compression cylinder tests. The tensile strength, ft, can be obtained from the tensile tests, or estimated from the compressive strength according to the suggestion of design codes. For the cohesion-softening behavior, the mode-I fracture energy
can be obtained from mode-I fracture tests, and the mode-II fracture energy
is assumed to be ten times
. The material parameters controlling the evolution of the shape of the failure surface, as well as the dilatation parameters, are determined according to the recommendations in [
38,
56].
The parameters of the interface elements for mortar joints in the infill wall are usually calibrated through a series of shear tests of mortar joints under different constant compressive stresses. The state parameters of the initial yielding and final failure surfaces can be determined by nonlinear fitting analyses using several groups of compressive stress and shear stress values. The mode-II fracture energy is obtained by continuously adjusting its value until the numerical shear stress displacement curves coincide with the experimental curves, and the mode-I fracture energy is then evaluated. Moreover, the dilatation parameters are calibrated by adjusting the analytical normal displacement-shear displacement curves to match the experimental results. In addition, the material properties of head joints and the frame-to-wall joints are assumed to be weaker than that of the bed joints due to the partial filling and the general poorer condition of these mortar joints.
The compressive parameters of masonry unit elements are calibrated with masonry prism tests to reflect the composite properties of a masonry assembly. The parameters for tensile and shear behaviors of the masonry units are calibrated in the same way as those for the concrete material.
The bare frame is firstly analyzed to verify the capability of the proposed modeling with regard to bare RC frames, and the analytical lateral load-bearing capacity curve for the bare frame, are compared with the envelope curve of hysteresis loops in the experiment, as shown in
Figure 9. It is concluded that the analysis predicts the experimental curve very well, with only the initial stiffness being overestimated.
Figure 10 displays the lateral load-bearing capacity curve of the infilled frame for the analytical and experimental results. It is shown that the relation at the ascend stage till the ultimate lateral load is well captured by the analysis, whereas a rapid decline from the post-peak point is not precisely predicted. This is because an out-of-plane failure at the upper part of the infill panel was observed at the post peak stage in the experiment, while it is not considered in the 2D finite element analysis.
More specifically, the differences of peak load, initial stiffness, and displacement corresponding to the peak load for the numerical and experimental results of two specimens are presented in
Table 3. It can be seen that the comparison of three parameters also confirms the results observed in the curves.
Next, the damage patterns for two specimens are discussed. For the bare frame specimen, the numerical result exhibits the damage pattern very well, successfully showing the flexural yielding at the ends of columns and beam, as well as the plastic hinges at the bottom of columns and at the two ends of the beam in the late stage of the test. For conciseness, the deformed mesh is not exhibited.
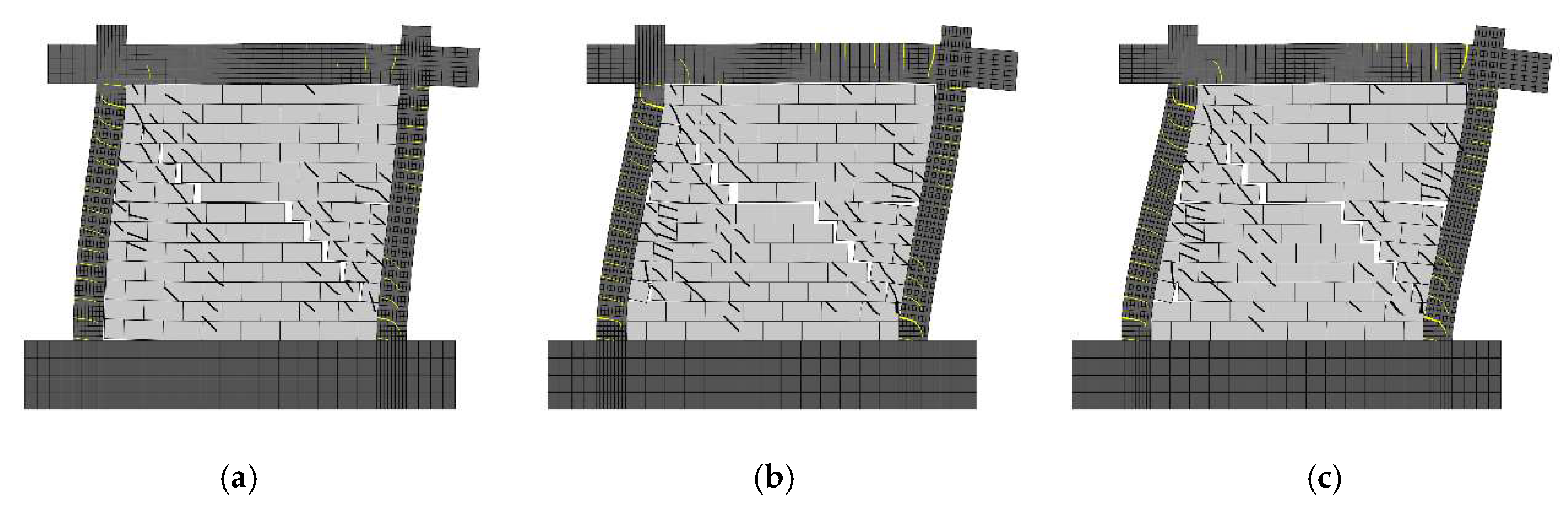
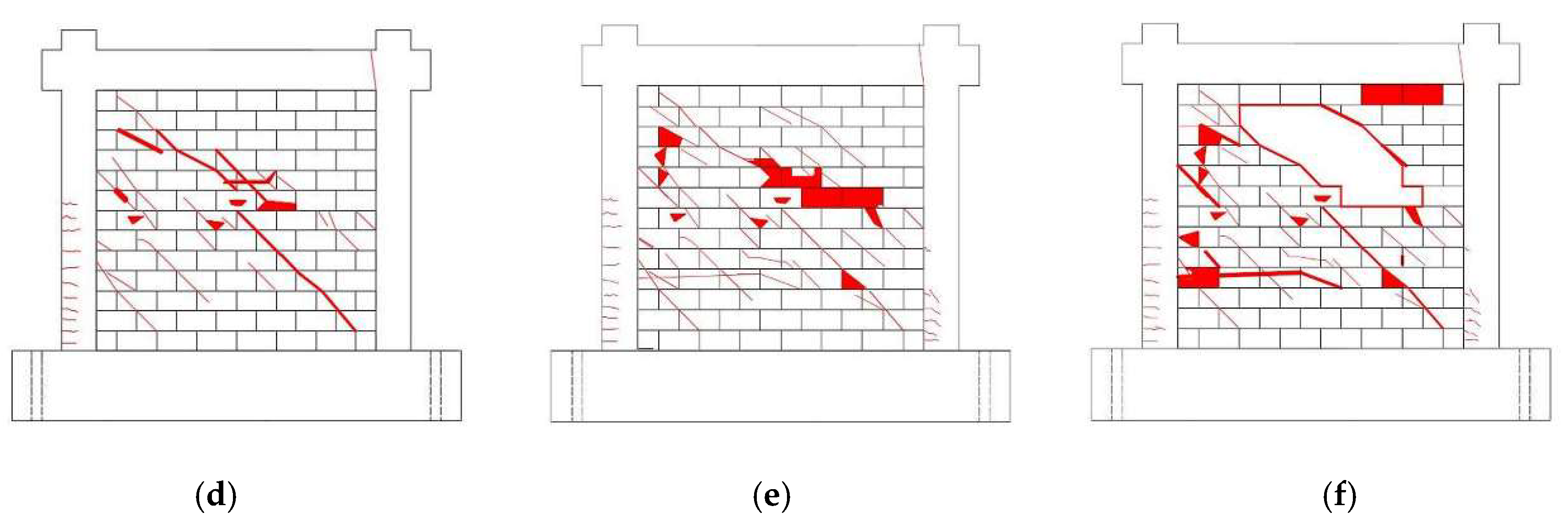
The damage patterns of the infilled frame for analytical and experimental results are compared in
Figure 11, and a reasonable prediction result is obtained by the numerical analysis. In both results, the damage to the columns and the beam is characterized by a series of flexural cracks, and the inflection point of columns derived from the crack distribution is located at the middle height. In the infill panel, some inclined cracks that start from the top-left corner and bottom-right corner are well captured by the analysis. As the load increases, the cracks and deformation gradually increase, and expand to the bottom-left corner and top-right corner. Finally, a diagonal compressive failure is formed, and a large number of cracks and larger deformation of masonry blocks are observed, which shows the serious damage that has occurred in the infill panel. However, the crack distribution at the top of columns predicted by the analysis is not clearly observed in the experiment, which may be due to the out-of-plane failure, which dramatically reduces the damage to columns.
5. Conclusions
In this paper, we presented the implementation procedure of finite element modeling within FEAP for the numerical analysis of masonry-infilled RC frames. In this modeling, XFEM is combined with interface elements to predict the complicated failure process of masonry-infilled RC frames, such as diagonal cracking, sliding and crushing in the infill wall, as well as the flexural and shear failure in RC frame members. The implementation is based on a user element subroutine; two user element subroutines with and without crack tip enrichment functions included within XFEM are built to model the nonlinear behavior of the concrete in RC frame members and the masonry blocks in the infill panel, respectively. Additionally, a macro command used to check the crack-propagation criterion and update the crack, and enrichment information is added to assist in the implementation of XFEM. Some critical and difficult issues related to the selection of enriched nodal degrees of freedom, input material parameters, information passing, numerical integration strategy, constitutive relations, assembly procedure of stiffness matrix and force vector, output for post-processing, and crack-propagation strategy are addressed.
A quasi-static test of two RC frames with and without infill walls is analyzed to verify the capability of the proposed finite element modeling. It revealed that the relative errors of peak load, displacement corresponding to peak load and initial stiffness for the two specimens are relatively small, and the load-bearing capacity curves are accurately predicted. Meanwhile, the failure process of the test specimens is well represented, especially for the cracking propagation in the concrete material and masonry units. These findings sufficiently demonstrate the efficacy of the XFEM implementation in FEAP and the effectiveness of the proposed modeling for representing the complicated behavior of masonry-infilled RC frames.
Further parametric studies using the proposed modeling can better understand the behavior of masonry-infilled RC frame buildings, which will contribute to the development of valuable seismic design advice and simplified approaches. Moreover, the proposed modeling is an effort to solve the fracture problems of practical structures using XFEM. The description of the implementation procedure will help readers to apply XFEM for a broader class of problems. The uncertainties in the mechanical properties of masonry units and mortar joints has a great impact on the performance of the infilled wall RC frame, and it is not considered in this study. In future research, the spatial variation in material properties in infill walls can be considered in the proposed finite element model to better understand the failure behavior of infilled wall RC frame structures.