Effect of Loading Frequency on the Fatigue Response of Adhesive Joints up to the VHCF Range
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material and Testing Devices
2.2. Specimen Mechanical Design
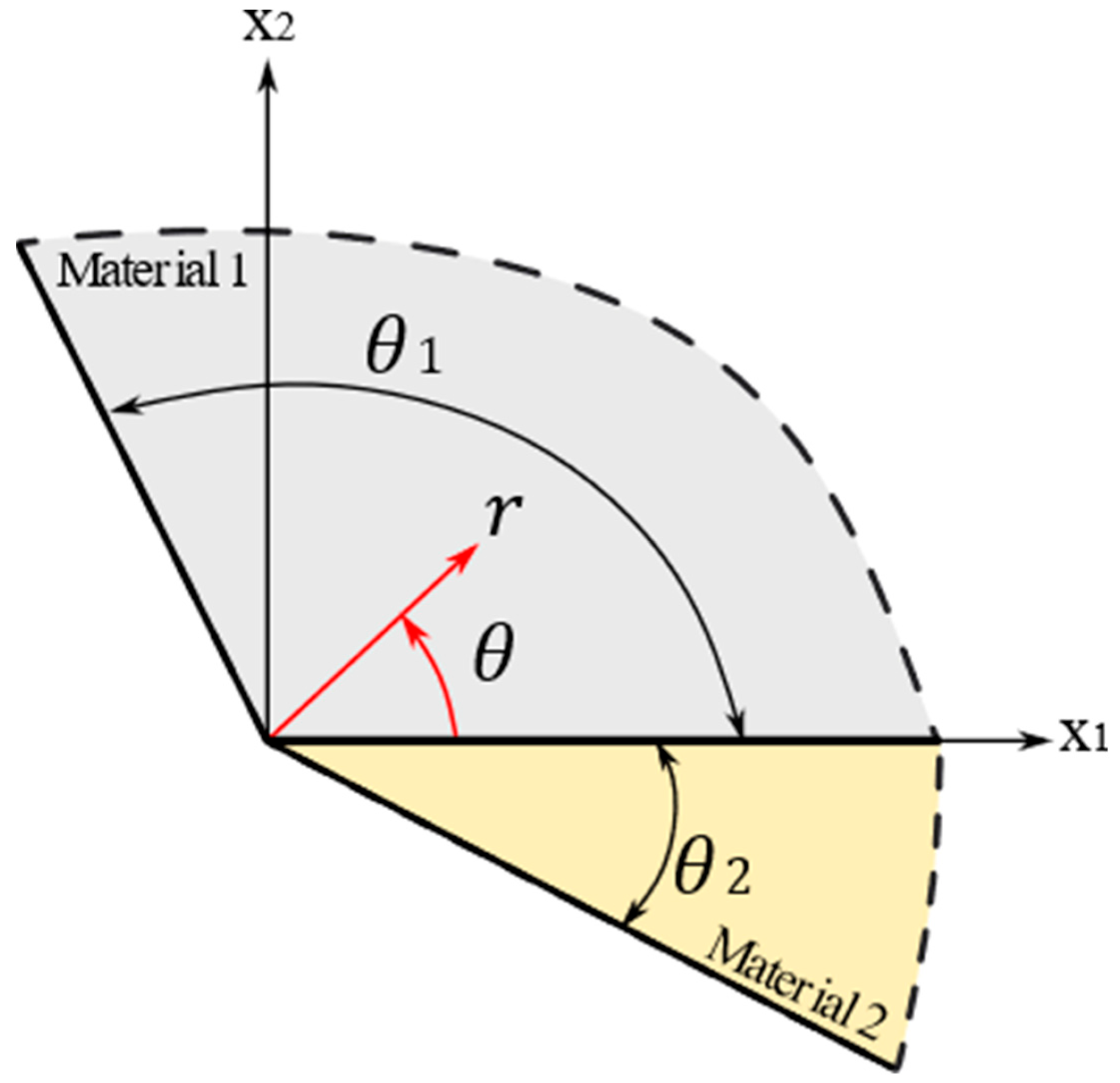
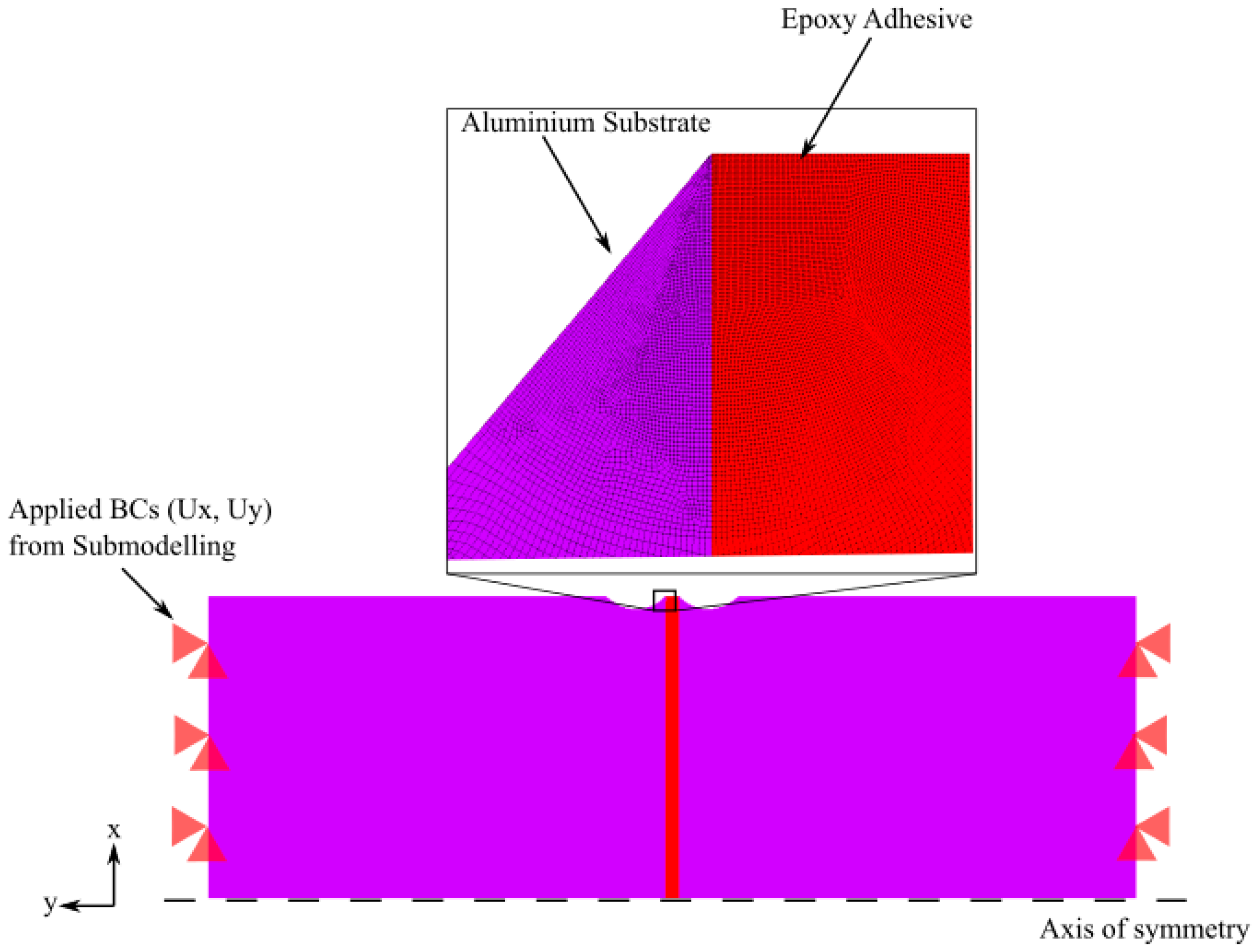
2.2.1. Removal of the Stress Singularity
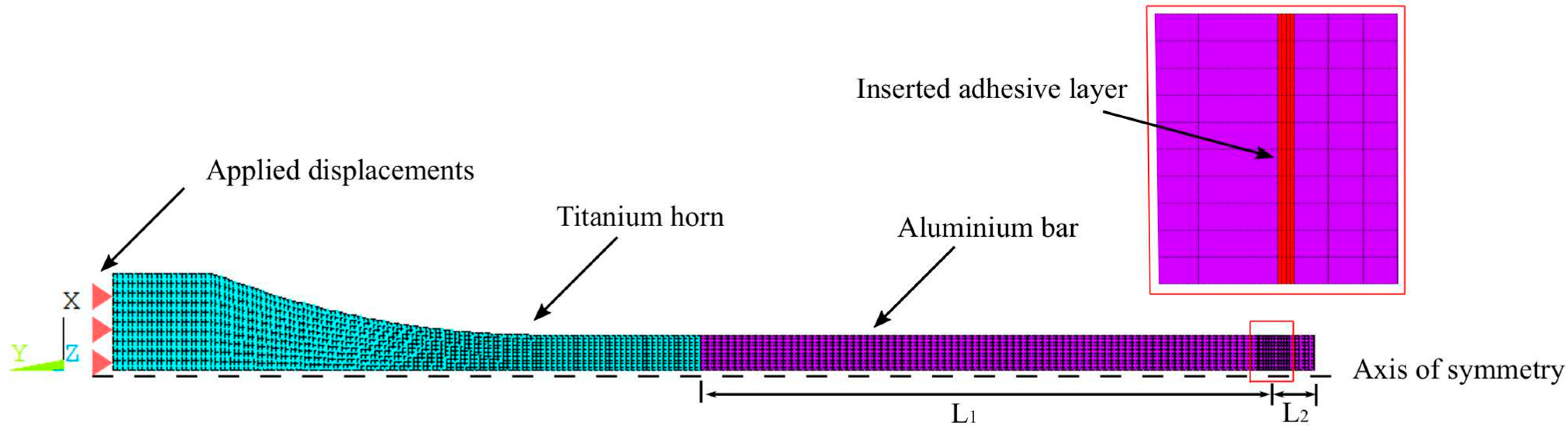
2.2.2. VHCF Specimen Design: FE Model Development and Analyses
- The numerical model of the titanium horn is first analyzed through a modal analysis under free–free conditions to collect the closest natural frequency and mode shape to the UFTM operative range. An operative frequency of Hz is thus selected and adopted for design purposes.
- The 1D elastic wave equations [58] reported in Equation (4) permit the definition of the specimen total length , where is the frequency of interest and are the mechanical properties of the aluminium. This calculation results in mm:
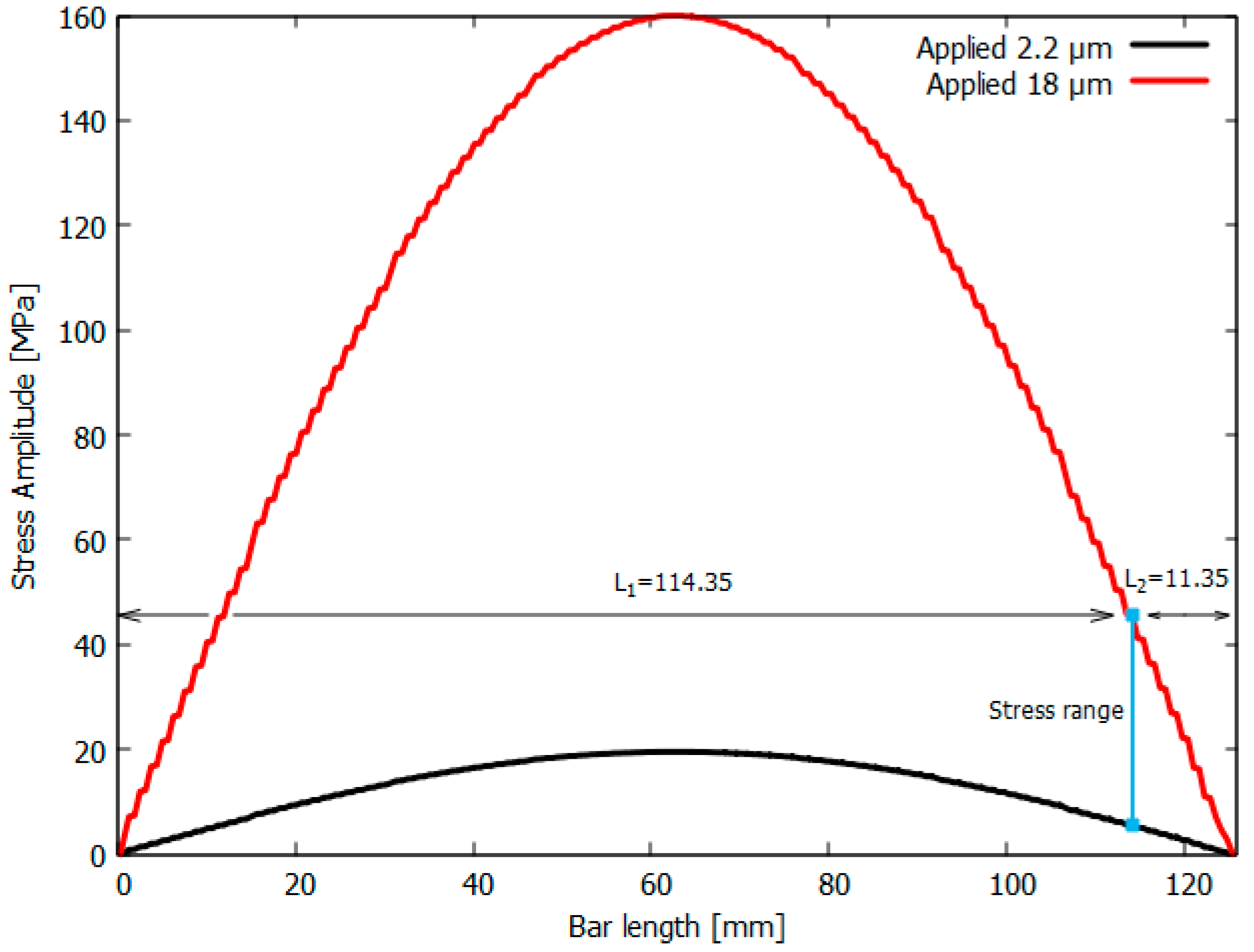
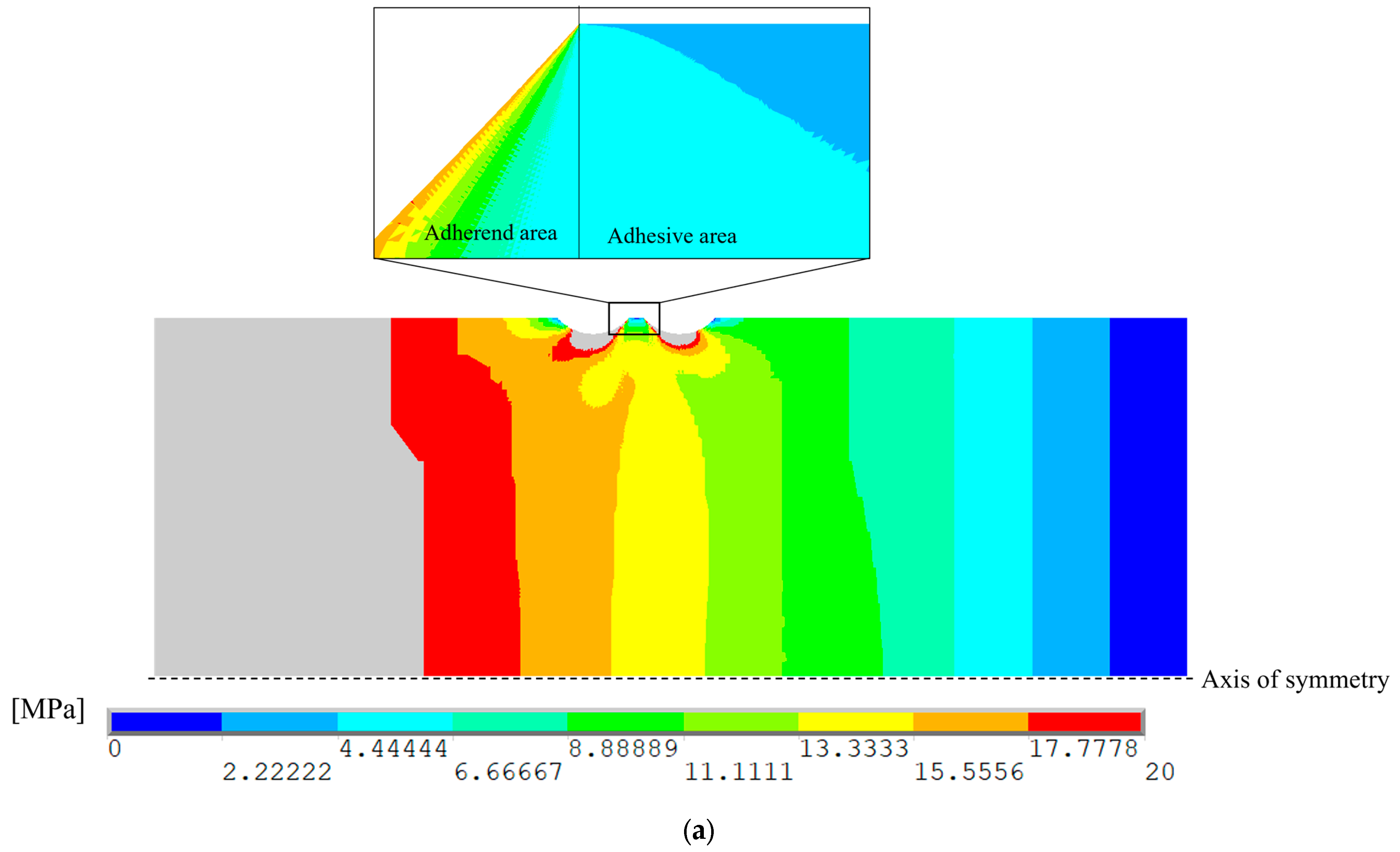
- A frequency response analysis (FRA) is run at Hz, where the current numerical model is composed using the of the titanium horn and the aluminum bar, with a displacement excitation at the horn base in the range of 2.2–18 , which corresponds to the capability of the UFTM. Longitudinal stress distributions are collected along the aluminium specimen axis and are depicted in Figure 5. This assessment was useful and necessary to explore the stress magnitudes applied to the whole specimen.
- A 0.3 mm thick adhesive layer is inserted into the mechanical system, thus dividing the aluminium bar in two separated components, now adhesively joined. The adhesive is placed at a suitable distance in order to impose the desired stress magnitude on the adhesive layer. In this work, the stress range from 5.5–46 MPa was selected. In this way, the is divided into = 114.15 mm and = 11.35 mm, as shown in Figure 5.
- A final numerical re-assessment is performed through an FRA.
3. Experimental Results
4. Discussion
5. Conclusions
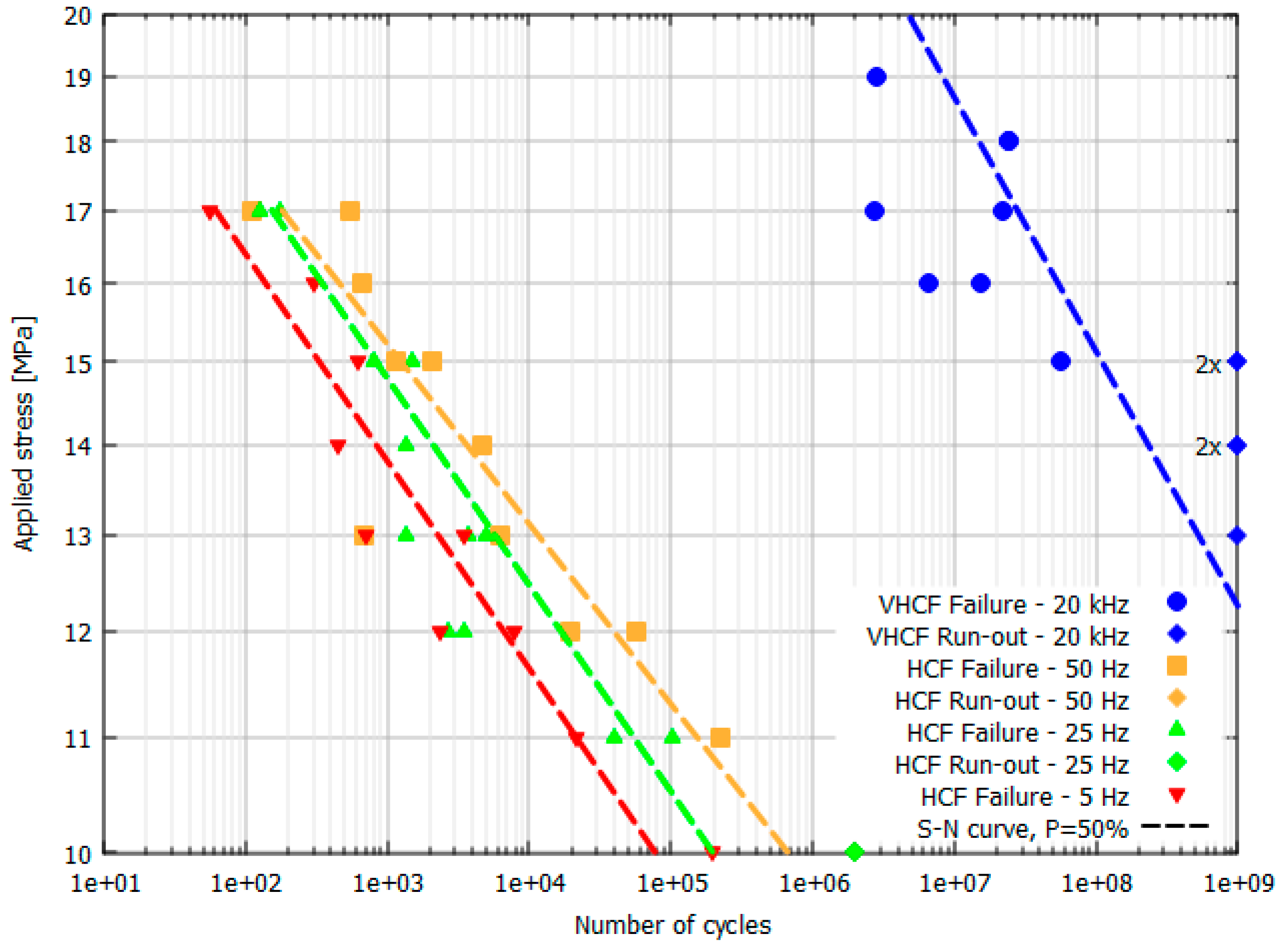
- At a fixed applied load, specimens tested at an ultrasonic frequency are prone to fail in the very high cycle fatigue range (N > 107), whereas specimens subjected to common frequencies fail in the high cycle fatigue range, thus confirming the presence of a frequency effect.
- Specimens tested at an ultrasonic frequency express run-out data below 15 MPa compared to 10 MPa in the case of 25 and 50 Hz frequencies. Specimens at 5 Hz do not present run-outs.
- There is an increase in fatigue performance among specimens tested in the low-frequency range, and this is visible through the S–N curve at the 50% probability level.
- Data scattering was investigated through standard deviations, and the experimental results demonstrated a minor impact on fatigue properties (i.e., 0.3038 at 5 Hz, 0.5763 at 25 Hz, 0.4687 at 50 Hz, and 0.7691 at 20 kHz);
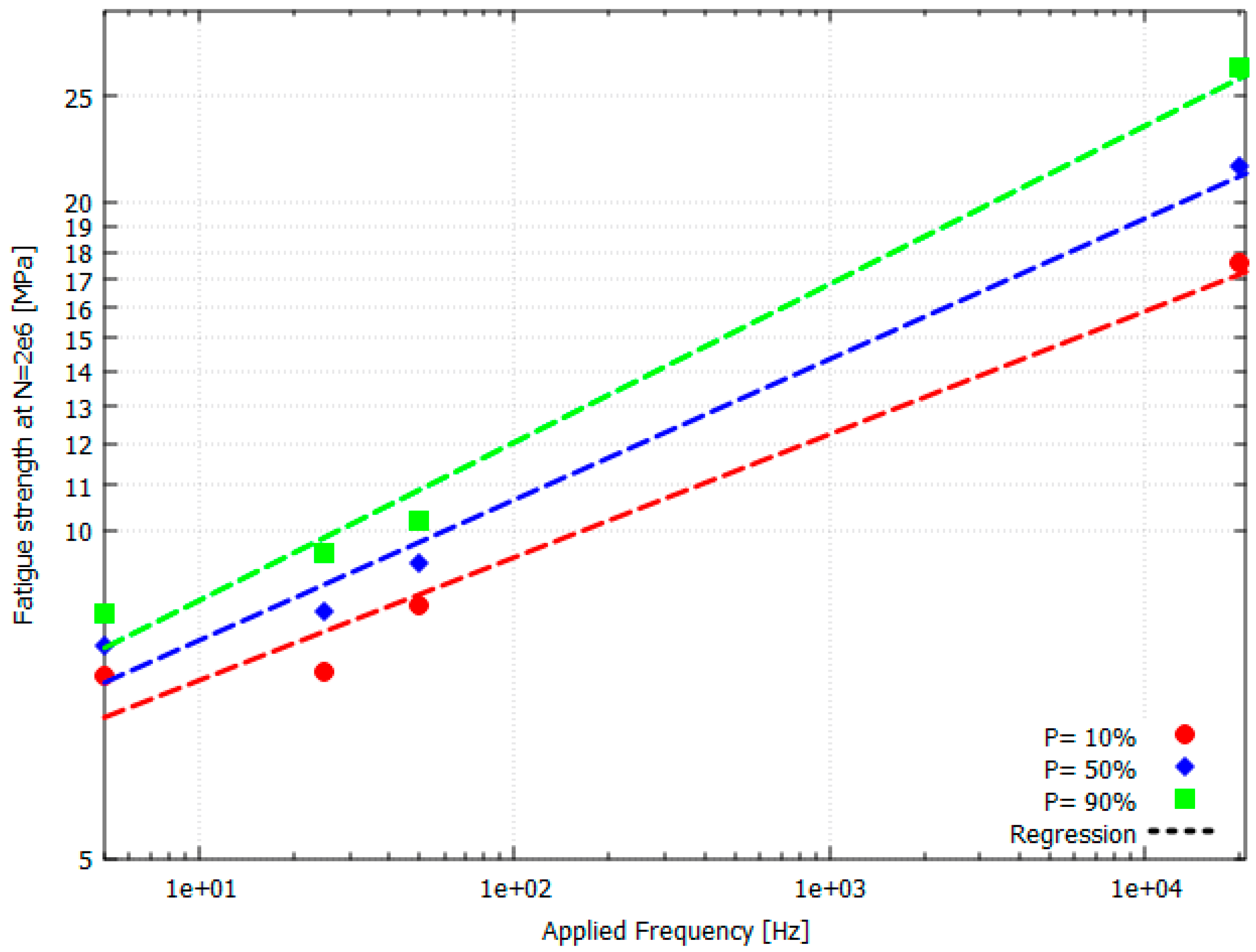
- Interpolating data at N = 2 × 106 for three probability levels (P = 10, 50, 90%) showed the possibility of strength prediction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Modulus of elasticity | |
| Probability density function of the fatigue life | |
| Cumulative distribution function of the fatigue life | |
| Conditional distribution of fatigue life | |
| Maximum likelihood function | |
| Number of failures | |
| Number of run-outs | |
| Tension–compression loading ratio | |
| Radial coordinate | |
| BCs | Boundary conditions |
| FE | Finite element |
| FRA | Frequency response analysis |
| ML | Maximum likelihood |
| PID | Proportional–integrative–derivative |
| SD | Standard deviation |
| UFTM | Ultrasonic fatigue testing machine |
| V | Viscosity |
| VHCF | Very high cycle fatigue |
| Dundurs parameters | |
| Local material angle | |
| Shear modulus | |
| Mean stress distribution | |
| Poisson’s ratio | |
| Density | |
| Stress vector | |
| Ultimate tensile strength |
References
- Decker, M. Vibration fatigue analysis using response spectra. Int. J. Fatigue 2021, 148, 106192. [Google Scholar] [CrossRef]
- Li, F.; Wu, H.; Wu, P. Vibration fatigue dynamic stress simulation under non-stationary state. Mech. Syst. Signal Process. 2021, 146, 107006. [Google Scholar] [CrossRef]
- Sui, G.; Zhang, Y. Response spectrum method for fatigue damage assessment of mechanical systems. Int. J. Fatigue 2023, 166, 107278. [Google Scholar] [CrossRef]
- ECSS-E-HB-32-26A; Spacecraft Mechanical Loads Analysis Handbook, ECSS Secretariat, Requirements & Standards Division, ESA-ESTEC. ECSS Standard: Noordwijk, The Netherlands, 2013.
- ECSS-E-ST-10-03C; Testing, ECSS Secretariat, Requirements & Standards Division, ESA-ESTEC. ECSS Standard: Noordwijk, The Netherlands, 2020.
- ECSS-E-ST-32-01C; Fracture Control, ECSS Secretariat, Requirements & Standards Division, ESA-ESTEC. ECSS Standard: Noordwijk, The Netherlands, 2021.
- Tahmasbi, K.; Alharthi, F.; Webster, G.; Haghshenas, M. Dynamic frequency-dependent fatigue damage in metals: A state-of-the-art review. Forces Mech. 2023, 10, 100167. [Google Scholar] [CrossRef]
- Jia, Z.; Hui, D.; Yuan, G.; Lair, J.; Lau, K.T.; Xu, F. Mechanical properties of an epoxy-based adhesive under high strain rate loadings at low temperature environment. Compos. Part B 2016, 105, 132–137. [Google Scholar] [CrossRef]
- Jia, Z.; Yuan, G.; Hui, D.; Feng, X.; Zou, Y. Effect of high strain rate and low temperature on mode II fracture toughness of ductile adhesive. Int. J. Adhes. Adhes. 2018, 86, 105–112. [Google Scholar] [CrossRef]
- Maio, L.; Monaco, E.; Ricci, F.; Lecce, L. Simulation of low velocity impact on composite laminates with progressive failure analysis. Compos. Struct. 2013, 103, 75–85. [Google Scholar] [CrossRef]
- Al-Zubaidy, H.; Zhao, X.L.; Al-Mahaidi, R. Mechanical characterisation of the dynamic tensile properties of CFRP sheet and adhesive at medium strain rates. Compos. Struct. 2013, 96, 153–164. [Google Scholar] [CrossRef]
- Liu, X.; Shao, X.; Li, Q.; Sun, G. Experimental study on residual properties of carbon fibre reinforced plastic (CFRP) and aluminum single-lap adhesive joints at different strain rates after transverse pre-impact. Compos. Part A 2019, 124, 105372. [Google Scholar] [CrossRef]
- Taniguchi, N.; Nishiwaki, T.; Kawada, H. Tensile strength of unidirectional CFRP laminate under high strain rate. Adv. Compos. Mater. 2007, 16, 167–180. [Google Scholar] [CrossRef]
- Wang, S.; Liang, W.; Duan, L.; Li, G.; Cui, J. Effects of loading rates on mechanical property and failure behavior of single-lap adhesive joints with carbon fiber reinforced plastics and aluminum alloys. Int. J. Adv. Manuf. Technol. 2020, 106, 2569–2581. [Google Scholar] [CrossRef]
- Ma, H.; Bai, X.; Ran, Y.R.; Wei, X.; An, Z. Modeling the Effect of Stress Ratio, Loading Frequency and Fiber Orientation on the Fatigue Response of Composite Materials. Polymers 2022, 14, 2772. [Google Scholar] [CrossRef]
- Banea, M.D.; Rosioara, M.; Carbas, R.J.C.; da Silva, L.F.M. Multi-material adhesive joints for automotive industry. Compos. Part B 2018, 151, 71–77. [Google Scholar] [CrossRef]
- Antelo, J.; Akhavan-Safar, A.; Carbas, R.J.C.; Marques, E.A.S.; Goyal, R.; da Silva, L.F.M. Replacing welding with adhesive bonding: An industrial case study. Int. J. Adhes. Adhes. 2022, 113, 103064. [Google Scholar] [CrossRef]
- Pazand, K.; Nobari, A.S. Investigation of damage effect on the effective dynamic mechanical properties of an adhesive in linear and nonlinear response regimes. J. Vib. Control 2017, 23, 2209–2220. [Google Scholar] [CrossRef]
- Kemiklioglu, U.; Baba, B.O. Investigation of mechanical properties and failure surfaces of adhesively bonded composites subjected to vibration loads. Mater. Res. Express 2019, 6, 115309. [Google Scholar] [CrossRef]
- Du, Y.; Shi, L. Effect of vibration fatigue on modal properties of single lap adhesive joints. Int. J. Adhes. Adhes. 2014, 53, 72–79. [Google Scholar] [CrossRef]
- Kemiklioglu, U.; Baba, B.O. Mechanical response of adhesively bonded composite joints subjected to vibration load and axial impact. Compos. Part B 2019, 176, 107317. [Google Scholar] [CrossRef]
- Challita, G. Analytical study of the dynamic behavior of a voided adhesively bonded lap joint under axial harmonic load. Int. J. Solids Struct. 2018, 141, 183–194. [Google Scholar] [CrossRef]
- Ramalho, L.D.C.; Sanchez-Arce, J.I.; Goncalves, D.C.; Belinha, J.; Campilho, R.D.S.G. Numerical analysis of the dynamic behaviour of adhesive joints: A review. Int. J. Adhes. Adhes. 2022, 118, 103219. [Google Scholar] [CrossRef]
- Yuan, W.; Yang, T.; Yang, G.; Liu, S.; Du, Y.; Liu, C. Enhancing mechanical properties of adhesive laminates joints using ultrasonic vibration-assisted preprocessing. Compos. Struct. 2019, 227, 111325. [Google Scholar] [CrossRef]
- Barroso, A.; Marin, J.C.; Mantic, V.; Paris, F. Premature failures in standard test specimens with composite materials induced by stress singularities in adhesive joints. Int. J. Adhes. Adhes. 2020, 97, 102478. [Google Scholar] [CrossRef]
- Williams, M.L. Stress Singularities Resulting from Various Boundary Conditions in Angular Corners of Plates in Extension. J. App. Mech. 1952, 19, 526–528. [Google Scholar] [CrossRef]
- Bogy, D.B. Edge bonded dissimilar orthogonal elastic wedge under normal and shear loading. J. Appl. Mech. 1968, 35, 460–466. [Google Scholar] [CrossRef]
- Bogy, D.B.; Wang, K.C. Stress singularities at interface corners in bonded dissimilar isotropic elastic materials. Int. J. Solid Struct. 1971, 7, 993–1005. [Google Scholar] [CrossRef]
- Bogy, D.B. Two Edge-Bonded Elastic Wedges of Different Materials and Wedge Angles Under Surface Tractions. J. Appl. Mech. 1971, 38, 377–386. [Google Scholar] [CrossRef]
- Groth, H.L. Stress singularities and fracture at interface corners in bonded joints. Int. J. Adhes. Adhes. 1988, 8, 107–113. [Google Scholar] [CrossRef]
- Kelly, P.A.; Hills, D.A.; Nowell, D. The Design of Joints Between Elastically Dissimilar Components. J. Strain Anal. 1992, 27, 15–20. [Google Scholar] [CrossRef]
- Wang, C.H.; Rose, L.R.F. Compact solutions for the corner singularity in bonded joints. Int. J. Adhes. Adhes. 2000, 20, 145–154. [Google Scholar] [CrossRef]
- Lazzarin, P.; Quaresimin, M.; Ferro, P. A two-term stress function approach to evaluate stress distribution in bonded joints of different geometries. J. Strain Anal. Eng. Des. 2002, 37, 385. [Google Scholar] [CrossRef]
- Goglio, L.; Rossetto, M. Evaluation of the Singular Stresses in Adhesive Joints. J. Adhes. Sci. Technol. 2009, 23, 1441–1457. [Google Scholar] [CrossRef]
- Sinclair, G.B. On ensuring structural integrity for configurations with stress singularities: A review. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 523–535. [Google Scholar] [CrossRef]
- Breto, R.; Chiminelli, A.; Lizaranzu, M.; Rodriguez, R. Study of the singular term in mixed adhesive joints. Int. J. Adhes. Adhes. 2017, 76, 11–16. [Google Scholar] [CrossRef]
- Galvez, P.; Noda, N.A.; Takaki, R.; Sano, Y.; Abenojar, J.; Martinez, M.A. Intensity of singular stress field variation as a function of the Young’s modulus in single lap adhesive joints. Int. J. Adhes. Adhes. 2019, 95, 102418. [Google Scholar] [CrossRef]
- Thouless, M.D.; Goutianos, S. Cohesive-zone models and singularities at corners and cracks in homogeneous materials. J. Mech. Phys. Solids 2023, 171, 105159. [Google Scholar] [CrossRef]
- Wu, Z. Design free of stress singularities for bi-material components. Compos. Struct. 2004, 65, 339–345. [Google Scholar] [CrossRef]
- Wu, Z. Stress concentration analyses of bi-material bonded joints without in-plane stress singularities. Int. J. Mech. Sci. 2008, 50, 641–648. [Google Scholar] [CrossRef]
- Xia, Z.; Chowdhuri, M.A.A.K.K.; Ju, F. A New Test Method for the Measurement of Normal-Shear Bonding Strength at Bi-Material Interface. Mech. Adv. Mater. Struct. 2015, 20, 571–579. [Google Scholar] [CrossRef]
- Barroso, A.; Lauke, B.; Mantic, V.; Paris, F. Tensile and shear strength of bimaterial interfaces within composite materials. Compos. Sci. Technol. 2016, 124, 81–88. [Google Scholar] [CrossRef]
- Pederbelli, D.; Tridello, A.; Paolino, D.S.; Goglio, L. Effects of singular and non-singular stress fields on Very High Cycle Fatigue life of adhesive joints. Fatigue Fract. Eng. Mater. Struct. 2023, 1–16. [Google Scholar] [CrossRef]
- Bathias, C.; Paris, P.C. Gigacycle Fatigue in Mechanical Practice; CRC Dekker: Boca Raton, FL, USA, 2005. [Google Scholar]
- Bathias, C. There is no infinite fatigue life in metallic materials. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 559–565. [Google Scholar] [CrossRef]
- Lia, X.; Xiang, O.; Pei, H.Y.; Wei, S. High-cycle and very-high-cycle fatigue behaviour of a stainless steel for air-conditioning compressor valve plates. Int. J. Struct. Integr. 2022, 13, 185–195. [Google Scholar]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Rossetto, M. VHCF response of H13 steels produced with different manufacturing processes. Procedia Eng. 2016, 160, 93–100. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Rossetto, M. Ultrasonic VHCF Tests on Very Large Specimens with Risk-Volume Up to 5000 mm3. App. Sci. 2020, 10, 2210. [Google Scholar] [CrossRef]
- Tridello, A.; Ciardiello, R.; Paolino, D.S.; Goglio, L. Fatigue response up to 109 cycles of a structural epoxy adhesive. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1555–1566. [Google Scholar] [CrossRef]
- Tridello, A.; Paolino, D.S.; Chiandussi, G.; Goglio, L. An innovative testing technique for assessing the VHCF response of adhesively bonded joints. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 84–96. [Google Scholar] [CrossRef]
- Tridello, A.; Boursier Niutta, C.; Berto, F.; Paolino, D.S. Size-effect in Very High Cycle Fatigue: A review. Int. J. Fatigue 2021, 153, 106462. [Google Scholar] [CrossRef]
- Mevada, H.; Patel, D. Experimental determination of structural damping of different materials. Procedia Eng. 2016, 144, 110–115. [Google Scholar] [CrossRef]
- ASTM E8-21; Standard Test Methods for Tension Testing of Metallic Materials. American Association State, Highway and Transportation Officials Standard: Washington, DC, USA, 2021.
- BS EN ISO 527-2-2012; Plastics—Determination of Tensile Properties, Part 2. CEN. European Committee for Standardization: Brussels, Belgium, 2012.
- SikaPower®-1277, Product Data Sheet. Version 04.01 (04-2022). Available online: https://industry.sika.com/content/dam/dms/gb01/7/sikapower_-1277.pdf (accessed on 15 October 2023).
- Takaki, R.; Noda, N.A.; Sano, Y.; Takase, Y.; Suzuki, Y.; Chao, C.K. Fractographic identification of fracture origin mainly controlled by the intensity of singular stress field (ISSF) in prismatic butt joint with corner fillet. Int. J. Adhes. Adhes. 2021, 106, 102810. [Google Scholar] [CrossRef]
- Ransom, J.B.; Knight, N.F. Global/Local Stress Analysis of Composite Panels. Comp. Struct. 1990, 37, 375–395. [Google Scholar] [CrossRef]
- Craig, R.R., Jr.; Kurdila, A.J. Fundamentals of Structural Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- ANSYS Mechanical APDL. Advanced Analysis Guide, Chapter 6; ANSYS Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Paolino, D.S.; Chiandussi, G.; Rossetto, M. A unified statistical model for S-N fatigue curves: Probabilistic definition. Fatigue Fract. Eng. Mater. Struct. 2012, 36, 187–201. [Google Scholar] [CrossRef]
- Paolino, D.S.; Tridello, A.; Chiandussi, G.; Rossetto, M. Statistical distributions of Transition Fatigue Strength and Transition Fatigue Life in duplex S–N fatigue curves. Theor. Appl. Fract. Mech. 2015, 80, 31–39. [Google Scholar] [CrossRef]






| Quantity | Symbol | Units | Materials | ||
|---|---|---|---|---|---|
| Ti-6Al-4V | Al. 7075 T6 | SikaPower®-1277 | |||
| Modulus of elasticity | E | MPa | 115,000 | 71,955 ± 224 | 2280 ± 533 |
| Poisson’s ratio | / | 0.34 | 0.3 | 0.33 | |
| Ultimate tensile strength | MPa | 950 | 610 ± 15 | 35.7 ± 1.4 | |
| Density | g/cc | 4.395 | 2.8 | 1.1 | |
| Loss factor | LF | / | 2.96 × 10−4 | 3.5 × 10−3 | 2 × 10−2 |
| Viscosity | V | Pa·s | / | / | 430 (at 20 °C) |
| Plane Stress | Plane Strain | |
|---|---|---|
| 10 | 179.6 | 179.6 |
| 20 | 179.3 | 179.2 |
| 30 | 178.8 | 178.7 |
| 40 | 177.9 | 177.5 |
| 50 | 175.5 | 171.8 |
| 60 | 121.2 | 70.28 |
| 70 | 61.35 | 51.09 |
| 80 | 51.68 | 45.7 |
| 90 | 48.17 | 43.5 |
| 100 | 46.97 | 42.64 |
| 110 | 47.78 | 42.65 |
| 120 | 60.60 | 44.83 |
| Failures at 5 Hz | Failures at 25 Hz | Failures at 50 Hz | Failures at 20 kHz | |
|---|---|---|---|---|
| Standard deviation (SD) | 0.3038 | 0.5763 | 0.4687 | 0.7691 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pederbelli, D.; Goglio, L.; Paolino, D.; Rossetto, M.; Tridello, A. Effect of Loading Frequency on the Fatigue Response of Adhesive Joints up to the VHCF Range. Appl. Sci. 2023, 13, 12967. https://doi.org/10.3390/app132312967
Pederbelli D, Goglio L, Paolino D, Rossetto M, Tridello A. Effect of Loading Frequency on the Fatigue Response of Adhesive Joints up to the VHCF Range. Applied Sciences. 2023; 13(23):12967. https://doi.org/10.3390/app132312967
Chicago/Turabian StylePederbelli, Davide, Luca Goglio, Davide Paolino, Massimo Rossetto, and Andrea Tridello. 2023. "Effect of Loading Frequency on the Fatigue Response of Adhesive Joints up to the VHCF Range" Applied Sciences 13, no. 23: 12967. https://doi.org/10.3390/app132312967
APA StylePederbelli, D., Goglio, L., Paolino, D., Rossetto, M., & Tridello, A. (2023). Effect of Loading Frequency on the Fatigue Response of Adhesive Joints up to the VHCF Range. Applied Sciences, 13(23), 12967. https://doi.org/10.3390/app132312967










