Abstract
Graph theory is a common topic that is introduced as part of the curricula of computing courses such as Computer Science, Computer Engineering, Data Science, Information Technology and Software Engineering. Understanding graphs is fundamental for solving many real-world problems, such as network routing, social network analysis, and circuit design; however, many students struggle to grasp the concepts of graph theory, as they often have difficulties in visualising and manipulating graphs. To overcome these difficulties, educational software can be used to aid in the teaching and learning of graph theory. This work focuses on the development of a Java system for graph visualisation and computation, called MaGraDa (Graphs for Discrete Mathematics), that can help both students and teachers of undergraduate or high school courses that include concepts and algorithms related to graphs. A survey on the use of this tool was conducted to explore the satisfaction level of students on a Discrete Mathematics course taken as part of a Computer Engineering degree at the University of Alicante (Spain). An analysis of the results showed that this educational software had the potential to enhance students’ understanding of graph theory and could enable them to apply these concepts to solve practical problems in the field of computer science. In addition, it was shown to facilitate self-learning and to have a significant impact on their academic performance.
1. Introduction
Topics related to graph theory are commonly introduced in academic programmes at the level of a baccalaureate degree in computing [1]. In particular, the curricula of computer science courses [2] include a knowledge unit related to graphs, trees and their representations [3], shortest path algorithms such as the Dijkstra and Floyd-Warshall algorithms [3,4], and minimum spanning tree algorithms, such as the Prim and Kruskal algorithms [5,6]. Other specific computing programmes such as Computer Engineering [7], Data Science [8], Information Technology [9] and Software Engineering [10] also include these concepts about graph theory, to a greater or lesser extent.
In these engineering curricula, there must be a strong relationship between theory and practice to make mathematics relevant and interesting to students [11]. In addition, making connections between mathematical content and the real world is essential for engineers [12]. To accomplish these goals, various types of resources can be used to teach mathematical concepts. In particular, an understanding of graphs is important for solving many real-world problems, such as network routing, social network analysis, and circuit design [13,14]; however, many students have trouble understanding graph theory, as they often find it challenging to visualise and manipulate graphs. To overcome these difficulties, educational software can be used to aid in the teaching and learning of graph theory. Several resources and software tools have been developed to allow students to handle graphs in classroom. In [15], various resources for teaching graph theory for engineering programmes were developed for an elementary course and made available to students via a Moodle platform [16]. These resources included tutorials, slideshows and Java and Python files with introductory activities. CABRI-Graph [17,18] is a system that can be used by students, teachers or researchers. It basically consists of a graph editor together with a toolkit that allows for several computations, such as some classical transformations and the evaluation of graph invariants. The user can construct graphs interactively, select algorithms or graph transformations from a menu, and view the results directly on the screen. It is written in C, meaning that it is platform-dependent. Gato [19] is another software application that visualises various graph algorithms and can solve several known problems such as the shortest path, minimum spanning tree, maximal flow, weighted and non-weighted matching, and min-cost flow. Gato runs on all platforms that can execute Python and Tcl/Tk. Tulip [20] is another information framework dedicated to the analysis and visualisation of graphs. Written in C++, this framework enables the development of algorithms, visual encodings, interaction techniques, data models, and domain-specific visualisations. It is also available to the Python community through the Tulip-Python bindings. Although the above-mentioned tools have great research potential, their use in an educational context may be limited; in particular, the capability for interactive editing of the graph structure is limited, and they do not offer a flexible way of creating graphs. GraphTea [21] is an educational framework that covers a wide range of topics related to graph theory and its algorithms. This framework creates a new graph from its graphical representation using the mouse. From a didactic point of view, however, it would be more interesting to be able to create a graph from its theoretical definition, by introducing a set of vertices and a collection of edges or arcs, or from its adjacency matrix (or weighted adjacency matrix, when the graph is weighted). Grafos [22] was developed to aid in the teaching and learning of graph theory and other related disciplines such as industrial organisation engineering, logistics, operations research and network design. It is perfectly suited for use in modelling and solving real problems of a certain size and complexity. GRIN (GRaph INterface [23]) is a computer software that was designed to allow university students and teachers to understand graph problems, and covers a wide range of well-known algorithms for graph theory and optimisation problems in network theory. Both the Grafos and GRIN computer software only work on the graphical representation of graphs, and are only available for MS Windows. Neo4j [24] is a native graph database, implemented in Java, that stores nodes, relationships and properties rather than tables or documents. It provides a compliant transactional backend that is intended to guarantee the validity of the data despite errors, power failures, and other mishaps. Neo4j discovers and analyses connections within the data to improve the accuracy of machine learning models, thus enabling more accurate predictions through the utilisation of existing data. However, its use in an educational context may be limited, due to its primary focus on business applications. Some graph traversal languages can be used with graph databases, such as the Gremlin query language [25]. Gremlin is a functional data-flow language that allows users to define complex queries about the property graph for their application. GrAlg [26,27] software was created in the Delphi environment, and primarily focuses on creating and modifying graphs; it also provides the option to visualise graph algorithms, which can offer valuable insights into the entire process and the data structures used. DIDAGRAPH [28] is a software tool for the visualisation and exploration of graph algorithms, and implements a wide range of graph-related algorithms. Neither GrAlg and DIDAGRAPH are accessible via the Internet. GraViz [29] is a graph visualisation and analysis prototype software tool, implemented in Java, which combines graph analysis algorithms with simple 2D visualisation techniques. Although GraViz was intended as a throwaway prototype, it continued to evolve, and has been used by the author as a prototype tool for other projects.
In addition, there are various computer programming languages that can be used for manipulating the concepts of graph theory. Some of these graph programming languages are explained in [13,30], such as GIRL (Graph Information Retrieval Language), GASP (Graph Algorithm Software Package) and GTPL (Graph Theoretic Programming Language). The main purpose of these languages is to enable the user to formulate operations on graphs in a compact and natural way. Grrr [31] is another visual graph rewriting programming language. The aim of Grrr is to enable the animation of graph-based algorithms, which can serve as a valuable debugging aid when programming in this language.
In this work, we focus on the development of a new graph visualisation and computational system with the aim of helping students and teachers of undergraduate or high school courses that include concepts related to graphs. The proposed software provides a specific set of features, not all of which are offered by existing programs. More specifically, this software is an educational tool specifically designed for teaching and learning graph-related concepts. It provides a user-friendly interface that allows students to interact with graphs visually and intuitively, and works with both the theoretical definition of a graph and its graphical representation. A new graph can be created from its sets of vertices and edges (or arcs, when the graph is directed), from its adjacency matrix (or weighted adjacency matrix, when the graph is weighted), or from its graphical view. It is a platform-independent application that runs on all platforms that support Java and can help students to understand graph-related problems. It can execute all algorithms step by step, mirroring the natural progression they would follow, and students can use it on their own, outside the classroom, without little difficulty.
To assess the level of satisfaction of the students with this software, a survey was conducted during the 2022–2023 academic year of a course in Discrete Mathematics (DM) at the University of Alicante. The survey collected data on socio-demographic aspects, the user-friendliness and usability of the software, the quality of its content, its usefulness for learning graphs, and its impact on academic performance.
Section 2 presents the proposed software, called MaGraDa (Graphs for Discrete Mathematics). After introducing the Integrated Development Environment (IDE) and the high-level, class-based, object-oriented Java programming language used to build the software, Section 2.1 presents a brief overview of the Java class structure of the graph application and the external Java libraries it uses. Section 2.2 describes the developed software, and gives examples of its main characteristics. Section 3 explains the questionnaire used to analyse the level of satisfaction of students with this software, presents an analysis of the reliability of the survey, and summarises the main features of the course in which the survey was carried out. Section 4 explores the underlying dimensions of the survey conducted in this study, and Section 5 analyses the opinions of students about the use of the proposed application for graph theory. The results demonstrate the capability of this educational software to enhance students’ grasp of concepts related to graph theory and their ability to apply these principles effectively to solve practical problems. In addition, the software is shown to significantly contribute to facilitating self-directed learning, and to positively impact academic performance. Finally, some conclusions are presented in Section 6.
2. MaGraDa Software Tool
The idea for a software tool in the context of graph theory was conceived in 2001, based on an initial approach that was used to teach the DM course as part of the Computer Engineering degree at the University of Alicante (Spain) [32]. Following years of feedback from students and teachers, we decided to develop a new software by rewriting, extending and improving that initial Java application. Although the new software includes important changes from the initial application, it is built under the same name (MaGraDa, or Graphs for Discrete Mathematics), thus maintaining continuity with its predecessor and familiarity to our students.
2.1. Structure and Design of the Software Tool
The new version of MaGraDa is a platform-independent Java application that was developed to help students and teachers of undergraduate or high school courses that include topics related to graphs. It was coded using version 2021-09 (4.21.0) of Eclipse IDE and the Java Development Kit (JDK) version 1.8. It runs on all platforms that support Java, including MS Windows, Mac OS X and Linux.
Figure 1 shows a schematic diagram of the class structure of MaGraDa. This is not a standard UML (Unified Modelling Language) diagram, but rather an illustrative scheme showing the interactions between the different components. The main method in the MaGraDa class sets several private variables and manages the initial frame with the language selection; it starts the frame called MainFrame which contains one of the two modes of operation, called the text mode. In this mode, the theoretical definition of a graph is the focus of operation. A graph G is defined as a doublet , where V is a non-empty set of elements called vertices and A is a collection of pairs of elements of V, which may be ordered or not, and are called arcs or edges, respectively (see e.g., [4,33]). From MainFrame, the user can access the second mode of operation, called the graphic mode. This mode was developed in the Java JDialog named DialogGraphicMode. It uses a canvas, defined as a class that extends a Java JPanel called DrawPane, to draw graphs. A graph is defined as an object of the class TGraph. The objects of this class have a set of attributes that are needed for handling the structure of the graph. The most important attributes of a TGraph object are the set of vertices, defined as objects of the TVertex class, and the collection of edges or arcs, defined in the TEdge and TArc classes, respectively. The TGraph class also contains all the methods needed to work with the algorithms, properties and operations included in the application. Finally, there is a set of classes and their constructors that are used to display the algorithms or methods invoked by each menu item in both the text and graphic modes.
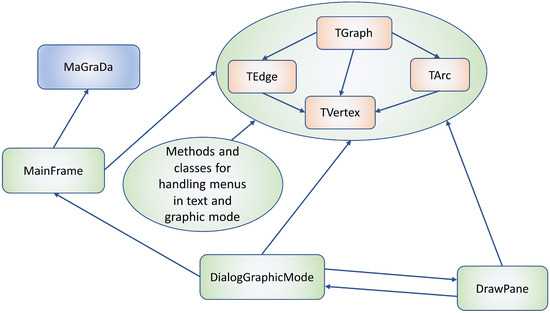
Figure 1.
Java structure of MaGraDa.
MaGraDa uses several external open-source Java libraries, such as JLaTeXMath [34], FlatLaf (Flat Look and Feel) [35], and JUNG (Java Universal Network/Graph) [36,37]. JLaTeXMath is a library for displaying mathematical formulas written in LaTeX [38], and is used to present a theoretical explanation of all the algorithms included in the application. FlatLaf is a modern cross-platform Look and Feel (L&F) for Java Swing desktop applications, and several of the L&Fs in MaGraDa are obtained from this library. Finally, the JUNG framework is a library that provides a common and extensible language for the manipulation, analysis, and visualisation of graphs, and is used to open and save graphs in GraphML format [39].
2.2. Description of the Visualisation and Computational Tool
As mentioned above, the MaGraDa Java application includes two modes of operation with similar options: the text mode and the graphic mode. Both modes offer the same functionalities, and the differences between them lie in the way in which the tool presents both the graphs themselves and the results of the algorithms and their explanation. In the text mode, the theoretical definition of a graph becomes relevant, while the graphic mode exploits the fact that most concepts and problems in graph theory can be expressed through the use of drawings. MaGraDa visualises graphs in the customary way in graph theory; that is, given a graph with a set of vertices V, MaGraDa uses points to represent vertices, line segments from to to represent an edge , and an arrow pointing from to to indicate the direction of an arc that starts at s and ends at t (see e.g., [33,40]). In each of the two modes, the results are presented to facilitate a comprehensive understanding of the algorithms and to demonstrate how they can be implemented. In addition, due to the ease of use of MaGraDa, students are able to use it on their own, outside the classroom, from the outset of the course.
MaGraDa works with directed and undirected graphs, and weighted and unweighted graphs. It can keep various graphs in memory so that at any time, the user can choose which graph to work with. In the text mode, an initial dialogue box displays the most relevant characteristics of the selected graph, such as the name of the graph, the number of vertices, the number of edges or arcs, and whether it is directed and weighted or not. For example, the initial text mode dialogue box in Figure 2a shows that the current graph, called Graph_1 and defined as , is directed and unweighted, and has five vertices and seven arcs. In the graphic mode, a graphical representation of the current graph is presented (see Figure 2b). We note that the graphic mode has four different zones: a menu bar for access to all the options it offers, a toolbar with the most commonly used options, a canvas on which graphs are drawn, and a status bar that gives information and helps the user with the handling of graphs and algorithms.
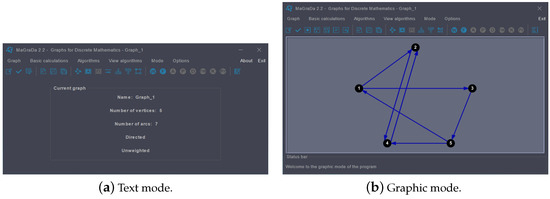
Figure 2.
Initial dialogue boxes of MaGraDa.
The Java application for graph processing is structured into six menus. Two of these are not related to graph theory, but allow the user to select the mode (text or graphic) and provide some other options (see Figure 3), such as the language used in the software (it currently offers three languages: English, Spanish and Valencian/Catalan), the aspect, or Java L&F, which allows the user to select between several L&Fs (Nimbus, Windows, Dark, …), the file format used to open and save a graph, and a check box to set the visibility of the toolbar. The options related to graph theory are presented in the other four menus, as follows:
- Graph menu: This allows for the handling of graphs.
- Basic calculations menu: This gives some basic properties of the current graph.
- Algorithms menu: This shows the algorithms that are available to apply to the current graph.
- View algorithms menu: This shows a detailed description of the algorithms included in the software.
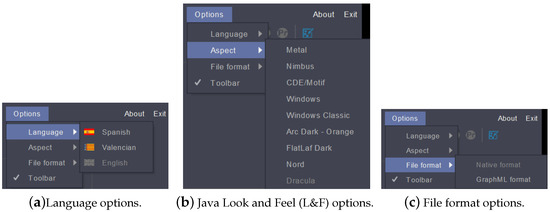
Figure 3.
Options menu.
2.2.1. Graph Menu
The Graph menu allows the user to create a new graph, modify the current graph, open a graph from a file, save a graph to a file, and select or delete a graph. In addition, a check box (Vertices with names) is included to indicate that all calculations will be presented with the name assigned to each vertex rather than using its number. In the graphic mode, this menu also offers an option to centre the current graph on the canvas. We note that MaGraDa can work with two different file formats: a native format, in which all the properties of a graph needed by MaGraDa are stored in a text file, and the GraphML format [39], an XML-based file format [41] used to describe the structural properties of a graph, which allows for the addition of application-specific data. This comprehensive and user-friendly file format for graphs is based on a core language for describing the structural properties of a graph and a flexible extension mechanism for adding application-specific data as needed. Graphs generated in this format can be opened by other graph visualisation programs such as Gephi [42] and yEd [43].
The most interesting parts of the Graph menu are those that relate to creating and modifying a graph. To create a new graph, MaGraDa opens a dialogue box in which the user must first input the main characteristics of the graph, that is, whether it is directed or undirected, weighted or unweighted, and the number of vertices, with the option to name each vertex (see Figure 4). From here, the way in which the user introduces edges or arcs (with or without weights) varies between the text and graphic modes. In the text mode, these elements can be entered either from the adjacency matrix (or weighted adjacency matrix, when the graph is weighted) or by explicitly entering each of the edges or arcs. The latter method of creating a graph helps students to understand its theoretical definition.
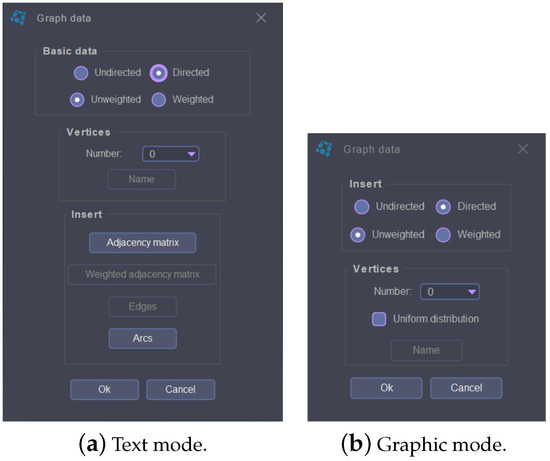
Figure 4.
Initial dialogue boxes used to create a graph.
Figure 5a shows the adjacency matrix used to create the graph in Figure 2, while Figure 5b shows the dialogue box that can be used as an alternative method to explicitly enter the seven arcs of this graph. In the graphic mode, after entering the main characteristics of the graph (see Figure 4b), vertices are drawn by clicking on their positions on the canvas. For simplicity, the user can also select a uniform distribution of vertices around a circle or an ellipse on the canvas (depending on the number of vertices in the graph). The edges or arcs are added by clicking on two adjacent vertices.

Figure 5.
Creating a new graph in the text mode.
To modify a graph in the text mode, users can access a dialogue box that allows them to add or remove edges or arcs, modify weights, and add, remove or rename vertices. Figure 6 shows this option for a directed and weighted graph named Graph_2. In the graphic mode, these modifications can be made by interacting with the canvas. For example, edges or arcs can be added or removed by clicking on the two adjacent vertices of the edge or arc. In addition, the vertices of a graph can be relocated on the canvas at any time by clicking on the current location of a vertex and dragging it to a new (free) place.

Figure 6.
Modifying a directed and weighted graph in the text mode.
In addition, the Graph menu has a submenu that allows the user to create a graph from a table of activities that represents a PERT (Project Evaluation and Review Technique). PERT analyses the time required to complete each activity of a project to determine the minimum time needed to complete the project [4]. This minimum time can be obtained with the critical path method, which gives the longest path from the start vertex to the end vertex of the graph representing the project. For simplicity, the MaGraDa activities table contains the list of activities or tasks, the expected time for each activity, and a list of prerequisites or tasks that need to be completed before a task begins [40]. MaGraDa informs the user if a prerequisite cannot be entered because the associated graph is cyclic, which would make the project impracticable. Figure 7 shows the dialogue box used to introduce an activities table. From this table, MaGraDa constructs the associated graph, which can be modified using a similar dialogue box. When this graph is saved to a file, the associated activities table is stored, so that this table can be recovered when the graph is opened again.
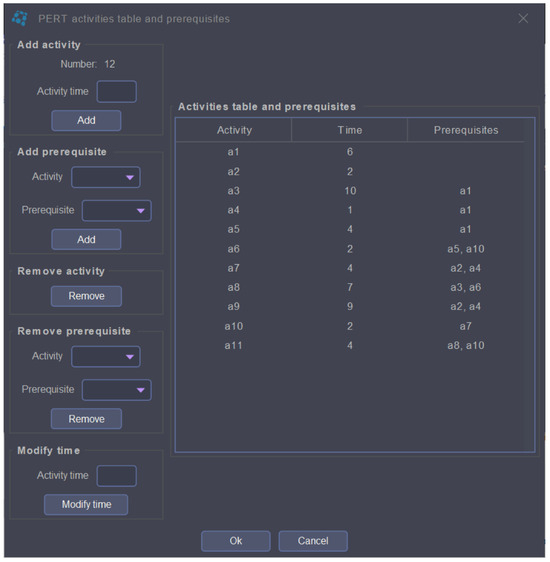
Figure 7.
Creating a new activities table for a PERT.
2.2.2. Basic Calculations Menu
The second menu, Basic calculations, includes a set of basic characteristics, properties and operations that can be obtained from the current graph. It gives the degree of the vertices, the adjacency matrix and the weighted adjacency matrix (when the graph is weighted). In addition, it shows the edges or arcs of the graph and indicates whether the graph is simple, cyclic, complete or connected in a reasoned way. When the current graph is directed, this menu also allows the user to obtain the associated undirected graph, and when it is undirected and connected, a spanning tree of the graph can be generated. Furthermore, this menu allows the user to ascertain whether two graphs are isomorphic (see e.g., [44]) by finding the correspondence between the vertices in both graphs. Before doing this, MaGraDa checks certain properties that two isomorphic graphs must have in common; that is, both graphs must be directed or undirected, they must have the same number of vertices and edges or arcs, and the same sequence of degrees. Another interesting option is the possibility of obtaining an isomorphic graph by permuting the vertices of the current graph. Finally, this menu gives the set of vertices that are reachable from a source vertex, the set of vertices reaching a vertex, and the connected components of the current graph. These options differ between the text and graphic modes; in the text mode, these options are displayed by a dialogue box with the answer to the question, while in the graphic mode, the user must click on a vertex to display its reachability or the connected component associated with it. In addition, the connected components of a graph can be computed through a set of steps. This involves obtaining the reachability matrix, denoted as R, the reaching matrix, denoted as Q, and the Hadamard or element-wise product of R and Q (), which yields the connected components [4]. The results of this process for the directed graph in Figure 2 are displayed in Figure 8.
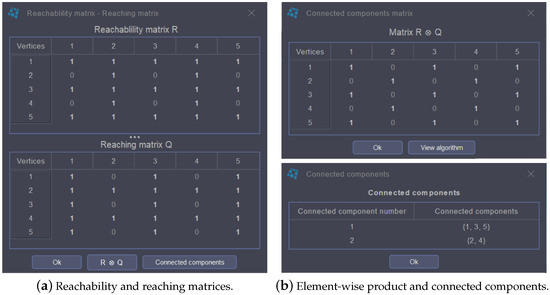
Figure 8.
Obtaining the connected components step by step.
In the graphic mode, the Basic calculations menu also has an option to zoom the graph using the scroll wheel of the mouse.
2.2.3. Algorithms and View Algorithms Menus
The third menu, Algorithms, implements some well-known algorithms in the context of graphs (see, e.g., [3,4,5,6,33,40,44,45,46]). For both weighted and unweighted graphs, this menu offers the Warshall algorithm [33,45] and the Fleury algorithm [4,33].
For the Warshall algorithm, MaGraDa displays all iterations needed to obtain the reachability matrix from the adjacency matrix, and highlights the changes from one iteration to the next. At each step of the recursive Warshall algorithm, the user can move forward and backwards through the iterations. The presentation of the Fleury algorithm, in which an Eulerian tour or Eulerian path is built, differs between the text mode and the graphic mode: in the text mode, an Eulerian tour or path is obtained as requested, whereas in the graphic mode, the application requests the user to build the Eulerian tour (or path), so that at each step, when the user selects an edge or arc to add to the tour (or path), the application determines whether it is suitable or not based on the Fleury algorithm.
The remainder of the algorithms listed in the third menu are related to weighted graphs. More specifically, MaGraDa implements the critical path algorithm for use with a PERT and the shortest path algorithm for acyclic graphs using Bellman equations [4]; the Dijkstra and Floyd-Warshall algorithms [3,4] to find the shortest paths from one vertex to the rest or between each pair of vertices, respectively; and the Kruskal and Prim algorithms [5,6], which obtain a minimum spanning tree from a weighted and undirected graph. All these algorithms are presented in such a way that the user can recognise the steps that have been followed in their execution, thus acquiring important pedagogical value. For example, Figure 9 shows the two first iterations of the Floyd-Warshall algorithm when applied to the graph defined by the weighted adjacency matrix . Note that the interface highlights the changes from one iteration to the next. As an application of the Floyd-Warshall algorithm, users can also obtain a specific shortest path between any two vertices by selecting the specific option included in MaGraDa. The solutions of these algorithms (shortest paths, critical paths and minimum spanning trees) are also displayed graphically on the canvas in the graphic mode.
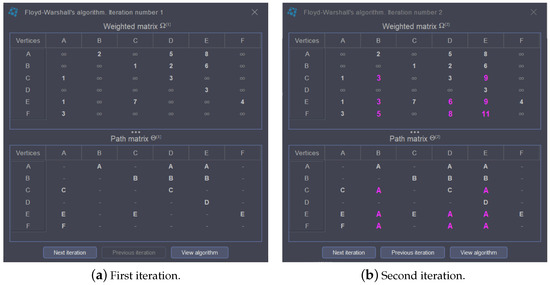
Figure 9.
First two iterations of the Floyd-Warshall algorithm.
The option from the Basic calculations menu that permutes the vertices of a graph can be used to teach and learn some characteristics of the Floyd-Warshall algorithm. More specifically, the Floyd-Warshall algorithm can be applied to obtain the shortest path between each pair of vertices with the constraint that each path contains only the intermediate vertices from a restricted set (see e.g., [4]). To solve this problem, a previous permutation of vertices is needed. For example, Figure 10 displays the last two iterations of the Floyd-Warshall algorithm, when the vertices of the graph of Figure 9 are permuted using the permutation . This permuted graph can be obtained with the above-mentioned option (see Figure 10a). Iteration 6 (where D is the sixth vertex in the permutation) in Figure 10b represents all the shortest paths, with the restriction that vertex D cannot appear as an intermediate vertex of any path. Obviously, iteration 7 in Figure 10c obtains all the shortest paths with no restrictions.
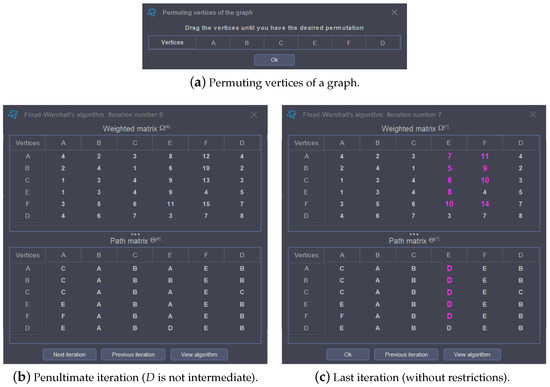
Figure 10.
Floyd-Warshall algorithm.
Figure 11 illustrates the output of the PERT algorithm when applied to the graph created from the activities table in Figure 7. Figure 11a shows the graph with the critical path (white arcs) and the minimum time required to complete each activity (yellow numbers at each vertex). Figure 11b provides information about the critical activities and the maximum allowable delay to complete a non-critical activity without affecting the project end date. Figure 12 shows the Bellman equations when applied both with the new vertex numbering required to calculate these equations, and the original numbering (properly ordered). Note that MaGraDa highlights the value at which the maximum is reached in each Bellman equation, which is used to identify the critical path.
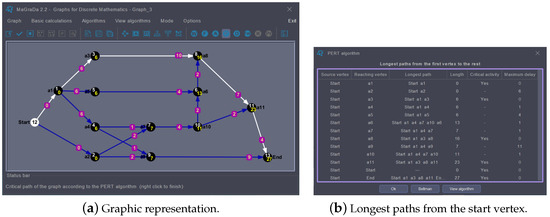
Figure 11.
PERT algorithm.
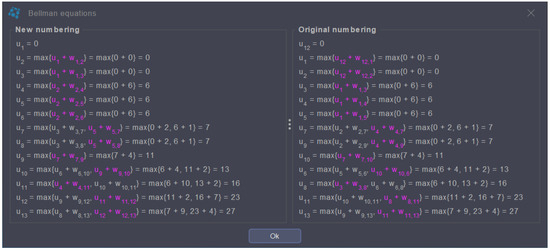
Figure 12.
Bellman equations (PERT algorithm).
The fourth menu, View algorithms, is a descriptive menu that shows a theoretical explanation of each algorithm included in the application. The descriptions included in this menu and the details offered when executing an algorithm are intended to help users overcome any difficulties in understanding graph theory. As an example, Figure 13 shows how the Warshall algorithm is described in this menu. The description of each algorithm can also be accessed when it is executed from the Algorithms menu (see e.g., Figure 10 and Figure 11b).

Figure 13.
Description of the Warshall algorithm.
3. Materials and Methods
To investigate the students’ level of satisfaction with the new software, we conducted a cross-sectional survey of students taking the DM course as part of the Computer Engineering degree at the University of Alicante, during the academic year 2022–2023. In the following, we describe this course, the way in which the tool was used, and the survey methodology used to analyse the students’ satisfaction with MaGraDa.
3.1. Description of the DM Course
Computer Engineering is a four-year degree with its courses distributed over eight semesters. DM is a mandatory course for the second semester (first year), with 30 h of lectures and 30 h of laboratory work. Moodle [16] is used as the main medium for e-learning, as it is one of the most commonly used web-based learning platforms for managing online learning within academia, including STEM (Science, Technology, Engineering, and Mathematics) education. E-learning has become one of the most valuable solutions for student education, especially following the COVID-19 measures [47]. The content of this course consists of graph theory (about 60%) and integer and modular arithmetic (about 40%). The content of the graph theory block is detailed in Table 1.

Table 1.
Content related to graph theory as part of the Discrete Mathematics (DM) course.
Laboratory classes provide students with first-hand experience of the concepts introduced on the course as well as the opportunity to explore the properties, operations, methods and algorithms described in lectures. To present content related to graph theory, classes (and especially laboratory classes) were conducted with the help of MaGraDa. Eight laboratory activities were offered that covered all the content related to graphs, as summarised in Table 2. The final grade for the DM course consisted of two parts: 50% was allocated based on the grade of a final exam with theoretical and practical exercises, and 50% was based on the lab score for three assessments that included practical exercises (two of which were related to graphs and the other to integer and modular arithmetic).

Table 2.
Laboratory activities undertaken as part of the DM course.
3.2. Survey Overview and Reliability
The survey was structured into several groups of questions: the first block contained items on socio-demographic characteristics, whereas the other four focused on the software tool. The survey concluded with an open-ended question to allow students to give comments and suggestions about MaGraDa (see Table 3). In addition, the survey asked the students for permission to access their grade for the laboratory sessions, to allow us to study the relationship between the use of MaGraDa and their final grade. The questionnaire blocks related to MaGraDa contained 18 items in which a five-point Likert scale was used to measure the level of agreement with each statement or question: strongly disagree (1), disagree (2), neither agree nor disagree (3), agree (4) and strongly agree (5) [48,49]. These questionnaire items were grouped into four sets of questions about the ease of use and friendliness of MaGraDa, its content, its didactic level, and general opinions about MaGraDa (see Figure 14), as follows:

Table 3.
Questions contained in the survey.
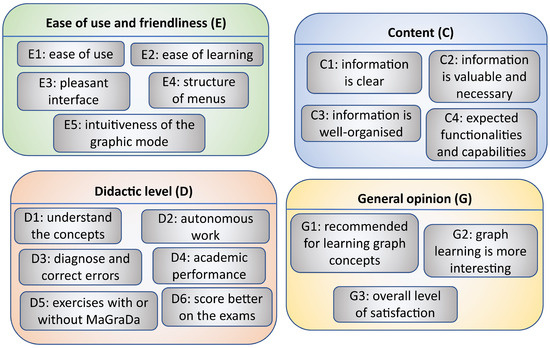
Figure 14.
Questionnaire items about MaGraDa using a five-point Likert scale.
- Questions about the ease of use and friendliness of MaGraDa (E): the users answered questions about their level of satisfaction with the ease of use of MaGraDa (E1), the ease of learning the software (E2), the pleasantness of the interface (E3), the structure of the menus (E4) and the intuitiveness of the graphic mode (E5).
- Questions about the content of MaGraDa (C): these covered aspects related to the information provided by the procedures and algorithms (C1), the need for the information contained in MaGraDa (C2), its organisation (C3), and the functionalities and capabilities offered by MaGraDa (C4).
- Questions about the didactic level of MaGraDa (D): the users answered questions about whether MaGraDa helped them to understand the concepts of graphs (D1), whether MaGraDa facilitated independent work (D2), whether MaGraDa helped them to identify, diagnose and correct errors in their graph exercises (D3), whether MaGraDa helped them in terms of their academic performance (D4), whether they would prefer to use MaGraDa rather than performing the exercises without computer assistance (D5), and finally their opinions about the help that MaGraDa could provide in terms of scoring better on the exams (D6).
- Questions about general opinions on MaGraDa (G): three questions were included about whether they would recommend MaGraDa for learning concepts about graphs (G1), whether MaGraDa made learning about graphs more interesting (G2), and an overall question about their level of satisfaction with MaGraDa (G3).
The anonymous questionnaire was distributed to students in laboratory classes using Google Forms. To avoid bias in the study, the students completed the questionnaire about MaGraDa when all the content related to graphs had been explained. A total of 116 students answered the questionnaire and were included in the study. The collected data were analysed with IBM SPSS Statistics 28.0 for Windows [50], using descriptive statistics, appropriate statistical tests, and multiple linear regression (MLR) with dummy variables [51].
Using a numeric scale from one to five to represent the values of the 18 input variables in Table 3, related to opinions about MaGraDa, we calculated the determinant of the Pearson correlation matrix. This determinant was approximately zero, suggesting that there were linear relationships among the variables. The variables for which the highest correlation coefficients were found were G1, G2 and G3, with coefficients ranging from 0.565 to 0.692 (general opinion block); the pairs (D3,D6), (D5,D6), (D2,D4), (D3,D4) and (D4,D6) of the didactic level block, with correlation coefficients of between 0.515 and 0.623; the pair (E1,E2) of the block related to the ease of use and friendliness of the software, with a correlation coefficient of 0.625; and the pairs (E2,G3), (E1,G3), (C2,G2), (D6,G1) and (C2,G1), with correlation coefficients of between 0.501 and 0.586. To enable us to explore, understand, and interpret the relationships between these variables, dimensionality reduction techniques were applied [52,53].
To assess the reliability of the measuring instrument, Cronbach’s alpha [54] was used. The reliability refers to the degree of internal consistency of the questionnaire and scale [55]. For all items combined, a value of 0.894 was found for Cronbach’s alpha (see Table 4), indicating a high level of internal consistency. The values obtained for the sets E, C, D and G of grouped items were 0.763, 0.709, 0.805 and 0.838, respectively. Table 5 summarises the statistics of the questionnaire as a whole and shows the values of Cronbach’ s alpha coefficient when each item is removed. It can be observed that when item E5 is removed, the overall reliability is 0.898. However, a decision was made to keep this item because it does not significantly affect the reliability of the instrument and is a priori relevant when evaluating the user-friendliness of MaGraDa.

Table 4.
Reliability statistics.

Table 5.
Item-total statistics (see Table 3 for a description of each variable).
4. Survey Exploratory Analysis
Factor analysis (FA) and principal component analysis (PCA) are multivariate statistical methods that are used in educational research to analyse measurement scales. Although both methods involve reducing the number of dimensions, they differ from a conceptual and mathematical point of view [52].
FA assumes that the correlations observed between variables result from unobserved latent factors influencing the observed variables. The main goal of this type of analysis is to identify, understand and model these underlying structures. In an FA model, each variable , is written as a linear combination of the common factors () plus a specific factor , that is, , where the scalars of these linear combinations , are called factor loadings. It is assumed that the common factors are standardised ( and ), and that the specific factors of the original variables are uncorrelated (, if ) and have a mean equal to zero ().
There are two types of FA: exploratory FA (EFA) and confirmatory FA (CFA). EFA is a multivariate statistical technique used for dimension reduction that seeks to discover the latent factors in a set of quantitative variables. In CFA, the factors are known a priori (and are usually previously described theoretically), and the objective is to verify whether this existing theoretical structure fits the data.
On the other hand, the goal of PCA is to reduce the dimensionality of a dataset while retaining the maximum possible variance from the original data. The aim is to represent the data as a new set of uncorrelated variables or principal components (, with , if ) that are linear combinations of the original variables, that is, , such that they efficiently capture the variability in the data.
Both FA and PCA have some limitations: firstly, they assume linear relationships between variables, and secondly, their interpretation is only reasonable if the variables are scaled at the numeric level (interval or ratio level of measurement) [53]. These assumptions are not always justified, which can render these reduction methods less suitable for certain contexts. Nonetheless, in specific fields such as social and education sciences, ordinal variables are sometimes treated as continuous variables, and the same principles and assumptions that apply to this type of data apply to ordinal data [56]. In addition, to overcome the limitations of these methods when using ordinal variables, we carried out a categorical PCA (CATPCA) [53]. The most important advantages of CATPCA over PCA are that it can deal with variables at their appropriate measurement level, including nominal or ordinal variables, and can handle and discover nonlinear relationships between variables. This means that CATPCA can be applied to ordinal scales such as the Likert scale used in our survey. CATPCA has the same purpose as PCA for categorical variables. Note that when all variables are scaled at the numeric level, CATPCA is equivalent to a standard PCA.
4.1. Exploratory Factor Analysis
To assess the suitability of using EFA, we used the Kaiser-Meyer-Olkin (KMO) measure and the Bartlett test of sphericity (see Table 6). The KMO value of 0.877 (i.e., greater than 0.8) suggested that the sample size was adequate [57,58]. The p-value for the Bartlett test of less than 0.001 indicated that the variables were not orthogonal and therefore correlated. We note that this test uses a chi-square distribution that assumes normality; nevertheless, many authors have shown, using theoretical distributions, that the Pearson correlation is robust to skewness and non-normality [56,59,60,61,62].

Table 6.
Results of Kaiser-Meyer-Olkin (KMO) and Bartlett tests.
To explore the latent factors, EFA was applied using the Principal Axis Factoring (PAF) method and the varimax rotation technique. To establish a cutoff for the eigenvalue, the Kaiser criterion was employed. In FA, the eigenvalues represent the variance explained by each factor, and when this criterion is used, factors with eigenvalues greater than one are retained.
Four factors were extracted that explained of the total variance (see Table 7). The first factor explained of the total variance, the second factor , the third and the fourth , with eigenvalues of 6.729, 2.162, 1.179 and 1.083, respectively. The extraction and rotation sums of the squared loadings displayed in Table 7 provide similar information but are based only on the shared variance among variables. The four extracted factors explained of this common variance. Table 8 displays the obtained rotated factor matrix. After examining the absolute loadings that exceeded 0.45, it was found that variables D2, D3, D4 and D6 were strongly loaded onto factor 1, while variables E1, E2, G2 and G3 had high loadings for factor 2, variables C2, C3, D5, G1 and G2 for factor 3, and variables E3, E4, E5 and C3 for factor 4. Factor 1 could be interpreted as the educational usefulness and academic benefits of MaGraDa, whereas factor 2 refers to the users’ perceptions of its usability. Factor 3 mainly represents the perceptions of the quality of its content as a tool for graph learning, while factor 4 seems to represent the perceptions of its user-friendliness.

Table 7.
Total variance explained by factor analysis (FA) with the principal axis factoring (PAF) extraction method.

Table 8.
Rotated factor matrix from FA with PAF extraction method, varimax rotation (see Table 3 for a description of each variable).
4.2. Principal Component Analysis
To reduce the dimensions of the data, we also applied PCA. Table 9 displays the total variance explained by the obtained principal components, while Table 10 shows the rotated component matrix using varimax with Kaiser normalisation. With four principal components, PCA explained of the total variance. The first component was highly correlated with variables E1, E2, E3, C1, C4, D1, G1, G2 and G3, and was therefore related to the user experience with the MaGraDa software. The second component, which was strongly correlated with variables D2, D3, D4 and D6, was mainly related to the educational usefulness and academic benefits of MaGraDa. The third component was strongly correlated with variables C2, C3, D5, D6 and G1. This component was mainly related to the users’ perceptions of the quality of the MaGraDa content as a tool for graph learning. The fourth component, which was correlated mainly with variables E4 and E5, was related to the users’ perceptions of the user–friendliness of MaGraDa.

Table 9.
Total variance explained by principal component analysis (PCA).

Table 10.
Rotated component matrix of PCA, varimax rotation (see Table 3 for a description of each variable).
4.3. Categorical Principal Component Analysis
The CATPCA solution was computed iteratively from the data, using the optimal scaling process of IBM SPSS to quantify the variables. Both ordinal and spline ordinal levels were considered, with the highest percentage of total variance being explained with the ordinal-level analysis. This is consistent with the recommendation to perform an ordinal-level analysis when the number of categories is small, and a monotonic spline-level analysis when the number of categories is large compared to the number of respondents [53].
CATPCA grouped the 18 variables into four principal components, which explained of the total variance (see Table 11 and Table 12). A high value of 0.976 for Cronbach’s alpha was also obtained for both CATPCA models, with and without rotation. This technique was able to identify the principal components or dimensions more clearly from the set of ordinal variables in this survey (see Table 13). The first principal component was strongly associated with the variables G1, G2, C2 and D2, and represented the usefulness of MaGraDa in terms of learning graphs. The second principal component was strongly associated with the variables E1, E2, E3, E4 and E5, and explained its user-friendliness and usability. The third principal component was primarily associated with variables D1, D3, D4, D5 and D6, and was therefore related to the impact of MaGraDa on academic performance. Finally, the fourth principal component, which was highly associated with variables C1, C3, C4, E1, E2, D1 and G3, was related to the quality of its content (procedures, algorithms and documentation). In summary, the CATPCA results showed that our survey comprehensively covered the most important aspects that, in our opinion, an educational software should encompass, that is, its usefulness for learning, its usability and user-friendliness, its effect on academic performance, and its content quality.

Table 11.
Categorical PCA (CATPCA) model summary.

Table 12.
CATPCA model summary, varimax rotation.

Table 13.
Rotated component loadings from CATPCA, varimax rotation (see Table 3 for a description of each variable).
5. Survey Results, Analysis and Discussion
In this section, we summarise the results of the survey designed to study the satisfaction level of students with MaGraDa. Table 14 displays the socio-demographic characteristics of the students. These demographic data show that the majority of respondents fell into the age group of 17–19 years (72.4%) followed by 20–29 years (25%) and over 29 years (2.6%). The percentage of males (82.8%) was much higher than that of females (12.9%), and was consistent with the total numbers of students taking the four-year degree course in Computer Engineering at the University of Alicante. In addition, a high percentage (81%) of students were enrolled in the first year of university, and 77.6% of students were taking the DM course for the first time.

Table 14.
Socio-demographic characteristics.
Figure 15 summarises the survey responses in regard to the ease of use and friendliness of MaGraDa. As can be seen, 79.3% of the students expressed a high level of satisfaction with its ease of use, while 87.1% found it easy to learn. Only a small percentage (3.5%) did not consider it well-structured, and 6% did not perceive its graphic mode as intuitive. In view of these results, and to improve its usability and structural organisation, the software was refined based on the feedback from the students, with the aim of meeting the expectations of more of the survey respondents. This feedback was obtained not only from the open-ended question, which included comments and suggestions about MaGraDa, but also through observation and feedback from students in the laboratory classes. The most significant changes that were introduced in regard to usability and user-friendliness, as suggested by the students, and included in the latest version of MaGraDa (reviewed in Section 2.2) are summarised in Table 15.
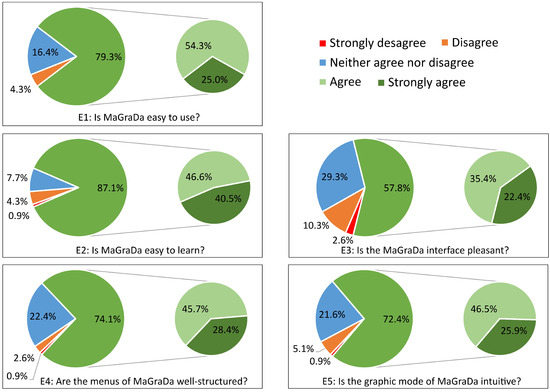
Figure 15.
Satisfaction with the ease of use and friendliness.

Table 15.
Changes to the latest version of MaGraDa, as suggested by students.
Regarding the educational content (see Figure 16), the majority of students considered that the information provided by this software was necessary and valuable (around 79%) and was aligned with their expectations for learning graph theory. However, 12.9% of students encountered problems understanding the information about procedures and algorithms. In the laboratory classes, some students reported difficulties in understanding certain algorithms and expressed a desire for the tool to apply all the algorithms step by step, similarly to the process of calculating them manually.
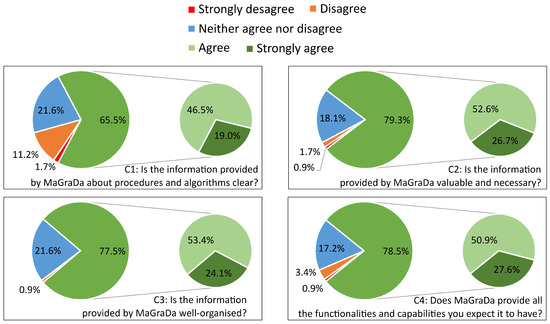
Figure 16.
Satisfaction with content.
To facilitate a better understanding of the software for all users, improvements were made to the documentation of some algorithms, and their outputs were explained in a more detailed way (see Table 15). In the current version, MaGraDa includes a feature that allows users to execute all algorithms step by step, corresponding to the theoretical explanations given in lectures.
Figure 17 displays the satisfaction of students with the didactic level of MaGraDa, including both its usefulness for learning graphs and the expected impact on their academic performance. The majority of students (78.4%) preferred to use this educational software to learn how to solve graph problems rather than the conventional method, while 13.8% had no particular preference, and only preferred to do the exercises without computer assistance. In fact, a high percentage of students considered that MaGraDa facilitated self-learning (82.8%) and the understanding of graph concepts (74.1%), and helped to identify, diagnose and correct possible errors in the exercises (76.7%). Regarding the impact of MaGraDa on academic performance, the survey results indicated that 65.5% of students believed that using MaGraDa would contribute to achieving better exam grades, while 26.7% of respondents expressed a neutral stance on this matter and only a minority of participants (7.8%) did not perceive MaGraDa as beneficial for improving their academic performance.
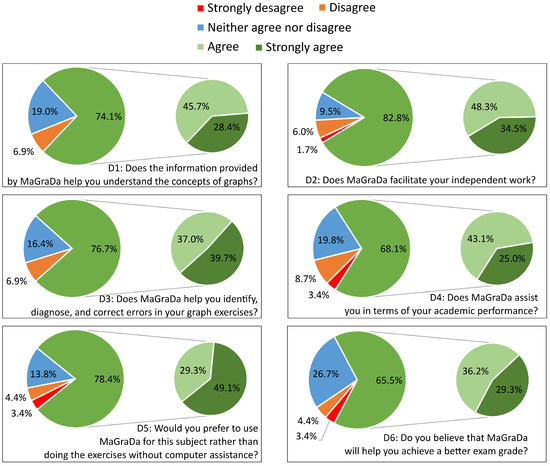
Figure 17.
Satisfaction with the didactic level.
A statistical summary of the survey variables is provided in Table 16 and Table 17. For most items, the mode and median were equal to four, indicating a generally positive assessment. In addition, items D3 (useful for diagnosis and error correction) and D5 (preference for using MaGraDa rather than conventional exercises) stood out with a mode score of five, highlighting a favourable experience with MaGraDa. These findings were aligned with the overall opinions expressed by students, as depicted in Figure 18. Specifically, the data indicated that a small percentage of users (6%) were not satisfied with this software, while a substantial percentage (79.3%) reported overall satisfaction. In addition, of students were willing to recommend MaGraDa for learning concepts related to graphs. Although approximately 15% of respondents remained neutral on these matters, it was noteworthy that all of the women answering the survey (100%) expressed overall satisfaction with this software.

Table 16.
Statistical summary of variables in blocks E and C (see Table 3 for a description of each variable).

Table 17.
Statistical summary of variables in blocks D and G (see Table 3 for a description of each variable).
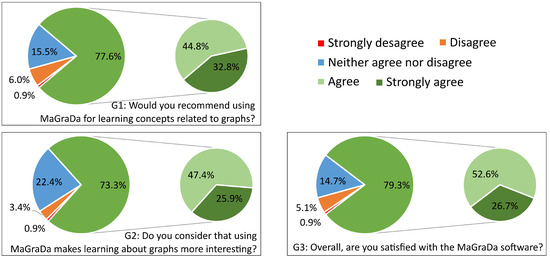
Figure 18.
General opinions.
To compare the opinions of the students by gender, the non-parametric Kruskal-Wallis H test was also used. The results showed statistically significant differences in the response distributions not only for overall satisfaction (p-value = 0.023) but also for other specific aspects explained by the variables E1 (p-value = 0.03), E2 (p-value = 0.01), E3 (p-value = 0.01), E4 (p-value = 0.004), D3 (p-value = 0.024), and G3 (p-value = 0.005). Figure 19 illustrates these differences for the surveyed students who specified their gender (111 from 116). It is apparent that female respondents had a more favourable perspective towards the software than male students. More specifically, 86.7% of female participants expressed the view that MaGraDa was easy to use, and 93.3% found it easy to learn. Furthermore, all female respondents affirmed that the software was well structured and helped in the identification, diagnosis, and rectification of errors in their exercises. Among male respondents, these percentages were slightly lower, with 80.2% perceiving it as easy to use and 86.5% finding it easy to learn. Moreover, 74% of male participants reported its effectiveness in terms of identifying errors. These findings offer valuable insights into the gender-based differences in opinions regarding MaGraDa, with the female cohort exhibiting a more favourable outlook across several key dimensions of assessment.
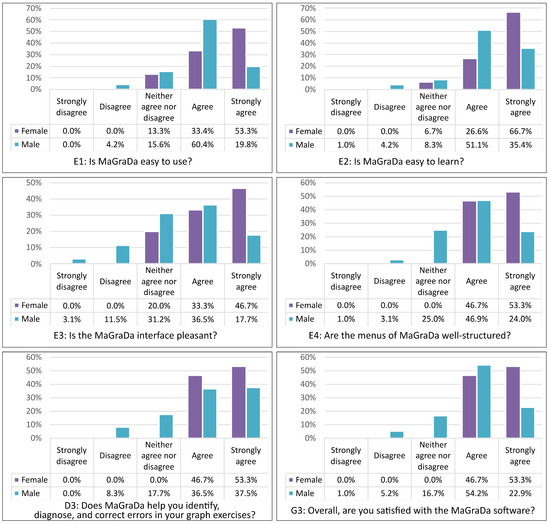
Figure 19.
Results by gender.
Mann-Whitney U and Kruskal-Wallis H tests were also employed to conduct comparisons based on the other characteristics of the surveyed population. The aim of this analysis was to determine whether there were differences in opinions based on the highest university year of the students, and whether it was the first time they had attended the DM course. In neither case were significant differences observed in the distribution of responses.
To analyse the effect of students’ socio-demographic profiles (described in Table 14) on the four dimensions obtained using CATPCA in Section 4.3, we also conducted a stepwise MLR analysis. The decision to use the dimensions obtained through CATPCA was based on its ability to identify the dimensions more clearly than EFA and PCA from the set of Likert scale variables used for the survey. Moreover, CATPCA explained a higher percentage of variance (71.179%) with 4 components, compared to FA and PCA. Since MLR treats independent variables as numerical, dummy variables were generated to represent the categorical variables. The gender variable accounted for approximately 3.6% of the variation in students’ opinions about the utility of MaGraDa for learning (dimension 1). With a p-value of 0.047, this variable emerged as the sole significant socio-demographic contributor to this dimension. As shown in Table 18, for similar profiles, female students rated the utility of MaGraDa for learning 0.556 points higher than male students. Furthermore, the categorised age of the students explained 4.9% of the variation in dimension 4, with students aged 20 to 29 rating the content quality of MaGraDa 0.472 points higher than the rest of students. The socio-demographic profile did not influence the students’ opinions about the usability and user-friendliness of the MaGraDa software (dimension 2) or its impact on academic performance (dimension 3).

Table 18.
Models obtained with stepwise multiple linear regression (MLR); Dependent variable in model A: object scores of dimension 1; Dependent variable in model B: object scores of dimension 4.
The final grades of students for the laboratory practice sessions were also compared with their opinions on each survey question. A preliminary statistical analysis to test the normality of the final grades was carried out using both the Shapiro-Wilk and Kolmogorov-Smirnov (with the Lilliefors correction) tests, which showed that there was no evidence to reject the assumption of normality in any group. The ANOVA (analysis of variance) test and the independent-samples t-test were therefore used to analyse the mean grades. Significant differences were observed in the mean grades achieved by students who expressed overall satisfaction with the MaGraDa software compared with those who were dissatisfied (see also Figure 20). Students who expressed satisfaction with MaGraDa achieved a mean grade of 6.87 and a median of 7, while their dissatisfied peers had a mean grade of 5.21 and a median of 5.5. These results indicated the influence of satisfaction with MaGraDa on academic performance. This was mainly because most of the satisfied students were able to use MaGraDa efficiently to learn about graphs and to identify, diagnose, and correct errors in their exercises, thus obtaining better grades for the laboratory sessions.
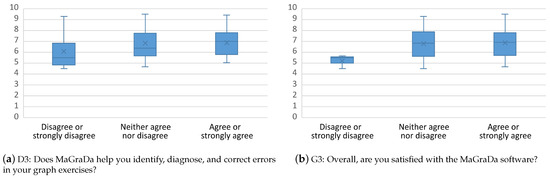
Figure 20.
Academic performance with MaGraDa.
6. Conclusions
In this work, we have presented MaGraDa, a Java-based graph visualisation and computational system designed to assist students and educators in undergraduate and high school courses involving concepts and algorithms related to graphs.
To analyse its effectiveness, a survey was conducted among students enrolled on a DM course as part of the Computer Engineering programme at the University of Alicante in Spain. A value of 0.894 for Cronbach’s alpha indicated the internal consistency of this survey. An exploratory analysis performed to reduce the dimensions of the data identified the most important aspects that an educational software should cover, that is, usefulness for learning, usability and user-friendliness, impact on academic performance, and content quality.
Based on the results of the survey and our analysis, MaGraDa is positioned as a valuable tool to facilitate the learning process and make abstract graph concepts more accessible. Through classroom assessments, we observed positive outcomes in terms of engagement, comprehension, and problem-solving skills. The visual representation of graphs and the ability to manipulate them in real time provided a hands-on learning experience, enabling students to understand graph structures and algorithms more effectively.
Furthermore, the ease of use of this software opens up possibilities for various applications within computer science education. It could be integrated into existing curricula, used as a supplementary tool for individual study, or even employed in online courses or distance learning programmes. The flexibility of this software allows educators to tailor the learning experience to the specific needs and learning styles of their students.
As with any educational tool, continuous improvement and refinement are necessary. Future iterations of MaGraDa could incorporate additional features such as interactive tutorials, more advanced graph algorithms, and customisable exercises. User feedback and ongoing research will play crucial roles in enhancing its functionality and usability, and will ensure its long-term effectiveness in terms of supporting graph theory education.
In summary, this educational software for teaching graph theory has been shown to have the potential to enhance the learning experiences of students and comprehension of this subject as part of computer science studies. By providing a visual and interactive platform, we aim to empower students to apply graph theory concepts confidently to solve practical and real-world problems. The results of this study, in which female students unanimously expressed satisfaction with the assessed software and only a small percentage (6%) of males reported dissatisfaction, underscore the motivating potential of this educational software. In addition, these findings show that MaGraDa could help to encourage female students pursuing STEM courses with graph-related content, thereby helping to address the gender gap in STEM fields.
Author Contributions
Conceptualisation, V.M. and J.P.; methodology, V.M. and J.P.; formal analysis, V.M. and J.P.; software, V.M. and J.P.; validation, V.M. and J.P.; investigation, V.M. and J.P.; data curation, V.M. and J.P.; writing—original draft preparation, V.M. and J.P.; writing—review and editing, V.M. and J.P.; supervision, V.M. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The current version 2.2 of the MaGraDa software implemented and presented in this manuscript is freely available from the University of Alicante website at https://web.ua.es/en/magrada, uploaded on 29 October 2023.
Acknowledgments
We would like to thank the students for their participation in the survey, and especially Manuel Ángel Caballero, who contributed to the initial concept for this software in 2001.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| MaGraDa | Graphs for Discrete Mathematics |
| DM | Discrete Mathematics |
| GRIN | Graph Interface |
| GIRL | Graph Information Retrieval Language |
| GASP | Graph Algorithm Software Package |
| GTPL | Graph Theoretic Programming Language |
| IDE | Integrated Development Environment |
| STEM | Science, Technology, Engineering, and Mathematics |
| JDK | Java Development Kit |
| FlatLaf | Flat Look and Feel |
| JUNG | Java Universal Network/Graph |
| L&F | Look and Feel |
| PERT | Program Evaluation Review Technique |
| MLR | Multiple linear regression |
| KMO | Kaiser-Meyer-Olkin |
| FA | Factor analysis |
| PCA | Principal component analysis |
| EFA | Exploratory factor analysis |
| CFA | Confirmatory factor analysis |
| CATPCA | Categorical principal component analysis |
| PAF | Principal axis factoring |
| ANOVA | Analysis of variance |
References
- CC2020 Task Force. Computing Curricula 2020: Paradigms for Global Computing Education; ACM: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Joint Task Force on Computing Curricula; ACM; IEEE Computer Society. Computer Science Curricula 2013: Curriculum Guidelines for Undergraduate Degree Programs in Computer Science; ACM: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Veerarajan, T. Discrete Mathematics with Graph Theory and Combinatorics; Computer Science Series; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Christofides, N. Graph Theory. An Algorithmic Approach; Academic Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Dierker, P.F.; Voxman, W.L. Discrete Mathematics; Harcourt Brace Jovanovich: San Diego, CA, USA, 1986. [Google Scholar]
- Grimaldi, R.P. Discrete and Combinatorial Mathematics. An Applied Introduction; Addison-Wesley: Boston, MA, USA, 2003. [Google Scholar]
- Joint Task Force on Computer Engineering Curricula; ACM; IEEE Computer Society. Computer Engineering Curricula 2016: Curriculum Guidelines for Undergraduate Degree Programs in Computer Engineering; ACM: New York, NY, USA, 2016; Available online: https://www.acm.org/binaries/content/assets/education/ce2016-final-report.pdf (accessed on 10 May 2023).
- ACM Data Science Task Force. Computing Competencies for Undergraduate Data Science Curricula; ACM: New York, NY, USA, 2021. [Google Scholar] [CrossRef]
- Task Group on Information Technology Curricula. Information Technology Curricula 2017: Curriculum Guidelines for Baccalaureate Degree Programs in Information Technology; ACM: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Joint Task Force on Computing Curricula; ACM; IEEE Computer Society. Curriculum Guidelines for Undergraduate Degree Programs in Software Engineering; ACM: New York, NY, USA, 2014. [Google Scholar]
- Flegg, J.; Mallet, D.; Lupton, M. Students’ perceptions of the relevance of mathematics in engineering. Int. J. Math. Educ. Sci. Technol. 2012, 43, 717–732. [Google Scholar] [CrossRef]
- Gueudet, G.; Quéré, P. “Making connections” in the mathematics courses for engineers: The example of online resources for trigonometry. In Proceedings of the Second Conference of the International Network for Didactic Research in University Mathematics; INDRUM2018; Durand-Guerrier, V., Hochmuth, R., Goodchild, S., Hogstad, N.M., Eds.; University of Agder and INDRUM: Kristiansand, Norway, 2018. [Google Scholar]
- Majeed, A.; Rauf, I. Graph Theory: A Comprehensive Survey about Graph Theory Applications in Computer Science and Social Networks. Inventions 2020, 5, 10. [Google Scholar] [CrossRef]
- Campbell, W.M.; Dagli, C.K.; Weinstein, C.J. Social Network Analysis with Content and Graphs. Linc. Lab. J. 2013, 20, 62–81. [Google Scholar]
- Tabchi, T.; Sabra, H.; Ouvrier-Buffet, C. Resources for teaching graph theory for engineers—Issue of connectivity. In Proceedings of the 3rd International Conference on Mathematics Textbook Research and Development; Rezat, S., Fan, L., Hattermann, M., Schumacher, J., Wuschke, H., Eds.; Universitätsbibliothek Paderborn: Paderborn, Germany, 2019; pp. 323–328. [Google Scholar]
- Gamage, S.H.P.W.; Ayres, J.R.; Behrend, M.B. A systematic review on trends in using Moodle for teaching and learning. Int. J. STEM Educ. 2022, 9, 9. [Google Scholar] [CrossRef] [PubMed]
- Carbonneaux, Y.; Laborde, J.M.; Madani, R.M. CABRI-Graph: A tool for research and teaching in graph theory. In Graph Drawing; Lecture Notes in Computer, Science; Brandenburg, F.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1027, pp. 123–126. [Google Scholar] [CrossRef]
- Baudon, O.; Laborde, J. Cabri-graph, a sketchpad for graph theory. Math. Comput. Simul. 1996, 42, 765–774. [Google Scholar] [CrossRef]
- Schliep, A.; Hochstättler, W. Developing Gato and CATBox with Python: Teaching graph algorithms through visualization and experimentation. In Multimedia Tools for Communicating Mathematics; Mathematics and, Visualization; Borwein, J., Morales, M.H., Rodrigues, J.F., Polthier, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 291–309. [Google Scholar] [CrossRef]
- Lambert, A.; Auber, D. Graph analysis and visualization with Tulip-Python. In Proceedings of the EuroSciPy 2012—5th European meeting on Python in Science, Brussels, Belgium, 23–27 August 2012. [Google Scholar]
- Rostami, M.A.; Azadi, A.; Seydi, M. GraphTea: Interactive graph self-teaching tool. In Communications, Circuits and Educational Technologies: 2014 International Conference on Education and Educational Technologies II (EET’14); Wseas Llc Staff: Prague, Czech Republic, 2014; pp. 48–51. [Google Scholar]
- Rodríguez-Villalobos, A. Grafos. Available online: https://arodrigu.webs.upv.es/grafos/doku.php (accessed on 15 September 2023).
- Pechenkin, V. GRIN (GRaph INterface). 2022. Available online: https://grin-software.net (accessed on 15 September 2023).
- Neo4j Connections: Generative AI and Knowledge Graphs. 2010. Available online: https://neo4j.com (accessed on 26 November 2023).
- Gremlin Query Language. 2009. Available online: https://tinkerpop.apache.org/gremlin.html (accessed on 26 November 2023).
- Ševčíková, A.; Milková, E. Multimedia applications: Graph algorithms visualization. In Proceedings of the 2016 IEEE 17th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 17–19 November 2016; pp. 231–236. [Google Scholar] [CrossRef]
- Sevcikova, A.; Milkova, E.; Moldoveanu, M.; Konvicka, M. Graph Theory: Enhancing Understanding of Mathematical Proofs Using Visual Tools. Sustainability 2023, 15, 10536. [Google Scholar] [CrossRef]
- Dagdilelis, V.; Satratzemi, M. DIDAGRAPH: Software for teaching graph theory algorithms. ACM SIGCSE Bull. 1998, 30, 64–68. [Google Scholar] [CrossRef]
- Hawick, K. Interactive Graph Algorithm Visualization and the GraViz Prototype; Technical Report CSTN-061; Institute of Information and Mathematical Sciences, Massey University: Auckland, New Zealand, 2010. [Google Scholar]
- Chaudhary, P.; Kumar, V. A Review on Applications of Graph Theory in Computer Science. J. Adv. Sci. Tecnol. 2020, 17, 82–87. [Google Scholar]
- Rodgers, P.J.; Vidal, N. Graph algorithm animation with Grrr. In Proceedings of the Applications of Graph Transformations with Industrial Relevance; Nagl, M., Schürr, A., Münch, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 379–394. [Google Scholar] [CrossRef]
- Caballero, M.; Migallón, V.; Penadés, J. MaGraDa: Una Herramienta para el tratamiento de grafos en matemática discreta. In Proceedings of the VII Jornadas de Enseñanza Universitaria de la Informática; Miró, J., Ed.; Universitat de les Illes Balears: Palma de Mallorca, Spain, 2001; pp. 478–481. [Google Scholar]
- Rosen, K.H. Discrete Mathematics and Its Applications; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- JLaTeXMath—A Java API to Render LaTeX—A Java Package to Display LaTeX Code in Mathematical Mode. 2021. Available online: https://github.com/opencollab/jlatexmath. (accessed on 3 September 2023).
- FlatLaf—Flat Look and Feel. 2022. Available online: https://www.formdev.com/flatlaf/ (accessed on 3 September 2023).
- JUNG (Java Universal Network/Graph). 2009. Available online: https://jung.sourceforge.net/doc/index.html (accessed on 3 September 2023).
- O’Madadhain, J.; Fisher, D.; Smyth, P.; White, S.; Boey, Y.B. Analysis and visualization of network data using JUNG. J. Stat. Softw. 2005, 10, 1–35. [Google Scholar] [CrossRef]
- Mittelbach, F.; Goossens, M.; Braams, J.; Carlisle, D.; Rowley, C. The LaTeX Companion, 2nd ed.; Pearson Education, Inc.: Boston, MA, USA, 2004. [Google Scholar]
- Brandes, U.; Eiglsperger, M.; Herman, I.; Himsolt, M.; Marshall, M.S. GraphML progress report structural layer proposal. In Proceedings of the Graph Drawing; Mutzel, P., Jünger, M., Leipert, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 501–512. [Google Scholar] [CrossRef]
- Grassmann, W.K.; Tremblay, J.P. Logic and Discrete Mathematics: A Computer Science Perspective; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- W3C. Extensible Markup Language (XML) 1.0. 2008. Available online: https://www.w3.org/TR/xml/ (accessed on 3 September 2023).
- Gephi—The Open Graph Viz Platform. 2008. Available online: https://gephi.org/ (accessed on 3 September 2023).
- yEd—Graph Editor. 2023. Available online: https://www.yworks.com/products/yed (accessed on 3 September 2023).
- Gross, J.L.; Yellen, J. Graph Theory and Its Applications; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Aho, A.V.; Alspach, B.; Archdeacon, D.; Arney, D.C.; Balbuena, C.; Beineke, L.W.; Blazewicz, J.; Bollobás, B.; Bonato, A.; Bonchev, D.; et al. Handbook of Graph Theory; Gross, J.L., Yellen, J., Zhang, P., Eds.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Migallón, V.; Penadés, J. Matemática Discreta; Puntero y Chip: Alicante, Spain, 2004. [Google Scholar]
- Secretary-General of the OECD. The Impact of COVID-19 On Education: Insights from Education at a Glance 2020. Available online: https://www.oecd.org/education/the-impact-of-covid-19-on-education-insights-education-at-a-glance-2020.pdf (accessed on 10 September 2023).
- Likert, R. A Technique for the Measurement of Attitudes. Arch. Psychol. 1932, 22, 5–55. [Google Scholar]
- Batterton, K.A.; Hale, K.N. The Likert Scale What It Is and How To Use It. Phalanx 2017, 50, 32–39. [Google Scholar]
- IBM Corp. IBM SPSS Statistics for Windows. 2023. Available online: https://www.ibm.com/uk-en/analytics/spss-statistics-software (accessed on 20 May 2023).
- Hardy, M.A. Regression with Dummy Variables; Sage University Paper Series on Quantitative Applications in the Social Science, 07-093; Sage: Newbury Park, CA, USA, 1993. [Google Scholar]
- Wang, F. Factor analysis and principal-components analysis. In International Encyclopedia of Human Geography, 2nd ed.; Kobayashi, A., Ed.; Elsevier: Oxford, UK, 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Linting, M.; Meulman, J.J.; Groenen, P.J.; van der Koojj, A.J. Nonlinear principal components analysis: Introduction and application. Psychol. Methods 2007, 12, 336–358. [Google Scholar] [CrossRef] [PubMed]
- Cronbach, L.J. Coefficient alpha and the internal structure of tests. Psychometrika 1951, 16, 297–334. [Google Scholar] [CrossRef]
- Tavakol, M.; Dennick, R. Making sense of Cronbach’s alpha. Int. J. Med. Educ. 2011, 2, 53. [Google Scholar] [CrossRef] [PubMed]
- Norman, G. Likert scales, levels of measurement and the “law” of statistics. Adv. Health Sci. Educ. 2010, 15, 625–632. [Google Scholar] [CrossRef] [PubMed]
- MacCallum, R.C.; Widaman, K.F.; Zhang, S.; Hong, S. Sample size in factor analysis. Psychol. Methods 1999, 4, 84–89. [Google Scholar] [CrossRef]
- Shrestha, N. Factor Analysis as a Tool for Survey Analysis. Am. J. Appl. Math. 2021, 9, 4–11. [Google Scholar] [CrossRef]
- Pearson, E.S. The Test of Significance for the Correlation Coefficient. J. Am. Stat. Assoc. 1931, 26, 128–134. [Google Scholar] [CrossRef]
- Pearson, E.S. The Test of Significance for the Correlation Coefficient: Some Further Results. J. Am. Stat. Assoc. 1932, 27, 424–426. [Google Scholar] [CrossRef]
- Havlicek, L.L.; Peterson, N.L. Robustness of the Pearson correlation against violations of assumptions. Percept. Mot. Skills 1976, 43, 1319–1334. [Google Scholar] [CrossRef]
- Fletcher, K.E.; French, C.T.; Irwin, R.S.; Corapi, K.M.; Norman, G.R. A prospective global measure, the Punum Ladder, provides more valid assessments of quality of life than a retrospective transition measure. J. Clin. Epidemiol. 2010, 63, 1123–1131. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).