Abstract
Despite receiving much attention from researchers in the field of naval architecture and marine engineering since the early stages of modern shipbuilding, the berthing phase is still one of the biggest challenges in ship maneuvering due to the potential risks involved. Many algorithms have been proposed to solve this problem. This paper proposes a new approach with a path-planning algorithm for automatic berthing tasks using deep reinforcement learning (RL) based on a maneuvering simulation. Unlike the conventional path-planning algorithm using the control theory or an advanced algorithm using deep learning, a state-of-the-art path-planning algorithm based on reinforcement learning automatically learns, explores, and optimizes the path for berthing performance through trial and error. The results of performing the twin delayed deep deterministic policy gradient (TD3) combined with the maneuvering simulation show that the approach can be used to propose a feasible and safe path for high-performing automatic berthing tasks.
1. Introduction
Since the early stages of modern shipbuilding, much attention has been paid to automated methods of ship navigation, particularly with the continuous advancements in artificial intelligence (AI). As a result, the number of autonomous ships has rapidly grown. Autonomous ship navigation offers substantial advantages in terms of safety, efficiency, reliability, and environmental sustainability. By harnessing advanced technologies such as sensor systems, data analysis, and artificial intelligence and by reducing the risk of human error, autonomous navigation systems ensure the safety of ship operations. These systems operate consistently and reliably, unhindered by human limitations, resulting in more predictable performance and fewer accidents. Autonomous ships can process vast amounts of data, enabling informed decision making, collision avoidance, and adaptation to changing conditions [1]. However, automatic ship berthing remains an extremely complex task, particularly under low-speed conditions where the hydrodynamic forces acting on the ship are highly nonlinear [2]. Controlling the ship becomes challenging and necessitates the expertise of an experienced commander. Numerous researchers have conducted extensive studies on the principles and algorithms for automatic ship berthing. Researchers have developed various ship control algorithms based on control theories and maneuverability assumptions [3,4,5,6,7,8,9]. These approaches proved effective under defined berthing conditions before the existence of AI. The development of AI algorithms has propelled the creation of algorithms and methods that enhance ship control performance, improve safety, and greatly reduce accidents in the marine industry. Many supervised learning algorithms based on neural networks have exhibited promising results with a high success rate, as in [10,11,12,13]. Applying AI algorithms eliminates the need to clearly understand the mathematical model of ships. However, acquiring a substantial number of labeled training data can be time-consuming and costly.
Unlike the aforementioned methods where the training dataset is not necessary, reinforcement learning techniques, which constitute an area of machine learning, allow the ship to learn and optimize its berthing maneuvers through interactions with a simulated environment. The application of RL in the automatic berthing task has shown good results when the ship can automatically learn the strategy and optimize the control policy to move to the berthing point [14,15].
In this paper, initial development of a novel path-planning algorithm for autonomous ship berthing that uses the latest technique in reinforcement learning, called twin delayed deep deterministic policy gradient (TD3), is proposed. The TD3 algorithm was introduced by Scott Fujimoto (2018) and is specifically designed for continuous action spaces. TD3 is an extension of deep deterministic policy gradients (DDPGs) and aims to address certain challenges and improve the stability of learning in complex environments. TD3 exploration algorithms allow the agent to explore the environment and gain new experiences that optimize rewards through trial and error. It employs two distinct value function estimators, which mitigate the overestimation bias and stabilize the learning process. Leveraging these two critics, TD3 provides more accurate value estimates and facilitates better policy updates. High performance and stability compared to other algorithms in the field of RL were shown in [16]. In combination with the MMG model, the solutions for ship-maneuvering motion simulation that were proposed by a research group maneuvering modeling group (MMG) in 1977 [17] suggest a feasible path, resulting in faster convergence and improved accuracy.
This article is organized into five parts. The first section introduces previous studies conducted in this field. Section 2 presents the equation of motion for the ship based on the MMG model along with hydrodynamic and interaction coefficients. Section 3 outlines the path-planning algorithm based on deep reinforcement learning TD3. Section 4 showcases and discusses simulation results for two berthing cases. Finally, Section 5 concludes this research.
2. Mathematical Model
2.1. Coordinated System
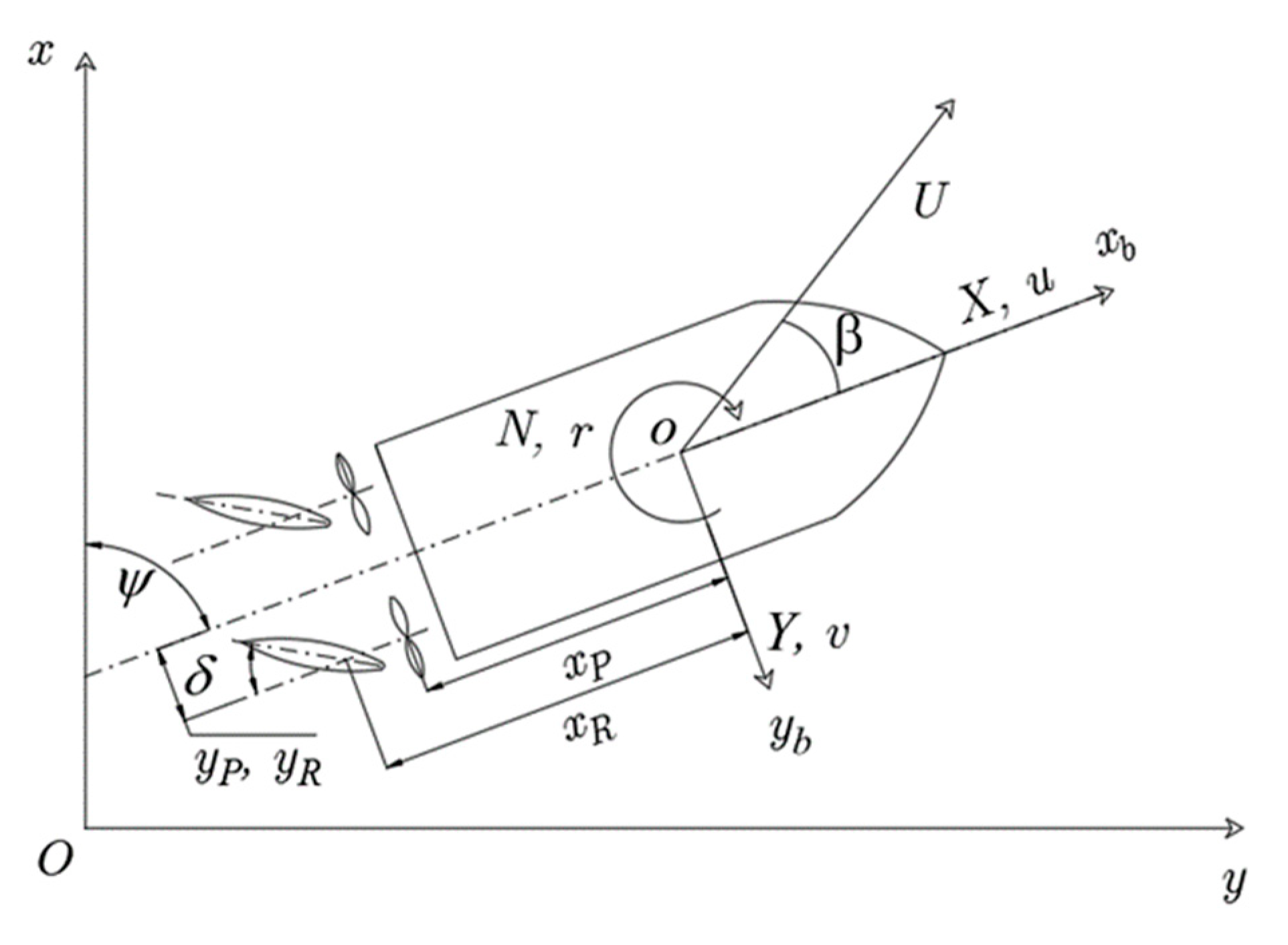
This paper focuses on the motions of USVs in horizontal planes only. Thus, two coordinate systems were defined for a maneuvering ship based on the right-hand rule, as shown in Figure 1. The earth-fixed coordinate system is , where the origin is located on the water surface and the body-fixed coordinate system is , where the origin is in the midship. The and axes point toward the ship’s bow and starboard, respectively. The heading angle represents the angle between the and axes.
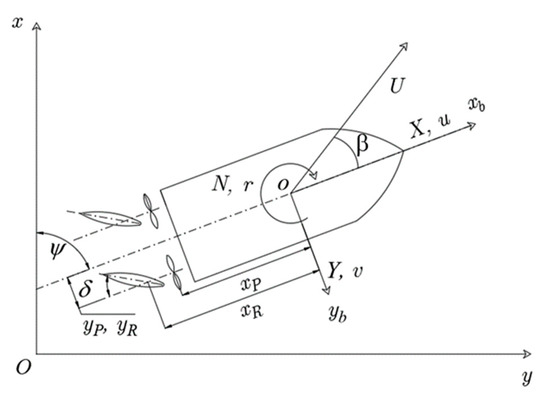
Figure 1.
Coordinate system of the twin-propeller and twin-rudder ship model.
2.2. Mathematical Model of USV
The motion equation with three degrees of freedom (3-DOF) is established based on Newton’s second law. In this paper, the berthing task assumed performing in the calm water, the disturbances from environments such as waves and wind in the port area are ignored due to the simplicity of the equation of motion. Thus, the heave, roll, and pitch motion are relatively small and not significantly affected in the equation of motion; thus, it can be neglected from the equation of motion. Furthermore, the low-speed condition made the 3-DOF motions sufficient to simulate the motion of the vehicle. Additionally, the main purpose of this paper is to focus on the path planning algorithm to generate the feasible path for the berthing task based on the maneuvering simulation. The application of the 3-DOF motion equations causes simplicity but retains characteristics of the system. The MMG model for the 3-DOF equation of motion suggested in [17] that the total ship force and moment can be divided into sub-components: the hull, thruster, and steering system. Thus, the 3-DOF motion equation is expressed as
where is the mass of the ship; is the longitudinal position of the center of gravity of the ship; denote the surge, sway, and yaw velocities, respectively; the symbol “” in the head of the variable denotes the derivative of the variable with respect to time; is the moment representing the mass moment of inertia with respect to the z-axis; , ,
and represent the surge force, lateral force, and yaw moments, respectively, at the midship; and the subscripts , , and denote the hull, rudder, and propeller, respectively.
Due to the operation conditions in the berthing phase, the hydrodynamic forces and moments around the midship acting on the ship hull were investigated at a low speed with a wide range of drift angles [2]. Thus, the equation of motion considers some of the high-order hydrodynamic coefficients and the hydrodynamic forces and moments caused by the hull, which are expressed as follows:
The hydrodynamic coefficients were described under the Taylor series expansion in terms of surge velocity, sway velocity, and yaw rate.
The ship model was equipped with twin-propeller and twin-rudder systems [18]. The thruster model is expressed as follows:
where is the propeller diameter; is the propeller revolutions per minute; denotes the thrust deduction factor; is the lateral position of the propeller from the centerline; and the superscripts and denote the side of the propeller (port and starboard).
The thrust coefficient is described as the function of the advanced ratio coefficient that was obtained through the propeller open water test
The parameter required for the estimation of thrust is given as
where the wake fraction at the propeller position was estimated using the wake fraction at the propeller in the straight motion ; the geometrical inflow angle to the propeller position is denoted by ; describe the wake-changing coefficients for plus and minus due to lateral motion; and denotes the longitudinal position from the midship.
Forces and moments due to the steering system for the twin rudder were calculated based on the normal force and are expressed as
where the normal force acting on the rudder is described as follows (Equation (7)).
The parameters required for estimating the rudder forces and moment during the maneuver are given as
where is the normal rudder force; , , and are the steering resistance deduction factor, the rudder increase factor, and the position of an additional lateral force component, respectively; is the resultant rudder inflow velocity; is the rudder lift gradient coefficient; is the rudder aspect ratio; is the effective inflow angle to the rudder; and are longitudinal and lateral inflow velocity components to the rudder; is a ratio of a wake fraction at the propeller and rudder position; is the flow straightening coefficient; and is the effective inflow angle to the rudder in the maneuvering motion.
2.3. Hydrodynamic and Interaction Coefficients
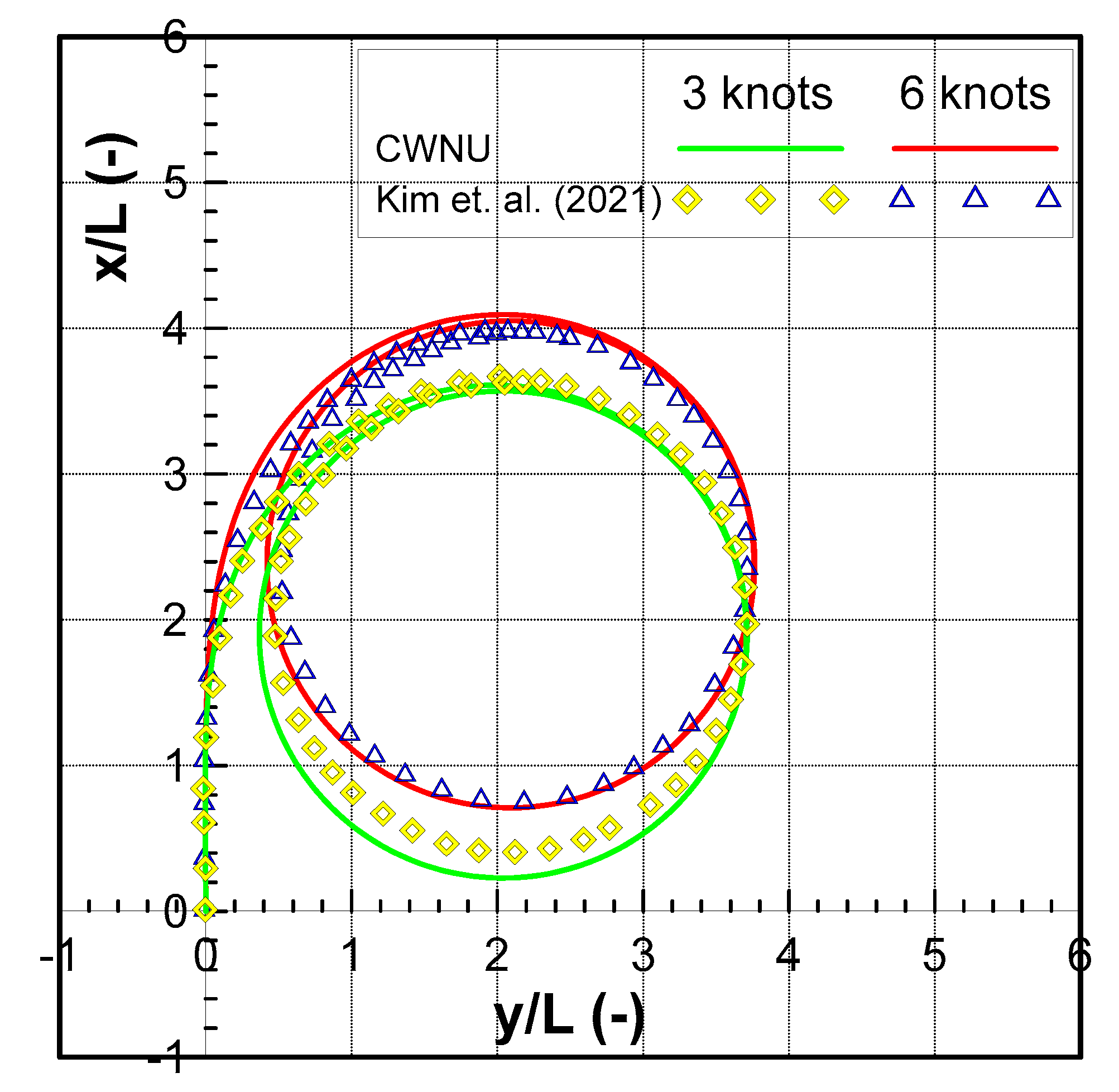
Previous studies were carried out by research groups at Changwon National University on hydrodynamic properties under operating conditions [19]. Experiments were conducted on the Korean autonomous surface ship (KASS) model, a ship model used in the project carried out by many universities and research institutes to develop autonomous ships. The main characteristics and the shape of the ship’s model are shown in Table 1 and Figure 2 The cross-comparison of the results between the previous studies and [20] shows similarities in the results. Figure 3 shows the comparison results of the turning maneuverability at a rudder angle of 35 degrees at three and six knots. Similarly, in order to obtain the feasible path for the automatic berthing task, the high-accuracy equation of motion and hydrodynamic coefficients of the USV should be investigated carefully using the Korean autonomous surface ship (KASS) model. In this paper, the hydrodynamic coefficients were estimated using the captive model test at Changwon National University and compared with the CFD method as presented in [21]. The coefficients relative to only the surge velocity were estimated through the resistance test. The hydrodynamic coefficients related to surge and sway velocity for forces and moments were estimated through a static drift test. The hydrodynamic coefficients related to the yaw rate were estimated using the circular motion test and the hydrodynamic coefficients related to the combined effect of sway velocity and yaw rate were estimated using the combined circular motion with drift test. The added mass and interaction coefficients were selected from [21]. The summary of hydrodynamics and interaction coefficients are shown in Table 2 and Table 3.

Table 1.
Principal dimensions.

Figure 2.
Geometry of an autonomous surface ship (KASS).
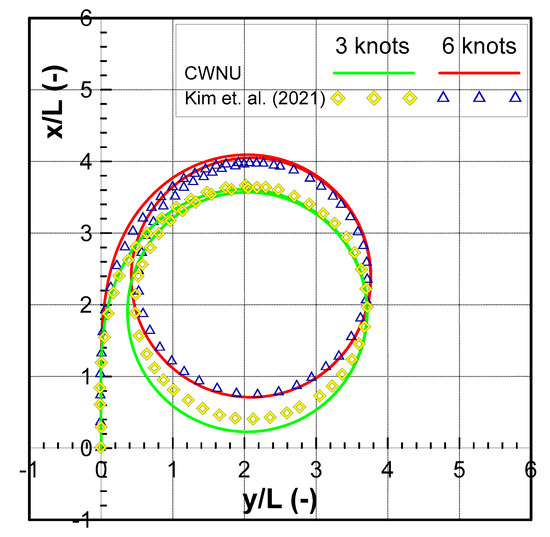
Figure 3.
Simulation results of turning trajectories at a rudder angle of 35 degrees at three and six knots [20].

Table 2.
Hydrodynamic force and moment coefficients.

Table 3.
Interaction coefficients.
2.4. Maneuverability
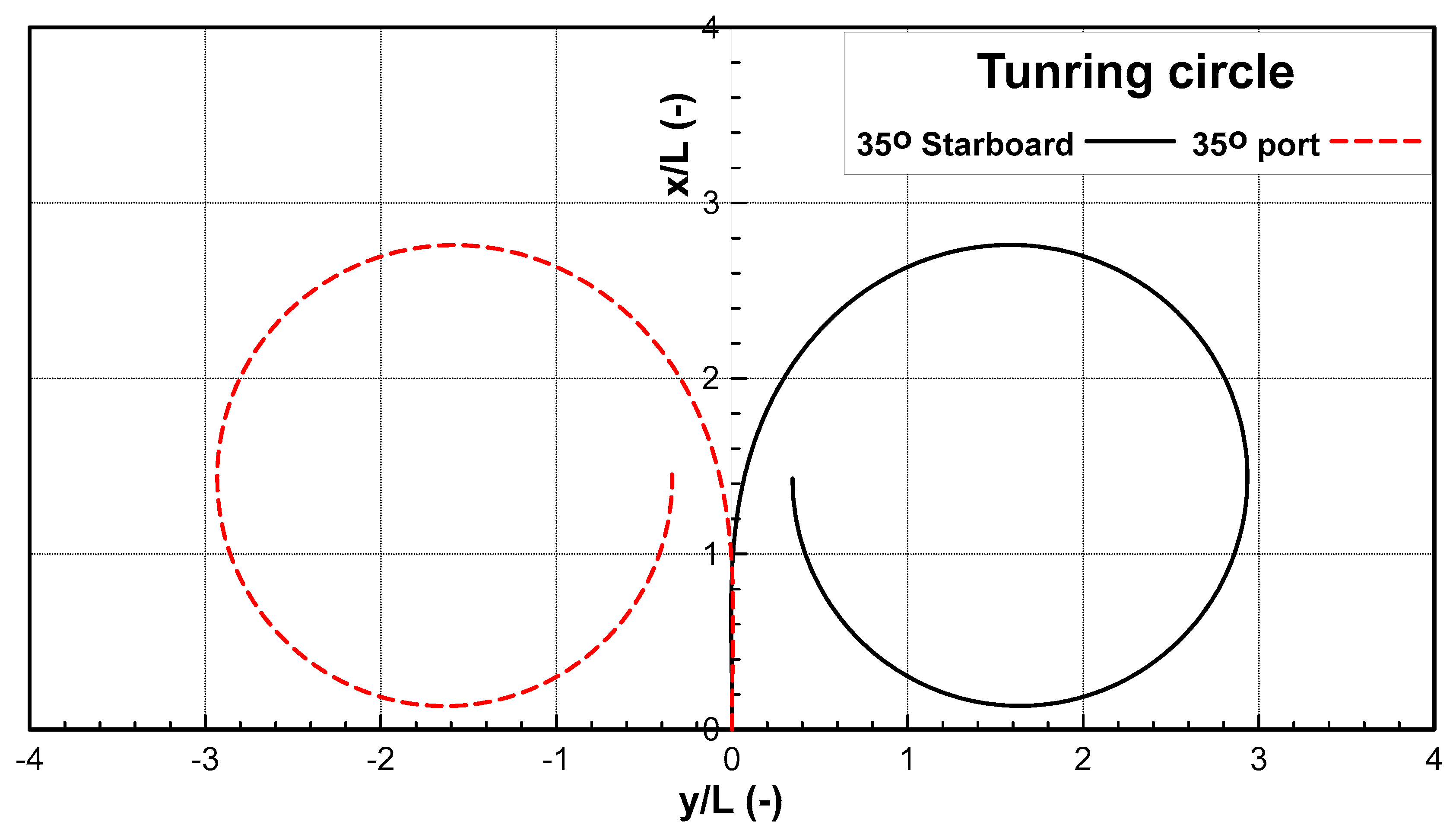
To define the problem, it is necessary to assess the maneuverability of the ship. Understanding the maneuverability makes it reasonable to determine where to start the automatic berthing process. The maneuvering simulation under low speed (1 knot) was conducted to investigate the ship-maneuvering characteristics in the port environment. Figure 4 shows the trajectory of the turning circle test at 35 degrees of a rudder angle at 1 knot. The simulation results show that this can easily turn into a range of approximately 3. Thus, the berthing area should be greater than three times that of from the berthing point. The maneuvering characteristics are shown in Table 4.
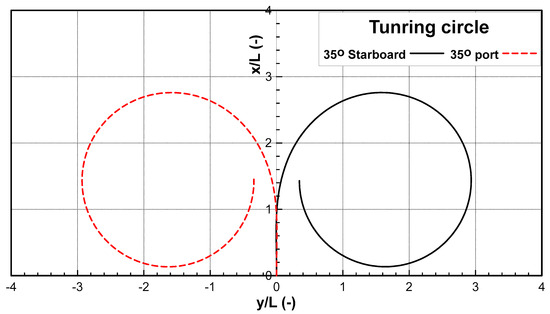
Figure 4.
Simulation results of turning trajectories at a rudder angle of 35 degrees.

Table 4.
Turning maneuverability characteristics.
3. Path-Planning Approach
In the last few decades, significant advancements have been made in the field of artificial intelligence, particularly reinforcement learning, a subfield of machine learning, which falls under the machine learning category. Reinforcement learning involves training data by assigning rewards and punishments based on behavior and state. Unlike supervised and semi-supervised learning, reinforcement learning does not rely on pairs of input data or true results and it does not explicitly evaluate near-optimal actions as true or false. As a result, reinforcement learning offers a solution to tackle complex problems, including the control of robots, self-driving cars, and even applications in the aerospace industry. A noteworthy advancement in reinforcement learning is the introduction of a twin delayed deep deterministic policy gradient in 2018. TD3 is an effective model-free policy reinforcement learning method. The TD3 agent is an actor–critic reinforcement learning agent that optimizes the expected long-term reward. Specifically, TD3 builds upon the success of the deep deterministic policy gradient algorithm developed in 2016. DDPG remains highly regarded and successful in the continuous action space, finding extensive applications in fields such as robotics and self-driving systems.
However, like many algorithms, DDPG has its limitations, including instability and the need for fine-tuning hyperparameters for each task. Estimation errors gradually accumulate during training, leading to suboptimal local states, overestimation, or severe forgetfulness on the part of the agent. To address these issues, TD3 was developed with a focus on reducing the overestimation bias prevalent in previous reinforcement learning algorithms. This is achieved through the incorporation of three key features:
- The utilization of twin critic networks, which work in pairs.
- Delayed updates of the actor.
- Action noise regularization.
By implementing these features, TD3 aims to enhance the stability and performance of reinforcement learning algorithms, ultimately improving their applicability in various domains.
3.1. Conception
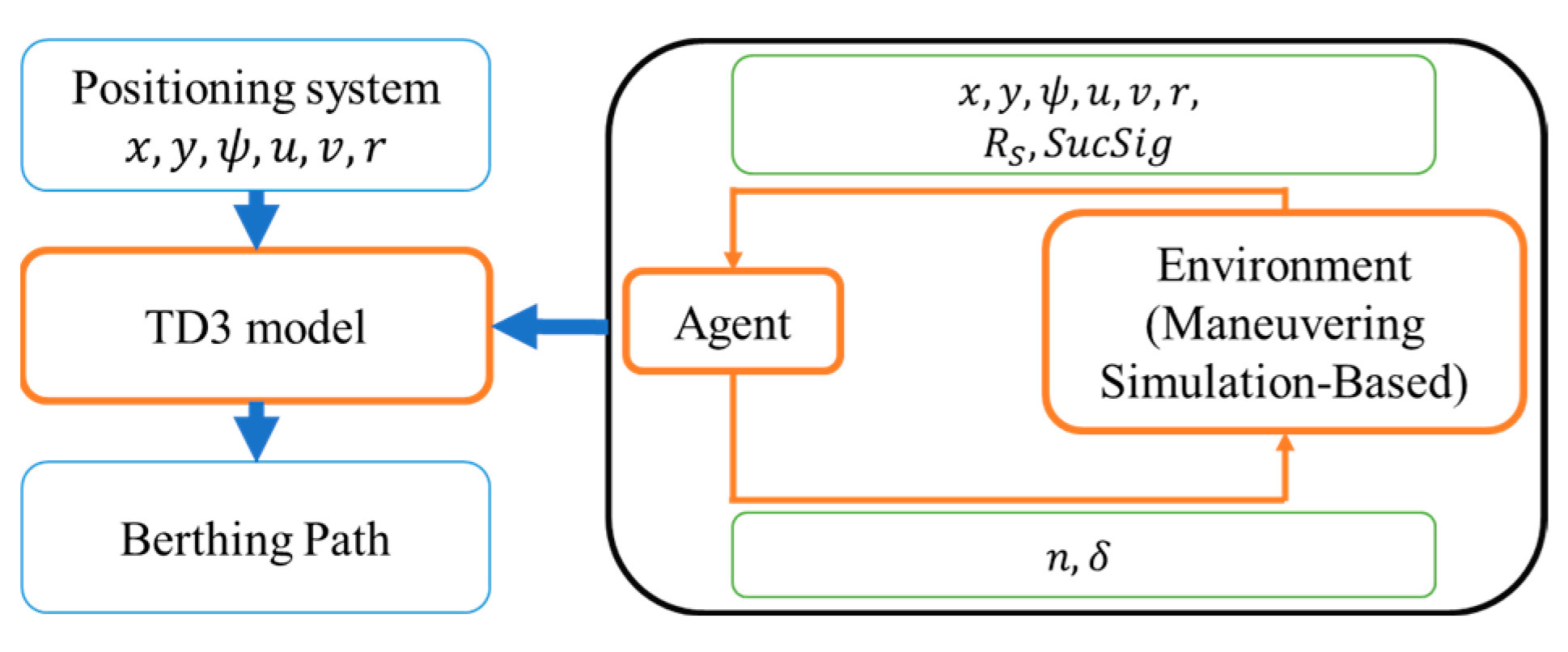
The path-planning algorithm in this paper was performed using the KASS model mentioned in Section 2.3. The port selected was the Busan port, whose geometry is shown in Figure 5. The objective of this result is to use the TD3 (the pseudocode as shown in Algorithm 1) for training the model that can generate the path for the berthing process. First, the TD3 algorithm trains the model with the combination of maneuvering simulations suggested by the MMG model. This approach allows for the integration of realistic ship motion dynamics into the training process. Then, this model is used to generate the desired path for the berthing task by inputting the state of the ship and predicting the control signal (propeller speed) and (rudder angle), based on the input ship state . The concept of path planning for automatic berthing tasks is shown in Figure 6.
| Algorithm 1: Pseudocode TD3 Algorithm | |
| 1 | Initialize the critic network and actor-network with random parameter |
| 2 | Initialize the target parameter to the main parameter |
| 3 | For to do: |
| 4 | Observe the state of the environment and choose the action |
| 5 | Execute action in the TD3 environment to observe the new state , reward , and done signal that gives the signal to stop training for this step. |
| 6 | Store training set in replay buffer D |
| 7 | If taking to the goal point, reset the environment state |
| 8 | If it is time for an update: For in range (custom decided) do: |
| 9 | Randomly sample a batch of transitions |
| 10 | Compute Target actions: |
| 11 | Compute targets: |
| 12 | Update Q-functions using gradient descent: |
| 13 | If mod policy delay == 0 then: Update policy by the one-step deterministic policy gradient ascent using |
| 14 | Update target networks: |
| 15 | End if End for End if End until convergence |
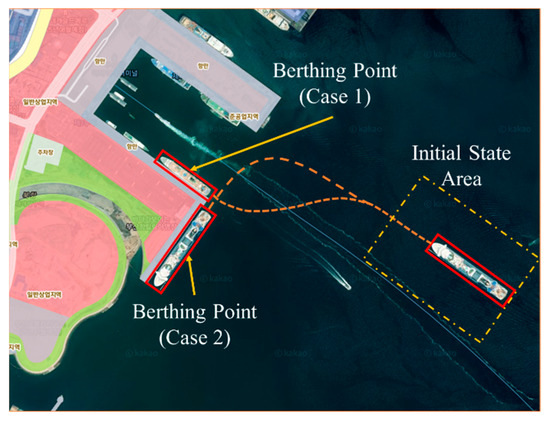
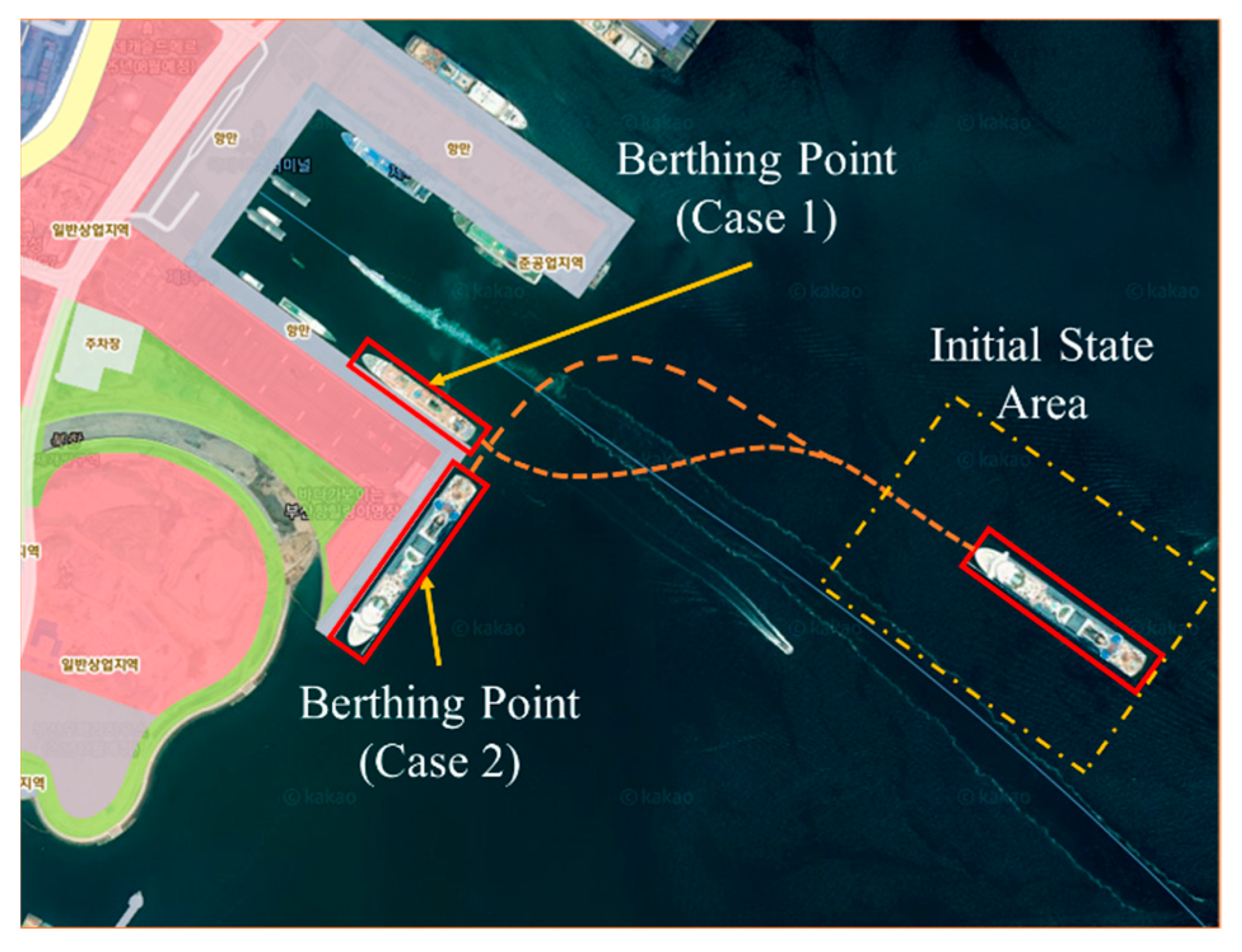
Figure 5.
Satellite image of the Busan port.

Figure 6.
Concept of the path-planning algorithm.
3.2. Setting for Reinforcement Learning
In this section, the parameters and variables for the TD3 algorithm to deal with the automatic berthing task were set as follows:
- Observation space and state: The observation space and state were defined as the set of physical velocity, position, and orientation. The state vector includes the position , as the element. The orientation is the heading angle. The linear velocity is , and the angular velocity is ;
- Action: The control action includes the control input of the thruster (revolution of propeller) and steering (rudder angle) system. The action signal is continuous in the range [−1, 1], where [−1, 1] = [−300, 100] rpm represents the thrust system and [−1, 1] where [−1, 1] = [−35, 35] is the degrees for the steering system.
- Reward function: This plays a crucial role in the design of a reinforcement learning application. It serves as a guide for the network training process and helps optimize the model’s performance throughout each episode. If the reward function does not accurately capture the objectives of the target task, the model may struggle to achieve desirable performance.
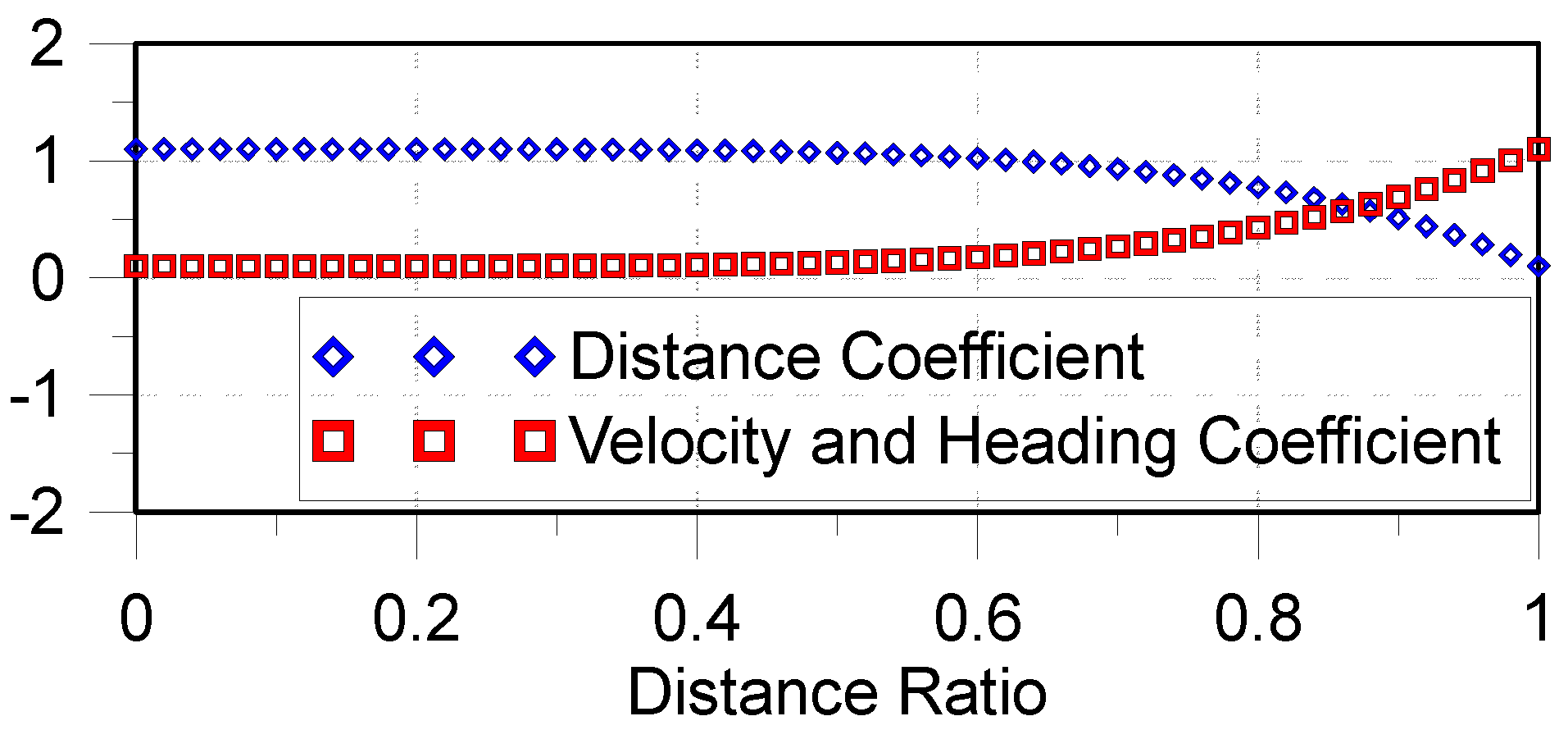
In this paper, based on the boundary state, the weights 100, 1000, 2000, and 1000 were assigned to the weight of distance, heading, linear, and angular velocity, respectively. The reward value was described as the sum of the reward in each time step. It received a positive value if the state variable changed to the required value and vice versa. Furthermore, for the faster convergence of rewards in the first stage of the berthing task, the distance is more prior to the target state than the speed and heading. Thus, the reward function of distance is multiplied by the distance coefficients. It is (1.1-Distance coefficients) in the case of the reward function of the heading, resultant velocity, and yaw rate. The reward coefficients are described in Figure 7.

Figure 7.
Reward coefficients.
- Environment: The environment receives the input as the control input and the state then returns the ship’s new state and the reward for this action. The environment function was built based on a maneuvering simulation that uses the MMG model as a mathematical simulation.
- Agent: The hyperparameters for the TD3 model were selected as follows: the number of hidden layers was set as two layers with 512 units for each. The learning rate for the actor and critic networks α and β was set to 0.0001. The discount factor was 0.99. The soft update coefficient was 0.005. The batch size was 128. This training process was set to 20,000/50,000 steps for the warmup of the model with the exploration noise set in Table 5.
 Table 5. Exploration rates.
Table 5. Exploration rates.
3.3. Boundary Conditions
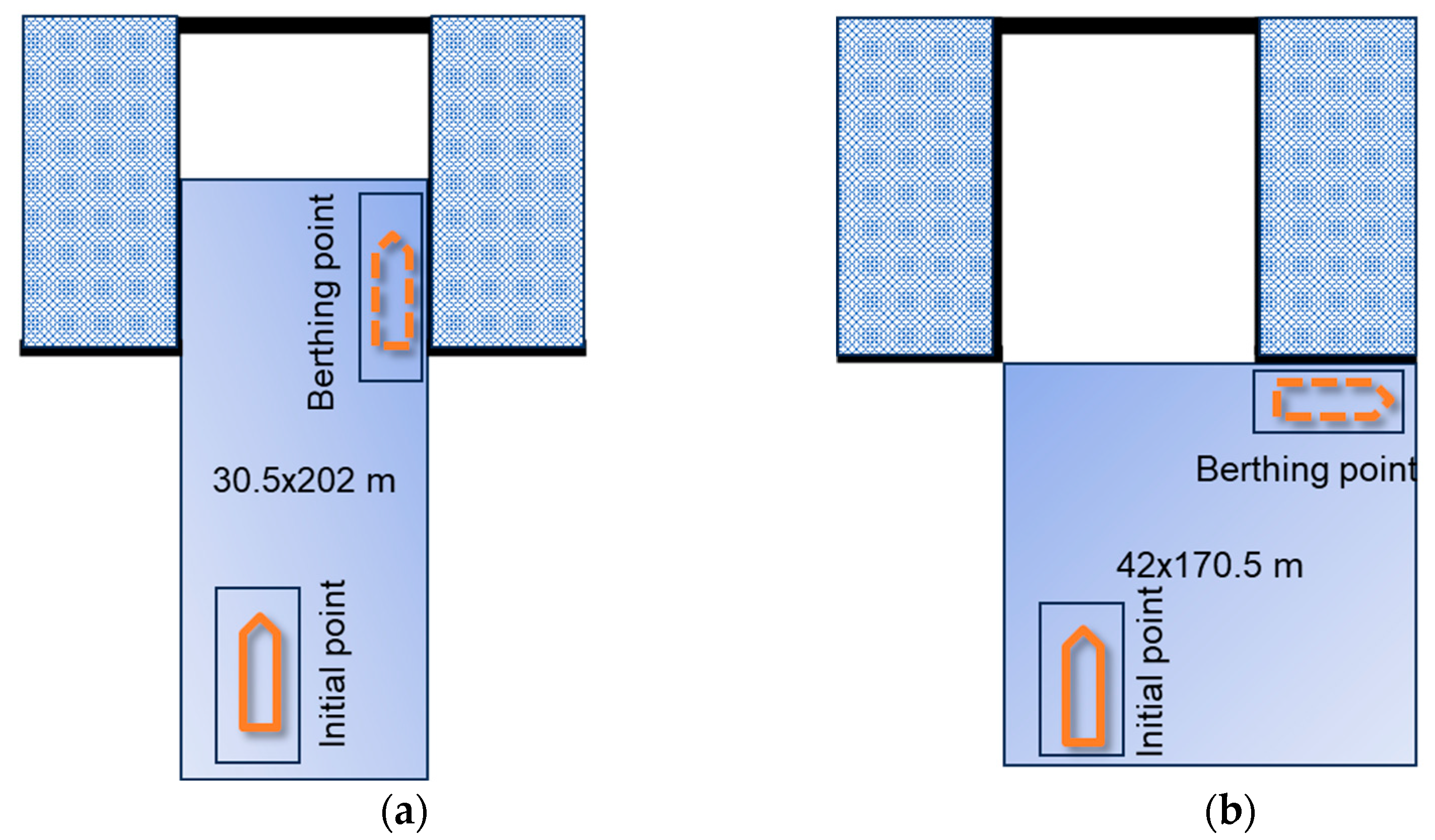
The simulations were performed at Busan port, with the satellite capture as in Figure 7. The geometry of this port was simplified as Figure 8. Considering the geometry of this port, two cases of berthing were selected to investigate the path-plan-generating system.

Figure 8.
Geometry of the port and berthing situation: (a) parallel berthing task (case 1) and (b) perpendicular berthing task (case 2).
Case 1: Parallel berthing task in a 30.5 × 202 m water area. In this case, the ship’s initial states were generated randomly, as described in Table 6. The berthing point was assumed, as shown in Table 7. The berthing task can be considered a success if the ship state is in the range of the values described in Table 7. The boundary area is described as a Figure 8a and Table 8.

Table 6.
Initial state values (case 1).

Table 7.
Target point (case 1).

Table 8.
Boundary values (case 1).
Case 2: Perpendicular berthing task in a 42 × 170.5 m water area. In this case, the ship’s initial states were generated randomly, as described in Table 9. The berthing point was assumed, as shown in Table 10. The berthing task can be considered a success if the ship state is in the range of the values described in Table 10. The boundary area is described as a Figure 8b and Table 11.

Table 9.
Initial state values (case 2).

Table 10.
Target point (case 2).

Table 11.
Boundary values (case 2).
4. Simulation Results and Discussion
The USV is considered to have successful berthing if it approaches the target berthing point with an error within the allowable range established in Section 3.3. The training process stops when the number of training episodes reaches 50,000.
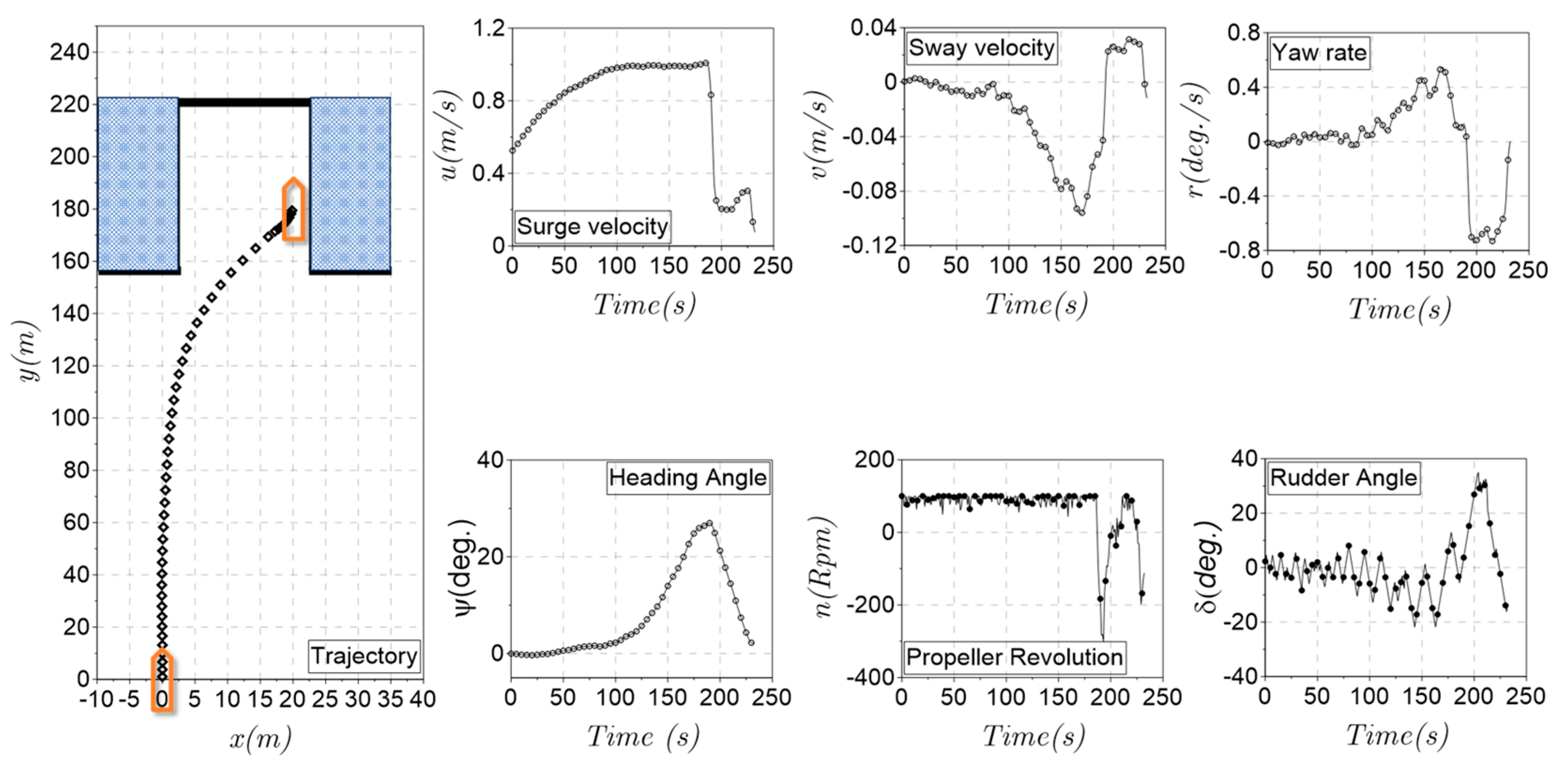
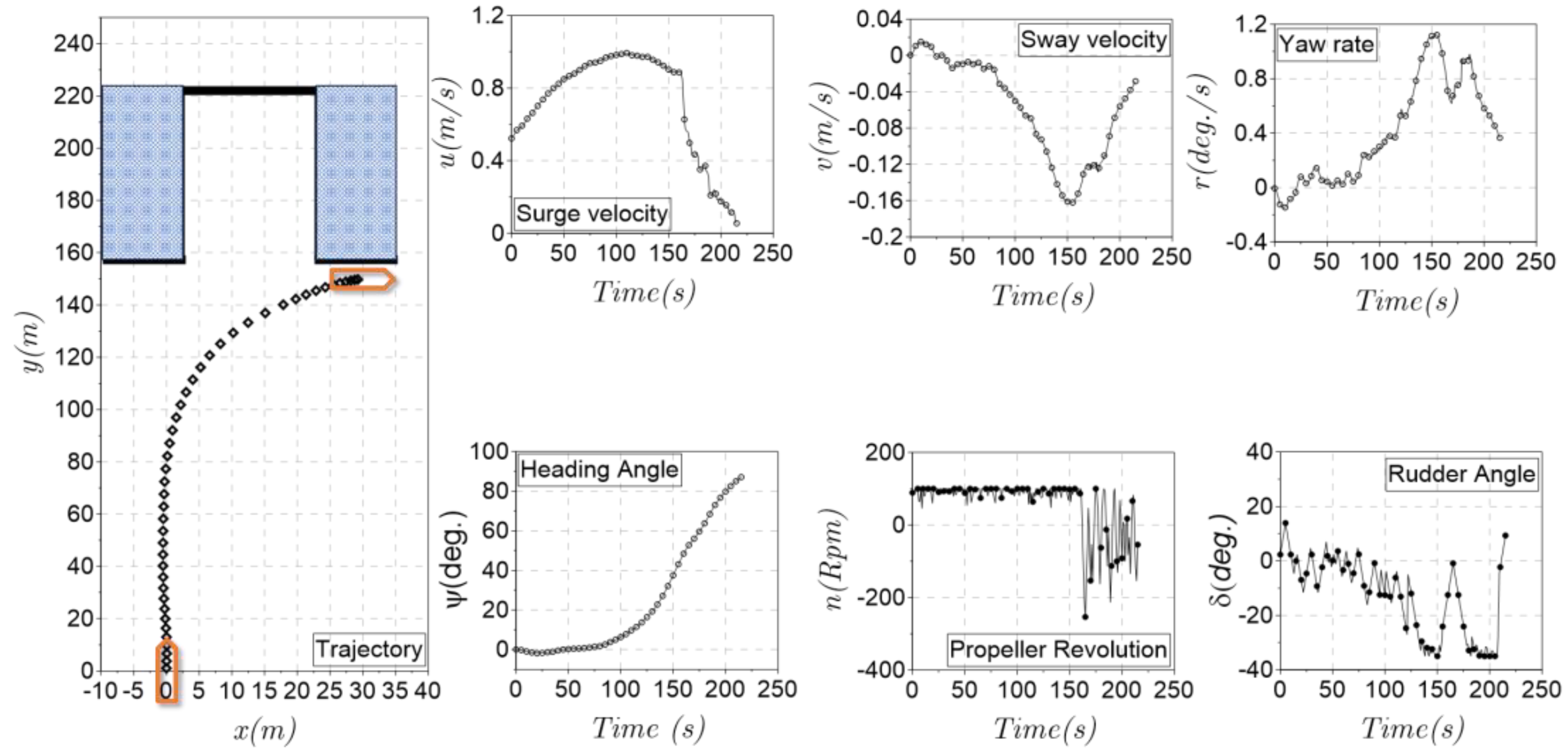
Figure 9 and Figure 10 sequentially present a set of information that includes the trajectory, surge, sway, yaw rate, heading angle, and control input as the propeller revolution and rudder angle. The USV starts from the random state shown in Section 3.3. Under the automatic control of the TD3 model, the ship has successfully berthed at the target location. The ship states gradually change from the initial state to the required range. In particular, the combination with the adjusted reward function made the ship berthing process happen faster and more optimally. The time series of surge velocity was shown in the first phase of the berthing process. The ship’s speed was increased to reduce the distance to the berthing point. However, the sway velocity and yaw rate did not change much in this phase. In the last phase of the berthing process, the importance of surge velocity, yaw rate, and heading angle is much more important than the distance in the first phase. So, the change in this value seems more sudden to adapt to the required value of the berthing process.
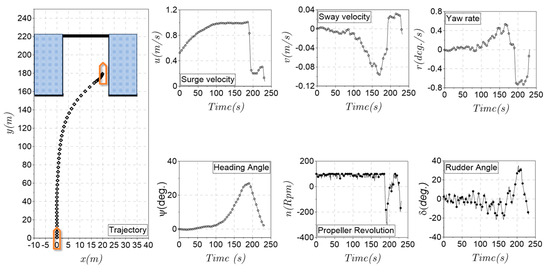
Figure 9.
Simulation results in a parallel berthing task (case 1).
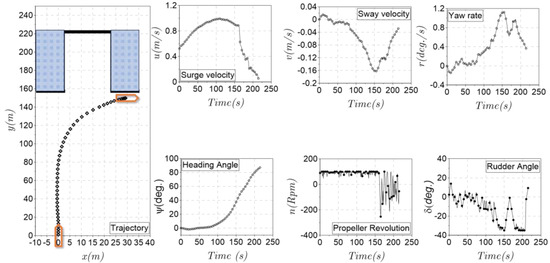
Figure 10.
Simulation results in the perpendicular berthing task (case 2).
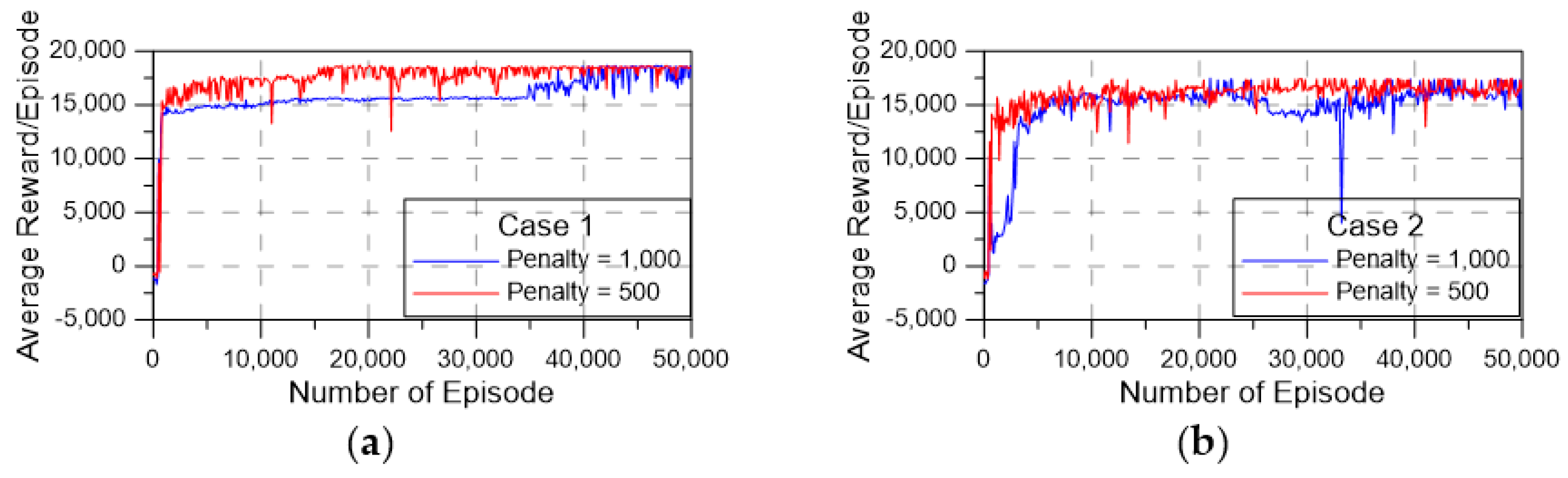
Figure 11a,b shows the learning performance of TD3 case 1 with 50,000 episodes. Although the warmup episode number is 20,000, the average reward shows that the model seems to be successfully berthing and stable before the warmup phase is finished. This demonstrates that TD3 provides good reinforcement learning for the automatic berthing process. To account for the difference in penalty values affecting the training process, too high a penalty will cause the model to misjudge the states, for instance, in cases where the vessel has moved reasonably close to the berthing position. However, it then collides with the wall and receives a heavy point deduction, causing the model to judge that process as wrong and try actions other than that process. This makes the training process longer. These results show that the method proposed in this paper has a high performance and success rate with a low penalty value.
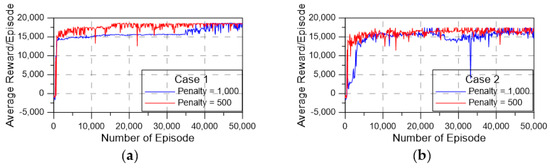
Figure 11.
Learning performance of TD3: (a) parallel berthing (case 1) and (b) perpendicular berthing task (case 2).
The simulation results show that the combination of TD3 and the maneuvering simulation proposes a powerful and accurate system for the automatic berthing process. Comparing the shape of the average reward to the results shown in [15] demonstrates that the stability of the TD3 algorithm is better than the older algorithm in the field of reinforcement learning. In particular, the method proposed in this paper is easier to apply because of the ability to learn, explore, and optimize the policy automatically. It can be used for another ship model if we know the ship’s hydrodynamic characteristics.
However, the limitations in this paper are evident. Firstly, the simplification of the port condition: due to the simplicity of the model, the effect of the disturbance was ignored in the simulation. This causes non-accuracy if there is wind or waves. The second limitation of this approach is the simplification of the obstacles and port geometry. It has a significant effect on the determination of the initial state and the berthing point. The presence of moving obstacles can make the training time increase significantly. So, the method proposed in this paper should only be used in the determined port and not for moving obstacles. Finally, this paper proposed the initial development of the path planning system. The results are performed based on maneuver simulation. The accuracy and performance of this approach in real-world operations need to be carefully considered and evaluated.
Although the approach in this paper uses the newest technique in reinforcement learning at present, the performance of this method should be investigated and compared carefully.
5. Conclusions and Remarks
In this study, the Korea autonomous surface ship (KASS) model was selected as the target ship to perform the training for path planning for the autonomous berthing task. A mathematical model and the hydrodynamics coefficients suggested in previous research conducted at Changwon National University provided an accurate model for solving the motion of a slow ship. By performing the path-planning algorithm based on the combination of TD3 and a maneuvering simulation, the automatic berthing task could be conducted with the automatic berthing problem and stable performance using reinforcement learning.
Even though the high performance of the path-planning system was shown, the complex environmental disturbance in the port area needs to be included in the model. It takes more time to train the model but is a necessary factor in the real situation. Additionally, several algorithms based on control theory must be considered for faster convergence.
Author Contributions
Conceptualization, H.K.Y. and A.K.V.; methodology, H.K.Y., A.K.V. and T.L.M.; software, A.K.V.; validation, A.K.V. and T.L.M.; formal analysis, A.K.V. and T.L.M.; investigation, A.K.V. and T.L.M.; resources, T.L.M.; data curation, A.K.V. and T.L.M.; writing—original draft preparation, A.K.V.; writing—review and editing, H.K.Y. and T.L.M.; visualization, A.K.V.; supervision, H.K.Y.; project administration, H.K.Y.; funding acquisition, H.K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Development of Autonomous Ship Technology (PJT201313, Development of Autonomous Navigation System with Intelligent Route Planning Function), funded by the Ministry of Oceans and Fisheries (MOF, Korea).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in this article (Tables and Figures).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Item | Unit | |
| - | Effective inflow angle to the rudder | |
| Drift angle of the ship | ||
| Inflow angle to the propeller | ||
| Inflow angle to the rudder | ||
| - | Flow straightening coefficient of the rudder | |
| Rudder angle | ||
| - | Propeller diameter to the rudder span ratio | |
| - | Rudder aspect ratio | |
| - | The experimental coefficient for longitudinal inflow velocity to the rudder | |
| Displacement of the ship | ||
| Heading angle of the ship | ||
| Water density | ||
| - | Ratio of the wake fraction at the propeller to the rudder | |
| Rudder profile area | ||
| - | Increase factor of the rudder force | |
| Breadth of ship | ||
| Average rudder chord length | ||
| - | Experimental constant due to wake characteristic in maneuvering | |
| Diameter of propeller | ||
| Draft of ship | ||
| Normal force of the rudder | ||
| Surge and sway force acting on the ship | ||
| - | Lift gradient coefficients of the rudder | |
| Span of rudder | ||
| Moment of inertial of ship | ||
| - | Advanced ratio of propeller | |
| - | Propeller thrust open water characteristic | |
| - | Coefficients relative to | |
| Ship length between two perpendicular | ||
| Effective longitudinal length of the rudder position | ||
| Yaw moment acting on the ship | ||
| Ship mass | ||
| Propeller revolutions per minute (rpm) | ||
| - | Earth-fixed coordinate system | |
| - | Body-fixed coordinate system | |
| - | Resistance of the ship in straight motion (-) | |
| Yaw rate | ||
| Reward | ||
| Longitudinal propeller force | ||
| Time | ||
| - | Thrust deduction factor | |
| - | Steering deduction factor | |
| Resultant velocity | ||
| Initial resultant velocity | ||
| Resultant inflow velocity to the rudder | ||
| Longitudinal and lateral velocity of the ship in the body-fixed coordinate system | ||
| Longitudinal and lateral inflow velocity to rudder position | ||
| - | Wake coefficient at the propeller in maneuvering motion | |
| - | Wake coefficient at the propeller at straight motion | |
| - | Wake coefficient at the rudder position | |
| Surge, sway force, and yaw moment around the midship | ||
| Surge, sway force, and yaw moment acting on ship’s Hull | ||
| Surge, sway force, and yaw moment due to the propeller | ||
| Surge, sway force, and yaw moment due to the rudder | ||
| Longitudinal position of the center of gravity | ||
| Longitudinal position of the acting point of addition lateral force | ||
| Longitudinal position of the propeller | ||
| Longitudinal position of the rudder |
Abbreviations
| Item | |
| AI | Artificial Intelligence |
| CFD | Computational Fluid Dynamics |
| DDPG | Deep Deterministic Policy Gradients |
| DRL | Deep Reinforcement Learning |
| MMG | Maneuvering Modeling Group |
| RL | Reinforcement Learning |
| TD3 | Twin Delayed DDPG (a variant of the DDPG algorithm) |
| USV | Unmanned Surface Vehicle |
References
- Chaal, M.; Ren, X.; BahooToroody, A.; Basnet, S.; Bolbot, V.; Banda, O.A.V.; van Gelder, P. Research on risk, safety, and reliability of autonomous ships: A bibliometric review. In Safety Science (Vol. 167); Elsevier B.V.: Amsterdam, The Netherlands, 2023. [Google Scholar] [CrossRef]
- Oh, K.G.; Hasegawa, K. Low speed ship manoeuvrability: Mathematical model and its simulation. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Nantes, France, 9–14 June 2013; p. 9. [Google Scholar] [CrossRef]
- Shouji, K. An Automatic Berthing Study by Optimal Control Techniques. IFAC Proc. Vol. 1992, 25, 185–194. [Google Scholar] [CrossRef]
- Skjåstad, K.G.; Barisic, M. Automated Berthing (Parking) of Autonomous Ships. Ph.D. Thesis, NTNU, Trondheim, Norway, 2018. [Google Scholar]
- Mizuno, N.; Uchida, Y.; Okazaki, T. Quasi real-time optimal control scheme for automatic berthing. IFAC-Pap. 2015, 28, 305–312. [Google Scholar] [CrossRef]
- Nguyen, V.S.; Im, N.K. Automatic ship berthing based on fuzzy logic. Int. J. Fuzzy Log. Intell. Syst. 2019, 19, 163–171. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.; Zhang, Q. Auto-berthing control of marine surface vehicle based on concise backstepping. IEEE Access 2020, 8, 197059–197067. [Google Scholar] [CrossRef]
- Sawada, R.; Hirata, K.; Kitagawa, Y.; Saito, E.; Ueno, M.; Tanizawa, K.; Fukuto, J. Path following algorithm application to automatic berthing control. J. Mar. Sci. Technol. 2021, 26, 541–554. [Google Scholar] [CrossRef]
- Wu, G.; Zhao, M.; Cong, Y.; Hu, Z.; Li, G. Algorithm of berthing and maneuvering for catamaran unmanned surface vehicle based on ship maneuverability. J. Mar. Sci. Eng. 2021, 9, 289. [Google Scholar] [CrossRef]
- Im, N.; Seong Keon, L.; Hyung Do, B. An Application of ANN to Automatic Ship Berthing Using Selective Controller. Int. J. Mar. Navig. Saf. Sea Transp. 2007, 1, 101–105. [Google Scholar]
- Ahmed, Y.A.; Hasegawa, K. Automatic ship berthing using artificial neural network trained by consistent teaching data using nonlinear programming method. Eng. Appl. Artif. Intell. 2013, 26, 2287–2304. [Google Scholar] [CrossRef]
- Im, N.; Hasegawa, K. Automatic ship berthing using parallel neural controller. IFAC Proc. Vol. 2001, 34, 51–57. [Google Scholar] [CrossRef]
- Im, N.K.; Nguyen, V.S. Artificial neural network controller for automatic ship berthing using head-up coordinate system. Int. J. Nav. Archit. Ocean. Eng. 2018, 10, 235–249. [Google Scholar] [CrossRef]
- Marcelo, J.; Figureueiredo, P.; Pereira, R.; Rejaili, A. Deep Reinforcement Learning Algorithms for Ship Navigation in Restricted Waters. Mecatrone 2018, 3, 151953. [Google Scholar] [CrossRef]
- Lee, D. Reinforcement Learning-Based Automatic Berthing System. arXiv 2021, arXiv:2112.01879. [Google Scholar]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. Int. Conf. Mach. Learn. 2018, 80, 1587–1596. [Google Scholar]
- Yasukawa, H.; Yoshimura, Y. Introduction of MMG Standard Method for Ship Maneuvering Predictions. J. Mar. Sci. Technol. 2015, 20, 37–52. [Google Scholar] [CrossRef]
- Khanfir, S.; Hasegawa, K.; Nagarajan, V.; Shouji, K.; Lee, S.K. Manoeuvring characteristics of twin-rudder systems: Rudder-hull interaction effect on the manoeuvrability of twin-rudder ships. J. Mar. Sci. Technol. 2011, 16, 472–490. [Google Scholar] [CrossRef]
- Vo, A.K.; Mai, T.L.; Jeon, M.; Yoon, H.k. Experimental Investigation of the Hydrodynamic Characteristics of a Ship due to Bank Effect. Port. Res. 2022, 46, 294–301. [Google Scholar] [CrossRef]
- Kim, D.J.; Choi, H.; Kim, Y.G.; Yeo, D.J. Mathematical Model for Harbour Manoeuvres of Korea Autonomous Surface Ship (KASS) Based on Captive Model Tests. In Proceedings of the Conference of Korean Association of Ocean Science and Technology Societies, Incheon, Republic of Korea, 13–14 May 2021. [Google Scholar]
- Vo, A.K. Application of Deep Reinforcement Learning on Ship’s Autonomous Berthing Based on Maneuvering Simulation. Ph.D. Thesis, Changwon National University, Changwon, Republic of Korea, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).