Abstract
Blasting is routinely carried out in urban quarry sites. Residents or houses around quarry sites are affected by the ground vibrations induced by blasting. Peak Particle Velocity (PPV) is used as a metric to measure ground vibration intensity. Therefore, many prediction models of PPV using experimental methods, statistical methods, and Artificial Neural Networks (ANNs) have been proposed to mitigate this effect. However, prediction models using experimental and statistical methods have a tendency of poor prediction accuracy. In addition, while prediction models using ANNs can produce a highly accurate prediction results, a large amount of measured data is necessarily collected. In an urban quarry site where the number of blastings is limited, it is difficult to collect a lot of measured data. In this study, a new PPV prediction method using Weighted Non-negative Matrix Factorization (WNMF) is proposed. WNMF is a method that approximates a non-negative matrix (including missing data) to the product of two low-dimensional matrices and predicts the missing data. In addition, WNMF is one of the unsupervised learning methods, so it can predict PPV regardless of the amount of data. In this study, PPV was predicted using measured data from 100 sites at the Mikurahana quarry site in Japan. As a result, the proposed method showed higher accuracy when using measured data at 60 sites rather than 100 sites, and the root mean square error for PPV prediction decreased from 0.1759 (100 points) to 0.1378 (60 points).
1. Introduction
In recent years, blast-induced ground vibrations from quarrying activities and their impact on structures and human beings have attracted significant attention in scientific and industrial communities. Researchers like Khandelwal and Singh have demonstrated through their studies the relationship between blast parameters and resulting ground vibrations [1,2,3]. These vibrations can potentially harm structures, especially if they are close to the blasting sites. Other researchers such as Faramarzi et al. and Navarro Torres et al. also contributed to this field of study by investigating the simultaneous effects of ground vibration and air blasts [4,5].
The prediction and control of ground vibrations induced by blasting have been extensively researched. Singh and Roy provided insights into the damage to surface structures due to these vibrations [6]. Artificial Neural Network approaches, as proposed by Khandelwal and Singh, have been employed for the prediction of these vibrations [1,3]. This method of prediction was further expanded by other researchers such as Monjezi et al., Hajihassani et al., and Saadat et al. [7,8,9].
Apart from neural network methods, multivariate analysis, as applied by Hudaverdi, has also been employed for the prediction of blast-induced ground vibrations [10]. Moreover, Australian and British standards provide guidelines related to the use of explosives and evaluation of human exposure to vibrations, respectively [11,12]. The studies by authors like Nicholls et al., Siskind et al., and Dowding offer in-depth knowledge on blasting vibrations and their effects on structures [13,14,15].
Historical perspectives on the topic have been provided by Duvall and Petkof and Langefors and Kihlström [16,17]. In addition, some research works like those by Roy and Kamali have proposed other models to predict vibrations [18,19]. With the rise in the relevance of technology, web-based visualization systems for predicting ground vibrations, as suggested by Kawamura et al., are gaining traction [20].
Recommendation systems using techniques like matrix factorization have also found application in this domain [21,22,23]. The critical essence is to find a balance between efficient blasting and minimizing the adverse impacts on the surroundings.
2. Related Work
2.1. Ground Vibrations from Blasting
In opencast mining, predicting blast-induced ground vibrations and their frequencies is essential for the safety of nearby structures and inhabitants. Researchers have employed various techniques to predict and control these vibrations, including neural network approaches which have shown promising results [1,2,3,4,24]. Various factors influence the intensity and frequency of ground vibrations, including the explosive type, blasting method, blast-to-structure distance, and the rock and soil’s geological properties. Studies over the years have provided insights into the impact of blasting on surrounding structures [6,13,14,15,25] and informed guidelines for explosive use and human vibration exposure in buildings [11,12]. Understanding explosion-generated strain pulses in rock is also crucial [16,17]. Previous work has emphasized the importance of controlling vibration in mines using advanced predictors [18]. Multivariate analysis for predicting blast-induced ground vibrations has also been explored [10]. In the domain of recommendation systems, matrix factorization techniques have been foundational. Koren et al. provided an overview of these techniques for recommender systems [21]. GroupLens introduced an architecture for collaborative netnews filtering [22], and Squires et al. investigated rank selection in non-negative matrix factorization [23]. For urban planning, visualizing predicted ground vibration is essential, and Web-GIS systems have been developed to aid this [20].
2.2. Traditional PPV Prediction Methods
Ground vibrations originating from blasts are usually recorded as Peak Particle Velocity (PPV). Given its correlation with the extent of potential structural damages, PPV has been deemed to be a crucial metric, especially in environmental considerations within the realm of resource development [6,11,12,14]. Over time, various methods have been devised to predict PPV. These methods can be broadly classified into experimental methods, statistical methods, and Artificial Neural Networks (ANNs). The most basic approach is the experimental method, which has been extensively employed by many researchers [13,14,16,17,18]. The PPV prediction model using this method can be expressed as
where V is the PPV (mm/s), D is the scaled distance (m/), and k, b are constants determined based on the specific site conditions. The scaled distance, D, is given by
where R represents the distance from the blasting site (m) and Q denotes the square root of the amount of explosive (kg). However, given the vast number of parameters involved in real-world blasting-induced ground vibrations, the experimental method shows limitations in its accuracy [2,20,24].
To overcome the limitations of experimental methods, statistical methods were introduced. These take into account a wide array of parameters, from the design of the blasts to the nature of the rock mass [10,19,26]. However, their predictive accuracy can be diminished when applied to new locations since they primarily rely on existing datasets [1,3,7].
Emerging from the domain of artificial intelligence (AI) during the 1980s, ANN enabled massive parallel computations, mimicking the human brain’s functionality. Khandelwal et al. [1] proposed an ANN-based PPV prediction model using data from 150 blasting sites, illustrating its superior predictive accuracy over traditional experimental methods. Monjezi et al. [7] and Dehghani et al. [27] also demonstrated high accuracy with ANN-based models. Recent innovations even incorporated advanced algorithms like particle swarm optimization (PSO) and the imperialism competitive algorithm (ICA) in PPV predictions [8,28]. Notably, a compilation of research on ANN-based PPV predictions can be seen in Table 1 [2,3,7,8,9,27,28,29]. However, the major challenge with ANN methods is the requirement for extensive datasets to build high-accuracy models. Urban quarries, due to their proximity to populated areas, face data collection challenges due to the limited opportunities for blasting.

Table 1.
Study on PPV prediction using ANN.
3. Target Site and Data Used
3.1. Target Site
In this study, we focused on the Mikurahana gravel pit operated by Toseki Material Co., Ltd., located in Akita, Japan. The primary objective was to predict the ground vibrations caused by blasting in this area. The Mikurahana gravel pit is an open-pit mine that employs the bench cut method. The primary rock type in this area is rhyolitic andesite. This rock formation significantly influences the blasting dynamics due to its specific lithological and geotechnical properties. The gravel pit has a production capacity of approximately 2000 t/day.
The lithological units at the site consist mainly of rhyolitic andesite, characterized by its high silica content and physical hardness. The geotechnical properties of this rock type, including its density, porosity, and fracture patterns, play a crucial role in determining the blast design and the resulting ground vibrations. These properties were carefully analyzed to optimize the blasting process and mitigate adverse effects on the surrounding environment.
The geographical relationship between the Mikurahana gravel pit and the surrounding area is illustrated in Figure 1. From Figure 1, it is evident that there are settlements and roads in the immediate vicinity of the gravel pit. The Mikurahana gravel pit conducts up to two blasts daily, making the surrounding areas susceptible to the effects of ground vibrations from these blasts.
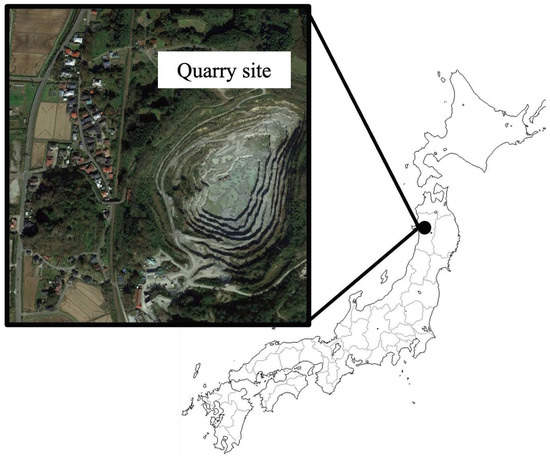
Figure 1.
Mikurahana quarry site.
A schematic of the blasting design at the Mikurahana gravel pit is shown in Figure 2. The scale of blasting is relatively small compared to overseas standards, with approximately 125 kg of explosives used for a single blast and a bench height of 10 m. The hole spacing is around 2–2.4 m, with blast hole lengths ranging from 9 to 9.5 m. Explosive materials such as ANFO, water gel explosives, and electric detonators are employed. The design includes five vertical holes and several horizontal holes, with a blasting interval of 25 mm/s. The corresponding vertical and horizontal holes are detonated simultaneously. From the obtained blast design information, geographical conditions during ground vibration measurements, and parameter values such as Peak Particle Velocity (PPV), we created a measurement data matrix to analyze the impact of these blasts.
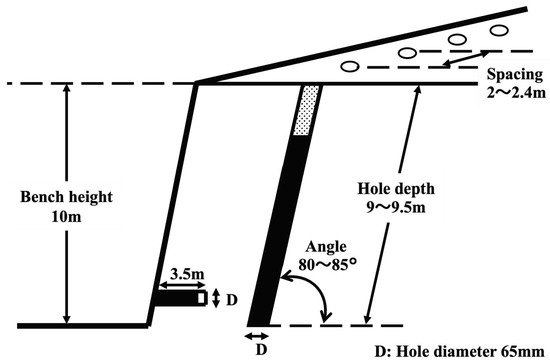
Figure 2.
Blast design at target site.
3.2. Data
Table 2 presents the types of data used for the measurement data matrix. In addition to the PPV, the parameters include the maximum instantaneous charge (MIC), which indicates the amount of explosive that detonates within 8 mm/s; the distance from the blasting point to the measurement point; the elevation difference between the blasting and measurement points; the direction, which denotes the angle of the line drawn between the blasting and measurement points; and the latitude and longitude of both the blasting and measurement points, totaling nine parameters. All these data were collected at 100 points around the Mikuranoseki quarry. Based on these data, we utilized a measurement data matrix (100 rows × 9 columns), where the rows represent measurement points and the columns represent the parameters.

Table 2.
Data used in the measurement data matrix.
4. Measurement of PPV
4.1. Collection of Ground Vibration Data
In this section, we discuss the method of collecting ground vibration data. To measure the ground vibrations caused by blasting, devices were placed in contact with the ground. Figure 3 shows a schematic of the experimental setup. The instruments for measuring ground vibrations due to blasting include the three-axis micro vibration detector MODEL-2205B (dimensions: 150 mm × 100 mm × 80 mm) by Showa Measuring Instruments Co. Tokyo, Japan) and accelerometers 608T No.E189, 608T No.E190 (dimensions: 13.8 mm × H 25 mm, resonance frequency: 30 kHz), 708LF C516, 708LF C518 (dimensions: 13.8 mm × H 28 mm, resonance frequency: 50 kHz) by Teac Corporation Tokyo, Japan). Although only one Teac accelerometer is illustrated in Figure 3, two–four accelerometers were used during measurements to increase measurement points. The amplifier used was Teac’s SA-611 CHARGE AMPLIFIER and the data logger used was the DM3100 by GRAPHTEC (Yokohama, Japan). The OPS021 application by the same company was used to set the measurement conditions. Using these devices, ground vibrations due to blasting were measured. When using the data logger outdoors, the engine was turned off and the ACC power source was used to eliminate the effects of vibrations from vehicles.
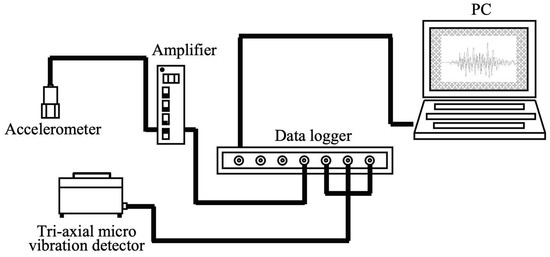
Figure 3.
Schematic diagram of experimental devices.
Figure 4a shows the ground vibration data measurement points used in this study. The map is cited from Google Maps. For the collection of ground vibration data, the measuring devices shown in Figure 4a were installed at about 50 points located around the marked quarry. Although the map indicates approximately 50 measurement points, in reality, multiple accelerometers were used at the same location, resulting in data from 100 measurement points. Typically, ground vibrations due to blasting decrease as the distance from the blasting point increases. Therefore, it is essential to set the measuring devices in advance to avoid measurement failures. The OPS021 settings used for data collection can be broadly categorized into amplifier settings, trigger settings, and memory settings. Figure 4b–d show the settings screens for the amplifier, memory, and trigger, respectively. In the amplifier settings (Figure 4b), one can set the name, input, range, and filter for each channel (CH). The name can be set freely for each CH. For the input, one can choose between DC and AC, with AC being chosen for this data collection. The accelerometers used in this experiment output vibration values in volts (V or mV). The range indicates the upper and lower limits of the vertical axis (voltage values) when displaying the measured ground vibration waves in the application. Care must be taken when setting this range; if the set range is exceeded, it becomes impossible to measure the peak vibration values. A range of 500 mV was set for collecting ground vibration data. Meanwhile, the filter excludes vibrations of a frequency higher than the set value, which helps in avoiding noise (high-frequency vibrations) and simplifying data processing. In this study, a filter of 500 Hz was set, so vibrations above 500 Hz were not measured.

Figure 4.
Various settings and data points: (a) measuring points for vibration data; (b) amplifier settings; (c) memory settings; (d) trigger settings.
In the memory settings (Figure 4c), one sets the sampling interval (sampling frequency), block size, and measurement duration. The sampling frequency indicates the interval for measuring vibration values, which affects the vibrational values that can be measured. Generally, the sampling frequency must be set to a value at least twice as high as the frequency one wishes to measure. Ground vibrations due to blasting are known to fall between 10 and 200 Hz and are known to be high-frequency waves compared to natural earthquakes. Considering these facts, the sampling frequency was generously set to 10 kHz for the collection of ground vibration data. The block size indicates how many times the measurement time is divided, and the measurement duration is determined by the sampling frequency and block size.
In the trigger settings (Figure 4d), one can set the timing (trigger) to start the measurement in percentage terms. Specifically, measurement starts when a vibration larger than the percentage value of the range set in the amplifier settings is detected. To ensure no vibrations before the start of the measurement are missed, a pre-trigger can be set in percentage terms. Vibrations occurring a percentage of the measurement time set in the memory settings before the triggers are recorded. In this study, the trigger and pre-trigger were set to 8% and 10%, respectively. After the measurement, the data were saved to a computer in comma-separated value (CSV) format. The location where the vibration measurement took place was also recorded on a Google Maps map, and the latitude and longitude coordinates of that measurement point were recorded simultaneously.
4.2. Conversion to Peak Particle Velocity (PPV)
This section details the methodology for processing ground vibration data acquired from quarry operations, utilizing Origin 2021 spreadsheet software. Raw data, in CSV format, was initially imported into Origin, presenting as voltage values. A sampling rate set at 10 kHz allowed for time series creation at 0.0001-s intervals, subsequently enabling the generation of graphs for time-dependent voltage, acceleration, and velocity. Figure 5a exemplifies a time–voltage graph for Z-axis ground vibrations, captured via a tri-axial micro-vibration detector.
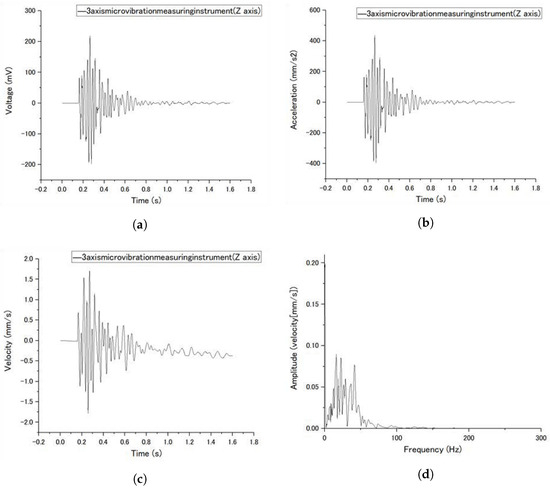
Figure 5.
Various time-related graphs and Fourier spectrum: (a) time–voltage graph; (b) time–acceleration graph; (c) time–velocity graph; (d) example of Fourier spectrum.
Utilizing the detector’s calibration coefficient of 2, voltage readings were transformed into acceleration units, depicted in a time–acceleration graph in Figure 5b. Velocity metrics were calculated by integrating the acceleration figures, an example of which is provided in Figure 5c, identifying the peak amplitude as the “Peak Particle Velocity” (PPV).
In instances of observed irregularities in the time–velocity graph, noise reduction was critical. This was accomplished with Origin’s Fast Fourier Transform (FFT) filter, particularly the band-pass type. A preliminary FFT analysis, converting time–velocity data to a frequency–amplitude graph, identified the significant frequency bands in the vibration data, essential for effective noise filtration. Figure 5d displays an FFT spectrum, highlighting a dominant 20–40 Hz frequency range, confirming these as the main contributors to blast-related ground vibrations. This insight directed the subsequent filtration of extraneous frequencies from the time–velocity data, ensuring an accurate PPV determination.
5. Methodology
5.1. WNMF
WNMF uses the non-negative measurement data matrix shown in Figure 6. Here, let the set of measurement points be and the set of parameters constituting the measurement data be . represents the value of parameter measured at the measurement point . Values of parameters not measured are incorporated into matrix A as missing values (=0). In WNMF, this matrix A is approximately decomposed into matrices and , and their inner product is taken to predict the missing values (values indicated as 0 in matrix A). This can be represented by Equation (3) as:
Here, k denotes the rank, which is smaller than m or n. Generally, as the rank increases, the prediction accuracy of the missing values increases, and as the rank decreases, the prediction accuracy decreases. However, too large a rank may increase the computational load and reduce prediction accuracy. Therefore, it is important to choose an appropriate rank when executing WNMF. WNMF is a learning method that aims to improve prediction accuracy for missing values by using only measured value elements [30]. WNMF learns matrices U and V by solving the optimization problem defined by Equation (4):

Figure 6.
Memory settings.
Here, initial values of matrices U and V are given randomly. Furthermore, ∘ represents element-wise matrix multiplication, and denotes the Frobenius norm of a matrix. The matrix represents a weight matrix and is defined by Equation (5):
Here, represents the set of measured values contained in matrix A, and represents the set of missing values contained in matrix A. Thus, when , it indicates that it is used for learning, and when , it indicates that it is not used for learning. The optimization problem in Equation (4) can be solved by updating matrices U and V t times until they converge, using Equations (6) and (7):
5.2. Prediction of PPV Using WNMF
WNMF allows for the prediction of any parameter value by replacing it with a missing value. By leveraging this feature, our proposed method integrates the PPV of the prediction site as a missing value in the matrix. This matrix is then approximated by WNMF to predict PPV. Figure 7 illustrates the flow of PPV prediction using WNMF. The matrix shown in the bottom right of Figure 7 represents measurement data using three parameters: PPV, amount of explosives, and distance. This shows the matrix calculation process in our proposed method. From Figure 7, our approach is divided into four steps: 1—data collection; 2—data processing; 3—matrix creation; 4—PPV prediction. Each step is detailed below.
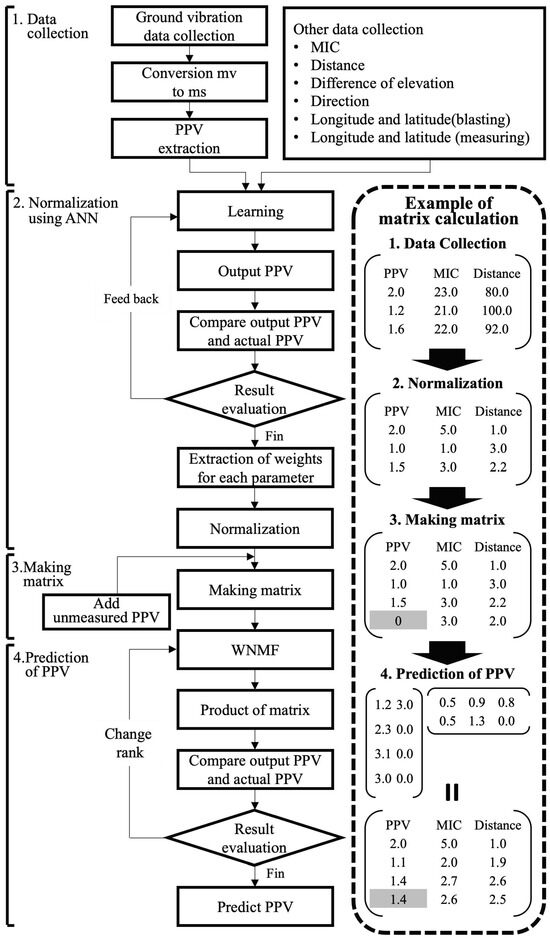
Figure 7.
Memory settings.
5.2.1. Step 1: Data Collection
Here, values for each parameter are measured at the target site. Ground vibration data resulting from blasting are converted to PPV. The type of parameter other than PPV can be arbitrarily chosen. In this study, we utilize nine parameters: MIC, distance, elevation difference, direction, latitude of the blasting site, longitude of the blasting site, latitude of the measurement site, and longitude of the measurement site.
5.2.2. Step 2: Data Processing
In Step 1, the range of values varies greatly for each parameter. Therefore, if these measurement data are used directly in WNMF, the learning may not proceed properly, potentially reducing the accuracy of PPV prediction. Thus, in Step 2, to apply WNMF for PPV prediction, normalization using ANN is performed on the measurement data from Step 1. Figure 8 presents a conceptual diagram of the neural network. During the learning process of the neural network, parameters are first input at the input layer. Then, in the hidden layer, “weights” are applied to each parameter, forming hidden neurons. The number of these hidden neurons can be pre-specified. Based on these hidden neurons, a single predicted value (PPV) is output in the output layer. The output predicted value is compared with the actual value to calculate the error. The neural network is then feedback-adjusted to optimize the “weight magnitude” for each parameter. This is the learning cycle of ANN. In our proposed method, the “weight magnitude” calculated by this ANN is quantified as the degree of influence on PPV, and the normalization value range is changed according to this weight magnitude. Parameters with a large influence on PPV are prioritized, and their normalization value range is made larger to prioritize their learning in WNMF. The method of normalization is min–max normalization. When aligning the value of the parameter at measurement point to an arbitrary value range , the normalized value is determined using Equation (8).
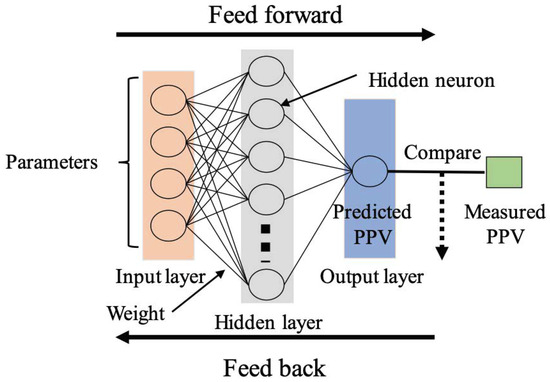
Figure 8.
Memory settings.
Here, indicates the set of values for the jth parameter. represents the maximum value of , and denotes its minimum value. In our proposed method, the impact on PPV is evaluated in three stages. Parameters with the highest influence have their normalization value range set to [1, 11], the second highest to [1, 6], and all other parameters to [1, 2]. The normalization value range for PPV is also set to [1, 2].
5.2.3. Step 3: Matrix Creation
In Step 3, a measurement data matrix is created based on the normalized parameter values. At this point, the PPV of the prediction site is integrated into the measurement data matrix as a missing value (shown as 0 in Figure 8). By applying WNMF to this measurement data matrix, the missing PPV can be predicted.
5.2.4. Step 4: PPV Prediction
In Step 4, the measurement data matrix, which includes missing values, is approximated into two matrices using WNMF. These approximated matrices are in a state where all values are filled. By multiplying these two matrices, the missing PPV is predicted. This is tried for all possible ranks, and the prediction error of PPV is calculated each time. The rank with the smallest prediction error is regarded as the optimal model, and the PPV value at that time is the final prediction result. Our proposed method can accommodate changes in quarry shape or the surrounding environment through integrating and corresponding.
6. Experiments and Results
6.1. Determination of Normalized Value Range
To determine the normalized value range for each parameter, training was performed using an ANN. The data used were measurements from 100 sites collected at the Mikurahana Quarry in Akita Prefecture. These data were divided into training data, validation data, and test data at a ratio of 80:10:10, respectively, and learning was conducted using MATLAB 2021. During the training of the ANN, the number of hidden neurons that make up the hidden layer of the neural network was varied as 2, 4, 6, 8, 10, and 12 to compare the prediction accuracy of each model. The mean square error (MSE) and the coefficient of determination () were used as evaluation metrics. A prediction model with an MSE close to 0 and close to 1 indicates a high prediction accuracy for PPV. As a result of the training, the predictive model with six hidden neurons showed the highest accuracy. Table 3 shows the learning results of the ANN. As shown in Table 3, the predictive model with six hidden neurons had an MSE of 0.0245 and of 0.8740, showing higher accuracy compared to other models. The sum of the weights (absolute values) of each parameter extracted from the predictive model with six hidden neurons is shown in Figure 9. As a result, it became clear that the weights of “MIC”, “Distance”, and “Longitude of the measurement point” were relatively large. Furthermore, although the weight for “Direction” was not as large compared to the previous three parameters, it showed a larger weight than the other parameters. Based on these results, it was judged that these four parameters have a large influence on PPV. Therefore, the normalization value ranges for “MIC”, “Distance”, and “Longitude of the measurement point”, which had the largest total weight value, were set to [1, 11], “Direction” to [1, 6], and all other parameters to [1, 2].

Table 3.
Comparison result of prediction model.
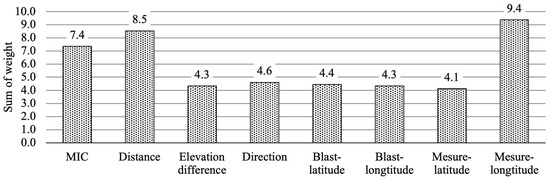
Figure 9.
Memory settings.
6.2. Effectiveness of Normalization Using ANN
To verify the effectiveness of normalization using an ANN, the prediction accuracy of PPV under three conditions was compared: the proposed method (Nor-ANN), a method in which the normalization value range of parameters is uniformly set to [1, 11] (Nor-1-11), and a case where normalization is not performed (Nor-None). In the experiment, PPV data randomly extracted from the measurement data matrix was replaced with unmeasured values (=0), and PPV prediction was performed using WNMF. This allowed for a comparison between the actually measured PPV and the predicted PPV. The number of unmeasured values (hereafter referred to as the number of unmeasured values) was set to 10, and the prediction accuracy of the WNMF for the number of unmeasured values was compared under each condition. When executing WNMF, the rank number was changed from 1 to 8, and the prediction accuracy for each rank was calculated. When comparing each condition, the rank with the highest prediction accuracy was used. The Root Mean Squared Error (RMSE) was used as an evaluation metric for prediction accuracy. RMSE is a metric commonly used to evaluate the prediction accuracy in recommendation systems. The calculation formula for RMSE is shown in Equation (9).
where Y represents the actual value of PPV, represents the predicted value of PPV, and t represents the number of missing values. As a result of WNMF, when normalization was performed using ANN, a higher prediction accuracy was shown than when normalization was uniformly performed or when normalization was not performed. Table 4 shows the PPV prediction results using WNMF. RMSE indicates higher prediction accuracy as the value is smaller. As shown in Table 4, Nor-ANN, Nor-1-11, and Nor-None all showed the smallest RMSE at rank 7. As a result of comparing the RMSE of each condition at rank 7, Nor-ANN showed a smaller value than Nor-11 or Nor-None. The results comparing the error ranges (difference between the actual value and the predicted value) for each condition are shown in Table 5. As a result, the error range of Nor-ANN was from to 0.2024, and the difference was 0.4306. This shows a smaller error range than Nor-1-11 or Nor-None. Through the above results, it became clear that the prediction accuracy of PPV improves more when normalized using ANN than when normalized uniformly or not normalized.

Table 4.
Prediction results of PPV using WNMF (comparison between Nor-ANN and Nor-1-11, Nor-None).

Table 5.
Range of error for Nor-ANN, Nor-1-11, and Nor-None.
6.3. Relationship between the Amount of Data and Prediction Accuracy
In this section, we examined the relationship between the amount of data used in the measurement data matrix and the prediction accuracy of the proposed method. Weighted Non-negative Matrix Factorization (WNMF) is a form of unsupervised learning. It can perform matrix factorization (i.e., prediction) even with a small amount of data. However, previous studies have not clearly shown how much the amount of data affects the prediction accuracy of WNMF. For this purpose, we prepared several measurement data matrices with different numbers of measurement points (rows) and conducted PPV prediction using WNMF. This allows us to verify the prediction accuracy of the proposed method according to the amount of data used in the measurement data matrix. Specifically, against the Matrix100 (100 rows × 9 columns) which uses all measurement data, we prepared conditions of Matrix20 (20 rows × 9 columns), Matrix40 (40 rows × 9 columns), Matrix60 (60 rows × 9 columns), and Matrix80 (80 rows × 9 columns). The measurement points (rows) to be deleted were randomly selected. Note that the measurement data of 100 points used in Matrix100 is one of the benchmarks for the amount of data required to create a PPV prediction model using ANN (refer to Section 2.2). Therefore, by comparing the prediction accuracy of PPV using Matrix100 and other conditions, we can clarify the effectiveness of the proposed method.
As for the experimental method, as in the previous experiment, 10 PPV data points were randomly extracted from each measurement data matrix condition and replaced with unmeasured values, and PPV prediction was performed using WNMF. When executing WNMF, the rank number was changed from 1 to 8, and the prediction accuracy for each rank was calculated. When comparing each condition, the rank with the highest prediction accuracy was used. RMSE was used as the evaluation metric for prediction accuracy.
As a result of WNMF, higher prediction accuracy was shown when using a smaller amount of data (60, 80 points) than the amount of data required for ANN learning (100 points of measurement data). On the other hand, low prediction accuracy was shown when using an extremely small amount of data (20, 40 points). Table 6 shows the PPV prediction results using WNMF. From Table 6, Matrix100, Matrix80, and Matrix40 showed the smallest RMSE at rank 7, Matrix60 at rank 6, and Matrix20 at rank 4. Therefore, this rank was used for comparison of prediction accuracy. As a result of comparing the prediction accuracy of Matrix100 with other conditions, Matrix80 and Matrix60 showed a smaller RMSE than Matrix100. On the other hand, conditions with extremely small amounts of data, Matrix40 and Matrix20, showed a larger RMSE than Matrix100. Table 6 shows the results of comparing the error range of each condition. As a result, Matrix80 and Matrix60 showed a smaller error range than Matrix100. On the other hand, Matrix40 and Matrix20 showed a larger error range than Matrix100.

Table 6.
Prediction results of PPV using WNMF (Comparison between Matrix100 and Matrix20–80).
From the above results, it became clear that by using the proposed method, it is possible to predict PPV with a smaller amount of data (60, 80 points) than the amount of data (100 points of measurement data) required for ANN learning. On the other hand, it became clear that the prediction accuracy of the proposed method decreases when using an extremely small amount of data (20, 40 points).
7. Discussion
7.1. Rank
In this experiment, the highest prediction accuracy was often observed when the rank was either 6 or 7, suggesting that an appropriate rank was selected. Many matrix factorization methods, including WNMF, have the characteristic of changing prediction accuracy depending on this rank. Generally, it is said that as the rank number increases, the prediction accuracy improves, and as the rank number decreases, the prediction accuracy drops [23]. However, an excessively large rank number might increase the computational cost, possibly reducing the prediction accuracy. Thus, selecting the appropriate rank number is crucial. In this experiment, the prediction accuracy was compared by changing the rank number from 1 to 8. Given that the highest prediction accuracy was observed at ranks 6 and 7, it can be inferred that the appropriate rank was chosen. Nonetheless, such a trial-and-error method requires significant time and computational cost. Assuming that the proposed method is used in actual settings, this approach could pose a significant challenge. Therefore, future research needs to develop a method to estimate the rank before executing WNMF. Already, cases where the rank is estimated before matrix factorization have been reported [23]. Building on these, the development of an optimal rank estimation method and the improvement of the proposed method are future challenges.
7.2. Normalization
Without normalization, the PPV prediction accuracy declined compared to using ANN for normalization. A possible reason is that the value ranges differed significantly among parameters, making it challenging to lead to an appropriate solution. In WNMF, the difference between the original matrix and the decomposed matrix is defined as the loss function, and updates are repeated to minimize it. If the value range in the original matrix varies greatly due to parameters, the computational cost increases, and there might be cases where it does not converge to the optimal solution. The data used in this study varied greatly in value range depending on the parameters, which could have led to a decline in prediction accuracy. Moreover, uniformly performing normalization resulted in a lower PPV prediction accuracy compared to using ANN for normalization. This could be attributed to setting the same normalization value range for all parameters. Despite each parameter possibly having different impacts on the PPV, the same normalization range was set for all parameters. It can be presumed that focusing on learning from parameters that have a significant impact on PPV would improve prediction accuracy. In contrast, with ANN-based normalization, the weights calculated by ANN were quantified as the impact on PPV, and the normalization value range was varied according to those weights. As a result, it’s conceivable that normalization using ANN resulted in higher prediction accuracy than uniform normalization.
7.3. Data Volume
In this experiment, Matrix100 showed a decline in PPV prediction accuracy compared to Matrix80 or Matrix60, which had less data. This might be because the large volume of data increased the computational load for WNMF, preventing the solution from converging. As previously mentioned, WNMF is an optimization problem that minimizes a loss function. However, this loss function may have local minima, and repeating the calculations might lead to different results [30]. In this experiment, since Matrix100 had more data than other matrices, it might have converged to a local solution. On the other hand, the PPV prediction accuracy for Matrix20 was clearly lower than for other matrices. The PPV prediction accuracy at rank 5, in particular, dropped significantly. This could be because the data volume used for the matrix was extremely limited, making WNNMF learning inadequate and preventing the solution from converging. Thus, while WNMF can learn with less data compared to ANN, there is a potential for non-convergence with extremely limited data.
8. Conclusions
In this study, we proposed a PPV (Peak Particle Velocity) prediction method using Weighted Non-negative Matrix Factorization (WNMF) based on measurement data from urban crushed stone sites. The method was further enhanced by normalization with Artificial Neural Networks (ANNs) to improve PPV prediction accuracy. This approach is particularly useful in scenarios where extensive measurement data are unavailable or contain missing values. The effectiveness of the proposed method was verified through various experiments, leading to the following key findings:
- Normalization with ANN resulted in higher accuracy compared to non-normalized methods. The PPV prediction error (root mean square error—RMSE) improved from 0.2219 to 0.1426.
- The method demonstrated high accuracy even with reduced measurement data (60 points) for ANN learning, decreasing the PPV prediction error from 0.1759 (with 100 points) to 0.1378 (with 60 points).
- The accuracy decreased when using extremely small amounts of measurement data (20 points), with the PPV prediction error increasing from 0.1759 (100 points) to 0.3630 (20 points).
Moreover, our proposed method is versatile, capable of predicting any parameter within the matrix. This feature can extend its application beyond PPV prediction. For instance, it can estimate the amount of explosives within a specific vibration value or predict the reach of vibrations over distance. We anticipate its future role as a valuable tool in blasting design for blasters. Further research should concentrate on enhancing the predictive accuracy and functional aspects of this method as a system.
Previous PPV prediction models, which relied on experimental, statistical methods, and ANN, faced issues like low prediction accuracy or the necessity for extensive data for accurate modeling. This study’s comprehensive verification of our method using actual data from urban crushed stone sites suggests a potential resolution to these longstanding challenges.
Nevertheless, our proposed method can be improved, particularly in establishing a rank estimation method for WNMF execution. The current practice of testing all conceivable ranks to select the one with the smallest prediction error is impractical due to its time and computational demands. Future research should aim to establish a more efficient rank estimation method, refining our approach into a highly accurate and universally applicable tool.
Author Contributions
Conceptualization, H.I., M.T. and T.A.; methodology, H.I., E.P. and Y.K.; software, H.I. and H.T.; validation, H.I., E.P. and B.B.S.; formal analysis, H.I. and H.T.; investigation, H.I., M.T. and B.B.S.; resources, H.I.; data curation, H.I.; writing—original draft preparation, H.I.; writing—review and editing, H.I., E.P. and Y.K.; visualization, H.I.; supervision, E.P. and Y.K.; project administration, E.P. and Y.K.; funding acquisition, M.T. and T.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created in this study.
Acknowledgments
We wish to extend my sincere thanks to Toseki Material Co. for allowing the use of the Mikurahana quarry site. Their generous support was crucial for the success of our research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khandelwal, M.; Singh, T.N. Prediction of blast induced ground vibrations and frequency in opencast mine: A neural network approach. J. Sound Vib. 2006, 289, 711–725. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T.N. Evaluation of blast-induced ground vibration predictors. Soil Dyn. Earthq. Eng. 2007, 27, 116–125. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T.N. Prediction of blast-induced ground vibration using artificial neural network. Int. J. Rock Mech. Min. Sci. 2009, 46, 1214–1222. [Google Scholar] [CrossRef]
- Faramarzi, F.; Farsangi, M.A.E.; Mansouri, H. Simultaneous investigation of blast induced ground vibration and airblast effects on safety level of structures and human in surface blasting. Int. J. Min. Sci. Technol. 2014, 24, 663–669. [Google Scholar] [CrossRef]
- Navarro Torres, V.F.; Silveira, L.G.C.; Lopes, P.F.T.; de Lima, H.M. Assessing and controlling of bench blasting-induced vibrations to minimize impacts to a neighboring community. J. Clean. Prod. 2018, 187, 514–524. [Google Scholar] [CrossRef]
- Singh, P.K.; Roy, M.P. Damage to surface structures due to blast vibration. Int. J. Rock Mech. Min. Sci. 2010, 47, 949–961. [Google Scholar] [CrossRef]
- Monjezi, M.; Ghafurikalajahi, M.; Bahrami, A. Prediction of blast-induced ground vibration using artificial neural networks. Tunn. Undergr. Space Technol. 2011, 26, 46–50. [Google Scholar] [CrossRef]
- Hajihassani, M.; Armaghani, D.J.; Marto, A.; Mohamad, E.T. Vibrations au sol prédiction dans quarry dynamitage à travers un réseau neural artificiel optimisé par une concurrence impérialiste algorithme. Bull. Eng. Geol. Environ. 2015, 74, 873–886. [Google Scholar] [CrossRef]
- Saadat, M.; Khandelwal, M.; Monjezi, M. An ANN-based approach to predict blast-induced ground vibration of Gol-E-Gohar iron ore mine, Iran. J. Rock Mech. Geotech. Eng. 2014, 6, 67–76. [Google Scholar] [CrossRef]
- Hudaverdi, T. Application of multivariate analysis for prediction of blast-induced ground vibrations. Soil Dyn. Earthq. Eng. 2012, 43, 300–308. [Google Scholar] [CrossRef]
- AS 2187.2-2006; Explosives—Storage and Use Part 2: Use of Explosives. Council of Standards Australia: Sydney, Australia, 2006.
- BS 6472-1:2008; Guide to Evaluation of Human Exposure to Vibration in Buildings. European Standard: Plzen, Czech Republic, 2008.
- Nicholls, H.R.; Johnson, C.F.; Duvall, W.I. Blasting Vibrations and Their Effects on Structures; U.S. Department of the Interior, Bureau of Mines: Washington, DC, USA, 1971; BM-BULL-656. [Google Scholar]
- Siskind, D.E.; Stagg, M.S.; Kopp, J.W.; Dowding, C.H. Structure Response and Damage Produced by Ground Vibration from Surface Mine Blasting; United States, Bureau of Mines: Washington, DC, USA, 1980. [Google Scholar]
- Dowding, C.H. Blast Vibration Monitoring and Control; Prentice-Hall: Hoboken, NJ, USA, 1985. [Google Scholar]
- Duvall, W.I.; Petkof, B. Spherical Propagation of Explosion-Generated Strain Pulses in Rock; U.S. Department of the Interior, Bureau of Mines: Washington, DC, USA, 1959. [Google Scholar]
- Langefors, U.; Kihlström, B. The Modern Technique of Rock Blasting; Wiley: Hoboken, NJ, USA, 1963. [Google Scholar]
- Pal Roy, P. Vibration control in an opencast mine based on improved blast vibration predictors. Min. Sci. Technol. 1991, 12, 157–165. [Google Scholar] [CrossRef]
- Kamali, M.; Ataei, M. Prediction of blast induced ground vibrations in Karoun III power plant and dam: A neural network. J. South. Afr. Inst. Min. Metall. 2010, 110, 481–490. [Google Scholar]
- Kawamura, Y.; Moriyama, Y.; Jang, H. Web-GIS Based Visualization System of Predicted Ground Vibration Induced by Blasting in Urban Quarry Sites. J. Geogr. Inf. Syst. 2019, 11, 17–31. [Google Scholar] [CrossRef]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix Factorization Techniques for Recommender Systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Resnick, P.; Iacovou, N.; Suchak, M.; Bergstrom, P.; Riedl, J. GroupLens: An open architecture for collaborative filtering of netnews. In Proceedings of the 1994 ACM Conference on Computer Supported Cooperative Work, CSCW 1994, Chapel Hill, NC, USA, 22–26 October 1994; pp. 175–186. [Google Scholar]
- Squires, S.; Prügel-Bennett, A.; Niranjan, M. Rank Selection in Nonnegative Matrix Factorization using Minimum Description Length. Neural Comput. 2017, 29, 2164–2176. [Google Scholar] [CrossRef] [PubMed]
- Singh, T.N.; Singh, V. An intelligent approach to prediction and control ground vibration in mines. Geotech. Geol. Eng. 2005, 23, 249–262. [Google Scholar] [CrossRef]
- Klæboe, R.; Amundsen, A.H.; Madshus, C.; Norén-Cosgriff, K.M.; Turunen-Rindel, I. Human reaction to vibrations from blasting activity - Norwegian exposure-effect relationships. Appl. Acoust. 2016, 111, 49–57. [Google Scholar] [CrossRef]
- Singh, T.N.; Dontha, L.K.; Bhardwaj, V. Study into blast vibration and frequency using ANFIS and MVRA. Min. Technol. 2008, 117, 116–121. [Google Scholar] [CrossRef]
- Dehghani, H.; Ataee-pour, M. Development of a model to predict peak particle velocity in a blasting operation. Int. J. Rock Mech. Min. Sci. 2011, 48, 51–58. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Hajihassani, M.; Mohamad, E.T.; Marto, A.; Noorani, S.A. Blasting-induced flyrock and ground vibration prediction through an expert artificial neural network based on particle swarm optimization. Arab. J. Geosci. 2014, 7, 5383–5396. [Google Scholar] [CrossRef]
- Mohamed, M.T. Performance of fuzzy logic and artificial neural network in prediction of ground and air vibrations. Int. J. Rock Mech. Min. Sci. 2011, 48, 845–851. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, W.; Ford, J.; Makedon, F. Learning from Incomplete Ratings Using Non-negative Matrix Factorization. In Proceedings of the 2006 SIAM International Conference on Data Mining, Bethesda, MD, USA, 20–22 April 2006; pp. 549–553. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).