A Damage Index for Assessing Seismic-Resistant Designs of Masonry Wall Buildings Reinforced with X-Bracing Concrete Frames
Abstract
:1. Introduction
2. Literature Review
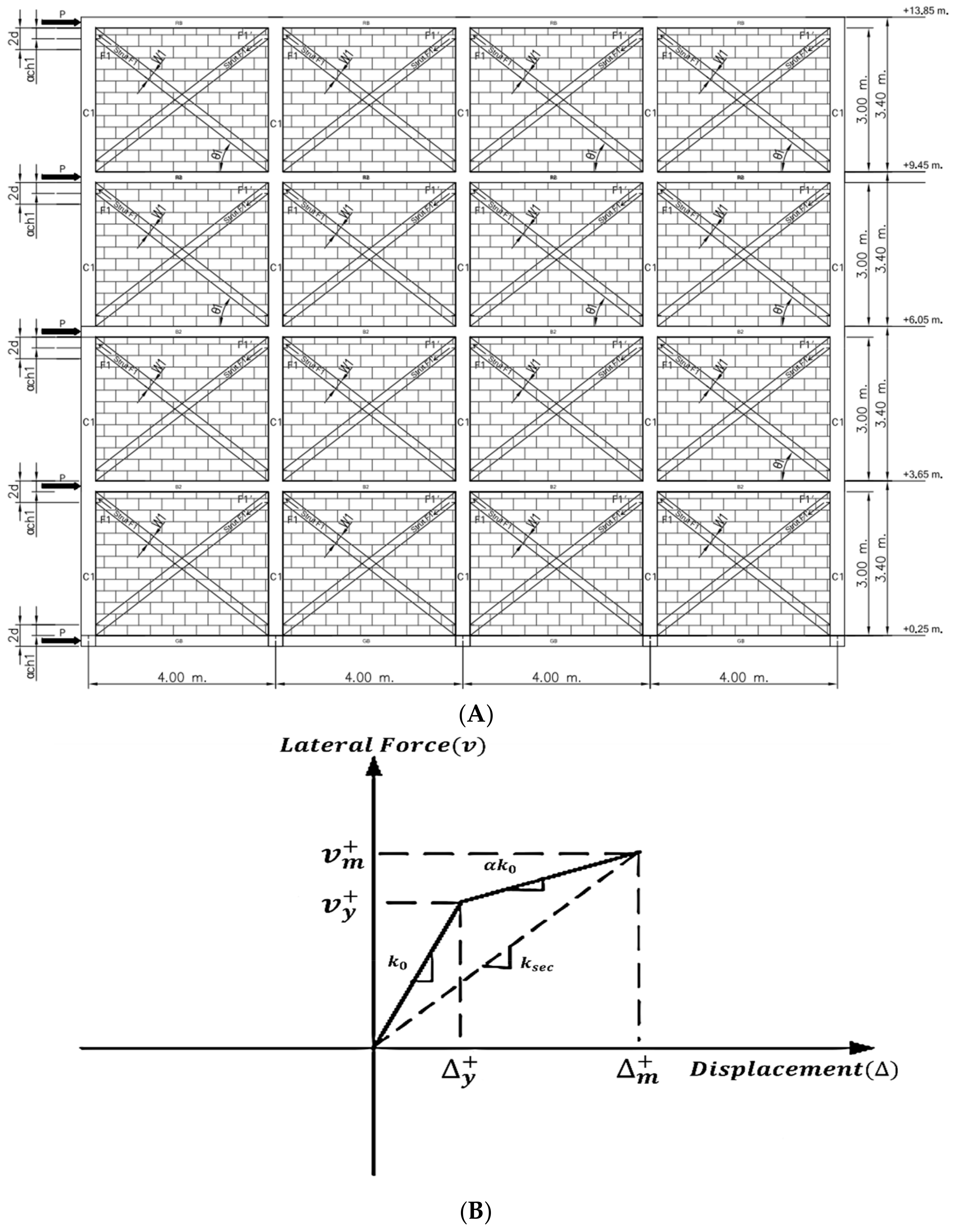
2.1. Park–Ang Damage Index
2.2. Structural Analysis of Model of Masonry Wall Building Reinforced with X-Bracing Concrete Frame
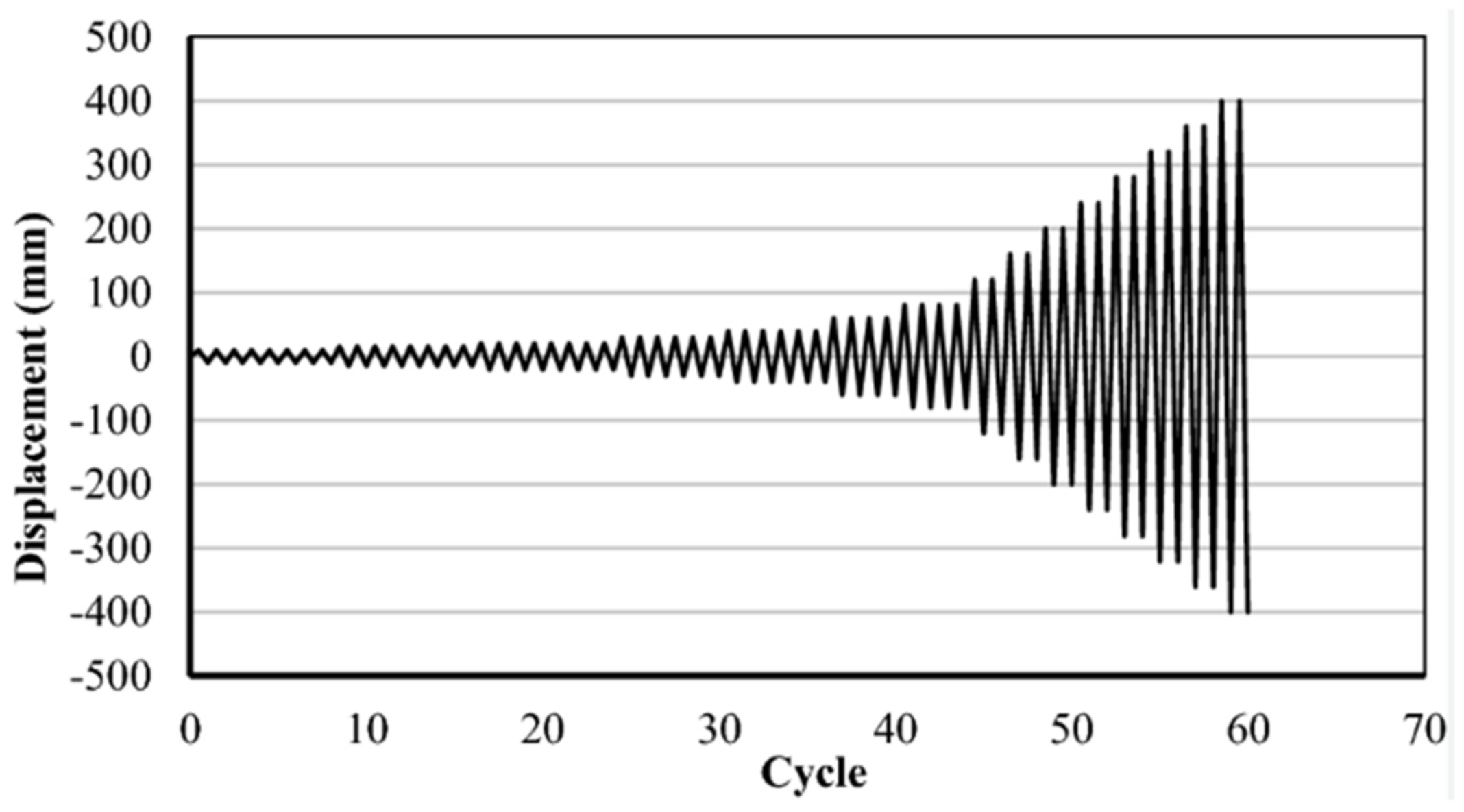
2.3. Coefficient Calibration of the Relationship between the Damage Level and Energy Decay
2.4. Damage Index of Study Sample to Assess Seismic-Resistant Design of Masonry Wall Buildings
3. Structural Analysis of Reinforcement X-Bracing Concrete Frames Used in the Model Samples from the Literature Review
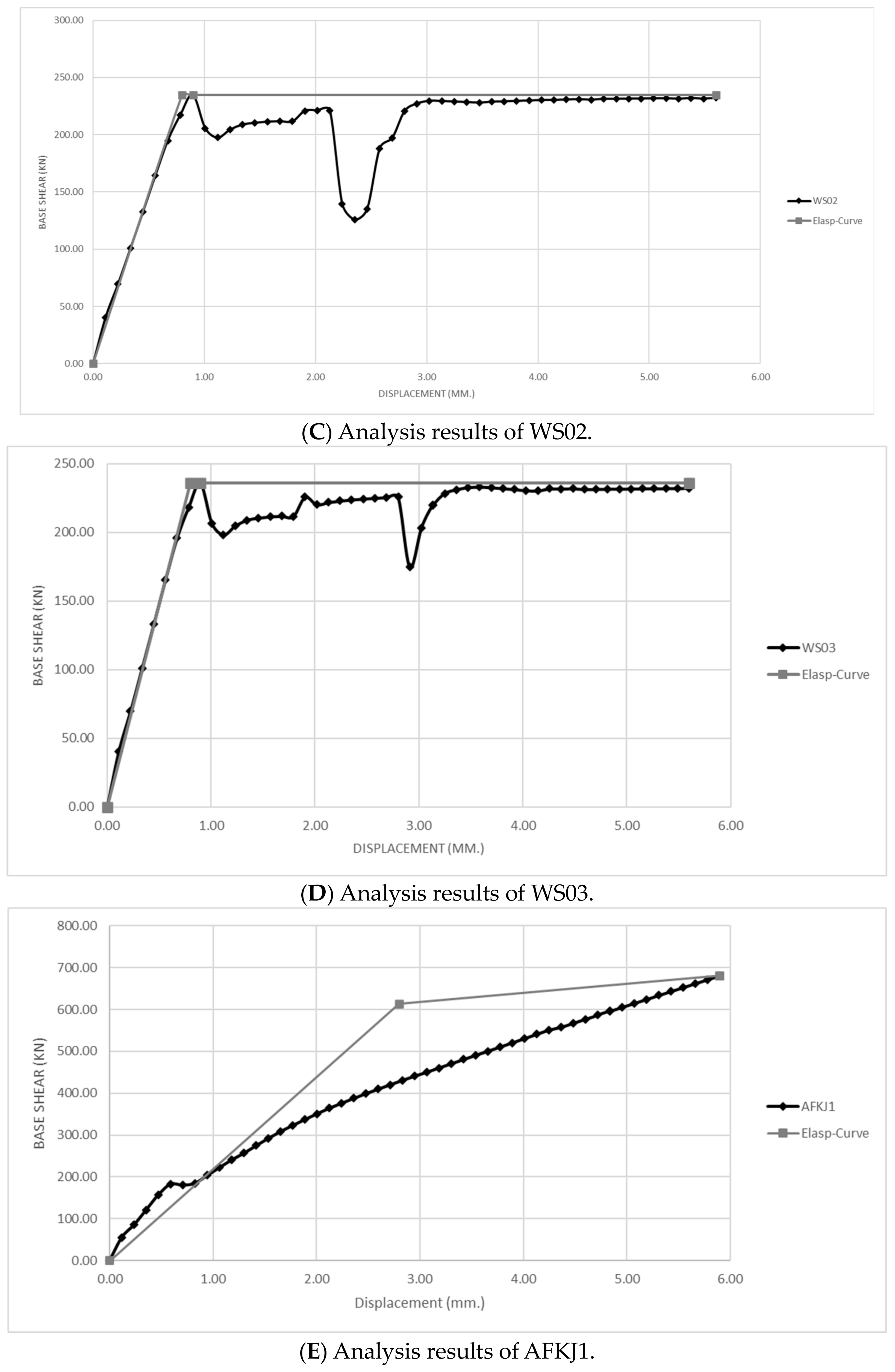
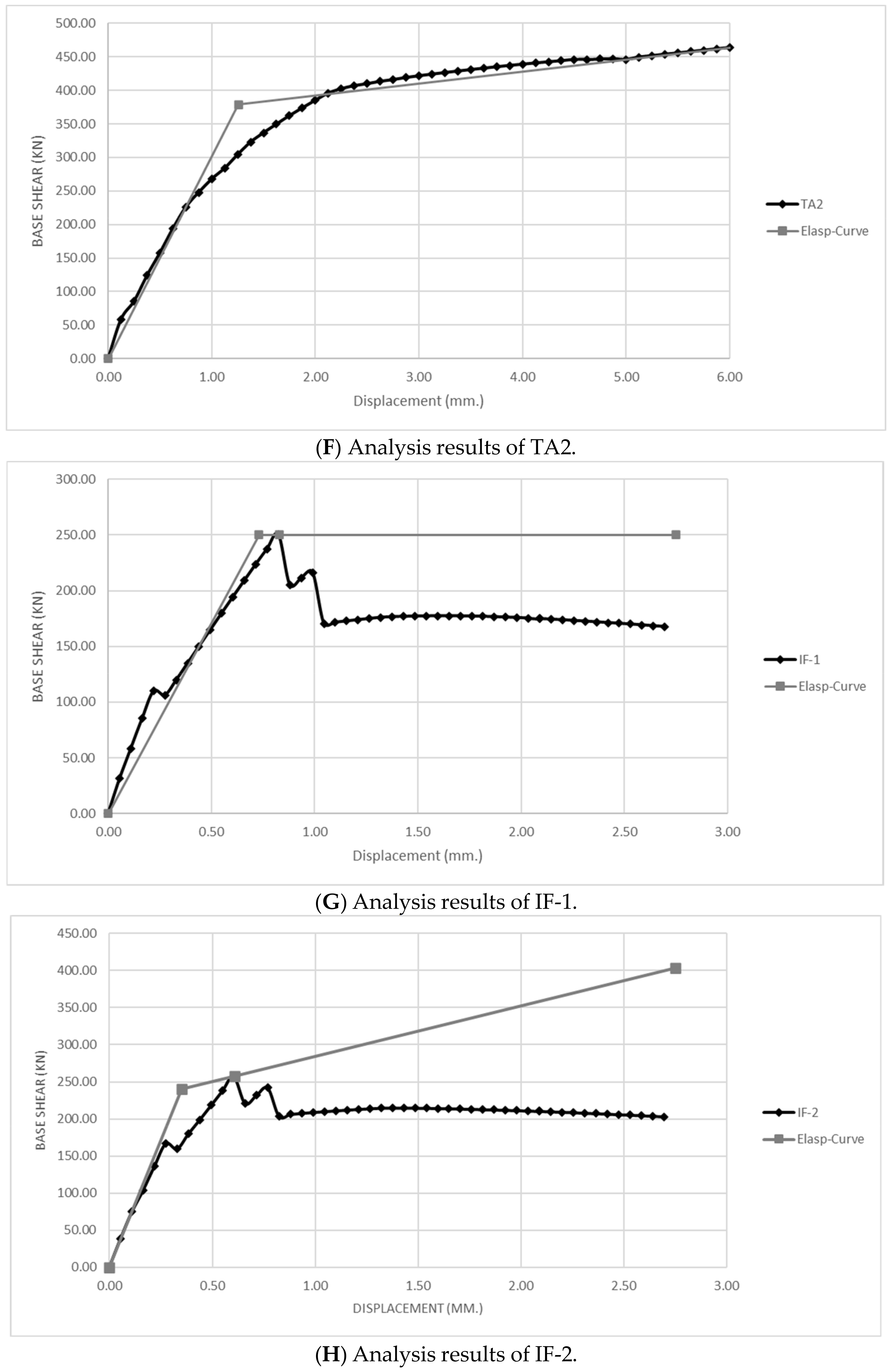
3.1. Damage Index Calculation Used in the Structural Analysis of Model Samples from the Literature Review
3.2. Determination of Damage Level for Assessing Seismic-Resistant Design of Masonry Wall Buildings
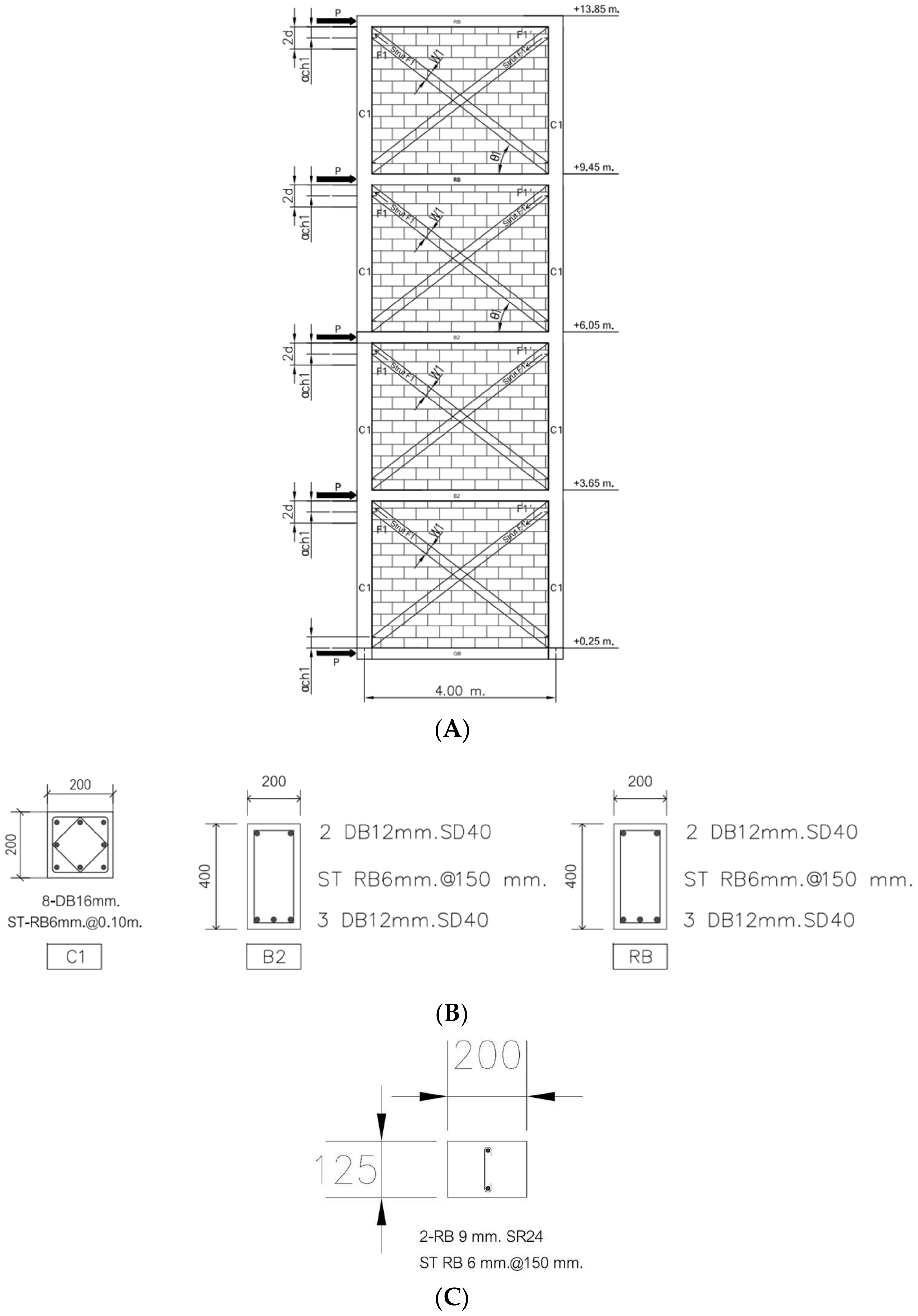
4. Case Study of Masonry Wall Building Reinforced with X-Bracing Concrete Frames
Case Study of Masonry Wall Building Reinforced with X-Bracing Concrete Frames
5. Analysis of Masonry Wall Building Reinforced with X-Bracing Concrete Frames
6. Conclusions
- The monotonic loading and cyclic loading conditions are analysed at the maximum lateral force. The analysis reveals that the results are consistent in the same direction and with the model structure analysis results.
- The correlation coefficient between the damage level and accumulated energy is appropriate for use in the calculation of the damage index using the Park–Ang equation. The Park–Ang equation for a masonry wall building is equal to 0.10–0.35.
- The criteria for the consideration of the damage level are defined as follows: when the damage index is between 0.25 and 0.50, the specimen has a minor damage level; when the damage index is between 0.50 and 0.80, the specimen has a moderate damage level; when the damage index is between 0.80 and 1.00, the specimen has a severe damage level; and when the damage index is more than 1.00, the specimen has a collapse damage level, resulting in the structure of the building experiencing a disaster.
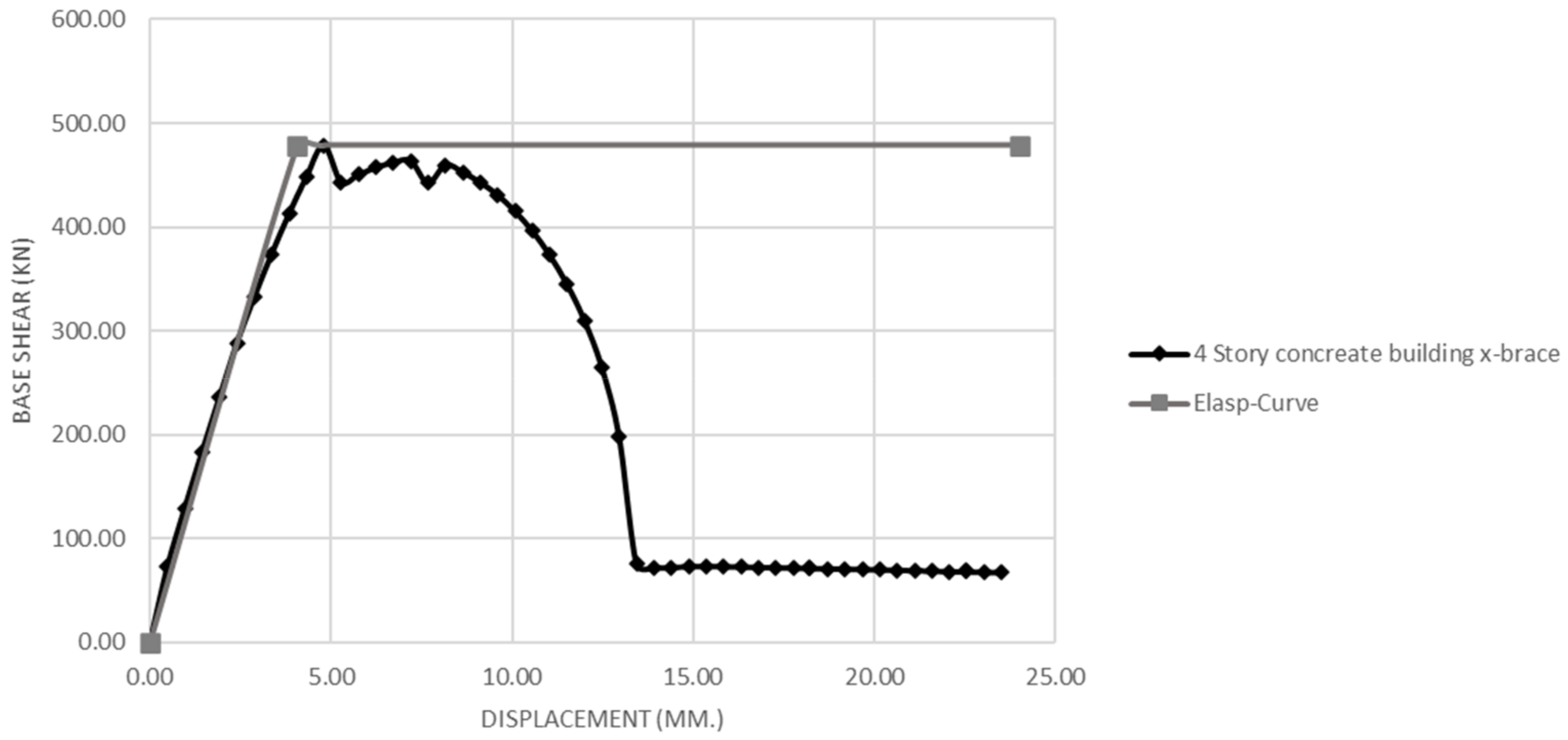
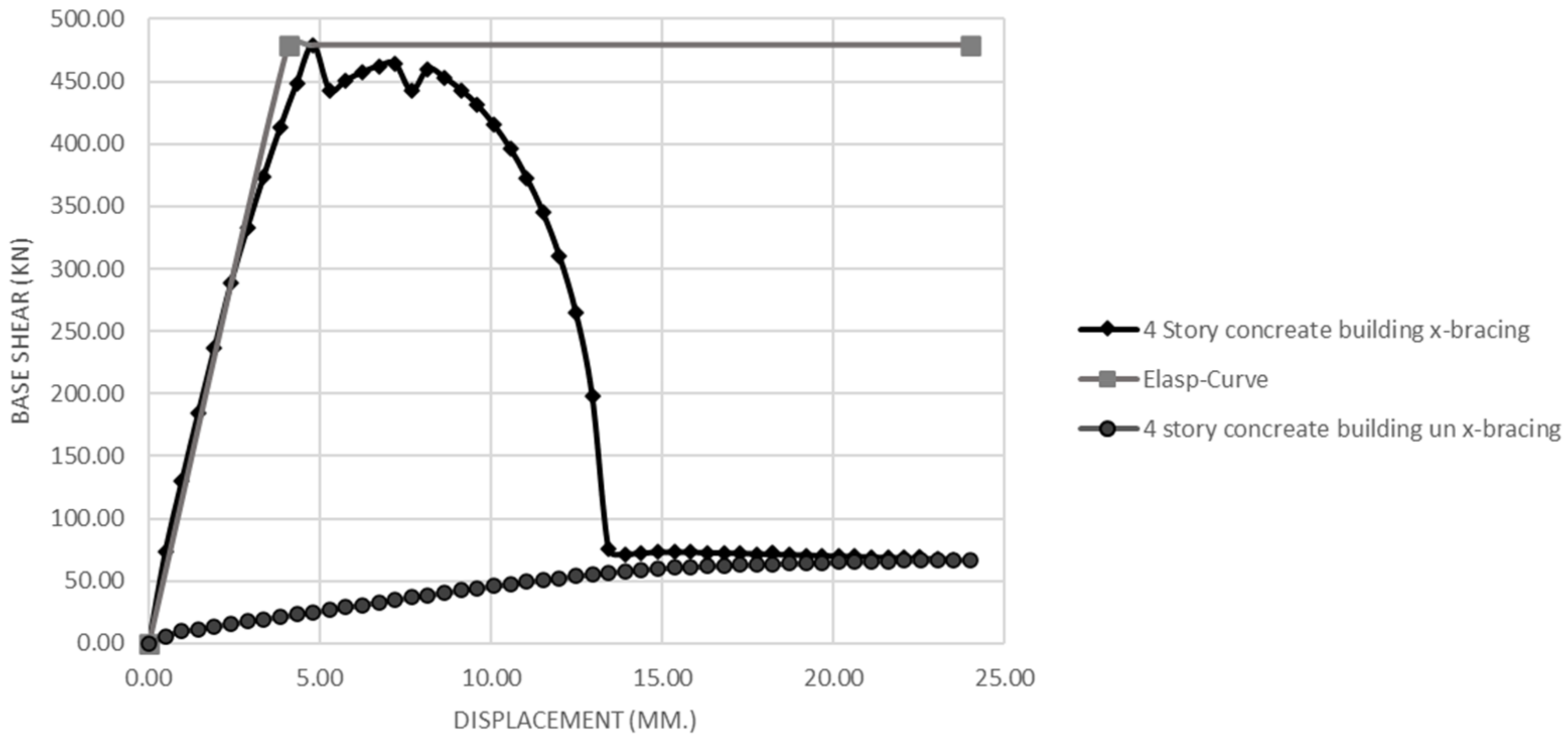
- The damage index for assessing the seismic-resistant design of masonry wall buildings reinforced with x-bracing concrete frames shows that they resist higher lateral force base shear values before lateral displacement than the original walls without x-bracing concrete frame structures, with values of 478.78 kN and at 67.16 kN, respectively, demonstrating an approximately 7.13 times difference in lateral forces. The masonry wall buildings reinforced with x-bracing concrete frames show extensive large cracks, and the damage index criterion (DI) is equal to 0.8 in the maximum lateral force base shear design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lukkunaprasit, P.; Ruangrassamee, A.; Boonyatee, T.; Chintanapakdee, C.; Jankaew, K.; Thanasisathit, N.; Chandrangsu, T. Performance of structures in the MW 6.1 mae lao earthquake in Thailand on May 5, 2014, and implications for future construction. J. Earthq. Eng. 2015, 20, 219–242. [Google Scholar]
- Park, Y.J.; Ang, A.H.S. Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 1985, 111, 723–732. [Google Scholar]
- DPT’s Standard 1301/1302. (2561); Earthquake Vibration Resistance Building Design Standards. Department of Public Works and Town & Country Planning: Bangkok, Thailand, 2018.
- Amornpunyapat, R.; Panyakapo, P.; Panyakapo, M. Development of Lightweight Concrete Interlocking Block Panel with Water Treatment Sludge and Expanded Metal Ferrocement. Eng. J. 2021, 25, 81–97. [Google Scholar]
- Saneinejad, A.; Hobbs, B. Inelastic design of infilled frames. J. Struct. Eng. ASCE 1995, 6682, 634–660. [Google Scholar]
- Mehrabi, A.B.; Shing, P.B.; Schuller, M.P.; Noland, J.L. Experimental evaluation of masonry-infilled RC frames. J. Struct. Eng. 1996, 122, 228–237. [Google Scholar]
- Wararuksajja, W.; Srechai, J.; Leelataviwat, S. Seismic design of RC moment-resisting frames with concrete block infill walls considering local infill-frame interactions. Bull. Earthq. Eng. 2020, 18, 6445–6474. [Google Scholar]
- Jiang, H.; Liu, X.; Mao, J. Full-scale experimental study on masonry infilled RC momentresisting frames under cyclic loads. Eng. Struct. 2015, 91, 70–84. [Google Scholar]
- Morandi, P.; Hak, S.; Magenes, G. Performancebased interpretation of in-plane cyclic tests on RC frames with strong masonry infills. Eng. Struct. 2018, 156, 503–521. [Google Scholar]
- Huang, Q.; Guo, Z.; Kuang, J.S. Designing infilled reinforced concrete frames with the ‘strong frame-weak infill’ principle. Eng. Struct. 2016, 123, 341–353. [Google Scholar]
- SeismoStruct user manual. Seismostruct User Manual; Seisomsoft Ltd.: Pavia, Italy, 2021. [Google Scholar]
- Kazemi, M.T.; Morshed, R. Seismic shear strengthening of R/C columns with ferrocement jacket. Cem. Concr. Compos. 2005, 27, 834–842. [Google Scholar]
- Leeanansaksiri, A.; Panyakapo, P.; Ruangrassme, A. Seismic capacity of masonry infilled RC frame strengthening with expanded metal ferrocement. Eng. Struct. 2018, 159, 110–127. [Google Scholar]
- Longthong, S.; Panyakapo, P.; Ruangrassamee, A. Seismic Strengthening of RC Frame and Brick Infill Panel using Ferrocement and Expanded Metal. Eng. J. 2020, 24, 45–59. [Google Scholar]
- Li, B.; Lam, E.S.S. Influence of interfacial characteristics on the shear bond behavior between concrete and ferrocement. Constr. Build. Mater. 2018, 176, 462–469. [Google Scholar]
- Panyamul, S.; Panyakapo, P.; Ruangrassame, A. Seismic shear strengthening of reinforced concrete short columns using fer-rocement with expanded metal. Eng. J. 2019, 23, 175–189. [Google Scholar]
- Salinas, S.; Guzman, A.; Carrillo, J. Performance evaluation of structures with reinforced concrete columns retrofitted with steel jacketing. J. Build. Eng. 2021, 33, 101510. [Google Scholar]
- Panyakapo, P. Seismic analysis of RC frame with brick infill panel strengthened by steel cage and expanded metal. Eng. J. 2021, 25, 29–44. [Google Scholar]
- Saiidi, M.; Sozen, M.A. Simple and Complex Models for Nonlinear Seismic Response of Reinforced Concrete Structures; Report UILU–ENG-79-2031; Department of Civil Engineering, University of Illinois: Urbana, IL, USA, 1979. [Google Scholar]
- Stewart, W.G. The Seismic Design of Plywood Sheathed Shear Walls. Ph.D. Thesis, Department of Civil Engineering, University of Canterbury, Christchurch, New Zealand, 1987. [Google Scholar]
- Naeim, F.; Kelly, J.M. Design of Seismic Isolated Structures: From Theory to Practice; John Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy Dissipation Systems for Seismic Applications: Current Practice and Recent Developments. J. Struct. Eng. 2007, 134, 3–21. [Google Scholar] [CrossRef]
- Kelly, J.M. The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 1999, 28, 3–20. [Google Scholar]
- Engle, T.; Mahmoud, H.; Chulahwat, A. Hybrid Tuned Mass Damper and Isolation Floor Slab System Optimized for Vibration Control. J. Earthq. Eng. 2015, 19, 1197–1221. [Google Scholar] [CrossRef]
- Matta, E.; De Stefano, A. Robust design of mass-uncertain rolling-pendulum TMDs for the seismic protection of buildings. Mech. Syst. Signal Process. 2009, 23, 127–147. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Optimal design and seismic performance of tuned mass damper inerter (TMDI) for structures with nonlinear base isolation systems. Earthq. Eng. Struct. Dyn. 2018, 47, 2539–2560. [Google Scholar] [CrossRef]
- Mantakas, A.G.; Kapasakalis, K.A.; Alvertos, A.E.; Antoniadis, I.A.; Sapountzakis, E.J. A Negative Stiffness Dynamic Base Absorber for Seismic Retrofitting of Residential Buildings. Struct. Control Health Monit. 2022, 29, e3127. [Google Scholar] [CrossRef]
- Kapasakalis, K.A.; Antoniadis, I.A.; Sapountzakis, E.J. Constrained Optimal Design of Seismic Base Absorbers Based on an Extended KDamper Concept. Eng. Struct. 2020, 226, 111312. [Google Scholar] [CrossRef]
- Kapasakalis, K.A.; Antoniadis, I.A.; Sapountzakis, E.J. Performance Assessment of the KDamper as a Seismic Absorption Base. Struct. Control Health Monit. 2019, 27, e2482. [Google Scholar] [CrossRef]
- Standard ASCE 41-17; Seismic Evaluation and Retrofit of Existing Buildings (41-17). American Society of Civil Engineers: Reston, VA, USA, 2017.



| Sample Name | H (mm) | L (mm) | D (mm) | W1 (mm) | (m) |
|---|---|---|---|---|---|
| Mehrabi et al. [6] | |||||
| No. 4 | 1537 | 2312 | 147 | 187 | 0.092 |
| Wararuksajja et al. [7] | |||||
| WS01 | 2800 | 4000 | 250 | 315 | 0.100 |
| WS02 | 2800 | 4000 | 250 | 331 | 0.100 |
| WS03 | 2800 | 4000 | 250 | 334 | 0.100 |
| Jiang et al. [8] | |||||
| AFKJ1 | 2950 | 5940 | 350 | 200 | 0.427 |
| Morandi et al. [9] | |||||
| TA2 | 3125 | 4587 | 300 | 350 | 0.370 |
| Huang et al. [10] | |||||
| IF-1 | 1375 | 2250 | 218 | 120 | 0.200 |
| IF-2 | 1375 | 2250 | 218 | 180 | 0.204 |
| Sample Name | Maximum Compressive Strength (Mpa) | Pending Strength (Mpa) | Compressive Stress | Pending Stress (mm) |
|---|---|---|---|---|
| No. 4 | 5.5 | 0.19 | 0.0010 | 0.0060 |
| WS01 | 9.4 | 0.20 | 0.0017 | 0.0050 |
| WS02 | 7.8 | 0.20 | 0.0017 | 0.0050 |
| WS03 | 6.8 | 0.20 | 0.0014 | 0.0018 |
| AFKJ1 | 3.8 | 0.47 | 0.0016 | 0.0060 |
| TA2 | 2.9 | 0.38 | 0.0011 | 0.0060 |
| IF-1 | 5.4 | 0.22 | 0.0020 | 0.0090 |
| IF-2 | 2.8 | 0.46 | 0.0014 | 0.0100 |
| Sample | Load Target | Result Model Structure Analysis | |
|---|---|---|---|
| Lateral Force (kN) | Maximum Lateral Force to Displacement (kN) | Maximum Lateral Displacement (mm) | |
| No. 4 | 502.39 | 210.74 | 3.07 |
| WS01 | 502.39 | 186.11 | 5.60 |
| WS02 | 502.39 | 234.690 | 5.60 |
| WS03 | 502.39 | 235.920 | 5.60 |
| AFKJ1 | 502.39 | 613.140 | 5.90 |
| TA2 | 502.39 | 378.470 | 6.25 |
| IF-1 | 502.39 | 250.110 | 2.75 |
| IF-2 | 502.39 | 239.860 | 2.75 |
| Sample Name | (kN) | (m) | (m) |
|---|---|---|---|
| No. 4 | 151.48 | 0.0111 | 0.014 |
| WS01 | 186.11 | 0.0134 | 0.017 |
| WS02 | 234.69 | 0.009 | 0.011 |
| WS03 | 235.92 | 0.009 | 0.011 |
| AFKJ1 | 680.86 | 0.059 | 0.074 |
| TA2 | 467.93 | 0.0625 | 0.078 |
| IF-1 | 250.11 | 0.0083 | 0.010 |
| IF-2 | 257.22 | 0.0061 | 0.008 |
| Sample Name | ||||||
|---|---|---|---|---|---|---|
| 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | |
| No. 4 | 0.818 | 0.837 | 0.846 | 0.846 | 0.855 | 0.864 |
| WS01 | 0.818 | 0.836 | 0.845 | 0.845 | 0.854 | 0.863 |
| WS02 | 0.810 | 0.819 | 0.824 | 0.824 | 0.829 | 0.834 |
| WS03 | 0.810 | 0.819 | 0.824 | 0.824 | 0.829 | 0.833 |
| AFKJ1 | 0.822 | 0.843 | 0.854 | 0.854 | 0.865 | 0.876 |
| TA2 | 0.833 | 0.867 | 0.883 | 0.883 | 0.900 | 0.917 |
| IF-1 | 0.808 | 0.817 | 0.821 | 0.821 | 0.825 | 0.829 |
| IF-2 | 0.806 | 0.812 | 0.815 | 0.815 | 0.818 | 0.821 |
| Average | 0.816 | 0.831 | 0.839 | 0.839 | 0.847 | 0.855 |
| SD. | 0.009 | 0.018 | 0.023 | 0.023 | 0.027 | 0.032 |
| Avg.+SD. | 0.825 | 0.849 | 0.862 | 0.862 | 0.874 | 0.887 |
| Avg.-SD. | 0.806 | 0.813 | 0.816 | 0.816 | 0.819 | 0.823 |
| Damage Characteristics | Damage Index (DI) | ||
|---|---|---|---|
| WS01 | WS02 | WS03 | |
| Total collapse of infill | 1.57 | 1.52 | 1.16 |
| Extensive large cracks | 1.07 | 1.03 | 0.84 |
| Corner crushing | 0.77 | 0.74 | 0.52 |
| First diagonal crack | 0.48 | 0.47 | 0.24 |
| Damage Level | Physical Characteristics | Damage Index |
|---|---|---|
| Collapse | Total collapse of infill | >1.00 |
| Severe | Extensive large cracks | 0.80–1.00 |
| Moderate | Corner crushing | 0.50–0.80 |
| Minor | First diagonal crack | 0.25–0.50 |
| Building | Size (mm.) | Main Reinforcement (mm.) | Stirrup Reinforcement (mm.) |
| C1 | 200 × 200 | 8DB16 | RB6@150 |
| B2 | 200 × 400 | 5DB16 | RB6@150 |
| RB | 200 × 400 | 5DB16 | RB6@150 |
| W1 | 125 × 200 | 2RB9 | RB6@150 |
| Parameter | Original Column | Reinforced X-Brace Concrete Frames |
|---|---|---|
| 30.05 | 30.05 | |
| - | 518.00 | |
| - | 548.05 | |
| 23.65 | 23.65 | |
| 11.19 | 190.57 |
| Parameter | Original Walls | Reinforced X-Brace Concrete Frames |
|---|---|---|
| 0.085 | 0.1176 | |
| - | 124.26 | |
| - | 75.52 | |
| 22.38 | 155.79 | |
| 22.38 | 231.31 | |
| 502.39 | 502.39 |
| Case Study | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (kN) | (m) | (m) | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | |
| Four-storey concrete building with x-bracing concrete frames | 478.780 | 0.048 | 0.06 | 0.83 | 0.85 | 0.86 | 0.86 | 0.88 | 0.89 |
| Four-storey concrete building without x-bracing concrete frames | 67.160 | 0.240 | 0.30 | 1.69 | 2.59 | 3.03 | 3.03 | 3.48 | 3.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chonratana, Y.; Chatpattananan, V. A Damage Index for Assessing Seismic-Resistant Designs of Masonry Wall Buildings Reinforced with X-Bracing Concrete Frames. Appl. Sci. 2023, 13, 12566. https://doi.org/10.3390/app132312566
Chonratana Y, Chatpattananan V. A Damage Index for Assessing Seismic-Resistant Designs of Masonry Wall Buildings Reinforced with X-Bracing Concrete Frames. Applied Sciences. 2023; 13(23):12566. https://doi.org/10.3390/app132312566
Chicago/Turabian StyleChonratana, Yossakorn, and Vuttichai Chatpattananan. 2023. "A Damage Index for Assessing Seismic-Resistant Designs of Masonry Wall Buildings Reinforced with X-Bracing Concrete Frames" Applied Sciences 13, no. 23: 12566. https://doi.org/10.3390/app132312566
APA StyleChonratana, Y., & Chatpattananan, V. (2023). A Damage Index for Assessing Seismic-Resistant Designs of Masonry Wall Buildings Reinforced with X-Bracing Concrete Frames. Applied Sciences, 13(23), 12566. https://doi.org/10.3390/app132312566







