Influence of Fastener Stiffness and Damping on Vibration Transfer Characteristics of Urban Railway Bridge Lines Using Vibration Power Flow Method
Abstract
:1. Introduction
2. Theoretical Analysis Model and Calculation Method
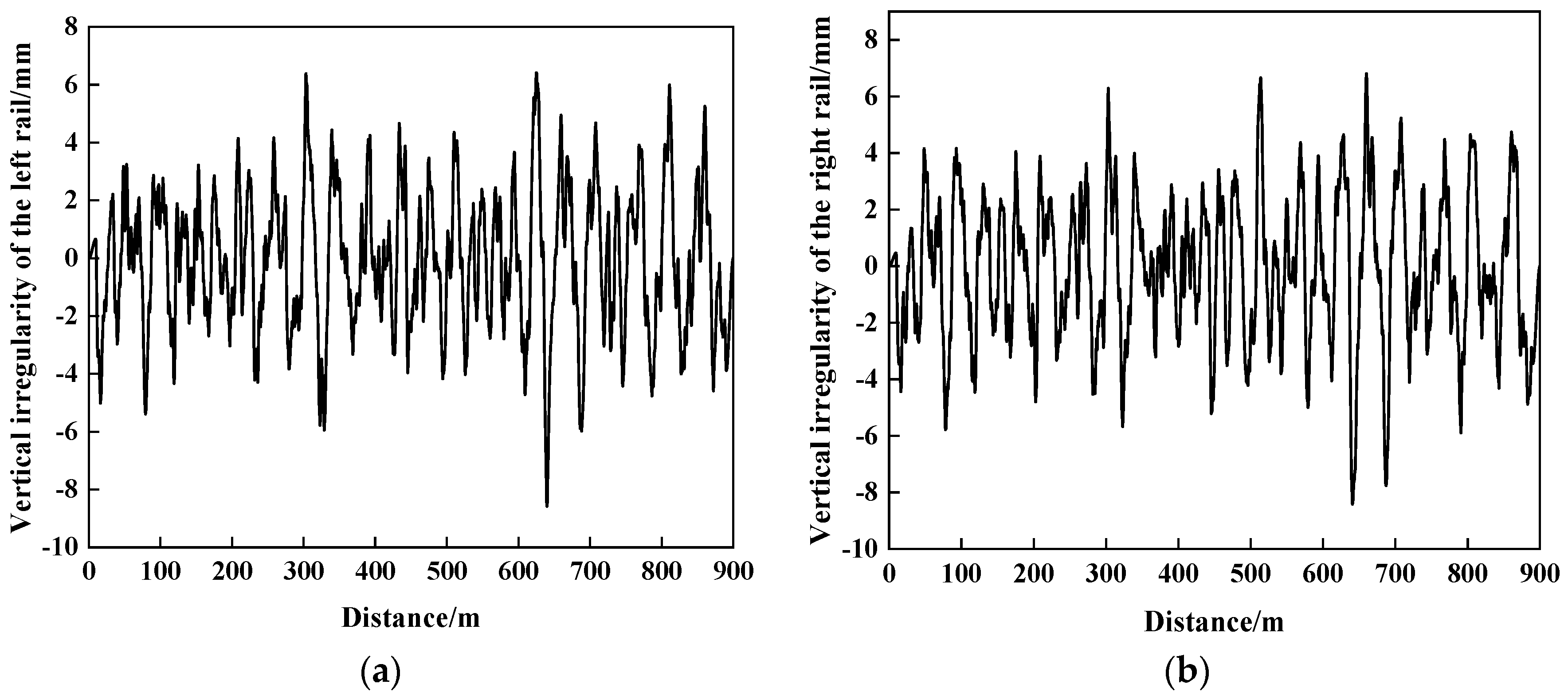
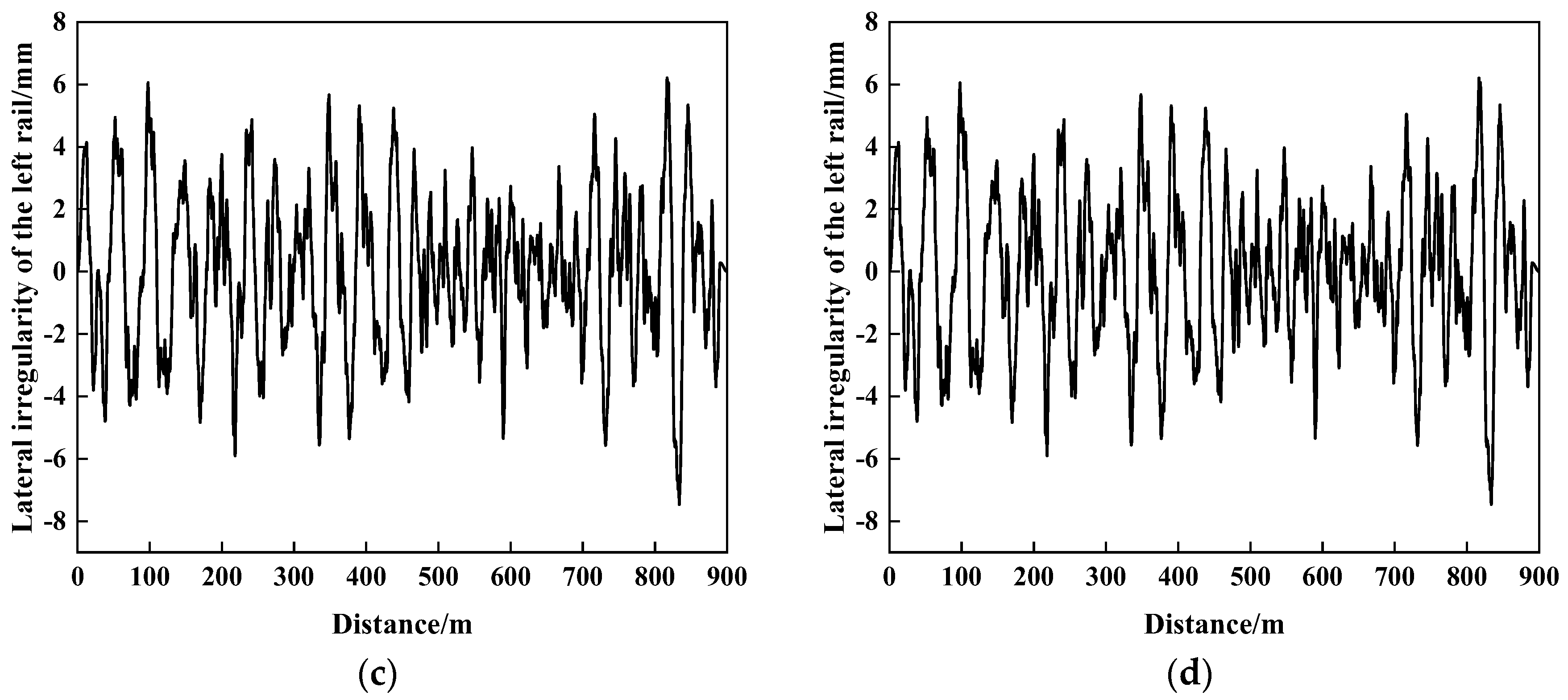
2.1. Establishment of Vehicle Model and Determination of Parameters
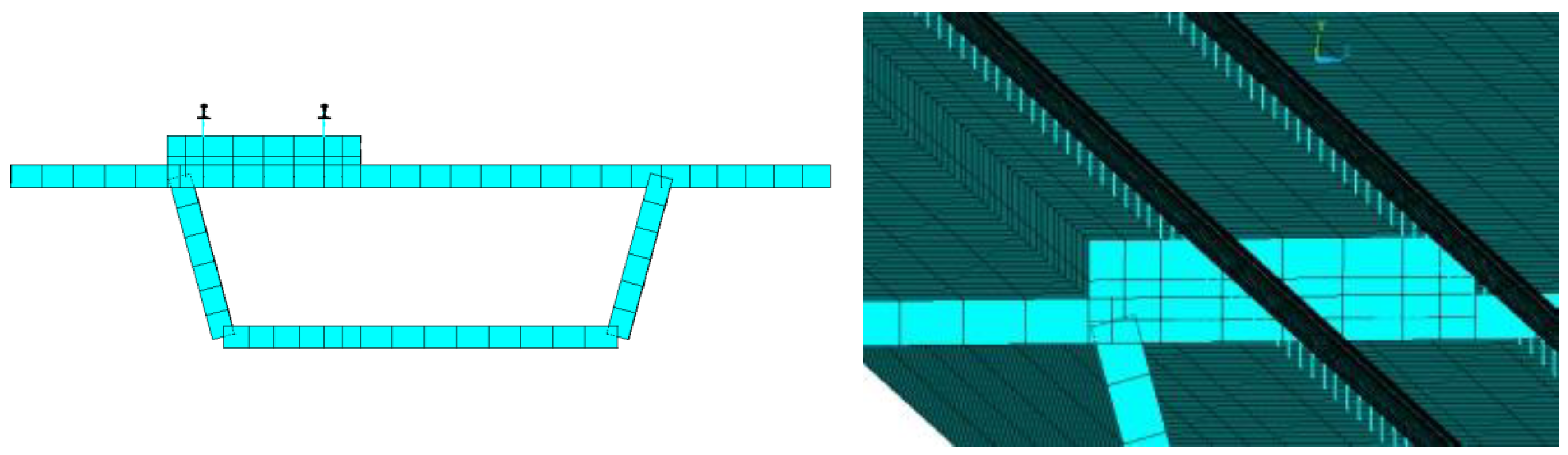
2.2. Finite-Element Model of Track–Box Girder Bridge
2.3. Method for Calculating Vibration Power Flow
3. Vibration Transmission Characteristics of Urban Track Transit Bridge Lines
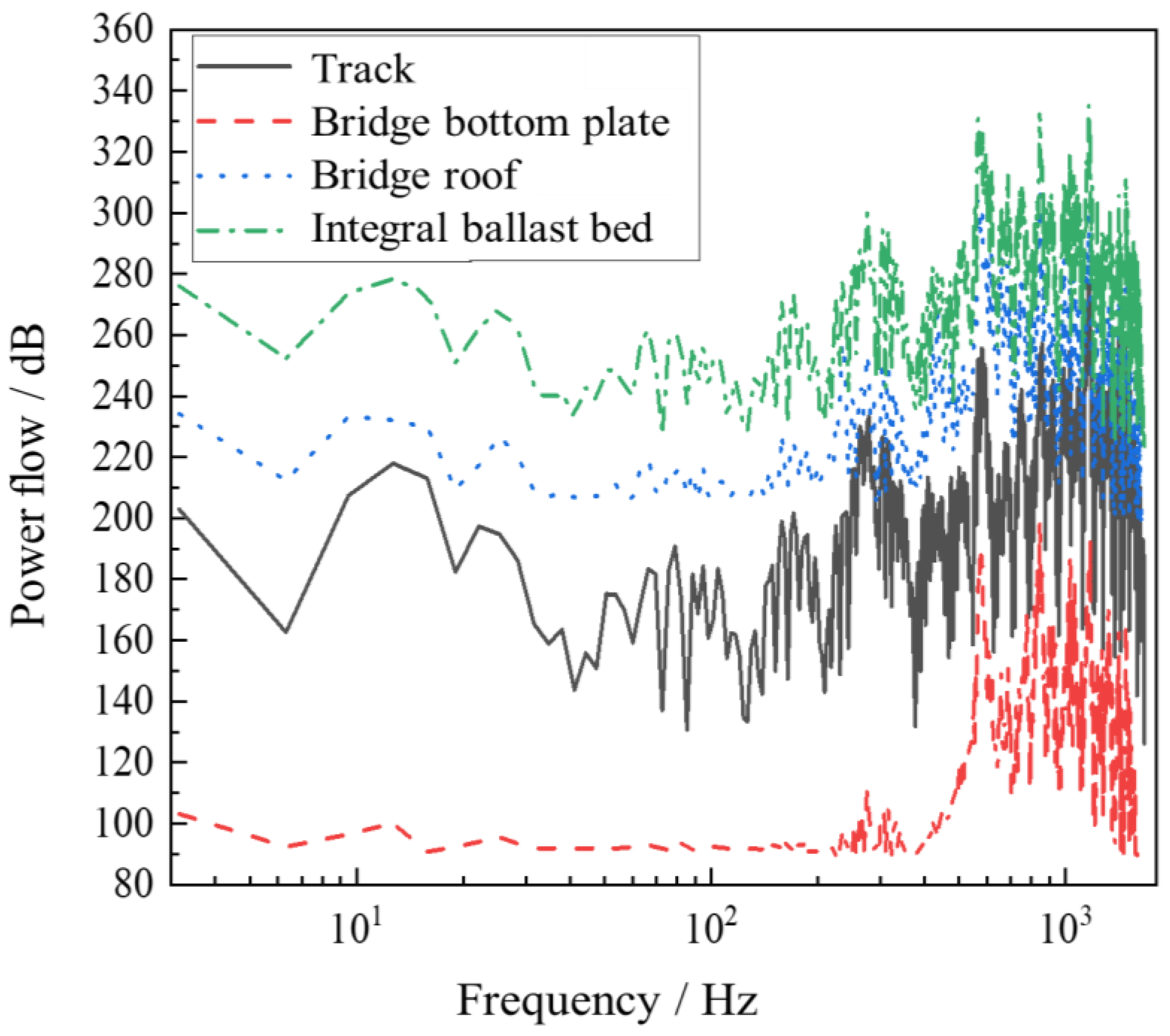
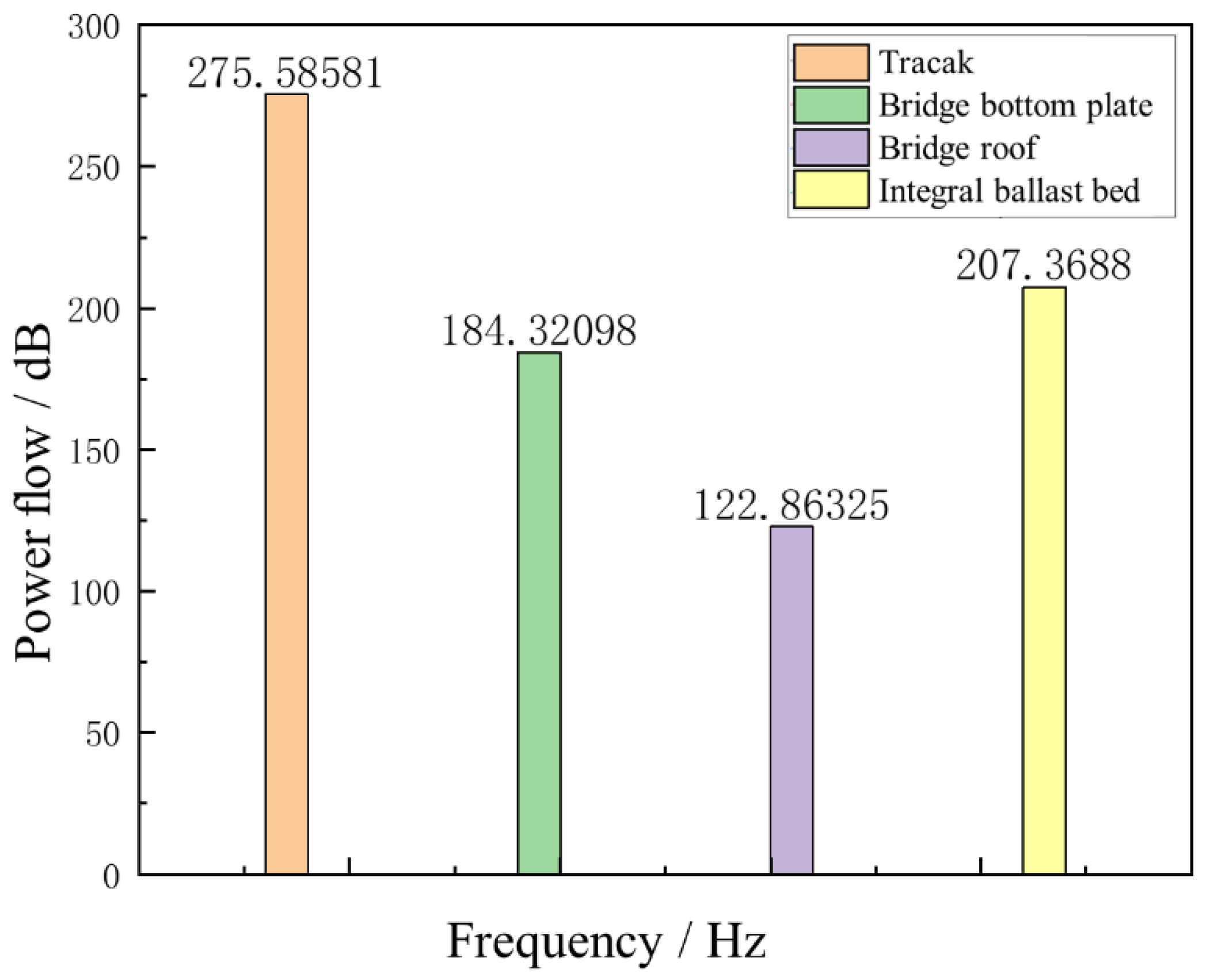
3.1. Vibration Energy Transfer Characteristics of Integral Ballast Bed Damping Track
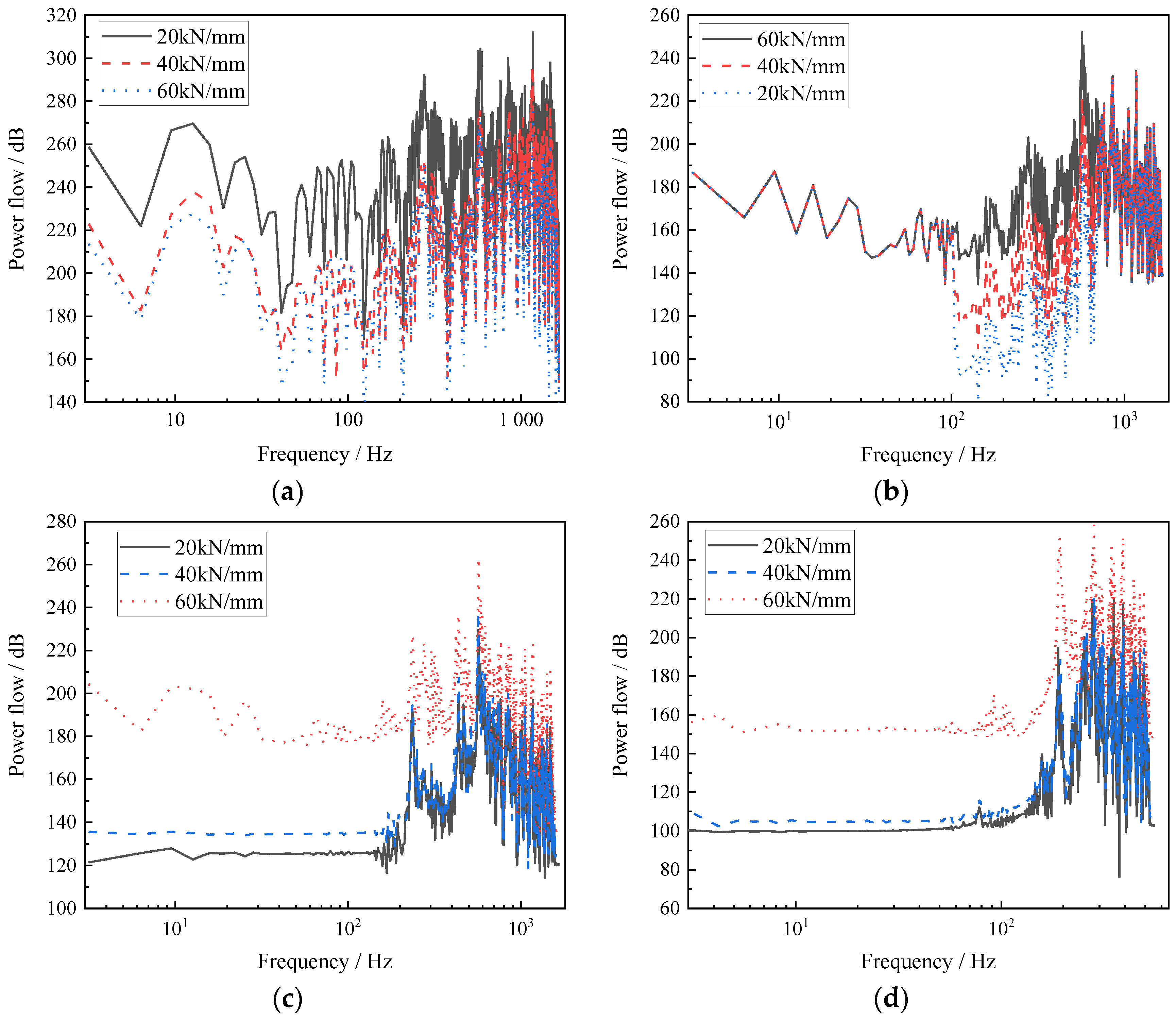
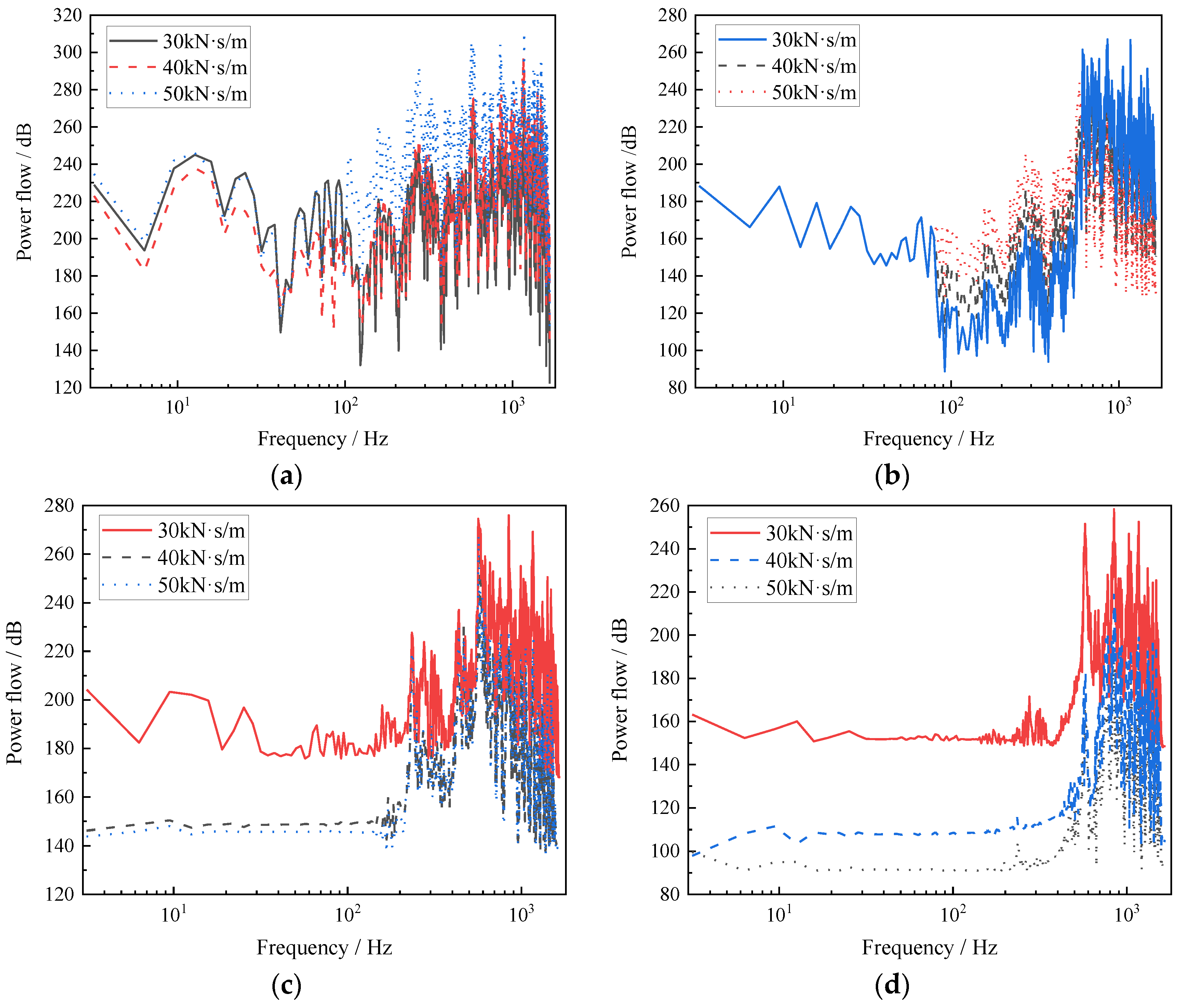
3.2. Effect of Fastener Parameters on System Power Flow Characteristics
3.2.1. Effect of Fastener Stiffness on Power Flow Transmission Characteristics
3.2.2. Impact of Fastener Damping on Power Flow Transmission Characteristics
4. Vertical Vibration Transmission Characteristics of Urban Track Transit Integral Ballast Bed–Box Girder Bridge
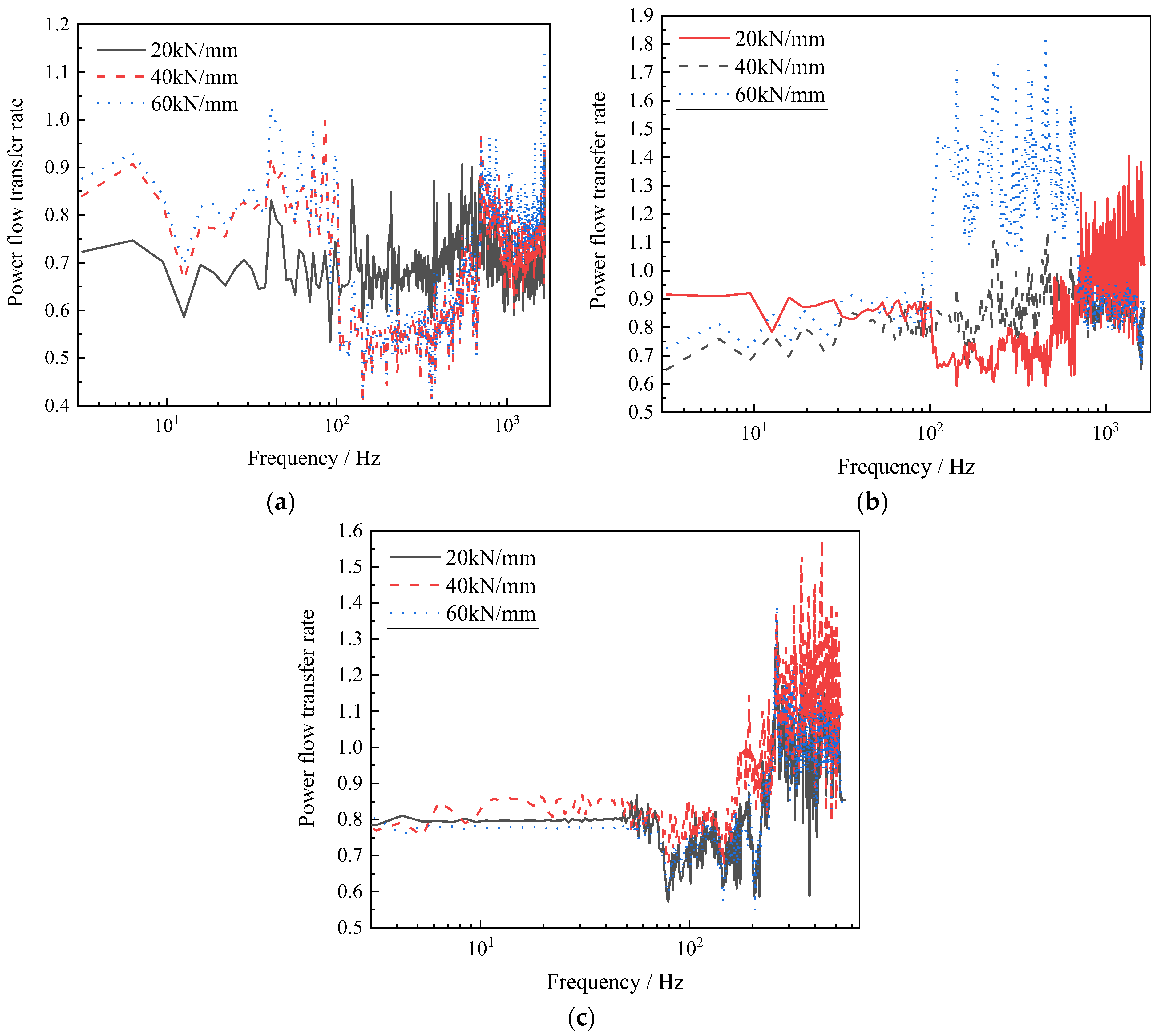
4.1. Analysis of Transmission Characteristics Based on Average Vibration Energy Level
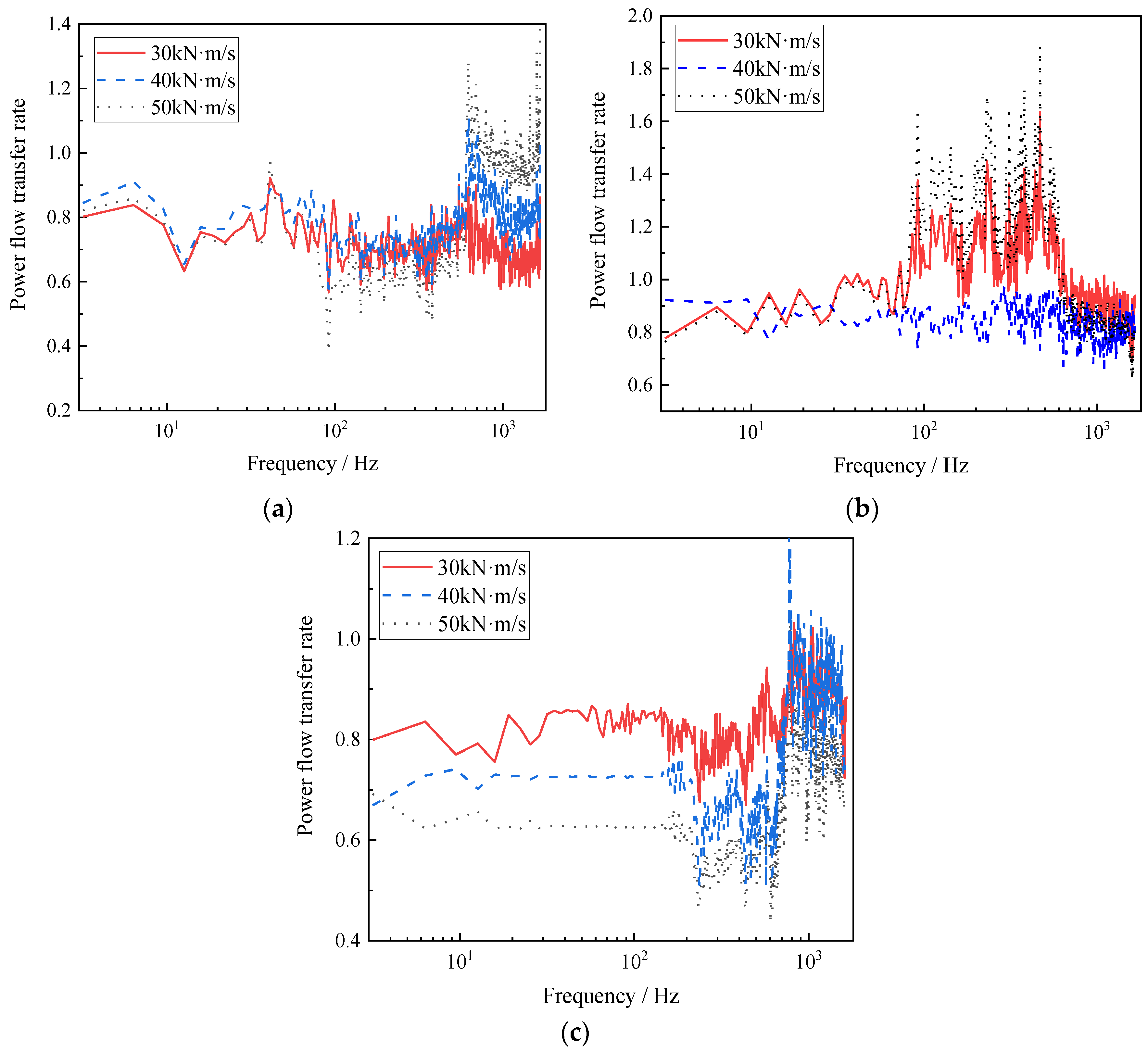
4.2. Impact of Fastener Parameters on the Power Flow Transfer Rate of the Entire System
5. Conclusions
- (1)
- The vibration energy caused by train operation in the low-frequency band is mainly concentrated in the integral ballast bed and the bridge roof and bottom plate of the box girder bridge. Most of the vibration energy will accumulate in the ballast bed. The vibration energy in the middle- and high-frequency band is mainly concentrated in the track position.
- (2)
- The fastener system, as the main vibration reduction component of the ordinary integral ballast, has a greater impact on the power flow in the low frequency range. Strategically reducing the stiffness of fasteners can effectively attenuate the transmission of low-frequency vibrations to the bridge, consequently leading to a reduction in the low-frequency vibrations experienced by the bridge structure. In the range of middle and low frequency, the accumulation of vibration energy of ballast decreases with the increase in damping of the fastener. However, with the increase in frequency, the accumulation state of vibration energy of the ballast bed and bridge will be intensified.
- (3)
- The fastener is the vibration reduction component of the ordinary integral ballast bed. In order to reduce the vibration and noise of the bridge on the bridge line, it is recommended to set the stiffness and damping of the fastener to 40 kN/mm and 50 kN·s/m, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, L.; Song, R.; Zhou, Y.-L.; Qin, J. Noise and vibration mitigation performance of damping pad under CRTS-III ballastless track in high speed rail viaduct. KSCE J. Civil. Eng. 2019, 23, 3525–3534. [Google Scholar] [CrossRef]
- Zhao, C.; Shi, D.; Zheng, J.; Niu, Y.; Wang, P. New floating slab track isolator for vibration reduction using particle damping vibration absorption and bandgap vibration resistance. Constr. Build. Mater. 2022, 336, 127561. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, W.; Jiang, L.; Peng, K.; Zu, L. Train effect on the vibration behavior of high-speed railway track-bridge system subjected to seismic excitation. Soil Dyn. Earthq. Eng. 2023, 172, 108049. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, D.; Zhang, X.; Yi, Q.; Wang, L.; Wang, P. Influence of vibration isolator failure on vehicle operation performance and floating slab track structure vibration reduction effectiveness. Shock. Vib. 2019, 2019, 8385310. [Google Scholar] [CrossRef]
- Zhou, X. Numerical analysis of influence of different track structures on vibration response of subway. Therm. Sci. 2020, 24, 1537–1543. [Google Scholar] [CrossRef]
- König, P.; Salcher, P.; Adam, C.; Hirzinger, B. Dynamic analysis of railway bridges exposed to high-speed trains considering the vehicle–track–bridge–soil interaction. Acta Mech. 2021, 232, 4583–4608. [Google Scholar] [CrossRef]
- Goyder, H.; White, R. Vibrational power flow from machines into built-up structures, part I: Introduction and approximate analyses of beam and plate-like foundations. J. Sound Vib. 1980, 68, 59–75. [Google Scholar] [CrossRef]
- Goyder, H.; White, R. Vibrational power flow from machines into built-up structures, part II: Wave propagation and power flow in beam-stiffened plates. J. Sound Vib. 1980, 68, 77–96. [Google Scholar] [CrossRef]
- Goyder, H.; White, R. Vibrational power flow from machines into built-up structures, part III: Power flow through isolation systems. J. Sound Vib. 1980, 68, 97–117. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, L.; Wang, S.; Chen, L.-Q. Vibration power flow characteristics of the whole-spacecraft with a nonlinear energy sink. J. Low Freq. Noise Vib. Act. Control 2019, 38, 341–351. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, G.; Yin, S.; Yuan, Y. Vibration transmission path analysis of underwater vehicle power plant based on TPA power flow. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2022, 236, 150–159. [Google Scholar] [CrossRef]
- Dai, W.; Shi, B.; Yang, J.; Zhu, X.; Li, T. Enhanced suppression of longitudinal vibration transmission in propulsion shaft system using nonlinear tuned mass damper inerter. J. Vib. Control 2023, 29, 2528–2538. [Google Scholar] [CrossRef]
- Fu, N.; Zhao, Z.; Liu, Y.; Li, Y. Vibrational Energy Properties of Twin-Block Ballastless Track with Anti-vibration Structure on Bridge by Power Flow Analysis. KSCE J. Civ. Eng. 2022, 26, 715–726. [Google Scholar] [CrossRef]
- Sudheesh, K.; Sujatha, C.; Krishnapillai, S. Vibration power flow analysis of simply supported uniform beams under moving point loads. Int. J. Dyn. Control 2023, 11, 1–16. [Google Scholar] [CrossRef]
- Ghangale, D.; Arcos, R.; Clot, A.; Cayero, J.; Romeu, J. A methodology based on 2.5D FEM-BEM for the evaluation of the vibration energy flow radiated by underground railway infrastructures. Tunn. Undergr. Space Technol. 2020, 101, 103392. [Google Scholar] [CrossRef]
- Zhai, W.; Xia, H.; Cai, C.; Gao, M.; Li, X.; Guo, X.; Zhang, N.; Wang, K. High-speed train–track–bridge dynamic interactions—Part I: Theoretical model and numerical simulation. Int. J. Rail Transp. 2013, 1, 3–24. [Google Scholar] [CrossRef]
- Zhai, W.; Han, Z.; Chen, Z.; Ling, L.; Zhu, S. Train–track–bridge dynamic interaction: A state-of-the-art review. Veh. Syst. Dyn. 2019, 57, 984–1027. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Wen, Z.; Zhao, Y. Numerical and experimental investigation into the mid- and high-frequency vibration behavior of a concrete box girder bridge induced by high-speed trains. J. Vib. Control 2018, 24, 5597–5609. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Zhang, Z.; Liu, Q.; Li, Y. Experimental research on noise emanating from concrete box-girder bridges on intercity railway lines. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2015, 229, 125–135. [Google Scholar] [CrossRef]
- Liang, L.; Li, X.; Yin, J.; Wang, D.; Gao, W.; Guo, Z. Vibration characteristics of damping pad floating slab on the long-span steel truss cable-stayed bridge in urban rail transit. Eng. Struct. 2019, 191, 92–103. [Google Scholar] [CrossRef]

| Degrees of Freedom | Hang Down | Rise and Fall | Nods |
|---|---|---|---|
| Train body | Zc | βc | |
| Front bogie | Zt1 | βt1 | |
| Rear bogie | Zt2 | βt2 | |
| First wheelset | Zw1 | - | βw1 |
| Second wheelset | Zw2 | - | βw2 |
| Third wheelset | Zw3 | - | βw3 |
| Fourth wheelset | Zw4 | - | βw4 |
| Parameters | Numerical Value |
|---|---|
| Body mass/kg | 4.566 × 104 |
| Height of vehicle center from track surface/m | 1.852 |
| Vehicle fixing distance/m | 15.7 |
| Quality of wheelsets/(kg·m2) | 1,985,110 |
| Fixed wheelbase/m | 1093 |
| Framing quality/kg | 2.5 |
| Primary longitudinal/transverse/vertical damping | 2081 |
| Two-system vertical/transverse/vertical damping (Ns/m) | 0/0/10,626 |
| Axlebox spring longitudinal/transverse stiffness | 0/2.9 × 104/1.1 × 104 |
| Wheel radius/m | 0.42 |
| Traction tie rod longitudinal stiffness (N/m) | 4.16 × 106 |
| Height of the upper plane of the gas spring from the track surface/m | 0.896 |
| Torsion bar spring stiffness (N/m) | 2.5 × 106 |
| Track Component | Cell Type | Correlation Parameter | Numerical Value |
|---|---|---|---|
| Track | Beam188 | Cross-sectional moment of inertia/(m4) | 2.1 × 1011 |
| Elastic modulus/(Pa) | 3.215 × 105 | ||
| Poisson’s ratio | 0.3 | ||
| Fastener | Combin14 | Linear density/(kg·m−1) | 60.64 |
| Stiffness/(N·m−1) | 4 × 107 | ||
| Damp/(N·s·m−1) | 2.26 × 104 | ||
| Integrated ballast bed | Solid45 | Density/(kg·m−3) | 2251 |
| Elastic modulus/GPa | 21 | ||
| Bridge | Shell63 | Elastic modulus/Pa | 3 × 1010 |
| Poisson’s ratio | 0.25 | ||
| Density/(kg·m−3) | 2500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Yang, L.; Li, P.; Xu, J.; Zhang, X. Influence of Fastener Stiffness and Damping on Vibration Transfer Characteristics of Urban Railway Bridge Lines Using Vibration Power Flow Method. Appl. Sci. 2023, 13, 12543. https://doi.org/10.3390/app132312543
Cao X, Yang L, Li P, Xu J, Zhang X. Influence of Fastener Stiffness and Damping on Vibration Transfer Characteristics of Urban Railway Bridge Lines Using Vibration Power Flow Method. Applied Sciences. 2023; 13(23):12543. https://doi.org/10.3390/app132312543
Chicago/Turabian StyleCao, Xingxiao, Li Yang, Peixuan Li, Jiangang Xu, and Xiaoyun Zhang. 2023. "Influence of Fastener Stiffness and Damping on Vibration Transfer Characteristics of Urban Railway Bridge Lines Using Vibration Power Flow Method" Applied Sciences 13, no. 23: 12543. https://doi.org/10.3390/app132312543
APA StyleCao, X., Yang, L., Li, P., Xu, J., & Zhang, X. (2023). Influence of Fastener Stiffness and Damping on Vibration Transfer Characteristics of Urban Railway Bridge Lines Using Vibration Power Flow Method. Applied Sciences, 13(23), 12543. https://doi.org/10.3390/app132312543






