Abstract
Various adjacent construction projects are inevitably encountered during the large-scale construction of urban underground transportation. The case of a twin shield tunnel excavated below an existing multi-arch culvert bridge in close vicinity has not yet been thoroughly studied. A case of a shield tunnel excavation below an existing multi-arch culvert bridge in Foshan is presented. First, a fully coupled three-dimensional model incorporating fluid and solid interactions was established to simulate the twin shield tunnel excavation below the existing multi-arch culvert bridge in close vicinity. Subsequently, the numerical model was validated using the modified Peck empirical formula. Finally, the influence of different foundation reinforcement deformation moduli, tunnel excavation face support pressures and grouting pressures on ground deformation was discussed. The results indicate that the area most significantly affected by the excavation of the tunnel passing underneath is not within the section of the multi-arch culvert bridge after applying the foundation reinforcement design. The area most significantly impacted is concentrated as the shield tunnel commences excavation and advances beneath the location corresponding to the 1-hole of the steel corrugated pipe. The range of influence of the ground disturbance extends approximately 7 m in front of the excavation face before the tunnel passed through. The range of ground disturbance decreases to 4–6 m in front of the excavation face after the tunnel passed through. The excavation face support pressure and grouting pressure have a minor impact on the settlement of the multi-arch culvert bridge under this reinforcement design. The results provide useful references for the reinforcement design for tunnel excavation adjacent to existing structures.
1. Introduction
The development of underground space can effectively address the issue of scarce urban land resources [1,2,3]. With the continuous development of urbanization, the scale of underground space development and utilization is constantly expanding [4]. During the process of underground space development and utilization, excavation of tunnels near existing structures is inevitable [5,6]. Tunnel excavation disrupts the original stress equilibrium of the surrounding strata with existing structures, leading to additional deformations in existing structures. Previous studies have shown that these structures experience significant deformations and even damage when tunnels are excavated near existing structures [7,8].
The interaction of tunnel–soil–existing structures is very complex, being related to many factors, such as the mechanical properties of soil layers [9,10], tunneling parameters [11], the distance between the tunnel and structures [12,13] and structural characteristics [14]. Some studies have used some empirical analysis methods to predict permanent ground subsidence caused by tunnel excavation to explore the impact of tunnel excavation on existing structures. Peck [15] explained that the settlement trough caused by tunnels can be fitted using a Gaussian function. The prediction of ground settlement deformation has evolved from two-dimensional to three-dimensional deformation and from single-track tunnels to multi-track tunnels [16,17] based on the continuous supplementation and modification of empirical formulas. Although empirical methods have been widely accepted in the tunneling industry, they lack a theoretical basis. Loganathan [18] proposed a theoretical method for predicting settlement and horizontal ground movement caused by tunnels, which is applicable to various ground conditions, tunnel geometries, construction techniques, and limited information about settlement distribution. However, due to the complexity of soil and tunnel excavation, empirical methods and theoretical methods cannot achieve completely accurate predictions.
With the development of computers, the advantages of numerical analysis methods in engineering have gradually become prominent. Huang et al. [19] analyzed the deformation of the rock mass around an existing tunnel caused by adjacent excavation based on a three-dimensional numerical model. Zhang et al. [20] discussed the influence of the construction disturbance of a super-large diameter shield tunnel on an existing tunnel through numerical simulation. Their results showed that the dynamic response amplitude of the segment at different positions is different. In addition to the numerical simulation to study the impact of tunnel excavation on the soil, the impact of tunnel excavation on nearby existing structures has also been extensively studied by numerical methods [21,22,23]. Xue and Zhang [24] established a two-dimensional granular flow numerical model for tunnel construction, investigating the relationship between the failure mode of the existing tunnel face, the support force, the excavation displacement, the longitudinal surface deformation and soil pressure distribution patterns. Ye et al. [25] studied the impact of excavation on the deformation of adjacent subway tunnels to ensure the safety of existing subway tunnel structures based on the PLAXIS 3D (CE V20) software. Yang et al. [26] explored the effects of different excavation sequences on the underlying existing tunnels based on numerical simulations using FLAC 3D. Zhang and Huang [11] analyzed the effects of shield tunnel construction for upper and lower cross tunnels through three-dimensional finite element simulation and simplified analysis methods. As can be seen above, most research is focused on the impact of tunnels on nearby individual structures. However, research on tunneling through a culvert bridge with multiple adjacent multi-arches is relatively scarce. Multi-arch culvert bridges differ from conventional single structures, as they consist of multiple culverts. There is a lack of research on the overall impact of tunnel excavation on the entire system formed by multiple culverts.
In this study, a case study involving the excavation of twin-line shield tunnels beneath an existing multi-arch culvert bridge in Foshan is presented. Initially, a fully coupled three-dimensional mode was established to simulate the excavation of twin shield tunnels in close proximity to the existing multi-arch culvert bridge. Subsequently, the numerical model was validated using the modified Peck empirical formula. Lastly, the influence of different foundation reinforcement deformation moduli, tunnel excavation face support pressures and grouting pressures on ground deformation was discussed. This study provides a useful reference for the reinforcement design for tunnel excavation adjacent to existing structures.
2. Project Overview
The Tongji Road west extension project is located in Foshan City, a coastal city of China. The road is 1.54 km in length and was built using the standard construction technique for first-class highways and urban roads. There is a multi-arch culvert bridge on the extension of the highway across a lake, as shown in Figure 1. The multi-arch culvert bridge spans approximately 140 m in length and 50 m in width. It runs parallel to the planned construction of twin-line subway tunnels. Figure 2 illustrates a section view of the multi-arch culvert bridge, tunnel location and strata condition. There are two types of corrugated steel pipes within the multi-arch culvert bridge. The corrugated pipes are labeled from left to right as 1-hole to 12-hole. The dimensions of the corrugated pipes for 4-hole to 9-hole are 7.77 m in height and 11 m in width, with a wall thickness of 9.75 mm. For the other holes, the corrugated pipes are 6.21 m in height and 8.7 m in width, with a wall thickness of 7.75 mm. The waveform specification of all steel corrugated pipes is 380 mm × 140 mm. The average spacing between the two tunnels is 5.76 m. with the minimum vertical distance between the culvert bridge and the tunnel is 3.8 m, located beneath 3-hole to 4-hole of the corrugated steel pipes. The shield excavation diameter is 6.7 m, and the tunnel segment thickness is 0.35 m, constructed using C50-grade concrete.
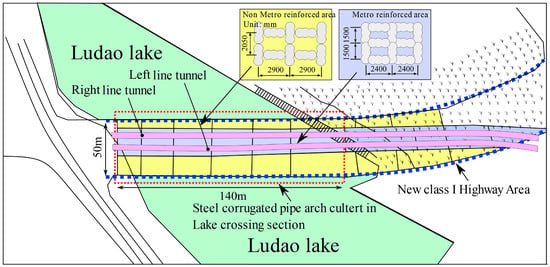
Figure 1.
Plane view of the arch culvert section.
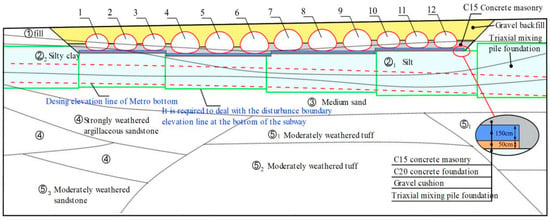
Figure 2.
Section view of the multi-arch culvert bridge, tunnel location and strata condition.
The construction of the multi-arch culvert bridge is situated on top of a complex soft soil foundation. The mechanical properties of the soil are presented in Table 1. The roadbed must possess high strength, stability and durability in engineering construction. However, the soft soil alone cannot meet these design requirements due to its high moisture content, low permeability, and low shear strength. A grid-type deep cement-soil triaxial mixing pile is a common ground improvement method used to address engineering issues such as uneven settlement and poor drainage in soft soil foundations [27]. A grid-type deep cement–soil triaxial mixing pile with a diameter of 850 mm was used to reinforce the foundation of the multi-arch culvert bridge in this engineering project. The reinforced area is divided into non-metro and metro reinforced areas. Figure 1 shows a plane view of the foundation treatment and the location of the tunnels. The center distances of the mixing piles in the non-metro and metro reinforced areas are 1.5 m × 2.4 m and 2.05 m × 2.9 m, respectively. The replacement rates of the metro-reinforced and non-metro reinforced areas are 59% and 72%, respectively. The treatment depth is 3 m below the tunnel excavation area. The results of triaxial tests show that the bearing capacities of the metro-reinforced area and non-metro reinforced area are 450 kPa and 300 kPa, respectively.

Table 1.
Parameters of soil.
3. Numerical Simulation
3.1. Finite Element Model
The influence area caused by tunnel excavation ranges from 1 to 2 times the diameter of the circular tunnel excavation [28]. Hence, the boundary settings for the model in this study extend beyond four times the tunnel diameter to avoid the boundary influence in numerical calculations. Due to the complexity of the engineering project, which involves 12 steel arch culverts and 2 tunnel structures, the computational workload for the finite element model is substantial. Therefore, some simplifications were applied to the establishment of the finite element model. The following assumptions were made:
- (1)
- Composite strata parameters were chosen for the non-subway reinforced areas from a safety perspective.
- (2)
- The pile-reinforced area was supposed to be a homogeneous horizontal layer.
- (3)
- The road surface of the multi-arch culvert bridge was treated as horizontally flat, while the geological layers were simplified to be horizontally distributed.
- (4)
- The spatial effects of the shield tunnel excavation were not considered.
This study combines the same type of soil layers due to the complexity of layering. Because the mechanical properties of the same type of soil are not significantly different, the impact on the simulation results is minimal. A three-dimensional finite element model was established based on the actual conditions of the project, which is shown in Figure 3 and Figure 4. The dimensions of the model are 250 m in length, 100 m in width, and 57 m in height. The average spacing between the two shield tunnels is 6.0 m. The mesh of the multi-arch culvert bridge, tunnels, and foundation reinforcement areas was refined to ensure computational accuracy. The C20 concrete foundations were simulated using liner structural elements with contact elements set on both sides. The final model comprises a total of 224,199 nodes and 210,972 elements.
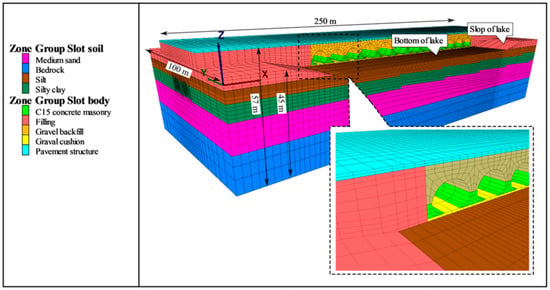
Figure 3.
3D finite element model.
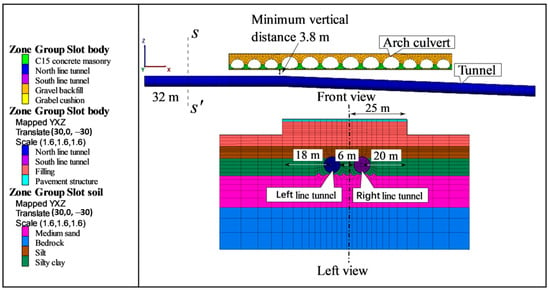
Figure 4.
The position of the tunnel and multi-arch culvert bridge in the s–s’ profile.
3.2. Parameter and Boundary Conditions
Due to the fact that this project spans across a lake, a fluid-structure coupling model has been established. The boundary conditions were set as follows:
- (1)
- The normal displacement of nodes on the four lateral sides of the model are constrained to be fixed.
- (2)
- The displacement in all three directions at the bottom nodes are set to be fixed.
- (3)
- The top boundary is an unconstrained free boundary.
- (4)
- The normal displacement of nodes on the sides along the longitudinal direction of the multi-arch culvert bridge is also set to be fixed.
- (5)
- Non-permeable boundaries are set at the four lateral side boundaries and bottom boundary of the model.
- (6)
- The boundary of the top surface is set as permeable.
Additionally, for the structural boundaries, constraints are applied to the nodes at the ends of the corrugated steel pipes, restricting the normal displacement. Since the water depth in the lake is 2 m, a vertically uniform load with a value of 20 kPa is applied to simulate the hydrostatic pressure of the water pressure. All geological layers are modeled using the Mohr–Coulomb constitutive model. The tunnel segments, corrugated steel pipes, and shield shells are modeled using linear elastic models. The computational parameters are listed in Table 2, Table 3 and Table 4.

Table 2.
Simulation parameters of soil layer.

Table 3.
Calculation parameters of multi-arch culvert bridge materials.

Table 4.
Calculation parameters of steel corrugated pipes.
3.3. Tunnel Excavation Simulation
The shield tunneling process induces disturbances in the soil at the excavation face, leading to a reduction in its strength. Hence, a modulus reduction method was employed for simulation, where the elastic modulus of the soil to be excavated in the next ring is reduced to 50% of its original value in the simulation. A simplified approach was adopted, assuming that the support pressure is equal to the initial horizontal stress at the tunnel axis of the excavation face.
A linear shrinkage of the shield diameter with a contraction rate of 0.4% is considered in this study. When the excavation diameter is 6.7 m, the over-excavation gap is approximately 13 mm. The state where the shield machine has fully entered the strata is taken as the initial condition, and the simulation of shield excavation and shield support is performed following the steps below:
- (1)
- Excavate the soil and create liner structural elements attached to the tunnel linings to simulate the shield shells.
- (2)
- Apart from the liner structural elements, fix the displacements of all nodes of the solid and structural elements, and only assign a radial inward velocity of 1 × 10−4 (m/step) to the liner structural element nodes. Iterate for 130 steps to achieve a uniform radial contraction of 13 mm, simulating the gap between of shield tunnel linings and shield shells.
- (3)
- Fix the displacements of liner structural element nodes and release the node constraints of other solid and structural elements (except for boundaries), and then solve for equilibrium.
- (4)
- After each shield excavation of one ring by 2 m, repeat steps (1) to (3) for a new liner structural element.
The implementation of the above method is based on the contact interface characteristics between liner structural elements and zone solid elements. As shown in Figure 5, when there is a gap between the shield shell and the tunnel lining, it is equivalent to the contact surface being subjected to tension and separation, and the interface tensile strength becomes 0. When the soil undergoes radial contraction and recontacts the shield shell, the contact surface is closed again, and the normal stress is generated.
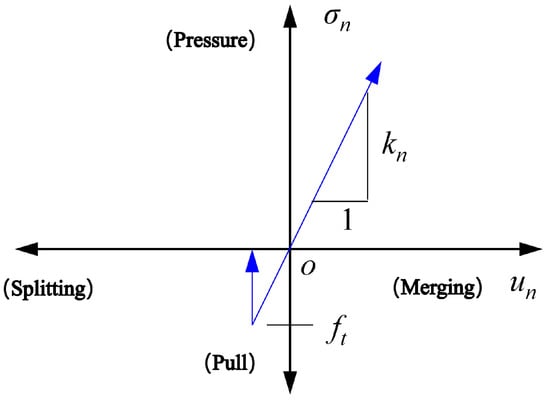
Figure 5.
The normal interface characteristics of contact surfaces.
A simplified measure was performed for simulating simultaneous grouting at the shield tail. The density of the grout obtained from tests was 20 kN/m3. When the grout is in a liquid state, it exerts radial outward grouting pressure on the tunnel linings. The grouting pressure was applied as a uniformly distributed surface load. After the grout has hardened, the simulation of the grouting pressure surface load was removed, and liner structural elements representing the grout layer were then established on the tunnel linings for support.
A comparative analysis of two different reinforcement conditions was conducted in this study, as shown in Table 5. Furthermore, different support pressures and grouting pressures were set for analysis based on the reinforcement scheme actually employed in engineering, as shown in Table 6.

Table 5.
Model settings of different reinforcement conditions.

Table 6.
Main parameters of shield.
3.4. Monitoring Point
The multi-arch culvert bridge is composed of two different types of corrugated steel pipes, so data-recording points need to be set at two different locations corresponding to these pipes. Data-recording points were established at the axial cross-sections of corrugated steel pipes at the 1-hole and 4-hole. These points are situated in the same cross-sectional plane as the central axis line of tunnel. Additionally, the base of the arch culvert is located at an elevation of 2 m below the lake surface. The distances of the measurement points from the west model boundary for the 1-hole and 4-hole are 59.4 m and 92.8 m, respectively. For the 1-hole and 4-hole, the distances of the measurement points from the south model boundary are 45 m and 57 m, respectively, as shown in the black points of Figure 6.
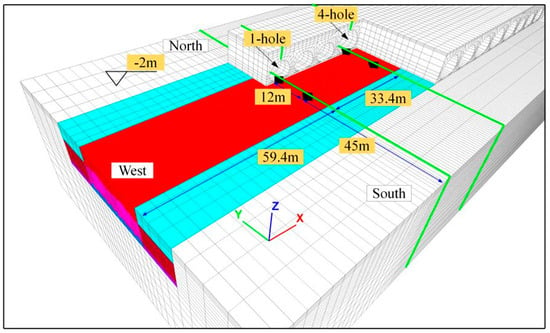
Figure 6.
Setting of data recording points.
4. Model Verification
As this project is still in the foundation treatment phase, there are no monitoring data available for model verification during tunnel excavation. Therefore, an empirical formula to predict surface settlement was used. Peck [15] proposed that ground settlement follows a normal distribution pattern by summarizing a substantial amount of field-measured settlement data caused by tunnel construction at that time. The surface settlement troughs induced by single-track tunnel excavation are calculated using the Peck empirical formula, which is presented as follows:
where A is the excavation area; s(x) is the surface settlement at a distance x from the tunnel centerline; i is the distance from the symmetry center of the settlement curve to the inflection point of the curve; and Vl is the stratum loss ratio.
Based on the superposition principle, the formula for calculating the surface settlement trough induced by the excavation of a twin-tunnel is obtained as follows:
where A1 and A2 are the cross-sectional areas of the first and second tunnels, respectively; Vl1 and Vl2 are the stratum loss ratios caused by the construction of the first and second tunnels, respectively; i1 and i2 are the widths of the settlement troughs induced by the construction of the first and second tunnels, respectively; and D is the distance between the centers of the two tunnels.
A verification was conducted using the non-arch culvert bridge section in the s–s’ profile (as shown in Figure 4). The distance from the tunnel axis to the surface at this cross-section is approximately 17.8 m. For the verification of a single tunnel, the natural stratum loss ratio was set at Vl = 0.7%, the coefficient was set at k = 0.6, and the settlement trough width coefficient was set at I = kZ0 (i = 10.68) based on regional engineering experience. Since the twin-line tunnels have the same burial depth and diameter, the parameter values for the two tunnels are the same as those for the single tunnel. The comparison of settlement trough results is shown in Figure 7. It can be observed from Figure 7 that the maximum subsidence of the settlement trough is located above the left-line tunnel during the excavation of a single tunnel. When the right-line tunnel is excavated, the centerline of the settlement trough gradually shifts away from the centers of both twin-line tunnels. Additionally, the empirical formula matches well in terms of magnitude and trend with the results of the numerical simulation, indicating the accuracy and validity of the numerical model. However, further model verification is needed for the section where the tunnel passes beneath the multi-arch culvert bridge.
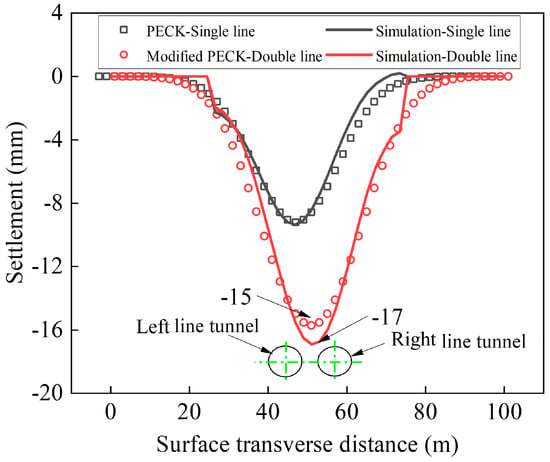
Figure 7.
Ground surface settlement curves of tunnel excavation.
5. Results Analysis
5.1. Analysis of Different Foundation Reinforcement Schemes
5.1.1. Foundation Settlement
Figure 8 shows the foundation settlement after twin-line tunnel excavation under two different foundation treatment conditions. It can be observed from Figure 8 that the two different reinforcement schemes have a minimal impact on foundation settlement. The maximum foundation settlement under different foundation treatment conditions differs by only 0.7%. This also implies that the reduction coefficient in the reinforcement scheme has a minimal effect on foundation settlement. Figure 8 shows that the maximum foundation settlement occurs at the tunnel crown, approximately 16 mm. The maximum foundation uplift occurs at the tunnel bottom, around 14 mm. The maximum settlement of the road surface without culverts is 9 mm, occurring in Area I, while the maximum settlement of the road surface in the culvert section is within 2 mm, occurring in Area II. The presence of culverts effectively reduces road surface settlement.
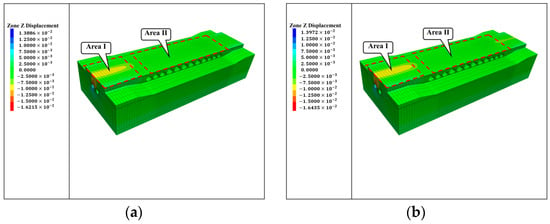
Figure 8.
Foundation settlement after twin-line tunnel excavation under two different foundation treatment conditions. (a) Condition JG-0; (b) condition JG-1.
Figure 9 shows the variation in settlement at the foundation bottom beneath the axis of the steel corrugated pipes with the distance from the tunnel excavation. It can be observed from the figure that there is no significant difference in settlement between the two reinforcement schemes. The difference in settlement caused by a 10% variation in the deformation modulus between the two schemes is within 1 mm. This is because the JG-0 design reinforcement scheme has a higher composite foundation-bearing capacity, and the cover soil above the steel corrugated pipe arch and the self-weight load of the culvert are not significant. Therefore, reducing the deformation modulus by 10% in the JG-1 reinforcement scheme does not result in significant settlement changes. It can be seen from Figure 9 that the settlement at P1ZD is greater than at P4ZD for both conditions. This is because the P1ZD point is located at the edge of the steel corrugated pipes and is more influenced by the shield tunnel excavation. For the P1ZD monitoring point, when the tunnel excavation reaches a distance of 7.3 m from the monitoring point, there is a sudden change in settlement at the monitoring point. After the tunnel excavation passes through, the settlement at the monitoring point slows down when it reaches a distance of 4.4 m from the point. This is because that the foundation modulus is different on both sides of the P1ZD monitoring point, with the foundation modulus in the reinforced area being higher than in the non-reinforced area. Therefore, the influence range of tunnel excavation on the weaker foundation is greater when it is above the reinforced area.
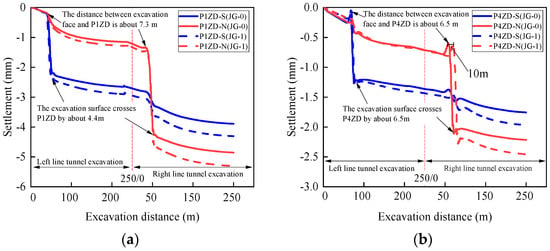
Figure 9.
Ground settlement at the bottom of the foundation above the tunnel crown. (a) 1-hole; (b) 4-hole.
Figure 10 shows the settlement at the foundation bottom along the excavation profiles of the 1-hole and 4-hole (axis profile locations indicated by the green lines in Figure 6). The maximum settlement at the 1-hole is approximately 2.5 mm greater than at the 4-hole. The settlement trough in the area enclosed by the red dashed lines does not follow a Gaussian distribution. This is because this location is situated at the edge of the steel corrugated pipes, where the soil treatment methods on either side are different. The difference of physical properties in soil leads to the appearance of a steep slope of settlement. Therefore, the maximum settlement has shifted by approximately 5 m to the right tunnel after the completion of the twin-line tunnel excavation, essentially aligning with the axis of the right tunnel.
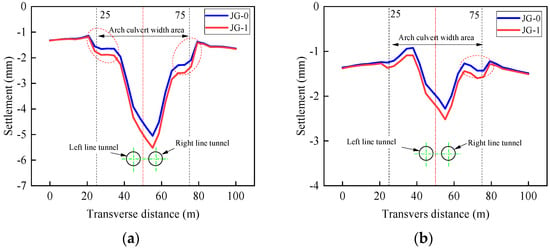
Figure 10.
Ground settlement at the bottom of the foundation of the steel corrugated axis section. (a) 1-hole; (b) 4-hole.
5.1.2. Pore Water Pressure
Figure 11 shows the pore pressure contour map along the excavation profile of the left tunnel during the excavation phase. The soil ahead of the excavation face experiences a rapid increase in pore water pressure due to the palm surface pressure. The most significant changes in pore water pressure occur within a range of 6 to 7 m ahead of the excavation face. As the distance from the face increases, the influence on pore water pressure gradually decreases. Pore water pressure rapidly decreases at the top and bottom of the tunnel due to the stress release caused by the shield over-excavation. Simultaneously, grouting causes an increase in the pore water pressure of strata near the tunnel lining.
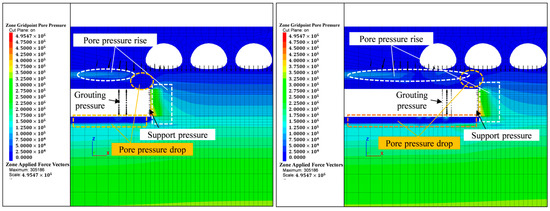
Figure 11.
Pore pressure contour of axis section of left line tunnel at a certain excavation stage.
Figure 12 shows the relationship between pore water pressure at the foundation bottom of the 1-hole and 4-hole and the excavation distance. The differences in pore water pressure changes caused by tunnel excavation under different reinforcement conditions are relatively small. The left tunnel is excavated first. When the excavation face is approximately 5.5 m away from P1ZD, the pore water pressure rapidly decreases from 20 kPa to 0, which marks point ①, where a sudden change occurs in Figure 12. When grouting pressure acts directly beneath P1ZD, the pore water pressure rapidly increases from 0 to 100 kPa, marked as point ② in Figure 12. As grouting pressure moves past P1ZD at a distance of approximately 11 m, the pore water pressure drops rapidly from 100 kPa to 65 kPa. Subsequently, the pore water pressure remains constant throughout the tunnel excavation process. Due to the low permeability of the foundation, the increase in pore water pressure caused by construction cannot dissipate quickly in a short time. Then, the right tunnel is excavated. The two sudden changes in pore water pressure, marked as ③ and ④ in Figure 12, occur for the same reasons as during the excavation of the left tunnel. Comparing the dashed and solid lines of the same color in the figure, it can be observed that under both reinforcement conditions, the construction of the twin-line tunnels does not significantly affect the pore water pressure changes at the other tunnel.
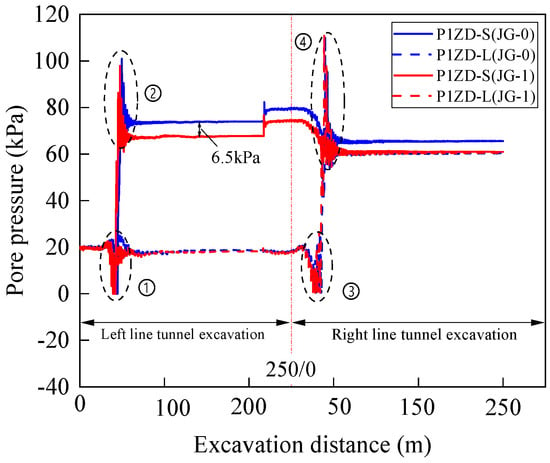
Figure 12.
Relation curve between pore water pressure and excavation distance.
5.2. Analysis of Supporting and Grouting Pressure
5.2.1. Foundation Settlement under Different Supporting Pressure
Figure 13 illustrates the variation in ground deformation with excavation distance under different excavation support pressures. When the support pressure at the excavation face is between 0.9 and 1.2 times the horizontal static soil pressure of the tunnel excavation axis, there is very little difference in settlement between P1ZD and P4ZD. This is because the ground deformation modulus after reinforcement is very large, and variations in the support pressure result in minimal ground deformation. Ultimately, the settlements for P1ZD-S and P1ZD-N are approximately 4 mm and 5 mm, respectively, while the settlements for P4ZD-S and P4ZD-N are approximately 1.7 mm and 2.3 mm, respectively.
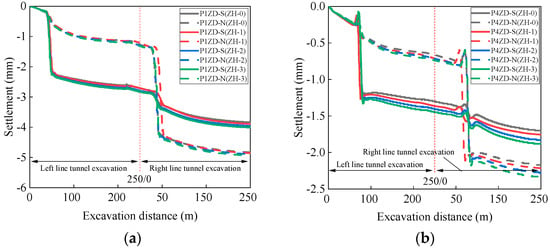
Figure 13.
Foundation settlement curve under different support pressures. (a) 1-hole; (b) 4-hole.
Figure 14 shows the ground settlement beneath the axis of the 1-hole under different excavation support pressures. It can be observed from the figures that different excavation support pressures have a minimal impact on ground settlement, which is consistent with the research conclusions of Yang et al. [30]. The ground settlement curves under different excavation support pressures almost overlap. Additionally, the maximum settlement has shifted by approximately 5 m northward after the completion of the twin-line tunnel excavation, positioning it along the axis of the right tunnel.
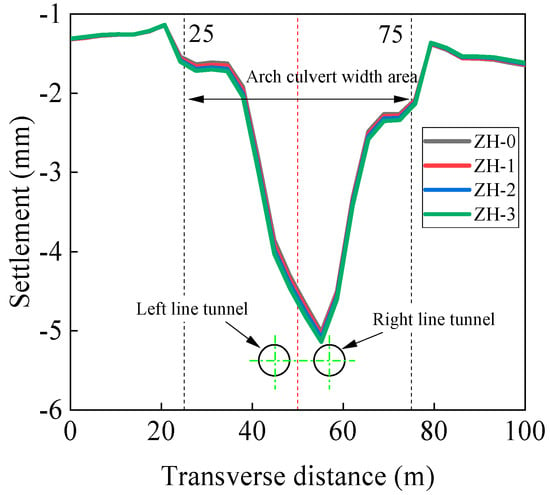
Figure 14.
Transverse foundation settlement under different support pressures.
5.2.2. Foundation Settlement under Different Grouting Pressures
Figure 15 shows the variation in ground deformation with excavation distance under different grouting pressures. During the excavation of the left tunnel, changes in grouting pressure have minimal influence on ground deformation. However, when the right tunnel is excavated, excavation of the left tunnel has already been completed. At this time, an increase in grouting pressure leads to reduced settlement caused by tunnel excavation. Specifically, when the grouting pressure at the tunnel crown is 0.9 times and 1.2 times the vertical stress of the same-depth ground layer after excavation stabilization, the difference in settlement is approximately 1 mm. Compared to changes in excavation support pressure, changes in grouting pressure have a more noticeable impact on ground settlement, which is consistent with the findings of references [31,32]. However, the large deformation modulus of the reinforced foundation appears to mitigate this impact to some extent in this study. The settlements for P1ZD-S and P1ZD-N range from 3 mm to 4 mm and 4 mm to 5 mm, respectively, while the settlements for P4ZD-S and P4ZD-N range from 1.4 mm to 1.7 mm and 1.7 mm to 2.4 mm, respectively.
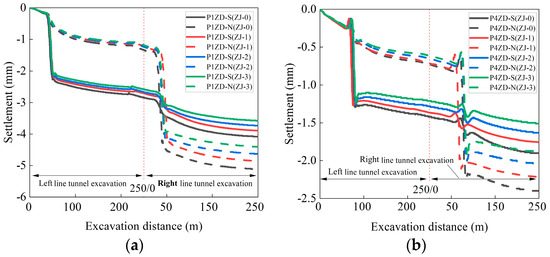
Figure 15.
Foundation settlement curves under different grouting pressures. (a) 1-hole; (b) 4-hole.
Figure 16 shows the ground settlement beneath the axis of the 1-hole under different grouting pressures. It can be observed from the figures that ground settlement gradually increases with an increase in grouting pressure, which is consistent with the research conclusions of Bao et al. [33]. The maximum difference in settlement caused by different grouting pressures is less than 0.5 mm. This indicates that different excavation support pressures and grouting pressures have a minimal effect on lateral ground settlement. Due to the influence of the excavation sequence, the maximum settlement has shifted approximately 5 m northward after the completion of the twin-line tunnel excavation, positioning it along the axis of the right tunnel.
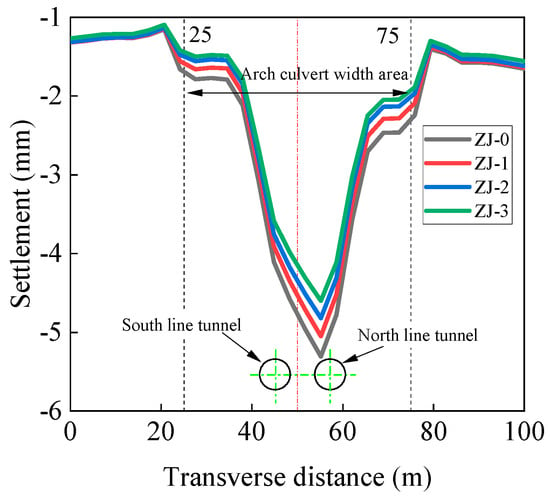
Figure 16.
Transverse foundation settlement under different grouting pressures.
6. Conclusions
In this study, the performance of twin-line shield tunnel excavation below an existing multi-arch culvert bridge in close vicinity was analyzed through numerical analysis. The following conclusions are drawn.
- (1)
- The lateral surface settlement caused by tunnel excavation follows a Gaussian distribution curve in areas outside the multi-arch culvert bridge, and the settlement is greater compared to the area beneath the arch culvert. The maximum settlement in these areas is approximately 9 mm. The ground improvement scheme employed in the engineering design involves high values of the ground deformation modulus and load-bearing capacity, which results in a relatively high overall stiffness of the multi-arch culvert bridge, making it less susceptible to the effects of tunnel excavation. The reinforcement measures of the foundation can be appropriately reduced to improve the economic benefits while ensuring safety.
- (2)
- Due to the varying deformation modulus of the soil on both sides of the multi-arch culvert bridge, the soil outside the foundation of the multi-arch culvert bridge is more affected by tunnel excavation. The deformation of the 1-hole at the edge of the steel corrugated pipes is more significantly influenced by the tunnel excavation. The transverse ground settlement trough exhibits an asymmetric distribution, with the maximum settlement trough shifting by approximately 5 m to the right tunnel. The later excavation of the right tunnel has a greater impact on the ground settlement compared to the earlier excavation of the left tunnel.
- (3)
- The range of influence of the ground disturbance extended approximately 7 m in front of the excavation face before the tunnel passed through. The range of ground disturbance decreased to 4–6 m in front of the excavation face after the tunnel passed through. Compared to the excavation face support pressure, the influence of grouting pressure on the ground is more significant. A reasonable grouting pressure can effectively control ground settlement. The foundation reinforced design with a high deformation modulus and high bearing capacity in this project resulted in relatively small settlement deformation caused by tunnel excavation, with the settlement of the multi-arch culvert bridge remaining within 2 mm. The chosen foundation reinforcement design appears to be reasonable.
Some simplifications were applied to the establishment of the finite element model to solve the computational workload, which may affect the calculation results in this study. Field monitoring data should be collected for the verification of the analysis in a following study. Furthermore, the spatial effects of shield tunnel excavation can be further considered based on this study after validating the model with on-site monitoring data.
Author Contributions
Conceptualization, X.B. and X.C.; methodology, Z.B.; validation, J.S., S.W. and S.Y.; formal analysis, S.W.; investigation, Z.B.; data curation, Z.B.; writing—original draft preparation, S.W.; writing—review and editing, J.S., Z.B.; supervision, X.B.; project administration, X.C.; funding acquisition, X.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China, grant number 2019YFC1511104, the National Natural Science Foundation of China (Grant No. 52090084) and the Technical Innovation Foundation of Shenzhen, grant number JCYJ20220531101214031.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Shuming Yang was employed by the company China Railway 22nd Bureau Group Shenzhen Construction Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Ng, C.; Boonyarak, T.; Masín, D. Three-dimensional centrifuge and numerical modeling of the interaction between perpendicularly crossing tunnels. Can. Geotech. J. 2013, 50, 935–946. [Google Scholar] [CrossRef]
- Talmon, A.M.; Bezuijen, A. Calculation of longitudinal bending moment and shear force for Shanghai Yangtze River Tunnel: Application of lessons from Dutch research. Tunn. Undergr. Space Technol. 2013, 35, 161–171. [Google Scholar] [CrossRef]
- Zhang, D.M.; Huang, Z.K.; Yin, Z.Y.; Ran, L.Z.; Huang, H.W. Predicting the grouting effect on leakage-induced tunnels and ground response in saturated soils. Tunn. Undergr. Space Technol. 2017, 65, 76–90. [Google Scholar] [CrossRef]
- Goel, R.K.; Singh, B.; Zhao, J. Underground Infrastructures: Planning, Design, and Construction; Butterworth-Heinemann: Oxford, UK, 2012; pp. 329–335. [Google Scholar] [CrossRef]
- Li, P.; Du, S.; Ma, X.; Yin, Z.; Shen, S. Centrifuge investigation into the effect of new shield tunnelling on an existing underlying large-diameter tunnel. Tunn. Undergr. Space Technol. 2014, 42, 59–66. [Google Scholar] [CrossRef]
- Chen, X.S.; Shen, J.; Bao, X.H.; Wu, X.L.; Tang, W.C.; Cui, H.Z. A review of seismic resilience of shield tunnels. Tunn. Undergr. Space Technol. 2023, 136, 105075. [Google Scholar] [CrossRef]
- Chang, C.-T.; Sun, C.-W.; Richard, W.S.D. Response of a Taipei Rapid Transit System (TRTS) tunnel to adjacent excavation. Tunn. Undergr. Space Technol. 2001, 16, 151–158. [Google Scholar] [CrossRef]
- Chen, R.P.; Meng, F.Y.; Li, Z.C.; Ye, Y.H.; Ye, J.N. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils. Tunn. Undergr. Space Technol. 2016, 58, 224–235. [Google Scholar] [CrossRef]
- Shi, J.W.; Zhang, X.; Chen, L.; Chen, L. Numerical Investigation of Pipeline Responses to Tunneling-Induced Ground Settlements in Clay. Soil Mech. Found. Eng. 2017, 54, 303–309. [Google Scholar] [CrossRef]
- Meng, F.Y.; Chen, R.P.; Wu, H.N.; Xie, S.W.; Liu, Y. Observed behaviors of a long and deep excavation and collinear underlying tunnels in Shenzhen granite residual soil. Tunn. Undergr. Space Technol. 2020, 103, 103504. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil. Comput. Geotech. 2014, 56, 121–132. [Google Scholar] [CrossRef]
- Zheng, Y.; Wu, K.; Sun, J.; Chen, R.; Li, Y.M.; Yang, S.F. Study on the Influence of Close Distance Construction of Urban Tunnel on the Existing Station. Geotech. Geol. Eng. 2021, 39, 4765–4780. [Google Scholar] [CrossRef]
- Zhang, H.; He, P.; Qin, D.; Li, L. Influence on Existing Tunnel Crossed Vertically by New Shield Tunnel. China Railw. Sci. 2013, 34, 66–70. [Google Scholar]
- Yu, S.H.; Geng, Y.C. Influence Analysis of Underground Excavation on the Adjacent Buildings and Surrounding Soil Based on Scale Model Test. Adv. Civ. Eng. 2019, 2019, 6527175. [Google Scholar] [CrossRef]
- Peck, R.B. Deep excavations and tunnelling in soft ground. In Proceedings of the 7th ICSMFE, Mexico City, Mexico, August 1969. [Google Scholar]
- Song, Z.P.; Tian, X.X.; Zhang, Y.W. A New Modified Peck Formula for Predicting the Surface Settlement Based on Stochastic Medium Theory. Adv. Civ. Eng. 2019, 2019, 7328190. [Google Scholar] [CrossRef]
- Tang, X.W.; Liang, J.X.; Liu, W.; Ye, Y.H.; Gan, P.L.; Zhao, W.F.; Yu, Y. Modification of Peck Formula to Predict Ground Surface Settlement of Twin Tunnels in Low Permeability Soil. Adv. Civ. Eng. 2021, 2021, 6698673. [Google Scholar] [CrossRef]
- Loganathan, N. Analytical Prediction for Tunneling-Induced Ground Movements in Clays. J. Geotech. Geoenviron. Eng. 1998, 124, 846–856. [Google Scholar] [CrossRef]
- Huang, F.; Zhang, M.; Wang, F.; Ling, T.H.; Yang, X.L. The failure mechanism of surrounding rock around an existing shield tunnel induced by an adjacent excavation. Comput. Geotech. 2020, 117, 103236. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M.X.; Javadi, A.A. Influence of a Super-Large Diameter Shield Tunnel Excavation on the Lining Structure of the Metro Lines in Operation. Iran. J. Sci. Technol.-Trans. Civ. Eng. 2023, 47, 3851–3866. [Google Scholar] [CrossRef]
- Liang, R.; Xia, T.; Hong, Y.; Yu, F. Effects of above-crossing tunnelling on the existing shield tunnels. Tunn. Undergr. Space Technol. 2016, 58, 159–176. [Google Scholar] [CrossRef]
- Reza, B.A.; Vojtech, G. 3D numerical parametric study of the influence of open-pit mining sequence on existing tunnels. Int. J. Min. Sci. Technol. 2017, 27, 459–466. [Google Scholar] [CrossRef]
- Zheng, G.; Yang, X.Y.; Zhou, H.Z.; Du, Y.M.; Sun, J.Y.; Yu, X.X. A simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavations. Comput. Geotech. 2018, 95, 119–128. [Google Scholar] [CrossRef]
- Xue, F.; Zhang, M.X. Excavation Face Stability of Shield Tunneling Closely Under Existing Tunnels: Particle Flow Simulation. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 497–506. [Google Scholar] [CrossRef]
- Ye, S.; Zhao, Z.; Wang, D. Deformation analysis and safety assessment of existing metro tunnels affected by excavation of a foundation pit. Undergr. Space 2021, 6, 421–431. [Google Scholar] [CrossRef]
- Yang, T.; Tong, L.Y.; Pan, H.S.; Wang, Z.S.; Chen, X.M.; Li, H.J. Effect of Excavation Sequence on Uplift Deformation of Underlying Existing Metro Tunnel. J. Perform. Constr. Facil. 2021, 35, 2. [Google Scholar] [CrossRef]
- Hu, Z.F.; Yue, Z.Q.; Zhou, J.; Tham, L.G. Design and construction of a deep excavation in soft soils adjacent to the Shanghai Metro tunnels. Can. Geotech. J. 2003, 40, 933–948. [Google Scholar] [CrossRef]
- Qian, W.P.; Qi, T.Y.; Zhao, Y.J.; Le, Y.Z.; Yi, H.Y. Deformation characteristics and safety assessment of a high-speed railway induced by undercutting metro tunnel excavation. J. Rock Mech. Geotech. Eng. 2019, 11, 88–98. [Google Scholar] [CrossRef]
- GB/T 50487-2008; Water Resources and Hydropower Engineering Geological Investigation Specification. Ministry of Water Resources and Electric Power of People’s Republic of China: Beijing, China, 2019.
- Yang, M.; Li, H.R.; Li, N.; Yang, S. Effect of Subway Excavation with Different Support Pressures on Existing Utility Tunnel in Xi’an Loess. Adv. Civ. Eng. 2020, 2020, 8818949. [Google Scholar] [CrossRef]
- Xie, X.Y.; Yang, Y.B.; Ji, M. Analysis of ground surface settlement induced by the construction of a large-diameter shield-driven tunnel in Shanghai, China. Tunn. Undergr. Space Technol. 2016, 51, 120–132. [Google Scholar] [CrossRef]
- Dias, D.; Kastner, R. Movements caused by the excavation of tunnels using face pressurized shields—Analysis of monitoring and numerical modeling results. Eng. Geol. 2013, 152, 17–25. [Google Scholar] [CrossRef]
- Bao, X.; Zhang, Y.; Xu, C.; Fu, Y.; Cui, H.; Xie, X. Factors Affecting the Settlement of Double-Line Shield Tunnel Construction. J. Chongqing Jiaotong Univ. Nat. Sci. 2020, 39, 51–60. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).