CPSR-HQKDN: A Hybrid Trusted Relay Quantum Key Distribution Network Routing Scheme Based on Classification of Packet Security Requirements
Abstract
:1. Introduction
2. Problem Statement
3. Network Model
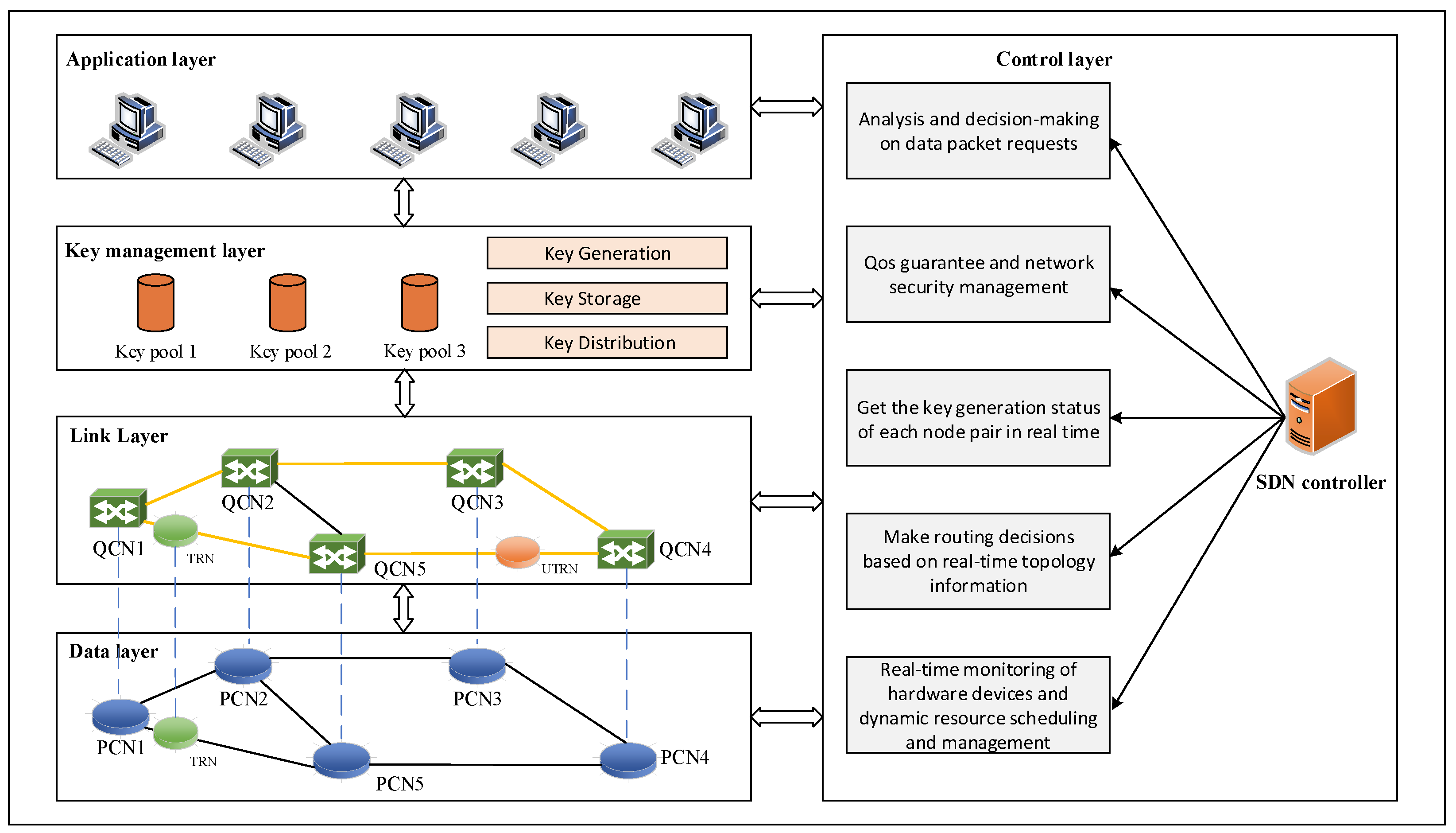
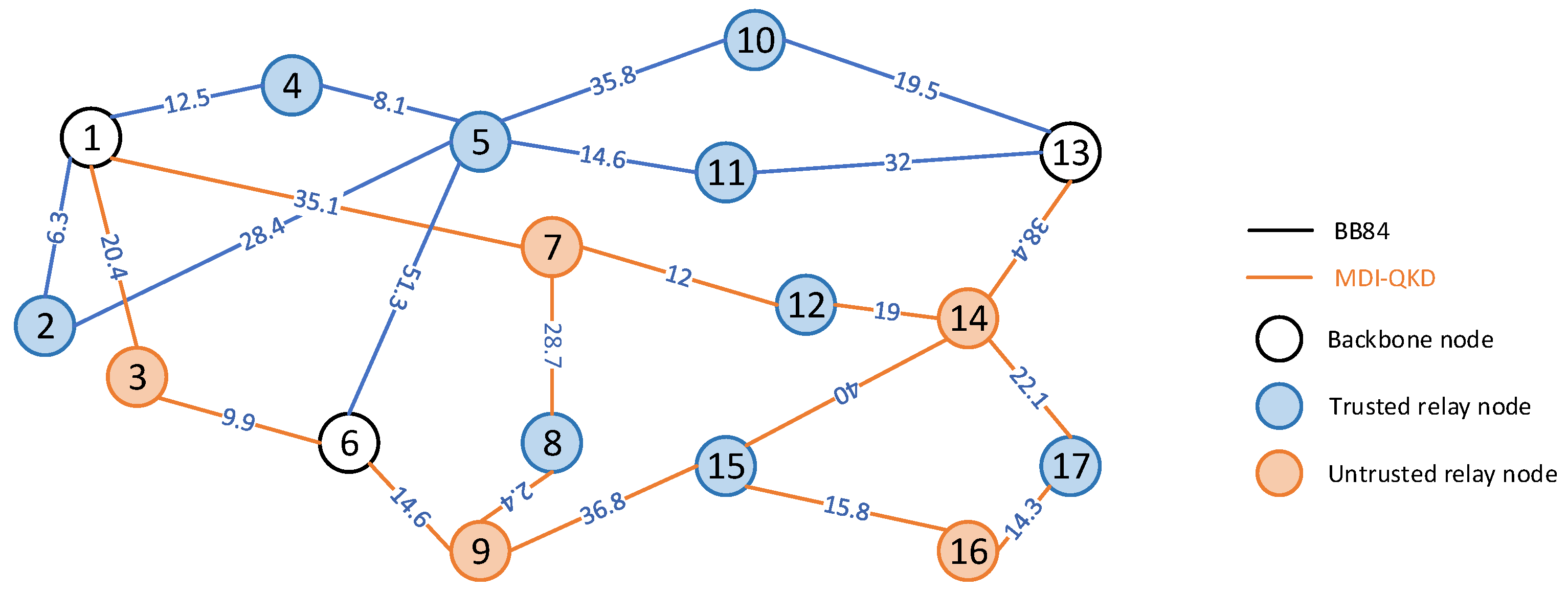
3.1. Quantum Key Distribution Luminescence Network Architecture Based on Hybrid Trusted Relay
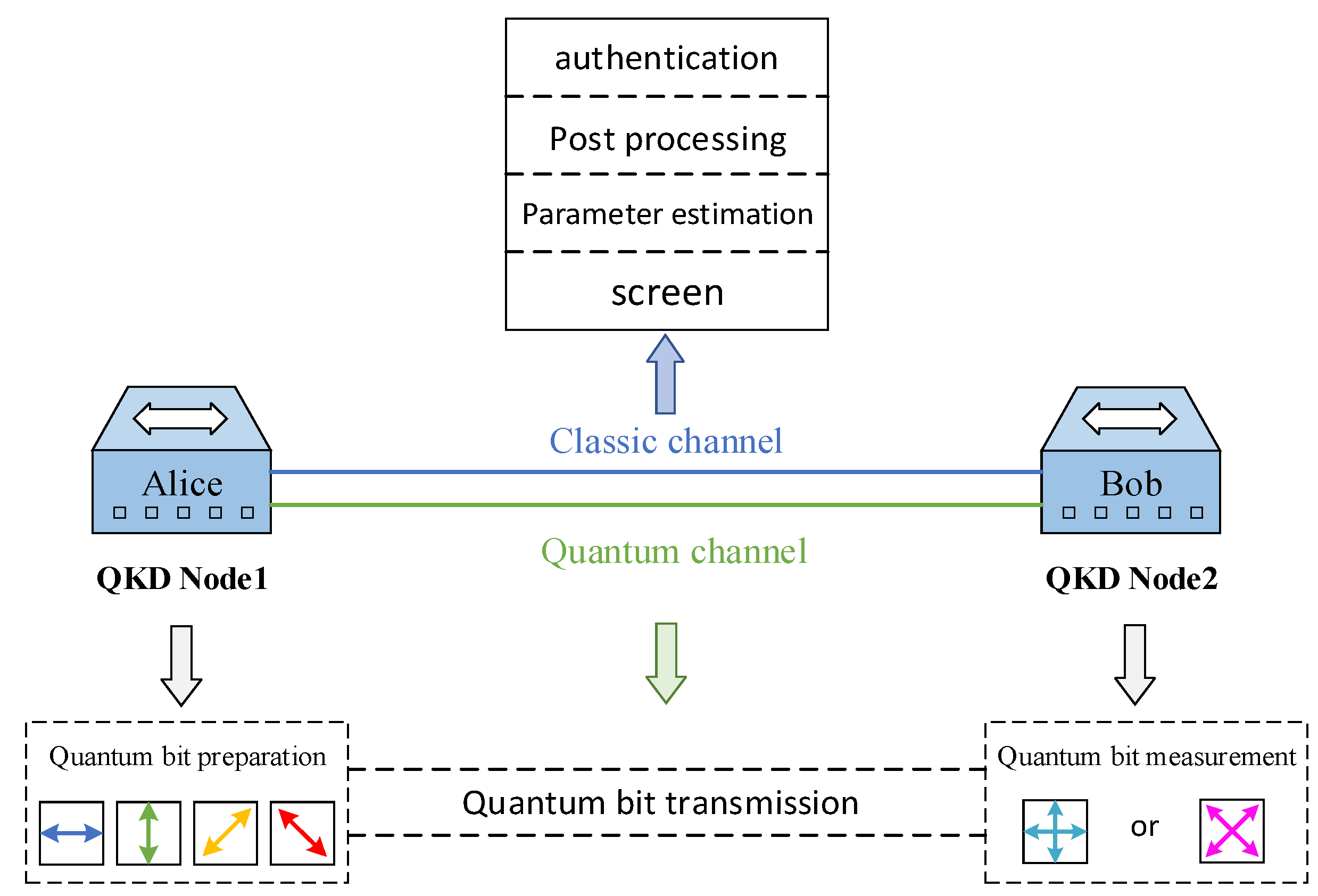
3.2. QKD Protocol, Model and Related Definitions
- QKD Link: A QKD link refers to the physical components involved in quantum key distribution, including optical transmitters, optical receivers, and the transmission medium. It is a virtual link abstracted between two quantum nodes, where the transmission and measurement of quantum bits based on QKD technology take place on the channel.
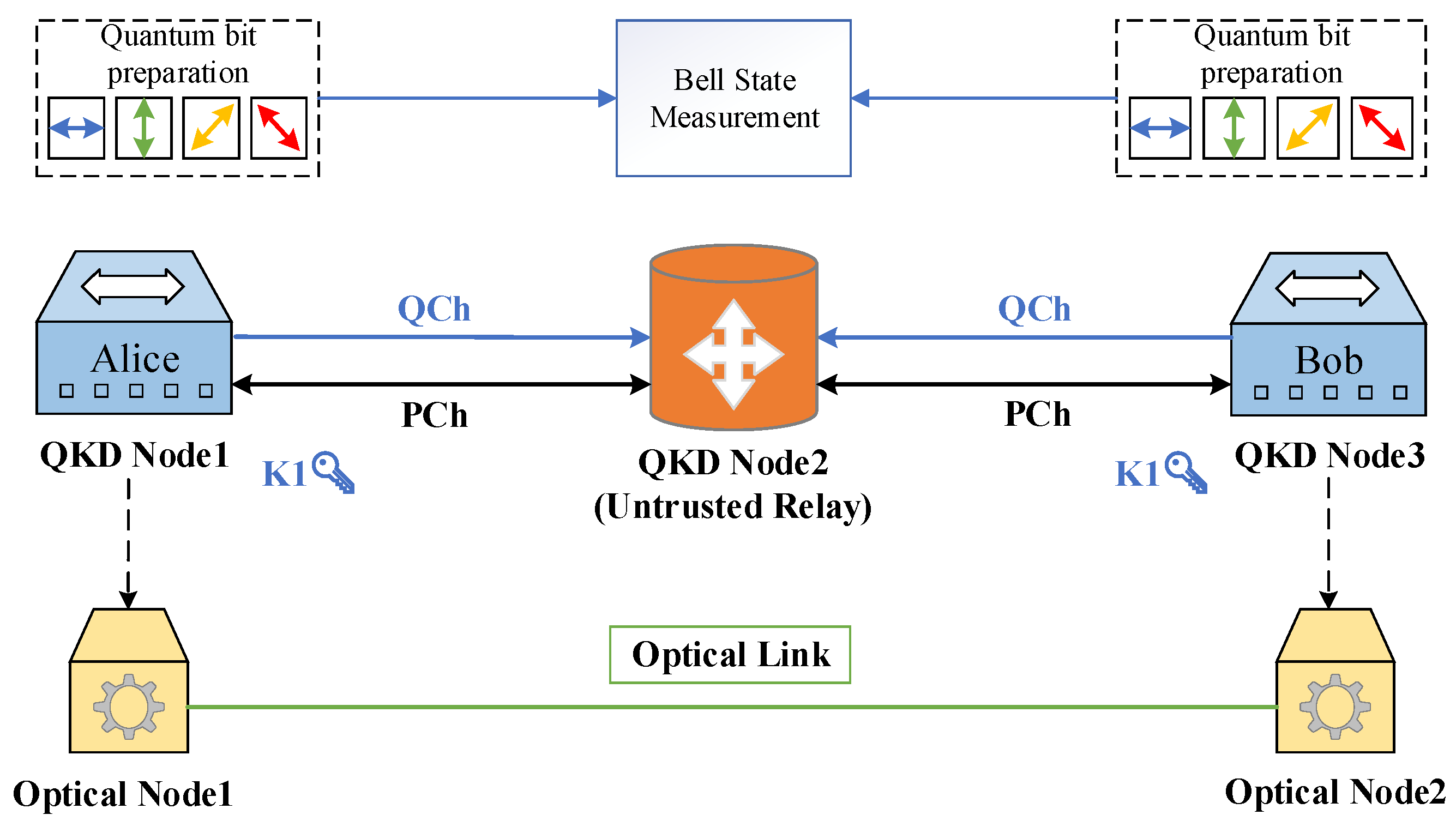
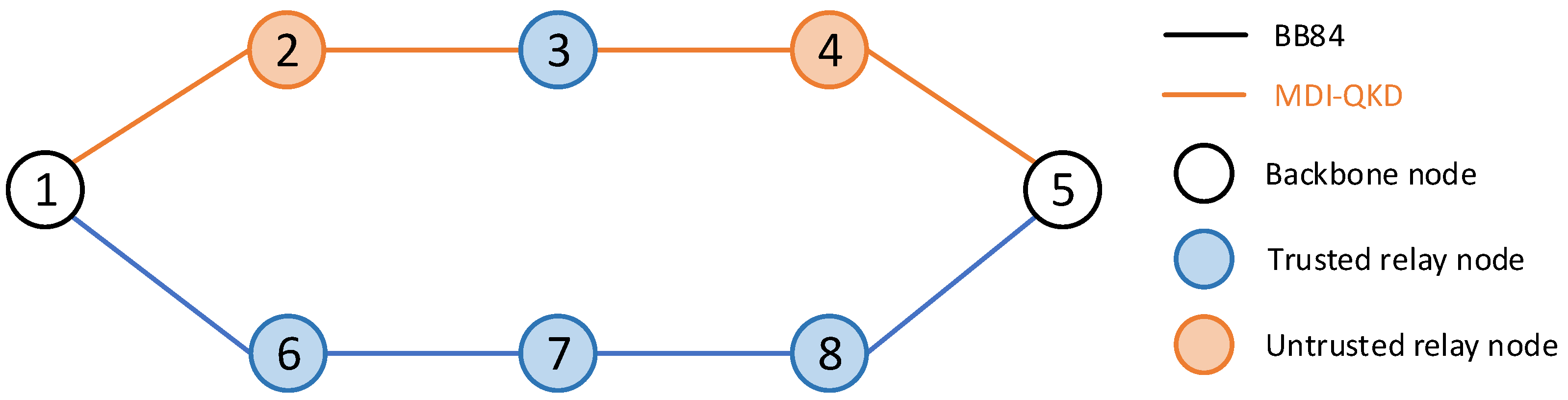
- Trusted Relay/Untrusted Relay: A trusted relay is an entity trusted by Alice and Bob, capable of establishing a secure communication link between them. Its functions mainly include channel enhancement, relay authentication, and key generation and distribution. Therefore, a trusted relay involves operations such as key storage and key utilization with the key pool. In MDI-QKD, an untrusted relay is considered an entity that cannot be trusted. Its functions mainly include the forwarding of quantum states, the measurement of Bell states, and noise filtering.
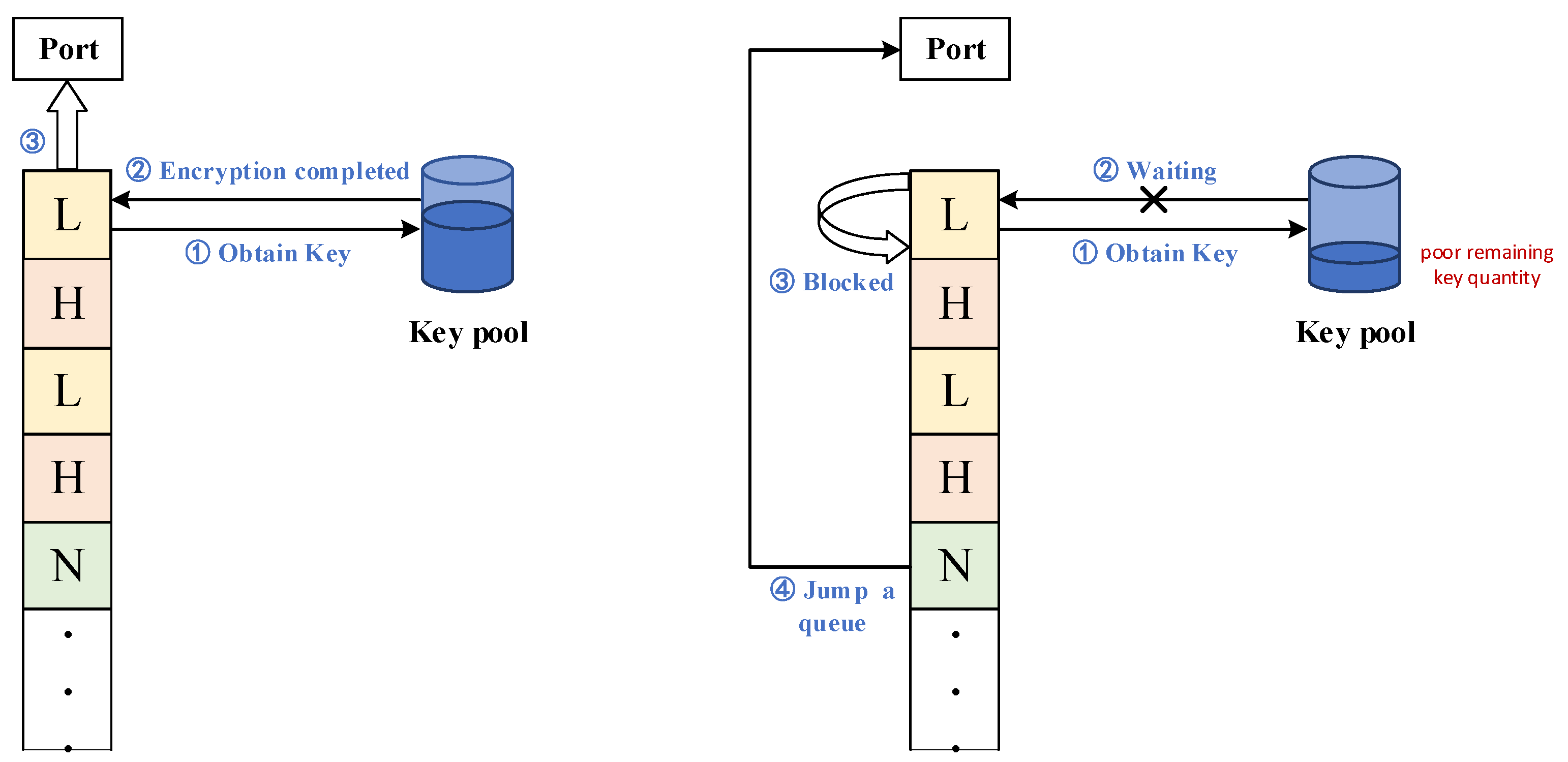
- Quantum Key Pool: The quantum key pool is a virtual concept that represents a series of quantum keys generated between a pair of quantum nodes in time slots. It also involves the issue of how to allocate keys to different data packets within the same time slot.
- Data Packet Security Requirement Levels: During the process of data transmission, not all data packets have the same security requirements. Some data packets may only require traditional encryption methods or even no encryption at all. Some data packets may be encrypted using quantum keys generated by the BB84 protocol. For the data packets with the highest security requirements, they will be encrypted using more valuable and secure quantum keys generated by the MDI-QKD protocol.
- Path Constraints: Different path selection constraints exist for data packets with different security requirements. First, for data packets that only require traditional encryption methods or no encryption at all, they do not need to pass through the QKD layer and can be directly processed at the traditional data layer. Therefore, they can choose the shortest path. Second, data packets encrypted using quantum keys generated by the BB84 protocol can only pass through backbone nodes and trusted relay nodes that utilize the BB84 protocol. Finally, data packets encrypted using quantum keys generated by the MDI-QKD protocol can only pass through backbone nodes, pairs of trusted relays, and untrusted relays located between the pairs of trusted relays that utilize the MDI-QKD protocol.
- Time Slot: In the field of communications, a time slot is a unit of time used for the allocation and management of resources in multiplexing techniques. Time slots divide time into non-overlapping intervals, with each time slot designated for the transmission of specific data or signals. One of the advantages of using time-division multiplexing is the efficient utilization of transmission resources and shared bandwidth. By allocating time slots appropriately, different users or channels can transmit data simultaneously over the same physical link, thereby improving transmission efficiency. In the CPSR-HQKDN scheme, time slots primarily serve the purpose of calculating the remaining quantity of keys and various key rates, among others, in preparation for addressing the routing issues of data packets.
- Key Update Rate: In QKD technology, the key update rate refers to the number of newly generated key bits successfully generated within a unit of time. In this scheme, the key update rate is calculated based on the total number of key bits successfully generated and the total time taken.
- Packet Encryption Request: Within the SDN network framework, a packet encryption request refers to a series of subsequent packet encryption requests issued by an application to the controller through the northbound interface. It plays a crucial role in determining the security requirements of the packets. The request involves a significant volume of packets, indicating that allocating resources for the current network will pose greater challenges and requires the comprehensive consideration of the existing network resource status.
3.3. CPSR-HQ KDN Routing Scheme
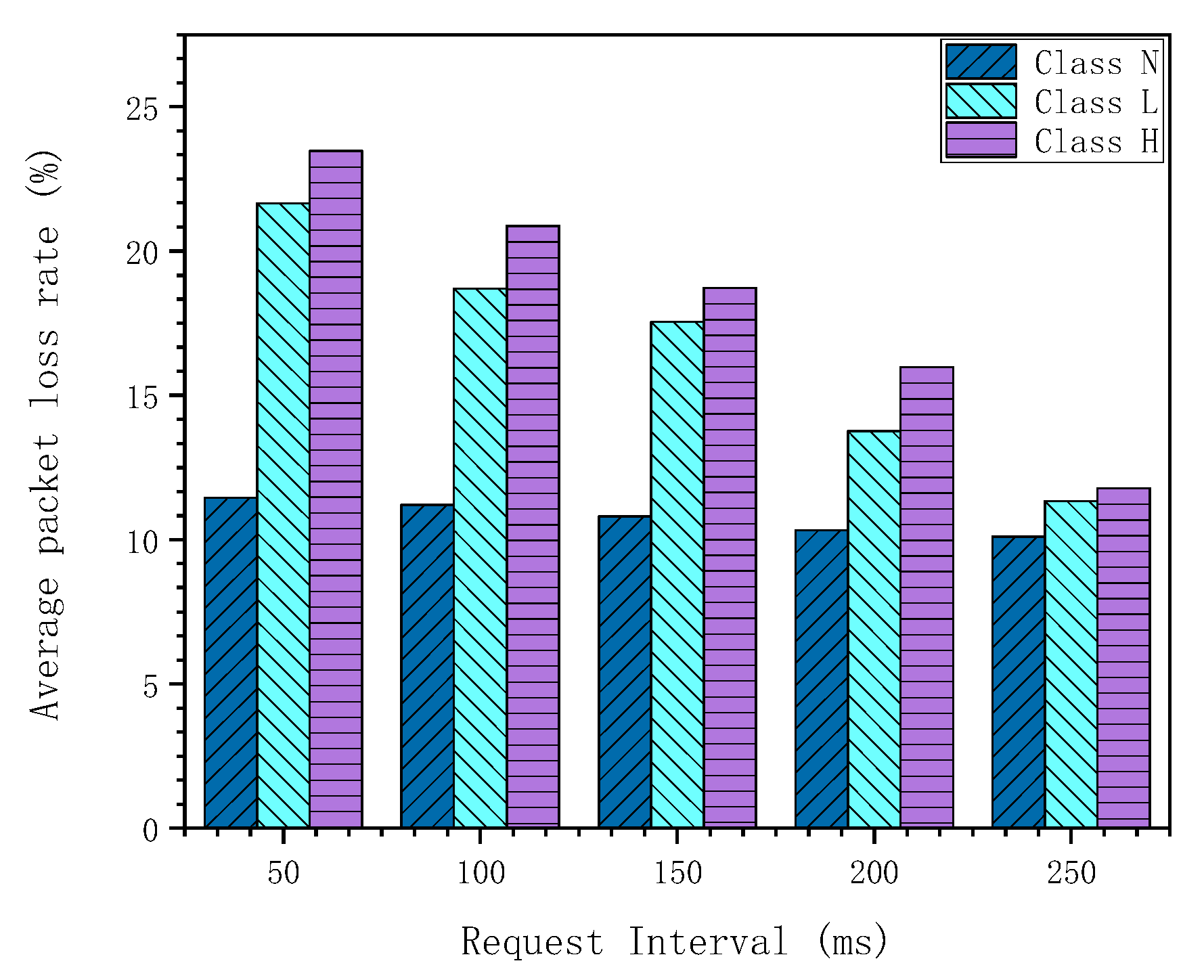
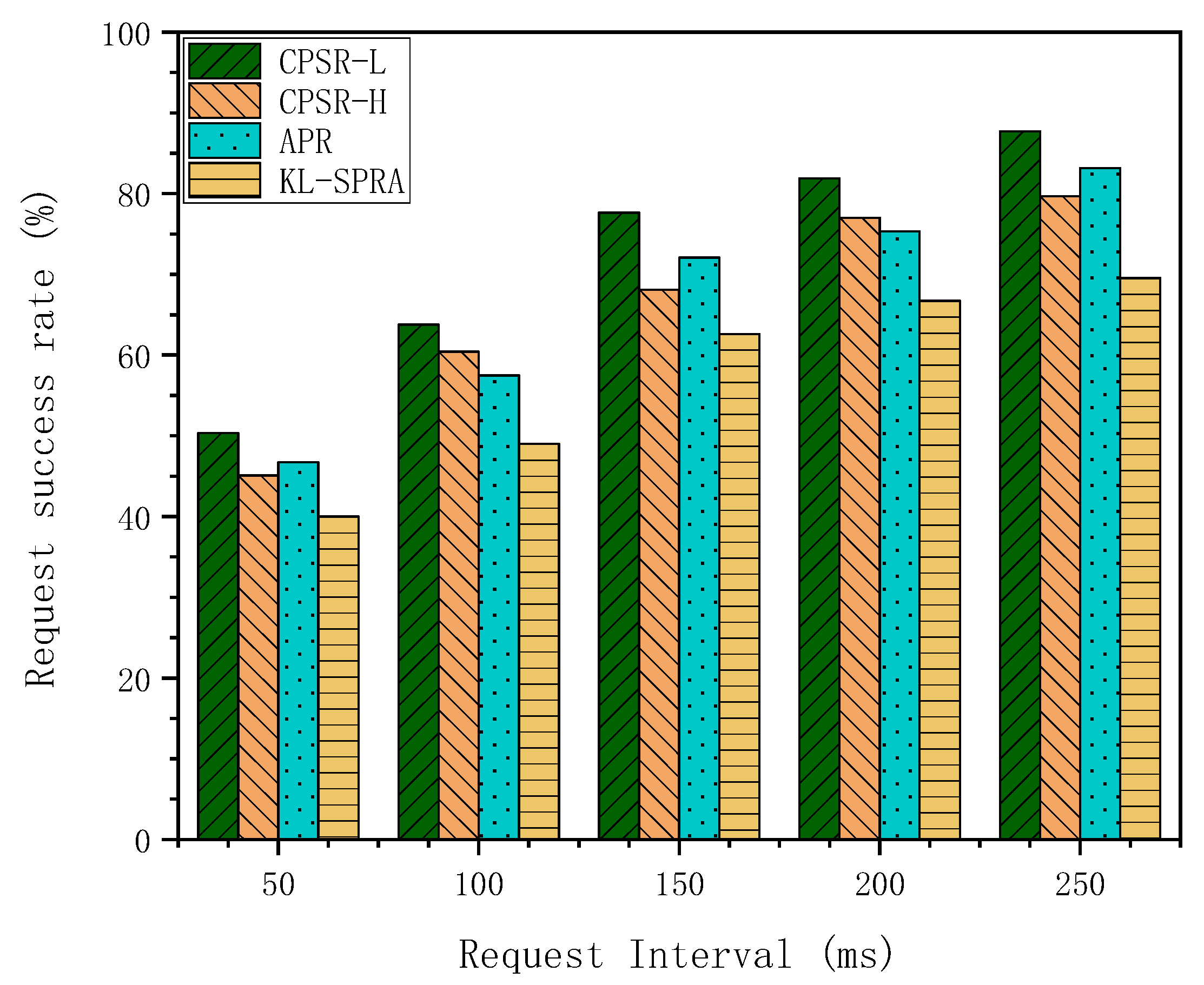
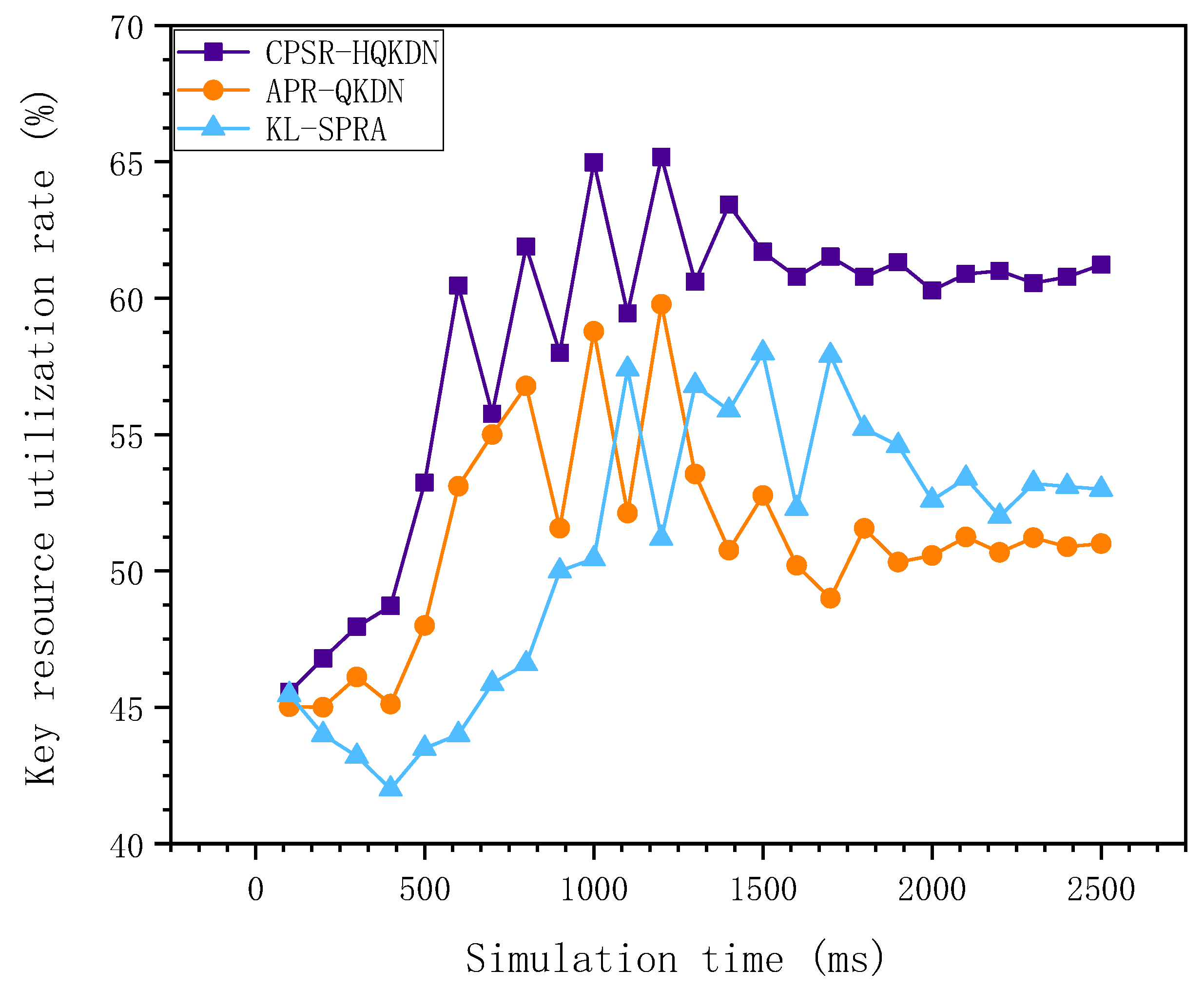
4. Network Simulation
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Milanov, E. The RSA algorithm. RSA Lab. 2009, 1–11. [Google Scholar]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Mallouli, F.; Hellal, A.; Saeed, N.S.; Alzahrani, F.A. A survey on cryptography: Comparative study between RSA vs ECC algorithms, and RSA vs. El-Gamal algorithms. In Proceedings of the 2019 6th IEEE International Conference on Cyber Security and Cloud Computing (CSCloud)/2019 5th IEEE International Conference on Edge Computing and Scalable Cloud (EdgeCom), Paris, France, 21–23 June 2019; pp. 173–176. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Diamanti, E.; Lo, H.-K.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. NPJ Quantum Inf. 2016, 2, 16025. [Google Scholar] [CrossRef]
- Lo, H.-K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photonics 2014, 8, 595–604. [Google Scholar] [CrossRef]
- Ahn, J.; Kwon, H.-Y.; Ahn, B.; Park, K.; Kim, T.; Lee, M.-K.; Kim, J.; Chung, J. Toward quantum secured distributed energy resources: Adoption of post-quantum cryptography (pqc) and quantum key distribution (qkd). Energies 2022, 15, 714. [Google Scholar] [CrossRef]
- Ahmad, I.; Shahabuddin, S.; Kumar, T.; Okwuibe, J.; Gurtov, A.; Ylianttila, M. Security for 5G and beyond. IEEE Commun. Surv. Tutor. 2019, 21, 3682–3722. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, F.; Chen, Y.A.; Peng, C.Z.; Pan, J.W. Large scale quantum key distribution: Challenges and solutions [Invited]. Opt. Express 2018, 26, 24260–24273. [Google Scholar] [CrossRef]
- Nawaz, S.J.; Sharma, S.K.; Wyne, S.; Patwary, M.N.; Asaduzzaman, M. Quantum machine learning for 6G communication networks: State-of-the-art and vision for the future. IEEE Access 2019, 7, 46317–46350. [Google Scholar] [CrossRef]
- Chong, S.-K.; Hwang, T. Quantum key agreement protocol based on BB84. Opt. Commun. 2010, 283, 1192–1195. [Google Scholar] [CrossRef]
- Lo, H.-K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, T.-Y.; Wang, L.-J.; Liang, H.; Shentu, G.-L.; Wang, J.; Cui, K.; Yin, H.-L.; Liu, N.-L.; Li, L. Experimental measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2013, 111, 130502. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Wang, Q.; Zhang, J.; Ng, S.X.; Hanzo, L. The evolution of quantum key distribution networks: On the road to the qinternet. IEEE Commun. Surv. Tutor. 2022, 24, 839–894. [Google Scholar] [CrossRef]
- Wang, S.; Yin, Z.-Q.; He, D.-Y.; Chen, W.; Wang, R.-Q.; Ye, P.; Zhou, Y.; Fan-Yuan, G.-J.; Wang, F.-X.; Chen, W. Twin-field quantum key distribution over 830-km fibre. Nat. Photonics 2022, 16, 154–161. [Google Scholar] [CrossRef]
- Zhang, W.; van Leent, T.; Redeker, K.; Garthoff, R.; Schwonnek, R.; Fertig, F.; Eppelt, S.; Rosenfeld, W.; Scarani, V.; Lim, C.C.-W. A device-independent quantum key distribution system for distant users. Nature 2022, 607, 687–691. [Google Scholar] [CrossRef]
- Pompili, M.; Hermans, S.L.; Baier, S.; Beukers, H.K.; Humphreys, P.C.; Schouten, R.N.; Vermeulen, R.F.; Tiggelman, M.J.; dos Santos Martins, L.; Dirkse, B. Realization of a multinode quantum network of remote solid-state qubits. Science 2021, 372, 259–264. [Google Scholar] [CrossRef]
- Qi, Z.; Li, Y.; Huang, Y.; Feng, J.; Zheng, Y.; Chen, X. A 15-user quantum secure direct communication network. Light Sci. Appl. 2021, 10, 183. [Google Scholar] [CrossRef]
- Wengerowsky, S.; Joshi, S.K.; Steinlechner, F.; Hübel, H.; Ursin, R. An entanglement-based wavelength-multiplexed quantum communication network. Nature 2018, 564, 225–228. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, Y.; Li, J.; Lin, R.; Zhang, J.; Chen, J. Hybrid Trusted/Untrusted Relay-Based Quantum Key Distribution over Optical Backbone Networks. IEEE J. Sel. Areas Commun. 2021, 39, 2701–2718. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, Y.Z.; Zhang, Q.; Pan, J.W. Device-independent quantum key distribution with random postselection. Phys. Rev. Lett. 2022, 128, 110506. [Google Scholar] [CrossRef]
- Ma, W.; Chen, B.; Liu, L.; Chen, H.; Shao, W.; Gao, M.; Wu, J.; Ho, P.-H. Equilibrium Allocation Approaches of Quantum Key Resources with Security Levels in QKD-Enabled Optical Data Center Networks. IEEE Internet Things J. 2022, 9, 25660–25672. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Y.; Zou, X.; Cao, Y.; Zhao, Y.; Nag, A.; Zhang, J. Secret-Key Provisioning With Collaborative Routing in Partially-Trusted-Relay-based Quantum-Key-Distribution-Secured Optical Networks. J. Light. Technol. 2022, 40, 3530–3545. [Google Scholar] [CrossRef]
- Wang, C.; Kon, W.Y.; Ng, H.J.; Lim, C.C. Experimental symmetric private information retrieval with measurement-device-independent quantum network. Light Sci. Appl. 2022, 11, 268. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Cao, L.; Shi, Y.; Wan, L.; Zhang, H.; Li, S.; Chen, G.; Li, Y.; Li, S.; Wang, Y.; et al. Recent progress in quantum photonic chips for quantum communication and internet. Light Sci. Appl. 2023, 12, 175. [Google Scholar] [CrossRef] [PubMed]
- Wang, S. Symmetric private information retrieval supported by quantum-secure key-exchange network. Light Sci. Appl. 2022, 11, 301. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.; Wang, Y.; Su, X. Hybrid quantum key distribution network. Sci. China Inf. Sci. 2022, 65, 200502. [Google Scholar] [CrossRef]
- Liu, R.; Rozenman, G.G.; Kundu, N.K.; Chandra, D.; De, D. Towards the industrialisation of quantum key distribution in communication networks: A short survey. IET Quantum Commun. 2022, 3, 151–163. [Google Scholar] [CrossRef]
- Nauerth, S.; Fürst, M.; Schmitt-Manderbach, T.; Weier, H.; Weinfurter, H. Information leakage via side channels in freespace BB84 quantum cryptography. New J. Phys. 2009, 11, 065001. [Google Scholar] [CrossRef]
- Bloom, Y.; Fields, I.; Maslennikov, A.; Rozenman, G.G. Quantum cryptography—A simplified undergraduate experiment and simulation. Physics 2022, 4, 104–123. [Google Scholar] [CrossRef]
- Wang, N.; Tian, X.; Zhang, X.; Lin, S. Quantum Secure Multi-Party Summation with Identity Authentication Based on Commutative Encryption. Photonics 2023, 10, 558. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Z.; Zhao, M.; Yu, K.; Liu, S. APR-QKDN: A Quantum Key Distribution Network Routing Scheme Based on Application Priority Ranking. Entropy 2022, 24, 1519. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zhang, H.; Su, J. The qkd network: Model and routing scheme. J. Mod. Opt. 2017, 64, 2350–2362. [Google Scholar] [CrossRef]


| Symbols | Meanings |
|---|---|
| Security requirement level for data packets, where N represents no use of QKD technology encryption, L represents the key generated using the BB84 protocol, and H represents the key generated using the MDI-QKD protocol. | |
| T | Lifetime of the network topology |
| t | A single time slot, where |
| The previous time slot, where | |
| Key requirement for a single data packet | |
| L | Set of all linkages in the network topology |
| Trusted relay link, where | |
| Untrusted relay link, where | |
| Current status of the link | |
| N | Set of all nodes |
| Untrusted relay node, where | |
| Trusted relay node, where | |
| Backbone node, where | |
| Length of the queue of data packets awaiting encryption at node n | |
| Remaining key amount for the current link | |
| Key update rate for the current link | |
| TD | Transmission delay for data packet transmission |
| Number of nodes a data packet goes through | |
| Amount of data packets waiting for forwarding at the current node |
| Input: t ∈ T, l ∈ L, n ∈ N, p, W Output: optimal path for a Class N Data Packet |
| Routing Algorithm for Class N Data Packets (topo, start, end): weights = {vertex: infinity for vertex in topo} weights[start] = 0 path = {} visited = set() while not all(weights[vertex] == infinity for vertex in topo): current_vertex = min((vertex, weights[vertex]) for vertex in topo - visited)[0] visited.add(current_vertex) for neighbor, weight in topo[current_vertex].items(): if weights[neighbor] > weights[current_vertex] + w: weights[neighbor] = weights[current_vertex] + w path[neighbor] = current_vertex shortest_path = [] current_vertex = end while current_vertex != start: shortest_path.append(current_vertex) current_vertex = path[current_vertex] shortest_path.append(start) shortest_path.reverse() return shortest_path, weights[end] |
| Input: t ∈ T, l ∈ L, n ∈ N, p, Output: optimal path for a Class L Data Packet or H Data Packet |
| Routing Algorithm for Class L and H Data Packets: Obtain the weight matrix X Check link status and update the weight matrix Get the packet waiting to be dequeued Get the waiting time slots of this packet If the waiting time slots are too long, just discard the packet directly Retrieve the required key amount for the packet, check if the remaining key amount in each link is sufficient, and update the different weight matrix according to to contain only the variable in the end for(int k = 1; k <= n; k++){ for(int i = 1;I <= n; i++){ if(k! = i){ int t = (k < i)?W[i][k]: W[k][i]; if(t == inf)continue; int temp = (k < i)?k:i; for(int j = 1; j <= temp; j++){ if(t + W[k][j] < W[i][j])W[i][j] = t + W[k][j]; } for(int j = k + 1; j <= i; j++){ if(t + W[k][j] < W[i][j])W[i][j] = t + W[j][k]; } } } } int start,end; if(start >= end)cout<<W[start][end]<<endl; else cout<<W[end][start]<<endl; Obtain the optimal path based on the final W matrix |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, L.; Wu, W.; Yuan, X.; Miao, M.; Di, X.; Jiang, Z. CPSR-HQKDN: A Hybrid Trusted Relay Quantum Key Distribution Network Routing Scheme Based on Classification of Packet Security Requirements. Appl. Sci. 2023, 13, 12284. https://doi.org/10.3390/app132212284
Bi L, Wu W, Yuan X, Miao M, Di X, Jiang Z. CPSR-HQKDN: A Hybrid Trusted Relay Quantum Key Distribution Network Routing Scheme Based on Classification of Packet Security Requirements. Applied Sciences. 2023; 13(22):12284. https://doi.org/10.3390/app132212284
Chicago/Turabian StyleBi, Lin, Weijie Wu, Xiaotong Yuan, Minghui Miao, Xiaoqiang Di, and Zhengang Jiang. 2023. "CPSR-HQKDN: A Hybrid Trusted Relay Quantum Key Distribution Network Routing Scheme Based on Classification of Packet Security Requirements" Applied Sciences 13, no. 22: 12284. https://doi.org/10.3390/app132212284
APA StyleBi, L., Wu, W., Yuan, X., Miao, M., Di, X., & Jiang, Z. (2023). CPSR-HQKDN: A Hybrid Trusted Relay Quantum Key Distribution Network Routing Scheme Based on Classification of Packet Security Requirements. Applied Sciences, 13(22), 12284. https://doi.org/10.3390/app132212284






