Pairing Hamiltonians of Nearest-Neighbor Interacting Superconducting Qubits on an IBM Quantum Computer
Abstract
:1. Introduction
2. Model
2.1. Pairing Hamiltonians in Superconductivity
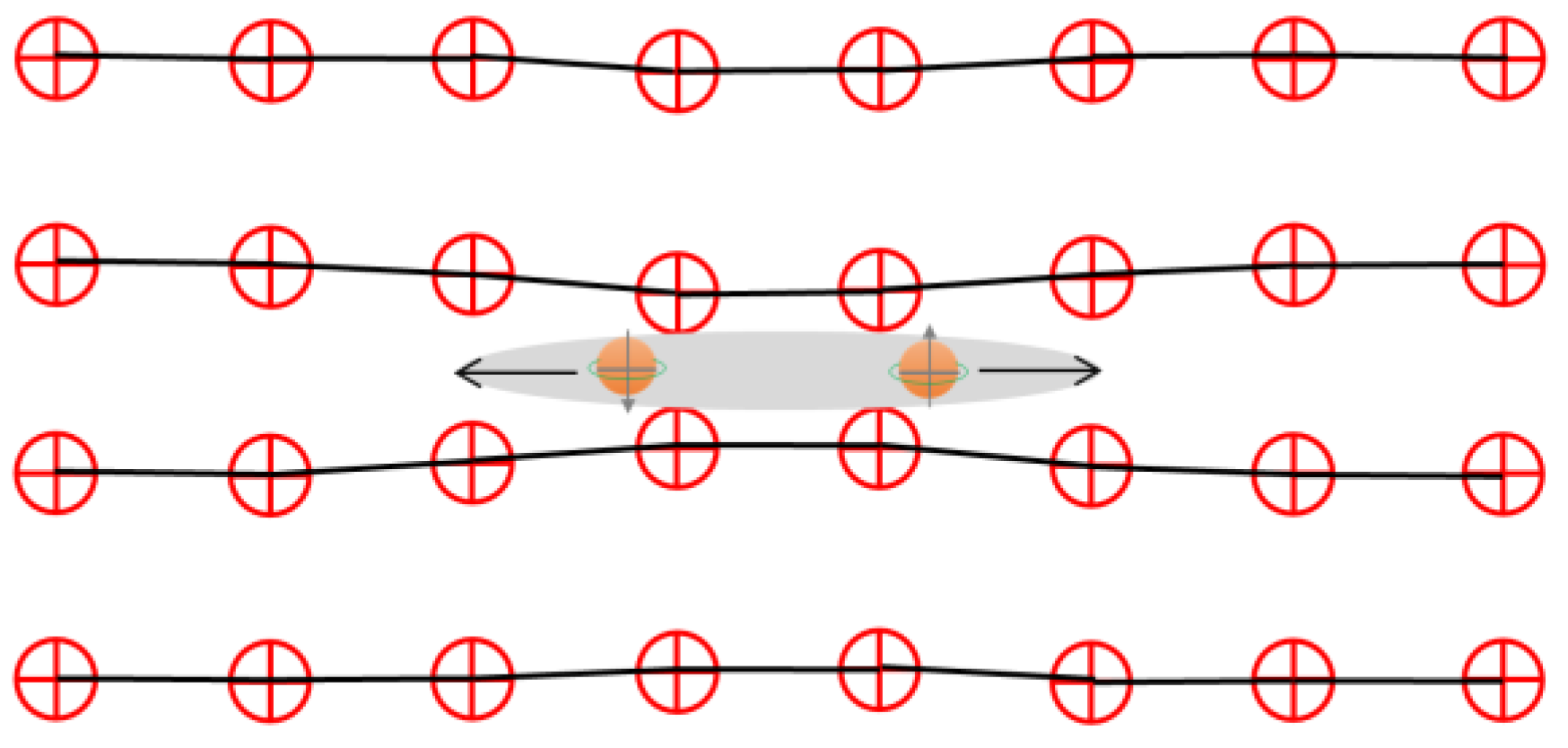
2.2. Nearest-Neighbor Coupling Interactions in Superconductivity
3. Methods of Simulation for Hamiltonian Operators
4. Results
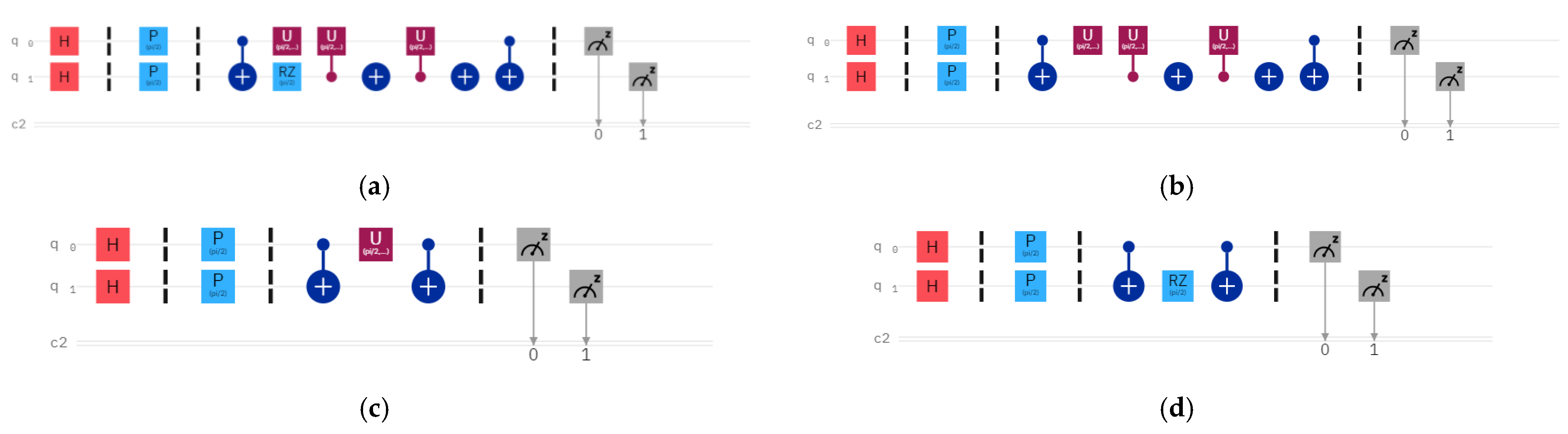
4.1. Initial State Preparation and Unitary Operation
- For the XX type of interaction: Comparing with the standard U3 gate (Equation (15)), the parameters for the gate are found to be , , and ;
- For the YY type of interaction: The parameters obtained for the U3 gate are , and . The parameters obtained for the gate are , , and ;
- For the ZZ type of interaction: Comparing with the standard U1 gate,
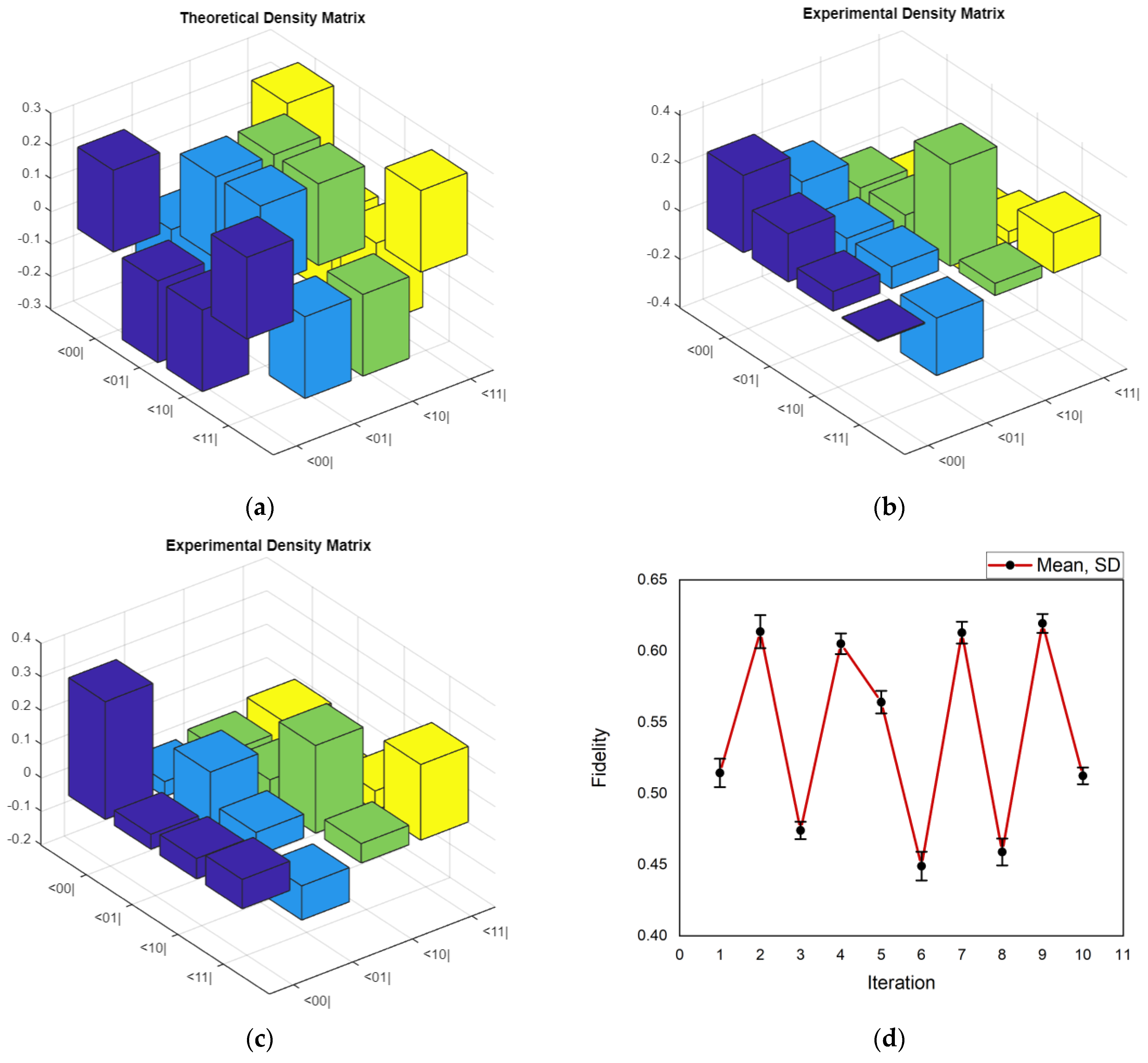
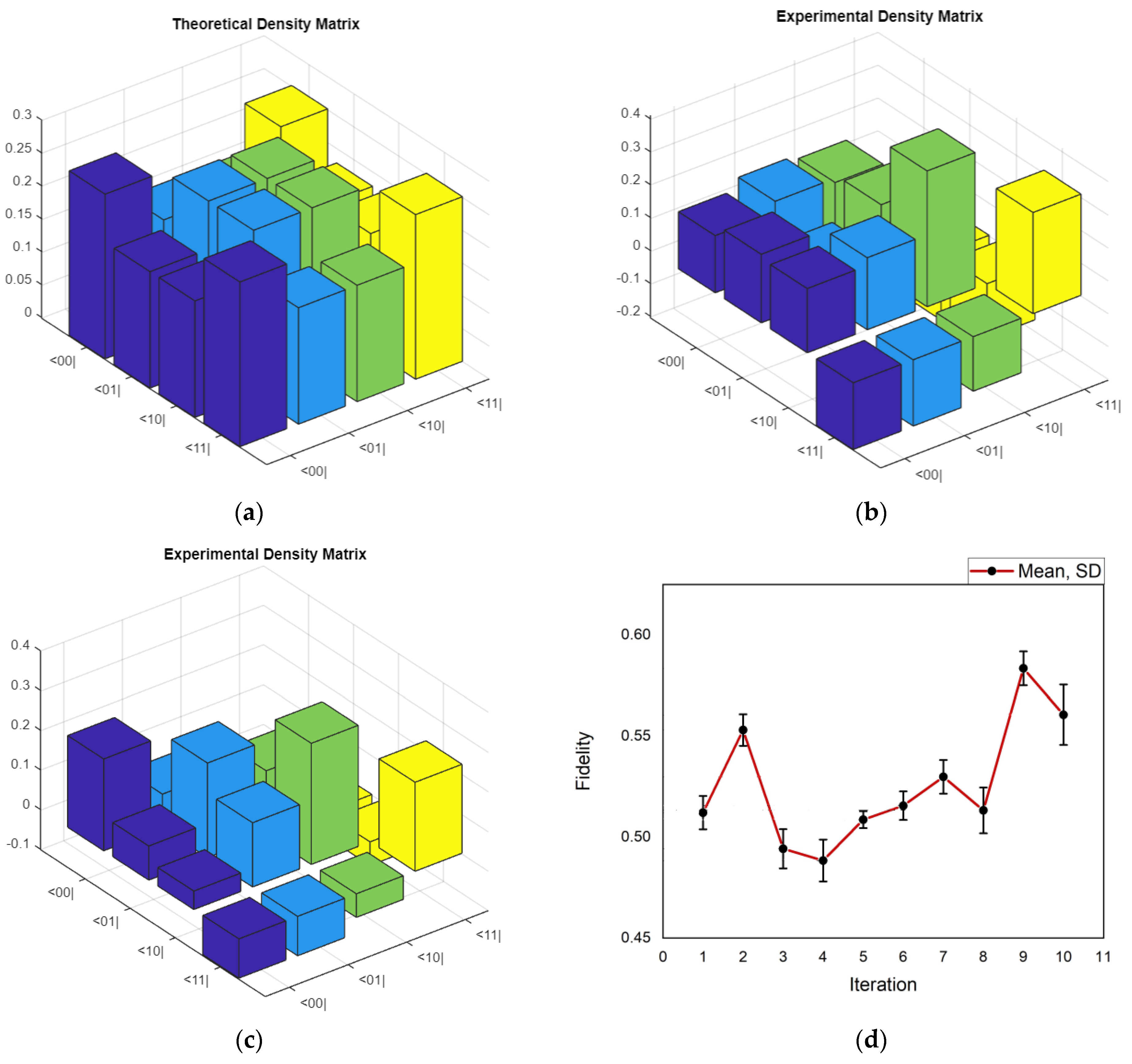
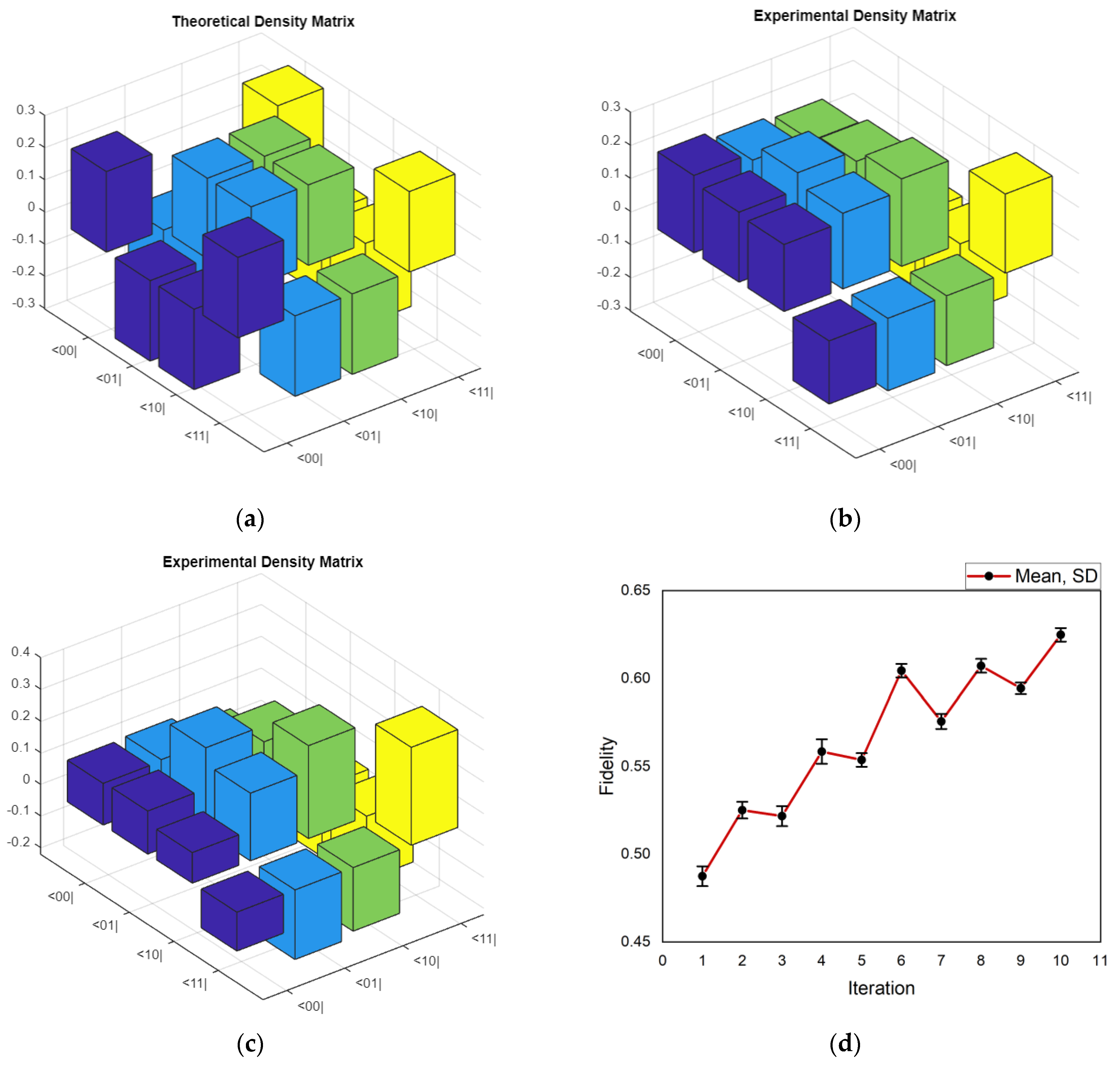
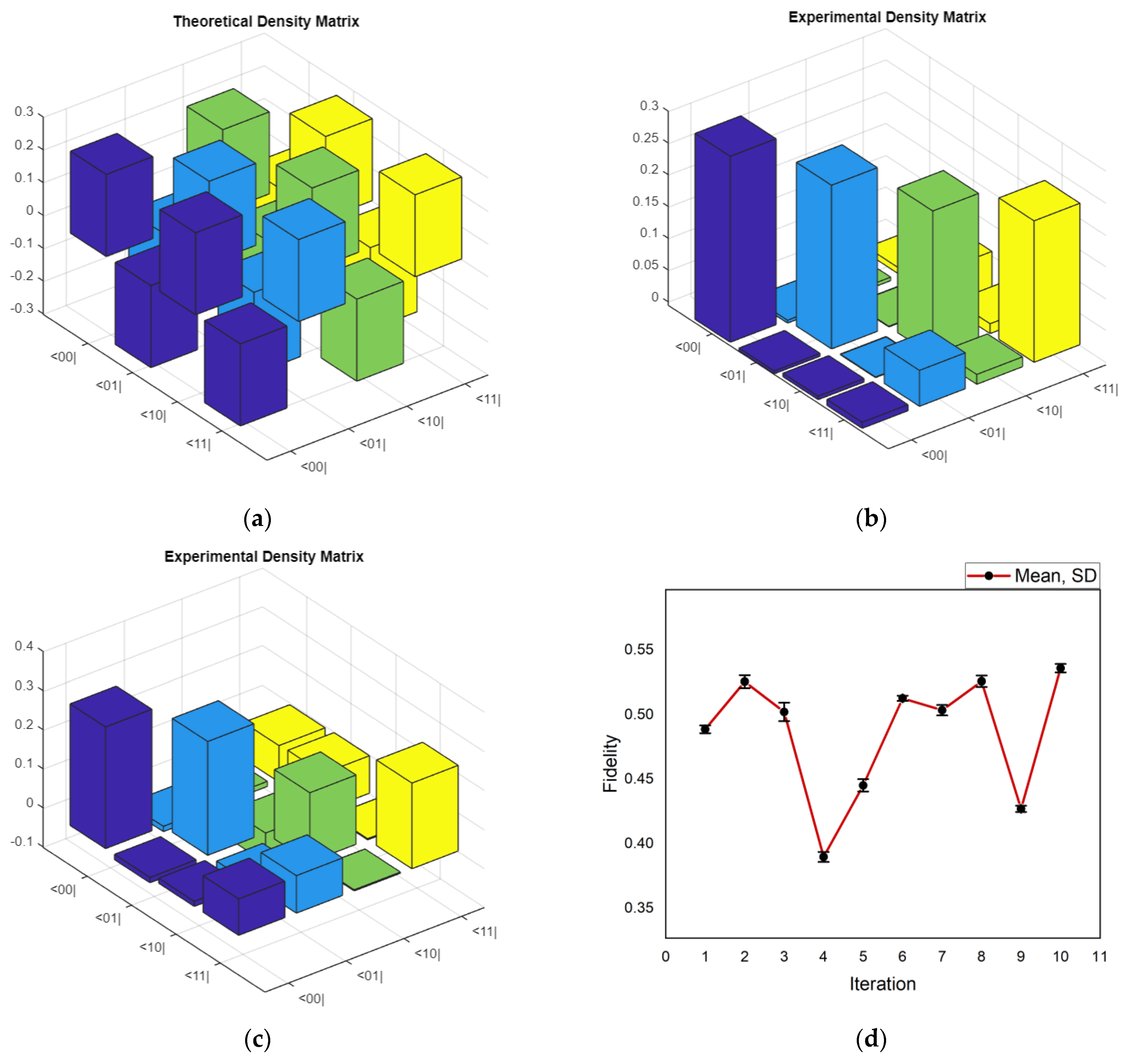
4.2. Quantum State Tomography for Suzuki–Trotter Decomposition of Quantum Circuits
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, A.; Kim, M.S.; Pollmann, F.; Knolle, J. Simulating quantum many-body dynamics on a current digital quantum computer. npj Quantum Inf. 2019, 5, 106. [Google Scholar] [CrossRef]
- Schirmer, S.G.; Pullen, I.C.; Solomon, A.I. Controllability of Quantum Systems. IFAC Proc. 2003, 36, 281–286. [Google Scholar] [CrossRef]
- Lloyd, S. Universal quantum simulators. Science 1996, 273, 1073–1078. [Google Scholar] [CrossRef] [PubMed]
- Shabani, A.; Mohseni, M.; Lloyd, S.; Kosut, R.L.; Rabitz, H. Rabitz Estimation of many-body quantum Hamiltonians via compressive sensing. Phys. Rev. A 2011, 84, 012107. [Google Scholar] [CrossRef]
- Nachman, B.; Provasoli, D.; De Jong, W.A.; Bauer, C.W. Quantum algorithm for high energy physics simulations. Phys. Rev. Lett. 2021, 126, 062001. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Xu, B.; Xu, N.; Li, Z.; Chen, H.; Peng, X.; Xua, R.; Du, J. Quantum chemistry simulation on quantum computers: Theories and experiments. Phys. Chem. Chem. Phys. 2012, 14, 9411–9420. [Google Scholar] [CrossRef] [PubMed]
- Langer, C. High Fidelity Quantum Information Processing with Trapped Ions; University of Colorado at Boulder: Boulder, CO, USA, 2006. [Google Scholar]
- Cohen, L.; Brady, A.J.; Huang, Z.; Liu, H.; Qu, D.; Dowling, J.P.; Han, M. Efficient Simulation of Loop Quantum Gravity: A Scalable Linear-Optical Approach. Phys. Rev. Lett. 2021, 126, 020501. [Google Scholar] [CrossRef]
- Saffman, M. Quantum computing with neutral atoms. Natl. Sci. Rev. 2019, 6, 24–25. [Google Scholar] [CrossRef]
- Salari, V.; Naeij, H.; Shafiee, A. Quantum Interference and Selectivity through Biological Ion Channels. Sci. Rep. 2017, 7, 41625. [Google Scholar] [CrossRef]
- DeMille, D. Quantum Computation with Trapped Polar Molecules. Phys. Rev. Lett. 2002, 88, 067901. [Google Scholar] [CrossRef]
- Shi, X.-F. Rydberg quantum computation with nuclear spins in two-electron neutral atoms. Front. Phys. 2021, 16, 1–18. [Google Scholar] [CrossRef]
- Milburn, G. Photons as qubits. Phys. Scr. 2009, 2009, 014003. [Google Scholar] [CrossRef]
- Blatt, R.; Roos, C.F. Quantum simulations with trapped ions. Nat. Phys. 2012, 8, 277–284. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: New York, NY, USA, 2011; p. 708. [Google Scholar]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153. [Google Scholar] [CrossRef]
- Ma, H.; Govoni, M.; Galli, G. Quantum simulations of materials on near-term quantum computers. npj Comput. Mater. 2020, 6, 85. [Google Scholar] [CrossRef]
- Babbush, R.; Berry, D.W.; McClean, J.R.; Neven, H. Quantum simulation of chemistry with sublinear scaling in basis size. npj Quantum Inf. 2019, 5, 92. [Google Scholar] [CrossRef]
- Outeiral, M.C.; Shi, S.J.; Morris, G.M.; Benjamin, S.C.; Deane, C.M. The prospects of quantum computing in computational molecular biology. WIREs Comp. Mol. Sci. 2020, 11, e1481. [Google Scholar] [CrossRef]
- Faroukh, Y.M. Quantum Computers vs Conventional Computers: A Study on the Larger Scale. 2018, p. 24. Available online: https://www.researchgate.net/publication/323993559_Quantum_Computers_Vs_Conventional_Computers_A_Study_on_the_Larger_Scale (accessed on 24 October 2023).
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Alhassid, K.N.Y. Nesterov Mesoscopic superconductivity in ultrasmall metallic grains. AIP Conf. Proc. 2014, 1619, 24. [Google Scholar]
- Yang, X.; Wang, A.M.; Xu, F.; Du, J. Experimental simulation of a pairing Hamiltonian on an NMR quantum computer. Chem. Phys. Lett. 2006, 422, 20–24. [Google Scholar] [CrossRef]
- Di Paolo, A.; Baker, T.E.; Foley, A.; Sénéchal, D.; Blais, A. Efficient modeling of superconducting quantum circuits with tensor networks. NPJ Quantum Inf. 2021, 7, 11. [Google Scholar] [CrossRef]
- Alferov, Z.I. The history and future of semiconductor heterostructures. Semiconductors 1998, 32, 1–14. [Google Scholar] [CrossRef]
- Loss, D.; Vincenzo, D.D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120. [Google Scholar] [CrossRef]
- Ortiz, G.; Gubernatis, J.E.; Knill, E.; Laflamme, R. Quantum algorithms for fermionic simulations. Phys. Rev. A 2001, 64, 022319. [Google Scholar] [CrossRef]
- Houck, A.; Tureci, H.; Koch, J. On-chip quantum simulation with superconducting circuits. Nat. Phys. 2012, 8, 292–299. [Google Scholar] [CrossRef]
- Barends, R.; Kelly, J.; Megrant, A.; Veitia, A.; Sank, D.; Jeffrey, E.; White, T.C.; Mutus, J.; Fowler, A.G.; Campbell, B.; et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 2014, 508, 500–503. [Google Scholar] [CrossRef]
- Pathak, A. Elements of Quantum Computation and Quantum Communication; Taylor & Francis: Milton Park, UK, 2013. [Google Scholar]
- Wikipedia. Quantum Logic Gate. Available online: https://en.wikipedia.org/wiki/Quantum_logic_gate (accessed on 12 February 2019).
- Devoret, M.H.; Schoelkopf, R.J. Schoelkopf. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef]
- Clarke, J.; Wilhelm, F.K. Superconducting quantum bits. Nature 2008, 453, 1031–1042. [Google Scholar] [CrossRef] [PubMed]
- You, J.Q.; Franco, N. Superconducting Circuits and Quantum Information. Phys. Today 2005, 58, 42–47. [Google Scholar] [CrossRef]
- Wu, L.A.; Byrd, M.S.; Lidar, D.A. Polynomial-time simulation of pairing models on a quantum computer. Phys. Rev. Lett. 2002, 89, 057904. [Google Scholar] [CrossRef] [PubMed]
- Orlando, T.P.; Mooij, J.E.; Tian, L.; van der Wal, C.H.; Levitov, L.S.; Lloyd, S.; Mazo, J.J. Superconducting persistent-current qubit. Phys. Rev. B 1999, 60, 15398. [Google Scholar] [CrossRef]
- You, J.Q.; Tsai, J.S.; Nori, F. Scalable Quantum Computing with Josephson Charge Qubits. Phys. Rev. Lett. 2002, 89, 197902. [Google Scholar] [CrossRef]
- Gangopadhyay, S.; Manabputra; Behera, B.K.; Panigrahi, P.K. Generalization and demonstration of an entanglement-based Deutsch-Jozsa-like algorithm using a 5-qubit quantum computer. Quantum Inf. Process. 2018, 17, 160. [Google Scholar] [CrossRef]
- Mandviwalla, A.; Ohshiro, K.; Ji, B. Implementing Grover’s Algorithm on the IBM Quantum Computers. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 2531–2537. [Google Scholar]
- Stenger, J.P.T.; Bronn, N.T.; Egger, D.J.; Pekker, D. Simulating the dynamics of braiding of Majorana zero modes using an IBM quantum computer. Phys. Rev. Res. 2021, 3, 033171. [Google Scholar] [CrossRef]
- Cattaneo, M.M.; Rossi, A.C.; García-Pérez, G.; Zambrini, S.R. Quantum Simulation of Dissipative Collective Effects on Noisy Quantum Computers. PRX Quantum 2023, 4, 010324. [Google Scholar] [CrossRef]
- Sarkar, K.; Behera, B.K.; Panigrahi, P.K. A Robust Tripartite Quantum Key Distribution Using Mutually Share Bell States and Classical Has Values Using a Complete Graph Network Architecture. 2019. Available online: https://www.researchgate.net/publication/333148981_A_robust_tripartite_quantum_key_distribution_using_mutually_shared_Bell_states_and_classical_hash_values_using_a_complete-graph_network_architecture (accessed on 24 October 2023).
- Agarwal, R.; Sethi, C.K.; Gupta, N.K.; Panigrahi, P.K. Comparison of Advantages in Quantum Teleportation Using Cluster State and Coined Quantum Walks. 2020. Available online: https://www.researchgate.net/publication/339528565_Comparison_of_advantages_in_quantum_teleportation_using_cluster_state_and_coined_quantum_walks?channel=doi&linkId=5e578b4092851cefa1c7fd92&showFulltext=true (accessed on 24 October 2023).
- Warke, A.; Behera, B.K.; Panigrahi, P.K. Experimental Realization of Three Quantum Key Distribution Protocols. Quantum Inf. Process. 2020, 19, 1–15. [Google Scholar] [CrossRef]
- Saini, R.; Papneja, A.; Behera, B.K.; Panigrahi, P.K. Experimental Realization of Differential Phase Shift Quantum Key Distribution on IBM QX. 2019. Available online: https://www.researchgate.net/publication/337685592_Experimental_Realization_of_Differential_Phase_Shift_Quantum_Key_Distribution_on_IBM_QX?channel=doi&linkId=5de5b14b4585159aa45cacc8&showFulltext=true (accessed on 24 October 2023).
- Behera, B.K.; Banerjee, A.; Panigrahi, P.K. Experimental realization of quantum cheque using a five-qubit quantum computer. Quantum Inf. Process. 2017, 16, 312. [Google Scholar] [CrossRef]
- Behera, B.K.; Reza, T.; Gupta, A.; Panigrahi, P.K. Designing Quantum Router in IBM Quantum Computer. Quantum Inf. Process. 2019, 18, 328. [Google Scholar] [CrossRef]
- Behera, B.K.; Seth, S.; Das, A.; Panigrahi, P.K. Demonstration of Entanglement Purification and Swap- ping Protocol to Design Quantum Repeater in IBM Quantum Computer. Quantum Inf. Process. 2019, 18, 108. [Google Scholar] [CrossRef]
- McDermott, R.; Simmonds, R.W.; Steffen, M.; Cooper, K.B.; Cicak, K.; Osborn, K.D.; Oh, S.; Pappas, D.P.; Martinis, J.M. Simultaneous state measurement of coupled Josephson phase qubits. Science 2005, 307, 1299–1302. [Google Scholar] [CrossRef]
- Isaac, D.W.L.; Chuang, L.; Yamaguchi, F.; Yamamoto, Y. Efficient implementation of coupled logic gates for quantum computation. Phys. Rev. A 2000, 61, 042310. [Google Scholar]
- Wang, Z.; Gu, X.; Wu, L.-A.; Liu, Y.-X. Quantum simulation of pairing hamiltonians with nearest-neighbor interacting qubits. Phys. Rev. A 2016, 93, 062301. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Quantum Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; ISBN 978-1-107-17986-8. OCLC 952389109. [Google Scholar]
- Altepeter, J.B.; James, D.F.; Kwiat, P.G. 4 Qubit Quantum State Tomography. In Quantum State Estimation; Lecture Notes in Physics; Paris, M., Řeháček, J., Eds.; Springer: Berlin, Heidelberg, 2004; Volume 649. [Google Scholar]
- Jozsa, R. Fidelity for Mixed Quantum States. J. Mod. Opt. 1994, 41, 2315–2324. [Google Scholar] [CrossRef]
- Uhlmann, A. The “transition probability” in the state space of a ∗-algebra. Rep. Math. Phys. 1976, 9, 273–279. [Google Scholar] [CrossRef]
- Pedersen, L.H.; Møller, N.M.; Mølmer, K. Fidelity of quantum operations. Phys. Lett. A 2007, 367, 47–51. [Google Scholar] [CrossRef]
- Carroll, M.; Rosenblatt, S.; Jurcevic, P.; Lauer, I.; Kandala, A. Dynamics of superconducting qubit relaxation times. NPJ Quantum Inf. 2022, 8, 132. [Google Scholar] [CrossRef]
- Choi, Y.; Joynt, R. Anisotropy with respect to the applied magnetic field of spin qubit decoherence times. NPJ Quantum Inf. 2022, 8, 70. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Müller, M.; Schindler, P.; Nigg, D.; Monz, T.; Chwalla, M.; Hennrich, M.; Roos, C.F.; Zoller, P.; Blatt, R. An open system quantum simulator with trapped ions. Nature 2011, 470, 486–491. [Google Scholar] [CrossRef]
- Tacchino, F.; Chiesa, A.; Carretta, S.; Gerace, D. Quantum computers as universal quantum simulators: State of art and perspectives. Adv. Quantum Technol. 2020, 3, 1900052. [Google Scholar] [CrossRef]

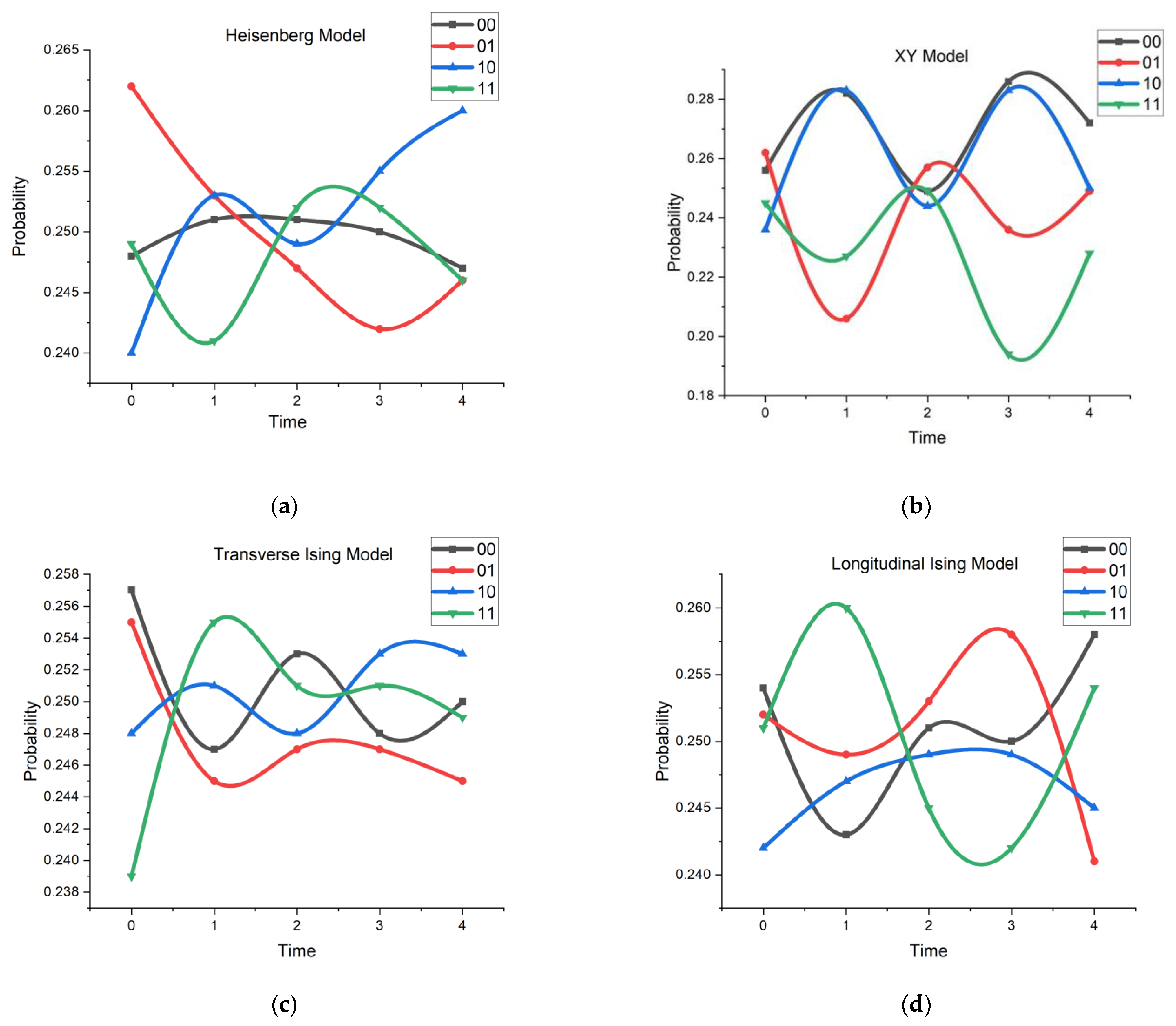

| Interaction Model | Interaction Hamiltonian |
|---|---|
| Heisenberg Model | |
| XY Model | |
| Transverse Ising Model | |
| Longitudinal Ising Model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, S.; Behera, B.K.; Seo, F.J. Pairing Hamiltonians of Nearest-Neighbor Interacting Superconducting Qubits on an IBM Quantum Computer. Appl. Sci. 2023, 13, 12075. https://doi.org/10.3390/app132112075
Chatterjee S, Behera BK, Seo FJ. Pairing Hamiltonians of Nearest-Neighbor Interacting Superconducting Qubits on an IBM Quantum Computer. Applied Sciences. 2023; 13(21):12075. https://doi.org/10.3390/app132112075
Chicago/Turabian StyleChatterjee, Shirshendu, Bikash K. Behera, and Felix J. Seo. 2023. "Pairing Hamiltonians of Nearest-Neighbor Interacting Superconducting Qubits on an IBM Quantum Computer" Applied Sciences 13, no. 21: 12075. https://doi.org/10.3390/app132112075
APA StyleChatterjee, S., Behera, B. K., & Seo, F. J. (2023). Pairing Hamiltonians of Nearest-Neighbor Interacting Superconducting Qubits on an IBM Quantum Computer. Applied Sciences, 13(21), 12075. https://doi.org/10.3390/app132112075







