Abstract
In this paper, to better evaluate the flight performance of pilot cadets, a flight performance evaluation index system was constructed based on the task of the traffic pattern, the flight training manual, and interviews with instructors. The fuzzy comprehensive evaluation model established by the G1 method was used to evaluate the flight performance of pilot cadets. The flight data of 30 flight cadets were collected to verify the applicability of the fuzzy comprehensive evaluation model. The results showed that the index system established in this paper can meet the requirements of flight performance evaluation. In addition, the fuzzy comprehensive evaluation results were consistent with the evaluation results of experts. Therefore, the system is effective and feasible for the evaluation of pilot cadets’ flight performance through the fuzzy comprehensive evaluation model established by the index system and G1 method.
1. Introduction
Safety is critical to the development of various industries, particularly civil aviation. The civil aviation industry plays an important role in the modern economy. An efficient and safe civil aviation transport network can promote commercial development and economic growth. At present, air travel is one of the most important means of long-distance travel and international communication. Ensuring safe flights is essential to protect the lives and property of passengers. In addition, maintaining a good safety record and implementing proactive safety measures can increase passenger confidence and loyalty, thereby contributing to the long-term growth and sustainability of the business. Aviation safety is, therefore, of vital importance to passengers, airlines, the economy, national security and the international community. A safe, reliable and sustainable civil aviation system can provide people with a better travel experience.
However, in current civil aviation transportation, there have been frequent unsafe flying incidents caused by crew factors. Statistical data show that the proportion of accidents caused by mechanical reasons is decreasing each year [1,2], whilst accidents caused by human factors account for over 70% of the total [3,4]. Pilot errors account for around 60% [5,6,7]. For example, the flight crew of Air China Flight 129 lost situational awareness during the flight and disregarded the height restrictions around the airport [8], while the captain of Asiana Airlines Flight 214 demonstrated poor manual flight skills and heavily relied on the autopilot system during the landing of a wide-body aircraft [9], which led to inadequate flight capabilities causing aviation accidents. These unsafe flight incidents reflect the insufficient knowledge and performance of existing pilots, the mismatch between pilot evaluation systems and industry development, and highlight the importance of conducting evaluations of pilot ability.
In recent research on pilot performance evaluations, researchers and scholars have primarily focused on methods and models. Hebbar and Pashilkar [10] performed a realistic approach and landing flight scenario using a reconfigurable flight simulator, and made subjective and quantitative measurements of pilot performance. Wojcik et al. [11] adapted the Demand Resource Evaluation Scores (DRES) as a metacognitive indicator to assess pilot students’ perceptions during simulated training of a novel manoeuvre. The research found that individual metacognitive evaluations of a stressful aviation manoeuvre might be important for progress in flight performance.
Some researchers also used quick access recorder (QAR) data to evaluate pilots’ flight performance. Wang et al. [12] developed an evaluation method for pilot’s performance during the landing phase based on flight QAR data. A flight landing operation performance evaluation system (FLOPES) was set up based on the evaluation model. Chen and Huang [13] used the Bayesian Network to perform flight crew performance evaluation. Based on an analysis of 484 aviation accidents caused by human factors, a flight crew performance model was constructed. Zhang et al. [14] studied the relationship between QAR data and pilot performance, and put forward one-dimensional convolutional neural networks (1-D CNN) that consider QAR metrics in an integrated manner. Then an approach was developed to achieve the state of pilot performance evaluations.
For this research’s method, studies found that fuzzy comprehensive evaluation refers to the use of fuzzy mathematics methods to assess the possibility of evaluating fuzzy objects influenced by multiple factors based on certain evaluation criteria [15,16,17]. The fuzzy comprehensive evaluation method has been widely applied in the research of evaluation modelling in various fields and has achieved good results [18,19,20].
In weight calculation, subjective weighting methods like the analytic hierarchy process (AHP) method and the order relationship analysis method (G1 method) are commonly used. The AHP method is a simple and practical method for handling complex problems with multiple objectives, criteria and levels. The AHP involves experts assigning values in the range from 1 to 9, or their reciprocals, to express the relative importance between two indicators [21]. After these valuations, a consistency check is performed [22]. However, when dealing with a large number of indicators, errors in assessing their importance can occur, resulting in inconsistent judgements [23], such as A being more important than B, B being more important than C, and C being more important than A. Thus, determining the importance between A and C becomes problematic.
In contrast, the G1 method is an improved index weighting method based on the AHP algorithm [24]. The G1 method avoids the consistency test required by the AHP algorithm by using the non-inferior relationship between indicators, and it has the characteristics of simple operation and wide applicability [25]. The G1 method initially requires experts to rank the importance of indicators according to their judgments and subsequently assign values to express the importance between them. This approach effectively circumvents the drawbacks of the AHP method. In the context of designing a flight trainee skill assessment, this study acknowledges that there may be a substantial number of indicators to consider. If the AHP method was employed, it could lead to consistency check failures. Moreover, repeatedly convening experts for the assessment of indicator importance is not very convenient. Consequently, the G1 method was chosen as the approach to calculating the indicator weights in this research.
Some scholars combined the G1 method with fuzzy comprehensive evaluation method for the construction research of evaluation models [26,27,28]. Thus, applying the G1 method [29] and the fuzzy evaluation method [30] to the assessment of pilot flight performance enables a comprehensive consideration of various factors exhibited by pilot flight performance. Based on the importance and evaluation results of each factor, the original qualitative evaluation can be quantified to better handle the multifactorial, fuzzy, and subjective judgments in the assessment of pilot flight performance.
Meanwhile, traffic pattern flight encompasses all flight processes, from take-off to landing, and flight training for pilot cadets primarily focuses on traffic pattern flight training [31]. Therefore, the detailed contributions and novelty of this paper are as follows:
(1) Based on the characteristics of flight tasks in the traffic pattern and the flight training manual, a flight performance evaluation index system that can accurately assess the flight performance of cadets in traffic pattern flight is derived.
(2) By determining the weight relations of various indicators through the G1 method, an evaluation model of flight performance for pilot cadets using the fuzzy comprehensive evaluation method is established.
(3) The flight data of pilot cadets are obtained through experiments. The evaluation results of flight performance of pilot cadets are calculated by inputting the data into the evaluation model. The results show that the evaluation index system and the method proposed in this paper are suitable for a flight performance evaluation of pilot cadets.
2. Flight Performance Evaluation Index System for Pilot Cadets
The traffic pattern flight is a major course for pilot cadets in their flight training. They can acquire flight performance such as take-off, climb, turn, cruise, descent, and landing from the traffic pattern flight training. Standard thresholds and scoring rules for monitoring indicators are set in advance to evaluate the flight performance. The real-time monitoring of flight data and overshoot situations is performed during traffic pattern flight training for pilot cadets.
2.1. Flight Process of Traffic Pattern
The traffic pattern flight is a flight subject that contains a complete flight process. The flight altitude of this subject generally does not exceed 1500 feet. For example, an airport with a runway magnetic heading of 359° is used for traffic pattern flight training. In this flight training, the maximum flight altitude is 1100 ft, and the pilot cadets are required to complete 11 flight phase tasks in sequence, including take-off, upwind flight, crosswind turn, crosswind flight, downwind turn, downwind flight, base turn, base flight, final turn, final flight and landing. Figure 1 shows the traffic pattern training process.
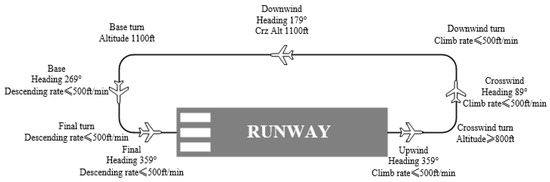
Figure 1.
Traffic pattern flight process.
There are a number of tasks to be completed during the traffic pattern flight. In the take-off phase, the pilot cadet’s control of the aircraft’s status is examined. The pilot cadet needs to control the aircraft to accelerate along the centerline of the runway and to pull the nose up when reaching the rotation speed. During various lateral flights, the pilot cadet needs to manage the aircraft’s track and energy, control the aircraft at the predetermined altitude and heading, and prevent the aircraft’s speed from exceeding the threshold. At each turning point during the flight, the pilot cadet needs to maneuver the aircraft to form a proper turning attitude at the appropriate position, monitor the bank angle so that it does not exceed the limit and promptly correct it before the turn is completed.
The approach and landing phase is the most challenging phase for the pilot cadet. At the end of the final turn, the pilot cadet should position the aircraft on the extended centerline of the runway and parallel to the runway heading. During the approach, the pilot cadet controls the energy, heading, and altitude of the aircraft based on the position of the glide slope and reference points. Before touchdown, the pilot cadet needs to ensure they will land within the touchdown area on the runway. The pilot cadet then controls the aircraft to slow down and taxi along the centerline of the runway.
2.2. Flight Performance Evaluation Index System
The selection of evaluation indicators is a crucial step in the evaluation of flight performance, as it directly affects the evaluation results of the pilot performance. In traffic pattern flight, the pilot cadet follows the training manual for flight operations, and each flight phase has corresponding operational requirements. The pilot cadet’s performance can be intuitively reflected by the relevant flight parameters [32].
The selected indicators should reflect the accuracy of the pilot cadet’s control of the aircraft during the traffic pattern flight, and achieve comprehensive monitoring. By considering the importance of various flight parameters and their practical value in flight performance evaluations, and based on the characteristics of flight tasks in various phases and the training manual, the evaluation indicators were selected.
According to the principles of systematicity, scientific quality, comparability, and practicability [33], the pilot cadet’s flight performance can be reflected by the control of the aircraft’s energy, flight attitude, flight trajectory during different flight phases in the traffic pattern flight. Therefore, based on the pilot cadet’s control over the aircraft’s energy, flight attitude, flight trajectory, a preliminary selection of evaluation indicators for the pilot cadet’s flight performance was made.
In terms of flight energy control, the pilot cadet’s assessment is based on parameters such as altitude, speed, and load factor. In terms of flight attitude control, the pilot cadet’s assessment is based on parameters such as pitch angle and bank angle. For flight trajectory control, the pilot cadet’s assessment is mainly based on trajectory parameters. Thus, for the flight energy control of the pilot cadet, nine evaluation indicators were selected, including altitude deviation in crosswind turn, altitude deviation in downwind, altitude deviation in runway threshold, rotation speed, maximum climb rate in upwind, maximum descent rate in approach, touchdown rate, touchdown overload, maximum flight overload. For the flight attitude control of the pilot, six evaluation indicators were selected, including maximum pitch angle in upwind, maximum pitch angle in final, maximum bank in crosswind turn, maximum bank in downwind turn, maximum bank in turning base, maximum bank in turning final. For the flight trajectory control of the pilot, six evaluation indicators were selected, including track deviation in upwind, track deviation in crosswind, track deviation in downwind, track deviation in approach, touchdown deviation, and taxing deviation.
Based on the characteristics of flight tasks in different phases and the flight training manual, this study provisionally identified 21 evaluation indicators for evaluating the flight performance of pilot cadets. To make the indicators more rational and scientific, the Delphi method was used to interview 168 flight school instructors, airline captains, instructors, experts and academics in the field of pilot training. After two rounds of expert interviews, 90.5% of the initially selected indicators were established as the evaluation criteria for the traffic pattern flight performance of the pilot cadet. The statistics of the experts including numbers and percentages for the interviews are shown in Table 1. The statistics for the Delphi questionnaires are presented in Table 2.

Table 1.
The statistics of experts.

Table 2.
The statistics for the Delphi questionnaires.
Through the collaborative analysis of expert opinions, two indicators of flight attitude control, maximum pitch angle in upwind and maximum pitch angle in final, were found to be repetitive, with two indicators of flight energy control, maximum climb rate in upwind and maximum descent rate in approach. The remaining 19 indicators had low repetitiveness and could effectively achieve the evaluation of flight performance for the pilot cadet’s traffic pattern flight throughout the entire process.
Based on the expert interviews, two flight attitude control indicators, maximum pitch angle in upwind and maximum pitch angle in final, were removed. The evaluation indicators for the flight performance of pilot cadets were then optimized. As a result, a total of 19 evaluation indicators in three dimensions were finalized. The flight performance evaluation index system for pilot cadets is shown in Figure 2.
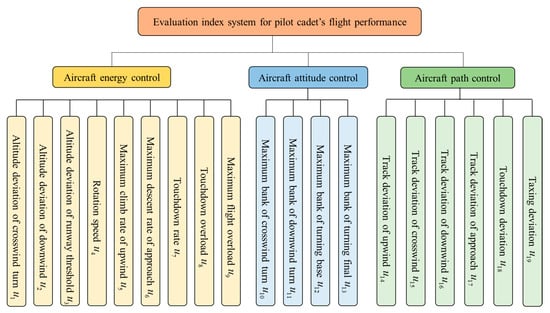
Figure 2.
Flight performance evaluation index system of the pilot cadet.
3. Method
The evaluation of pilot cadets’ flight performance is a complex system, and the selection of appropriate evaluation methods and the establishment of a proper evaluation model will lead to a more accurate assessment of pilot cadets’ traffic pattern flight performance. In this study, the G1 method and the fuzzy comprehensive evaluation method are used to establish an evaluation model of pilot cadets’ traffic pattern flight performance and to evaluate their flight performance.
3.1. Subjective Weight Calculation by G1 Method
To divide a complex problem into a hierarchical structure model with interrelation and subordination, the complex problem is decomposed into several indicators, level by level. The weights can be obtained by determining the importance ranking and degree of each indicator in the hierarchical structure model. In this paper, is used to represent the weight of the main criteria indicators’ level and is used to represent the weight of the sub-criteria indicators’ level. The implementation method of the G1 method was as follows:
- Determine the order relationship of indicators. For a set of flight performance evaluation indicators , experts ranked the importance of these evaluation indicators from high to low based on their personal understanding and experience. Let this ranking be denoted as .
- Assign importance values to adjacent indicators. and are two adjacent indicators, and the relative importance between the two indicators can be represented by . The assigned values of are shown in Table 3.where , and represent the weights of the indicator and the indicator.
 Table 3. Relative importance assignment for adjacent indicators.
Table 3. Relative importance assignment for adjacent indicators.
- Calculate the weight of each indicator. Based on the relative importance value of adjacent indicators, the weight of the evaluation indicator is calculated using Equation (2):
- After obtaining the weight of indicator , the weight of the remaining indicator can be calculated step by step using Equation (3):
- An expert group determines the weight vector. If there are experts involved in the process of determining the indicator weights, different experts may provide different order relationships and weight coefficients among the indicators. To solve this problem, Equation (4) is used to calculate the total weight coefficients for all experts regarding the indicators:where represents the weight coefficient of the expert on the evaluation indicator .
3.2. Multi-Level Fuzzy Comprehensive Evaluation
3.2.1. Grading Standard
The grading standard of evaluation indicators is the basis of the evaluation system for the flight performance of flight cadets. We divided the grading standard into four levels: excellent, good, medium, and bad. Therefore, the comment set V = { Excellent, Good, Medium, Bad} was established for fuzzy comprehensive evaluation.
By consulting the flight training manual for the maximum threshold requirements of flight control and flight parameters in the traffic pattern flight, the threshold relationship between the flight performance level of the pilot cadet and the corresponding evaluation indicators for each flight performance is derived. Table 4 shows the relationship between the grading standards of 19 evaluation indicators and the flight performance levels. Each grading standard corresponds to a deviation value, which serves as the basis for the membership function.

Table 4.
Flight performance evaluation threshold standards.
3.2.2. Membership Function
The fuzzy membership degrees of each factor are determined using membership functions. Figure 3 shows a graphical representation of the triangular fuzzy membership function Figure 3a and the trapezoidal fuzzy membership function Figure 3b.

Figure 3.
Fuzzy membership function.
As shown in Table 4, the deviation value thresholds corresponding to the different levels of the 19 criteria can be categorized into two scenarios. In the first scenario, the thresholds have a center-symmetric distribution around zero. In the second scenario, the thresholds are spread over a range and spread in both directions. In this context, if the deviation value of flight data falls to the left of the threshold of the Excellent level or to the right of the threshold of the Bad level, it can also be considered Excellent or Bad, with a membership degree of 1. If the deviation value of flight data falls between the thresholds of two levels, this study postulates that the value is a membership with the level to the left and simultaneously with the level to the right. Furthermore, when the deviation value is exactly at the threshold of a particular level threshold, this research assumes that the value has the highest degree of membership with that particular level, with a membership degree of 1. Therefore, the trapezoidal membership function is used to deal with the boundary thresholds and the triangular membership functions for the intermediate levels.
By using a combination of triangular fuzzy membership function and trapezoidal fuzzy membership function, a hybrid membership function is established to evaluate the flight performance of pilot cadets in the traffic pattern flight. The hybrid membership function is shown in Equation (5):
The graphical representation of the hybrid membership function is shown in Figure 4.
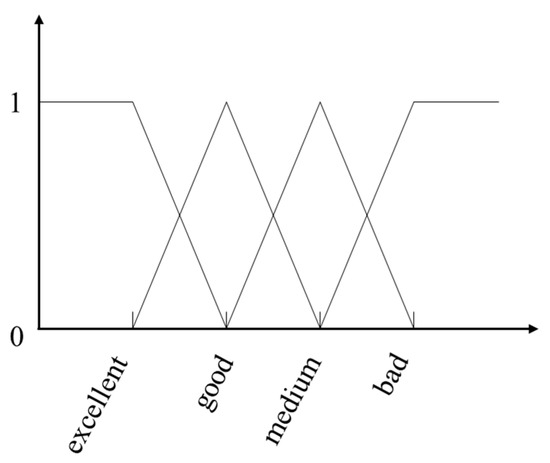
Figure 4.
The hybrid membership function.
3.2.3. Evaluation Matrix
Based on the experimental data that were obtained and the hybrid membership functions, the main criteria element evaluation matrix of each pilot cadet is calculated. Each is considered as a main criteria element and is denoted as . For example, Equation (6) is the evaluation matrix of :
where means the evaluation matrix of the main criteria element . The in is calculated based on the deviation data obtained from the experiment and the membership function. refers to the number of indices of and refers to the number of grading standard in the comment set .
3.2.4. Fuzzy Comprehensive Evaluation
The fuzzy comprehensive evaluation model of a main criteria element is calculated by Equation (7):
where symbol is the fuzzy synthesis operator. represents the membership degree corresponding to each grading. By using the maximum membership rule to deal with , the final fuzzy comprehensive evaluation result can be obtained. In addition, to better reflect the impact of various indices in the evaluation of pilot cadet’s flight performance on traffic pattern, the weighted average fuzzy synthesis operator was chosen in this paper, and the is shown in Equation (8):
Equation (8) can comprehensively consider the evaluation indicators and comprehensive evaluation results, which makes the fuzzy comprehensive evaluation results more practical. After obtaining the evaluation results of the main criteria element, the evaluation results of the main criteria element need to be normalized, while the in the calculation result. A new fuzzy comprehensive evaluation matrix is formed using the normalized results. Then, the product-weighted fuzzy synthesis operator is used to recalculate and obtain the comprehensive evaluation results of the pilot cadet’s flight performance on the traffic pattern flight.
4. Results and Discussions
The pilot cadets evaluated are selected from a flight school in China that trains approximately 320 pilot cadets per year. In terms of training equipment, the school is equipped with a professional flight simulator training room that can accommodate up to 90 pilot cadets for simulator training. At present, the evaluation of the cadets’ traffic pattern flight performance is mainly based on subjective scoring, which has low accuracy and is highly influenced by the evaluators’ subjectivity. In order to obtain more accurate evaluation results, this study attempts to utilize the flight data collected during the cadets’ training and apply a fuzzy comprehensive evaluation method to objectively evaluate the cadets’ traffic pattern flight performance.
4.1. Experimental Design and Data Pre-Processing
In order to obtain flight data and expert judgements on the training performance of the pilot cadets, which were used to validate the flight performance evaluation model, a flight experiment was designed specifically for the pilot cadets in the traffic pattern flight. The specific experimental procedure is shown in Figure 5.
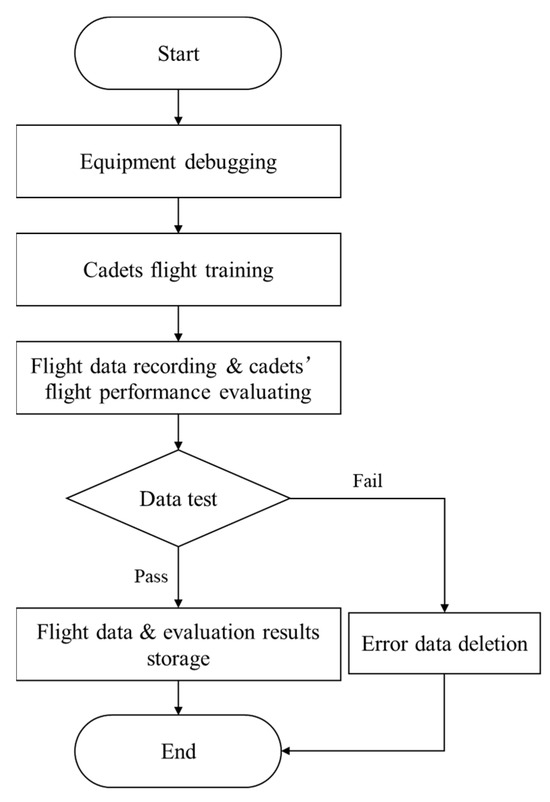
Figure 5.
The experimental process of the traffic pattern flight.
A total of 30 male student pilots aged between 18 and 20 years old, healthy and well-rested prior to the test, and three flight instructors with more than 5 years’ experience and valid flight certificates, participated in the experiment.
The flight experiment used the Cessna 172R flight simulator. During the experiment, control deviation data were recorded as the pilot cadets operated the flight simulator. After the experiment, the three instructors evaluated the flight performance of the cadets based on the maximum deviation values recorded during the flight experiments, using the evaluation threshold table for flight evaluation indicators. The expert evaluation results were then obtained by calculating the average scores given by the three instructors. The maximum deviation values obtained for each indicator and the expert evaluation results were then verified, and the complete and accurate data were stored. Finally, the dataset of the maximum deviation values and the expert evaluation results for the 30 pilot cadets in the 19 evaluation indicators were obtained. The statistical analysis of the maximum deviation values for the 30 cadets across the 19 evaluation indicators is shown in Table 5.

Table 5.
The statistical analysis of the maximum deviation values for the 30 cadets across the 19 evaluation indicators.
4.2. Calculation of Indicator Weights
The weights of the 19 evaluation indicators were calculated using the G1 method. A total of 168 experts were invited to rate the importance of the indicators, and 131 survey responses were collected. Based on the collected survey results, the weights of each indicator were calculated and are presented in Table 6.

Table 6.
The weights of each indicator.
In Table 6, the most important concern is aircraft energy control , the second is the aircraft path control , and the least important element is the aircraft attitude control . The weight of the 19 indicators is = [0.0279, 0.0316, 0.0863, 0.0437, 0.0886, 0.2081, 0.1684, 0.1296, 0.2158], = [0.2559, 0.2004, 0.2228, 0.3209], = [0.1251, 0.0882, 0.1295, 0.2089, 0.2440, 0.2043].
4.3. Flight Performance Evaluation
Based on the calculation results of the weights, the evaluation results of the main criteria element of the pilot cadets’ traffic pattern flight performance are calculated using a fuzzy evaluation model. Taking the pilot cadet 1 as an example, a comprehensive evaluation of this pilot cadet’s traffic pattern flight performance is conducted using a fuzzy comprehensive evaluation method. The maximum deviations of the first pilot cadet in the 19 evaluation indicators are shown in Table 7.

Table 7.
The maximum deviations of the first pilot cadet in the 19 evaluation indicators.
Based on the deviations shown in Table 7, the evaluation matrix (see Equations (9)–(11)) of the main criteria elements for the pilot cadet 1 is calculated using the membership function Equation (5).
According to Equation (7), the evaluation results of the pilot cadet 1 can be calculated as follows:
Following the principle of maximum membership degree, the evaluation results of the pilot cadet 1 at the level of the main criteria elements are shown in Table 8.

Table 8.
The evaluation results of the pilot cadet 1 at the main criteria elements’ level.
Since the calculation results show that , it is not necessary to normalize the evaluation results of the main criteria elements when constructing a comprehensive evaluation matrix for the pilot cadet 1. Therefore, the comprehensive evaluation matrix for flight performance can be obtained.
By synthesizing the comprehensive evaluation matrix with the weight matrix using the weighted average fuzzy synthesis operator, the comprehensive evaluation results of pilot cadet 1 can be obtained.
Based on the maximum membership degree obtained from the calculation results, the flight performance evaluation result of pilot cadet 1 is excellent.
Then, by repeating the steps of the above fuzzy comprehensive evaluation of flight performance, the evaluation results of traffic pattern flight performance for all 30 pilot cadets can be calculated. The evaluation results of the flight performance for the 30 pilot cadets are shown in Table 9.

Table 9.
The evaluation results of flight performance for the 30 pilot cadets.
4.4. Results Analysis
The evaluation results show that among the 30 pilot cadets that were evaluated, 14 cadets’ evaluation results are excellent, 2 cadets’ evaluation results are good, 9 cadets’ evaluation results are medium, and 5 cadets’ evaluation results are poor. By examining the flight theory learning and simulated flight training performance of the selected pilot cadets during their daily schooling, it is clear that the evaluation results have a strong correlation with their performance. The cadets who are rated as excellent have better theoretical learning performance and a better performance in the hard simulated flight training test while the cadets with poor evaluation results have a weak learning performance and poor training performance. Therefore, it can be verified that the evaluation model of pilot cadets’ traffic pattern flight performance established by the fuzzy comprehensive evaluation method in this paper can evaluate pilot cadets’ handling performance in traffic pattern flights. To verify the reliability of the model evaluation results and their consistency with the expert evaluation results, the model evaluation results were compared with the expert evaluation results.
Figure 6 shows the evaluation results by the experts and the method proposed in this paper. By comparing the model evaluation results with the expert evaluation results, it can be concluded that the model evaluation results obtained in this paper are basically consistent with the expert evaluation results, which proves the accuracy of the modelling method for evaluating the flight performance of pilot cadets in traffic pattern flight. It also confirms the good practical application effect of the fuzzy evaluation method used in this paper. Through the evaluation of pilot cadets’ flight performance, flight instructors and flight schools can clearly identify the differences in aircraft energy control, flight attitude control, and flight trajectory control among different pilot cadets, as well as the overall level of pilot cadets’ flight performance within the group. This provides an important theoretical basis for instructors to develop personalized training plans in a timely and accurate manner.
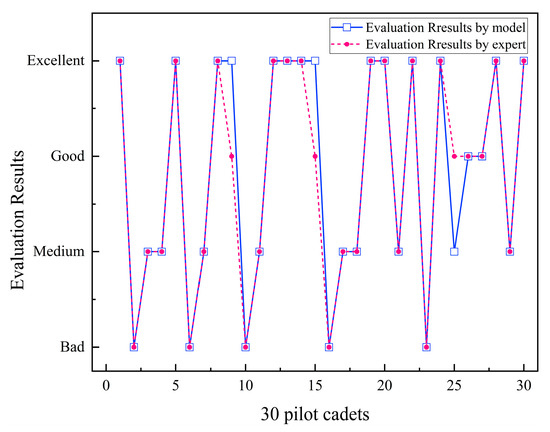
Figure 6.
Comparison between expert evaluation results and fuzzy comprehensive evaluation method evaluation results.
5. Conclusions
In this paper, an evaluation model of pilot cadets’ flight performance in traffic pattern flight was established using the Delphi method, the G1 method, and the fuzzy comprehensive evaluation method. For the evaluation of pilot cadets’ flight performance, a traffic pattern flight was selected as the flight subject for the evaluation of flight performance. Combined with the flight training manual and expert interviews with flight instructors, a total of 19 flight parameters were selected as evaluation indicators, forming a flight performance evaluation index system for pilot cadets. The weight of the evaluation indicators determined by the G1 method incorporates the judgments of numerous experts on the degree of impact of the indicators. The evaluation model established by the fuzzy comprehensive evaluation method avoids the errors in the evaluation results caused by the subjective factors of the instructors. Then, the flight data of pilot cadets were obtained through simulated flight training experiments. By inputting the flight data into the evaluation model, the flight performance evaluation results were calculated for each pilot caded. The results show the evaluation index system established in this paper accurately reflects the flight performance of the pilot cadets. The evaluation model based on the G1 method and the fuzzy comprehensive evaluation method established in this paper has consistent evaluation results with expert results. Therefore, the evaluation model has good rationality, accuracy, and applicability in evaluating the performance of pilot cadets.
The contribution of this study is to propose an evaluation model that assesses the flight performance of pilot cadets during their traffic pattern flight training. By using this evaluation model to assess their current level of flight proficiency, it could help them to identify weaknesses in their flight operations and provide scientific support for the development of personalized training plans. In addition, the evaluation of pilot cadets’ flight performance will also help to promote safer and more sustainable civil aviation operations in the future.
Author Contributions
Conceptualization, H.S. and G.L.; methodology, G.L. and H.W.; validation, G.L. and T.P.; investigation, T.P. and H.L.; data curation, G.L.; writing—original draft preparation, G.L.; writing—review and editing, G.L. and H.L.; supervision, H.S. and H.W.; funding acquisition, H.S. and H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the Fundamental Research Funds for the Central Universities under Grant NS2022094; National Natural Science Foundation of China and Civil Aviation Administration of China under Grant No. U2033202; and Experimental Technology Research and Development Project of Nanjing University of Aeronautics and Astronautics Project under Grant SYJS202207Y.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to their containing information that could compromise the privacy of the experimental participants and these data need to be protected.
Conflicts of Interest
The author(s) declared that they have no potential conflicts of interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Lu, Y.; Zhang, S.G.; Hao, L.; Huangfu, H.Y.; Sheng, H. System dynamics modeling of the safety evolution of blended-wing-body subscale demonstrator flight testing. Saf. Sci. 2016, 89, 219–230. [Google Scholar] [CrossRef]
- Mao, Y.; Lu, Y.; Huang, D.; Fu, S. Simulation study on civil aviation human reliability learning from incidents using system dynamics. In Proceedings of the International Conference on Aerospace System Science and Engineering, Singapore, 14–16 July 2021. [Google Scholar]
- Sant, D.A.L.M.; Hilal, A.V.G. The impact of human factors on pilots’ safety behavior in offshore aviation companies: A brazilian case. Saf. Sci. 2021, 140, 105272. [Google Scholar] [CrossRef]
- Xiao, Q.; Luo, F.; Li, Y.; Pan, D. Risk prediction and early warning of pilots’ unsafe behaviors using association rule mining and system dynamics. J. Air Transp. Manag. 2023, 110, 102422. [Google Scholar] [CrossRef]
- ICAO. Safety Reports; International Civil Aviation Organization: Montreal, QC, Canada, 2023; Available online: https://www.icao.int/safety/Documents/ICAO_SR_2023_20230823.pdf (accessed on 5 September 2023).
- Kelly, D.; Efthymiou, M. An analysis of human factors in fifty controlled flight into terrain aviation accidents from 2007 to 2017. J. Saf. Res. 2019, 69, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Perboli, G.; Gajetti, M.; Fedorov, S.; Giudice, S.L. Natural Language Processing for the identification of Human factors in aviation accidents causes: An application to the SHEL methodology. Expert Syst. Appl. 2021, 186, 115694. [Google Scholar] [CrossRef]
- Mckinney, D. Circling traps. Bus. Commer. Aviat. 2018, 114, 58–62. [Google Scholar]
- Tabibzadeh, M.; Shapeti, V.; Mokhtari, M. Systematic investigation of the Asiana Airlines 214 air crash using the AcciMap methodology. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2019, 63, 606–610. [Google Scholar] [CrossRef]
- Hebbar, P.A.; Pashilkar, A.A. Pilot performance evaluation of simulated flight approach and landing manoeuvres using quantitative assessment tools. Sādhanā 2017, 42, 405–415. [Google Scholar] [CrossRef]
- Wojcik, D.Z.; Moulin, C.J.A.; Fernandez, A. Assessment of metacognition in aviation pilot students during simulated flight training of a demanding maneuver. Appl. Ergon. 2021, 95, 103427. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Dong, C.; Sun, H.; Ren, Y. A method of applying flight data to evaluate landing operation performance. Ergonomics 2019, 62, 171–180. [Google Scholar] [CrossRef]
- Chen, W.; Huang, S. Evaluating flight crew performance by a Bayesian network model. Entropy 2018, 20, 178. [Google Scholar] [CrossRef]
- Zhang, S.; Huo, Z.; Sun, Y.; Li, F.; Jia, B. Pilot maneuvering performance analysis and evaluation with deep learning. Int. J. Aerosp. Eng. 2023, 2023, 6452129. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Z.; Han, L.; Mei, N. Fuzzy comprehensive evaluation method for energy management systems based on an internet of things. IEEE Access 2017, 5, 21312–21322. [Google Scholar] [CrossRef]
- Zadeh, L.A. Quantitative fuzzy semantics. Inf. Sci. 1971, 3, 159–176. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic = computing with words. IEEE Trans. Fuzzy Syst. 1996, 4, 103–111. [Google Scholar] [CrossRef]
- Jiang, L.; Tao, T.; Zhang, C.; Jiang, H.; Wang, J. Summary of the port shoreline resource evaluation based on triangular fuzzy analytic hierarchy process. Pol. Marit. Res. 2017, 24, 16–22. [Google Scholar] [CrossRef][Green Version]
- Lee, S. Determination of priority weights under multiattribute decision-making situations: AHP versus fuzzy AHP. J. Constr. Eng. Manag. 2015, 141, 05014015. [Google Scholar] [CrossRef]
- Mo, H.; Yan, K.; Zhao, X.; Zeng, Y.; Wang, X.; Wang, F.Y. Type-2 fuzzy comprehension evaluation for tourist attractive competency. IEEE Trans. Comput. Soc. Syst. 2019, 6, 96–102. [Google Scholar] [CrossRef]
- Russo, R.F.S.M.; Camanho, R. Criteria in AHP: A systematic review of literature. Procedia Comput. Sci. 2015, 55, 1123–1132. [Google Scholar] [CrossRef]
- Al-Harbi, K.M.A.S. Application of the AHP in project management. Int. J. Proj. Manag. 2001, 19, 19–27. [Google Scholar] [CrossRef]
- Xie, X.J. Research on material selection with multi-attribute decision method and G1 method. Adv. Mater. Res. 2014, 952, 20–24. [Google Scholar] [CrossRef]
- Lu, J.; Wang, Y. A safety assessment of China’s crude oil import based on G1 method. Procedia Soc. Behav. Sci. 2013, 96, 1738–1744. [Google Scholar]
- Ye, F.; Sun, J.; Wang, Y.; Nedjah, N.; Bu, W. A novel method for the performance evaluation of institutionalized collaborative innovation using an improved G1-CRITIC comprehensive evaluation model. J. Innov. Knowl. 2023, 8, 100289. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, M.; Tian, Z.; Lu, Y.; Chen, K. Evaluation method of storage assignment for intelligent pharmaceutical warehouse. In Proceedings of the 2019 IEEE Eurasia Conference on IOT, Communication and Engineering (ECICE), Yunlin, China, 3–6 October 2019. [Google Scholar]
- Zhao, Y.; Lv, X.; Shen, X.; Wang, G.; Li, Z.; Yu, P.; Luo, Z. Determination of weights for the integrated energy system assessment index with electrical energy substitution in the dual carbon context. Energies 2023, 16, 2039. [Google Scholar] [CrossRef]
- Zhou, W.; Liu, M.; Xu, Z.; Herrera-Viedma, E. Global fusion of multiple order relations and hesitant fuzzy decision analysis. Appl. Intell. 2022, 52, 6866–6888. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y.; Jin, S. Research on flight fatigue risk comprehensive evaluation index system based on G1 method. J. China Saf. Sci. 2010, 20, 21–26. [Google Scholar]
- Kelemen, M.; Polishchuk, V.; Kelemen, M.; Sabo, J. A hybrid model for evaluating the outcomes of student pilots within the didactic system of aviation education. Aerospace 2023, 10, 281. [Google Scholar] [CrossRef]
- Wang, Y. Study on Flight Quality Evaluation Model of Flight Cadets. Master’s Thesis, Civil Aviation Flight University of China, Guanghan, China, 2019. [Google Scholar]
- Wang, L.; Ren, Y.; Sun, H.; Dong, C. A landing operation performance evaluation system based on flight data. In Proceedings of the Engineering Psychology and Cognitive Ergonomics: Cognition and Design, Vancouver, BC, Canada, 9–14 July 2017. [Google Scholar]
- Li, Y.H.; Zeng, S.S. Modeling and analysis of football players’ specific physical ability based on training evaluation index. Secur. Commun. Netw. 2021, 2021, 1446971. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).