Numerical Analysis of Vibroacoustic Response of Timber Floor Panels Damped with Porous Materials
Abstract
:Featured Application
Abstract
1. Introduction
2. General Structural Design
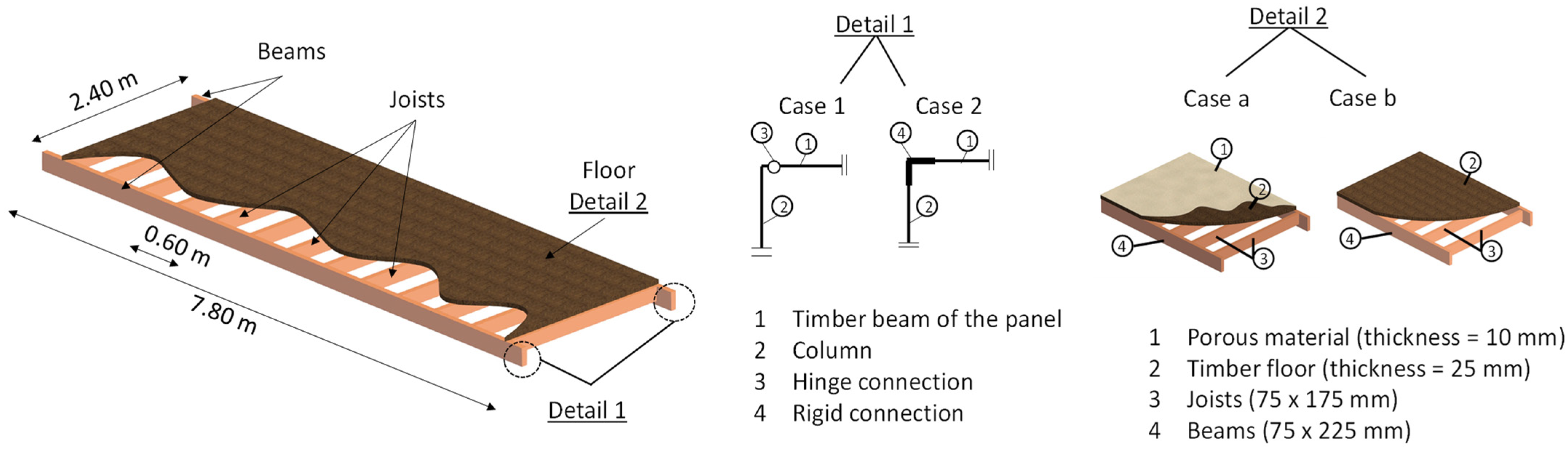
2.1. Floor Panel Description
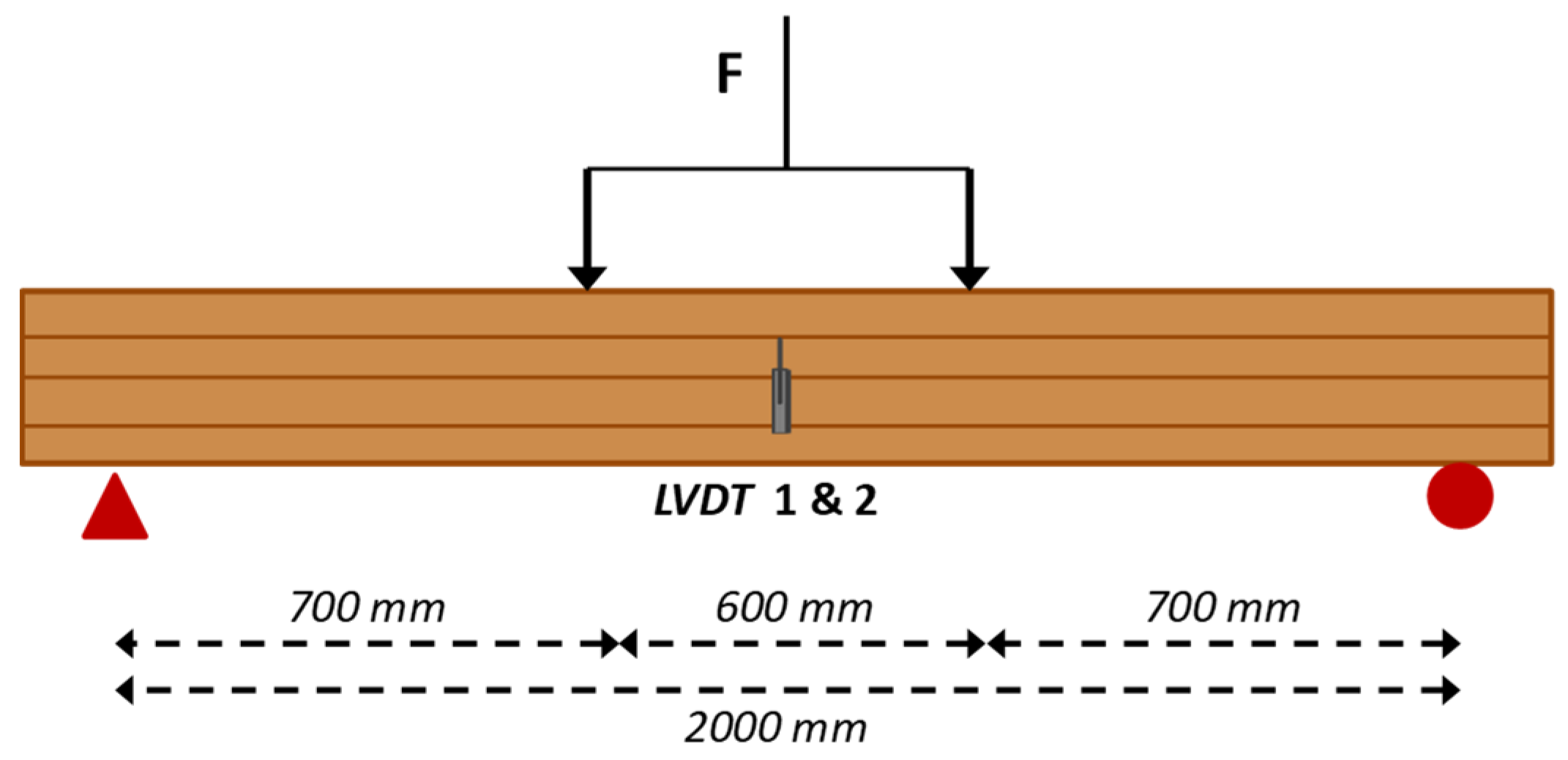
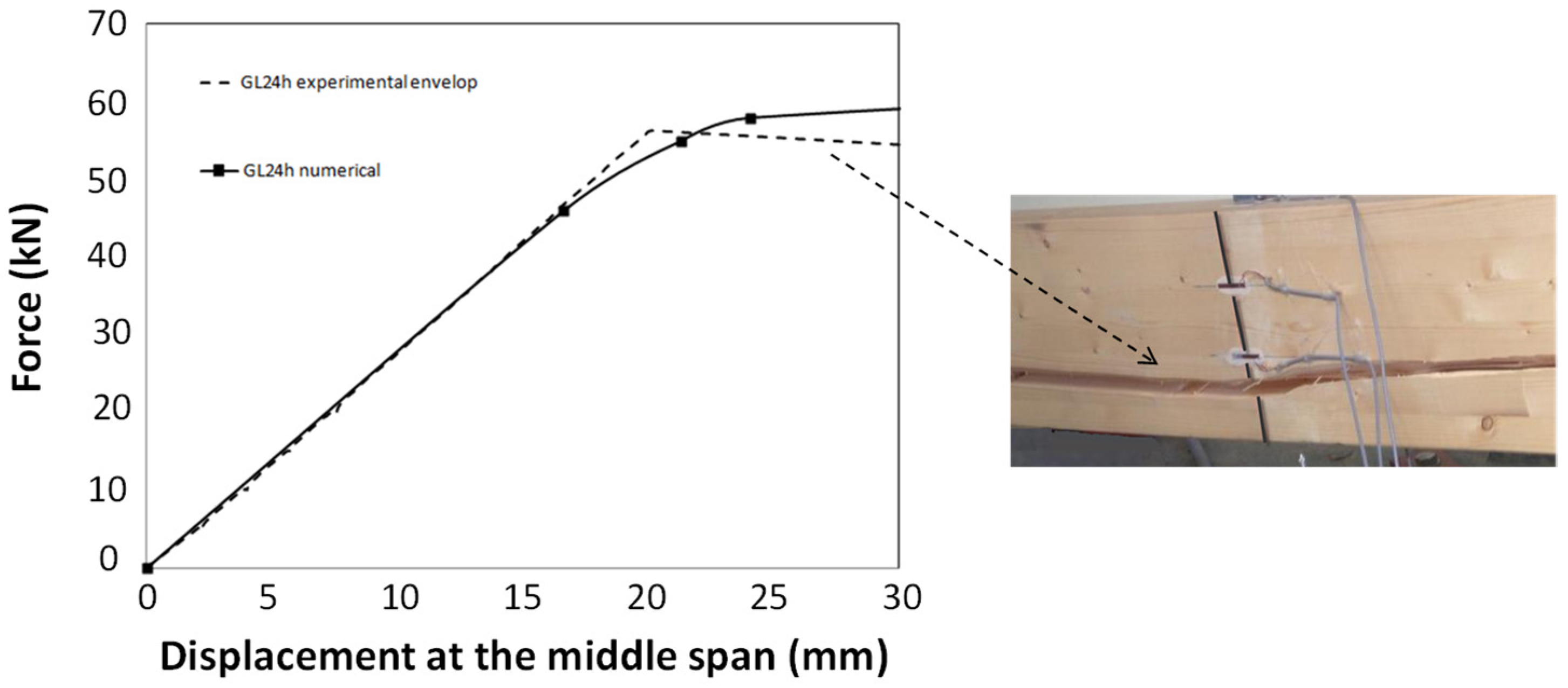
2.2. Experimental and Numerical Determination of the Mechanical Properties of Glued Laminated Timber
3. Finite Element Formulation of Sound Radiation of an Elastic Structure with a Poroelastic Layer
3.1. Local Equations
- Elastic structure:
- Poroelastic material (solid phase):
- Poroelastic material (fluid phase):
3.2. Variational Formulation
- Elastic structure:
- Poroelastic material (solid phase):
- Poroelastic material (fluid phase):
3.3. Finite Element Discretization
3.4. Prediction of Radiated Sound Power
4. Dynamic Analyses and Parametric Study
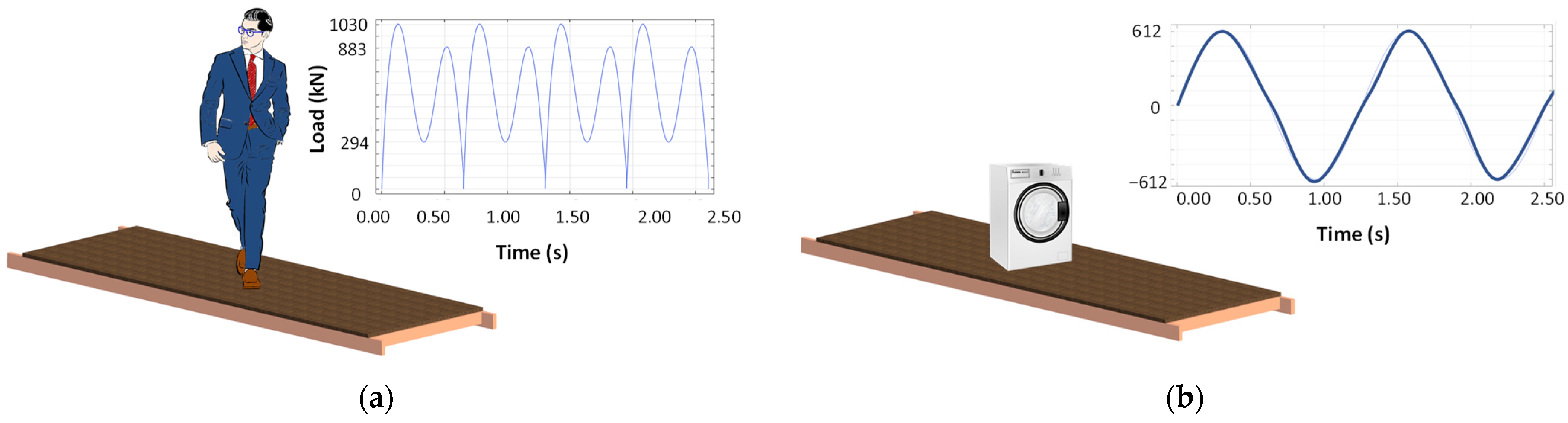
4.1. Loading
- Walking time history
- Washing machine time history
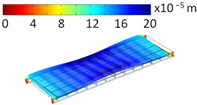
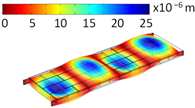
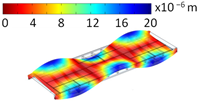
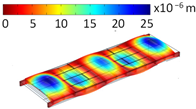
4.2. Fundamental Frequencies
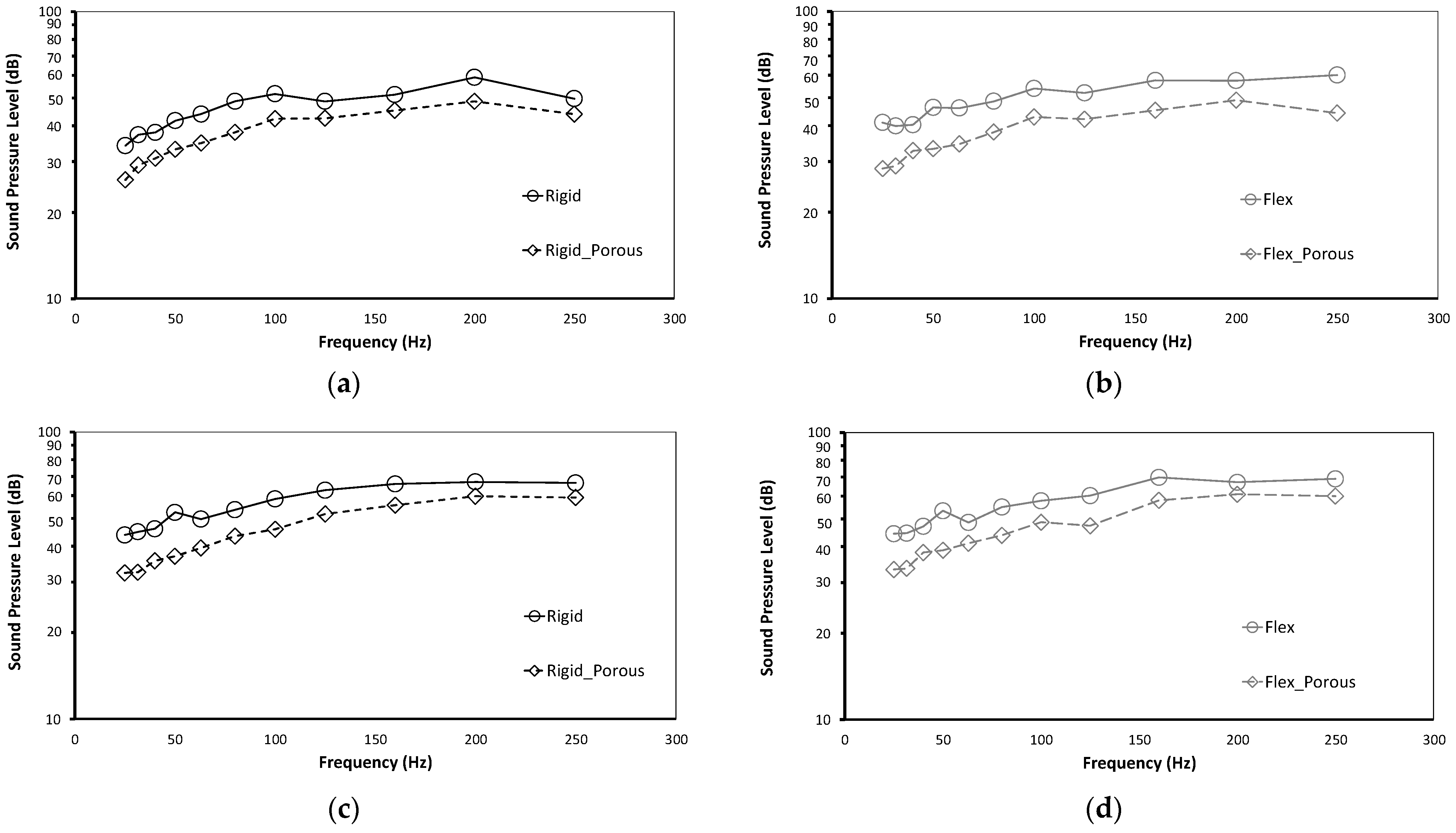
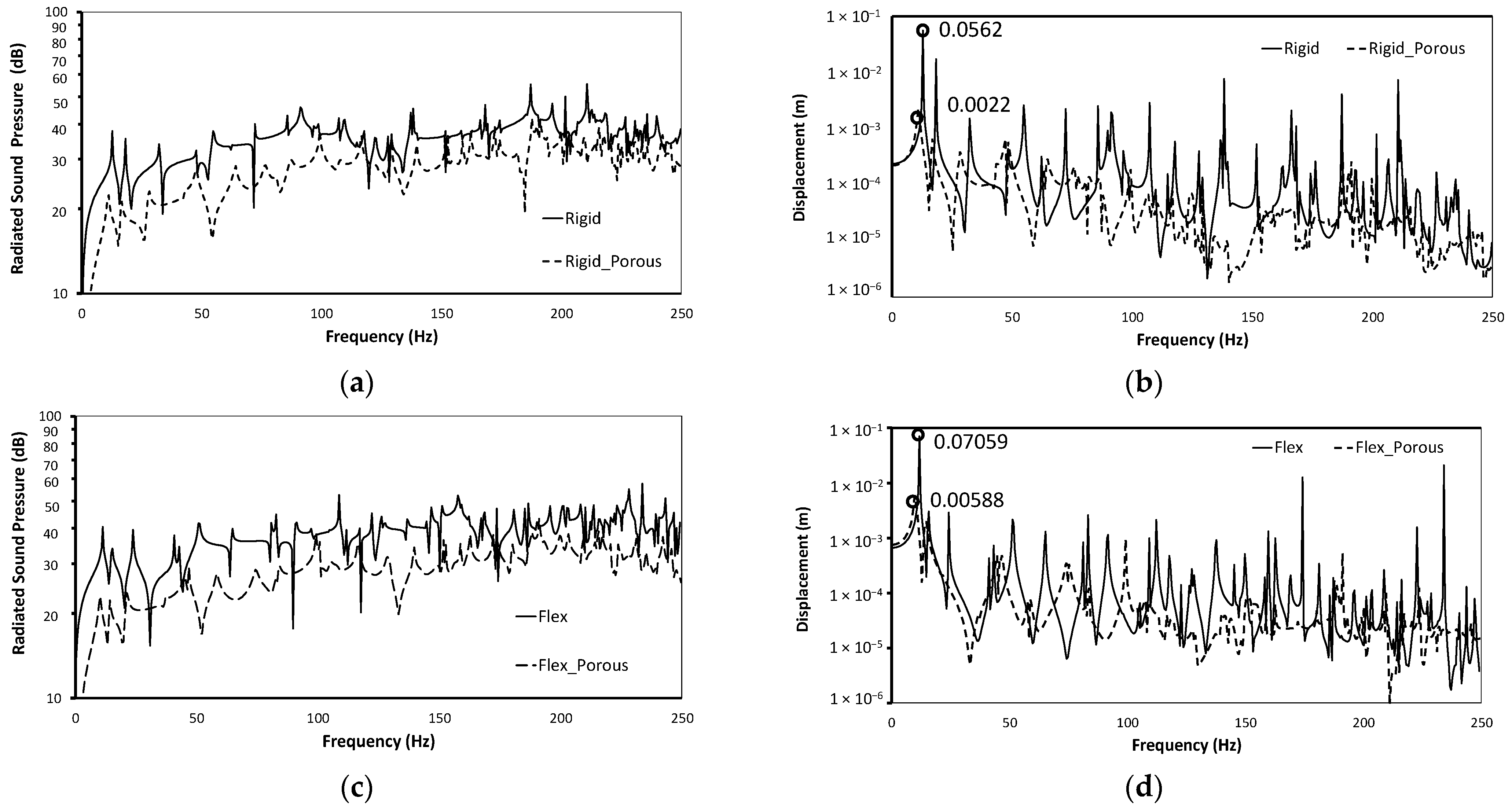
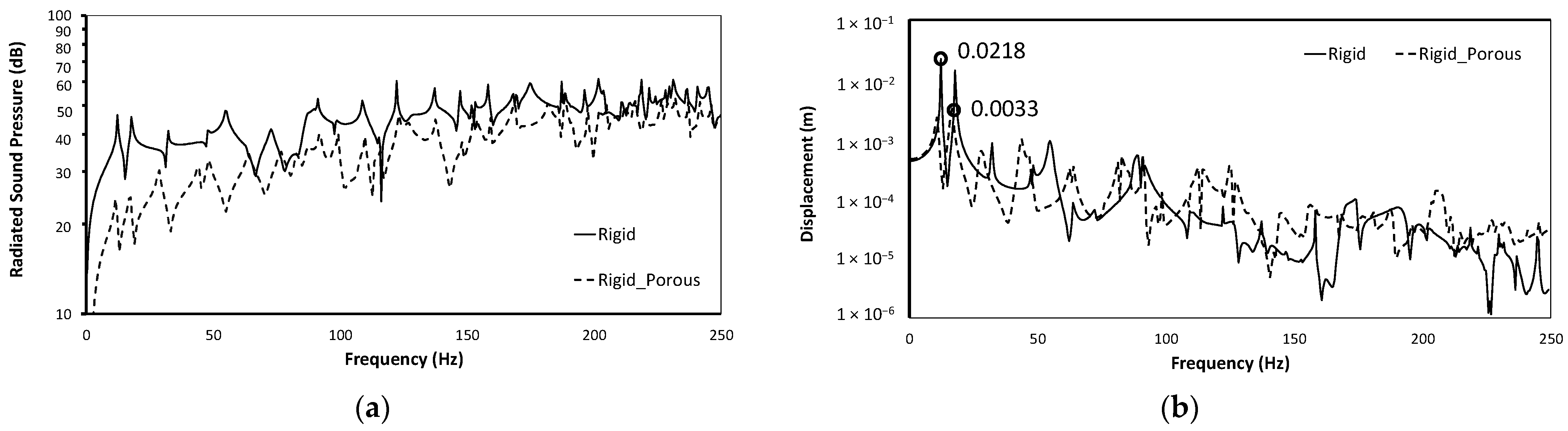
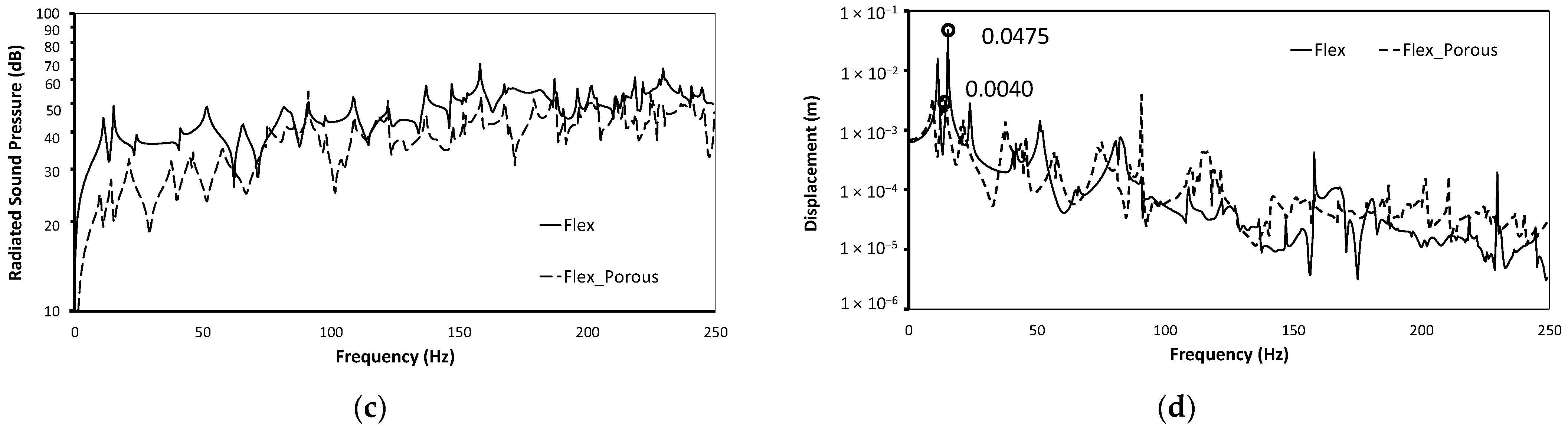
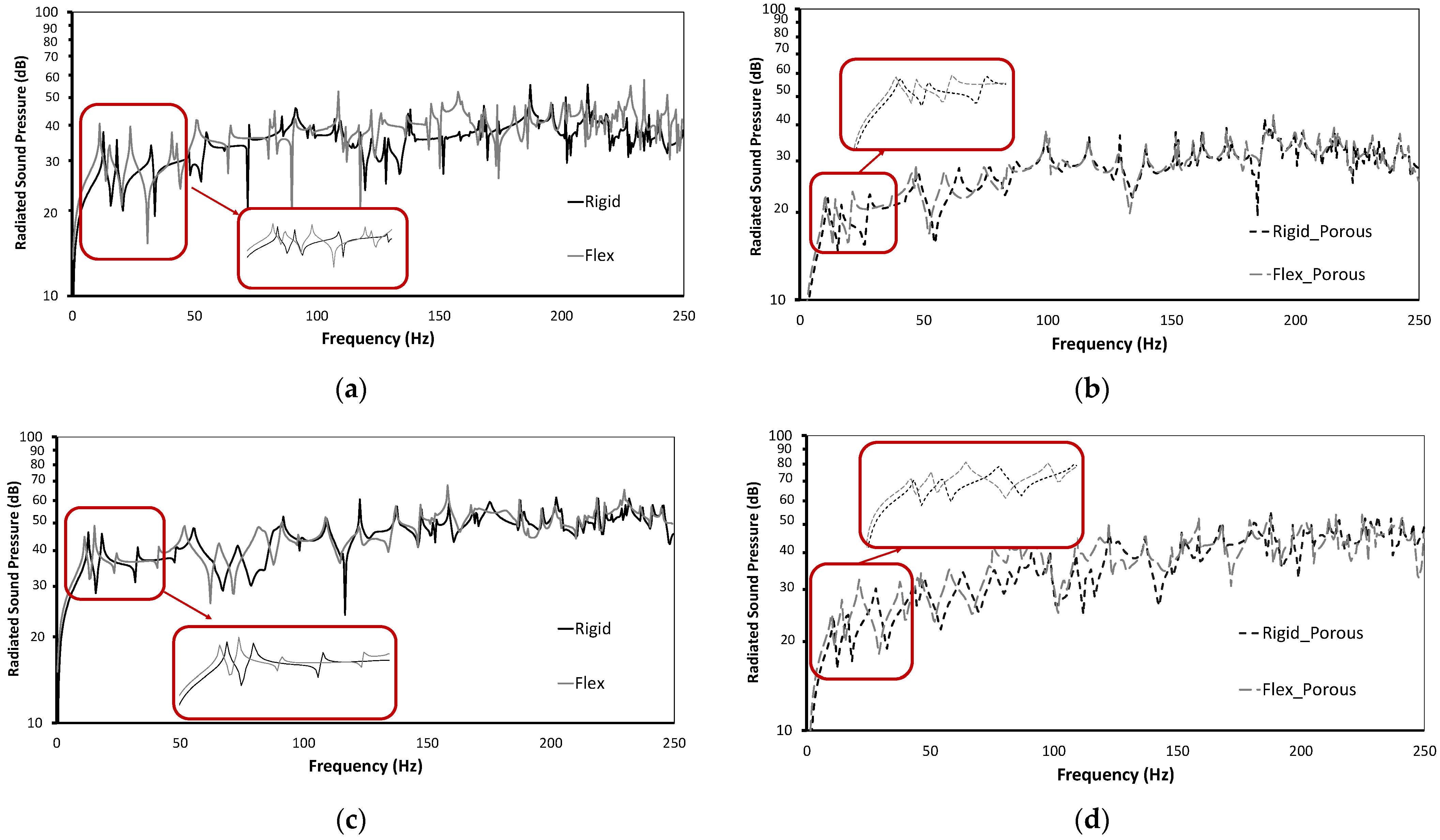
4.3. Effect of Porous Material
4.4. Effect of Boundary Conditions
5. Conclusions
- Experimental tests are conducted to determine the mechanical properties of the glued laminated timber, and numerical models are developed using the finite element method (FEM). The material properties obtained from the experimental tests are used as input data in the FEM model to predict the behavior of the floor panel.
- A finite element formulation of sound radiation from an elastic structure with a poroelastic layer is presented. The poroelastic material is characterized using Biot theory, and its behavior is coupled with that of the elastic structure using a symmetrical coupling term. The porous material has two phases: solid and fluid, which are represented in the formulation by the displacement field for the solid phase and the pressure field for the fluid phase. This original approach has the benefit of lower computing costs and facilitates connectivity between all domains.
- The dynamic analyses and parametric study of the timber floor panel are performed considering different loading conditions and the presence of the porous material. The study shows that the incorporation of the porous layer leads to a significant reduction in sound levels (approximately 18%) by acting as an efficient sound absorber. The porous material not only attenuates sound but also dampens structural vibrations, contributing to improved overall noise reduction. This is owing to the porous sound-absorbing material’s damping effect on timber floor panels displacement, in which vibration energy is released as heat and absorbed by the porous sound-absorbing material’s solid skeleton. The porous sound-absorbing material also reduces noise due to thermal and viscous effects. Further research can focus on optimizing the properties of the porous material used in the floor panel to achieve maximum noise reduction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aloisio, A.; Pasca, D.; De Santis, Y.; Hillberger, T.; Giordano, P.; Rosso, M.; Tomasi, R.; Limongelli, M.; Bedon, C. Vibration issues in timber structures: A state-of-the-art review. J. Build. Eng. 2023, 76, 107098. [Google Scholar] [CrossRef]
- Rigobert, S.; Sgard, F.; Atalla, N. Investigation of dissipative effects in a poroelastic layer coated plate. J. Acoust. Soc. Am. 1999, 105, 1295. [Google Scholar] [CrossRef]
- Conta, S.; Homb, A. Sound radiation of hollow box timber floors under impact excitation: An experimental parameter study. Appl. Acoust. 2020, 161, 107190. [Google Scholar] [CrossRef]
- Titirla, M.; Michel, L.; Ferrier, E. Mechanical behavior of hybridal floor panels to timber columns joints. In Proceedings of the 9th International Conference on Fibre-Reinforced Polymer (FRP) Composites in Civil Engineering, CICE 2018, Paris, France, 17–19 July 2018. [Google Scholar]
- Titirla, M.; Benakli, S.; Larbi, W. Dynamic and vibroacoustic response of timber floor panels. Measurements and non-linear numerical simulations. In Proceedings of the 8th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, COMPDYN 2021, Athens, Greece, 28–30 June 2021. [Google Scholar]
- CEN. 2004. EN 1995-1-1:2004; Eurocode 5: Design of Timber Structures. Part 1–1: General Common Rules and Rules for Buildings. European Committee for Standardization: Brussel, Belgium, 2004.
- Bachmann, H.; Ammann, W. Vibrations in Structures Induced by Man and Machines; IABSE—AIPC—IVBH: Zurich, Switzerland, 1987. [Google Scholar]
- Williams, M.S.; Waldron, P. Evaluation of methods for predicting occupantin-duced vibrations in concrete floors. Struct. Eng. 1994, 72, 334–340. [Google Scholar]
- Da Silva, J.G.S.; da SVellasco, P.C.G.; de Andrade, S.A.L.; da Soeiro, F.J.C.P.; Werneck, R.N. An evaluation of the dynamical performance of composite slabs. Comput. Struct. 2003, 81, 1905–1913. [Google Scholar] [CrossRef]
- Hicks, S. Vibration characteristics of steel-concrete composite floor system. Prog. Struct. Eng. Mater. 2004, 4, 21–38. [Google Scholar] [CrossRef]
- Ebrahimpour, A.; Sack, R.L. A review of vibration serviceability criteria for-floor structures. Comput. Struct. 2005, 83, 2488–2494. [Google Scholar] [CrossRef]
- Bernard, E.S. Dynamic serviceability in lightweight engineered timber floors. ASCE J. Struct. Eng. 2008, 134, 258–268. [Google Scholar] [CrossRef]
- Yang, Y.; Fenemore, C.; Kingan, M.; Mac, B. Analysis of the vibroacoustic characteristics of cross laminated timber panels using a wave and finite element method. J. Sound Vib. 2021, 494, 115842. [Google Scholar] [CrossRef]
- Caniato, M.; Bettarello, F.; Fausti, P.; Ferluga, A.; Marsich, L.; Schmid, C. Impact sound of timber floors in sustainable buildings. Build. Environ. 2017, 120, 110–122. [Google Scholar] [CrossRef]
- Filippoupolitis, M.; Hopkins, C.; Völtl, R.; Schanda, U.; Mahn, J.; Krajči, L. Structural dynamics of a dowelled-joist timber floor in the low-frequency range modelled using finite element simulation. Eng. Struct. 2017, 148, 602–620. [Google Scholar]
- Proença, M.; Neves e Sousa, A.; Garrido, M.; Correia, J.R. Acoustic performance of composite sandwich panels for building floors: Experimental tests and numerical-analytical simulation. J. Build. Eng. 2020, 32, 101751. [Google Scholar]
- Granzotto, N.; Arianna Marzi, A.; Gasparella, A. Cross-Laminated Timber Floor: Analysis of the Acoustic Properties and Radiation Efficiency. Appl. Sci. 2022, 12, 3233. [Google Scholar] [CrossRef]
- Titirla, M.; Ferrier, E.; Michel, L. On the mechanical behaviour of innovative moment connections between composite floor panels and glulam columns. Int. J. Archit. Herit.-Conserv. Anal. Restor. 2021, 15, 321–333. [Google Scholar]
- EN 1194:1999; Timber Structures—Glued Laminated Timber—Strength Classes and Determination of Characteristic Values (Withdrawn), 1999. British Standards Institution: London, UK, 1999.
- EN 384; Structural Timber—Determination of Characteristic Values of Mechanical Proper-Ties and Density; CEN/TC 124. British Standards Institution: London, UK, 2016.
- Allard, J.F.; Atalla, N. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Larbi, W.; Deü, J.-F.; Ohayon, R. Vibroacoustic analysis of double-wall sandwich panels with viscoelastic core. Comput. Struct. 2016, 174, 92–103. [Google Scholar]
- Panneton, R.; Atalla, N. Numerical prediction of sound transmission through finite multilayer systems with poroelastic materials. J. Acoust. Soc. Am. 1996, 100, 346–354. [Google Scholar]
- Atalla, N.; Hamdi, M.A.; Panneton, R. Enhanced weak integral formulation for the mixed (u, p) poroelastic equations. J. Acoust. Soc. Am. 2001, 109, 3065–30684. [Google Scholar]
- Atalla, N.; Panneton, R.; Debergue, O. A mixed displacement-pressure formulation for poroelastic materials. J. Acoust. Soc. Am. 1998, 104, 1444–1452. [Google Scholar]
- Larbi, W. Numerical modeling of sound and vibration reduction using viscoelastic materials and shunted piezoelectric patches. Comput. Struct. 2020, 232, 105822. [Google Scholar]
- Larbi, W.; Deü, J.-F.; Ohayon, R. Finite element reduced order model for noise and vibration reduction of double sandwich panels using shunted piezoelectric patches. Appl. Acoust. 2016, 108, 40–49. [Google Scholar]
- Fahy, F.; Gardonio, P. Sound and Structural Vibration, Radiation, Transmission and Response, 2nd ed.; Academic Press Inc.: Cambridge, MA, USA, 2006. [Google Scholar]
- Harper, C.; Warlow, W.J.; Clarke, B.L. The forces applied to the floor by the foot in walking. Wear 1961, 4, 495–497. [Google Scholar]
- Elliott, S.J.; Johnson, M.E. Radiation modes and the active control of sound power. J. Acoust. Soc. Am. 1993, 94, 2194–2204. [Google Scholar] [CrossRef]
- Fuller, C.C.; Elliott, S.; Nelson, P.A. Nelson, Active Control of Vibration; Academic Press: London, UK, 1996. [Google Scholar]
- Larbi, W.; Pereira da Silva, L.; Deü, J.-F. An efficient FE approach for attenuation of acoustic radiation of thin structures by using passive shunted piezoelectric systems. Appl. Acoust. 2017, 128, 3–13. [Google Scholar]
- Groby, J.-P.; Ogam, E.; De Ryck, L.; Sebaa, N.; Lauriks, W. Analytical method for the ultrasonic characterization of homogeneous rigid porous materials from transmitted and reflected coefficients. J. Acoust. Soc. Am. 2010, 127, 764–772. [Google Scholar]
- Yang, T.; Saati, F.; Groby, J.-P.; Xiong, X.; Petrů, M.; Mishra, R.; Militký, J.; Marburg, S. Characterization on Polyester Fibrous Panels and Their Homogeneity Assessment. Polymers 2020, 12, 2098. [Google Scholar] [PubMed]

| (MPa) | (MPa) | (MPa) | (MPa) | (kg/m3) | |||
|---|---|---|---|---|---|---|---|
| 11,300 | 373 | 373 | 23.5 | 0.35 | 0.35 | 0.09 | 350 |
| Mode Shape | Eigenfrequencies [Hz] | |
|---|---|---|
| Hinge Connection | Rigid Connection | |
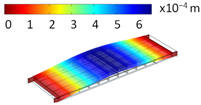 | ||
 | ||
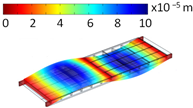 | ||
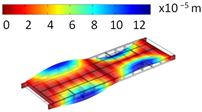 | ||
 | ||
 | ||
 | ||
 | ||
 | ||
| Symbol | Value | Description |
|---|---|---|
| Young’s modulus | ||
| Density | ||
| Airflow resistivity | ||
| Viscous characteristic length | ||
| Thermal characteristic length | ||
| Porosity | ||
| Tortuosity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Titirla, M.; Larbi, W. Numerical Analysis of Vibroacoustic Response of Timber Floor Panels Damped with Porous Materials. Appl. Sci. 2023, 13, 11931. https://doi.org/10.3390/app132111931
Titirla M, Larbi W. Numerical Analysis of Vibroacoustic Response of Timber Floor Panels Damped with Porous Materials. Applied Sciences. 2023; 13(21):11931. https://doi.org/10.3390/app132111931
Chicago/Turabian StyleTitirla, Magdalini, and Walid Larbi. 2023. "Numerical Analysis of Vibroacoustic Response of Timber Floor Panels Damped with Porous Materials" Applied Sciences 13, no. 21: 11931. https://doi.org/10.3390/app132111931
APA StyleTitirla, M., & Larbi, W. (2023). Numerical Analysis of Vibroacoustic Response of Timber Floor Panels Damped with Porous Materials. Applied Sciences, 13(21), 11931. https://doi.org/10.3390/app132111931






