Abstract
The critical problem restricting the development and application of phase change energy piles is that adding phase change materials to concrete generally reduces its thermal conductivity. Therefore, exploring a scheme to improve the heat transfer performance of phase change energy piles is necessary. In this study, steel fibers were added to energy piles to enhance the heat exchange capacity between the pile and the surrounding soil. The model tests were conducted on two types of energy piles: a fiber-reinforced pile and a fiber-reinforced phase change pile. Based on laboratory tests, a three-dimensional thermo–hydro–mechanical coupled finite-element model was established to characterize the phase transformation process of FRPC piles accurately. Then, the thermal parameters of the phase change concrete pile were optimized and analyzed to explore the feasibility of improving the application of the phase change pile. The results reveal that the cooling condition where the initial ground temperature was higher than the phase change temperature was more suitable for the FRPC pile. When the flow rate was increased by 50%, the peak heat power of the FRPC pile increased by 25.7%. There is an optimal economic flow rate to balance the system’s energy consumption and heat power in different conditions. Increasing thermal conductivity and specific heat capacity are effective solutions to improve the heat transfer capacity of concrete piles. The energy pile that was enhanced with the high-thermal-conductivity PCM is a good choice to improve long-term operation performance.
1. Introduction
In recent years, energy piles have gained prominence in engineering as an innovative technology derived from ground source heat pumps [1,2,3]. These piles have the dual functions of bearing loads and transferring heat. In addition to supporting the structural load of upper buildings, they also play a crucial role in facilitating heat exchange between piles and the surrounding soil. Energy piles harness geothermal energy and minimize adverse environmental impacts. Nowadays, energy piles are widely used in several developed nations, such as Austria, Germany, and the United Kingdom [4,5,6,7]. Moreover, research focused on energy pile technologies is increasing. Stewart et al. [8] conducted an energy pile test on a silty clay foundation and discovered that repeated heating and cooling cycles could lead to a settlement between the pile top and the soil surface. Yavari et al. [9] conducted tests on energy piles in saturated clay and observed that repeated thermal cycles caused the irreversible settlement of the piles. Park et al. [10] analyzed the thermal performance of a large-diameter bored pile on a soft soil foundation. They investigated how fluid circulation and temperature variations within the formation impact the thermal performance of the energy pile.
The thermal–mechanical response of energy piles is not only affected by external thermal and force loads but also depends on the properties of the piles [11,12,13]. By adding steel fiber to a pile, the thermal conductivity of the pile can be improved, which will enhance the heat transfer efficiency of the energy pile [14,15,16]. On the other hand, the mechanical properties of a pile can be effectively improved. In recent years, many scholars have studied the properties of steel fiber-reinforced concrete piles. Guo [17] studied the effect of steel fiber inclusion on the mechanical properties of steel fiber-reinforced concrete. The results showed that the strength of the specimen increased, and the overall mechanical properties of the steel fiber-reinforced concrete specimen were significantly better than that of a plain concrete specimen, which indicates that steel fiber can effectively improve the toughness of concrete and prevent cracks. To clarify the influence of fiber volume fraction on the thermal properties of cement concrete, Liu et al. [18] studied the thermal conductivity of steel fiber concrete and carbon fiber concrete through experiments and composite theoretical models. The results show that the volume fraction of steel fiber significantly affects the thermal properties of concrete, and steel fiber forms a network structure that effectively improves the heat conduction of concrete.
Cyclic thermal loading causes significant thermal stress between a pile and the soil, resulting in the irreversible settlement of the pile. Introducing phase change material (PCM) into energy piles can help mitigate the impact of thermal loading [19,20]. PCM can maintain a constant temperature and supply latent heat through changes in its state [21,22,23]. PCM possesses the characteristics of high energy density and minimal temperature fluctuations; this is why PCM has been incorporated into pile systems [24,25,26]. By incorporating expanded graphite and a nanoscale composite PCM, Bao et al. [27] developed an integrated cement-based composite material suitable for energy piles. They subsequently conducted experimental tests to assess its mechanical properties. The results indicated an increase in the bending strength of the cement-based composite materials with an increase in the content of composite PCM. Yang et al. [28] introduced an expanded graphite base and a graphite nano matrix composite PCM to an energy pile. The results showed that the strength of the energy pile, which was incorporated with 10% composite PCM, reached 37 MPa. Yang et al. [29] enhanced energy piles by incorporating PCM into the concrete within a pile. This modification improved heat exchange efficiency, increased heat storage capacity, and enhanced temperature stability in both the piles and the surrounding soil. However, it is worth noting that thermal interference among the heat exchange tubes may influence heat transfer calculations due to the small size of the model pile. Bao et al. [30] conducted a thermal response test on a PCM pile in unsaturated clay. The results clearly show that using PCM energy piles is an efficient engineering approach for improving heat exchange capacity and saving underground space resources compared to traditional concrete piles. Their investigation revealed that PCM piles exhibited a reduced temperature fluctuation range compared to traditional piles, effectively reducing heat accumulation in the surrounding soil. However, the pile accumulated plastic strain during the temperature cycling process. While PCM can enhance the energy density of piles and improve heat exchange efficiency compared to traditional concrete piles [31], it also reduces the thermal conductivity of piles. Furthermore, there is still a lack of clarity in characterizing the phase change process for PCM in concrete. The ambiguity primarily arises due to the dispersion of PCM when incorporated into the concrete, making it challenging to assess its thermal behavior through experiments.
The size limitations of model tests and the high cost of field experiments have limited research on energy piles. Consequently, many scholars have employed numerical methods to further investigate energy piles’ thermodynamic characteristics [31,32,33]. Li et al. [34] and Andrea et al. [35] conducted multidimensional analyses using the finite element method and comprehensively validated their findings through experiments. Their research confirmed that the heat within the soil medium resulted in only a slight vertical temperature gradient on the pile surface and a relatively constant temperature was observed across each horizontal cross-section. Qi et al. [36] conducted a comparative simulation analysis of the thermal properties of various backfill materials, including soil, paraffin, ordinary acid, and reinforced acid, in a ground source heat pump (GSHP) system. Their findings revealed that, compared to soil, the use of PCMs as backfill materials reduced the thermal effect radius by approximately 15% to 35%. Han and Yu [37] and Lyu et al. [38] indicated that the spacing between piles should be greater than 6.8 times the diameter of each pile to reduce the impact of interference. There are few existing studies on the simulation of the phase change process in phase change piles, so it is urgent to establish a simulation method for phase change piles.
To address the issues of inadequate thermal conductivity and observe the phase transition process within PCM inside a pile, two types of energy piles were designed in this study: a fiber-reinforced concrete pile (FR pile) and a fiber-reinforced phase change pile (FRPC pile). The equivalent substitution method established a thermo–hydro–mechanical multi-physics coupling three-dimensional numerical model to simulate the phase transformation process. The thermal performance of the FR and FRPC piles was investigated through a combination of model tests and numerical simulations. By analyzing the phase change process and temperature distribution in both piles and soil, this study provides valuable insights into designing and implementing phase change energy piles.
2. Model Test
2.1. Test Device
In this study, two different piles were tested simultaneously. The two piles had the same specifications except for the pile material. The size of the model pile was 0.15 m in diameter and 1.5 m in length. The heat transfer pipe inside the pile was made of a double U-shaped cross-steel pipe with a wall thickness of 1 mm. The mass mix ratio of the FR pile was “water:cement:sand:stone = 0.4:1:1.94:2.09”, and 5% of the total volume of steel fiber was added. The FRPC pile used paraffin wax as a phase change material. To enhance the thermal conductivity of the FRPC pile, paraffin wax was encapsulated in a hollow steel ball with a wall thickness of 0.3 mm and a diameter of 19 mm. The steel ball was converted by an equal volume method to replace the coarse aggregate in concrete. The other materials were consistent with the FR pile except for the phase change steel ball. Through the uniaxial compressive test, the representative values of compressive strength of the FR and FRPC piles were 63.78 MPa and 31.92 MPa, respectively. The schematic diagram of the pile structures is shown in Figure 1.
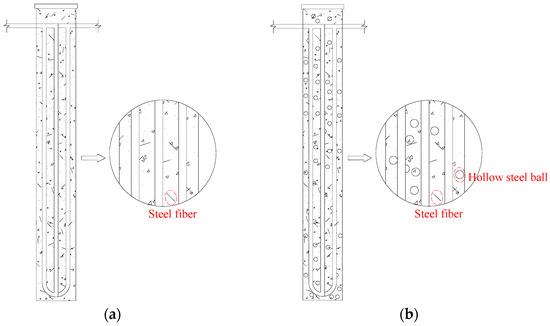
Figure 1.
Two types of energy concrete piles. (a) FR pile. (b) FRPC pile.
The laboratory test device mainly comprised a model tank and a temperature circulation system. The plane size of the model tank was 2.45 m × 2.45 m and the height was 2 m. To prevent rusting in the tank, the inside and outside of the tank were sprayed with anti-rust paint, and a waterproof cushion was arranged inside of the tank. Two model energy piles were installed in the tank filled with saturated sand. A polystyrene foam insulation board was arranged outside the tank to isolate the heat exchange between the ambient temperature and the model tank. The temperature circulation system comprised a water circulation temperature control machine and a water tank. The temperature control range of the water circulation was 10~120 °C, which could be used to simulate the heating condition. The circulation system was connected to the heat exchange tube, the flow meter, and the pile to form a heat exchange loop. The entire test system is shown in Figure 2.
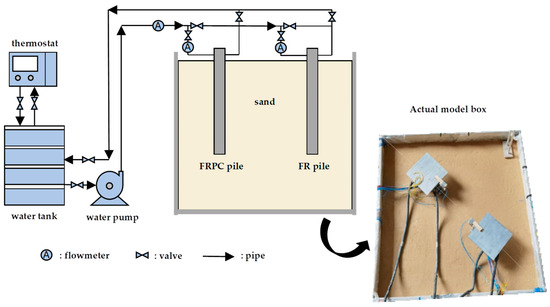
Figure 2.
Model tests system for energy piles.
2.2. Test Conditions
The inlet water temperature was at 45 °C within the heat exchange pipe. The model piles were heated at two flow rates of 1500 mL/min and 3000 mL/min, respectively, for 140 h. The initial temperatures before testing are summarized in Table 1. The arrangement of the temperature measurement is shown in Figure 3. The upper thermocouples were arranged at the depth of 25 mm, and one layer was arranged every 300 mm, and the arrangement at the bottom of the pile was intensively treated. Each layer of thermocouples was arranged to measure points on both sides of the pile 0.5, 1, 2, or 3 times the diameter of the pile to monitor the temperature change in the horizontal direction.

Table 1.
The average value of initial soil temperature before the test.
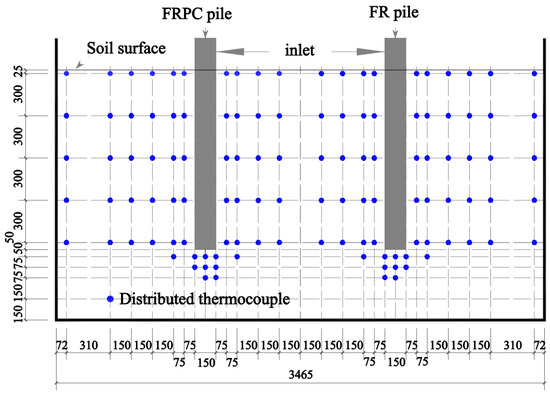
Figure 3.
Layout of thermocouples in soil (unit: mm).
2.3. Thermal Parameters of Materials
The thermal parameters of the soil and piles were measured before the beginning of the test. The measurement details can be found in the previous study [39]. The primary thermal parameters of the soil and pile materials are shown in Table 2.

Table 2.
Thermal parameters of soil and pile materials.
2.4. Test Error Analysis
In this test, direct and indirect measurement errors were used to reflect the reliability of the test results. The direct error is the inevitable error caused by the uncertainties of the test instrument reading, and the indirect error is caused by the direct error calculation in the calculation process. Through the direct error, the relative error can be calculated by Equation (1)
where is the maximum relative error. indicates the accuracy of the test instrument. is the largest range of test instruments. is the minimum value measured. Based on the above methods, the main parameter errors of this experiment are presented in Table 3.

Table 3.
Relative errors of the major parameters in the test.
3. Numerical Simulation
The limited number of measuring points posed challenges in observing the comprehensive diffusion of soil temperature across the entire range. Therefore, a three-dimensional thermo–hydro–mechanical multi-physics coupled heat transfer transient model was established. The finite element model was verified through the results of model tests. The internal force of the piles and the total heat transfer power were observed and analyzed based on the numerical results.
3.1. Basic Assumption
Considering the complexity of the FR and FRPC pile structures, the following assumptions were made in establishing the numerical model:
- Changes in the thermal parameters of materials, such as thermal conductivity, elastic modulus, and specific heat capacity, were not considered when there was a temperature change.
- It was assumed that heat exchange occurred only through heat conduction between the sand and water, without considering the heat convection of the soil’s pore water.
3.2. Governing Equations
The coupled heat transfer between the water and soil was achieved by utilizing a non-isothermal pipe flow and a solid heat transfer module. The soil was added to the solid heat transfer module as a porous medium. In addition, the phase change interface was introduced to simulate the phase change process of the PCM, and the apparent heat capacity method was used to describe the latent heat. The control equation is as follows:
- (1)
- Non-isothermal pipe flow
- (2)
- Heat transfer in solids
Equation (4) describes the heat exchange between the fluid and the pipe wall. Assuming that the soil was a porous medium material, the model did not consider the heat exchange phenomenon caused by groundwater flow and convective heat transfer.
- (3)
- Phase change interface
The material parameters of PCM change during the phase transition process. The changes in its key parameters of volume density and thermal conductivity were calculated by the following formula [36]:
where θ(T) is the phase mass fraction, phase 1 represents the solid phase of PCM, and phase 2 represents the liquid phase of PCM.
The equivalent heat capacity method was used to simulate the phase change process through the interface of PCM in a solid heat transfer module. During the test, a hollow steel ball with a wall thickness of 0.3 mm and a diameter of 19 mm was used to enclose the phase change paraffin. Due to the substantial quantity of steel balls in the FRPC pile, equivalent material parameters for the FRPC pile were experimentally determined and used as input parameters for the finite element model. The specific heat capacity of the phase change material was related to latent heat and calculated as follows:
where is a smooth transition function to prevent the numerical instability caused by the rapid change in the specific heat capacity. The equation for calculation is as follows:
This parameter only works during the time interval of the phase transition temperature. In this study, the phase transition interval was 2 °C; a smaller interval would result in a sharper transition edge.
This study aimed to investigate the effect of steel fibers and PCM on the performance of energy piles. It was assumed that the thermal properties of the soil, as shown in Table 3, remain unchanged in temperature variations. The parameters for paraffin are summarized in Table 4.

Table 4.
Thermophysical parameters of paraffin.
3.3. Finite Element Model
The numerical model of the soil, piles, and heat exchange pipes is shown in Figure 4. All the conditions were the same with the model tests. For the heat transfer process in the non-isothermal pipeline flow, the pipeline flow was simplified to a one-dimensional flow, ignoring the radial heat exchange inside the pipeline. This method can avoid the problem of pipeline grid division caused by the relatively large length and radius. Based on the results of finite element analysis with or without reinforcing bars in concrete, the influence of reinforcing bars was ignored to improve computational efficiency. The heat transfer phenomenon in the tube domain played a leading role in the whole numerical analysis. To ensure accuracy and save calculation time, the double U-shaped heat exchange tube adopted a refined boundary grid, in which the inlet and outlet grid were super-refined. The concrete structure and soil were modeled using free tetrahedral mesh elements. To optimize computational costs, meshes were chosen with a minimum length of 0.045 m and an average size of 0.6 m, and the non-uniform mesh from dense to sparse was used to reduce the computational cost, resulting in the generation of 52,026 elements, which was sufficient to meet the accuracy requirements.
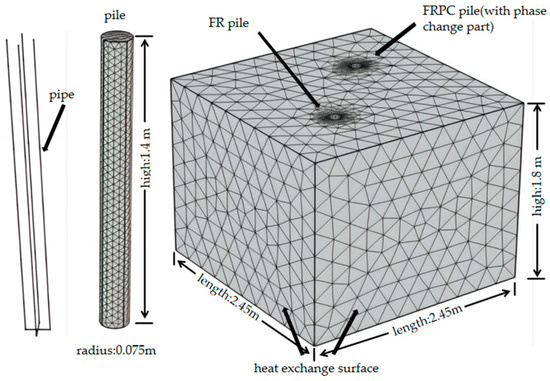
Figure 4.
Numerical model of the pile, heat exchange pipe, and soil.
Boundaries and initial conditions were set based on the model test, assuming that the fluid was an incompressible Newtonian. The pipe parameters were defined using the Churchill friction model, with a surface roughness of profiled steel (0.046 mm). The inlet temperature (Tin) was set at 45 °C, and the same volume flow rate was used in the model test and numerical simulation. The outer surfaces of the model tank were insulated by wrapping the foam board to avoid heat exchange with the external environment. All soil surfaces in the finite element model were designated as thermally insulating boundary conditions.
In the following, the model’s validity was verified by comparing the experimental data with the simulated data, and the thermal–mechanical response of the two different piles was further explored.
4. Results and Discussions
4.1. Comparison of Tests and Simulation Results
4.1.1. Horizontal Temperature Change
Figure 5 shows the temperature change in the horizontal direction of the soil at various positions around the FR and FRPC piles, with a burial depth of 1150 mm. In general, the numerical results in the horizontal direction of the soil were in good agreement with the test results. During the first 10 h, the soil temperature at the FR pile side underwent significant temperature variations, followed by a gradual decrease in the rate of change. The most significant changes in soil temperature occurred at distances of 0.5 D and 1 D from the side of the pile. The temperature variations at 2 D and 3 D from the side of the pile were relatively general in comparison. It is worth noting that the heat transfer in the horizontal direction in soil was 1–2 D over the initial 3 h and extended to 2–3 D over the subsequent 3 to 10 h. Furthermore, due to its high energy density, the temperature increase amplitude and rate in the soil near the FRPC pile was smaller than that of the FR pile.
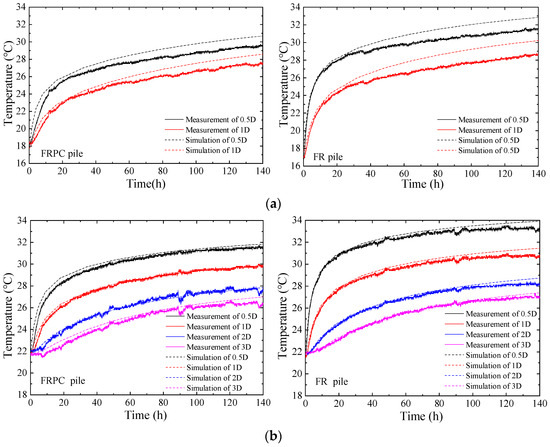
Figure 5.
The temperature change of soil in the horizontal direction at different distances from the FRPC pile and FR pile at different flow rates (burial depth of 1.15 m). (a) 1500 mL/min. (b) 3000 mL/min.
4.1.2. Temperature Change with Depth
Figure 6 shows the temperature variation in the soil at different times along the depth, located at a distance of 0.5 D. In the figure, M represents measurement and S represents simulation. The numerical results of the soil temperature at a horizontal distance of 0.5 D were consistent with the trend observed in the test results. It is worth noting that the numerical results of the FR pile better fit the test results than those of the FRPC pile. This is because the FRPC pile was modeled as a homogeneous material, and the phase change steel balls in the pile were not modeled separately. However, the results still demonstrated the thermal response characteristics of the phase change pile. The numerical results of the FRPC and FR piles reasonably described the test results. The findings of Singh et al. [41] corroborated the observed patterns in the numerical results.
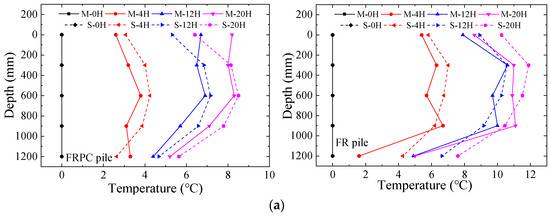
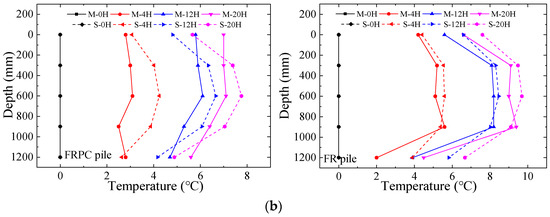
Figure 6.
The soil temperature variation along the depth at horizontal distance of 0.5 D from the piles within the initial 20 h of heating at different flow rates (M—measurement; S—simulation). (a) 1500 mL/min. (b) 3000 mL/min.
4.2. Simulation Results
4.2.1. Phase Transition Progression inside the Pile
Figure 7 illustrates the progression of phase transition in the FRPC pile at different times at a flow rate of 1500 mL/min. The initial soil temperature was about 16 °C, and the paraffin was solid. The inlet temperature was set at 45 °C, causing the paraffin to gradually absorb heat and transition from a solid to a liquid state. The phase change process of the PCM near the heat exchange pipe was completed within 0.1 h. At 1 h, the phase transition of the pile was almost complete, finishing at 140 h.
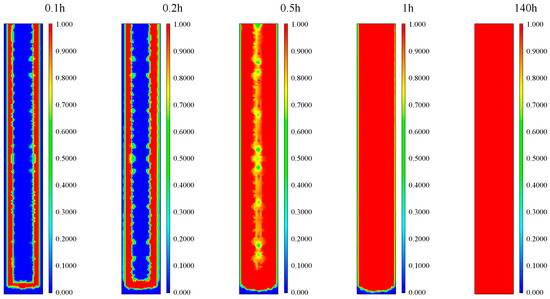
Figure 7.
Liquid phase fraction of PCM in FRPC pile under 1500 mL/min flow at different times.
4.2.2. Temperature Distribution in Pile–Soil
Figure 8 presents the sectional temperature distributions of the soil and piles at the flow rate of 1500 mL/min. The results show that the soil temperature on the FRPC pile side was lower than that on the FR pile side. The heat transfer process first occurred in the pile. When the temperature in the pile was close to the temperature of the heat exchange tube, the heat influence range in the soil further expanded. The numerical results indicated that the thermal diffusion range reached the soil boundary at 140 h. However, the thermal influence range of the FRPC pile was always smaller than that of the FR pile.
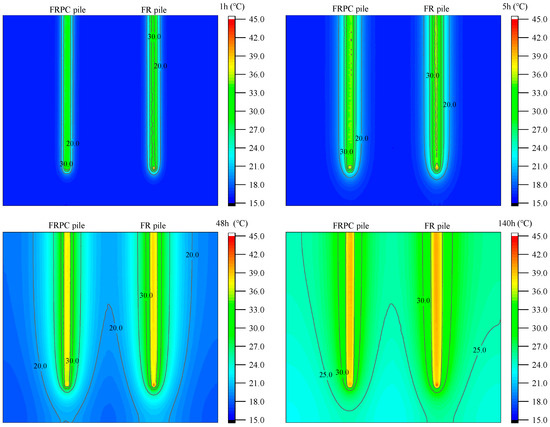
Figure 8.
The internal temperature distribution of piles and soil at different times under the flow rate of 1500 mL/min.
4.2.3. Heat Power
A mathematical model was used to calculate the heat transfer efficiency per unit area of the model pile at a specific time. In the model test, the circulating water flowed into the energy pile at a constant temperature and flowed into the water tank after exchanging heat with the soil. According to the circulating water flow, the pile’s total heat transfer power could be calculated based on the fluid’s inlet and outlet water temperature using the following equation:
where is the heat transfer power (W), is the circulating water flow rate (m3/s), is the water outlet temperature (K), is the water inlet temperature (K), is the water density (kg/m3), and is the specific heat of the water [J/(kg·K)].
To analyze the influence of specific heat enhancement measures on heat transfer, an ordinary concrete pile (OC pile) and an FR pile were introduced to make a comparison. Referring to previous studies, the thermal conductivity of the OC pile was set to 1.6 W/(m·K) and the specific heat capacity was set to 880 J/(kg·K). Figure 9a–c compare the heat power of the FR and FRPC piles at different flow rates. At the beginning of the test, heat transfer was the highest. The total heat power showed a downward trend over time. However, it still did not reach stability at 140 h. Figure 9d,e show the pile’s maximum and minimum heat power during operation. Under three different flow rates of 1500 mL/min, 3000 mL/min, and 4500 mL/min, the maximum heat power was 655.9 W,801.8 W, 1008.1 W for the FRPC pile, 698.3 W, 941.8 W, 1231.2 W for the FR pile, and 664.3 W, 850.5 W, and 1095.7 W for the OC pile, respectively. Similarly, the minimum heat power was 148.5 W, 160.2 W, 162.1 W for the FRPC pile, 160.8 W, 174.9 W, 177.1 W for the FR pile, and 156.5 W, 170.1 W, 171.8 W for the OC pile, respectively. By integrating heat power over time, the quantity of heat transfer of different piles in the whole heat transfer process could be obtained, as shown in Figure 9f. Under three different flow rates of 1500 mL/min, 3000 mL/min, and 4500 mL/min, the quantity of heat transfer was 93.8 MJ, 104.3 MJ, and 106.2 MJ for the FRPC pile, 102.8 MJ, 116.1 MJ, and 118.4 MJ for the FR pile, and 99.2 MJ, 111.5 MJ, and 113.7 MJ for the OC pile, respectively.
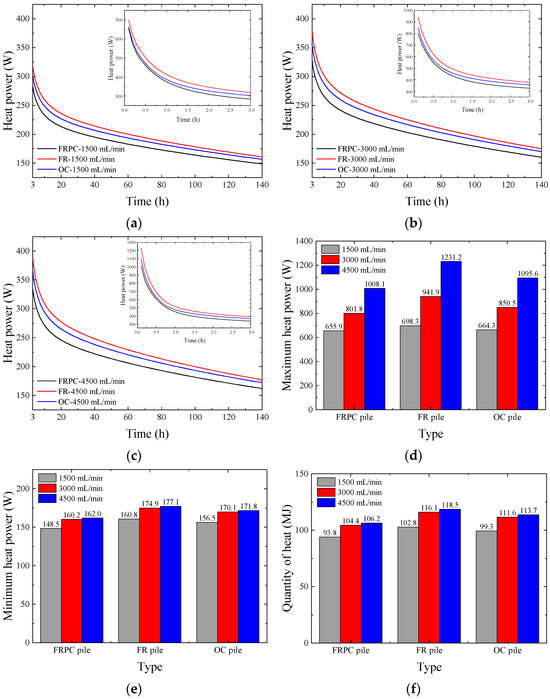
Figure 9.
Comparison of the simulated results of the unit heat power of different piles under different flow rates. (a) Heat power under 1500 mL/min flow. (b) Heat power under 3000 mL/min flow. (c) Heat power under 4500 mL/min flow. (d) Maximal heat power under different flow. (e) Minimal heat power under different flow. (f) Quantity of heat under different flow.
4.2.4. Pile–Soil Displacement
Figure 10 illustrates the displacement and temperature changes in simulations at the top of the energy piles and adjacent soil when operating with a 1500 mL/min flow rate. The positive values represent upward displacement. The top displacement of the FRPC pile with a maximum of 3.115 mm exceeded that of the FR pile with a maximum value of 2.831 mm. The expansion of the soil was more pronounced in the vicinity of the two piles. The maximum soil expansion outside the FRPC and FR piles was 4.702 mm and 4.815 mm, respectively, which were close. However, soil expansion in the center of the two piles reached 5.677 mm due to the accumulated thermal loading by the two piles.
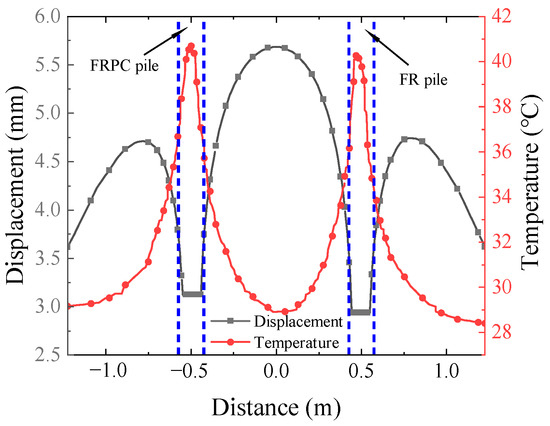
Figure 10.
Displacement and temperature changes at the top of the energy piles and soil near the pile under continuous heating for 140 h at a flow rate of 1500 mL/min.
4.2.5. Pile Internal Stress and Side Friction
Table 5 and Figure 11 show the variations in the axial stress of the energy piles under continuous heating for 140 h at the flow rate of 1500 mL/min. Negative values represent compressive stress, while positive values indicate tensile stress. From Figure 11, it can be observed that there was a gradual transformation of the axial stress in the piles, shifting from compressive stress to tensile stress during the heating process. The internal stress of the FR pile gradually decreased as the depth increased. The maximum tensile stress occurred at a depth of 0.25 m for the FR pile with a value of 0.405 MPa and 750 mm for the FRPC pile with a value of 0.184 MPa. The stress difference in the two energy piles reached the maximum at the buried depth of 250 mm, with values of 0.308 MPa and 0.348 MPa when heating for 12 h and 140 h, respectively.

Table 5.
Stress values at different buried depths in the piles at different times under continuous heating conditions with a flow rate of 1500 mL/min.
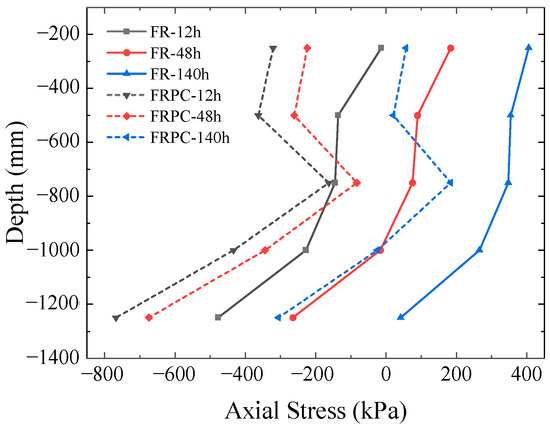
Figure 11.
Stress changes in two energy piles along the depth at a 1500 mL/min flow rate.
The thermal stress difference at different buried depths was used to calculate the pile side friction. Under the continuous thermal load, the piles’ and soil’s thermal expansion caused relative displacement, resulting in pile-side friction. The pile-side friction resistance at different depths was calculated using Equation (11):
where D represents the pile diameter, is the stress difference between the adjacent two measuring points, and is the distance between the two strain measuring points. The side friction resistance was assumed to be positive upwards and negative downwards.
Figure 12 compares the variation in side friction between the FRPC pile and the FR pile after continuous heating of 140 h at a flow rate of 1500 mL/min. It can be observed that the pile-side frictional resistance of the FR pile was entirely downward, indicating that the entire pile expanded and moved upward. In contrast, the FRPC pile exhibited upward frictional resistance at a depth of 0.25–0.5 m.
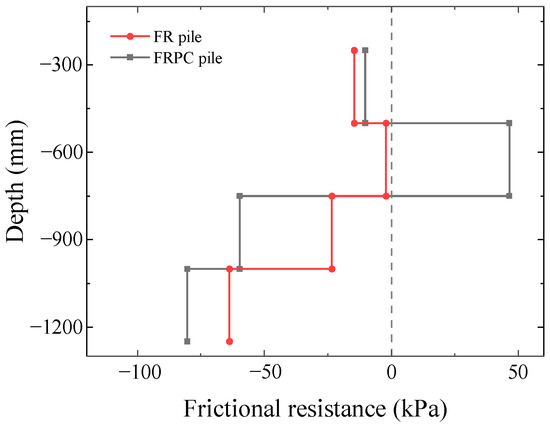
Figure 12.
Comparison of side friction between the FRPC pile and the FR pile after continuous heating for 140 h at a flow rate of 1500 mL/min.
4.3. Parametric Optimization Results
Due to the limitation of laboratory tests, using different phase change materials to make energy piles for analysis is difficult. Although the FRPC pile adopted in this study could reduce the mechanical response of the pile structure, it still had shortcomings in overall heat transfer performance compared with the ordinary concrete pile. Therefore, it was necessary to conduct further analysis on the heat transfer and heat storage capacity of phase change concrete piles. Based on the above numerical analysis, parameter optimization was carried out for the phase change pile’s thermal conductivity and specific heat capacity. All the results were obtained at a fixed flow rate of 1500 mL/min. The heat power and maximum tensile stress of the FRPC pile with thermal conductivity of 1.6 W/(m·K), 1.9 W/(m·K), and 2.2 W/(m·K) for the solid phase (1.4 W/(m·K), 1.7 W/(m·K), and 2.0 W/(m·K) for the liquid phase) and specific heat capacity of 1200 J/(kg·K), 1500 J/(kg·K), and 1800 J/(kg·K) were compared with those of the FR pile. The results are shown in Figure 13.
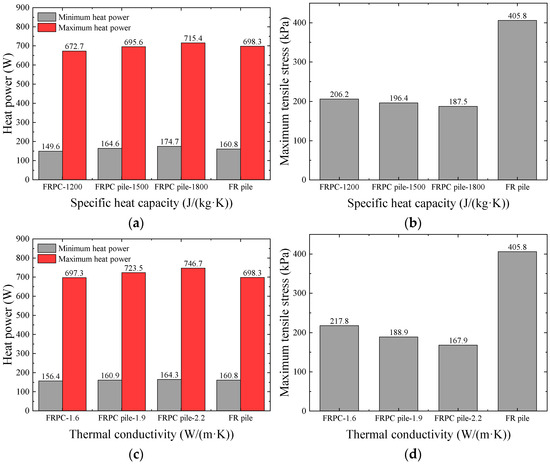
Figure 13.
Optimization results for different thermal conductivities and specific heat capacities. (a) Heat power of different specific heat capacities. (b) Structural maximum tensile stress of different specific heat capacities. (c) Heat power of different thermal conductivity. (d) Structural maximum tensile stress of different thermal conductivity.
4.4. Discussion
4.4.1. Thermo–Mechanical Response Behavior of the FRPC Pile
The phase change process of the PCM near the heat exchange pipe was completed within 0.1 h (see Figure 7). The liquid phase distribution at 0.5 h indicated that the phase change inside the pile was completed more quickly than that on the outer surface because the surface of the pile exchanged heat with the soil. At 1 h, the phase transition of the pile was almost complete, and the PCM existed in a liquid phase, which further reduced the FRPC pile’s thermal conductivity and led to a further decrease in the heat power of the phase change pile in the later stage.
Figure 8 shows that at the end of heat transfer, the boundary of the model box on the side of the FR pile intersected with the isotherm of 25 °C. The isotherm in the center of the two piles also overlapped, which suggested a boundary effect in the laboratory test, the same phenomenon was also observed in the study of Yin et al. [42]. The thermal influence radius was about 0.5 times the pile diameter at 5 h of operation and about 3.5 times the pile diameter at the end of operation, producing strong thermal interference between piles and affecting the heat transfer capacity.
The results of Figure 9d–f show that the increase in flow rate had a greater impact on the initial peak heat power. When the heat transfer was gradually stabilized, the benefit of flow increase was greatly reduced due to the decrease in temperature difference between the components. Taking the FR pile as an example, when the flow rate increased from 1500 to 3000 mL, the maximum and minimum heat power increased by 34.8% and 8.7%, respectively. When the flow rate increased from 3000 mL to 4500 mL, the maximum and minimum values of heat power increase became 30.7% and 1.3%. Correspondingly, the quantity of heat increase caused by the increase of two flows was 12.9% and 2.0%, respectively. Therefore, there is an optimal economic flow rate to balance the system’s energy consumption and heat power.
Figure 10 shows that the expansion at the top of the FRPC pile was greater than that of the FR pile. However, it is worth noting that the numerical model used in this study did not consider the foundation consolidation but only the influence of the pile-side friction resistance. The addition of phase change materials had a positive effect on the mechanical properties of the pile, especially the tensile strength. As shown in Figure 11, it is worth noting that both types of piles experienced tensile stress at the end of the heat exchange. However, there were both tensile and compressive stresses in the FRPC pile, which indicated that the deformation of the FRPC pile was not uniform along the vertical direction during the heat exchange process. Therefore, engineering designs should pay attention to the bearing capacity of energy piles.
4.4.2. Parametric Analysis
The results in Figure 13a,b show that with the increase in specific heat capacity, the maximum and minimum heat power of the FRPC pile increased. When the specific heat capacity increased by 25% and 20%, the maximum heat power increased by 3.4% and 2.8%, showing a linear relationship. The minimum heat power increased by 10.0% and 6.13%, respectively. The maximum tensile stress decreased by 4.7% and 4.5%, respectively. This phenomenon was because the energy density of the FRPC pile increased with the increase in specific heat capacity when the thermal conductivity was unchanged. This slowed down the temperature rise of the pile body. Thus, a higher temperature difference between the pile and the water inlet was maintained. The temperature difference between the pile and the water inlet improved the heat power of the pile.
The results in Figure 13c,d show that, similar to the law of specific heat capacity, the maximum and minimum heat power of the FRPC pile increased with the increase in thermal conductivity. When the thermal conductivity increased by 18.7% and 15.8%, the maximum heat power increased by 3.75% and 3.2%, the minimum heat power increased by 2.9% and 2.1%, and the maximum tensile stress decreased by 13.2% and 11.7%, respectively. As the thermal conductivity rose, the heat transfer efficiency and the amount of heat exchange simultaneously increased, which caused the increase in heat exchange.
Increasing thermal conductivity and specific heat capacity are effective solutions to improving the heat transfer capacity of phase change concrete piles. During long-term operation, the heat transfer power is close to the minimum heat power, so increasing the specific heat capacity that is more sensitive to the minimum heat power can effectively improve the heat transfer capacity of piles. The volume content of phase change material can improve the specific heat capacity and energy density, and the energy pile that was enhanced with the high thermal conductivity PCM is a good choice to improve the long-term operation performance of energy piles.
5. Conclusions
This study introduced two reinforced energy piles designed to enhance latent heat and thermal conductivity by incorporating PCM and steel fibers. The pile temperature, phase change processes, soil temperature variations, heat transfer power, and thermo–mechanical responses were analyzed by a three-dimensional transient heat transfer finite element model. At the same time, targeted parameter analysis was carried out. The key findings are as follows.
- The FRPC pile effectively reduced the thermal influence radius surrounding the pile. However, incorporating PCM introduced uneven temperature distribution within the FRPC pile and a 9.4% reduction in heat transfer capacity compared to the FR pile. Compared with the heating condition, the FRPC pile is more suitable for cooling conditions.
- The mechanical response of energy piles under thermal loading can be effectively reduced through PCM in pile concrete. Under long-term heat transfer conditions, the axial stress change at the top of the FRPC pile caused by thermal loading could be reduced by 85.9%. The pile-side friction generally shows a downward trend in heating conditions.
- The phase change path of the phase change material in the pile is that the heat exchange tube gradually starts the phase change to the pile surface, and the phase change is completed quickly. Since the thermal conductivity of the phase change material in the liquid phase is generally lower than that in the solid phase, the FRPC pile is more suitable for cooling conditions compared with the heating condition.
- The increase in flow rate had a greater impact on the initial peak heat power of the PCM pile. However, the relationship between the two was not proportionally linear. There is an optimal economic flow rate to balance the system’s energy consumption and heat power in different conditions.
- The improvement in the thermal conductivity of energy pile concrete enhanced the overall heat transfer capacity and reduced the mechanical response of the pile structures. Compared with the OC pile, the FRPC pile is more suitable for long-term heat exchange operations.
In this study, due to the influence of the model tank size, the boundary effect was amplified. In the next study on PCM concrete piles, more emphasis should be placed on eliminating the influence of the boundary effect, and the heat transfer capacity of PCM concrete piles should be more accurately evaluated.
Author Contributions
Conceptualization, X.B. and H.C.; methodology, J.S.; validation, Y.L., J.S. and H.C.; formal analysis, G.C. and J.H.; investigation, J.H.; data curation, H.C. and G.C.; writing—original draft preparation, J.S.; writing—review and editing, Y.L. and X.B.; supervision, X.B.; project administration, H.C.; funding acquisition, X.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Key Program of the National Natural Science Foundation of China, grant number 51938008, and the National Natural Science Foundation of China, grant number 51925804.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
Author Jinxin Hu was employed by the company Sinohydro Bureau 14 Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Fadejev, J.; Simson, R.; Kurnitski, J.; Haghighat, F. A review on energy piles design, sizing and modelling. Energy 2017, 122, 390–407. [Google Scholar] [CrossRef]
- Sani, A.K.; Singh, R.M.; Amis, T.; Cavarretta, I. A review on the geothermal energy pile foundation’s performance, design process, and applications. Renew. Sust. Energ. Rev. 2019, 106, 54–78. [Google Scholar] [CrossRef]
- Faizal, M.; Bouazza, A.; Singh, R.M. Heat transfer enhancement of geothermal energy piles. Renew. Sust. Energ. Rev. 2016, 57, 16–33. [Google Scholar] [CrossRef]
- Bourne-Webb, P.J.; Amatya, B.; Soga, K.; Amis, T.; Davidson, C.; Payne, P. Energy pile test at Lambeth College, London: Geotechnical and thermodynamic aspects of pile response to heat cycles. Geotechnique 2009, 59, 237–248. [Google Scholar] [CrossRef]
- Laloui, L.; Nuth, M.; Vulliet, L. Experimental and numerical investigations of the behaviour of a heat exchanger pile. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 763–781. [Google Scholar] [CrossRef]
- Amatya, B.L.; Soga, K.; Bourne-Webb, P.J.; Amis, T.; Laloui, L. Thermo-mechanical behaviour of energy piles. Geotechnique 2012, 62, 503–519. [Google Scholar] [CrossRef]
- Akrouch, G.A.; Sanchez, M.; Briaud, J.L. Thermo-mechanical behavior of energy piles in high plasticity clays. Acta Geotech. 2014, 9, 399–412. [Google Scholar] [CrossRef]
- Stewart, M.A.; Mccartney, J.S. Centrifuge Modeling of Soil-Structure Interaction in Energy Foundations. J. Geotech. Geoenviron. Eng. 2014, 140, 04013044. [Google Scholar] [CrossRef]
- Yavari, N.; Tang, A.M.; Pereira, J.M.; Hassen, G. Mechanical behaviour of a small-scale energy pile in saturated clay. Géotechnique 2016, 66, 878–887. [Google Scholar] [CrossRef]
- Park, S.; Lee, D.; Lee, S.; Chauchois, A.; Choi, H. Experimental and numerical analysis on thermal performance of large-diameter cast-in-place energy pile constructed in soft ground. Energy 2017, 118, 297–311. [Google Scholar] [CrossRef]
- Han, C.J.; Shen, Y.; Chen, K.H.; Gong, C.; Liu, T.L.; Qu, B. Characteristics and energy performance of novel MicroPCM C50 energy pile in cooling mode. Energy Build. 2022, 274, 112442. [Google Scholar] [CrossRef]
- Wang, Y.X.; Du, G.Y.; Shi, G.; Liu, S.Y. Experimental Study of High-Thermal Conductivity SiC Concrete Energy Piles. Int. J. Civ. Eng. 2023, 21, 647–664. [Google Scholar] [CrossRef]
- Qu, B.; Liu, T.L.; Gong, C.; Liu, J.X.; Shen, Y.; Chen, K.H.; Han, C.J. Investigation of microencapsulate phase change material-based energy pile group: Energy analysis and optimization design. J. Clean. Prod. 2022, 381, 135204. [Google Scholar] [CrossRef]
- Ren, X.; Ding, Y.X.; Liu, Q.F.; Chen, S.J.; Song, F. Effect of different volume fraction of steel fiber/graphite on thermal conductivity and compressive properties of concrete. Front. Mater. 2022, 9, 1003830. [Google Scholar] [CrossRef]
- Li, H.Y.; Chen, B.G.; Zhu, K.C.; Gong, X.L. Flexural Toughness Test and Inversion Research on a Thermal Conductivity Formula on Steel Fiber-Reinforced Concrete Components Post-Fire. Materials 2022, 15, 5103. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.Z.; Zou, J.P.; Gong, Z.; Zheng, D.P.; Bao, X.H.; Chen, X.S. Study on the thermal and mechanical properties of steel fibre reinforced PCM-HSB concrete for high performance in energy piles. Constr. Build. Mater. 2022, 350, 128822. [Google Scholar] [CrossRef]
- Guo, G. Preparation and mechanical properties of steel fiber reinforced concrete. J. Funct. Mater. 2020, 51, 012037. [Google Scholar]
- Liu, K.; Lu, L.; Wang, F.; Liang, W. Theoretical and experimental study on multi-phase thermal conductivity model for fiber reinforced concrete. Constr. Build. Mater. 2017, 148, 465–475. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Li, F.; Zhang, L. Experimental Investigation and the Development of Phase Change Heat Storage Device Adapted to the Solar Energy Heat Pump. Adv. Mater. Res. 2014, 860, 191–195. [Google Scholar] [CrossRef]
- Chang, H.; Jin, L. Preparation and Heat Transfer Performance of Steel Ball Phase Change Concrete. J. New Mat. Electrochem. Syst. 2020, 23, 204–212. [Google Scholar] [CrossRef]
- Ling, Z.; Wang, F.; Fang, X.; Gao, X.; Zhang, Z. A hybrid thermal management system for lithiumion batteries combining phase change materials with forced-air cooling. Appl. Energy 2015, 148, 403–409. [Google Scholar] [CrossRef]
- Gulfam, R.; Zhang, P.; Meng, Z. Advanced thermal systems driven by paraffin-based phase change materials—A review. Appl. Energy 2019, 238, 582–611. [Google Scholar] [CrossRef]
- Veerakumar, C.; Sreekumar, A. Phase change material based cold thermal energy storage: Materials, techniques and applications—A review. Int. J. Refrig. 2016, 67, 271–289. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, G.; Zheng, M.; Shi, S. Model test on thermal response of phase change pile in saturated silt ground. Rock Soil Mech. 2022, 43, 282–290. [Google Scholar]
- Shahidi, S.; Hajialilue-Bonab, M.; Tohidvand, H.R.; Khosravi, A. Experimental investigation on the efficiency of the phase change materials for enhancing the thermal performance of energy piles in sandy soils. Energy Build. 2023, 298, 113544. [Google Scholar] [CrossRef]
- Yang, W.B.; Sun, T.F.; Yang, B.B.; Wang, F. Laboratory study on the thermo-mechanical behaviour of a phase change concrete energy pile in summer mode. J. Energy Storage 2021, 41, 102875. [Google Scholar] [CrossRef]
- Bao, X.; Memon, S.A.; Yang, H.; Dong, Z.; Cui, H. Thermal Properties of Cement-Based Composites for Geothermal Energy Applications. Materials 2017, 10, 462. [Google Scholar] [CrossRef]
- Yang, H.; Memon, S.A.; Bao, X.; Cui, H.; Li, D. Design and Preparation of Carbon Based Composite Phase Change Material for Energy Piles. Materials 2017, 10, 391. [Google Scholar] [CrossRef]
- Yang, W.; Lu, P.; Chen, Y. Laboratory investigations of the thermal performance of an energy pile with spiral coil ground heat exchanger. Energy Build. 2016, 128, 491–502. [Google Scholar] [CrossRef]
- Bao, X.H.; Qi, X.D.; Cui, H.Z.; Tang, W.C.; Chen, X.S. Experimental study on thermal response of a PCM energy pile in unsaturated clay. Renew. Energy 2022, 185, 790–803. [Google Scholar] [CrossRef]
- Lu, H.-W.; Jin, X.; Jiang, G.; Liu, W.-Q. Numerical Analysis of the Thermal Performance of Energy Pile with U-Tube. Energy Procedia 2017, 105, 4731–4737. [Google Scholar] [CrossRef]
- Wya, B.; Lz, A.; Hz, A.; Feng, W.A.; Xl, C. Numerical investigations of the effects of different factors on the displacement of energy pile under the thermo-mechanical loads. Case Stud. Therm. Eng. 2020, 21, 100711. [Google Scholar]
- Gao, J.; Xu, Z.; Liu, J.; Li, K.; Jie, Y. Numerical and experimental assessment of thermal performance of vertical energy piles: An application. Appl. Energy 2008, 85, 901–910. [Google Scholar] [CrossRef]
- Li, T.; Yu, X.; Lei, G.; Habibzadeh-Bigdarvish, O.; Hurley, M. Numerical analyses of a laboratory test of a geothermal bridge deck externally heated under controlled temperature. Appl. Therm. Eng. 2020, 174, 115255. [Google Scholar] [CrossRef]
- Ferrantelli, A.; Fadejev, J.; Kurnitski, J. Energy Pile Field Simulation in Large Buildings: Validation of Surface Boundary Assumptions. Energies 2019, 12, 770. [Google Scholar] [CrossRef]
- Qi, D.; Pu, L.; Sun, F.; Li, Y. Numerical investigation on thermal performance of ground heat exchangers using phase change materials as grout for ground source heat pump system. Appl. Therm. Eng. 2016, 106, 1023–1032. [Google Scholar] [CrossRef]
- Han, C.; Yu, X.B. An innovative energy pile technology to expand the viability of geothermal bridge deck snow melting for different United States regions: Computational assisted feasibility analyses. Renew. Energy 2018, 123, 417–427. [Google Scholar] [CrossRef]
- Lyu, W.; Pu, H.; Chen, J.N. Thermal Performance of an Energy Pile Group with a Deeply Penetrating U-Shaped Heat Exchanger. Energies 2020, 13, 5822. [Google Scholar] [CrossRef]
- Bao, X.H.; Li, Y.B.; Feng, T.J.; Cui, H.Z.; Chen, X.S. Investigation on thermo-mechanical behavior of reinforced concrete energy pile with large cross-section in saturated sandy soil by model experiments. Undergr. Space 2020, 5, 229–241. [Google Scholar] [CrossRef]
- Han, C.; Yu, X.B. Sensitivity analysis of a vertical geothermal heat pump system. Appl. Energy 2016, 170, 148–160. [Google Scholar] [CrossRef]
- Singh, R.M.; Bouazza, A.; Wang, B. Near-field ground thermal response to heating of a geothermal energy pile: Observations from a field test. Soils Found. 2015, 55, 1412–1426. [Google Scholar] [CrossRef]
- Yin, Y.; Li, Q.W.; Qiao, L. Response of energy pile-soil structure and pile group effect: An indoor similarity simulation study. J. Build. Eng. 2022, 51, 104247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).