Hybrid Parallel Ant Colony Optimization for Application to Quantum Computing to Solve Large-Scale Combinatorial Optimization Problems

Abstract

Quantum computing is a promising technology that may provide breakthrough solutions to today’s difficult problems such as breaking encryption and solving large-scale combinatorial optimization problems. An algorithm referred to as Quantum Approximate Optimization Algorithm (QAOA) has been recently proposed to approximately solve hard problems using a protocol know as bang–bang. The technique is based on unitary evolution using a Hamiltonian encoding of the objective function of the combinatorial optimization problem. The QAOA was explored in the context of several optimization problems such as the Max-Cut problem and the Traveling Salesman Problem (TSP). Due to the relatively small node-size solution capability of the available quantum computers and simulators, we developed a hybrid approach where sub-graphs of a TSP tour can be executed on a quantum computer, and the results from the quantum optimization are combined for a further optimization of the whole tour. Since the local optimization of a sub-graph is prone to becoming trapped in a local minimum, we overcame this problem by using a parallel Ant Colony Optimization (ACO) algorithm with periodic pheromone exchange between colonies. Our method exceeds existing approaches which have attempted partitioning a graph for small problems (less than 48 nodes) with sub-optimal results. We obtained optimum results for benchmarks with less than 150 nodes and results usually within 1% of the known optimal solution for benchmarks with around 2000 nodes.

1. Introduction

Searching for an intelligent algorithm inspired by nature has always been a research hotspot [1]. All practical but computationally challenging problems are often addressed by heuristic algorithms using classical computers. However, these algorithms were empirically shown to be effective but not analytically proven to be the best approaches to outperform previous approaches. Due to the growing research in quantum computing and the promising development of quantum hardware, quantum computing will soon help us experiment and solve many problems, obtaining results even beyond those reachable by today’s largest supercomputers [2]. We are in the era of quantum computing, which holds the potential to be the next industrial revolution and help solve existential challenges.

Quantum computing is a promising technology based on the unique properties of quantum physics such as superposition, entanglement, and quantum interference. Quantum computers consist of qubits that can be either 0 or 1 or a superposition of both 0 and 1, which provides them with a computational power that grows exponentially as the number of qubits increases. There has been considerable effort in building quantum-centric supercomputers by large corporations such as IBM, Google, Microsoft, Intel, IonQ, D-Wave systems, etc. In addition, to foster their adoption and improve their computation capacity, numerous improvements are being made to the middleware applications to streamline hybrid quantum-classical integrations. Primarily, there have been two approaches to building quantum computers, one of which is quantum gate-based, while the other is based on quantum annealing. In quantum gate-based quantum computers, qubits are initialized to a known state, and gates are used for manipulating the states, encoding the problem, and performing the computations. In contrast, in quantum computers based on quantum annealing, the formulation starts off with a set of qubits, whose interactions at their lowest energy state, called the ground state, represent the optimal answer that we are attempting to solve. Notably, quantum annealing is mainly used for optimization problems, and D-Wave has been following this approach and released quantum computers with 500 qubits [3]. In contrast, the IBM Osprey quantum processor released in November 2022 has 433 qubits and is based on superconducting transmon qubits.

Optimization problems with discrete variables are classified as combinatorial optimization problems and typically involve finding a grouping, ordering, or assignment of a discrete, finite set of objects that satisfies given conditions. In other words, in any given discrete but large configuration space, combinatorial optimization is the process of searching either maxima or minima, based on the goal of an objective function F. It has important applications in several fields including Artificial Intelligence (AI) and Machine Learning (ML). A few popular examples of problems in this category are the travelling salesman problem (TSP), the minimum spanning tree problem (MST), the knapsack problem, the job-shop scheduling problem, protein structure prediction, etc.

In this paper, we focused on solving large-scale combinational optimization problems, specifically the TSP, employing hybrid quantum and classical computing environments. While quantum computing has the potential to optimally solve the TSP, which is an NP-hard problem, the number of qubits needed for an n-node TSP is O(n²). So far, the number of reliable quantum operations have been limited by noise and decoherence as well as by the available qubit size, and therefore, hybrid quantum-classical algorithms have been introduced in recent years. Thus, efficient algorithms that partition a TSP with a large number of nodes and combine the optimized partitioned solutions via metaheuristics, such that the overall solution is near optimal, are of fundamental importance.

Ant Colony Optimization (ACO) is a population-based metaheuristic for solving hard computational problems. ACO can be effectively used to find approximate solutions to difficult optimization problems like the TSP. Note that other metaheuristics can also be used for the TSP instead of Ant Colony Optimization (ACO); however, for the TSP, ACO has an extremely quick execution time as compared to other metaheuristics [4]. Furthermore, ACO is also efficiently parallelizable, and our new parallel ACO uses cooperation between ant colonies to yield better optimization results. For solving TSPs with a relatively large number of nodes, even parallel ACO is slow and does not produce optimal solutions. Thus, the aim of this paper was the development of an approach for partitioning large-scale TSPs into sub-graphs, solving these sub-graphs optimally on quantum computers, assembling the sub-graphs results, and then optimizing them using parallel ACO.

For the quantum aspect of our hybrid approach, a good candidate was the Quantum Approximate Optimization Algorithm (QAOA), which alternates between applying a cost function-based Hamiltonian and a mixing Hamiltonian [2]. Farhi et al. introduced the QAOA in 2014 with the goal to maximize a cost function [5,6,7]. It is a polynomial-time algorithm for finding a nearly optimal solution to an optimization problem. Considering a given NP-hard problem, an approximate algorithm solves it in polynomial time with some guaranteed bound on the expectation. The criterion to judge the approximate algorithm is the ratio between the quality of the polynomial time solution and the quality of the true solution. One of the reasons for the great interest in the QAOA is its potential to exhibit quantum supremacy [8]. The QAOA is a hybrid quantum-classical variational algorithm that attempts to approximately solve hard problems using a protocol known as bang–bang [9].

Contributions of This Study and Paper Organization

In this work, we developed a Hybrid Quantum Optimization Algorithm (QAOA) with a classical parallel ACO algorithm for solving large-scale combinatorial optimization problems such as the TSP. Our algorithm, termed Hybrid Parallel Ant Colony Optimization (HPACO) algorithm, can be applied to quantum computing to solve large-scale optimization problems. Our contributions can be summarized as follow:

• Development of a TSP sub-graph partitioning algorithm for applications to quantum computing where each sub-graph can be optimally solved on a quantum computer.
• Novel combined optimization of individually optimized sub-graphs by our new parallel cooperating ant colony algorithm with periodic pheromone exchange that produces optimal results for TSP instances with up to 150 nodes.
• To avoid the local minima due to partitioning of the graph, recreation by our algorithm of sub-graphs after each optimization iteration such that the partitioning boundaries are selected differently from the previous iteration to avoid local minima in the overall TSP optimization.

The remainder of the paper is organized as follows. Section 2 provides a brief background on the combinatorial optimization and the QAOA. In Section 3, we discuss some of the related work that was proven successful for finding high-quality solutions to relatively large combinatorial optimization problems. In Section 4, we include the details of our parallel ACO algorithm with cooperating ant colonies. Section 5 presents the extension of parallel ACO for graph partitioning. Section 6 highlights our results for some of the TSP benchmarks, while Section 7 includes a further discussion. Finally, Section 8 provides a brief conclusion and suggests future work.

2. Background

Problems with discrete variables are classified as combinatorial optimization problems. Combinatorial optimization is the process of finding an optimal or close-to-optimal solution among a finite set of possibilities. Formally, an instance of an optimization problem I is a pair (F, c), where F is the domain of feasible points, and c is the cost function [10], and the goal is to find a globally optimal solution $f\in F$ to the given instance I so that

$$c\left(f\right)\le c\left(y\right) \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} y\in F$$

(1)

In other words, we look for an object (integer, set, permutation, or graph) from a finite or, possibly, countably infinite set. In classical computing, some of these problems can be solved exactly using branch and bound techniques. But in many cases, such as the TSP (an NP-hard problem), exact algorithms are infeasible, and therefore, randomized-search algorithms, such as the genetic algorithm, particle swarm optimization, simulated annealing, and alike, are used [4]. Due to the constraints and the complexities of such problems, at the very core, two important factors are to be considered—the time to find an optimal solution, and the quality of that solution. The optimal solution is obtained from a finite set of solutions.

The TSP is a classic combinatorial optimization problem that can be described as follows. Given the (x, y) positions of n different cities, we need to find the shortest possible path that visits each city exactly once. The TSP belongs to a class of NP-complete combinatorial problems and is classified as an NP-hard problem because for n cities, (n − 1)! possible combinations are needed to search for the solution, and the number of combinations grows fast as n increases. This cycle of visiting each city once, where each city represents a unique vertex in a graph, and returning to the starting city is known as a Hamiltonian cycle. Each city is connected to other cities with a specific cost associated to each connection.

Quantum data are remarkably interesting as information can be in the superposition of states. When we increase the number of qubits, the Hilbert space (the state space), grows exponentially with the number of qubits, as ${\left(\right|0⟩+|1⟩)}^n.$ If $n=50$, the operation can be handled by today’s supercomputers; however when $n=300$, then we will have more states than atoms in the universe.

Thus far, the number of reliable quantum operations have been limited by noise and decoherence, and therefore, hybrid quantum-classical algorithms were introduced with the aim to combine the best of both worlds. The QAOA [7] and the variational quantum eigensolver [11] are examples of such hybrid quantum-classical algorithms aimed to address some of the classical combinatorial optimization problems. These algorithms use a quantum circuit depending on a set of parameters which are determined by a classical optimizer. The QAOA is a promising algorithm to tackle these problems in the Noisy Intermediate-Scale Quantum (NISQ) technology.

The QAOA applies alternatively a cost function-based Hamiltonian and a mixing Hamiltonian. The goal is to maximize the cost function. It is a polynomial-time algorithm for finding a nearly optimal solution to an optimization problem. We are interested in combinatorial optimization problems specified by n bit binary strings and m clauses [7]. The objective function $C\left(z\right)$, which is the sum of the individual cost functions from m clauses, is:

$$C\left(z\right)=\sum _{\alpha =1}^m{C}_{\alpha }\left(z\right)$$

(2)

where $z=z_1{\cdots z}_n$ is the bit string, and $C_{\alpha }\left(z\right)$ depends on only a few of the n bits, and its satisfiability is described as:

$${ C}_{\alpha }\left(z\right)=\left\{\begin{array}{ll}1& \to satisfies\\ 0& \to does not satisfy\end{array}\right.$$

(3)

The maximum of the cost function $C_{max}$ is:

$$C_{max}=\underset{z}{\max } C\left(z\right)$$

(4)

The goal is to find a string z that achieves the highest approximate ratio of the calculated cost divided by the maximum cost, which is presented as:

$$Approximate Ratio=\frac{C\left(z\right)}{C_{max}}$$

(5)

The QAOA would like this value to be large, since this is a maximization problem. To encode the above as a quantum algorithm, we will need to define unitary operators. The first one depends on an angle $\gamma$ and it is:

$$U\left(C,\gamma \right)=e^{-i\gamma c}=\prod _{\alpha =1}^m{e}^{-i\gamma C_{\alpha } }$$

(6)

The above cost function, also known as the cost Hamiltonian $H_c$, is unitary and depends on the angle $\gamma \in \left[0, 2\pi \right)$. Further, this unitary function can be written as the product of m unitary functions because each $C_{\alpha }$ commutes. There is another operator, $B$, which is the sum of ${\sigma }^x$ operators and is defined as:

$$B=\sum _{j=1}^n{\sigma }_j^x$$

(7)

Another unitary operator, also known as the mixing Hamiltonian $H_B$, depends on the angle $\beta \in \left[0, \pi \right)$ and can be written as the product of n individual rotations of qubits by an angle $\beta$ and is given as:

$$U\left(B, \beta \right)=e^{-i\beta B}=\prod _{j=1}^n{e}^{-i\beta {\sigma }_j^x}$$

(8)

Finally, the initial state $|s⟩$, the uniform superpositions of all the bitstrings $z$, is expressed as:

$$|s⟩=\frac{1}{\sqrt{2n}} \sum _z|z⟩$$

(9)

For any integer $p\ge 1$ and a set of $2p$ angles ${\gamma }_1\cdots {\gamma }_p\equiv \gamma$ and ${\beta }_1\cdots {\beta }_p\equiv \beta$, the QAOA quantum circuit produces the following angle-dependent quantum state:

$$|\gamma ,\beta ⟩=U\left(B,{\beta }_p\right)U\left(C,{\gamma }_p\right)\cdots U\left(B,{\beta }_1\right)U\left(C,{\gamma }_1\right)|s⟩$$

(10)

The corresponding state is defined as:

$$\left|\overrightarrow{\gamma },\overrightarrow{\beta }⟩=\exp \left(-i{\beta }_{p}B\right)\exp \left(-i{\gamma }_{p}C\right)\cdots \exp \left(-i{\beta }_{1}B\right)\exp \left(-i{\gamma }_{1}C\right)\right|s⟩$$

(11)

The goal is to find the $2p$ angles $\gamma$ and $\beta$ so that

$$⟨\overrightarrow{\gamma },\overrightarrow{\beta } |C| \overrightarrow{\gamma },\overrightarrow{\beta }⟩$$

(12)

is maximized. It is not obvious how to choose good angles in advance, but there are several ways to find the optimal angles with classical optimizers using optimized iterations.

Considering the above definitions, we started our study with the initial parameters, constructed the corresponding states, measured those states, and updated the angles. With layering and multiple iterations, the circuit was optimized, and the measurements of the output state provided an approximate solution. The steps of a high-level QAOA can be summarized as:

Step 1: start with an initial state $|\psi ⟩=|s⟩$;

Step 2: using a classical algorithm, initialize the $2p$ parameters $\gamma$ and $\beta$;

Step 3: construct $|\gamma ,\beta ⟩$ using the angles from step 2 and update the state ${|\psi ⟩}_{new}$;

Step 4: measure the state from step 3 and obtain a value $|z⟩;$

Step 5: using a classical algorithm, calculate $C\left(z\right);$

Step 6: repeat steps 1 to 4 several times, each time keep track and store the values of $|\gamma ,\beta ⟩$ and $|z⟩$;

Step 7: select a new set of $2p$ parameters $\beta$ and $\gamma$, and repeat steps 3 to 6. Choose the largest value for this distribution. Continue until the objective is met.

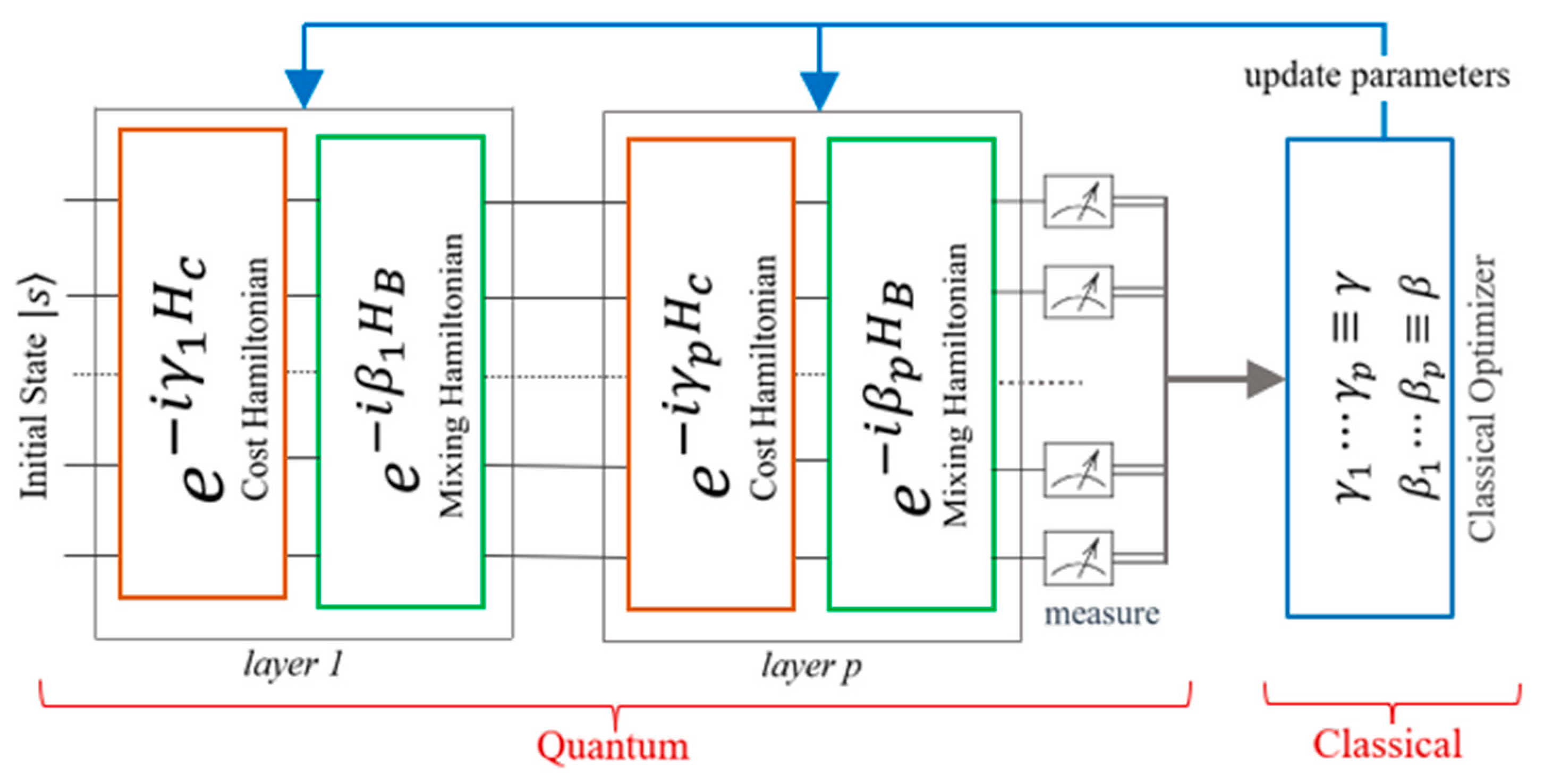
Furthermore, a p-layer QAOA can be constructed by repeating the non-H gates (not Hadamard gates) for p times as shown in Figure 1. Each of the layers consists of cost Hamiltonian followed by mixing Hamiltonian, with the measurement being performed after the final p-layer resulting in the final quantum state. As demonstrated in Figure 1, the classical optimizer evaluates the objective and updates the gate parameters ($\gamma , \beta )$ until convergence is reached and the objective is met.

3. Related Work

An essential but missing approach for understanding and deploying the QAOA is a constructive one to carry out the outer-loop classical optimization [12]. Recent work showed that for large enough problem sizes, algorithms suffer from barren plateaus with a very low probability to escape, resulting in algorithms to settle at a sub-optimal result [2].

In 2014, Farhi et al. showed that the QAOA with p = 1 achieved an approximate ratio of 0.6924 when performing Max-Cut on three-regular graphs. Unfortunately, it did not outperform the best classical algorithm available. In 2002, Halperin et al. achieved a significantly better approximation ratio of 0.9326 with a semidefinite programming-based approach [13]. In 2018, Crooks showed that the QAOA for Max-Cut could achieve far better approximation ratios [14] than the classical Goemans–Williamson algorithm [15]. In 2019, Streif et al. showed that the QAOA is arguably one of the strongest candidates for demonstrating quantum advantage over classical approaches in the current NISQ era [16].

It was observed that while the QAOA has a simple description, its effectiveness is not clear beyond the case of p = 1 [12]. To be able to achieve quantum supremacy over classical algorithms, it is important that its mechanisms are analyzed and understood for depths p > 1. Perhaps, because of lack of this understanding, the QAOA has not shown a greatly improved performance on bounded-degree graphs when the depth p is shallow [17,18]. It was conjectured in [12] that the reason for this limited performance of the QAOA could be due to the fact that the algorithm cannot “see” the entire graph at low depth. Perhaps, a solution to this might be to increase the depth of the QAOA with the system size (e.g., p ≥ log n). For example, for the Max-Cut problem, through numerical evidence, it seems that the QAOA yields the ratio (Equation (5)) r ≥ (2p + 1)/(2p + 2). In another case of Grover’s unstructured search problem among n items, the QAOA was able to find the target state with p = Θ(√n), achieving the optimal query complexity within a constant factor [19].

The QAOA for Max-Cut has been widely studied since Farhi et al. initially introduced the algorithm. Recently, in 2021, Li et al. introduced a “divide-and-conquer” approach to solve a large-scale Max-Cut graph. The authors demonstrated that recursively partitioning a large graph into smaller ones and applying combination policy helped them achieve a higher approximation ratio than that obtained with classical methods [20]. This approach utilizes a partitioning heuristic to split a large graph into two sub-graphs with equal nodes and sharing two common nodes. The sub-graphs are then solved by the QAOA and classically combined in the end to retrieve the results. Furthermore, the authors stated this approach only applies to input graphs with connectivity less than the maximum allowed qubit size. Nonetheless, this approach is not appropriate for our enhanced methodology to solve the TSP.

Related Work on TSP Optimization with Quantum Computers

Unlike for the use of the QAOA for Max-Cut, very few attempts have been made to use the QAOA for TSPs with a large number of nodes, i.e., with n > 4. This is mainly due to the limited qubit size and scalable quantum simulators available. In 2018, Karthik et al. proposed a quantum algorithm to solve the TSP using the phase estimation technique. The authors encoded the distances between the cities as phases and applied the phase estimation algorithm to compute the total distances for all the possible routes [21]. Though a quadratic speedup over the classical brute force method for a large number of cities was claimed, the actual demonstration was performed only for a four-node TSP using an IBM quantum simulator.

Some initial attempts to adapt quantum formulation to graph optimization using ACO were reported in [22,23]. The solution of the TSP with time windows (TSPTW) in quantum computers was developed in [24]. It looks for a tour with the minimum cost where each city is visited within an associated time frame, namely, between its earliest start time and its due time. The authors investigated the implementation of this solution on a D-Wave computer with only up to five nodes. Recent work [25] formulated the TSP as Quadratic Unconstrained Binary Optimization (QUBO) and showed how the number of resources (qubits) can be reduced. For example, to solve a seven-node TSP, the authors used 43 qubits.

Another study on the TSP using the QAOA was reported [26]. A 48-node TSP was examined by partitioning it into smaller problems (9 nodes for the 48-city problem) and solving the sub-problems on a D-wave quantum computer. While optimal solutions were obtained for the smaller problems, only an approximate solution was achieved for the 48-node problem.

In short, the current approaches to partitioning the TSP to find the optimal solution using quantum computers reported limited success for small TSPs. This was our primary motivation to develop a new approach that can handle large-scale problems by a partitioning approach such that individual partitions can be optimized on a quantum computer, and when these optimized sub-graphs are combined, the resulting optimization is near optimum. Note that a hybrid approach involving quantum computers and classical computing is needed because the number of qubits needed to solve a combinatorial optimization problem is O(n²). Solving TSP instances containing over a few dozen nodes is beyond the scope of the current and near-future quantum computers. For example, a 1000-node TSP optimization will require a 1 million-qubit quantum computer. Thus, a hybrid approach consisting in dividing the problem into sequences of smaller TSP sub-graphs and then further optimizing the resulting individual optimized sub-graphs is the only viable solution in the near future.

4. Our Hybrid Quantum-Classical Optimization Algorithm

Combinatorial optimization problems are solved by encoding them to minimize a binary quadratic form, which can be translated to finding the minimal eigenvalue of a Hamiltonian. The number of qubits needed is the dimension of the Hamiltonian. To solve an n-node TSP problem, the qubits needed become (n − 1)². Clearly, the QAOA cannot effectively handle a large-scale combinatorial optimization problem with the current qubit size, and therefore, the QAOA is far from achieving quantum advantage at this time.

Our approach to solving the TSP is based on a hybrid parallel ACO algorithm and possibly a quantum computer to optimize the sub-tours present in a large tour. After an initial parallel ACO of the entire tour, we partitioned the tour into disjoint sub-tours. Each sub-tour could then potentially be optimized on a quantum computer, and the optimized sub-tours could be assembled and further optimized to provide the complete tour. Figure 2 depicts this scenario.

We repeated the partitioning and optimization process until the solution converged to an optimal or near-optimal value. Note that the optimization of the partitioned sub-graphs lost the global perspective, and thus the resulting assembled solution should be globally optimized. The steps of our optimization algorithm are as follows:

• Partition the TSP graph in sub-graphs. The number of nodes in the sub-graphs is chosen according to the available number of qubits in the quantum computer.
• Optimize each sub-graph on a quantum computer using the QAOA algorithm.
• Assemble the sub-graphs and optimize the complete graph using the parallel ACO algorithm for a few iterations.

Repeat steps 1–3 until the solution converges.

In the next sub-section, we describe the details of our new parallel ACO algorithm for achieving a global optimization of the solution to the TSP.

4.1. Parallel ACO Algorithm with Cooperating Ant Colonies

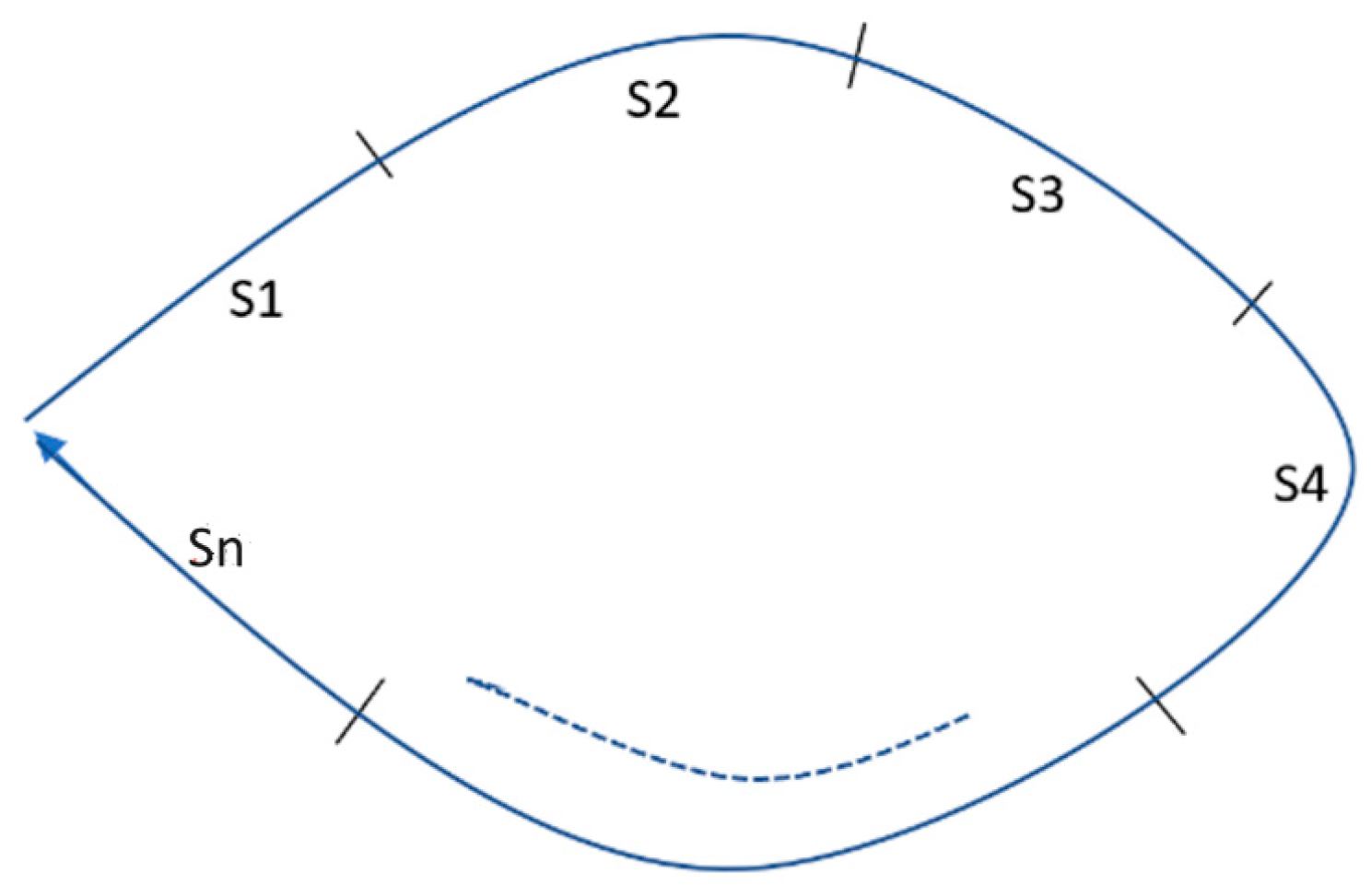
The Ant Colony Optimization (ACO) algorithm was proposed by Dorigo in 1992 [27]. Since then, many different variations of the ACO have been reported [28], e.g., the Ant System, the Ant Colony System, the Max–Min Ant System, the Rank-Based Ant System, etc. Of these, the Ant Colony System (ACS) and the Max–Min Ant System have demonstrated the best performance on large benchmarks. For a better exploration of the search space, we used both of these algorithms in our new parallel algorithm. For completeness, we briefly describe the key features of these individual ACO algorithms before incorporating them into our novel parallel optimization algorithm. The general outline of the ACO algorithm for solving the TSP is shown below in Figure 3:

The ACS and the Max–Min ACO algorithms differ in the initialization of the pheromone matrix, the tour construction, and the pheromone update after the iteration-best tour is determined.

4.1.1. ACS Algorithm

Pheromone Initialization

In the ACS, the initial tour cost is determined by creating a greedy tour, and the pheromone on each link is set as:

$$\mathrm{P}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{e}\left[i, j\right]={\tau }_{i,j}=1.0/\left(cityCount\times tourCost\right)$$

(13)

where cityCount is the total number of nodes.

Tour Construction

In the ACS, each ant k at node i decides to go to an unvisited node j in the tth iteration by following the pseudorandom proportional action choice rule described as follows:

if the generated random number (between 0 and 1) > q,

select the node j with the highest value of ${\tau }_{i,j}\times {[ {\eta }_{i,j}]}^{\beta }$

else

the probability of visiting node j from the unvisited set $N_{j,k} \mathrm{i}\mathrm{s}:$

$$p_{i,j}^k\left(t\right)=\frac{{\left[{\tau }_{i,j}\left(t\right)\right]}^{\alpha }{[ {\eta }_{i,j}]}^{\beta } }{{\sum }_{l \in { N}_{i,k}}{\left[{\tau }_{i,l}\left(t\right)\right]}^{\alpha }{[ {\eta }_{i,l}]}^{\beta }} j\in { N}_{i,k}$$

(14)

where ${\eta }_{i,j}=1/dist\left(i,j\right)$ is a popular heuristic, and $\alpha$ and $\beta$ are the hyper-parameters of the ACO system. The parameter $\alpha$ contributes to the weight given to a trail according to the pheromone on it, whereas $\beta$ takes into account the distance of the next unvisited node that can be selected from the current node. The typical value of $\alpha$ is 1, and $\beta$ is usually selected between 2 and 10. Note that a higher $\beta$ favors the exploration of different paths [29].

Pheromone Update

In the ACS, only pheromones on the trails of the global best tour are updated as:

$${\tau }_{i,j}^{\left(t+1\right)}={\tau }_{i,j}^{\left(t\right)}\left(1-\rho \right)+\rho /costOfGlobalBestTour$$

(15)

There is no evaporation of pheromone values in the ACS algorithm.

4.1.2. Max–Min Algorithm:

The Max–Min algorithm uses the following parameters:

$\rho =pheromoneupdate constant;$ //typical value is 0.1;

${\tau }_{max}=1/\left(\rho \times cityCount\right);$//max pheromone value;

${\tau }_{min}={\tau }_{max}/\left(2\times cityCount\right);$//min pheromone value.

Pheromone Initialization

The Max–Min algorithm initializes the pheromone on each link to its maximum value according to:

$$\mathrm{P}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{e}\left[i, j\right]={\tau }_{max}; //\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{e} \mathrm{t}\mathrm{o} \mathrm{m}\mathrm{a}\mathrm{x}$$

(16)

Tour Construction

The Max–Min algorithm uses the same tour construction as the ACS algorithm. Note that, since the initial pheromone values are high in the Max–Min algorithm, i.e., ${\tau }_{max},$ it favors an early exploration compared to the ACS algorithm.

Pheromone Update

Since the pheromone values are set to ${\tau }_{max}$ in the beginning, evaporation on all links is first carried out according to the following equation:

$${\tau }_{i,j}^{\left(t+1\right)}={\tau }_{i,j}^{\left(t\right)}\left(1-\rho \right)$$

(17)

The pheromone values on the links of the best iteration tour or the best global tour are updated as:

$${\tau }_{i,j}^{\left(t+1\right)}={\tau }_{i,j}^{\left(t\right)}\left(1-\rho \right)+1/costOfIterationOrGlobalBestTour$$

(18)

Since the ACS and the Max–Min algorithms offer different exploration characteristics (e.g., the Max–Min algorithm favors an early exploration), we combined both of these algorithms in a parallel multi-colony system. To further improve the learning of the optimal paths, we implemented a periodic pheromone exchange between the different colonies that resulted in a more collaborative and efficient exploration of the search space.

Note that the graph partitioning approach to solving the TSP was proposed in many different papers [30,31,32,33]. The approach in [30] used the K-means-based partitioning of the global graph into sub-graphs and optimized the overall solution by using the Lin–Kernighan algorithm. In [31], a heuristic based on cutting the TSP cycle in time proportionally to the number of edges in the graph was used to partition the graph. The partitions were assembled and optimized further. While the partitioning approach does reduce the time complexity of the entire optimization, it often results in sub-optimal performance as compared to the approach optimizing the entire tour as a whole. The main reason is that a node s_i in a sub-tour is not swapped with a node in a different sub-tour, s_j, during the optimization of the individual sub-tours. Further, the initial breakdown of the sub-tours can have a major impact on the overall tour optimization if the sub-tours are not properly chosen. We addressed the initial partitioning and the combined optimization of the optimized sub-tours through a significantly improved and novel parallel ACO algorithm. We will first describe the details of our novel parallel ACO algorithm and then present a hybrid parallel ACO sub-graph-partitioning version of it for use in a quantum environment.

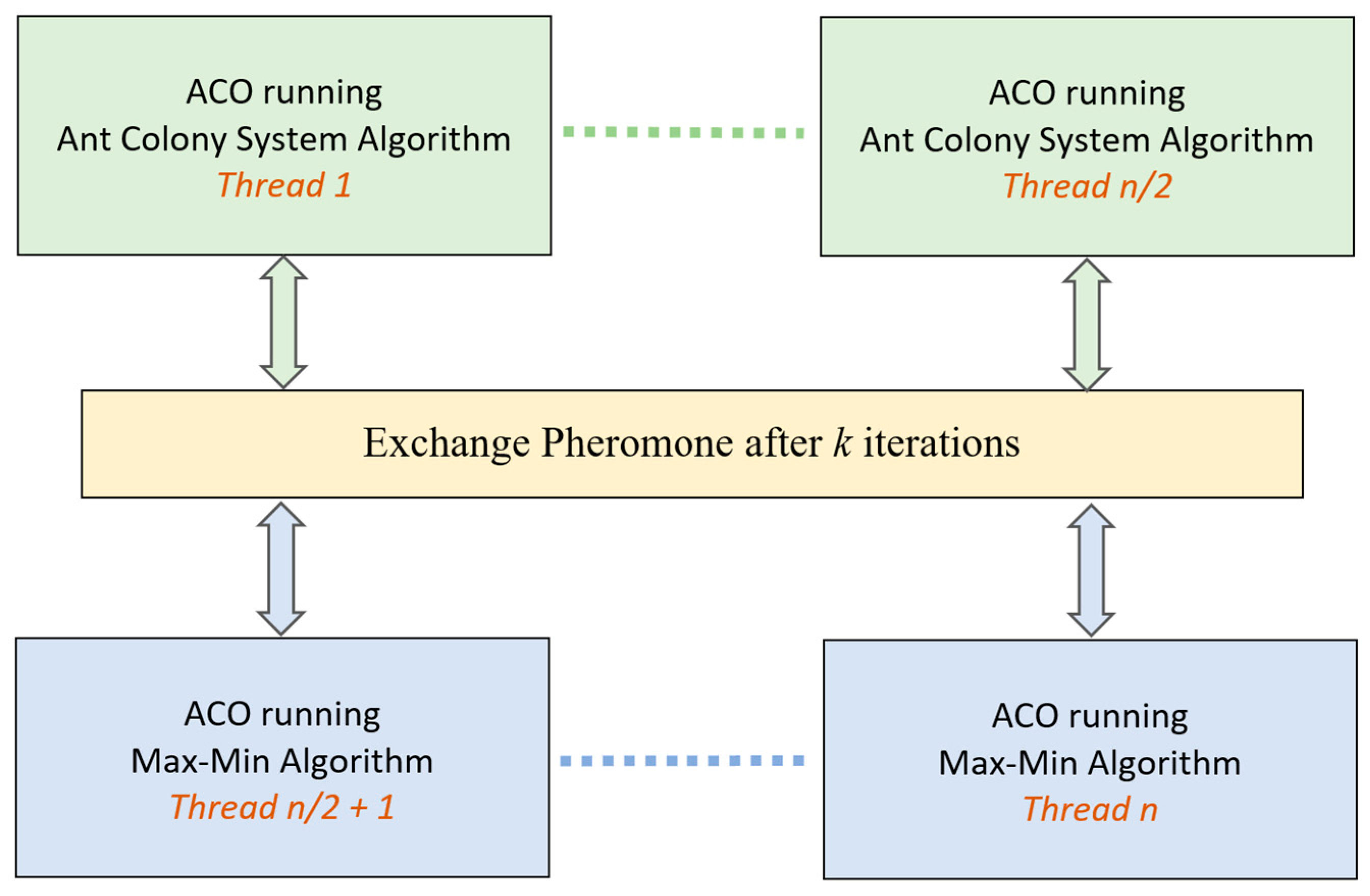
The parallel multi-colony ACO algorithm developed in this work is multithreaded, and each thread runs either the ACS or the Max–Min algorithm. Generally, better results are obtained when half the colonies execute the ACS algorithm, and the other half the Max–Min algorithm. The different threads are periodically synchronized via barrier synchronization and perform pheromone exchange between colonies according to a selected pheromone exchange policy. The general architecture of our parallel implementation is shown in Figure 4.

After a specified number of iterations of the individual ACO algorithm running in each thread, the threads were synchronized and performed a pheromone exchange. The reason for doing this was to learn which paths were most commonly used, so that more weight could be attributed to those commonly used sub-paths during the exploration of an optimal path. In fact, “the best route between two given cities” will most likely involve the major highways connecting them, while the roads that connect to these major highways may offer alternative routes. We implemented the following different pheromone exchange policies after a fixed number k of iterations.

4.2. Averaging of the Pheromone Value on All Links (APAL)

After k iterations, the pheromone value on a link in each colony was updated to the average value from all colonies. A similar idea was presented in [34], where only two ant colonies were used. We generalized this concept to n colonies.

4.3. Increase in Pheromone Value on Common Links and Decrease in Pheromone Value on Uncommon Links between Best Solutions from Two Randomly Selected Colonies (ICDU)

After k iterations, a number of different colonies were chosen at random, and the common links between them were determined. The pheromone value on the common links between them increased, while the pheromone value on the uncommon links was reduced. The number of random colony pairs that took part in this exchange is a hyper-parameter, and its setting depends on the total number of parallel ant colonies being used. When a large number of colonies is used, the percentage of colonies taking part in this exchange is usually relatively low. The increase in the pheromone value on the common links was determined according to Equation (15) if the colony was running the ACS algorithm and according to Equation (17) if the Max–Min algorithm was used.

4.4. No Pheromone Exchange (PIR)

A situation in which ant colonies do not exchange any pheromone information with each other is described by the Parallel Independent Runs (PIR) model reported in [27], where the final solution is the best result amongst all parallel colonies. We implemented this scheme for comparison purposes.

In our parallel ACO algorithm, the individual ant colonies executed the following algorithm as shown in Figure 5. Note that the individual ants in an ant colony were further launched in parallel to complete an individual tour.

5. Extension of the Parallel ACO for Graph Partitioning

While our parallel ACO algorithm with cooperating ant colonies provided an elegant and efficient solution, we enhanced it further to perform graph partitioning, where a given graph was partitioned into sub-tours, and each partition could be individually optimized using our parallel ACO algorithm, as described in Section 4. We had two reasons for enhancing the algorithm in this way. First, this would allow its application to larger optimization problems. Secondly, the sub-graphs could be optimally solved on a quantum computer, and the final assembly of sub-tours could be further optimized using our parallel ACO algorithm.

There are two major challenges in a graph partitioning approach. First, the initial partitioning has to be such that most of the nodes in a partition are part of the final optimal solution, otherwise, even though the sub-tours may be optimal within themselves, the overall tour is likely to be sub-optimal. Secondly, the assembly of the final optimized sub-tours further need to be globally optimized so that the nodes within a partition can move to a spot in another partition. We propose to solve both problems with our parallel algorithm. We executed the parallel ACO algorithm for a few iterations to obtain an approximate tour. The tour was partitioned into non overlapping sub-graphs, and each sub-graph could be optimized using the same parallel ACO algorithm or, preferably, a quantum computer.

The optimized sub-tours were further assembled and optimized globally using our parallel ACO algorithm. This process was repeated until convergence was reached. Figure 6 shows the overall hybrid parallel ACO algorithm (HPACO) for TSP optimization.

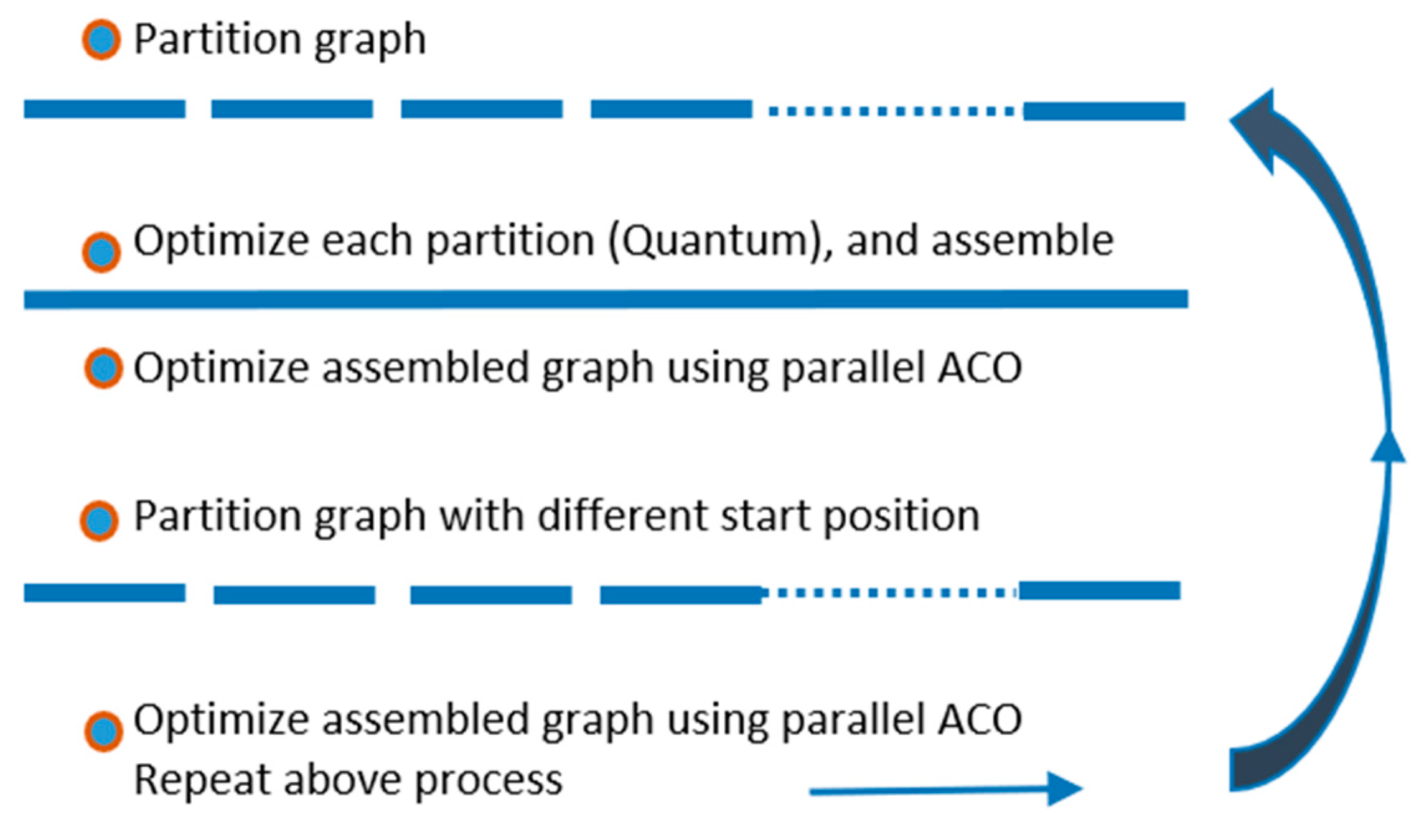
Note that the partitioning of the graph in the above algorithm was performed on a partially optimized tour by selecting a fixed-size sub-tour. Thus, we avoided becoming trapped in a local minimum. The start point where the partition started was randomly chosen. For example, if the number of nodes was 1000 and we decide to partition the tour into sub-tours of 50 nodes each, the sub-tours would start randomly between position 1 and 49, e.g., the first sub-tour to be optimized could start from position 23 to position 72, the second sub-tour from position 73 to 122, and so on. Second time in the while loop in the above algorithm, the partitions to be optimized may be from 17 to 66, and 67 to 116 etc.… After each sub-graph optimization and the assembly of the sub-graphs, a global local search was conducted, and a parallel ACO was applied on the entire tour for a limited number p of iterations to continue improving the global optimization. Also note that, in the optimization of the sub-graph, the end nodes were fixed and not allowed to change in the optimization process, i.e., the sub-tours were not cyclic, unlike the global tour in the TSP, which went back to the start node.

Since the optimization of the entire graph can be time-consuming for large tours, we here present a slight modification of the HPACO algorithm. In this case, after the initial partitioning into sub-graphs, the assembly of the optimized sub-graphs did not require applying the HPACO on the entire graph. Instead, a k-opt was used to swap a node between sub-tours, and if this resulted in a lower overall tour cost, then the sub-graphs that were changed were optimized again. This modified HPACO that is particularly efficient in a quantum environment is shown in Figure 7.

Note that the key difference between our new algorithm and that presented in our previous work [29] is that the new algorithm is based on the partitioning of sub-graphs and their assembly and repartitioning, whereas the previous parallel ACO algorithm operates on the entire graph.

6. Results

To implement the HPACO with quantum optimization for sub-tours, we used the IBM Qiskit quantum simulator. The current Qiskit simulator is only able to handle a three-node TSP problem. For the optimization of a four-node problem, the simulator takes almost 30 min, and often errors are made. This phenomenon was also reported in [35]. Thus, we first considered a relatively small-size problem, i.e., a 51-node TSP (eil51 from the TSPLib benchmark), and used our HPACO algorithm to optimize it. A tour cost of 426 was obtained (the known optimal cost for this benchmark is 426). In the rest of the experiments, we replaced the QAOA with the parallel ACO algorithm, as detailed in Figure 7, so that we could assess the effectiveness of our hybrid approach, without being limited by the size of the current quantum computers or simulators in the optimization of the sub-graphs.

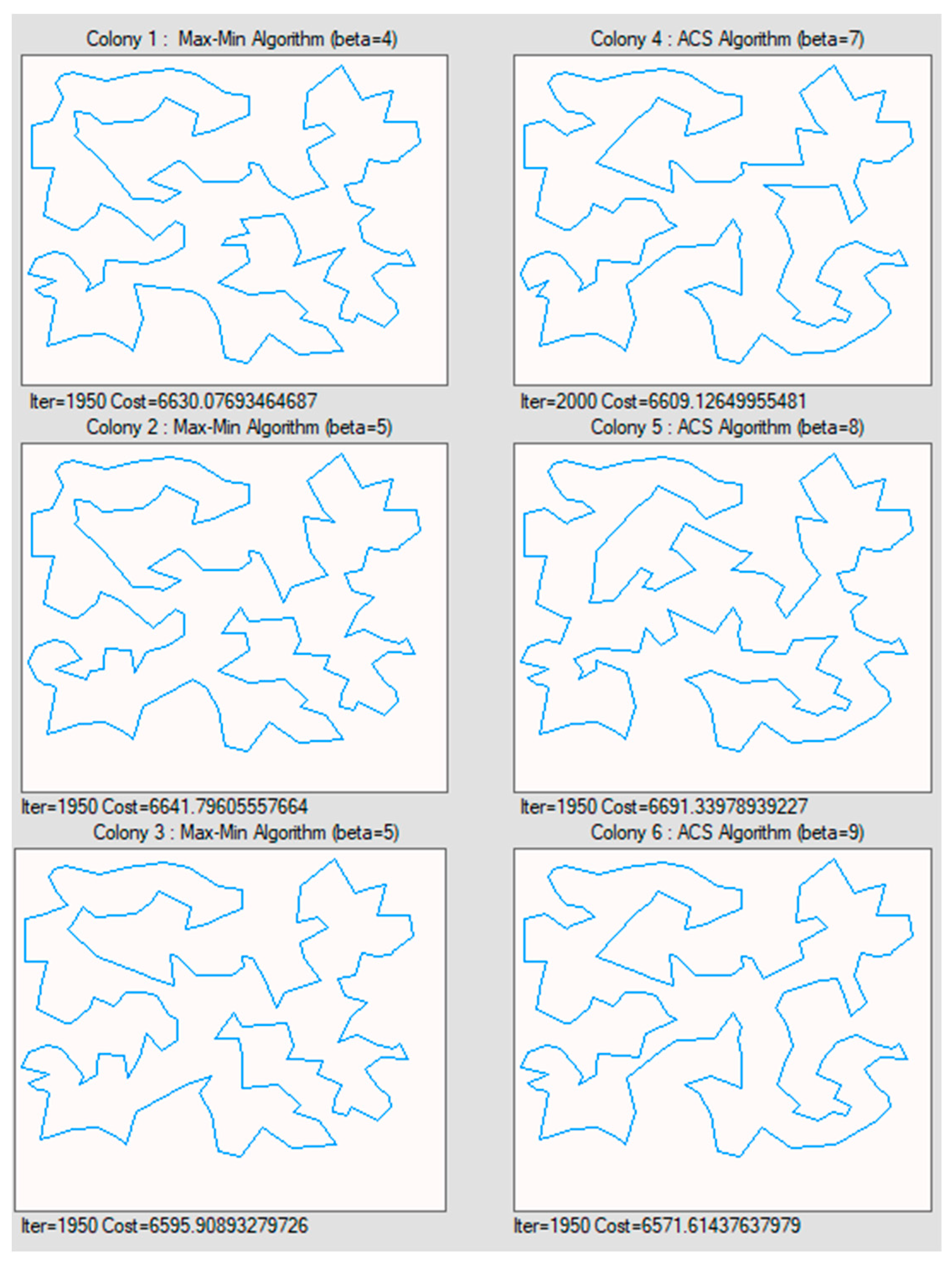
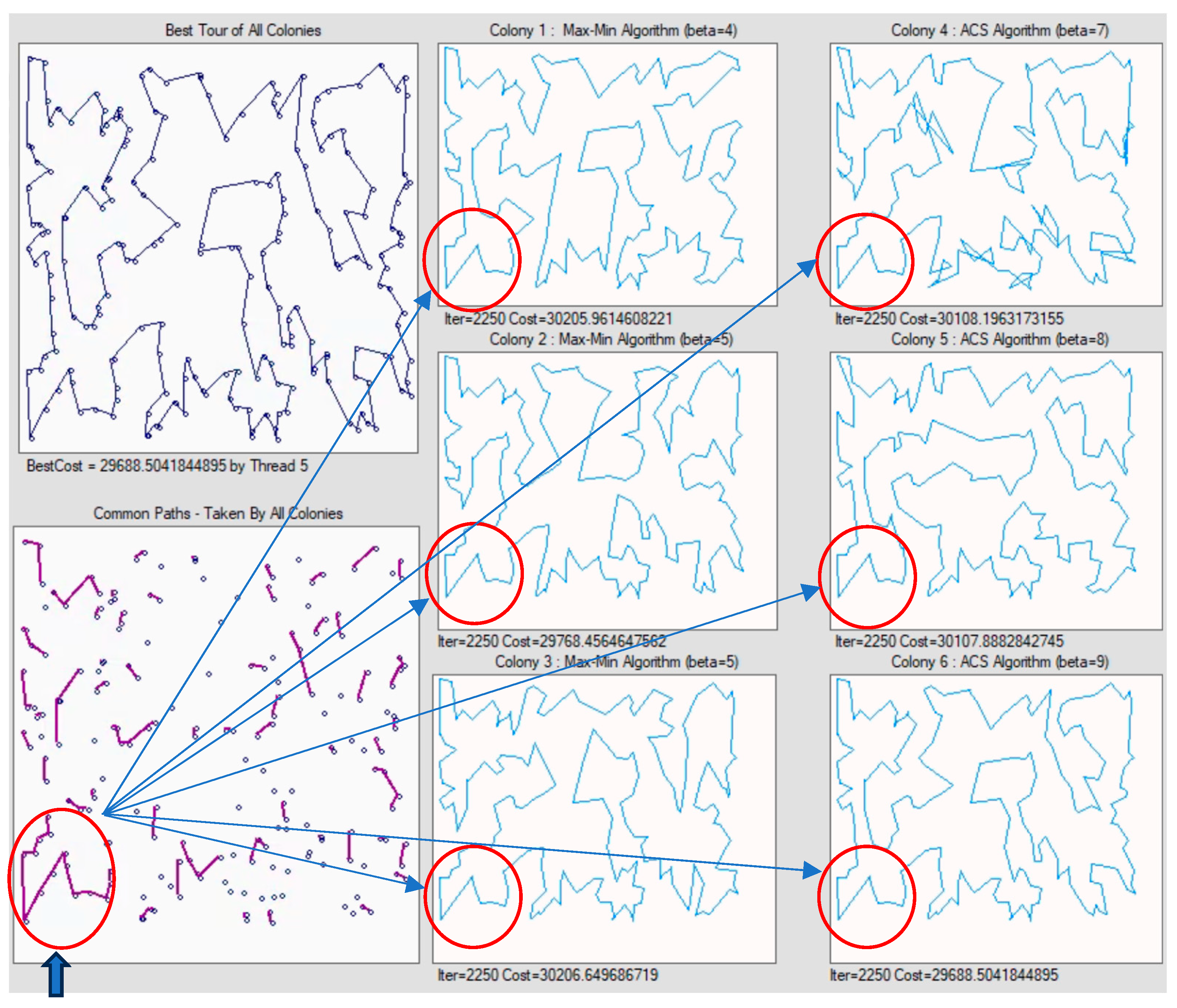
One of the key strengths of our parallel ACO algorithm is the cooperation between different ant colonies. In our experimental setup, the algorithm was implemented using C#. Our computing platform was a 48-core Xeon processor with 128 GB RAM allowing us to run multiple ant colonies. The progress of different ant colonies during the optimization of the Ch150 (150 nodes) benchmark is shown in Figure 8.

The parallel ACO algorithm periodically used the information on the common paths taken by different colonies to increase the pheromone value on these common paths. Figure 9 shows the common paths taken by the ant colonies during the optimization of the Ch150 benchmark.

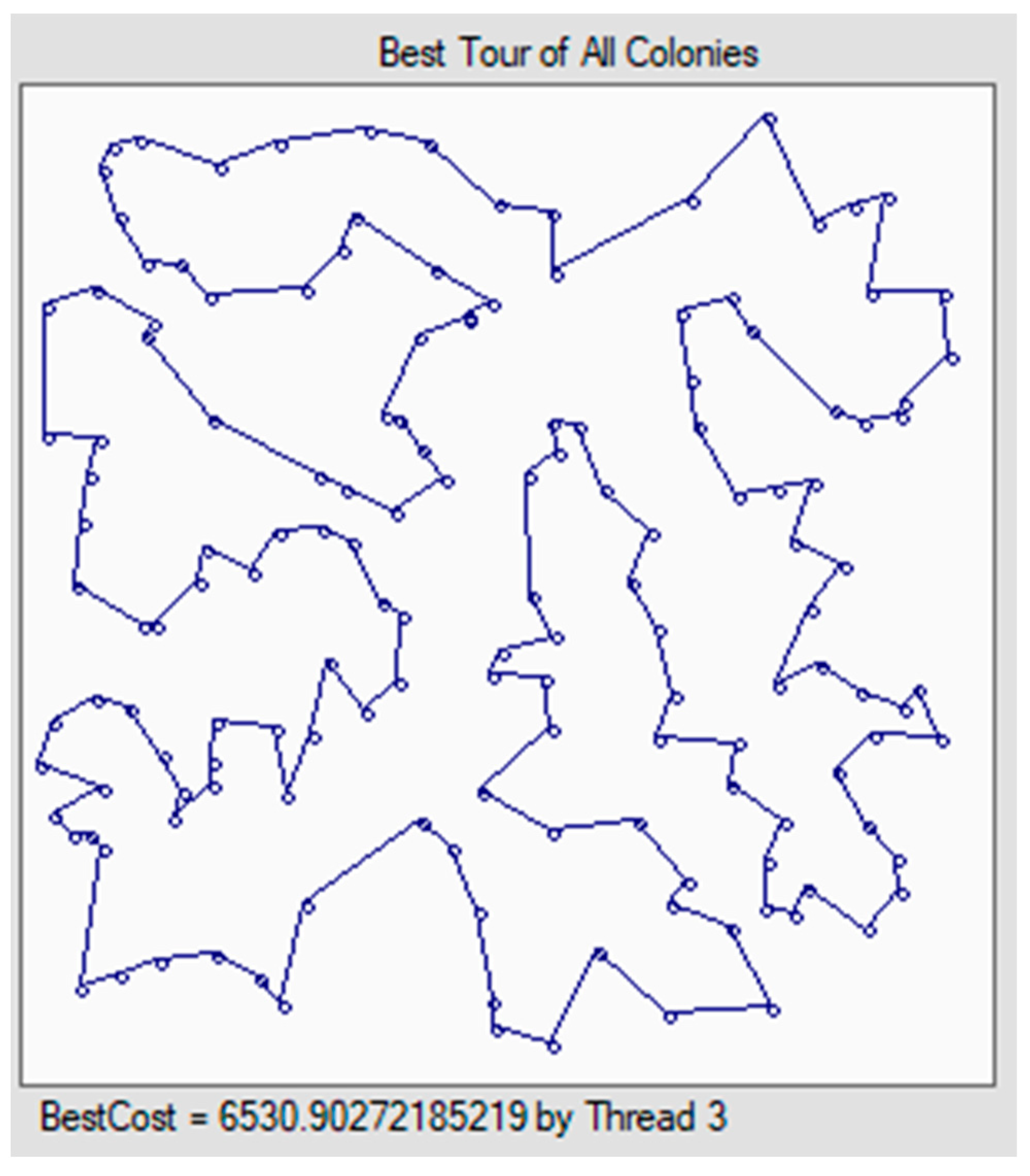
Our HPACO algorithm, as described in Section 5, obtained optimal results for TSPLIB benchmarks with up to 150 nodes, partitioning sub-graphs of 30–50 nodes. For example, for the 150-node Ch150 benchmark, the optimum value obtained by our HPACO algorithm was 6530.90. The optimal tour is shown in Figure 10.

• Optimal tour (Ch150): 1 98 103 82 95 107 5 100 143 97 146 26 75 18 142 85 65 132 137 50 55 58 141 83 56 90 46 92 54 138 134 131 32 23 38 67 43 109 51 20 25 110 81 29 86 135 70 108 102 114 99 19 2 37 6 28 9 42 120 47 139 40 53 118 24 12 116 101 41 57 39 127 69 36 61 11 148 130 17 66 60 140 117 129 27 31 123 74 13 106 91 119 68 128 45 71 44 64 112 136 145 144 147 49 72 80 14 122 77 133 15 78 21 150 115 4 104 22 125 149 62 3 113 10 94 88 121 79 59 16 111 105 33 126 52 93 124 35 96 89 8 7 84 30 63 48 73 76 34 87 1.

As can be seen from the progress of optimization in Figure 8, there are many Hamiltonian cycles possible that are near optimal (without intersecting edges). Without our parallel ACO algorithm which uses periodic cooperation between ant colonies, the optimization can easily get trapped in a local minimum. The six ant colonies depicted in Figure 8 used a slightly different evolutionary strategy (ACS or Max–Min) with different optimization parameters, which further aided the optimization as the algorithm progressed. Regarding the cooperation between ant colonies, we focused on the common paths taken by all colonies and, especially, on those path choices for which there was a disagreement between the colonies. The paths highlighted in Figure 9 were determined to be the common paths for the optimization of the Ch150 benchmark, with about 2000 iterations of the optimization process.

Figure 11 shows the progress of the different ant colonies during the optimization of the kroA200 benchmark as well as the common paths taken by the ant colonies during the optimization of kroA200 benchmark.

Table 1. Comparison of the tour lengths for different variations of the parallel ACO algorithm for TSPLIB benchmarks (* indicates the optimal value).

TSPLIB Benchmark	Exchange Policy APAL	Exchange Policy PIR	Exchange Policy ICDU	HPACO
Eli51	429.48	428.98	428.98	428.98 *
Berlin52	7544.36	7544.36	7544.36	7544.36 *
Rd100	7918	7910.39	7910.39	7909.10 *
Ch130	6156.27	6144.32	6114.02	6110.73 *
Ch150	6576.54	6547.32	6538.76	6530.90 *
kroA200	29,644.3	29,744.5	29,492.2	29,443
pr439	108,537	108,425	108,208	107,744
				(0.5% of Optimal)
d2103	81,518	81,469	81,296	81,283
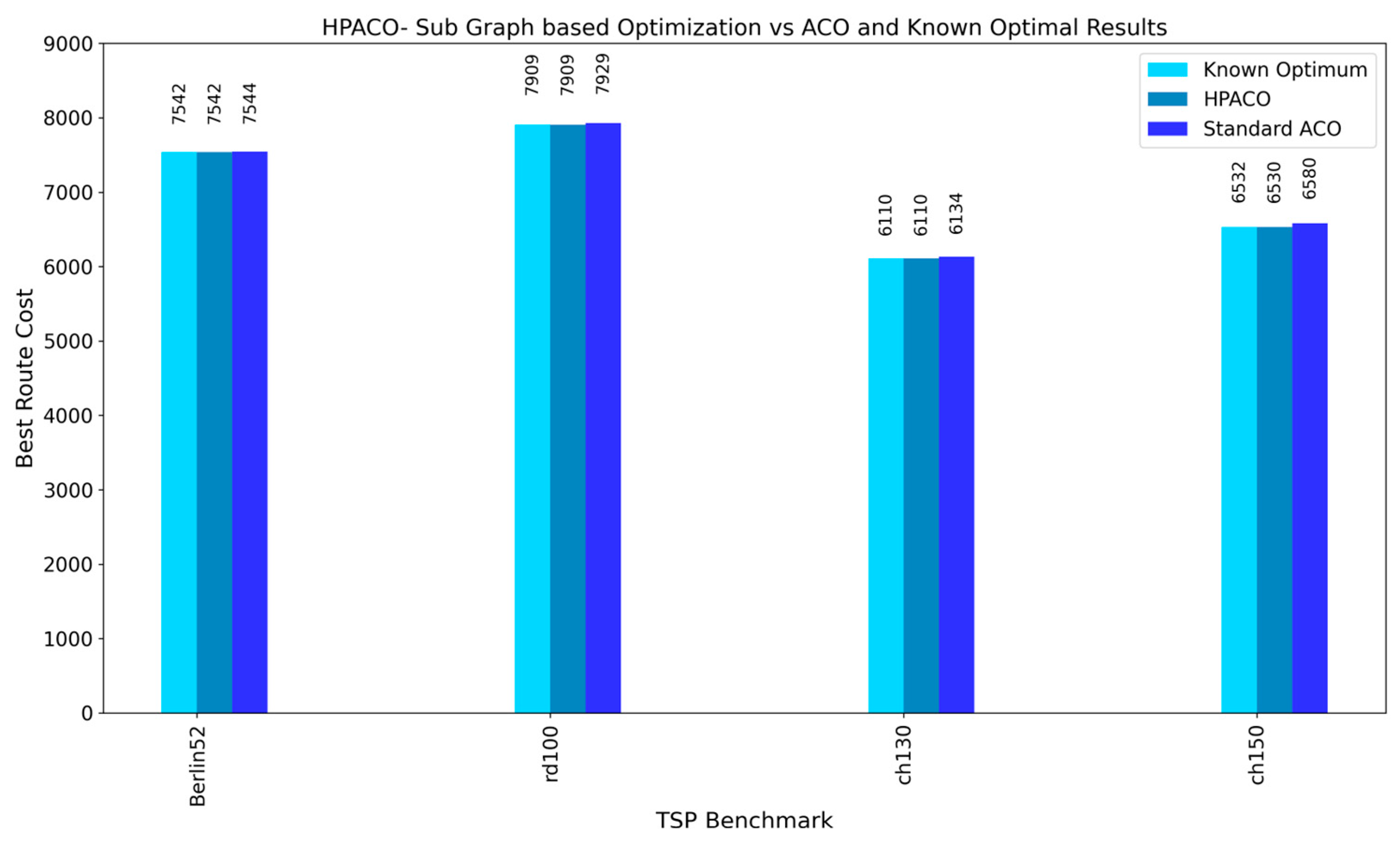
				(1.03% of Optimal)

shows the optimization results for the different pheromone exchange policies and the HPACO.

Evidently, the pheromone exchange policy ICDU, which increased the pheromone value on common links and reduced the pheromone value on uncommon links between two randomly selected colonies, produced better results when the entire tour was optimized without breaking it into sub-graphs. When we used the HPACO algorithm (as described in Section 5), it produced the best results. Note that this algorithm starts out as a parallel ACO on the entire graph, partially op-timizes it, then partitions it into disjoint sub-tours that are individually optimized in parallel, and finally the assembled sub-tours as a whole are optimized using the paral-lel ACO algorithm of Section 4. The optimization of the individual sub-tours can be carried out by a quantum computer implementing the QAOA algorithm. The size of the partitioned sub-tours then depends on the number of qubits available in the quantum computer. The number of nodes that can be currently optimized using a quantum computer is less than 50.

Figure 12 shows the results of the modified version of the HPACO algorithm, where after the partitioned sub-tours were optimized, only one iteration of k-opt (2-opt) was used on the entire graph. After determining a better swap of the nodes, the sub-graphs were generated again and optimized. This process was repeated. This implementation will allow for the most efficient execution time in a quantum environment. As can be seen from the algorithm in Figure 6, the modified HPACO algorithm obtained optimal results for benchmarks with up to 150 nodes, as observed for the HPACO algorithm in Section 5, but its execution was much more efficient, as can be seen from the code in Figure 7. For larger problems, the algorithm allowed achieving a result within 1% of the known optimal result for graphs containing up to a few thousand nodes.

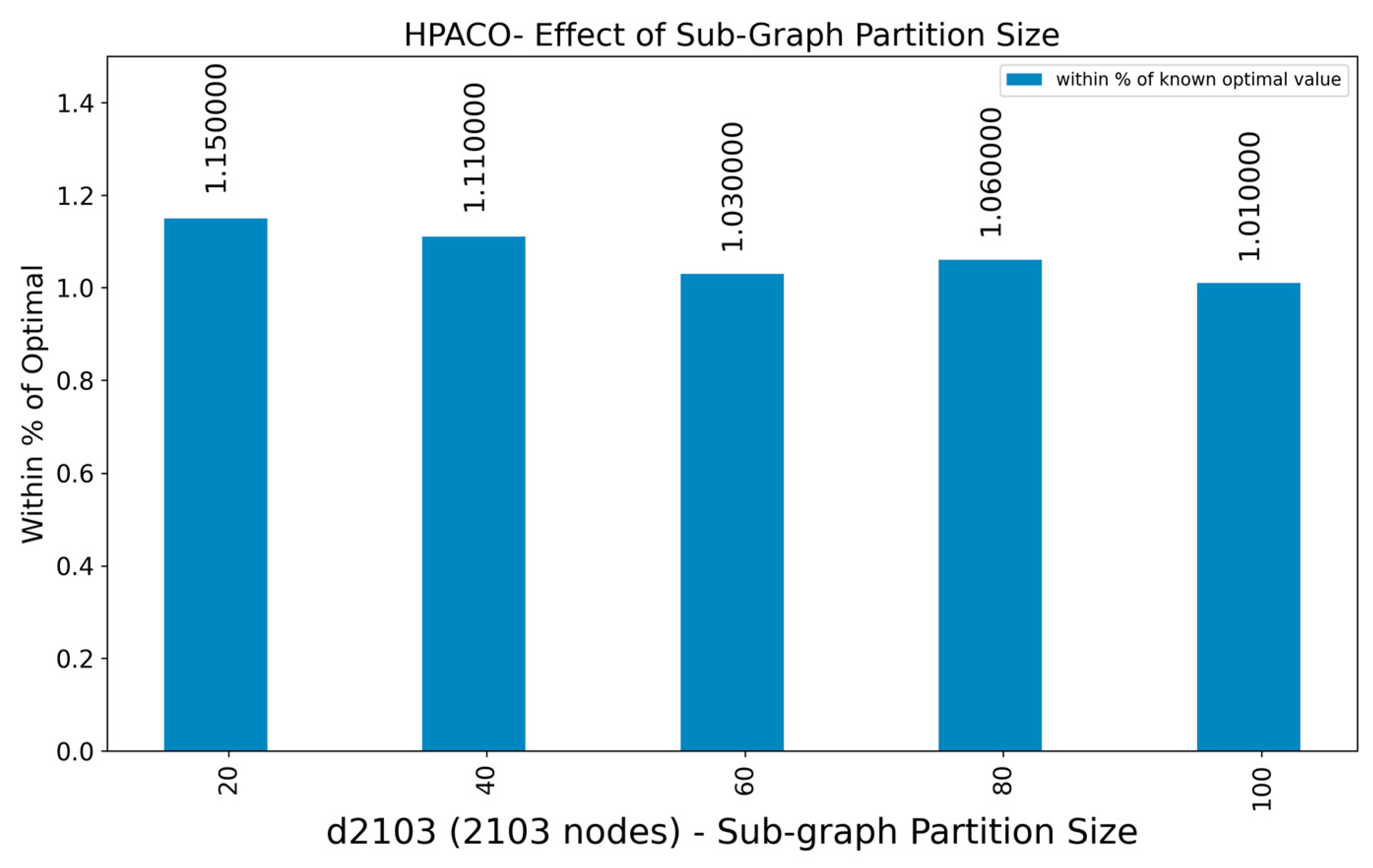
Figure 13 shows the effect of the sub-graph size on the tour cost with respect to the known optimal value for the d2103 benchmark with 2103 nodes. As can be seen, and as intuitively expected, as the sub-graph size increased, the tour cost decreased if the sub-graphs were optimal. In Figure 13, each sub-graph was optimized using the HPACO algorithm and executed for 500 iterations. If a quantum computer is available, then sub-graph optimization can be carried out instantaneously.

One of the interesting observations is that the difference in the optimization results between a sub-graph with a size of 20 and a sub-graph with a size of 100 was relatively small. This can be attributed to the capability of our parallel ACO algorithm that is able to overcome the less optimal merge of sub-graphs into a better optimization via periodic pheromone exchange between the colonies. Another advantage of our hybrid approach is that it can overcome, to some extent, the noise and decoherence issues occurring when using quantum computers for sub-graph optimization. In the case of an invalid tour returned by the quantum computer, we can substitute a duplicate or missing node in the Hamiltonian cycle and let the parallel ACO optimize the sub-graph.

7. Discussion

For TSP optimization, the search space for the optimal solution becomes complex as the problem’s size increases. We used the parallel ant colony system to explore the optimal path. Rather than just relying on brute force parallelization, our implementation periodically exchanges information in terms of pheromone value, so that the common paths taken by different colonies are likely optimal, and the exploration can be focused on paths for which the different ant colonies disagree. This is analogous to driving from one source address to a destination address, with highways most likely covering the shortest distance, and side roads leading to the highways offering alternatives routes. Our parallel ACO with pheromone exchange discovered this, as depicted in Figure 8 and Figure 9. All colonies shown in Figure 8 took the sub-paths indicated by solid lines in Figure 9. Further, as can be seen in Table 1, our approach achieved optimal routes for the TSPLIB benchmarks with sizes up to a few hundred nodes. The value of the optimal tour for some of the TSPLIB benchmarks is publicly available on the TSPLIB website; therefore, we could compare our results to these values. The optimal solution consists in the shortest path from the start node and back to it, visiting each node only once.

The ability of quantum computing to optimally solve NP-hard problems such as the TSP is great. An issue lies in the size of quantum computers, i.e., the large number of qubits needed. To address this issue, we developed a hybrid algorithm that allowed us to partition a large TSP in sub-graphs, which could then be optimized on a quantum computer. Even though partitioning approaches were attempted previously, the novelty of our approach lies in the assembly of individually optimized sub-graphs using a parallel ACO algorithm with pheromone exchange, so that the negative effect of partitioning on the overall optimization is overcome by the cooperating ant colonies, which allows refining the assembled solution. Furthermore, we performed iterations; we produced the partitions, assembled them, optimize them, then partitioned the system again until convergence. The size of each partition depends upon the available number of qubits.

In Figure 13, it can be seen that the larger the partition size, the better the overall optimization. Intuitively, the partitioning causes fixed end nodes in individual sub-graph optimization. By using a different partitioning in each iteration, as shown in Figure 14, we were able to overcome the slight loss in optimization quality.

Note that other metaheuristics can be used for the TSP instead of ACO; however, for the TSP, ACO allows an extremely quick execution time as compared to other metaheuristics. Further, it is easily parallelizable, and our parallel ACO uses cooperation between ant colonies to yield better optimization results.

8. Conclusions

We developed a new approach to solve large-scale combinatorial optimization problems, focusing on the Travelling Salesman Problem (TSP), using hybrid parallel computing and quantum platforms. While a quantum computer has the potential to solve large combinatorial optimization problems fast, it requires n² qubits for TSP-like optimization. Due to the relatively small number of qubits available in current quantum computers, a hybrid approach, in which sub-graphs of a TSP tour are executed on a quantum computer, and the results from the quantum optimization are combined for further optimization of the whole tour, is a viable approach. Since the simple optimization of aggregated locally optimized sub-graphs is prone to be trapped in a local minimum, we developed a parallel ACO with periodic pheromone exchange between ant colonies. Further, we repeated the above process by creating different sub-graphs from the previously optimized iteration, so that the boundaries of the adjacent sub-graphs changed, which avoiding obtaining a sub-optimal solution.

Our results are encouraging. We obtained optimum results for benchmarks with less than 150 nodes, and within 1% of the optimal solution for benchmarks with a few thousand nodes. The execution time required by our parallel ACO algorithm increases significantly for TSPs with a large number of nodes, as many iterations are needed to arrive at a good solution. If the sub-graphs are solved using the ACO, instead of a quantum computer, the execution time is of the order of a few days for problems involving a few thousand nodes. Thus, quantum computing can optimally solve some NP-hard problems, such as TSP. However, as the qubit size increases in the newer quantum processors, and quantum computers become widely accessible, our hybrid approach presented herein will allow solving relatively large optimization problems.

Recently, the use of AI techniques to advance the optimization of the TSP has been attempted via Graph Neural Networks (GNNs), e.g., as reported in a work [36] that attempted to speed up local search via GNNs. This is needed to keep the real-time execution constraint. Our future work will attempt to use a GNN-based local search in our hybrid framework to further improve the execution time in place of the k-opt based local search that we currently use.