Abstract
This article proposes a design method for a “slow connect”-type clutch with unequal-length wedges, which ensures the wedges’ wear life while improving the engagement reliability of the clutch. A finite element model of the dynamics of an unequal-length wedge clutch was constructed. Compared with an ordinary clutch, the output shaft impact was reduced by more than 30%, and the response time and engagement time were reduced by approximately 50%. It was found that for every 0.005 mm increase in the length of the middle section of the wedge, the critical detachment speed of the wedge increased by approximately 2.2%. Finally, the excellent engagement response performance of the unequal-length wedge slant support clutch was verified through experiments.
1. Introduction
The slant support-type overrunning clutch has a large bearing capacity and stable power transmission and can adapt to different working conditions [1]. NASA began studying high-speed aviation slant support clutches in the 1970s. Kish et al. [2] used the high-speed clutch in the helicopter as the research object, proposed a preliminary dimension design method and stress analysis at 20,000 rpm, and applied it in the design of the UH-60A Black Hawk helicopter. Chen et al. [3] used a combination of finite element analysis and experimental tests to study the influence of wedge contour changes on contact performance and transmitted torque but did not study the disengagement process. Lowen et al. [4] established a damping model with variable preload displacement and constant amplitude attenuation ratio, based on which an analytical model of the overrunning clutch was constructed, ignoring the influence of wedge contour changes. Liu et al. [5] established a new multi-circular-arc wedge-block oblique-braced clutch and proposed an improved geometric variable coordination method to improve the model accuracy, but no experimental verification was carried out. Huang et al. [6,7] established a piecewise-wedged dynamic model for a diagonal clutch-quasi rigid rotor system (SC-QRRS, SPRAG clutch-quasi rigid rotor system), based on which combined dynamic models of an SC-QRRS with multi-arc and logarithmic spirals were established. Qing et al. [8,9], aiming at the problem of the wear of the wedge and the inner and outer rings due to the contact cyclic force, established the wear formula by an analytical method and proposed the failure criterion method of the wear limit value but did not carry out the optimization study of the dynamic engagement. Liu et al. [10], considering factors such as the meshing stiffness of the time-varying gears, static transmission error, and nonlinear backlash, established the transmission system model of a double-shaft assembly of an inclined brace clutch; the dynamic response of the inclined-brace clutch under different operating conditions was studied. Yan et al. [11] established a four-degree-of-freedom nonlinear transverse and torsional vibration model of a two-shaft system with a diagonally braced clutch and provided a solution for the dynamic design and vibration control of the system, but the dynamic characteristics of clutch dynamic engagement and disengagement were not studied. Wang [12] established a model of the center of gravity of a wedge block and studied its influence on the contact force, engagement, and release performance of an inclined-brace clutch. Wen et al. [13] studied the wear performance of a clutch support spring in an overrunning state, which provided a reference for the design and optimization of support springs. Huang [14] established an analytical model of the internal interaction of multi-circular-arc surfaces in the process of engagement and further proposed the analytical modeling and optimization of a logarithmic-surface clutch with profile modification; the possibility of extrusion failure and low-cycle fatigue of the upper and lower cams was reduced. Tao et al. [15] analyzed the law of spring fatigue fracture caused by abnormal wear and extrusion of an inclined stay clutch from the perspective of macro and micromorphology. Ma et al. [16] improved the clutch engagement failure problem by adjusting the spring parameters, ignoring the influence of wedge design on the engagement process. Xue et al. [17] proposed a new double-arc sprag overrunning clutch, which overcomes the disadvantages of poor transmission capacity and low torsional rigidity of transmission devices but lacks quantitative analysis between contact stress and fatigue life. Liu et al. [18] evaluated the differential engagement time and impact load of a high-speed oblique-braced clutch, which can provide a reference for the impact load estimation of similar clutches. It includes, primarily, the analysis of dynamic and static performance and has formed a complete standard design method of centrifugal-combined inclined-brace clutches.
In summary, the impact of the centrifugal off-type inclined-braced clutch from the overrunning state to the transition state of the output shaft is excessively large and the engagement is unstable. The proposed method can improve the critical speed of the wedge by changing its center of gravity and maintaining contact between the wedge and inner ring at the rated speed. This paper designs an oblique-supporting clutch with unequal-length wedges to realize the “slow-connecting” demand of oblique-supporting clutches to reduce the impact during the differential engagement process and eliminate wedge-block wear during the overrunning process.
The rest of the paper is organized as follows: Section 2 introduces the working principle of the slant support clutch and studies the main contents and methods of the design of unequal wedge blocks. Section 3 details the design of various wedge layouts and analyzes the differential engagement dynamic characteristics of the clutch. Section 4 studies the response of the clutch in a critical disengagement state. Section 5 verifies the effectiveness of the model through critical detachment experiments. The total research flowchart of this article is shown in Figure 1.
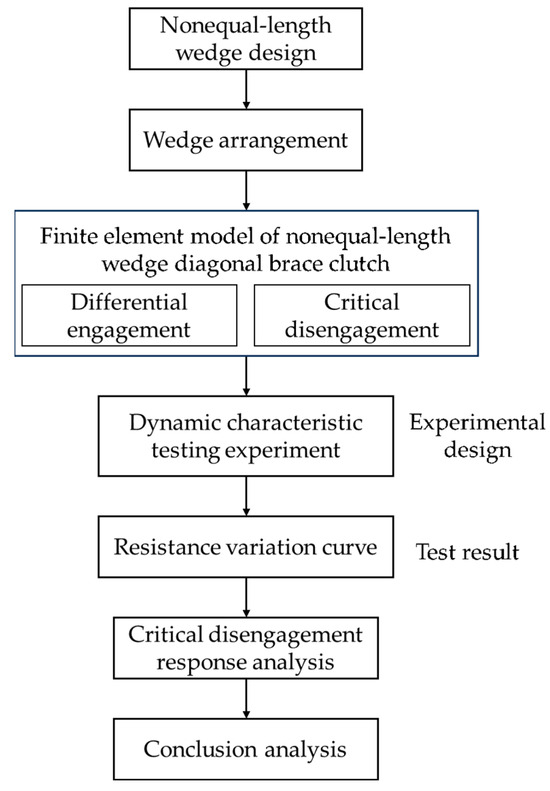
Figure 1.
Total research flowchart of slow coupling clutch.
2. Unequal-Length Wedge Diagonal Brace Clutch Design
2.1. Working Principle of Unequal-Length Wedge Diagonal Brace Clutch
“Non-isometric” wedge diagonal clutch design refers to a nonstandard design method of two or more sets of wedges with different geometric dimensions in one clutch. By modifying the parameters, such as the length of the middle segment of the wedge and the number of wedges, the diagonal brace clutch wedge presents a “segmented engagement” effect. This reduces the overshoot of the diagonal clutch-output shaft speed and extends the diagonal clutch engagement time. Owing to its engagement characteristics, the new clutch is called a “slow coupling”-type diagonal clutch.
Figure 2a shows a 3D view of the sprag clutch. When a centrifugal-disengagement diagonal brace clutch is in the outer-ring overrun state, the wedge is subjected to the centrifugal moment generated by the centrifugal force under the non-inertial reference frame, and the inner ring and wedge tend to separate. As the rotational speed of the outer ring increases, the wedge completely detaches from the inner ring. When the differential engagement of the slow coupling clutch is made, the theoretical engagement process starts from the clutch part of the wedge contacting the inner and outer rings at the same time and ends with the complete torque transmission of the clutch; the entire differential engagement process is displayed in Figure 2b. Stage A: the clutch starts differential engagement; Stage B: the inner ring speed increases, the outer ring speed decreases, and the difference between the inner and outer ring speeds causes the clutch part of the wedge to experience engagement conditions; Stage C: part of the wedge is engaged, which can transmit a small torque between the inner and outer rings, and the speed of the outer ring continues to decrease such that other wedges contact the inner ring and produce joint conditions; and Stage D: the diagonal clutch is fully engaged.
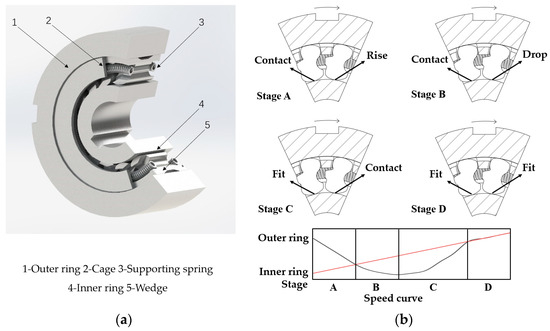
Figure 2.
(a) 3D view of the clutch; (b) differential engagement process of slow coupling clutch.
2.2. Unequal-Length Wedge Design
2.2.1. Wedge Difference Quantity
The wedge difference is an important part of unequal-length wedge design and directly influences the clutch wear life, impact torque, and critical off speed, defined as the difference in the middle section length of the different wedges. The unequal-length wedge in the clutch is divided into a short wedge block and long wedge block, where the short wedge block is the original wedge block in the clutch and the long wedge block is the wedge block obtained by extending the middle segment of the wedge block. The shape and size of the upper and lower cams are identical; only the length of the middle segment and distance between the center of the cam on the wedge and center of the lower cam on the wedge are different, as indicated in Figure 3.
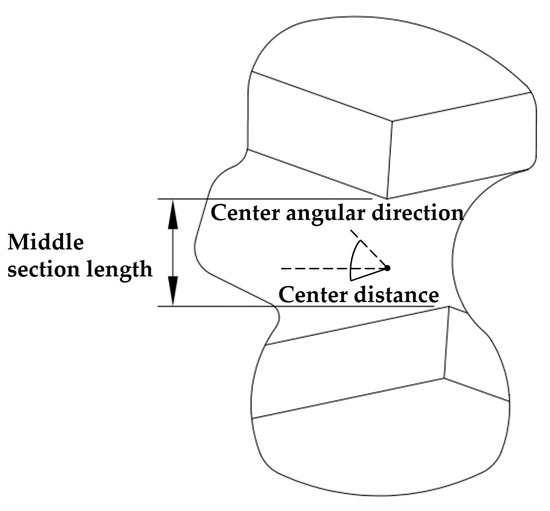
Figure 3.
Design of unequal-length wedge difference.
The materials for the inner and outer rings, cage, and wedge of the clutch are 16Cr3NiWMoVNbE-YJ.0225, 1Cr11Ni2W2MoV, and GCr15, respectively. For engineering applications, the precision of the wedge can reach IT4 accuracy standard or higher with a change in the clutch. The length of the middle section varies by about 0.005 mm, the length of the wedge is 6.100 mm, wedge width is 4.540 mm, and center distance is 0.324 mm. Therefore, 0.005 mm is used as the gradient for the wedge differential design. To investigate the influence of the wedge difference on the clutch differential engagement characteristics, five wedges were designed, as listed in Table 1.

Table 1.
Main design parameters of five different wedges.
2.2.2. Wedge Distribution
The wedges are uniformly distributed in the circular direction before the inner and outer rings in the inclined stay clutch; there are numerous uniform or nonuniform arrangements for two or more wedges when different wedges are used, which influences the dynamic characteristics of the diagonal clutch. There is also a large coaxiality deviation between the incomplete and even distribution of wedge blocks and the assembly of the inclined stay clutch, which leads to the wear of specific wedges in the clutch and causes unexpected structural damage to the inner and outer rings, greatly reducing the operating life of the clutch. Considering the design requirements for the life and smooth operation of the inclined-brace clutch, all wedges of unequal length were assembled in a uniform manner.
2.2.3. Number of Wedges
Based on a certain type of conventional clutch, the number of wedges was set to 15. A multibody dynamics simulation was performed by changing the number of wedges, and the influence of the number of wedges on the differential engagement characteristics of the clutch was obtained. Two different wedges were combined and arranged to design the model of an unequal-length wedge-inclined supported clutch. As indicated in Figure 4, the 15 wedges were divided evenly into three parts, and the wedges in each part were arranged in the same manner. Taking one of the sectors as an example, we could obtain 20 different ways of arranging the wedges by replacing the wedges in the small sectors numbered 1–4 with Wedges A–E; that is, 20 models of unequal-length wedge clutches were designed.
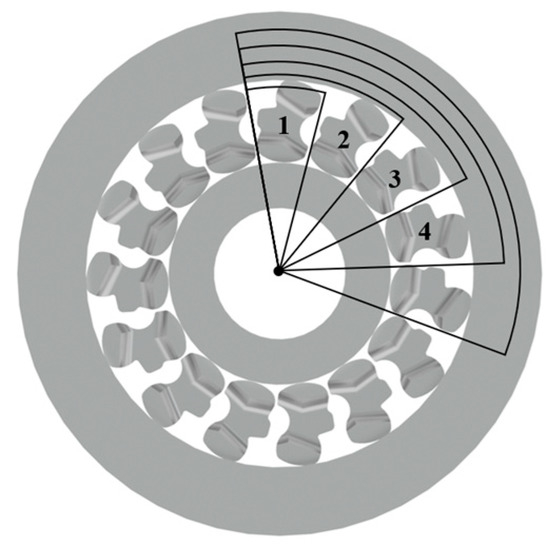
Figure 4.
Schematic of unequal-length wedge arrangement.
Based on the method mentioned above, a model of an inclined-brace clutch with three groups of unequal-length wedges was built; Wedges B and D were used as examples. The concrete arrangements are listed in Table 2. The corresponding wedges were replaced by Wedges B or D; the remainder were conventional wedges.

Table 2.
Design of four kinds of wedge slant support clutch.
2.2.4. Verification of Design Parameters
It is difficult to calculate the different wedges in a diagonal clutch; it was assumed that a single wedge was used in each diagonal clutch to validate the clutch design parameters. The clutch performance parameters of different types of wedges were obtained using the calculation method in [19], as listed in Table 3. The force on the wedge is displayed in Figure 5, which primarily includes the spring support force Fr, contact forces Fi and Fo of the inner and outer rings, respectively, and centrifugal force Fc. O and O′ are, respectively, the center of the upper and lower arc surfaces of the wedge, and A and B are the contact points between the wedge and the inner and outer ring. The included angle between AB and AO is the external wedge angle W, and the angle between AB and O′ is the internal wedge angle V.

Table 3.
Performance parameters of different wedge-block inclined-support clutches.
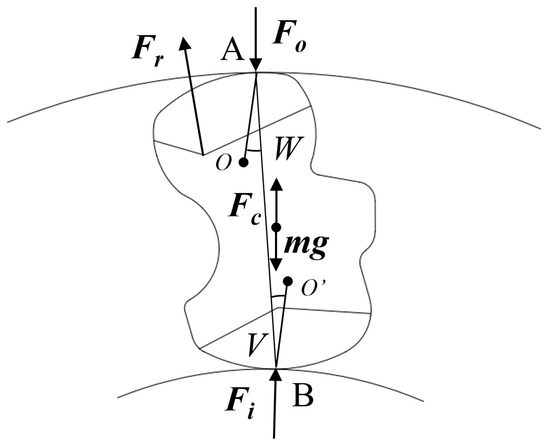
Figure 5.
Schematic diagram of wedge force analysis.
According to the ISO standard [20], four aspects of the clutch wedge—angle, lift, PCE continuous output, and strength constraints—were verified, and all wedges met the usage requirements. In addition, considering the situation where certain wedges engage first during the engagement process of the “slow connect”-type clutch, the primary consideration is the stability of clutch engagement. The calculation of the limit situation for certain wedges during engagement verified that certain wedges could fully transmit torque near the limit angle. After the calculation, the required number of wedges for complete torque transmission under the limit conditions of each modified wedge was as follows: the minimum number of Wedges A, B, and C was four. The minimum number of Wedges D and E was five.
It can be observed that during the dynamic engagement process of the “slow connect”-type clutch, the initial torque transmission capacity of certain long wedges could possibly not be sufficient, resulting in the clutch exceeding the limit angle, causing the PCE phenomenon and significant wear and impact. Therefore, in subsequent optimization design, the minimum number of wedges in the table above should be ensured. However, under actual working conditions, within an extremely short period of time after certain wedges are engaged, the remaining wedges are fully engaged, and further simulation analysis is required for their specific differential working characteristics.
3. Analysis of Dynamic Characteristics of Differential Engagement of Slant Support Clutch
3.1. Establishment of Dynamic Model for Clutch Differential Engagement
The engagement process of the clutch is simulated by RecurDyn, as its object-oriented modeling language is beneficial to the nonlinear, high-speed, and large deformation dynamic models of complex mechanical systems. The main steps were as follows: (1) we imported the 3D model of the clutch; (2) we defined the rotation constraints for the inner ring, outer ring, and cage; (3) we defined the contact between the wedge block and inner and outer ring wedge block and the cage as well as between the wedge blocks; (4) we calculated the GeoSur contact between the wedge and inner and outer rings using the impact method for parameter input and used the default collision parameters for the calculation between the other components; and (5) we added a constant resistance torque to the outer ring to simulate the load torque on the clutch outer ring. The outer ring is the active component in the overtaking state, whereas the passive component in the engagement state applies the active speed to the outer ring in the overtaking state. When the inner ring speed reaches 90%, the outer ring rotates freely under the load. The inner ring is a passive component in the overtaking state and an active component in the engaged state. Through the above steps, the slant support clutch simulation models were obtained, as displayed in Figure 6.
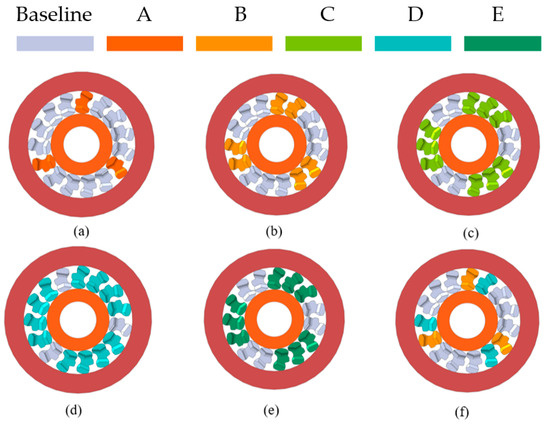
Figure 6.
Multibody dynamic model of partial clutch with unequal-length wedges: (a) three A wedges; (b) six B wedges; (c) nine C wedges; (d) twelve D wedges; (e) nine E wedges; (f) three B and three D wedges.
3.2. Analysis of Simulation Results
3.2.1. Conventional Slant Support Clutch
The time-domain curves of the internal and external ring speeds of the conventional slant support clutch during engagement are displayed in Figure 7. It can be observed that a long period elapses from the first synchronization of the inner and outer ring speeds to the maximum speed difference, which defines the engagement response time. The speed of the outer ring of the clutch suddenly changes at approximately 0.528 s. The maximum speed difference between the inner and outer rings was 74.52 rad/s and the instantaneous angular acceleration of the outer ring was 7673.64 rad/s2. Based on the analysis of the wedge pose during the simulation, the following can be concluded.
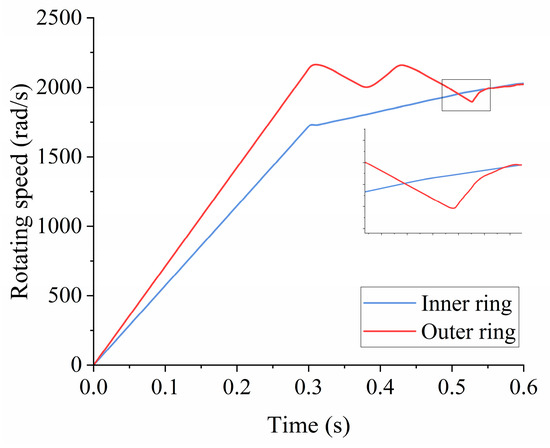
Figure 7.
Time domain curve of speed of inner and outer rings of conventional slant support clutch.
- Approximately 0.1 s after the speed of the clutch outer ring is withdrawn, the speed of the inner and outer rings remains the same. During this period, the speed decrease rate of the outer ring of the clutch remains constant until 0.526 s. At this point, the wedge is completely detached from the inner ring until the speed of the outer ring decreases to approximately 1900 rad/s and the bonding conditions are re-established.
- The phenomenon of PCE on the wedge block is speculated to be caused by the excessive deformation between the inner and outer rings of the clutch and wedge block.
- Owing to the excessive impact, the wedge deflects further, which is similar to the phenomenon of overload deflection in an all-phase clutch. There is always a certain difference between the speed of the outer ring and that of the inner ring of the clutch, and the torque transmission performance of the slanted support clutch declines significantly.
- During the simulation process, there was an overload deflection phenomenon, and under actual working conditions, the clutch could have been in a failed or damaged state and, thus, unable to meet the usage requirements.
3.2.2. Two Sets of Unequal-Length Wedge Slant Support Clutch
The differential engagement dynamic model of the unequal-length wedge slant support clutch can be solved, and the time-domain diagram of the differential engagement inner and outer ring speed curves can be obtained, as displayed in Figure 8, A–F corresponds to different wedge arrangement schemes in Figure 6. Except for the slant support clutch with the A wedge, the engagement response duration of all other ”slow contact” clutches was extended; that is, the speed of the outer ring dropped freely first. When the speed was consistent with that of the inner ring, certain wedges were engaged to transmit torque, delaying the rate of decline of the outer ring speed. The remaining wedges were then engaged, and the speeds of the inner and outer rings remained consistent.
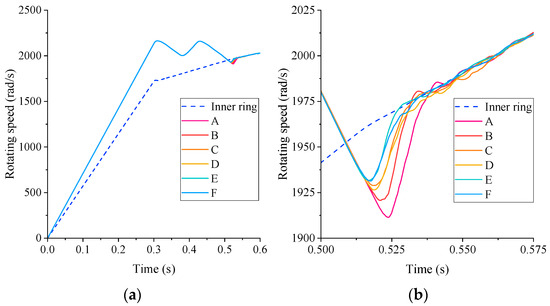
Figure 8.
Time domain curve of speed of inner and outer ring of slant support clutch for two groups of unequal-length wedges: (a) the entire process of jointing; (b) partial enlarged view.
The differential engagement performance of the slanted support clutch with unequal-length wedges was comprehensively evaluated in terms of response time, engagement time, and instantaneous angular acceleration. Figure 9 shows the performance of the slanted support clutch with five wedges under different wedge numbers.
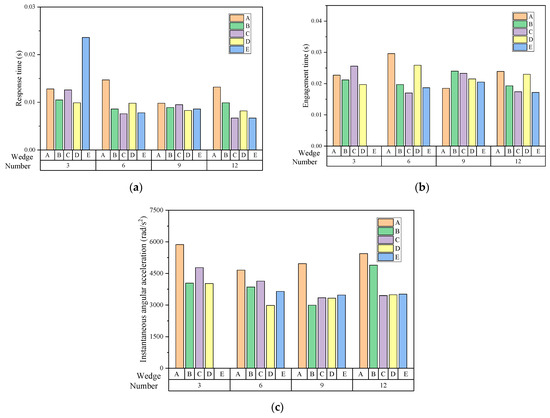
Figure 9.
Performance of slant support clutch with five wedges under different wedge numbers (a) response time; (b) engagement time; (c) instantaneous angular acceleration.
The difference in clutch differential engagement performance with different wedge numbers was obtained by comparing the response time, engagement time, and instantaneous angular acceleration, as indicated in Figure 10 and Figure 11.
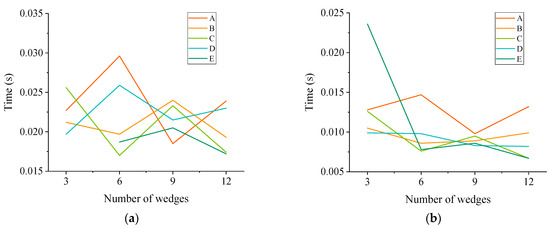
Figure 10.
Dynamic characteristics of clutches under different numbers: (a) engagement time; (b) response time.
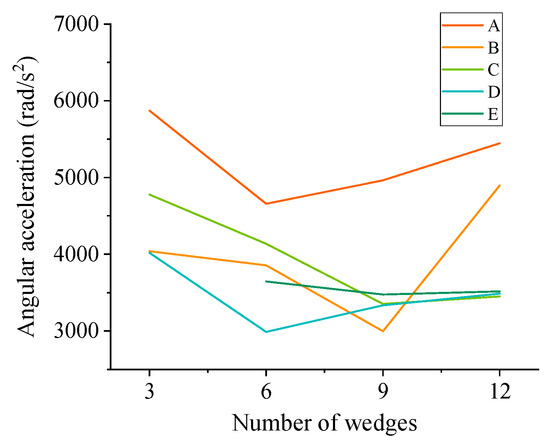
Figure 11.
Instantaneous angular acceleration curve of clutch outer ring under different numbers.
It can be observed from Figure 10 that except for the “slow connect” slant support clutch with three E wedges, which cannot transmit torque owing to an insufficient number of long wedges, the other unequal-length wedges arranged and combined function normally. A comparison of the data between the same type of wedges revealed that the response and engagement times of the clutch decreased as the number of wedges increased. By comparing the data of the different wedges, it was found that the response and engagement times of the clutch demonstrated a decreasing trend with an increase in the length of the middle section of the wedge. The relationship between the instantaneous angular acceleration of the clutch outer ring and number of wedges was analyzed, as displayed in Figure 11. It can be observed that as the number of wedges increased, instantaneous angular acceleration first decreased and then increased. Comparing the simulation results between different wedges, it can be observed that as the length of the middle section of the wedge increased, the instantaneous angular acceleration of the outer ring decreased. A further comparative analysis of the differences between clutches using different wedges is presented in Table 4.

Table 4.
Average differential engagement performance using different wedges.
It can be observed from Table 4 that, based on the simulation data of conventional clutches, the instantaneous angular acceleration of the outer ring of the “slow”-type slant support clutch pair was reduced by approximately 32% to 55%, response time was reduced by approximately 33% to 56%, and engagement time was reduced by approximately 39% to 50%. This improved the long engagement response times of conventional slant support clutches and effectively improved the dynamic performance of differential engagement. As the length of the middle section of the wedge increased, the clutch engagement time decreased significantly, and its instantaneous angular acceleration also exhibited a significant downward trend. The average response time decreased by approximately 34%, average engagement time decreased by approximately 17%, and average instantaneous angular acceleration of the outer ring decreased by approximately 34%.
3.2.3. Three Sets of Unequal-Length Wedge Slant Support Clutch
The analysis method for the differential engagement performance of the slanted support clutch with three groups of unequal-length wedges was the same as above. Four different wedge combination modes, G–J, respectively, were designed. The time-domain curves of the internal and external ring speeds displayed in Figure 12 were obtained through simulation; a comprehensive performance comparison is presented in Table 5.
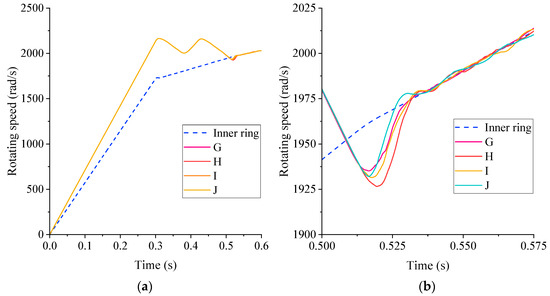
Figure 12.
Time domain curve of speed of inner and outer rings of slant support clutch with three groups of unequal-length wedges: (a) the entire process of jointing; (b) partial enlarged view.

Table 5.
Performance characterization parameters of slant support clutch with three sets of wedges.
Comparing the results in Table 5, it can be concluded that there is no significant relationship between the instantaneous angular acceleration value of the clutch outer ring and number of B wedges when using D wedges. The instantaneous angular acceleration of the clutch outer ring using three B wedges increased by 17%; the instantaneous angular acceleration of the clutch outer ring using six B wedges decreased by 3%. After increasing the number of D wedges to six, the instantaneous angular acceleration of the clutch outer ring significantly decreased. Compared with the slant support clutch with only six D wedges, the relative error of the instantaneous angular acceleration of the outer ring of the clutch with 3 B wedges was less than 1%, and the difference of the instantaneous angular acceleration of the outer ring of the clutch with six B wedges was approximately 8%.
In summary, it was found that using a longer wedge (D wedge) and adding a shorter wedge (B wedge) had a smaller influence on the differential engagement performance of the clutch. Considering that in the process of design, assembly, and use, an excessive number of wedge types leads to engineering problems, such as assembly difficulties and spare part warehouse redundancy, two different wedges are used in the subsequent research to design the “slow connect”-type slant support clutch.
4. Dynamic Characteristics Analysis of Critical Disengagement of Slant Support Clutch
4.1. Critical Disengagement State of Clutch
As shown in Figure 2, the center of mass of the wedge is at the flange side of the connection line A and B, between the wedge and the inner and outer rings, i.e., opposite to the joint direction. Therefore, the torque generated by the centrifugal force of the wedge is opposite to the pre-joint torque generated by the ring spring. Considering that the closing moment of wedge to outer ring contact point A is zero, there is:
where Lc, Lr, Lg, and Li are the arms of Fc, Fr, mg, and Fi with respect to the outer contact point A, respectively. As there is no large displacement of the wedge under the overrun state, the torque of the ring spring Mc and the heavy torque Mg can be regarded as fixed values. According to the above formula, with the increase in the centrifugal force Fc, the contact force Fi between the wedge and the inner ring gradually decreases until Fi = 0, the outer ring reaches the critical clutch disengagement speed.
The theoretical model in [21] was used to solve the critical disengagement speed of the slanted support clutch in the overrunning state; the wedge parameters were substituted to obtain the above formula. The calculation results are listed in Table 6. There was a significant positive correlation between the theoretical critical disengagement speed of the clutch and length of the middle section of the wedge; that is, the critical disengagement speed of the wedge increased with the length of the middle section of the wedge. Increasing the speed at which the wedge disengages can improve the differential engagement performance of the clutch. The gravity of the wedge had a significant influence on its critical detachment speed, with the critical detachment speed band accounting for approximately 5% of the total critical detachment speed value.

Table 6.
Theoretical critical disengaging speed of wedge block.
4.2. Simulation Analysis of Critical Disengaging Speed
In the overrunning state of the slanted support clutch, friction occurs between the outer ring and wedge before it is fully disengaged. The wedge accelerates to rotate in the same direction under the force of the outer ring. With an increase in the speed, the centrifugal force of the wedge increases, and the wedge further compresses the outer ring. As the wedge gradually rises, the friction force with the inner ring gradually decreases and, finally, completely disengages from the inner ring. Therefore, by simulating and reading the moment when the contact force between the clutch wedge and inner ring is zero, it can be determined that the clutch wedge and inner ring have already disengaged. At this point, the instantaneous speed of the clutch exceeds the critical disengagement speed. Using the dynamic model in Section 3.1, with the outer ring of the clutch as the active component, the loading curve of the model is displayed in Figure 13.
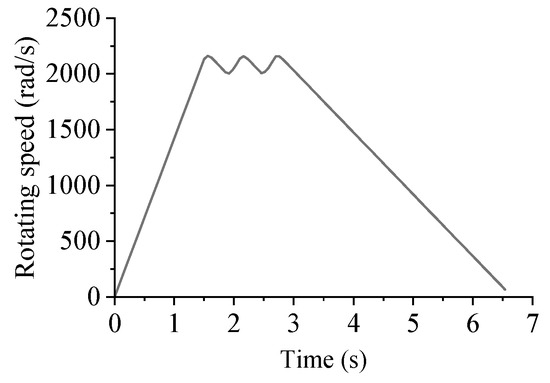
Figure 13.
Critical exceeding simulation loading curve.
Simulation analysis was performed on 15 wedges of six clutches, and the critical disengagement speed change rates of the different wedges were calculated based on the simulation results of the original wedges. The results are summarized in Table 7.

Table 7.
Critical detachment speeds of different wedges.
By comparing and analyzing the data in Table 6 and Table 7, it was found that the simulated critical detachment speed of the wedge was within the range calculated theoretically, with an error of no more than 4%. For every 0.005 mm increase in the length of the middle section of the wedge, the critical detachment speed of the wedge increased by approximately 2.2%.
5. Dynamic Characteristic Testing Experiment
By comparing the data in Section 3.2 and Section 4.2, it can be observed that the differential engagement performance of the slanted support clutch with six E wedges was superior; therefore, the slanted support clutch was selected for the experiment. The unequal-length wedge slant support clutch was composed primarily of nine original wedges, six No. 5 wedges, a cage, the inner ring of the clutch, end caps on both sides, the outer ring of the clutch, two support springs, and two 6008 zirconia ceramic bearings. The explosion and physical diagrams of the wedge are displayed in Figure 14 and Figure 15, respectively.

Figure 14.
Exploded view of “slow”-type slant support clutch model.

Figure 15.
Comparison of unequal-length wedge blocks: short wedge block (left) and long wedge block (right).
A DC resistance tester was connected to the inner and outer rings of the clutch using an electric brush. The resistance values between the inner and outer rings of the clutch were collected in real time; the sudden change range of the resistance values of the inner and outer rings of the clutch was further subdivided by the target speed of the outer ring of the clutch. Gradually, the load was increased in increments of 10 rpm, and the resistance values between the inner and outer rings were recorded at each speed. The relationship between the resistances of the inner and outer rings of the clutch and the speed of the outer ring was obtained experimentally, as indicated in Figure 16.
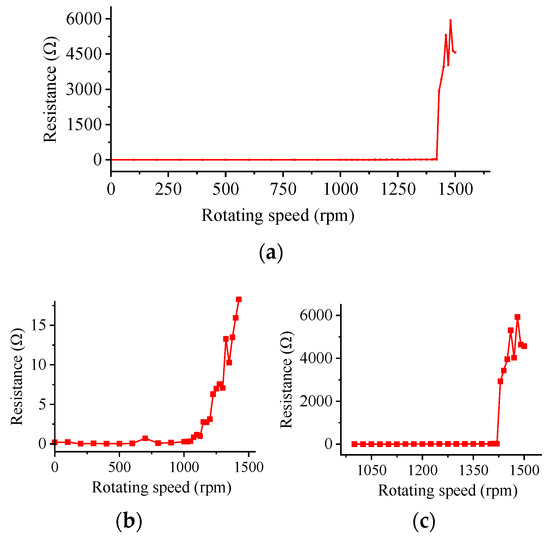
Figure 16.
(a) Curve of resistance of inner and outer rings of clutch as function of speed, (b) low-resistance zone, and (c) high-resistance zone.
As indicated in Figure 16, the overrunning process of the clutch had a segmented release feature. At approximately 1100 rpm, the resistance between the inner and outer rings increased to greater than 1 Ω, indicating that the wedge between the inner and outer rings was gradually disengaged. When the outer ring speed reached 1325 rpm to 1420 rpm, the resistance slowly increased from 15 Ω to approximately 20 Ω. When the outer ring speed was 1430 rpm, the resistance demonstrated a geometric increase, increasing to approximately 3000 Ω and increasing to approximately 5000 Ω at approximately 1500 rpm. Using the analytical method described in Section 4.1 to calculate the clutch model after expansion and contraction, the theoretical values of the theoretical critical detachment speed of the wedge were obtained, as listed in Table 8.

Table 8.
Comparison between the critical detachment speed of the wedge and experimental data.
In summary, the critical disengagement speed of the conventional slant support clutch was approximately 1325 rpm; that of the slant support clutch with an unequal-length wedge was approximately 1430 rpm. In addition, the critical disengagement process of the unequal-length wedge clutch exhibited a segmented effect. The slanted support clutch with an unequal-length wedge had a wider critical disengagement speed range than the conventional slanted support clutch, and the differential engagement performance was significantly improved.
6. Conclusions
Aimed at the problems of long response time and the large impact of the output shaft of centrifugal-disengaged slant support clutches in actual working conditions, this paper proposed a design method for a slant support clutch with unequal-length wedges to achieve the goal of “slow connection” in the process of differential engagement.
- The design parameters of unequal-length wedge were provided, and the wedge angle constraint, lift constraint, PCE constraint, and other conditions were verified. A series of “slow contact” clutch design schemes were determined, and the engagement performance of the unequal-length wedge slant support clutch was verified through experiments.
- Under the condition of using the same type of wedge, the instantaneous angular acceleration of the outer ring of the “slow connect”-type clutch demonstrated a significant trend of first decreasing and then increasing with the increase in the number of long wedges. The response and engagement times of the clutch demonstrated a decreasing trend with an increase in the number of long wedges. Under the same number of wedges, the instantaneous angular acceleration, clutch response time, and engagement time of the outer ring of the clutch decreased with an increase in the wedge difference.
- There is a direct proportional relationship between the wedge difference and critical detachment speed. For every 0.005 mm increase in wedge difference, the critical detachment speed of the wedge increased by approximately 2%. The effectiveness of the critical detachment mathematical model was demonstrated through experimental verification.
Author Contributions
Conceptualization, C.Z.; methodology, J.W. and M.L.; software, X.W.; supervision, C.Z. and H.Y.; validation, X.W. and M.L.; writing—original draft, J.W.; writing—review and editing, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the National Natural Science Foundation of China (Grant no. 52075552).
Data Availability Statement
All data, models, and codes generated or used in the study are included in this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xue, H.; Liu, G.; Yang, X.; Han, B. Key technologies research of helicopter transmissions. AMM 2015, 743, 55–60. [Google Scholar] [CrossRef]
- Kish, J. Helicopter Freewheel Unit Design Guide; [Department of Defense, Department of the Army], Army Research and Technology Laboratories, Applied Technology Laboratory: Adelphi, MD, USA, 1977.
- Chen, L.W.; Chen, Y.C. Wedge-shaped track design and contact analysis of overrunning clutches. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2008, 222, 1647–1656. [Google Scholar] [CrossRef]
- Xu, T.; Lowen, G.G. A New Damping Model for Nonlinear Stiffness Systems With Variable Preload Displacements and Constant Amplitude Decay Ratios. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Scottsdale, AZ, USA, 13–16 September 1992; American Society of Mechanical Engineers: New York, NY, USA, 1992; Volume 9402. [Google Scholar]
- Huang, C.; Liu, M.; Zhao, Y. An Analytical Model of Multiarc Sprag Clutch considering Geometry and Internal Interaction during Engagement. Shock Vib. 2017, 2017, 2393578. [Google Scholar] [CrossRef]
- Huang, C.; Zhao, Y.; Liu, M.; Fu, Z. Dynamic modelling and vibration analysis of dual-rotor system with inter-shaft sprag clutch and bearings. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019. [Google Scholar]
- Huang, C. Wedging Optimization and Vibration Characteristics of Slant Support Clutch Rotor System. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Qing, M.; Yan, H.; Tan, W. Research on the Failure Judgment of Sprag Clutch Based on Wear Loss. AMM 2013, 378, 329–334. [Google Scholar] [CrossRef]
- Qing, M.; Yan, H.; Tan, W. The Effects of the Manufacturing Errors of a Group of Sprags on the Engagement Properties of Sprag Clutch. Adv. Mater. Res. 2013, 744, 18–22. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, H.; Cao, Y. Design and analysis of logarithmic spiral type sprag one-way clutch. J. Cent. South Univ. 2015, 22, 4597–4607. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, H.; Cao, Y.; Lai, Y. Bifurcation and Chaos Analysis of the Spur Gear Transmission System for One-Way Clutch, Two-Shaft Assembly. Shock Vib. 2017, 2017, 8621514. [Google Scholar] [CrossRef]
- Yan, H.; Wang, Z.; Zhu, C. The influence of the position of the wedge center of gravity on the performance of the slant support clutch. Chin. J. Mech. Eng. 2021, 32, 253. [Google Scholar]
- Yan, H.; Wen, B.; Wang, Z. Wear Analysis of Support Spring of Sprag Clutch during State of Overrunning. Math. Probl. Eng. 2022, 2022, 3417760. [Google Scholar] [CrossRef]
- Huang, C.; Zhao, Y.; Liu, M. Analytical modeling and optimization of logarithmic sprag clutch considering profile modification. Shock Vib. 2018, 2018, 4190303. [Google Scholar] [CrossRef]
- Han, T.; Bai, Z.; Quan, J. Failure analysis of overrunning clutch for turbine starter. Bearing 2023, 7, 56–61. [Google Scholar]
- Ma, L.; Meng, H.; Han, H. Research on the Wear and Failure of Cylindrical Rollers in Alien Wheel Overrunning Clutch. Met. Process. (Cold Work.) 2020, 1, 84–86. [Google Scholar]
- Xue, Y.; Wang, Z.; Chen, D.; Tao, S.; Lu, Y. Design and Test of a New Type of Overrunning Clutch. Machines 2022, 10, 1188. [Google Scholar] [CrossRef]
- Liu, H.; Ning, F. High speed overrunning slant support clutch differential engagement impact load estimation. Mech. Transm. 2011, 35, 21–22. [Google Scholar]
- Zhu, Z. Research on Design Technology of High Speed Overrunning Slant Support Clutch. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2004. [Google Scholar]
- ISO 24195:2022(EN); Road Vehicles—Vocabulary and Characteristics for Engineering of Starting Devices. ISO: Geneva, Switzerland, 2022.
- China Aerospace Shenyang Engine Research Institute. A Method for Determining the Release Speed of Ratchet Clutch. China Patent No. CN202011628428.2, 19 October 2021.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).