Feasibility Analysis of Online Uncertainty Metrics for PMU-Based State Estimation
Abstract
:1. Introduction
Paper Contributions
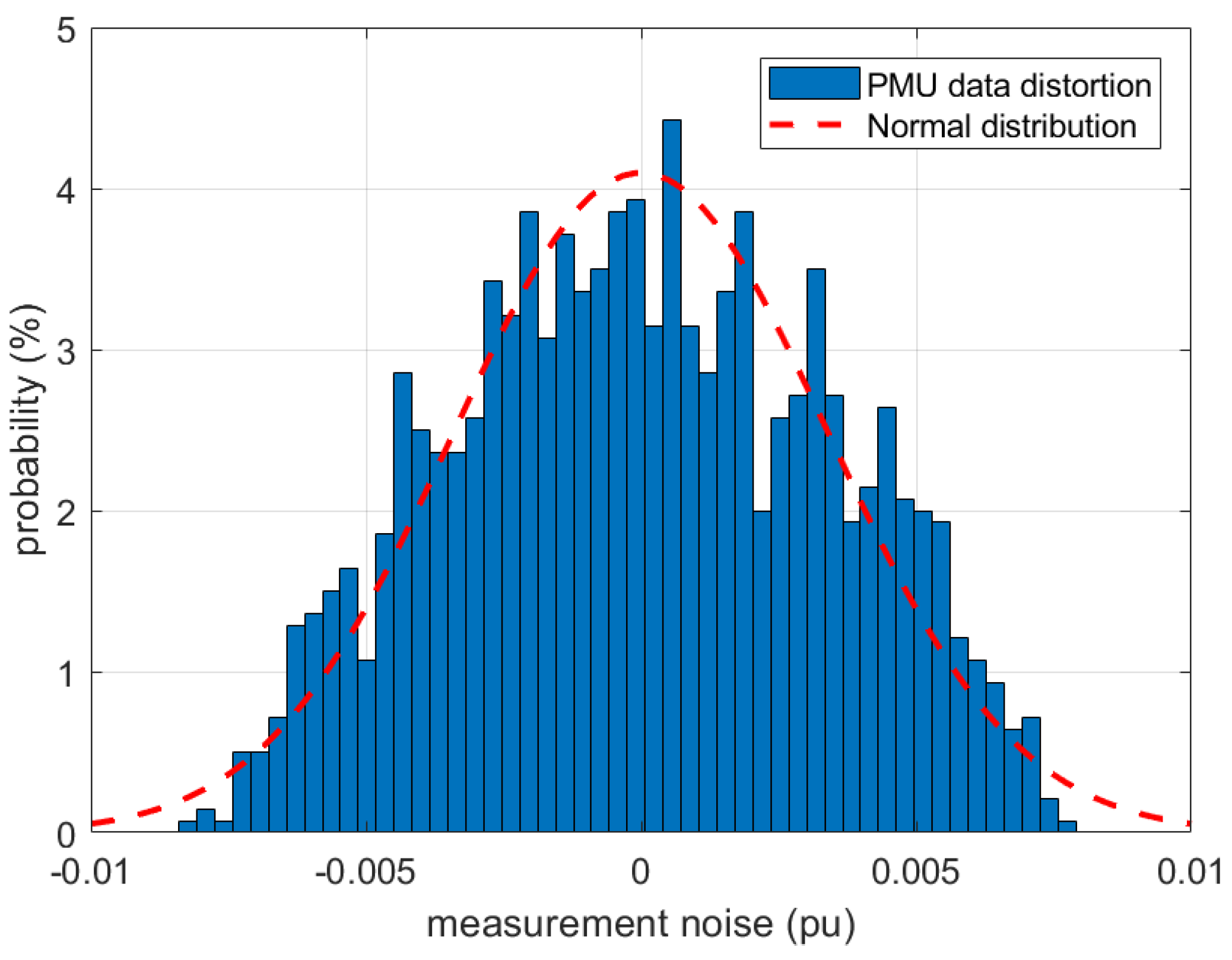
2. Uncertainty Contributions in the PMU Measurement Chain
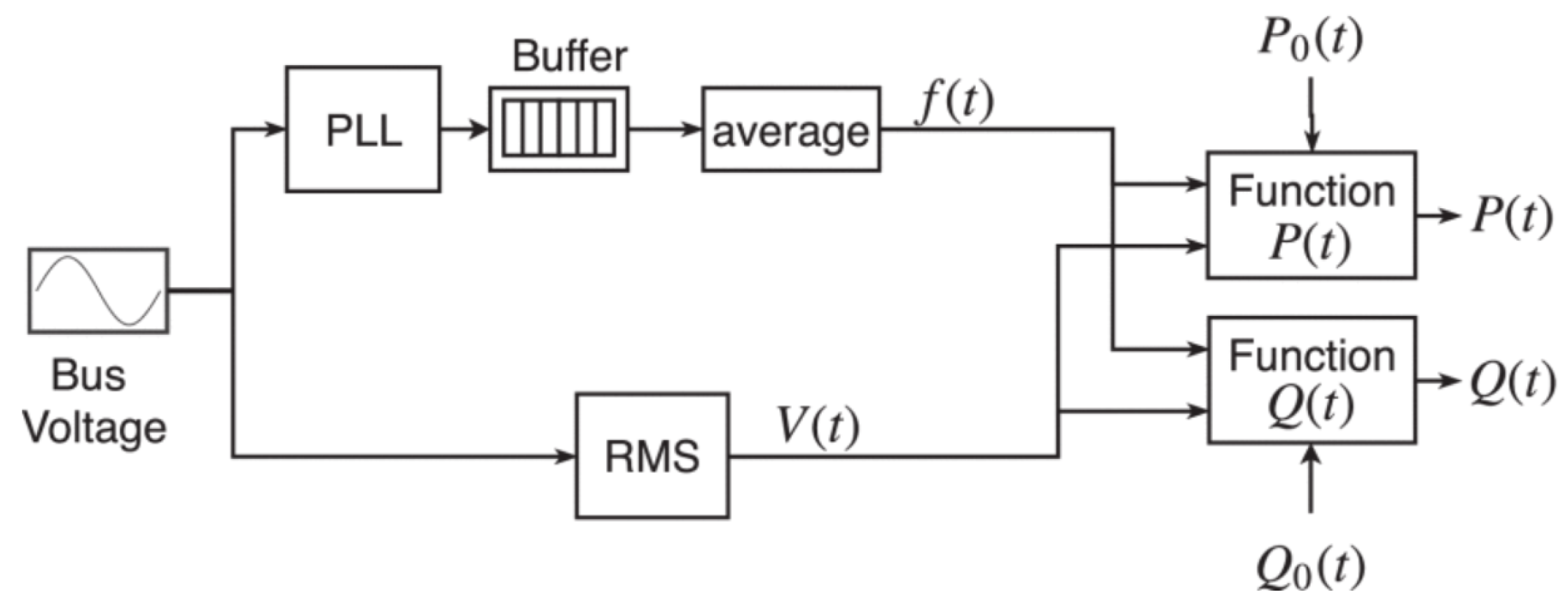
3. Online Performance Assessment
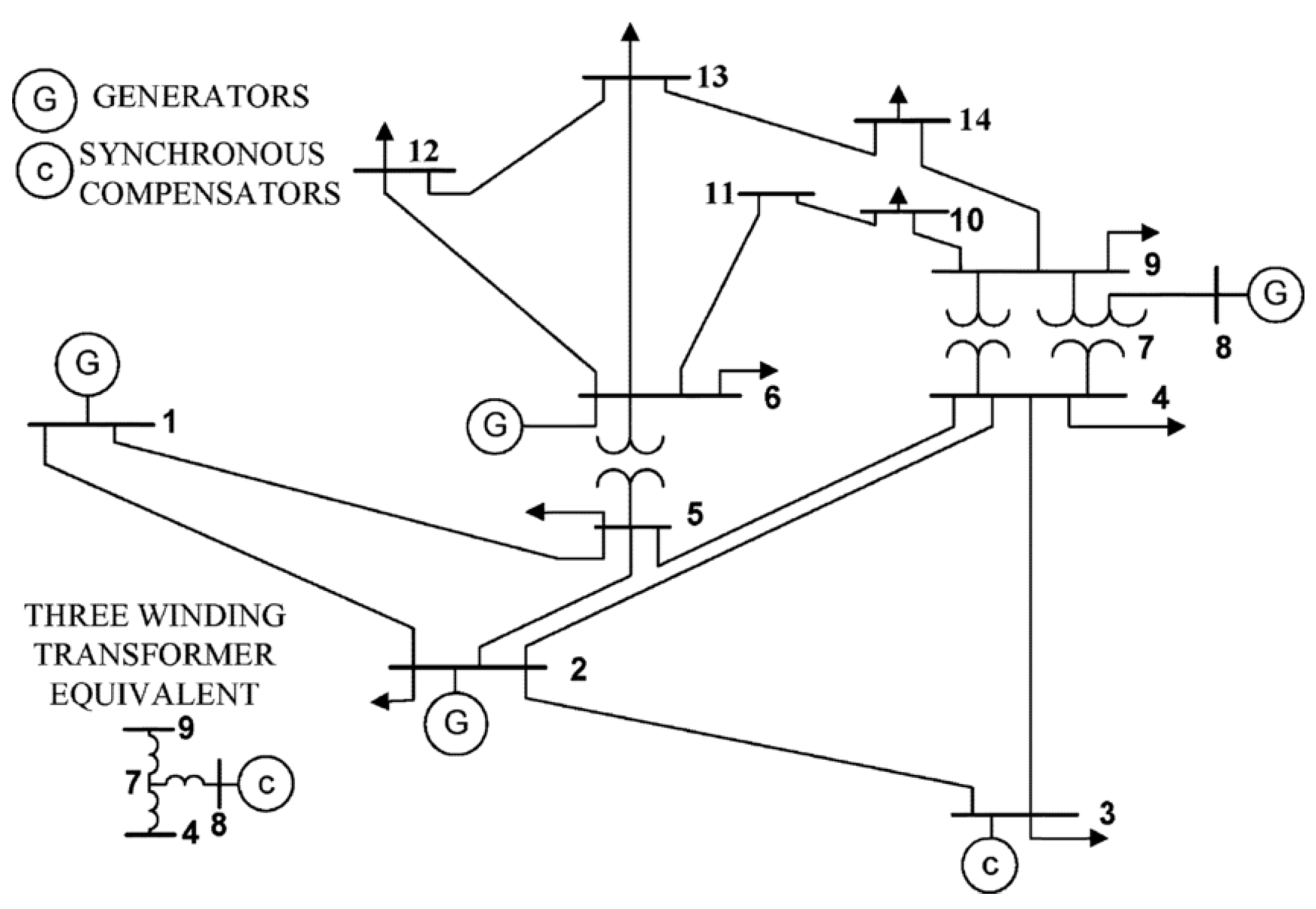
4. State Estimation Scenario
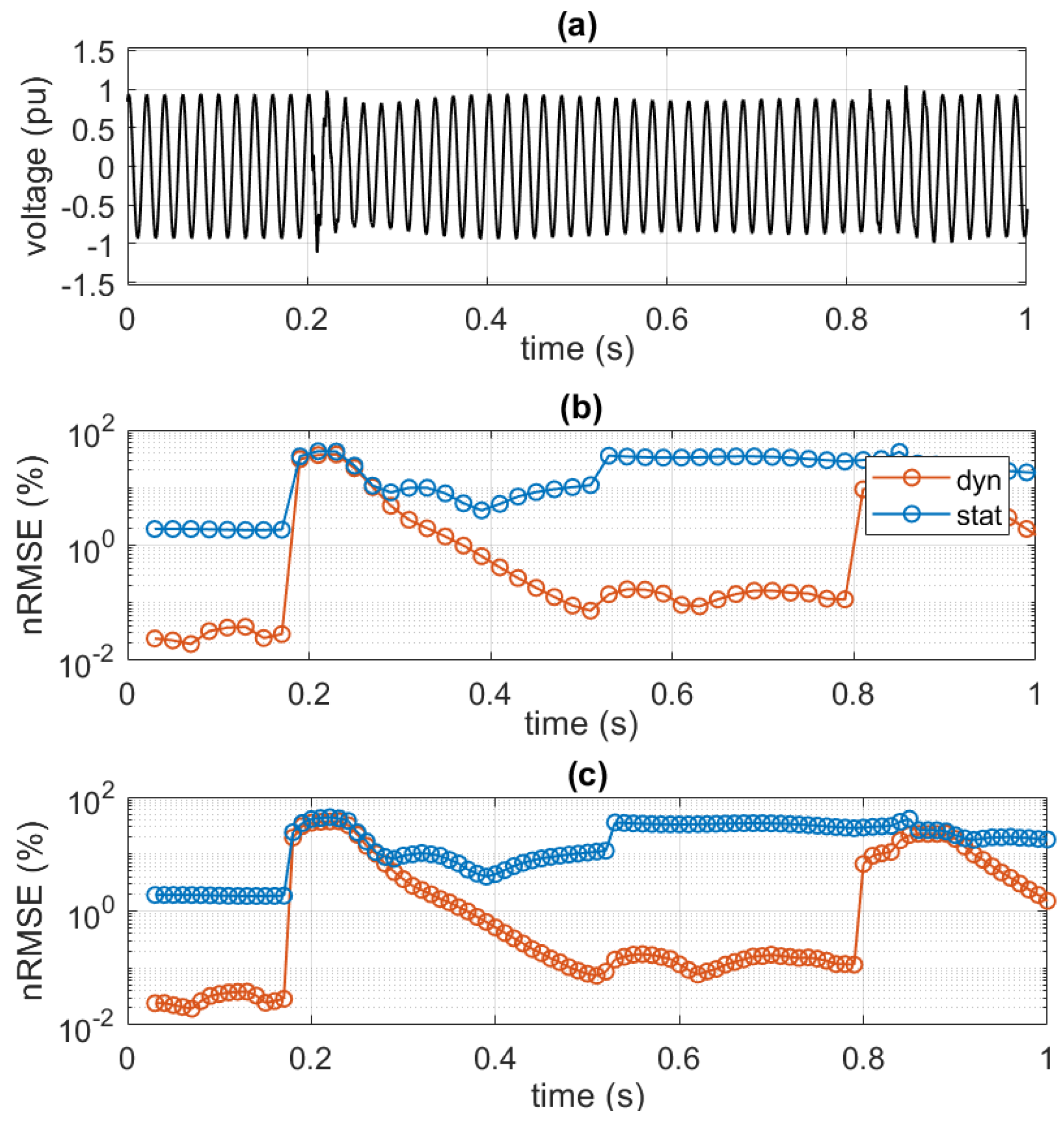
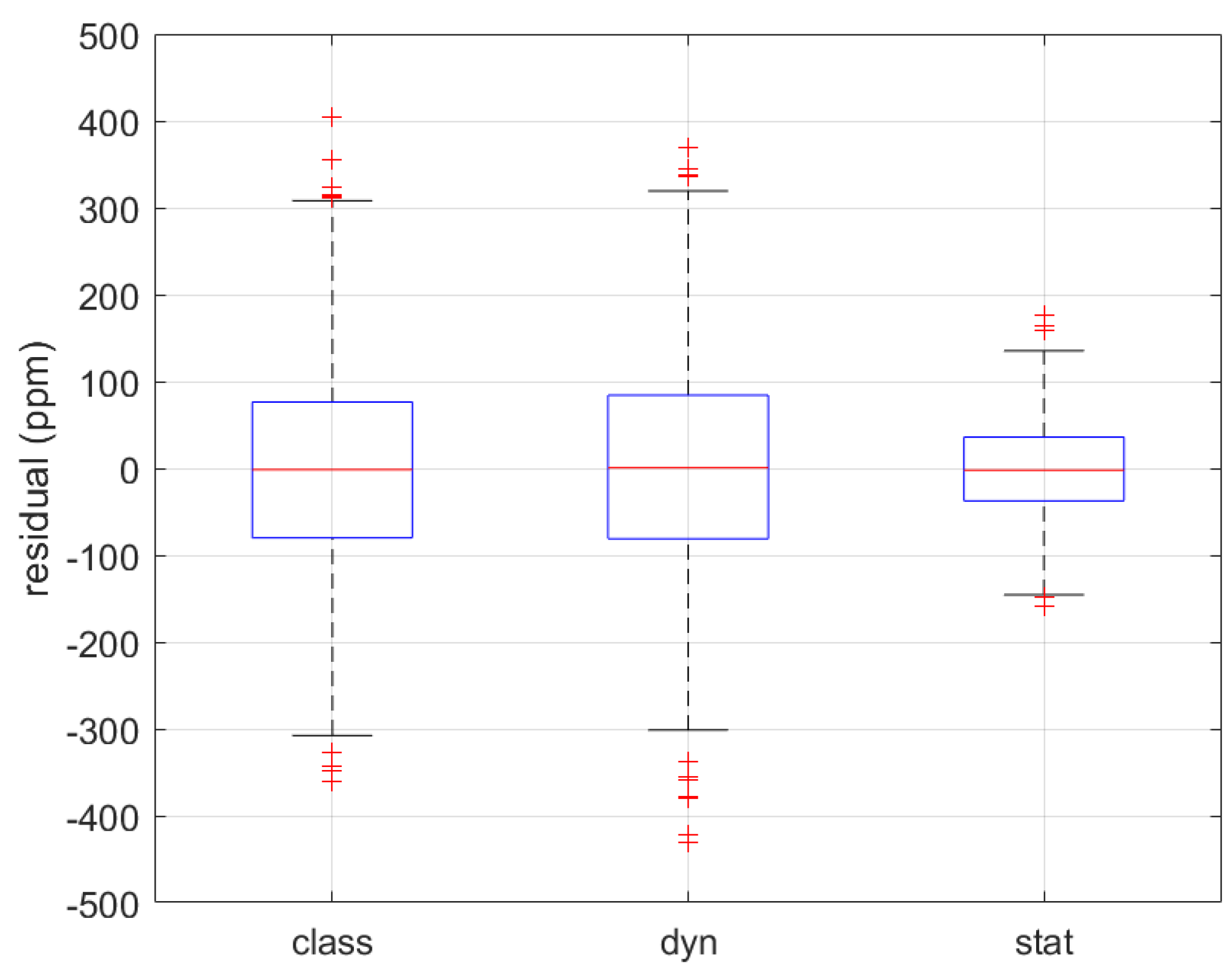
- static: considering only the zero-order parameters, i.e., amplitude, frequency, phase, and ROCOF, as in (4);
- dynamic: considering all the derivative terms, i.e., accounting also for the parameter variations within the considered window.
5. Simulation Results
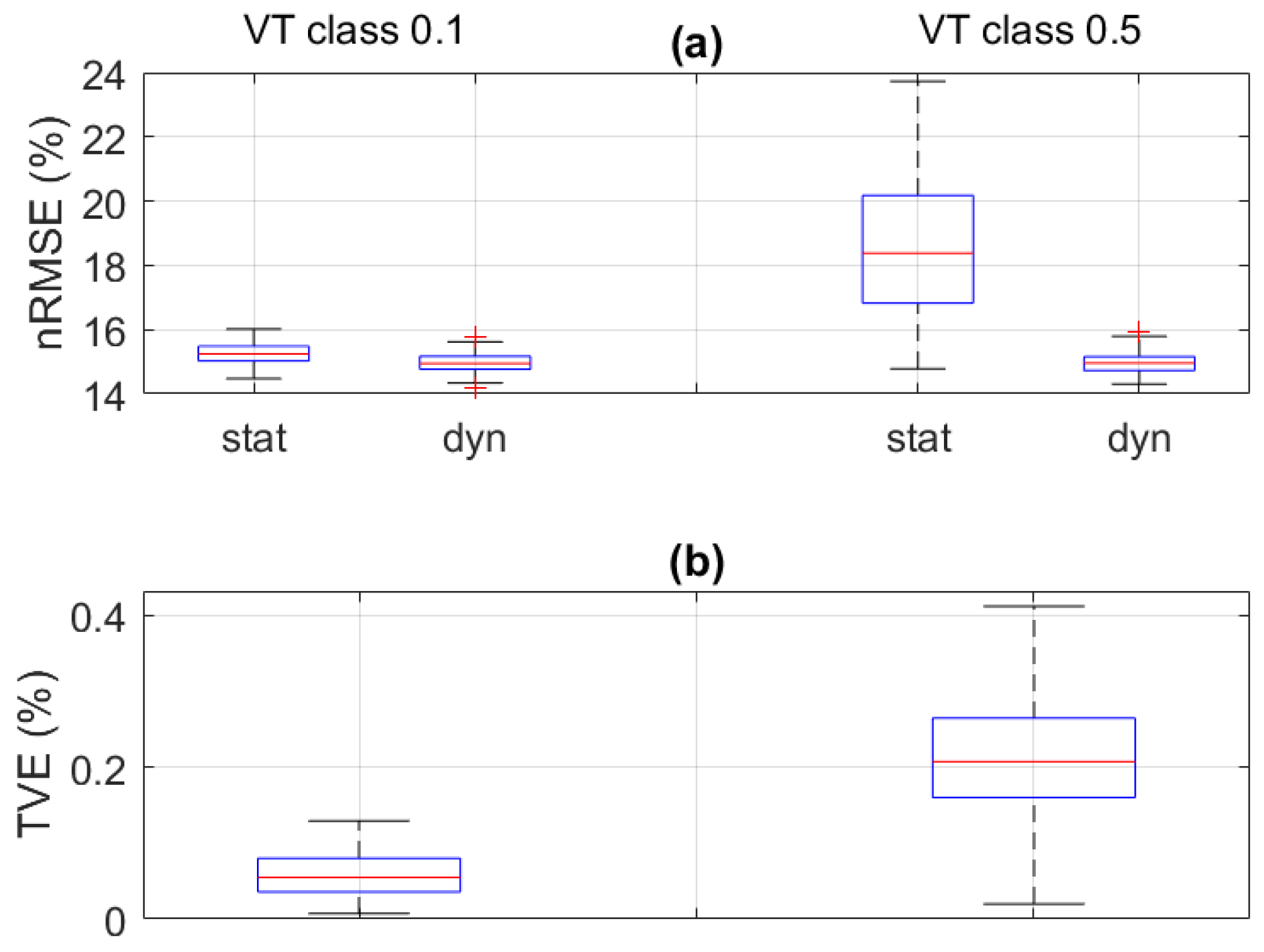
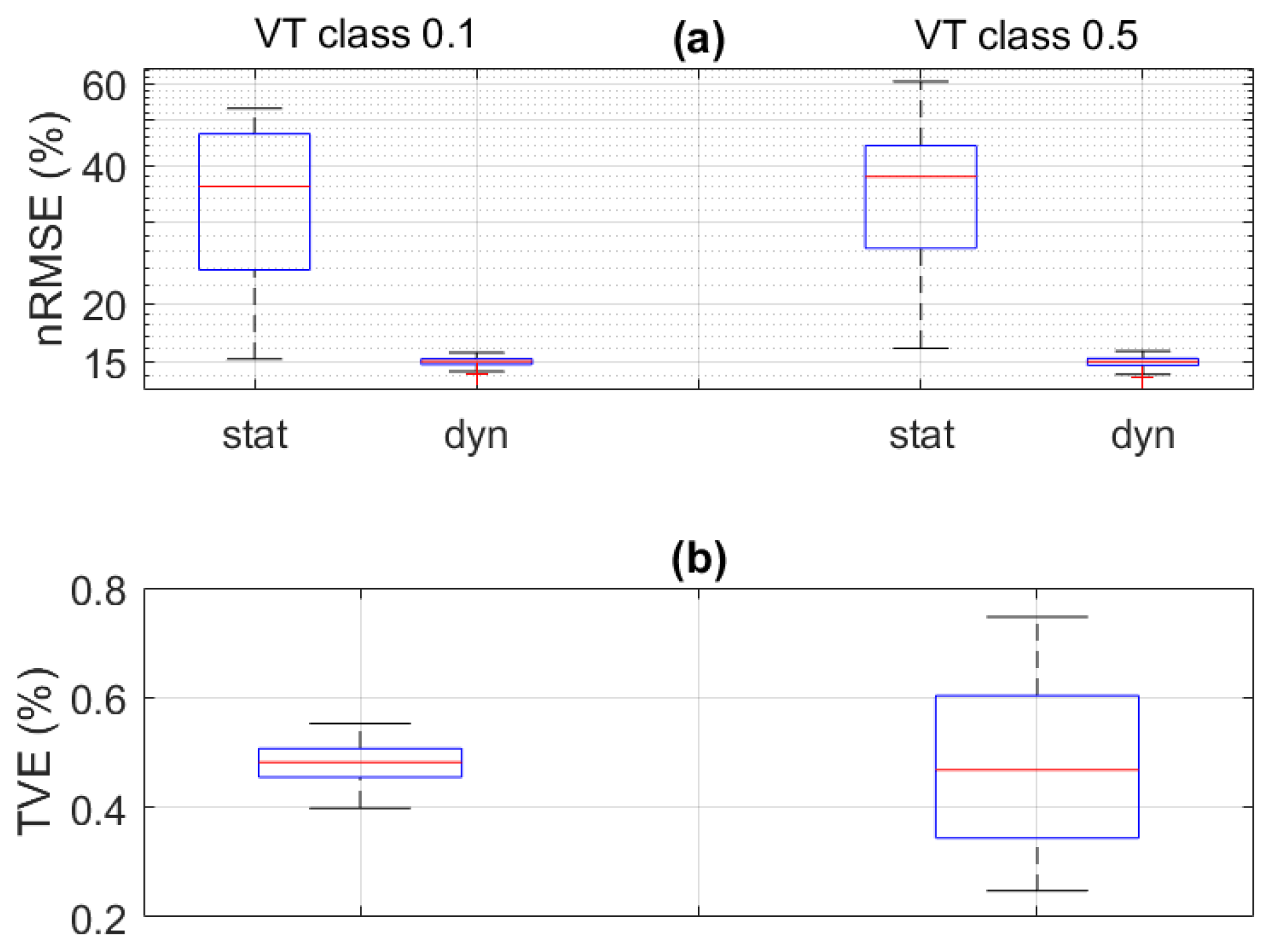
5.1. Sensitivity Analysis
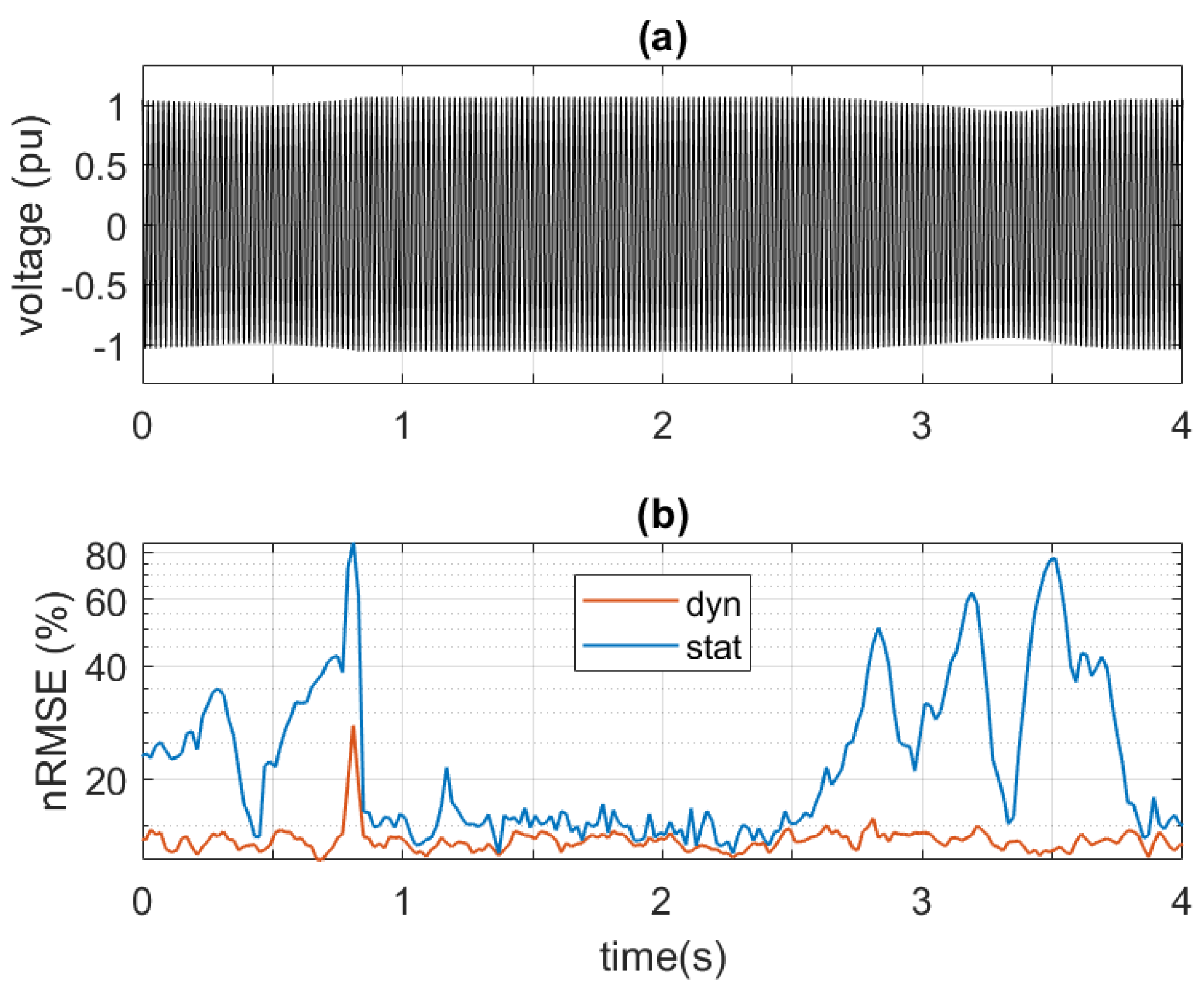
5.2. Feasibility Analysis in Real-World Scenarios
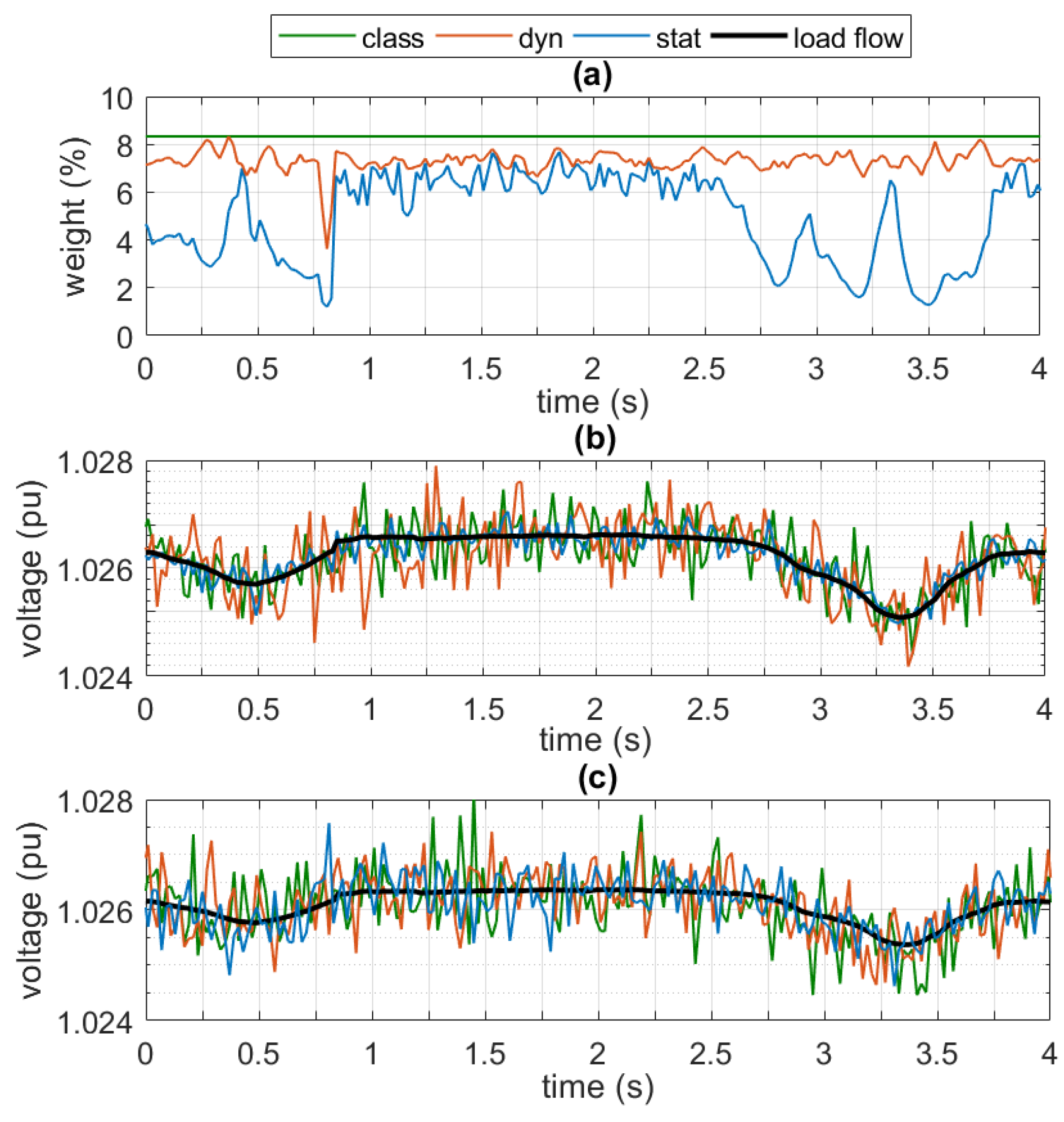
5.3. PMU-Based State Estimation
6. Conclusions
Future Activities
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Terzija, V.; Valverde, G.; Cai, D.; Regulski, P.; Madani, V.; Fitch, J.; Skok, S.; Begovic, M.M.; Phadke, A. Wide-Area Monitoring, Protection, and Control of Future Electric Power Networks. Proc. IEEE 2011, 99, 80–93. [Google Scholar] [CrossRef]
- Rueda Torres, J.; Kumar, N.V.; Rakhshani, E.; Ahmad, Z.; Adabi, E.; Palensky, P.; van der Meijden, M. Dynamic Frequency Support for Low Inertia Power Systems by Renewable Energy Hubs with Fast Active Power Regulation. Electronics 2021, 10, 1651. [Google Scholar] [CrossRef]
- Stojković, J.; Stefanov, P. A Novel Approach for the Implementation of Fast Frequency Control in Low-Inertia Power Systems Based on Local Measurements and Provision Costs. Electronics 2022, 11, 1776. [Google Scholar] [CrossRef]
- Paolone, M.; Gaunt, T.; Guillaud, X.; Liserre, M.; Meliopoulos, S.; Monti, A.; Van Cutsem, T.; Vittal, V.; Vournas, C. Fundamentals of power systems modelling in the presence of converter-interfaced generation. Electr. Power Syst. Res. 2020, 189, 106811. [Google Scholar] [CrossRef]
- Rietveld, G.; Braun, J.P.; Martin, R.; Wright, P.; Heins, W.; Ell, N.; Clarkson, P.; Zisky, N. Measurement Infrastructure to Support the Reliable Operation of Smart Electrical Grids. IEEE Trans. Instrum. Meas. 2015, 64, 1355–1363. [Google Scholar] [CrossRef]
- Rouhani, A.; Abur, A. Linear Phasor Estimator Assisted Dynamic State Estimation. IEEE Trans. Smart Grid 2018, 9, 211–219. [Google Scholar] [CrossRef]
- Feng, G.; Abur, A. Fault Location Using Wide-Area Measurements and Sparse Estimation. IEEE Trans. Power Syst. 2016, 31, 2938–2945. [Google Scholar] [CrossRef]
- Ding, F.; Booth, C.D.; Roscoe, A.J. Peak-Ratio Analysis Method for Enhancement of LOM Protection Using M-Class PMUs. IEEE Trans. Smart Grid 2016, 7, 291–299. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, H.; Yin, X.; Han, J.; Wang, Y.; Chen, G. A Load-Shedding Model Based on Sensitivity Analysis in on-Line Power System Operation Risk Assessment. Energies 2018, 11, 727. [Google Scholar] [CrossRef]
- De La Ree, J.; Centeno, V.; Thorp, J.S.; Phadke, A.G. Synchronized Phasor Measurement Applications in Power Systems. IEEE Trans. Smart Grid 2010, 1, 20–27. [Google Scholar] [CrossRef]
- Livanos, N.A.I.; Hammal, S.; Giamarelos, N.; Alifragkis, V.; Psomopoulos, C.S.; Zois, E.N. OpenEdgePMU: An Open PMU Architecture with Edge Processing for Future Resilient Smart Grids. Energies 2023, 16, 2756. [Google Scholar] [CrossRef]
- 60255-118-1:2018; Measuring Relays and Protection Equipment—Part 118-1: Synchrophasor for Power Systems—Measurements. International Standard; IEC: Geneva, Switzerland, 2018.
- IEEE Std C37.242-2013; IEEE Guide for Synchronization, Calibration, Testing, and Installation of Phasor Measurement Units (PMUs) for Power System Protection and Control. IEEE: Piscataway, NJ, USA, 2013; pp. 1–107. [CrossRef]
- Tang, Y.H.; Stenbakken, G.N.; Goldstein, A. Calibration of Phasor Measurement Unit at NIST. IEEE Trans. Instrum. Meas. 2013, 62, 1417–1422. [Google Scholar] [CrossRef]
- Kirkham, H.; Riepnieks, A. Dealing with non-stationary signals: Definitions, considerations and practical implications. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Qian, C.; Kezunovic, M. A Novel Time-Frequency Analysis for Power System Waveforms Based on “Pseudo-Wavelets”. In Proceedings of the 2018 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Denver, CO, USA, 16–19 April 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Wright, P.S.; Davis, P.N.; Johnstone, K.; Rietveld, G.; Roscoe, A.J. Field Measurement of Frequency and ROCOF in the Presence of Phase Steps. IEEE Trans. Instrum. Meas. 2019, 68, 1688–1695. [Google Scholar] [CrossRef]
- Kirkham, H. The measurand: The problem of frequency. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Taipei, Taiwan, 23–26 May 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Riepnieks, A.; Kirkham, H. An Introduction to Goodness of Fit for PMU Parameter Estimation. IEEE Trans. Power Deliv. 2017, 32, 2238–2245. [Google Scholar] [CrossRef]
- Frigo, G.; Colangelo, D.; Derviškadić, A.; Pignati, M.; Narduzzi, C.; Paolone, M. Definition of Accurate Reference Synchrophasors for Static and Dynamic Characterization of PMUs. IEEE Trans. Instrum. Meas. 2017, 66, 2233–2246. [Google Scholar] [CrossRef]
- Yousof, H.M.; Goual, H.; Emam, W.; Tashkandy, Y.; Alizadeh, M.; Ali, M.M.; Ibrahim, M. An Alternative Model for Describing the Reliability Data: Applications, Assessment, and Goodness-of-Fit Validation Testing. Mathematics 2023, 11, 1308. [Google Scholar] [CrossRef]
- Frigo, G.; Grasso Toro, F. On-line performance assessment for improved sensor data aggregation in power system metrology. Meas. Sens. 2021, 18, 100186. [Google Scholar] [CrossRef]
- Rahmatian, M.; Chen, Y.C.; Dunford, W.G.; Rahmatian, F. Incorporating Goodness-of-Fit Metrics to Improve Synchrophasor-Based Fault Location. IEEE Trans. Power Deliv. 2018, 33, 1944–1953. [Google Scholar] [CrossRef]
- Frigo, G.; Toro, F.G. Metrological Significance and Reliability of On-Line Performance Metrics in PMU-based WLS State Estimation. In Proceedings of the 2022 International Conference on Smart Grid Synchronized Measurements and Analytics (SGSMA), Split, Croatia, 24–26 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Paolone, M.; Le Boudec, J.Y.; Sarri, S.; Zanni, L. Static and recursive PMU-based state estimation processes for transmission and distribution power grids. In Advanced Techniques for Power System Modelling, Control and Stability Analysis; IET: London, UK, 2015; pp. 189–239. [Google Scholar]
- Fotopoulou, M.; Petridis, S.; Karachalios, I.; Rakopoulos, D. A Review on Distribution System State Estimation Algorithms. Appl. Sci. 2022, 12, 11073. [Google Scholar] [CrossRef]
- Illinois Center for a Smarter Electric Grid. IEEE 14-Bus System. 2021. Available online: https://icseg.iti.illinois.edu/ieee-14-bus-system/ (accessed on 9 October 2021).
- Frigo, G.; Derviškadić, A.; Zuo, Y.; Bach, A.; Paolone, M. Taylor-Fourier PMU on a Real-Time Simulator: Design, Implementation and Characterization. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- 62586-2:2017+AMD1:2021; Power Quality Measurement in Power Supply Systems—Part 2: Functional Tests and Uncertainty Requirements. International Standard; IEC: Geneva, Switzerland, 2021.
- Roscoe, A.J.; Blair, S.M.; Dickerson, B.; Rietveld, G. Dealing with Front-End White Noise on Differentiated Measurements Such as Frequency and ROCOF in Power Systems. IEEE Trans. Instrum. Meas. 2018, 67, 2579–2591. [Google Scholar] [CrossRef]
- Arefin, A.A.; Baba, M.; Singh, N.S.S.; Nor, N.B.M.; Sheikh, M.A.; Kannan, R.; Abro, G.E.M.; Mathur, N. Review of the Techniques of the Data Analytics and Islanding Detection of Distribution Systems Using Phasor Measurement Unit Data. Electronics 2022, 11, 2967. [Google Scholar] [CrossRef]
- Zuo, Y.; Derviskadic, A.; Frigo, G.; Paolone, M. IEEE-39-Bus-4WG-Power-System. 2018. Available online: https://github.com/DESL-EPFL/IEEE-39-bus-4WG-power-system (accessed on 29 August 2022).
- Mingotti, A.; Betti, C.; Peretto, L.; Tinarelli, R. Simplified and Low-Cost Characterization of Medium-Voltage Low-Power Voltage Transformers in the Power Quality Frequency Range. Sensors 2022, 22, 2274. [Google Scholar] [CrossRef] [PubMed]
- Pegoraro, P.A.; Castello, P.; Muscas, C.; Brady, K.; von Meier, A. Handling Instrument Transformers and PMU Errors for the Estimation of Line Parameters in Distribution Grids. In Proceedings of the 2017 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Liverpool, UK, 20–22 September 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Price, W.W. Load representation for dynamic performance analysis (of power systems). IEEE Trans. Power Syst. 1993, 8, 472–482. [Google Scholar] [CrossRef]
- Ferrero, R.; Pegoraro, P.A.; Toscani, S. Impact of Capacitor Voltage Transformers on Phasor Measurement Units Dynamic Performance. In Proceedings of the 2018 IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Kummerow, A.; Monsalve, C.; Brosinsky, C.; Nicolai, S.; Westermann, D. A Novel Framework for Synchrophasor Based Online Recognition and Efficient Post-Mortem Analysis of Disturbances in Power Systems. Appl. Sci. 2020, 10, 5209. [Google Scholar] [CrossRef]
- Pes, I. Benchmark Systems for Small-Signal Stability Analysis and Control; Technical report; IEEE: Austin, TX, USA, 2015. [Google Scholar]
- Gomez-Exposito, A.; Abur, A.; de la Villa Jaen, A.; Gomez-Quiles, C. A Multilevel State Estimation Paradigm for Smart Grids. Proc. IEEE 2011, 99, 952–976. [Google Scholar] [CrossRef]
- Muscas, C.; Pau, M.; Pegoraro, P.A.; Sulis, S. Uncertainty of Voltage Profile in PMU-Based Distribution System State Estimation. IEEE Trans. Instrum. Meas. 2016, 65, 988–998. [Google Scholar] [CrossRef]
- Kettner, A.M.; Paolone, M. Sequential Discrete Kalman Filter for Real-Time State Estimation in Power Distribution Systems: Theory and Implementation. IEEE Trans. Instrum. Meas. 2017, 66, 2358–2370. [Google Scholar] [CrossRef]
- Zhao, J.; Gómez-Expósito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; et al. Power System Dynamic State Estimation: Motivations, Definitions, Methodologies, and Future Work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- Asprou, M.; Kyriakides, E.; Albu, M. The Effect of Variable Weights in a WLS State Estimator Considering Instrument Transformer Uncertainties. IEEE Trans. Instrum. Meas. 2014, 63, 1484–1495. [Google Scholar] [CrossRef]


| Type | Class | (%) | (mrad) | Nodes |
|---|---|---|---|---|
| VT | 0.1 | 0.1 | 1.45 | 1, 2, 5, 7, 8 |
| 0.5 | 0.5 | 5.82 | 3, 4, 6, 9, 10–14 | |
| CT | 0.2 | 0.2 | 2.91 | 1, 2, 5, 7, 8 |
| 0.5 | 0.5 | 8.73 | 3, 4, 6, 9, 10–14 |
| Test | Model | Corr (%) | p-Value (%) | Conf (%) | |||
|---|---|---|---|---|---|---|---|
| VT | 0.1 | 0.5 | 0.1 | 0.5 | 0.1 | 0.5 | |
| SS | stat | 96.32 | 93.20 | 0.01 | 0.01 | 3.89 | 5.43 |
| dyn | 13.82 | 1.73 | 17.71 | 89.44 | 39.16 | 39.88 | |
| PM | stat | 36.23 | 33.79 | 0.03 | 1.28 | 14.84 | 19.83 |
| dyn | 8.64 | 5.87 | 39.99 | 56.78 | 39.60 | 39.76 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frigo, G.; Grasso-Toro, F. Feasibility Analysis of Online Uncertainty Metrics for PMU-Based State Estimation. Appl. Sci. 2023, 13, 11670. https://doi.org/10.3390/app132111670
Frigo G, Grasso-Toro F. Feasibility Analysis of Online Uncertainty Metrics for PMU-Based State Estimation. Applied Sciences. 2023; 13(21):11670. https://doi.org/10.3390/app132111670
Chicago/Turabian StyleFrigo, Guglielmo, and Federico Grasso-Toro. 2023. "Feasibility Analysis of Online Uncertainty Metrics for PMU-Based State Estimation" Applied Sciences 13, no. 21: 11670. https://doi.org/10.3390/app132111670
APA StyleFrigo, G., & Grasso-Toro, F. (2023). Feasibility Analysis of Online Uncertainty Metrics for PMU-Based State Estimation. Applied Sciences, 13(21), 11670. https://doi.org/10.3390/app132111670






