Numerical Investigation of the Pile–Soil Interaction Problem under Dynamic Loads
Abstract
:1. Introduction
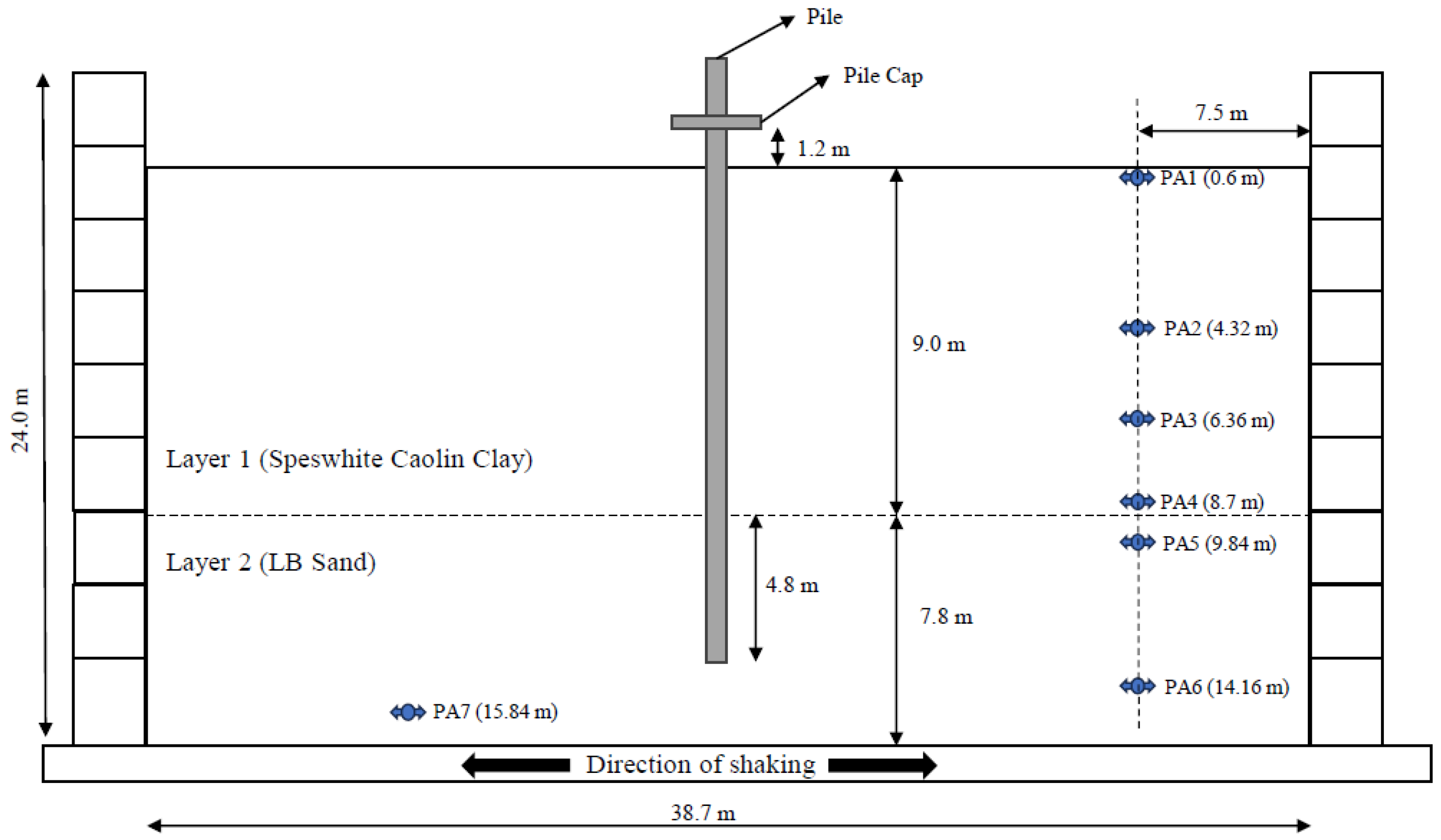
2. Description of Problem
3. Finite Element Analysis
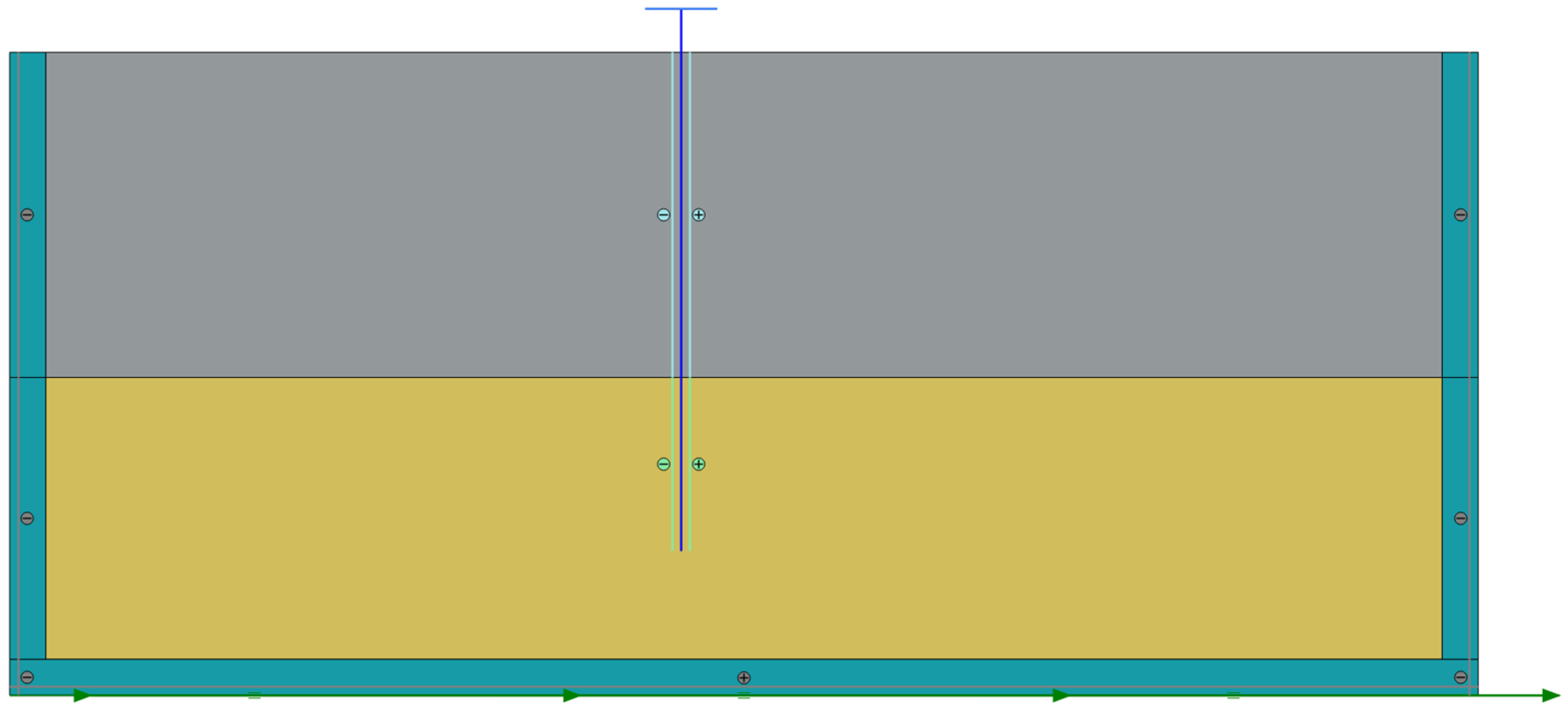
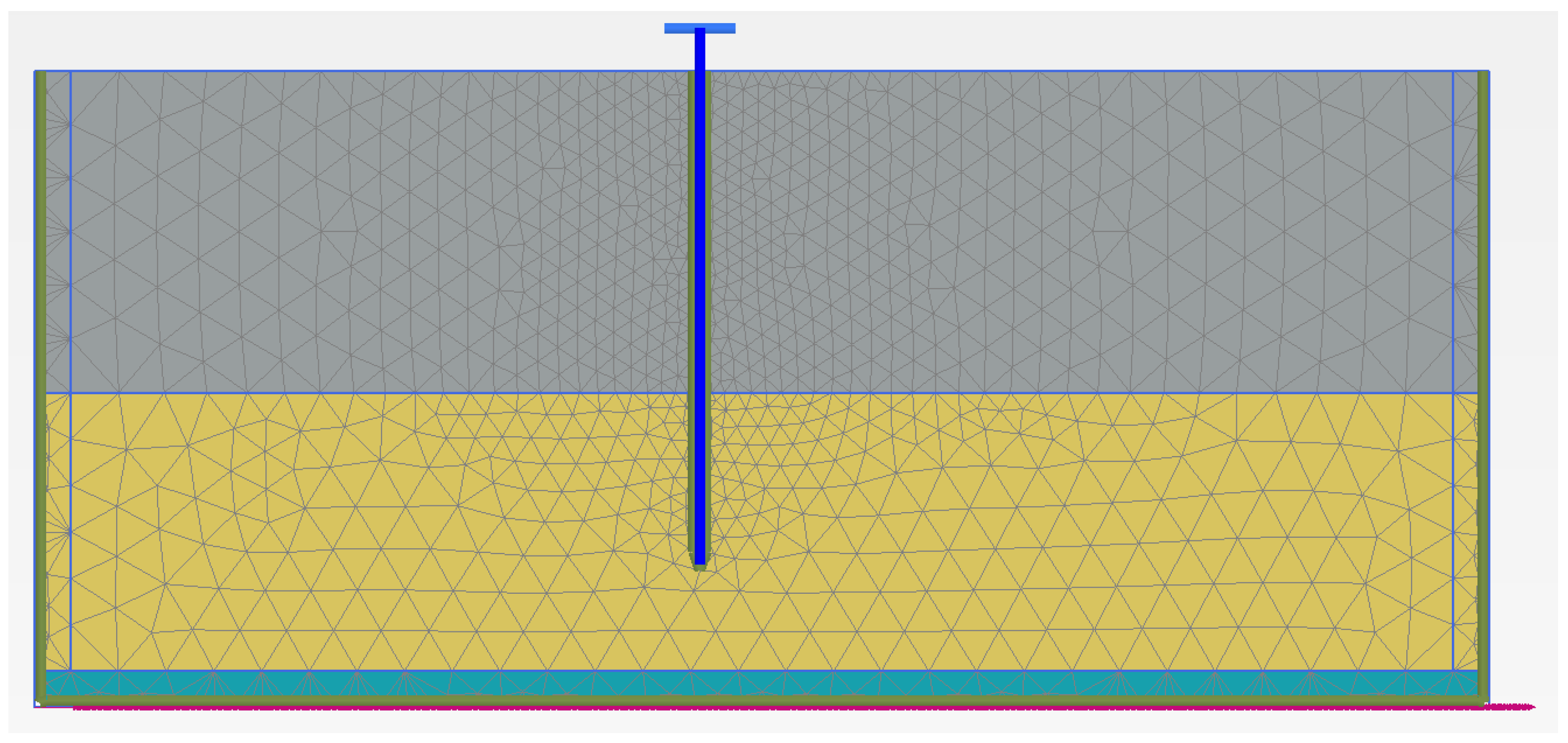
3.1. Numerical Modeling
3.2. Soil Parameters
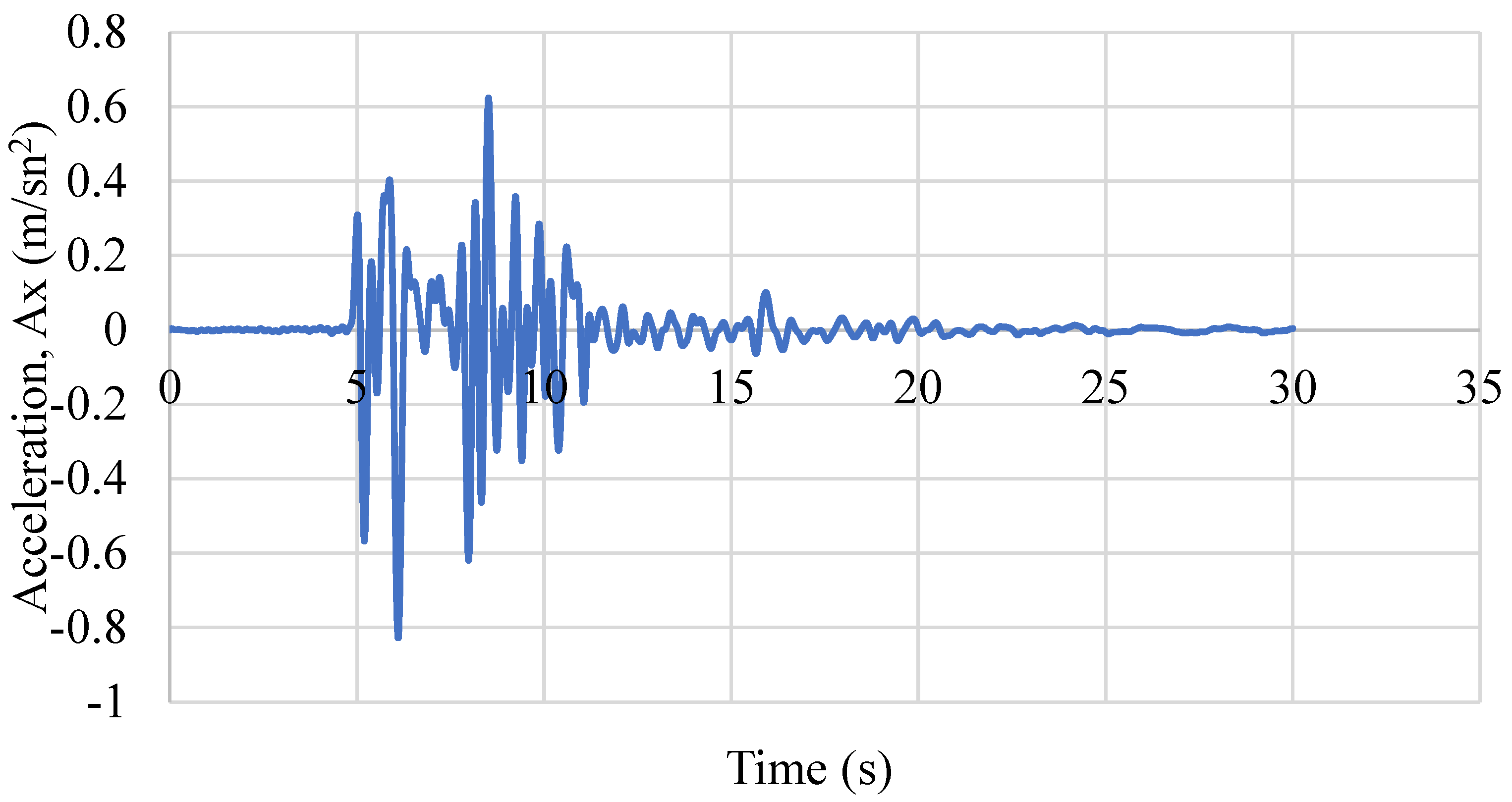
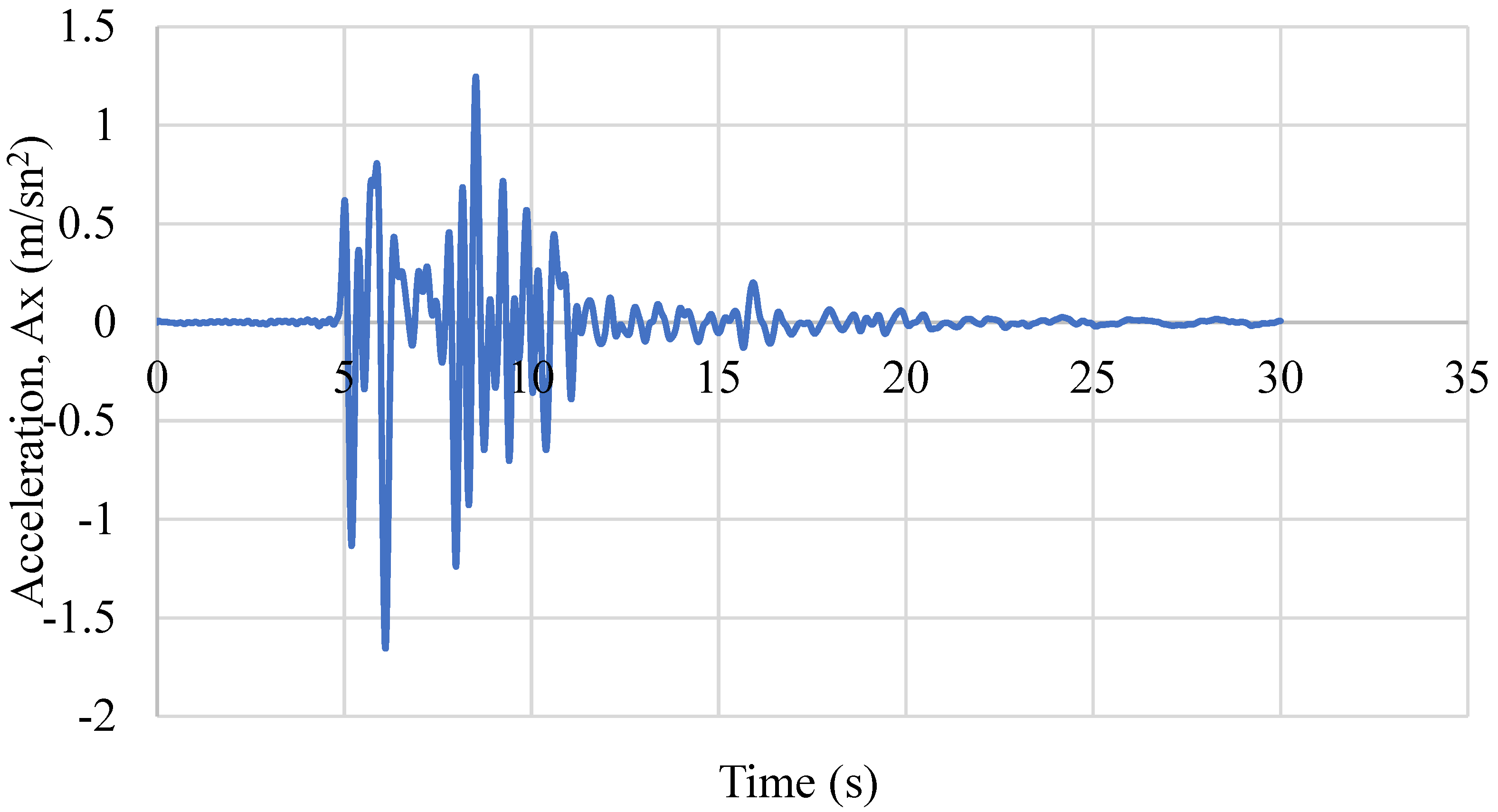
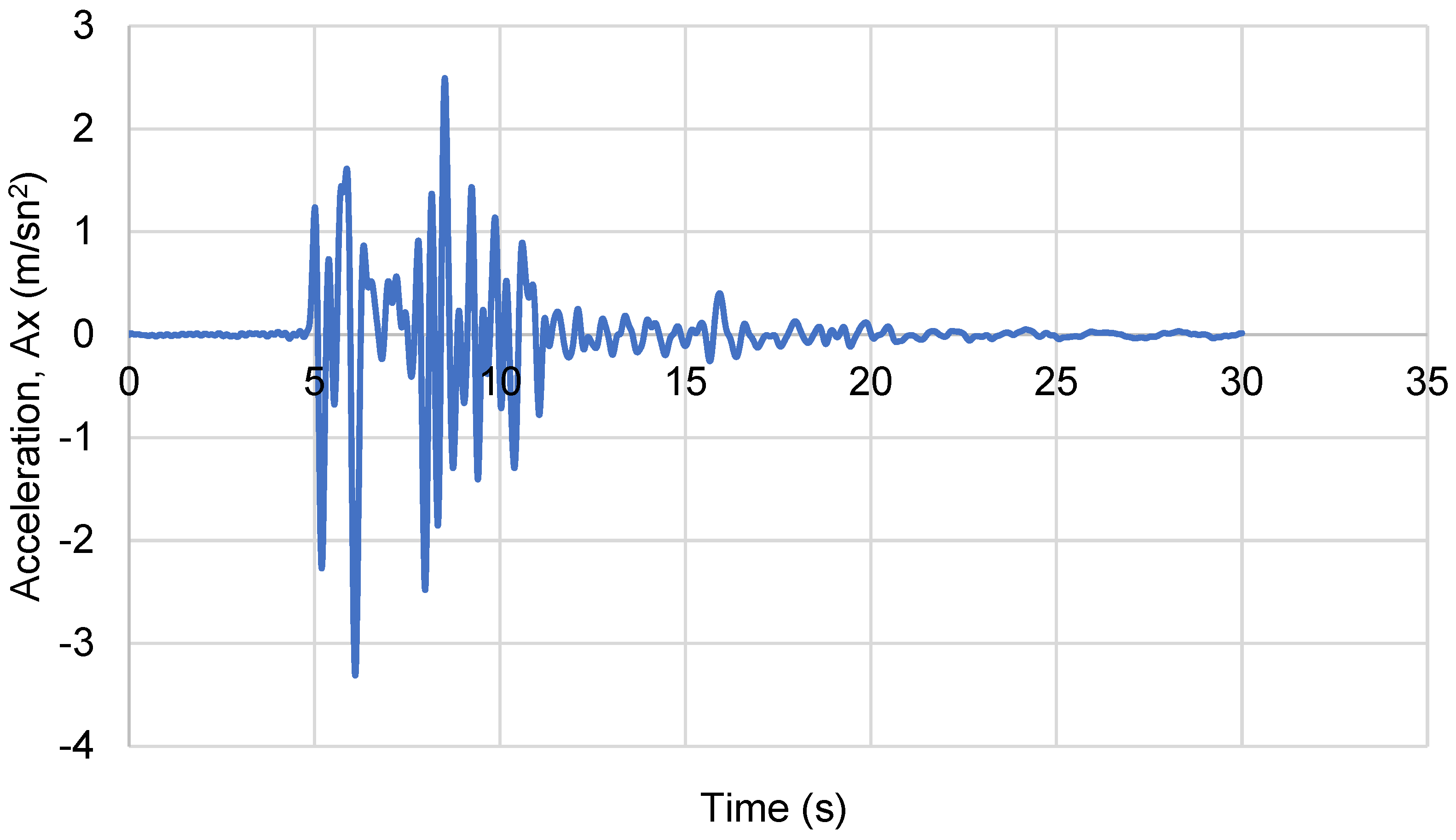
3.3. Input Earthquakes
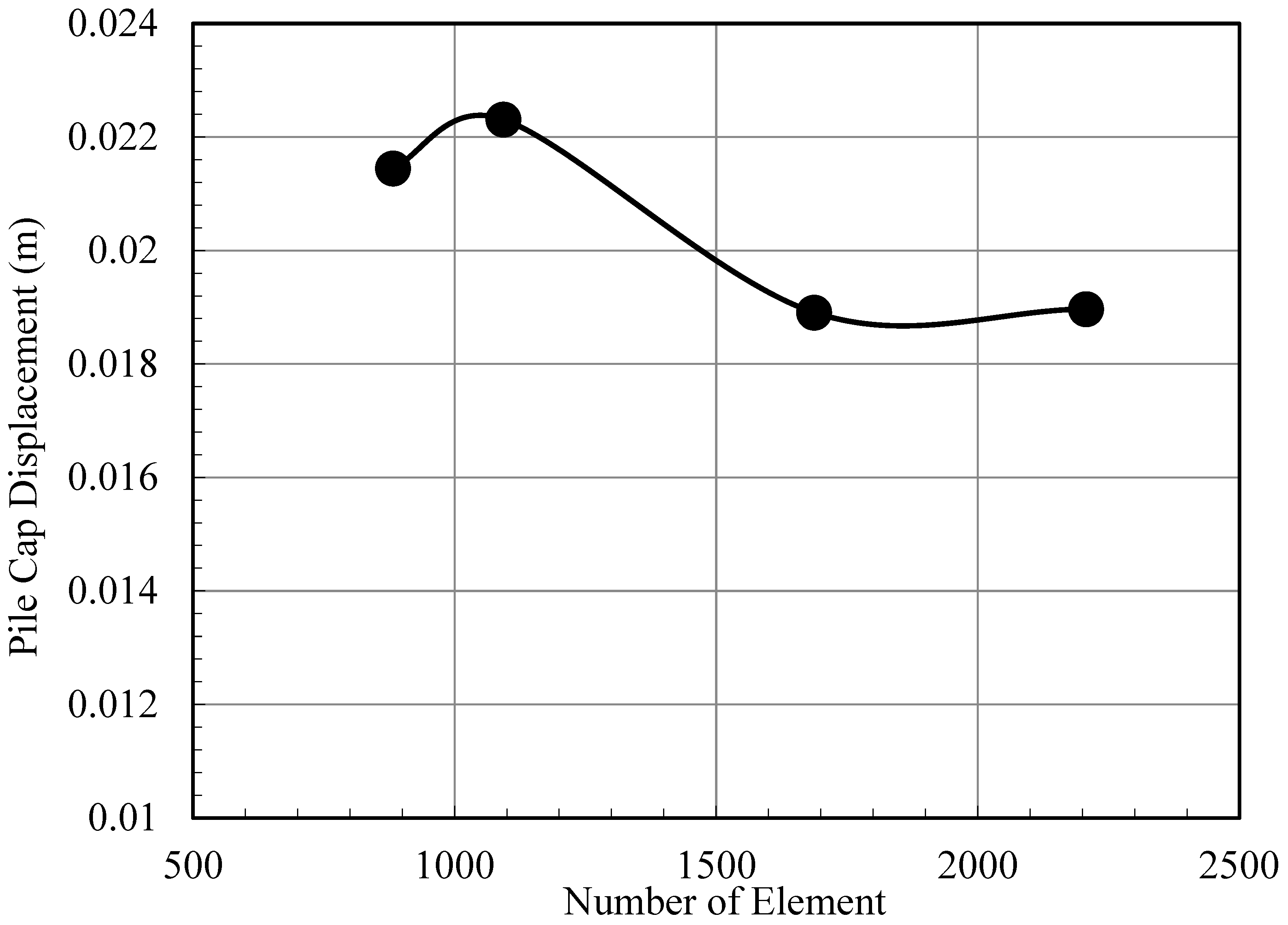
3.4. Mesh Analysis
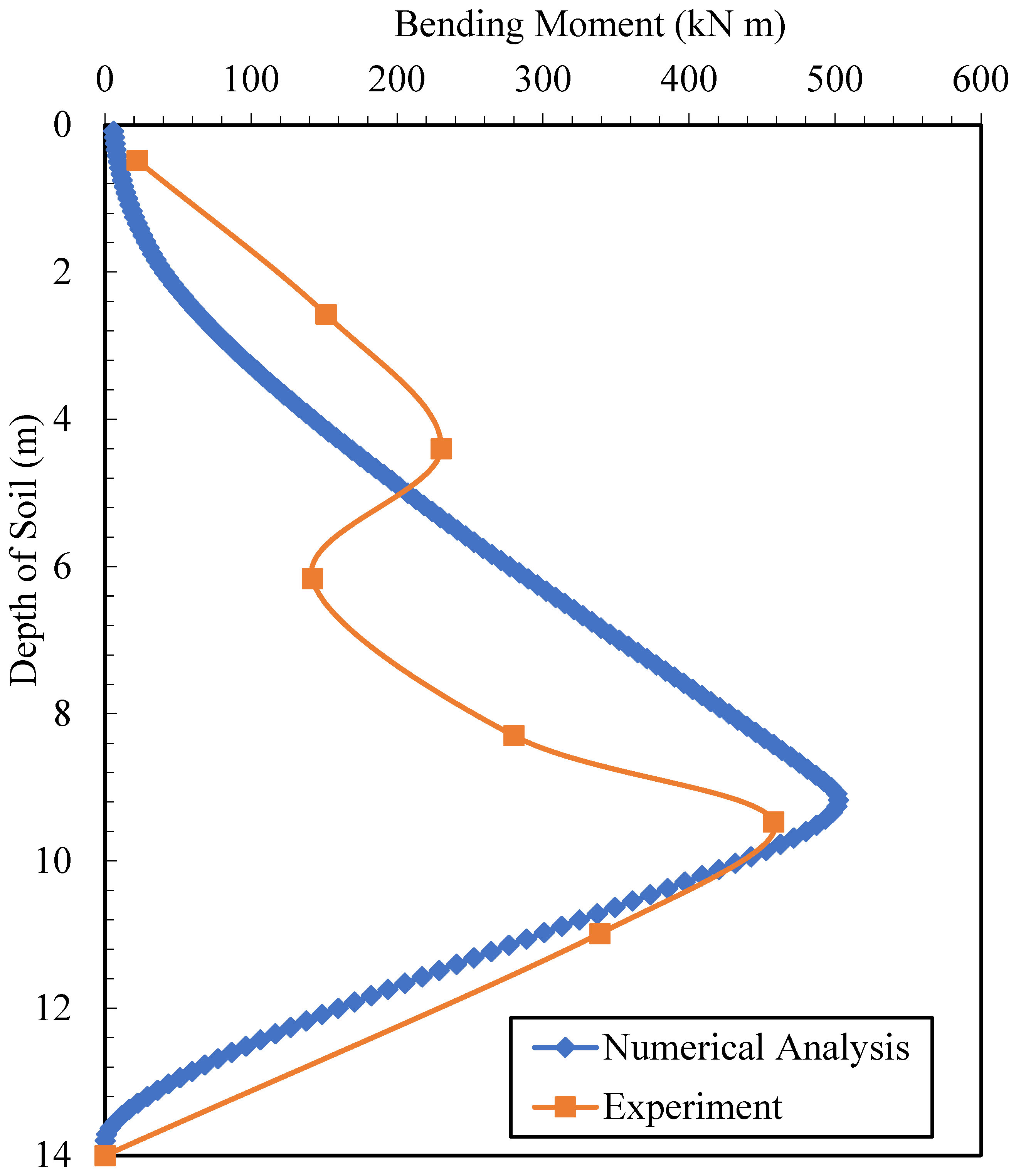
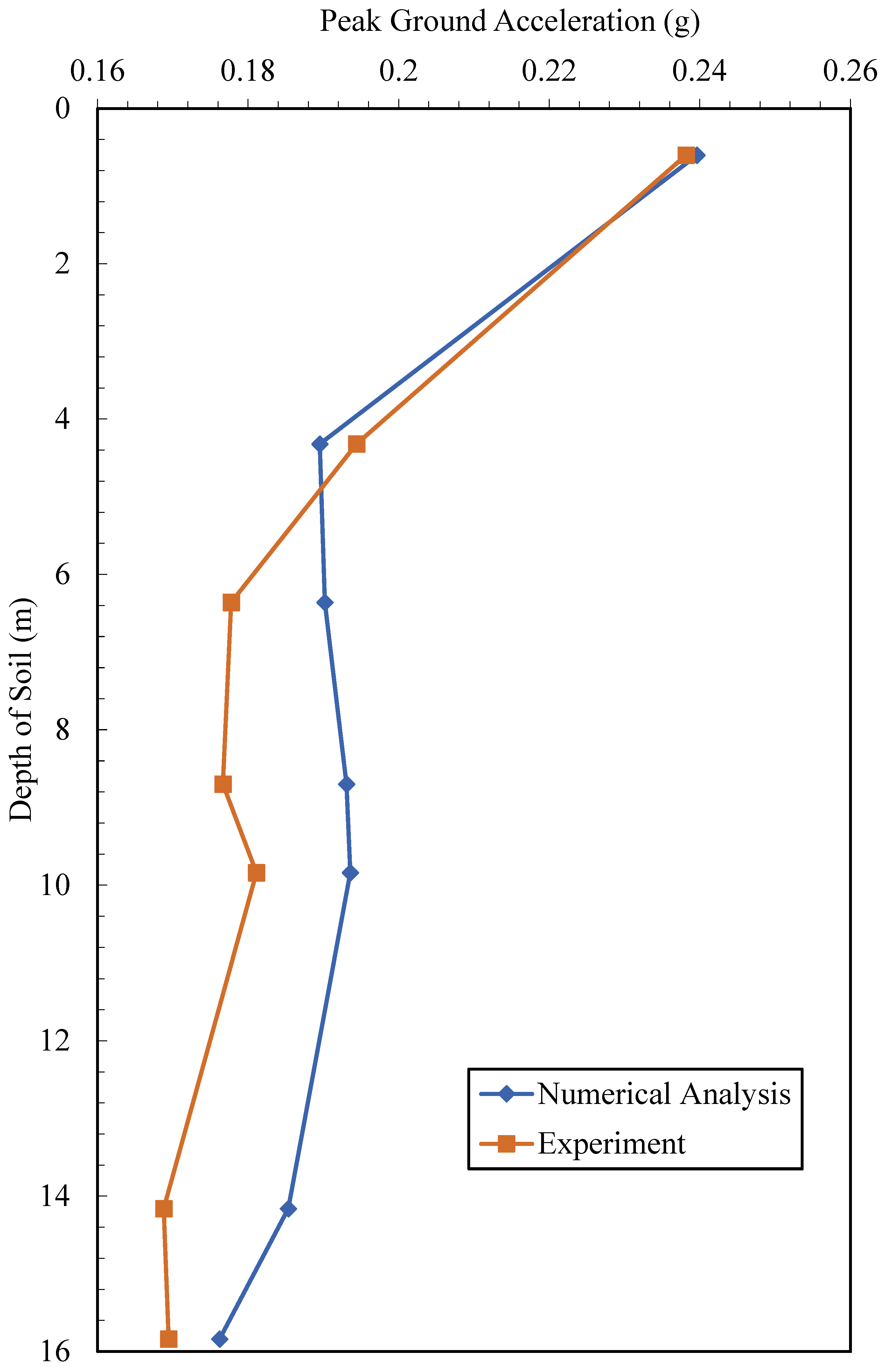
3.5. Numerical Verification of the Experiment
4. Parametric Studies
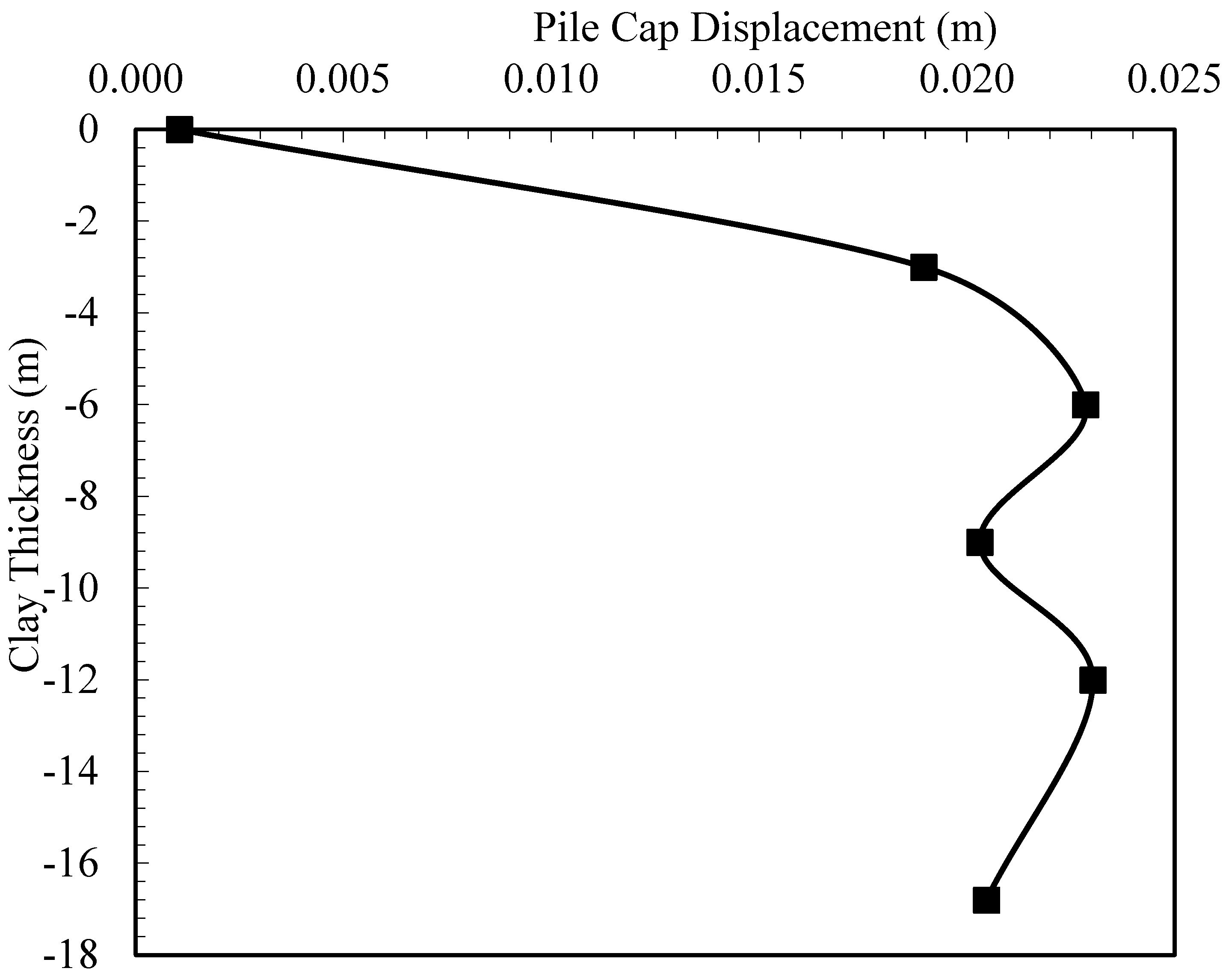
4.1. Effect of Clay Liner Thickness
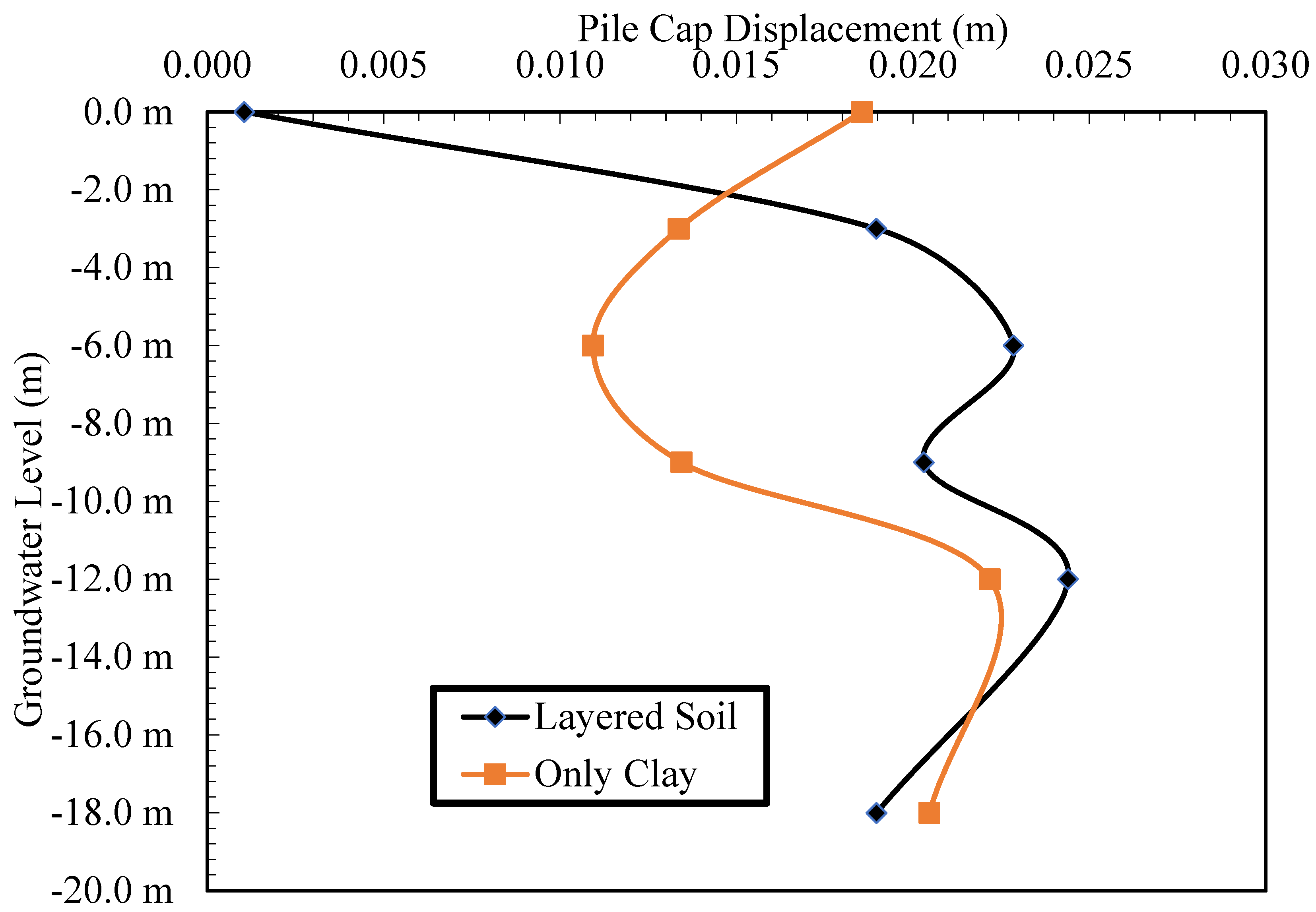
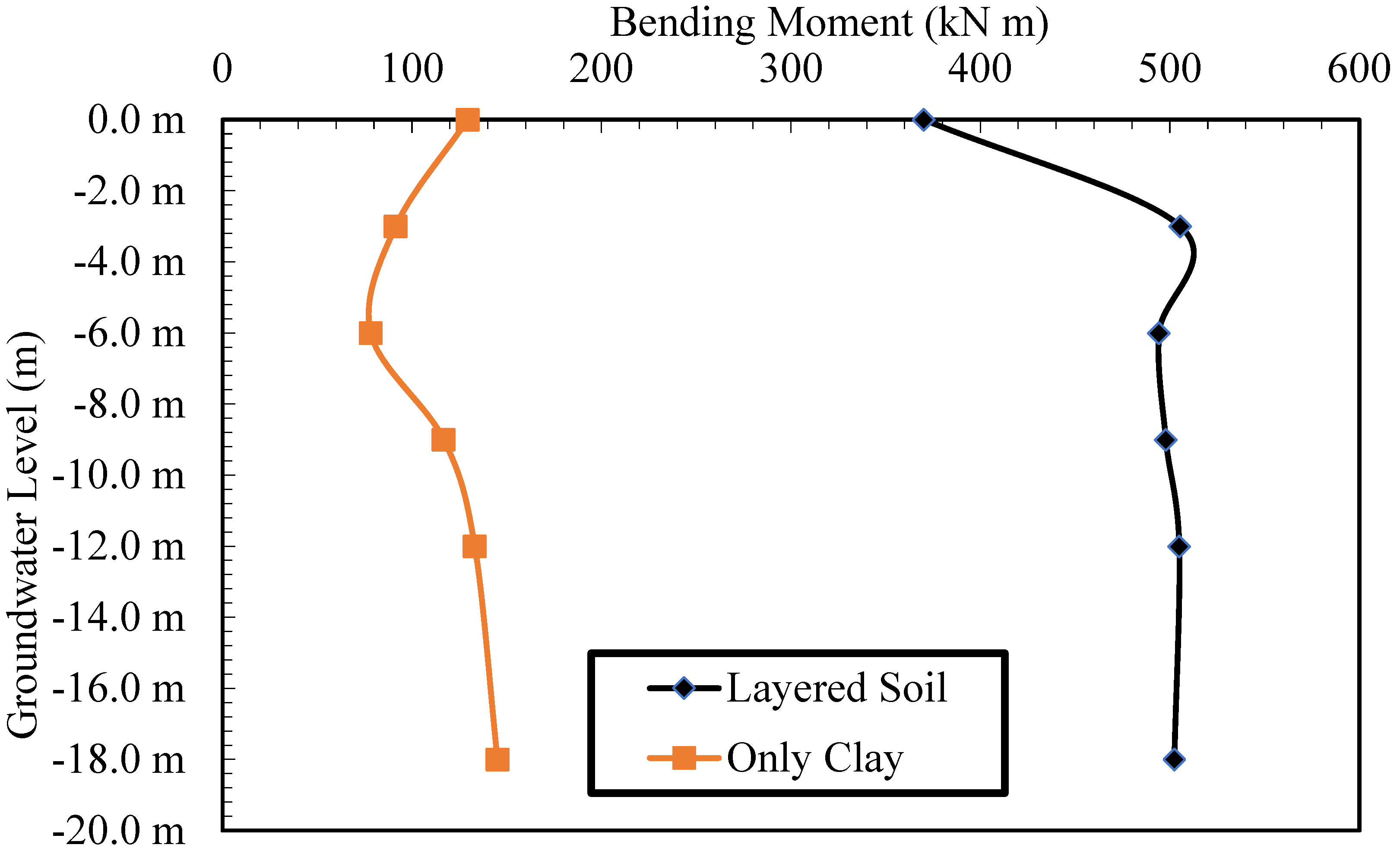
4.2. Effect of Groundwater Level
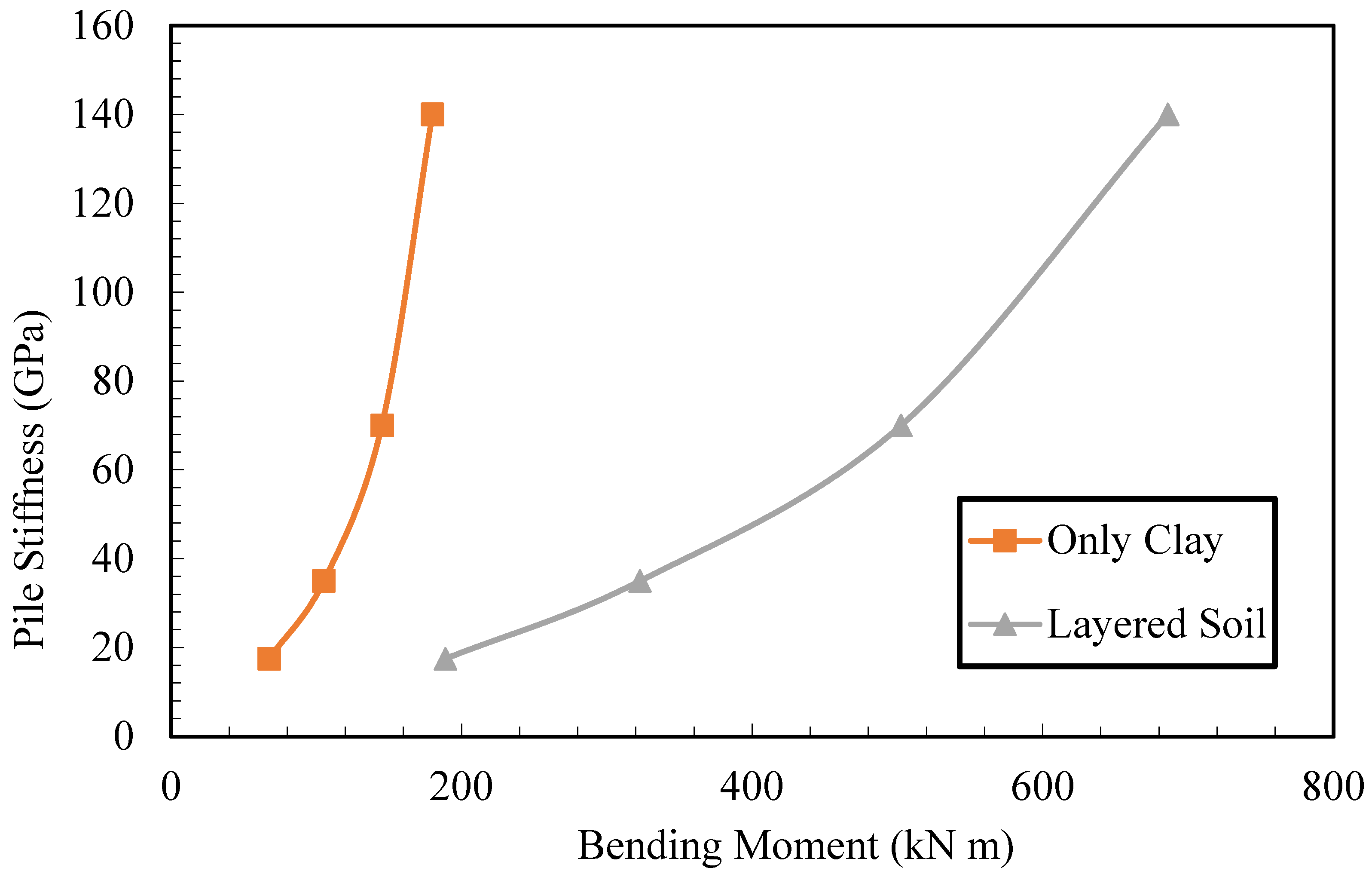
4.3. Effect of Pile Stiffness
4.4. Effect of Earthquake Magnitude
5. Conclusions
- The results obtained from the centrifuge experiment by Garala et al. [13] were confirmed with numerical analysis results obtained using a finite element program in this study.
- In the kinematic interaction analyses, with the increase in the weak soil layer thickness in layered soil conditions, although there was no significant increase in the displacement values at first, significant increases were observed in the pile cap displacement at the depth where the clay layer thickness reached approximately 75% of the total pile length. No significant increase in displacements was observed as the clay layer thickness reached larger values. This was due to the fact that the pile behaves more flexible under kinematic conditions as the number of sockets in the dense sand decreased.
- In the analyses of the investigation of the effect of the groundwater level, considering the stratified situation, it was seen that the displacement increased with the increase in the depth of the groundwater level, and there was no significant change in displacement after the water level reached -6 m. This situation was caused by the groundwater level approaching the underlying sand layer, and the effect of the groundwater level remaining in the sand on deformation decreased.
- In the only-clay soil, it was observed that as the groundwater level increased, the deformation first decreased, and then the deformation increased. The decrease in the groundwater level caused the upper layer to behave more rigidly and the deformation to decrease up to a certain level. As the water level decreased below the bottom elevation of the pile, the pile behaved flexibly, and its deformation increased.
- In the analyses examining the effect of pile stiffness, it was observed that deformation decreased as the elasticity modulus increased in the layered case, and there was no change in deformation after the elasticity modulus reached the 70 GPa value used in the experiments. For the only-clay soil, it was seen that the deformation increased with the increase in the elasticity modulus, and there was no change in deformation after reaching the value of 70 GPa. In this case, it is understood that the elasticity modulus was effective as it approached the soil elasticity modulus, and the effect decreased after a certain stiffness.
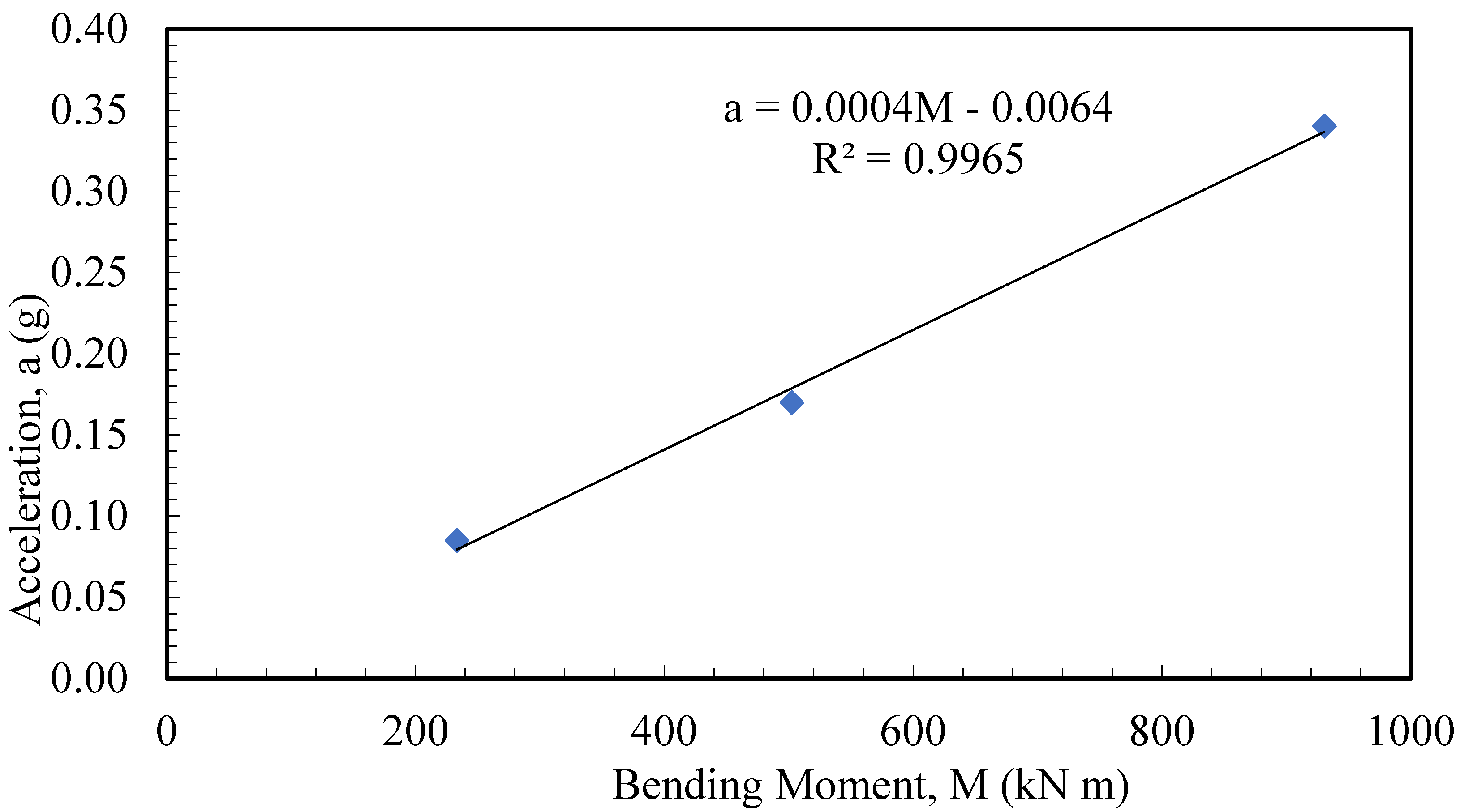
- In the analysis examining the earthquake magnitude effect, it was seen that displacements and moments increased linearly with the increase in earthquake acceleration. The results obtained show that the earthquake magnitude is the most important parameter affecting the results.
- When the results obtained are evaluated from a practical engineering perspective, it is understood that the piles, which are adequate for design under static loads, are exposed to significant bending moments under dynamic loads. Therefore, it is of great importance to take dynamic loads into consideration in the design stage. In addition, under dynamic loads in weak soil conditions, the largest displacement occurs in the pile head, while the highest bending moment occurs in the transition between soil layers. Additional precautions should be taken by increasing the steel reinforcement ratios in the pile foundation connection areas and in the transition between soil layers.
- Earthquake forces are one of the most important factors that directly affect the design of pile systems. Therefore, using accurate earthquake data is important for design. Selecting earthquake data by taking local soil conditions into consideration will make the design more realistic.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mizuno, H. Pile damage during earthquakes in Japan. Dyn. Response Pile Found. 1987, 53–78. [Google Scholar]
- Gazetas, G.; Tazoh, T.; Shimizu, K.; Fan, K. Seismic response of the pile foundation of Ohba-Ohashi bridge. In Proceedings of the 3rd Conference of the International Conference on Case Histories in Geotechnical Engineering, St. Louis, MO, USA, 1–9 June 1993. [Google Scholar]
- Kaynia, A.M. Dynamic Stiffness and Seismic Response of Pile Groups. Ph.D. Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 1982. [Google Scholar]
- Fan, K.; Gazetas, G.; Kaynia, A.; Kausel, E.; Ahmad, S. Kinematic seismic response of single piles and pile groups. J. Geotech. Eng. 1991, 117, 1860–1879. [Google Scholar] [CrossRef]
- Kavvads, M.; Gazetas, G. Kinematic seismic response and bending of free-head piles in layered soil. Geotechnique 1993, 43, 207–222. [Google Scholar] [CrossRef]
- Haigh, S.K. Effects of Earthquake-Induced Liquefaction on Pile Foundations in Sloping Ground. Doctoral Dissertation, University of Cambridge, Cambridge, UK, 2002. [Google Scholar]
- Brandenberg, S.J.; Boulanger, R.W.; Kutter, B.L.; Chang, D. Behavior of pile foundations in laterally spreading ground during centrifuge tests. J. Geotech. Geoenviron. Eng. 2005, 131, 1378–1391. [Google Scholar] [CrossRef]
- Castelli, F.; Maugeri, M.; Mylonakis, G. Numerical analysis of kinematic soil—Pile interaction. In Proceedings of the AIP Conference Proceedings, American Institute of Physics, Reggio Calabria, Italy, 8–11 July 2008; Volume 1020, pp. 618–625. [Google Scholar]
- Madabhushi, G.; Haigh, S.; Knappett, J. Design of Pile Foundations in Liquefiable Soils; World Scientific: Singapore, 2009. [Google Scholar]
- Haskell, J.J.M. Guidance for the Design of Pile Groups in Laterally Spreading Soil. Doctoral Dissertation, University of Cambridge, Cambridge, UK, 2014. [Google Scholar]
- Luo, X.; Li, S.; Xu, H. Results of real-time kinematic positioning based on real GPS L5 data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1193–1197. [Google Scholar] [CrossRef]
- Mallick, M.; Mandal, K.K.; Sahu, R.B. Effects of axial loading on dynamic response of laterally loaded single piles in liquefiable layered soil of Kolkata city considering nonlinearity of soil. SN Appl. Sci. 2022, 4, 297. [Google Scholar] [CrossRef]
- Garala, T.K.; Madabhushi, G.S.; Di Laora, R. Experimental investigation of kinematic pile bending in layered soils using dynamic centrifuge modelling. Géotechnique 2022, 72, 146–161. [Google Scholar] [CrossRef]
- Garala, T.K.; Madabhushi, G.S. Comparison of seismic behaviour of pile foundations in two different soft clay profiles. In Physical Modelling in Geotechnics; CRC Press: Boca Raton, FL, USA, 2018; Volume 2, pp. 1359–1364. [Google Scholar]
- Sahare, A.; Ueda, K.; Uzuoka, R. Influence of the sloping ground conditions and the subsequent shaking events on the pile group response subjected to kinematic interactions for a liquefiable sloping ground. Soil Dyn. Earthq. Eng. 2022, 152, 107036. [Google Scholar] [CrossRef]
- Yamashita, K.; Shigeno, Y.; Hamada, J.; Chang, D.W. Seismic response analysis of piled raft with grid-form deep mixing walls under strong earthquakes with performance-based design concerns. Soils Found. 2018, 58, 65–84. [Google Scholar] [CrossRef]
- Kaynia, A.M. Effect of kinematic interaction on seismic response of offshore wind turbines on monopiles. Earthq. Engng. Struct. Dyn. 2021, 50, 777–790. [Google Scholar] [CrossRef]
- Al-Jeznawi, D.; Jais, I.B.M.; Albusoda, B.S.; Khalid, N. Numerical modeling of single closed and open-ended pipe pile embedded in dry soil layers under coupled static and dynamic loadings. J. Mech. Behav. Mater. 2022, 31, 587–594. [Google Scholar] [CrossRef]
- Hu, H.; Gan, G.; Bao, Y.; Guo, X.; Xiong, M.; Han, X.; Chen Cui, L.; Wang, L. Nonlinear stochastic seismic response analysis of three-dimensional reinforced concrete piles. Buildings 2023, 13, 89. [Google Scholar] [CrossRef]
- Huang, W.; Liu, J.; Wang, H.; Ayasrah, M.; Qiu, H.; Wang, Z. Study on dynamic response of inclined pile group foundation under earthquake action. Buildings 2023, 13, 2416. [Google Scholar] [CrossRef]
- Tipsunavee, T.; Arangjelovski, G.; Jongpradist, P. Numerical analysis on effects of soil improvement on pile forces on existing high-rise building. Buildings 2023, 13, 1523. [Google Scholar] [CrossRef]
- FEMA. NEHRP, Prestandard and Commentary for the Seismic Rehabilitation of Buildings (No. 356); Report; FEMA: Washington, DC, USA, 2000.
- American Association of State Highway Transportation Officials (AASHTO). Guide Specifications for Seismic Isolation Design; American Association of State Highway Transportation Officials (AASHTO): Washington, DC, USA, 1999. [Google Scholar]
- European Committee for Standardization. EC8 Eurocode 8 (EN 1998-1, EN 1998-5): Seismic Design of Building; European Committee for Standardization: Bruxelles, Belgium, 2004. [Google Scholar]
- Turkish Building and Earthquake Regulation (TBDY). 2018.
- ASTM D854; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D4254; Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM D4253; Standard Test Methods for Maximum Index Density and Unit Weight of Soils Using a Vibratory Table. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM D6913; Standard Test Methods for Particle-Size Distribution (Gradation) of Soils Using Sieve Analysis. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D7181; Standard Method for Consolidated Drained Triaxial Compression Test for Soils. ASTM International: West Conshohocken, PA, USA, 2011.
- Kok, S.; Huat, B.B. Numerical Modeling of Laterally Loaded Piles. Am. J. Appl. Sci. 2008, 5, 1403–1408. [Google Scholar] [CrossRef]
- Van der Kwaak, B. Modelling of Dynamic Pile Behaviour during an Earthquake Using PLAXIS 2D: Embedded Beam (Row). Master’s Thesis, Delf University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Rathod, D.; Muthukkumaran, K.; Sitraham, T.G. Dynamic response of single pile located in soft clay underlay by sand. Int. J. Geomate 2016, 11, 2563–2567. [Google Scholar] [CrossRef]
- Kardogan, P.S.O.; Stacul, S.; Pagnini, F.; Squeglia, N.; Bhattacharya, S. 2D FEM Analyses for the Evaluation of Seismic Performance of Single Pile and Pile Group-Supported Structure in Liquefiable Soil; Associazione Geotecnica Italiana: Rome, Italy, 2019; ISBN 978-0-367-14328-2. [Google Scholar]
- Deendayal, R. Finite element analysis of a single pile under cyclic loading. Int. J. Civ. Eng. Technol. IJCIET 2017, 8, 918–924. [Google Scholar]
- Deendayal, R.; Nigitha, D. Response of single pile under dynamic loading. In Proceedings of the Indian Geotechnical Conference 2017 GeoNEst, Guwahati, India, 14–16 December 2017. [Google Scholar]
- Plaxis 2D Reference Manual; PLAXIS B.V.: Delft, The Netherlands, 2023.
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Design equations and curves. J. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Snyder, J.L. Full Scale Test Lateral Load Tests of a 3 × 5 Pile Group in Soft Clays and Silts. Master’s Thesis, Brigham Young University, Provo, UT, USA, 2004. [Google Scholar]
- Lau, B.H. Cyclic Behaviour of Monopile Foundations for Offshore Wind Turbines in Clay. Ph.D. Dissertation, University of Cambridge, Cambridge, UK, 2015. [Google Scholar]
- Brinkgreve RB, J.; Engin, E.; Engin, H.K. Validation of empirical formulas to derive model parameters for sands. Numer. Methods Geotech. Eng. 2010, 1, 137–142. [Google Scholar]
- Phoban, H.; Seeboonruang, U.; Lueprasert, P. Numerical modeling of single pile behaviors due to groundwater level rising. Appl. Sci. 2021, 11, 5782. [Google Scholar] [CrossRef]


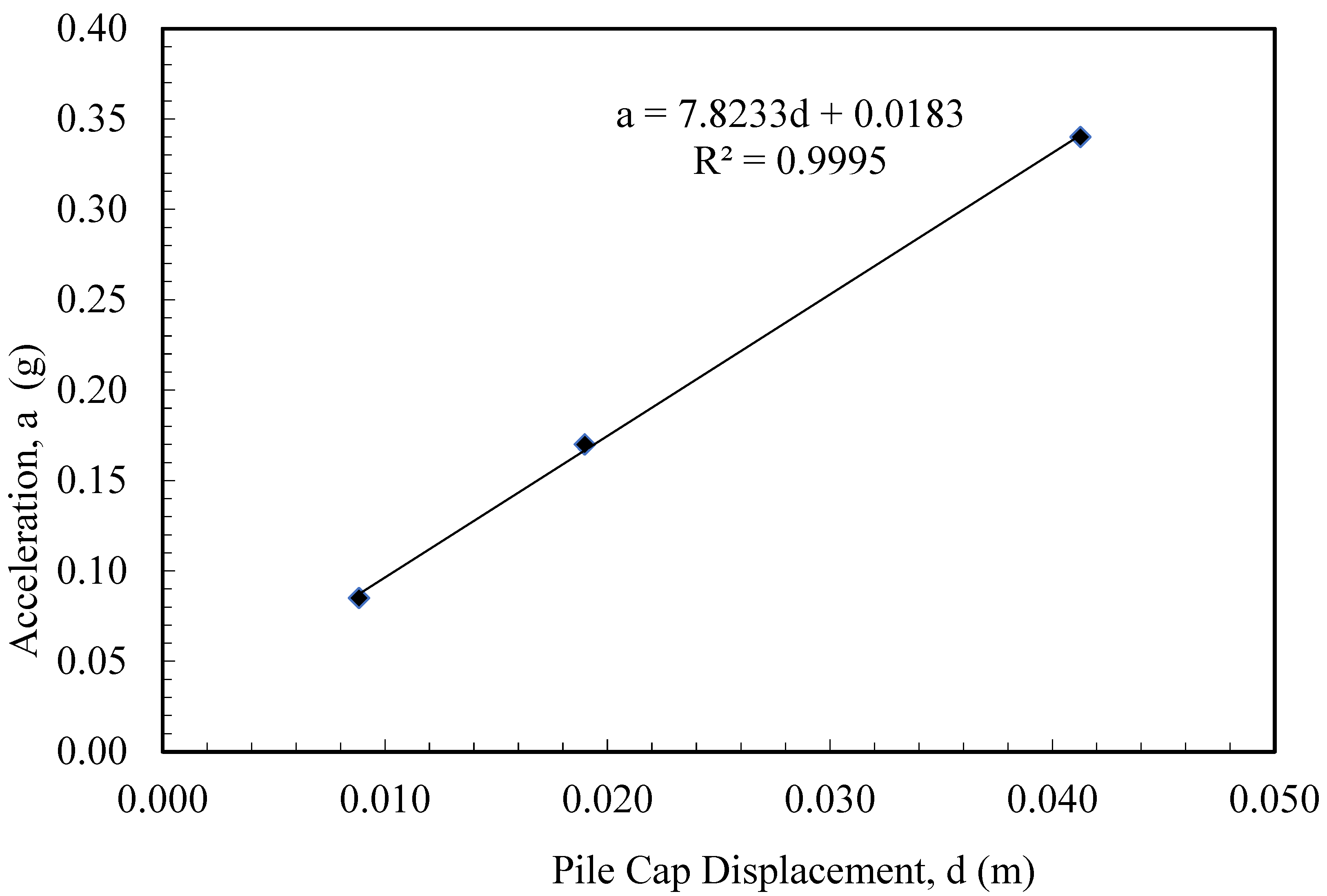
| Property | Standard | Value |
|---|---|---|
| Specific gravity, Gs | ASTM D854 [26] | 2.65 |
| Maximum void ratio, emax | ASTM D4254 [27] | 0.767 |
| Minimum void ratio, emin | ASTM D4253 [28] | 0.49 |
| Effective particle size, D10 (mm) | ASTM D6913 [29] | 0.68 |
| Average particle size, D50 (mm) | ASTM D6913 [29] | 0.80 |
| Coefficient of uniformity, Cu | ASTM D6913 [29] | 1.221 |
| Coefficient of curvature, Cc | ASTM D6913 [29] | 0.97 |
| Relative density, Dr (%) | ASTM D4254 [27] | 85 |
| Peak friction angle, ϕp (°) | ASTM D7181 [30] | 37.2 |
| Property | Value |
|---|---|
| Plastic limit, PL (%) | 30 |
| Liquid limit, LL (%) | 63 |
| Plasticity index, PI (%) | 33 |
| Specific gravity, Gs | 2.60 |
| Slope of critical state line (CSL) in q-p′ plane | 0.90 |
| Slope of an unload-reload line, (κ) | 0.039 |
| Intercept of CSL at p′ = 1 kPa (Γ) | 3.31 |
| Slope of normal consolidation line (λ) | 0.22 |
| Parameters | Unit | Speswhite Kaolin Clay | Leighton Buzzard Sand | LE |
|---|---|---|---|---|
| Material type | - | HS Small | HS Small | Linear Elastic |
| Drainage type | - | Undrained | Drained | Drained |
| γunsat, Unsaturated unit weight | kN/m3 | 16.2 | 18.4 | 24.00 |
| γsat, Saturated unit weight | kN/m3 | 16.4 | 20.36 | 24.00 |
| einit, initial void ratio | - | 0.50 | 0.50 | 0.50 |
| Rayleigh, α | - | 0.09425 | 0.09425 | 0.00 |
| Rayleigh, β | - | 7.958 × 10−4 | 7.96 × 10−4 | 0.00 |
| ν′, Poisson’s ratio (linear elastic) | - | - | - | 0.20 |
| G′, Shear modulus | kN/m2 | - | - | 1.04 × 107 |
| E′, Elasticity modulus | kN/m2 | - | - | 2.50 × 107 |
| Vs, S wave velocity | m/s | - | - | 2063.00 |
| Vp, P wave velocity | m/s | - | - | 3370.00 |
| E50ref, Secant stiffness | kN/m2 | 1500 | 5.10 × 104 | |
| Eoedref, Tangent stiffness | kN/m2 | 750 | 5.10 × 104 | |
| Eurref, Unloading/reloading stiffness | kN/m2 | 8000 | 1.5 × 105 | |
| m, Rate of stress-dependency | - | 0.8 | 0.4344 | |
| c′, Cohesion | kN/m2 | 1 | 0.00 | |
| Ø, Internal friction angle | ° | 21 | 37.20 | |
| Ψ, dilatation angle | ° | 0 | 8.625 | |
| γ0.7, Shear strain at 0.7G0 | - | 2.00 × 10−4 | 1.15 × 10−4 | |
| G0ref, Small strain stiffness | kN/m2 | 1.398 × 104 | 1.178 × 105 | |
| ν′ur, Poisson’s ratio | - | 0.20 | 0.20 | |
| Pref, Reference stress | kN/m2 | 100.00 | 100.00 | |
| K0nc, Stress ratio | - | 0.64 | 0.3954 | |
| Rinter, Interface factor | - | 0.50 | 0.70 |
| Parameter | Unit | Pile Cap | Pile |
|---|---|---|---|
| Material type | - | Elastic | Elastic |
| EA1 | kN/m | 9.90 × 105 | 9.30 × 106 |
| EA2 | kN/m | 9.90 × 105 | 9.930 × 106 |
| EI | kN/m2/m | 7425 | 3.439 × 105 |
| d | m | 0.3 | 0.6661 |
| w | kN/m/m | 3.5 | 2.8 |
| ν | - | 0.37 | 0.3 |
| Rayleigh α | - | 0.2827 | 0.2827 |
| Rayleigh β | - | 2.39 × 10−3 | 2.39 × 10−3 |
| Mesh Type | Number of Element | Pile Cap Displacement (m) |
|---|---|---|
| Coarse | 882 | 0.021 |
| Medium | 1093 | 0.022 |
| Fine | 1687 | 0.018 |
| Very Fine | 2207 | 0.018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bildik, S.; Tanrıöver, H. Numerical Investigation of the Pile–Soil Interaction Problem under Dynamic Loads. Appl. Sci. 2023, 13, 11653. https://doi.org/10.3390/app132111653
Bildik S, Tanrıöver H. Numerical Investigation of the Pile–Soil Interaction Problem under Dynamic Loads. Applied Sciences. 2023; 13(21):11653. https://doi.org/10.3390/app132111653
Chicago/Turabian StyleBildik, Selçuk, and Haluk Tanrıöver. 2023. "Numerical Investigation of the Pile–Soil Interaction Problem under Dynamic Loads" Applied Sciences 13, no. 21: 11653. https://doi.org/10.3390/app132111653
APA StyleBildik, S., & Tanrıöver, H. (2023). Numerical Investigation of the Pile–Soil Interaction Problem under Dynamic Loads. Applied Sciences, 13(21), 11653. https://doi.org/10.3390/app132111653






