Performance Analysis of Interval Type-2 Fuzzy
Abstract
:1. Introduction
2. Interval Type-2 Fuzzy Sets
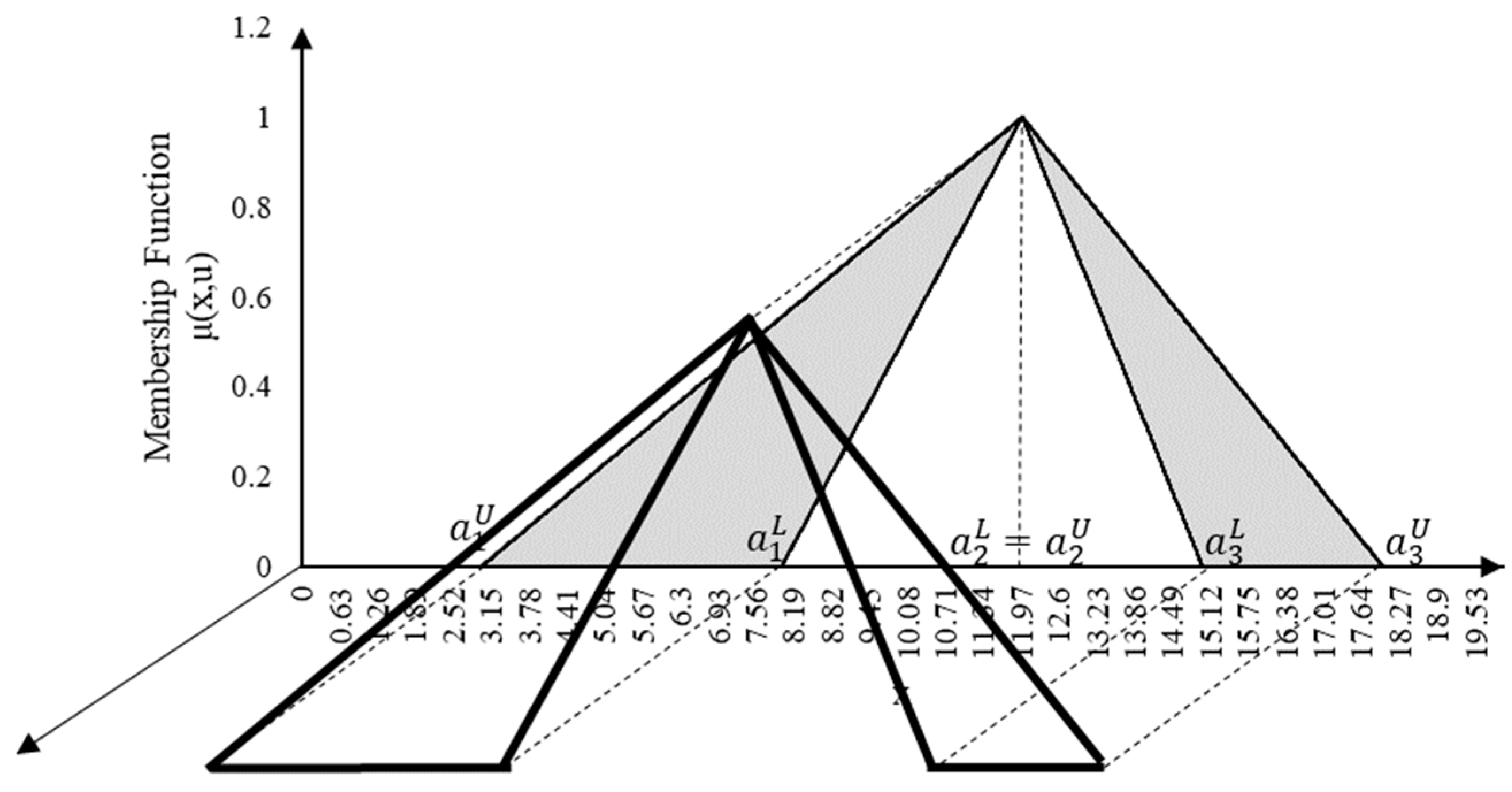
2.1. Interval Type-2 Triangular Fuzzy Sets
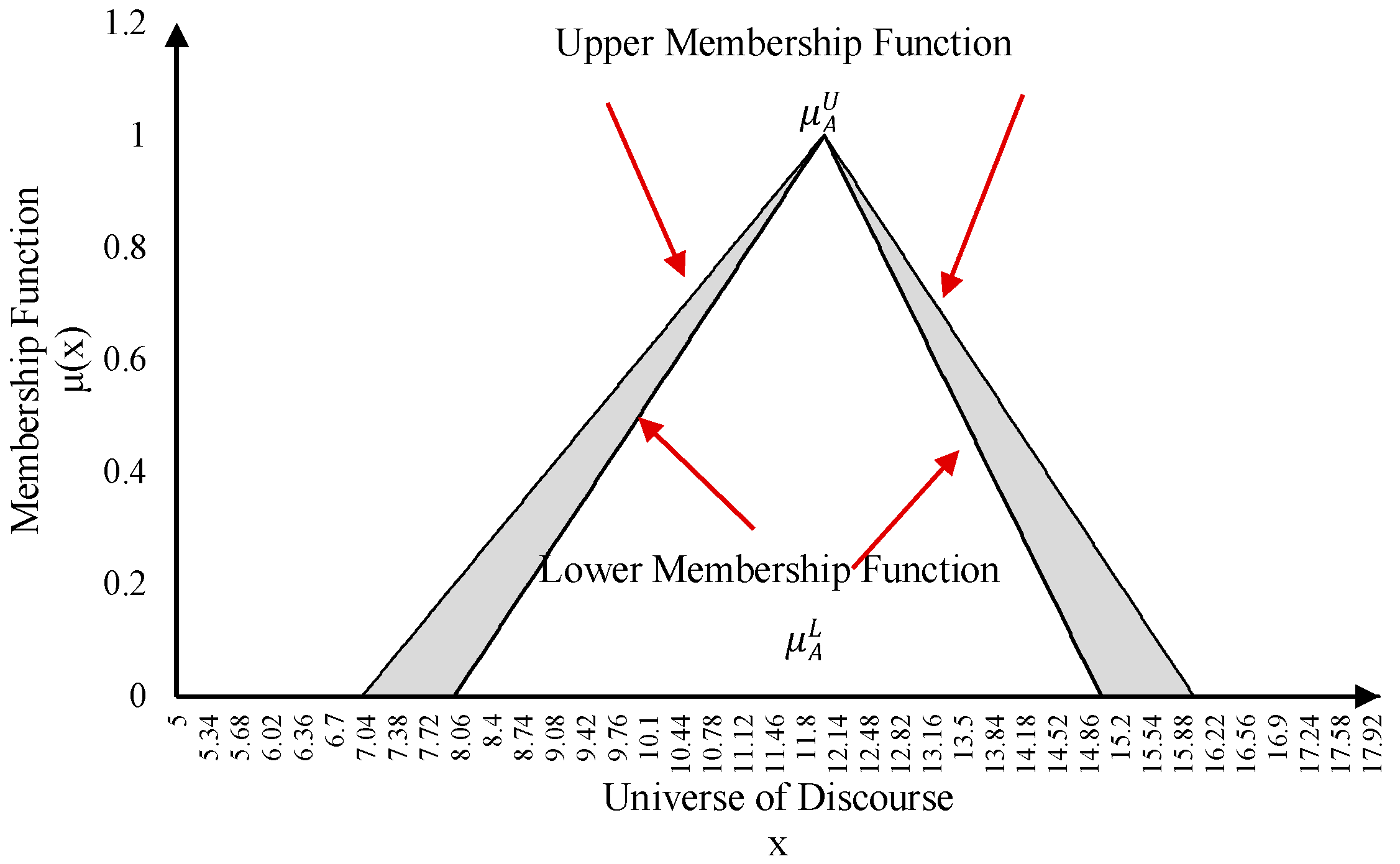
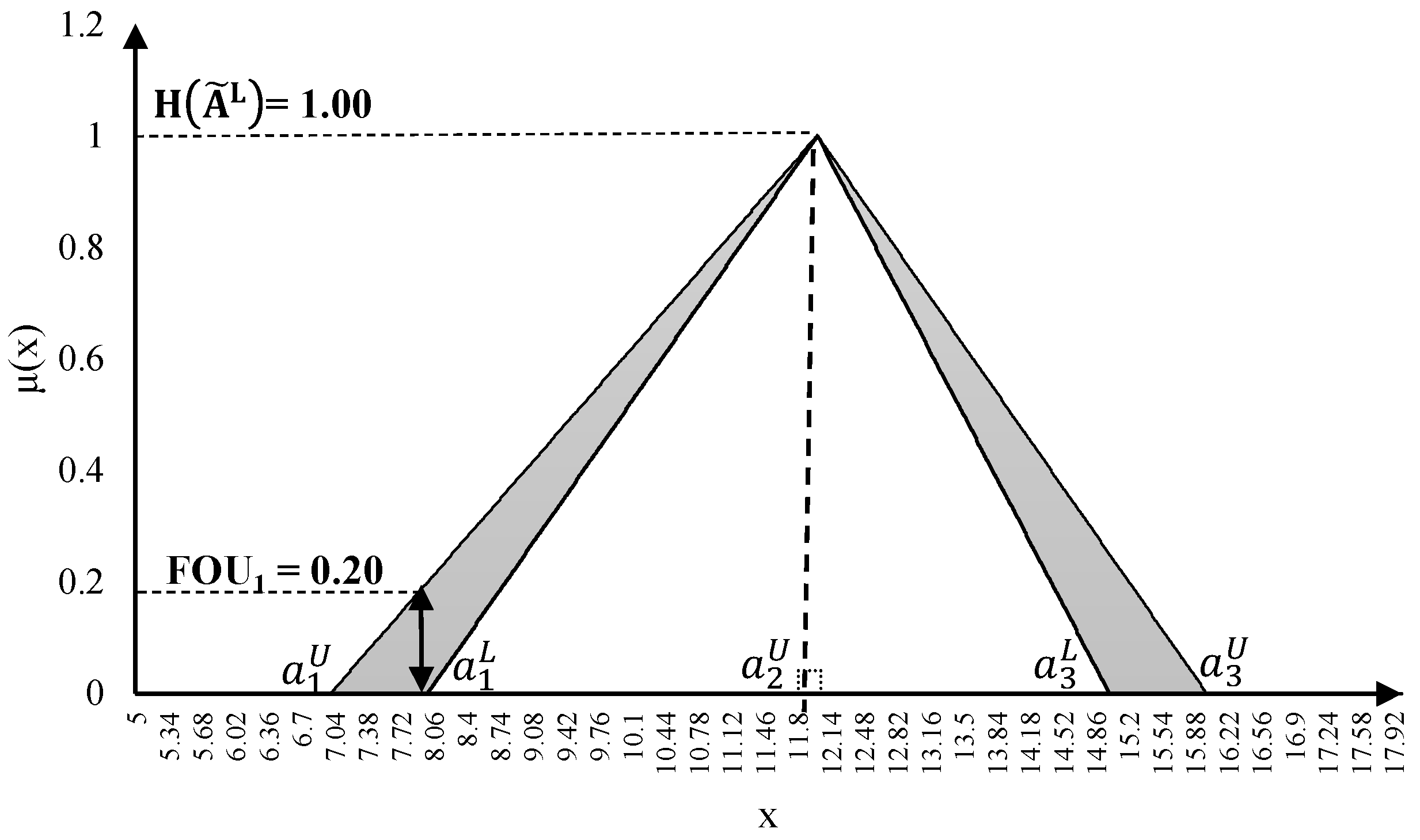
2.2. Footprint of Uncertainty and Membership Functions
3. Interval Type-2 Fuzzy and R Control Charts
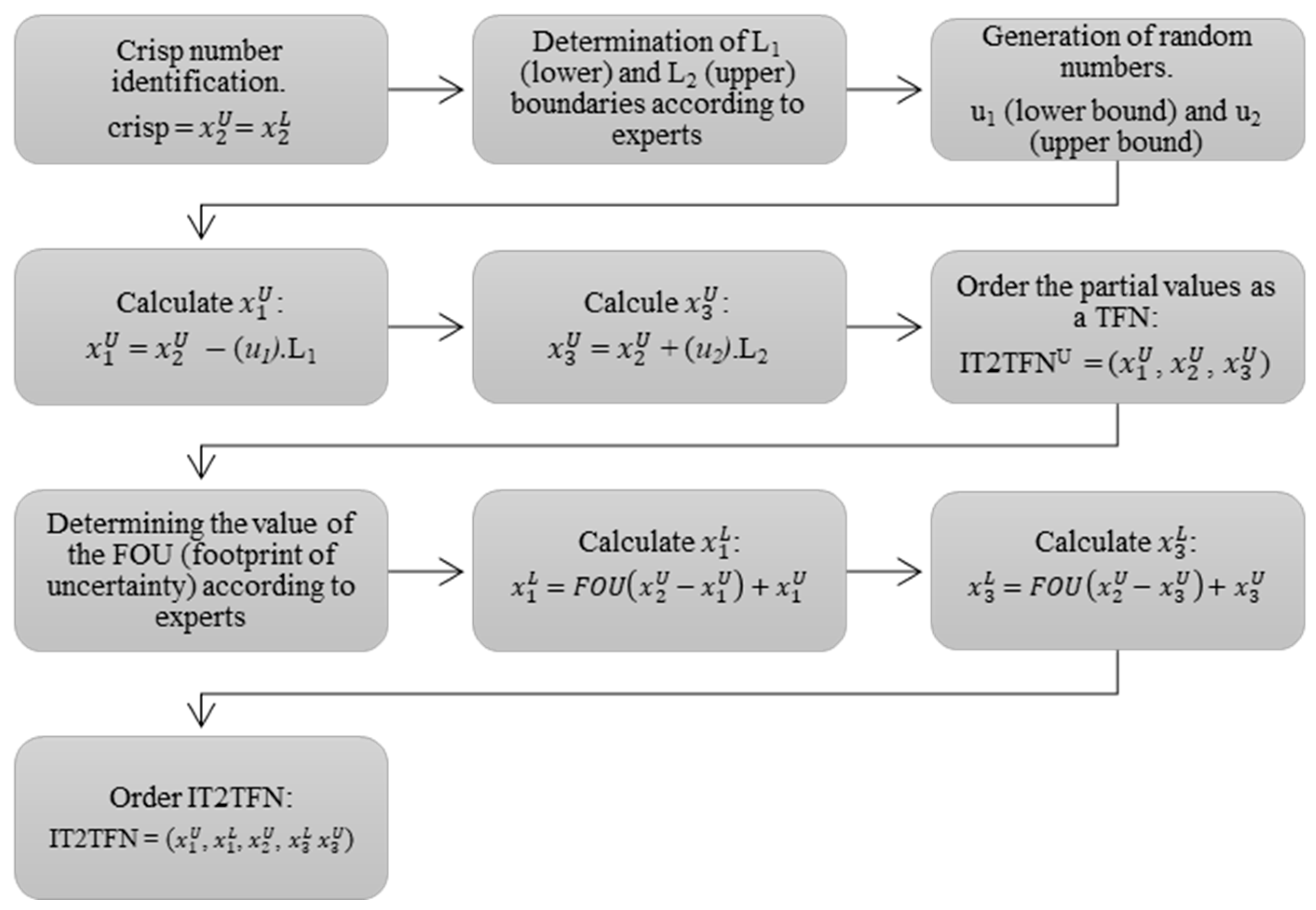
3.1. Fuzzification Method
3.2. Type Reduction and Defuzzification Method
4. Control Chart Performance Measures
5. Results and Discussion
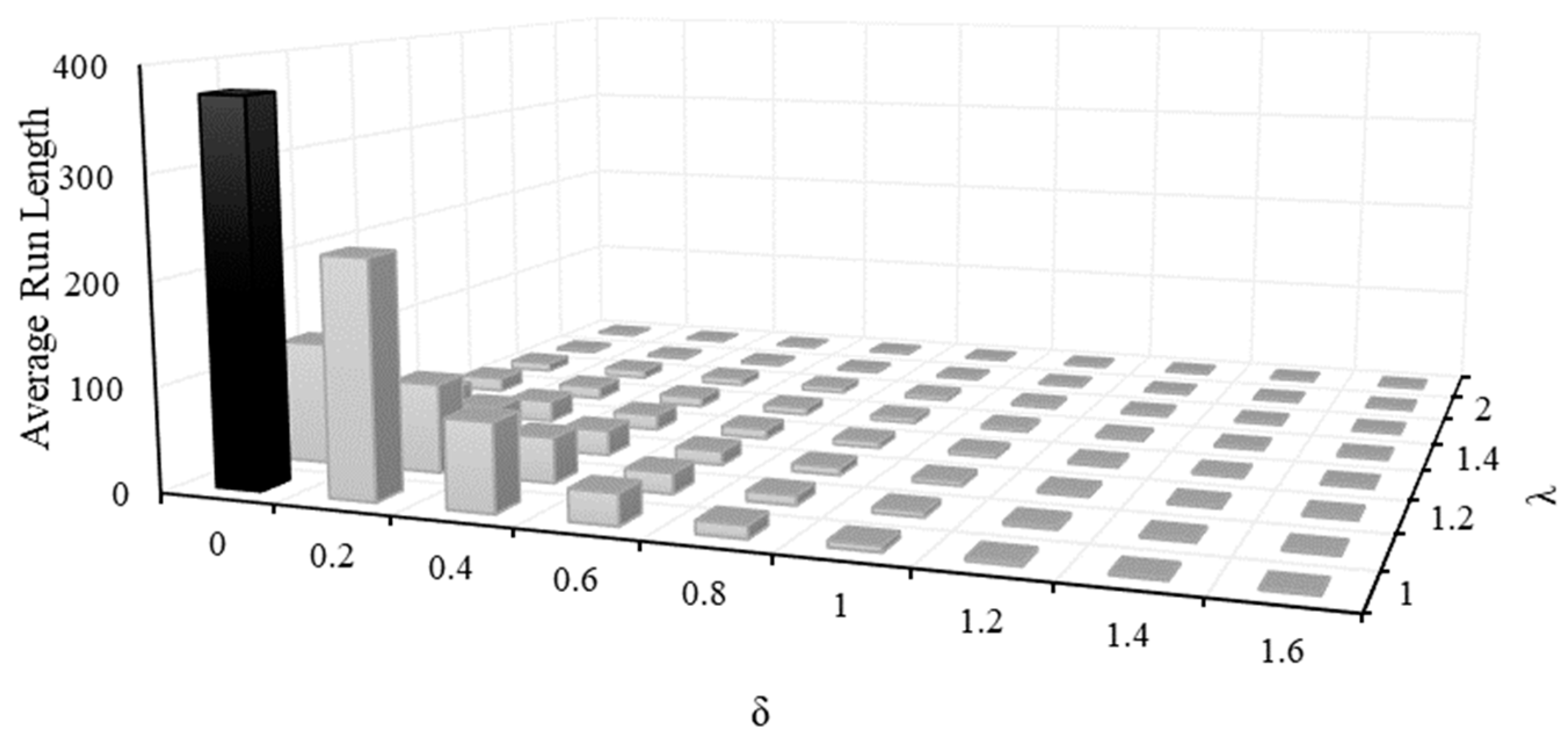
5.1. Average Run Length (ARL) and Standard Deviation Run Length (SDRL) for -R Control Charts
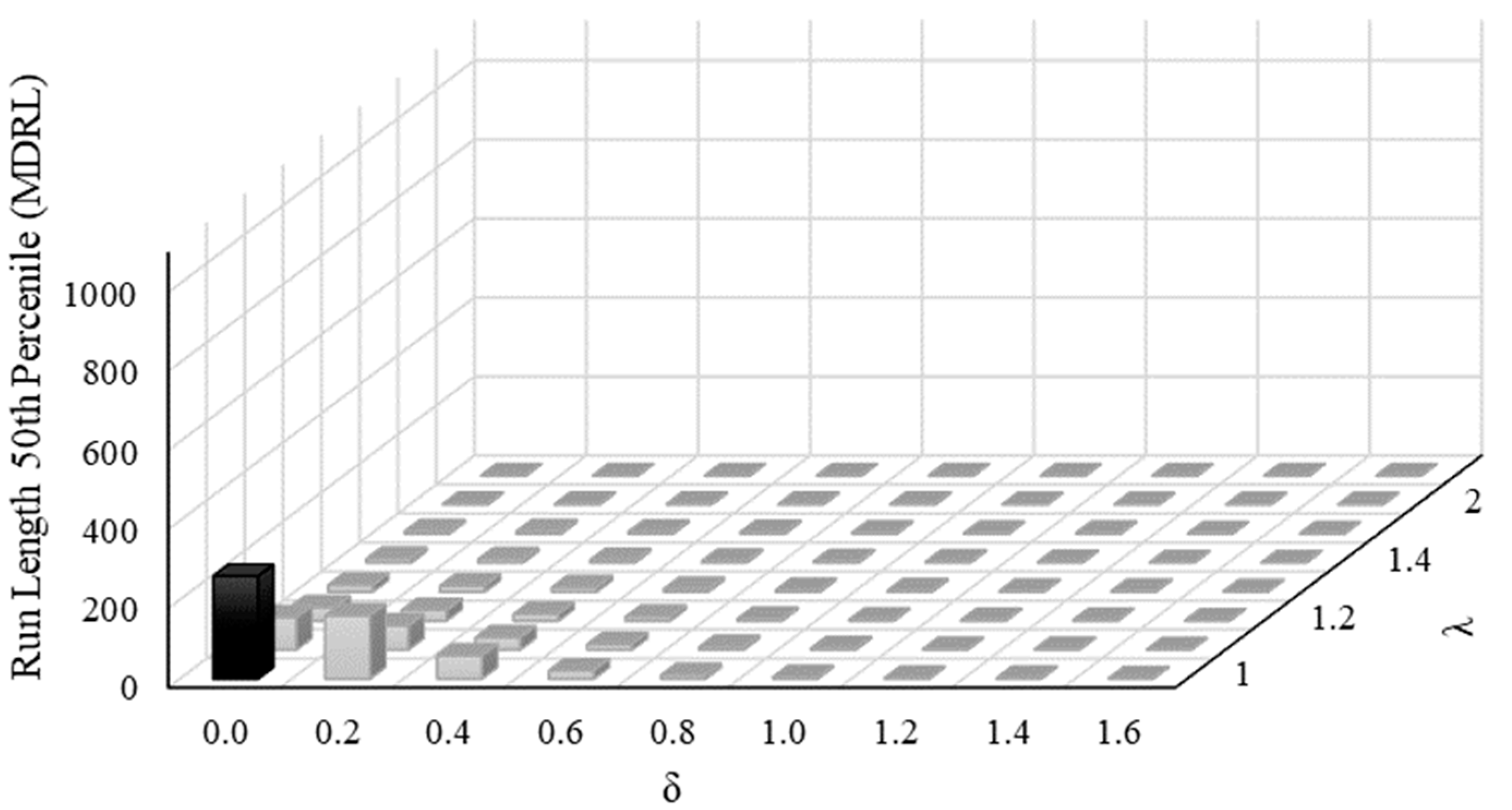
5.2. Run Length Percentile Analysis for -R Control Charts
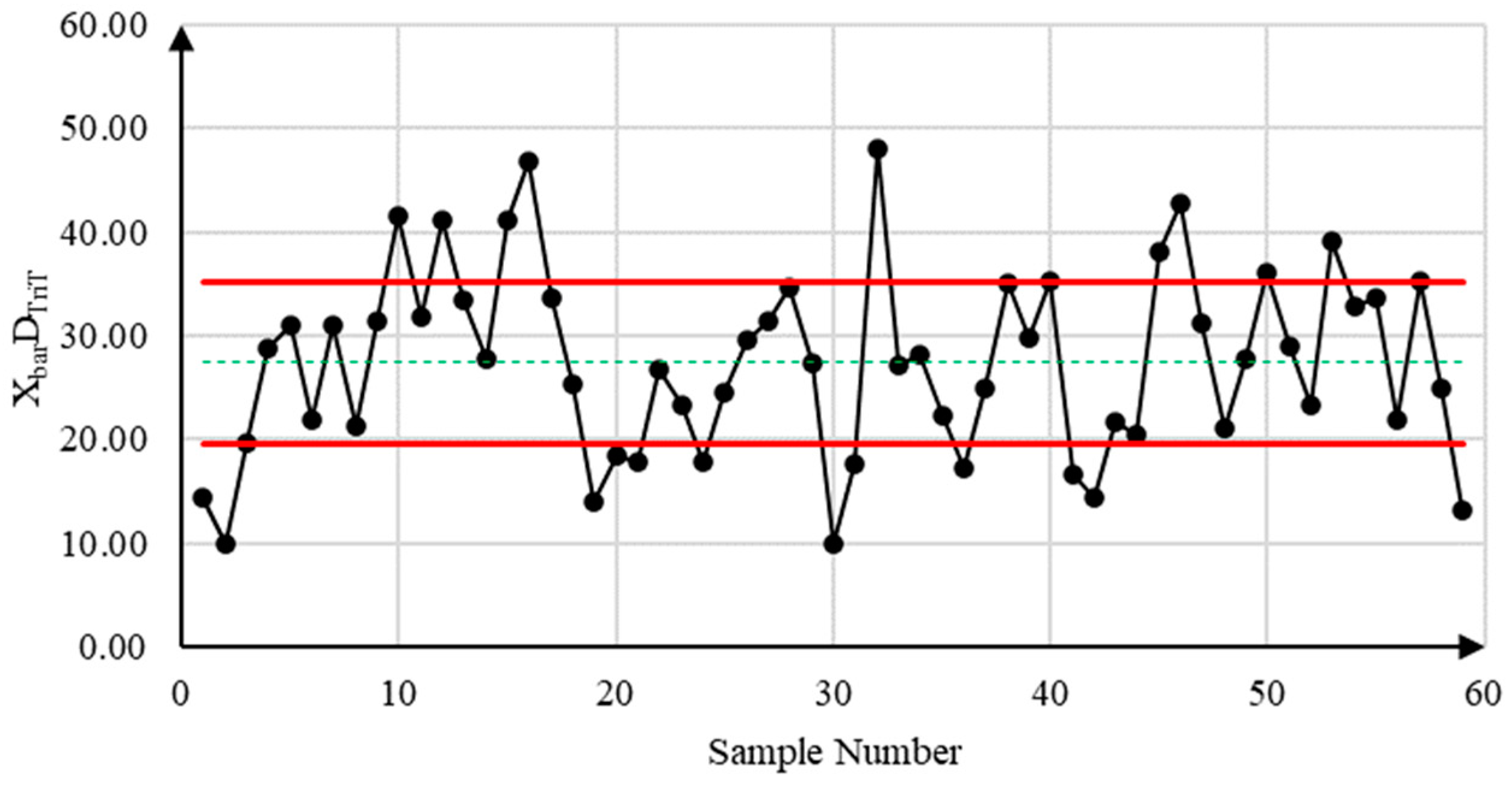
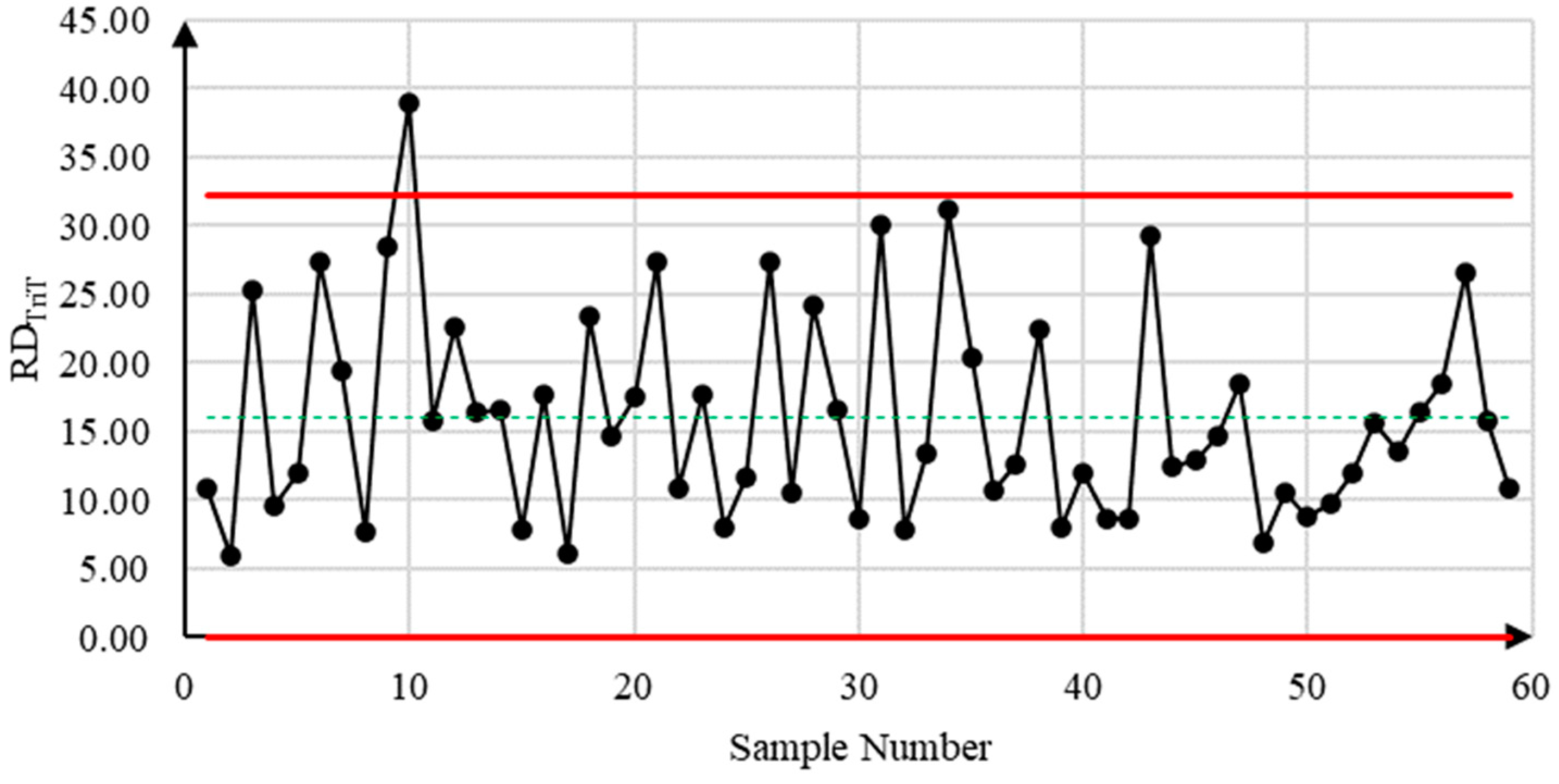
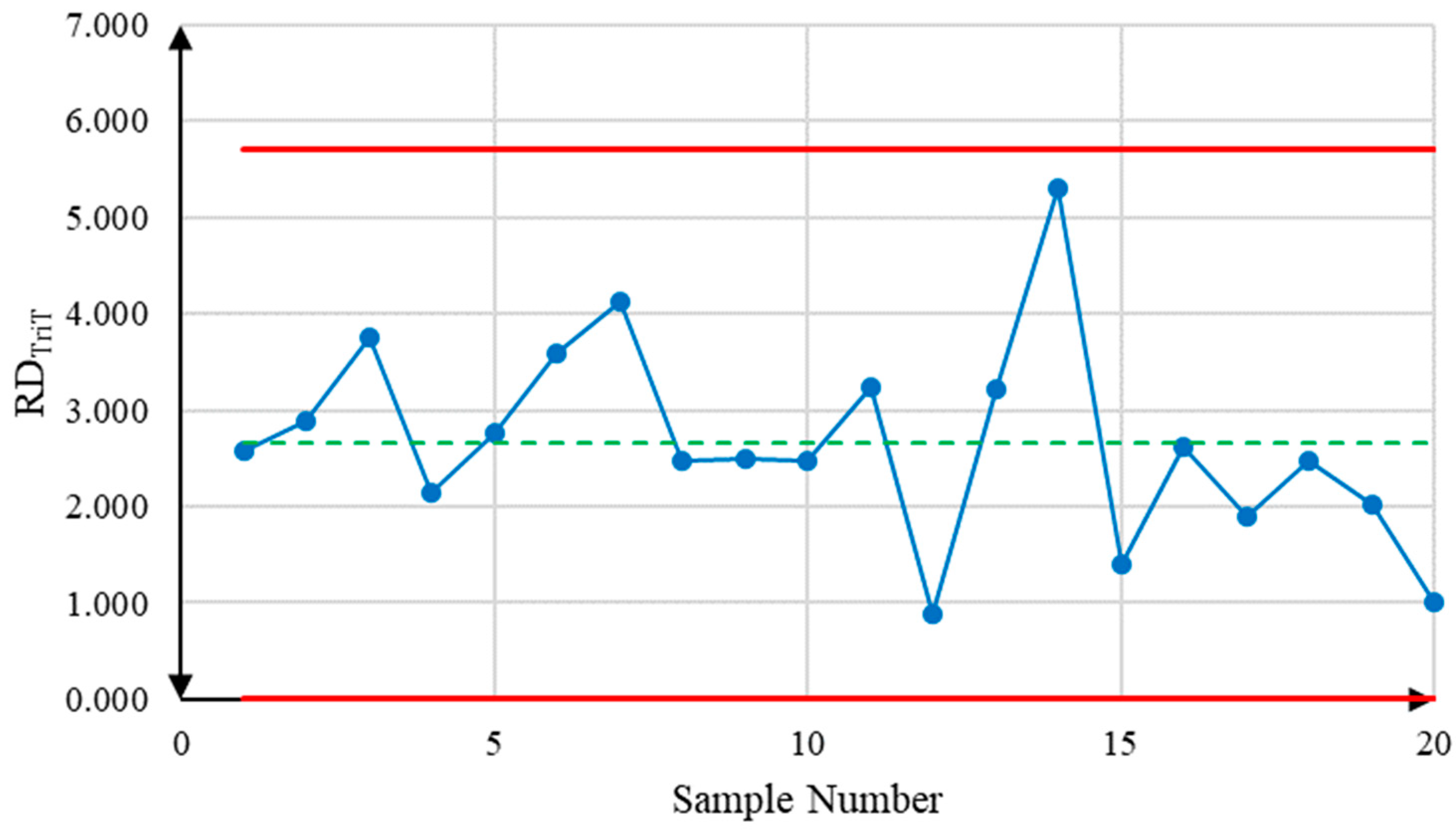
5.3. Illustrative Example
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oakland, J.; Oakland, R. Statistical Process Control, 7th ed.; Routledge: New York, NY, USA, 2019. [Google Scholar]
- Stapenhurst, T. Mastering Statistical Process Control, 1st ed.; Elsevier Butterwoth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Ozdemir, A. Development of fuzzy -S control charts with unbalanced fuzzy data. Soft Comput. 2021, 25, 4015–4025. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets and Systems 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Mendel, J.M. Uncertain Rule-Based Fuzzy Logic Systems—Introduction and New Directions, 1st ed.; Prentice Hall: Hoboken, NJ, USA, 2001. [Google Scholar]
- JCGM (Joint Commettee for Guides in Metrology). Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement, 1st ed.; BIPM (Bureau International des Poids et Mesures): Sèvres, France, 2008. [Google Scholar]
- Mendes, A.S.; Machado, M.A.G.; Rocha Rizol, P.M.S. Fuzzy control chart for monitoring mean and range of univariate processes. Pesqui. Oper. 2019, 39, 339–357. [Google Scholar] [CrossRef]
- Khan, M.Z.; Khan, M.F.; Aslam, M.; Mughal, A.R. A study on average run length of fuzzy EWMA control chart. Soft Comput. 2022, 26, 9117–9124. [Google Scholar]
- Mendel, J.M.; John, R.I.B. Type-2 Fuzzy Sets Made Simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Kaya, I.; Turgut, A. Design of variable control charts based on type-2 fuzzy sets with real case study. Soft Comput. 2021, 25, 613–633. [Google Scholar]
- Chen, C.; Shen, Q. Transformation-Based Fuzzy Rule Interpolation Using Interval Type-2 Fuzzy Sets. Algorithms 2017, 10, 91. [Google Scholar] [CrossRef]
- Javanmard, M.; Nehi, H.M. Solving interval type-2 fuzzy linear programming problem with a new ranking function method. In Proceedings of the Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS), Qazvin, Iran, 7–9 March 2017. [Google Scholar]
- Teksen, H.E.; Anagün, A.S. Different methods to fuzzy -R control charts used in production: Interval type-2 fuzzy set example. J. Enterp. Inf. Manag. 2018, 31, 848–866. [Google Scholar]
- Karnik, N.N.; Mendel, J.M. Introduction to Type-2 Fuzzy Logic Systems. In Proceedings of the IEEE FUZZ Conference, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar]
- Karnik, N.N.; Mendel, J.M.; Liang, Q. Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 1999, 7, 643–658. [Google Scholar] [CrossRef]
- Raj, R.; Yang, J.-M. Analytical Structure and Performance of Interval Type-2 Fuzzy Two-Term Controllers with Varying Footprint of Uncertainty. Int. J. Comput. Intell. Syst. 2022, 15, 106. [Google Scholar]
- Zhang, C.; Zhou, H.; Li, Z.; Ju, X.; Tan, S.; Duan, J. Analysis of the difference between footprints of uncertainty for interval type-2 fuzzy PI controllers. Soft Comput. 2022, 26, 9993–10005. [Google Scholar]
- Costa, A.F.B.; Rahim, M.A. A Synthetic Control Chart for Monitoring the Mean and Variance. J. Qual. Maint. Eng. 2006, 12, 81–88. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Gulbay, M.; Kahraman, C. An alternative approach to fuzzy control charts: Direct fuzzy approach. Inf. Sci. 2007, 177, 1463–1480. [Google Scholar] [CrossRef]
- Sentürk, S.; Erginel, N. Development of fuzzy -R and -S control charts using α-cuts. Inf. Sci. 2009, 179, 1542–1551. [Google Scholar] [CrossRef]
- Hesamian, G.; Akbari, M.G.; Ranjbar, E. Exponentially Weighted Moving Average Control Chart Based on Normal Fuzzy Random Variables. Int. J. Fuzzy Syst. 2019, 21, 1187–1195. [Google Scholar]
- Zabihinpour, M.; Ariffin, M.K.A.; Tang, S.H.; Azfanizam, A.S. Construction of fuzzy -S control charts with an unbiased estimation of standard deviation for a triangular fuzzy random variables. J. Intell. Fuzzy Syst. 2015, 28, 2735–2747. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Type-2 Fuzzy Logic: Theory and Applications. In Proceedings of the IEEE International Conference on Granular Computing (GRC), San Jose, CA, USA, 2–4 November 2007. [Google Scholar]
- Kahraman, C.; Oztaysi, B.; Sari, I.U.; Turanoglu, E. Fuzzy Analytic Hierarchy Process with Interval Type-2 Fuzzy Sets. Knowl. Based Syst. 2014, 59, 48–57. [Google Scholar] [CrossRef]
- Jensen, W.A.; Jones-Farmer, L.A.; Champ, C.W.; Woodall, W.H. Effects of parameter estimation on control chart properties: A literature review. Int. J. Qual. Technol. 2006, 38, 349–364. [Google Scholar]
- Chen, G. The Mean and Standard Deviation of the Run Length Distribution of Charts when Control Limits are Estimated. Stat. Sin. 1997, 7, 789–798. [Google Scholar]
- Saleh, N.A.; Mahmoud, M.A.; Keefe, M.J.; Woodall, W.H. The Difficulty in Designing Shewhart X-bar and X Control Charts with Estimated Parameters. J. Qual. Technol. 2015, 47, 127–138. [Google Scholar] [CrossRef]
- Chakraborti, S. Run Length Distribution and Percentiles: The Shewhart Chart with Unknown Parameters. Qual. Eng. 2007, 19, 119–127. [Google Scholar] [CrossRef]
- Khoo, M.B.C. Performance measures for the Shewhart control chart. Qual. Eng. 2004, 16, 585–590. [Google Scholar] [CrossRef]
- Fang, J.; Wang, H.; Deng, W. Design of EWMA Control Charts for Assuring Predetermined Production Process Quality. Res. J. Appl. Sci. 2013, 5, 3010–3014. [Google Scholar] [CrossRef]
- Costa, A.F.B.; Magalhães, M.S.; Epprecht, E.K. Monitoring the process mean and variance using synthetic control chart with two-stage testing. Int. J. Prod. Res. 2009, 47, 5067–5086. [Google Scholar]
- Domangue, R.; Patch, S.C. Some omnibus exponentially weighted moving average statistical process monitoring schemes. Technometrics 1991, 33, 299–313. [Google Scholar] [CrossRef]




| Target | FOU Values (θ) | FOU Relationship |
|---|---|---|
| Faster response | 0.00 < θ1 = θ2 = θ ≤ 0.50 | They should be equal and small |
| Response with lower or no overshoot | 0.50 ≤ θ1 = θ2 = θ < 1.00 | They should be equal and larg |
| Smaller overshoot and faster response | 0.30 ≤ θ1 = θ2 = θ < 0.90 | They should be equal and medium sized |
| Traditional -R Control Chart ARL | |||||||||
| λ | δ (Shift) | ||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 |
| 1.0 | 370.5 | 228.0 | 84.9 | 30.8 | 12.6 | 6.0 | 3.3 | 2.1 | 1.5 |
| 1.1 | 119.2 | 88.2 | 44.1 | 20.1 | 9.7 | 5.2 | 3.1 | 2.1 | 1.6 |
| 1.2 | 48.8 | 40.3 | 25.0 | 13.8 | 7.7 | 4.5 | 2.9 | 2.1 | 1.6 |
| 1.3 | 24.2 | 21.3 | 15.3 | 9.8 | 6.2 | 4.0 | 2.8 | 2.0 | 1.6 |
| 1.4 | 13.9 | 12.8 | 10.1 | 7.2 | 5.0 | 3.5 | 2.6 | 2.0 | 1.6 |
| 1.5 | 8.9 | 8.4 | 7.1 | 5.5 | 4.2 | 3.1 | 2.4 | 1.9 | 1.6 |
| 2.0 | 2.6 | 2.5 | 2.4 | 2.3 | 2.1 | 1.9 | 1.7 | 1.5 | 1.4 |
| 2.5 | 1.6 | 1.6 | 1.5 | 1.5 | 1.5 | 1.4 | 1.4 | 1.3 | 1.2 |
| Traditional -R Control Chart SDRL | |||||||||
| λ | δ (Shift) | ||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 |
| 1.0 | 370.0 | 227.5 | 84.4 | 30.2 | 12.1 | 5.5 | 2.8 | 1.5 | 0.9 |
| 1.1 | 118.7 | 87.7 | 43.6 | 19.6 | 9.2 | 4.7 | 2.6 | 1.5 | 1.0 |
| 1.2 | 48.3 | 39.8 | 24.4 | 13.3 | 7.1 | 4.0 | 2.4 | 1.5 | 1.0 |
| 1.3 | 23.7 | 20.8 | 14.8 | 9.3 | 5.6 | 3.5 | 2.2 | 1.4 | 1.0 |
| 1.4 | 13.4 | 12.2 | 9.5 | 6.7 | 4.5 | 3.0 | 2.0 | 1.4 | 1.0 |
| 1.5 | 8.4 | 7.9 | 6.5 | 5.0 | 3.6 | 2.6 | 1.8 | 1.3 | 1.0 |
| 2.0 | 2.0 | 2.0 | 1.8 | 1.7 | 1.5 | 1.3 | 1.1 | 0.9 | 0.8 |
| 2.5 | 0.9 | 0.9 | 0.9 | 0.9 | 0.8 | 0.8 | 0.7 | 0.6 | 0.6 |
| IT2TFN -R Control Chart ARL | |||||||||
| λ | δ (Shift) | ||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 |
| 1.0 | 372.45 | 228.54 | 85.32 | 30.43 | 12.55 | 5.93 | 3.35 | 2.11 | 1.56 |
| 1.1 | 118.56 | 87.10 | 44.23 | 20.32 | 9.56 | 5.17 | 3.11 | 2.10 | 1.59 |
| 1.2 | 48.54 | 39.54 | 24.89 | 13.77 | 7.67 | 4.54 | 2.95 | 2.08 | 1.58 |
| 1.3 | 24.10 | 21.09 | 15.45 | 9.71 | 6.14 | 4.03 | 2.76 | 2.00 | 1.60 |
| 1.4 | 13.91 | 12.61 | 9.77 | 7.27 | 4.99 | 3.50 | 2.56 | 1.97 | 1.60 |
| 1.5 | 8.70 | 8.33 | 7.06 | 5.52 | 4.10 | 3.08 | 2.41 | 1.92 | 1.59 |
| 2.0 | 2.56 | 2.50 | 2.42 | 2.29 | 2.05 | 1.87 | 1.70 | 1.54 | 1.42 |
| 2.5 | 1.57 | 1.55 | 1.54 | 1.50 | 1.45 | 1.40 | 1.36 | 1.29 | 1.26 |
| IT2TFN -R Control Chart SDRL | |||||||||
| λ | δ (Shift) | ||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 |
| 1.0 | 371.141 | 226.537 | 84.860 | 29.844 | 12.081 | 5.298 | 2.807 | 1.515 | 0.942 |
| 1.1 | 119.090 | 85.087 | 43.340 | 19.960 | 9.167 | 4.605 | 2.551 | 1.528 | 0.972 |
| 1.2 | 47.318 | 39.034 | 24.456 | 13.138 | 7.122 | 3.997 | 2.400 | 1.491 | 0.964 |
| 1.3 | 23.366 | 20.641 | 14.992 | 9.222 | 5.628 | 3.549 | 2.208 | 1.407 | 0.968 |
| 1.4 | 13.220 | 12.266 | 9.299 | 6.628 | 4.510 | 3.012 | 1.981 | 1.397 | 0.987 |
| 1.5 | 8.180 | 7.808 | 6.506 | 4.924 | 3.534 | 2.526 | 1.880 | 1.346 | 0.964 |
| 2.0 | 2.042 | 1.975 | 1.879 | 1.735 | 1.482 | 1.296 | 1.094 | 0.910 | 0.774 |
| 2.5 | 0.938 | 0.938 | 0.918 | 0.869 | 0.827 | 0.742 | 0.697 | 0.614 | 0.576 |
| 5th | λ | δ (Shift) | 25th | λ | δ (Shift) | ||||||||||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | ||
| 1.0 | 19 | 12 | 5 | 2 | 1 | 1 | 1 | 1 | 1 | 1.0 | 107 | 66 | 25 | 9 | 4 | 2 | 1 | 1 | 1 | ||
| 1.1 | 7 | 5 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 1.1 | 35 | 26 | 13 | 6 | 3 | 2 | 1 | 1 | 1 | ||
| 1.2 | 3 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1.2 | 14 | 12 | 8 | 4 | 3 | 2 | 1 | 1 | 1 | ||
| 1.3 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.3 | 7 | 6 | 5 | 3 | 2 | 2 | 1 | 1 | 1 | ||
| 1.4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.4 | 4 | 4 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | ||
| 1.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.5 | 3 | 3 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | ||
| 2.0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2.0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 2.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 50th (MDRL) | λ | δ (Shift) | |||||||||||||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | ||||||||||||
| 1.0 | 257 | 158 | 59 | 21 | 9 | 4 | 2 | 2 | 1 | ||||||||||||
| 1.1 | 83 | 61 | 31 | 14 | 7 | 4 | 2 | 2 | 1 | ||||||||||||
| 1.2 | 34 | 28 | 17 | 10 | 5 | 3 | 2 | 2 | 1 | ||||||||||||
| 1.3 | 17 | 15 | 11 | 7 | 4 | 3 | 2 | 2 | 1 | ||||||||||||
| 1.4 | 10 | 9 | 7 | 5 | 4 | 3 | 2 | 1 | 1 | ||||||||||||
| 1.5 | 6 | 6 | 5 | 4 | 3 | 2 | 2 | 1 | 1 | ||||||||||||
| 2.0 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | ||||||||||||
| 2.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||
| 75th | λ | δ (Shift) | 95th | λ | δ (Shift) | ||||||||||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | ||
| 1.0 | 513 | 316 | 117 | 42 | 17 | 8 | 4 | 3 | 2 | 1.0 | 1109 | 682 | 253 | 91 | 37 | 17 | 9 | 5 | 3 | ||
| 1.1 | 165 | 122 | 61 | 28 | 13 | 7 | 4 | 3 | 2 | 1.1 | 356 | 263 | 131 | 59 | 28 | 14 | 8 | 5 | 3 | ||
| 1.2 | 67 | 56 | 34 | 19 | 10 | 6 | 4 | 3 | 2 | 1.2 | 145 | 120 | 74 | 40 | 22 | 13 | 8 | 5 | 4 | ||
| 1.3 | 33 | 29 | 21 | 13 | 8 | 5 | 4 | 3 | 2 | 1.3 | 72 | 63 | 45 | 28 | 17 | 11 | 7 | 5 | 4 | ||
| 1.4 | 19 | 17 | 14 | 10 | 7 | 5 | 3 | 2 | 2 | 1.4 | 41 | 37 | 29 | 21 | 14 | 10 | 7 | 5 | 4 | ||
| 1.5 | 12 | 11 | 10 | 7 | 6 | 4 | 3 | 2 | 2 | 1.5 | 26 | 24 | 20 | 15 | 11 | 8 | 6 | 5 | 4 | ||
| 2.0 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2.0 | 7 | 6 | 6 | 6 | 5 | 4 | 4 | 3 | 3 | ||
| 2.5 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 2.5 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | ||
| 5th | λ | δ (Shift) | 25th | λ | δ (Shift) | ||||||||||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | ||
| 1.0 | 20 | 13 | 5 | 2 | 1 | 1 | 1 | 1 | 1 | 1.0 | 107 | 67 | 25 | 9 | 4 | 2 | 1 | 1 | 1 | ||
| 1.1 | 7 | 5 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 1.1 | 34 | 26 | 13 | 6 | 3 | 2 | 1 | 1 | 1 | ||
| 1.2 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1.2 | 15 | 12 | 8 | 4 | 3 | 2 | 1 | 1 | 1 | ||
| 1.3 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.3 | 7 | 6 | 5 | 3 | 2 | 2 | 1 | 1 | 1 | ||
| 1.4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.4 | 4 | 4 | 3 | 3 | 2 | 1 | 1 | 1 | 1 | ||
| 1.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1.5 | 3 | 3 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | ||
| 2.0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2.0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 2.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 50th (MDRL) | λ | δ (Shift) | |||||||||||||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | ||||||||||||
| 1.0 | 260 | 160 | 59 | 21 | 9 | 4 | 2 | 2 | 1 | ||||||||||||
| 1.1 | 82 | 61 | 31 | 14 | 7 | 4 | 2 | 2 | 1 | ||||||||||||
| 1.2 | 34 | 27 | 17 | 10 | 5 | 3 | 2 | 2 | 1 | ||||||||||||
| 1.3 | 17 | 15 | 11 | 7 | 4 | 3 | 2 | 2 | 1 | ||||||||||||
| 1.4 | 10 | 9 | 7 | 5 | 4 | 3 | 2 | 1 | 1 | ||||||||||||
| 1.5 | 6 | 6 | 5 | 4 | 3 | 2 | 2 | 1 | 1 | ||||||||||||
| 2.0 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | ||||||||||||
| 2.5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||
| 75th | λ | δ (Shift) | 95th | λ | δ (Shift) | ||||||||||||||||
| # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | # | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | ||
| 1.0 | 517 | 317 | 118 | 42 | 17 | 8 | 4 | 3 | 2 | 1.0 | 1098 | 682 | 258 | 91 | 37 | 17 | 9 | 5 | 3 | ||
| 1.1 | 164 | 122 | 61 | 28 | 13 | 7 | 4 | 3 | 2 | 1.1 | 358 | 257 | 130 | 60 | 28 | 14 | 8 | 5 | 4 | ||
| 1.2 | 67 | 55 | 34 | 19 | 10 | 6 | 4 | 3 | 2 | 1.2 | 142 | 118 | 75 | 41 | 22 | 12.1 | 8 | 5 | 4 | ||
| 1.3 | 33 | 29 | 21 | 13 | 8 | 5 | 4 | 3 | 2 | 1.3 | 71 | 62 | 46 | 28 | 17 | 11 | 7 | 5 | 4 | ||
| 1.4 | 19 | 17 | 13 | 10 | 7 | 5 | 3 | 2 | 2 | 1.4 | 41 | 37 | 29 | 20 | 14 | 9 | 7 | 5 | 4 | ||
| 1.5 | 12 | 11 | 10 | 8 | 5 | 4 | 3 | 2 | 2 | 1.5 | 25 | 24 | 20 | 15 | 11 | 8 | 6 | 5 | 3 | ||
| 2.0 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2.0 | 7 | 6 | 6 | 6 | 5 | 4 | 4 | 3 | 3 | ||
| 2.5 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 2.5 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | ||
| Sample Number | Measures (Crisp Values) | Variables | Decision | |||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x5 | R | |||
| 1 | −0.547 | −0.551 | 1.866 | −0.418 | −0.706 | −0.071 | 2.572 | In control |
| 2 | −0.382 | 0.075 | −1.504 | 1.395 | −0.152 | −0.114 | 2.899 | In control |
| 3 | 0.694 | −0.444 | −1.559 | 1.975 | −1.800 | −0.227 | 3.776 | In control |
| 4 | 0.050 | −0.520 | −1.425 | −0.194 | 0.721 | −0.273 | 2.146 | In control |
| 5 | 1.368 | 0.014 | −0.207 | 0.518 | −1.400 | 0.059 | 2.769 | In control |
| 6 | 1.615 | 0.706 | −0.783 | −0.620 | −1.980 | −0.212 | 3.595 | In control |
| 7 | −2.426 | 1.077 | 0.569 | 1.686 | −0.859 | 0.009 | 4.112 | In control |
| 8 | 1.824 | 0.195 | −0.659 | −0.415 | −0.581 | 0.073 | 2.483 | In control |
| 9 | 0.646 | −0.241 | −1.400 | −1.045 | 1.090 | −0.190 | 2.490 | In control |
| 10 | 1.101 | −0.685 | 1.772 | 0.372 | −0.337 | 0.445 | 2.457 | In control |
| 11 | 0.259 | −2.005 | 1.247 | 1.204 | 0.223 | 0.186 | 3.252 | In control |
| 12 | −0.104 | −0.320 | −0.968 | −0.484 | −0.337 | −0.443 | 0.864 | In control |
| 13 | −2.235 | −0.614 | 0.234 | 0.991 | −0.096 | −0.344 | 3.226 | In control |
| 14 | 2.216 | −0.527 | −3.062 | 0.176 | 0.155 | −0.208 | 5.278 | In control |
| 15 | 0.960 | 0.729 | 0.772 | 0.304 | 1.699 | 0.893 | 1.395 | In control |
| 16 | −0.199 | 2.435 | 0.528 | 0.906 | 0.547 | 0.843 | 2.634 | In control |
| 17 | 1.416 | −0.461 | −0.244 | 0.202 | −0.058 | 0.171 | 1.878 | In control |
| 18 | 1.633 | −0.748 | −0.642 | −0.832 | 0.872 | 0.056 | 2.465 | In control |
| 19 | 0.064 | 0.758 | −0.515 | 1.516 | 0.671 | 0.499 | 2.031 | In control |
| 20 | 0.292 | −0.551 | −0.362 | 0.309 | 0.449 | 0.027 | 1.000 | In control |
| Sample Number | x1 | x2 | x3 | x4 | x5 | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −0.587 | −0.575 | −0.547 | −0.526 | −0.517 | −0.566 | −0.561 | −0.551 | −0.535 | −0.528 | 1.838 | 1.846 | 1.866 | 1.890 | 1.900 | −0.461 | −0.448 | −0.418 | −0.391 | −0.380 | −0.736 | −0.727 | −0.706 | −0.696 | −0.692 |
| 2 | −0.418 | −0.407 | −0.382 | −0.349 | −0.335 | 0.028 | 0.042 | 0.075 | 0.078 | 0.080 | −1.534 | −1.525 | −1.504 | −1.485 | −1.477 | 1.346 | 1.361 | 1.395 | 1.406 | 1.411 | −0.177 | −0.170 | −0.152 | −0.144 | −0.140 |
| 3 | 0.687 | 0.689 | 0.694 | 0.698 | 0.700 | −0.466 | −0.459 | −0.444 | −0.410 | −0.395 | −1.608 | −1.593 | −1.559 | −1.556 | −1.555 | 1.932 | 1.945 | 1.975 | 1.996 | 2.004 | −1.817 | −1.812 | −1.800 | −1.770 | −1.758 |
| 4 | 0.008 | 0.021 | 0.050 | 0.079 | 0.091 | −0.538 | −0.532 | −0.520 | −0.488 | −0.474 | −1.428 | −1.427 | −1.425 | −1.402 | −1.392 | −0.209 | −0.204 | −0.194 | −0.167 | −0.155 | 0.690 | 0.700 | 0.721 | 0.743 | 0.752 |
| 5 | 1.341 | 1.349 | 1.368 | 1.372 | 1.374 | −0.025 | −0.013 | 0.014 | 0.041 | 0.053 | −0.241 | −0.231 | −0.207 | −0.205 | −0.204 | 0.482 | 0.493 | 0.518 | 0.537 | 0.545 | −1.406 | −1.404 | −1.400 | −1.377 | −1.367 |
| 6 | 1.607 | 1.609 | 1.615 | 1.624 | 1.628 | 0.661 | 0.674 | 0.706 | 0.726 | 0.735 | −0.822 | −0.810 | −0.783 | −0.749 | −0.734 | −0.623 | −0.622 | −0.620 | −0.599 | −0.589 | −1.989 | −1.986 | −1.980 | −1.967 | −1.961 |
| 7 | −2.475 | −2.460 | −2.426 | −2.409 | −2.401 | 1.067 | 1.070 | 1.077 | 1.112 | 1.127 | 0.537 | 0.547 | 0.569 | 0.576 | 0.579 | 1.664 | 1.671 | 1.686 | 1.701 | 1.708 | −0.866 | −0.864 | −0.859 | −0.849 | −0.845 |
| 8 | 1.810 | 1.815 | 1.824 | 1.840 | 1.847 | 0.165 | 0.174 | 0.195 | 0.218 | 0.229 | −0.673 | −0.669 | −0.659 | −0.631 | −0.618 | −0.441 | −0.433 | −0.415 | −0.412 | −0.410 | −0.611 | −0.602 | −0.581 | −0.567 | −0.561 |
| 9 | 0.626 | 0.632 | 0.646 | 0.646 | 0.647 | −0.249 | −0.247 | −0.241 | −0.232 | −0.228 | −1.409 | −1.406 | −1.400 | −1.395 | −1.393 | −1.046 | −1.046 | −1.045 | −1.024 | −1.015 | 1.087 | 1.088 | 1.090 | 1.113 | 1.122 |
| 10 | 1.100 | 1.100 | 1.101 | 1.120 | 1.128 | −0.724 | −0.712 | −0.685 | −0.681 | −0.679 | 1.737 | 1.748 | 1.772 | 1.796 | 1.806 | 0.323 | 0.338 | 0.372 | 0.381 | 0.385 | −0.350 | −0.346 | −0.337 | −0.321 | −0.315 |
| 11 | 0.236 | 0.243 | 0.259 | 0.270 | 0.275 | −2.014 | −2.011 | −2.005 | −1.982 | −1.973 | 1.206 | 1.218 | 1.247 | 1.254 | 1.257 | 1.201 | 1.202 | 1.204 | 1.222 | 1.230 | 0.220 | 0.221 | 0.223 | 0.252 | 0.265 |
| 12 | −0.111 | −0.109 | −0.104 | −0.076 | −0.064 | −0.341 | −0.335 | −0.320 | −0.308 | −0.303 | −1.018 | −1.003 | −0.968 | −0.940 | −0.927 | −0.502 | −0.497 | −0.484 | −0.468 | −0.461 | −0.354 | −0.349 | −0.337 | −0.312 | −0.302 |
| 13 | −2.281 | −2.267 | −2.235 | −2.203 | −2.189 | −0.662 | −0.648 | −0.614 | −0.609 | −0.607 | 0.197 | 0.208 | 0.234 | 0.265 | 0.279 | 0.973 | 0.979 | 0.991 | 1.006 | 1.012 | −0.112 | −0.107 | −0.096 | −0.088 | −0.085 |
| 14 | 2.214 | 2.215 | 2.216 | 2.246 | 2.259 | −0.569 | −0.556 | −0.527 | −0.508 | −0.501 | −3.088 | −3.080 | −3.062 | −3.061 | −3.061 | 0.140 | 0.150 | 0.176 | 0.206 | 0.218 | 0.150 | 0.151 | 0.155 | 0.184 | 0.197 |
| 15 | 0.950 | 0.953 | 0.960 | 0.971 | 0.975 | 0.680 | 0.695 | 0.729 | 0.744 | 0.750 | 0.763 | 0.766 | 0.772 | 0.797 | 0.808 | 0.263 | 0.276 | 0.304 | 0.309 | 0.312 | 1.656 | 1.669 | 1.699 | 1.703 | 1.705 |
| 16 | −0.244 | −0.230 | −0.199 | −0.176 | −0.166 | 2.389 | 2.403 | 2.435 | 2.444 | 2.447 | 0.499 | 0.508 | 0.528 | 0.538 | 0.543 | 0.878 | 0.886 | 0.906 | 0.913 | 0.917 | 0.524 | 0.531 | 0.547 | 0.576 | 0.589 |
| 17 | 1.401 | 1.405 | 1.416 | 1.450 | 1.465 | −0.494 | −0.484 | −0.461 | −0.439 | −0.430 | −0.286 | −0.274 | −0.244 | −0.242 | −0.242 | 0.160 | 0.172 | 0.202 | 0.217 | 0.223 | −0.101 | −0.088 | −0.058 | −0.032 | −0.021 |
| 18 | 1.632 | 1.632 | 1.633 | 1.633 | 1.634 | −0.780 | −0.771 | −0.748 | −0.714 | −0.699 | −0.659 | −0.654 | −0.642 | −0.622 | −0.613 | −0.844 | −0.840 | −0.832 | −0.827 | −0.825 | 0.855 | 0.860 | 0.872 | 0.896 | 0.906 |
| 19 | 0.015 | 0.030 | 0.064 | 0.098 | 0.113 | 0.740 | 0.745 | 0.758 | 0.774 | 0.781 | −0.521 | −0.519 | −0.515 | −0.490 | −0.480 | 1.491 | 1.498 | 1.516 | 1.546 | 1.559 | 0.650 | 0.656 | 0.671 | 0.703 | 0.717 |
| 20 | 0.269 | 0.276 | 0.292 | 0.295 | 0.297 | −0.575 | −0.568 | −0.551 | −0.549 | −0.548 | −0.412 | −0.397 | −0.362 | −0.352 | −0.347 | 0.278 | 0.288 | 0.309 | 0.343 | 0.358 | 0.420 | 0.429 | 0.449 | 0.457 | 0.461 |
| Sample Number | Defuzzified | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DTriT | RDTriT | |||||||||||
| 1 | −0.102 | −0.093 | −0.071 | −0.052 | −0.043 | 2.529 | 2.542 | 2.572 | 2.617 | 2.636 | −0.072 | 2.578 |
| 2 | −0.151 | −0.140 | −0.114 | −0.099 | −0.092 | 2.822 | 2.846 | 2.899 | 2.931 | 2.945 | −0.118 | 2.890 |
| 3 | −0.254 | −0.246 | −0.227 | −0.209 | −0.201 | 3.690 | 3.715 | 3.776 | 3.808 | 3.821 | −0.227 | 3.764 |
| 4 | −0.295 | −0.289 | −0.273 | −0.247 | −0.235 | 2.082 | 2.101 | 2.146 | 2.170 | 2.180 | −0.269 | 2.138 |
| 5 | 0.030 | 0.039 | 0.059 | 0.074 | 0.080 | 2.708 | 2.726 | 2.769 | 2.777 | 2.780 | 0.057 | 2.755 |
| 6 | −0.233 | −0.227 | −0.212 | −0.193 | −0.184 | 3.568 | 3.576 | 3.595 | 3.610 | 3.617 | −0.210 | 3.594 |
| 7 | −0.014 | −0.007 | 0.009 | 0.026 | 0.033 | 4.065 | 4.079 | 4.112 | 4.161 | 4.183 | 0.009 | 4.119 |
| 8 | 0.050 | 0.057 | 0.073 | 0.090 | 0.097 | 2.429 | 2.445 | 2.483 | 2.510 | 2.521 | 0.073 | 2.478 |
| 9 | −0.198 | −0.196 | −0.190 | −0.179 | −0.174 | 2.480 | 2.483 | 2.490 | 2.519 | 2.531 | −0.188 | 2.499 |
| 10 | 0.417 | 0.426 | 0.445 | 0.459 | 0.465 | 2.417 | 2.429 | 2.457 | 2.508 | 2.530 | 0.443 | 2.466 |
| 11 | 0.170 | 0.175 | 0.186 | 0.203 | 0.211 | 3.179 | 3.201 | 3.252 | 3.265 | 3.271 | 0.188 | 3.236 |
| 12 | −0.465 | −0.459 | −0.443 | −0.421 | −0.411 | 0.816 | 0.830 | 0.864 | 0.927 | 0.954 | −0.440 | 0.876 |
| 13 | −0.377 | −0.367 | −0.344 | −0.326 | −0.318 | 3.162 | 3.181 | 3.226 | 3.273 | 3.293 | −0.346 | 3.227 |
| 14 | −0.231 | −0.224 | −0.208 | −0.187 | −0.177 | 5.275 | 5.276 | 5.278 | 5.327 | 5.347 | −0.206 | 5.297 |
| 15 | 0.863 | 0.872 | 0.893 | 0.905 | 0.910 | 1.344 | 1.360 | 1.395 | 1.428 | 1.442 | 0.889 | 1.394 |
| 16 | 0.809 | 0.820 | 0.843 | 0.859 | 0.866 | 2.555 | 2.579 | 2.634 | 2.674 | 2.691 | 0.840 | 2.628 |
| 17 | 0.136 | 0.146 | 0.171 | 0.191 | 0.199 | 1.831 | 1.845 | 1.878 | 1.934 | 1.959 | 0.169 | 1.887 |
| 18 | 0.041 | 0.045 | 0.056 | 0.073 | 0.081 | 2.457 | 2.459 | 2.465 | 2.474 | 2.477 | 0.059 | 2.466 |
| 19 | 0.475 | 0.482 | 0.499 | 0.526 | 0.538 | 1.970 | 1.988 | 2.031 | 2.065 | 2.080 | 0.503 | 2.028 |
| 20 | −0.004 | 0.006 | 0.027 | 0.039 | 0.044 | 0.968 | 0.978 | 1.000 | 1.025 | 1.035 | 0.023 | 1.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almeida, T.S.; dos Santos Mendes, A.; Rocha Rizol, P.M.S.; Machado, M.A.G.
Performance Analysis of Interval Type-2 Fuzzy
Almeida TS, dos Santos Mendes A, Rocha Rizol PMS, Machado MAG.
Performance Analysis of Interval Type-2 Fuzzy
Almeida, Túlio S., Amanda dos Santos Mendes, Paloma M. S. Rocha Rizol, and Marcela A. G. Machado.
2023. "Performance Analysis of Interval Type-2 Fuzzy
Almeida, T. S., dos Santos Mendes, A., Rocha Rizol, P. M. S., & Machado, M. A. G.
(2023). Performance Analysis of Interval Type-2 Fuzzy






