You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Applied Sciences
Download PDF
  • Article
  • Open Access

18 October 2023

Classification of Skin Lesion Images Using Artificial Intelligence Methodologies through Radial Fourier–Mellin and Hilbert Transform Signatures

,
,
,
and
1
Facultad de Ingeniería, Arquitectura y Diseño, Universidad Autónoma de Baja California, Km. 103 Carretera Tijuana-Ensenada, Ensenada 22860, Baja California, Mexico
2
Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE), Baja California, Carretera Ensenada-Tijuana No. 3918, Zona Playitas, Ensenada 22860, Baja California, Mexico
3
SolexVintel, Santa Margarita 117, Colonia Insurgentes San Borja, Alcaldía Benito Juárez, Cd. De Mexico C. P. 03100, Mexico
*
Author to whom correspondence should be addressed.
Appl. Sci.2023, 13(20), 11425;https://doi.org/10.3390/app132011425
This article belongs to the Special Issue New Trends in Machine Learning for Biomedical Data Analysis
Version Notes
Order Reprints

Abstract

This manuscript proposes the possibility of concatenated signatures (instead of images) obtained from different integral transforms, such as Fourier, Mellin, and Hilbert, to classify skin lesions. Eight lesions were analyzed using some algorithms of artificial intelligence: basal cell carcinoma (BCC), squamous cell carcinoma (SCC), melanoma (MEL), actinic keratosis (AK), benign keratosis (BKL), dermatofibromas (DF), melanocytic nevi (NV), and vascular lesions (VASCs). Eleven artificial intelligence models were applied so that eight skin lesions could be classified by analyzing the signatures of each lesion. The database was randomly divided into 80% and 20% for the training and test dataset images, respectively. The metrics that are reported are accuracy, sensitivity, specificity, and precision. Each process was repeated 30 times to avoid bias, according to the central limit theorem in this work, and the averages and ± standard deviations were reported for each metric. Although all the results were very satisfactory, the highest average score for the eight lesions analyzed was obtained using the subspace k-NN model, where the test metrics were 99.98% accuracy, 99.96% sensitivity, 99.99% specificity, and 99.95% precision.

1. Introduction

The skin is the largest organ in the body; it covers and protects externally. Its condition and appearance show the state of health and wellbeing of a person; however, due to exposure to the environment and other factors, specific skin injuries may occur; these can vary in size and shape. Different types of skin diseases vary according to the symptoms. The presence of any mild skin condition can lead to severe complications and even death. Skin cancer is a serious disease and one of the most common carcinomas. It is mainly classified into basal cell carcinoma (BCC), squamous cell carcinoma or epidermoid carcinoma (SCC), and melanoma (MEL) [1,2,3,4]. BCC is the most frequent skin cancer in the worldwide population, and its growth is slow. It can grow and destroy the skin. It is generally observed as a flat or raised lesion and its color is reddish [1,5,6,7]. SCC is a malignant tumor that appears as red spots with raised growths like warts; it is the second most common skin cancer [1,2]. Melanoma is the most aggressive skin cancer, appearing as a pigmented lesion, usually beginning on normal skin as a new, small, pigmented growth [2]. Other common skin diseases are actinic keratosis (AK), benign keratosis (BKL), dermatofibromas (DF), melanocytic nevi (NV), and vascular lesions (VASCs), among others.
Actinic keratosis occurs due to frequent exposure to ultraviolet rays from the sun or tanning beds; it usually appears as small rough spots and presents color variations. Some areas are generally malignant, causing squamous cell carcinoma [7,8,9]. Seborrheic keratoses or benign keratoses are benign tumors that frequently occur in the geriatric population. This type of tumor consists of a brown, black, or light brown spot or lesion. In some cases, it is often confused with basal cell carcinoma or melanoma [10,11]. Dermatofibroma is a benign skin lesion; it appears as a slow-growing papule, and its color varies from light to dark brown, purple to red, or yellowish. Its clinical diagnosis is simple; however, sometimes it is difficult to differentiate it from other tumors, such as malignant melanoma [12,13]. Melanocytic nevi or moles are the most common benign lesions and have smooth, flat, or palpable surfaces. They form as a brown spot or freckle that varies in size and thickness [14,15]. Vascular lesions are disorders of the blood vessels. They become evident on the skin’s surface, forming red structures, dark spots, or scars, presenting an aesthetic problem. Some VASCs develop over time due to environmental changes, temperature, poor blood circulation, or sensitive skin [16,17]. The skin can warn of a health problem; its care is critical for physical and emotional aspects. Different conditions can affect the skin; some are present at birth, whereas others are acquired throughout life. Some lesions may have similar characteristics, making it difficult to differentiate them from the most common malignant neoplasms. Skin diseases are a significant health problem. The development of new digital tools and technologies based on artificial intelligence (AI) to detect and treat diseases is due to the ability to analyze large amounts of data. The latest developments based on artificial intelligence tools help identify health problems in the early stages. These developments are also based on image processing, where the recognition of visual patterns through images represents a potential solution for the failure of the human eye to detect disease. Applying algorithms based on artificial intelligence allows the development of non-invasive tools in the health area.
In recent decades, machine learning (ML) techniques have been used in impressive applications in many research areas and are still growing. Since many studies about medical imaging are focused on automating skin lesion identification from dermatological images to provide an adequate diagnosis and treatment to patients, ML techniques can be a powerful tool to detect malignant lesions automatically, quickly, and reliably.
Some ML techniques, such as convolutional neural networks (CNNs), are the most popular as they represent the closest technique to the learning process of human vision. CNNs are based on the mathematical operator of the convolution between the image and filters to extract information. Even though CNNs have provided successful results for image classification, their high computational cost, as well the non-invariance properties under rotation, scale, and translation of the convolution operation, make CNNs, in practice, an ineffective tool to implement in the identification or classification of some images, especially for those corresponding to skin lesions where vital information could be lost due to the low contrast that often exists between the lesion and healthy skin. This low contrast can mean that during the segmentation carried out by some filters, information on the lesion is not extracted correctly [18,19]. In this context, other ML techniques, such as the support vector machine (SVM), k-nearest neighbor (k-NN), or ensemble classifiers, have shown acceptable performance [20,21].
Although the SVM, k-NN, and ensemble classifiers have been successfully implemented to classify skin lesions, digital images under rotation, scaling, or translation were not considered. The application of the fractional radial Fourier transform in pattern recognition for digital images is invariant to translation, scale, and rotation, and the results obtained to classify phytoplankton species showed a high level of confidence (greater than 90%) [22]. In this paper, we implemented the Hilbert mask on the module of the Fourier–Mellin Transform to obtain a unique signature of the skin lesion called the radial Fourier–Mellin signature, which is invariant to rotation, scale, and translation. Additionally, we included as a signature the extraction of the uniform local binary pattern (LBP-U) image features. The classification task was obtained using the k-NN, SVM, and ensemble classifiers. Section 2 contains the description and image dataset pre-processing procedure and methods used to achieve its skin lesion classification. Section 3 presents the results using these supervised machine learning methods. In Section 4, we discuss the obtained results.

2. Materials and Methods

2.1. Image Dataset

The images used in our study were obtained from the 2019 challenge training data of the “International Skin Imaging Collaboration” (ISIC) [23]. Some examples are shown in Figure 1. This dataset consists of 25,331 digital images of 8 types of skin lesions. A total of 3323 basal cell carcinoma (BCC) digital images, 628 digital images of squamous cell carcinoma (SCC), 4522 melanoma (MEL) digital images, 867 actinic keratosis (AK) skin lesion digital images, 2624 benign keratosis (BKL) skin lesion images as solar lentigo, seborrheic keratosis, and lichen planus-like keratosis, 239 dermatofibroma (DF) digital skin lesion images, 12,875 melanocytic nevus (NV) digital images, and 253 images of vascular skin lesions (VASCs). However, we proceeded to eliminate the skin lesion images that contained noise, such as hair, measurement artifacts, and other noise types that made it difficult to segment the lesions. The image dataset debugging reduced the data to 9067 dermatologic skin lesions, where 6747 images were for NV, 1032 for MEL, 512 for BCC, 471 for BKL, 130 for VASC, 67 for DF, 62 for SCC, and 46 for AK. This dramatic reduction motivated us to include a data augmentation procedure resulting in 362,680 dermatologic skin lesion images, and we randomly selected images to classify using the SVM, k-NN, and ensemble classifier machine learning methodologies. To avoid classification bias, we homogenized the classes in the database using 1840 images for each type of skin lesion. Each of these 14,720 randomly selected dataset images were transformed into their radial Fourier signatures and texture descriptors using the Hilbert transform.
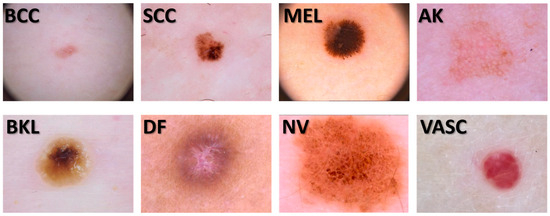
Figure 1. Some digital skin lesion images from our dataset.

2.2. The Signatures

We generated several signature vectors for each RGB channel and gray-scale images using our dataset (362,680) obtained through data augmentation. The data augmentation procedure considered five image scale percentages (100%, 95%, 90%, 85%, and 80%) and eight rotation angle values (45°, 90°, 135°, 180°, 225°, 270°, 315°, and 360°). These signatures or descriptors used invariance properties to the translation and scale of the modules of the Fourier transform and the Mellin transform, respectively. To include the invariant object rotation property, we used the Hilbert transform. To calculate the unique signatures of the image, we summed the pixel value for each ring obtained after using the Hilbert masks as a filter. We incorporated the texture signatures or descriptors on the previously generated radial Fourier signatures. The process to obtain this one-dimensional skin lesion digital image representation or signature is shown in Figure 2 and Figure 3. The original image ( I m ( x , y ) ) contains three matrix channels in RGB (red, green, and blue channels). Thus, the picture was segmented into these three primary color channels to apply the radial Fourier–Mellin method and the uniform LBP image features extraction. In addition, we considered the gray-scale skin lesion digital image obtained by a weighted sum of RGB values defined by: 0.299R + 0.587G + 0.114B.
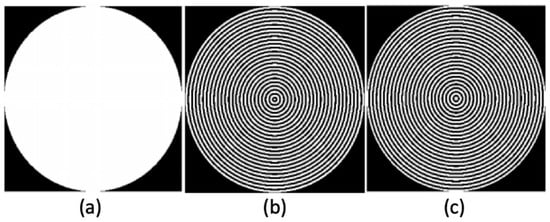
Figure 2. (a) Binary disk. (b) H R mask. (c) H I mask.
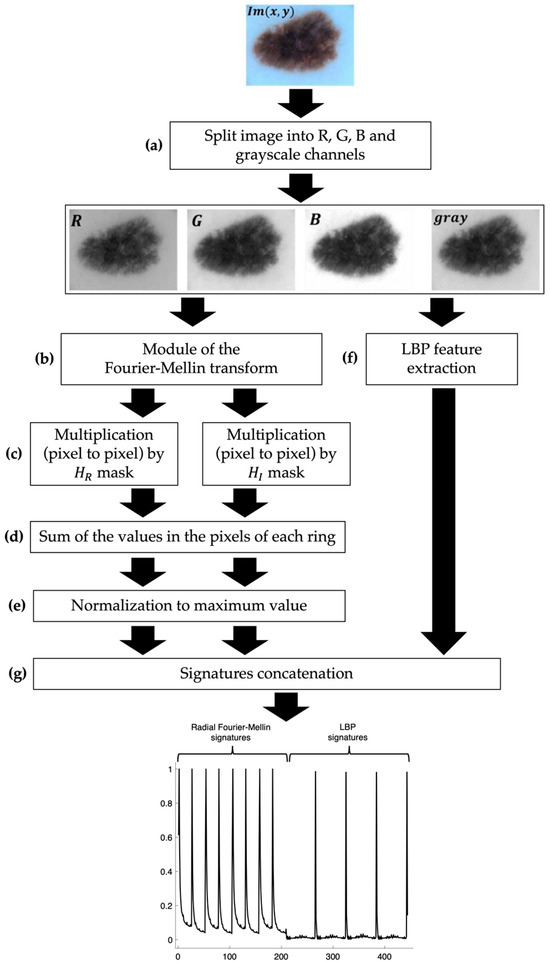
Figure 3. Description of the methodology for the image signature generation.

2.3. Radial Fourier–Mellin Signatures through Hilbert Transform

To generate the radial Fourier–Mellin signatures, first the image was split into its RGB channels and gray scale (Figure 3a). Then, the module of the Fourier–Mellin (FM) transforms of each skin digital image, named I m ( x , y ) , was obtained using the next equation [24,25,26] (Figure 3b).
| F M s , t | = ∬ 0 ∞ | F T [ I m ( x , y ) ] | x s − 1 y t − 1 d x d y = M | F T [ I m ( x , y ) ] |
where | F M s , t | is the module of the Mellin transform, which give us a scale invariance of an object in the image that is necessary as the skin lesion digital images were obtained from different lesion to camera distances. Thus, the lesion region is smaller for longer lesion to camera distances and the images contain a larger lesion region when the opposite is true. Moreover, ( s , t ) represents the 2D coordinates of the transformed x , y pixel coordinates on Mellin’s plane. Notice that these pixel coordinates x , y correspond to the module Fourier transform of the image ( | F T [ I m ( x , y ) ] | ), taking advantage of its translation invariance. Therefore, at this moment, the object (skin lesion) in the image is invariant to translation and scale.
Now, using the Hilbert transform, we also achieve the skin lesion in the image being invariant to rotation. The Hilbert transform of the image is given by [22,26,27,28,29]:
F H r [ I m ( x , y ) ] = e i p θ F T I m x , y = e i p θ F u , v
where p is the order of the radial Hilbert transform, θ is the angle on frequency domain/space of the pixel coordinates in the image ( x , y ) after being transformed to the Fourier plane coordinates as ( u , v ) . Therefore, this angle is determined by θ = a c o s ⁡ ( u / u 2 + v 2 ) . Then, using the Euler’s formula, we calculated the binary ring masks of the RGB channels and gray-scale skin lesion digital image, using both the real ( H R ) and imaginary ( H I ) parts of the radial Hilbert transform of the image as follows (Figure 2), [22,26,27,28,29].
H R = R e [ H r u , v ] = 1 ,   i f   s i n ⁡ = p θ > 0       0 ,     o t h e r w i s e
H I = I m [ H r u , v ] = 1 ,   i f   c o s p θ > 0       0 ,     o t h e r w i s e
The binary ring masks obtained above were applied to filter the skin lesion digital images that were previously processed using the module of the Fourier–Mellin transform (Figure 3c). The results require the sum of the values in the pixels of each ring obtaining two unique signatures of each skin gray-scale lesion image ( S g r a y H R   a n d   S g r a y H I ) and its RGB channels given by: S R H R , S R H I , S G H R , S G H I , S B H R , and S B H I (Figure 3d). Finally, each signature is normalized by its maximum value (Figure 3e,g).
To include texture descriptors, we used the uniform local binary pattern (LBP) technique (Figure 3f). This is a texture analysis tool in computer vision and image processing [30].
It is a simple and efficient descriptor that describes textures, edges, corners, spots, and flat regions. Taking blocks of 3 × 3 pixels, the intensity of each of the eight neighboring pixels is compared with the intensity of the central pixel (defined as the threshold). Suppose the intensity of the adjacent pixel is greater than or equal to the intensity of the central pixel; in this case, the position of the neighboring pixel is assigned a value of 1 (or otherwise a value of 0). Once all the pixels are compared, we obtain a set of zeros and ones that represent a binary number. Each position of the binary number is multiplied by its corresponding decimal value and then all the values are added. This sum is the LBP value that labels the central pixel. Figure 4 shows an example of the LBP calculation on any pixel for P = 8 neighborhood pixels.
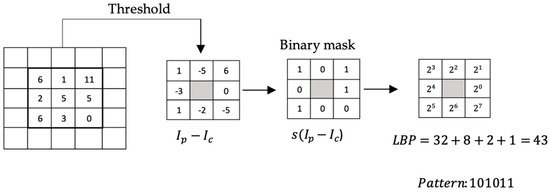
Figure 4. LBP calculation procedure.
To calculate the LBP on a gray-scale image, the following equation is used:
L B P x c , y c = ∑ p = 0 P − 1 s ( I p − I c ) 2 p ,
where x c , y c represents the position of the central pixel, P is the number of pixels in the neighborhood, I p is the intensity of the neighboring pixels, I c is the intensity of the central pixel, and s is the function:
s x = 1 ,                                                 x ≥ 0 0 ,                   a n o t h e r   v a l u e .
The so-called uniform LBP (LBP-U) is a variant of the LBP that reduces the original LBP characteristic vector; this technique allows invariance against rotations. An LBP is uniform when there are at most two transitions from 1 to 0 and from 0 to 1; for example, the binary patterns 11111111 (0 transitions), 11111000 (1 transition), and 11001111 (2 transitions) are uniform, whereas the patterns 11010110 (6 transitions) and 110010001 (4 transitions) are not. In a neighborhood of eight pixels, 256 patterns can be identified; of which, 58 will be uniform. In this way, 58 labels are obtained for the uniform patterns, and for the non-uniform patterns, the same label is assigned, which will be 59. In this work, we use the LBP-U.
After calculating the uniform LBP value for each pixel in the image, we create a histogram of the uniform LBP values to represent the distribution of different image features of both the RGB and gray-scale images L B P R , L B P G , L B P B , and L B P g r a y . We concatenate these signatures to obtain 444 components of one-dimensional objects/signatures (Figure 3g).

2.4. Signature Classification

We generated radial Fourier and texture signature vectors for each RGB channel and gray-scale dermatological digital image in our dataset. These descriptors are invariant to scale, rotation, illumination, and noise on the image being analyzed. A data augmentation procedure considering scale and rotation was included. To homogenize the classes in the database, we used 1840 images for each type of skin lesion. The signature classification was performed with the support vector machine (SVM), k-nearest neighbor (k-NN), and ensemble classifiers.
Variations of these methods were implemented. In the case of the SVM, four different kernels were used [31]: Quadratic SVM works by implementing a polynomial of degree = 2 as a kernel, whereas the cubic SVM method uses a polynomial of degree = 3. The fine Gaussian SVM method uses a Gaussian kernel with a kernel scale = 5.3. The medium Gaussian SVM works with a wider Gaussian kernel, using a kernel scale = 21.
Additionally, five k-NN variations were explored [32,33]: Fine k-NN works using the Euclidean distance and a k = 1 neighbor. The medium k-NN algorithm also uses Euclidean distance, but the number of neighbors is k = 10. The cosine k-NN algorithm implements the cosine distance with k = 10 neighbors. The Minkowski distance, with exponent p = 3, is used for the cubic k-NN method. For the weighted k-NN, the same length and number of neighbors were used as in the medium k-NN, but for this case, the neighbors are weighted based on the square inverse of the distance.
Finally, two ensemble classifiers were used. These classifiers aggregate the predictions of a group of predictors to obtain better forecasts than the best individual predictor [34]. The bagged trees method implements decision trees using bootstrap aggregation (bagging) [35]. The subspace k-NN method uses the random subspace method for k-NN classification [36,37].
In total, 11 algorithms were explored; these are shown in Table 1.
Table 1. This table shows a description of the 11 algorithms implemented.
MATLAB 2022b was used to carry out the classification process, using the same dataset for all 11 algorithms. The dataset was balanced by selecting 1840 signatures from each skin lesion. Therefore, the dataset consists of 14,720 signatures.

3. Results

The data were divided by randomly selecting 80% of the data to train and 20% of the data to test each methodology used. In the training process, k-fold cross-validation with k = 5 was used. For the training dataset and the testing dataset, the accuracy, sensitivity, specificity, and precision [33] were calculated for each class. These parameters are given by
a c c u r a c y C i = T P i + T N i T P i + T N i + F P i + F N i
s e n s i t i v i t y C i = T P i T P i + F N i      
s p e c i f i c i t y C i = T N i T N i + F P i    
p r e c i s i o n C i = T P i T P i + F P i    
where:
  • T P i : true positives for class i .
  • T N i : true negatives for class i .
  • F P i : false positives for class i .
  • F N i : false negatives for class i .
Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11 and Table 12 show the results for each algorithm.
Table 2. Results for quadratic SVM.
Table 3. Results for cubic SVM.
Table 4. Results for fine Gaussian SVM.
Table 5. Results for medium Gaussian SVM.
Table 6. Results for fine k-NN.
Table 7. Results for medium Gaussian k-NN.
Table 8. Results for cosine k-NN.
Table 9. Results for cubic k-NN.
Table 10. Results for weighted k-NN.
Table 11. Results for bagged trees.
Table 12. Results for subspace k-NN.
Because the splitting, training, and testing process described above was performed randomly, it was repeated 30 times to avoid bias according to the central limit theorem, and the mean ±1 standard deviation was calculated for each metric to determine the repeatability of each implemented method.
An example of the subspace k-NN method’s performance in each cycle is presented. In Figure 5, the ROC curve for the training and test sets from an example cycle of the subspace k-NN method is shown. Both curves have excellent performance for each of the eight classes.
Figure 5. ROC curve for one example subspace k-NN process. (a) Training ROC. (b) Testing ROC.
The confusion matrix for the training and testing of the example process of the subspace k-NN method are shown in Figure 6.
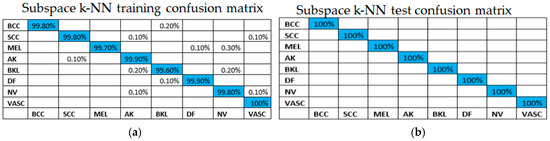
Figure 6. Confusion matrix for one example subspace k-NN process: (a) training, (b) testing.

4. Discussion

The results obtained from this new methodology for classifying skin lesions by employing eleven artificial intelligence algorithms using concatenated signatures were promising. This methodology proposes using several integral transforms (Fourier, Mellin, and Hilbert) along with the uniform LBP method of texture features to obtain a series of concatenated signatures for each lesion. This methodology works quite well for those images of skin lesions that lack noise. It is important to note that the concatenation of the signatures was achieved using the three color spaces (RGB) and the gray image to extract as much information as possible. This allows the artificial intelligence algorithms to detect the most subtle differences between the lesions. The eleven tables show excellent results for the accuracy, sensitivity, specificity, and precision metrics of the method, both for the training set and the test set. The group of lesions used to test this methodology was absent in the set of images used to train the various artificial intelligence algorithms. For both the training and test sets, the algorithms were run 30 times, thus obtaining an average and a ±standard deviation for each case. When defining the best classifier from the eleven presented in this work for this class of images, we observed that the classifier with the best performance was the subspace k-NN classifier, which had the best results for the test set. The same happens when we compare the metrics regarding the training of the various classifiers. The remaining ten classifiers also performed well. Using these classifiers when the input consists of concatenated signatures that are invariant to rotation, scale, and translation is an excellent contribution to this work. This work aligns with previous studies on the classification of skin lesions using artificial intelligence algorithms. For example, ref. [38] presented a dataset of 2241 histopathological images from 2008 to 2018. They employed two deep learning architectures, namely VGG19 and ResNet50. The results showed a high accuracy for distinguishing melanoma from nevi, with an average F1 score of 0.89, a sensitivity of 0.92, a specificity of 0.94, and an AUC of 0.98. In reference [39], the authors present an automated skin lesion detection and classification technique utilizing an optimized stacked sparse autoencoder (OSSAE)-based feature extractor with a backpropagation neural network (BPNN), named the OSSAE-BPNN technique, that reached a testing accuracy of 0.947, a sensitivity of 0.824, a specificity of 0.974, and a precision of 0.830. More studies in these areas are described in Table 13. Table 13 compares our work with other approaches, and our results are generally better. However, the results show that training and validation data metrics are around 99%. The signatures are invariant to each image’s rotation, scale, and displacement.
Table 13. Literature review. Works that implement machine learning techniques for skin lesion classification.
These studies demonstrate the potential of artificial intelligence algorithms in the classification of skin lesions, and this work furthers our understanding of how to achieve the best results. Our methodology is a breakthrough in classifying skin lesions using artificial intelligence algorithms and concatenated signatures. Indeed, the main contribution of this manuscript is how the images have been converted into linked signatures using the different integral transforms mentioned above, as well as the uniform LBP vectors.
This is a promising development in medical diagnosis and has the potential to revolutionize how medical professionals diagnose and treat skin lesions. It is worth mentioning that concatenated signatures cannot only be used for classifying skin lesions; they can be used for other medical imaging tasks, such as identifying tumors or categorizing brain scans. Furthermore, this technique can be applied to other areas, such as facial recognition or the categorization of satellite images.

Author Contributions

Methodology, L.F.L.-Á., E.G.-R., J.Á.-B. and E.G.-F.; Software, L.F.L.-Á., E.G.-R., J.Á.-B. and E.G.-F.; Validation, J.Á.-B., E.G.-F., L.F.L.-Á. and C.A.V.-B.; Data curation, E.G.-R. and C.A.V.-B.; Visualization, E.G.-R. and J.Á.-B.; Supervision, J.Á.-B.; Project administration, J.Á.-B.; Funding acquisition, J.Á.-B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE), Baja California, grant number F0F181.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Available online: https://challenge.isic-archive.com/data/#2019, accessed on 10 January 2019.

Acknowledgments

Luis Felipe López-Ávila holds a postdoc in Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE) supported by CONAHCYT, with postdoc application number 4553917, CVU 693156, Clave: BP-PA-20230502163027674-4553917. Claudia Andrea Vidales-Basurto holds a postdoc in Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE) supported by CONAHCYT, with postdoc application number 2340213, CVU 395914, Clave: BP-PA-20220621205655995-2340213.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lomas, A.; Leonardi-Bee, J.; Bath-Hextall, F. A systematic review of worldwide incidence of nonmelanoma skin cancer. Br. J. Dermatol. 2012, 166, 1069–1080. [Google Scholar] [CrossRef] [PubMed]
  2. Gordon, R. Skin cancer: An overview of epidemiology and risk factors. Semin. Oncol. Nurs. 2013, 29, 160–169. [Google Scholar] [CrossRef] [PubMed]
  3. Cameron, M.C.; Lee, E.; Hibler, B.P.; Barker, C.A.; Mori, S.; Cordova, M.; Nehal, K.S.; Rossi, A.M. Basal cell carcinoma: Epidemiology; pathophysiology; clinical and histological subtypes; and disease associations. J. Am. Acad. Dermatol. 2019, 80, 303–317. [Google Scholar] [CrossRef] [PubMed]
  4. Zhang, W.; Zeng, W.; Jiang, A.; He, Z.; Shen, X.; Dong, X.; Feng, J.; Lu, H. Global, regional and national incidence, mortality and disability-adjusted life-years of skin cancers and trend analysis from 1990 to 2019: An analysis of the Global Burden of Disease Study 2019. Cancer Med. 2021, 10, 4905–4922. [Google Scholar] [CrossRef]
  5. Born, L.J.; Khachemoune, A. Basal cell carcinosarcoma: A systematic review and reappraisal of its challenges and the role of Mohs surgery. Arch. Dermatol. Res. 2023, 315, 2195–2205. [Google Scholar] [CrossRef]
  6. Naik, P.P.; Desai, M.B. Basal Cell Carcinoma: A Narrative Review on Contemporary Diagnosis and Management. Oncol. Ther. 2022, 10, 317–335. [Google Scholar] [CrossRef]
  7. Reinehr, C.P.H.; Bakos, R.M. Actinic keratoses: Review of clinical, dermoscopic, and therapeutic aspects. An. Bras. De Dermatol. 2019, 94, 637–657. [Google Scholar] [CrossRef]
  8. Del Regno, L.; Catapano, S.; Di Stefani, A.; Cappilli, S.; Peris, K. A Review of Existing Therapies for Actinic Keratosis: Current Status and Future Directions. Am. J. Clin. Dermatol. 2022, 23, 339–352. [Google Scholar] [CrossRef]
  9. Casari, A.; Chester, J.; Pellacani, G. Actinic Keratosis and Non-Invasive Diagnostic Techniques: An Update. Biomedicines 2018, 6, 8. [Google Scholar] [CrossRef]
  10. Opoko, U.; Sabr, A.; Raiteb, M.; Maadane, A.; Slimani, F. Seborrheic keratosis of the cheek simulating squamous cell carcinoma. Int. J. Surg. Case Rep. 2021, 84, 106175. [Google Scholar] [CrossRef]
  11. Moscarella, E.; Brancaccio, G.; Briatico, G.; Ronchi, A.; Piana, S.; Argenziano, G. Differential Diagnosis and Management on Seborrheic Keratosis in Elderly Patients. Clin. Cosmet. Investig. Dermatol. 2021, 14, 395–406. [Google Scholar] [CrossRef] [PubMed]
  12. Jiahua, X.; Yi, C.; Liwu, Z.; Yan, S.; Yichi, X.; Lingli, G. Innovative combined therapy for multiple keloidal dermatofibromas of the chest wall: A novel case report. CJPRS 2022, 4, 182–186. [Google Scholar] [CrossRef]
  13. Endzhievskaya, S.; Hsu, C.-K.; Yang, H.-S.; Huang, H.-Y.; Lin, Y.-C.; Hong, Y.-K.; Lee, J.Y.W.; Onoufriadis, A.; Takeichi, T.; Lee, J.Y.-Y.; et al. Loss of RhoE Function in Dermatofibroma Promotes Disorganized Dermal Fibroblast Extracellular Matrix and Increased Integrin Activation. J. Investig. Dermatol. 2023, 143, 1487–1497. [Google Scholar] [CrossRef] [PubMed]
  14. Park, S.; Yun, S.J. Acral Melanocytic Neoplasms: A Comprehensive Review of Acral Nevus and Acral Melanoma in Asian Perspective. Dermatopathology 2022, 9, 292–303. [Google Scholar] [CrossRef] [PubMed]
  15. Frischhut, N.; Zelger, B.; Andre, F.; Zelger, B.G. The spectrum of melanocytic nevi and their clinical implications. J. Der Dtsch. Dermatol. Ges. 2022, 20, 483–504. [Google Scholar] [CrossRef] [PubMed]
  16. Hu, K.; Li, Y.; Ke, Z.; Yang, H.; Lu, C.; Li, Y.; Guo, Y.; Wang, W. History, progress and future challenges of artificial blood vessels: A narrative review. Biomater. Transl. 2022, 28, 81–98. [Google Scholar] [CrossRef]
  17. Liu, C.; Dai, J.; Wang, X.; Hu, X. The Influence of Textile Structure Characteristics on the Performance of Artificial Blood Vessels. Polymers 2023, 15, 3003. [Google Scholar] [CrossRef]
  18. Folland, G.B. Fourier Analysis and Its Applications; American Mathematical Society: Providence, RI, USA, 2000; pp. 314–318. [Google Scholar]
  19. Al-masni, M.A.; Al-antari, M.A.; Choi, M.T.; Han, S.M.; Kim, T.S. Skin lesion segmentation in dermoscopy images via deep full resolution convolutional networks. Comput. Meth. Prog. Biomed. 2018, 162, 221–231. [Google Scholar] [CrossRef]
  20. Afza, F.; Sharif, M.; Khan, M.A.; Tariq, U.; Yong, H.-S.; Cha, J. Multiclass Skin Lesion Classification Using Hybrid Deep Features Selection and Extreme Learning Machine. Sensors 2022, 22, 799. [Google Scholar] [CrossRef]
  21. Surówka, G.; Ogorzalek, M. On optimal wavelet bases for classification of skin lesion images through ensemble learning. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014. [Google Scholar] [CrossRef]
  22. López-Ávila, L.F.; Álvarez-Borrego, J.; Solorza-Calderón, S. Fractional Fourier-Radial Transform for Digital Image Recognition. J. Signal Process. Syst. 2021, 2021, 49–66. [Google Scholar] [CrossRef]
  23. ISICCHALLENGE. Available online: https://challenge.isic-archive.com/data/#2019 (accessed on 10 January 2019).
  24. Casasent, D.; Psaltis, D. Scale invariant optical correlation using Mellin transforms. Opt. Commun. 1976, 17, 59–63. [Google Scholar] [CrossRef][Green Version]
  25. Derrode, S.; Ghorbel, F. Robust and efficient Fourier—Mellin transform approximations for gray-level image reconstruction and complete invariant description. Comput. Vis. Image Underst. 2001, 83, 57–78. [Google Scholar] [CrossRef]
  26. Alcaraz-Ubach, D.F. Reconocimiento de Patrones en Imágenes Digitales Usando Máscaras de Hilbert Binarias de Anillos Concéntricos. Bachelor Thesis, Science Faculty, Universidad Autónoma de Baja California, Ensenada, México, 2015. [Google Scholar]
  27. Davis, J.A.; McNamara, D.E.; Cottrell, D.M.; Campos, J. Image processing with the radial Hilbert transform: Theory and experiments. Opt. Lett. 2000, 25, 99–101. [Google Scholar] [CrossRef] [PubMed]
  28. Pei, S.C.; Ding, J.J. The generalized radial Hilbert transform and its applications to 2D edge detection (any direction or specified directions). In Proceedings of the 2003 IEEE International Conference on Acoustics, Speech, and Signal, Hong Kong, China, 6–10 April 2003. [Google Scholar] [CrossRef]
  29. King, F.W. Hilbert Transforms; Cambridge University Press: Cambridge, UK, 2009; pp. 1–858. [Google Scholar] [CrossRef]
  30. Ojala, T.; Pietikainen, T.; Maenpaa, T. Multiresolution grayscale and rotation invariant texture classification with local binary patterns. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
  31. Rogers, S.; Girolami, M. A First Course in Machine Learning, 2nd ed.; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2017; pp. 185–195. [Google Scholar]
  32. K-Nearest Neighbor. Available online: http://scholarpedia.org/article/K-nearest_neighbor (accessed on 16 August 2023).
  33. Mucherino, A.; Papajorgji, P.J.; Pardalos, P.M.; Mucherino, A.; Papajorgji, P.J.; Pardalos, P.M. K-nearest neighbor classification. In Data Mining in Agriculture. Springer Optimization and Its Applications, 2nd ed.; Springer: New York, NY, USA, 2009; Volume 34, pp. 83–106. [Google Scholar] [CrossRef]
  34. Gerón, A. Hands-On Machine Learnign with Scikit-Learn, Keras & TensorFlow, 2nd ed.; O’Reily: Sebastopol, CA, USA, 2019; pp. 189–212. [Google Scholar]
  35. Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
  36. Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
  37. Ma, X.; Yang, T.; Chen, J.; Liu, Z. k-Nearest Neighbor algorithm based on feature subspace. In Proceedings of the 2021 International Conference on Big Data Analysis and Computer Science (BDACS), Kunming, China, 25–27 June 2021. [Google Scholar] [CrossRef]
  38. Xie, P.; Zuo, K.; Zhang, Y.; Li, F.; Yin, M.; Lu, K. Interpretable classification from skin cancer histology slides using deep learning: A retrospective multicenter study. arXiv 2019, arXiv:1904.06156. [Google Scholar] [CrossRef]
  39. Ogudo, K.A.; Surendran, R.; Khalaf, O.I. Optimal Artificial Intelligence Based Automated Skin Lesion Detection and Classification Model. Comput. Syst. Sci. Eng. 2023, 44, 693–707. [Google Scholar] [CrossRef]
  40. Ballerini, L.; Fisher, R.B.; Aldridge, B.; Rees, J. Non-melanoma skin lesion classification using colour image data in a hierarchical k-nn classifier. In Proceedings of the 2012 9th IEEE International Symposium on Biomedical Imaging (ISBI), Barcelona, Spain, 2–5 May 2012; pp. 358–361. [Google Scholar]
  41. Ozkan, I.A.; Koklu, M. Skin Lesion Classification using Machine Learning Algorithms. Int. J. Intell. Syst. Appl. Eng. 2017, 5, 285–289. [Google Scholar] [CrossRef]
  42. Nasir, M.; Attique Khan, M.; Sharif, M.; Lali, I.U.; Saba, T.; Iqbal, T. An improved strategy for skin lesion detection and classification using uniform segmentation and feature selection based approach. Microsc. Res. Tech. 2018, 81, 528–543. [Google Scholar] [CrossRef]
  43. Chatterjee, S.; Dey, D.; Munshi, S. Integration of morphological preprocessing and fractal based feature extraction with recursive feature elimination for skin lesion types classification. Comput. Methods Programs Biomed. 2019, 178, 201–218. [Google Scholar] [CrossRef] [PubMed]
  44. Fisher, R.; Rees, J.; Bertrand, A. Classification of Ten Skin Lesion Classes: Hierarchical KNN versus Deep Net. In Medical Image Understanding and Analysis, Proceedings of the 23rd Conference, MIUA 2019, Liverpool, UK, 24–26 July 2019; Communications in Computer and Information Science (CCIS); Springer: Berlin/Heidelberg, Germany, 2020; Volume 1065, pp. 86–98. [Google Scholar] [CrossRef]
  45. Molina-Molina, E.O.; Solorza-Calderón, S.; Álvarez-Borrego, J. Classification of Dermoscopy Skin Lesion Color-Images Using Fractal-Deep Learning Features. Appl. Sci. 2020, 10, 5954. [Google Scholar] [CrossRef]
  46. Afza, F.; Khan, M.A.; Sharif, M.; Saba, T.; Rehman, A.; Javed, M.Y. Skin Lesion Classification: An Optimized Framework of Optimal Color Features Selection. In Proceedings of the 2020 2nd International Conference on Computer and Information Sciences (ICCIS), Sakaka, Saudi Arabia, 13–15 October 2020; pp. 1–6. [Google Scholar]
  47. Ghalejoogh, G.S.; Kordy, H.M.; Ebrahimi, F. A hierarchical structure based on Stacking approach for skin lesion classification. Expert Syst. Appl. 2020, 145, 113127. [Google Scholar] [CrossRef]
  48. Moldovanu, S.; Damian Michis, F.A.; Biswas, K.C.; Culea-Florescu, A.; Moraru, L. Skin Lesion Classification Based on Surface Fractal Dimensions and Statistical Color Cluster Features Using an Ensemble of Machine Learning Techniques. Cancers 2021, 13, 5256. [Google Scholar] [CrossRef]
  49. Shetty, B.; Fernandes, R.; Rodrigues, A.P.; Chengoden, R.; Bhattacharya, S.; Lakshmanna, K. Skin lesion classification of dermoscopic images using machine learning and convolutional neural network. Sci. Rep. 2022, 12, 18134. [Google Scholar] [CrossRef]
  50. Mohanty, N.; Pradhan, M.; Reddy, A.V.N.; Kumar, S.; Alkhayyat, A. Integrated Design of Optimized Weighted Deep Feature Fusion Strategies for Skin Lesion Image Classification. Cancers 2022, 14, 5716. [Google Scholar] [CrossRef] [PubMed]
  51. Camacho-Gutiérrez, J.A.; Solorza-Calderón, S.; Álvarez-Borrego, J. Multi-class skin lesion classification using prism- and segmentation-based fractal signatures. Expert Syst. Appl. 2022, 197, 116671. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Novel Microfluidic Septum to Optimize Energy Recovery in Single-Chamber Microbial Fuel Cells
Previous
Progress and Prospects in Assessing the Multidimensional Environmental Impacts of Global Vegetation Restoration
Next