Abstract
This paper develops a multi-objective optimization model for national high-speed railway network planning. Three objectives are proposed from the macro, meso, and micro perspectives, and these three objectives are considered simultaneously. Using real data, case studies are conducted to optimize China’s “four east–west and four north–south railway lines” network, which includes Beijing, Shanghai, Wuhan, Guangzhou, and Zhengzhou as main hubs. The results show that, on the one hand, the optimization model reduces the overlap between long-distance passengers and short-distance passengers on the high-speed railway line, facilitates the travel of passengers, and improves the line service capability; on the other hand, optimization of the network shortens the travel time of the passengers, reduces the cost of the railway, and improves the operation efficiency of the high-speed railway line network. The results show that the total travel time of all high-speed railway passengers in the optimization model is reduced by 18.4%, while the benefit rate of the operator increased by 21.99%.
1. Introduction
As a symbol of modern technology and scientific development, the high-speed railway is considered the most competitive passenger transport technology [1]. It is the most complex engineering industry after the aerospace industry [2]. Although the high-speed railway derives from the traditional railway, it has broken from the concept of the traditional railway and developed into a new transport system compatible with the conventional railway network [3] High-speed railways in countries such as China, Japan, France, Germany, and Spain have developed rapidly on a large scale [4]. By the end of 2021, China’s high-speed railway had reached 40,000 km, ranking first in the world.
China’s high-speed railway network not only plays a critical role in meeting residents’ requirements for fast and comfortable travel but also drives the economic development of towns along the railway and the growth of the national economy [5,6]. The construction of the high-speed railway requires a large amount of investment, for example, the construction cost of the Beijing–Shanghai high-speed railway in China was USD 1.29 million per kilometer. Therefore, it is necessary to develop an optimal route structure for the railway network at the planning level. Nevertheless, the existing high-speed railway network is not fully optimized, due to a lack of knowledge on developing high-speed railways [7]. Therefore, the motivation of this study was to propose an optimization framework for high-speed railway network planning. The innovation of this study lies in the simultaneous consideration of macro, meso, and micro-objectives, which capture the interests of travelers, the benefits of operators, and the efficiency of managers. To be more specific, (1) the micro-objective was to minimize the generalized travel cost of the high-speed railway for travelers; (2) the meso-objective was to maximize the operators’ profit; (3) the macro-objective was to minimize the energy consumption of the high-speed railway system.
The rest of this paper is organized as follows. Section 2 discusses previous related works and establishes the contributions of this paper. Section 3 introduces the three objectives, the multi-objective optimization model, and the solution method. Section 4 conducts a case study using real data. Finally, Section 5 concludes this paper and provides directions for future research.
2. Literature Review
There have been a considerable number of studies on high-speed railway optimization in the scientific literature. Table 1 is a representative list of the most advanced approaches in chronological order, mainly focusing on three aspects, namely, the type of research perspective, the number of objectives, and the method applied to solve the proposed model.

Table 1.
A summary of high-speed railway optimization studies.
In terms of research perspectives, railway optimization has been studied from the meso-level [8,9,10,13,16,18,20,23,24,26] and micro-level [9,11,12,17,18,21,22,26,27,28] perspectives. Studies from the micro-level perspective have attempted to capture the interests of travelers. For instance, Castillo et al. [17] proposed a time partitioning technique to optimize the schedule of a few trains. Rui et al. [11] evaluated the railway station location using accessibility and travel time consumption. Wang et al. [12] studied the timetable rescheduling problem based on the delay period and the number of trains impacted. Meanwhile, Xu et al. [28] formulated two mixed-integer programming models to simultaneously assign locomotives to trains and schedule trains so that delays were minimized. At the meso-level, Xu et al. [13] proposed using system utility to optimize resource allocation in high-speed railway wireless networks. Zheng and Liu [19] applied the total revenue of the train system to identify the optimal ticket fare for a single high-speed train. Wang et al. [20] employed optimum rail profiles to improve the stability of high-speed railway vehicles. Lin et al. [24] used the total costs to determine whether high-speed trains needed maintenance. Considering the application of the total turnaround time into maintenance, Wang et al. [25] studied high-speed train unit routing problems. Nevertheless, the above-mentioned studies suffer a shortcoming because they ignored the trade-off between the travelers’ costs and operators’ benefits. Chen et al. [18] overcame this disadvantage by integrating the interests of travelers and operators and applied a stop cost for railway corporations and the convenience of travelling for travelers to optimize the stop schedules. Both Zhang et al. [21] and Han and Ren [26], in line with Chen et al. [18], analyzed the optimization problem associated with the high-speed railway network and formed the micro- and meso-level perspectives. Zhang et al. [21] implemented a trade-off between a track occupation time and the total walking distance to solve the track allocation problem. Han and Ren [26] focused on the stop plan and ticket allocation problems that were significantly affected by passenger satisfaction and average seat occupancy rate. In addition, Binder et al. [29] focused on the railway timetable rescheduling problem in cases of large disruptions from a macroscopic point of view. Based on population coverage, budget constraints, and origin–destination flows, Blanco et al. [30] proposed a model for expanding transportation networks from a macro perspective.
However, the high-speed railway system is a multi-factor, multi-objective, and multi-function stochastic dynamic system. Therefore, in recent years, a few studies on optimizing high-speed railway problems have considered multi-objective models [8,15]. Sun et al. [14] proposed a multi-objective optimization model for train routing on a high-speed railway network, thereby providing an important reference for train planning to provide better services. Fernández-Rodríguez et al. [31] described the train scheduling problem as a dynamic multi-objective optimization model that utilizes accurate results provided by detailed real-time train simulations. Mateus et al. [32] described a multi-criteria decision analysis approach that identified the best alternative from a given set of possible alternatives. Based on the Beijing–Shanghai high-speed railway and the existing railway network, Ma et al. [33] established a multi-objective model for high-speed and medium-speed trains. At present, the model has been applied to the train diagram system of the Beijing–Shanghai high-speed railway. Nevertheless, the above studies only described the high-speed railway as a multi-objective model but did not optimize it.
As shown in the above review, existing models and tools are mainly concerned with high-speed railway management. Most of them use a single objective to compute the location of high-speed railway systems, and their output is an analysis of different indexes that reflect the characteristics of the systems. Some scholars have focused on optimizing the high-speed railway strictly according to the given operation management, which means that robustness characteristics are seldom considered. However, various disturbances can influence real-world high-speed railway operations. Therefore, if we use these results to evaluate high-speed railway operation management, we will obtain incorrect outcomes because of the neglected disturbances. To address the above issues, this paper describes the high-speed railway line problem as a dynamic multi-objective model and carries out optimization research to provide accurate results. Rather than just focusing on a single perspective, this paper proposes a more realistic model that takes into account multiple perspectives: macro, meso, and micro. An optimization model is used to solve the dimension problems of the different objective functions using the economic transformation coefficient, and the best operation scheme for the high-speed railway is obtained.
It is well known that there are many methods for solving optimization models. For highly complex and large-scale optimization models, an optimization algorithm is often used, such as the neural network algorithm [34,35,36], tabu search algorithm [22], genetic algorithm [9,14,18,25,36,37], or simulated annealing algorithm [11,21,24]. However, the process of improving the applicability of the algorithm to multi-objective optimization problems remains to be further studied.
In this paper, a multi-objective optimization model of the high-speed railway system is constructed by comprehensively considering the micro-, meso-, and macro-objectives. The Pareto optimization algorithms can offer a means to find a set of Pareto-optimal solutions in a single run [10,38,39]. Therefore, the main purpose of this paper was to introduce a novel Pareto frontier optimization algorithm to solve the tri-objective model and determine the optimal decision within the Pareto-optimal solution set range.
3. Methodology
3.1. Objectives for Optimizing the High-Speed Railway Network
The train operation scheme for the high-speed railway is an important part of the transportation organization problems, and the train stop scheme is the key link in the operation scheme. Therefore, this paper comprehensively considers the passenger transport cost, the passenger transport demand, and the energy consumption; establishes a multi-objective model to improve the network efficiency, and optimizes the train stop scheme, all while using ‘whether a railway station’ as the decision variable in this paper.
3.1.1. Micro-Objective for Traveler’s Demand
The proposed micro-objective is to minimize the generalized travel cost of passengers. Based on the interests of travelers, the optimization function for the high-speed railway line was constructed from two aspects: travel time and travel cost. To maximize the benefit for passengers, this section mainly builds on the optimization function at the micro-level. Based on the basic concepts and properties of the uncertainty theory, the proposed model is described as a quantitative linear model.
- Passenger travel time function of travelers: The travel time for high-speed railway passengers is defined as the total time between the starting point (origin, O) and the endpoint (destination, D). It includes the time from the travel point to the corresponding train station, the transfer times at different stations, the travel time of the train, and the time from the train station to the travel destination. Figure 1 shows a high-speed railway line.
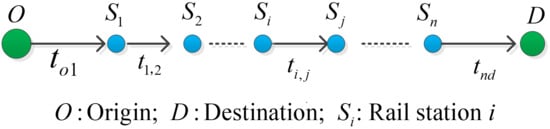 Figure 1. A high-speed railway line.When a passenger travels between (origin and destination are and ), they need to traverse a set of railway stations. The set of stations is denoted as . For an pair, their travel time is defined as:where represents the travel time between the origin and the first railway station, represents the travel time between stations; , , and represent the travel time between the last railway station and the destination.
Figure 1. A high-speed railway line.When a passenger travels between (origin and destination are and ), they need to traverse a set of railway stations. The set of stations is denoted as . For an pair, their travel time is defined as:where represents the travel time between the origin and the first railway station, represents the travel time between stations; , , and represent the travel time between the last railway station and the destination. - Passengers’ travel cost function: The travel cost, which is the total fare, includes all the expenses for high-speed railway travelling, and is the main factor for passengers in choosing a method of travel. This paper provides general fares, not the actual fare. The general fare is the comparable fare rate per kilometer per person on different routes, determined by the administrative department. The actual fare is the fare between the starting point and the ending point for each person, and it is uncertain due to seasonal fare discounts and other factors. We assume that the high-speed train journey takes place along an itinerary consisting of m sections along a route and that these are sequential. The lower the fare, the more attractive it is to passengers. Thus, the relative function of the cost per passenger can be described as:where is the fare for a passenger traveling by high-speed railway; is the distance traveled by passengers on the i-th section of the high-speed railway; is the fare rate per kilometer per person of the i-th section of the high-speed railway line, and it is determined by the operating speed ; is the number of high-speed railway lines.
- Micro-objective model for optimizing the high-speed railway network: The micro-objective is to minimize the generalized travel cost for passengers on high-speed railway travel: their travel expenses and travel time. It is the constraint condition that a high-speed train can go from 0 to 350 km/h in about 10 min, while it also takes about 10 min to decelerate from 350 km/h to 0. A high-speed train runs for at least 20 min, and 20 min is also the constraint condition (). Therefore, the micro-objective function is constructed based on the two optimization objectives in Equations (1) and (2).where is the micro-objective model for optimizing the high-speed railway network and is the value of time in monetary terms used to solve the dimension problem of the different objective functions.
3.1.2. Meso-Objective for Operator’s Supply
The line optimization function of a high-speed railway is established to maximize the benefit to the operators, which includes both the financial cost and the income of the operators.
- The financial cost function of the operators: As the responsible person and transporter of the high-speed railway, operators bear not only the construction costs of the high-speed railway but also the responsibility for its operation and maintenance. This paper assumes that the service operator and infrastructure owner are the same (as in the case of China), and the cost structure is as follows:where is the operating cost of the line, is the construction and maintenance costs of the high-speed railway lines, is the construction and maintenance costs of a high-speed station, and is the purchase and maintenance costs of a high-speed train. We can calculate , , and , respectively, according to Equations (5)–(7).where is the annual amortization cost and are the operating costs and the annual maintenance costs for passengers who traveled on the i-th high-speed railway line, respectively. and are the annual construction costs and the maintenance cost of the station for the j-th high-speed railway line, respectively, and is the number of stations on the high-speed railway line. and are the annual purchase cost and the annual maintenance cost of the k-th high-speed train, respectively, and is the number of high-speed trains.
- Financial income function of the operator. High-speed railway operators must consider costs (operation and maintenance, etc.) and income (financial gain). The yield rate is the best indicator for measuring the operating efficiency of a high-speed railway. The relationship between the yield rates of the high-speed railway operators is as follows:where is the annual operating income of the high-speed railway lines, and , , and are the annual operating income (depending on the fare and the number of passengers), the annual staff expenses, and the other annual expenses for the i-th high-speed railway line traveled by passengers, respectively.
- Meso-objective model for optimizing the high-speed railway network: The meso-objective aims to determine the operating requirements for the high-speed railway and to maximize its benefits. According to Chinese official documents, it costs (), on average, USD 1.29 million per kilometer to build a high-speed railway track, which allows a train to travel at 350 km/h, while it costs, on average, USD 0.89 million per kilometer to build a track, which allows a train to travel at 250 km/h. F2 is the constraint condition in high-speed railway enterprises minimizing costs and maximizing income. Therefore, the micro-objective function can be constructed based on two optimization objectives, as shown in Equations (4) and (8).
3.1.3. Macro-Objective for Government Management
Considering national interests, a macro-level line optimization function for a high-speed railway should include energy consumption and line efficiency. This paper focuses on low-carbon traffic optimization by the government at the macro level.
- Energy consumption function by the government: As a high-speed train is a fast vehicle that uses electrical power, energy consumption should be minimized. The relative function of energy consumption is:where denotes the energy consumption of a high-speed railway line; , , and are the number, the operating speed, and the energy consumption per kilometer of the k-th train on the i-th high-speed railway line, respectively; is the number of high-speed trains in operation.
- Efficiency function of the government: The line efficiency of a high-speed railway is the main indicator to comprehensively evaluate its operating state. The greater the line efficiency is, the better the operating state of the high-speed railway. The relative line efficiency function is:where is the line efficiency of the high-speed railway, the general requirement is that line efficiency should be more than 70%; and are the passenger flow and the passenger demand for the i-th high-speed railway line station to station , respectively.
- Macro-objective model for optimizing the high-speed railway network: The macro-objective aims to optimize the efficiency of the high-speed railway line in terms of energy consumption, as line efficiency is an important indicator. Then, the macro-objective model is constructed based on the two optimization objectives in Equations (10) and (11).where and are weight coefficients used to synthesize the line efficiency and the energy consumption .
3.2. Multi-Objective Optimization Model
Multi-objective optimization is a vector optimization problem, which aims to find the design variables and optimize a vector of the objective function, subject to several constraints and bounds. The multi-objective optimization is often formulated as follows:
the optimization of the high-speed railway lines adopts a scientific method to optimize the operating line. The main purpose is to make the passenger flow distribution equal to the actual passenger flow and facilitate passengers to travel, improve the efficiency of enterprises, and promote the sustainable development of high-speed railways. The line optimization problem for high-speed railways is a management problem in the tri-objective system. The principle is that high-level management sends certain information to the lower-level management, and the low-level management responds according to their interests or preferences. Then, the high-level management makes decisions to meet their overall interests. When developing a tri-objective model to optimize high-speed railway lines, this paper considers the macro- (the country, i.e., the manager), meso- (enterprises, i.e., operators), and micro- (individuals, i.e., travelers) level aspects.
Since the tri-objective model for line optimization is a multi-objective non-linear programming problem with multiple targets, in practical application, the model should be simplified rationally and practically. Therefore, a tri-objective model for high-speed railway line optimization is constructed based on Equations (3), (9) and (12):
where is a tri-objective model for high-speed railway line optimization; is the minimum time for high-speed railway lines to operate between two stations. is the fare between the starting point and the ending point for each person; is the operating distance of a high-speed railway line; is the average cost per kilometer to build a high-speed railway; is the minimum line efficiency for the high-speed railway.
3.3. Solution Method
The route planning of the high-speed railway is a vector optimization problem. Considering that the multi-objective optimization problem usually has multiple Pareto non-inferior solutions, the purpose of the multi-objective railway network planning method based on Pareto optimization is to search the complete and evenly distributed Pareto non-inferior solution set as the optimization scheme, and then, make the final decision based on certain principles and preferences in the optimization scheme [14].
This paper applies an improved PE algorithm to solve the tri-objective model. During the modeling, we considered the macro, meso, and micro disturbances, used various functions to describe the differences and applied an improved PE algorithm as the modeling tool. The flow chart of the improved PE algorithm for the tri-objective model is shown in Figure 2.
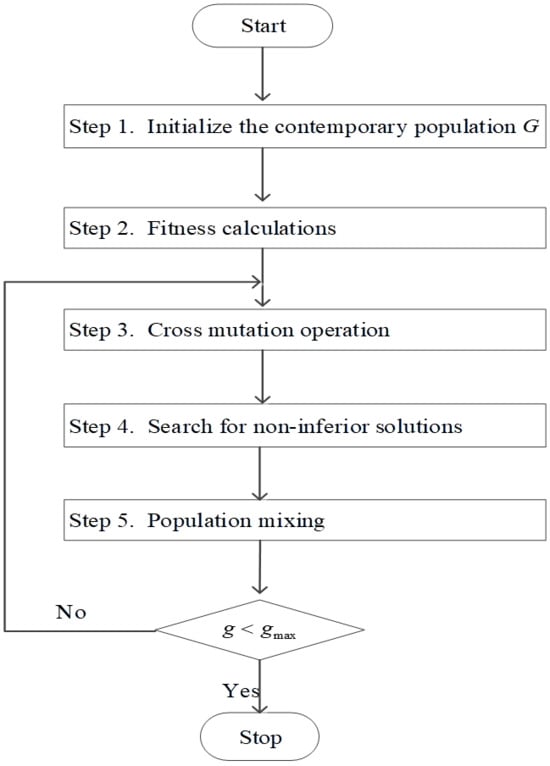
Figure 2.
Flowchart of the improved PE algorithm.
The specific process is as follows:
- Step 1.
- Initialize the contemporary population
The elite population is generated and set empty. Then, the non-inferior solution of the contemporary population is found and stored in the elite population .
- Step 2.
- Fitness calculations
The fitness of the elite population and contemporary population individuals is calculated, while the maximum number of iterations is set as .
- Step 3.
- Cross-mutation operation
A new population is formed via cross-mutation operations, and the objective function values of the individuals in the new species group are calculated.
- Step 4.
- Search for non-inferior solutions
The set of non-inferior solutions is solved, which is denoted as .
- Step 5.
- Population mixing
The repeated individuals in the population and the elite population are eliminated, and the elite population is copied into the population to form a new contemporary population .
- Step 6.
- Obtain the elite population
If , the function returns to Step 3; otherwise, the algorithm is terminated.
4. Case Study
We selected the “four east–west and four north–south” railway network of China’s national high-speed railway as the research object to explain the rationality of the single-objective model. The high-speed railways incorporated into the “four east–west and four north–south” railway network connect almost all of the large cities in China. The details are shown in Table 2.

Table 2.
“Four east–west and four north–south” railway lines.
In this paper, eight high-speed railway lines in the “four east–west and four north–south” railway network are analyzed. From July to September 2015, our research team investigated and analyzed the above eight high-speed railways and obtained some valid and relevant data that were published by the Ministry of Transport of the People’s Republic of China. The operating status of these eight high-speed railways was also analyzed using the optimization model.
4.1. Results of the Single Objective
In this section, we used Equations (3), (9) and (12) to study the “four east–west and four north–south” railway networks of China’s National Railway. The values are defined as , , , , and . The optimized and unoptimized indicators are shown in Figure 3, Figure 4 and Figure 5.
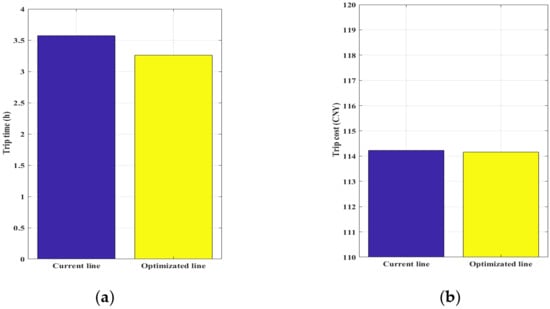
Figure 3.
Comparison of the performance indicators based on the micro-objective optimization model. (a) Travel time (h); (b) travel cost (CNY).
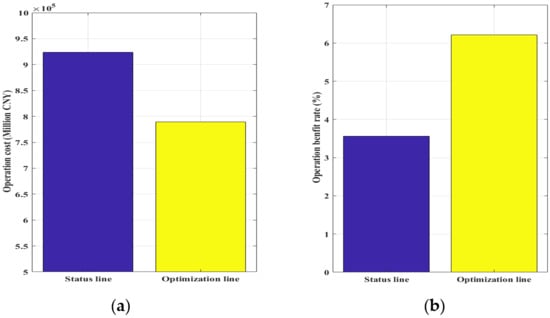
Figure 4.
Comparison of performance indicators based on the meso-objective optimization model. (a) Operation cost (million CNY); (b) operation benefit rate (%).
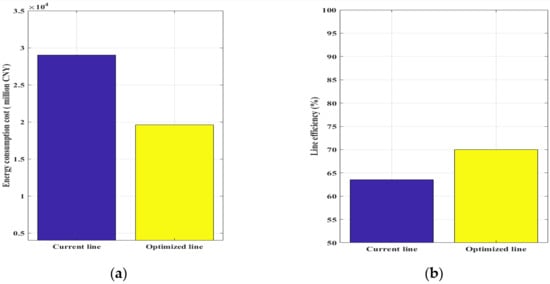
Figure 5.
Comparison of performance indicators based on the macro-objective optimization model. (a) Energy consumption cost (million CNY); (b) line efficiency (%).
As shown in Figure 3, Figure 4 and Figure 5, the total travel time of all high-speed railway passengers in the optimization model was reduced by 8.68%, and the benefit rate of the operator increased by 21.99%. This means that the proposed model can improve the operating ability of the high-speed railway, reduce passengers’ travel time, and improve the overall benefit of high-speed railways. The index comparison between the current and the optimized high-speed railway is shown in Table 3.

Table 3.
Index comparison between the current and optimized high-speed railway.
4.2. Result of the Multi-Objective Model
As shown in Table 2, this network is composed of eight lines, and each line is optimized by PE. The optimization process for the “four east–west and four north–south” railway network is shown in Figure 6.
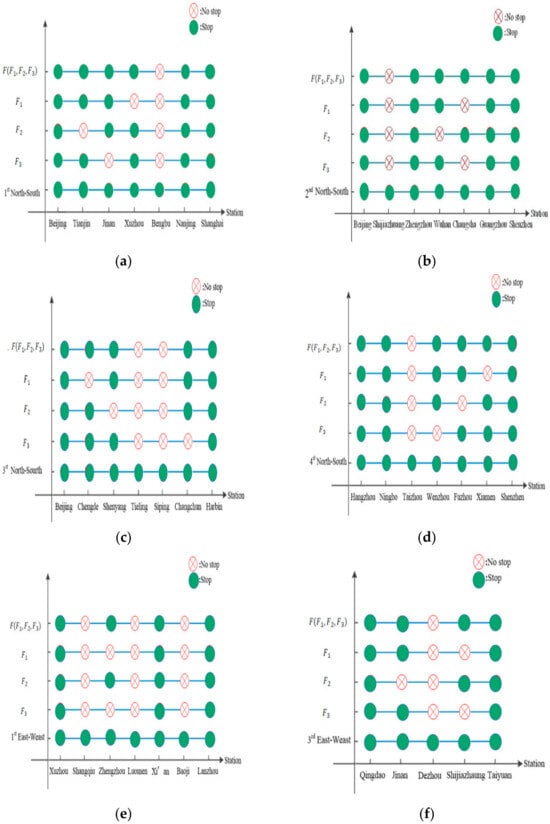
Figure 6.
The optimization process for the “four north–south and four east–west” railway lines. (a) The 1st north–south railway line; (b) the 2nd north–south railway line; (c) the 3rd north–south railway line; (d) the 4th east–west railway line; (e) the 1st east–west railway line; (f) The 3rd east–west railway line.
The optimized “four east–west and four north–south” railway network is shown in Table 4. The second east–west and the fourth east–west lines are unchanged, while the others (the first, second, third, and fourth north–south and the first and third east–west lines) are changed. Specifically, for the first north–south line, Bengbu station is not a stop; for the second north–south line, Shijiazhuang is not a stop; for the third north–south line, the Tieling and Siping stations are not stops; for the fourth north–south line, the Taizhou station is not a stop; for the first east–west line, the Shangqiu and Luomen stations are not stops; for the third east–west line, the Dezhou station is not a stop. Thus, the network becomes optimal after optimizing the transportation hubs of Beijing, Shanghai, Wuhan, Guangzhou, and Zhengzhou using the tri-objective model.

Table 4.
Optimized “four east–west and four north–south” railway network.
5. Conclusions
This paper comprehensively studied a high-speed railway operating problem by using the uncertain mathematics theory. Eight high-speed railway lines in the “four east–west and four north–south” railway network were selected for analysis. First, three single-objective models are proposed to optimize the railway network. Through optimization, the total travel time and travel cost for passengers are reduced by 18.04% and 0.063%, respectively. The operation costs and energy consumption costs of the high-speed railway are reduced by 17.08% and 21.99%, respectively. The line efficiency of the high-speed railway is increased by 10.20%. Second, based on the optimization function of the high-speed railway operation, a tri-objective model for line optimization is established. The improved Pareto efficient algorithm was selected to solve the tri-objective model. According to the optimization results, we suggest that the second east–west and the fourth east–west lines remain unchanged, while some stations in the first, second, third, and fourth north–south lines and the first and third east–west lines do not stop. The multi-objective optimization also provides the average speed for each line. Of course, the speed of some lines is quite different from their original speed, such as the first, second, third, and fourth north–south lines. The relevant results obtained by using the improved PE algorithm still need further verification, or even practical investigation, to prove their feasibility.
These results match the related national planning policies of the Beijing, Shanghai, Wuhan, Guangzhou, and Zhengzhou main hubs. The new PE railway line-optimizing method proposed in this work is especially suitable for optimization problems, although it can also be used as a general-purpose optimization method. This approach provides decision-makers with a Pareto set of choices. The solutions obtained through this method can reflect the entire Pareto optimal frontier. This approach also automatically captures the Pareto optimal frontier without any formal optimization process. It uses an approximation to guide the sampling process and does not require an accurate approximation model. Through testing and application, the PE method was found to be robust and efficient. This optimization model can be used in future research on high-speed railway network planning problems.
Author Contributions
Conceptualization, Q.H. and L.B.; methodology, J.L.; resources, M.T.; writing—original draft preparation, Q.H.; writing—review and editing, L.B. and J.L.; supervision, M.T.; funding acquisition, Q.H. and L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51178157, High-level Project of the Top Six Talents in Jiangsu Province, grant number JXQC021, Key Science and Technology Program in Henan Province, grant number 182102310004. China Scholarship Council No. 201906840033, 202106840078.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hou, Y. Agglomeration spillover, accessibility by high-speed rail, and urban innovation in China: A focus on the electronic information industry. Habitat Int. 2022, 126, 102618. [Google Scholar] [CrossRef]
- Liu, J.; Xing, X. Introduction to High-Speed Railway; China Railway Press: Beijing, China, 2013. [Google Scholar]
- Zhang, D.; Peng, Y.; Xu, Y.; Du, C.; Zhang, Y.; Wang, N.; Chong, Y.; Wang, H.; Wu, D.; Liu, J. A high-speed railway network dataset from train operation records and weather data. Sci. Data 2022, 9, 244. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liu, W.; Peng, K. Research on high speed rail broadband communication resource management algorithm based on Cloud Computing. In Proceedings of the 2021 4th International Conference on Information Systems and Computer Aided Education, Dalian, China, 24–26 September 2021; pp. 2830–2835. [Google Scholar]
- Jiabao, Y.; Zhuo, F. An optimization method for high-speed motor train unit crew roundtrip routing problem with immediate turn-back. J. Railw. Sci. Eng. 2018, 15, 24–31. [Google Scholar]
- Ning, B.; Tang, T.; Dong, H.; Wen, D.; Liu, D. An Introduction to Parallel Control and Management for High-Speed Railway Systems. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1473–1483. [Google Scholar] [CrossRef]
- Deng, D.; Wu, M.; Chen, Z. An optimized relay handover algorithm in TD-LTE along high-speed railway. In Proceedings of the TENCON 2013–2013 IEEE Region 10 Conference, Xi’an, China, 22–25 October 2013; p. 31194. [Google Scholar]
- Min, L.X.; Yong, W.J.; Yuan, Y.; Yan, X.W. Multiobjective optimization of preventive maintenance schedule on traction power system in high-speed railway. In Proceedings of the Reliability & Maintainability Symposium, Fort Worth, TX, USA, 26–29 January 2009; pp. 365–370. [Google Scholar]
- Maji, A.; Jha, M.K. Multi-objective highway alignment optimization using a genetic algorithm. J. Adv. Transp. 2010, 43, 481–504. [Google Scholar] [CrossRef]
- Sayarshad, H.R.; Javadian, N.; Tavakkoli-Moghaddam, R.; Forghani, N. Solving multi-objective optimization formulation for fleet planning in a railway industry. Ann. Oper. Res. 2010, 181, 185–197. [Google Scholar] [CrossRef]
- Xiang, R.; Gongyuan, L.; Dong, H. Simulated annealing algorithm for solving a bi-level optimization model on high-speed railway station location. In Proceedings of the 2010 Third International Conference on Information and Computing, Wuxi, China, 4–6 June 2010; pp. 159–162. [Google Scholar]
- Wang, L.; Qin, Y.; Xu, J.; Limi, J. A Fuzzy Optimization Model for High-Speed Railway Timetable Rescheduling. Discret. Dyn. Nat. Soc. 2012, 2012, 827073. [Google Scholar] [CrossRef]
- Xu, S.F.; Zhu, G.; Shen, C.; Lei, Y.; Zhong, Z.D. Analysis and Optimization of Resource Control in High-Speed Railway Wireless Networks. Math. Probl. Eng. 2014, 2014, 781654. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, C.; Wu, C. Multi-objective optimization of train routing problem combined with train scheduling on a high-speed railway network. Transp. Res. Part C Emerg. Technol. 2014, 44, 1–20. [Google Scholar] [CrossRef]
- Shangguan, W.; Yan, X.H.; Cai, B.G.; Wang, J. Multiobjective Optimization for Train Speed Trajectory in CTCS High-Speed Railway With Hybrid Evolutionary Algorithm. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2215–2225. [Google Scholar] [CrossRef]
- Xie, Z.; Qin, Y.; Yu, F. Sensor Networks Hierarchical Optimization Model for Security Monitoring in High-Speed Railway Transport Hub. J. Sens. 2015, 2015, 951242. [Google Scholar] [CrossRef]
- Castillo, E.; Grande, Z.; Moraga, P.; Sánchez-Vizcaíno, J. A Time Partitioning Technique for Railway Line Design and Timetable Optimization. Comput. Aided Civ. Infrastruct. Eng. 2016, 31, 599–616. [Google Scholar] [CrossRef]
- Chen, D.; Ni, S.; Xu, C.; Lv, H.; Wang, S. High-speed train stop-schedule optimization based on passenger travel convenience. Math. Probl. Eng. 2016, 2016, 8763589. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, J. The Research on Ticket Fare Optimization for China’s High-Speed Train. Math. Probl. Eng. 2016, 2016, 5073053. [Google Scholar] [CrossRef]
- Wang, P.; Ma, X.; Wang, J.; Xu, J.; Chen, R. Optimization of Rail Profiles to Improve Vehicle Running Stability in Switch Panel of High-Speed Railway Turnouts. Math. Probl. Eng. 2017, 2017, 2856030. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, X.; Wang, L. Track allocation optimization in high-speed railway stations from infrastructure management and service perspectives. Meas. Control 2018, 51, 243–259. [Google Scholar] [CrossRef]
- Feng, Z.; Cao, C.; Liu, Y.; Zhou, Y. A Multiobjective Optimization for Train Routing at the High-Speed Railway Station Based on Tabu Search Algorithm. Math. Probl. Eng. 2018, 2018, 8394397. [Google Scholar] [CrossRef]
- Cheng, R.; Song, Y.; Chen, D.; Ma, X. Intelligent Positioning Approach for High Speed Trains Based on Ant Colony Optimization and Machine Learning Algorithms. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3737–3746. [Google Scholar] [CrossRef]
- Lin, B.; Wu, J.; Lin, R.; Wang, J.; Wang, H.; Zhang, X. Optimization of high-level preventive maintenance scheduling for high-speed trains. Reliab. Eng. Syst. Saf. 2019, 183, 261–275. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Y.; Yu, X.; Hansen, I.A.; Miao, J. Optimization models for high-speed train unit routing problems. Comput. Ind. Eng. 2019, 127, 1273–1281. [Google Scholar] [CrossRef]
- Han, B.; Ren, S. Optimizing stop plan and tickets allocation for high-speed railway based on uncertainty theory. Soft Comput. 2020, 24, 6467–6482. [Google Scholar] [CrossRef]
- Aguado, J.A.; Racero, A.J.S.; Torre, S.D.L. Optimal Operation of Electric Railways with Renewable Energy and Electric Storage Systems. IEEE Trans. Smart Grid 2018, 9, 993–1001. [Google Scholar] [CrossRef]
- Xu, X.; Li, K.; Lu, X. Simultaneous locomotive assignment and train scheduling on a single-track railway line: A simulation-based optimization approach. Comput. Ind. Eng. 2019, 127, 1336–1351. [Google Scholar] [CrossRef]
- Binder, S.; Maknoon, Y.; Bierlaire, M. The multi-objective railway timetable rescheduling problem. Transp. Res. Part C Emerg. Technol. 2017, 78, 78–94. [Google Scholar] [CrossRef]
- Blanco, V.; Puerto, J.; Ramos, A.B. Expanding the Spanish high-speed railway network. Omega 2011, 39, 138–150. [Google Scholar] [CrossRef]
- Fernández-Rodríguez, A.; Fernández-Cardador, A.; Cucala, A.P. Real time eco-driving of high speed trains by simulation-based dynamic multi-objective optimization. Simul. Model. Pract. Theory 2018, 84, 50–68. [Google Scholar] [CrossRef]
- Mateus, R.; Ferreira, J.; Carreira, J. Multicriteria decision analysis (MCDA): Central Porto high-speed railway station. Eur. J. Oper. Res. 2007, 187, 1–18. [Google Scholar] [CrossRef]
- Ma, J.; Hu, S.; Xu, H.; Jiang, F. A multi-objective model on train working diagram for Jinghu high-speed railway line. In Proceedings of the International Conference on Traffic & Transportation Studies, Wuhan, China, 29–31 December 2023. [Google Scholar]
- Çodur, M.Y.; Tortum, A. An Artificial Neural Network Model for Highway Accident Prediction: A Case Study of Erzurum, Turkey. Promet Traffic Traffico 2015, 27, 217–225. [Google Scholar] [CrossRef]
- Jiang, H.; Gao, L. Optimizing the rail profile for high-speed railways based on artificial neural network and genetic algorithm coupled method. Sustainability 2020, 12, 658. [Google Scholar] [CrossRef]
- Wacholder, E.; Han, J.; Mann, R.C. A neural network algorithm for the multiple traveling salesmen problem. Biol. Cybern. 1989, 61, 11–19. [Google Scholar] [CrossRef]
- Zhou, F.H.; Liao, Z.Z. A Particle Swarm Optimization Algorithm. Appl. Mech. Mater. 2013, 303–306, 1369–1372. [Google Scholar] [CrossRef]
- Azzeh, M.; Nassif, A.B.; Banitaan, S.; Almasalha, F. Pareto efficient multi-objective optimization for local tuning of analogy-based estimation. Neural Comput. Appl. 2016, 27, 2241–2265. [Google Scholar] [CrossRef]
- Hombach, L.E.; Walther, G. Pareto-efficient legal regulation of the (bio) fuel market using a bi-objective optimization model. Eur. J. Oper. Res. 2015, 245, 286–295. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, X.; Sheng, X.; Li, Z. Sound Source Localisation for a High-Speed Train and Its Transfer Path to Interior Noise. Chin. J. Mech. Eng. 2019, 32, 178–193. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).