Discrete Element Simple Shear Test Considering Particle Shape
Abstract
:1. Introduction
2. Numerical Simulation
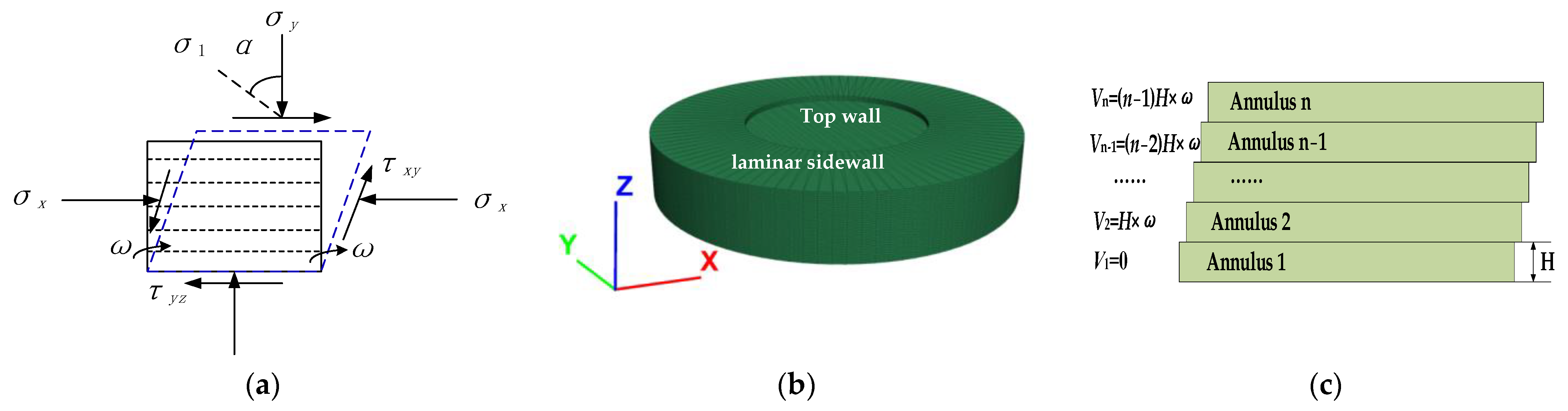
2.1. Simple Shear Test Model
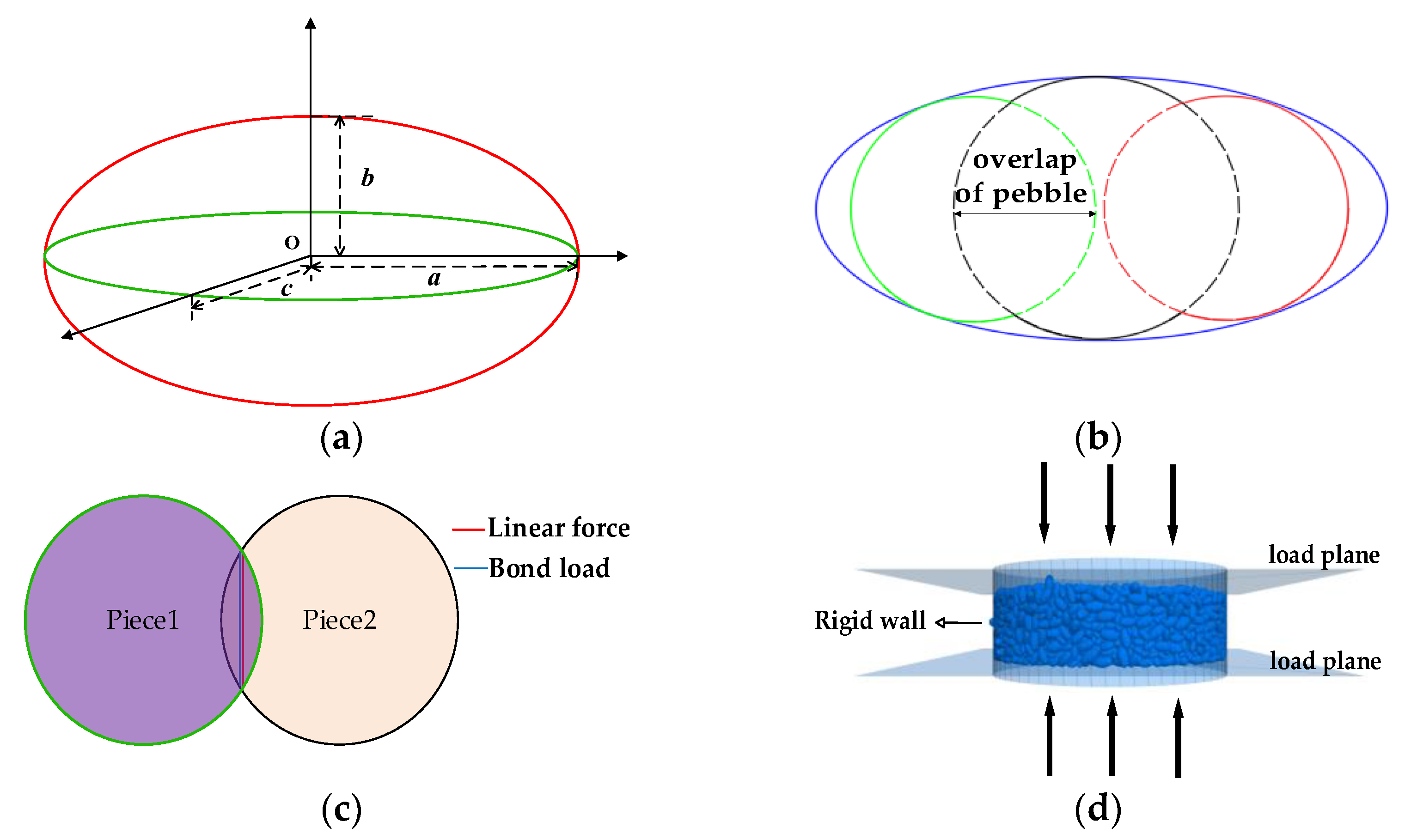
2.2. Sample Preparation and Parameter Setting
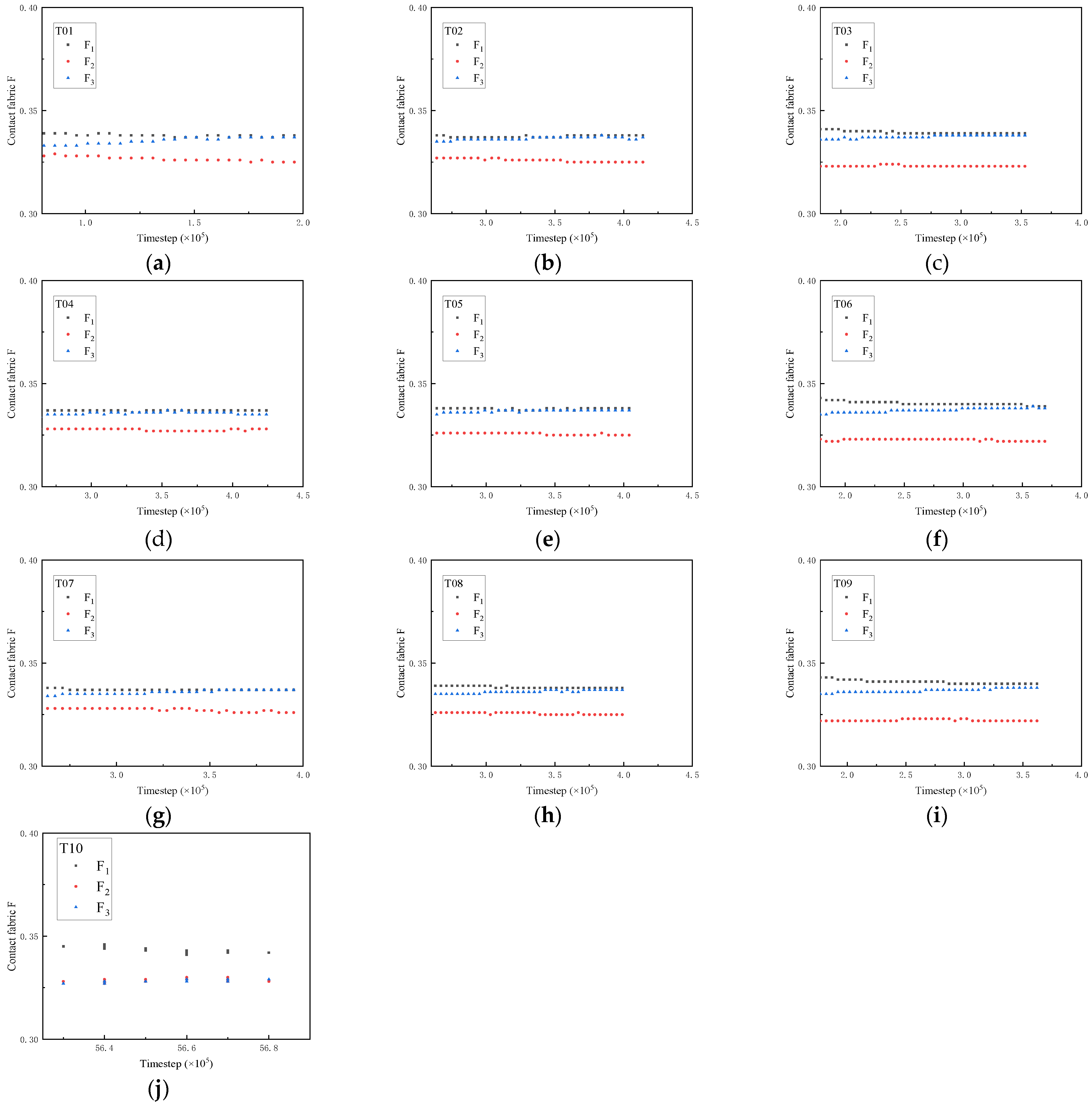
2.3. Test Scheme and Variable Monitoring
3. Results and Analysis
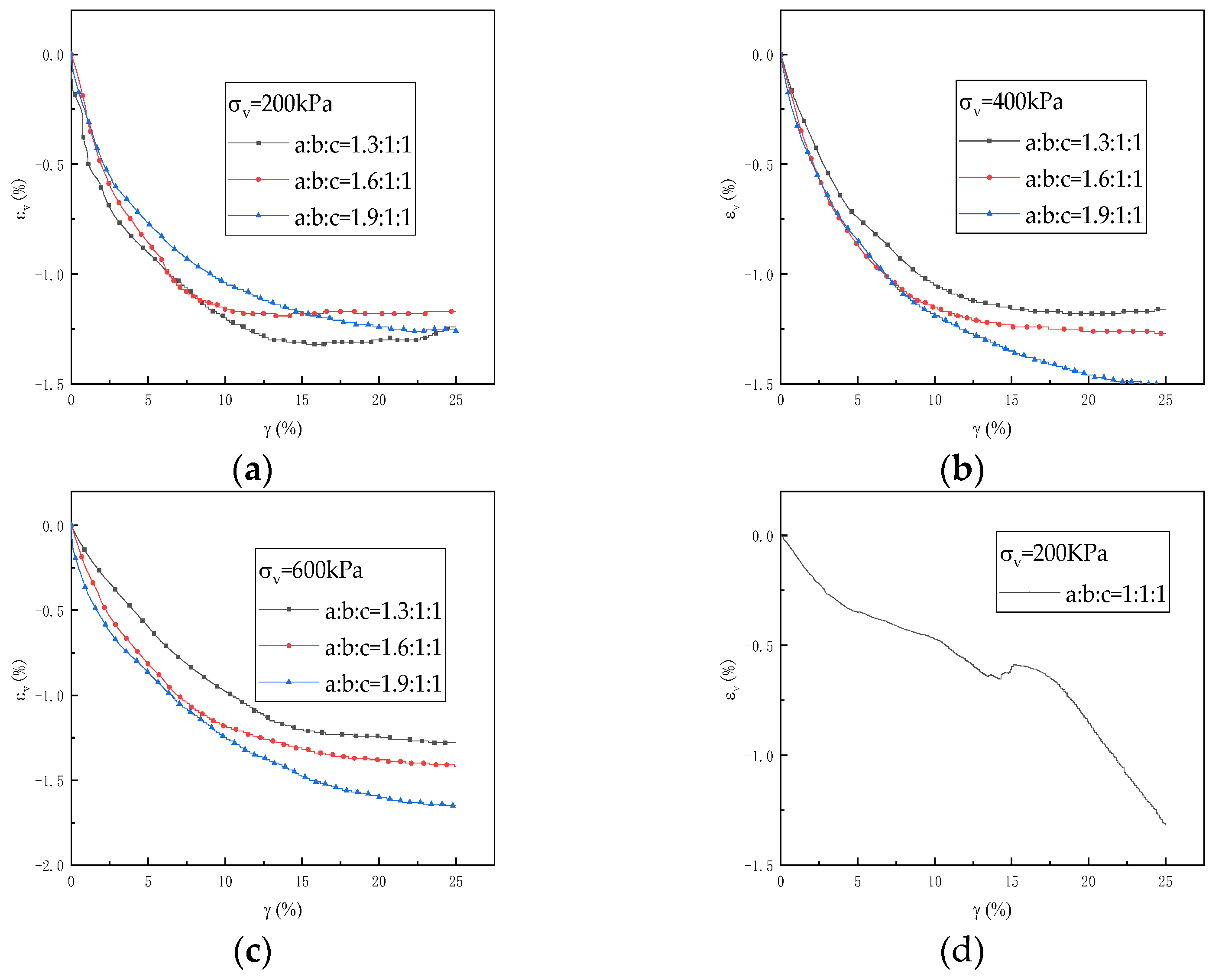
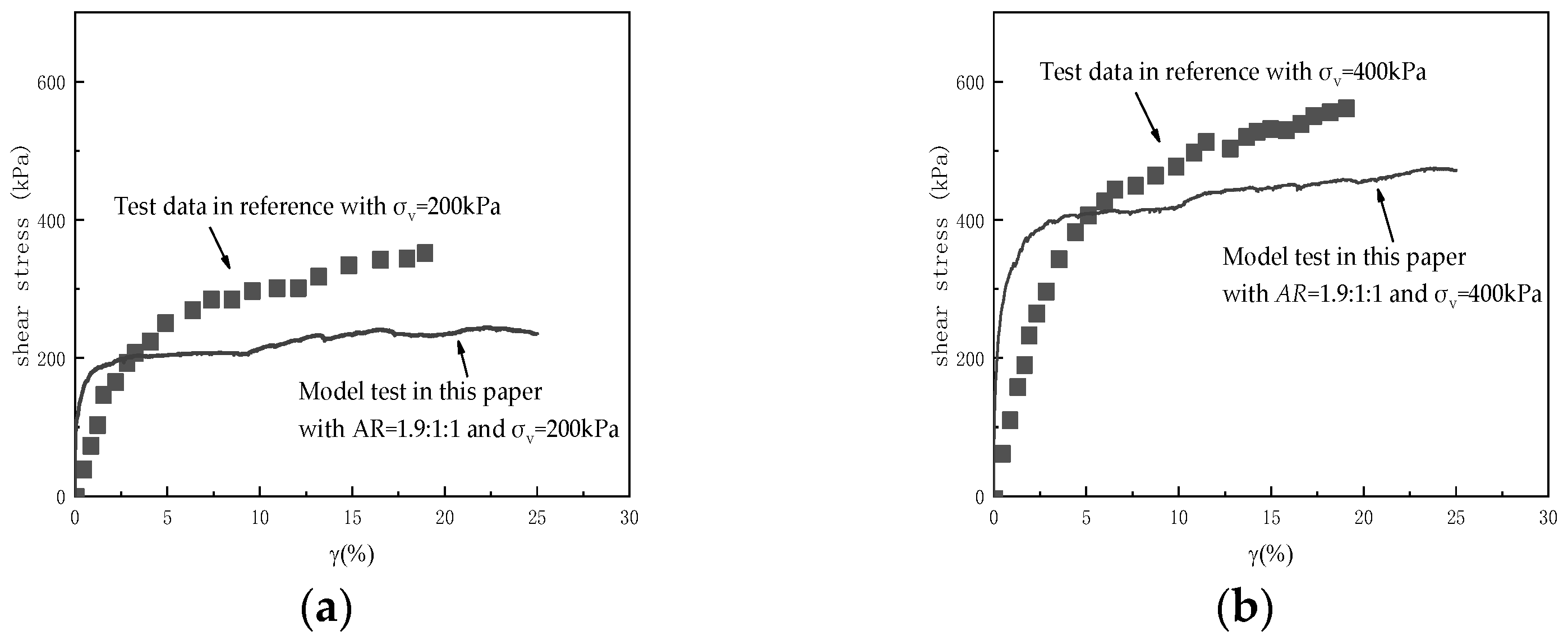
3.1. Stress–Strain Relationship
3.2. Micro Mechanical Properties
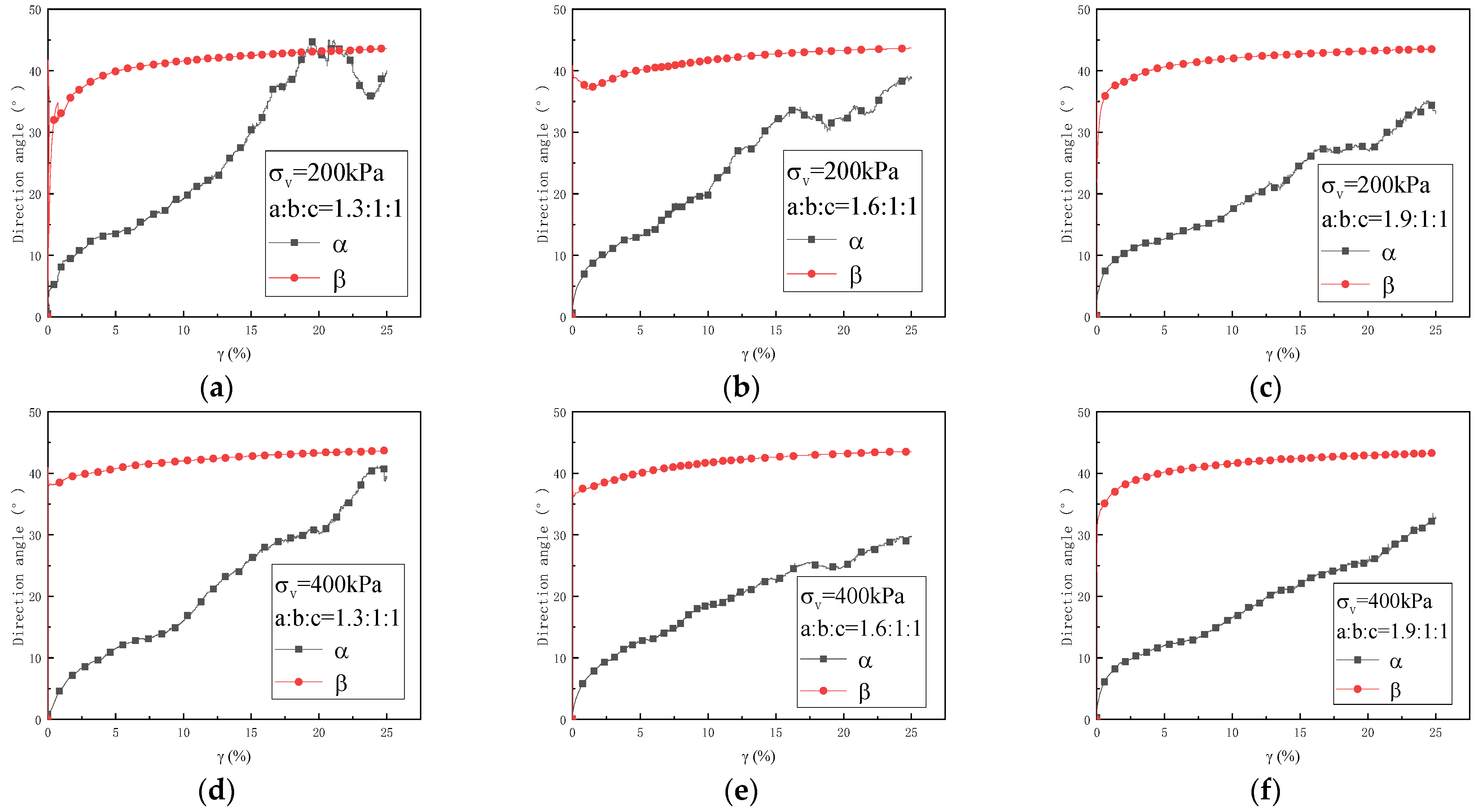
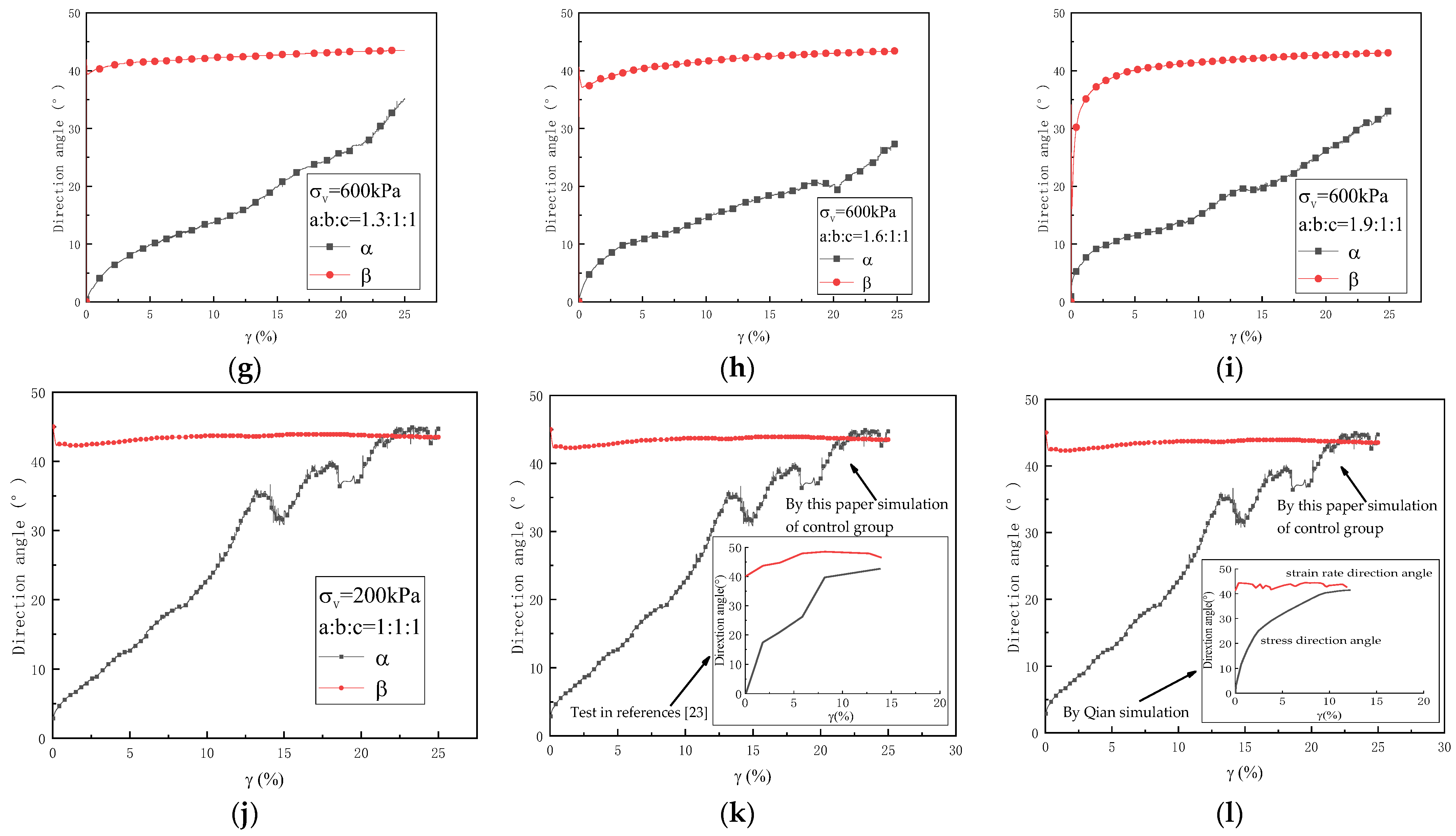
3.3. Noncoaxiality
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pradel, D.; Ishihara, K.; Gutierrez, M. Yielding and flow of sand under principal stress axes rotation. Soils Found. 1990, 30, 87–99. [Google Scholar] [CrossRef]
- Hu, P.; Teng, Y.; Ma, S.K.; Liu, Y.; Zhang, X.W.; Chen, Y.L. Non-proportional loading deformation characteristics of silty fine sand under principal stress rotation. J. Shandong Univ. (Eng. Sci.) 2022, 52, 89–95. [Google Scholar]
- Kjellman, W. Testing the shear strength of clay in Sweden. Geotechnique 1951, 2, 225–232. [Google Scholar] [CrossRef]
- Mortezaie, A.R.; Vucetic, M. Effect of frequency and vertical stress on cyclic degradation and pore water pressure in clay in the NGI simple shear device. J. Geotech. Geoenviron. Eng. 2013, 139, 1727–1737. [Google Scholar] [CrossRef]
- Oda, M.; Konishi, J. Microscopic deformation mechanism of granular material in simple shear. Soils Found. 1974, 14, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Xiong, H.; Guo, L.; Cai, Y.Q. Effect of non-coaxiality on dilatancy of sand involving principal stress axes rotation. Rock Soil Mech. 2017, 38, 133–140. [Google Scholar]
- Ishihara, K.; Towhata, I. Sand response to cyclic rotation of principal stress direction as induced by wave loads. Soils Found. 1983, 23, 11–16. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Z. Unified anisotropic elastoplastic model for sand. J. Eng. Mech. 2015, 142, 4015056. [Google Scholar] [CrossRef]
- Gutierrez, M.; Ishihara, K. Non-coaxiality and energy dissipation in granular materials. Soils Found. 2000, 40, 49–59. [Google Scholar] [CrossRef]
- Lashkari, A.; Latifi, M. A non-coaxial constitutive model for sand deformation under rotation of principal stress axes. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1051–1086. [Google Scholar] [CrossRef]
- Li, X.F.; Yuan, Q.; Wang, X. A critical state anisotropic model with state-dependent of sand. J. Civ. Archit. Environ. Eng. 2015, 37, 70–78. [Google Scholar]
- Li, X.F.; Huang, M.S.; Qian, J.G. Failure criterion of anisotropic sand with method of macro-meso incorporation. Chin. J. Rock Mech. Eng. 2010, 29, 1885–1892. [Google Scholar]
- Zhang, D.; Liu, Y.; Wu, S.C. Simulation of strength characteristics of granular materials in true triaxial test for different stress paths and its mesoscopic mechanism analysis. Rock Soil Mech. 2016, 37, 509–520. [Google Scholar]
- Li, K.F.; Li, X.F. On non-coaxiality and fabric evolution of granular media in circular shear simulated by DEM. Granul. Matter 2023, 25, 48. [Google Scholar] [CrossRef]
- Thornton, C.; Zhang, L. A numerical examination of shear banding and simple shear non-coaxial flow rules. Philos. Mag. 2006, 86, 3425–3452. [Google Scholar] [CrossRef]
- Lin, J.; Wu, W. A comparative study between DEM and micropolar hypoplasticity. Powder Technol. 2016, 293, 121–129. [Google Scholar] [CrossRef]
- Jiang, M.J.; Liu, J.D.; Arroyo, M. Numerical evaluation of three non-coaxial kinematic models using the distinct element method for elliptical granular materials. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 2468–2488. [Google Scholar] [CrossRef]
- Jiang, M.J.; Li, T.; Shen, Z.F. Fabric rates of elliptical particle assembly in monotonic and cyclic simple shear tests: A numerical study. Granul. Matter 2016, 18, 54. [Google Scholar] [CrossRef]
- Ruan, X.; Chen, S.; Li, S. Structural evolution and breakage of dense agglomerates in shear flow and Taylor-Green vortex. Chem. Eng. Sci. 2019, 211, 115261. [Google Scholar] [CrossRef]
- Maqsood, Z.; Koseki, J.; Ahsan, M.K.; Shaikh, M.; Kyokawa, H. Experimental study on hardening characteristics and loading rate dependent mechanical behaviour of gypsum mixed sand. Constr. Build. Mater. 2020, 262, 119992. [Google Scholar] [CrossRef]
- Maqsood, Z.; Koseki, J.; Miyashita, Y.; Xie, J.; Kyokawa, H. Experimental study on the mechanical behaviour of bounded geomaterials under creep and cyclic loading considering effects of instantaneous strain rates. Eng. Geol. 2020, 276, 105774. [Google Scholar] [CrossRef]
- Xu, X.; Wei, H.Z.; Meng, Q.S.; Wei, C.F.; Ai, D.H. Effects of shear rate on shear strength and deformation characteristics of coarse-grained soils in large-scale direct shear tests. Chin. J. Geotech. Eng. 2013, 35, 728–733. [Google Scholar]
- Qian, J.G.; Huang, Z.P.; Huang, M.S. Anisotropic characteristics of granular materials under simple shear. J. Cent. South Univ. 2013, 20, 2275–2284. [Google Scholar] [CrossRef]
- Zabihi, N.; Athanasopoulos-Zekkos, A. Discrete Element Modelling of Large Scale Stacked-Ring Simple Shear Test of Steel Spheres. In Proceedings of the Geo-Congress, Minneapolis, MN, USA, 25–28 February 2020; American Society of Civil Engineers: Reston, VA, USA, 2020. [Google Scholar] [CrossRef]
- Shi, D.D.; Xue, J.F.; Zhao, Z.Y.; Shi, J.Y. A DEM investigation on simple shear behavior of dense granular assemblies. J. Cent. South Univ. 2015, 22, 4844–4855. [Google Scholar] [CrossRef]
- Cheng, Z.; Hou, M.; Wang, J.F. Discrete element modeling of the mechanical behaviour of cemented carbonate sand consider the effects of particle shape and breakage. Chin. J. Comput. Mech. 2022, 39, 315–323. [Google Scholar]
- Asadzadeh, M.; Soroush, A. Fundamental investigation of constant stress simple shear test using dem. Powder Technol. 2016, 292, 129–139. [Google Scholar] [CrossRef]
- Shen, C.K.; O’Sullivan, R.; Jardine, R.J. A micromechanical investigation of drained simple shear tests. In Proceedings of the International Symposium on Deformation Characteristics of Geomaterials, Seoul, Republic of Korea, 1–3 September 2011; pp. 314–321. [Google Scholar]
- Zhou, L.L.; Chu, X.H.; Xu, Y.J. Breakage behavior of sand under true triaxial stress based on discrete element method. Chin. J. Geotech. Eng. 2017, 39, 839–847. [Google Scholar]
- McDowell, G.R.; Harireche, O. Discrete element modelling of soil particle fracture. Geotechnique 2002, 52, 131–135. [Google Scholar] [CrossRef]
- Wang, J.F.; Yan, H.B. DEM analysis of energy dissipation in crushable soil. Soils Found. 2012, 52, 644–657. [Google Scholar] [CrossRef]
- Oda, M. Initial fabrics and their relations to mechanical properties of granular materials. Soils Found. 1972, 12, 17–36. [Google Scholar] [CrossRef]
- Li, X.F.; Wang, Q.; Liu, J.F.; Wu, W.; Meng, F.C. Quantitative Description of Microscopic Fbric Based on Sand Particle Shapes. China J. Highw. Transp. 2016, 29, 29–53. [Google Scholar]
- Li, Y.; Yang, Y.M.; Yu, H.S.; Roberts, G.; Li, A. Principal stress rotation under bidirectional simple shear loadings. KSCE J. Civ. Eng. 2018, 22, 1651–1660. [Google Scholar] [CrossRef]
- Huang, M.S.; Sun, H.Z.; Qian, J.G. Non-coaxial behavior of coarse granular aggregates simulated by DEM. J. Hydraul. Eng. 2010, 2, 173–181. [Google Scholar] [CrossRef]
- Yamada, Y.; Ishihara, K. Anisotropic Deformation Characteristics of Sand Under Three Dimensional Stress Conditions-Science Direct. Soils Found. 1979, 19, 79–94. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Fei, W.; Yu, H.-S.; Ooi, J.; Rotter, M. Experimental study of anisotropy and non-coaxiality of granular solids. Granular Matter. 2015, 17, 189–196. [Google Scholar] [CrossRef]




| Parameters | Values |
|---|---|
| Clump_normal stiffness/(kPa) | 1 × 107 |
| Clump_tangential stiffness/(kPa) | 1 × 107 |
| Porosity/(%) | 0.45 |
| Density/(Kg/m3) | 2.7 × 103 |
| Elastic modulus/(kPa) | 1 × 107 |
| Coefficient of friction | 0.5 |
| Damp/(Pa∙s) | 0.7 |
| Test Number | AR | Cell Pressure (kPa) | Clump Number |
|---|---|---|---|
| T01 | 1.3:1:1 | 200 | 16,536 |
| T02 | 1.6:1:1 | 200 | 22,088 |
| T03 | 1.9:1:1 | 200 | 27,310 |
| T04 | 1.3:1:1 | 400 | 16,536 |
| T05 | 1.6:1:1 | 400 | 22,088 |
| T06 | 1.9:1:1 | 400 | 27,310 |
| T07 | 1.3:1:1 | 600 | 16,536 |
| T08 | 1.6:1:1 | 600 | 22,088 |
| T09 | 1.9:1:1 | 600 | 27,310 |
| T10 | 1:1:1 | 200 | 1011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Li, X.; Lv, L.; Yuan, Q. Discrete Element Simple Shear Test Considering Particle Shape. Appl. Sci. 2023, 13, 11382. https://doi.org/10.3390/app132011382
Zhu H, Li X, Lv L, Yuan Q. Discrete Element Simple Shear Test Considering Particle Shape. Applied Sciences. 2023; 13(20):11382. https://doi.org/10.3390/app132011382
Chicago/Turabian StyleZhu, Houying, Xuefeng Li, Longlong Lv, and Qi Yuan. 2023. "Discrete Element Simple Shear Test Considering Particle Shape" Applied Sciences 13, no. 20: 11382. https://doi.org/10.3390/app132011382
APA StyleZhu, H., Li, X., Lv, L., & Yuan, Q. (2023). Discrete Element Simple Shear Test Considering Particle Shape. Applied Sciences, 13(20), 11382. https://doi.org/10.3390/app132011382







